Учимся на отлично! — Виды задач на движение

ВИДЫ ЗАДАЧ НА ДВИЖЕНИЕ

В задачах на движение  рассматриваются три взаимосвязанные величины:

S — расстояние (пройденный путь),

t — время движения и

V — скорость – расстояние, пройденное за единицу времени.

• Расстояние – это произведение скорости на время движения;

S = V • t

• Скорость – это расстояние, которое тело проходит за единицу времени;
• Скорость  — это частное от деления расстояния на время движения;

V = S : t

• Время – это частное от деления расстояния на скорость движения

t = S : V

 

Какие могут быть ситуации?

 

Встречное  движение     

Два объекта движение начинают одновременно навстречу друг другу.

 

 Движение в противоположных направлениях из одного пункта

 

 

Два объекта движение начинают одновременно в противоположных направлениях.

 

Движение в одном направлении

Два объекта движение начинают одновременно в одном направлении.

При решении этих задач надо использовать понятия «скорость сближения» и « скорость удаления».

 

ЗАДАЧА 1

В данный момент расстояние между двумя таксистами 345 км. На каком расстоянии будут находиться таксисты через два часа, если скорость одного 72 км /ч., а другого  -68 км /ч., и они выезжают навстречу друг другу одновременно?

Первый способ решения
1) 72 + 68 =140 (км /ч.) – скорость сближения таксистов.
2) 140 • 2 = 280 (км) – на такое расстояние таксисты    приблизятся друг к другу за 2 часа.
3) 345 – 280 = 145 (км) – на таком расстоянии будут таксисты через 2 часа.
Ответ: 145 км.

Второй способ решения

1) 72 • 2 =144 (км) – такое расстояние проедет один таксист за 2 часа.

2)  68 • 2 = 136 (км) – такое расстояние проедет другой таксист за 2 часа.

3) 144+ 136 =280 (км) – на такое расстояние таксисты приблизятся друг к другу за 2 часа.

4) 345 – 280 = 145 (км) – на таком расстоянии будут таксисты через 2 часа.

Ответ: 145 км.

ЗАДАЧА 2

Расстояние между городами А и В 720км. Из А в В вышел скорый поезд со скоростью 80 км /ч. Через 2 часа навстречу ему  из В в А  вышел

пассажирский поезд  со  скоростью 60 км /ч. Через  сколько  часов после   выхода  пассажирского  поезда  эти  поезда встретятся?

Решение

1) 80 • 2=160(км) -прошёл скорый поезд за 2 часа.

2) 720-160=560(км) -осталось пройти поездам.

3) 80+60=140(км/ч) -скорость сближения 2 поездов.

4) 560:140=4(ч) -был в пути пассажирский поезд.

Ответ: 4часа.

ЗАДАЧА 3

Из двух пунктов навстречу друг другу одновременно выехали два автобуса.  Скорость  одного  автобуса  45 км /ч,  а скорость другого автобуса 72 км /ч. Первый автобус до встречи проехал 135км.
Найдите расстояние между пунктами.

Решение

Первый способ решения
1) 135 : 45 = 3 (часа) – ехали автобусы до встречи.
2) 72 • 3 = 216 (км) – проехал второй автобус до встречи.
3) 135 + 216 = 351 (км) – расстояние между пунктами.
Ответ: 351 км.

Второй способ решения

1) 135 : 45 = 3 (часа) – ехали автобусы до встречи.

2) 45 +72 = 117 (км/ ч.). – скорость сближения автобусов .

3) 117 • 3 = 351 (км) – расстояние между пунктами.

Ответ: 351 км.

Что такое скорость сближения?

ЗАДАЧА 4

Машина и автобус выехали из двух городов, находящихся на расстоянии 740 км навстречу друг другу со скоростями 70 км/ч и 50 км/ч.  Какое расстояние будет между машинами через 5 часов?

Решение

Первый способ решения

1) 50 • 5 = 250 (км) – проедет машина до встречи.

2) 70 • 5 = 350 (км) – проедет автобус до встречи.

3) 250 + 350 = 600 (км) — на такое расстояние они приблизятся друг к другу.

4) 740 — 600 = 140 (км)  — такое расстояние будет между ними через 5 часов.

Ответ: 140 км.

Второй способ решения

1) 50 + 70 = 120 (км /ч.) – скорость сближения автобуса и машины.

2) 120 • 5 = 600 (км) – на такое расстояние они приблизятся друг к другу.

3) 740 – 600 = 140 (км) – такое расстояние будет между ними через 5 часов.

Ответ: 140 км.

ЗАДАЧА 5

Две гоночные машины выехали навстречу друг другу. Расстояние между ними было 660 км. Одна ехала со скоростью 100 км/ч, а другая 120 км/ч.  Через какое время они встретятся?

Решение

1) 100+120=220(км/ч)- скорость сближения машин .

2) 660:220=3(ч) -через такое время встретятся гоночные машины.

Ответ: через 3 часа.

ЗАДАЧА 6

Из одного логова одновременно в противоположных направлениях выбежало два тигра. Скорость одного тигра 48 км / ч.,  а  другого  – 54 км ч. Какое расстояние будет между тиграми через 3 часа?

Решение

Первый способ решения

1) 48 • 2 = 96 (км) – пробежит один тигр за 2 часа.

2) 54 • 2 = 108 (км) – пробежит другой тигр за 2 часа.

3) 96 + 108 = 204 (км) – будет между тиграми через 2 часа.

Ответ: 204 км.

Второй способ решения

1) 48 + 54 =102 (км /ч.) – скорость удаления тигров.

2) 102 • 2 =204 (км) – будет между тиграми через 2 часа.

Ответ: 204 км.

ЗАДАЧА 7

Максим и Саша вышли из школы со скоростью 50 м/мин. Рома вышел вслед за ними через 6 минут со скоростью 80 м/мин. Через сколько минут  Рома догонит Максима и Сашу?

Решение

1) 80 — 50 = 30 (км /ч.) –скорость сближения мальчиков.

2) 50 • 6 = 300 (км) – такое расстояние было между мальчиками перед выходом из школы Ромы.

3) 300 : 30 = 10 (мин.) – через такое время Рома догонит друзей.

Ответ: через 10 мин.

 

ИТОГИ

1) При решении задач на движении двух объектов применяются понятия «скорость сближения» и «скорость удаления».

2) При решении задач на встречное движение  и движение в противоположных направлениях скорость сближения и скорость удаления находятся сложением скоростей движущихся объектов.

3) При решении задач на движение в одном направлении скорость сближения и скорость удаления находятся вычитанием скоростей движущихся объектов.

teplyakova.ucoz.com

Методика решения задач на движение

методика решения задач на движение в 5-6 классах

Решение текстовых задач – важная составляющая курса математики школы. Умение решать текстовые задачи является одним из основных показателей уровня математического развития школьника. Математическая задача неизменно помогает ученику вырабатывать правильные математические понятия, глубже выяснять различные стороны взаимосвязей в окружающей его жизни, дает возможность применять изучаемые теоретические положения. Решение задач способствует формированию у детей полноценных знаний, определяемых программой. Задачи дают возможность связать теорию с практикой, обучение с жизнью. Через решение задач дети знакомятся с важными в познавательном и воспитательном отношении фактами.

Давно не секрет, что математику любят в основном те ученики, которые умеют решать задачи. Следовательно, научив детей владеть умением решения задачи, мы окажем существенное влияние на их интерес к предмету, на развитие мышления и речи. Сам процесс решения задач при определенной методике оказывает весьма положительное влияние на умственное развитие школьников, поскольку он требует выполнения умственных операций: анализа и синтеза, конкретизации и абстрагирования, сравнения и обобщения.

Но на практике большинство учителей мало уделяют внимание решению задач. Учащиеся нередко не умеют выделить искомые и данные, установить связь между величинами, входящими в задачу; составить план решения; выполнить проверку полученного результата. Необоснованно много внимания и неоправданных затрат времени идет на оформление краткой записи и решения задачи. При этом основное внимание направлено на реализацию единственно цели – получение ответа на вопрос задачи.

В задачах на движение есть две стандартные модели: движение навстречу друг другу и движение вдогонку. В первой модели рассматривается как бы совместная скорость сближения, как сумма двух скоростей и поэтому время сближения считается так: t=Sv1+v2 . Во второй модели время, за которое объект, идущий сзади с большей скоростью v1, догонит другой объект, идущий с меньшей скоростью v2, считается так: t=Sv1−v2, где S — расстояние между объектами в начальный момент времени.

Задача 1. Из городов А и В, расстояние между которыми 480 км, навстречу друг другу выехали два автомобиля. Из города А со скоростью 55 км/ч, а из города В со скоростью 65 км/ч. Найдите расстояние от города А где они встретятся.

Решение: Время до встречи считается по формуле t=Sv1+v2 и равно 4 часа. Расстояние от города А до места встречи равно S=455=220 км.

Задача 2. Два пешехода отправляются из аптеки в одном направлении на прогулку по набережной. Скорость первого на 0,5 км/ч больше скорости второго. Найдите время в минутах, когда расстояние между ними станет 200 м.

Решение: Время в часах, за которое расстояние станит между ними 200 м, т.е. 0,2 км, считается по формуле t=0502=04 часа. Значит, через 24 минуты расстояние между ними будет 200

Решение задач на движение.

Предположим, вы неплохо поняли, как решать задачи по математике. Умеете выкачивать всю спрятанную информацию из задачи и записывать её в виде математических выражений с иксом. Но задачки на движение – не идут… Ну не хватает информации, и всё тут! Почему? А вот почему!

Для успешного решения задач на движение нужно кое-что твёрдо держать в голове. А именно – формулу-ключ, в которой связаны путь, время и скорость. В любой задаче дают кучу информации, но эту формулу – никогда! Это должно быть ваше знание! Кстати, эта формула нужна и в компетентностных задачах, и в обыденной жизни.

Чтобы эту формулу-ключ хорошо и осмысленно запомнить, достаточно ответить самому себе на простой вопрос: «Если я еду со скоростью 60 километров в час, какое расстояние я проеду за 2 часа?». Очевидно, умножив 60 на 2, получим 120 километров. Вот вы и запомнили нехитрую формулу скорости, пути, времени:

S — это пройденный путь, или расстояние,

V – скорость движения,

t – время движения.

Всё. Это вся посторонняя информация (из физики), которая необходима для решения задач на движение. Всё остальное – в тексте задачи.

Зная эту формулу (для расстояния), вы можете легко вывести из неё формулу для скорости, или времени. Ведь эта формула – тоже уравнение. Стало быть, к ней применимы тождественные преобразования. Если нас интересует не путь, а скорость – поделим обе части формулы на t, получим:

V = S/t

Если интересует время, делим на V:

t = S/V

Запомнили? Если считать задачу замком, то эти формулы – ключи, который должен быть всегда при вас. Ибо без ключа замок открывать неудобно…

Что нам даёт этот ключ? Он нам даёт дополнительную информацию! Которой, как раз, и не хватает. Скажем, в задаче даны скорость и расстояние. А нам позарез нужно время. Так найти время из формулы-ключа за 6 секунд можно! То есть, можно считать, что время тоже дано. Если формулу-ключ помните. И вообще, если даны любые две величины из формулы, можно считать, что и третья величина известна. Вот и всё.

Решение задач – это работа несколько необычная, а именно умственная работа. А чтобы научиться какой-либо работе, нужно предварительно хорошо изучить тот материал, над которым придётся работать, те инструменты, с помощью которых выполняется эта работа.

Значит, для того чтобы научиться решать задачи, надо разобраться в том, что собой они представляют, как они устроены, из каких составных частей они состоят, каковы инструменты, с помощью которых производится решение задач.

Каждая задача – это единство условия и цели. Если нет одного из этих компонентов, то нет и задачи. Это очень важно иметь в виду, чтобы проводить анализ текста задачи с соблюдением такого единства. Это означает, что анализ условия задачи необходимо соотносить с вопросом задачи и, наоборот, вопрос задачи анализировать направленно с условием. Их нельзя разрывать, так как они составляют одно целое.

Математическая задача – это связанный лаконический рассказ, в котором введены значения некоторых величин и предлагается отыскать другие неизвестные значения величин, зависимые от данных и связанные с ними определенными соотношениями, указанными в задачах.

infourok.ru

Как научить ребенка решать задачи на движение

В четвертом классе многих детей и родителей пугают задачи на движение. Сегодня мы поделимся, как одно небольшое изменение подачи формулы, может научить ребенка щелкать подобные задачи, словно орешки.

Пример задач на движение:

Лыжник шел со скоростью 18 км/ч и был в пути 3 часа. Сколько времени потребуется пешеходу, чтобы пройти такое же расстояние, если его скорость 9 км час

Расстояние между селами 48 км. Через сколько часов встретятся два пешехода, которые вышли одновременны навстречу друг другу, если скорость одного 3 км/ч, а другого 5 км/ч?

В этой статье вы узнаете простую технику, которая позволяет детям легко применять практически первую в их жизни серьезную математическую формулу (до этого дети применяли формулу вычисления площади и периметра)

В школе, по традиционной программе, детей знакомят с формулой в линейной структуре, записывая ее на доске и поясняя S=v*t

Опытный учитель не только расскажет, что S — расстояние v — скорость t — время, а обязательно объяснит, почему обозначение происходит именно такими буквами.

Дальше ребенку последовательно предлагается блок задач, сначала на применение прямой формулы S=v*t

Потом обратной. V=S:t t=S:v

Конечно ребенку нужно будет выучить правило нахождения расстояния, времени или скорости.  Правила с одной стороны, очень понятны взрослым, с другой очень трудны для детей.

Потому что читая задачу, маленький ученик, который только учится решать задачи, в голове прокручивает алгоритм:

1. Известно, что …
2. Надо узнать…
3. Чтобы ответить на вопрос, надо … (тут происходит процесс определения нужной формулы, обычно это самая трудная часть)
4. Можем сразу ответить на вопрос? Нет. Сразу мы не можем ответить на вопрос задачи, так как не знаем…
5. Поэтому в первом действии мы узнаем …
6. Во втором действии мы ответим на вопрос задачи. Для этого …

Сложный алгоритм, но именно так решают задачи младшие школьники! Некоторые делают это очень быстро, а некоторые продумывают каждый шаг.

Упростите ребенку решение задач. Станьте для него магом и лучшим проводником по школе.

Нарисуйте вместе с ним треугольник. И впишите в него формулу следующим образом:

Закройте карточкой или рукой то, что нужно найти (например, время) Тогда сразу найдется «нужная формула»

Горизонтальная черта в треугольнике обозначает деление. Вертикальная — умножение. Ребенку можно поставить точку (знак умножения), что будет для него подсказкой.

Так подбор правильной формулы для решения задачи на движение становится не только простым, но и интересным ребенку.

У меня дети просили все больше и больше задач, закрывали разные части формулы, и тем самым, запоминали ее.

Если речь идет о двух, трех движущихся объектах, то треугольник с формулой применяется для каждого в отдельности. Хотя об этом обычно догадываются сами дети.

Взаимодействие и обмен полезными техниками между родителями и учениками может помочь ребенку как добиться хороших результатов в учебе, так и улучшить свою самооценку.

Используйте техники эффективного обучения, помогайте детям учиться.

Ведь очень часто одно простое действие может убрать непонимание, слезы, истерики, нежелание ребенка учиться, замотивировать его на учебу и показать ему простые и легкие способы решения сложных для него задач.

• Можно стирать белье руками, а можно в стиральной машинке
• Можно идти пешком, а можно доехать на автомобиле
• Можно делать дырку в стене ручной дрелью, а можно перфоратором
• Можно решеть задачи по-старинке, а можно дать ребенку техники эффективного решения задач.

Результат одинаков — усилие разное

Именно для этих целей, создана Школа умных детей.

В каждом классе по курсу «Математика», в уроках школы по блоку «решение задач» Вы узнаете:

• Как научить ребенка понимать текст задачи
• Как научить ребенка оформлять краткую запись
• Как научить ребенка определить, как решать задачу
• Сможете объяснить разницу между 2*9 и 9*2 в задаче
• Получите простой Алгоритм-инструкцию «Как решать задачи»
• Узнаете типы задач 1 класса и способы простого объяснения
• Узнаете типы задач 2 класса и способы простого объяснения
• Узнаете типы задач 3 класса и способы простого объяснения
• Узнаете типы задач 4 класса и способы простого объяснения
• Узнаете Формулу «треугольник» для решения задач на движение, цену, количество и стоимость и все тонкости ее применения

Присоединяйтесь прямо сейчас, пока действует специальная цена на участие

Хочу учить ребенка эффективно>>

Вам понравилась статья? Сохраните себе на стену, чтобы не потерять

Похожее

gladtolearn.ru

Учебно-методическое пособие по математике (4 класс) на тему: Задачи на движение (математические формулы)

                         

                              t- время

                                                               S

V сближения = V1 + V2

S=(V1 + V2) • t

t = S: ( V1 + V2)

                                                                                                                                          d

                         t- время                                           t- время

                             

                                                               S

V удаления = V1 + V2

S= V удаления • t + d

                                                                                                                                         

                         t- время                                          t- время

                             

                                                               S

V удаления = V1 + V2

S= V удаления • t

                                                                                                                                                                                                                                     V1 > V2

                                               

          d                          t- встречи

V сближения = V1 — V2

S= (V1 — V2) • t встречное — d                          t встречное = S: V сближения

V1 = S: t + V2

                                                                                                                                                                                                                                    V1

t- время                                                                                                                                             

                                               

              d                             s

V удаления = V1 — V2

S= (V1 — V2) • t  + d

t= S: (V1 — V2)    d-расстояние между точками

1.Задачи на встречное движение

2. Движение в противоположных

направлениях

3. Движение в противоположных

направлениях

4. Движение вдогонку

5. Движение с остановками

Эта книжка – помощница будет полезна учащимся 4 класса, учителям, родителям, желающим помочь своим детям научиться решать задачи «на движение».

В книжке представлены математические модели и формулы по решению задач на разные виды движения. Это основная группа задач, которые считаются трудными для учеников начальных классов.

Научиться преодолевать трудности в решении задач на движение – это значит научиться  определять зависимость между величинами: скорость, время, расстояние. 

nsportal.ru

Задачи на сближение и удаление

Для начала вспомним формулы, которые используют при решении подобных задач:  S = υ·t,   υ = S : t,   t = S : υ
где S – расстояние, υ – скорость движения, t – время движения.

Когда два объекта движутся равномерно с разными скоростями, то расстояние между ними за каждую единицу времени или увеличивается, или уменьшается.

Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.
Скорость удаления – это расстояние, на которое удаляются объекты за единицу времени.

Движение на сближение можно разделить на два вида: встречное движение и движение вдогонку. Движение на удаление можно разделить на два вида: движение в противоположных направлениях и движение с отставанием.

Трудность для некоторых учеников заключается в том, чтобы правильно поставить «+» или «–» между скоростями при нахождении скорости сближения объектов или скорости удаления.

Рассмотрим таблицу.

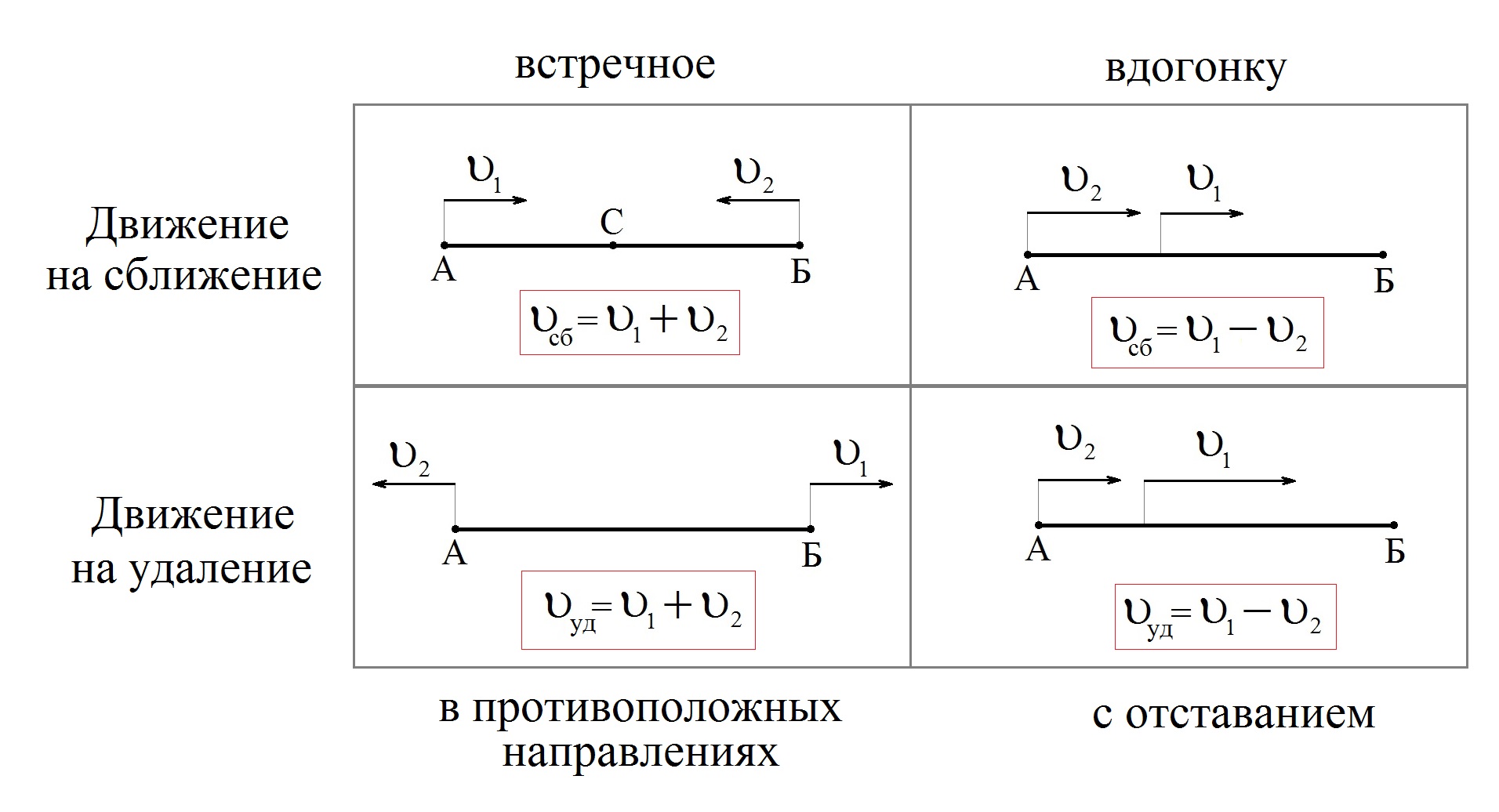
Из неё видно, что при движении объектов в противоположные стороны их скорости складываются. При движении в одну сторону – вычитаются.

Примеры решения задач.

Задача №1.  Две автомашины движутся навстречу друг другу со скоростями 60км/ч и 80 км/ч. Определите скорость сближения машин.
υ₁ = 60 км/ч
υ₂ = 80 км/ч
Найти υ_сб
Решение.
υ_сб = υ₁ + υ₂ – скорость сближения (знак «+» так как из условия понятно, что машины движутся в разных направлениях)
υ_сб = 60 + 80 = 140 (км/ч)
Ответ:  скорость сближения 140 км/ч.

Задача №2. Из одного пункта в противоположных направлениях выехали две автомашины со скоростями 60 км/ч и 80 км/ч. Определите скорость удаления машин.
υ₁ = 60 км/ч
υ₂ = 80 км/ч
Найти υ_уд
Решение.
υ_уд = υ₁ + υ₂ – скорость удаления (знак «+» так как из условия понятно, что машины движутся в разных направлениях)
υ_уд = 80 + 60 = 140 (км/ч)
Ответ: скорость удаления 140 км/ч.

Задача №3. Из одного пункта в одном направлении выехали сначала автомобиль со скоростью 60 км/ч, а затем мотоцикл со скоростью 80 км/ч. Определите скорость сближения машин.
(Видим, что здесь случай движения вдогонку, поэтому находим скорость сближения)
υ_ав = 60 км/ч
υ_мот = 80 км/ч
Найти υ_сб
Решение.
υ_сб =  υ₁ – υ₂– скорость сближения (знак «–» так как из условия понятно, что машины движутся в одном направлении)
υ_сб = 80 – 60 = 20 (км/ч)
Ответ: скорость сближения 20 км/ч.

То есть название скорости – сближения или удаления – не влияют на знак между скоростями. Имеет значение только направление движения.

Рассмотрим другие задачи.

Задача № 4. Из одного пункта в противоположных направлениях вышли два пешехода. Скорость одного из них 5 км/ч, другого – 4 км/ч. Какое расстояние будет между ними через 3 ч?
υ₁ = 5 км/ч
υ₂ = 4 км/ч
t = 3 ч
Найти S
Решение.
υ_уд = υ₁ + υ₂ – скорость удаления (знак «+» так как из условия понятно, что пешеходы движутся в разных направлениях)
υ_уд = 5 + 4 = 9 (км/ч)
(Пройденное расстояние находим по формуле)
S = υ_уд·t
S =  9·3 = 27 (км)
Ответ: через 3 ч расстояние будет 27 км.

Задача № 5. Два велосипедиста одновременно выехали навстречу друг другу из двух пунктов, расстояние между которыми 36 км. Скорость первого 10 км/ч, второго 8 км/ч. Через сколько часов они встретятся?
S = 36 км
υ₁ = 10 км/ч
υ₂ = 8 км/ч
Найти t
Решение.
υ_сб = υ₁ + υ₂ – скорость сближения (знак «+» так как из условия понятно, что машины движутся в разных направлениях)
υ_сб = 10 + 8 = 18 (км/ч)
(время встречи можно рассчитать по формуле)
t = S : υ_сб
t = 36 : 18 = 2 (ч)
Ответ:  встретятся через 2 ч.

Задача №6. Два поезда отошли от одной станции в противоположных направлениях. Их скорости 60 км/ч и 70км/ч. Через сколько часов расстояние между ними будет 260 км?
υ₁ = 60 км/ч
υ₂ = 70 км/ч
S = 260 км
Найти t
Решение.
1 способ
υ_уд = υ₁ + υ₂ – скорость удаления (знак «+» так как из условия понятно, что пешеходы движутся в разных направлениях)
υ_уд = 60 + 70 = 130 (км/ч)
(Пройденное расстояние находим по формуле)
S = υ_уд·t    ⇒   t = S : υ_уд
t =  260 : 130 = 2 (ч)
Ответ: через 2 ч расстояние между ними будет 260 км.
2 способ
Сделаем пояснительный рисунок:

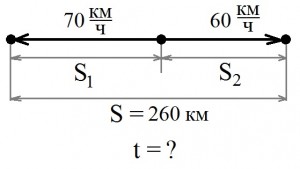
Из рисунка видно, что
1) через заданное время расстояние между поездами будет равно сумме расстояний, которые прошли каждый из поездов:
S = S₁ + S₂;
2) каждый из поездов ехал одинаковое время (из условия задачи), значит, 
S₁ =υ₁· t — расстояние которое проехал 1 поезд
S₂ =υ₂· t — расстояние которое проехал 2 поезд
Тогда,
S = S₁ + S₂ = υ₁· t  + υ₂· t  =  t · (υ₁ + υ₂) = t · υ_уд  
t = S : (υ₁ + υ₂)  — время за которое оба поезда проедут 260 км
t =  260 : (70 + 60) = 2 (ч)
Ответ:  расстояние между поездами будет 260 км через 2 ч . 

1. Два пешехода одновременно вышли навстречу друг другу из двух пунктов, расстояние между которыми 18 км. Скорость одного из них 5 км/ч, другого – 4 км/ч. Через сколько часов они встретятся? (2 ч)
2. Два поезда отошли от одной станции в противоположных направлениях. Их скорости 10 км/ч и 20 км/ч. Через сколько часов расстояние между ними будет 60 км? (2 ч)
3. Из двух сел, расстояние между которыми 28 км, одновременно навстречу друг другу вышли два пешехода. Скорость первого 4 км/ч, скорость второго 5 км/ч. На сколько километров за час пешеходы сближаются друг с другом? Какое расстояние будет между ними через 3 часа? (9 км, 27 км)
4. Расстояние между двумя городами 900 км. Два поезда вышли из этих городов навстречу друг другу со скоростями 60 км/ч и 80 км/ч. На каком расстоянии друг от друга были поезда за 1 час до встречи? Есть ли в задаче лишнее условие? (140 км, есть)
5. Велосипедист и мотоциклист выехали одновременно из одного пункта в одном направлении. Скорость мотоциклиста 40 км/ч, а велосипедиста 12 км/ч. Какова скорость их удаления друг от друга? Через сколько часов расстояние между ними будет 56 км? (28 км/ч, 2 ч)
6. Из двух пунктов, удаленных друг от друга на 30 км, выехали одновременно в одном направлении два мотоциклиста. Скорость первого 40 км/ч, второго 50 км/ч. Через сколько часов второй догонит первого?
7. Расстояние между городами А и В 720 км. Из А в В вышел скорый поезд со скоростью 80 км/ч. Через 2 часа навстречу ему из В в А вышел пассажирский поезд со скоростью 60 км/ч. Через сколько часов они встретятся?
8. Из села вышел пешеход со скоростью 4 км/ч. Через 3 часа вслед за ним выехал велосипедист со скоростью 10 км/ч. За сколько часов велосипедист догонит пешехода?
9. Расстояние от города до села 45 км. Из села в город вышел пешеход со скоростью 5 км/ч. Через час навстречу ему из города в село выехал велосипедист со скоростью 15 км/ч. Кто из них в момент встречи будет ближе к селу?
10. Старинная задача.  Некий юноша пошел из Москвы к Вологде. Он проходил в день 40 верст. Через день вслед за ним был послан другой юноша, проходивший в день 45 верст. Через сколько дней второй догонит первого?
11. Старинная задача. Собака усмотрела в 150 саженях зайца, который пробегает в 2 минуты по 500 сажен, а собака за 5 минут – 1300 сажен. Спрашивается, в какое время собака догонит зайца?
12. Старинная задача. Из Москвы в Тверь вышли одновременно 2 поезда. Первый проходил в час 39 верст и прибыл в Тверь двумя часами раньше второго, который проходил в час 26 верст. Сколько верст от Москвы до Твери?

www.easyphysics.in.ua

Движение вдогонку (формула). Решение задач на движение вдогонку — OneKu

Содержание статьи:

Движение является способом существования всего, что человек видит вокруг себя. Поэтому задачи на перемещение разных объектов в пространстве являются типичными проблемами, которые предлагается разрешить школьникам. В данной статье подробно рассмотрим движение вдогонку и формулы, которые необходимо знать, чтобы уметь решать задачи такого типа.

Что такое движение?

Перед тем, как переходить к рассмотрению формул движения вдогонку, необходимо разобраться с этим понятием подробнее.

Вам будет интересно:Что собой представляет симбиоз грибов и деревьев?

Под движением подразумевают изменение пространственных координат объекта за определенный промежуток времени. Например, автомобиль, который движется по дороге, самолет, который летит в небесах, или кошка, бегущая по траве, — все это примеры движения.

Важно отметить, что рассматриваемый движущийся объект (автомобиль, самолет, кошка) считают безмерным, то есть его размеры не имеют совершенно никакого значения для решения проблемы, поэтому ими пренебрегают. Это своего рода математическая идеализация, или модель. Для подобного объекта существует название: материальная точка.

Движение вдогонку и его особенности

Вам будет интересно:Франц Гальдер, немецкий генерал: биография, арест и концлагерь Дахау

Теперь перейдем к рассмотрению популярных школьных задач на движение вдогонку и формул для него. Под этим видом движения понимают перемещение двух или более объектов в одном направлении, которые отправляются в свой путь из разных пунктов (материальные точки имеют разные начальные координаты) или/и в разное время, но из одного и того же пункта. То есть создается ситуация, при которой одна материальная точка пытается догнать другую (другие), поэтому эти задачи получили такое название.

Согласно определению, особенностями движения вдогонку являются следующие:

• Наличие двух и более движущихся объектов. Если двигаться будет только одна материальная точка, то ей «некого» будет догонять.
• Прямолинейное перемещение в одном направлении. То есть объекты осуществляют движение вдоль одной и той же траектории и в одном направлении. Движение навстречу друг другу не входит в число рассматриваемых задач.
• Пункт отправления играет важную роль. Идея заключается в том, чтобы в момент начала движения объекты были разделены в пространстве. Такое разделение будет иметь место, если они стартуют в одинаковое время, но из разных пунктов или же из одного пункта, но в разное время. Старт двух материальных точек из одного пункта и в одинаковое время к задачам вдогонку не относится, поскольку в этом случае один объект будет постоянно удаляться от другого.

Формулы движения вдогонку

В 4 классе общеобразовательной школы обычно рассматриваются подобные задачи. Это означает, что формулы, которые необходимы для решения, должны быть максимально простыми. Такому случаю удовлетворяет равномерное прямолинейное движение, в котором фигурируют три физических величины: скорость, пройденный путь и время движения:

• Скорость — величина, показывающая расстояние, которое проходит тело за единицу времени, то есть она характеризует быстроту изменения координат материальной точки. Обозначается скорость латинской буквой V и измеряется, как правило, в метрах в секунду (м/с) или в километрах в час (км/ч).
• Путь — это расстояние, которое проходит тело за время своего движения. Он обозначается буквой S (D) и выражается обычно в метрах или километрах.
• Время — период движения материальной точки, который обозначается буквой T и приводится в секундах, минутах или часах.

Описав основные величины, приведем формулы движения вдогонку:

• s = v*t;
• v = s/t;
• t = s/v.

Решение любой задачи рассматриваемого типа базируется на применении этих трех выражений, которые необходимо запомнить каждому школьнику.

Пример решения задачи №1

Приведем пример задачи движения вдогонку и решения (формулы, необходимые для него, приведены выше). Проблема формулируется следующим образом: «Грузовик и легковой автомобиль одновременно выезжают из пунктов A и B со скоростями 60 км/ч и 80 км/ч соответственно. Оба транспортных средства движутся в одном направлении так, что автомобиль приближается к пункту A, а грузовик удаляется от обоих пунктов. Через какое время автомобиль догонит грузовик, если расстояние между A и B составляет 40 км?».

Перед тем как решать задачу, необходимо научить ребят определять суть проблемы. В данном случае она заключается в неизвестном времени, которое проведут оба транспортных средства в пути. Предположим, что это время равно t часам. То есть через время t автомобиль догонит грузовик. Найдем это время.

Рассчитаем расстояние, которое пройдет каждый из движущихся объектов за время t, имеем: s1 = v1*t и s2 = v2*t, здесь s1, v1 = 60 км/ч и s2, v2 = 80 км/ч — пройденные пути и скорости движения грузовика и автомобиля до того момента, когда второй догонит первого. Поскольку расстояние между пунктами A и B равно 40 км, то автомобиль, догнав грузовик, пройдет путь на 40 км больше, то есть s2 — s1 = 40. Подставляя в последнее выражение формулы для путей s1 и s2, получим: v2*t — v1*t = 40 или 80*t — 60*t = 40, откуда t = 40/20 = 2 ч.

Отметим, что данный ответ можно получить, если использовать понятие скорости сближения между движущимися объектами. В задаче она равна 20 км/ч (80-60). То есть при этом подходе возникает ситуация, когда один объект движется (автомобиль), а второй относительно него стоит на месте (грузовик). Поэтому достаточно поделить расстояние между пунктами A и B на скорость сближения, чтобы решить задачу.

Пример решения задачи №2

Приведем еще один пример задач на движение вдогонку (формулы для решения используются те же): «Из одного пункта выезжает велосипедист, а через 3 часа в ту же сторону выезжает автомобиль. Через какое время после начала своего движения автомобиль догонит велосипедиста, если известно, что он движется в 4 раза быстрее?».

Решать эту задачу следует так же, как и предыдущую, то есть необходимо определить, какой путь пройдет каждый участник движения до момента, когда один догонит другого. Предположим, что автомобиль догнал велосипедиста через время t, тогда получаем следующие пройденные пути: s1 = v1*(t+3) и s2 = v2*t, здесь s1, v1 и s2, v2 — пути и скорости велосипедиста и автомобиля соответственно. Заметим, что до того, как автомобиль догнал велосипедиста, последний находился в пути t + 3 часа, так как он выехал на 3 часа раньше.

Зная, что оба участника отправились из одного пункта, и пройденные ими пути будут равны, получаем: s2 = s1 или v1*(t+3) = v2*t. Скорости v1 и v2 нам не известны, однако в условии задачи сказано, что v2 = 4*v1. Подставляя это выражение в формулу для равенства путей, получим: v1*(t+3) = 4*v1*t или t+3 = 4*t. Решая последнее, приходим к ответу: t = 3/3 = 1 ч.

Некоторые советы

Формулы движения вдогонку являются простыми, тем не менее школьников в 4 классе важно научить мыслить логически, понимать значение величин, с которыми они имеют дело, и осознавать проблему, которая перед ними стоит. Ребят рекомендуется призывать к рассуждениям вслух, а также к командной работе. Кроме того, для наглядности задач можно использовать компьютер и проектор. Все это способствует развитию у них абстрактного мышления, коммуникативных навыков, а также математических способностей.

Источник

1ku.ru

Решение задач на движение вдогонку. 4-м классе

Цель урока:  познакомить учащихся с новым видом задач на движение (вдогонку).

Задачи:

• обучающие: учиться читать и записывать информацию, представленную в виде различных математических моделей, строить высказывания, продолжать учиться называть цели конкретного задания, алгоритм (план работы), проверять, исправлять и оценивать результаты работы так, как это было описано ранее.
• развивающие: способствовать развитию математического мышления, познавательной активности обучающихся,  умения пользоваться математической терминологией.
• воспитательные: продолжить работу по воспитанию взаимопомощи, культуры общения, способствующей созданию благоприятного психологического климата;
• воспитывать внимание, самостоятельность, самоконтроль, аккуратность, прививать интерес к предмету.

Тип урока:  Урок изучения и первичного закрепления новых знаний

Методы и приемы: словесные, наглядные, частично-поисковые.

Используемые учебники и учебные пособия: Учебник “Математика” Алматы “Атамра” 2011

Используемое оборудование: 

• интерактивное оборудование (мультимедийный проектор), компьютер,
• интер.доска. 

Ход урока

1. Вводно-мотивационная часть

Загадка.

Всем она давно знакома —
Ждёт послушно возле дома,
Только выйдешь из ворот-
Куда хочешь поведёт.

(дорога)

— Какое действие совершают машины по дороге?

— Прочитайте дружно, хором наш девиз:

Смело иди вперед,
Не стой на месте,
Чего не сделает один,
Сделаем вместе!

2. Актуализация знаний. Минутка чистописания

— Запишите формулы нахождения расстояния, скорости и времени.

S = V x t

V = S : t

t = S : V

— Чем отличаются величины: расстояние и скорость?

— Расстояние – это путь, пройденный за несколько единиц времени;

— Cкорость – это путь, пройденный за одну единицу времени

3. Устный счёт (задачи на движение)

Задача №1

Шофер все сильнее давит на газ
Скорость – сто километров в час.
Тебе нетрудно будет сказать,
Сколько проедет за три часа
Автомобиль со скоростью этой?
Решай поскорее – жду ответа!

Решение:

S = U х t

100 х 3 = 300 (км)

Задача №2

За 5 часов один пешеход
Тридцать пять километров пройдет.
Должен быть ответ поскорее готов:
Сколько пройдет он за восемь часов
Если скорость свою не изменит?
Решай – и учитель ответ оценит!

Решение:

1) 35 : 5 = 7 (км/ч)

2) 7 х 8 = 56 (км)

Задача №3

Возьми-ка ручку,
Открой чистый лист,
Задачу послушай: “Прошел турист
Со скоростью пять километров в час
Сто километров.” Ответ найди:
Сколько часов он был в пути?

Решение: 100 : 5 = 20 (час.)

Задача №4

Лора задачу быстро решила:
“Пятьсот километров проедет машина
За десять часов. Какова же скорость?”
Лора решала, не беспокоясь:
Пятьсот умножает на десять скоро.
Ответ получает. Права ли Лора?

Решение:

Лора не права!

500 : 10 = 50 ( км/ч)

4. Закрепление пройденного.

— С какими видами движения вы знакомы?

— Встречное движение

— Движение в противоположных направлениях.

— Движение с отставанием.

— С какой темой мы познакомились на прошлых уроках? (- Одновременное движение с отставанием.)

Работа по группам

(Группам раздаются карточки со схемами к задачам)

Задание: Какое направление движения соответствует решению?

14 км/ч+12км/ч=26км/ч

14 км/ч-12км/ч=2км/ч

5. Проблемная ситуация. Решите задачи по схемам.

— Почему не удалось решить вторую задачу? — Это задача на движение вдогонку.

— Не умеем находить скорость сближения при движении вдогонку.

Постановка учебной задачи.

— Какова же тема нашего урока? Задачи на движение вдогонку.

— Какие цели мы поставим?

• познакомиться со скоростью сближения при движении вдогонку;
• научиться решать задачи на движение вдогонку.

7. “Открытие” учащимися нового знания.

а) Работа над задачей стр. 230 №3

— Вначале понаблюдаем, что происходит с объектами при движении вдогонку. Заполним таблицу, чтобы сделать верные выводы.

(Текст задачи на стр.230 №3, чертежи с числовым лучом, таблица у каждого ученика.)

— Прочитайте условие вслух.

Из городов, длина пути между которыми 240км, одновременно в одном направлении выехали автомобиль и автобус. Скорость автомобиля 80 км/ч, а скорость автобуса 56км/ч. Сколько километров будет между ними через 2 часа?

Разбор задачи:

— В какой точке находится автомобиль? В точке 0.

— А автобус? В точке 240.

— Какое между ними расстояние до начала движения? 240 км

— Занесите в таблицу.

— Покажите на числовом луче, где будет находиться автомобиль через час.

В точке 80.

— И где через час будет находиться автобус. В точке 296 .

— Как изменилось расстояние между ними? Расстояние между объектами за каждую единицу времени будет уменьшаться на одно и то же число.

— Как это записать? (Vб — Vм)

— Составьте выражение и внесите запись в таблицу. 240 – (80-56) x 1 = 216 км

— Покажите на числовом луче, в каких точках будут находиться автомобиль и автобус через два часа. В точках 160 и 352

— Как изменилось расстояние между объектами через два часа? Уменьшилось еще на (80-56) x 2

Узнайте, какое расстояние стало между ними через два часа, запишите выражение в таблицу 240 – (80-56) x 2 = 192 км

— Сделайте вывод, с помощью какой формулы мы узнали, как изменяется расстояние при движении вдогонку? d = S – (V ₁– V ₂) x t

— Запишите формулы зависимости между величинами: S, t, V.

Vсбл= (V ₁– V ₂) Sп = Vсбл. x t,

t встр.= S : (V ₁– V ₂), V ₁= S : t – V ₂

d = S – (V ₁– V ₂) x t

8. Для закрепления работа над задачей стр.231 №9

 

9. Рефлексия.

— Что такое скорость сближения.

(- Скорость сближения – расстояние, при котором объекты сближаются за единицу времени.)

— Как найти скорость сближения при движении вдогонку?

Vсбл = (Vб – Vм),

— Какие еще знания необходимы, чтобы успешно решать задачи на движение вдогонку?

Sп = Vсбл. x t,

t встр.= S : (Vб – Vм), V1= S : t – V2

d = S – (Vб – Vм) x t

Презентация.

urok.1sept.ru