Быстро найти нужную формулу для расчета онлайн. Геометрия. Алгебра.

---

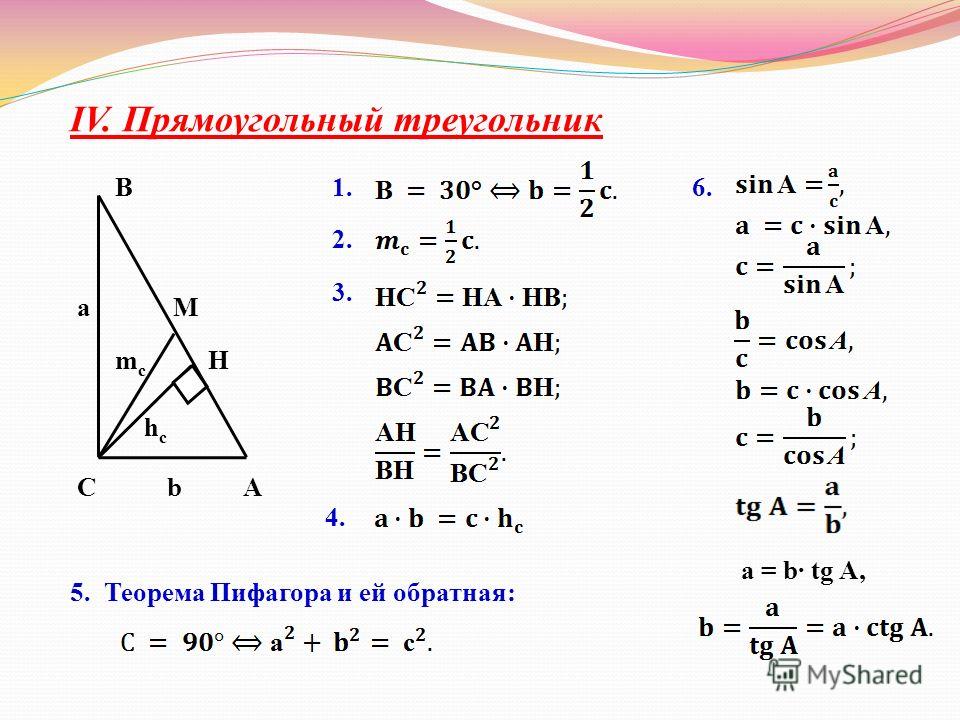
Как найти,

гипотенузу или катеты в прямоугольном треугольнике.

 

a, b — катеты

c — гипотенуза

α, β — острые углы

 

Формулы для катета, (a):

 

Формулы для катета, (b):

 

 

Формулы для гипотенузы, (c):

 

Формулы сторон по теореме Пифагора, (a,b):

 

---

---

---

Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)

a — равные стороны

α — углы при основании

β — угол образованный равными сторонами

 

 

Формулы длины стороны (основания), (b):

 

 

Формулы длины равных сторон , (a):

 

---

---

---

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

 

 

a, b, c — стороны произвольного треугольника

α, β, γ — противоположные углы

 

 

Формула  длины через две стороны и угол (по теореме косинусов), (a):

* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение

 

 

Формула  длины через сторону и два угла (по теореме синусов), (a):

 

---

---

---

В прямоугольном треугольнике катеты, являются высотами. Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.

 

H — высота из прямого угла

a, b — катеты

с — гипотенуза

c₁ , c₂ — отрезки полученные от деления гипотенузы, высотой

α, β — углы при гипотенузе

 

Формула длины высоты через стороны, (H):

 

 

Формула длины высоты через гипотенузу и острые углы, (H):

 

Формула длины высоты через катет и угол, (H):

 

Формула длины высоты через составные отрезки гипотенузы , (

H):

---

---

---

Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).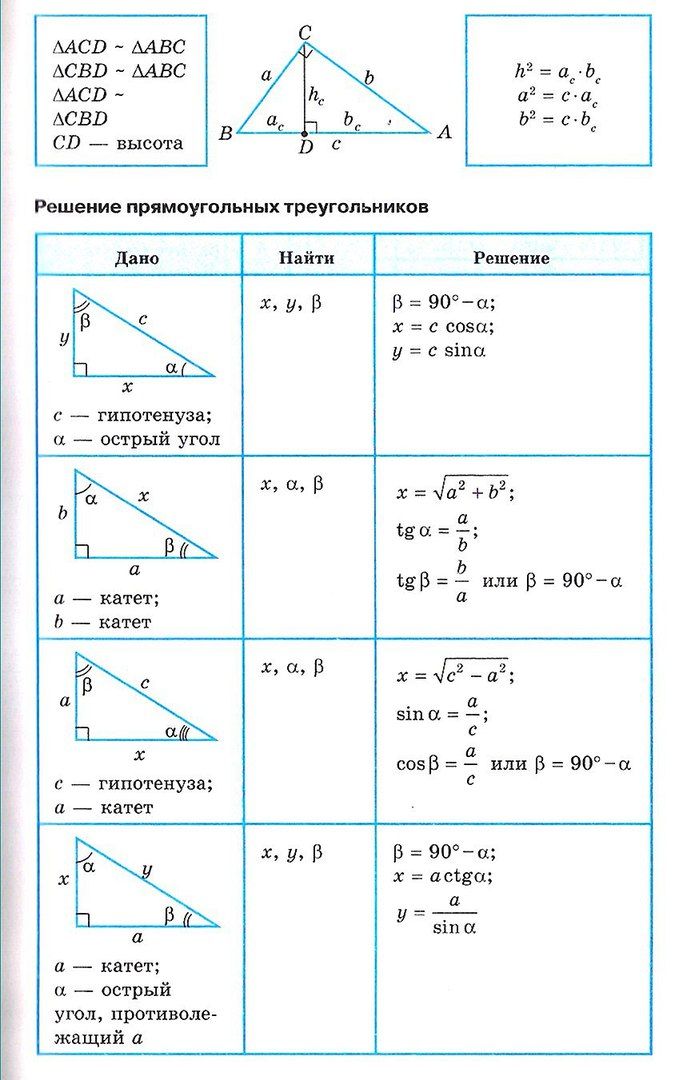

Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

 

H — высота треугольника

a — сторона, основание

b, c — стороны

β, γ — углы при основании

p — полупериметр, p=(a+b+c)/2

R — радиус описанной окружности

S — площадь треугольника

 

Формула длины высоты через стороны, (H):

 

 

Формула длины высоты через сторону и угол, (H):

 

Формула длины высоты через сторону и площадь, (H):

 

Формула длины высоты через стороны и радиус, (H):

 

 

---

---

---

Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.

Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).

 

M — медиана

R — радиус описанной окружности

O — центр описанной окружности

с — гипотенуза

a, b

— катеты

α — острый угол CAB

 

Медиана равна радиусу и половине гипотенузы, (M):

 

 

Формула длины через катеты, (M):

 

Формула длины через катет и острый угол, (M):

 

 

---

---

---

Медиана — отрезок |AO|, который выходит из вершины A и делит противолежащею сторону  c пополам.

Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.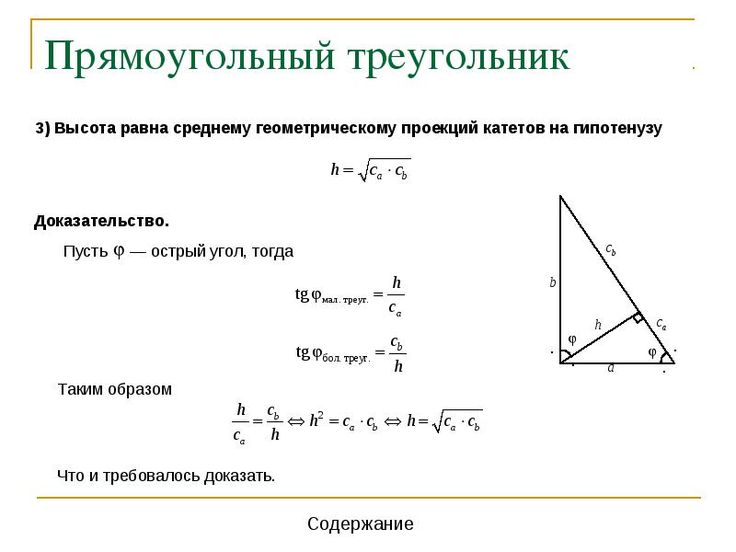

 

 

M — медиана, отрезок |AO|

c — сторона на которую ложится медиана

a, b — стороны треугольника

γ — угол CAB

 

Формула длины медианы через три стороны, (M):

 

 

Формула длины медианы через две стороны и угол между ними, (M):

---

---

---

Формула для вычисления высоты = биссектрисы = медианы.

В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.

 

L — высота=биссектриса=медиана

a — сторона треугольника

 

 

Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):

 

 

Калькулятор — вычислить, найти медиану, биссектрису, высоту

 

---

---

---

Формулы для вычисления высоты, биссектрисы и медианы.

В равнобедренном треугольнике: высота, биссектриса и медиана, исходящие из угла образованного равными сторонами, один и тот же отрезок.

 

L — высота = биссектриса = медиана

a — одинаковые стороны треугольника

b — основание

α — равные углы при основании

β — угол образованный равными сторонами

 

Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):

 

 

 

 

Формула высоты, биссектрисы и медианы, через стороны, (L):

 

---

---

---

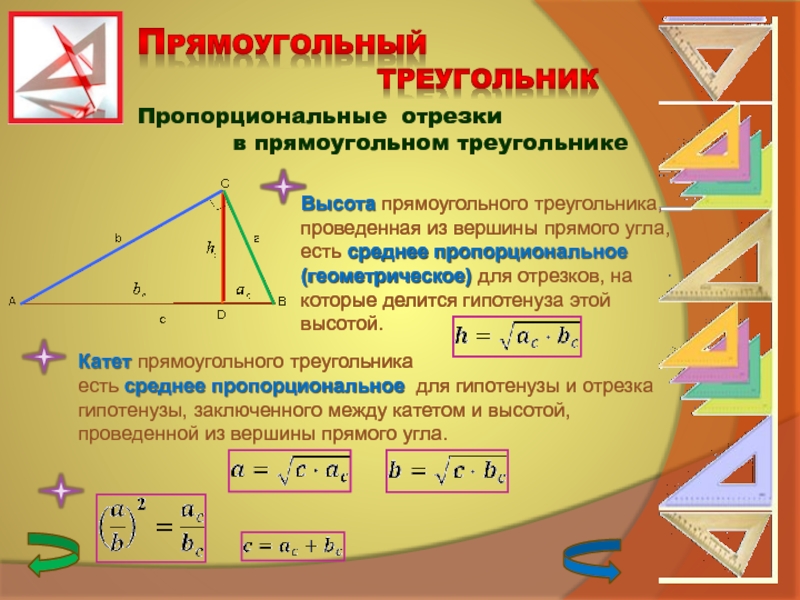
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:

 

L — биссектриса, отрезок ME ,  исходящий из прямого угла (90 град)

a, b — катеты прямоугольного треугольника

с — гипотенуза

α — угол прилежащий к гипотенузе

 

Формула длины биссектрисы через катеты, ( L):

 

Формула длины биссектрисы через гипотенузу и угол, ( L):

 

 

2. Найти по формулам длину биссектрисы из острого угла на катет:

 

L — биссектриса, отрезок ME ,  исходящий из острого угла

a, b — катеты прямоугольного треугольника

с — гипотенуза

α, β

— углы прилежащие к гипотенузе

 

Формулы длины биссектрисы через катет и угол, (L):

 

Формула длины биссектрисы через катет и гипотенузу, (L):

 

---

---

---

L— биссектриса, отрезок |OB|, который делит угол ABC пополам

a, b — стороны треугольника

с — сторона на которую опущена биссектриса

d, e — отрезки полученные делением биссектрисы

γ — угол ABC , разделенный биссектрисой пополам

p — полупериметр, p=(a+b+c)/2

 

Длина биссектрисы через две стороны и угол, (L):

 

Длина биссектрисы через полупериметр и стороны, (L):

 

 

Длина биссектрисы через три стороны, (L):

 

Длина биссектрисы через стороны и отрезки d, e, (L):

 

 

 

Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.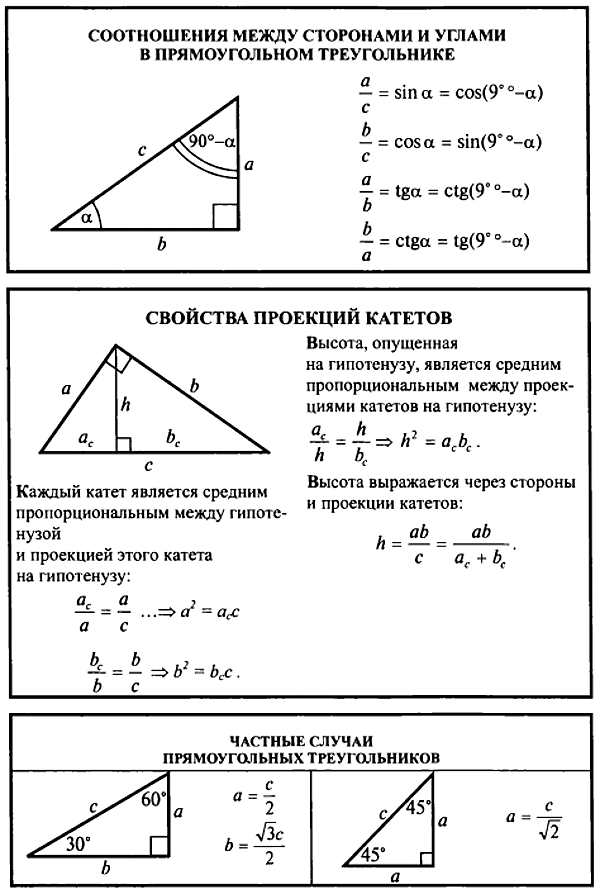

---

---

Теорема Пифагора — формула, доказательство, задачи

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные понятия

Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Гипотенуза — сторона, лежащая напротив прямого угла.

Катет — одна из двух сторон, образующих прямой угол.

Формула Теоремы Пифагора

выглядит так:

a² + b² = c²,

где a, b — катеты, с — гипотенуза.

Из этой формулы можно вывести следующее:

• a = √c² − b²
• b = √c² − a²
• c = √a² + b²

Запоминаем

в любом прямоугольном треугольнике сумма квадратов длин двух катетов равна квадрату длины гипотенузы.

Для треугольника со сторонами a, b и c, где c — большая сторона, действуют следующие правила:

• если c² < a² + b², значит угол, противолежащий стороне c, является острым.
• если c² = a² + b², значит угол, противолежащий стороне c, является прямым.
• если c² > a² +b², значит угол, противолежащий стороне c, является тупым.

Теорема Пифагора: доказательство

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано: ∆ABC, в котором ∠C = 90º.

Доказать: a² + b² = c².

Пошаговое доказательство:

• Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
• Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:

∠ACB =∠CHA = 90º,

∠A — общий.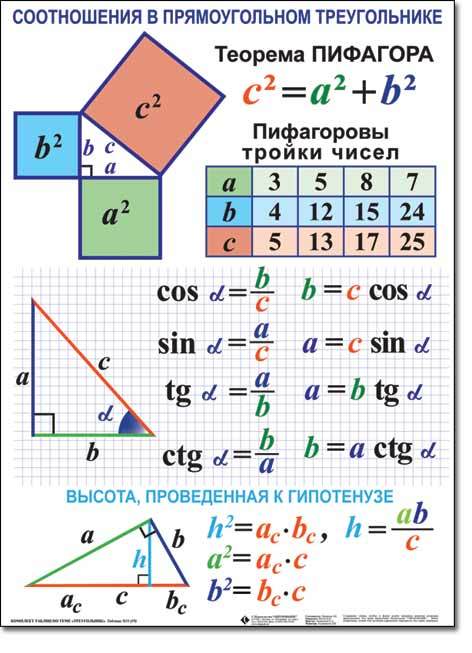

• Также прямоугольная фигура ∆CBH подобна ∆ABC:

∠ACB =∠CHB = 90º,

∠B — общий.

• Введем новые обозначения: BC = a, AC = b, AB = c.

• Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.

• Значит a² = c * HB, b² = c * AH.
• Сложим полученные равенства:

a² + b² = c * HB + c * AH

a² + b² = c * (HB + AH)

a² + b² = c * AB

a² + b² = c * c

a² + b² = c²

Теорема доказана.

Обратная теорема Пифагора: доказательство

Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.

Дано: ∆ABC

Доказать: ∠C = 90º

Пошаговое доказательство:

• Построим прямой угол с вершиной в точке C₁.
• Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.

• Проведём отрезок A₁B₁.
• Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.

• В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁² = A₁C₁² + B₁C₁².
• Таким образом получится:

• Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:

1. C₁A₁ = CA и C₁B₁ = CB по результату построения,
2. A₁B₁ = AB по доказанному результату.

• Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
• Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.

Обратная теорема доказана.

Решение задач

Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 8 см. Какое значение у гипотенузы?

Как решаем:

• Пусть катеты a = 6 и b = 8.

• По теореме Пифагора c² = a² + b².

• Подставим значения a и b в формулу:
  c² = 6² + 8² = 36 + 64 = 100
  c = √100 = 10.

Ответ: 10.

Задание 2. Является ли треугольник со сторонами 8 см, 9 см и 11 см прямоугольным?

Как решаем:

• Выберем наибольшую сторону и проверим, выполняется ли теорема Пифагора:

11² = 8² + 9²

121 ≠ 145

Ответ: треугольник не является прямоугольным.

---

---

 

Прямоугольный треугольник

Прямоугольный треугольник — это треугольник, у которого один из углов — прямой, то есть равен 90 градусам.

• Сторона, противолежащая прямому углу называется гипотенузой (на рисунке обозначена как c или AB)
• Сторона, прилежащая к прямому углу, называется катетом. Каждый прямоугольный треугольник имеет два катета (на рисунке обозначены как a и b или AC и BC)

Формулы и свойства прямоугольного треугольника

Обозначения формул:

(см. рисунок выше)

a, b — катеты прямоугольного треугольника

c — гипотенуза

α, β — острые углы треугольника

S — площадь

h — высота, опущенная из вершины прямого угла на гипотенузу

m_a— медиана, проведенная к стороне a из противолежащего угла (α)

m_b — медиана, проведенная к стороне b из противолежащего угла (β)

m_c — медиана, проведенная к стороне c из противолежащего угла (γ)

В прямоугольном треугольнике любой из катетов меньше гипотенузы (Формулы 1 и 2). Данное свойство является следствием теоремы Пифагора.

Косинус любого из острых углов меньше единицы (Формулы 3 и 4). Данное свойство следует из предыдущего. Так как любой из катетов меньше гипотенузы, то из соотношение катета к гипотенузе всегда меньше единицы.

Квадрат гипотенузы равен сумме квадратов катетов (теорема Пифагора). (Формула 5). Это свойство постоянно используется при решении задач.

Площадь прямоугольного треугольника равна половине произведения катетов (Формула 6)

Сумма квадратов медиан к катетам, равна пяти квадратам медианы к гипотенузе и пяти квадратам гипотенузы, деленных на четыре (Формула 7). Кроме указанной, есть еще 5 формул, поэтому рекомендуется ознакомиться также и с уроком «Медиана прямоугольного треугольника», в котором более подробно изложены свойства медианы.

Высота прямоугольного треугольника равна произведению катетов, деленному на гипотенузу (Формула 8)

Квадраты катетов обратно пропорциональны квадрату высоты, опущенной на гипотенузу (Формула 9). Данное тождество также является одним из следствий теоремы Пифагора.

Длина гипотенузы равна диаметру (двум радиусам) описанной окружности (Формула 10). Гипотенуза прямоугольного треугольника является диаметром описанной окружности. Это свойство часто используется при решении задач.

Радиус вписанной в прямоугольный треугольник окружности можно найти как половину от выражения, включающего в себя сумму катетов этого треугольника минус длину гипотенузы. Или как произведение катетов, деленное на сумму всех сторон (периметр) данного треугольника. (Формула 11)
Синус угла А (α, альфа) в прямоугольном треугольнике будет равен отношению противолежащего данному углу катета к гипотенузе (по определению синуса). (Формула 12). Данное свойство используется при решении задач. Зная величины сторон, можно найти угол, который они образуют.

Косинус угла А (α, альфа) в прямоугольном треугольнике будет равен отношению прилежащего данному углу катета к гипотенузе (по определению синуса). (Формула 13)

См. также Соотношения между углами и сторонами прямоугольного треугольника изучает Тригонометрия.

Содержание главы:
 Подобие треугольников. Использование в задачах | Описание курса | Прямоугольный треугольник 

   

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК формулы площади, периметра, радиуса

Прямоугольный треугольник – это треугольник, у которого один из углов прямой (90°).

Другие виды треугольников:

Любой прямоугольный треугольник характеризуется катетами a и b и гипотенузой c (см. рисунок).

Катет – это сторона прямоугольного треугольника, образующая прямой угол с другой стороной (также катетом).

Гипотенуза – это сторона прямоугольного треугольника, лежащая напротив прямого угла.

Именно эти характеристики используются в формулах прямоугольного треугольника при вычислении площади, периметра, а также радиусов вписанной и описанной окружностей.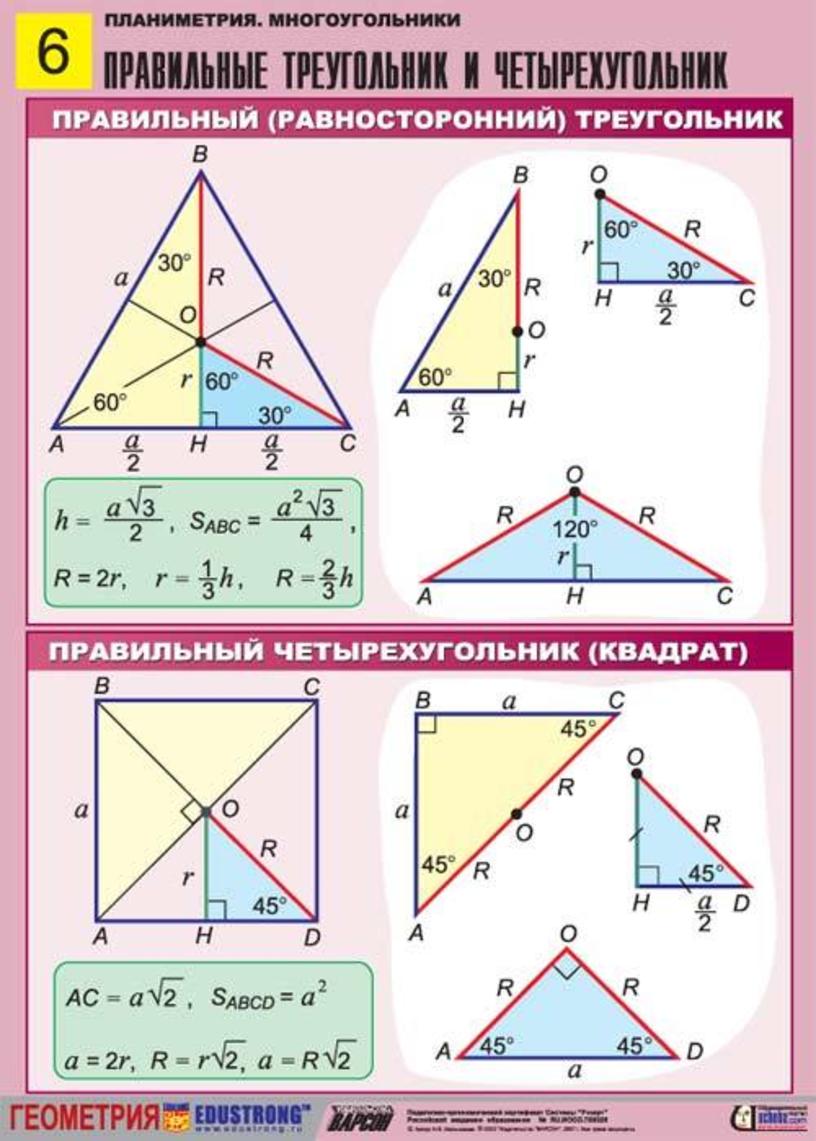

Формула радиуса вписанной окружности для прямоугольного треугольника

Радиус вписанной окружности r можно вычислить, зная стороны прямоугольного треугольника:

Формула радиуса описанной окружности для прямоугольного треугольника

Радиус описанной окружности R можно вычислить, зная гипотенузу прямоугольного треугольника:

Формула периметра прямоугольного треугольника

Периметр P прямоугольного треугольника можно получить, зная его стороны:

При вычислении площади прямоугольного треугольника часто требуется знать его полупериметр:

Формулы площади прямоугольного треугольника

При вычислении площади прямоугольного треугольника можно пользоваться формулами, которые применяются для вычисления площади произвольного треугольника, так как прямоугольный треугольник является частным случаем для треугольников.

Площадь прямоугольного треугольника S можно вычислить, зная его катеты a и b:

Еще одна формула позволяет вычислить площадь прямоугольного треугольника по его катетам a и b и полупериметру p (формула Герона):

S = (p – a) ⋅ (p – b)

Прямоугольные треугольники — урок.

Геометрия, 7 класс.

Свойства прямоугольного треугольника

Сумма двух острых углов прямоугольного треугольника равна 90°.

Сумма углов треугольника равна 180°, а прямой угол равен 90°, поэтому сумма двух острых углов прямоугольного треугольника&angmsd; \(1\) \(+\) &angmsd; \(2 =\) 90°.

Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы (гипотенуза в два раза длиннее катета, лежащего против угла в \(\)30°\(\)).

 

Рассмотрим прямоугольный треугольник \(ABC\), в котором &angmsd; \(A\) — прямой, &angmsd; \(B =\) 30°, и значит, что &angmsd; \(C =\) 60°.

 

Докажем, что \(BC = 2 AC\).
Приложим к треугольнику \(ABC\) равный ему треугольник \(ABD\), как показано на рисунке.

Получим треугольник \(BCD\), в котором &angmsd; \(B =\) &angmsd; \(D =\) 60°, поэтому \(DC = BC\). Но \(DC = 2 AC\). Следовательно, \(BC = 2 AC\).

 

Справедливо и обратное суждение.

Если катет прямоугольного треугольника равен половине гипотенузы (или гипотенуза в два раза длиннее катета), то угол, лежащий против этого катета, равен 30°.

Признаки равенства прямоугольных треугольников

Основываясь на общих признаках равенства треугольников для прямоугольных треугольников можно сформулировать свои признаки равенства, потому что в прямоугольном треугольнике угол между двумя катетами — прямой, а любые два прямых угла равны.

1. Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.

 

2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.

 

3. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.

 

4. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.

Формула площади прямоугольного треугольника

В элементарной геометрии прямоугольным треугольником называется фигура, состоящая из трёх отрезков соединённых в точках, с углами два из которых острые, а один прямой (то есть равен 90°). Прямоугольный треугольник характеризуется целым рядом важных свойств, многие из которых составляют основу тригонометрии (например, соотношения между его сторонами и углами). Еще со школьной скамьи все мы знаем, как вычислить площадь прямоугольного треугольника, а в повседневной жизни встречаемся с этой геометрической фигурой достаточно часто, порой даже не замечая этого. Достаточно широкое применение находит она в технике и поэтому такую задачу, как нахождение площади прямоугольного треугольника, часто приходится решать инженерам, конструкторам и архитекторам.

Зодчим определять эту величину требуется тогда, когда они проектируют здания с фронтонами, которые являются завершением фасадов и имеют треугольную форму ограниченную карнизом, а по бокам – скатами крыши. Нередко угол между скатами бывает прямой, и в таких случаях фронтон имеет форму прямоугольного треугольника. Определять его площадь требуется по той простой причине, что необходимо точно знать количество строительного материала, необходимого для его обустройства. Следует заметить, что фронтоны являются обязательными элементами малоэтажных строений (загородных домов, коттеджей, дач).

Нахождение площади прямоугольного треугольника

Формула расчёта площади прямоугольного треугольника

 

 

a – катет

b – катет

S – площадь прямоугольного треугольника

Форму прямоугольного треугольника имеют многие детали, из которых изготавливается современная мебель. Как известно, для того чтобы наиболее рационально использовать площадь помещений, все элементы обстановки должны размещаться в ней оптимальным образом. С пользой задействовать такие зоны, как углы, можно с помощью столов треугольной формы, столешницы которых в большинстве случаев представляют собой прямоугольные треугольники с катетами, вплотную прилегающими к стенам. При проектировании и расчете этих элементов конструкторы мебельного производства применяют формулу, по которой нахождение площади прямоугольного треугольника осуществляется на основе длины его сторон. Кроме того, им нередко приходится разрабатывать конструкции столиков, крепящихся непосредственно к стенам, в состав которых входят опорные элементы, также представляющие собой прямоугольные треугольники.

Строителям, занимающимся облицовочными работами, нередко в своей профессиональной деятельности приходится использовать керамическую плитку, имеющую форму прямоугольного треугольника с катетами одинаковой или различной длины. Им также приходится определять площадь этих элементов для того, чтобы выяснить необходимое их количество.

Форму прямоугольного треугольника имеет и такой важный и необходимый измерительный инструмент, как угольник. С его помощью производится построение и контроль прямых углов, а используется он очень широко и многими: от обычных школьников на уроках геометрии до конструкторов суперсовременной техники.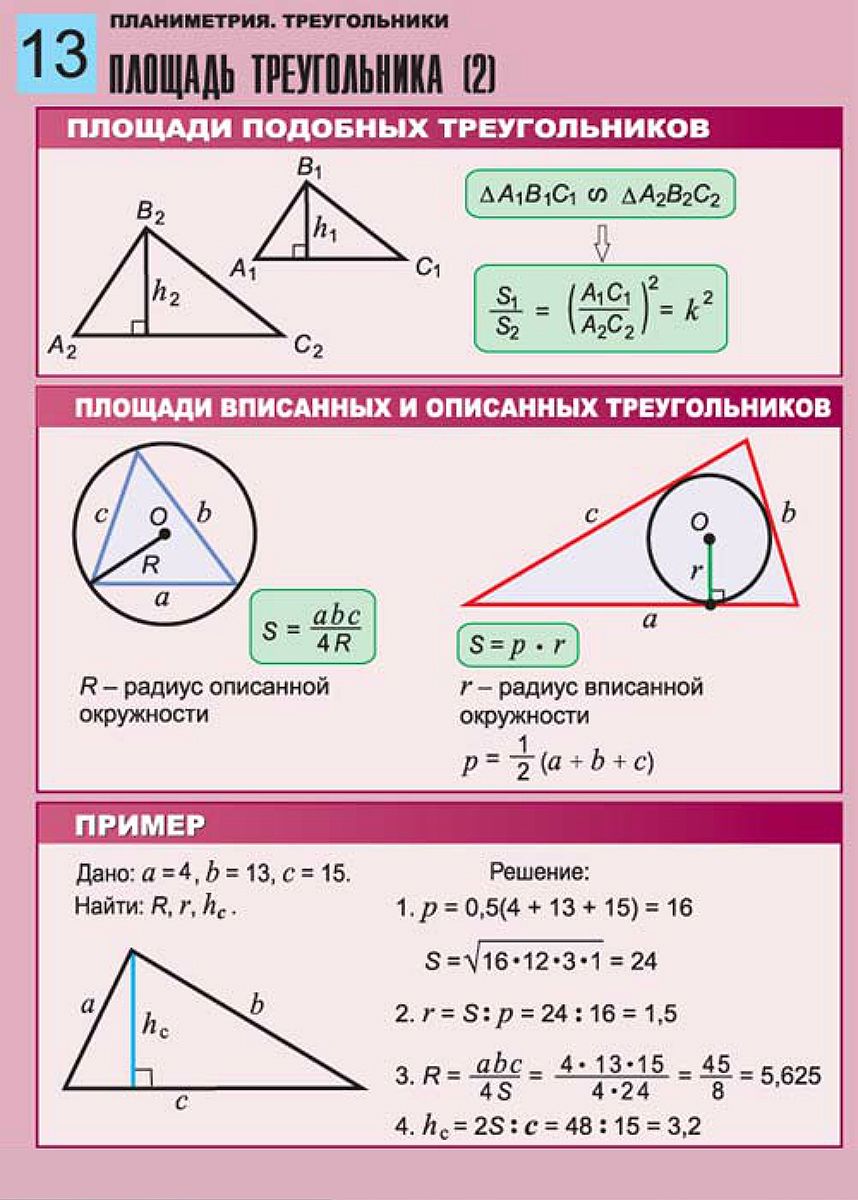

Некоторые свойства прямоугольных треугольников

Вспомним, что прямоугольным называют треугольник, который содержит прямой угол. Две стороны, образующие прямой угол, называют катетами, а противолежащую сторону — гипотенузой прямоугольного треугольника.

Теорема:

Сумма углов треугольника равна 180 градусов.

Свойство:

Сумма двух острых углов прямоугольного треугольника равна 90 градусов.

Доказательство:

Пусть АВС — прямоугольный треугольник, у которого ∠С=90 градусов.

Так как сумма углов треугольника равна 180 градусов, то:

Что и требовалось доказать.

Свойство:

Катет прямоугольного треугольника, лежащий против угла в 30 градусов, равен половине гипотенузы.

Пусть АВС — прямоугольный треугольник, у которого ∠С=90 градусов, а ∠А=30 градусов.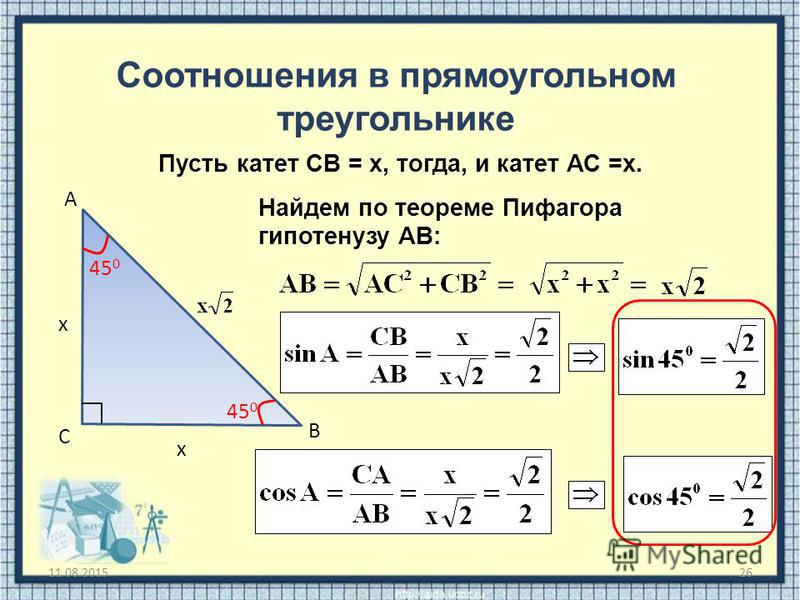 А тогда по теореме о сумме углов треугольника ∠В=60 градусов. Докажем, что катет ВС равен половине гипотенузы АВ.

Приложим к треугольнику АВС равный ему треугольник АСD следующим образом:

Получили, что у треугольника АВD все углы равны по 60 градусов, то есть он является равносторонним. Получаем:

Что и требовалось доказать.

Свойство:

Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30 градусов.

Доказательство:

Пусть АВС — прямоугольный треугольник, у которого катет ВС равен половине гипотенузы АВ. Докажем, что угол ВАС=30 градусов.

Приложим к треугольнику АВС равный ему треугольник АСD следующим образом:

Получили равносторонний треугольник АВD. Известно, что все углы равностороннего треугольника равны 60 градусам. Полуаем:

Что и требовалось доказать.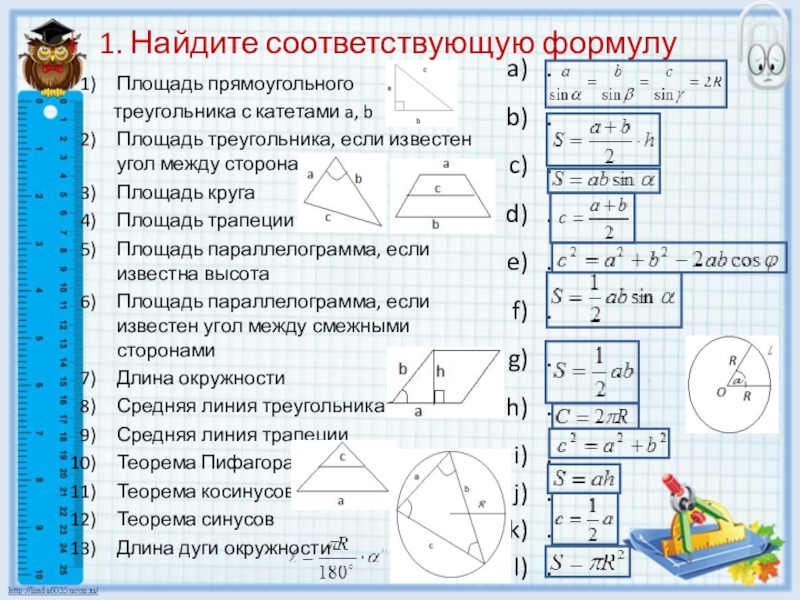

Пример.

Сумма гипотенузы и катета, лежащего против угла в 30 градусов, равна 15 сантиметров. Найти длину гипотенузы.

Пусть АВС — прямоугольный треугольник. ∠А=30 градусов. Получим:

Подставим это в предыдущее равенство и получаем:

Пример.

В прямоугольном треугольнике АВС, ∠С=90 градусов, а ∠ВАС=60 градусов. Найти длину катета ВС, если высота СD треугольника АСВ равна 5 сантиметров.

Рассмотрим прямоугольный треугольник АВС. ∠АСВ=90 градусов, ∠ВАС=60 градусов. А так как сумма острых углов прямоугольного треугольника равна 90 градусов, то ∠АВС=90-60=30 градусов.

Рассмотрим треугольник ВСD, который является прямоугольным, так как СD - высота и ∠СВD=30 градусов, то катет СD лежит против угла в 30 градусов. Следовательно, по выше доказанному свойству, гипотенуза ВС=2*5=10 см.

Пример.

Отрезок СD - высота прямоугольного треугольника АВС с прямым углом С, ВС=2*ВD.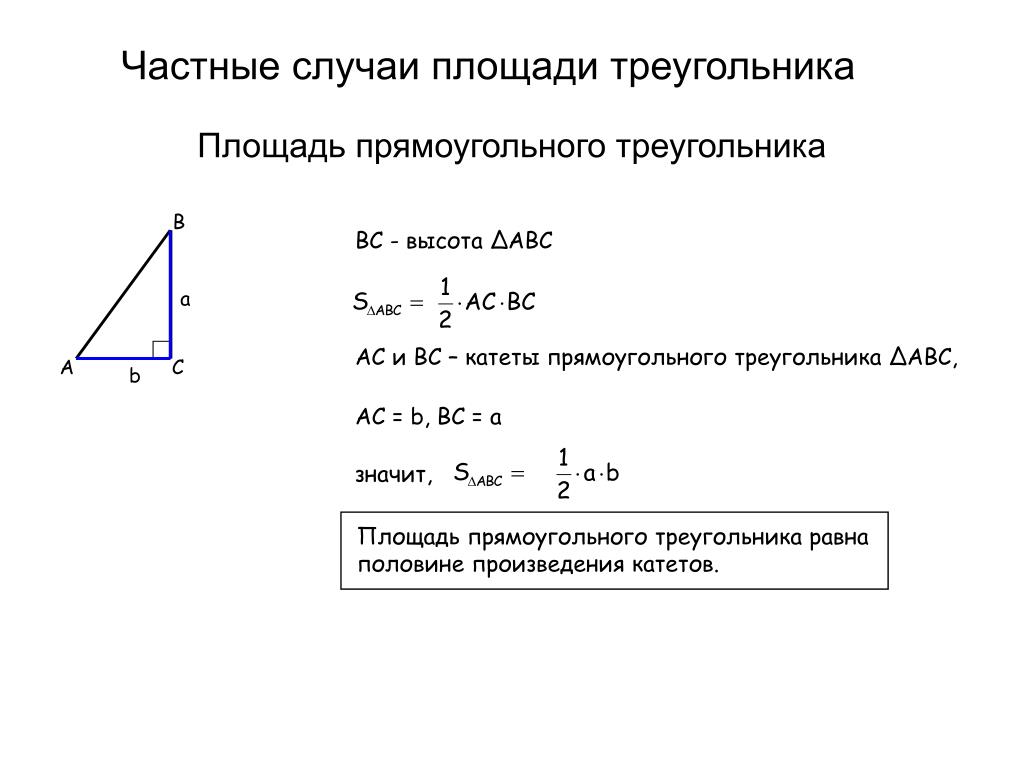 Доказать, что АВ=4*ВD.

Рассмотрим прямоугольный треугольник BCD:

У него ∠ВСD=30 градусов, так как по условию ВС=2*ВD.

По условию задачи ∠АСВ=90 градусов, а ∠ВСD=30 градусов, значит, ∠АСD=60 градусов.

Так как СD - высота, то треугольник АСD - прямоугольный. ∠АСD=60 градусов. Следовательно, ∠САD=30 градусов.

Теперь рассмотрим треугольник АВС. У него ∠ВАС=30 градусов. Следовательно, гипотенуза АВ=2*ВС, так как катет ВС лежит против угла в 30 градусов. По условию задачи ВС=2*ВD.

Получаем, что АВ=4*ВD.

Сводка тригонометрических формул

Сводка тригонометрических формул

Эти формулы связывают длины и площади определенных кругов или треугольников. На следующей странице вы найдете личности. Тождества не относятся к конкретным геометрическим фигурам, но справедливы для всех углов.

Формулы для дуг и секторов окружностей

Вы можете легко найти длину дуги и площадь сектора для угла θ в окружности радиусом r .

Длина дуги. Длина дуги равна радиусу r , умноженному на угол θ , где угол измеряется в радианах. Чтобы перевести градусы в радианы, умножьте количество градусов на π /180.
Площадь сектора. Площадь сектора равна половине квадрата радиуса, умноженного на угол, где, опять же, угол измеряется в радианах.

Формулы для прямоугольных треугольников

Наиболее важными формулами тригонометрии являются формулы прямоугольного треугольника.Если θ — один из острых углов в треугольнике, то синус теты — это отношение противолежащего катета к гипотенузе, косинус — отношение прилежащего катета к гипотенузе, а тангенс — это отношение противоположная сторона соседней стороне.

Эти три формулы вместе известны мнемоникой SohCahToa. Кроме того, есть очень важная формула Пифагора, которая гласит, что квадрат гипотенузы равен сумме квадратов двух других сторон.

Зная, что два острых угла дополняют друг друга, то есть дают в сумме 90°, можно решить любой прямоугольный треугольник:

• Зная две из трех сторон, можно найти третью сторону и оба острых угла.
• Если вы знаете один острый угол и одну из трех сторон, вы можете найти другой острый угол и две другие стороны.

Формулы для косоугольных треугольников

Эти формулы работают для любого треугольника, острого, тупоугольного или прямоугольного.Мы будем использовать стандартные обозначения, в которых три вершины треугольника обозначены прописными буквами A , B и C , а три противоположные им стороны соответственно обозначены строчными буквами a , б и в .

Есть две важные формулы для косых треугольников. Они называются законом косинусов и законом синусов.

Закон косинусов обобщает формулу Пифагора на все треугольники.Он говорит, что c ² , квадрат одной стороны треугольника, равен a ²  +  b ² , сумма квадратов двух других сторон минус 2. ab  cos&nbsp C , удвоенное произведение их на косинус противоположного угла. Когда угол C правильный, он становится формулой Пифагора.

Закон синусов гласит, что отношение синуса одного угла к противоположной стороне одинаково для всех трех углов.

С помощью этих двух формул вы можете решить любой треугольник:

• Зная два угла и сторону, можно найти третий угол и две другие стороны.
• Если известны две стороны и угол между ними, то можно найти третью сторону и оба других угла.
• Если известны две стороны и угол, противолежащий одной из них, то для угла, противолежащего другой, возможны два варианта (один острый и один тупой), и для обоих вариантов можно определить оставшийся угол и оставшуюся сторону.

Формулы площади треугольников

Существует три различных полезных формулы площади треугольника, и какую из них использовать, зависит от имеющейся у вас информации.

Половина основания, умноженная на высоту. Обычно используется, так как он самый простой, и у вас обычно есть эта информация. Выберите любую сторону для вызова базы b . Тогда, если h — это расстояние от противоположной вершины до b , то площадь равна половине bh .
Формула Герона. Это полезно, когда вы знаете три стороны a , b и c треугольника, и все, что вы хотите знать, это площадь. Пусть s будут половиной их суммы, называемой полупериметром . Тогда площадь равна квадратному корню из произведения s , s  —  a , s  —  b и s  —  c .
Формула «бок-угол-бок». Используйте это, когда вы знаете две стороны, a и b , и прилежащий угол, C . Площадь равна половине произведения двух сторон на синус прилежащего угла.

Прямоугольник

: типы, свойства и формулы — видео и расшифровка урока

Что делает прямоугольник прямоугольником?

Есть несколько вещей, которые делают прямоугольники особенными и отличают их от других форм. Первые два уже упоминались, но здесь они снова вместе с некоторыми другими:

• У него должно быть четыре стороны.
• Все четыре угла должны быть прямыми по 90 градусов.
• Прямоугольник является частным случаем параллелограмма; его противоположные стороны параллельны. Как и у параллелограмма, противоположные стороны равны по длине друг другу. Есть две пары противоположных сторон, и каждая пара может иметь разную длину, но стороны каждой пары будут равны друг другу.
• Диагонали прямоугольника равны по длине друг другу и в точке пересечения делятся пополам.Когда вы проведете линию, которая разрезает прямоугольник на два треугольника, а затем сделаете то же самое с двумя другими углами, эти две линии будут равны по длине друг другу. Эти две линии также пересекаются точно посередине каждой. Таким образом, каждая диагональ делит другую пополам.

Все вышеперечисленное должно быть выполнено, чтобы фигура считалась прямоугольником. Даже с учетом этих требований существуют прямоугольники, которые относятся к своим особым типам.

Особые типы прямоугольников

Существует два особых типа прямоугольников, к которым предъявляются еще более строгие требования, чем к обычным прямоугольникам.

• Первый квадрат . Квадрат — это прямоугольник с дополнительным требованием, чтобы все стороны были равны по длине. Вы можете поместить квадрат в прямоугольник, ширина которого равна ширине квадрата, учитывая, что длина прямоугольника больше ширины.
• Второй прямоугольник Фибоначчи . Этот специальный прямоугольник добавляет требование, чтобы отношение длины к ширине составляло 1,618. Другими словами, длина в 1,618 раза больше ширины.Итак, если ширина равна 2, то длина 2 умножить на 1,618 или 3,236.

Этот особый тип прямоугольника также называют золотым прямоугольником, потому что его отношение является золотым сечением 1,618. Глядя на картину Моны Лизы, математики заметили, что прямоугольник, идущий от ее головы к правой руке и левому локтю, имеет пропорции золотого прямоугольника.

Использование прямоугольников в реальном мире

При использовании прямоугольников в реальном мире для решения задач необходимо помнить лишь несколько формул.Они относятся к площади, периметру и диагоналям прямоугольника.

Как и другие формулы, они просты в использовании и требуют подстановки значений в соответствующие места.

Допустим, ваш деловой партнер недавно купил офисное здание и хочет отремонтировать его, уложив новый пол в главном конференц-зале. Чтобы вычислить, сколько квадратных метров пола ему нужно, он может использовать формулу для площади прямоугольника .

Если размеры комнаты 20 футов на 30 футов, то ему потребуется 20 * 30 = 600 квадратных футов пола для проведения ремонта.

Если он хочет добавить плинтус по всей комнате, он может использовать формулу периметра . Это дало бы ему 2(20) + 2(30) = 100 футов необходимого плинтуса.

Если он хочет добавить перегородку в комнату, чтобы ее можно было разделить на две треугольные комнаты, он может использовать диагональную формулу , чтобы вычислить, какой длины перегородка ему нужна. 2 = 400 + 900 = 1300, а затем извлеките из него квадратный корень, чтобы получить 36,05551275463989. Если округлить, то ему потребуется примерно 36,06 фута для разделителя.

Резюме урока

Чтобы считаться прямоугольником , фигура должна иметь четыре стороны с четырьмя прямыми углами, противоположные стороны которых параллельны и равны по длине друг другу с диагоналями одинаковой длины и пересекающимися в их серединах.

Для прямоугольников необходимы три формулы: площадь , периметр и диагональ .

Прямоугольники Термины и определения

Специальный прямоугольник

Условия	Определения
Прямоугольник	любая четырехсторонняя фигура, которая также имеет четыре прямых угла (углы 90 градусов)
Квадрат	прямоугольник с добавленным требованием, чтобы все стороны были равны по длине
Прямоугольник Фибоначчи	добавляет требование, чтобы отношение длины к ширине было равно 1. 618
Площадь прямоугольника	длина умножить на ширину
Формула периметра	суммирование всех четырех сторон
Диагональная формула	найти квадратный корень из длины в квадрате плюс ширина в квадрате

Результаты обучения

Вы закончили этот урок, поэтому вы должны быть готовы:

• Определить «прямоугольник»
• Опишите виды прямоугольников
• Определите, как найти площадь, периметр и диагональ прямоугольника

Обзор геометрической формулы | Пурпурная математика

Пурпурная математика

Существует много геометрических формул, и они связывают высоту, ширину, длину или радиус и т. д. с периметром, площадью, площадью поверхности или объемом и т. д.Некоторые формулы довольно сложны, и вы их почти никогда не видите, не говоря уже о том, чтобы ими пользоваться. Но есть несколько основных формул, которые вам действительно следует запомнить, потому что ваш инструктор вполне разумно ожидает, что вы их знаете.

Например, очень легко найти площадь A прямоугольника: это всего лишь длина l , умноженная на ширину w :

Справка по математике.ком

«Прямоугольник» в приведенной выше формуле является нижним индексом, указывающим, что найденная площадь » A » является площадью прямоугольника. Поскольку я буду обсуждать формулы площади, объема и т. д. для различных фигур, я использую нижние индексы, чтобы прояснить форму, к которой относится конкретная формула (используя « A » для «площади», « SA «для «площади», « P » для «периметра» и « V » для «объема»).Подписка такого рода может быть полезной техникой для ясности вашего смысла, поэтому постарайтесь держать это в уме для возможного использования в будущем.

Если вы посмотрите на изображение прямоугольника и вспомните, что «периметр» означает «длина по внешней стороне», вы увидите, что периметр прямоугольника P представляет собой сумму длин верхней и нижней части l и ширина слева и справа w :

Квадраты еще проще, потому что их длина и ширина одинаковы.Площадь A и периметр P квадрата со стороной s определяются как:

Вы должны знать формулу площади треугольника; его легко запомнить, и он имеет тенденцию неожиданно всплывать посреди текстовых задач. Учитывая размеры основания b и высоты h треугольника, площадь A треугольника равна:

Конечно, периметр P треугольника будет просто суммой длин трех сторон треугольника.

---

Вы должны знать формулы длины окружности C и площади A круга, учитывая радиус r :

(«π» — это число, приближенное к 3,14159 или дроби 22/7)

Помните, что радиус окружности — это расстояние от центра до внешней стороны окружности. Другими словами, радиус находится только на полпути. Если они дают вам длину диаметра, представляющую собой длину линии, проходящей через середину круга, то вам сначала придется разделить это значение пополам, чтобы применить приведенные выше формулы.

---

Все вышеперечисленное является «плоскими», двумерными формами. Иногда вам придется иметь дело с трехмерными фигурами, такими как кубы или конусы. Для таких форм вы найдете площадь поверхности (если вы рисовали объект, это площадь, которую вам нужно было бы покрыть) и объем (внутреннее пространство, которое вы могли бы заполнить, если бы форма пустой).

Формула для объема V куба проста, так как длина, ширина и высота имеют одно и то же значение s :

Формула для площади поверхности (площадь, которую вы измерили бы, если бы вам нужно было покрасить куб снаружи) также довольно проста, поскольку все стороны имеют одинаковую квадратную площадь s ² .Есть шесть сторон (верхняя, нижняя, левая, правая, передняя и задняя), поэтому площадь поверхности SA составляет:

Формулы немного усложняются для «прямоугольной призмы», которая является техническим термином для кирпича. Объем V по-прежнему довольно прост: длина умножается на ширину, умноженную на высоту:

.

Формула площади поверхности немного более витиеватая. (Постарайтесь следовать рассуждениям, которые я собираюсь использовать, потому что вы, вероятно, забудете формулу, но ее легко воссоздать, если вы просто потратите немного времени и подумаете об этом.) Верх и низ «кирпича» имеют одинаковую площадь, т. е. длину, умноженную на ширину. Левая и правая стороны кирпича имеют одинаковую площадь, т. е. ширину, умноженную на высоту. И передняя, ​​и задняя часть кирпича имеют одинаковую площадь, т. е. длину, умноженную на высоту. (Нарисуйте рисунок, обозначив размеры, если вы в этом не уверены.) Тогда формула для площади поверхности SA кирпича:

Цилиндры

(похожие на трубки, но с заглушками на концах) тоже попадаются изредка.Объем V цилиндра легко определить: это площадь конца (которая является просто площадью круга), умноженная на высоту h :

Площадь поверхности SA — это площадь концов (которые представляют собой просто круги) плюс площадь стороны, которая равна длине окружности круга, умноженной на высоту h цилиндра:

В зависимости от класса, который вы изучаете, вам также может понадобиться знать формулу объема V конуса с радиусом основания r и высотой h :

. ..или объем V сферы (шара) с радиусом r :

Вы можете заметить, что другие формулы появляются в вашей домашней работе или упражнениях в классе. Возможно, вам придется запомнить эти другие формулы (их много!), поэтому обязательно проконсультируйтесь со своим инструктором перед тестом, чтобы узнать, какие из них вы должны знать.

Некоторые преподаватели предоставляют все геометрические формулы, поэтому в вашем тесте будет список всего, что вам может понадобиться.Но не все инструкторы такие, и вы не можете ожидать, что каждый инструктор, каждый отдел или «общие», общеотдельные или иным образом стандартизированные тесты дадут вам всю эту информацию. Спросите своих преподавателей об их правилах, но помните, что наступает момент (средняя школа? SAT? ACT? колледж? «реальная жизнь»?), когда вы должны выучить хотя бы некоторые из этих основных формул. Начните запоминать прямо сейчас!

---

URL-адрес: https://www. Purplemath.com/modules/geoform.htm

Как решать геометрические задачи с участием прямоугольников и треугольников

 

o Точка

o Строка

o Отрезок линии

или Рэй

o Угол

o Прямоугольник

o Периметр

o Район

o Квадрат

o Треугольник

 

Объективы

 

o Познакомиться с некоторыми основными геометрическими фигурами

o Вычислить периметр и площадь прямоугольника

o Вывести формулу площади треугольника

 

Геометрия изучает точки, линии, фигуры, углы и отношения между ними.Мы рассмотрим некоторые простые формы, такие как треугольники и прямоугольники, и обсудим, как вычислить некоторые их свойства.

 

Элементы геометрии

 

Прежде чем рассматривать некоторые более сложные фигуры, мы должны иметь представление о некоторых терминах, которые используются при изучении геометрии. Несколько основных геометрических понятий включают точки, линии и углы. Точка , по сути, является местоположением — ее часто представляют с помощью маленькой точки, и она представляет собой местоположение в пространстве и не имеет ни длины, ни ширины, ни глубины.Несколько точек показаны ниже.

 

 

 

Линия в геометрии имеет почти те же характеристики, что и в реальной жизни (и в алгебре). Геометрическая линия прямая и бесконечно простирается в противоположных направлениях. Если две прямые пересекаются в одной точке, то говорят, что они пересекаются на 90 475. Пример строки показан ниже; обратите внимание, что на концах линии есть стрелки, указывающие на то, что линия продолжается бесконечно.

 

Конечный участок линии называется отрезком линии . Отрезки линий имеют длины, которые являются конечными (ограниченными) числами, в отличие от линий, длина которых бесконечна (неограничена). Отрезок линии показан ниже; концы отрезка показаны точками.

 

Луч — это часть линии только с одной конечной точкой, как показано ниже. Его длина по-прежнему бесконечна, но у него есть один опознаваемый конец.

 

 

Когда пересекаются две прямые, отрезки, лучи или их комбинации, они образуют угол . Пример угла показан ниже.

 

 

Углы можно измерять в градусах (°) в диапазоне от 0° до 360°. Некоторые примеры угловых измерений показаны ниже.

 

 

Используя эти основные геометрические термины и фигуры, мы можем теперь перейти к изучению некоторых более сложных фигур.

 

Прямоугольники

 

Прямоугольник — это особый вид замкнутой геометрической фигуры с четырьмя сторонами; пример прямоугольника показан ниже.

 

 

Прямоугольники можно описать двумя их размерами: длиной (которую мы можем обозначить как l ) и шириной (которую мы можем обозначить как w ). Противоположные стороны прямоугольника равны по длине, а все «внутренние» углы равны 90°; таким образом, мы можем нарисовать прямоугольник, как показано ниже.

 

 

Одной из характеристик прямоугольников, которую мы можем легко вычислить, является его периметр, который представляет собой сумму длин всех сторон. Периметр P следующий:

 

P = л + ш + л + ш

 

Мы можем упростить это выражение, превратив сложение одинаковых членов в умножение:

 

P = л + л + ш + ш

P =2 л + 2 ш

 

Например, рассмотрите прямоугольник ниже.

 

 

Поскольку противоположные стороны равны по длине, у прямоугольника есть две стороны длиной 6 единиц и две стороны длиной 3 единицы. Таким образом, периметр следующий:

 

 

Периметр 18 единиц. (Обратите внимание, что «единицей» могут быть дюймы, футы, метры или любой другой тип измерения длины. Если единица измерения указана, используйте эту конкретную единицу; в противном случае достаточно общего термина «единицы».)

 

Практическая задача : Вычислите периметр прямоугольника ниже. Все измерения указаны в футах.

 

 

Решение : Напомним, что противоположные стороны прямоугольника равны по длине. Таким образом, этот прямоугольник имеет две стороны длиной 10 футов и две стороны длиной 2 фута. Тогда периметр P будет следующим:

 

 

В качестве альтернативы мы могли бы просто использовать формулу, полученную выше.

 

 

 

Практическая задача : Некоторый прямоугольник имеет периметр 50 метров и длину 14 метров. Какова его ширина?

 

Решение : Мы можем решить эту задачу, внимательно изучив представленную информацию и применив наши знания о решении уравнений. Прежде всего мы знаем, что периметр P прямоугольника подчиняется следующей формуле, где l — длина, а w — ширина.

 

Постановка задачи говорит нам, каков периметр ( P ), а также какова длина ( l ). Давайте введем эти значения в приведенное выше уравнение, а затем максимально упростим результат.

 

 

Чтобы найти ширину прямоугольника, нам нужно только найти w , используя тот же подход, который мы использовали при решении линейных уравнений.

 

 

Таким образом, ширина прямоугольника равна 11 метрам. Давайте проверим этот результат, чтобы убедиться, что он работает. Из условия задачи мы знаем, что длина прямоугольника равна 14 метрам.

 

 

Итак, ответ проверен.

 

 

Мы также можем вычислить площадь прямоугольника, которая является мерой того, сколько места он занимает. Рассмотрим прямоугольник шириной 4 единицы и длиной 2 единицы.

 

 

Давайте разделим каждую сторону на сегменты длиной 1, как показано ниже.

 

 

Теперь, используя эти деления, мы нарисуем сетку, которая разделит прямоугольник.

 

 

Обратите внимание, что сетка разделена на более мелкие области, каждая сторона которых имеет длину 1 единицу.

 

Каждая из этих меньших областей представляет собой квадрат (прямоугольник, длина и ширина которого равны) со стороной, равной 1. Мы определяем одну из этих областей как 1 квадратную единицу — квадрат, размеры которого (длина и ширина) равны 1 единице. Теперь обратите внимание, что прямоугольник имеет в общей сложности 8 квадратных единиц, которые разделены на два ряда по четыре или четыре ряда по два (в зависимости от того, как вы смотрите на диаграмму). Но вычислить количество объектов (в данном случае квадратных единиц) в строках и столбцах можно путем умножения: обратите внимание, что количество квадратных единиц в прямоугольнике — это просто произведение длины и ширины. Таким образом, площадь A прямоугольника с длиной l и шириной w равна произведению l и w:

 

 

Эта формула применима к любому прямоугольнику, независимо от длины его сторон.(То есть длины могут быть целыми положительными, дробными, десятичными, рациональными или иррациональными числами.)

 

Допустим, у нас есть прямоугольник длиной 5 дюймов и шириной 3 дюйма, как показано ниже.

 

Наша цель состоит в том, чтобы вычислить, сколько квадратов со стороной в 1 дюйм может поместиться в этот прямоугольник. Результатом будет общая площадь прямоугольника. Располагая квадраты краем к краю, мы можем разместить пять из них поперек прямоугольника и три по прямоугольнику.

 

 

Из диаграммы видно, что в прямоугольник можно поместить 15 квадратов со стороной один квадратный дюйм — таким образом, площадь прямоугольника составляет 15 квадратных дюймов. Разумеется, на это указывает и формула:

.

 

 

 

Практическая задача : Вычислите площадь прямоугольника шириной 32 дюйма и длиной в дюйм.

 

Решение : Формула площади прямоугольника применяется независимо от используемых чисел (конечно, если они положительные). Таким образом, давайте просто воспользуемся формулой площади А:

 

 

 

Треугольники

 

Мы также можем рассмотреть некоторые характеристики другой распространенной геометрической фигуры: треугольника.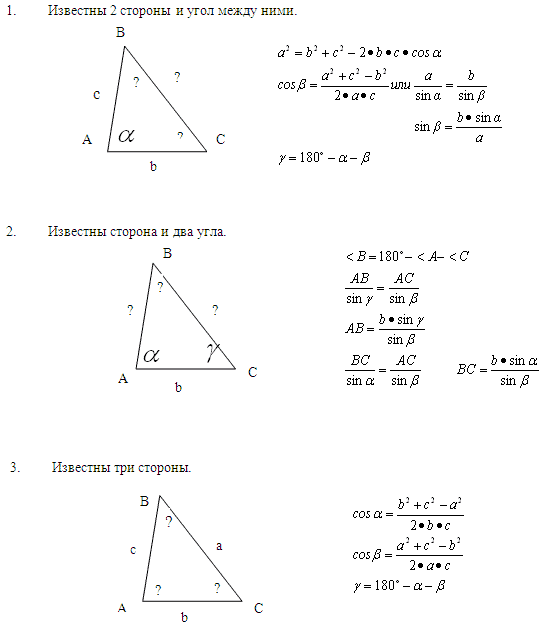 Треугольник — замкнутая геометрическая фигура с тремя сторонами; примеры треугольников показаны ниже.

 

 

Периметр треугольника вычисляется примерно так же, как и периметр прямоугольника: просто сложить длины сторон треугольника (в этом случае у фигуры всего три стороны, и все эти стороны могут быть разной длины ). Однако рассчитать площадь несколько сложнее. Для прямоугольников мы смогли увидеть площадь просто как ряды и столбцы квадратов. Из-за формы треугольника мы не можем аккуратно вписать в него квадраты.

 

 

Мы должны применить несколько иной подход к нахождению площади треугольника. Давайте рассмотрим общий треугольник, показанный ниже; этот треугольник не имеет особых свойств.

 

 

Теперь давайте определим два характерных размера этого (или любого) треугольника: длину основания (которую мы назовем b ) и высоту (которую мы назовем h ). Основание — это просто длина стороны «на земле» или внизу фигуры. Тогда высота является максимальным расстоянием, на которое треугольник достигает «над землей».

 

 

Площадь треугольника равна A. Если бы у нас было два таких треугольника абсолютно одинаковой формы, общая площадь двух треугольников была бы равна 2 A. Давайте воспользуемся этим фактом, чтобы попытаться построить более знакомую фигуру. .

 

 

Сначала разрежем один из треугольников по высоте.

 

 

Обратите внимание, что оба разделенных треугольника имеют высоты х (как мы определили для исходного треугольника), а их основания равны х и у, , где х + у равно б. Мы не знаем, что такое x и y , но поскольку мы разрезали треугольник, мы знаем, что эти два основания должны в сумме давать основание исходного треугольника. Теперь давайте попробуем переставить части так, чтобы получился прямоугольник!

 

Давайте теперь рассмотрим характеристики этой новой фигуры (помните, что она имеет площадь 2 A, , где A площадь исходного треугольника).

 

 

Фигура представляет собой прямоугольник — обратите внимание, что противоположные стороны равны по длине (помните, что x + y = b ). Но мы знаем, как вычислить площадь прямоугольника: это просто произведение длины и ширины (в данном случае b и h ). Однако эта общая площадь равна 90 328, удвоенной по 90 329 площади исходного треугольника. Таким образом, произведение b и h равно 2 А.

 

 

Изучая линейные уравнения, мы узнали, как решать для определенной переменной. В этом случае мы можем выделить A , умножив обе части выражения на .

 

 

Итак, мы вывели формулу площади треугольника. Этот вывод, хотя и не показан в полной математической строгости, дает правильную формулу площади для всех треугольников, а не только для показанного выше.Процесс вычисления высоты треугольника 90 328 и 90 329 может быть несколько сложным, но если вы знаете основание и высоту, то теперь вы можете вычислить площадь треугольника.

 

 

Практическая задача : Вычислите площадь приведенного ниже треугольника.

Решение : Если мы повернем треугольник так, чтобы 10-футовая сторона оказалась внизу, мы увидим, что отрезок пунктирной линии представляет собой высоту треугольника.

 

 

Затем мы можем вычислить площадь треугольника, используя формулу, которую мы вывели на уроке.

 

 

Калькулятор треугольной призмы

Треугольная форма призмы

а = длина стороны а
b = длина стороны b = основание нижнего треугольника b
c = длина стороны c
h = высота призмы
H = высота нижнего треугольника
В = объем
A _to = общая площадь поверхности = все стороны
A _lat = площадь боковой поверхности = все прямоугольные стороны
A _{верхняя часть} = площадь верхней поверхности = верхний треугольник
A _бот = площадь нижней поверхности = нижний треугольник

Треугольная призма представляет собой твердое геометрическое тело с треугольником в основании. Это трехсторонняя призма, в которой основание и вершина представляют собой равные треугольники, а остальные 3 стороны — прямоугольники.

Использование калькулятора

Этот калькулятор находит объем, площадь поверхности и высоту треугольной призмы. Расчеты площади поверхности включают верхнюю, нижнюю, боковые стороны и общую площадь поверхности. Высота вычисляется по известному объему или площади боковой поверхности.

Единицы: Единицы показаны для удобства, но не влияют на расчеты.Ответы будут одинаковыми в футах, футах ² , футах ³ или метрах, м ² , м ³ или любых других единицах измерения.

Значащие цифры: Выберите количество значащих цифр или оставьте значение авто, чтобы калькулятор определял точность чисел.

Треугольная призма Формулы для высоты и длин сторон треугольника a, b и c:

Объем треугольной призмы Формула

Находит трехмерное пространство, занимаемое треугольной призмой.

\[ V = \dfrac{1}{4}h \sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)} \]

\[ V = \dfrac{1}{4}h \sqrt{(c+ab)(a+bc)} \\\times \sqrt{(a+b+c)(b+ca)} \]

Площадь верхней поверхности треугольной призмы Формула

Находит площадь треугольной поверхности в верхней части призмы. Это та же площадь, что и площадь нижней поверхности.

\[ A_{top} = \dfrac{1}{4} \sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)} \]

\[ A_{top} = \dfrac{1}{4} \sqrt{\begin{align}(a+&b+c)(b+ca)\\&\times(c+ab)(a+bc )\конец{выровнено}} \]

Площадь нижней поверхности треугольной призмы Формула

Находит площадь треугольной поверхности в нижней части призмы.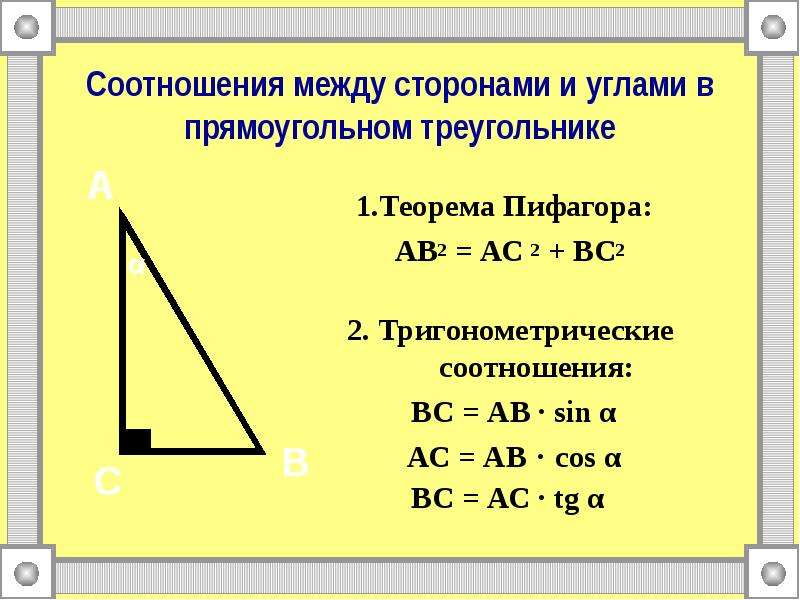 Это та же площадь, что и площадь верхней поверхности.

\[ A_{bot} = \dfrac{1}{4} \sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)} \]

\[ A_{bot} = \dfrac{1}{4} \sqrt{\begin{align}(a+&b+c)(b+ca)\\&\times(c+ab)(a+bc )\конец{выровнено}} \]

Площадь боковой поверхности треугольной призмы Формула

Находит общую площадь трех прямоугольных сторон призмы. Площадь боковой поверхности можно представить как общую площадь поверхности призмы за вычетом двух треугольных площадей вверху и внизу призмы.

\[ A_{широта} = h (a+b+c) \]

Общая площадь поверхности треугольной призмы Формула

Находит общую площадь всех сторон треугольной призмы. Общая площадь поверхности призмы включает площадь верхней и нижней треугольных сторон призмы, а также площадь всех трех прямоугольных сторон.

\[ A_{tot} = A_{top} + A_{bot} + A_{lat} \]

Формула высоты треугольной призмы в единицах объема

Находит высоту треугольной призмы, решая Формулу объема для высоты. Высота h рассчитывается исходя из объема V и длин сторон a, b и c.

\[ h = \dfrac{4V}{\sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)}} \]

\[ h = 4V \div \left[ \, \sqrt{(c+ab)(a+bc)} \\\times \sqrt{(a+b+c)(b+ca)} \, \ справа] \]

Высота треугольной призмы Формула через площадь боковой поверхности

Находит высоту треугольной призмы, решая формулу площади боковой поверхности для высоты.Высота h рассчитывается по площади боковой поверхности A _lat и длинам сторон a, b и c.

\[ч = \dfrac{A_{широта}}{(a+b+c)} \]

Артикул

Вайсштейн, Эрик В. «Зона треугольника». Из MathWorld — веб-ресурса Wolfram, Площадь треугольника.

Какова формула площади поверхности прямоугольной пирамиды?

Площадь поверхности будет равна сумме прямоугольного основания и #4# треугольников, в которых есть #2# пар конгруэнтных треугольников.

Площадь прямоугольного основания

Основание просто имеет площадь #lw#, так как это прямоугольник.

#=>лв#

Площадь переднего и заднего треугольников

Площадь треугольника находится по формуле #A=1/2(«основание»)(«высота»)#.

Здесь основание равно #l#. Чтобы найти высоту треугольника, мы должны найти наклонную высоту на этой стороне треугольника.

Наклонную высоту можно найти, найдя гипотенузу прямоугольного треугольника внутри пирамиды.2)#

Это не та формула, которую вы должны пытаться запомнить. Скорее, это упражнение на правильное понимание геометрии треугольной призмы (а также немного алгебры).

Искусство решения задач

В математике площадь относится к размеру области, которую занимает двумерная фигура. Размер области в более высоких измерениях называется объемом.

Часто можно элементарными средствами найти площадь области, ограниченной частями окружностей и отрезками. Можно найти площадь еще более сложных областей с помощью исчисления.

Прямоугольники — самые основные фигуры, площадь которых мы можем изучать. Имеет смысл, что площадь прямоугольника с длиной и шириной просто равна .

Зная площадь прямоугольника, мы можем легко найти площадь треугольника, просто заметив, что если наш треугольник имеет основание и высоту , то площадь прямоугольника с длиной и шириной ровно в два раза больше площади исходного треугольника. Таким образом, площадь треугольника равна

Теперь мы можем найти площадь любого многоугольника, разбив его на треугольники.

Ознакомительные видео

https://youtu.be/51K3uCzntWs?t=842\

Обозначение

Буквы и часто используются для обозначения площади. Когда рассматривается несколько регионов, часто используются нижние индексы: могут использоваться для обозначения областей определенных регионов или . Например, будет означать площадь шестиугольника.

Альтернативным обозначением является использование квадратных скобок вокруг названия региона для обозначения его площади, т.е.г. для площади треугольника.

Площадь правильных многоугольников

Площадь любого правильного многоугольника можно найти следующим образом:

Впишите фигуру со сторонами длиной , в круг и проведите линию из двух соседних вершин в центр описанной окружности. Это создает треугольник общей площади (в качестве примера рассмотрим правильный восьмиугольник ниже).

Рисование апофемы создает два прямоугольных треугольника, каждый с углом в верхней вершине. Если у многоугольника есть длина стороны, высота треугольника может быть найдена с помощью тригонометрии, чтобы быть длиной.

Площадь каждого треугольника равна произведению основания на высоту, что также может быть выражено как и площадь всего многоугольника равна .

Площадь треугольника

Есть много способов найти площадь треугольника. Во всех этих формулах будет использоваться для обозначения площади.

Площадь четырехугольника

Чтобы найти площадь большинства четырехугольников, вы должны разделить четырехугольник на меньшие треугольники и найти площадь каждого треугольника. Однако для некоторых четырехугольников есть специальные формулы для нахождения их площадей.Опять же, это площадь.

• Воздушный змей — где s представляют длины диагоналей воздушного змея.

• Параллелограмм — , где основание и высота до этого основания.

• Трапеция — , где s параллельные стороны и расстояние между этими основаниями.

• Ромб — частный случай воздушного змея и параллелограмма, поэтому здесь можно использовать любую формулу.

• Прямоугольник — , где длина прямоугольника, а ширина.(Это частный случай формулы параллелограмма, где высота и сторона совпадают.)

• Квадрат — , где — длина стороны.

См. также

Теорема Пика

Теорема о шнурках

.