Прямоугольный треугольник — Википедия

Прямоугольный треугольник

Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то есть 90 градусов).

Соотношения между сторонами и углами прямоугольного треугольника лежат в основе тригонометрии.

• Сторона, противоположная прямому углу, называется гипотенузой (сторона c на рисунке выше).
• Стороны, прилегающие к прямому углу, называются катетами. Сторона a может быть идентифицирована как прилежащая к углу В и противолежащая углу A, а сторона b — как прилежащая к углу A и противолежащая углу В.

• Если длины всех трёх сторон прямоугольного треугольника являются натуральными числами, то треугольник называется пифагоровым треугольником, а длины его сторон образуют так называемую пифагорову тройку.

Признаки равенства прямоугольных треугольников[править | править код]

• По двум катетам: если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.

  Этот признак немедленно следует из первого признака равенства треугольников, так как у двух треугольников будут равны по два катета и прямой угол.

• По катету и прилежащему острому углу: если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны

  Этот признак немедленно следует из второго признака равенства треугольников, так как у двух треугольников будут равен один катет, прилежащий к нему угол и прямой угол.

• По гипотенузе и острому углу: если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.

  Этот признак следует из второго признака равенства треугольников, так как вторые острые углы будут равны по теореме о сумме углов треугольника и у треугольников будут равны гипотенузы и два прилежащих к ней угла.

• По гипотенузе и катету: если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

  Этот признак докажем так. Наложим два треугольника друг на друга так, чтобы получить равнобедренный треугольник, то есть совместим их равными катетами так, чтобы углы, лежащие при этих катетах, лежали в разных плоскостях. Так как гипотенузы равны, получившийся треугольник — равнобедренный, тогда углы при основании равны. Тогда два прямоугольных треугольника будут равны по гипотенузе и острому углу.

• По катету и противолежащему острому углу: если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.

  Этот признак доказывается так: если один из острых углов первого треугольника равен острому углу второго треугольника, то второй острый угол будет известен по теореме о сумме углов треугольника. Так как второй острый угол прилегает к катету, то далее равенство треугольников будет доказываться по предыдущей теореме.

Далее предполагаем, что a{\displaystyle a} и b{\displaystyle b} длины катетов, а c{\displaystyle c} длина гипотенузы

• Площадь прямоугольного треугольника равна половине произведения двух его катетов. То есть,

  S=12ab.{\displaystyle S={\tfrac {1}{2}}ab.}

• Для медиан ma{\displaystyle m_{a}}, mb{\displaystyle m_{b}} и mc{\displaystyle m_{c}} выполняется следующее соотношение:

  ma2+mb2=5mc2=54c2.{\displaystyle m_{a}^{2}+m_{b}^{2}=5m_{c}^{2}={\frac {5}{4}}c^{2}.}

  • В частности, медиана, падающая на гипотенузу, равна половине гипотенузы.

Высота[править | править код]

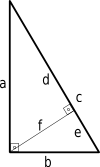Высота прямоугольного треугольника.

Если высота проведена к гипотенузе, то треугольник делится на два меньших треугольника, подобных исходному и подобных друг другу. Из этого следует, что в обозначениях, показанных на диаграмме:^[1]

f2=de,{\displaystyle \displaystyle f^{2}=de,} (иногда это называют теоремой высоты прямоугольного треугольника)

b2=ce,{\displaystyle \displaystyle b^{2}=ce,}

a2=cd{\displaystyle \displaystyle a^{2}=cd}

• В прямоугольном треугольнике высота, опущенная из вершины прямого угла на гипотенузу, делит гипотенузу в таком отношении, в каком находятся квадраты прилежащих катетов, то есть

d:e=a2:b2,{\displaystyle \displaystyle d:e=a^{2}:b^{2},}

Кроме того высота, опущенная на гипотенузу, связана с катетами прямоугольного треугольника соотношением:^[2][3]

1a2+1b2=1f2.{\displaystyle {\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}={\frac {1}{f^{2}}}.}

и

f=abc.{\displaystyle f={\frac {ab}{c}}.}

Также если прямоугольный треугольник является равнобедренным, то высота, опущенная на гипотенузу будет равна:

f=rδS =r(1+2){\displaystyle f=r\delta _{S}\ =r(1+{\sqrt {2}})}, где r{\displaystyle r} — это радиус вписанной окружности, а δS{\displaystyle \delta _{S}} — серебряное сечение.

Характеристики[править | править код]

Треугольник ABC со сторонами a, b, c (где c — самая длинная сторона), с описанной окружностью радиуса R является прямоугольным треугольником тогда и только тогда, когда верно любое из следующих соотношений:^[4]

Тригонометрические соотношения[править | править код]

Тригонометрические функции для острых углов можно определить как отношения сторон прямоугольного треугольника. Для любого данного угла можно построить прямоугольный треугольник, содержащий такой угол, и со сторонами: противолежащим катетом, прилежащим катетом и гипотенузой, связанными с этим углом определёнными выше соотношениями. Эти отношения сторон не зависят от конкретного выбранного прямоугольного треугольника, а зависят только от заданного угла, так как все треугольники, построенные таким образом, являются подобными. Если для заданного угла α, противолежащий катет, прилежащий катет и гипотенузу обозначить a, b и c соответственно, то тригонометрические функции имеют вид:

sin⁡α=ac,cos⁡α=bc,tg⁡α=ab,ctg⁡α=ba,sec⁡α=cb,csc⁡α=ca.{\displaystyle \sin \alpha ={\frac {a}{c}},\,\cos \alpha ={\frac {b}{c}},\,\operatorname {tg} \alpha ={\frac {a}{b}},\,\operatorname {ctg} \alpha ={\frac {b}{a}},\sec \alpha ={\frac {c}{b}},\,\,\csc \alpha ={\frac {c}{a}}.}

И таким образом:

• Катет, противолежащий углу, равен произведению гипотенузы на синус этого угла

a=c⋅sin⁡α,b=c⋅sin⁡β.{\displaystyle a=c\cdot \sin \alpha ,\,b=c\cdot \sin \beta .}

• Катет, прилежащий углу, равен произведению гипотенузы на косинус этого угла

a=c⋅cos⁡β,b=c⋅cos⁡α.{\displaystyle a=c\cdot \cos \beta ,\,b=c\cdot \cos \alpha .}

• Катет, противолежащий углу, равен произведению второго катета на тангенс угла

a=b⋅tg⁡α,b=a⋅tg⁡β.{\displaystyle a=b\cdot \operatorname {tg} \alpha ,\,b=a\cdot \operatorname {tg} \beta .}

• Катет, прилежащий углу, равен произведению второго катета на котангенс угла

a=b⋅ctg⁡β,b=a⋅ctg⁡α.{\displaystyle a=b\cdot \operatorname {ctg} \beta ,\,b=a\cdot \operatorname {ctg} \alpha .}

• Гипотенуза равна отношению катета к синусу противолежащего угла, и/или частному отношению катета и косинуса прилежащего угла (угла между ними)

c=asin⁡α=bsin⁡β=acos⁡β=bcos⁡α.{\displaystyle c={\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {a}{\cos \beta }}={\frac {b}{\cos \alpha }}.}

Специальные прямоугольные треугольники[править | править код]

Значения тригонометрических функций можно точно оценить для определённых углов, используя прямоугольные треугольники с особыми значениями углов. К таким треугольникам относятся треугольник 30-60-90, который можно использовать для оценки тригонометрических функций для любых значений, кратных π/6, и треугольник 45-45-90 (равнобедренный прямоугольный), который можно использовать для оценки тригонометрических функций для значений, кратных π/4. В частности,

• Катет, лежащий против острого угла в 30° (и соответственно, прилежащий к углу в 60°), равен половине гипотенузы.

Теорема Фалеса[править | править код]

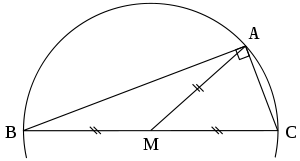Медиана прямого угла треугольника

Теорема Фалеса утверждает, что если какая-нибудь точка A лежит на окружности диаметра BC (за исключением самих точек B и C), то △ABC представляет собой прямоугольный треугольник с прямым углом

A. Обратное утверждение таково: если прямоугольный треугольник вписан в окружность, то гипотенуза будет её диаметром. Следствием является то, что длина гипотенузы равна удвоенному расстоянию от вершины прямого угла до середины гипотенузы. Верно также, что центр окружности, описывающей прямоугольный треугольник, является серединой гипотенузы, а её радиус равен половине длины гипотенузы.

Другие свойства[править | править код]

Радиус вписанной окружности в прямоугольный треугольник с катетами a и b и гипотенузой c равен:

r=a+b−c2=aba+b+c.{\displaystyle r={\frac {a+b-c}{2}}={\frac {ab}{a+b+c}}.}

Если отрезки длиной p и q, исходящие из вершины C, делят гипотенузу на три равных отрезка длины c/3, то:^{[5]:pp. 216-217}

p2+q2=5(c3)2.{\displaystyle p^{2}+q^{2}=5\left({\frac {c}{3}}\right)^{2}.}

Прямоугольный треугольник является единственным треугольником с двумя, а не тремя, отличными друг от друга вписанными квадратами.^[6]

Пусть h и s (h>s) сторонами двух квадратов, вписанных в прямоугольный треугольник с гипотенузой c. Тогда:

1c2+1h3=1s2.{\displaystyle {\frac {1}{c^{2}}}+{\frac {1}{h^{2}}}={\frac {1}{s^{2}}}.}

Периметр прямоугольного треугольника равен сумме двух радиусов вписанной и четырех описанных окружностей:

P=2r+4R{\displaystyle P=2r+4R}

Если заданы S и r, то стороны треугольника находятся по формулам:

a=12(r+Sr−r2−6S+S2r2){\displaystyle a={\frac {1}{2}}\left(r+{\frac {S}{r}}-{\sqrt {r^{2}-6S+{\frac {S^{2}}{r^{2}}}}}\right)}

b=12(r+Sr+r2−6S+S2r2){\displaystyle b={\frac {1}{2}}\left(r+{\frac {S}{r}}+{\sqrt {r^{2}-6S+{\frac {S^{2}}{r^{2}}}}}\right)}

c=Sr−r{\displaystyle c={\frac {S}{r}}-r}

Во всех прямоугольных треугольниках медиана, опущенная на гипотенузу, равна половине гипотенузы.

1. ↑ Wentworth p. 156
2. ↑ Voles, Roger, «Integer solutions of a−2+b−2=d−2{\displaystyle a^{-2}+b^{-2}=d^{-2}},» Mathematical Gazette 83, July 1999, 269—271.
3. ↑ Richinick, Jennifer, «The upside-down Pythagorean Theorem, » Mathematical Gazette 92, July 2008, 313—317.
4. ↑ Andreescu, Titu and Andrica, Dorian, «Complex Numbers from A to…Z», Birkhäuser, 2006, pp. 109—110.
5. ↑ Posamentier, Alfred S., and Salkind, Charles T. Challenging Problems in Geometry, Dover, 1996.
6. ↑ Bailey, Herbert, and DeTemple, Duane, «Squares inscribed in angles and triangles», Mathematics Magazine 71(4), 1998, 278—284.

Треугольник | Формулы и расчеты онлайн

Треугольник — многоугольник с тремя сторонами. Стороны треугольника часто обозначаются малыми буквами, соответствующими обозначению противоположных вершин.

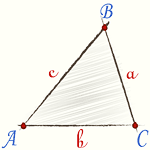Остроугольный треугольник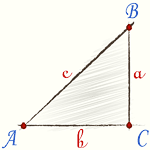

Прямоугольный треугольник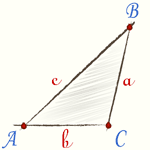

Тупоугольный треугольник

Если все три угла острые, то треугольник — остроугольный.

Если один из углов прямой, то треугольник — прямоугольный.

Стороны, образующие прямой угол, называются катетами. Сторона против прямого угла — гипотенузой.

Если один из углов тупой — то треугольник тупоугольный.

Равнобедренный треугольник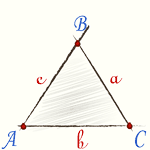

Равносторонний треугольник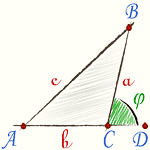

Внешний угол треугольника

Треугольник равнобедренный, когда две его стороны равны.

Треугольник равносторонний или правильный, когда все три его стороны равны.

Равные стороны равнобедренного треугольника называются боковыми. Третья сторона — основанием.

Во всяком треугольнике против большей стороны лежит больший угол. Против равных сторон — равные углы, Равносторонний треугольник вместе с тем равноугольный.

Сумма углов в треугольнике

Во всяком треугольнике сумма углов равна 180°.
В равностороннем треугольнике каждый угол равен 60°.

\[ A + B + C = 180° \]

Продолжив одну из сторон треугольника, получим внешний угол ∠BCD Внешний угол равен сумме внутренних, с ним не смежных углов.

\[ ∠BCD = ∠DAB + ∠ABC \]

В помощь студенту

Треугольник	стр. 230

Прямоугольный треугольник. Подробная теория с примерами.

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

В задачах прямой угол вовсе не обязательно – левый нижний, так что тебе нужно научиться узнавать прямоугольный треугольник и в таком виде,

и в таком

Что же хорошего есть в прямоугольном треугольнике? Ну…, во-первых, есть специальные красивые названия для его сторон.

Стороны, между которыми прямой угол, называются катеты, а третья сторона (самая длинная) называется гипотенуза. Внимание на рисунок!

Запомни и не путай: катетов – два, а гипотенуза – всего одна (единственная, неповторимая и самая длинная)!

Ну вот, названия обсудили, теперь самое важное: Теорема Пифагора.

Эта теорема – ключик к решению многих задачек с участием прямоугольного треугольника. Её доказал Пифагор в совершенно незапамятные времена, и с тех пор она принесла много пользы знающим её. А самое хорошее в ней то, что она – простая.

Помнишь шутку: «Пифагоровы штаны на все стороны равны!»?

Давай нарисуем эти самые пифагоровы штаны и посмотрим на них.

Правда, похоже на какие – то шорты? Ну и на какие стороны и где она равны? Почему и откуда возникла шутка? А шутка эта связана как раз с теоремой Пифагора, точнее с тем, как сам Пифагор формулировал свою теорему. А формулировал он её так:

«Сумма площадей квадратов, построенных на катетах, равна площади квадрата, построенного на гипотенузе».

Правда, немножко по-другому звучит? И вот, когда Пифагор нарисовал утверждение своей теоремы, как раз и получилась такая картинка.

На этой картинке сумма площадей маленьких квадратов равна площади большого квадрата. А чтобы дети лучше запоминали, что сумма квадратов катетов равна квадрату гипотенузы, кто-то остроумный и выдумал эту шутку про Пифагоровы штаны.

Почему же мы сейчас формулируем теорему Пифагора

Понимаешь, в древние времена не было… алгебры! Не было никаких обозначений   и так далее. Не было надписей  . Представляешь, как бедным древним ученикам было ужасно запоминать всё словами??! А мы можем радоваться, что у нас есть простая формулировка теоремы Пифагора. Давай её ещё раз повторим, чтобы лучше запомнить:

Ну вот, самую главную теорему о прямоугольном треугольнике обсудили. Если тебе интересно, как она доказывается, читай следующие уровни теории, а сейчас пойдём дальше… в тёмный лес… тригонометрии! К ужасным словам синус, косинус, тангенс и котангенс.

 

На самом деле все совсем не так страшно. Конечно, «настоящее» определение синуса, косинуса, тангенса и котангенса нужно смотреть в статье «Синус, косинус…». Но очень не хочется, правда? Можем обрадовать: для решения задач про прямоугольный треугольник можно просто заполнить следующие простые вещи:

А почему же всё только про угол  ? Где же угол  ? Для того, чтобы в этом разобраться, нужно знать, как утверждения 1 — 4 записываются словами. Смотри, понимай и запоминай!

1.  
Вообще-то звучит это так:

Синус острого угла в прямоугольном треугольнике равен отношению противоположного катета к гипотенузе.

А что же угол  ? Есть ли катет, который находится напротив угла  , то есть противолежащий (для угла  ) катет? Конечно, есть! Это катет  !

Значит,

2.  

Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе.

А как же угол  ? Посмотри внимательно. Какой катет прилегает к углу  ? Конечно же, катет  . Значит, для угла   катет   – прилежащий, и

 .

А теперь, внимание! Посмотри, что у нас получилось:

 

Видишь, как здорово:

Это очень удобно – если тебе дан в задаче синус одного угла прямоугольного треугольника, то ты знаешь и косинус другого! Итак, запомни очень твёрдо:

В прямоугольном треугольнике синус одного острого угла равен косинусу другого и наоборот.

Теперь перейдём к тангенсу и котангенсу.

3.  

Как это теперь записать словами? Катет   каким является по отношению к углу  ? Противолежащим, конечно – он «лежит» напротив угла  . А катет  ? Прилегает к углу  . Значит, что у нас получилось?

Тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему.

4.  

Видишь, числитель и знаменатель поменялись местами?

Котангенс острого угла в прямоугольном треугольнике равен отношению прилежащего катета к противолежащему.

Вспомним теперь про угол  . Что будет для него? Правильно:

И теперь снова углы   и   совершили обмен:

 

В прямоугольном треугольнике тангенс одного острого угла равен котангенсу другого.

Резюме

Давай вкратце запишем всё, что мы узнали.

Теорема Пифагора:

 

Запомни эту табличку как таблицу умножения – и ты сможешь решить много задач про прямоугольный треугольник.

Во всяком случае, все задачи первой части ЕГЭ, в которых участвует прямоугольный треугольник, тебе точно будут «по зубам»!

Если тебе нужно научиться решать более сложные задачи, сдать ЕГЭ на отлично и поступить на бюджет в топовый ВУЗ…

…иди на следующий уровень!  

 

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК. СРЕДНИЙ УРОВЕНЬ.

Треугольник называется прямоугольным, если один из его углов – прямой, то есть равен  .

Главная теорема о прямоугольном треугольнике – теорема Пифагора.

Теорема Пифагора

Сумма квадратов катетов равна квадрату гипотенузы.

В буквах это будет так:   или так:

Кстати, хорошо ли ты помнишь, что такое катеты и гипотенуза? Если не очень, то смотри на рисунок – освежай знания

Вполне возможно, что ты уже много раз использовал теорему Пифагора, а вот задумывался ли ты, почему же верна такая теорема. Как бы её доказать? А давай поступим, как древние греки. Нарисуем квадрат со стороной  .

Видишь, как хитро мы поделили его стороны на отрезки длин   и  !

А теперь соединим отмеченные точки

Тут мы, правда ещё кое что отметили, но ты сам посмотри на рисунок и подумай, почему так.

Чему же равна площадь большего квадрата?

Правильно,  .

А площадь меньшего?

Конечно,  .

Осталась суммарная площадь четырех уголков. Представь, что мы взяли их по два и прислонили друг к другу гипотенузами.

Что получилось? Два прямоугольника. Значит, площадь «обрезков» равна  .

Давай теперь соберем всё вместе.

 

Преобразуем:  

то есть  

Вот и побывали мы Пифагором – доказали его теорему древним способом.

Прямоугольный треугольник и тригонометрия

 

 

Для прямоугольного треугольника выполняются следующие соотношения:

I.  

Синус острого угла равен отношению противолежащего катета к гипотенузе

II.  

Косинус острого угла равен отношению прилежащего катета к гипотенузе.

III.  

Тангенс острого угла равен отношению противолежащего катета к прилежащему катету.

IV.  

Котангенс острого угла равен отношению прилежащего катета к противолежащему катету.

И ещё раз всё это в виде таблички:

Заметил ли ты одну очень удобную вещь? Посмотри на табличку внимательно.

В прямоугольном треугольнике синус одного острого угла равен косинусу другого, а тангенс острого угла равен котангенсу другого.

 

Это очень удобно!

Признаки равенства прямоугольных треугольников

I. По двум катетам

 

Прямоугольные треугольники равны, если два катета одного треугольника соответственно равны двум катетам другого треугольника.

 

II. По катету и гипотенузе

 

 

Прямоугольные треугольники равны, если катет и гипотенуза одного треугольника соответственно равны катету и гипотенузе другого.

 

III. По гипотенузе и острому углу

 

 

Прямоугольные треугольники равны, если гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого.

 

IV. По катету и острому углу

 

 

a)

b)

Прямоугольные треугольники равны, если катет и острый угол одного треугольника соответственно равны катету и острому углу другого треугольника.

 

Внимание! Здесь очень важно, чтобы катеты были «соответствующие». Например, если будет так:

То ТРЕУГОЛЬНИКИ НЕ РАВНЫ, несмотря на то, что имеют по одному одинаковому острому углу.

Нужно, чтобы в обоих треугольниках катет был прилежащим, или в обоих – противолежащим.

Ты заметил, чем отличаются признаки равенства прямоугольных треугольников от обычных признаков равенства треугольников?

Загляни в тему «Треугольник» и обрати внимание на то, что для равенства «рядовых» треугольников нужно равенство трех их элементов: две стороны и угол между ними, два угла и сторона между ними или три стороны.

А вот для равенства прямоугольных треугольников достаточно всего двух соответственных элементов. Здорово, правда?

Примерно такая же ситуация и с признаками подобия прямоугольных треугольников.

Признаки подобия прямоугольных треугольников

I. По острому углу

 

 

Если прямоугольные треугольники имеют по одинаковому острому углу, то они подобны.

 

 

II. По двум катетам

 

 

Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого, то эти треугольники подобны.

 

III. По катету и гипотенузе

 

 

Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе другого, то эти треугольники подобны.

Медиана в прямоугольном треугольнике

В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равна половине гипотенузы

Почему это так?

Рассмотрим вместо прямоугольного треугольника целый прямоугольник.

Что видим? Треугольник   – половина прямоугольника.

Проведём диагональ   и рассмотрим точку   — точку пересечения диагоналей. Что известно про диагонали прямоугольника?

Точкой пересечения диагонали делятся пополам Диагонали равны

И что из этого следует?

Вот и получилось, что

1.   – медиана:
2.  

Запомни этот факт! Очень помогает!

А что ещё более удивительно, так это то, что верно и обратное утверждение.

 

Если медиана, проведенная к какой-нибудь стороне треугольника, оказалась равна половине этой стороны, то треугольник – прямоугольный.

Что же хорошего можно получить из того, что медиана, проведенная к гипотенузе, равна половине гипотенузы? А давай посмотрим на картинку

Здесь   – медиана и равна  . Что же это получилось за точка  ?

Посмотри внимательно. У нас есть:  , то есть расстояния от точки   до всех трёх вершин треугольника оказались равны. Но в треугольнике есть всего одна точка, расстояния от которой о всех трёх вершин треугольника равны, и это – ЦЕНТР ОПИСАННОЙ ОКРУЖНОСТИ. Значит, что получилось?

В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы.

 

 

Высота в прямоугольном треугольнике

Высота в прямоугольном треугольнике, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника. Кроме того, каждый из этих треугольников подобен исходному.

Вот давай мы начнём с этого «кроме того…».

Посмотрим на   и  .

У них общий  , и они оба – прямоугольные. Значит (вспоминаем только что прочитанные признаки подобия прямоугольных треугольников) – они подобны!

Еще раз:

Но у подобных треугольников все углы равны!

(Посмотри на рисунок)

То же самое можно сказать и про   и  

А теперь нарисуем это вместе:

Что видим? У   и   одинаковые острые углы!

Какую же пользу можно извлечь из этого «тройственного» подобия.

Ну, например – две формулы для высоты прямоугольного треугольника.

Чтобы писать меньше букв, обозначим:  ;  ;  ;   (посмотри на рисунке). Применяем подобие: .

Запишем отношения соответствующих сторон:

Для нахождения высоты решаем пропорцию и получаем первую формулу «Высота в прямоугольном треугольнике»:

Ну вот, теперь, применяя и комбинируя эти знания с другими, ты решишь любую задачу с прямоугольным треугольником!

 

Как же получить вторую?

А теперь применим подобие треугольников   и  .

Но сначала обозначим   и   ( смотри на рисунок)

Итак, применим подобие:  .

Значит,

Что теперь получится?

Опять решаем пропорцию и получаем вторую формулу «Высота в прямоугольном треугольнике»:

  ,то есть  

Обе эти формулы нужно очень хорошо помнить и применять ту, которую удобнее.

Запишем их ещё раз

 

 

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК. КРАТКОЕ ИЗЛОЖЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ

Прямоугольный треугольник — треугольник, у которого один из углов – прямой =  .

— катеты   — гипотенуза В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.

Теорема Пифагора: 

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:  .

Признаки равенства прямоугольных треугольников:

• по двум катетам:  
• по катету и гипотенузе:   или  
• по катету и прилежащему острому углу:     или    
• по катету и противолежащему острому углу:     или    
• по гипотенузе и остром углу:     или    .

Признаки подобия прямоугольных треугольников:

• одному острому углу:   или  
• из пропорциональности двух катетов:  
• из пропорциональности катета и гипотенузы:   или  .

Синус, косинус, тангенс, котангенс в прямоугольном треугольнике

• Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе:  
• Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе:  
• Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему:  
• Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему:  .

Высота, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника. Каждый из этих треугольников подобен исходному:

Высота прямоугольного треугольника:   или  .

В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равна половине гипотенузы:  .

Центр описанной окружности совпадает с серединой гипотенузы (точка О). Радиус описанной окружности:  .

Радиус вписанной в прямоугольный треугольник окружности:

Площадь прямоугольного треугольника:

• через катеты:  
• через катет и острый угол:  .

 

А также получить доступ к учебнику YouClever без ограничений…

Соотношения между сторонами и углами прямоугольного треугольника

На данном уроке мы вспомним основные теоретические факты о прямоугольном треугольнике, рассмотрим связи между его сторонами и углами, вспомним формулы, связывающие тригонометрические функции острого угла.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Основы геометрии»

Тема: Повторение курса геометрии 8 класса

Урок: Соотношения между сторонами и углами прямоугольного треугольника

Нарисуем прямоугольный треугольник 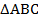, угол  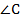прямой. 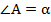, катет 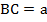, , 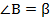катет . Гипотенуза 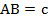 (см. Рис. 1).

Соотношения между углами и сторонами в прямоугольном треугольнике задаются тригонометрическими функциями – синусом, косинусом, тангенсом, котангенсом.

Рис. 1

Определение

Синусом острого угла прямоугольного треугольника называется отношение противолежащего ему катета к гипотенузе.

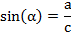
Определение

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего ему катета к гипотенузе.

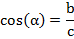
Определение

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего ему катета к прилежащему.

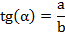
Определение:

Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего ему катета к противолежащему.

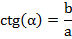
Кроме того, важный факт касается углов прямоугольного треугольника: сумма острых углов прямоугольного треугольника составляет .

Для удобства выпишем выражения для всех сторон треугольника через тригонометрические соотношения.

Правило нахождения катета через гипотенузу:

Катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего ему угла или на косинус прилежащего ему угла.

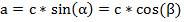
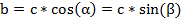
Правило нахождения катета через второй катет:

Катет прямоугольного треугольника равен произведению второго катета на тангенс противолежащего искомому катету угла или на котангенс прилежащего искомому катету угла.

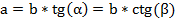
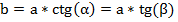
Напомним другие важные тригонометрические соотношения:

1. 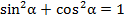      – основное тригонометрическое тождество;

Доказательство:

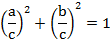
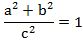
Вспомним теорему Пифагора, согласно которой сумма квадратов катетов равна квадрату гипотенузы:

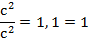
α=b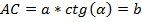

Согласно правилу нахождения гипотенузы:

 

АВ=аsinα=c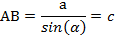

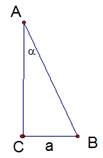
Рис. 2

 

Итак, мы рассмотрели основные соотношения, связывающие углы и стороны в прямоугольном треугольнике. Вспомнили основные формулы, которые связывают тригонометрические функции острого угла. Кроме того, мы решили несколько типовых задач.

 

Список литературы

1. Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
2. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
3. Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Uztest.ru (Источник).
2. Terver.ru (Источник).
3. Bymath.net (Источник).

 

Домашнее задание

1. Задание 1: в равнобедренном треугольнике ∆КРО с основанием РО проведена высота КН. Найдите угол ∠ОKН, если угол ∠Р=54°.
2. Задание 2: один из углов прямоугольного треугольника 60°, а сумма гипотенузы и меньшего из катетов равна 26,4с м. Найдите гипотенузу треугольника.
3. Задание 3: в прямоугольном треугольнике ∆АВС с прямым углом ∠С внешний угол при вершине А равен 120°. АС+АВ = 18 см, найдите длины АС и АВ.

Высота в прямоугольном треугольнике ℹ️ свойства и признаки, основные теоремы, формула углов и сторон, нахождение периметра, площади, примеры задач с решениями

Общие сведения

Следует отметить, что в геометрии существуют элементы, используя которые можно строить простые и сложные фигуры. Простейшим из них считается точка. С ее помощью можно создать прямую, луч, отрезок и угол. Точкой называется базовый «кирпич» геометрии, позволяющий осуществлять построение других элементов математической науки.

Прямая — совокупность множества точек, лежащих в одной плоскости и соединенных между собой таким образом, чтобы образовалась некоторая линия без перегибов и переломов. У нее нет вообще границ. Если говорят, что нужно провести прямую, то чертится только ее часть, а затем обозначается произвольной строчной буквой (a, b, c и т. д.). Простейшая фигура не имеет начала и конца. Математически границы записываются следующим образом: (- ∞; ∞). Следовательно, левая граница находится в точке — ∞, а правая — ∞.

Луч — разновидность прямой линии, имеющей только одну границу (точку). Из последней исходит прямая в бесконечность. Примером этой модели является Солнце, испускающее пучки световой энергии. Оно является источником света, который может проходить не только через Солнечную систему, но и уходить за ее пределы в бесконечность (космическое пространство). Луч обозначается также строчной литерой. Однако точку-источник следует обозначать прописной буквой.

Отрезком является часть прямой или луча, имеющая некоторые ограничения. Они обозначаются прописными литерами. Моделями являются следующие объекты и процессы: луч Солнца, идущий к Земле (Солнце — Земля), линейка, карандаш и т. д.

Плоским углом называется элементарная фигура, состоящая из общей точки и двух лучей, исходящих из нее и не лежащих на одной прямой. Измеряется в градусах и радианах. Далее следует разобрать виды прямоугольных треугольников.

Прямоугольный треугольник

Прямоугольным называется треугольник, имеющий угол, градусная мера которого эквивалентна 90. Он состоит из трех сторон, вершин и углов. К дополнительным параметрам можно отнести следующие:

• Периметр.
• Площадь.
• Высота.
• Медиана.
• Биссектриса.

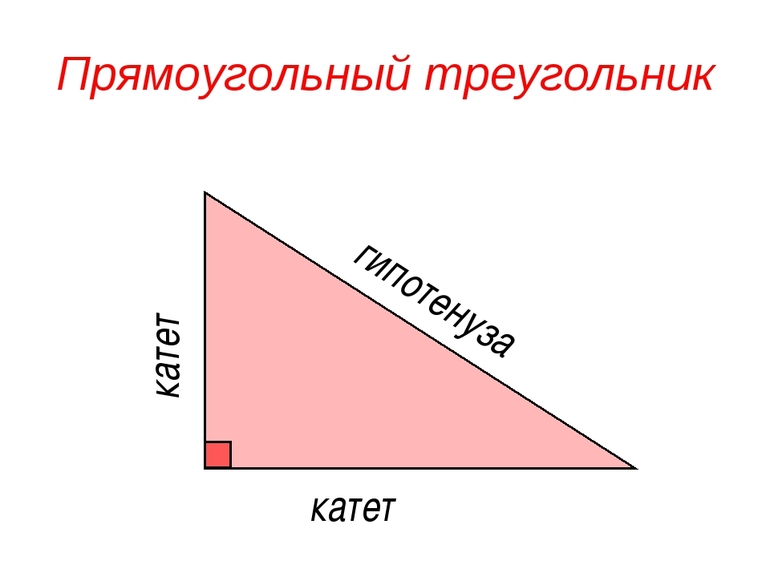
Стороны, образующие прямой угол, называются катетами. Третья сторона, соединяющая их, является гипотенузой. Все остальные углы являются острыми. Если сумма углов любого треугольника эквивалентна 180 градусам, то 180 — 90 = 90. Следовательно, сумма двух остальных углов составляет 90, а значит, они являются острыми.

Периметр — вспомогательная величина, характеризующая суммарное значение сторон фигуры. Существует также понятие полупериметра. Последним называется полусумма всех его сторон. Площадью называется характеристика треугольника, показывающая его размерность.

Высота в прямоугольном треугольнике, проведенная к гипотенузе — отрезок, опущенный перпендикулярно относительно этой стороны. Ее еще называют проекцией. Медиана — отрезок, соединяющий вершину с серединой стороны. Если она проведена из прямого угла, то эквивалентна половине гипотенузы. Биссектрисой является некоторая прямая, которая делит искомый угол на два равных значения.

Следует отметить, что этот тип треугольника бывает двух видов — разносторонний и равнобедренный. В последнем три последних параметра не совпадают (медиана, высота и биссектриса).

Следует рассмотреть свойства высоты в прямоугольном треугольнике равнобедренного типа. Она является медианой и биссектрисой. Далее следует обратить внимание на теорему, которая применяется для взаимосвязи сторон фигуры.

Теорема Пифагора

Для удобства треугольник следует обозначить символом «Δ». Связь между сторонами прямоугольного Δ была открыта древнегреческим ученым Пифагором. Утверждение имеет следующую формулировку: в произвольном прямоугольном Δ (со сторонами a, b и c) должно выполняться равенство между квадратом гипотенузы c и алгебраической суммой квадратов двух катетов a и b. Следует отметить, что при несоблюдении этого условия заданная фигура не содержит прямой угол. Математическая запись теоремы имеет такой вид: a^2 + b^2 = c^2.

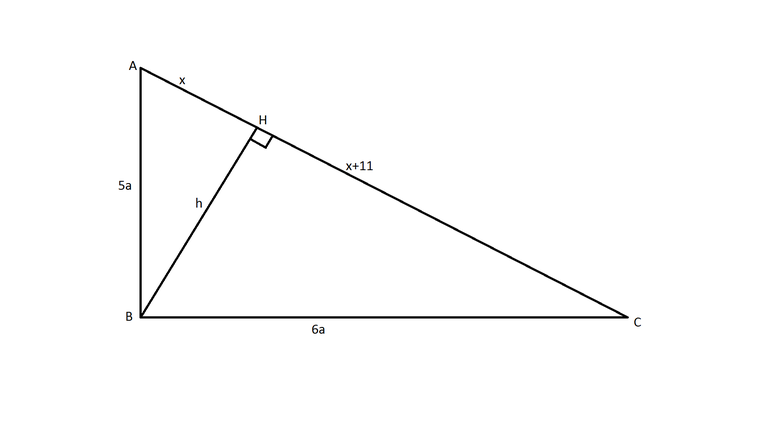
Доказательств теоремы существует огромное количество, поскольку применяются различные подходы. Однако наибольшей популярностью пользуется способ, полученный из аксиом. Кроме того, дополнительно применяется алгебраическая методика. Для выполнения операции по доказательству соотношения a^2 + b^2 = c^2 необходимо построить прямоугольный Δ с такими сторонами: BC = a, AC = b и AB = c. После этого проводится высота к гипотенузе из вершины, которая является точкой пересечения двух катетов.

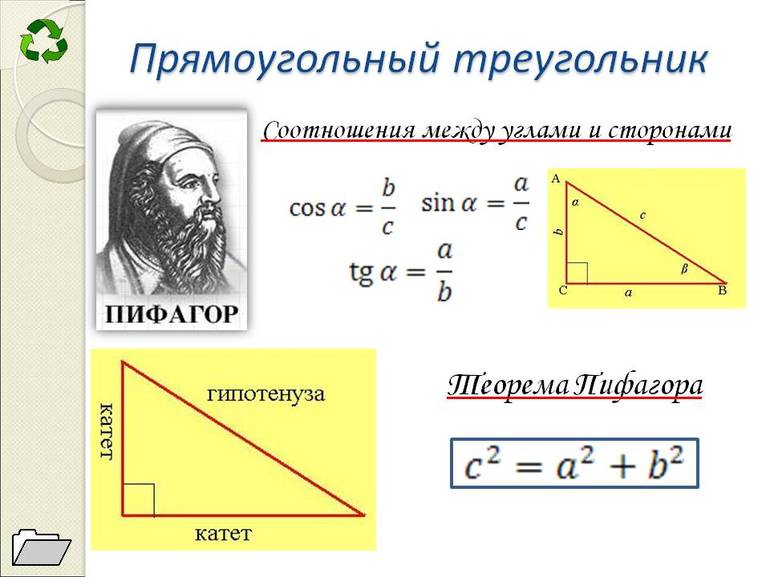
В результате образовались два равных угла ∠АНС и ∠ВНС. Кроме того, они являются прямыми по свойству высоты. Затем нужно рассмотреть Δ АВС и Δ АСН (Δ СВН), которые подобны по двум углам. На основании признака подобия можно вывести такие соотношения в виде пропорций:

• а / с = НВ / а.
• b / с = АН / b.

Далее нужно перемножить крайние и средние члены двух формул: а ² = c * НВ и b ² = c * AH. После этого для окончательного доказательства утверждения необходимо только сложить части. Получается равенство такого вида: а^2 + b ² = c * [НВ + AH] = c ² .

Утверждение о высоте

Для прямоугольного Δ и высоты была выведена специальная теорема, позволяющая оптимизировать процесс вычисления основных его параметров. Ее формулировка имеет следующий вид: в прямоугольном ΔABC высота CE, опущенная на гипотенузу, делит ее по соотношению квадратов катетов к частям гипотенузы. Для доказательства нужно использовать такой алгоритм:

• Построить ΔABC (∠C = 90).
• Провести высоту к CE к гипотенузе AB.
• Следует доказать соотношение BE / EA = (BC^2) / (AC^2).
• Используя теорему о пропорциональности отрезков прямоугольного Δ, можно сделать вывод о подобии ΔABC и ΔACE.
• На основании 4 пункта получается формула: CA / AB = EA / CA.
• Перемножив крайние и средние члены по свойству пропорции, можно вывести CA^2 = AB * EA.
• Нужно рассмотреть ΔABC и ΔBCE. Их подобие доказывается аналогично пункту 4.
• Пропорция имеет такой вид: BC / AB = BE / BC. Окончательно: BC^2 = AB * BE.
• Разделить полученные равенства в 8 и 6 пунктах на AC^2. Формулу можно править таким образом: BC^2 / AC^2 = BE / EA.

​Теорема доказана. Существуют и другие утверждения о высоте в прямоугольном Δ. Их необходимо также рассмотреть, но без доказательств.

Тригонометрические функции

Полезными при решении различных задач считаются тригонометрические функции. Их всего четыре:

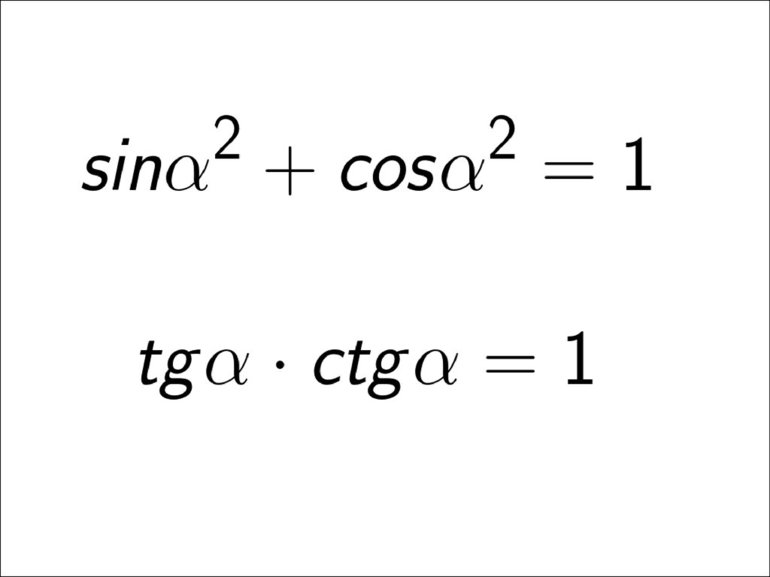
• Синус (sin) эквивалентен отношению противолежащего катета к гипотенузе Δ: sin (∠CBA) = a / c.
• Косинусом (cos) искомого угла называется величина, характеризующая отношение противолежащего катета к гипотенузе: cos (∠CBA) = b / c.
• Тангенс (tg) — это значение отношения двух катетов (противолежащего к прилежащему): tg (∠CBA) = a / b.
• Котангенс (ctg) является обратной величиной для функции tg (∠CBA). Он характеризует отношение прилежащего к противолежащему. Записывается в математическом виде следующим образом: ctg (∠CBA) = b / a или ctg (∠CBA) = 1 / (tg (∠CBA)= 1 / (a / b) = b / a.

Математики выделяют 4 обратные тригонометрические функции: arcsin, arccos, arctg и arcctg. Применяются они, когда получено одно из значений тригонометрической функции. На основании этого можно найти градусную меру угла. Расчет выполняется с использованием специальных таблиц (Брадиса) или при помощи онлайн-калькуляторов.

Другие соотношения

Формулы для нахождения длины высоты происходят от некоторых теорем. Их необходимо знать, поскольку это позволит существенно сэкономить время и избежать множества ошибок при вычислениях. Для этих целей необходимо начертить прямоугольный ΔABC, у которого ∠BAD = 90, а больший катет эквивалентен величине а. Основные теоремы о высоте, проведенной из прямого угла, имеют такие формулировки:

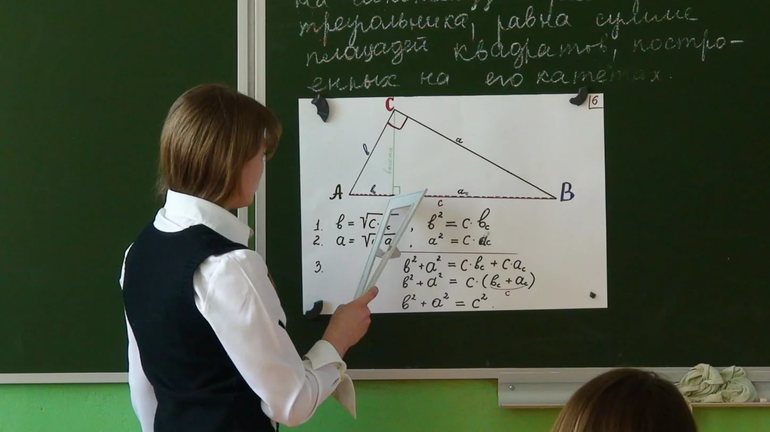
• Высота делит гипотенузу на проекции катетов: Ca = a^2 / c и Cb = b^2 / c.
• Высота эквивалентна средней геометрической величине проекций катетов: h = [Сa * Cb]^(1/2).
• Проведенная из угла 90 высота делит исходный треугольник на 2 ему подобных.
• Длина искомой высоты соответствует отношению произведения катетов к линейному значению гипотенузы: h = (a * b) / c.
• Если медиана проведена из угла прямого типа, то она эквивалентна 1/2 гипотенузы. Кроме того, ее основание совпадает с центром описанной около Δ окружности, радиус которой равен медиане.
• Радиус вписанного круга в Δ эквивалентен соотношению r = (a + b — c) / 2.
• Размерность прямоугольного Δ или площадь S соответствуют величине, равной 1/2 от произведения катетов: S = (1/2) * a * b.

Следует отметить, что величину размерности можно найти из производных формул: S = (1/2) * c^2 * sin(∠CBA) * sin(∠BAC) = (1/2) * c^2 * sin(∠CBA) * cos(∠CBA) = (1/2) * c^2 * sin(∠BAC) * cos(∠BAC) = (1/2) * a^2 * tg(∠BAC) = (1/2) * a^2 * ctg(∠CBA).

Примеры решения задач

Для закрепления теоретических знаний специалисты рекомендуют решить несколько задач. Они делятся на простые и сложные. Первые решаются при помощи одной или нескольких элементарных операций. Таких примеров в интернете очень много. Однако попадаются и сложные варианты, которые позволяют использовать полученные знания на все 100%.

В интернете встречаются онлайн-приложения, позволяющие найти решение. Этот инструмент нужно использовать для проверки результата. Хотя многие им злоупотребляют, а затем не получают правильного результата. Для начала необходимо взять готовый решенный пример и ознакомиться с ним. Далее попытаться воспроизвести его на бумаге. Подсматривать в исходник нельзя. При помощи такого приема происходит формирование алгоритма решения в головном мозге.

Сложное задание

Условие задачи следующее: имеется ΔMNO (∠MNO = 90) с высотой NP и стороной NM = 3, а также с известным значением тригонометрической функции cos между большим катетом и гипотенузой (cos(∠NOM) = (35)^(1/2) / 6). Следует найти OP. Для этого необходимо следовать такому алгоритму:

• Найти sin(∠NOM): [sin(∠NOM)]^2 + [cos(∠NOM)]^2 = 1. Отсюда следует, что sin(∠NOM) = [1 — [cos(∠NOM)]^2]^(1/2) = [1 — 35/36]^(1/2) = 1/6.
• Вычислить длину гипотенузы: MO = MN / (sin(∠NOM)) = 3 / 1/6 = 18 (ед).
• Рассмотреть ΔMNP: MN = 3, sin(∠NOM) = sin(∠MNP) = 1/6.
• Найти MP: MP = MN * sin(∠MNP) = 3 * 1/6 = 1/2.
• Искомая величина ОР высчитывается таким образом: OP = MO — MP = 18 — 1/2 = 17,5 (ед).

На основании пятого пункта можно сделать вывод, что длина искомого отрезка равна 17,5 (ед). Если проанализировать решение упражнения, то станет понятно, что очень часто применяются соотношения на основе тригонометрических функций.

Уровень турбо

В некоторых источниках задачи повышенной сложности называют «для турбо». К ним принадлежат все типы, которые имеют минимальный объем известных данных. Пусть дан равнобедренный ΔSTU (∠STU = 90). Гипотенуза на 2 больше катета. Необходимо найти его высоту TV, проведенную из прямого угла. Решение следует выполнять по такой инструкции:

• Обозначить катет неизвестной «y», тогда ST = TU = y и SU = y + 2.
• Записать формулу определения высоты: h = (a * b) / c.
• Составить уравнение: (y + 2) = y^2 + y^2.
• Раскрыть скобки и привести подобные слагаемые: y^2 + 4 * y + 4 — 2 * y^2 = -y^2 + 4 * y + 4 = y^2 — 4 * y — 4 = 0.
• Найти величину дискриминанта: D = 16 + 16 = 32.
• Первый корень: y1 = [-4 — 32^(1/2)] / 2 = [-4 — 4 * 2^(1/2)] / 2.
• Второй: [-4 + 4 * 2^(1/2)] / 2 = -2 + 2 * 2^(1/2).
• Первый не подходит, поскольку является величиной отрицательной.
• ST = TU = -2 + 2 * 2^(1/2) и SU = -2 + 2 * 2^(1/2) + 2 = 2 * 2^(1/2).
• Расчет высоты TV: TV = (-2 + 2 * 2^(1/2))^2 / 2 * 2^(1/2) = (4 — 8 * 2^(1/2) + 2) / 2 * 2^(1/2) = (6 — 8 * 2^(1/2)) / 2 * 2^(1/2) = 3 — 4 * 2^(1/2) / 2^(1/2) (ед).

Следует отметить, что в скобках необходимо указывать единицу измерения. Если размерность последней не дана, то нужно указывать ее условно.

Таким образом, для решения сложных задач по геометрии следует знать формулу высоты в прямоугольном треугольнике. Это позволяет оптимизировать решение и не совершать ошибок при вычислениях.

Все основные формулы площади прямоугольного треугольника

Прямоугольный треугольник, так же как и любой другой треугольник, имеет три стороны и три угла. Разница только в том, что один угол прямой, т. е. 90 градусов и два остальных, острых угла в сумме составляют, тоже 90 градусов.
Две стороны, которые формируют прямой угол, называют катетами, а третья сторона напротив прямого угла, называется — гипотенуза

---

1. Если известны только катеты

a, b — катеты треугольника

 

Формула площади треугольника через катеты ( S ) :

 

 

2. Если известны острый угол и гипотенуза или катет

c — гипотенуза

a, b — катеты

α, β — острые углы

 

Формулы площади прямоугольного треугольника через гипотенузу и угол ( S ) :

 

Формулы площади прямоугольного треугольника через катет и угол ( S ) :

 

---

Как известно, сумма острых углов в прямоугольном треугольнике равна 90 градусов, а если

то справедливы следующие тождества:

 

---

 

 

3. Если известны радиус вписанной окружности и гипотенуза

c — гипотенуза

c₁, c₂ — отрезки полученные делением гипотенузы, точкой касания окружности

r — радиус вписанной окружности

О — центр вписанной окружности

 

Формулы площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу ( S ) :

 

Сферический треугольник — Википедия

Материал из Википедии — свободной энциклопедии

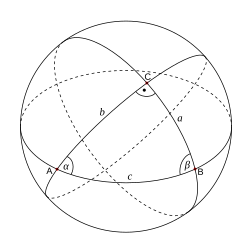Сферический треугольник

Сферический треугольник — геометрическая фигура на поверхности сферы, состоящая из трёх точек и трёх дуг больших кругов, соединяющих попарно эти точки. Три больших круга на поверхности сферы, не пересекающихся в одной точке, образуют восемь сферических треугольников. Соотношения между элементами сферических треугольников изучает сферическая тригонометрия.

Сторона сферического треугольника измеряется величиной опирающегося на неё центрального угла. Угол сферического треугольника измеряется величиной двугранного угла между плоскостями, в которых лежат стороны этого угла. Сферический треугольник, все стороны которого меньше половины большого круга, а углы меньше π, называется эйлеровым^[1]:9. Далее рассматриваются эйлеровы треугольники.

• Помимо трёх признаков равенства плоских треугольников, для сферических треугольников верен ещё один: два сферических треугольника равны, если их соответствующие углы равны^[1]:16. В евклидовой геометрии такие треугольники являются подобными. В сферической геометрии любое преобразование подобия является изометрическим (то есть коэффициент подобия всегда равен единице), поэтому в сферической геометрии нет неравных подобных фигур (то есть фигур, переводящихся друг в друга преобразованием подобия).
• Полярным для данного сферического треугольника (ABC) называется такой сферический треугольник (A’B’C’), вершины которого A’, B’, C’ являются полюсами^[a] по отношению к сторонам BC, CA, AB соответственно. При этом точки A и A’, B и B’, C и C’ лежат по одну сторону относительно BC, CA, AB соответственно.^[3]
  • Для любого полярного треугольника выполняются следующие правила: K′=π−k{\displaystyle K’=\pi -k}; k′=π−K{\displaystyle k’=\pi -K}, где угол K=α,β,γ{\displaystyle K=\alpha ,\beta ,\gamma } и сторона k=a,b,c{\displaystyle k=a,b,c}.
  • Сферический треугольник, все стороны которого равны прямому углу, будет полярным к самому себе.
  • Полярный треугольник, построенный к полярному треугольнику для некоего сферического, совпадает с исходным.

• Для сторон сферического треугольника выполняются 3 неравенства треугольника: каждая сторона меньше суммы двух других сторон и больше их разности^[1]:11.

• Сумма всех сторон a+b+c{\displaystyle a+b+c} всегда меньше 2π{\displaystyle 2\pi }^[1]:11.
  • Величина 2π−(a+b+c){\displaystyle 2\pi -(a+b+c)} называется сферическим дефектом^[4][5].

• Если от двух углов сферического треугольника отнимем третий, получим угол, меньший π{\displaystyle \pi }^[1]:15.
• В отличие от плоского треугольника, у сферического треугольника может быть два или три прямых или тупых угла.

Прямоугольный сферический треугольник полностью определяется двумя элементами, остальные три находятся при помощи мнемонического правила Непера. А чтобы решить косоугольный сферический треугольник, необходимо знать три его элемента. Для решения можно использовать следующие соотношения между ними^{[1]:102—139}:

• Формула половины стороны и формула половины угла — при решении по трём сторонам и трём углам;
• Формулы аналогии Непера — при решении по двум сторонам и углу между ними и по двум углам и прилежащей к ним стороне;
• Теорема синусов и формулы аналогии Непера — при решении по двум сторонам и противолежащему одной из них углу и по двум углам и противолежащей одному из них стороне.

1. ↑ Полюсом по отношению к AB называется называется такая точка X сферы, что отрезок OX (здесь O — центр сферы) перпендикулярен плоскости большого круга AB.^[2] Имеется две таких точки. Например, если AB — дуга экватора, то полюсы AB — это северный и южный полюс.

1. ↑ ^{1 2 3 4 5 6 7 8} Степанов Н. Н. Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — 154 с.
2. ↑ Энциклопедия элементарной математики, 1963, с. 521.
3. ↑ Энциклопедия элементарной математики, 1963, с. 530.
4. ↑ ^{1 2} Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1974.
5. ↑ Сферический треугольник
6. ↑ Статья в «Успехах физических наук»
7. ↑ Weisstein, Eric W. Сферический треугольник (англ.) на сайте Wolfram MathWorld.
8. ↑ Вентцель М. К. Сферическая тригонометрия. — 2 изд, ИГКЛ, 1948, 115 с. (доступно на bookfi.org). Строгое доказательство пропорциональности площади сферическому избытку — на с. 82
9. ↑ Васильев Н., Гутенмахер В. Сумма углов сферического многоугольника // «Квант», № 2, 1988

• Прасолов В. В. Геометрия Лобачевского. — М., 1995. (§1. Сферическая геометрия.)
• Основные понятия сферической геометрии и тригонометрии // Энциклопедия элементарной математики. — Физматгиз, 1963. — Т. 4 (геометрия). — С. 518-558.