Функции и их графики — математика, уроки
Цель, стоящая перед обучающимися: показать знания, умения и навыки, полученные при изучении предыдущего материала.
Цель, строящая перед педагогом: определить уровень усвоения материала, активизировать деятельность детей, подготовить учащихся к решению заданий из ГИА
Методы: словесный, практический, наглядный, интерактивный метод контроля (письменный: работа по карточкам), устный.
Критерии достижения цели:
— мотивирование на отдаленную перспективу; стимулирование оценкой к дальнейшему достижению поставленной цели
Совместная деятельность: фронтальная работа с классом;
Методы стимулирования учебной активности:
оценочный, убеждение, создание комфортных взаимоотношений, взаимодоверия.
Критерии оценивания ответов:
— оценивание по уровню подготовленности, качества выполненного задания и полноты ответа; активности.
2
Дома вы должны были повторить материал по данной теме, давайте посмотрим ,как вы справились с этим заданием
Фронтальная работа с классом по вопросам
1Так что же такое функция?
2 Что называют областью определения функции?
3 Что называется областью значения функции?
4 Что называется графиком функции?
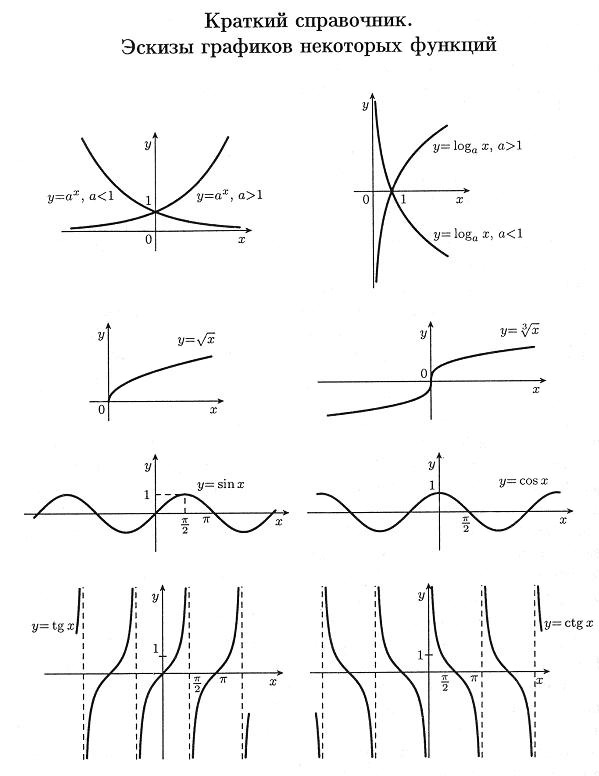
5 Давайте вспомним все функции, которые мы изучали, формулы их задающие , и их графики.
(После того, как дети назовут все функции и формулы показать
Слайд 3
6 Что вы мне можете рассказать об этих функциях, какими свойствами они обладают?
Слайд 4
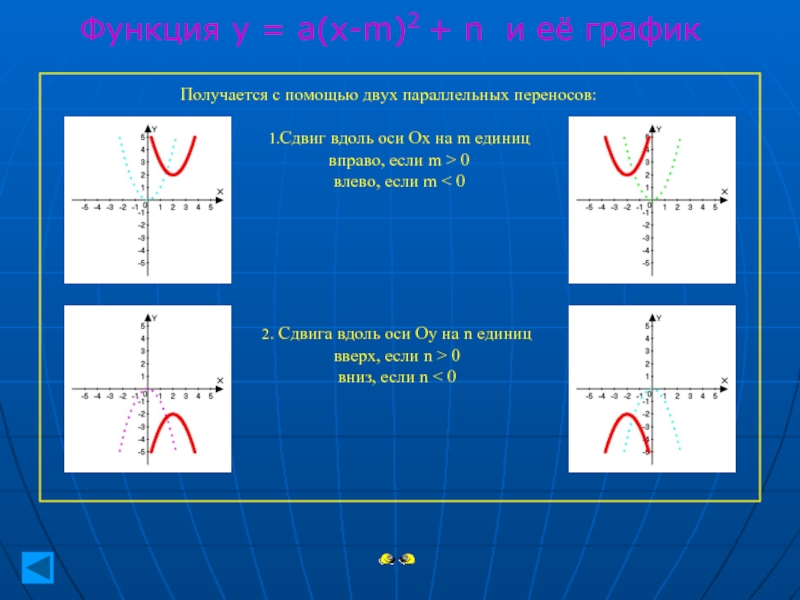
7 Давайте вспомним преобразование графиков (Работа с презентацией преобразование графиков)
Как из графика функции у =ах2 можно получить график функции: У=ах2+п у=а(х –m)2
у=а(х-m)2+п
8 Какой график соответствует функции у = ?
Слайд 5
9 Какой график соответствует функции у=-2(х-2)2+2
Слайд 6
10 Какой график соответствует функции у=|x-2|+2? Слайд 7
11 Какой из формул задается график данных функций? Слайды 8-11
Слайды 12-14
| 1. |
Формула степенной функции
Сложность: лёгкое |
1 |
| 2. |
График степенной функции (чётный/отрицательный показатель степени)
Сложность: лёгкое |
1 |
| 3. |
Вычисление значения функции по значению аргумента (целое число)
Сложность: лёгкое |
2 |
4.
|
Формула функции
Сложность: лёгкое |
2 |
| 5. | Сложность: среднее |
2 |
| 6. |
Показатель степенной функции
Сложность: среднее |
2 |
7.
|
График функции вида y = k/x + a
Сложность: среднее |
3 |
| 8. |
График функции вида y = k/(x + a)
Сложность: среднее |
3 |
| 9. |
График функции вида y = 1/(x + a) + b
Сложность: среднее |
3 |
10.
|
Чётность степенной функции (отрицательный показатель степени)
Сложность: среднее |
3 |
| 11. |
Монотонность степенной функции (отрицательный показатель степени)
Сложность: среднее |
3 |
| 12. |
Наименьшее и наибольшее значения функции (показатель степени больше единицы)
Сложность: среднее |
4 |
13.
|
Построение графика степенной функции (положительный показатель степени, меньший единицы)
|
3 |
| 14. |
Построение графика степенной функции (положительный показатель степени, больший единицы)
Сложность: сложное |
3 |
цикл проектных уроков, устанавливающих связь между коэффициентами формулы функции и видом ее графика
Евсеева А.А.,
учитель математики
ГБОУ г. Москвы «Школа № 687»
Григорова О.Т.,
учитель математики
ГБОУ г. Москвы «Школа № 687»
Зотова М.О.,
учитель математики
ГБОУ г. Москвы «Школа № 687»
Функции и их графики изучаются в курсе алгебры, начиная с 7 класса. И, казалось бы, такой простой тип заданий, как задания на распознавание, с приходом ОГЭ не должен вызывать много трудностей у учеников. Однако, по статистике, выпускники 9 классов справляются с этими заданиями далеко не так успешно, как хотелось бы. Речь идет о номере 5 части «Алгебра» из ОГЭ.
Однако, по статистике, выпускники 9 классов справляются с этими заданиями далеко не так успешно, как хотелось бы. Речь идет о номере 5 части «Алгебра» из ОГЭ.
Причины возникновения затруднений мы увидели в том, что каждая функция в курсе алгебры с 7 по 9 класс изучается отдельно, с большими временными перерывами между темами. И нет объединяющей линии, позволяющей рассматривать задания на нахождение связи между коэффициентами формул и видом графика, как метапредметное умение. Если проанализировать банк заданий по данной теме, мы увидим некоторую закономерность. Вне зависимости от вида функции и буквенного обозначения, коэффициенты несут одинаковую смысловую нагрузку. Так, например, свободный член в формуле отвечает за пересечение графика с осью у, а старший коэффициент за монотонность функции.
Чтобы красной линией провести работу с коэффициентами различных функций через весь курс алгебры до ОГЭ, мы разработали цикл уроков-проектов, идущих под одним названием «Азбука графиков». Каждый ученик на таком уроке проходит практически через все ступени абстрактно-логического метода научного исследования.
Абстрактно-логический метод исследования, приобретающий с развитием науки все большее значение, включает следующую совокупность научных приемов: индукции и дедукции, анализа и синтеза, аналогии, сопоставлений, системно-структурный прием, формализации, моделирования, прогнозирования. Подробнее о методах научного познания можно прочитать по ссылке, а о том, как абстрактно-логический метод исследования реализуется на уроке, рассмотрим подробно в одной из таблиц.
Цикл уроков «Азбука графиков в 7-9 классах включает следующие темы:
1. «Линейная функция (начало 7 класса)»;
2. «Квадратичная функция вида у = (х – m)² + n (конец 7 класса, тема расширена специально под данный цикл уроков)»;
3. «Функция у=√х (8 класс)»;
4. «Функция у = ΙхΙ (8 класс)»;
5. «Функция у = к/х (8 класс)»;
6. «Квадратичная функция вида у = ах2+bx+c (8 класс)»;
7. «Степенная функция (9 класс)».
«Степенная функция (9 класс)».
Каждый такой урок состоит из трех ступеней, на которых деятельность учеников в корне различна. На первой ступени ученик строит несколько (количество зависит от работоспособности ученика и сложности функции) графиков функции с различными коэффициентами. На второй ступени в группе учеников классифицируются построенные графики, в зависимости от их вида, и собирается банк графиков в виде одной большой таблицы на класс. На третьей ступени ученик заполняет индивидуальную азбуку, в которой по виду графика он дает сравнительную характеристику коэффициентам функции.
Остановимся подробно на плане подготовки урока «Азбука графиков».
1. Работа по подготовке к уроку-проекту начинается с формулировки задания для групп. Пример такого задания для урока «Азбука графиков»:
Задание для групп
Заполнить «Азбуку графиков», установив связи между коэффициентами в формуле функции и видом её графика.
Инструкция
Для этого вам потребуется: распределить роли в группе; распределить каждому по одной функции с карточки, обращая внимание на уровень сложности. В тетради каждый пишет название функции, составляет таблицу для 2 точек, чертит систему координат с названием осей х и у, строит график, выписывает коэффициенты m и к. Контролер проверяет правильность заполнения таблицы и построения графиков. Каждый переносит свой график и формулу на маленький листочек по образцу. Листочек расположить горизонтально! Выложить все начерченные графики в центр стола. Определить по знаку коэффициентов в формуле, в какую часть плаката приклеить график. Приклеить график на плакат. Заполнить все колонки в «Азбуке графиков». Руководитель по эталону проверяет правильность заполнения «Азбуки графиков». Для домашнего задания взять карточку с «Банком функций» и доделать оставшиеся графики. Записать название функции, графика, выписать коэффициенты m и к.
2. Создается лист планирования и продвижения по заданию, который заполняет руководитель группы. Образец листа планирования и продвижения по заданию:
Образец листа планирования и продвижения по заданию:
Лист планирования и продвижения по заданию
группы №________ 7 класса «____»
| Дата: | |||
| Тема урока | |||
Распределение ролей: | Руководитель: | ||
| Контролер: | |||
| Советник: | |||
| Докладчик: | |||
| Цель урока: | |||
| Гипотеза: | |||
| План урока: | Отметка о выполнении плана | ||
3. Создается оценочный лист.
Лист оценивания
Число:____________________Группа:_№______________Класс____________
Тема:______________________________________________________________
| № | Список группы | Роли | Баллы за 1 график | Баллы за роль в группе | Баллы за «Азбуку» | Всего баллов | Оценка |
| 2-5 | 1-3 | 0-5 | 13 | ||||
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| 4 | |||||||
| 5 |
Критерии баллов за графики:
«5» – полностью правильно и самостоятельно заполнена таблица и построен график.
«4» – в самом начале получена подсказка, как надо делать, затем задание выполнено самостоятельно.
«3» – была вычислительная ошибка в таблице.
«2» – постоянно оказывалась помощь при заполнении таблицы и построении графика.
Критерии баллов за «Азбуку»:
«5» – правильно и самостоятельно определил все коэффициенты в «Азбуке графиков».
«4» – допущены 1–2 ошибки при определении коэффициентов в «Азбуке графиков».
«3» – допущены 3–4 ошибки при определении коэффициентов в «Азбуке графиков» «2» – постоянно пользовался помощью соседей.
«1» – коэффициенты не определены, но записаны формулы (или наоборот).
«0» – коэффициенты не определены, формулы не записаны.
Критерии баллов за «Роль»:
«3» – успешно выполнены все функции по роли от начала до конца работы.
«2» – есть замечания по работе.
«1» – роль выполнена неудачно.
4. Учитель создает банк функций, графики которых будут строить дети на уроке.
Пример такого банка для урока «Азбука графиков линейной функции»:
| 1 группа | 2 группа | 3 группа | 4 группа |
| у=2х+3 | у=3х+2 | у=х+4 | у=4х+1 |
| у= –2х+3 | у= –3х+2 | у= –х+4 | у= –4х+1 |
| у=2х–3 | у= –3х-2 | у=х–4 | у= –4х-1 |
| у= –2х | у=3х | у= –х | у=4х |
| у= 3 | у= –2 | у=4 | у= –1 |
Банк функций включает в себя различные сочетания коэффициентов в формулах, что позволит потом собрать разнообразную коллекцию графиков.
Функций в банке может быть меньше или больше, в зависимости от количества учеников в классе и их работоспособности, а также от времени, выделенного на данный проект.
5. Создается, распечатывается и склеивается большая таблица для банка функций.
Пример такой таблицы для урока «Азбука графиков линейной функции»:
| Банк графиков линейной функции y = kx + m | |||
| m = 0 | m ˃ 0 | m ˂ 0 | |
k = 0 | |||
k ˃ 0 | |||
k ˂ 0 | |||
6. Необходимо приготовить маленькие листочки в клетку, размером с четверть тетрадного листа. На них каждый ученик будет строить свой график и приклеивать его к общей таблице банка.
На фотографии представлено, как выглядит готовый банк графиков на примере темы «Функция у = IxI»:
7. Создается таблица самой азбуки графиков, которая выдается каждому ученику. Пример: см. ссылку.
8. Создается эталон заполненной азбуки графиков для проверки руководителем по итогу урока. Пример: см. ссылку.
План проведения урока «Азбука графиков»
1. Класс разбивается на группы так, чтобы в одной группе было от 4 до 6 человек (группа более 6 и менее 4 участников малопродуктивна), причем в каждой группе должны быть ученики, способные выполнять функции руководителя, контролера, советника и докладчика.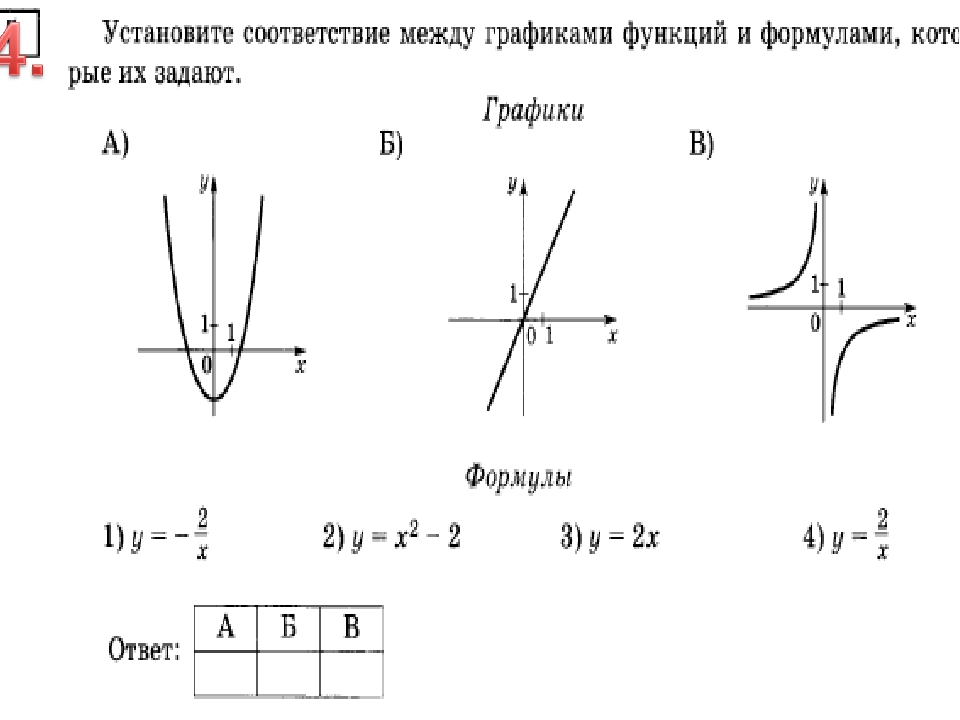
Функционал участников группы
Руководитель – координирует работу группы, отвечает за составление плана работы и следование этому плану, заполняет отчеты (лист планирования и продвижения по заданию), следит за временными рамками, оценивает правильность заполнения «Азбуки графиков» по эталону и выполнение роли в группе (а группа оценивает выполнение роли руководителем).
Контролер – контролирует полноценную работу каждого участника группы, следит за записями и другими видами работы участников группы. Проверяет правильность построенных графиков (если необходимо помогает исправить) и оценивает их. Собирает и сдает все нужные бумаги (тетради) в конце занятия.
Советник – может обратиться за помощью к преподавателю или участникам других групп. Приводит в порядок рабочий стол группы.
Докладчик – отвечает за теоретический материал. По результатам общих обсуждений в группе и сделанных выводов готовит доклад. Представляет проект.
9. Учитель выдает пакет документов, в который входят:
– Задание для групп.
– Банк функций.
– Лист планирования и продвижения по заданию.
– Лист оценивания.
– Листочки для построения графиков.
– Листы «Азбука графиков».
– Учащиеся знакомятся с заданием. Обсуждают и формулируют цель и задачи урока.
Формулируют гипотезы о связи вида графиков и коэффициентов функции. Руководитель начинает заполнять лист планирования и продвижения по заданию.
1. Руководитель раздает задания из банка функций и участники группы приступают к построению графиков в тетради.
2. Контролер проверяет правильность построенных графиков, оценивает их и разрешает переносить график на листочек в клетку по образцу в задании. Руководитель следит за временем и подгоняет отстающих.
3. Когда все графики проверены и перенесены на листочки по образцу, они выкладываются в центр стола, и группа приступает к их обсуждению, в результате которого учащиеся делают первичные выводы о зависимости вида графика от коэффициентов функции и решают в какую ячейку на плакате «Банка графиков» разместить свои чертежи.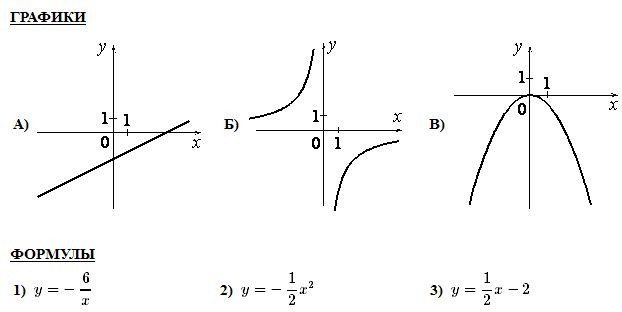
4. Когда ученик подходит к таблице «Банка графиков», и ищет место для своего чертежа он может обнаружить, что его график не соответствует виду формулы (проанализировав другие чертежи) или не понимает куда его разместить. В этот момент у ученика есть возможность исправить свою ошибку и получить консультацию у одноклассников.
5. Когда плакат «Банк графиков» заполнен полностью учащиеся приступают к сводному анализу, по результатам которого заполняется «Азбука графиков». На этом этапе происходит совместное обсуждение основных закономерностей, выявляются раннее допущенные ошибки в гипотезах первичного обсуждения.
6. После совместного обсуждения участники групп приступают к заполнению листов «Азбуки графиков», в которой по виду графика восстанавливают название функции, и знаки коэффициентов к и т. Руководитель по эталону, предоставленному учителем, проверяет правильность заполнения «Азбуки» и выставляет оценки в оценочный лист.
7. По результатам общих обсуждений в группе и сделанных выводов докладчик готовит речь и проводит защиту проекта.
8. Учитель подводит итоги и дает краткую оценку работы групп.
9. На следующем уроке целесообразно провести проверочную работу по данной теме. Пример проверочной работы:
На рисунках изображены графики функции вида у=кх+т. Установите соответствие между графиками и коэффициентами к и т.
1) к˃0, т˃0;
2) к˂0, т=0;
3) к˂0, т˂0;
4) к˃0, т˂0.
Аналогичные задания можно найти в сборнике подготовки к ОГЭ.
План проведения урока с примерами на основе темы «Линейная функция»
| Номер этапа | Название этапа | Что делает учитель | Что делают ученики |
| 1 | Организационный | Выдает пакет документов группам | Распределяют роли в группе |
| 2 | Знакомство с заданием | Читают задание для групп | |
| 3 | Целеполагание и планирование | Направляет и корректирует | Формулируют цель и задачи |
| 4 | Построение графиков | Контактирует с советниками по необходимости | Строят графики в тетради и после проверки контролером переносят на листочек в клетку по образцу |
| 5 | Первичный анализ зависимости вида графика от коэффициентов | Контактирует с советниками по необходимости | Просматривают все графики, полученные в группе, и совместно решают, где разместится каждый график на плакате «Банк графиков». Приклеивают листочки с графиками в нужную ячейку плаката. Приклеивают листочки с графиками в нужную ячейку плаката. |
| 6 | Сводный анализ | По заполненному плакату «Банк графиков линейной функции» в результате совместных обсуждений, делают окончательный вывод о влиянии коэффициентов к и т на вид графика ( на монотонность, на угол наклона с положительным направлением оси Ох, на точку пересечения с осью Оу. | |
| 7 | Рефлексия 1 | В конце этапа выдает руководителю группы эталон для проверки правильности заполнения «Азбуки графиков» | Заполняют «Азбуку графиков» в которой по виду графика восстанавливают формулу функции, название функции, знак коэффициентов к и т, либо их отсутствие. |
| 8 | Рефлексия 2. Защита проекта | Руководит прениями, задает вопросы для уточнения, высказывает свое мнение о качестве проделанной работы. | Докладчик озвучивает выводы группы о влиянии коэффициентов функции на вид её графика и предполагает наличие аналогичных зависимостей у других функций. |
Сопоставление этапов урока с научными приемами абстрактно-логического метода исследования
| Номер этапа | Название этапа | Название приема | Определение приема |
| 1 | Организа-ционный | ||
| 2 | Знакомство с заданием | Гипотеза | Гипотеза— положение, выдвигаемое в качестве предварительного, условного объяснения некоторого явления. |
| 3 | Целепо-лагание и плани-рование | ||
| 4 | Построе-ние графиков | ||
| 5 | Первичный анализ зависимости вида графика от коэффициентов | Анализ и синтез, сопоставление, аналогия | Анализ — представляет собой мысленное разложение или расчленение процессов на составляющие части, элементы с целью определения их места, роли и функций в целом объекте и установления взаимосвязи и взаимозависимости между ними. Сопоставление — это прием, при котором выявляются различия во вновь сформулированных категориях с ранее установленными. Аналогия — это прием научного познания, когда на основе сходства двух или нескольких признаков изучаемого явления делается вывод о сходстве других признаков и свойств. Для повышения достоверности выводов необходимо, чтобы аналогия базировалась на большом количестве существенных общих признаков и связи между ними были довольно тесными. Установление взаимосвязи с помощью приема аналогии требует дополнительной проверки в общественной практике (с помощью логических выводов или специального опыта). |
| 6 | Итоговый анализ | Индукция | Индукция (наведение) представляет собой способ изучения явления, в процессе которого от отдельных фактов, единичных случаев совершается переход к общим положениям, к обобщениям и утверждениям. При таком логическом умозаключении отдельные факты как бы наводят на общее положение. |
| 7 | Рефлексия 1 | Сопоставление, формализация, дедукция | Сопоставление — это прием, при котором выявляются различия во вновь сформулированных категориях с ранее установленными. Формализация. Суть этого приема состоит в том, что при изучении исследователь отвлекается от конкретного содержания изучаемых явлений, рассматривает их в правильном общем виде, исходя из законов диалектической логики. Дедукция — логическое умозаключение на основе перехода от общих суждений (доказательств) к частным. |
| 8 | Рефлексия 2. Защита проекта | Моделирование, прогнозирование | Моделирование — это прием научной абстракции, при котором на основании проведенного системно-структурного анализа формируется модель, которая отражает математическую закономерность в целом со всеми свойствами и взаимосвязями. Прогнозирование — это аргументированное представление о возможных путях развития изучаемого явления. |
В заключении хочется сказать, что значительные затраты учителя на подготовку и проведение таких уроков окупаются тем, что каждый ученик создает для себя целостную картину о взаимосвязи коэффициентов различных функций и видом их графиков, глубоко погружается в данную тему, проходит хорошую школу абстрактно-логического метода исследования. А также, такие глобальные системы уроков активизируют память, внимание, абстрактное мышление. А если говорить о развитии метапредметных умений на таких уроках, то можно написать ещё одну статью.
Мнение редакции может не совпадать с мнением авторов.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
значения функции по значению аргумента при различных способах задания функции описывать по Формулы преобразования суммы тригонометрических функций в произведение и произведения в сумму.
Министерство образования, науки и молодежной политики
Краснодарского края
Государственное бюджетное образовательное учреждение
дополнительного профессионального образования
«Институт развития образования»
Краснодарского края
Авторская программа для общеобразовательных организаций Краснодарского края: Алгебра и начала математического анализа. 10 – 11 классы (автор-составитель Е.А. Семенко).
10 – 11 классы (автор-составитель Е.А. Семенко).
Краснодар
2016
Пояснительная записка
Цели обучения математике в общеобразовательной школе определяются её ролью в развитии общества в целом и формировании личности каждого отдельного человека. К ним относятся:
овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для продуктивной жизни в обществе;
формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности;
формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.
Образовательные и воспитательные задачи обучения математике должны решаться комплексно с учетом возрастных особенностей учащихся, специфики математики как науки и учебного предмета, определяющей ее роль и место в общей системе школьного обучения и воспитания.
Принципиальным положением организации школьного математического образования является уровневая дифференциация обучения. Осваивая общий курс математики, одни школьники в своих результатах ограничиваются уровнем обязательной подготовки, зафиксированной в стандарте образования, другие в соответствии со своими склонностями и способностями достигают более высоких рубежей. При этом достижение уровня обязательной подготовки становится непременной обязанностью ученика в его учебной работе. В то же время, каждый учащийся имеет право самостоятельно решить, ограничиться этим уровнем или же продвигаться дальше. Следует всемерно способствовать удовлетворению потребностей и запросов школьников, проявляющих интерес, склонности и способности к математике. Для таких школьников следует разрабатывать индивидуальные программы и задания, их необходимо привлекать к участию в математических кружках, олимпиадах, факультативных занятиях, рекомендовать дополнительную литературу.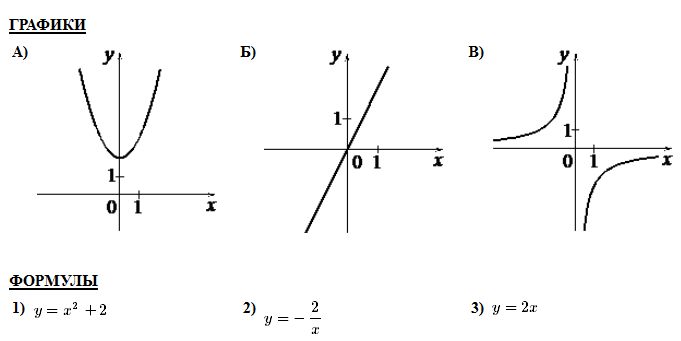 Развитие интереса к математике является важнейшей целью учителя.
Развитие интереса к математике является важнейшей целью учителя.
Критерием успешной работы учителя служит качество математической подготовки школьников, выполнение поставленных образовательных и воспитательных задач, а не формальное использование какого-то метода, приема или средства обучения.
Настоящая программа разработана в соответствии с требованиями федерального компонента Государственного образовательного стандарта среднего (полного) общего образования по математике, на основе примерной программы среднего (полного) общего образования по математике.
Основное отличие предложенной программы от всех программ, представленных в сборниках, в последовательности изложения материала. Это связано с тем, что в результате эксперимента по введению единого государственного экзамена по математике в нашем крае выявлены недостатки в изучении тем «Логарифмическая функция», «Логарифмические уравнения», «Логарифмические неравенства». Отмечено, что учащиеся, изучавшие эти темы в 10 классе, на ЕГЭ справились с заданиями, проверяющими усвоение этих тем, лучше, нежели школьники, изучившие указанные темы лишь в 11 классе.
Для построения единого образовательного пространства и для управления качеством математического образования на Кубани необходима единая программа.
Программа предполагает подробное изучение тригонометрии в 10 классе, а также изучение степенной, показательной и логарифмической функций. При этом знакомство с решением показательных и логарифмических уравнений и неравенств в 10 классе происходит на базовом уровне (т.е. рассматриваются простейшие уравнения и неравенства).
В 11 классе программой предусматривается возврат к темам «Показательные и логарифмические уравнения и их системы», «Показательные и логарифмические неравенства и их системы». Это позволит учащимся, слабо усвоившим соответствующие темы в 10 классе, еще раз вернуться к ним, а учащимся, которые хорошо усвоили эти темы на базовом уровне, можно предлагать задачи повышенного и высокого уровня сложности.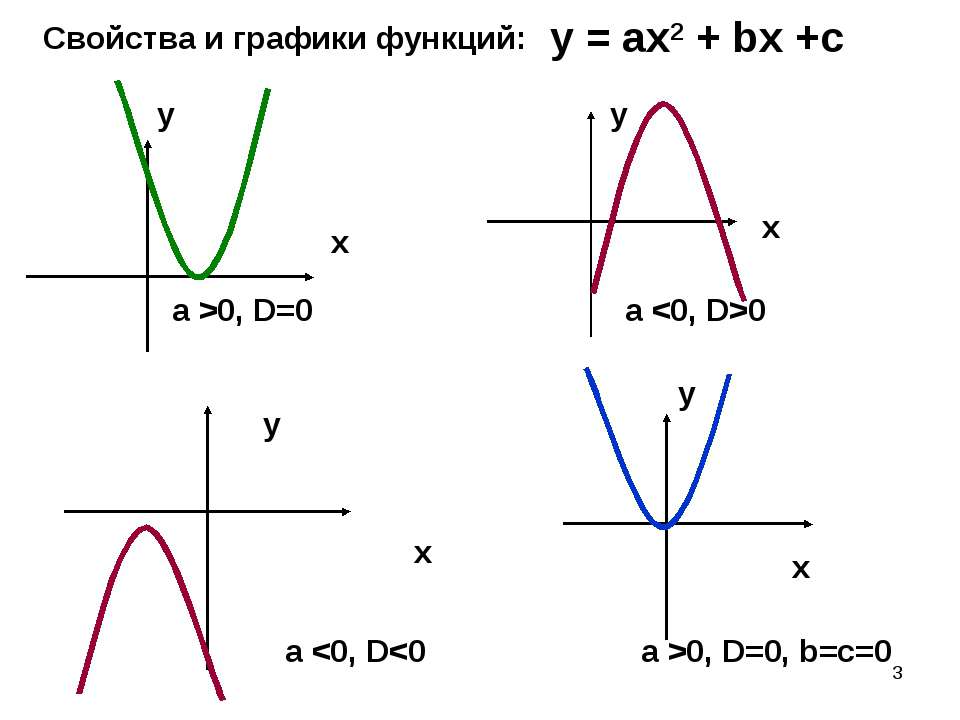 В 11 класс перенесены все элементы математического анализа. Предполагается, что на протяжении 10 класса, параллельно с изучением новых тем, будет проводиться повторение курса алгебры основной школы, а в 11 классе в повторение будут включаться разделы, изученные в 10 классе. Таким образом, наиболее сложные для усвоения темы будут рассмотрены с учащимися дважды, что позволит им лучше подготовиться к итоговой аттестации.
В 11 класс перенесены все элементы математического анализа. Предполагается, что на протяжении 10 класса, параллельно с изучением новых тем, будет проводиться повторение курса алгебры основной школы, а в 11 классе в повторение будут включаться разделы, изученные в 10 классе. Таким образом, наиболее сложные для усвоения темы будут рассмотрены с учащимися дважды, что позволит им лучше подготовиться к итоговой аттестации.
Календарно-тематическое планирование по данной программе разработано на 34 учебных недели в трех вариантах: I вариант, для профильных классов гуманитарного направления, в которых преподавание алгебры и начал анализа ведется в объеме 2,5 часа в неделю (если учебным планом в профильном классе предусмотрено 35 учебных недель, то 2,5 часа необходимо добавить к блоку итогового повторения), II вариант для общеобразовательных классов – 3 часа в неделю, III вариант для профильных классов – 4 часа в неделю.
АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА
Базовый уровень
Требования к уровню математической подготовки
выпускников 10 класса
В результате изучения курса алгебры и математического анализа в 10 – м классе учащиеся должны уметь:
находить значения корня натуральной степени, степени с рациональным показателем, логарифма, значения тригонометрических выражений на основе определений и основных свойств, пользоваться оценкой и прикидкой при практических расчетах;
выполнять тождественные преобразования тригонометрических, иррациональных, степенных, показательных и логарифмических выражений;
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
определять значения функции по значению аргумента при различных способах задания функции;
описывать по графику и в простейших случаях по формуле поведение и свойства функций;
строить графики линейной, квадратичной, тригонометрических, степенной, показательной и логарифмической функций;
решать уравнения и неравенства, используя свойства функций и их графики;
решать рациональные, тригонометрические, иррациональные, показательные (простейшие) и логарифмические (простейшие) уравнения;
решать рациональные, показательные (простейшие) и логарифмические (простейшие) неравенства;
составлять уравнения и неравенства по условию задачи;
использовать графический метод для приближенного решения уравнений и неравенств.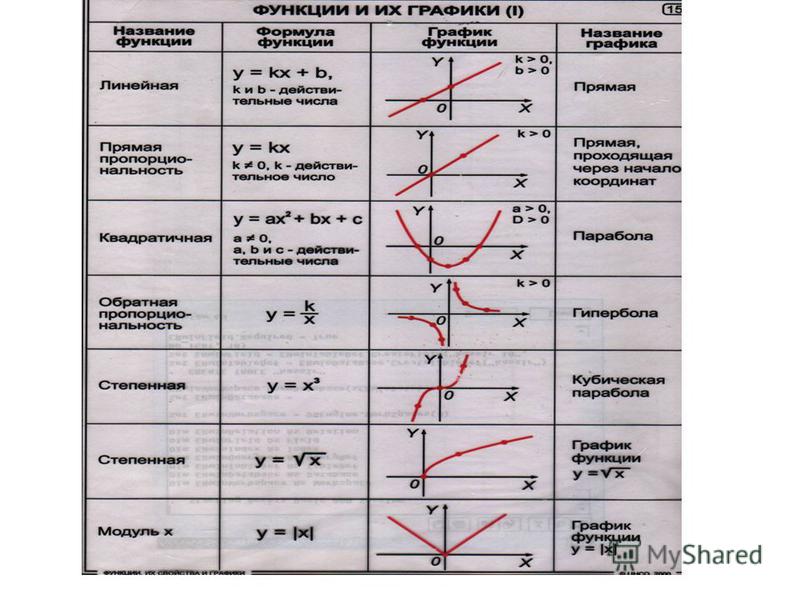
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
построения и исследования простейших математических моделей.
Содержание курса в 10 классе
Повторение.
Решение рациональных уравнений (линейных, дробно – линейных и квадратных).
Решение рациональных неравенств (линейных, дробно – линейных и квадратных) методом интервалов.
Действительные числа.
Натуральные и целые числа. Признаки делимости. Рациональные, иррациональные и действительные числа. Свойства арифметических операций над действительными числами. Числовая (действительная) прямая. Модуль действительного числа.
Тригонометрические выражения.
Понятие числовой окружности. Радианное измерение углов.
Определение синуса, косинуса, тангенса, котангенса любого действительного числа, связь этих определений с определениями тригонометрических функций, введенных в курсе планиметрии.
Соотношения между тригонометрическими функциями одного и того же аргумента (угла, числа). Знаки тригонометрических функций в зависимости от расположения точки, изображающей число на числовой окружности.
Формулы приведения, вывод, их применение.
Формулы сложения (косинус и синус суммы и разности двух углов), их применение.
Формулы двойных и половинных углов.
Формулы преобразования суммы тригонометрических функций в произведение и произведения в сумму.
Применение основных тригонометрических формул к преобразованию выражений.
Тригонометрические функции и их графики.
Функция, определение, способы задания, свойства функций. Общая схема исследования функции (область определения, множество значений, нули функции, четность и нечетность, возрастание и убывание, экстремумы, наибольшие и наименьшие значения, ограниченность, промежутки знакопостоянства).
Свойства и графики функций 13 EMBED Equation.DSMT4 1415, 13 EMBED Equation.DSMT4 1415, 13 EMBED Equation.DSMT4 1415, 13 EMBED Equation.DSMT4 1415. Периодичность, основной период.
Преобразования графиков: параллельный перенос, симметрия относительно осей координат и относительно начала координат, растяжение и сжатие вдоль осей координат. Исследование тригонометрических функций и построение их графиков*.
Тригонометрические уравнения (неравенства).
Определение арксинуса, арккосинуса, арктангенса действительного числа.
Формулы решений простейших тригонометрических уравнений 13 EMBED Equation.DSMT4 1415, 13 EMBED Equation.DSMT4 1415, 13 EMBED Equation.DSMT4 1415. Решение простейших тригонометрических уравнений. Решение простейших тригонометрических неравенств.*
Решение тригонометрических уравнений (уравнения, сводящиеся к простейшим заменой неизвестного, применение основных тригонометрических формул для решения уравнений, однородные уравнения).
Степенная функция.
Степень с натуральным и целым показателем. Свойства степеней. Арифметический корень натуральной степени. Свойства корней. Степень с рациональным показателем. Свойства степеней. Понятие степени с иррациональным показателем.
Степенная функция, ее свойства и график.
Равносильные уравнения и неравенства. Иррациональные уравнения.
Показательная функция.
Показательная функция, ее свойства и график.
Показательные уравнения (простейшие). Показательные неравенства (простейшие).
Логарифмическая функция.
Определение логарифма числа. Свойства логарифмов. Десятичные и натуральные логарифмы.
Понятие об обратной функции. Область определения и множество значений обратной функции. График обратной функции.
Логарифмическая функция, ее свойства и график.
Логарифмические уравнения (простейшие). Логарифмические неравенства (простейшие).
Итоговое повторение курса алгебры и начал математического анализа за 10 класс.
Преобразование рациональных, степенных, иррациональных и логарифмических выражений.
Преобразование тригонометрических выражений.
Решение тригонометрических уравнений.
Решение иррациональных уравнений.
Решение показательных и логарифмических уравнений (простейших).
Решение показательных и логарифмических неравенств (простейших).
Требования к уровню математической подготовки
выпускников 11 класса
В результате изучения курса алгебры и математического анализа 11 класса учащиеся должны уметь:
находить значения корня натуральной степени, степени с рациональным показателем, логарифма, значения тригонометрических выражений на основе определений и основных свойств, пользоваться оценкой и прикидкой при практических расчетах;
выполнять тождественные преобразования тригонометрических, иррациональных, степенных, показательных и логарифмических выражений;
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
определять значения функции по значению аргумента при различных способах задания функции;
описывать по графику и в простейших случаях по формуле поведение и свойства функций;
строить графики линейной, квадратичной, тригонометрических, степенной, показательной и логарифмической функций;
решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
решать рациональные, тригонометрические, иррациональные, показательные и логарифмические уравнения, их системы;
решать рациональные, показательные и логарифмические неравенства, их системы;
составлять уравнения и неравенства по условию задачи;
использовать для приближенного решения уравнений и неравенств графический метод;
изображать на координатной плоскости множества решений простейших уравнений и их систем;
вычислять производные и первообразные элементарных функций;
исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
вычислять в простейших случаях площади с использованием первообразной;
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
вычислять в простейших случаях вероятности событий на основе подсчета числа исходов.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
построения и исследования простейших математических моделей.
Содержание курса в 11 классе
Уравнения, неравенства, системы
Свойства степени с натуральным, целым и рациональным показателем. Преобразование степенных и иррациональных выражений.
Свойства логарифмов. Преобразование логарифмических выражений.
Решение показательных и логарифмических уравнений. Решение показательных и логарифмических неравенств.
Системы линейных уравнений и неравенств. Графический метод решения систем.
Системы квадратных уравнений и неравенств.
Системы показательных уравнений и неравенств.
Системы логарифмических уравнений и неравенств.
Смешанные системы и совокупности уравнений от одной и двух переменных. Смешанные системы и совокупности неравенств от одной и двух переменных .
Производная
Приращение аргумента и приращение функции. Понятие о производной функции. Ее геометрический и физический смысл. Уравнение касательной к графику функции.
Понятие о непрерывности функции. Примеры.
Правила вычисления производных (суммы, произведения, частного). Таблица производных основных элементарных функций. Вычисление производных.
Производная функции вида 13 EMBED Equation.DSMT4 1415.
Применение производной
Признак возрастания (убывания) функции. Критические точки функции. Максимумы и минимумы функции.
Наибольшее и наименьшее значения функции на промежутке.
Исследование функции и построение графиков с применением производной.
Первообразная и её применение
Определение первообразной. Основное свойство первообразной.
Правила нахождения первообразных. Таблица первообразных основных элементарных функций.
Площадь криволинейной трапеции. Формула Ньютона-Лейбница. Вычисление площадей плоских фигур с помощью первообразной.
Элементы комбинаторики, статистики и теории вероятностей
Статистическая обработка данных. Статистические понятия дискретного ряда (мода, медиана, среднее, размах вариации, частота признака). Диаграмма, гистограмма, полигон.
Статистические понятия дискретного ряда (мода, медиана, среднее, размах вариации, частота признака). Диаграмма, гистограмма, полигон.
Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач.
Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля.
Элементарные и сложные события. Понятие о вероятности события. Вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события. Решение практических задач с применением вероятностных методов.
Итоговое повторение курса алгебры и начал математического анализа
Функция, определение, способы задания, свойства функций, сведенные в общую схему исследования функции.
Линейная функция. Систематизация ее свойств на основе общей схемы исследования функций. Решение задач с использованием свойств функции.
Функция 13 EMBED Equation.DSMT4 1415. Систематизация ее свойств на основе общей схемы исследования функций. Решение задач с использованием свойств функции.
Квадратичная функция 13 EMBED Equation.DSMT4 1415 и 13 EMBED Equation.DSMT4 1415. Систематизация ее свойств на основе общей схемы исследования функций. Решение задач с использованием свойств функции.
Показательная функция 13 EMBED Equation.DSMT4 1415, её свойства и график. Решение задач с использованием свойств функции.
Логарифмическая функция 13 EMBED Equation.DSMT4 1415, её свойства и график. Решение задач с использованием свойств функции.
Тригонометрические функции (13 EMBED Equation.DSMT4 1415, 13 EMBED Equation.DSMT4 1415, 13 EMBED Equation.DSMT4 1415, 13 EMBED Equation.DSMT4 1415), их свойства и графики. Решение задач с использованием свойств функций.
Тождественные преобразования степеней с рациональным показателем, иррациональных и логарифмических выражений.
Тождественные преобразования тригонометрических выражений.
Решение рациональных и иррациональных уравнений (в том числе содержащих модули и параметры13 EMBED Equation. DSMT4 1415).
DSMT4 1415).
Решение показательных и логарифмических уравнений и их систем (в том числе содержащих модули и параметры13 EMBED Equation.DSMT4 1415).
Решение тригонометрических уравнений, (в том числе содержащих модули и параметры13 EMBED Equation.DSMT4 1415).
Решение задач с использованием производной.
АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА
Профильный уровень
ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ВЫПУСКНИКОВ2
В результате изучения математики на профильном уровне ученик должен:
знать/понимать
значение математической науки для решения задач, возникающих в теории и практике; широту и ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки;
идеи расширения числовых множеств как способа построения нового математического аппарата для решения практических задач и внутренних задач математики;
значение идей, методов и результатов алгебры и математического анализа для построения моделей реальных процессов и ситуаций;
возможности геометрии для описания свойств реальных предметов и их взаимного расположения;
универсальный характер законов логики математических рассуждений, их применимость в различных областях человеческой деятельности;
различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных наук, на практике;
роль аксиоматики в математике; возможность построения математических теорий на аксиоматической основе; значение аксиоматики для других областей знания и для практики;
вероятностный характер различных процессов и закономерностей окружающего мира.
Числовые и буквенные выражения
уметь
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
применять понятия, связанные с делимостью целых чисел, при решении математических задач;
находить корни многочленов с одной переменной, раскладывать многочлены на множители;
выполнять действия с комплексными числами, пользоваться геометрической интерпретацией комплексных чисел. В простейших случаях находить комплексные корни уравнений с действительными коэффициентами;
В простейших случаях находить комплексные корни уравнений с действительными коэффициентами;
проводить преобразования числовых и буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
Функции и графики
уметь
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций, выполнять преобразования графиков;
описывать по графику и по формуле поведение и свойства функций;
решать уравнения, системы уравнений, неравенства, используя свойства функций и их графические представления.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания и исследования с помощью функций реальных зависимостей, представления их графически; интерпретации графиков реальных процессов.
Начала математического анализа
уметь
находить сумму бесконечно убывающей геометрической прогрессии;
вычислять производные и первообразные элементарных функций, применяя правила вычисления производных и первообразных, используя справочные материалы;
исследовать функции и строить их графики с помощью производной;
решать задачи с применением уравнения касательной к графику функции;
решать задачи на нахождение наибольшего и наименьшего значения функции на отрезке;
вычислять площадь криволинейной трапеции.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения геометрических, физических, экономических и других прикладных задач, в том числе задач на наибольшие и наименьшие значения с применением аппарата математического анализа.
Уравнения и неравенства
уметь
решать рациональные, показательные и логарифмические уравнения и неравенства, иррациональные и тригонометрические уравнения и их системы;
доказывать несложные неравенства;
решать текстовые задачи с помощью составления уравнений и неравенств, интерпретируя результат с учетом ограничений условия задачи;
изображать на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем;
находить приближенные решения уравнений и их систем, используя графический метод;
решать уравнения, неравенства и системы с применением графических представлений, свойств функций, производной.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
построения и исследования простейших математических моделей.
Элементы комбинаторики, статистики и теории вероятностей
уметь
решать простейшие комбинаторные задачи методами перебора, а также с использованием известных формул, вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля;
вычислять вероятности событий на основе.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
анализа реальных числовых данных, представленных в виде диаграмм, графиков; для анализа информации статистического характера.
Содержание курса в 10 классе
Действительные числа.
Натуральные и целые числа. Признаки делимости. Рациональные, иррациональные и действительные числа. Свойства арифметических операций над действительными числами. Числовая (действительная) прямая. Модуль действительного числа. Метод математической индукции.
Тригонометрические выражения.
Понятие числовой окружности. Радианное измерение углов.
Определение синуса, косинуса, тангенса, котангенса любого действительного числа, связь этих определений с определениями тригонометрических функций, введенных в курсе планиметрии.
Соотношения между тригонометрическими функциями одного и того же аргумента (угла, числа). Знаки тригонометрических функций в зависимости от расположения точки, изображающей число на числовой окружности.
Формулы приведения, вывод, их применение.
Формулы сложения (косинус и синус суммы и разности двух углов), их применение.
Формулы двойных и половинных углов.
Формулы преобразования суммы тригонометрических функций в произведение и произведения в сумму.
Преобразование выражения 13 EMBED Equation.DSMT4 1415 к виду 13 EMBED Equation.DSMT4 1415.
Применение основных тригонометрических формул к преобразованию выражений.
Тригонометрические функции и их графики.
Функция, определение, способы задания, свойства функций. Общая схема исследования функции (область определения, множество значений, нули функции, четность и нечетность, возрастание и убывание, экстремумы, наибольшие и наименьшие значения, ограниченность, промежутки знакопостоянства).
Свойства и графики функций 13 EMBED Equation.DSMT4 1415, 13 EMBED Equation.DSMT4 1415, 13 EMBED Equation.DSMT4 1415, 13 EMBED Equation.DSMT4 1415. Периодичность, основной период.
Преобразования графиков: параллельный перенос, симметрия относительно осей координат и относительно начала координат, растяжение и сжатие вдоль осей координат. Исследование тригонометрических функций и построение их графиков.
Тригонометрические уравнения (неравенства).
Обратные тригонометрические функции.
Формулы решений простейших тригонометрических уравнений 13 EMBED Equation.DSMT4 1415, 13 EMBED Equation.DSMT4 1415, 13 EMBED Equation.DSMT4 1415. Решение простейших тригонометрических уравнений. Решение простейших тригонометрических неравенств.
Решение тригонометрических уравнений (уравнения, сводящиеся к простейшим заменой неизвестного, применение основных тригонометрических формул для решения уравнений, однородные уравнения).
Комплексные числа.
Комплексные числа в алгебраической форме и арифметические операции над ними.
Тригонометрическая форма записи комплексного числа.
Решение квадратных уравнений с отрицательным дискриминантом и комплексными коэффициентами.
Возведение комплексного числа в степень. Извлечение квадратного и кубического корня из комплексного числа.
Степенная функция.
Степень с натуральным и целым показателем. Свойства степеней. Арифметический корень натуральной степени. Свойства корней. Степень с рациональным показателем. Свойства степеней. Понятие степени с иррациональным показателем.
Степенная функция, ее свойства и график.
Равносильные уравнения и неравенства. Иррациональные уравнения.
Показательная функция.
Показательная функция, ее свойства и график.
Показательные уравнения (простейшие). Показательные неравенства (простейшие).
Логарифмическая функция.
Определение логарифма числа. Свойства логарифмов. Десятичные и натуральные логарифмы.
Понятие об обратной функции. Область определения и множество значений обратной функции. График обратной функции.
Логарифмическая функция, ее свойства и график.
Логарифмические уравнения (простейшие). Логарифмические неравенства (простейшие).
Комбинаторика и вероятность.
Формулы числа перестановок, сочетаний, размещений. Правило умножения. Решение комбинаторных задач.
Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля.
Случайные события и вероятности.
Итоговое повторение курса алгебры и начал анализа 10 класса.
Преобразование рациональных, степенных, иррациональных и логарифмических выражений.
Преобразование тригонометрических выражений.
Решение тригонометрических уравнений.
Решение иррациональных уравнений.
Решение показательных и логарифмических уравнений (простейших).
Решение показательных и логарифмических неравенств (простейших).
Содержание курса в 11 классе.
Многочлены.
Многочлены от одной переменной. Делимость многочленов. Деление многочленов с остатком. Многочлены от нескольких переменных. Рациональные корни многочленов с целыми коэффициентами. Уравнения высших степеней. Решение целых алгебраических уравнений.
Уравнения, неравенства, системы
Свойства степени с натуральным, целым и рациональным показателем. Преобразование степенных и иррациональных выражений.
Свойства логарифмов. Преобразование логарифмических выражений.
Решение показательных и логарифмических уравнений. Решение показательных и логарифмических неравенств.
Системы линейных уравнений и неравенств. Графический метод решения систем.
Системы квадратных уравнений и неравенств.
Системы показательных уравнений и неравенств.
Системы логарифмических уравнений и неравенств.
Смешанные системы и совокупности уравнений от одной и двух переменных. Смешанные системы и совокупности неравенств от одной и двух переменных.
Решение текстовых задач на проценты, пропорции, с помощью уравнений.
Производная
Числовые последовательности. Понятие о пределе последовательности. Существование предела монотонной ограниченной последовательности. Предел функции, понятие о непрерывности функции.
Приращение аргумента и приращение функции. Понятие о производной функции. Ее геометрический и физический смысл. Уравнение касательной к графику функции.
Правила вычисления производных (суммы, произведения, частного). Таблица производных основных элементарных функций. Вычисление производных.
Дифференцирование сложной функции. Дифференцирование обратной функции
Применение производной
Признак возрастания (убывания) функции. Критические точки функции. Максимумы и минимумы функции.
Наибольшее и наименьшее значения функции на промежутке. Решение задач на оптимизацию с помощью производной.
Исследование функции и построение графиков с применением производной.
Первообразная и её применение
Определение первообразной. Основное свойство первообразной.
Правила нахождения первообразных. Таблица первообразных основных элементарных функций.
Площадь криволинейной трапеции. Формула Ньютона-Лейбница. Вычисление площадей плоских фигур с помощью первообразной.
Элементы комбинаторики, статистики и теории вероятностей
Статистическая обработка данных. Статистические понятия дискретного ряда (мода, медиана, среднее, размах вариации, частота признака). Диаграмма, гистограмма, полигон.
Решение текстовых задач с помощью графиков зависимостей.
Гауссова кривая. Закон больших чисел.
Элементарные и сложные события. Понятие о вероятности события. Вероятность суммы несовместных событий, вероятность противоположно события. Понятие о независимости событий. Вероятность и статистическая частота наступления события. Решение практических задач с применением вероятностных методов.
Итоговое повторение курса алгебры и начал математического анализа
Функция, определение, способы задания, свойства функций, сведенные в общую схему исследования функции.
Линейная функция. Систематизация ее свойств на основе общей схемы исследования функций. Решение задач с использованием свойств функции.
Функция 13 EMBED Equation.DSMT4 1415. Систематизация ее свойств на основе общей схемы исследования функций. Решение задач с использованием свойств функции.
Квадратичная функция 13 EMBED Equation.DSMT4 1415 и 13 EMBED Equation.DSMT4 1415. Систематизация ее свойств на основе общей схемы исследования функций. Решение задач с использованием свойств функции.
Показательная функция 13 EMBED Equation.DSMT4 1415, её свойства и график. Решение задач с использованием свойств функции.
Логарифмическая функция 13 EMBED Equation.DSMT4 1415, её свойства и график. Решение задач с использованием свойств функции.
Тригонометрические функции (13 EMBED Equation.DSMT4 1415, 13 EMBED Equation.DSMT4 1415, 13 EMBED Equation.DSMT4 1415, 13 EMBED Equation.DSMT4 1415), их свойства и графики. Решение задач с использованием свойств функций.
Тождественные преобразования степеней с рациональным показателем, иррациональных и логарифмических выражений.
Тождественные преобразования тригонометрических выражений.
Решение рациональных и иррациональных уравнений (в том числе содержащих модули и параметры).
Решение показательных и логарифмических уравнений и их систем (в том числе содержащих модули и параметры).
Решение тригонометрических уравнений, (в том числе содержащих модули и параметры).
Решение задач с использованием производной.
Пункты, выделенные курсивом, не применяются при контроле уровня подготовки выпускников профильных классов гуманитарного направления.
Пункты, выделенные курсивом, не применяются при контроле уровня подготовки выпускников профильных классов гуманитарного направления.
Предисловие
13PAGE 147615
13PAGE 14215
Root EntryEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation Native
Построение графиков тригонометрических функций с использованием MS Excel
Тип урока: урок обобщения и систематизации знаний
Цели:
- научить строить графики тригонометрических функций средствами MS Excel
- закрепить навыки работы в электронных таблицах,
- углубить представления учащихся о взаимосвязи предметов и прикладной ориентации курса информатики.
ХОД УРОКА
Если вычислений много, а времени мало, то доверьтесь электронным таблицам
1. Сообщение целей и задач урока
– Ребята, сегодня мы продолжим знакомиться с
возможностями электронных таблиц Excel. Давайте
вспомним, для чего предназначены электронные
таблицы? (Автоматизация расчетов).
– Что вы уже умеете делать в электронных
таблицах? (Создавать и форматировать таблицу,
работать с типами данных, решать задачи
используя относительную и абсолютную ссылки,
строить диаграммы).
– На уроках математики вы изучили
тригонометрические функции и их графики. При
построении графиков тригонометрических функций
необходимо учесть множество нюансов. Начертить
синусоиду или косинусоиду красиво – это уже
искусство, а если необходимо график растянуть,
сжать или симметрично отобразить относительно
какой-либо оси – это может вызвать затруднения. И
здесь нам на помощь нам придут электронные
таблицы MS Excel. Вы узнаете как с их помощью быстро и
красиво построить график.
Сегодня на уроке мы познакомимся с алгоритмом
построения графика тригонометрической функции.
Эпиграфом к уроку я взяла слова «Если
вычислений много, а времени мало, то доверьтесь
электронным таблицам»
2. Актуализация знаний
Фронтальный опрос (за правильный ответ даем красную карточку)
- С чего начинается ввод формулы в ячейку? (Со знака равенства)
- На каком языке набирается формула в MS Excel? (Английском)
- Как скопировать формулу в другие ячейки?(С помощью маркера автозаполнения)
- Как изменить число десятичных знаков после запятой в отображаемом числе? (Выделить, Формат, Ячейки, вкладка Число, Числовой формат, …..)
- Что означает запись ###### в ячейке? (Длина водимых данных превышает ширину ячейки)
- Каким образом набирается формула, содержащая какую-либо функцию? (Выделить ячейку, в которую нужно вставить первое значение функции;Вставка, Функция, выбрать Категорию и саму функцию)
- Каким образом набирается формула, содержащая сложную функцию, например, y = |x2|? (Вставляется внешняя функция с пустым аргументом, затем левее строки редактирования формул из раскрывающегося списка выбирается внутренняя функция)
- Как вставить какой-либо символ, например, математический в ячейку? (Вставка, Символ, в появившемся диалоговом окне выбрать шрифт Symbol и нужный символ)
На прошлом уроке вы строили графики элементарных функций. Давайте повторим алгоритм построения графика (Учащиеся называют шаги построения графика функции, а учитель показывает соответствующий пункт алгоритма на доске (используется проектор) и если необходимо дополняет ответ учеников) (см. Приложение 1).
3. Изучение нового
С использованием презентации (см. Приложение 2) учитель рассказывает, как строится график тригонометрической функций, а затем выполняет его построение в электронных таблицах.
Задание. Построить в MS Excel графики функций y = Sin x и y = |1 – sin x| на промежутке [–360о; 360о] с шагом 15о.
Построенные графики смотри в Приложении 3
4. Закрепление полученных знаний
Каждому ученику даётся карточка с заданием и оценочный лист, который после выполнения задания отдается учителю (Каждый пункт в оценочном листе является шагом построения графика тригонометрической функции с использованием MSExcel). Презентация находится в сетевой папке, и любой ученик может ею воспользоваться при выполнении своего задания.
Задание. Построить в MS Excel графики функций на промежутке [–36о;36о] с шагом 15о.
5. Проверка построенных графиков и разбор нюансов
Один из учеников строил график y = |Sin x| / Sin x на промежутке [–360о;360о] с шагом 15о. На доске демонстрируется этот график и график, построенный традиционным алгебраическим способом.
С помощью этого примера обращается внимание учащихся, что существуют функции, графики которых в электронных таблицах строятся неточно. Учащихся можно попросить найти неточности в графике, построенном с помощью MS Excel и попросить объяснить их.
График, построенный традиционным алгебраическим
График, построенный с использованием МS Exel
6. Подведение итогов
Учеников просят ответить на вопросы:
- В чем достоинства и недостатки алгебраического метода построения графиков функций и построения графиков с использованием электронных таблиц?
- Каким образом можно использовать полученные на уроке знания в учебе?
Вывод. MS Excel облегчает построение графиков функций, но без глубоких математических знаний построить точные графики сложных функций (тригонометрических функций, функций с модулем, функций имеющих точки разрыва) невозможно.
Математика – это царица всех наук!
7. Постановка Д/З.
Построить график функции y= 1 + 0,5*ctg(X–П/4) на промежутке [–360о;360о] с шагом 15о.
8. Рефлексия
Оцени свое настроение на уроке
Оценочный лист
Фамилия, имя |
Количество баллов |
| Создание заголовка таблицы | 0,2 |
| Заполнение ряда значений аргумента х в градусах | 0,1 |
| Заполнение ряда значений аргумента х в радианах (перевод градусов в радианы) | 0,5 |
| Запись формулы для вычисления значений сложной функции | 1 |
| Запись формулы для вычисления значений элементарной функции | 0,5 |
| Заполнение рядов значений функций (для обеих функций) | 0,1 |
| Установка числового формата данных | 0,2 |
| Построение графиков функций | 1 |
| Перенос оси | 0,2 |
| Подпись значений х на оси абсцисс (в градусах) | 0,2 |
| Создание ряда значений аргумента х (в радианах, например П/3) | 0,7 |
| Подпись значений х на оси абсцисс (в радианах, например П/3) | 0,5 |
ИТОГО |
5 |
| Если вы обращаетесь к учителю, то ставится 0 баллов |
|
Нахождение уравнения графической линии — Задача 1
Чтобы найти уравнение построенной на графике линии, найдите точку пересечения по оси Y и наклон, чтобы записать уравнение в форме точки пересечения по оси Y (y = mx + b). Наклон — это изменение y по сравнению с изменением x. Найдите две точки на линии и нарисуйте наклонный треугольник, соединяющий две точки. Обозначьте стороны треугольника. Это сообщит вам значение роста (изменение y, числитель) и значение пробега (изменение x, знаменатель).Пересечение оси y происходит от точки, где линия проходит ось y. Значение Y координаты — это точка пересечения по оси Y или значение «b». Подключите наклон m и точку пересечения оси y b к форме линии пересечения с уклоном.
Задачи этого типа используются во всем курсе алгебры 1. Под типом задачи я подразумеваю, когда вам дается график и вас просят написать его уравнение.Поэтому, когда вы это делаете, есть много разных подходов к этому. Мой личный любимый способ — найти наклон и точку пересечения оси y. Особенно в таких графиках, где такие вещи бросаются в глаза. Вот что я имею в виду.
Для уравнения прямой, я думаю, y равно mx плюс форма b. Мне нужен наклон и точка пересечения по оси Y. Эта буква y и эта буква x останутся в моем уравнении, так что давайте продолжим и пощупаем пробелы.
Мой номер наклона можно найти по изменению y поверх изменения x.Один из способов сделать это — найти две любые точки, через которые проходит линия, и нарисовать наклонный треугольник. Итак, давайте посмотрим, эта линия проходит точно через эту точку, а эта точка прямо там. Итак, я хочу нарисовать треугольник наклона, который их соединяет, хорошо, а затем я помечу стороны, которые будут говорить мне о моем подъеме и моем беге, а затем наклон — это вертикальное изменение поверх горизонтального изменения. Так что в моем случае наклон будет +3/2. Я почти закончил. +3/2, милая, не так уж и плохо. Последнее, что мне нужно из моего уравнения y равно mx плюс b, — это точка пересечения y.
Помните, что y — это вертикальная ось, поэтому точка пересечения y происходит от того места, где графическая линия пересекает эту вертикальную ось. Вот и все, координаты 0 для x, 3 для y. 3 — важная часть, которая будет моим значением b для моего пересечения с y. Уравнение для линии будет y равно 3 / 2x плюс 3.
Вот и все. Когда у вас есть такой график, и особенно когда он нанесен на миллиметровую бумагу, например, графическая сетка, очень легко найти уравнение в форме наклон-пересечение.Первое, что вам нужно сделать, это найти угол наклона, а второе — найти точку пересечения оси y, а затем просто подключить их.
Графические линейные уравнения
График линейного уравнения с двумя переменными представляет собой линию (поэтому его называют линейный ).
Если вы знаете, что уравнение линейно, вы можете построить его график, найдя любые два решения.
( Икс 1 , y 1 ) а также ( Икс 2 , y 2 ) ,
нанесение этих двух точек на карту и построение линии, соединяющей их.
Пример 1:
Изобразите уравнение Икс + 2 y знак равно 7 .
Вы можете найти два решения, соответствующие Икс -перехватывает а также y -перехватывает графика, установив сначала Икс знак равно 0 а потом y знак равно 0 .
Когда Икс знак равно 0 , мы получили:
0 + 2 y знак равно 7 y знак равно 3.5
Когда y знак равно 0 , мы получили:
Икс + 2 ( 0 ) знак равно 7 Икс знак равно 7
Итак, две точки ( 0 , 3.5 ) а также ( 7 , 0 ) .
Постройте эти две точки и проведите линию, соединяющую их.
Если уравнение находится в форма пересечения склонов или же точечно-наклонная форма , вы также можете использовать склон чтобы помочь вам построить график.
Пример 2:
Постройте линию y знак равно 3 Икс + 1 .
Из уравнения мы знаем, что y -перехват 1 , точка ( 0 , 1 ) и наклон 3 .Постройте точку ( 0 , 1 ) и оттуда идти вверх 3 единиц и вправо 1 единицы и нанесите на график вторую точку. Проведите линию, содержащую обе точки.
Горизонтальные и вертикальные линии иметь очень простые уравнения.
Пример 3:
Горизонтальная линия: y знак равно 3
Вертикальная линия: Икс знак равно — 2
3.6 Графики функций — Промежуточная алгебра 2e
Цели обучения
К концу этого раздела вы сможете:
- Используйте тест вертикальной линии
- Определить графики основных функций
- Считать информацию с графика функции
Будьте готовы 3.16
Перед тем, как начать, пройдите тест на готовность.
Оцените: 2323 32,32.
Если вы пропустили эту проблему, просмотрите Пример 1.5.
Будьте готовы 3.17
Оценить: ⓐ | 7 || 7 | Ⓑ | −3 |. | −3 |.
Если вы пропустили эту проблему, просмотрите Пример 1.14.
Будьте готовы 3.18
Оцените: ⓐ 44 ⓑ 16,16.
Если вы пропустили эту проблему, просмотрите Пример 1.41.
Используйте тест вертикальной линии
В предыдущем разделе мы узнали, как определить, является ли отношение функцией. Рассматриваемые нами отношения были выражены в виде набора упорядоченных пар, отображения или уравнения. Теперь мы посмотрим, как определить, является ли график графиком функции.
Упорядоченная пара (x, y) (x, y) является решением линейного уравнения, если уравнение является истинным утверждением, когда x — и y -значения упорядоченной пары подставляются в уравнение .
График линейного уравнения — это прямая линия, где каждая точка на прямой является решением уравнения, а каждое решение этого уравнения является точкой на этой прямой.
На рисунке 3.14 мы видим, что на графике уравнения y = 2x − 3, y = 2x − 3 для каждого значения x существует только одно значение y , как показано в прилагаемой таблице. .
Рисунок 3.14
Отношение является функцией, если каждый элемент домена имеет ровно одно значение в диапазоне. Таким образом, отношение, определяемое уравнением y = 2x − 3y = 2x − 3, является функцией.
Если мы посмотрим на график, каждая вертикальная пунктирная линия пересекает линию только в одной точке. Это имеет смысл, как и в функции, для каждого значения x существует только одно значение y .
Если вертикальная линия дважды коснется графика, значение x будет сопоставлено с двумя значениями y , и поэтому график не будет представлять функцию.
Это приводит нас к тесту вертикальной линии. Набор точек в прямоугольной системе координат является графиком функции, если каждая вертикальная линия пересекает график не более чем в одной точке. Если какая-либо вертикальная линия пересекает график более чем в одной точке, график не представляет функцию.
Тест вертикальной линии
Набор точек в прямоугольной системе координат является графиком функции, если каждая вертикальная линия пересекает график не более чем в одной точке.
Если какая-либо вертикальная линия пересекает график более чем в одной точке, график не представляет функцию.
Пример 3.51
Определите, является ли каждый график графиком функции.
ⓐ Поскольку любая вертикальная линия пересекает график не более чем в одной точке, график является графиком функции.
Ⓑ Одна из вертикальных линий, показанных на графике, пересекает его в двух точках. Этот график не представляет функцию.
Попробуйте 3.101
Определите, является ли каждый график графиком функции.
Попробуйте 3.102
Определите, является ли каждый график графиком функции.
Определите графики основных функций
Мы использовали уравнение y = 2x − 3y = 2x − 3 и его график при разработке теста вертикальной линии. Мы сказали, что отношение, определяемое уравнением y = 2x − 3y = 2x − 3, является функцией.
Мы можем записать это в обозначениях функций как f (x) = 2x − 3.f (x) = 2x − 3. Это по-прежнему означает то же самое. График функции — это график всех упорядоченных пар (x, y) (x, y), где y = f (x).у = f (х). Таким образом, мы можем записать упорядоченные пары как (x, f (x)). (X, f (x)). Выглядит иначе, но график останется прежним.
Сравните график y = 2x − 3y = 2x − 3, ранее показанный на рис. 3.14, с графиком f (x) = 2x − 3f (x) = 2x − 3, показанным на рис. 3.15. Ничего не изменилось, кроме обозначений.
Рисунок 3.15
График функции
График функции — это график всех упорядоченных пар (x, y) (x, y) или с использованием обозначения функции (x, f (x)) (x, f (x)), где y = f (Икс).у = f (х).
f имя функции x x координата упорядоченной пары f (x) координата y упорядоченной пары f имя функции x x координата упорядоченной пары f (x) координата y упорядоченной парыПо мере продвижения нашего исследования полезно ознакомиться с графиками нескольких основных функций и уметь их идентифицировать.
Благодаря нашей предыдущей работе мы знакомы с графиками линейных уравнений. Процесс, который мы использовали, чтобы решить, является ли y = 2x − 3y = 2x − 3 функцией, применим ко всем линейным уравнениям.Все нелинейные линейные уравнения являются функциями. Вертикальные линии не являются функциями, поскольку значение x имеет бесконечно много значений y .
Мы написали линейные уравнения в нескольких формах, но здесь будет наиболее полезно использовать форму линейного уравнения с пересечением угла наклона. Форма линейного уравнения с угловым пересечением: y = mx + b.y = mx + b. В обозначении функции эта линейная функция принимает вид f (x) = mx + bf (x) = mx + b, где m, — наклон прямой, а b — интервал пересечения y .
Домен — это набор всех действительных чисел, а диапазон — это также набор всех действительных чисел.
Линейная функция
Мы будем использовать методы построения графиков, которые мы использовали ранее, для построения графиков основных функций.
Пример 3.52
График: f (x) = — 2x − 4.f (x) = — 2x − 4.
| f (x) = — 2x − 4f (x) = — 2x − 4 | |
| Мы признаем это линейной функцией. | |
| Найдите наклон и точку пересечения y . | м = −2м = −2 b = −4b = −4 |
| График с использованием точки пересечения наклона. |
Попробуйте 3.103
График: f (x) = — 3x − 1f (x) = — 3x − 1
Попробуйте 3.104
График: f (x) = — 4x − 5f (x) = — 4x − 5
Следующая функция, график которой мы рассмотрим, называется постоянной функцией, и ее уравнение имеет вид f (x) = b, f (x) = b, где b — любое действительное число. Если мы заменим f (x) f (x) на y, мы получим y = b.у = б. Мы узнаем это как горизонтальную линию, пересечение которой y равно b . График функции f (x) = b, f (x) = b также является горизонтальной линией, пересечение которой y равно b .
Обратите внимание, что для любого действительного числа, которое мы вводим в функцию, значение функции будет b . Это говорит о том, что диапазон имеет только одно значение: b .
Постоянная функция
Пример 3.53
| f (x) = 4f (x) = 4 | |
| Мы признаем это постоянной функцией. | |
| График представляет собой горизонтальную линию, проходящую через (0,4). (0,4). |
Попробуйте 3.105
График: f (x) = — 2. f (x) = — 2.
Идентификационная функция, f (x) = xf (x) = x, является частным случаем линейной функции. Если мы запишем это в линейной форме функции, f (x) = 1x + 0, f (x) = 1x + 0, мы увидим, что наклон равен 1, а интервал y равен 0.
Функция идентификации
Следующая функция, которую мы рассмотрим, не является линейной функцией.Так что график не будет линией. Единственный метод, который у нас есть для построения графика этой функции, — это точечное построение. Поскольку это незнакомая функция, мы выбираем несколько положительных и отрицательных значений, а также 0 для наших значений x.
Пример 3.54
Выбираем x -значения. Мы подставляем их, а затем создаем диаграмму, как показано.
Глядя на результат в примере 3.54, мы можем резюмировать особенности функции квадрата. Мы называем этот граф параболой.Когда мы рассматриваем домен, обратите внимание, что любое действительное число может использоваться как значение x . Домен — это все реальные числа.
Диапазон не всех действительных чисел. Обратите внимание, что график состоит из значений и , которые никогда не опускаются ниже нуля. Это имеет смысл, поскольку квадрат любого числа не может быть отрицательным. Итак, диапазон квадратной функции — это все неотрицательные действительные числа.
Квадратная функция
Следующая функция, которую мы рассмотрим, также не является линейной функцией, поэтому график не будет линией.Мы снова будем использовать точечный график и обязательно выберем несколько положительных и отрицательных значений, а также 0 для наших значений x .
Пример 3.55
Выбираем x -значения. Подставляем их, а затем создаем диаграмму.
Попробуй 3.110
График: f (x) = — x3.f (x) = — x3.
Глядя на результат в примере 3.55, мы можем резюмировать особенности функции куба. Когда мы рассматриваем домен, обратите внимание, что любое действительное число может использоваться как значение x .Домен — это все реальные числа.
Диапазон состоит из действительных чисел. Это имеет смысл, поскольку куб любого ненулевого числа может быть положительным или отрицательным. Итак, диапазон функции куба — это все действительные числа.
Функция куба
Следующая функция, которую мы рассмотрим, не возводит в квадрат и не кубирует входные значения, а, скорее, извлекает квадратный корень из этих значений.
Давайте изобразим график функции f (x) = xf (x) = x, а затем суммируем характеристики функции. Помните, что мы можем извлекать квадратный корень только из неотрицательных действительных чисел, поэтому нашей областью будут неотрицательные действительные числа.
Пример 3.56
Выбираем x -значения. Поскольку мы будем извлекать квадратный корень, мы выбираем числа, которые являются точными квадратами, чтобы облегчить нашу работу. Подставляем их, а затем создаем диаграмму.
Попробуй 3.112
График: f (x) = — x.f (x) = — x.
Функция квадратного корня
Наша последняя основная функция — это функция абсолютного значения, f (x) = | x | .f (x) = | x |. Имейте в виду, что абсолютное значение числа — это его расстояние от нуля.Поскольку мы никогда не измеряем расстояние как отрицательное число, мы никогда не получим отрицательное число в диапазоне.
Пример 3.57
График: f (x) = | x | .f (x) = | x |.
Выбираем x -значения. Подставляем их, а затем создаем диаграмму.
Попробуй 3.113
График: f (x) = | x | .f (x) = | x |.
Попробуй 3.114
График: f (x) = — | x | .f (x) = — | x |.
Функция абсолютного значения
Чтение информации из графика функции
В науке и бизнесе данные часто собираются, а затем отображаются в виде графиков.График анализируется, информация получается из графика, а затем часто на основе данных делаются прогнозы.
Мы начнем с чтения домена и диапазона функции по ее графику.
Помните, что домен — это набор всех значений x в упорядоченных парах функции. Чтобы найти домен, мы смотрим на график и находим все значения x , которым соответствуют соответствующие значения на графике. Следуйте значению x вверх или вниз по вертикали.Если вы нажмете на график функции, тогда x находится в домене.
Помните, что диапазон — это набор всех значений y в упорядоченных парах функции. Чтобы найти диапазон, мы смотрим на график и находим все значения y , которым соответствуют соответствующие значения на графике. Следуйте значению y влево или вправо по горизонтали. Если вы нажмете на график функции, тогда y находится в диапазоне.
Пример 3.58
Используйте график функции, чтобы найти ее домен и диапазон.Запишите домен и диапазон в виде интервалов.
Чтобы найти домен, мы смотрим на график и находим все значения x , которые соответствуют точке на графике. Домен выделен красным на графике. Область — [−3,3]. [- 3,3].
Чтобы найти диапазон, мы смотрим на график и находим все значения y , которые соответствуют точке на графике. Диапазон выделен синим цветом на графике. Диапазон составляет [−1,3]. [- 1,3].
Попробуй 3.115
Используйте график функции, чтобы найти ее домен и диапазон. Запишите домен и диапазон в виде интервалов.
Попробуй 3.116
Используйте график функции, чтобы найти ее домен и диапазон. Запишите домен и диапазон в виде интервалов.
Теперь мы собираемся прочитать информацию с графика, которую вы можете увидеть в будущих математических классах.
Пример 3.59
Используйте график функции, чтобы найти указанные значения.
ⓐ Найдите: f (0) .f (0).
Ⓑ Найдите: f (32π) .f (32π).
Ⓒ Найдите: f (−12π) .f (−12π).
Ⓓ Найдите значения для x , когда f (x) = 0. f (x) = 0.
Ⓔ Найдите точки пересечения x .
Ⓕ Найдите точки пересечения и .
Ⓖ Найдите домен. Запишите это в интервальной записи.
Ⓗ Найдите диапазон. Запишите это в интервальной записи.
ⓐ Когда x = 0, x = 0, функция пересекает ось y в точке 0. Итак, f (0) = 0. f (0) = 0.
Ⓑ Когда x = 32π, x = 32π, значение y функции равно -1.−1. Итак, f (32π) = — 1. f (32π) = — 1.
Ⓒ Когда x = −12π, x = −12π, значение функции y равно −1. − 1. Итак, f (−12π) = — 1. f (−12π) = — 1.
Ⓓ Функция равна 0 в точках, (−2π, 0), (- π, 0), (0,0), (π, 0), (2π, 0). (- 2π, 0), (- π, 0), (0,0), (π, 0), (2π, 0). Значения x при f (x) = 0f (x) = 0 равны −2π, −π, 0, π, 2π, −2π, −π, 0, π, 2π.
Ⓔ Перехват x происходит, когда y = 0. y = 0. Таким образом, перехват x происходит, когда f (x) = 0. f (x) = 0. x -перехваты: (−2π, 0), (- π, 0), (0,0), (π, 0), (2π, 0).(−2π, 0), (- π, 0), (0,0), (π, 0), (2π, 0).
Ⓕ Перехват y происходит, когда x = 0.x = 0. Таким образом, перехват y происходит в f (0) .f (0). Перехват y равен (0,0). (0,0).
Ⓖ Эта функция имеет значение для всех значений x . Следовательно, область в обозначении интервалов равна (−∞, ∞) (- ∞, ∞)
Ⓗ Значения этой функции или y -значения изменяются от -1-1 до 1. Следовательно, диапазон в обозначении интервала равен [-1,1]. [-1,1].
Попробуй 3.117
Используйте график функции, чтобы найти указанные значения.
ⓐ Найдите: f (0) .f (0).
Ⓑ Найдите: f (12π) .f (12π).
Ⓒ Найдите: f (−32π) .f (−32π).
Ⓓ Найдите значения для x , когда f (x) = 0. f (x) = 0.
Ⓔ Найдите точки пересечения x .
Ⓕ Найдите точки пересечения и .
Ⓖ Найдите домен. Запишите это в интервальной записи.
Ⓗ Найдите диапазон. Запишите это в интервальной записи.
Попробуй 3.118
Используйте график функции, чтобы найти указанные значения.
ⓐ Найдите: f (0).f (0).
Ⓑ Найдите: f (π) .f (π).
Ⓒ Найдите: f (−π) .f (−π).
Ⓓ Найдите значения для x , когда f (x) = 0. f (x) = 0.
Ⓔ Найдите точки пересечения x .
Ⓕ Найдите точки пересечения и .
Ⓖ Найдите домен. Запишите это в интервальной записи.
Ⓗ Найдите диапазон. Запишите это в интервальной записи.
Раздел 3.6. Упражнения
Практика ведет к совершенству
Используйте тест вертикальной линии
В следующих упражнениях определите, является ли каждый график графиком функции.
338. ⓐ
ⓑ
ⓐ
ⓑ
Графики основных функций
В следующих упражнениях ⓐ построите график каждой функции ⓑ укажите ее домен и диапазон. Запишите домен и диапазон в виде интервалов.
343.f (x) = — x − 2f (x) = — x − 2
344.f (x) = — 4x − 3f (x) = — 4x − 3
Считывание информации из графика функции
В следующих упражнениях используйте график функции, чтобы найти ее домен и диапазон.Запишите домен и диапазон в виде интервалов.
378. 380. 382.В следующих упражнениях используйте график функции, чтобы найти указанные значения.
383. ⓐ Найдите: f (0) .f (0).
Ⓑ Найдите: f (12π) .f (12π).
Ⓒ Найдите: f (−32π) .f (−32π).
Ⓓ Найдите значения для x , когда f (x) = 0. f (x) = 0.
Ⓔ Найдите точки пересечения x .
Ⓕ Найдите точки пересечения и .
Ⓖ Найдите домен. Запишите это в интервальной записи.
Ⓗ Найдите диапазон. Запишите это в интервальной записи.
ⓐ Найдите: f (0) .f (0).
Ⓑ Найдите: f (π) .f (π).
Ⓒ Найдите: f (−π) .f (−π).
Ⓓ Найдите значения для x , когда f (x) = 0. f (x) = 0.
Ⓔ Найдите точки пересечения x .
Ⓕ Найдите точки пересечения и .
Ⓖ Найдите домен. Запишите это в интервальной записи.
Ⓗ Найдите диапазон. Запишите его в обозначении интервала
ⓐ Найдите: f (0) .f (0).
Ⓑ Найдите: f (−3) .f (−3).
Ⓒ Найдите: f (3).f (3).
Ⓓ Найдите значения для x , когда f (x) = 0. f (x) = 0.
Ⓔ Найдите точки пересечения x .
Ⓕ Найдите точки пересечения и .
Ⓖ Найдите домен. Запишите это в интервальной записи.
Ⓗ Найдите диапазон. Запишите это в интервальной записи.
ⓐ Найдите: f (0) .f (0).
Ⓑ Найдите значения для x , когда f (x) = 0. f (x) = 0.
Ⓒ Найдите точки пересечения x .
Ⓓ Найдите точки пересечения и .
Ⓔ Найдите домен.Запишите это в интервальной записи.
Ⓕ Найдите диапазон. Запишите его в обозначении интервала
Письменные упражнения
387.Объясните своими словами, как найти домен по графику.
388.Объясните своими словами, как найти диапазон по графику.
389.Объясните своими словами, как использовать тест вертикальной линии.
390.Нарисуйте эскиз функций квадрата и куба. В чем сходство и различие графиков?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что вы сделаете, изучив этот контрольный список, чтобы стать уверенным в достижении всех целей?
Стандартная форма Уравнение линии с примерами, графиками и формулой
Обзор различных форм уравнения линии
Есть много разных способов выразить уравнение линии.Есть форма пересечения откоса, форма точечного откоса, а также тема этой страницы. Каждый из них выражает уравнение линии, и у каждого есть свои плюсы и минусы. Например, форма точечного наклона позволяет легко найти уравнение линии, когда вы знаете только наклон и одну точку на линии. Стандартная форма также имеет несколько различных применений, но об этом позже.
Определение стандартной формы уравнения
Уравнение стандартной формы линии имеет следующую формулу:$ \ text {Формула}: \\ Ax + By = C \\ A \ ne 0 \\ B \ ne 0 $
Общая формула для пересечений по осям x и y
Для уравнения прямой в стандартной форме $$ Ax + By = C $$ где $$ A \ ne 0 $$ а также $$ B \ ne 0 $$, вы можете использовать приведенные ниже формулы, чтобы найти точки пересечения по осям x и y.
$ \ text {X Intercept:} \\ \ frac C A = \ frac 6 3 = 2 $
$ \ text {Y Intercept:} \\ \ frac C B = \ frac 6 2 = 3 $
Примерные и не примерные уравнения
| Примеры стандартной формы | Без примеров |
| $$ 3x + 5y = 3 $$ | $$ 2y = 4x + 2 $$ |
| $$ 2x — y = 6 $$ | $$ x = 6 — y $$ |
| $$ -2x + y = 7 $$ | $$ y = 2x + 7 $$ |
Когда полезна стандартная форма?
Когда другие формы более полезны?
Видеоурок по уравнению прямой в стандартной форме
Пример 1
Найдите точки пересечения и изобразите следующее уравнение: 3x + 2y = 6
Как найти точку пересечения по оси x:
| Установить y = 0 | 3x + 2 (0) = 6 |
| Решить относительно x |
Как найти точку пересечения оси Y:
| Установить x = 0 | 3 (0) + 2y = 6 |
| Решить для y |
Как построить график из стандартной формы
Пример 2
Постройте точки пересечения по осям x и y и проведите линию на миллиметровой бумаге!
Задача 1
Определите, какие уравнения внизу справа имеют стандартную форму.
Покажи ответ- Уравнение 1: 2x + 5 = 2y
- Уравнение 2: 2x + 3y = 4
- Уравнение 3: y = 2x + 3
- Уравнение 4: 4x — $$ \ frac 1 2 $$ y = 11
Уравнение 2 и уравнение 4 — единственные в стандартной форме.
Уравнение 3 имеет форму пересечения наклона.
Задача 2
Определите, какие уравнения внизу справа имеют стандартную форму.
Покажи ответ- Уравнение 1: 11 = ¼x + ½y
- Уравнение 2: 2x + 5 + 2y = 3
- Уравнение 3: y — 2 = 3 (x — 4)
- Уравнение 4: $$ \ frac 1 2 $$ y — 4x = 0
Уравнение 1 и уравнение 4 — единственные в стандартной форме.
Уравнение 3 имеет форму точечного наклона.
Задача 3
Найдите точки пересечения и затем изобразите следующее уравнение 2x + 3y = 18.
Сначала найдите точки пересечения, установив y, а затем x равные нулю.Это довольно просто, поскольку линия уже имеет стандартную форму.
Покажи ответЗадача 4
Найдите точки пересечения и затем изобразите следующее уравнение 3x + 5y = 15.
Покажи ответЗадача 5
Найдите точки пересечения и затем изобразите следующее уравнение 3y — 2x = -12.
Покажи ответкак написать уравнение с помощью графика?
Я не могу помочь вам получить точный ответ, не видя графика, но могу дать вам несколько советов, которые могут вам помочь.
1. Поскольку вы заявили, что график представляет собой диагональную линию, я знаю, что вы ищете линейное уравнение .Линейные уравнения можно записать в виде y = mx + b .
Чтобы получить точное уравнение, нам нужно найти значения m и b (вы оставите th2.e y и x в окончательном ответе).
2. Знак на значении м (наклон линии) определяется тем, идет ли оно вверх или вниз при движении вправо. Если линия идет вправо, m положительно. Если линия идет вправо, m отрицательно.
3. Предположим, вы видите оси x и y с отметками решетки (жирные вертикальные и горизонтальные линии с небольшими отметками, равномерно расположенными вдоль них), вы можете найти vlaue м (наклон линии).Наклон определяется путем подсчета того, насколько линия перемещается вверх или вниз на расстояние, перемещаясь справа налево.
Например, вы можете обнаружить, что в одной точке линии вы находитесь на одну отметку над осью x и две отметки справа от оси y. Двигаясь по линии, вы можете обнаружить, что находитесь на четыре метки над осью x и четыре метки над осью y. Наклон определяется путем сравнения изменения высоты (1 метка вверх дает 4 метки) и изменения длины (2 метки дают 4 метки). Соотношение 3 (4-1) к 2 (4-2), поэтому наклон (м) равен 3/2.
4. Если вы видите, где линия пересекает ось Y (жирная вертикальная линия), у вас есть значение b.
5. Если вы не видите, где линия пересекает ось Y, вы все равно можете найти значение b. Просто найдите точку на линии. Подставьте значения x и y точки вместе с наклоном (m) в формулу пересечения наклона (y = mx + b) и решите относительно b.
6. Напишите форму пересечения наклона уравнения со значениями, которые вы нашли для m и b.
Еще один быстрый совет: если у вас есть хэши на оси x и оси y, но не записаны числа, предположите, что каждый хеш представляет 1.
Математическая сцена — Уравнения III — Урок 3
Математическая сцена — Уравнения III — Урок 3 — Квадратные уравнения| 2008 Rasmus ehf и Jhann sak | Уравнения III |
Урок 3 Пересечение точек графиков
Как приступить к поиску точек, в которых два графика y = f (x) и y = g (x) пересекаются?
Мы уже знаем, как найти график
f (x) пересекает ось x.Здесь y = 0. Мы вычисляем его, решая
уравнение f (x) = 0.
Когда графики y = f (x) и y =
g (x) пересекаются, оба графа имеют
точно такие же значения x и y. Итак, мы можем найти точку или точки
пересечения путем решения уравнения f (x)
= g (x). Решение этого уравнения даст нам значение (я) x
точка (и) пересечения. Затем мы можем найти значение y, поместив значение для
x, который мы нашли в одном из исходных уравнений.То есть путем расчета
либо f (x), либо g (x).
Пример 1
Рассчитать точку пересечение двух прямых f (x) = 2x — 1 и g (x) = x + 1. Сначала давайте посмотрим на график двух функций. Мы видим смысл пересечение есть (2, 3).
Рассчитываем точку пересечения по решение уравнения f (x) = g (x). То есть:
2х — 1 = х + 1
2х — х = 1 + 1
х = 2
Координата Y теперь может быть найдена вычисление f (2):
f (2) = 2 × 2 — 1 = 3
Точка пересечения — (2, 3) .
Пример показывает, что мы можем найти точку
пересечения двумя способами.
Либо графически, нарисовав два графика в одной системе координат, либо
алгебраически, решив уравнение, подобное тому, которое приведено в приведенном выше примере.
Некоторые уравнения нельзя решить алгебраически, но мы можем найти решения, которые исправляем до любого количества значащих цифр, используя компьютеры и калькуляторы.
Пример 2
Решите уравнение x 2 — 2x — 3 = 2x — 3 сначала графически, а затем алгебраически.
Рисуем графики f (x) = x 2 — 2x — 3 и g (x) = 2x — 3, составив таблицу значений и построив график точки. Как из графика, так и из таблицы значений видно, что графики пересекаются при x = 0 и x = 4 .
Решает алгебраически:
x 2 — 2x — 3 = 2x — 3
x 2 — 4x = 0
х (х — 4) = 0
Даем решения x = 0 и x = 4 .
Пример 3
Решите уравнение x 2 — 1 = 2x — 3
Сначала переместите все термины перейдите к левой части уравнения и упростите.
Это дает x 2 — 2x + 2 = 0
Используем формулу корней квадратного уравнения с a = 1, b = −2 и c = 2.
Число под знаком квадратного корня:
отрицательный, что означает, что это уравнение не имеет решения.
Чтобы понять, почему это так, мы рисуем графики левой части оригинала.
уравнение
f (x) = x 2 — 1 и правая часть g (x) = 2x — 3.
Мы видим, что парабола f (x) и прямая g (x) не пересекаются.Легко видеть, что мы не может вычислить точку пересечения просто потому, что такой точки нет.
Пример 4
Решите уравнение x 3 — 3x + 2 = x 2 — 2x + 1
Как и в предыдущем примере, мы перемещаем все слагаемые в левую часть уравнения.
х 3 — 3x + 2 = x 2 — 2x + 1
x 3 — x 2 — x + 1 = 0
(x 3 — x 2 ) — (x — 1) = 0
x 2 (x — 1) — (x — 1) = 0
(х — 1) (х 2 — 1) = 0
(х — 1) (х — 1) (х + 1) = 0
Расчеты показывают, что их всего два решений, x = 1 и x = −1, но кубическое уравнение может иметь три решения.График показывает нам, что происходит.
Графики f (x) = x 2 — 2x + 1 и g (x) = x 3 — 3x + 2 пересекаются только в двух местах, где x = −1 и x = 1, которые были решениями уравнение.
Пример 5
Решите уравнение x 2 = x
Легко видеть, что x = 0 и x = 1 являются решения уравнения, но есть ли еще решения? Это не очень вероятно, но давайте посмотрим на графики.
Назовите левую часть f (x) = x 2 и правую часть g (x) = x. Помните, что g (x) не может принимать отрицательные значения x, поэтому не может быть никаких отрицательные точки пересечения.
На графике видно, что точек всего две
пересечения и, следовательно, только два решения уравнения. х = 0 и х =
1.
Вот как решить уравнение расчетом:
| x 2 = x х 4 = х х 4 — х = 0 х (х 3 — 1) = 0 | Квадрат обе стороны уравнения, чтобы избавиться от квадратного корня . |
Это дает решение x = 0 и x = 1 .
Пример 6
Решите уравнение ln x = x 2 — 1
Это уравнение не так-то просто решить. Если мы помните определение логарифма, мы видим, что x = 1 делает обе стороны уравнение равно 0 и, следовательно, является одним решением уравнения. Мы рисуем графики, чтобы увидеть, есть ли другие решения.
График показывает нам, что есть два решения. Одно решение — это ровно x = 1, поскольку e 0 = 1.
Обратите внимание, что мы выбираем значения x так, чтобы значения y становятся все ближе и ближе друг к другу в таблице значений. Таким образом мы можем выбрать значение x, чтобы получить желаемую точность.| Пример 7 | EXCEL |
Если мы воспользуемся графическим калькулятором, то сможем найти решение уравнения ln x = x 2 — 1 намного проще.
Рисуем графики обеих сторон уравнение и используйте Zoom (сдвиг F2), а затем Trace (сдвиг F1), чтобы найти точка пересечения.
Еще проще использовать G-Solve (F5) и затем функция пересечения ISCT (F5). 2-ln (B2)
Теперь выберите Инструменты а затем «Поиск цели» в строке меню.В на экране появляется следующее:
Пишем D2, 1 и B2 в промежутках, как показано. Мы просим Excel сделать значение ячейки D2 равным к значению 1, изменив значение в B2.
Когда нажимаем ОК, появляется следующая информация.
Это говорит нам о том, что аппроксимация x ≈ 0,45, которую мы нашли графически в примере 6, довольно хорошо.Решение x ≈ 0.4500289, найденный с помощью EXCEL, не намного лучше.
Попробуйте пройти тест 3 по уравнениям III.
Не забудьте использовать контрольный список для следите за своей работой.
Линейные функции. Уравнение прямой
9
Набросок графика
Форма откоса-пересечения
Доказательство
МЫ НАЧИНАЕМ ИЗУЧЕНИЕ ГРАФИКОВ полиномиальных функций.
Мы обнаружим, что график каждой степени оставляет свою характерную подпись на плоскости x — y .
График полинома первой степени всегда представляет собой прямую линию. График полинома второй степени — это кривая, известная как парабола. Полином третьей степени имеет вид, показанный справа. Навык координатной геометрии состоит в распознавании этой связи между уравнениями и их графиками. Следовательно, ученик должен знать, что график любого многочлена первой степени y = ax + b является прямой линией, и, наоборот, любая прямая линия имеет в своем уравнении y = ax + б .
Рисование графика уравнения первой степени должно быть базовым навыком. См. Урок 33 алгебры.
Пример. Отметьте точки пересечения x и y и нарисуйте график
.y = 2 x + 6.
Решение .
Перехват x — это корень. Это решение 2 x + 6 = 0.Перехват
x равен −3.
Перехват y — постоянный член, 6.
Итак, что означает утверждение, что y = 2 x + 6 является «уравнением» этой линии?
Это означает, что каждая пара координат ( x , y ), которая есть на графике, решает это уравнение. (Это означает, что координирующая пара находится на графике любого уравнения.) Каждая координированная пара ( x , y ) на этой линии равна
( x , 2 x + 6).
Таким образом, эта линия называется графиком уравнения y = 2 x + 6. А y = 2 x + 6 называется уравнением этой линии.
Каждое уравнение первой степени имеет график прямой. (Мы докажем это ниже.) По этой причине функции или уравнения первой степени, где 1 — старший показатель степени, называются линейными функциями или линейными уравнениями.
Проблема 1.Отметьте точки пересечения x и y и нарисуйте график
.y = −3 x -3
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Перехват x — это решение для −3 x — 3 = 0. Это x = −1. Перехват y — постоянный член, −3.
Задача 2. Нарисуйте график y = −4.
Уравнение вида y = Число, представляет собой горизонтальную линию.
См. Урок алгебры 33, раздел «Вертикальные и горизонтальные линии».
Форма откоса-пересечения
Эта линейная форма
y = ось + b
называется формой с пересечением наклона уравнения прямой.Потому что, как мы сейчас докажем, a — это наклон прямой (Тема 8), а b — постоянный член — это интервал y .
Эта форма первой степени
Ax + По + C = 0
, где A , B , C — целые числа, называется общей формой уравнения прямой.
Теорема. Уравнение
y = ось + b
— это уравнение прямой с наклоном a и y — пересечение b .
Для, прямая линия может быть указана с указанием ее наклона и координаты одной точки на нем. (Теорема 8.3.)
Следовательно, пусть наклон линии будет a , и пусть одна точка на ней будет ее пересечением y , (0, b ).
Тогда, если ( x , y ) являются координатами любой точки на этой линии, ее уклон
| y — b x — 0 | = | y — b x | = a . |
На решение для y ,
y = ax + b .
Следовательно, поскольку переменные x и y являются координатами любой точки на этой прямой, это уравнение представляет собой уравнение прямой с наклоном a и y с интервалом b . Это то, что мы хотели доказать.
Наклон прямой линии — это число — указывает скорость, с которой значение y изменяется по отношению к значению x .(Тема 8.)
Задача 3. Назовите наклон каждой линии и укажите значение каждого наклона.
а) y = 2 x + 6
Наклон равен 2. Это означает, что y увеличивается на 2 единицы на каждую 1 единицу x .
| б) y = — | 2 3 | x + 4 |
| Уклон — | 2 3 | .Это означает, что y уменьшается на 2 единицы на каждые |
| 3 шт. По x . | ||
в) y = x
Наклон равен 1.
 Алгебра, 11 класс: уроки, тесты, задания.
Алгебра, 11 класс: уроки, тесты, задания.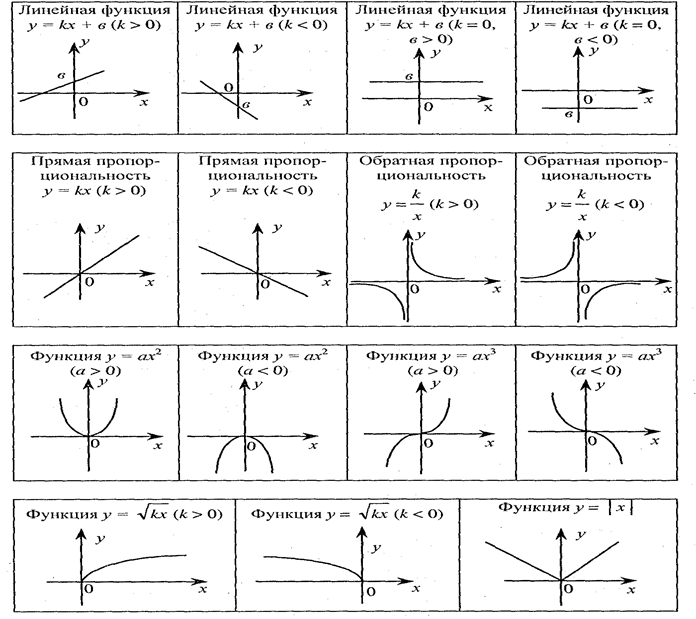 Анализ — это сложный исследовательский процесс, включающий не только изучение сущности явлений и закономерностей их развития, но и использование полученных выводов в практике. Синтез — это мысленное составление целостного объекта из его частей. Анализ и синтез выступают в аналитическом процессе в их единстве. Без анализа нет синтеза, как синтеза без анализа. Вместе взятые они служат мощным средством познания. Аналитические материалы помогают вскрыть не только поверхностные явления, внутреннюю структуру объекта, но и вскрыть глубинные процессы, дать развернутую характеристику объекта явления.
Анализ — это сложный исследовательский процесс, включающий не только изучение сущности явлений и закономерностей их развития, но и использование полученных выводов в практике. Синтез — это мысленное составление целостного объекта из его частей. Анализ и синтез выступают в аналитическом процессе в их единстве. Без анализа нет синтеза, как синтеза без анализа. Вместе взятые они служат мощным средством познания. Аналитические материалы помогают вскрыть не только поверхностные явления, внутреннюю структуру объекта, но и вскрыть глубинные процессы, дать развернутую характеристику объекта явления.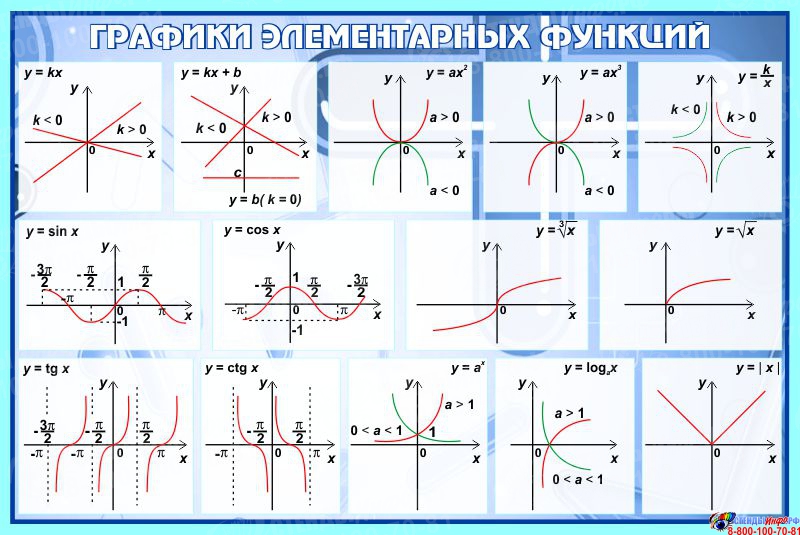 Поэтому обобщенная сущность явления всегда представляет собой определенный уровень формализации. Из существа этого приема вытекает использование при научных разработках логических выводов и обоснований, различных схем, формул, символики, абстрактно-логико-математических и знаковых моделей и т.д.
Поэтому обобщенная сущность явления всегда представляет собой определенный уровень формализации. Из существа этого приема вытекает использование при научных разработках логических выводов и обоснований, различных схем, формул, символики, абстрактно-логико-математических и знаковых моделей и т.д.