Кинематика — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Система СИ
К оглавлению…
Основные единицы измерения величин в системе СИ таковы:
- единица измерения длины — метр (1 м),
- времени — секунда (1 с),
- массы — килограмм (1 кг),
- количества вещества — моль (1 моль),
- температуры — кельвин (1 К),
- силы электрического тока — ампер (1 А),
- Справочно: силы света — кандела (1 кд, фактически не используется при решении школьных задач).
При выполнении расчетов в системе СИ углы измеряются в радианах.
Если в задаче по физике не указано, в каких единицах нужно дать ответ, его нужно дать в единицах системы СИ или в производных от них величинах, соответствующих той физической величине, о которой спрашивается в задаче. Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.
Для удобства в задачах по физике часто приходится использовать дольные (уменьшающие) и кратные (увеличивающие) приставки. их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
Таблица дольных и кратных приставок в физике:
Путь и перемещение
К оглавлению…
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Всякое тело имеет определенные размеры. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой. Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Интуитивно понятно, что характеристики движения (скорость, траектория и т.д.) зависят от того, откуда мы на него смотрим. Поэтому для описания движения вводится понятие системы отсчета. Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает в данной СО некоторую линию, которую называют траекторией движения тела.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.
Пройденный путь равен длине траектории, пройденной телом за некоторое время. Путь – скалярная величина. Путь не может уменьшаться. Путь только возрастает либо остается постоянным (если тело не движется). При движении тела по криволинейной траектории модуль (длина) вектора перемещения всегда меньше пройденного пути.
При равномерном (с постоянной скоростью) движении путь L может быть найден по формуле:где: v – скорость тела, t – время в течении которого оно двигалось. При решении задач по кинематике перемещение обычно находится из геометрических соображений. Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.
Средняя скорость
К оглавлению…
Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Средняя скорость пути – это отношение всего пути ко всему времени движения:
где: Lполн – весь путь, который прошло тело, tполн – все время движения.
Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:
Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
- При решении задач по кинематике не совершайте очень распространенную ошибку. Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
- И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.
Равноускоренное прямолинейное движение
К оглавлению…
Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела. Ускорением тела называют отношение изменения скорости к промежутку времени, в течение которого происходило изменение скорости:
где: v0 – начальная скорость тела, v – конечная скорость тела (то есть спустя промежуток времени t).
Далее, если иное не указано в условии задачи, мы считаем, что если тело движется с ускорением, то это ускорение остается постоянным. Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.
Равноускоренное движение бывает собственно ускоренным, когда тело увеличивает скорость движения, и замедленным, когда скорость уменьшается. Для простоты решения задач удобно для замедленного движения брать ускорение со знаком «–».
Из предыдущей формулы, следует другая более распространённая формула, описывающая изменение скорости со временем при равноускоренном движении:
Перемещение (но не путь) при равноускоренном движении рассчитывается по формулам:
В последней формуле использована одна особенность равноускоренного движения. При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):
С расчетом пути все сложнее.
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Аналогичные формулы получаются для остальных координатных осей. Формула для тормозного пути тела:
Свободное падение по вертикали
К оглавлению…
На все тела, находящиеся в поле тяготения Земли, действует сила тяжести. В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли. Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением.
Это значит, что свободное падение всех тел вблизи поверхности Земли является равноускоренным (но не обязательно прямолинейным) движением. Вначале рассмотрим простейший случай свободного падения, когда тело движется строго по вертикали. Такое движение является равноускоренным прямолинейным движением, поэтому все изученные ранее закономерности и фокусы такого движения подходят и для свободного падения. Только ускорение всегда равно ускорению свободного падения.
Традиционно при свободном падении используют направленную вертикально ось OY. Ничего страшного здесь нет. Просто надо во всех формулах вместо индекса « х» писать «у». Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.
Вариантов 2: вверх или вниз.
Приведем несколько формул, которые являются решением некоторых конкретных задач по кинематике на свободное падение по вертикали. Например, скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Горизонтальный бросок
К оглавлению…
При горизонтальном броске с начальной скоростью v0 движение тела удобно рассматривать как два движения: равномерное вдоль оси ОХ (вдоль оси ОХ нет никаких сил препятствующих или помогающих движению) и равноускоренного движения вдоль оси OY.
Скорость в любой момент времени направлена по касательной к траектории. Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна vx = v0. А вертикальная возрастает по законам ускоренного движения vy = gt. При этом полная скорость тела может быть найдена по формулам:
Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна vx = v0. А вертикальная возрастает по законам ускоренного движения vy = gt. При этом полная скорость тела может быть найдена по формулам:
При этом важно понять, что время падения тела на землю никоим образом не зависит от того, с какой горизонтальной скоростью его бросили, а определяется только высотой, с которой было брошено тело. Время падения тела на землю находится по формуле:
Пока тело падает, оно одновременно движется вдоль горизонтальной оси. Следовательно, дальность полета тела или расстояние, которое тело сможет пролететь вдоль оси ОХ, будет равно:
Угол между горизонтом и скоростью тела легко найти из соотношения:
Также иногда в задачах могут спросить о моменте времени, при котором полная скорость тела будет наклонена под определенным углом к вертикали. Тогда этот угол будет находиться из соотношения:
Тогда этот угол будет находиться из соотношения:
Важно понять, какой именно угол фигурирует в задаче (с вертикалью или с горизонталью). Это и поможет вам выбрать правильную формулу. Если же решать эту задачу координатным методом, то общая формула для закона изменения координаты при равноускоренном движении:
Преобразуется в следующий закон движения по оси OY для тела брошенного горизонтально:
При ее помощи мы можем найти высоту на которой будет находится тело в любой момент времени. При этом в момент падения тела на землю координата тела по оси OY будет равна нулю. Очевидно, что вдоль оси OХ тело движется равномерно, поэтому в рамках координатного метода горизонтальная координата изменятся по закону:
Бросок под углом к горизонту (с земли на землю)
К оглавлению…
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т. е. тело бросали, например, с земли на землю):
е. тело бросали, например, с земли на землю):
Минимальная скорость тела брошенного под углом к горизонту – в наивысшей точке подъёма, и равна:
Максимальная скорость тела брошенного под углом к горизонту – в моменты броска и падения на землю, и равна начальной. Это утверждение верно только для броска с земли на землю. Если тело продолжает лететь ниже того уровня, с которого его бросали, то оно будет там приобретать все большую и большую скорость.
Сложение скоростей
К оглавлению…
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными. Таким образом, покой и движение тела относительны. Классический закон сложения скоростей:
Таким образом, абсолютная скорость тела равна векторной сумме его скорости относительно подвижной системы координат и скорости самой подвижной системы отсчета. Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Равномерное движение по окружности
К оглавлению…
Движение тела по окружности является частным случаем криволинейного движения. Такой вид движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит и при движении по окружности (см. рисунок). Равномерное движение тела по окружности характеризуется рядом величин.
Период – время, за которое тело, двигаясь по окружности, совершает один полный оборот. Единица измерения – 1 с. Период рассчитывается по формуле:
Частота – количество оборотов, которое совершило тело, двигаясь по окружности, в единицу времени. Единица измерения – 1 об/с или 1 Гц. Частота рассчитывается по формуле:
В обеих формулах: N – количество оборотов за время t. Как видно из вышеприведенных формул, период и частота величины взаимообратные:
Как видно из вышеприведенных формул, период и частота величины взаимообратные:
При равномерном вращении скорость тела будет определяется следующим образом:
где: l – длина окружности или путь, пройденный телом за время равное периоду T. При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряемое в радианах. Угловой скоростью ω тела в данной точке называют отношение малого углового перемещения Δφ к малому промежутку времени Δt. Очевидно, что за время равное периоду T тело пройдет угол равный 2π, следовательно при равномерном движении по окружности выполняются формулы:
Угловая скорость измеряется в рад/с. Не забывайте переводить углы из градусов в радианы. Длина дуги l связана с углом поворота соотношением:
Связь между модулем линейной скорости v и угловой скоростью ω:
При движении тела по окружности с постоянной по модулю скоростью изменяется только направление вектора скорости, поэтому движение тела по окружности с постоянной по модулю скоростью является движением с ускорением (но не равноускоренным), так как меняется направление скорости. В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
Модуль центростремительного ускорения связан с линейной v и угловой ω скоростями соотношениями:
Обратите внимание, что если тела (точки) находятся на вращающемся диске, шаре, стержне и так далее, одним словом на одном и том же вращающемся объекте, то у всех тел одинаковые период вращения, угловая скорость и частота.
Кинематика. Формулы
Кинематика. Формулы| Номер | Название формулы | Запись формулы | Примечание |
| (1) | Закон равноускоренного криволинейного движения | vS0 — модуль начальной скорости; aS — ускорение | |
| (2) | Скорость равномерного прямолинейного движения | ||
| (3) | Скорость | ||
| (4) | Ускорение | ||
| (5) | Касательное ускорение | dv = dl/dt, т.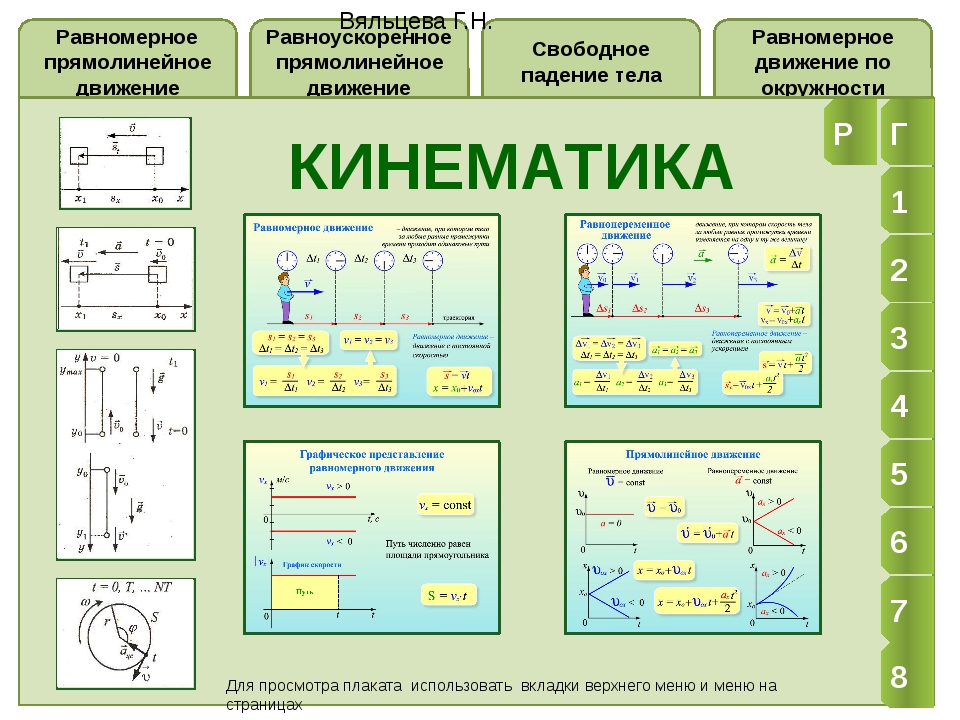 е. путевая скорость вдоль рассматриваемой траектории е. путевая скорость вдоль рассматриваемой траектории | |
| (6) | Нормальное ускорение | ||
| (7) | Скорость свободного падения тела | ||
| (8) | Время тела при свободном падении | ||
| (9) | Время при равномерном движении по окружности | ||
| (10) | Скорость равномерного движения по окружности | ||
| (11) | Угловая (мгновенная) скорость равномерного движения по окружности | Единица измерения угловой скорости — радианы в секунду | |
| (12) | Скорость равноускоренного движения по окружности | ||
| (13) | Угловая (мгновенная) скорость равноускоренного движения по окружности |
— версия для печати
- Определение
- Кинематикой называется раздел физики, занимающийся исследованием законов движения идеальных тел
- Пояснение
- Под чертой вверху буквы подразумевается знак вектора.

| Если у вас есть мысли или идеи по поводу данной таблицы или, например, вы считаете, что полезно было бы создать определенную вспомогательную памятку, то мы обязательно рассмотрим ваше предложение, которое можно изложить по ссылке (где вы также можете поделиться с нами любыми мыслями по поводу сайта scolaire.ru). Мы готовы устранить любые неудобства, связанные с использованием данной таблицы, или ей подобных, которые можно найти в разделе «Физика». |
© Школяр. Лингвистика (при поддержке «Ветвистого древа») 2009—2021
Осн. формулы и метод. рекомендации по решению задач на кинематику МТ
Ближайшие темы будут посвящены решению задач на движение тел, без учета причин, вызвавших это движения, т.е. решению задач по кинематике.
Но для того, чтобы начать рассмотрение решений задач по данной
теме, необходимо вспомнить основные формулы, связанные с этим разделом.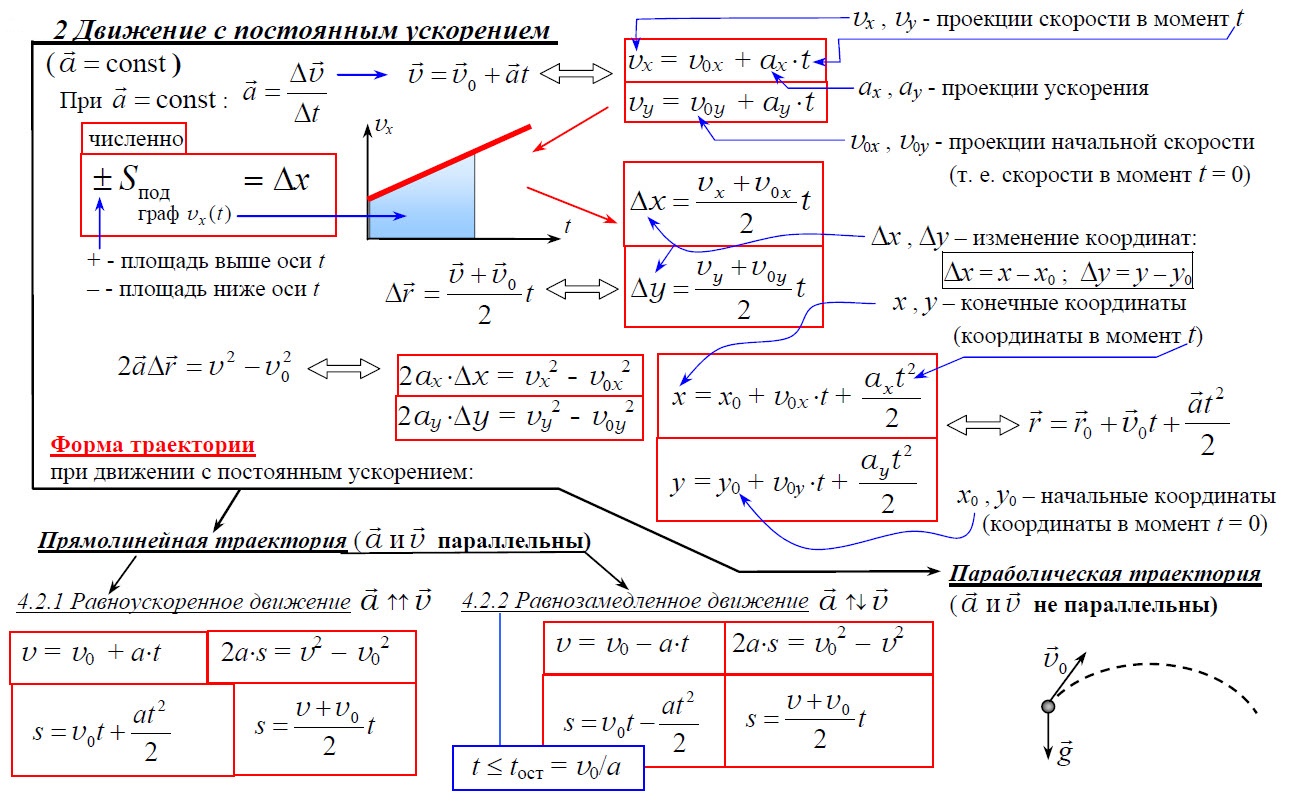 Для удобства,
сведём все формулы в таблицу.
Для удобства,
сведём все формулы в таблицу.
Основные формулы равномерного прямолинейного движения
|
Формула |
Описание формулы |
|
Перемещение тела за промежуток времени t, где – скорость тела, sx, vx – проекции перемещения и скорость на ось Ох. |
|
|
Путь за промежуток времени t. |
|
|
Закон сложения скоростей в классической механике. |
|
|
Кинематическое
уравнение равномерного движения, где х — координата тела в момент
времени t, х0 — начальная
координата тела. |
Основные формулы равноускоренного прямолинейного движения
|
Формула |
Описание формулы |
|
Скорость тела в момент времени t, где – ускорение тела, – скорость тела в начальный момент времени. |
|
|
Перемещение тела за промежуток времени t. |
|
|
Кинематическое уравнение равноускоренного движения. |
Основные формулы движения тела по окружности с постоянной по модулю скоростью.
|
Формула |
Описание формулы |
|
Линейная
скорость тела, где l — длина дуги окружности,
пройденной телом за промежуток времени Δt. |
|
|
Угловая скорость тела, где Dj – угол поворота радиус-вектора движущегося по окружности тела за промежуток времени Dt. |
|
|
Связь линейной скорости с угловой, где R — радиус окружности. |
|
|
Период вращения, где N — число оборотов тела за промежуток времени Δt. |
|
|
Частота вращения. |
|
|
Связь между линейной скоростью, периодом вращения и частотой. |
|
|
Центростремительное
ускорение. |
Известно, что для большей наглядности движение можно описывать с помощью графиков.
Давайте рассмотрим в сравнении графики для равномерного и равноускоренного движения.
Известно, что при равномерном движении скорость тела не изменяется с течением времени. Поэтому графиком скорости, в этом случае, будет прямая линия, параллельная оси времени. При равноускоренном движении тела, неизменной величиной является ускорение. Поэтому графиком ускорения будет являться также прямая линия, параллельная оси времени.
По графику скорости для равномерного движения, можно определить путь, пройденный телом за некоторый промежуток времени. Для этого достаточно определить площадь прямоугольника, образованного графиком скорости и осью времени.
Известно, что перемещение тела при равномерном движении линейно зависит от времени, поэтому графиком перемещения является прямая линия вида
y = kx.
Наклон же графика к оси времени зависит от модуля скорости. При равноускоренном движении линейно зависимой величиной является скорость тела. Поэтому графиком скорости является прямая линия вида
y = kx +b.
Используя график скорости для равноускоренного движения можно определить перемещение тела за некоторый промежуток времени. Для этого необходимо определить площадь прямоугольной трапеции или прямоугольного треугольника, ограниченных графиком скорости и осью времени.
График зависимости координаты от времени при равномерном движении, то есть график движения, представлен на рисунке ниже. По этому графику можно определить: координату тела в любой момент времени, путь, пройденный телом за некоторый промежуток времени, кратчайшее расстояние между телами в любой момент времени, а также момент и место встречи тел.
А графиком перемещения при равноускоренном движении
является парабола, положение вершины которой зависит от направлений
начальной скорости и ускорения. Так, если проекция ускорения отрицательна,
то возможны следующие три вида графика перемещения:
Так, если проекция ускорения отрицательна,
то возможны следующие три вида графика перемещения:
– когда проекция начальной скороститела равна нулю;
– когда проекция начальной скорости тела меньше нуля;
– когда проекция начальной скорости тела больше нуля.
Если проекция ускорения положительна, то здесь также возможны три случая:
– когда начальная скорость тела равна нулю;
– когда проекция начальной скорости больше нуля;
– когда проекция начальной скорости меньше нуля.
Методические рекомендации по решению задач на кинематику материальной точки
1) Сделать схематический рисунок, который лучше всего представить в виде траектории движущейся точки с изображением векторов перемещения, скорости и ускорения.
2) Выбрать систему отсчета (то есть тело отсчета, связанную с
ним систему координат и начало отсчета времени) на основании тщательного
анализа условия задачи. Рациональный выбор системы отсчета, как правило,
значительно упрощает решение задачи. При выборе положительных направлений
координатных осей необходимо руководствоваться направлением движения (то есть
направлением вектора скорости) или направлением вектора ускорения.
Рациональный выбор системы отсчета, как правило,
значительно упрощает решение задачи. При выборе положительных направлений
координатных осей необходимо руководствоваться направлением движения (то есть
направлением вектора скорости) или направлением вектора ускорения.
3) Составить на основании законов движения систему уравнений в векторном виде для всех тел, участвующих в движении. А затем в скалярной форме, спроецировав на координатные оси эти векторные уравнения движения. При записи этих уравнений не забыть привести в соответствие знаки проекций скорости и ускорения с направлением координатных осей. При необходимости дополнить систему уравнений соотношениями, составленными на основе данных задачи и конкретной ситуации, описанной в ней.
4) Решить полученную систему уравнений относительно искомых величин в общем виде, убедиться в соответствии единиц измерения и проделать числовые расчеты.
Следование этим простым рекомендациям позволит вам успешнее
справляться с решением задач на кинематику материальной точки.
Свободное падение. Кинематика — 10 класс
Свободное падение. Кинематика — 10 класс
- Подробности
- Просмотров: 692
Кинематика — это просто!
Свободное падение — это движение тела только лишь под действием силы тяжести.
Свободное падение — это движение с постоянным ускорением, когда ускорение равно ускорению свободного падения (g=9,8 м/c2).
P.S.Ускорение свободного падения g всегда направлено вертикально вниз!
При расчетах движения для большинства падающих тел вблизи поверхности Земли силу сопротивления воздуха можно не учитывать, т.к. ускорение свободного падения практически не меняется.
Существуют 2 варианта свободного падения:
1. с прямолинейной траекторией,
когда векторы скорости V и ускорения g направлены одинаково или противоположны друг другу.
…. а) падение тела с высоты вертикально вниз
…. б) бросок тела вертикально вверх.
2. с криволинейной траекторией,
когда векторы скорости V и ускорения g направлены под углом друг к другу.
Например, когда тело брошено под углом к горизонту.
Для расчета любого варианта свободного падения годятся уже знакомые вам формулы для движения с постоянным ускорением,
достаточно в них заменить ускорение а на ускорение свободного падения g:
а) в векторном виде
б) расчетные формулы в координатной форме
Пример решения задачи на свободное падение
Задача
Шишка, висевшая на ели, оторвалась и за 2 секунды достигла земли.
На какой высоте висела шишка?
Какую скорость она имела у самой земли?
Помни!
1. В данной задаче начальная скорость тела равна нулю, и формулы становятся проще!
2. Будем грамотны! Рассчитываем проекцию вектора, но ответ должен быть в модулях! В последней записи перед ответом переходим от проекции к модулю.
Будем грамотны! Рассчитываем проекцию вектора, но ответ должен быть в модулях! В последней записи перед ответом переходим от проекции к модулю.
Кинематика — Класс!ная физика
Прямолинейное равномерное движение и решение задач — Закон сложения скоростей и решение задач — Движение с постоянным ускорением и решение задач — Свободное падение — Движение тела, брошенного под углом к горизонту — Решение задач. Тело, брошенное под углом к горизонту — Криволинейное движение
Движение с постоянным ускорением и решение задач. Кинематика — 10 класс
Движение с постоянным ускорением и решение задач. Кинематика — 10 класс
- Подробности
- Просмотров: 748
Кинематика — это просто!
В общем случае движение может быть криволинейным и неравномерным.
Тогда вектор скорости будет меняться и по направлению, и по величине, а это значит, что тело движется с ускорением.
Ускорение показывает быстроту изменения скорости.
Ускорение — это векторная величина, которая характеризуется модулем и направлением.
Единица измерения ускорения в системе СИ:
Частным случаем такого движения является прямолинейное движение с постоянным ускорением.
Постоянное ускорение — это когда ускорение не меняется ни по модулю, ни по направлению.
Прямолинейное движение с постоянным ускорением подразделяется на:
1. равноускоренное, когда при движении модуль скорости тела увеличивается (тело разгоняется).
Здесь векторы скорости и ускорения совпадают по направлению.
2. равнозамедленное, когда при движении модуль скорости тела уменьшается (тело тормозит).
Здесь векторы скорости и ускорения направлены противоположно друг другу.
Формула ускорения:
1. в векторном виде
2. расчетная формула в координатной форме (для решения задач)
расчетная формула в координатной форме (для решения задач)
Отсюда «вытекает» уравнение скорости, которое выражает мгновенную скорость тела в любой момент времени:
1. в векторном виде
2. расчетная формула в координатной форме
Графики ускорения
Перемещение
1. формула перемещения в векторном виде
2. Расчетная формула в координатной форме
Графики перемещения
Уравнение движения (или иначе уравнение координаты)
1. в векторном виде
2. расчетная формула в координатной форме
Примеры решения задач на движение с постоянным ускорением
Задача 1
Тело движется согласно уравнению х=2-4t-2t2.
Дать описание движения тела.
Составить уравнение скорости движущегося тела.
Определить скорость тела и координату через 10 секунд после начала движения.
Решение
Сравниваем заданное уравнение движения х=2-4t-2t2 с формулой:
тогда
По полученным данным даем описание движения тела:
— тело движется из точки с координатами 2 метра относительно начала координат с начальной скоростью 4 м/с противоположно направлению координатной оси ОХ с постоянным ускорением 4 м/с2, разгоняется, т. к. направление вектора скорости и вектора ускорения совпадают.
к. направление вектора скорости и вектора ускорения совпадают.
Составляем уравнение скорости, глядя на расчетную формулу для скорости:
Расчитываем скорость и координату тела через 10 секунд после начала движения:
Задача 2
Уравнение движения тела x=-3+t+t2
Дать описание движения тела.
Определить скорость и координату тела через 2 секунды после начала движения.
Решение
Рассуждаем аналогично вышерассмотренной задаче:
Тело движется из точки с координатами -3 метра относительно начала координат с начальной скоростью 1 м/с в направлении координатной оси ОХ с постоянным ускорением 2м/с2, разгоняется, т.к. проекции вектора скорости и ускорения имеют одинаковые знаки, значит оба векторв направлены одинаково.
Кинематика — Класс!ная физика
Прямолинейное равномерное движение и решение задач —
Закон сложения скоростей и решение задач —
Движение с постоянным ускорением и решение задач —
Свободное падение —
Движение тела, брошенного под углом к горизонту —
Решение задач. Тело, брошенное под углом к горизонту —
Криволинейное движение
Тело, брошенное под углом к горизонту —
Криволинейное движение
Все формулы по физике за 7 класс с пояснениями — таблица и шпаргалки
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Шпаргалки по физике за 7 класс
В рамках одной статьи сложно охватить весь курс по физике, но мы осветили основные темы за 7 класс и этого достаточно, чтобы освежить знания в памяти. Скачайте и распечатайте обе шпаргалки — одна из них (подробная) пригодится для вдумчивой подготовки к ОГЭ и ЕГЭ, а вторая (краткая) послужит для решения задач.
Скачать PDF со всеми формулами и определениями по физике за 7 класс.
Скачать PDF со всеми формулами и определениями по физике за 7 класс (мелко на одной странице).
Для тех, кто находится на домашнем обучении или вынужден самостоятельно изучать материал ввиду пропусков по болезни, рекомендуем также учебник по физике А. В. Перышкина с формулами за 7 класс и легкими, доступными пояснениями по всем темам. Он был написан несколько десятилетий назад, но до сих пор очень популярен и востребован.
В. Перышкина с формулами за 7 класс и легкими, доступными пояснениями по всем темам. Он был написан несколько десятилетий назад, но до сих пор очень популярен и востребован.
Измерение физических величин
Измерением называют определение с помощью инструментов и технических средств числового значения физической величины. Результат измерения сравнивают с неким эталоном, принятым за единицу. В итоге значением физической величины считается полученное число с указанием единиц измерения. |
В курсе по физике за 7 класс изучают правила измерений с использованием приборов со шкалой. Если цена деления шкалы неизвестна, узнать ее можно с помощью следующей формулы:
ЦД = (max − min) / n, где ЦД — цена деления, max — максимальное значение шкалы, min — минимальное значение шкалы, n — количество делений между ними.
Вместо максимального и минимального можно взять любые другие значения шкалы, числовое выражение которых нам известно.
Выделяют прямое и косвенное измерение:
при прямом измерении результат можно увидеть непосредственно на шкале инструмента;
при косвенном измерении значение величины вычисляется через другую величину (например, среднюю скорость определяют на основе нескольких замеров скорости).
Для удобства и стандартизации измерений в 1963 году была принята Международная система единиц СИ. Она регламентирует, какие единицы измерения считать основными и использовать для формул. Обозначения этих единиц также учат в программе по физике за 7 класс.
Механическое движение: формулы за 7 класс
Механическое движение — перемещение тела в пространстве, в результате которого оно меняет свое положение относительно других тел. Закономерности такого движения изучают в рамках механики и конкретно ее раздела — кинематики. |
Для того, чтобы описать движение, требуется тело отсчета, система координат, а также инструмент для измерения времени.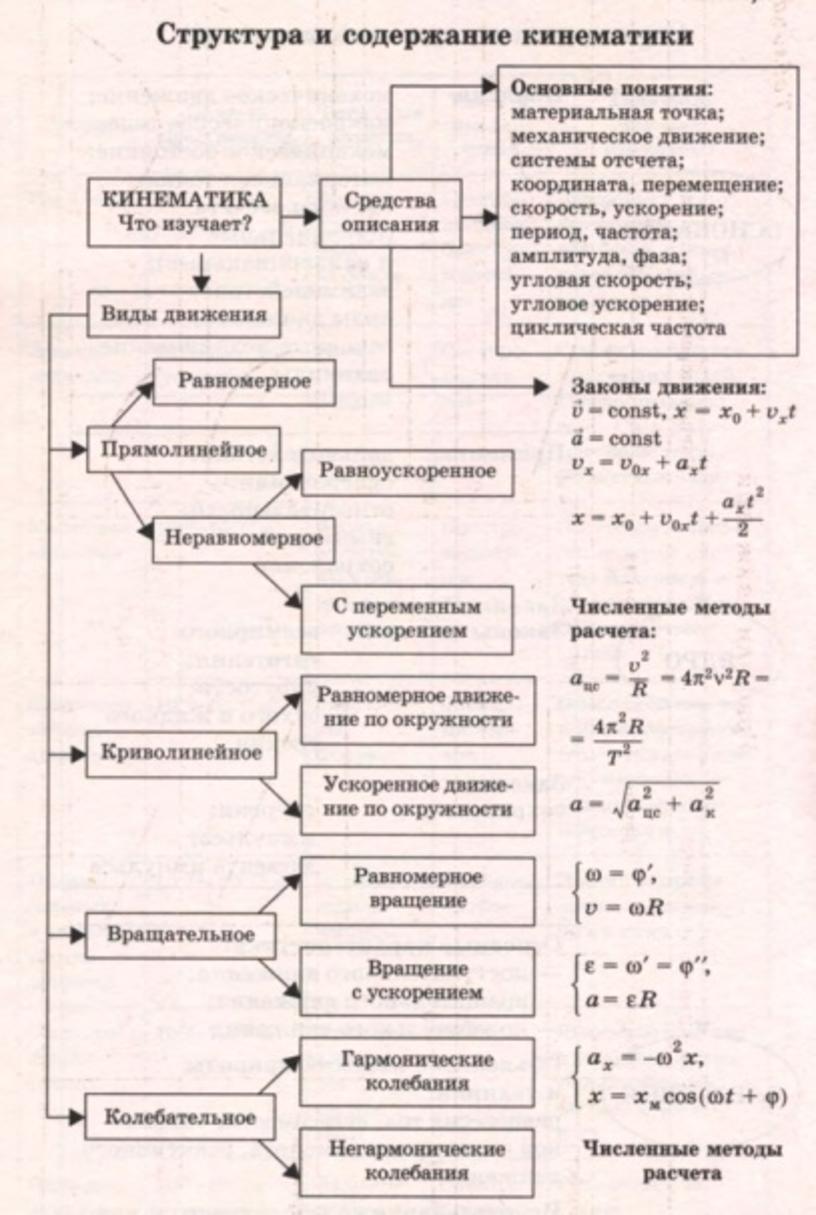 Это составляющие системы отсчета.
Это составляющие системы отсчета.
Изучение механического движения в курсе по физике за 7 класс включает следующие термины:
Перемещение тела — вектор, проведенный из начальной точки в конечную.
Траектория движения — мысленная линия, вдоль которой перемещается тело.
Путь — длина траектории тела от начальной до конечной точки.
Скорость — быстрота перемещения тела или отношение пройденного им пути ко времени прохождения.
Ускорение — быстрота изменения скорости, с которой движется тело.
Равномерное прямолинейное движение означает, что тело движется вдоль прямой с одинаковой скоростью. В таком случае перемещение тела и его путь будут равны. |
Формула скорости равномерного прямолинейного движения:
V = S / t, где S — путь тела, t — время, за которое этот путь пройден.
Формула скорости равномерного криволинейного движения:
где S1 и S2 — отрезки пути, а t1 и t2 — время, за которое был пройден каждый из них.
Единица измерения скорости в СИ: метр в секунду (м/с).
Формула скорости равноускоренного движения:
V = V0 + at, где V0— начальная скорость, а — ускорение.
Единица измерения ускорения в СИ: м/с2.
Сила тяжести, вес, масса, плотность
Формулы, понятия и определения, описывающие эти физические характеристики, изучают в 7 классе в рамках такого раздела физики, как динамика.
Вес тела или вещества — это векторная величина, которая характеризует, с какой силой оно действует на горизонтальную поверхность или вертикальный подвес. Не следует путать эту величину с массой, которая является скалярной величиной. |
Вес тела измеряется в ньютонах, масса тела — в граммах и килограммах.
Формула веса:
P = mg, где m — масса тела, g — ускорение свободного падения.
Ускорение свободного падения возникает под действием силы тяжести, которой подвержены все находящиеся на нашей планете тела.
g = 9,806 65 м/с2 или 9,8 Н/кг
Если тело находится в покое или в прямолинейном равномерном движении, его вес равен силе тяжести.
Fтяж = mg
Но эти понятия нельзя отождествлять: сила тяжести действует на тело ввиду наличия гравитации, в то время как вес — это сила, с которой само тело действует на поверхность.
Плотность тела или вещества — величина, указывающая на то, какую массу имеет данное вещество, занимая единицу объема. Плотность прямо пропорциональна массе и обратно пропорциональна объему. |
Формула плотности:
ρ = m / V, где m — масса тела или вещества, V — занимаемый объем.
Единица измерения плотности в СИ: кг/м3.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Механический рычаг, момент силы
О механическом рычаге говорил еще Архимед, когда обещал перевернуть Землю, если только найдется подходящая точка опоры. Это простой механизм, который помогает поднимать грузы, закрепленные на одном его конце, прилагая силу к другому концу. При этом вес груза намного превосходит прилагаемое усилие. В 7 классе физические формулы, описывающие этот процесс, изучаются в том же разделе динамики.
Рычаг — это некое твердое тело, способное вращаться вокруг неподвижной точки опоры, на один конец которого действует сила, а на другом находится груз. Перпендикуляр, проведенный от точки опоры до линии действия силы, называется плечом силы. |
Рычаг находится в равновесии, если произведение силы на плечо с одной его стороны равно произведению силы на плечо с другой стороны.
Уравнение равновесия рычага:
F1 × l1 = F2 × l2
Из этого следует, что рычаг уравновешен, когда модули приложенных к его концам сил обратно пропорциональны плечам этих сил.
Момент силы — это векторная величина, числовую характеристику которой можно описать как произведение модуля силы на плечо. |
Формула момента силы:
M = F × l, где F — модуль силы, l — длина плеча.
Единица измерения момента силы в СИ: ньютон-метр (Н·м).
Эта формула верна, если сила приложена перпендикулярно оси рычага. Если же она прилагается под углом, такой случай выходит за рамки курса физики за 7 класс и подробно изучается в 9 классе.
Правило моментов: рычаг уравновешен, если сумма всех моментов сил, которые поворачивают его по часовой стрелке, равна сумме всех моментов сил, которые поворачивают его в обратном направлении. |
Можно сказать иначе: рычаг в равновесии, если сумма моментов всех приложенных к нему сил относительно любой оси равна нулю.
М1 + М2 + Мn + … = 0
Давление, сила давления
Прилагая одну и ту же силу к предмету, можно получить разный результат в зависимости от того, на какую площадь эта сила распределена. Объясняют этот феномен в программе 7 класса физические термины «давление» и «сила давления».
Давление — это величина, равная отношению силы, действующей на поверхность, к площади этой поверхности. Сила давления направлена перпендикулярно поверхности. |
Формула давления:
p = F / S, где F — модуль силы, S — площадь поверхности.
Единица измерения давления в СИ: паскаль (Па).
1 Па = 1 Н/м2
Понятно, что при одной и той же силе воздействия более высокое давление испытает та поверхность, площадь которой меньше.
Формулу для расчета силы давления вывести несложно:
F = p × S
В задачах по физике за 7 класс сила давления, как правило, равна весу тела.
Давление газов и жидкостей
Жидкости и газы, заполняющие сосуд, давят на его стенки. Это давление зависит от высоты столба данного вещества и от его плотности.
Формула гидростатического давления:
р = ρ × g × h, где ρ — плотность вещества, g — сила тяжести, h — высота столба.
g = 9,8 м/с2
Единица измерения давления жидкости или газа в СИ: паскаль (Па).
Однородная жидкость или газ давит на стенки сосуда равномерно, поскольку это давление создают хаотично движущиеся молекулы. И внешнее давление, оказываемое на вещество, тоже равномерно распределяется по всему его объему.
Закон Паскаля: давление, производимое на поверхность жидкого или газообразного вещества, одинаково передается в любую его точку независимо от направления. |
Внешнее давление, оказываемое на жидкость или газ, рассчитывается по формуле:
p = F / S, где F — модуль силы, S — площадь поверхности.
Сообщающиеся сосуды
Сообщающимися называются сосуды, которые имеют общее дно либо соединены трубкой. Уровень однородной жидкости в таких сосудах всегда одинаков, независимо от их формы и сечения. |
Если ρ1 = ρ2, то h1 = h2 и ρ1gh1 = ρ2gh2, где:
p — плотность жидкости,
h — высота столба жидкости,
g = 9,8 м/с2.
Если жидкость в сообщающихся сосудах неоднородна, т. е. имеет разную плотность, высота столба в сосуде с более плотной жидкостью будет пропорционально меньше.
Высоты столбов жидкостей с разной плотностью обратно пропорциональны плотностям.
Гидравлический пресс — это механизм, созданный на основе сообщающихся сосудов разных сечений, заполненных однородной жидкостью. Такое устройство позволяет получить выигрыш в силе для оказания статического давления на детали (сжатия, зажимания и т. д.). |
Если под поршнем 1 образуется давление p1 = f1/s1, а под поршнем 2 будет давление p2 = f2/s2, то, согласно закону Паскаля, p1 = p2
Следовательно,
Силы, действующие на поршни гидравлического пресса F1 и F2, прямо пропорциональны площадям этих поршней S1 и S2.
Другими словами, сила поршня 1 больше силы поршня 2 во столько раз, во сколько его площадь больше площади поршня 2. Это позволяет уравновесить в гидравлической машине с помощью малой силы многократно бóльшую силу.
Закон Архимеда
Сила выталкивания тела, погруженного в жидкость или газ, равна весу данной жидкости или газа в таком же объеме, как у этого тела. |
Формула архимедовой силы:
Fa = ρ × g × V, где ρ — плотность жидкости, V — объем жидкости, g — ускорение 9,8 м/с2.
Закон Архимеда помогает рассчитать, как поведет себя тело при погружении в среды разной плотности. Верны следующие утверждения:
если плотность тела выше плотности среды, оно уйдет на дно;
если плотность тела ниже, оно всплывет на поверхность.
Другими словами, тело поднимется на поверхность, если архимедова сила больше силы тяжести.
Работа, энергия, мощность
Механическая работа — это скалярная величина, которая равна произведению перемещения тела на модуль силы, под действием которой было выполнено перемещение. Подразумевается, что перемещение произошло в том же направлении, в котором действует сила. |
Формула работы в курсе физики за 7 класс:
A = F × S, где F — действующая сила, S — пройденный телом путь.
Единица измерения работы в СИ: джоуль (Дж).
Такое понятие, как мощность, описывает скорость выполнения механической работы. Оно говорит о том, какая работа была совершена в единицу времени.
Мощность — это скалярная величина, равная отношению работы к временному промежутку, потребовавшемуся для ее выполнения. |
Формула мощности:
N = A / t, где A — работа, t — время ее совершения.
Также мощность можно вычислить, зная силу, воздействующую на тело, и среднюю скорость перемещения этого тела.
N = F × v, где F — сила, v — средняя скорость тела.
Единица измерения мощности в СИ: ватт (Вт).
Тело может совершить какую-либо работу, если оно обладает энергией — кинетической и/или потенциальной.
Кинетической называют энергию движения тела. Она говорит о том, какую работу нужно совершить, чтобы придать телу определенную скорость.
Потенциальной называется энергия взаимодействия тела с другими телами или взаимодействия между частями одного целого. Потенциальная энергия тела, поднятого над Землей, характеризует, какую работу должна совершить сила тяжести, чтобы опустить это тело снова на нулевой уровень.
Таблица с формулами по физике за 7 класс для вычисления кинетической и потенциальной энергии:
Кинетическая энергия | Пропорциональна массе тела и квадрату его скорости. | Ek = mv2/2 |
Потенциальная энергия | Равна произведению массы тела, поднятого над Землей, на ускорение свободного падения и высоту поднимания. | Ep= mgh |
Полная механическая энергия | Складывается из кинетической и потенциальной энергии. | E = Ek+Ep |
Сохранение и превращение энергии | Если механическая энергия не переходит в другие формы, то сумма потенциальной энергии и кинетической представляет собой константу. | Ek+ Ep= const |
Для того, чтобы понять, какая часть совершенной работы была полезной, вычисляют коэффициент полезного действия или КПД. С его помощью определяется эффективность различных механизмов, инструментов и т. д.
д.
Коэффициент полезного действия (КПД) отражает полезную часть выполненной работы. Также его можно выразить через отношение полезно использованной энергии к общему количеству полученной энергии. |
Формула для расчета КПД:
где Ап— полезная работа, Аз— затраченная работа.
КПД выражается в процентах и составляет всегда меньше 100%, поскольку часть энергии затрачивается на трение, повышение температуры воздуха и окружающих тел, преодоление силы тяжести и т. д.
Удачи на экзаменах!
+50 формул по физике за 7-11 класс с пояснением
Основные формулы по физике: кинематика, динамика, статика
Итак, как говорится, от элементарного к сложному. Начнём с кинетических формул:
Также давайте вспомним движение по кругу:
Медленно, но уверенно мы перешли более сложной теме – к динамике:
Уже после динамики можно перейти к статике, то есть к условиям равновесия тел относительно оси вращения:
После статики можно рассмотреть и гидростатику:
Куда же без темы “Работа, энергия и мощность”. Именно по ней даются много интересных, но сложных задач. Поэтому без формул здесь не обойтись:
Именно по ней даются много интересных, но сложных задач. Поэтому без формул здесь не обойтись:
Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Заказать работу
Основные формулы термодинамики и молекулярной физики
Последняя тема в механике – это “Колебания и волны”:
Теперь можно смело переходить к молекулярной физике:
Плавно переходим в категорию, которая изучает общие свойства макроскопических систем. Это термодинамика:
Основные формулы электричества
Для многих студентов тема про электричество сложнее, чем про термодинамика, но она не менее важна. Итак, начнём с электростатики:
Переходим к постоянному электрическому току:
Далее добавляем формулы по теме: “Магнитное поле электрического тока”
Электромагнитная индукция тоже важная тема для знания и понимания физики. Конечно, формулы по этой теме необходимы:
Конечно, формулы по этой теме необходимы:
Ну и, конечно, куда же без электромагнитных колебаний:
Основные формулы оптической физики
Переходим к следующему разделу по физике – оптика. Здесь даны 8 основных формул, которые необходимо знать. Будьте уверены, задачи по оптике – частое явление:
Основные формулы элементов теории относительности
И последнее, что нужно знать перед экзаменом. Задачи по этой теме попадаются реже, чем предыдущие, но бывают:
Основные формулы световых квантов
Этими формулами приходится часто пользоваться в силу того, что на тему “Световые кванты” попадается немало задач. Итак, рассмотрим их:
На этом можно заканчивать. Конечно, по физике есть ещё огромное количество формул, но они вам не столь не нужны.
Это были основные формулы физики
В статье мы подготовили 50 формул, которые понадобятся на экзамене в 99 случая из 100.
Совет: распечатайте все формулы и возьмите их с собой.
Во время печати, вы так или иначе будете смотреть на формулы, запоминая их. К тому же, с основными формулами по физике в кармане, вы будете чувствовать себя на экзамене намного увереннее, чем без них.
Надеемся, что подборка формул вам понравилась!
P.S. Хватило ли вам 50 формул по физике, или статью нужно дополнить? Пишите в комментариях.
Кинематические уравнения
Целью этого первого раздела «Класса физики» было исследование разнообразных средств, с помощью которых может быть описано движение объектов. Разнообразие представлений, которые мы исследовали, включает словесные представления, графические представления, числовые представления и графические представления (графики положения-времени и графики скорости-времени). В Уроке 6 мы исследуем использование уравнений для описания и представления движения объектов.Эти уравнения известны как кинематические уравнения.
Есть множество величин, связанных с движением объектов — смещение (и расстояние), скорость (и скорость), ускорение и время.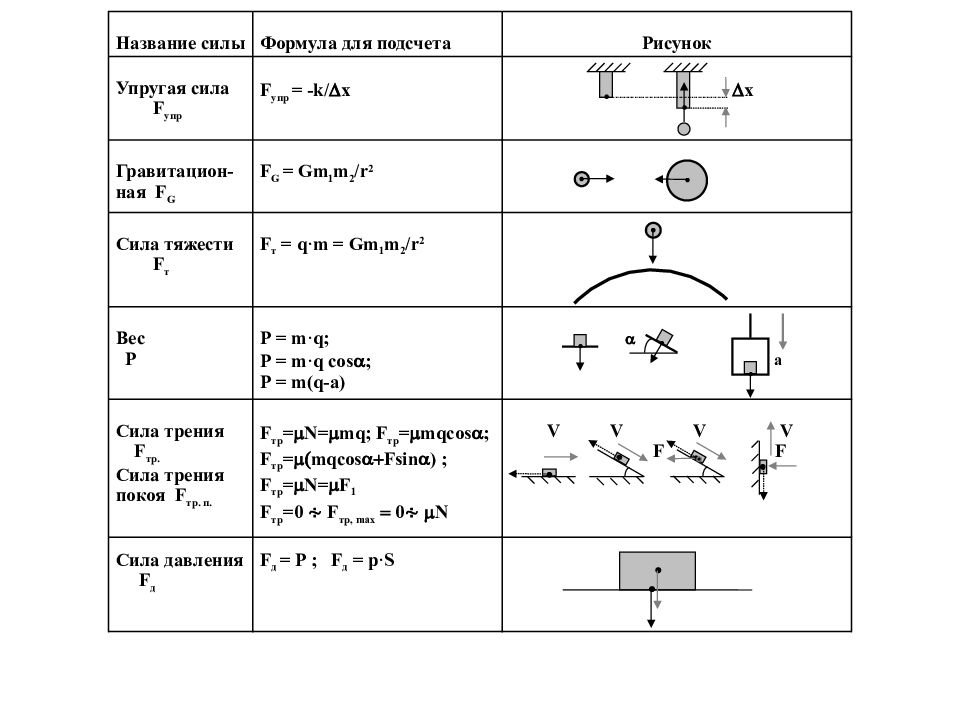 Знание каждой из этих величин дает описательную информацию о движении объекта. Например, если известно, что автомобиль движется с постоянной скоростью 22,0 м / с, на север в течение 12,0 секунд для смещения на север на 264 метра, то движение автомобиля полностью описано.И если известно, что вторая машина ускоряется из положения покоя с ускорением на восток 3,0 м / с 2 в течение 8,0 секунд, обеспечивая конечную скорость 24 м / с, восток и смещение на восток 96 метров. , то полностью описывается движение этой машины. Эти два утверждения обеспечивают полное описание движения объекта. Однако не всегда такая полнота известна. Часто бывает так, что известны лишь некоторые параметры движения объекта, а остальные неизвестны.Например, приближаясь к светофору, вы можете узнать, что ваша машина развивает скорость 22 м / с, восток и способна к заносу 8,0 м / с 2 , запад. Однако вы не знаете, какое смещение испытает ваша машина, если бы вы резко нажали на тормоз и занесло до полной остановки; и вы не знаете, сколько времени потребуется, чтобы остановиться.
Знание каждой из этих величин дает описательную информацию о движении объекта. Например, если известно, что автомобиль движется с постоянной скоростью 22,0 м / с, на север в течение 12,0 секунд для смещения на север на 264 метра, то движение автомобиля полностью описано.И если известно, что вторая машина ускоряется из положения покоя с ускорением на восток 3,0 м / с 2 в течение 8,0 секунд, обеспечивая конечную скорость 24 м / с, восток и смещение на восток 96 метров. , то полностью описывается движение этой машины. Эти два утверждения обеспечивают полное описание движения объекта. Однако не всегда такая полнота известна. Часто бывает так, что известны лишь некоторые параметры движения объекта, а остальные неизвестны.Например, приближаясь к светофору, вы можете узнать, что ваша машина развивает скорость 22 м / с, восток и способна к заносу 8,0 м / с 2 , запад. Однако вы не знаете, какое смещение испытает ваша машина, если бы вы резко нажали на тормоз и занесло до полной остановки; и вы не знаете, сколько времени потребуется, чтобы остановиться. В таком случае неизвестные параметры могут быть определены с использованием принципов физики и математических уравнений (кинематических уравнений).
В таком случае неизвестные параметры могут быть определены с использованием принципов физики и математических уравнений (кинематических уравнений).
БОЛЬШОЙ 4
Кинематические уравнения — это набор из четырех уравнений, которые можно использовать для предсказания неизвестной информации о движении объекта, если известна другая информация. Уравнения можно использовать для любого движения, которое можно описать как движение с постоянной скоростью (ускорение 0 м / с / с) или движение с постоянным ускорением. Их нельзя использовать в течение какого-либо периода времени, в течение которого изменяется ускорение.Каждое из кинематических уравнений включает четыре переменные. Если известны значения трех из четырех переменных, то можно рассчитать значение четвертой переменной. Таким образом, кинематические уравнения предоставляют полезные средства прогнозирования информации о движении объекта, если известна другая информация. Например, если известно значение ускорения, а также начальное и конечное значения скорости буксирующего автомобиля, то смещение автомобиля и время можно предсказать с помощью кинематических уравнений. Урок 6 этого модуля будет посвящен использованию кинематических уравнений для прогнозирования числовых значений неизвестных величин для движения объекта.
Урок 6 этого модуля будет посвящен использованию кинематических уравнений для прогнозирования числовых значений неизвестных величин для движения объекта.
Четыре кинематических уравнения, описывающие движение объекта:
В приведенных выше уравнениях используются различные символы. Каждый символ имеет свое особое значение. Символ d обозначает смещение объекта. Символ t обозначает время, в течение которого объект двигался.Символ a обозначает ускорение объекта. А символ v обозначает скорость объекта; нижний индекс i после v (как в v i ) указывает, что значение скорости является начальным значением скорости, а нижний индекс перед f (как в v f ) указывает, что значение скорости является конечным значением скорости.
Каждое из этих четырех уравнений надлежащим образом описывает математическую связь между параметрами движения объекта. По сути, их можно использовать для прогнозирования неизвестной информации о движении объекта, если известна другая информация. В следующей части Урока 6 мы исследуем процесс этого.
В следующей части Урока 6 мы исследуем процесс этого.
Кинематические уравнения и кинематические графики
Урок 4 этого модуля в классе физики был посвящен использованию графиков скорость-время для описания движения объектов. В этом уроке было подчеркнуто, что наклон линии на графике скорость-время равен ускорению объекта, а площадь между линией и осью времени равна смещению объекта.Таким образом, графики скорость-время можно использовать для определения числовых значений и соотношений между величинами смещения (d), скоростью (v), ускорением (a) и временем (t). В Уроке 6 основное внимание уделялось использованию четырех кинематических уравнений для описания движения объектов и прогнозирования числовых значений одного из четырех параметров движения — смещения (d), скорости (v), ускорения (a) и время (t). Таким образом, теперь доступны два метода решения проблем, связанных с числовыми соотношениями между перемещением, скоростью, ускорением и временем. В этой части Урока 6 мы исследуем взаимосвязь между этими двумя методами.
В этой части Урока 6 мы исследуем взаимосвязь между этими двумя методами.
Рассмотрим объект, который движется с постоянной скоростью +5 м / с в течение 5 секунд, а затем ускоряется до конечной скорости +15 м / с в течение следующих 5 секунд. Такое словесное описание движения может быть представлено графиком скорость-время. График показан ниже.
Горизонтальная часть графика изображает движение с постоянной скоростью в соответствии со словесным описанием.Участок графика с положительным уклоном (т. Е. С наклоном вверх) показывает положительное ускорение, соответствующее словесному описанию объекта, движущегося в положительном направлении и ускоряющегося от 5 до 15 м / с. Наклон линии можно вычислить, используя коэффициент превышения пробега. Между 5 и 10 секундами линия поднимается с 5 до 15 м / с и длится от 5 до 10 с. Это общий подъем +10 м / с и общий пробег 5 с. Таким образом, уклон (отношение подъема / хода) составляет (10 м / с) / (5 с) = 2 м / с 2 .Используя график скорость-время, определено, что ускорение объекта составляет 2 м / с 2 в течение последних пяти секунд движения объекта. Смещение объекта также можно определить с помощью графика скорость-время. Область между линией на графике и осью времени представляет смещение; эта область принимает форму трапеции. Как обсуждалось в Уроке 4, площадь трапеции можно приравнять к площади треугольника, лежащего поверх площади прямоугольника.Это показано на диаграмме ниже.
Таким образом, уклон (отношение подъема / хода) составляет (10 м / с) / (5 с) = 2 м / с 2 .Используя график скорость-время, определено, что ускорение объекта составляет 2 м / с 2 в течение последних пяти секунд движения объекта. Смещение объекта также можно определить с помощью графика скорость-время. Область между линией на графике и осью времени представляет смещение; эта область принимает форму трапеции. Как обсуждалось в Уроке 4, площадь трапеции можно приравнять к площади треугольника, лежащего поверх площади прямоугольника.Это показано на диаграмме ниже.
Общая площадь равна площади прямоугольника плюс площадь треугольника. Расчет этих площадей показан ниже.
| Прямоугольник | Треугольник |
|---|---|
| Площадь = основание * высота Площадь = (10 с) * (5 м / с) Площадь = 50 м | Площадь = 0,5 * основание * высота Площадь = 0.5 * (5 с) * (10 м / с) Площадь = 25 м |
Общая площадь (прямоугольник плюс треугольник) равна 75 м. Таким образом, перемещение объекта составляет 75 метров за 10 секунд движения.
Таким образом, перемещение объекта составляет 75 метров за 10 секунд движения.
Вышеупомянутое обсуждение показывает, как можно использовать графическое представление движения объекта для извлечения числовой информации об ускорении и смещении объекта. После построения график скорость-время можно использовать для определения скорости объекта в любой момент в течение 10 секунд движения.Например, скорость объекта в 7 секунд может быть определена путем считывания значения координаты y в координате x 7 секунд. Таким образом, графики скорость-время могут использоваться для выявления (или определения) числовых значений и соотношений между величинами смещения (d), скоростью (v), ускорением (a) и временем (t) для любого заданного движения.
Пример проблемы — решение с использованием кинематического уравнения Теперь рассмотрим то же словесное описание и соответствующий анализ с использованием кинематических уравнений.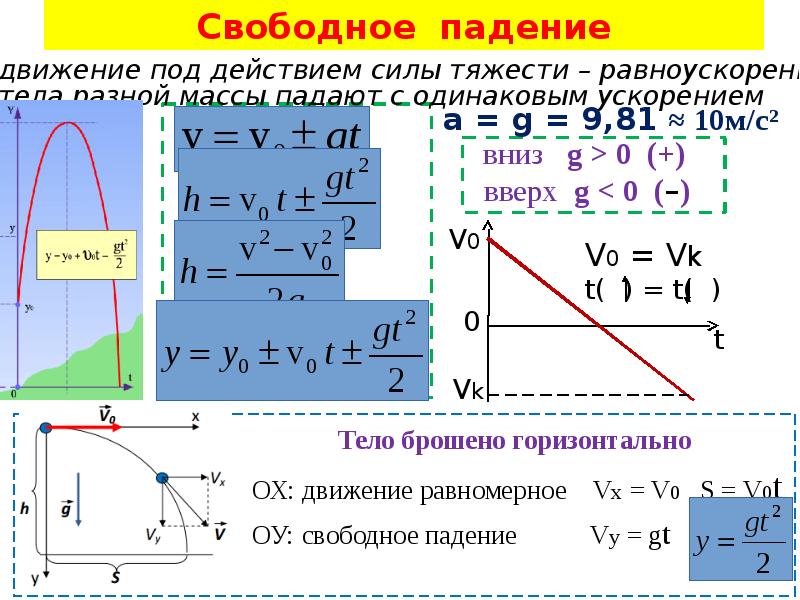 Словесное описание движения было:
Словесное описание движения было:
Объект, который движется с постоянной скоростью +5 м / с в течение 5 секунд, а затем ускоряется до конечной скорости +15 м / с в течение следующих 5 секунд
Кинематические уравнения могут применяться к любому движению, для которого ускорение постоянно. Поскольку это движение имеет две отдельные стадии ускорения, любой кинематический анализ требует, чтобы параметры движения в течение первых 5 секунд не смешивались с параметрами движения в течение последних 5 секунд.В таблице ниже перечислены указанные параметры движения.
| t = 0 с — 5 с | t = 5 с — 10 с |
|---|---|
| v i = 5 м / с v f = 5 м / с t = 5 с a = 0 м / с 2 | v i = 5 м / с v f = 15 м / с t = 5 с |
Обратите внимание, что ускорение в течение первых 5 секунд указано как 0 м / с 2 , несмотря на то, что это явно не указано. Фраза с постоянной скоростью указывает движение с нулевым ускорением. Ускорение объекта за последние 5 секунд можно рассчитать с помощью следующего кинематического уравнения.
Фраза с постоянной скоростью указывает движение с нулевым ускорением. Ускорение объекта за последние 5 секунд можно рассчитать с помощью следующего кинематического уравнения.
v f = v i + a * t
Здесь показаны подстановка и алгебра.
15 м / с = 5 м / с + a * (5 с)15 м / с — 5 м / с = a * (5 с)
10 м / с = a * (5 с)
(10 м / с) / (5 с) = a
a = 2 м / с 2
Это значение ускорения объекта за время от 5 до 10 с согласуется со значением, определенным по наклону линии на графике скорость-время.
Смещение объекта в течение всех 10 секунд также можно рассчитать с помощью кинематических уравнений. Поскольку эти 10 секунд включают два совершенно разных интервала ускорения, расчеты для каждого интервала должны выполняться отдельно. Это показано ниже.
| t = 0 с — 5 с | t = 5 с — 10 с |
|---|---|
| d = v i * t + 0,5 * a * t 2 d = (5 м / с) * (5 с) +0. 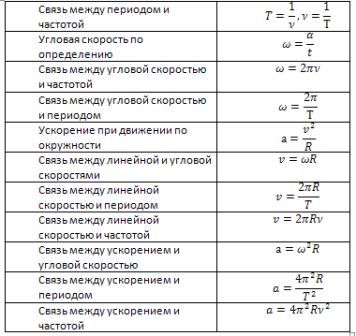 5 * (0 м / с 2 ) * (5 с) 2 5 * (0 м / с 2 ) * (5 с) 2 d = 25 м + 0 м d = 25 м | d = ((v i + v f ) / 2) * t d = ((5 м / с + 15 м / с) / 2) * (5 с) d = (10 м / с) * (5 с) d = 50 м |
Общее смещение в течение первых 10 секунд движения составляет 75 метров, что соответствует значению, определенному по площади под линией на графике скорость-время.
Анализ этого простого движения иллюстрирует ценность этих двух представлений движения — графика скорости-времени и кинематических уравнений.Каждое представление может использоваться для извлечения числовой информации о неизвестных величинах движения для любого заданного движения. Приведенные ниже примеры предоставляют полезную возможность для тех, кому требуется дополнительная практика.
Проверьте свое понимание
1. Rennata Gas движется по городу со скоростью 25,0 м / с и начинает ускоряться с постоянной скоростью -1,0 м / с 2 . В конце концов Ренната полностью останавливается.
В конце концов Ренната полностью останавливается. а. Изобразите ускоренное движение Реннаты, нарисовав график скорости-времени.Используйте график скорость-время, чтобы определить это расстояние.
г. Используйте кинематические уравнения, чтобы рассчитать расстояние, которое Ренната преодолеет при замедлении.
а. Изобразите 15 секунд движения Отто Эмиссии, нарисовав график скорости-времени.Используйте график, чтобы определить расстояние, которое Отто преодолел за все 15 секунд.
г. Наконец, разделите движение на два сегмента и используйте кинематические уравнения для расчета общего расстояния, пройденного за все 15 секунд.
 Люк ускоряется с постоянным ускорением вниз -10,0 м / с 2 (приблизительное значение ускорения свободного падения).
Люк ускоряется с постоянным ускорением вниз -10,0 м / с 2 (приблизительное значение ускорения свободного падения). а. Нарисуйте график скорости-времени для первых 8 секунд движения Люка.
б. Используйте кинематические уравнения, чтобы определить время, необходимое Люку Отбелу, чтобы вернуться к исходной высоте обрыва. Укажите это время на графике.
а. Нарисуйте график скорости-времени движения Чака Вагона. Используйте график скорость-время, чтобы определить общее расстояние, пройденное Чаком Вэгоном за 12 минут движения.
г. Наконец, разделите движение на два сегмента и используйте кинематические уравнения, чтобы определить общее расстояние, пройденное Чаком Вагоном.
 Вера смотрит вперед и наблюдает за аварией, которая привела к налету посреди дороги.К тому времени, как Вера хлопает по перерывам, она находится в 50,0 м от pileup. Она замедляется со скоростью -10,0 м / с 2 .
Вера смотрит вперед и наблюдает за аварией, которая привела к налету посреди дороги.К тому времени, как Вера хлопает по перерывам, она находится в 50,0 м от pileup. Она замедляется со скоростью -10,0 м / с 2 . а. Постройте график скорости-времени для движения Веры Сайд. Используйте график, чтобы определить расстояние, которое Вера должна пройти до полной остановки (если она не столкнется с pileup).
г. Используйте кинематические уравнения, чтобы определить расстояние, которое Вера Сайд должна пройти до полной остановки (если она не столкнется с pileup). Ударится ли Вера по машинам в pileup? То есть проездит Вера больше 50.0 метров?
а. Постройте график скорости-времени для движения Эрла Э. Берда. Используйте график, чтобы определить общее пройденное расстояние.
б. Разделите движение Эрла Э. Берда на два временных отрезка и используйте кинематические уравнения для расчета полного смещения.
Берда на два временных отрезка и используйте кинематические уравнения для расчета полного смещения.
Решения вышеуказанных вопросов
Решение вопроса 1 а.График скорость-время для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени.
Площадь = 0,5 * b * h = 0,5 * (25,0 с) * (25,0 м / с)
Площадь = 313 м
г. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Дано:
| Находят: d = ?? |
(0 м / с) 2 = (25,0 м / с) 2 + 2 * (-1,0 м / с 2 ) * d
0. 0 м 2 / с 2 = 625,0 м 2 / с 2 + (-2,0 м / с 2 ) * d
0 м 2 / с 2 = 625,0 м 2 / с 2 + (-2,0 м / с 2 ) * d
0,0 м 2 / с 2 — 625,0 м 2 / с 2 = (-2,0 м / с 2 ) * d
(-625,0 м 2 / с 2 ) / (- 2,0 м / с 2 ) = d
313 м = d
а.График скорость-время для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади треугольника плюс площадь прямоугольника 1 плюс площадь прямоугольника 2.
Площадь = 0,5 * b tri * h tri + b rect1 * h rect1 + b rect2 * h rect2
Площадь = 0.5 * (5,0 с) * (10,0 м / с) + (5,0 с) * (25,0 м / с) + (10,0 с) * (35,0 м / с)
Площадь = 25 м + 125 м + 350 м
Площадь = 500 м
г. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Сначала найдите d для первых 5 секунд:
Дано:
| Находят: d = ?? |
d = v i * t + 0,5 * a * t 2
d = (25,0 м / с) * (5,0 с) + 0.5 * (2,0 м / с 2 ) * (5,0 с) 2
d = 125 м + 25,0 м
d = 150 м
Теперь найдите d за последние 10 секунд:
Дано:
| Находят: d = ?? |
(Примечание: скорость на отметке 5 секунд можно определить, зная, что автомобиль ускоряется с 25,0 м / с при +2,0 м / с 2 за 5 секунд. Это приводит к изменению скорости на a * t = 10 м / с, а значит, скорость 35,0 м / с.)
d = v i * t + 0.5 * а * т 2
d = (35,0 м / с) * (10,0 с) + 0,5 * (0,0 м / с 2 ) * (10,0 с) 2
d = 350 м + 0 м
d = 350 м
Общее расстояние за 15 секунд движения является суммой этих двух вычислений расстояния (150 м + 350 м):
расстояние = 500 м
a.График скорость-время для движения:
г. Время для подъема и падения до исходной высоты в два раза больше времени, чтобы подняться на вершину. Итак, решение состоит в том, чтобы найти время, чтобы подняться до пика, а затем удвоить его.
Итак, решение состоит в том, чтобы найти время, чтобы подняться до пика, а затем удвоить его.
Дано:
| Находят: т вверх = ?? 2 * т вверх = ?? |
v f = v i + a * t вверх
0 м / с = 40 м / с + (-10 м / с2) * t вверх
(10 м / с 2 ) * t вверх = 40 м / с
т вверх = (40 м / с) / (10 м / с 2 )
т до = 4.0 с
2 * t вверх = 8,0 с
а. График скорость-время для движения:
График скорость-время для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади прямоугольника плюс площадь треугольника.
Площадь = b прямоугольник * h прямоугольник + 0,5 * b tri * h tri
Площадь = (10,0 мин) * (0,50 миль / мин) + 0,5 * (2,0 мин) * (0,50 миль / мин)
Площадь = 5 миль + 0,5 миль
Площадь = 5.5 миль
г. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Сначала найдите d для первых 10 минут:
Дано:
| Находят: d = ?? |
d = v i * t + 0,5 * a * t 2
d = (0,50 миль / мин) * (10. 0 мин) + 0,5 * (0,0 миль / мин 2 ) * (10,0 мин) 2
0 мин) + 0,5 * (0,0 миль / мин 2 ) * (10,0 мин) 2
d = 5.0 миль + 0 миль
d = 5.0 миль
Теперь найдите d за последние 2 минуты:
Дано:
| Находят: d = ?? |
d = v i * t + 0,5 * a * t 2
d = (0,50 миль / мин) * (2,0 мин) + 0,5 * (- 0,25 м / с 2 ) * (2,0 мин) 2
d = 1,0 мили + (-0,5 мили)
d = 0.5 миль
Общее расстояние за 12 минут движения является суммой этих двух вычислений расстояний (5.0 миль + 0,5 миль):
расстояние = 5.5 миль
a. График скорость-время для движения:
График скорость-время для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени.
Площадь = 0.5 * b * h = 0,5 * (4,5 с) * (45,0 м / с)
Площадь = 101 м
г.
Дано:
| Находят: d = ?? |
v f 2 = v i 2 + 2 * a * d
(0 м / с) 2 = (45.0 м / с) 2 + 2 * (-10,0 м / с 2 ) * d
0,0 м 2 / с 2 = 2025,0 м 2 / с 2 + (-20,0 м / с 2 ) * d
0,0 м 2 / с 2 -2025,0 м 2 / с 2 = (-20,0 м / с 2 ) * d
(-2025,0 м 2 / с 2 ) / (- 20,0 м / с 2 ) = d
101 м = d
Так как место аварии находится менее чем в 101 м от Веры, она действительно ударится по скоплению, прежде чем полностью остановится (если только она не свернет в сторону).
a. График скорость-время для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади треугольника плюс площадь прямоугольника 1 плюс площадь прямоугольника 2.
Площадь = 0,5 * b tri * h tri + b 1 * h 1 + b 2 * h 2
Площадь = 0,5 * (5,0 с) * (15,0 м / с) + (10,0 с) * (30,0 м / с) + (5,0 с) * (30,0 м / с)
Площадь = 37,5 м + 300 м + 150 м
Площадь = 488 м
г. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Сначала найдите d для первых 10 секунд:
Дано:
| Находят: d = ?? |
d = v i * t + 0. 5 * а * т 2
5 * а * т 2
d = (30,0 м / с) * (10,0 с) + 0,5 * (0,0 м / с 2 ) * (10,0 с) 2
d = 300 м + 0 м
d = 300 м
Теперь найдите d за последние 5 секунд:
Дано:
| Находят: d = ?? |
d = v i * t + 0,5 * a * t 2
d = (30,0 м / с) * (5,0 с) + 0,5 * (3,0 м / с 2 ) * (5,0 с) 2
d = 150 м + 37,5 м
д = 187.5 м
Общее расстояние за 15 секунд движения является суммой этих двух вычислений расстояний (300 м + 187,5 м):
расстояние = 488 м
Формула кинематических уравнений
Кинематика — это исследование движущихся объектов и их взаимосвязей. Есть четыре (4) кинематических уравнения, которые относятся к смещению D, скорости v, времени t и ускорению a.
Есть четыре (4) кинематических уравнения, которые относятся к смещению D, скорости v, времени t и ускорению a.
a) D = v i t + 1/2 при 2 b) (v i + v f ) / 2 = D / t
c) a = (v f — v i ) / t d) v f 2 = v i 2 + 2aD
D = смещение
a = ускорение
t = время
v f = конечная скорость
v i = начальная скорость
Вопросы по формулам кинематических уравнений.
1) Боб едет на велосипеде в магазин со скоростью 4 м / с, когда перед ним выбегает кошка. Он быстро тормозит до полной остановки, с ускорением — 2м / с 2 . Какое у него перемещение?
Ответ: Поскольку Боб остановлен, конечная скорость v f = 0. Его начальная скорость v i = 4 м / с. Ускорение, a = -2 м / с 2 . Время не указано, поэтому используйте уравнение (d) для смещения, D, потому что оно не зависит от времени.
Время не указано, поэтому используйте уравнение (d) для смещения, D, потому что оно не зависит от времени.
v f 2 = v i 2 + 2aD
(0) 2 = (4 м / с) 2 +2 (- 2 м / с 2 ) D
0 = 16 м 2 / с 2 + (- 4 м / с 2 ) D
-16 м 2 / с 2 = (- 4 м / с 2 ) D
16 м 2 / с 2 = 4 м / с 2 ) D
(16 м 2 / с 2 ) / (4 м / с 2 ) = D
Водоизмещение полное 4 м.
2) Вы путешествуете с постоянной скоростью 11 м / с в течение 5 минут. Как далеко ты проехал?
Ответ: При постоянной скорости v i = v f = 11 м / с. Время t = 5 мин или t = (60 сек / мин x 5 мин) = 300 сек. Теперь используйте уравнение (b), чтобы найти смещение D.
(v i + v f ) / 2 = D / t
D = [(v i + v f ) / 2] t
D = [(11 м / с + 11 м / с) / 2] x 300 с
D = (22 м / с) / 2 x 300 с
D = 11 м / с x 300 с
D = 3300 м.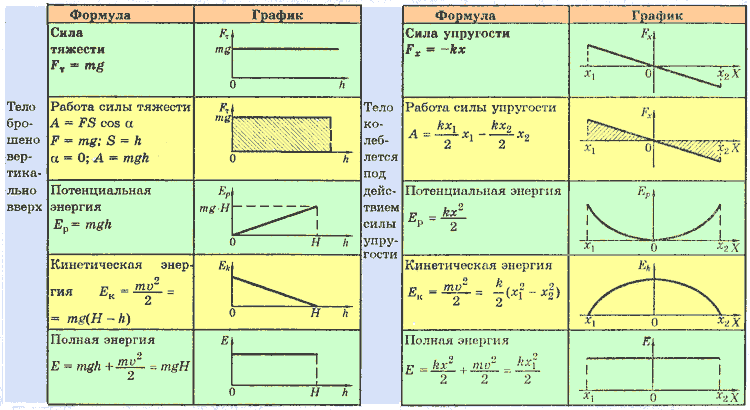 Водоизмещение полное 3,300 м.
Водоизмещение полное 3,300 м.
3) Каково ускорение автомобиля, который разгоняется с 11 до 40 м / с за 10 секунд?
Ответ: V i = 11 м / с. V f = 40 м / с. Время, t = 10 с. Используйте кинематическое уравнение c), чтобы найти ускорение.
a = (v f — v i ) / t
a = (40 м / с — 11 м / с) / 10 с
a = (29 м / с) / 10 с = 2,9 м / с 2
4) Если автомобиль разгоняется на 3.0 м / с 2 от полной остановки, сколько времени потребуется, чтобы проехать 3000 м?
Ответ: Ускорение a = 2,9 м / с 2 и перемещение D = 3000 м. Автомобиль был неподвижен, поэтому v i = 0. Используйте уравнение a), чтобы найти время.
D = v i t + 1/2 при 2
3000 м = 0t + 1/2 (3,0 м / с 2 ) t 2
3000 м = 1/2 (3,0 м / с 2 ) / т 2
3000 м / 1.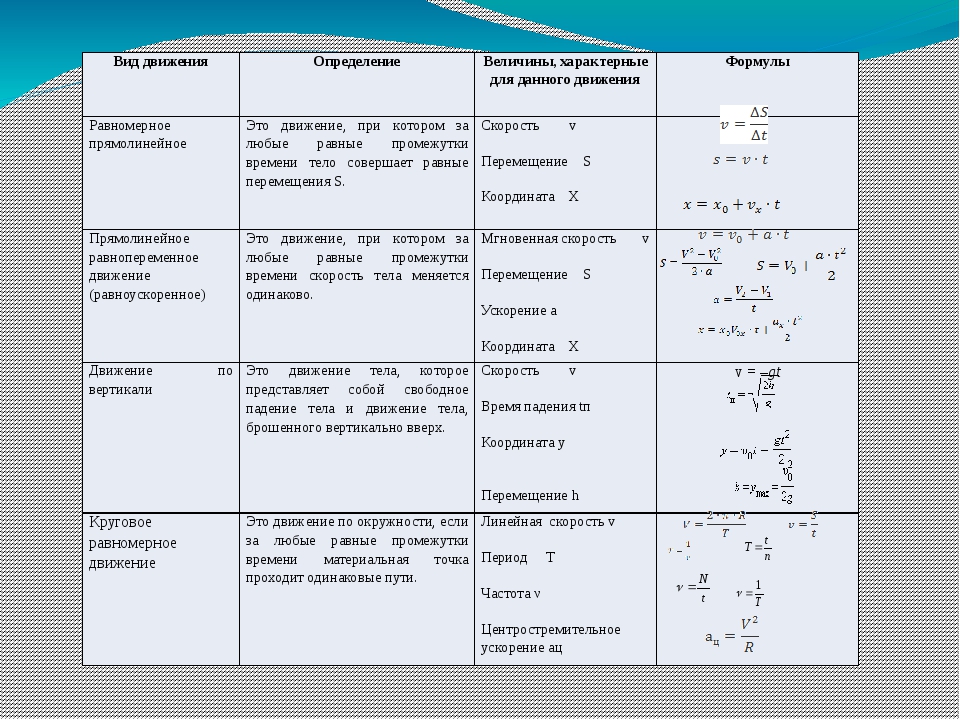 5 м / с 2 = t 2
5 м / с 2 = t 2
2000 с 2 = t 2
t = 44,72 сек
21,7 Уравнения движения | Движение в одном измерении
21.7 Уравнения движения (ESAHG)
В этом разделе мы рассмотрим третий способ описания движения. Мы рассмотрели описание движения с точки зрения слова и графики. В этом разделе мы исследуем уравнения, которые можно использовать для описания движения.
Этот раздел посвящен решению задач, связанных с равноускоренным движением.{-1} $} \ text {в момент} t \\ \ vec {s} & = \ text {displacement} \ text {(m)} \ end {выровнять *}
Галилео Галилей из Пизы, Италия, был первым, кто определил правильный математический закон ускорения:
общее пройденное расстояние, начиная с покоя, пропорционально квадрату времени. Он также пришел к выводу, что
объекты сохраняют свою скорость, если на них не действует сила — часто трение —
принял гипотезу Аристотеля о том, что объекты «естественным образом» замедляются и останавливаются, если не действует сила
на них. {2} + 2 \ vec {a} \ Delta \ vec {x} \ qquad (4)
\ end {выровнять *}
{2} + 2 \ vec {a} \ Delta \ vec {x} \ qquad (4)
\ end {выровнять *}
Вопросы могут быть разными, но следующий метод ответа на них всегда подойдет. Используйте это, когда попытаться задать вопрос, связанный с движением с постоянным ускорением. Вам нужны любые три известные величины (\ ({\ vec {v}} _ {i} \), \ ({\ vec {v}} _ {f} \), \ (\ Delta \ vec {x} \), \ (t \) или \ (\ vec {a} \)), чтобы можно было вычислить четвертый.
Стратегия решения проблем:
Внимательно прочтите вопрос, чтобы определить указанные количества.Запишите их.
Определите используемое уравнение. Запишите !!!
Убедитесь, что все значения указаны в правильных единицах измерения, и введите их в уравнение.
Рассчитайте ответ и проверьте свои единицы.
Рабочий пример 7: Уравнения движения
Гоночная машина едет на север. {- 1} $} \ text {(поскольку объект начинается с места)} \\
\ Delta \ vec {x} & = \ text {64} \ text {m} \\
т & = \ текст {4} \ текст {s} \\
\ vec {a} & =? \\
\ vec {v} _ {f} & =? \\
t & =? \ text {на половине расстояния} \ Delta \ vec {x} = \ text {32} \ text {m} \\
\ Delta \ vec {x} & =? \ text {в половине случаев} t \ text {2} \ text {s}
\ end {выровнять *}
{- 1} $} \ text {(поскольку объект начинается с места)} \\
\ Delta \ vec {x} & = \ text {64} \ text {m} \\
т & = \ текст {4} \ текст {s} \\
\ vec {a} & =? \\
\ vec {v} _ {f} & =? \\
t & =? \ text {на половине расстояния} \ Delta \ vec {x} = \ text {32} \ text {m} \\
\ Delta \ vec {x} & =? \ text {в половине случаев} t \ text {2} \ text {s}
\ end {выровнять *}
Все величины указаны в единицах СИ.{-2} $} \ text {Восток} \ end {выровнять *}
Конечная скорость : Найдите подходящее уравнение для расчета конечной скоростиМы можем использовать уравнение 1 — помните, что теперь мы также знаем ускорение объекта.
\ [{\ vec {v}} _ {f} = {\ vec {v}} _ {i} + \ vec {a} t \]Подставьте значения и рассчитайте окончательную скорость
\ begin {align *} {\ vec {v}} _ {f} & = {\ vec {v}} _ {i} + at \\ {\ vec {v}} _ {f} & = \ text {0} \ text {m · s $ ^ {- 1} $} + \ left (\ text {8} \ text { m · s $ ^ {- 2} $} \ right) \ left (\ text {4} \ text {s} \ right) \\ & = \ text {32} \ text {m · s $ ^ {- 1} $} \ text {Восток} \ end {выровнять *} Время на половине расстояния : Найдите уравнение для вычисления времениМы можем использовать уравнение 3:
\ begin {align *} \ Delta \ vec {x} & = {\ vec {v}} _ {i} + \ frac {1} {2} \ vec {a} {t} ^ {2} \\ \ text {32} \ text {m} & = \ left (\ text {0} \ text {m · s $ ^ {- 1} $} \ right) t + \ frac {1} {2} \ left ( \ текст {8} \ текст { m · s $ ^ {- 2} $} \ right) {\ left (t \ right)} ^ {2} \\ \ text {32} \ text {m} & = 0 + \ left (\ text {4} \ text {m · s $ ^ {- 2} $} \ right) {t} ^ {2} \\ \ text {8} \ text {s $ ^ {2} $} & = {t} ^ {2} \\ т & = \ текст {2,83} \ текст {s} \ end {выровнять *} Расстояние за половину времени : Найдите уравнение, связывающее расстояние и время В половине случаев это \ (\ text {2} \) \ (\ text {s} \), поэтому мы имеем \ ({\ vec {v}} _ {i} \), \ (\ vec {a} \) и \ (t \) все в
правильные единицы. {-1} $} \) в \ (\ text {8} \) \ (\ text {s} \). Рассчитайте необходимое ускорение и
общее расстояние, которое он прошел за это время.
{-1} $} \) в \ (\ text {8} \) \ (\ text {s} \). Рассчитайте необходимое ускорение и
общее расстояние, которое он прошел за это время.
Решение пока недоступно
Расширение: поиск уравнений движения (ESAHH)
Следующее не является частью учебной программы и может считаться дополнительной информацией.
Вывод уравнения 1
По определению ускорения:
\ [\ vec {a} = \ frac {\ Delta \ vec {v}} {t} \]где \ (\ Delta \ vec {v} \) — изменение скорости, т.е.е. \ (\ Delta v = {\ vec {v}} _ {f} — {\ vec {v}} _ {i} \). Таким образом, мы иметь
\ begin {align *} \ vec {a} & = \ frac {{\ vec {v}} _ {f} — {\ vec {v}} _ {i}} {t} \\ {\ vec {v}} _ {f} & = {\ vec {v}} _ {i} + \ vec {a} t \ end {выровнять *}Вывод уравнения 2
Мы видели, что смещение можно рассчитать по площади под графиком зависимости скорости от времени. За равномерно ускоренное движение наиболее сложный график зависимости скорости от времени, который мы можем получить, — это прямой
линия.Посмотрите на график ниже — он представляет объект с начальной скоростью \ ({\ vec {v}} _ {i} \) , ускоряясь до конечной скорости \ ({\ vec {v}} _ {f} \) за все время т .
За равномерно ускоренное движение наиболее сложный график зависимости скорости от времени, который мы можем получить, — это прямой
линия.Посмотрите на график ниже — он представляет объект с начальной скоростью \ ({\ vec {v}} _ {i} \) , ускоряясь до конечной скорости \ ({\ vec {v}} _ {f} \) за все время т .
Чтобы рассчитать окончательное смещение, мы должны вычислить площадь под графиком — это просто площадь прямоугольник добавлен к площади треугольника. Эта часть графика заштрихована для ясности.
\ begin {align *} {\ text {Area}} _ {△} & = \ frac {1} {2} b \ times h \\ & = \ frac {1} {2} t \ times \ left ({v} _ {f} — {v} _ {i} \ right) \\ & = \ frac {1} {2} {v} _ {f} t — \ frac {1} {2} {v} _ {i} t \ конец {выравнивание *} \ begin {выравнивание *} {\ text {Area}} _ {\ square} & = l \ times b \\ & = t \ times {v} _ {i} \\ & = {v} _ {i} т \ конец {выравнивание *} \ begin {выравнивание *} \ text {Displacement} & = {\ text {Area}} _ {\ square} + {\ text {Area}} _ {△} \\ \ Delta \ vec {x} & = {v} _ {i} t + \ frac {1} {2} {v} _ {f} t — \ frac {1} {2} {v} _ {i} т \\ \ Delta \ vec {x} & = \ frac {\ left ({v} _ {i} + {v} _ {f} \ right)} {2} t \ end {выровнять *}Вывод уравнения 3
Это уравнение просто выводится путем исключения конечной скорости \ ({v} _ {f} \) в уравнении 2.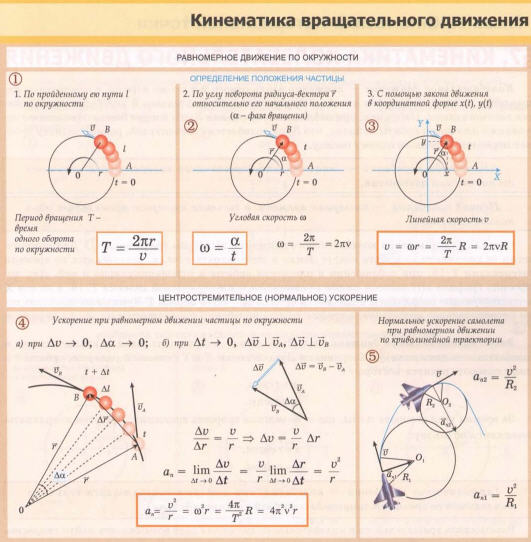 {2} + 2 \ vec {a} \ Delta \ vec {x}
\ end {выровнять *}
{2} + 2 \ vec {a} \ Delta \ vec {x}
\ end {выровнять *}
Это дает нам конечную скорость с точки зрения начальной скорости, ускорения и смещения и составляет не зависит от временной переменной.{-2} $} \). Его время реакции, чтобы ударить тормоза составляет \ (\ text {0,5} \) секунд. Будет ли грузовик сбить ребенка?
Проанализировать проблему и определить, какая информация предоставляется
Полезно нарисовать временную шкалу, подобную этой:
Нам необходимо знать следующее:
Какое расстояние водитель проезжает, прежде чем нажать на тормоз.
Как долго грузовик останавливается после нажатия на тормоз.
Общее расстояние, которое грузовик преодолевает до остановки.
Рассчитать расстояние \ (AB \)
Прежде чем водитель нажмет на тормоз, грузовик движется с постоянной скоростью. Нет ускорения
и поэтому уравнения движения не используются. Чтобы найти пройденное расстояние, мы используем:
Нет ускорения
и поэтому уравнения движения не используются. Чтобы найти пройденное расстояние, мы используем:
Грузовик преодолевает \ (\ text {5} \) \ (\ text {m} \) до того, как водитель нажмет на тормоз.{-2} $} \ right) t \\ т & = \ текст {8} \ текст {s} \ end {выровнять *}
Рассчитать расстояние \ (BC \)
Для расстояния мы можем использовать Уравнение 2 или Уравнение 3. Мы будем использовать Уравнение 2:
\ begin {align *} \ Delta \ vec {x} & = \ frac {\ left ({\ vec {v}} _ {i} + {\ vec {v}} _ {f} \ right)} {2} t \\ \ Delta \ vec {x} & = \ frac {10 + 0} {2} \ left (8 \ right) \\ \ Delta \ vec {x} & = \ text {40} \ text {m} \ end {выровнять *}Напишите окончательный ответ
Общее расстояние, которое преодолевает грузовик, составляет \ ({d} _ {AB} + {d} _ {BC} = \ text {5} + \ text {40} = \ text {45} \)
метров. Ребенок находится на \ (\ text {50} \) метрах впереди. Грузовик не ударит ребенка.
Ребенок находится на \ (\ text {50} \) метрах впереди. Грузовик не ударит ребенка.
ПРИМЕЧАНИЯ: Класс X, ФИЗИКА, «Кинематика»
ОПРЕДЕЛЕНИЕ СИЛЫ«Это раздел физики, который занимается описанием движения без ссылки на любую противодействующую или внешнюю силу».
ДВИЖЕНИЕ
«Когда тело меняет свое положение по отношению к окружающему, так что тело считается находящимся в состоянии движения».
ВИДЫ ДВИЖЕНИЯ
Есть три типа движения:
1, линейное или поступательное движение
2, вращательное движение
3, вибрационное движение
1.Линейное или поступательное движение
Если тело движется по прямой траектории, то оно должно быть в линейном или поступательном движении.
Пример
Автобус движется по дороге, Человек бежит по земле.
2. Вращательное движение
Если тело вращается или вращается от фиксированной точки, то оно должно находиться во вращательном движении.
Пример
Лопасти движущегося вентилятора, Колесо движущегося автомобиля.
3.Вибрационное движение
Движение вперед и назад вокруг средней точки, поэтому тело должно находиться в вибрационном движении.
Пример
Движение пружины.
ОТДЫХ
«Когда тело не меняет своего положения по отношению к своему окружению, так что тело считается находящимся в состоянии покоя».
Пример
Книга лежит на столе, Человек стоит на полу, Дерево в саду.
СКОРОСТЬ
«Расстояние, которое преодолевает тело за единицу времени, называется скоростью.»
OR
» Скорость изменения расстояния называется скоростью. «
FORMULA
или V = S / t
UNIT
Единица измерения скорости в системе СИ в системе MKS — метр / сек. .
или м / с
Виды скорости
1. Равномерная скорость
Если тело преодолевает равное расстояние за равный интервал времени, то считается, что тело движется с постоянной скоростью.
2. Переменная скорость
Если тело не преодолевает равное расстояние за равные промежутки времени, то говорят, что тело движется с переменной скоростью.
СКОРОСТЬ
«Расстояние, пройденное телом за единицу времени в определенном направлении, называется скоростью».
OR
«Скорость изменения смещения называется скоростью».
OR
«Скорость в определенном направлении называется скоростью».
FORMULA
Скорость = Смещение / Время
или V = S / t
UNIT
Единицей измерения скорости S.I в системе M.K.S является метр в секунду.
или м / с
Виды скорости
1.Равномерная скорость
Если тело преодолевает равное расстояние за равный интервал времени в постоянном направлении, то говорят, что тело имеет равномерную скорость.
2. Переменная скорость
Если тело не преодолевает равное расстояние за равный интервал времени в определенном направлении, то говорят, что тело движется с переменной скоростью.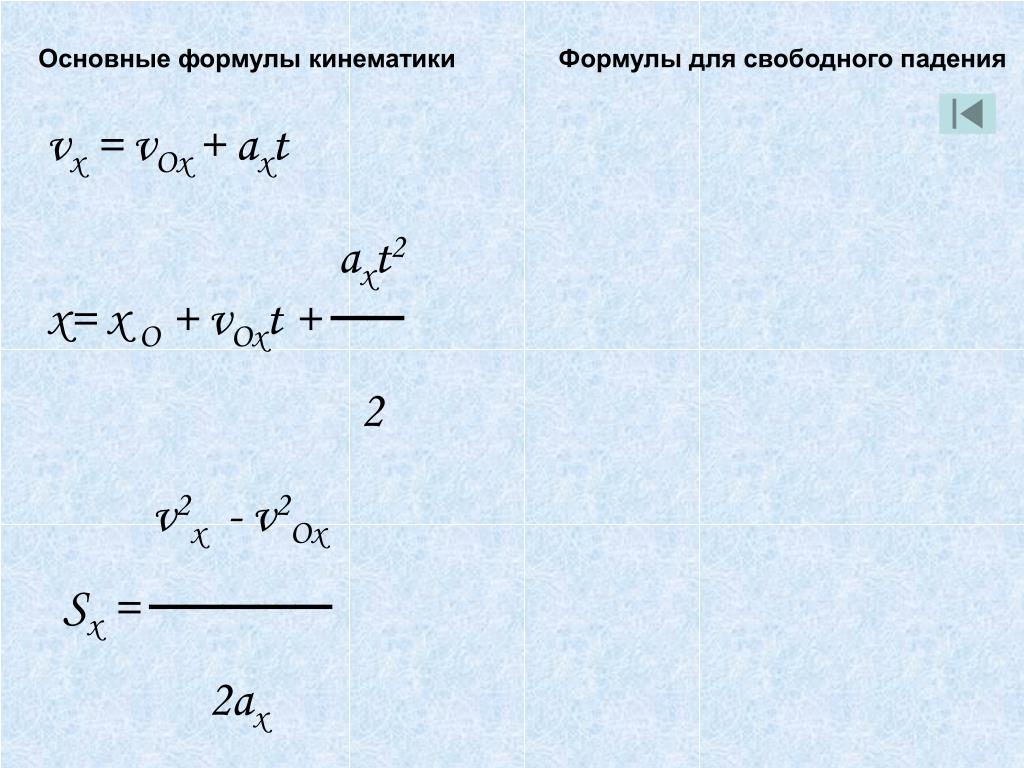
УСКОРЕНИЕ
«Скорость изменения скорости называется ускорением».
OR
«Ускорение зависит от скорости, если скорость непрерывно увеличивается или уменьшается, ускорение будет производиться.»
1. Положительное ускорение
Если скорость постоянно увеличивается, то ускорение будет положительным.
2. Отрицательное ускорение
Если скорость непрерывно уменьшается, то ускорение будет отрицательным.
FORMULA
Ускорение = изменение скорость / время
или
a = (Vf-Vi) / t
UNIT
Единица измерения скорости в системе MKS: метр / секунду + квадрат
или м / с
УРАВНЕНИЕ ДВИЖЕНИЯ
соотношение начальной скорости, конечной скорости, ускорения, времени и линейного расстояния.
ПЕРВОЕ УРАВНЕНИЕ ДВИЖЕНИЯ
предположим, что объект движется с начальной скоростью «Vi» за время «t» и преодолевает расстояние «S» с ускорением «a», а конечная скорость объекта становится «Vf»
Согласно определению ускорения «Скорость изменения скорости называется ускорением»
т. е. Ускорение = Изменение скорости / время
е. Ускорение = Изменение скорости / время
=> a = Vf — Vi / t
ПРОИЗВОДСТВО
a = Vf — Vi / t
at = Vf — Vi
или Vf = Vi + at
ВТОРОЕ УРАВНЕНИЕ ДВИЖЕНИЯ
Согласно определению ускорения «Скорость изменения скорости называется ускорением».
т.е. ускорение = изменение скорости / времени
=> a = Vf — Vi / t
при = Vf — Vi
или Vf = Vi + при ————- ( 1)
Подставляем среднюю скорость:
Vav = (Vi + Vf) / 2 ———— (2)
Расстояние, пройденное телом в единице:
S = Vav / t
Вычисление значения Vav из уравнения 2:
S = [(Vi + Vf) / 2] * t
Вычисление значения Vf из уравнения 1:
S = [(Vi + Vi + at) / 2] * t
S = [(2Vi + at) / 2] * t
S = (Vi + at / 2} * t
S = (Vit + 1 / 2at2) {Здесь 2 — квадрат времени «t».Не пишите это предложение в экзамене}
ТРЕТЬЕ УРАВНЕНИЕ ДВИЖЕНИЯ
Согласно определению ускорения «Скорость изменения скорости называется ускорением».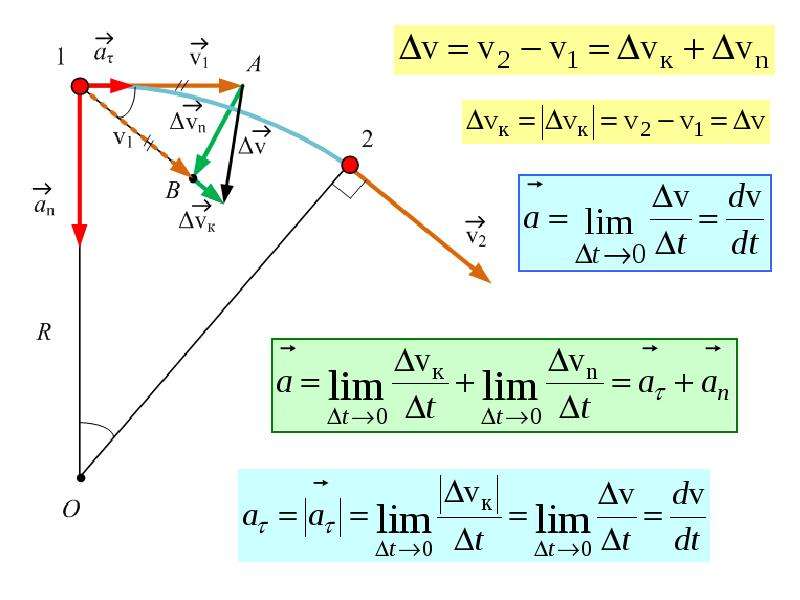
Ускорение = Изменение скорости / время
=> a = (Vf — Vi) / t
=> at = Vf — Vi
или t = (Vf — Vi) / a ——- —— (1)
Подставляем среднюю скорость:
Vav = (Vi + Vf) / 2 ———— (2)
Мы знаем, что:
Vav = S / t
=> S = Vav * t
Подставляем значение Vav из уравнения 2 и значение t из уравнения 1:
S = [(Vi + Vf) / 2] * [(Vf-Vi ) / a]
S = Vi2 — Vf2 / 2a, поскольку {(a + b) (ab) = a2 — b2}
или 2as = Vf2 — Vi2
УСКОРЕНИЕ ИЗ-ЗА ГРАВИТАЦИИ ИЛИ СВОБОДНОГО ПАДАЮЩИХ ОБЪЕКТОВ
«Galileo был первым ученым, который осознал, что, пренебрегая эффектом сопротивления воздуха, все тела в свободном падении вблизи поверхности Земли ускоряются вертикально вниз с одинаковым ускорением, а именно 9.8 м / с2 «
Пример
Если мяч брошен вертикально вверх, он поднимается на определенную высоту и затем падает обратно на землю. Однако это происходит из-за притяжения земли, которое притягивает объект к земле»
ХАРАКТЕРИСТИКА СВОБОДНО ПАДАЮЩИХСЯ ТЕЛ
1, Когда тело отбрасывается вертикально вверх, его скорость непрерывно уменьшается и становится равной нулю на определенной высоте.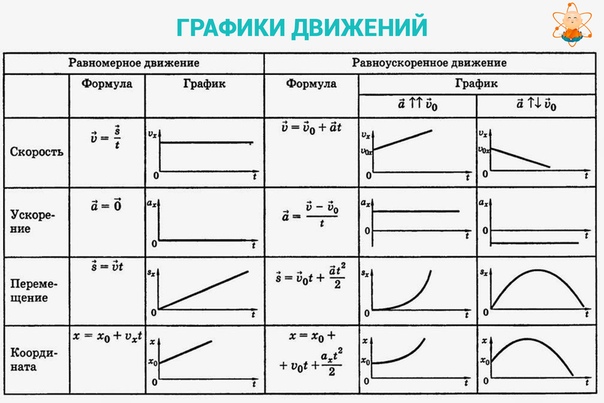 Во время этого движения значение ускорения отрицательное и Vf равно нулю (a = -9 .8 м / с2, Vf = 0).
Во время этого движения значение ускорения отрицательное и Vf равно нулю (a = -9 .8 м / с2, Vf = 0).
2, Когда тело падает обратно на землю, его скорость непрерывно увеличивается и становится максимальной на определенной высоте. Во время этого движения значение ускорения положительное, а Vi равно нулю (a = 9,8 м / с2, Vi = 0 ).
3, Ускорение свободного падения обозначено буквой a, его значение составляет 9,8 м / с2.
4, Уравнение движения для свободно падающих тел можно записать как:
Vf = Vi + gt
h = Vit + 1/2 gt2
2gh = Vf2 — Vi2
Уравнения кинематики — определение, параметры, и ответы на часто задаваемые вопросы
Целью этого первого раздела, относящегося к классу физики, было исследование разнообразия средств, с помощью которых можно описывать движение объектов.Разнообразие представлений, которые мы уже изучили и исследовали, также включает словесные представления, которые являются графическими представлениями, а также числовые представления и графические представления, которые представляют собой графики положения-времени и графики скорости-времени.
Определение кинематических уравнений
Раздел физики, который обычно определяет движение, относящееся к времени и пространству и игнорирующее причину этого движения, называется кинематикой. Уравнение, которое называется кинематикой, представляет собой набор уравнений, которые могут вывести неизвестный аспект движений тела, если другие аспекты предоставлены.
Эти уравнения связывают пять кинематических переменных:
Смещение, обозначаемое Δx.
Начальная скорость, которая задается как v 0 , которая называется Конечной скоростью и обозначается v. Временной интервал обозначается t Постоянное ускорение, обозначаемое a.
По сути, мы можем сказать, что кинематические уравнения, которые могут выводить одну или несколько из этих переменных, если другие заданы. Эти уравнения, которые мы видели, определяют движение либо с постоянной скоростью, либо с постоянным ускорением. Поскольку мы можем сказать, что уравнения кинематики применимы только при постоянном ускорении или постоянной скорости, мы не можем использовать их, если одно из двух меняется.
Эти уравнения, которые мы видели, определяют движение либо с постоянной скоростью, либо с постоянным ускорением. Поскольку мы можем сказать, что уравнения кинематики применимы только при постоянном ускорении или постоянной скорости, мы не можем использовать их, если одно из двух меняется.
Параметры кинематического уравнения
Знание каждой из различных величин обычно обеспечивает описательную информацию о движении объекта. Например, мы можем сказать, что если известно, что автомобиль движется с постоянной скоростью 22.0 м / с, север в течение 12,0 секунд для смещения на север, равного 264 метрам. Тогда можно сказать, что движение автомобиля полностью описано.
Если мы возьмем вторую машину, то известно, что она ускоряется из положения покоя с ускорением на восток 3,0 м / с 2 в течение 8,0 секунд, а конечная скорость составляет 24 м / с. . Направление смещения на восток и на восток составляет 96 метров, и тогда мы можем сказать, что движение этой машины полностью описано.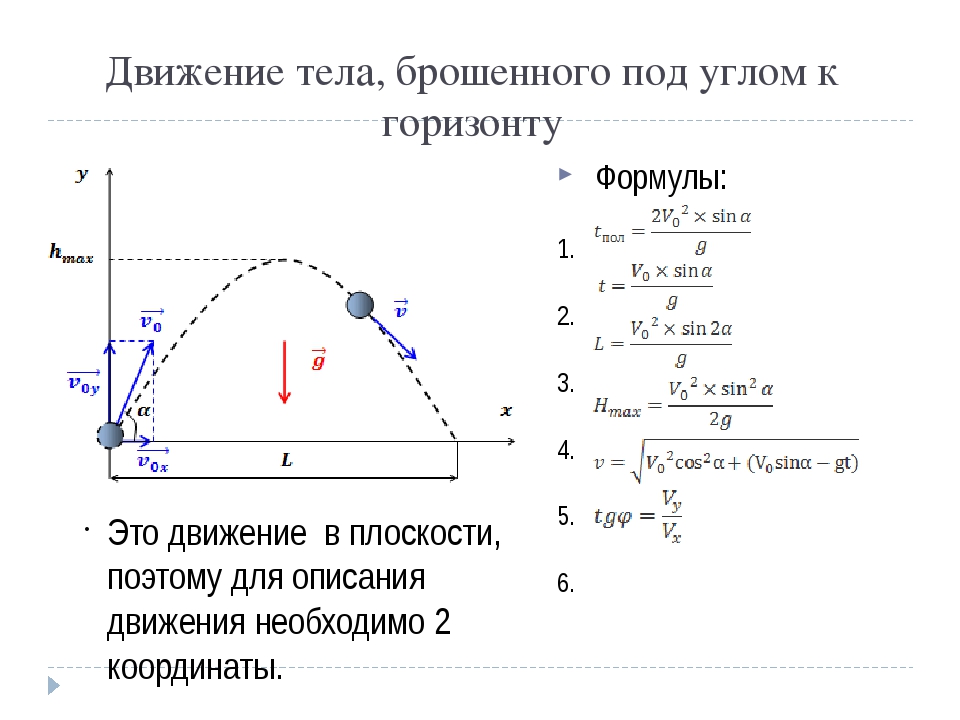
Эти два утверждения, которые мы видели, обеспечивают полное описание движения объекта. Однако можно сказать, что такая полнота не всегда известна.
Часто видно, что известны лишь некоторые параметры движения объекта, а остальные неизвестны. Например, мы можем сказать, что, приближаясь к светофору, мы можем узнать, что автомобиль имеет скорость 22 м / с, движется в восточном направлении и способен к заносу 8,0 м / с 2 и в западном направлении.Однако мы не знаем, какое смещение испытала бы наша машина, если бы мы резко нажали на тормоза и резко остановились. а затем, после этого, мы не знаем, сколько времени потребуется, чтобы остановиться. В таком случае, как этот, мы можем сказать, что неизвестные параметры, которые могут быть определены с использованием физических принципов и математических уравнений, являются кинематическими уравнениями.
Что такое кинематическое уравнение?
Уравнения, которые могут быть использованы для любого движения, которое в целом можно описать как постоянное движение, которое имеет скорость движения, которая является ускорением 0 м / с / с, или мы можем сказать движение с постоянным ускорением. Можно сказать, что они никогда не будут использоваться в течение какого-либо периода времени, в течение которого изменяется ускорение. Каждое из уравнений, которые являются кинематическими уравнениями, включает четыре переменные. Если нам известны значения трех из четырех переменных, то можно просто вычислить значение четвертой переменной.
Можно сказать, что они никогда не будут использоваться в течение какого-либо периода времени, в течение которого изменяется ускорение. Каждое из уравнений, которые являются кинематическими уравнениями, включает четыре переменные. Если нам известны значения трех из четырех переменных, то можно просто вычислить значение четвертой переменной.
Таким образом, мы можем сказать, что уравнение, которое является кинематическим уравнением, предоставляет полезные средства прогнозирования информации о движении объекта, если другая информация нам уже известна.Например, мы можем сказать, что если значение ускорения, а также начальное и конечное значения скорости буксирующего автомобиля известны, то мы можем сказать, что смещение автомобиля и время можно предсказать с помощью кинематических уравнений. Здесь мы сосредоточимся на использовании кинематических уравнений, которые должны предсказывать численные значения неизвестных величин для движущихся объектов.
Четыре кинематических уравнения, описывающие движение объекта, приведены ниже:
\ [d = v_ {i} \ times t + \ frac {1} {2} \ times a \ times t ^ {2} \] \ [v_ {f} ^ {2} = v_ {i} ^ {2} + 2 \ times a \ times d \]
\ [v_ {f} = v_ {i} + a \ times t \] \ [ d = \ frac {v_ {i} + v_ {f}} {2} \ times t \]
В приведенных выше уравнениях, которые мы видели, используются различные символы. Каждый символ, который мы видели, имеет свое особое значение. d обозначает смещение объекта, t обозначает время, в течение которого объект перемещался, a обозначает ускорение объекта, v обозначает скорость объекта, v указывает, что значение скорости является начальным, а vf указывает, что значение скорости является окончательным.
Каждый символ, который мы видели, имеет свое особое значение. d обозначает смещение объекта, t обозначает время, в течение которого объект перемещался, a обозначает ускорение объекта, v обозначает скорость объекта, v указывает, что значение скорости является начальным, а vf указывает, что значение скорости является окончательным.
Каждое из этих четырех уравнений, которые мы видели, надлежащим образом описывает математическую взаимосвязь между параметрами движения объекта.Таким образом, мы можем сказать, что их можно использовать для прогнозирования неизвестной информации о движении объекта, если известна другая информация. В следующей части мы исследуем процесс этого.
Кинематические уравнения: список и пример — стенограмма видео и урока
Уравнения кинематики
Есть пять основных кинематических уравнений, которые необходимо знать для решения задач.
В этих пяти уравнениях:
- t — время, измеренное в секундах
- vi — начальная скорость, измеренная в метрах в секунду
- vf — конечная скорость, измеренная в метрах в секунду
- a — ускорение, измеренное в метрах в секунду в квадрате
- y (или иногда x ) — смещение, измеряемое в метрах
Также важно отметить, что для падающих объектов ускорение ( a ) — это ускорение свободного падения ( g ), которое всегда отрицательно 9.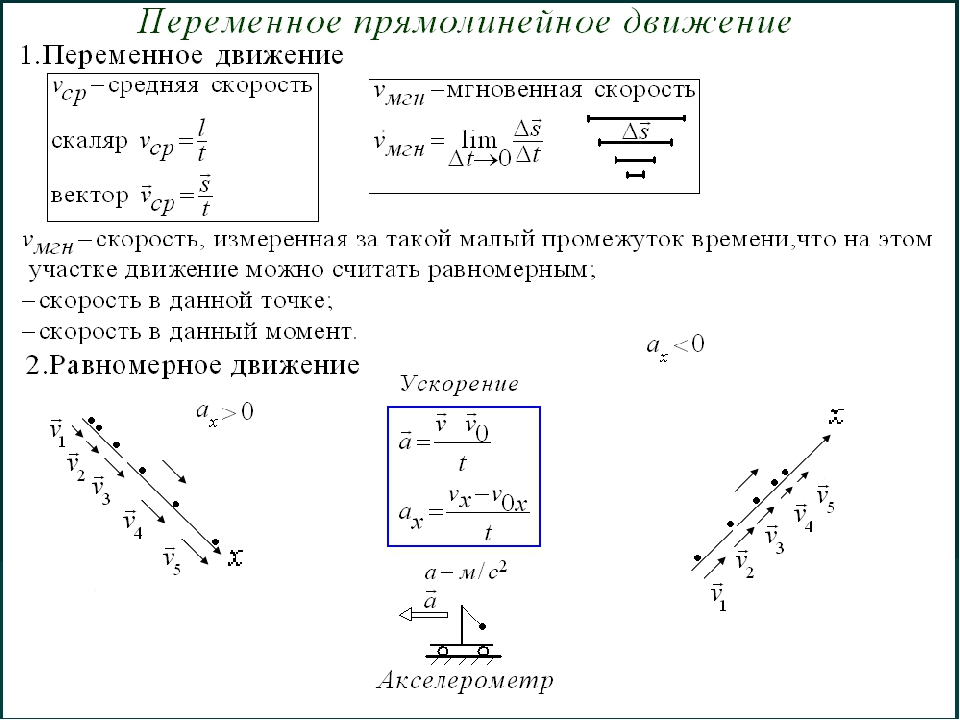 8 метров на секунду в квадрате.
8 метров на секунду в квадрате.
Каждое из пяти уравнений содержит четыре переменные, при этом одна переменная отсутствует. Каждый раз, когда вы решаете задачи кинематики, вам следует дать три числа и попросить найти четвертое. Итак, все, что вам нужно сделать, это найти уравнение с этими четырьмя величинами в нем, подставить числа и решить.
Пример задачи движения
Давайте рассмотрим пример использования уравнений. Допустим, мяч падает с высоты 6 метров, и он падает, пока не достигнет земли.Сколько времени нужно, чтобы достичь земли?
Ну, в первую очередь надо записать то, что мы знаем. Водоизмещение y составляет -6 метров. Почему отрицательный? Что ж, падает вниз. Обычно в физике мы называем восходящий положительный и нисходящий отрицательный. Однако это довольно произвольно, и если все ваши признаки совпадают, вы должны получить один и тот же ответ.
Хорошо, теперь у нас есть потенциальная проблема: в вопросе нет других номеров. Но вопрос говорит нам о вещах, которые тайком дают нам другие числа, которые мы можем использовать. Во-первых, мяч падает, то есть падает под действием силы тяжести. Таким образом, ускорение, как и для всех падающих предметов, составляет -9,8. Опять же, отрицательный, потому что ускорение направлено вниз.
И вопрос также говорит нам, что мяч упал, а это значит, что начальная скорость равна нулю. Когда вы бросаете мяч, в тот момент, когда вы его отпускаете, он не движется и его скорость равна нулю.И нас просят найти время, t , поэтому t =?.
Итак, мы знаем три числа, и нас просят найти четвертое. Так что эта проблема разрешима.
Нам нужно найти уравнение из пяти, которое содержит y , vi , a и t . И это уравнение таково:
Мы подставляем числа в это уравнение, например:
Первый член равен нулю, поэтому эта часть исчезает. Затем измените порядок так, чтобы получилось t , и введите числа в калькулятор. И получаем t = 1,1 секунды. И это все; это наш ответ.
Затем измените порядок так, чтобы получилось t , и введите числа в калькулятор. И получаем t = 1,1 секунды. И это все; это наш ответ.
Краткое содержание урока
Кинематика — это исследование движения без ссылки на силы, вызывающие движение. В кинематике есть пять важных величин: смещение (изменение положения), начальная скорость, конечная скорость, ускорение и время. Начальная скорость — это скорость движения объекта при t = 0. Конечная скорость — это скорость движения объекта по истечении времени t . Водоизмещение — насколько изменилось положение за время т . Ускорение — это скорость, с которой скорость изменялась за время t . А время просто … ну, самое время.
Есть пять основных кинематических уравнений, которые вам нужно знать для решения задач. В этих пяти уравнениях:
- t — время, измеренное в секундах
- vi — начальная скорость, измеренная в метрах в секунду
- vf — конечная скорость, измеренная в метрах в секунду
- a — ускорение, измеренное в метрах в секунду в квадрате
- y (или иногда x ) — смещение, измеряемое в метрах
Также важно отметить, что для падающих объектов ускорение a — это ускорение свободного падения g , которое всегда отрицательно 9.



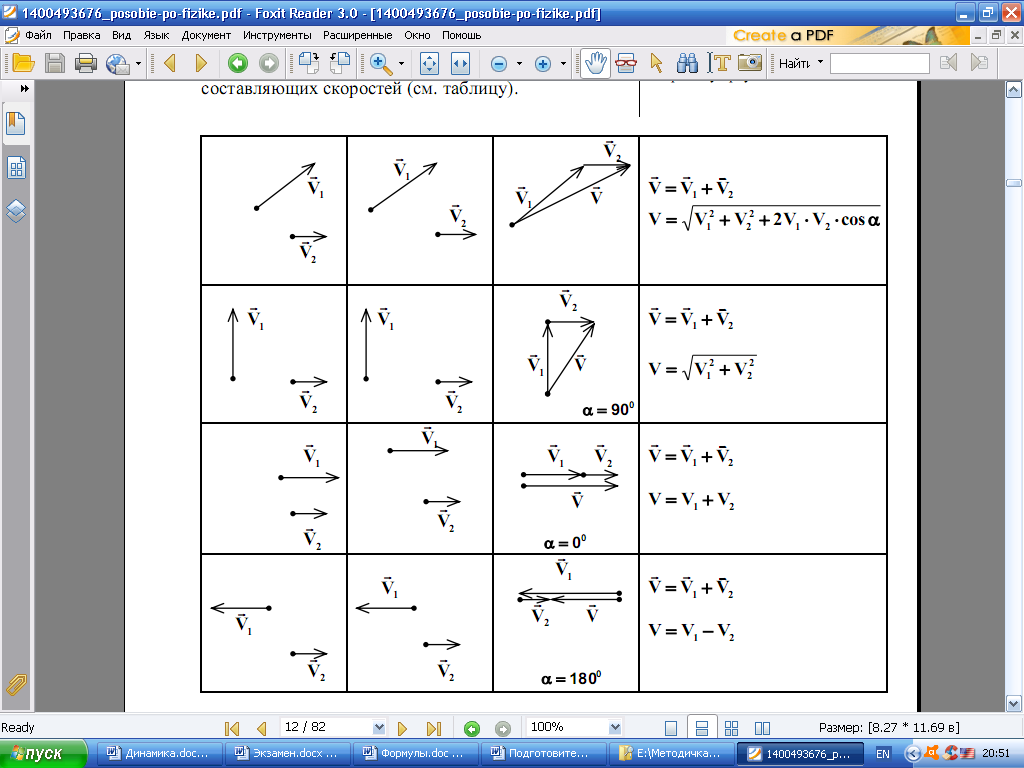




 Во время печати, вы так или иначе будете смотреть на формулы, запоминая их. К тому же, с основными формулами по физике в кармане, вы будете чувствовать себя на экзамене намного увереннее, чем без них.
Во время печати, вы так или иначе будете смотреть на формулы, запоминая их. К тому же, с основными формулами по физике в кармане, вы будете чувствовать себя на экзамене намного увереннее, чем без них. 0 м / с 2
0 м / с 2