прямой, тупой, острый и развернутый угол

Давайте начнем с определения того, что такое угол. Во-первых, он является геометрической фигурой. Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).

Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине.

Существует несколько их разновидностей. Рассмотрим подробнее каждый вид.

Основных типов углов всего четыре — прямой, тупой, острый и развернутый угол.

Прямой

Он выглядит так:

Его градусная мера всегда составляет 90^о, иначе говоря, прямой угол — это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник.

Тупой

Он имеет такой вид:

Градусная мера тупого угла всегда больше 90^о, но меньше 180^о. Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.

Острый

Он выглядит так:

Градусная мера острого угла всегда меньше 90^о. Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма.

Развернутый

Развернутый угол имеет такой вид:

В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить смежные углы, проведя из его вершины один или несколько лучей в любых направлениях.

Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:

1. Нулевой

Он выглядит так:

Само название угла уже говорит о его величине. Его внутренняя область равняется 0^о, а стороны лежат друг на друге так, как показано на рисунке.

2. Косой

Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие — он не должен равняться 0^о, 90^о, 180^о, 270^о.

3. Выпуклый

Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы. Как вы уже поняли, градусная мера выпуклого угла — от 0^о до 180^о.

4. Невыпуклый

Невыпуклыми являются углы с градусной мерой от 181^о до 359^о включительно.

5. Полный

Полным является угол с градусной мерой 360^о.

Это все типы углов по их величине. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.

1. Дополнительные

Это два острых угла, образовывающие один прямой, т.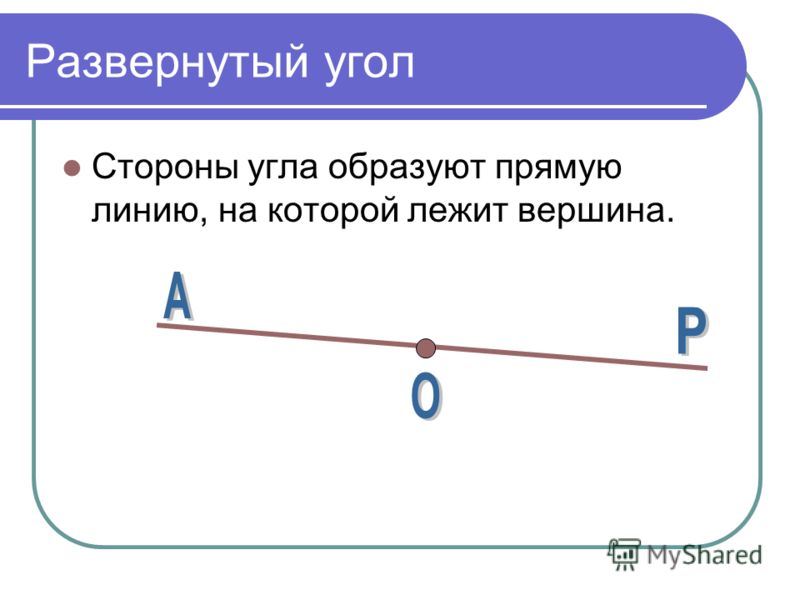 е. их сумма 90^о.

2. Смежные

Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180^о.

3. Вертикальные

Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны.

Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный.

1. Центральный

Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами.

2. Вписанный

Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается.

Это все, что касается углов. Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.

Угол, виды углов и их измерение

Определение. Угол — это часть плоскости, ограниченная двумя лучами, исходящими из одной точки, называемой вершиной угла.

Если плоскость круга разделить на 360 равных частей радиусами, то часть круга — это угловой градус, который обозначается знаком « ° » (читается — «градус»).

Следовательно, 1° = часть круга.

Круг составит * 360 = 1° * 360 = 360°.

Угол, равный плоскости круга, составляет 360° и называется полным углом.

Если плоскость круга разделить диаметром (двумя радиусами, расположенными на одной прямой линии) на две равные части, то плоскость полукруга составит угол в 360′: 2 = 180°.

Угол, равный полуплоскости круга, составляет 180° и называется развернутым углом.

Если плоскость круга разделить двумя диаметрами (горизонтальной и вертикальной линиями) на четыре равные части, то плоскость одной части составит угол в 360° : 4 = 90°.

Угол, равный четвертой части круга, составляет 90° и называется прямым углом.

Отвлекаясь от плоскости, в которой расположен круг, изобразим углы таким образом:

Углы равны, если равны их градусные меры или у них при наложении одного угла на другой совпадают вершины и соответствующие стороны углов.

Например, прямой угол (рис. 1) мы трижды развернули вокруг вершины угла, при этом на двух рисунках (рис. 2 и 4) мы передвинули вершину угла по плоскости листа.

Инструментом для измерения углов служит транспортир.

Для измерения угла следует совместить вершину угла и штрих с цифрой 0 на шкале транспортира. Одна сторона угла должна совпадать с прямой линией транспортира, на которой стоит 0, а вторая сторона угла пересекать шкалу транспортира (полуокружность с разметкой в угловых градусах).

На пересечении стороны угла и шкалы транспортира считывается градусная мера данного угла.

Мы рассмотрели полный, развернутый и прямой углы. Существует еще два типа углов: острые и тупые. Все острые углы имеют градусную меру в пределах: больше 0° и меньше 90°.

Например. острые углы:

Углы, градусная мера которых больше 90°, но меньше 180°*, называются тупыми углами.

Тупые углы (штриховой линией обозначен прямой угол в составе тупого угла) приведены на рис. 5, 6,7.

Чтобы построить заданный в градусной мере угол, необходимо иметь транспортир, линейку и карандаш.

Что такое Угол? Определение, виды, как обозначают? Примеры

Определение угла

Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.
Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.

Если нам дана прямая a на плоскости, и на ней есть некоторая точку O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.

Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:

Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.

В математике существует специальный символ для обозначения угла, вот он: ∠.

Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.

Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре. При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA.

Иногда можно встретить обозначение в виде цифр — так тоже можно.

Для наглядности — все способы обозначения углов:

Что такое вершина и стороны угла:

• Стороны угла — лучи, из которых состоит угол.
• Вершина угла — общее начало сторон угла.

Биссектриса — это луч, который исходит из вершины угла и делит его на два равных угла.

Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:

При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.

Единица измерения углов — градусы. Символ для обозначения градуса угла: °.

Совет 2: Как возвести угол

Углом именуется геометрическая фигура, которая образована двумя лучами – сторонами угла, исходящими из одной точки – вершины угла. Традиционно для построения плоского угла в планиметрии применяется транспортир, с подмогой которого дозволено легко отложить угол с заданной градусной мерой, но как быть, если под рукой этого инструмента нет?Для построения угла дозволено воспользоваться тригонометрическими функциями и построением прямоугол ьного треугол ьника.

Вам понадобится

Определение смежных и вертикальных углов

Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Таким образом два смежных угла составляют развернутый угол. Общая сторона двух смежных углов называется наклонной к прямой, на которой лежат другие стороны, при условии, что смежные углы не равны.

Вертикальные углы — это пара углов, у которых есть общая вершина, при этом стороны одного угла составляют продолжение сторон другого угла.

При пересечении прямых получается четыре пары смежных и две пары вертикальных углов. Вот как это выглядит:

Измерение вертикальных углов теодолитом – как сделать это самостоятельно?

Вначале прибор необходимо достаточно надежно закрепить на штативе. Далее выбирают две точки объекта, проводимых измерений. Зрительную трубу при помощи винта и диоптрийного кольца наводят на выбранные точки.

После этого вертикальная нить зрительной трубы совмещается с одной из точек и проводится считывание данных с горизонтального круга. Постепенно ослабляя винт фиксации, трубу перемещают по часовой стрелке на другую точку и также снимаются показания.

Измерение углов теодолитом иногда делают с применением кругового приема, который целесообразен в случае, когда приходится проводить измерения из одной точки. Для этого теодолит устанавливается в нужном месте. Лимб должен быть как можно ближе к нулю.

Затем начинают вращать алидаду до полного совмещения нулевого штриха микроскопа с нулевым штрихом на лимбе. Далее следует немного ослабить зажим и направить трубу на точку. По окончании замеров, затягивают стопорный винт и делают расчеты.

Измерение горизонтальных углов теодолитом проводится вне зависимости от его положения. Для проведения таких замеров зрительную трубу поочередно наводят на пару точек, между которыми необходимо провести замер и одновременно проводится отсчет по горизонтальному кругу. Величину угла определяют на основании разницы отсчетов.

Измерение горизонтальных углов с использованием теодолита проходит в две или три стадии, в зависимости от типа устройства. Если используется классический теодолит, к двум измерительным добавится одна вычислительная.

Принимая, что вершиной искомого угла является установленный прибор, оператор наводит вертикальную нить сетки зрительной трубки на первую отметку и фиксирует значение на горизонтальном лимбе. В современных теодолитах с электронной «начинкой» отметка определяется на лимбе автоматически и закрепляется как 0 с помощью кнопок на панели прибора; в традиционных – отмечается оператором через окуляр отсчетного устройства и заносится в журнал измерений.

После этого по часовой стрелке трубка наводится на вторую отметку. Электронный прибор, при этом, высчитает угол сам и выведет показания на экран. При работе с традиционным устройством, оператор должен будет через микроскоп снять показания с горизонтального лимба и, путем геометрических операций, вычислит значение искомого угла.

Виды углов

Есть разные типы углов и у каждого своё название:

• острый
• прямой
• тупой
• развернутый
• выпуклый
• полный

Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.

Острый угол — это угол, который меньше прямого угла, то есть < 90°.

Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол всегда равен половине развернутого угла, то есть = 90°.

Если два смежных угла равны между собой, то каждый из них является прямым. Для удобства прямой угол обозначается уголком. Вот так:

На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.

Развернутый угол — это открытый угол, который образован двумя лучами и равен сумме двух прямых углов. Развернутый угол равен 180°. Как выглядит развернутый угол показано на первой картинке.

Неразвернутый угол — это любой угол, который не является развернутым, то есть не равен 180°.

Тупой угол — это угол, который больше прямого угла, но меньше развернутого: 90° < тупой угол < 180°.

Выпуклый угол — это угол, который больше развернутого угла, но меньше полного: 180° < выпуклый угол < 360°.

Полный угол — это угол, обе стороны которого совпадают с одним лучом. Он равен сумме четырех прямых углов, то есть = 360°.

Прилежащие углы — это пара углов с общей вершиной и стороной, другие стороны при этом лежат по разные стороны от общей стороны.

На картинке мы видим два прилежащих угла ∠AOB и ∠BOC, общую вершину O и общую сторону OB.

Можно сформулировать определение по-другому: если из вершины любого угла провести луч, разделяющий угол на два, то образованные углы будут прилежащими.

Чтобы найти угол, который разделен лучом, нужно сложить полученные углы: ∠AOB = ∠AOC + ∠COB. Из этого можно выделить следующие верные разности:

• ∠AOC = ∠AOB — ∠COB,
• ∠COB = ∠AOB — ∠AOC.

Инструкция для изготовления транспортира

Для этого понадобится:

Инструкция

1. Нужно убедиться, что у принтера имеется разрешение по всем координатам. Открываем графический редактор, рисуем квадрат и распечатываем. Берем линейку и перепроверяем все стороны квадрата, они должны быть равными. Если, вдруг не получилось с первого раза, то, распечатайте в другом разрешении.
2. Сохраненный рисунок с изображением транспортира масштабируем до нужных нам размеров в графической программе с соблюдением пропорций. Если же у принтера есть такая функция печати на пленке, это только плюс. Так как при работе с ним, вы сможете видеть, то что находиться под ним. Но если нет, то ваш инструмент получиться не прозрачным, что совершенно не страшно, потому, как на точность данных никакого влияния не окажет.
3. По размеченным линиям вырезаем шаблон. Приложите распечатанный трафарет к орг. стеклу и сведите с него контур.
4. По получившемуся силуэту вырезаем лобзиком заготовку транспортира. Не отесанные края стоит обработать напильником, чтобы не были острыми. Затем приклеиваем к болванке, подготовленное ранее из пленки или бумаги изображение транспортира. При использовании пленки, лучше применять прозрачный клей.
5. После того, как клей высох, сверлим небольшое отверстие. Оно располагается строго по центру, диаметр которого равен 2мм. Это отверстие будет для карандаша и, как правило, обозначается окружностью. У инструмента имеется прямая, обратная, и шкалы полукруга разделенного делениями, что и является угломерной шкалой от 0 до 180°. А при использовании цветной печати отмечается градация делений, через каждые 30 градусов, что значительно облегчит работу с ним.

Транспортир — это инструмент, который используют в математике для измерения углов в градусах. Транспортир может понадобиться вам для выполнения домашней работы по геометрии или при создании чертежей, поэтому полезно знать, как можно сделать его своими руками. Можно распечатать шаблон транспортира на бумаге, начертить самому или сделать его из квадратного листа бумаги.

Метод 1 Распечатка транспортира на бумаге

1. 1 Возьмите плотную или прозрачную бумагу. Найдите лист открыточной или другой плотной бумаги, которая подходит для вашего принтера. Транспортир из плотной бумаги прослужит дольше. Можно также использовать прозрачную бумагу, чтобы легче было измерять углы.
2. Прежде чем приступить к печати, загляните в инструкцию к принтеру и убедитесь в том, что для него можно использовать прозрачную бумагу.
3. 2 Скачайте шаблон транспортира для печати. Загрузите подходящее вам изображение транспортира. Такое изображение можно найти в интернете.
4. Для лучшего качества выберите достаточно большое изображение. Отчетливость распечатанного рисунка будет определяться тем, насколько велик графический файл. Поищите изображения размером по меньшей мере 540X620.
5. 3 Распечатайте изображение транспортира. Распечатайте изображение транспортира на принтере. Предварительно убедитесь в том, что изображение полностью поместится на лист бумаги.
6. Измените размер изображения, чтобы он подходил вам. Как правило, прямой край транспортира должен иметь длину от 7,5 до 15 сантиметров.
7. 4 Вырежьте транспортир. С помощью ножниц вырежьте транспортир из бумаги. Не забудьте вырезать центральную часть транспортира.
8. 5 Совместите прямой край транспортира с одной стороной угла. Приложите нижний край транспортира к одной из сторон измеряемого вами угла. В той точке, где вторая сторона угла пересечет изогнутый край транспортира, вы найдете искомую величину угла.

Читать также: Домашний шиномонтаж своими руками чертежи

Метод 2 Изготовление карманного транспортира

1. 1 Вырежьте из листа бумаги квадрат. Возьмите лист бумаги формата А4 (210×297 мм) и вырежьте из него квадрат.
2. Отмерьте линейкой 21 сантиметр вдоль длинной стороны листа и поставьте метку на этом расстоянии.
3. С помощью линейки проведите прямую линию между сделанной меткой и противоположным краем листа.
4. Разрежьте бумагу по этой линии. В результате у вас получится квадрат 21 x 21 сантиметр.
5. 2 Сложите квадратный лист пополам. Согните левый край над правым, так чтобы складка прошла посредине листа. Затем разогните бумагу.
6. Аккуратно совместите края листа, чтобы складка пролегла точно посередине квадрата.
7. Точность измерения углов зависит от того, насколько аккуратно вы сделаете складки.
8. 3 Согните правый верхний угол треугольником. Возьмитесь за правый верхний угол листа и согните его вниз так, чтобы его вершина легла на сделанную ранее складку посередине квадрата.
9. При этом угол закроет примерно ⅔ складки посередине листа.
10. В результате на листе бумаги у вас получится треугольник с углами 30°, 60° и 90°.
11. Следует сложить лист так, чтобы в его верхней левой вершине получился острый угол.
12. 4 Заверните нижний правый угол вверх, чтобы образовать второй треугольник. Возьмитесь за нижний правый угол листа и согните его к верхнему краю первого треугольника. При этом правый край листа должен совпасть с правой складкой первого треугольника.
13. В результате у вас получится второй треугольник с углами 30°,60° и 90°.
14. 5 Согните вверх левый нижний угол. Возьмитесь за левый нижний угол и загните его вверх, так чтобы левый край листа совпал с краем первого треугольника, который вы сделали ранее вверху листа. Эти два края должны совместиться.
15. Подоткните левый нижний угол под второй треугольник с углами 30°, 60° и 90°, который вы сделали перед этим.
16. 6 Пометьте углы на получившемся транспортире. Стороны треугольников образуют различные углы, которые следует надписать. Положите лист на стол длинной стороной вверх.
17. В вершине транспортира находится два угла. Левый угол составляет 15°, а правый — 30°.
18. Левая вершина транспортира также содержит два угла. Верхний угол равен 45°, а нижний — 30°.
19. Правый угол транспортира составляет 60°.
20. Угол на правой стороне транспортира, там где складка пересекает край треугольника, равен 90°.
21. Нижний левый край содержит два угла: 45° справа и 30° слева.
22. 7 Используйте свой карманный транспортир. С его помощью можно измерять различные углы: просто прикладывайте к ним транспортир и смотрите, каким углам они соответствуют.
23. Оценивайте с помощью транспортира величину углов, которые имеют промежуточные значения.
24. Можно поделить углы на еще меньшие сегменты, согнув треугольники пополам.
25. 8 Приложите транспортир к измеряемому вами углу. Поверните транспортир так, чтобы одна из его вершин совпала с измеряемым углом.
26. Подберите угол транспортира, который ближе всего подходит к измеряемому углу. Таким образом вы определите величину искомого угла.

Читать также: Не горит диод на выключателе

Метод 3 Вычерчивание транспортира

1. 1 С помощью линейки проведите горизонтальную линию. Начертите на листе бумаги прямую линию длиной 127 миллиметров. Можно просто отмерить это расстояние вдоль края листа.
2. Отметьте середину линии на расстоянии 63,5 миллиметра от обоих концов.
3. 2 С помощью циркуля проведите полуокружность. Установите иглу циркуля в центр отрезка и соедините дугой его края.
4. Раздвиньте ножки циркуля на 127 миллиметров.
5. Соедините концы отрезка полуокружностью с центром в его середине.
6. 3 Сложите квадратный лист бумаги, чтобы с его помощью измерить углы. Возьмите квадратный лист бумаги и сложите его точно пополам и вдоль каждой диагонали.
7. Можно использовать квадратный лист поделочной бумаги.
8. Можно также вырезать ровный квадрат из обычного листа бумаги. Для этого загните верхний угол листа так, чтобы его край совпал с боковой стороной. Проведите линию вдоль наложившегося края и разрежьте бумагу вдоль нее.
9. Нанесите на транспортир угол 90º с помощью развернутого квадратного листа. Для этого приложите сторону квадрата к нижнему краю транспортира. Совместите угол квадрата с центром прямого отрезка и проведите линию вдоль вертикальной стороны квадрата.
10. 4 Обозначьте углы на транспортире. Когда вы сложите квадрат пополам вдоль диагонали, у вас получится угол 45 градусов. Приложите получившийся треугольник к нижнему краю транспортира и отметьте точку, в которой сторона треугольника пересекает дугу транспортира. Это будет угол 45 градусов.
11. Загните верхний левый угол треугольника к центру его нижней стороны. В результате у вас получится угол 60º. Таким же образом загните правую сторону, чтобы получить угол 120º. Отметьте эти углы на транспортире. Загибайте обе стороны треугольника, чтобы отмерить дополнительные углы с двух сторон транспортира.
12. Сложите новый треугольник. Загните внутренний край треугольника, который проходит от верхнего левого угла к центру листа. Угол треугольника слегка сдвинется вправо от центра, и воображаемая линия будет соединять угол листа с центром его нижнего края. В результате у вас получатся углы 75º и 105º.
13. Переверните свернутый лист и совместите его край с углом 90 градусов на транспортире. При этом край треугольника отсечет углы 15 и 165º.
14. 5 Вырежьте транспортир. Возьмите ножницы и аккуратно вырежьте полукруг транспортира.
15. Вырежьте небольшой полукруг в центре транспортира, чтобы были видны стороны измеряемых углов.
16. 6 Измерьте углы. Приложите нижний край транспортира к одной стороне угла. Совместите вторую сторону угла с дугой транспортира. Отметьте точку, в которой сторона угла пересекает дугу транспортира, и определите величину угла.
17. При этом следует поместить центр нижнего края транспортира в вершину угла.

Читать также: Виды изделий из пластика

Сравнение углов

Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:

При этом развернутые углы всегда являются равными.

Совмещение углов ∠

Сколько сумма смежных углов. Смежные углы

1. Смежные углы.

Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (рис. 72): ∠АВС и ∠СВD, у которых одна сторона ВС общая, а две другие, АВ и ВD, составляют прямую линию.

Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.

Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.

Например, ∠АDF и ∠FDВ — углы смежные (рис. 73).

Смежные углы могут иметь самые разнообразные положения (рис. 74).

Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 180°

Отсюда прямой угол можно определить как угол, равный своему смежному углу.

Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.

Например, если один из смежных углов равен 54°, то второй угол будет равен:

180° — 54° = l26°.

2. Вертикальные углы.

Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На рисунке 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные.

Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.

Пусть ∠1 = \(\frac{7}{8}\) ⋅ 90°(рис. 76). Смежный с ним ∠2 будет равен 180° — \(\frac{7}{8}\) ⋅ 90°, т. е. 1\(\frac{1}{8}\) ⋅ 90°.

Таким же образом можно вычислить, чему равны ∠3 и ∠4.

∠3 = 180° — 1\(\frac{1}{8}\) ⋅ 90° = \(\frac{7}{8}\) ⋅ 90°;

∠4 = 180° — \(\frac{7}{8}\) ⋅ 90° = 1\(\frac{1}{8}\) ⋅ 90° (рис. 77).

Мы видим, что ∠1 = ∠3 и ∠2 = ∠4.

Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.

Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.

Убедиться в справедливости свойства вертикальных углов необходимо путём доказательства.

Доказательство можно провести следующим образом (рис. 78):

∠a + ∠c = 180°;

∠b + ∠c = 180°;

(так как сумма смежных углов равна 180°).

∠a + ∠c = ∠b + ∠c

(так как и левая часть этого равенства равна 180°, и правая его часть тоже равна 180°).

В это равенство входит один и тот же угол с .

Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: ∠a = ∠b , т. е. вертикальные углы равны между собой.

3. Сумма углов, имеющих общую вершину.

На чертеже 79 ∠1, ∠2, ∠3 и ∠4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.

∠1 + ∠2 + ∠3 + ∠4 = 180°.

На чертеже 80 ∠1, ∠2, ∠3, ∠4 и ∠5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. ∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 360°.

Другие материалы

Геометрия — это весьма многогранная наука. Она развивает логику, воображение и интеллект. Конечно, из-за своей сложности и огромного количества теорем и аксиом, она не всегда нравится школьникам. Кроме этого, существует необходимость постоянно доказывать свои выводы, используя общепринятые стандарты и правила.

Смежные и вертикальные углы — это неотъемлемая составляющая геометрии. Наверняка многие школьники просто обожают их по той причине, что их свойства понятны и просты в доказательстве.

Образование углов

Любой угол образуется путем пересечения двух прямых или проведения двух лучей из одной точки. Они могут называться либо одной буквой, либо тремя, которые последовательно обозначают точки построения угла.

Углы измеряются в градусах и могут (в зависимости от их значения) по-разному называться. Так, существует прямой угол, острый, тупой и развернутый. Каждому из названий соответствует определенная градусная мера или ее промежуток.

Острым называется угол, мера которого не превышает 90 градусов.

Тупым является угол, превышающий 90 градусов.

Угол называется прямым в том случае, когда его градусная мера равна 90.

В том случае, когда он образован одной сплошной прямой, и его градусная мера равна 180, его называют развернутым.

Углы, имеющие общую сторону, вторая сторона которых продолжает друг друга, называются смежными. Они могут быть как острыми, так и тупыми. Пересечение линией образует смежные углы. Свойства их следующие:

1. Сумма таких углов будет равна 180 градусам (существует теорема, доказывающая это). Поэтому можно легко вычислить один из них, если известен другой.
2. Из первого пункта следует, что смежные углы не могут быть образованы двумя тупыми или двумя острыми углами.

Благодаря этим свойствам, можно всегда вычислить градусную меру угла, имея значение другого угла или, по крайней мере, отношение между ними.

Вертикальные углы

Углы, стороны которых являются продолжением друг друга, называются вертикальными. В качестве такой пары могут выступать любые их разновидности. Вертикальные углы всегда равны между собой.

Они образуются при пересечении прямых. Совместно с ними всегда присутствуют и смежные углы. Угол может быть одновременно смежным для одного и вертикальным для другого.

При пересечении произвольной линией также рассматривают еще несколько видов углов. Такая линия называется секущей, она и образует соответственные, односторонние и накрест лежащие углы. Они равны между собой. Их можно рассматривать в свете свойств, которые имеют вертикальные и смежные углы.

Таким образом, тема углов представляется довольно простой и понятной. Все их свойства легко запомнить и доказать. Решение задач не представляется сложным до тех пор, пока углам соответствует числовое значение. Уже дальше, когда начнется изучение sin и cos, придется запоминать множество сложных формул, их выводов и следствий. А до того времени можно просто наслаждаться легкими задачками, в которых необходимо найти смежные углы.

2)Сколько общих точек могут иметь 2 прямые?
3)Объясните что такое отрезок?
4)Объясните что такое луч. Как обозначаются лучи?
5)Какая фигура называется углом?Объясните что такое вершина и стороны угла?
6)Какой угол называется развернутым?
7)Какие фигуры называют равными?
8)Объясните как сравнить 2 отрезка
9)Какая точка называется серединой отрезка?

10)Объясните как сравнить 2 угла.
11)Какой луч называется биссектрисой угла?
12)Точка С делит отрезок АВ на 2 отрезка.Как найти длину отрезка АВ если известны длины отрезков АС и СВ?
13)Какими инструментами пользуются для измерения расстояний?
14)Что такое градусная мера угла?
15)Луч ОС делит угол АОВ на 2 угла. Как найти градусную меру угла АОВ если известны градусные меры углов АОС и СОВ?
16)Какой угол называется острым?прямым?тупым?
17)Какие углы называют смежными?Чему равна сумма смежных углов?
18)Какие углы называются вертикальными?Каким свойством обладают вертикальные углы?
19)Какие прямы называются перпендикулярными?
20)Объясните почему 2 прямые перпендикулярные к 3-ей не пересекаются?
21)Какие приборы применяют для построения прямых углов на местности?

1сколько прямых можно провести через две точки?

2сколько общих точек могут иметь две прямые?
3обьясните что такое отрезок
4обьясните что такое луч.

Как обозначаются лучи?
5какая фигура называется углом? обьясните что такое вершина и стороны угла
6какой угол называется развёрнутым
7какие фигуры называются равными
8обьясните как сравнить два отрезка
9какая точка называется серединой отрезка
10обьясните как сравнить два угла
11какой луч называется биссектрисой угла
12точка с делит отрезок аб на два отрезка.Как найти длину отрезка аб если известны длины отрезков ас и сб
13какими инструментами пользуются для измерения расстояний
14что такое градусная мера угла
15луч ос делит угол аоб на два угла.Как найти градусную меру угла аоб,если известны меры углов аос в соб
16какой угол называется острым?,прямым?,тупым?.
17какие углы называются смежными?чему равна сумма смежных углов?
18какие углы называются вертикальными?каким свойством обладают вертикальные углы
19какие прямые называются перпендикулярными
20обьясните почему две прямые перпендикулярные к третьей не пересикаются
21какие приборы применяют для построения прямых углов на местности?

1)что такое градусная мера угла? 2)какие фигуры называются равными 3)какие углы называются смежными,чему равна сумма смежныхуглов 4)какие углы называются

вертикальными каким свойством обладают вертикальные углы 5)

Помогите плиз, !! плизз=**

7. Докажите, что если две параллельные прямые пересекаются третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180 градусов.

8. Докажите, что две прямые, перпендикулярные третьей, параллельны. Если прямая перепендикулярна одной из двух параллелных прямых, то она перепендикулярна и другой.

9. Докажите, что сумма углов треугольника равна 180 градусов.

10. Докажите, что у любого треугольника по крайней мере два угла острые.

11. Что такое внешний угол треугольника?

12. Докажите, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

13. Докажите, что внешний угол треугольника больше любого внутреннего угла, не смежного с ним.

14. Какой треугольник называется прямоугольным?

15. Чему равна сумма острых углов прямоугольного треугольника?

16. Какая сторона прямоугольного треугольника называется гипотенузой? Какие стороны называются катетами?

17. Сформулируйте признак равенства прямоугольных треугольников по гипотенузе и катету.

18. Докажите, что из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один.

19. Что называется расстоянием от точки до прямой?

20. Объясните, что такое расстояние между параллельными прямыми.

Что такое смежный угол

Угол – это геометрическая фигура (рис.1), образованная двумя лучами OA и OB (стороны угла), исходящими из одной точки O (вершина угла).

СМЕЖНЫЕ УГЛЫ — два угла, сумма которых равна 180°. Каждый из этих углов дополняет другой до развернутого угла.

Смежные углы — (Agles adjacets) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через.

Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.

рис. 2

На рисунке 2 углы a1b и a2b смежные. У них общая сторона b, а стороны a1, a2 — дополнительные полупрямые.

рис. 3

На рисунке 3 изображена прямая AB, точка C расположена между точками A и B. Точка D — точка не лежащая на прямой AB. Получается, что углы BCD и ACD смежные. У них общая сторона CD, а стороны CA и CB дополнительные полупрямые прямой AB, так как точки A, B разделены начальной точкой C.

Теорема о смежных углах

Теорема: сумма смежных углов равна 180°

Доказательство:
Углы a1b и a2b смежные (см. рис. 2) Луч b проходит между сторонами a1, и a2 развернутого угла. Следовательно, сумма углов a1b и a2b равна развернутому углу, то есть 180°. Теорема доказана.

Угол, равный 90° называется прямым. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом также прямой угол. Угол, меньший 90° называется острым, а угол больше 90° — тупым. Так как сумма смежных углов равна 180°, значит угол, смежный с острым углом — тупой угол. А угол смежный с тупым углом — острый угол.

Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.

Определение 1. Углом называется часть плоскости, ограниченная двумя лучами с общим началом.

Определение 1.1. Углом называют фигуру, состоящую из точки — вершины угла — и двух различных полупрямых, исходящих из этой точки, — сторон угла.
Например, угол ВОС на рис1 Рассмотрим сначала две пересекающиеся прямые. При пересечении прямые образуют углы. Есть частные случаи:

Определение 2. Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым.

Определение 3. Прямой угол — это угол величиной в 90 градусов.

Определение 4. Угол, меньший 90 градусов, называется острым углом.

Определение 5. Угол, больший 90 градусов и меньший 180 градусов, называется тупым углом.
пересекающиеся прямые.

Определение 6. Два угла, одна сторона которых общая, а другие стороны лежат на одной прямой, называются смежными.

Определение 7. Углы, стороны которых продолжают друг друга, называются вертикальными углами.
На рисунке 1:
смежные: 1 и 2; 2 и 3; 3 и 4; 4 и 1
вертикальные: 1 и 3; 2 и 4
Теорема 1. Сумма смежных углов равна 180 градусов.
Для доказательства рассмотрим на рис. 4 смежные углы АОВ и ВОС. Их суммой является развернутый угол АОС. Поэтому сумма данных смежных углов равна 180 градусов.

рис. 4

Связь математики с музыкой

«Раздумывая об искусстве и науке, об их взаимных связях и противоречиях, я пришел к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая духовная деятельность человека и, что между ними размещается все, что человечество создало в области науки и искусства.»
Г. Нейгауз
Казалось бы, искусство — весьма отвлеченная от математики область. Однако связь математики и музыки обусловлена как исторически, так и внутренне, несмотря на то, что математика — самая абстрактная из наук, а музыка — наиболее отвлеченный вид искусства.
Консонанс определяет приятное для слуха звучание струны
В основе этой музыкальной системы были два закона, которые носят имена двух великих ученых — Пифагора и Архита. Вот эти законы:
1. Две звучащие струны определяют консонанс, если их длины относятся как целые числа, образующие треугольное число 10=1+2+3+4, т.е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n:(n+1) (n=1,2,3), тем созвучнее получающийся интервал.
2. Частота колебания w звучащей струны обратно пропорциональна ее длине l .
w = a: l ,
где а — коэффициент, характеризующий физические свойства струны.

Так же предложу вашему внимаю забавную пародию про спор двух математиков =)

Геометрия вокруг нас

Геометрия в нашей жизни имеет немаловажное значение. Ввиду того, что когда оглядеться вокруг, то не сложно будет заметить, что нас окружают различные геометрические фигуры. Мы с ними сталкиваемся повсюду: на улице, в классе, дома, в парке, в спортивном зале, в школьной столовой, в принципе везде, где бы мы с вами не находились. Но темой сегодняшнего урока являются смежные угли. Поэтому давайте оглянемся вокруг и попытаемся в этом окружении найти углы. Если вы внимательно посмотрите в окно, то можете увидеть, что некоторые ветки дерева образуют смежные углы, а в перегородках на воротах можно заметить множество вертикальных углов. Приведите свои примеры смежных углов, которые вы наблюдаете в окружающей обстановке.

Задание 1.

1. Вот на столе на книжной подставке стоит книга. Какой угол она образует?
2. А вот ученик работает за ноутбуком. Какой угол вы видите здесь?
3. Какой угол образует фото рамка на подставке?
4. Как вы думаете, возможно ли, чтобы два смежных угла были равными?

Задание 2.

Перед вами изображена геометрическая фигура. Что это за фигура, назовите ее? А теперь назовите все смежные углы, которые вы можете увидеть на этой геометрической фигуре.

Задание 3.

Перед вами изображение рисунка и картины. Рассмотрите их внимательно и скажите, какие виды улов вы видите на картине, а какие углы на рисунке.

Решение задач

1) Даны два угла, относящиеся друг к другу как 1: 2, а смежные с ними — как 7: 5. Нужно найти эти углы.
2) Известно, что один из смежных углов больше другого в 4 раза. Чему равны смежные углы?
3) Необходимо найти смежные углы, при условии, что один из них на 10 градусов больше от второго.

Математический диктант на повторение ранее выученного материала

1) Выполните рисунок: прямые a I b пересекаются в точке А. Отметьте меньший из образованных углов цифрой 1, а остальные углы – последовательно цифрами 2,3,4; дополняющие лучи прямой а — через а1 и а2, а прямой b — через b1 i b2.
2) Пользуясь выполненным рисунком, впишите нужные значения и объяснения в места пропусков в тексте:
а) угол 1 и угол …. смежные, поскольку. ..
б) угол 1 и угол …. вертикальные, поскольку…
в) если угол 1 = 60°, то угол 2 = …, потому что…
г) если угол 1 = 60°, то угол 3 = …, потому что…

Решите задачи:

1. Может ли сумма 3-х углов, образованных при пересечении 2-х прямых, равняться 100°? 370°?
2. На рисунке найдите все пары смежных углов. А теперь вертикальных углов. Назовите эти углы.

3. Нужно найти угол, когда он втрое больше, чем смежный с ним.
4. Две прямые пересеклись между собой. В результате этого пересечения образовались четыре угла. Определите величину любого из них, при условии что:

а) сумма 2-х углов из четырех 84°;
б) разность 2-х углов из них равна 45°;
в) один угол в 4 раза меньше чем второй;
г) сумма трех из данных углов равна 290°.

Итог урока

1. назовите углы, которые образуются при пересечении 2-х прямых?
2. Назовите все возможные пары углов, находящихся на рисунке, и определите их вид.

Домашнее задание:

1. Найдите отношение градусных мер смежных углов, когда один из них на 54° больше второго.
2. Найдите углы, которые образуются при пересечении 2-х прямых, при условии, что один из углов равняется сумме 2-х других углов, смежных с ним.
3. Необходимо найти смежные углы, когда биссектриса одного из них образует со стороной второго угол, который больше чем второй угол на 60°.
4. Разница 2-х смежных углов равна трети от суммы этих двух углов. Определите величины 2-х смежных углов.
5. Разница и сумма 2-х смежных углов относятся как 1: 5 соответственно. Найдите смежные углы.
6. Разница двух смежных составляет 25% от их суммы. Как относятся величины 2-х смежных углов? Определите величины 2-х смежных углов.

Вопросы:

1. Что такое угол?
2. Какие бывают типы углов?
3. Какая особенность смежных углов?

Предмети > Математика > Математика 7 класс

Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.

Сумма смежных углов равна 180°

Теорема 1. Сумма смежных углов равна 180°.

Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .

Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.

Вертикальные углы равны

Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).

Теорема 2. Вертикальные углы равны.

Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1 ∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.

Отсюда заключаем, что ∠ АОВ = ∠ COD.

Следствие 1. Угол, смежный с прямым углом, есть прямой угол.

Рассмотрим две пересекающиеся прямые АС и BD (рис. 3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.

Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.

АН — перпендикуляр к прямой

Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.

Чертежный угольник

Справедлива следующая теорема.

Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис. 5).

Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.

Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».

Пример 1. Один из смежных углов равен 44°. Чему равен другой?

Решение. Обозначим градусную меру другого угла через x , тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.

Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?

Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1. 2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.
∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.

Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.

Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.

Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.

Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° — 50° = 130°.

Измерение углов. Транспортир. Видеоурок. Математика 5 Класс

Транспортир — это простой и удобный инструмент для измерения и построения углов. В основном распространены транспортиры полукруглой формы, хотя существуют и круглые транспортиры, рассчитанные на 360 градусов. Если вы впервые столкнулись с транспортиром и не знаете, как им пользоваться, прочитайте эту статью! Это совсем несложно: несколько простых шагов, и вы как следует освоите этот полезный инструмент.

Транспортиром пользуются для измерения углов.

Условно выделим в транспортире две части — «линейку», называемую также прямолинейной шкалой (нижняя часть на рисунке), и полукруга, называемого также угломерной шкалой. На полукруге находятся метки градусов от 0° до 180°. Назовем разделение на градусы «градусной сеткой».

Транспортиры бывают разного вида, но использование их сводится к следующему. У транспортира есть центральная метка. На рисунке выше это маленький кружок с отверстием в центре. Однако центральная метка может обозначаться просто черточкой. Эту метку нужно совместить с вершиной угла. При этом одна из сторон угла должна пройти через метку с числом 0 на полукруге транспортира.

На транспортире может быть две «нулевых» метки: справа и слева. Понятно, что следует смотреть на ту, через которую проходит сторона угла. Но самое главное, понять на какую градусную сетку смотреть при измерении величины угла: верхнюю или нижнюю. Если сторона угла прошла через 0, который находятся с внешней стороны, то в дальнейшем мы пользуемся внешней градусной сеткой. Если же сторона угла прошла через «внутренний» 0, то в дальнейшем пользуемся внутренней градусной сеткой транспортира (на внешнюю не обращаем внимания).

Итак, одна сторона угла должна пройти через метку 0, а вторая сторона угла должна оказаться со стороны полукруга (угломерной шкалы), то есть как бы пересекать его.

Что такое транспортир?

Транспортиром называют предмет, с помощью которого каждый из нас может не только измерять углы, но и строить их. Внешне он напоминает полукруглую линейку со шкалой и делениями. Внизу, на ровной поверхности, расположена привычная нам прямая линейка для измерения отрезков. В верхней части — полукруг с двойной шкалой для измерений. В каждом из направлений шкала рассредоточена по транспортиру от 0 до 180 градусов.

Презентация к уроку

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели:

• Образовательные:

• познакомить учащихся с единицей измерения углов, с прибором для измерения углов;
• научить пользоваться транспортиром.

Развивающие:развивать внимание, мышление учащихся;развивать самостоятельность учащихся, используя проблемные ситуации, творческие задания;развивать познавательный интерес к предмету.Воспитательные:воспитывать чувство взаимоуважения;воспитывать у учащихся навыки учебного труда.
I. Организационный момент

II. Вступительное слово учителя

Мы познакомимся с измерительным прибором (как он называется, вы узнаете немного позже), научимся с его помощью измерять, а затем и строить углы. Вы покажите свои знания, докажите насколько внимательны. Будем учиться не только математике, но и умению общаться, уважению друг к другу. Для того чтобы достичь наших целей, вы должны быть волевыми, настойчивыми, целеустремленными, поэтому эпиграфом нашего урока будут слова:

Правила пользования

В школе объясняют, что такое транспортир, на уроках математики. Именно здесь есть необходимость в измерениях.

Для того чтобы нам узнать, чему равен один градус, нужно окружность поделить на 360 равных частей. Одна из таких частей и будет равна 1 градусу. Величина окружности никак не повлияет на градус! Это легко проверить.

Нарисуем две окружности разного диаметра и поделим каждую на 360 равных частей. Затем наложим меньшую окружность на большую и увидим, что линии совпали.

Измеряем угол

Транспортир помогает построить и измерить угол. Градус — это общепринятая единица, которой пользуются для измерения углов. Встречается несколько разновидностей углов:

• Острый. Таким называют угол до 90 градусов.
• Прямым является угол, равный 90 градусам.
• Тупой угол варьируется в диапазоне от 90 до 180 градусов.
• Развёрнутый угол представляет собой прямую линию или 180 градусов.
• Полный угол выглядит как окружность и составляет 360 градусов.

Нетрудно разобраться, как измерить угол. Для того чтобы узнать, какова величина угла, нам необходимо установить транспортир таким образом, чтобы его центр располагался в вершине угла, а прямая сторона совпала с одной из его сторон. Шкала укажет нам количество градусов данного угла. Вот таким нехитрым способом мы можем узнать, что за угол перед нами.

Для построения угла с заданным градусом следует приложить прямую часть транспортира к линии, а его центр — к началу линии. Впоследствии эта точка будет являться вершиной угла. Затем на шкале отыскиваем заданное число и ставим точку. Теперь транспортир можно снять и соединить отрезком начало линии (вершину угла) с отмеченной точкой.

Школьные канцтовары, произведенные разными компаниями, отличаются по материалу, цвету, размеру. Так вот: тем, у кого транспортир оказался больше длины угла, и не представляется возможным определить его величину, сторону угла необходимо продлить, используя прямую линейку.

Вывод

Вот, как просто можно вычислить прямой угол без использования каких-либо строительных инструментов и приборов. Использовать можно самое простое, но в то же время весьма действенное средство, которое вкупе с использованием имеющихся знаний и бесхитростных расчётов, может помочь произвести измерение.

При использовании предложенных величин, ключевым становится финальный замер между двумя отметками, которые были сделаны ранее. Расстояние, которое будет равняться точно 5 метрам, покажется, что он прямой. Если же величина будет больше или меньше 5 метров, это будет означать, что он прямым не является.

Набор школьника

Неспроста учащиеся младшего звена не знакомы с транспортиром. При его применении должна быть заложена некая база знаний. Для полноценной работы с ним на уроке ребята изучают ряд сопутствующих предметов. Прежде чем узнать, что такое транспортир, школьники должны в совершенстве овладеть прямой линейкой, чертить ровные линии, изучить сложение и вычитание, освоить циркуль, знать геометрические фигуры и так далее. Весь этот процесс занимает время, и только окончив начальную школу, ученик может добавить транспортир в свой набор инструментов.

Ученикам сейчас предлагаются школьные канцтовары в огромном выборе. Транспортир не исключение. Производители стараются угодить самым требовательным запросам покупателей. Инструменты изготавливают в различной цветовой гамме. Яркие цвета всегда нравятся детям. Порой даже в одном классе не сыскать одинаковых транспортиров, что облегчает при утрате их поиск. Формы и размеры каждый выбирает на свой вкус.

Большинство таких товаров выпускают из пластмассы, и это значительно уменьшает его стоимость. Но есть деревянные и даже железные транспортиры. Как показывает практика, металлические хоть и непрозрачны, но практичнее в том плане, что шкала не стирается, а это позволяет гораздо дольше применять его в действии, с точностью определяя углы.

Транспортир не так востребован школьниками, как линейка, но он сопровождает учеников вплоть до выпускного экзамена. Некоторые из выпускников школы выбирают специальности, которые связаны с измерением и построением углов, проектированием зданий и сооружений, работой с чертежами. В силу своих профессий им постоянно приходится сталкиваться с транспортирами и его производными. Но и бывшие одноклассники нынешних инженеров, порой даже с глубочайшим гуманитарным уклоном, без труда вспомнят навыки обращения с этим предметом и определят количество градусов у любого угла.

Сегодня современные дети привыкли добывать любую информацию из интернета. Однако он никак не поможет в измерении углов. Лишь только умение пользоваться транспортиром даст возможность правильно их определять. Будущим инженерам и проектировщикам это бесспорно пригодится в работе, да и каждый образованный человек должен обладать навыками работы с транспортирами, поэтому уметь пользоваться таким инструментом должен каждый!

Итог

Сегодня современные дети привыкли добывать любую информацию из интернета. Однако он никак не поможет в измерении углов. Лишь только умение пользоваться транспортиром даст возможность правильно их определять. Будущим инженерам и проектировщикам это бесспорно пригодится в работе, да и каждый образованный человек должен обладать навыками работы с транспортирами, поэтому уметь пользоваться таким инструментом должен каждый!

На уроке мы вспомним, что такое единицы измерения, узнаем какими единицами можно измерять углы, познакомимся с такой единицей измерения, как градус, научимся измерять углы в градусах и чертить их с помощью транспортира. Также мы узнаем о других единицах измерения углов, которые применяются в различных ситуациях.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок и

Какие-то вещи можно измерить, какие-то нельзя. Например, нельзя измерить дружбу или любовь. А расстояние, вес, температуру вполне можно. Чтобы что-то измерять, нужно всем договориться о единицах измерения.

Метр, дюйм, аршин — это и есть такие договоренности при измерении длины. Эталонный метр хранится во Франции, в Палате мер и весов. Килограмм, фунт, пуд — это договоренности для измерения массы. Эталонный килограмм тоже хранится в Палате мер и весов.

Единицы измерения придуманы для конкретных величин. В секундах не измерить вес, а в аршинах — время.

В геометрии такая же ситуация. Есть сантиметры, для измерения длин отрезков, но они не подходят для измерения углов. Для измерения углов есть свои единицы измерения. На этом уроке мы рассмотрим одну из них, а именно градусы.

Разделим полный угол на 360 равных частей. Для этого удобно использовать окружность. Поделим ее на 360 частей и соединим каждое полученное деление с центром. Получим 360 равных углов (см. Рис. 1).

Рис. 1. Окружность, разделенная на 360 равных углов

Один такой маленький угол назовем углом в 1° (см. Рис. 2).

Рис. 2. 1 градус

Не важно, какого размера будет окружность, которую мы делим. Поделим обе окружности на 360 частей, получим равные углы в 1°, хотя стороны одного угла визуально длиннее, чем у другого (см. Рис. 3).

Рис. 3. Углы равны

Стороны углов можно продолжать бесконечно, от этого размер угла не меняется (см. Рис. 4).

Рис. 4. Более явный пример равенства углов

Величина любого угла — это сколько раз в него умещается угол в 1°.

Вот мы видим угол 13° (см. Рис. 5).

Рис. 5. Угол 13°

Понятно, что полный угол

состоит из 360 таких углов. То есть он равен 360° (см. Рис. 6).

Рис. 6. Полный угол

Развернутый угол

— это половина полного угла. Он равен (см. Рис. 7).

Рис. 7. Развернутый угол

Прямой угол

является половиной развернутого и равен 90° (см. Рис. 8).

Рис. 8. Прямой угол

Эталон градуса нет нужды где-то хранить. Если нужно, то всегда можно полный угол разделить на 360 частей, или развернутый — на 180, или прямой — на 90.

Линейка нужна для того, чтобы измерить имеющийся отрезок или начертить отрезок нужной длины. Чтобы измерить угол или начертить угол нужной величины, мы тоже используем линейку, только не прямую, а круглую. Она называется транспортиром (см. Рис. 9).

Рис. 9. Транспортир

Единицы измерения на ней — градусы. Шкала начинается с нуля и заканчивается 180°.То есть максимальный угол, который мы можем измерить или начертить, — это 180°, развернутый.

Транспортиры могут быть разных размеров, но это не влияет на то, какого размера углы ими измеряют. Для более крупного транспортира у углов нужно чертить стороны длиннее.

1. Измерим пару углов.

Прямая часть транспортира совмещается с одной стороной угла, центр транспортира с вершиной угла. Смотрим, где оказалась вторая сторона угла, — 54° (см. Рис. 10, 11).

Рис. 10. Измерение угла

Проделаем то же самое со вторым углом, 137°.

Рис. 11. Измерение угла

Если сторона угла не достает до шкалы, то ее нужно сначала продлить.

2. Начертим углы 29°, 81° и 140°.

Сначала чертим одну сторону угла по линейке (см. Рис. 12).

Рис. 12. Построение одной стороны угла

Отмечаем вершину. Совмещаем с транспортиром. Отмечаем точкой нужное значение угла — 29° (см. Рис. 13).

Рис. 13. Использование транспортира для построения углов

Убираем транспортир. Соединяем полученную точку с вершиной (см. Рис. 14).

Рис. 14. Угол 29°

Точно так же строим два других угла (см. Рис. 15).

Рис. 15. Построение углов

Итак, мы с вами обсудили, что для измерения углов люди договорились использовать градусы. Градус

— это полного угла.

Инструментом для измерения и построения углов является транспортир.

Можно не использовать названия углов — полный, развернутый, прямой. Мы можем просто говорить — 360 градусов, 180 или 90 градусов.

На самом деле бывает, когда мы одни величины измеряем единицами, казалось бы, для них не предназначенными, «чужими» единицами.

Можно ли измерить расстояние в минутах? Да, мы часто используем этот способ. «От моего дома до школы 5 минут». Если быть точнее, то «5 минут пешком». Мы здесь используем известную всем величину — скорость пешехода. И величина «5 минут» на самом деле означает «расстояние, которое пешеход проходит за 5 минут». Скорость пешехода — 5 км/ч, 5 минут — это часа, умножим одно на другое. Получаем примерно 400 метров. Не очень точно, зато удобно.

Точно по такому же принципу устроена другая единица измерения расстояния — световой год. Световой год — расстояние, которое проходит свет за 1 год. С помощью этой единицы меряют расстояния между звездами.

Очень распространенный пример использования «чужой» единицы измерения — это измерять вес в килограммах. На самом деле килограмм — единица измерения массы, а вес — это другая физическая величина. Если хотите подробнее узнать, в чем разница между массой и весом, и почему измерять вес в килограммах не верно, то наберите в поисковой системе «масса и вес» и получите множество пояснений по этому поводу.

Атмосферное давление мы до сих пор измеряем в миллиметрах (миллиметрах ртутного столба).

Хотя для угла есть свои «родные» единицы измерения — градусы, которые мы и проходим на этом уроке, все-таки его можно измерять и с помощью линейных величин, например сантиметров. Если нужно измерить угол , то можно достроить его до треугольника, так чтобы один угол был прямым, и разделить длину одной стороны на другую.

Получим величину угла , которая называется тангенсом.

Если увеличить треугольник, то ничего не изменится (см. Рис. 16).

Рис. 16. Тангенс

Ведь во сколько раз увеличилась одна сторона, во столько и вторая.

То есть величины часто можно измерять «чужими» единицами, но это чуть сложнее, там нужны некоторые дополнительные договоренности.

Существуют и другие единицы измерения углов.

1.
Минуты и секунды.
Как и метр можно делить на дециметры, сантиметры, миллиметры для более точных измерений, так и градусы делятся на более мелкие единицы измерения.

Если угол в 1° разделить на 60 равных частей, то величина полученного угла называется минута, 1′.

Если минуту поделить на 60 частей, то полученная величина называется секундой. Секунда — уже очень маленькая величина, но ее тоже можно делить дальше.

Почему вообще стали делить на 360 частей полный угол, ведь это не очень удобно? В древнем Вавилоне была шестидесятеричная система (у нас десятеричная). Им было удобно делить на 60.

2.
Грады.
Чтобы сделать измерение углов ближе к нашей десятичной системе счисления, были предложены грады. Для этого прямой угол делится на 100 частей. Полученная величина называется град. Полный угол составляет тогда 400 градов. Система не прижилась, и сейчас ее не используют.

3.
Радиан.
Если взять два радиуса окружности так, чтобы кусочек окружности между ними тоже был равен радиусу, то угол между радиусами мы и примем за новую единицу измерения. Он называется 1 рад (радиан). Эта мера используется наравне с градусной. У нее есть свои преимущества и свои недостатки по сравнению с градусами (см. Рис. 17).

Рис. 17. Радианы

Например, теперь полный угол (вся окружность) состоит не из целого числа единичных углов. Полный угол состоит из 6 с лишним единичных углов. Не очень удобно, зато теперь длина дуги (части окружности) и угол хорошо связаны. Если взять окружность радиуса 1 см, то величина угла совпадает с длиной дуги. Угол 1 рад — дуга 1 см, угол 2 рад — длина дуги 2 см.

Список литературы

1. Зубарева И.И., Мордкович А.Г. Математика. 5 класс. — М.: Мнемозина, 2013.
2. Виленкин Н.Я. и др. Математика. 5 кл. — М.: Мнемозина, 2013.
3. Ерина Т.М. Математика 5кл. Раб. тетрадь к уч. Виленкина, 2013. — М.: Мнемозина, 2013.

1. Shkolo.ru ().
2. Cleverstudents.ru ().
3. Festival.1september.ru ().

Домашнее задание

1. Зубарева И.И., Мордкович А.Г. Математика. 5 класс. — М.: Мнемозина, 2013. Стр. 144 № 522.
2. Начертите углы: 23°, 167°, 84°.
3. Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 5 класса (5-е изд.) — 2010. Стр. 163 № 3.

Пусть в результате тщательного и искусного наблюдения та или шая цель вами найдена. Очевидно, этого еще мало: нужно определись местоположение цели, чтобы наша артиллерия знала, куда стрелять. Как это сделать?

Местоположение цели определяют обычно по отношению к ориентиру, — именно по отношению к тому ориентиру, который находится ближе всего к цели. Достаточно знать две координаты цели — ее дальность, то-естъ расстояние от наблюдателя или от орудия до цели, и угол, под которым цель видна нам правее или левее ориентира, — и тогда местоположение цели будет определено достаточно точно.

Предположим, ради простоты, что цель находится от нас на том же расстоянии, что и ориентир. Расстояние до этого ориентира нам известно заранее. Пусть оно равно 1000 метрам. Одна координата цели, следовательно, уже определена. Остается определить другую: угол между целью и ориентиром. Чем же и как артиллеристы измеряют углы?

В обыденной жизни вам не раз приходилось измерять углы: вы измеряли их в градусах и минутах. Артиллеристам же приходится не толшо измерять углы, но и быстро в уме по угловым величинам находить линейные величины и, наоборот, — по линейным величинам находить угловые. Пользоваться в таких случаях градусной системой измерения углов неудобно. Поэтому артиллеристы приняли совсем иную меру углов. Мера эта — «тысячная», или, как ее называют иначе, деление угломера.

Представим себе окружность, разделенную на 6000 равных частей.

Примем за основную меру для измерения углов одну шеститысячную долю этой окружности и попробуем определить ее величину в долях радиуса.

Известно, что радиус (R

) любой окружности укладывается по ее длине приблизительно 6 раз, следовательно, можно считать, что длина окружности равна 6
R
. Мы же разделили окружность на 6000 равных частей; отсюда 6
R
= 6000 частей окружности. Теперь легко узнать, какую часть радиуса будет составлять одна шеститысячная часть окружности. Очевидно, что она будет в 6000 раз меньше величины 6
R
, то-есть будет равна или одной тысячной радиуса . Поэтому-то артиллерийская мера углов — деление угломера — и носит название «тысячной» (рис. 212). Такой мерой пользоваться для измерения углов очень удобно. {243}

Вспомните, что в поле зрения бинокля вы видели сетку с делениями, то-есть короткие и длинные черточки, которые расположены вправо, влево и вверх от перекрестия, находящегося в центре поля зрения бинокля (рис. 213). Эти деления и есть «тысячные». Маленькое деление сетки (между короткой и длинной черточками) равно 5 «тысячным», а большое деление (между длинными черточками) — 10 «тысячным».

На рис. 213 эти деления обозначены не просто числами 5 и 10, а с приставленными слева нолями — 6-05. и 0-10. Так пишут и произносят артиллеристы все угловые величины в «тысячных», чтобы избежать ошибок в командах. Например, если нужно передать в команде угол, равный 185 «тысячным» или 8 «тысячным», то произносят эти числа как номер телефона: «один восемьдесят пять» или «ноль ноль восемь», и соответственно пишут 1-85 или 0-08.

Зная теперь, как устроена сетка бинокля, вы можете измерить по ней угол между двумя предметами (точками местности), которые ввдны с вашего наблюдательного пункта. Взгляните опять на рис. 213. Вы видите, что между перекрестком дорог, куда направлено перекрестие, и отдельно стоящим деревом (вправо от перекрестка дорог) укладывается два больших деления и одно маленькое, то-есть 25 «тысячных» или 0-25. Это и есть угол между перекрестком дорог и деревом. Точно так же вы можете определить угол между перекрестком дорог и домиком (влево от перекрестка дорог). Он равен 0-40. {244}

Сетка с делениями, примерно такая же как в бинокле, имеется и в поле зрения стереотрубы. Но у стереотрубы для измерения углов есть еще угломерная шкала снаружи.

На рис. 214 показаны те части стереотрубы (лимб и барабан лимба), при помощи которых можно более точно, чем по сетке, измерять горизонтальные углы.

Окружность лимба разделена на 60 частей, и поворот стереотрубы на одно деление лимба соответствует таким образом 100 «тысячным». Окружность же барабана лимба разделена на 100 частей, и при полном обороте барабана стереотруба поворачивается всего только на одно деление лимба (т. е. на 100 «тысячных»). Следовательно, деление барабана соответствует не 100 «тысячным», а всего лишь одной «тысячной». Это позволяет уточнять показания лимба в 100 раз и дает возможность измерять углы с точностью до одной «тысячной».

Чтобы измерить угол между двумя точками, пользуясь лимбом и барабаном, совмещают перекрестие стереотрубы сначала с правой тачкой; для этого, подведя указатель лимба к делению 30 и деление барабана 0 к его указателю (рис. 215), поворачивают трубу в нужную сторону при помощи маховичка точной наводки (см. рис. 214). Затем, вращая барабан лимба, совмещают перекрестие стереотрубы с левой точкой. При этом указатель лимба передвинется и покажет новый отсчет. Разность между полученным отсчетом и первоначальной установкой (30-00) и будет равна искомому углу (рис. 215).

Но не только при помощи этих сложных приборов можно измерять углы.

Ваша ладонь и ваши пальцы могут стать неплохим угломерным прибором, если только вы запомните, сколько в них заключается «тысячных» или, как говорят артиллеристы, какова «цена» ладони и пальцев. Хотя разные люди имеют разную ширину ладони и пальцев, но все же «цена» их не будет сильно отличаться от указанной на рис. 216. Вытянув перед собой руку на полную ее длину, вы можете быстро измерить угол между любыми точками местности (рис. 217). Чтобы не делать больших ошибок при измерении углов таким приемом, надо проверить «цену» своих пальцев. Для этого нужно вытянуть руку на уровне {245}

глаз и заметить, какую часть пространства закрыл собой палец (или ладонь руки), а затем измерить это пространство при помощи стереотрубы, поставленной на то же место.

Понятно, что подобным же простейшим «угломером» может служить всякий предмет, «цену» которого вы заблаговременно определили. На рис. 218 показаны такие предметы и их примерная «цена» в «тысячных».

Ознакомившись с приемами измерения углов, вы можете теперь убедиться в том, что, пользуясь «тысячными», можно весьма просто по угловым величинам определять линейные величины, а по линейным величинам — угловые. Для этого рассмотрим два примера. {246}

Первый пример (рис. 219). С наблюдательного пункта вы видите впереди проволочные заграждения противника; они протянулись полосой от мельницы влево до сухого дерева. Расстояние до мельницы, а следовательно, и до проволочных заграждений вы определили по карте; оно равно 1500 метрам. Вам поставлена задача — узнать длину наблюдаемой полосы проволочных заграждений. Как это сделать? Карта здесь вам не поможет, так как на ней нет сухого дерева, на ней есть только мельница.

Чтобы решить данную задачу, вы прежде всего определяете угол, под которым видна с наблюдательного пункта полоса проволочных заграждений, то-есть угол между направлениями на мельницу и на сухое дерево. Вы измерили этот угол по сетке бинокля; он оказался рашым 100 «тысячным», или 1-00.

Дальше задача решается просто. Надо лишь представить себе, что ваш наблюдательный пункт — это центр той окружности, которая описана радиусом, равным расстоянию от вас до мельницы. Радиус этот равен 1500 метрам. Углу в одну «тысячную» соответствует, как вы знаете, расстояние, равное одной тысячной радиуса, то-есть в данном случае 1,5 метра. А так как угол между мельницей и сухим деревом равен не одной, а 100 «тысячным», то значит расстояние между мельницей и сухим деревом равно не 1,5 метра, а 150 метрам. Это и будет длина полосы проволочных заграждений {247}

Второй пример (рис. 220). В канаве около шоссе вы обнаружили пулемет, по которому решили открыть огонь. Вам надо вычислить расстояние до пулемета или, что то же, — до шоссе.

Для решения этой задачи воспользуйтесь телеграфными столбами на шоссе; высота их известна — она равна 6 метрам. Измерьте теперь по вертикальной сетке бинокля угол, под которым вы видите телеграфный столб (угол между верхним концом столба и его основанием). Тогда вы будете иметь все данные для определения расстояния.

Допустим, что этот угол оказался равен 3 «тысячным». Очевидно, что если углу 3 «тысячных» с этого расстояния соответствует 6 метров на местности, то одной «тысячной» будет соответствовать 2 метра, а всему радиусу, то-есть расстоянию от вас до шоссе, будет соответствовать величина, в 1000 раз большая. Нетрудно сообразить, что расстояние от вас до шоссе будет равно 2000 метрам.

На рассмотренных примерах вы убедились, что принятая в артиллерии мера для измерения углов позволяет без всякого труда находить одну «тысячную» от любой величины расстояния. Для этого только надо в числе, выражающем величину расстояния, отделить справа три знака. Все это проделывается очень быстро в уме.

А вот что получилось бы, если за меру углов принять не «тысячную», а обычную, применяемую в геометрии меру углов: один градус или одну минуту. Углу в один градус соответствовала бы линейная величина, равная 1/60 радиуса, а углу в одну минуту — 1/3600 радиуса; следовательно, при решении любой из приведенных задач пришлось бы делить числа, выражающие расстояния до целей, не на 1000, а на 60 или на 3600.

Попробуйте проделать это деление с любым выбранным наугад числом и вы сейчас же убедитесь, что без карандаша и бумаги вам здесь не обойтись. Вот почему артиллерийская мера углов практически является несравненно более удобной. {248}

Измерить угол

— значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.

Обычно за единицу измерения углов принимают градус. Градус

— это угол, равный части развёрнутого угла. Для обозначения градусов в тексте, используется знак °, который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).

История изобретения

Происхождение этого математического инструмента восходит к жрецам в Египте и Вавилоне, которые установили меру углов в градусах, минутах и секундах. Однако до времён классической Греции тригонометрия не использовалась в математике.

Во втором веке до нашей эры астроном Гиппарх из Никии изобрёл тригонометрический стол, для измерения треугольников. Затем Птолемей включил в свою великую астрономическую книгу «Альмагест» таблицу, с угловыми приращениями от 0 до 180°, с погрешностью менее 1/3600 единиц. Он также объяснил метод составления этой таблицы, и на протяжении всей книги приводил много примеров того, как вычислять с помощью неё неизвестные элементы фигур.

Птолемей также был автором, так называемой теоремы Менелая для решения сферических треугольников, и на протяжении многих веков его тригонометрия была основным пособием для астрономов.

Где еще используются

Очень часто при проведении ремонтных работ, составления таблиц в журналах и тетрадях, создании различных изделий мастерами различных профессий, домохозяйками, рабочими применяется данный инструмент. Для чего нужна линейка, например, бухгалтеру? При занесении данных из листов в компьютер накладывает линейку на ту строку, с которой нужно работать. Так он не потеряет место, где остановился.

Вот такие полезные свойства у линейки и траспортира! А стоят они недорого и доступны каждому.

Процессор – системный блок — предназначен для вычислений, обработки информации и управления работой компьютера. 2 типа корпуса Desctop — настольный вариант Tower — башня Кнопки: power (вкл/выкл), reset (перезагрузка) Индикаторы: power (вкл/выкл), hdd (ЖД)

Монитор — устройство визуального представления данных. Его потребительские параметры: 1. Размер – по диагонали: 17, 20, 21 дюйм 2. Шаг маски – шаг между отверстиями специальной панели: 0,25-0,27 мм 3. Частота регенерации –обновление изображения, частота кадров: от 100 Гц 4. Класс защиты – стандарт техники безопасности

Устройства системного блока Внутренние Внешние — устройства, находящиеся внутри системного блока. — устройства, подключаемые к системному блоку снаружи. — блок питания — материнская плата — видеокарта — сетевая плата — дисководы ЖМД — монитор — клавиатура — принтер — мышь — сканер — модем — колонки

Задание 5, стр. 55 Информация — сведения об интересующем вас предмете. Компьютер — универсальное программно управляемое устройство для обработки информации. Процессор — устройство, предназначенное для вычислений, обработки информации и управления работой компьютера. Оперативная память — информация в ней находиться только во время работы компьютера. Жёсткий диск — используется для длительного хранения информации.

Задание 5, стр. 55 Клавиатура — устройство для ввода информации путём нажатия клавиш. Монитор — устройство визуального отображения информации. Мышь — устройство для быстрого перемещения по экрану и выбору нужной информации. Принтер — устройство для печати информации на бумаге. Данные — информация, представленная в форме, пригодной для обработки компьютером. Аппаратное обеспечение — совокупность всех устройств компьютера.

Транспортир представляет собой геометрический инструмент, используемый для измерения углов.

Разновидности и использование

Транспортир — это простой гониометр для измерения или создания угла. Он выглядит как круглый или полукруглый диск с делением. Диск может быть изготовлен из пластика, прочной бумаги или листового металла. Типичными являются диаметры от 8 до 15 см и деления на 1° и 0,5°, при измерении также 0,5 Гон (новый градус). Точность составляет от 0,1 до 0,5° в зависимости от диаметра шкалы. Более точные приборы имеют поворотную рейку со шкалой (длина до миллиметра).

Частично из-за различного использования их изготавливают во многих формах: знакомый полукруг, а также круги, прямоугольники, квадраты или четверть круга (квадранты). Они также могут иметь различные диаметры. Их изготавливают из латуни, стали, дерева, слоновой кости или пластика. Самой распространённой формой является полукруг с ограничительной шкалой в 180 градусов.

Угловой транспортир — градуированный круглый инструмент с одной поворотной рукой; используется для измерения или разметки. В строительстве часто требуется отмерить угол в 90 градусов. Иногда прилагается шкала Вернье, чтобы дать более точные показания. Прибор широко применяется для изготовления архитектурных и механических чертежей, хотя его использование уменьшилось с появлением современного программного обеспечения для рисования.

Универсальные транспортиры скоса используются изготовителями инструментов; поскольку они делают измерения посредством механического контакта с предметом, то классифицируются как механические транспортиры.

Угловой транспортир применяется для того, чтобы измерить и проверить углы с очень жёсткими допусками. Он считывает до 5 угловых минут (5 или 1/12°) и может измерять от 0 до 360°.

Сегодня также применяются электронные приборы, которые обычно работают с поворотным датчиком. Кроме того, связанными с транспортиром приборами являются:

• теодолит;
• оптический транспортир в строительной промышленности и геодезии;
• инклинометр для определения уклонов и косвенной альтиметрии;
• секстант для навигации.

Назначение линейки

Линейка — это длинная узкая прямоугольная полоса с нанесенной по верхнему краю (на некоторых линейках и по нижнему) шкалой и цифрами.

Для чего нужна линейка человеку? Во-первых, для измерения небольших расстояний, длины, высоты и ширины различных предметов; во-вторых, для проведения ровных прямых линий при помощи карандаша, ручки, фломастера. То есть линейка имеет две основные функции: измерение и проведение ровных линий. Нередко используются сразу обе, например, нужно нарисовать прямоугольник со сторонами 5 см и 7 см. Берем линейку, прикладываем на лист в нужном месте сначала горизонтально, карандашом проводим от 0 до 7 см, затем рисуем перпендикулярные стороны по концам по 5 см и завершаем верхнюю сторону 7 см.

С другой стороны, линейка используется не для построений, а просто для измерений. Например, вам нужно измерить длину ручки, чтобы понять, поместится она в миниатюрную карандашницу или нет.

Измерение градусов угла

Для того чтобы научиться пользоваться транспортиром инструкция нужна на начальном этапе. Для его освоения достаточно нескольких минут и примеров (смотреть онлайн) того, как можно измерить и построить угол с помощью этого прибора.

Измерить угол, значит найти его величину. Углы разделяют на три типа: острый, тупой и прямой. Прямоугольный имеет 90 градусов. Все углы что имеют больше этого значения называются тупыми, и соответственно меньше 90 градусов называются острыми. Развёрнутый угол имеет 180 градусов.

Понимание того, что углы являются частями окружностей, полезно, потому что тогда конструкция транспортира обретает смысл. Поскольку полный круг имеет 360º, отдельный угол должен быть меньше этого числа, потому что он часть круга.

Алгоритм измерения следующий: для того чтобы измерить угол транспортиром необходимо приложить его центр верхней кромки линейки к вершине измеряемого угла. Вершина — это точка, в которой две из трёх сторон треугольника пересекаются.

Нижнюю планку (основание) транспортира нужно выставить горизонтально. Каждый транспортир имеет точку, спроектированную в центре основания, Эта средняя точка располагается на вершине угла, который должен быть измерен или нанесён на график. Другая сторона должна пересекать транспортир в одной из точек его дуги.

Если вторая сторона (линия) до дуги не доходит нужно продолжить её с помощью простой или масштабной линейки. То число, на шкале дуги, которое будет пересечено линией и есть величина угла в градусах.

Для удобства на большинстве транспортиров сделано две шкалы, внутренняя и внешняя, которые отображают числа в каждой строке.

Инструкция

• Если под рукой нет ничего кроме листа бумаги и карандаша, то можно обойтись даже этими принадлежностями. Для этого очень аккуратно сверните лист бумаги вчетверо, при этом хорошо заглаживая сгибы. В результате на месте двойного сгиба получите прямой угол, который имеет 90°. Сложите угол еще раз пополам, и получится искомый угол в 45°. Правда в этом случае проявится небольшая погрешность в виде потери нескольких градусов. Для более точного рисунка обведите прямой угол карандашом на чистый лист бумаги, аккуратно вырежьте его и сложите пополам – это даст угол в 45°.
• Можно начертить угол с помощью прямоугольных треугольников, которые могут быть разными – с углами 90°, 45°, 45° и 90°, 60°, 30°. Возьмите треугольник (с углами 90°, 45°, 45°) и обведите на листе бумаги острый угол в 45°. Если имеется только треугольник с углами 90°, 60°, 30°, то на другом листе бумаги обведите прямой угол, вырежьте его, сложите пополам и обведите на нужном чертеже. Это и будет угол в 45°.
• Самым точным будет вариант построения, при котором используется транспортир. Начертите на листе бумаги линию, отметьте на ней угловую точку, приложите транспортир и отметьте точкой 45° , после чего соедините их между собой.
• Интересно, что даже с помощью циркуля можно также изобразить угол в 45° . Для этого достаточно иметь перед собой изображенный угол в 90° (например, с помощью прямоугольного треугольника или путем сгибания бумаги вчетверо). Затем от угловой точки циркулем проведите окружность.

Построение угла

Берётся чистый лист бумаги в клетку. На нём карандашом отмечается точка, от которой проводиться прямая линия, как одна из сторон будущего угла. Эта черта служит для того, чтобы задать направление второй стороне. В простых упражнениях, для приобретения навыка построения угла, линия проводится горизонтально.

Центр основы транспортира располагается на любом из концов черты, который будет вершиной угла. Эта точка отмечается на бумаге карандашом. И именно к этому месту, внутри отверстия и присоединяется вершина угла, одна из сторон которого должна совпадать в горизонтальной плоскости с внутренней стороной линейки транспортира.

Затем на шкале отмечается необходимый градус. С внутренней стороны отверстия также обозначается точка возле этого градуса. И от вершины проводится прямая линия к этой точке. Таким образом, получается необходимый угол.

Для того чтобы правильно пользоваться транспортиром очень важно его выровнять, и точно прикладывать, для получения верных измерений.

Пересечённые линии в верхней части прямой кромки линейки должны совпадать с вершиной (конечной точкой), где соединяются два луча.

Ответ

Пошаговое объяснение:

Для начала надо иметь в руках транспортир, примерно такой, как на фото. Этот почти антиквариат — из СССР — 8 копеек стоит.

Действие первое — нужно иметь изображение угла, который мы хотим измерить. Угол — это два луча исходящие из одной точки.

При обозначении угла из трех букв обозначение вершины — это центральная буква. Например,∠АОС — вершина О и два луча ОА и ОС.

Действие второе: Совместить вершину угла О с центром транспортира, а его развернутый угол с одним из лучей.

Действие третье, самое сложное: Определить значение самого угла. Находим показание транспортира — место где второй луч пересекает шкалу транспортира. Возможно для этого понадобится продлить луч до пересечения со шкалой. На шкале транспортира две шкалы, одна на увеличение — от 0° до 180°, другая — на уменьшение — от 180° до 0°.

На рисунке это и +140° и -40°. Думаем: какое показание взять за результат. Просто думаем.

В приложении и второй рисунок: 20°, 25° и 70°.

Как пользоваться транспортиром

Условно выделим в транспортире две части — «линейку», называемую также прямолинейной шкалой (нижняя часть на рисунке), и полукруга, называемого также угломерной шкалой. На полукруге находятся метки градусов от 0° до 180°. Назовем разделение на градусы «градусной сеткой».

Транспортиры бывают разного вида, но использование их сводится к следующему. У транспортира есть центральная метка. На рисунке выше это маленький кружок с отверстием в центре. Однако центральная метка может обозначаться просто черточкой. Эту метку нужно совместить с вершиной угла. При этом одна из сторон угла должна пройти через метку с числом 0 на полукруге транспортира.

На транспортире может быть две «нулевых» метки: справа и слева. Понятно, что следует смотреть на ту, через которую проходит сторона угла. Но самое главное, понять на какую градусную сетку смотреть при измерении величины угла: верхнюю или нижнюю. Если сторона угла прошла через 0, который находятся с внешней стороны, то в дальнейшем мы пользуемся внешней градусной сеткой. Если же сторона угла прошла через «внутренний» 0, то в дальнейшем пользуемся внутренней градусной сеткой транспортира (на внешнюю не обращаем внимания).

Итак, одна сторона угла должна пройти через метку 0, а вторая сторона угла должна оказаться со стороны полукруга (угломерной шкалы), то есть как бы пересекать его.

По тому месту, где вторая сторона угла пересекает угломерную шкалу транспортира, определяется величина угла.

Введение

Какие-то вещи можно измерить, какие-то нельзя. Например, нельзя измерить дружбу или любовь. А расстояние, вес, температуру вполне можно. Чтобы что-то измерять, нужно всем договориться о единицах измерения.
Метр, дюйм, аршин – это и есть такие договоренности при измерении длины. Эталонный метр хранится во Франции, в Палате мер и весов. Килограмм, фунт, пуд – это договоренности для измерения массы. Эталонный килограмм тоже хранится в Палате мер и весов.

Единицы измерения придуманы для конкретных величин. В секундах не измерить вес, а в аршинах – время.

В геометрии такая же ситуация. Есть сантиметры, для измерения длин отрезков, но они не подходят для измерения углов. Для измерения углов есть свои единицы измерения. На этом уроке мы рассмотрим одну из них, а именно градусы.

Измерение угла транспортиром

1. Оцените, к какому типу относится интересующий вас угол. Углы можно разделить на три класса: острые, тупые и прямые.

Острые углы относительно узки (менее 90 градусов), тупые углы шире (более 90 градусов), а величина прямых углов составляет 90 градусов (их стороны перпендикулярны друг другу). Оцените на глаз, к какому типу принадлежит тот угол, который вы собираетесь измерить. Предварительная оценка поможет вам определить необходимый диапазон и правильно выбрать шкалу транспортира. На первый взгляд мы можем сказать, что выше изображен острый угол, то есть его величина меньше 90 градусов.

Теорема Пифагора

Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы

. В виде формулы записывается это так:

Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.

Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!

А теперь применим теорему на практике.

видео-инструкция как шпаклевать своими руками, цена, фото

Процедура выравнивания поверхности стен при помощи листов гипсокартона сегодня довольно распространена, поскольку этот материал позволяет в кратчайшие сроки выровнять самые неровные стены, к тому же материал сравнительно недорогой и экологически чистый. При работе с ним, главное освоить такую процедуру как шпаклевка углов гипсокартона.

Приобретение этих навыков позволит существенно снизить затраты на ремонт, не привлекая к работе сторонних специалистов.

Нанесенная шпаклевка на изгибе перегородки из гипсокартона.

Важные аспекты

Перед тем как начинать работу с гипсокартоном, необходимо изучить несколько важнейших моментов при его отделке, которые позволят вам добиться высокого результата своими руками.

Если работы были выполнены в неправильной последовательности и без соблюдения технологии, то, скорее всего, вам придется нанимать квалифицированных специалистов, которые будут переделывать всё вновь. Сам материал достаточно хрупкий и требует бережного обращения в процессе работ.

Особое внимание стоит уделить внутренним и наружным углам. Для их качественной обработки существуют специальные металлические или пластиковые уголки, которые накладываются на стыки в прямых углах и заделываются шпаклевкой.

Также для создания ровных внутренних углов используются специальные угловые шпатели, поскольку вывести идеально ровный угол при помощи обычного прямого шпателя, особенно для начинающего, крайне сложно, а точнее – практически невозможно.

Рассмотрим подробно, как шпаклевать углы гипсокартона и какие инструменты и материалы для этого использовать.

На фото представлен угловой шпатель.

Необходимые материалы и инструменты

Перед началом работ с гипсокартоном, рекомендуется заранее приобрести все необходимые расходные материалы и подготовить нужный инструмент. Это позволит значительно ускорить манипуляции и существенно повысит их качество.

Итак, для данного мероприятия вам потребуются:

• стартовая шпаклевка;
• финишная шпаклевка;
• строительная сетка;
• специальные металлические или пластиковые уголки с перфорацией;
• флизелиновая лента для дополнительного укрепления швов;
• плоский и угловой шпатель;
• строительный нож;
• емкость для замешивания раствора шпаклевки;
• дрель с насадкой миксером для качественного замешивания смеси.

Инструменты, которые максимально облегчат производимые действия.

Совет: Если в помещении будут использованы арочные конструкции или другие элементы с изгибами, то для их оформления понадобятся специальные арочные уголки, одна сторона которых имеет вырезанные плоскости, обеспечивая равномерный изгиб.
Такое приспособление позволит создать идеально ровные углы на различных закруглённых и волнистых конструкциях, которые часто используют для декорации помещения или визуального разделения зон (зонирования) в квартирах, домах и административных учреждениях.

Шпаклевание: способы

Для того чтобы четко понимать, как зашпаклевать углы из гипсокартона, рассмотрим несколько вариантов решения этого вопроса с использованием различных материалов и технологии.

Использование пластикового уголка типа AquaBead

Образец пластиковой полосы.

AquaBead представляет собой обычный пластиковый уголок, внутренняя часть которого покрыта специальной бумагой с клеем. Для его установки не требуется предварительное нанесение клеящего слоя шпаклевки.

Клеевая поверхность бумаги смачивается обычной водой, которая активирует основу и уголок можно просто приклеивать на предусмотренное место.

Процесс работы выглядит так:

• поверхность необходимо проверить на ровность при помощи лазерного или водяного уровня;
• смочить клейкую часть бумаги на уголке мокрой кисточкой или пульверизатором;
• через 20-30 секунд можно фиксировать уголок на подготовленное место, предварительно проверив уровень клейкости касанием пальца;

Примечание!
Если после размачивания клейкой основы вы не успели установить уголок и клей застыл, то достаточно просто его ещё раз намочить.

На развернутый угол наклеиваем пластиковую полосу.

• через 15-20 минут после приклеивания, можно наносить выравнивающий слой шпаклевки.

Эту немаловажную деталь на клейкой основе для угла можно приобрести практически в каждом строительном магазине, однако его цена на порядок выше, чем у аналогичных изделий без клея.

Металлический перфорированный уголок

При использовании обычного металлического уголка, процесс монтажа выглядит следующим образом:

• поверхность проверяется на ровность при помощи уровня;
• подготавливается уголок нужного размера;
• приготавливается небольшое количество раствора для приклеивания изделия по всей длине угла;
• раствор наносят на обе стороны поверхности небольшими порциями;
• прикладывают уголок и вдавливают его в смесь (фото), регулируя ровность угла уровнем.

Вдавливаем уголок в раствор.

После вдавливания, через отверстия в уголке будет выступать клеящая смесь, которую после выравнивания необходимо равномерно распределить по всей высоте при помощи шпателя с добавлением новой порции шпаклевки.

В некоторых случаях, возможно применить и другую схему крепления металлического уголка к гипсокартону – при помощи обычного монтажного степлера.

К сведению!
Обычно это применяется в тех конструкциях, где угол строения больше или меньше угла металлического изделия и его приходится укладывать с небольшим нажимом.
Шпаклевочная смесь в таких случаях не сможет удержать изделие на нужном месте, поэтому используется степлер.

Полукруглый уголок из пластика

Такой тип изделия не имеет острого угла и предназначается для установки в тех местах помещения, где возможность механического повреждения наиболее высока. Изделие изготавливают из прочного ABS пластика.

Перед его установкой, необходимо торец гипсокартона обрезать по всей высоте на 1,5-2 см под углом примерно в 45 градусов. Перед установкой наносится толстый слой стартовой шпаклевки, и изделие устанавливают в обработанный торец.

Перед тем как шпаклевать угол из гипсокартона, положение пластикового уголка корректируется при помощи лазерного или водяного уровня. При необходимости, уголок можно дополнительно зафиксировать монтажным степлером в нескольких местах. После выравнивания торца, лишнюю смесь снимают с полукруглого изделия при помощи влажной тряпки или губки.

Полукруглый арочный уголок, закрепленный степлером.

Шпаклевка внутренних углов

Для оформления внутренних углов некоторые мастера используют специальные пластиковые уголки, которые продаются с уже установленной на них монтажной сеткой для дополнительного армирования стыков. Однако при наличии специального углового шпателя, можно обойтись и без него, используя только монтажную сетку.

Перед тем как шпаклевать внутренние углы гипсокартона, необходимо обеспечить надёжное соединение листов на стыке, поскольку при сильных вибрациях листов, во внутренних углах может появиться трещины и щели.

Процесс шпаклевки выглядит следующим образом, инструкция:

• на стыки накладывается монтажная сетка таким образом, чтобы центр полосы был четко по центру стыка;

Укладываем сетку на стыки.

• поверх монтажной сетки наносят заранее подготовленную шпаклевку по всей высоте угла;

Наносим раствор поверх монтажной сетки.

• после этого угол выравнивается специальным угловым шпателем.

Лучше всего выравнивать каждую плоскость внутреннего угла по очереди и не пытаться выровнять обе стороны одновременно, поскольку шпатель будет затрагивать другую сторону. Если у вас уже есть необходимый опыт работы и специальные навыки, то можно попробовать выровнять сразу обе плоскости внутреннего угла.

Совет: На всех этапах работ с установкой пластиковых или металлических уголков, в качестве клеящего вещества используется стартовая шпаклевка, которая отличается от финишной более крупной зернистостью и лучшим сцеплением с поверхностью.

Выравниваем угол специальным инструментом.

Заключительный этап

Если вы подготавливаете стены под оклейку флизелиновыми или другими видами обоев с плотной основой или фактурным рисунком, то достаточно просто зачистить углы специальной сеткой или наждачной бумагой. Но если стены готовятся под покраску или для бумажных обоев без теснения, то они должны быть идеально гладкими. (См. также статью Как шпаклевать стены под покраску своими руками.)

В таких случаях рекомендуется дополнительно обработать и плоскость, и все углы финишной шпаклевкой, которая скроет все мелкие неровности и придаст поверхности красивый эстетический вид.

Отделываем гипсокартон финишной шпаклевкой.

Перед тем как зашпаклевать гипсокартон в углах финишной шпаклевкой, необходимо их дополнительно загрунтовать. После нанесения слоя финишной смеси, поверх ещё не застывшей шпаклевки наклеивается специальная флизелиновая лента и осторожно ровняется шпателем. Впоследствии, лента пропитывается и застывает, обеспечивая дополнительное армирование и устойчивость к механическим повреждениям.

Затирка

По окончанию нанесения финишной выравнивающей смеси, нужно подождать 2-3 дня до полного её высыхания и производить затирку. Затирка осуществляется при помощи наждачной бумаги или затирочной сетки, которые крепятся на деревянный брусок или специальный инструмент с зажимами. Затирка окончательно сглаживает все неровности и придаёт поверхности идеальный внешний вид. (См. также статью Шпаклевка швов гипсокартона: особенности работ.)

Шлифуем поверхность.

Заключение

Ознакомившись с этой инструкцией, вы знаете, как шпаклевать углы гипсокартона без привлечения сторонних специалистов. Это поможет вам значительно сэкономить бюджет и приобрести опыт, который вам в дальнейшем может ещё не раз пригодится для осуществления ремонтных работ. Еще много полезного – в видео в этой статье.

Понравилась статья? Подписывайтесь на наш канал Яндекс.Дзен Добавить в избранное Версия для печати

Как извлечь данные из exe файла. Распаковка инсталляционных файлов с помощью Universal Extractor. Universal Extractor

Два угла размещнные на одной прямой и имеющие одну вершину называются смежными.

Иначе — если сумма двух углов на одной прямой равна 180 градусам и одна сторона у них общая, то это смежные углы.

1 смежный угол + 1 смежный угол = 180 градусов.

Смежные углы -это два угла, у которых одна сторона общая, а две другие стороны в целом образуют прямую линию.

Сумма двух смежных углов всегда равна 180 градусам. К примеру, если один угол 60 градусов, то второй обязательно будет равен 120 градусам (180-60).

Углы АОС и ВОС являются смежными углами, потому что соблюдается все условия характеристики смежных углов:

1.ОС -общая сторона двух углов

2.АО -сторона угла АОС, ОВ -сторона угла ВОС. Вместе эти стороны образуют прямую линию АОВ.

3.Угла два и сумма их равна 180 градусов.

Вспоминая школьный курс геометрии, про смежные углы мы можем сказать следующее:

у смежных углов — одна сторона общая, а другие две стороны принадлежат одной прямой, то есть находятся на одной прямой. Если по рисунку, то углы СОВ и ВОА — это смежные углы, сумма которых всегда равна 180 , так как они разделяют развернутый угол, а развернутый угол всегда равен 180 .

Смежные углы понятие легкое в геометрии. Смежные углы, угол плюс угол дают 180 градусов в общей сумме.

Два смежных угла — это будет один развернутый угол.

Есть еще несколько свойств. Со смежными углами задачи решать и теоремы доказывать легко.

Смежные углы образуются при проведении луча из произвольной точки прямой. Тогда эта произвольная точка оказывается вершиной угла, луч — общей стороной смежных углов, а прямая от которой проведен луч — двумя оставшимися сторонами смежных углов. Смежные углы могут быть как одинаковыми в случае перпендикуляра, так и отличатся при наклонном луче. Легко понять, что сумма смежных углов равна 180 градусов или попросту прямой линии. По другому этот угол можно объяснить простым примером — вы сперва шли в одном направлении по прямой, потом передумали, решили вернуться назад и развернувшись на 180 градусов отправились по той же прямой в обратном направлении.

Итак, что же такое смежный угол? Определение:

Смежными называются два угла с общей вершиной и одной общей стороной, причем две другие стороны этих углов лежат на одной прямой.

И небольшой видео урок, где толково показано про смежные углы, вертикальные углы, плюс про перпендикулярные прямые, которые являются частным случаем смежных и вертикальных углов

Смежные углы — это углы, у которых одна сторона общая, а вторая является одной линией.

Смежные углы — это углы, зависящие друг от друга. То есть если общую строну слегка повернуть, то один угол уменьшится на сколько-то градусов и автоматически второй угол увеличится на столько же градусов. Это свойство смежных углов позволяет в Геометрии решать различные задачи и осуществлять доказательства различных теорем.

Общая же сумма смежных углов всегда равна 180 градусов.

Из курса геометрии, (насколько я помню за 6 класс) смежными называются два угла, у которых одна сторона общая, а другие стороны являются дополнительными лучами, сумма смежных углов равна 180. Каждый из двух смежных углов, дополняет другой до развернутого угла. Пример смежных углов:

Смежные углы это два угла с общей вершиной, одна из сторон которых общая, а оставшиеся стороны лежат на одной прямой (не совпадая).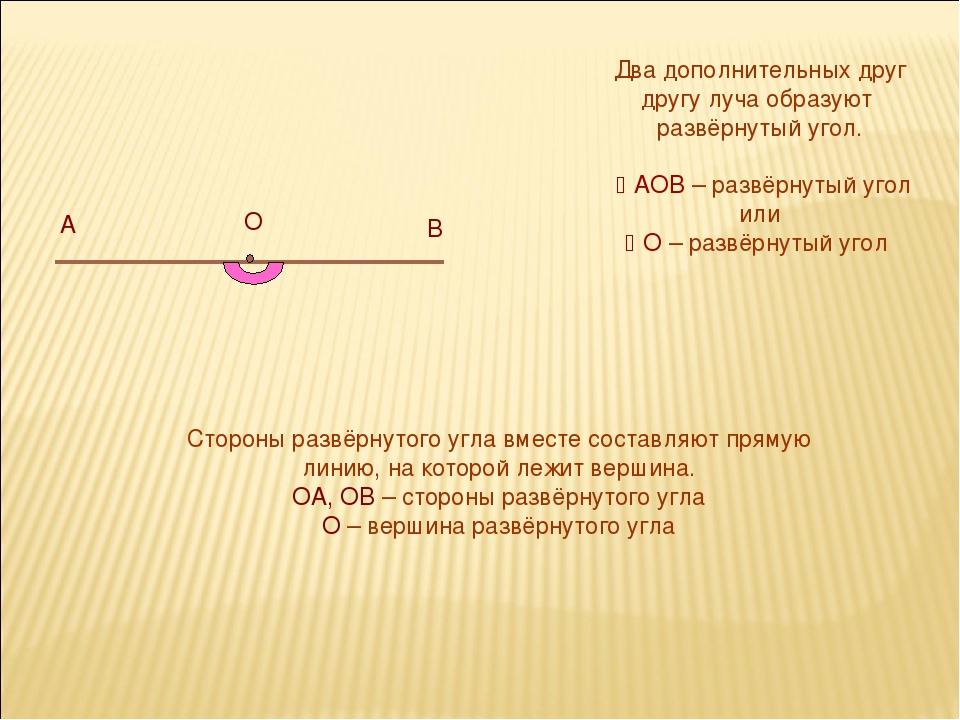 Сумма смежных углов равна ста восьмидесяти градусам. А вообще все это очень легко находится в гугле или учебнике геометрии.

Два угла называются смежными, если у них есть общие вершина и одна сторона, а две другие стороны составляют прямую линию. Сумма смежных углов равна 180 градусам.

На рисунке углы АОВ и ВОС являются смежными.

Смежными называются углы имеющие общую вершину, одну общую сторону, а другие стороны являются продолжением друг друга и образуют развернутый угол. Замечательным свойством смежных углов является — сумма этих углов всегда равна 180 градусам.

Углы с общей вершиной и одной общей стороной в геометрии называются смежными

Сумма смежных углов равна 180 градусов

Нужно отметить тот факт, что у смежных углов синусы равны

Что бы узнать больше про смежные углы — читайте вот здесь

Углы, у которых одна сторона общая, а другие стороны лежат на одной прямой (на рис. углы 1 и 2 смежные). Рис. к ст. Смежные углы … Большая советская энциклопедия

СМЕЖНЫЕ УГЛЫ — углы, имеющие общую вершину и одну общую сторону, а две др. их стороны лежат на одной прямой … Большая политехническая энциклопедия

См. Угол … Большой Энциклопедический словарь

СМЕЖНЫЕ УГЛЫ, два угла, сумма которых равна 180°. Каждый из этих углов дополняет другой до развернутого угла … Научно-технический энциклопедический словарь

См. Угол. * * * СМЕЖНЫЕ УГЛЫ СМЕЖНЫЕ УГЛЫ, см. Угол (см. УГОЛ) … Энциклопедический словарь

— (Angles adjacents) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие С. углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через вершину … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

См. Угол … Естествознание. Энциклопедический словарь

Две прямые пересекаются, создавая пару вертикальных углов. Одна пара состоит из углов A и B, другая из C и D. В геометрии, два угла называются вертикальными, если они созданы пересечением двух … Википедия

Пара комплементарных углов, дополняющих друг друга до 90 градусов Комплементарные углы это пара углов, которые дополняют друг друга до 90 градусов. Если два комплементарных угла являются соседними (т.е. имеют общую вершину и разделяются только… … Википедия

Пара дополнительных углов, дополняющих друг друга до 90 градусов Дополнительные углы это пара углов, которые дополняют друг друга до 90 градусов. Если два дополнительных угла являются с … Википедия

Книги

• О доказательстве в геометрии , Фетисов А.И.. Эта книга будет изготовлена в соответствии с Вашим заказом по технологии Print-on-Demand. Однажды, в самом начале учебного года, мне пришлось услышать разговор двух девочек. Старшая из них…
• Комплексная тетрадь для контроля знаний. Геометрия. 7 класс. ФГОС , Бабенко Светлана Павловна, Маркова Ирина Сергеевна. В пособии представлены контрольно-измерительные материалы (КИМы) по геометрии для проведения текущего, тематического и итогового контроля качества знаний учащихся 7 класса. Содержание пособия…

Г Л А В А I.

ОСНОВНЫЕ ПОНЯТИЯ.

§11. СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ.

1. Смежные углы.

Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (черт. 72): / А ВС и / СВD, у которых одна сторона ВС общая, а две другие АВи ВD составляют прямую линию.

Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.

Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.
Например, / АDF и / FDВ — углы смежные (черт. 73).

Смежные углы могут иметь самые разнообразные положения (черт. 74).

Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 2d.

Отсюда прямой угол можно определить как угол, равный своему смежному углу.

Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.

Например, если один из смежных углов равен 3 / 5 d , то второй угол будет равен:

2d — 3 / 5 d = l 2 / 5 d .

2. Вертикальные углы.

Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На чертеже 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные.

Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.

Пусть / 1 = 7 / 8 d (черт. 76). Смежный с ним / 2 будет равен 2d — 7 / 8 d , т. е. 1 1 / 8 d .

Таким же образом можно вычислить, чему равны / 3 и / 4.
/ 3 = 2d — 1 1 / 8 d = 7 / 8 d ; / 4 = 2d — 7 / 8 d = 1 1 / 8 d (черт. 77).

Мы видим, что / 1 = / 3 и / 2 = / 4.

Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.

Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.

Убедиться в справедливости свойства вертикальных углов необходимо путём рассуждения, путём доказательства.

Доказательство можно провести следующим образом (черт. 78):

/ a + / c = 2d ;
/ b + / c = 2d ;

(так как сумма смежных углов равна 2d ).

/ a + / c = / b + / c

(так как и левая часть этого равенства равна 2d , и правая его часть тоже равна 2d ).

В это равенство входит один и тот же угол с .

Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: / a = / b , т. е. вертикальные углы равны между собой.

При рассмотрении вопроса о вертикальных углах мы сначала объяснили, какие углы называются вертикальными, т. е. дали определение вертикальных углов.

Затем мы высказали суждение (утверждение) о равенстве вертикальных углов и в справедливости этого суждения убедились путём доказательства. Такие суждения, справедливость которых надо доказывать, называются теоремами . Таким образом, в данном параграфе мы дали определение вертикальных углов, а также высказали и доказали теорему об их свойстве.

В дальнейшем при изучении геометрии нам постоянно придётся встречаться с определениями и доказательствами теорем.

3. Сумма углов, имеющих общую вершину.

На чертеже 79 / 1, / 2, / 3 и / 4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.
/ 1+ / 2+/ 3+ / 4 = 2d .

На чертеже 80 / 1, / 2, / 3, / 4 и / 5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. / 1 + / 2 + / 3 + / 4 + / 5 = 4d .

Упражнения.

1. Один из смежных углов равен 0,72 d. Вычислить угол, составленный биссектрисами этих смежных углов.

2. Доказать, что биссектрисы двух смежных углов образуют прямой угол.

3. Доказать, что если два угла равны, то равны и их смежные углы.

4. Сколько пар смежных углов на чертеже 81?

5. Может ли пара смежных углов состоять из двух острых углов? из двух тупых углов? из прямого и тупого угла? из прямого и острого угла?

6. Если один из смежных углов прямой, то что можно сказать о величине смежного с ним угла?

7. Если при пересечении двух прямых линий один угол прямой, то что можно сказать о величине остальных трёх углов?

Что такое смежный угол

Угол – это геометрическая фигура (рис. 1), образованная двумя лучами OA и OB (стороны угла), исходящими из одной точки O (вершина угла).

СМЕЖНЫЕ УГЛЫ — два угла, сумма которых равна 180°. Каждый из этих углов дополняет другой до развернутого угла.

Смежные углы — (Agles adjacets) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через.

Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.

рис. 2

На рисунке 2 углы a1b и a2b смежные. У них общая сторона b, а стороны a1, a2 — дополнительные полупрямые.

рис. 3

На рисунке 3 изображена прямая AB, точка C расположена между точками A и B. Точка D — точка не лежащая на прямой AB. Получается, что углы BCD и ACD смежные. У них общая сторона CD, а стороны CA и CB дополнительные полупрямые прямой AB, так как точки A, B разделены начальной точкой C.

Теорема о смежных углах

Теорема: сумма смежных углов равна 180°

Доказательство:
Углы a1b и a2b смежные (см. рис. 2) Луч b проходит между сторонами a1, и a2 развернутого угла. Следовательно, сумма углов a1b и a2b равна развернутому углу, то есть 180°. Теорема доказана.

Угол, равный 90° называется прямым. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом также прямой угол. Угол, меньший 90° называется острым, а угол больше 90° — тупым. Так как сумма смежных углов равна 180°, значит угол, смежный с острым углом — тупой угол. А угол смежный с тупым углом — острый угол.

Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.

Определение 1. Углом называется часть плоскости, ограниченная двумя лучами с общим началом.

Определение 1.1. Углом называют фигуру, состоящую из точки — вершины угла — и двух различных полупрямых, исходящих из этой точки, — сторон угла.
Например, угол ВОС на рис1 Рассмотрим сначала две пересекающиеся прямые. При пересечении прямые образуют углы. Есть частные случаи:

Определение 2. Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым.

Определение 3. Прямой угол — это угол величиной в 90 градусов.

Определение 4. Угол, меньший 90 градусов, называется острым углом.

Определение 5. Угол, больший 90 градусов и меньший 180 градусов, называется тупым углом.
пересекающиеся прямые.

Определение 6. Два угла, одна сторона которых общая, а другие стороны лежат на одной прямой, называются смежными.

Определение 7. Углы, стороны которых продолжают друг друга, называются вертикальными углами.
На рисунке 1:
смежные: 1 и 2; 2 и 3; 3 и 4; 4 и 1
вертикальные: 1 и 3; 2 и 4
Теорема 1. Сумма смежных углов равна 180 градусов.
Для доказательства рассмотрим на рис. 4 смежные углы АОВ и ВОС. Их суммой является развернутый угол АОС. Поэтому сумма данных смежных углов равна 180 градусов.

рис. 4

Связь математики с музыкой

«Раздумывая об искусстве и науке, об их взаимных связях и противоречиях, я пришел к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая духовная деятельность человека и, что между ними размещается все, что человечество создало в области науки и искусства.»
Г. Нейгауз
Казалось бы, искусство — весьма отвлеченная от математики область. Однако связь математики и музыки обусловлена как исторически, так и внутренне, несмотря на то, что математика — самая абстрактная из наук, а музыка — наиболее отвлеченный вид искусства.
Консонанс определяет приятное для слуха звучание струны
В основе этой музыкальной системы были два закона, которые носят имена двух великих ученых — Пифагора и Архита. Вот эти законы:
1. Две звучащие струны определяют консонанс, если их длины относятся как целые числа, образующие треугольное число 10=1+2+3+4, т. е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n:(n+1) (n=1,2,3), тем созвучнее получающийся интервал.
2. Частота колебания w звучащей струны обратно пропорциональна ее длине l .
w = a: l ,
где а — коэффициент, характеризующий физические свойства струны.

Так же предложу вашему внимаю забавную пародию про спор двух математиков =)

Геометрия вокруг нас

Геометрия в нашей жизни имеет немаловажное значение. Ввиду того, что когда оглядеться вокруг, то не сложно будет заметить, что нас окружают различные геометрические фигуры. Мы с ними сталкиваемся повсюду: на улице, в классе, дома, в парке, в спортивном зале, в школьной столовой, в принципе везде, где бы мы с вами не находились. Но темой сегодняшнего урока являются смежные угли. Поэтому давайте оглянемся вокруг и попытаемся в этом окружении найти углы. Если вы внимательно посмотрите в окно, то можете увидеть, что некоторые ветки дерева образуют смежные углы, а в перегородках на воротах можно заметить множество вертикальных углов. Приведите свои примеры смежных углов, которые вы наблюдаете в окружающей обстановке.

Задание 1.

1. Вот на столе на книжной подставке стоит книга. Какой угол она образует?
2. А вот ученик работает за ноутбуком. Какой угол вы видите здесь?
3. Какой угол образует фото рамка на подставке?
4. Как вы думаете, возможно ли, чтобы два смежных угла были равными?

Задание 2.

Перед вами изображена геометрическая фигура. Что это за фигура, назовите ее? А теперь назовите все смежные углы, которые вы можете увидеть на этой геометрической фигуре.

Задание 3.

Перед вами изображение рисунка и картины. Рассмотрите их внимательно и скажите, какие виды улов вы видите на картине, а какие углы на рисунке.

Решение задач

1) Даны два угла, относящиеся друг к другу как 1: 2, а смежные с ними — как 7: 5. Нужно найти эти углы.
2) Известно, что один из смежных углов больше другого в 4 раза. Чему равны смежные углы?
3) Необходимо найти смежные углы, при условии, что один из них на 10 градусов больше от второго.

Математический диктант на повторение ранее выученного материала

1) Выполните рисунок: прямые a I b пересекаются в точке А. Отметьте меньший из образованных углов цифрой 1, а остальные углы – последовательно цифрами 2,3,4; дополняющие лучи прямой а — через а1 и а2, а прямой b — через b1 i b2.
2) Пользуясь выполненным рисунком, впишите нужные значения и объяснения в места пропусков в тексте:
а) угол 1 и угол …. смежные, поскольку…
б) угол 1 и угол …. вертикальные, поскольку…
в) если угол 1 = 60°, то угол 2 = …, потому что…
г) если угол 1 = 60°, то угол 3 = …, потому что…

Решите задачи:

1. Может ли сумма 3-х углов, образованных при пересечении 2-х прямых, равняться 100°? 370°?
2. На рисунке найдите все пары смежных углов. А теперь вертикальных углов. Назовите эти углы.

3. Нужно найти угол, когда он втрое больше, чем смежный с ним.
4. Две прямые пересеклись между собой. В результате этого пересечения образовались четыре угла. Определите величину любого из них, при условии что:

а) сумма 2-х углов из четырех 84°;
б) разность 2-х углов из них равна 45°;
в) один угол в 4 раза меньше чем второй;
г) сумма трех из данных углов равна 290°.

Итог урока

1. назовите углы, которые образуются при пересечении 2-х прямых?
2. Назовите все возможные пары углов, находящихся на рисунке, и определите их вид.

Домашнее задание:

1. Найдите отношение градусных мер смежных углов, когда один из них на 54° больше второго.
2. Найдите углы, которые образуются при пересечении 2-х прямых, при условии, что один из углов равняется сумме 2-х других углов, смежных с ним.
3. Необходимо найти смежные углы, когда биссектриса одного из них образует со стороной второго угол, который больше чем второй угол на 60°.
4. Разница 2-х смежных углов равна трети от суммы этих двух углов. Определите величины 2-х смежных углов.
5. Разница и сумма 2-х смежных углов относятся как 1: 5 соответственно. Найдите смежные углы.
6. Разница двух смежных составляет 25% от их суммы. Как относятся величины 2-х смежных углов? Определите величины 2-х смежных углов.

Вопросы:

1. Что такое угол?
2. Какие бывают типы углов?
3. Какая особенность смежных углов?

Предмети > Математика > Математика 7 класс

Рейд на бен Ладена: внутри оперативного зала Фото

Во вселенной исторических фотографий немногие являются более знаковыми, чем это изображение ключевых политиков Белого дома, наблюдающих и ожидающих подтверждения того, что команде SEAL Six удалось поймать или убить Усаму бен Ладена. .

Хотя эта фотография известна как фотография «Ситуационная комната», фотограф Белого дома Пит Соуза на самом деле сделал ее втиснутой в угол небольшого соседнего конференц-зала, в который вошел президент Барак Обама, чтобы посмотреть видеотрансляцию в режиме реального времени. .Тарелка с бутербродами и другими закусками, принесенная ранее в тот же день в Costco сотрудником Белого дома, была оставлена ​​в главной ситуационной комнате.

Результат: момент почти ощутимого напряжения и беспокойства среди молчаливой группы высших руководителей. Мы не видим директора ЦРУ Леона Панетту, который принес первые новости о резиденции бен Ладена в Абботтабаде восемью месяцами ранее, всего за несколько дней до девятой годовщины терактов 11 сентября. Мы также не видим вице-адмирала Уильяма Макрейвена, главы JSOC (Объединенного командования специальных операций), ветерана специальных операций, который командовал или участвовал в более чем тысяче подобных опасных предприятий.Он находился в Джелалабаде, Афганистан, и руководил оттуда миссией группы SEAL. Тем не менее, изображение запечатлело решающий момент в истории, предлагая редкий взгляд на то, кем были ключевые игроки Белого дома и о чем они думали, ожидая услышать слова «Джеронимо (кодовое имя бен Ладена) EKIA (враг убит в действие).»

ПОДРОБНЕЕ: Как SEAL Team Six уничтожил Усаму бен Ладена

Сидят, слева направо:

Джо Байден, вице-президент президента, а затем избранного президентом, перебирал свои четки, наблюдая за развитием событий.

Убежденный католик Байден опасался рейда, вспоминал Обама в своих мемуарах. Сам Байден позже настаивал на том, что его совет заключался в том, чтобы просто подождать, чтобы убедиться, что это правильное решение. Фотография действительно передает часть этой двойственности и беспокойства, в большей степени, чем это можно увидеть на каменных лицах других противников рейда, таких как министр обороны Роберт Гейтс. Когда команда SEAL подтвердила, что Усама мертв, вице-президент схватил Обаму за плечо, сжал его и мягко сказал: «Поздравляю, босс.

Барак Обама, президент

Президент Барак Обама и советник по национальной безопасности Том Донилон во время встречи в ситуационной комнате Белого дома, обсуждающей миссию по поимке или убийству Усамы бен Ладена, 1 мая 2011 года.

Пит Соуза /The White House/Getty Images

44-й ^-й -й президент Соединенных Штатов, восседающий на том, что Соуза назвал складным черным стулом, является одним из самых неформально одетых людей в комнате и одновременно самым сосредоточенным на что разворачивалось перед ним. Обама в самом начале своего первого президентского срока решил, что хочет привлечь Усаму бен Ладена к ответственности. «Я хотел напомнить миру… что эти террористы были не чем иным, как бандой заблудших злобных убийц», — вспоминал он позже в своих мемуарах. Президент, все еще одетый в ту же одежду, в которой он играл в гольф ранее днем ​​(чтобы никого не предупредить о том, что в Белом доме происходит что-то необычное), держался подальше от своей команды, пока не прилетели вертолеты. прибыл на комплекс.Он написал, что не хочет отвлекать их, заставляя перефразировать все планы и стратегии, которые они будут использовать для устранения любых сбоев.

Когда он понял, что в небольшом конференц-зале предлагается прямой вид с воздуха на комплекс, он направился туда; вот так самая могущественная фигура в комнате оказалась сбоку от изображения. «Это был первый и единственный раз в качестве президента, когда я наблюдал за развертыванием военной операции в режиме реального времени», — писал он позже. Когда один из вертолетов был поврежден при посадке, «в голове прокрутилась катушка катастрофы.Ожидание и наблюдение, писал он, было «мучительным».

Маршалл Б. Уэбб, бригадный генерал

В центре стола, в центральном командирском кресле, сидит «Брэд» Уэбб, генерал ВВС, который смотрит видео в прямом эфире и контролирует все коммуникации со спецслужбами. силы. Когда Обама вошел в небольшой конференц-зал из главного ситуационного зала, Уэбб попытался уступить Обаме свое место, но президент сказал ему оставаться на месте. Когда он поднял голову, чтобы оглядеть комнату, Уэбб позже вспомнил, как подумал про себя: «Я должен сходить с ума прямо сейчас», когда все руководство страны наблюдало за ним.Вместо этого он оставался спокойным и «в зоне».

Денис МакДонаф, заместитель советника по национальной безопасности

Тот факт, что Макдонаф был достаточно быстр, чтобы последовать за президентом и занять место за небольшим столом в конференц-зале, оставив позади своего босса Тома Донилона, может дать нам намек на его растущее влияние в администрации Обамы; он станет главой администрации президента, когда начнется второй срок Обамы. Макдонаф, участвовавший в планировании операции с самого начала, «потел над деталями», как вспоминал Обама.

Хиллари Родэм Клинтон, госсекретарь

Советник по национальной безопасности Том Донилон, госсекретарь Хиллари Клинтон и директор национальной разведки Джеймс Клэппер слушают выступление Леона Панетты, директора ЦРУ, во время встречи в Оперативной комнате 1 мая. 2011 год в Вашингтоне, округ Колумбия 

Пит Соуза/Белый дом Фото/Getty Images

Обама позже вспоминал, что раздались слышимые вздохи, когда группа получила подтверждение смерти бен Ладена. На этом фото Хиллари Клинтон пытается сдержать вздох или подавить кашель из-за весенней аллергии? Даже она не могла потом ясно вспомнить.«Это были 38 самых напряженных минут», — сказала она позже. «Риски были огромными». Несмотря на явно выраженное на лице Клинтон напряжение, она поддержала решение о проведении рейда. Она также была обеспокоена решением президента следить за видеотрансляцией в режиме реального времени. «Как вы думаете, это хорошая идея для президента посмотреть это?» — спросила она у сотрудника службы национальной безопасности, который заверил ее, что не будет напрямую чем-либо управлять. Отдав свой голос за рейд, Клинтон явно по-прежнему беспокоилась о последствиях любых неудач для президентства Обамы.

Роберт Гейтс, министр обороны

Гейтс был одним из тех, кто опасался проведения рейда в Абботтабаде, напомнив Обаме о том, что произошло в 1980 году, когда американские войска попытались использовать вертолеты для спасения 53 американцев, взятых в заложники в посольстве в Тегеране. (Миссия была прервана, когда один вертолет разбился в пути в пустыне; восемь военнослужащих погибли.) Он считал, что более безопасным вариантом было бы использовать бомбы, чтобы полностью уничтожить комплекс. Тем не менее, он назвал бы решение президента провести рейд «смелым».”

ПОДРОБНЕЕ: 9 неожиданных вещей Морские котики обнаружены в комплексе Усамы бен Ладена 1 мая 2011 г. в Вашингтоне, округ Колумбия

Пит Соуза/Белый дом Фото/Getty Images

Майк Маллен, председатель Объединенного комитета начальников штабов (стоит позади генерала Уэбба, в коричневой рубашке и темном галстуке)

«Если бы он потерпел неудачу той ночью, я думаю, это стоило бы Обаме президентства», — сказал позже Маллен, ссылаясь на мысль, которая преследовала его, когда он и другие наблюдали за развертыванием рейда.Заинтересовавшись, о чем он думал в тот самый момент, когда фотограф Пит Соуза щелкнул затвором, Маллен позже спросил, есть ли на фотографии временная метка. Это не так.

Томас Донилон, советник по национальной безопасности (стоит со скрещенными руками, в синей рубашке, рядом с Малленом)

Донилон был одним из первых, кто узнал о решимости Обамы найти бен Ладена во время встречи в Овальном кабинете в мае 2009 года, во время которой президент поручил ему помочь разработать официальный план и издать президентскую директиву. Как и Клинтон, он хотел избежать впечатления, что Обама руководил рейдом на микроуровне, и предложил президенту не общаться напрямую с Макрейвеном в Джелалабаде. Именно по предложению Донилона Уэбб и его видеотрансляция были размещены в меньшем конференц-зале.

Билл Дейли, глава администрации Белого дома (в темном пиджаке, рядом с Донилоном)

Дейли, который в течение года до января 2012 года занимал пост главы администрации Обамы, единственный человек в комнате, одетый в полный костюм и галстук, благодаря настойчивости его жены, чтобы он признал важный характер дня.«Так или иначе, это президентство либо закончилось, либо мы еще дышим», — вспоминал он мысли. Для Дейли, единственного человека, присутствовавшего на каждом совещании на этапах планирования рейда, который не был сотрудником разведки или органов национальной безопасности, это было правильное решение. На следующее утро он проснулся с осознанием того, что «если меня уволят сегодня, все будет в порядке».

ПОДРОБНЕЕ: 8 фактов о последнем убежище Усамы бен Ладена

Энтони Блинкен, советник Байдена по национальной безопасности (видны голова и плечи, заглядывает через плечо Дейли)

В 2021 году Блинкен добился общенационального авторитета в качестве секретаря президента Джо Байдена государства. В то время, когда был сделан этот снимок, он был практически неизвестен за пределами Кольцевой дороги и вашингтонского сообщества. Вскоре после того, как культовая фотография Соузы была опубликована, Дэвид Леттерман взял интервью у Маллена в своем ток-шоу и, создавая фотографию, указал на Блинкена. «Кто этот парень? Ему явно не место на фотографии», — вспоминал Блинкен шутку Леттермана. — Он только что вернулся с экскурсии по Белому дому?

Одри Томасон, директор по борьбе с терроризмом (видна только ее голова)

Единственная другая женщина в комнате и самый молодой член этой высокопоставленной группы политиков, Томасон стала широко известна благодаря фотографии.Но сама женщина и ее мысли остаются загадкой, вероятно, из-за подпольного характера ее работы в Совете национальной безопасности.

Джон Бреннан, помощник президента Обамы по внутренней безопасности и борьбе с терроризмом (стоит за Клинтон)

Вместе с Донилоном Бреннану было поручено попытаться представить, как будет выглядеть рейд в Абботтабаде. Несмотря на то, что он поддерживал миссию, которая была отчасти его детищем, его костяшки пальцев побелели на протяжении всей атаки.«Минуты казались часами», — вспоминал он, даже после того, как члены группы «морских котиков» вернулись на борт своих вертолетов с телом бен Ладена и массивом данных, извлеченных из лагеря. Он знал, что им еще предстояло благополучно покинуть воздушное пространство Пакистана. Обама назначил Бреннана главой ЦРУ в 2013 году.

Джеймс Р. Клэппер, директор национальной разведки (в бледно-голубой рубашке, последний человек, чье лицо полностью видно на правой руке фотографии)

«Вплоть до в последнюю минуту мы не смогли подтвердить, что он был там», — вспоминает Клэппер, пенсионер из США.С. Генерал-лейтенант ВВС, который с 2010 по 2017 год был высшим должностным лицом разведки при президенте Обаме. суждения». На этом изображении он ждет, чтобы узнать, был ли этот вотум доверия оправдан.

ПОДРОБНЕЕ: Почему войска США похоронили тело Усамы бен Ладена в море?

0424-2838-MTDC, Ограждение дикой природы Пластиковыми сетчатыми заборами и электрическими заборами, контролируемыми спутниковой телеметрией

Ограждение дикой природы
Заборы из пластиковой сетки и электрические заборы Контролируется спутниковой телеметрией

Высокопрочная стальная электрическая Изгородь

Этот семиметровый забор высотой 6 футов поддерживается деревянными угловыми стойками со стекловолоконными стержнями, используемыми в качестве столбов (1 ½ дюймов в диаметре) или остается (5/8 дюйма в диаметр). Тяжелый, 10-футовый, Деревянное натяжение диаметром 6 дюймов столбы закапывают на глубину 2,5 фута в углы и ворота. Брекеты из деревянные столбы диаметром от 3 до 4 дюймов, помочь поддержать углы и проемы ворот (рис. 12). Тяжелые столбы и скобы необходимы, потому что до ¼ мили проволока может быть натянута между натяжными сообщения.

Рисунок 12—Угловые стойки высокопрочного ограждения утоплены в
на глубину 3 фута. ямы, вырытые вручную, затем поддерживается плавающим коленным бандажом.Низкий
конец скобы сидит на плоском камне или доске и привязан к базе
угловой столб с высокопрочной проволокой. Заостренный конец
сообщение до пролить воду.

Фарфоровые изоляторы были привязаны к деревянные столбы на расстоянии 10 дюймов (рис. 13), используя высокопрочную проволоку. Семь высокопрочных проводов были привязаны к изоляторы и натяжные с Галлахером Быстродействующие натяжители проволоки (рис. 14а и 14б).Проволочная катушка (спиннинг Дженни) для развертывание высокопрочной проволоки может сэкономить много разочарований, пытаясь раскрутить петли. Если пробег между угловыми стойками короткий, как и в нашем случае, проволока проходит через пластиковые изоляторы, прибитые к внешней стороне деревянного столба, а затем следующий пост. Быстрый провод Галлахера Натяжители очень удобны для натяжная проволока и веревка. Галлахер продает специальный инструмент (G645004) для Rapid Натяжители проволоки, которые делают натяжение легко для одного человека.На относительно плоской грунт, пробеги ¼ мили и более возможно между угловыми стойками утопленными 3 футов глубиной и поддерживается плавающим коленный бандаж.

Рисунок 13—Высокопрочные провода могут проходить через изоляторы, прибитые снаружи
угловой стойки и затем привяжите к следующему столбу, если провода короче
чем 800 футов и земля относительно плоская

Рис. 14а—Регулируемые натяжители упрощают натяжение и повторное натяжение
в высокопрочная проволока без ее разрезания.

Рисунок 14б—Детальный вид регулируемого натяжитель.

Опорные стойки из стеклопластика (рис. 15) вбиты в землю на глубину от 12 до 18 дюймов каждые 60 футов между деревянными столбами. Через каждые 20 футов использовались стойки из стекловолокна. чтобы помочь сохранить интервал между провода между столбами. Клипы, которые скользили через отверстия в стойках из стекловолокна и удерживает высокопрочные провода на месте (рис. 16а и 16б).Стекловолокно делает не проводит электричество, поэтому в идеале подходит для электрических заборов. Галлахер Энерджайзер B160 подал электроэнергию на забор. Этот забор был подключен как чередование горячего и заземляющего проводов система с трехстержневым заземлением система.

Рисунок 15—Стойки и распорки из стекловолокна помогают удерживать высокопрочные провода
вертикально и на правильном расстоянии.

Рисунок 16а—Специальные зажимы прикрепляют провод к стеклопластиковым стойкам после
. провод был натянут.

Рисунок 16b—Зажимы, используемые для стекловолоконных распорок.

Эффект складок и складок в Photoshop

Как создать эффект складок и складок

Шаг 1. Добавьте новый пустой слой

Давайте начнем с добавления нового пустого слоя в наш документ. Щелкните значок «Новый слой » в нижней части панели «Слои»:

.

Щелкните значок «Новый слой».

В окне документа ничего не произойдет, потому что наш новый слой пуст, но если мы посмотрим на панель «Слои», мы увидим новый слой, который Photoshop назвал «Слой 1», расположенный над исходным изображением на фоновом слое:

Новый слой появляется над фоновым слоем.

Шаг 2. Включите линейки

Мы собираемся перетащить несколько горизонтальных и вертикальных направляющих, чтобы помочь нам, и для этого нам сначала нужно включить линейки Photoshop. Перейдите к меню View в строке меню в верхней части экрана и выберите Rulers . Или нажмите Ctrl+R (Win) / Command+R (Mac) на клавиатуре, чтобы включить линейки с помощью сочетания клавиш:

Выберите Вид > Линейки.

Линейки появятся вверху и слева от окна документа:

Линейки отображаются сверху и слева от изображения.

Шаг 3. Вытащите две вертикальные направляющие

Щелкните в любом месте внутри линейки слева, затем, удерживая нажатой кнопку мыши, начните перетаскивать вправо. Вы увидите вертикальную направляющую, выходящую из линейки. Перетащите направляющую примерно на треть изображения, затем отпустите кнопку мыши, чтобы разместить направляющую. Не беспокойтесь о правильном размещении. Пока это близко к одной трети пути, все в порядке:

Нажмите на левую линейку и перетащите вертикальную направляющую на треть изображения.

Щелкните еще раз внутри линейки слева и, снова удерживая нажатой кнопку мыши, вытащите вторую вертикальную направляющую, разместив ее примерно на двух третях изображения:

Щелкните и перетащите вторую вертикальную направляющую, разместив ее на две трети поперек изображения.

Наконец, щелкните в любом месте внутри линейки вверху и, удерживая нажатой кнопку мыши, перетащите горизонтальную направляющую, поместив ее в середину изображения.Когда вы закончите, у вас должно быть две вертикальные направляющие и одна горизонтальная направляющая, разделяющие изображение на шесть примерно равных частей:

.

Щелкните и перетащите горизонтальную направляющую из верхней линейки, поместив ее посередине изображения.

Шаг 4. Выберите инструмент «Прямоугольная область»

Выберите инструмент Rectangular Marquee Tool на панели инструментов или нажмите букву M на клавиатуре, чтобы быстро захватить его с помощью сочетания клавиш:

Выберите инструмент «Прямоугольная область».

Шаг 5. Перетащите контур выделения вокруг первой секции

Выбрав инструмент Rectangular Marquee Tool, обведите контур выделения вокруг первой секции (тот, что в верхнем левом углу изображения):

Нарисуйте прямоугольное выделение вокруг первой части в левом верхнем углу изображения.

Шаг 6. Выберите инструмент «Градиент»

Выберите инструмент Gradient Tool на панели инструментов или нажмите букву G на клавиатуре, чтобы выбрать его с помощью сочетания клавиш (сочетания клавиш для инструментов Rectangular Marquee Tool и Gradient Tool пригодятся через мгновение):

Выберите инструмент «Градиент».

Шаг 7. Выберите черно-белый градиент

Выбрав инструмент «Градиент», щелкните правой кнопкой мыши (Win) / , удерживая нажатой клавишу Control, щелкните (Mac) в любом месте окна документа, чтобы быстро открыть средство выбора градиента Photoshop , затем выберите градиент «Черный, белый » двойным нажатием нажав на его миниатюру (третья миниатюра слева, верхний ряд). Двойной щелчок по миниатюре выберет градиент и закроет вас из средства выбора градиента:

Дважды щелкните эскиз черно-белого градиента.

Шаг 8.

Нарисуйте градиент от черного к белому по выделенной области

С помощью инструмента «Градиент» и градиента «Черный, белый», выбранного в палитре градиентов, щелкните и перетащите градиент от черного к белому внутри выделения. Я собираюсь перетащить свою по диагонали из нижнего левого угла в верхний правый угол:

Нарисуйте градиент от черного к белому внутри выделения.

Шаг 9. Нарисуйте контур выделения вокруг следующей секции

Вернитесь к инструменту Rectangular Marquee Tool , нажав букву M на клавиатуре, затем выделите следующий участок (тот, что в центре вверху):

Растяните контур выделения вокруг верхней средней части.

Шаг 10. Нарисуйте градиент от черного к белому по выделенной области в другом направлении

Нажмите букву G на клавиатуре, чтобы быстро переключиться на Gradient Tool , затем щелкните и перетащите градиент от черного к белому внутри этого второго выделения. Однако убедитесь, что вы рисуете его в другом направлении, чтобы оба градиента выглядели по-разному. Это добавит разнообразия нашему световому эффекту, как мы вскоре увидим:

.

Нарисуйте второй градиент под углом, отличным от первого.

Шаг 11: повторите шаги 9 и 10 для остальных разделов

Нам нужно сделать то же самое для всех шести разделов, но это всего лишь вопрос повторения одних и тех же шагов для каждого из них. Сначала нажмите букву M на клавиатуре, чтобы переключиться на инструмент Rectangular Marquee Tool и обведите контур выделения вокруг секции, затем нажмите букву G на клавиатуре, чтобы переключиться на инструмент Gradient Tool и нарисуйте градиент от черного к белому внутри выделения, рисуя каждый градиент под другим углом, чтобы добавить разнообразия.Когда вы закончите, у вас должен быть градиент в каждой секции. Нажмите Ctrl+D (Win) / Command+D (Mac) на клавиатуре после того, как вы нарисовали окончательный градиент, чтобы удалить контур выделения вокруг него:

Каждый раздел должен иметь собственный градиент от черного к белому.

Шаг 12. Скройте линейки и направляющие

Нам больше не нужны линейки или направляющие, поэтому, чтобы скрыть линейки, либо вернитесь в меню View вверху экрана и повторно выберите Rulers , либо нажмите Ctrl+R (Win) / Command+R (Mac) на клавиатуре.Чтобы скрыть направляющие, перейдите в меню View , выберите Show , затем выберите Guides или нажмите Ctrl+; (Победа) / Команда+; (Mac), чтобы отключить их с клавиатуры:

Выберите Вид > Показать > Направляющие, чтобы скрыть направляющие, когда они видны на экране.

Шаг 13. Измените режим наложения на Мягкий свет

Перейдите к параметру Режим наложения в верхнем левом углу панели «Слои» и измените режим наложения слоя градиентов с Нормального (настройка по умолчанию) на Мягкий свет :

Измените режим наложения слоя на Мягкий свет.

Это превращает наши градиенты в серию бликов и теней на изображении, и мы можем начать видеть, как обретает форму наш эффект «складок и складок»:

Изображение после изменения режима наложения на Мягкий свет.

Шаг 14. Применение пластикового фильтра

Чтобы немного подчеркнуть линии сгиба, мы воспользуемся фильтром Photoshop Plastic Wrap. Перейдите в меню Filter в верхней части экрана, выберите Artistic , затем выберите Plastic Wrap :

Выберите «Фильтр» > «Художественное оформление» > «Пластиковая пленка».

Откроется большая Галерея фильтров , в которой установлен пластиковый фильтр. Параметры фильтра находятся в верхней части правого столбца. Установите Highlight Strength на 20 и Smoothness на 15 , перетащив оба ползунка вправо. Затем установите параметр Detail где-то между 5 и 10. Чем выше значение детализации, тем плотнее будет эффект вокруг линий сгиба, поэтому следите за большим окном предварительного просмотра слева, когда перетаскиваете ползунок. и выберите значение, которое, по вашему мнению, лучше всего подходит.Я собираюсь установить значение детализации на 10:

.

Параметры фильтра «Пластиковая пленка».

Когда закончите, нажмите OK, чтобы закрыть галерею фильтров. Линии сгиба теперь выглядят немного сильнее:

Изображение после применения фильтра Plastic Wrap.

Шаг 15. Добавьте еще один новый пустой слой

Щелкните значок New Layer в нижней части панели «Слои», чтобы добавить еще один новый пустой слой, на этот раз над слоем градиентов:

Добавьте в документ еще один новый слой.

Шаг 16. Выберите инструмент «Кисть»

Чтобы еще больше усилить эффект, давайте добавим несколько линий износа на сгибы, и мы сделаем это с помощью специальной кисти. Выберите инструмент «Кисть» на панели «Инструменты» или нажмите букву B , чтобы выбрать его с помощью сочетания клавиш:

.

Выберите инструмент «Кисть».

Шаг 17. Выберите кисть «Брызги» в палитре кистей

С выбранным инструментом «Кисть» щелкните правой кнопкой мыши (Win) / Удерживая клавишу Control, щелкните (Mac) в любом месте окна документа, чтобы быстро открыть средство выбора кистей и выбрать кисть Spatter 59 пикселей , дважды щелкнув на ее миниатюре, которая выберет кисть и закроет вас из палитры кистей (если у вас включены подсказки по инструментам в настройках Photoshop, вы увидите, как имя кисти появляется при наведении курсора мыши на миниатюру):

Дважды щелкните кисть Spatter 59 пикселей, чтобы выбрать ее.

Шаг 18. Откройте панель кистей и выберите параметры формы кончика кисти

После того, как вы выбрали кисть Брызги, нажмите клавишу F5 на клавиатуре, чтобы быстро открыть полную панель Photoshop Кисти , и нажмите на слова Форма кончика кисти в верхнем левом углу панели. Установите Roundness кисти примерно на 10% , затем увеличьте параметр Spacing до 50% :

Установите Roundness на 10% и Spacing на 50% в параметрах формы кончика кисти.

Шаг 19. Выберите параметры динамики формы

В левой части панели «Кисти» находится столбец, в котором перечислены различные категории параметров кисти («Динамика формы», «Рассеяние», «Текстура» и т. д.). Прежде чем идти дальше, убедитесь, что ни одна из этих категорий не выбрана, сняв отметку с любой из них, рядом с названием которой стоит галочка.

Затем щелкните непосредственно слова Shape Dynamics в верхней части левого столбца, чтобы просмотреть различные параметры Shape Dynamics в основной части панели Brushes.Убедитесь, что вы нажимаете прямо на слова «Динамика формы». Не устанавливайте флажок рядом со словами, иначе вы просто включите категорию, не получив доступа к каким-либо фактическим параметрам динамики формы.

Увеличьте значение Size Jitter до 100 %, перетащив ползунок вправо до упора, затем установите для параметра Angle Control значение Direction . Пока не закрывайте панель, нам нужно выбрать еще одну категорию:

.

Установите для параметра Size Jitter значение 100%, а для параметра Angle Control значение Direction в параметрах Shape Dynamics.

Шаг 20. Выберите параметры двойной кисти

Нажмите непосредственно на слова Двойная кисть в столбце слева, чтобы переключиться на параметры двойной кисти в основной части панели кистей. Эти параметры позволяют нам смешать вторую кисть с нашей оригинальной. Выберите кисть Spatter 27 пикселей , щелкнув ее миниатюру, затем измените Mode в верхней части панели Brushes на Multiply . Наконец, увеличьте Size кисти примерно до 55 px и Spacing примерно до 55% . Когда вы закончите, нажмите F5 на клавиатуре, чтобы закрыть панель кистей:

Выберите кисть Брызги 27 пикселей, установите режим наложения на Умножение, Размер на 55 пикселей и Интервал на 55%.

Шаг 21. Установите белый цвет переднего плана

Мы собираемся рисовать белым цветом , и Photoshop использует текущий цвет переднего плана в качестве цвета кисти, что означает, что нам нужно убедиться, что наш цвет переднего плана установлен на белый, прежде чем мы начнем рисовать.Самый простой способ сделать это — сначала нажать букву D на клавиатуре, что вернет цвета переднего плана и фона к значениям по умолчанию (сделав цвет переднего плана черным, а цвет фона — белым). Затем нажмите на клавиатуре букву X , чтобы поменять местами цвета, что сделает цвет переднего плана белым. Вы можете увидеть текущие цвета переднего плана и фона в образцах цветов в нижней части панели инструментов:

Образцы цветов переднего плана (вверху слева) и фона (внизу справа).

Шаг 22. Закрасьте линии сгиба

Если вы работаете в плавающем окне документа, как я делал до сих пор, нажмите букву F на клавиатуре, чтобы переключиться на первый из полноэкранных режимов Photoshop , что облегчит следующий шаг. (нажатие F еще пару раз будет переключать вас через полноэкранные режимы, а затем обратно в режим плавающего окна документа). Вместо того, чтобы рисовать мазки вручную, щелкните кистью прямо над первой вертикальной линией сгиба (та, что слева).Не нажимайте и не перетаскивайте, просто нажмите:

Щелкните непосредственно над первой вертикальной линией сгиба.

Затем, удерживая нажатой клавишу Shift , щелкните непосредственно под той же линией сгиба. Photoshop автоматически нарисует мазок кистью по прямой линии между двумя точками, на которые вы нажали. Вы увидите тонкий белый мазок кисти вдоль линии сгиба, придающий ей изношенный вид:

Удерживая нажатой клавишу Shift, щелкните непосредственно под той же линией сгиба, чтобы нарисовать прямой мазок кистью между двумя точками.

Если угол или положение мазка кисти выглядят немного не так, просто нажмите Ctrl+Z (Win) / Command+Z (Mac) на клавиатуре, чтобы отменить действие, а затем повторите попытку. Чтобы увеличить интенсивность эффекта потертости, добавьте еще несколько мазков поверх первого. Изменение размера кисти с каждым мазком добавит больше разнообразия. Нажатие клавиши в левой скобке ( [ ) на клавиатуре уменьшит размер кисти. Нажатие клавиши правой скобки ( ] ) сделает его больше.Просто щелкните над линией сгиба, затем, удерживая нажатой клавишу Shift, щелкните под линией сгиба, чтобы добавить каждый новый мазок кисти:

Изображение после добавления нескольких мазков к первой вертикальной линии сгиба.

Повторите те же действия со второй вертикальной линией сгиба, чтобы нарисовать несколько мазков по ней, затем проделайте то же самое с горизонтальной линией сгиба, щелкнув кистью слева от линии, затем, удерживая Shift, щелкнув вправо линии. Если это поможет, вы можете снова включить направляющие, нажав Ctrl+; (Победа) / Команда+; (Mac) на клавиатуре, что может упростить выравнивание.Нажмите сочетание клавиш еще раз, чтобы отключить их. Вот мое изображение после добавления мазков кистью по всем трем линиям сгиба:

Изображение после добавления мазков кистью.

Шаг 23. Уменьшите непрозрачность слоя (необязательно)

Наконец, если мазки кисти выглядят слишком белыми и интенсивными, вы можете сделать их более плавными, уменьшив непрозрачность слоя. Вы найдете опцию Opacity прямо напротив опции Blend Mode в верхней части панели слоя.По умолчанию непрозрачность установлена ​​на 100%. Я уменьшу свой до 70%:

Уменьшите непрозрачность слоя, чтобы при необходимости уменьшить интенсивность мазков кистью.

На этом мы закончили! Вот мой окончательный эффект «складки и складки»:

Окончательный результат.

samoa Corner Настенные художественные принты Камалы Нахас

Бумага без кислоты и лигнина, роскошная пигментная печать

О работе

Этот фрагмент является частью фоторепортажа, снятого во время пандемического лета в Северной Калифорнии. Эта работа посвящена блужданию в одиночестве, вдали от других. Когда я шел по полям и песку, я протягивал руки, чтобы почувствовать связь с природой — со всеми ее колючими, зернистыми, мягкими и пушистыми частями, которые защищают и соблазняют. Одна из восьми фотографий в коллекции Самоа, доступных в холодных, теплых и монохромных тонах.

5 x 7 дюймов

8 x 10 дюймов

11 x 14 дюймов

16 x 20 дюймов

18 x 24 дюйма

24 x 30 дюймов

30 x 40 дюймов

40 x 54 дюйма

44 x 60 дюймов

48 x 70 дюймов

Художественная бумага премиум-класса

Художественные репродукции премиум-класса

Minted печатаются на музейном качестве. хлопковая тряпичная архивная бумага с архивными пигментными чернилами.В результате получается потрясающий отпечаток музейного качества с насыщенным изображением. и яркие цвета. Этот метод бумаги и печати используется на всех премиальных художественных принтах.

Стандартная художественная бумага

Стандартные художественные репродукции

Minted напечатаны на кислоте. и не содержащая лигнина матовая художественная бумага с роскошными пигментными чернилами. В результате получается красивая печать с яркими цветами. Этот метод бумаги и печати используется для всех репродукций Standard Art.

Профессиональное обращение

Для защиты каждый художественный принт поставляется в бескислотной и рукав без лигнина.

О художнике

Камала родом из прибрежной Южной Калифорнии. Она проводит большую часть своего времени на пляжах или в походах со своей семьей и собаками в горном чапарале, который их граничит. Она живет со своей семьей, собаками и одним самоуверенным котом.

О работе

Этот фрагмент является частью фоторепортажа, снятого во время пандемического лета в Северной Калифорнии.Эта работа посвящена блужданию в одиночестве, вдали от других. Когда я шел по полям и песку, я протягивал руки, чтобы почувствовать связь с природой — со всеми ее колючими, зернистыми, мягкими и пушистыми частями, которые защищают и соблазняют. Одна из восьми фотографий в коллекции Самоа, доступных в холодных, теплых и монохромных тонах.

Защитите свою печать

Мы рекомендуем обрамить ваш художественный принт Minted Art Print, чтобы наилучшим образом новая покупка и для защиты качества бумаги и печати.Minted предлагает профессиональное обрамление для всех художественных репродукций размером 40 x 54 дюйма. и меньше.

Художественные репродукции премиум-класса в рамке представлены изготовленные на заказ архивные материалы для обрамления. Каждое произведение искусства Minted Premium Art в рамке оснащено все деревянные молдинги, архивный покровитель, УФ-плексигласовое стекло и готовые бамперы для защиты вашей стены, и подвесной провод.

Стандартные репродукции в рамке оснащены прочным плексигласом и отделаны защитная подложка, бамперы и подвесная проволока.

Пожалуйста, смотрите информацию о размерах здесь.

Декларация независимости и Рука времени

Осень 2016 г., Том. 48, № 3

Мэри Линн Ритценталер и Кэтрин Николсон

 

Каждый год более миллиона посетителей посещают здание Национального архива в Вашингтоне, округ Колумбия.C., чтобы увидеть Декларацию независимости.

Иногда их можно увидеть в Ротонде, терпеливо ожидающих удобного места перед футляром с Декларацией. Они низко наклоняются над стеклом, пытаясь разобрать бледный почерк и узнать имена подписавших.

Декларация продолжает вызывать чувство благоговения. Но сам физический документ сильно пострадал за эти годы. Его разборчивость значительно ухудшилась, и сегодня документ сильно отличается по внешнему виду от того, когда он был написан в 1776 году.По сравнению с удобочитаемостью Конституции США (1787 г.) и Билля о правах (1791 г.), которые лишь немногим более поздние, различия поразительны.

Так что же случилось с этим почитаемым документом?

Существует мало письменных свидетельств того, что могло произойти — или когда — изменить документ. Однако, собрав воедино историю и путешествия Декларации, а также изучив ключевые фотографии, мы можем ответить на некоторые вопросы о том, как документ пришел к своему нынешнему состоянию.

 

Создание физического документа

После провозглашения независимости

19 июля 1776 г. Континентальный конгресс приказал выучить Декларацию независимости или написать крупным разборчивым почерком. Тимоти Мэтлак, клерк в Государственной палате Пенсильвании, был писцом, которому было поручено это задание.Работа Мэтлака включала размещение текста на пергаменте, определение полей и промежутков между строками, а также расчет пространства, которое потребуется внизу документа для подписей.

Между 19 июля и 2 августа (когда делегаты начали подписывать документ) Мэтлак написал текст на большом листе пергамента. Он выбрал лучшую кожу, которая была доступна, подготовил свои перья и убедился, что у него достаточно чернил.

Мэтлак сочинил новый заголовок, отличающийся визуально, большими буквами и росчерками: «Единогласная Декларация тринадцати Соединенных Штатов Америки.Под этим заголовком строки текста занимают почти всю ширину пергамента.

Хотя пергамент и не является идеальным прямоугольником, его размеры примерно 29½ на 24 дюйма. Во времена Мэтлака он был немного больше, о чем свидетельствуют различия в чистых и грязных краях, особенно вдоль верхнего края кожи. Чрезвычайно грязные края, появившиеся в результате многолетнего обращения с голым пергаментом, являются оригинальными и отражают полный размер документа, в то время как более чистые края свидетельствуют о обрезке в прошлом.Почему края были обрезаны? Возможности включают в себя желание подровнять неровный край, необходимость удалить зазубренный кусок пергамента, который может за что-то зацепиться и порваться, или желание выпрямить край перед установкой документа для выставки.

 

Чернила железной желчи,

Красивые прямые линии

Железно-галловые чернила, которые обычно использовались во времена Мэтлака, включали дубильную кислоту (из дубовых галлов), железо (из гвоздей или железных обрезков), связующее вещество (часто гуммиарабик) и иногда краситель. Светлые по цвету при нанесении чернила темнели по мере окисления до интенсивного пурпурно-черного цвета. Со временем железно-желчные чернила стареют до теплого коричневого цвета.

Строки текста Матлака довольно прямые. Переписчики часто прокалывали поля булавками и чертили на листе линейные линии, чтобы направлять перо. Сегодня в тексте нет доказательств ни булавочных уколов, ни линейных линий. Конечно, слегка нанесенные линейки могли исчезнуть в результате обработки и истирания.

Однако область подписи имеет вертикальные линейки, которые служат для выравнивания подписей в столбцах. Эти светло-серые линии правил бледны. Но если вы посмотрите очень внимательно — слева от столбцов с первого по четвертый и слева от столбца шесть, вы сможете их увидеть.

Сегодня на Декларации осталось относительно немного оригинальных чернил. Этому убытку способствовало множество факторов. В местах нанесения тяжелых чернил, например в заголовке и некоторых подписях, чернила отслаивались в результате многократного скручивания и складывания документа.

Снижение интенсивности и, следовательно, удобочитаемости чернил также может быть связано с длительным воздействием света во время выставки, что привело к некоторому выцветанию. Кроме того, влага, нанесенная на документ во время процессов копирования с влажным переносом, могла удалить некоторое количество чернил. Текст, который мы видим сегодня, внешне изменился в результате этих коллективных действий.

 

Ранние путешествия с Конгрессом

Грубая декларация

Декларация путешествовала с Континентальным Конгрессом по суше и по воде во время Войны за независимость.В 1789 году, находясь под опекой нового Государственного департамента, он продолжал путешествовать по мере перемещения столицы.

Один лист пергамента можно было свернуть для транспортировки или, что вполне вероятно, сложить, чтобы поместить в седельную сумку или деревянный сундук. Примитивные условия упаковки и транспортировки, в которых он путешествовал с другими документами, были опасны и подвергали пергамент резким перепадам температуры и относительной влажности.

Эти изменения оставили свой след.На Декларации все еще видны следы предыдущего складывания и скручивания: две основные вертикальные линии сгиба проходят сверху вниз, и есть многочисленные горизонтальные линии сгиба, особенно в нижней части документа. Небольшие складки или изгибы в целом на пергаменте возникли в результате скручивания документа до плотного диаметра, а некоторые складки могли возникнуть в результате смятия или сплющивания пергамента во время скручивания. Декларация была свернута, начиная с верхнего края, по направлению к тексту. Это защитит текст от элементов и обработки, оставив пустую оболочку в качестве внешнего слоя.Идентификационным ярлыком служила надпись в нижней части оборотной стороны пергамента, которая гласила: «Первоначальная декларация независимости от 4 июля 1776 года».

 

Воспроизведение декларации

Чтобы все это видели

В конце войны 1812 года Декларацию видели очень немногие.В воздухе витала идея создания печатных изображений Декларации.

Пенман и учитель каллиграфии Бенджамин Оуэн Тайлер создали украшенный каллиграфическим текстом Декларации и заказали гравировку Питера Маверика с факсимиле всех подписей ниже.

Тайлер потребовал от исполняющего обязанности госсекретаря Ричарда Раша сравнить текст доказательства с исходным документом и подтвердить его правильность. Удостоверение Раша было воспроизведено факсимиле на гравюре Тайлера 1818 года и отметило влияние «руки времени» на оригинал.Это заявление о том, что Декларация начала изнашиваться через 35 лет после ее написания, является первым письменным отчетом о ее состоянии. В 1819 году филадельфийский издатель Джон Биннс опубликовал большую орнаментированную гравюру текста Декларации с факсимильными подписями ниже и заявление государственного секретаря Джона Куинси Адамса, подтверждающее точность текста.

Хотя гравюры передавали письменные слова Декларации и включали точные копии подписей, им не хватало возможности передать полное присутствие документа.Поэтому Адамс, окруженный конкурирующими переписчиками, решил, что Государственный департамент должен заказать полноразмерное факсимиле Декларации, которое можно было бы увидеть во всех штатах.

Где-то после середины 1820 года Адамс обратился к молодому политическому стороннику Уильяму Стоуну и поручил ему выгравировать полноразмерное изображение на медной пластине. Медная пластина, на создание которой ушло несколько лет и с которой позже были заказаны гравюры на пергаменте, датирована 4 июля 1823 года.

Во время пребывания Адамса на посту государственного секретаря, с 1817 по 1825 год, почти любой мог войти в Государственный департамент и попросить показать Декларацию. С созданием этого культового факсимиле переписчикам — или случайным посетителям — больше не будет разрешен доступ к оригиналу в Государственном департаменте.

Доказательства, оставленные переписчиками на Декларации, — это уменьшение чернил в местах текста и особенно в подписях.На всех гравюрах, связанных с Тайлером, Биннсом и Стоуном, были факсимильные подписи, а на гравюре Стоуна также был факсимильный текст.

Поскольку фотография еще не была изобретена, переписчики должны были работать непосредственно с оригинала, чтобы запечатлеть точные изображения подписей и слов. Хотя при копировании можно было использовать и другие методы, использование влажной бумаги или ткани для прижимания к водорастворимым чернилам было быстрым методом, который создавал зеркальное изображение, необходимое для гравировальной пластины. Кажется вероятным, что подписи подвергались мокрому копированию более одного раза, вероятно, всеми тремя попытками копирования.

Адамс предполагал, что создание полноразмерного факсимиле Декларации защитит исходный пергамент от излишней обработки и ограничит количество посетителей, приходящих в его офис, чтобы увидеть настоящий документ. Хотя копии действительно помогли ограничить обращение, на горизонте маячили и другие риски.

 

Эпоха выставок

берет свое

Начиная с 1841 года Декларация выставлялась в новом здании Патентного ведомства, в котором располагался первый публичный выставочный зал в Вашингтоне.В здании, считавшемся «огнестойким», на верхнем этаже был большой Зал моделей, где Декларация была выставлена ​​в одной рамке с комиссией Джорджа Вашингтона в качестве главнокомандующего. окна. В каталоге выставки 1859 года отмечается расположение Декларации на стене между двумя окнами, затененными массивным фронтоном, выходящим на юг. В то время как Декларация висела на стене с некоторой тенью с юга, кумулятивное воздействие света в пространстве — особенно за 35 лет выставки — было экстремальным.

В течение 19 века Декларация выставлялась более полувека: 35 лет в Зале моделей, один год в Зале независимости и 17 лет в библиотеке Государственного департамента в неконтролируемых условиях окружающей среды. Кроме того, не было широко изучено вредное воздействие избыточного света на чернила. Одним из физических изменений в Декларации в результате долгой выставки стало изменение цвета чернил на теплый, бледно-коричневый.

В 1876 году президент Улисс С.Грант одобрил отправку Декларации в Филадельфию для демонстрации на выставке столетия США, которую посетили почти 10 миллионов человек. Гравюра на камне сделала общедоступным общий дизайн Декларации, но не ее фактическое состояние. Зрители, увидевшие оригинальный пергамент в Филадельфии, были поражены его поврежденным видом. Опубликованные отчеты прокомментировали выцветший вид чернил. Некоторые специально отметили, что большинство подписей были «стерты» или «неразборчивы».

Желание принять меры привело к Совместной резолюции Конгресса (19 Stat. 216), принятой в августе 1876 года, когда документ все еще находился на рассмотрении в Филадельфии. В резолюции содержится призыв к совместной комиссии глав Смитсоновского института, Библиотеки Конгресса и Министерства внутренних дел изучить вопрос о восстановлении рукописного текста и подписей на документе.

 

Государственный департамент в качестве хранителя:

Консервативный и осторожный

В конце выставки, посвященной столетию, несмотря на растущую обеспокоенность состоянием Декларации, она была возвращена в новое несгораемое здание Государственного, военного и военно-морского флота и выставлена ​​на обозрение в библиотеке Государственного департамента.

Совместная комиссия обратилась в Национальную академию наук в 1880 году с просьбой сформировать комитет для определения целесообразности восстановления чернил. В отчете комитета НАН за январь 1881 г. приводились доводы против любых попыток восстановить чернила химическими средствами, но вместо этого рекомендовалось хранить Декларацию в темноте и не делать копии для печати в будущем. Этот отчет не привел к немедленным изменениям.

В 1883 году вашингтонский фотограф Левин С. сделал первую известную фотографию Декларации.Удобно. Однако, несмотря на длительные поиски, найти его не удалось. Коллотипная фотография Декларации, сделанная вашингтонским печатником Альбертом Г. Гедни в том же году, сохранилась в редких экземплярах. Копия коллотипа была ненадолго одолжена в Национальном архиве одним из потомков Гедни и сфотографирована в 1980-х годах.

В 1894 году Государственный департамент объявил, что Декларация будет заменена в витрине факсимиле, а оригинал должен храниться «завернутым и помещенным в стальной футляр. К Декларации по-прежнему иногда обращались. Он был сфотографирован и напечатан в специальном памятном выпуске Ladies’ Home Journal за 1898 год. В подписи к фотографии говорится, что документ все еще находится в читаемом состоянии, хотя подписи были «размыты» из-за избыточного освещения.

Государственный департамент обеспокоен состоянием Декларации. В 1903 году госсекретарь Джон Хэй обратился к Национальной академии наук за рекомендациями по сохранению Декларации.Был сформирован новый комитет НАН меньшего размера, председателем которого стал профессор химии Чарльз Ф. Чандлер, работавший в комитете 1880 года.

Комиссия Чендлера быстро подготовила первый подробный отчет о состоянии документа: признаки скручивания и складывания, уменьшение количества чернил в результате копирования в прессе, выцветание из-за избыточного воздействия света, но нет признаков плесени или активного износа. Комитет категорически против применения каких-либо химикатов, восстановления чернил или нанесения покрытия на пергамент.

Члены Комитета

отметили, что фотография 1883 года помогла им оценить документ, когда они изучали его с начальником Бюро списков и библиотеки Государственного департамента. Они дали важную рекомендацию фотографировать Декларацию и снова через определенные промежутки времени в будущем. Они посоветовали продолжать хранить Декларацию в темноте, в как можно более сухих условиях и никогда не выставлять ее напоказ. Примечательно, что комитет не упомянул о наличии линий прилива или повреждений водой.

Секретарь

Хэй немедленно отреагировал на рекомендации. Он снова сфотографировал Декларацию Л. К. Хэнди в апреле 1903 года. На больших стеклянных негативах имперского формата запечатлено удивительно подробное изображение документа, которое позволяет тщательно сравнить состояние Декларации в том виде, в котором она была в 1903 году, с тем, как она выглядит сегодня. Фотография Хэнди ясно показывает, что с 1903 года произошел ряд изменений и переделок.

В апреле 1920 г. государственный секретарь назначил новый комитет для консультирования по вопросам ухода и сохранения «первоначальной Декларации независимости, Конституции…. . Договоры, прокламации и законы. . . хранится в Государственном департаменте». В начале мая комитет сообщил, что Декларация и Конституция находятся в тонких сейфах со стальными стенками, которые не являются огнеупорными или безопасными, и что в библиотеке разрешено курить.

Изучив Декларацию без рамки, они пришли к выводу, что повреждение явилось результатом неосторожного обращения в прошлом. Они заявили: «Мы не видим причин, по которым оригинал документа не должен быть выставлен, если…. . освещается только рассеянным светом». Кроме того, они рекомендовали Государственному департаменту передать оригинальные документы Континентального конгресса, включая Декларацию независимости, в Библиотеку Конгресса. Это было сделано в следующем году.

 

Другое путешествие —

В Библиотеку Конгресса

В 1921 году госсекретарь предложил новому президенту Уоррену Г. Хардингу, чтобы первоначальные Декларация и Конституция были переданы в Библиотеку Конгресса, в которой есть «специалисты по архивному хранению, в здании современной несгораемой конструкции, где они могут быть безопасно выставлены многим посетителям, которые теперь желают их увидеть. ”

Хардинг издал указ по этому поводу в сентябре. Когда библиотекарь Конгресса Герберт Патнэм получил заказ, он сразу же отправился к госсекретарю.Документы в больших дубовых рамах отнесли в почтовый грузовик библиотеки и положили на груду кожаных почтовых сумок для поездки в библиотеку. Драгоценные документы были помещены в сейф кабинета библиотекаря.

Новый мраморный храм, освященный в феврале 1924 года, был построен в Большом зале здания Джефферсона у внешней стены между большими западными окнами, которые пропускали в пространство обильный свет. Сам Патнэм установил Декларацию, которая была закреплена в зеленом бархатном оконном коврике, в вертикальную раму святыни, а внизу были выставлены листы Конституции. Декларация и Конституция оставались выставленными до 1952 года (с некоторыми перерывами) за двойными стеклами с желтыми желатиновыми фильтрами, предназначенными для блокировки вредного света.

 

Выжившие насекомые,

Влажность и война

Однако к началу 1940-х у храма возникло несколько проблем. Жуки, питающиеся белком, были обнаружены в нижнем регистре, где отображалась Конституция, в то время как Конституция и Декларация подвергались неконтролируемой влажности, что было обычным явлением до появления кондиционеров.При высокой влажности клей, удерживающий края декларации на коврике для дисплея, размягчался. Затем, когда влажность упала, пергамент сжался, и сильное напряжение между пергаментом, клеем и циновкой привело к тому, что пергамент порвался. Охранники сообщили о слезах в правом верхнем углу документа; эти слезы со временем становились длиннее.

Если этого было недостаточно для беспокойства, растущая озабоченность по поводу риска, связанного со Второй мировой войной, привела к секретным планам в апреле 1941 года по эвакуации важнейших документов библиотеки в хранилище драгоценных металлов в Форт-Ноксе, штат Кентукки.Эти планы были реализованы после нападения на Перл-Харбор 7 декабря 1941 года.

На протяжении многих лет было сделано много заявлений о состоянии Декларации, но только в ноябре 1940 года реставратор — Джордж Стаут из Гарвардского музея Фогга — исследовал ее в Библиотеке Конгресса и записал подробные наблюдения о ее состоянии.

Стаут отметил наличие отверстий и разрывов, самые большие из которых в правом верхнем углу, вызванные техникой крепления, а также следы предыдущих ремонтов с помощью бумаги и скотча.Что касается состояния пергамента, Стаут отметил, что он кажется «твердым и прочным» и что «чернила на письме стали тусклыми либо из-за выцветания, либо из-за меления». Его отчет также включает первое известное упоминание о «неясном отпечатке руки» в левом нижнем углу пергамента.

В мае 1942 года хранитель бумаги и пергамента Музея Стаута и Фогга Эвелин Эрлих изучила и обработала Декларацию в Форт-Ноксе. Их отчет включает первое известное письменное упоминание о «больших водяных пятнах».«Глядя на Декларацию сегодня, эти пятна и линии отлива, созданные водой, которая растворяла и повторно осаждала чернила, являются доминирующей чертой документа и представляют собой один из самых значительных повреждений.

Обработка Стаутом и Эрлихом стабилизировала документ: старые починки и клей (паста, клей и целлофановая самоклеящаяся лента) были удалены, а на обороте заделаны разрывы и дыры. Они заткнули дыры новым пергаментом и зашили бумагой из тутового волокна, смазанной рисовой пастой.Стаут и Эрлих отметили наличие цветных носителей на некоторых подписях, включая подпись Хэнкока.

Наиболее заметными изменениями после их обработки были исправление и закрепление порванного верхнего правого угла и заполнение близлежащих отверстий в коже, что помогло как физически, так и визуально интегрировать документ и сделать его менее уязвимым для будущих разрывов.

 

Новый вид дисплея

И последнее путешествие

Реагируя на проблемы с насекомыми в витринах и колебаниями относительной влажности, Библиотека Конгресса обратилась в Национальное бюро стандартов (NBS) с просьбой разработать герметичные корпуса для защиты Декларации и Конституции.

Полученные корпуса были дальновидными и современными для 1950-х годов. Они включили свободно плавающий кусок стекла, лежащий на пергаменте, чтобы он оставался плоским, с атмосферой увлажненного гелия, чтобы предотвратить появление насекомых и порчу. Оглядываясь назад, можно сказать, что вес стекла, лежащего непосредственно на документе, вероятно, сжал плотные выпуклые выступы на пергаменте.

Президенты Герберт Гувер и Франклин Д.Рузвельт заявил о своем намерении разместить Декларацию и Конституцию в Национальном архиве, и здание Национального архива было построено в 1930-х годах со специальной святыней в Ротонде для демонстрации наших учредительных документов. Только в декабре 1952 года — после многих лет обсуждений и переговоров — документы были переданы из Библиотеки Конгресса для постоянной экспозиции вместе с Биллем о правах в Национальный архив.

В течение 50 лет кожухи NBS превосходно выполняли двойную задачу обеспечения сохранности и обеспечения доступа.Однако с ростом знаний о методах отображения и материаловедении, включая опасения по поводу износа стекла, лежащего непосредственно на пергаменте, к началу 2000-х годов пришло время для нового подхода.

 

Новый корпус

Для нового века

Возможность спроектировать и изготовить новые корпуса, отражающие текущую практику консервации, появилась в 1990-х годах, когда планировалось отремонтировать здание Национального архива.Декларация и другие хартии были изъяты из экспозиции в 2001 году, но сотрудники Национального архива в сотрудничестве с коллегами из Национального института стандартов и технологий (NIST, преемник NBS) и другими экспертами уже приступили к разработке новых корпусов.

В 2002 году авторы этой статьи открыли корпус NBS и вынули Декларацию, выставив ее на воздух впервые за десятилетия. После тщательного осмотра наша команда зафиксировала его состояние в письменных заметках и отчетах, а также с помощью многочисленных фотографий.Мы использовали эту оценку состояния в качестве основы для разработки плана лечения, чтобы стабилизировать Декларацию для нового тысячелетия.

Экспертиза показала, что Декларация является физическим свидетельством многолетнего обращения, скручивания, складывания, выставления на свет, копирования и монтажа для выставки. На протяжении десятилетий чернила впитывались в пергамент, отслаивались во время обращения с документом и его прокатки и удалялись во время процессов копирования методом мокрого переноса, используемых для создания факсимиле.

В результате остается мало оригинальных чернил. Повреждение и потеря чернил заставили кого-то в прошлом улучшить некоторые подписи, в первую очередь жирный отчетливый почерк Джона Хэнкока.

Исправления и заделки, выполненные в 1942 году, все еще были в безопасности, что привело к решению 2002 года принять эту работу и оставить ее на месте. Одна большая потеря края ниже правого верхнего угла была заполнена японской бумагой, чтобы создать более устойчивый край.Мы заметили ряд ранее незадокументированных небольших Y-образных проколов по краям, которые, предположительно, были сделаны для того, чтобы закрепить пергамент в оправе в начале его истории. Поверхность пергамента была аккуратно очищена только по краям, но старая грязь осталась.

Не было предпринято никаких попыток уменьшить отпечаток руки, который прочно укоренился в пергаменте и теперь является частью истории Декларации, хотя его происхождение неизвестно. Пергамент уже был относительно плоским, и испорченное состояние кожи поддержало решение пассивно расплющить его под легким весом, не вводя влагу или влажность.

Мы использовали обработку 1942 года, но использовали легкое прикосновение, чтобы обеспечить дополнительную стабильность разрывов и потерь краев без существенного изменения внешнего вида документа.

 

Хранение пергамента

Квартира: вызов

Поскольку пергамент реагирует на изменения влажности, расширяясь, сжимаясь и скручиваясь, его трудно удерживать ровно в выставочном шкафу или в рамке.

За годы выставления в Патентном ведомстве Декларация сохранила небольшие Y-образные проколы по краям. По-видимому, они были сделаны для шнуровки креплений для струн, чтобы края оставались плоскими и на месте. Дырочки видны по низу и справа там, где края пергамента сильно загрязнены и не обрезаны.

Декларация, должно быть, была в новой рамке, когда отправлялась на выставку столетия в Филадельфии, так как она больше не была с комиссией Вашингтона.По возвращении в библиотеку Государственного департамента он был выставлен вертикально, вероятно, за счет плотного прижатия к стеклу корпуса, до 1894 года. Затем Декларация и Конституция были зажаты между тяжелыми стеклами, чтобы они оставались относительно плоскими в дубовых рамах для хранения. . Позже в Библиотеке Конгресса Декларация была прикреплена к подставке с помощью клея, нанесенного на оборотную сторону по всем четырем краям.

На протяжении многих лет применялись различные методы, чтобы сохранить пергамент плоским для демонстрации, и каждый из них в той или иной степени влиял на состояние документа.Вес тяжелого стекла сжал и разгладил существующие складки и извитости. Крепления для шнурков по краям кожи сохраняли натяжение пергамента, но оставляли проколы. Клей, нанесенный по краям документа, привел к разрывам пергамента, когда он сжался и оторвался от держателя.

В отличие от этого, нынешний метод крепления Декларации отошел от традиции попыток контролировать этот живой материал и использовал мягкое сдерживание без клея: язычки из полиэфирной пленки по краям слегка нажимали, чтобы прикрепить пергамент к его платформе. Этот метод монтажа, наряду с контролируемой относительной влажностью, предназначен для сведения к минимуму физического движения пергамента и сохранения его плоского состояния, но при этом он может прогибаться, если пергамент сжимается.

 

слов привели к факсимиле. . .

И, Тогда . . . к фотографиям

Фотография — наиболее часто используемый сегодня инструмент для записи и передачи информации о состоянии объекта.Прежде чем реставраторы обработают важные документы или картины, они делают серию фотографий, чтобы задокументировать состояние.

Однако первые 63 года существования Декларации фотографии не существовало. Поэтому люди использовали слова, чтобы описать состояние документа. Ричард Раш в 1818 году заявил, что документ свидетельствует о последствиях «руки времени». Что именно он имел в виду? Без подробного описания сложно сказать. Ясно то, что беспокойство по поводу физического состояния документа привело к созданию факсимиле, как для защиты оригинала, так и для распространения содержания документа по всей стране.

Внимательно изучив ранние фотографии Декларации, можно проследить ее состояние с течением времени.

 

Фотография как доказательство;

Тайна отпечатка руки

Сегодня документ выглядит иначе, чем на подробной фотографии 1903 года; некоторые изменения незаметны, другие более поразительны.На фотографии 1903 года, а также на коллотипе Гедни 1883 года и фотографии 1898 года Ladies Home Journal показан документ, несмотря на некоторое уменьшение чернил, с полностью разборчивым текстом, без пятен воды и линий прилива. Подписи более уменьшены, но все подписи, видимые на каменной гравюре, присутствуют в правильно выровненных колонках.

Сегодня, внимательно рассмотрев левый нижний угол Декларации, вы увидите отчетливое изображение отпечатка руки, впервые отмеченное в 1940 году, которого нет на фотографии 1903 года.Тайна отпечатка руки — как он появился, когда и кем — до сих пор не разгадана.

Также замечаются линии прилива, размытость и общая потеря разборчивости многих слов в тексте. Еще одно существенное изменение — в разделе подписи. Некоторые подписи, такие как подпись Джона Хэнкока, были улучшены, а другие были переписаны, чтобы сделать их более заметными. Показательно, что на фотографии 1903 года не видно ни отпечатка руки, ни линий прилива, ни размытого и неразборчивого чернильного текста, ни изменений в подписях.Ранние фотографии доказывают, что определяющий ущерб, который сделал Декларацию такой, какой она является сегодня, не был результатом копирования или чрезмерной демонстрации в 19 веке, а был нанесен в 20 веке.

В 1922 году Библиотека Конгресса попросила Хэнди сфотографировать Декларацию, чтобы задокументировать ее состояние при получении. Но, несмотря на многочисленные усилия, начиная с усилий Вернера Клэппа из Библиотеки Конгресса в 1940-х годах, никому не удалось найти работу Хэнди 1922 года.Эта фотография будет иметь ключевое значение для отслеживания изменений в Декларации и того, когда они произошли.

Клапп, однако, преуспел в своих усилиях в 1940-х годах восстановить программу регулярного фотографирования Декларации. Фотографии, сделанные в Библиотеке Конгресса в 1940, 1941 и 1942 годах, документируют первую современную реставрацию Декларации.

Между 1903 годом, когда Государственный департамент заказал фотографии для комитета Национальной академии наук, и 1940 годом кто-то, имевший доступ к документу, предпринял решительные шаги, которые значительно изменили документ.На сегодняшний день не было найдено никаких современных письменных документов, описывающих то, что можно описать только как искажение — пусть даже непреднамеренное — Декларации.

 

Хартия Америки

И Рука Времени

Так что же говорит нам этот поток слов, копий, фотографий и, главное, сама Декларация, когда мы смотрим на нее сегодня?

Безусловно, Декларация очень понравилась американскому народу.Его перенесли, чтобы уберечь от войн. Он был скопирован, а затем выставлен на всеобщее обозрение. Но методы, используемые для обеспечения безопасности и доступности, иногда сказывались на пергаменте и чернилах.

Тайны сохраняются.

Многие связывают поврежденное состояние Декларации с чрезмерным воздействием света во время длительной выставки в старом патентном ведомстве (ныне Национальная портретная галерея). Но легкое выцветание привело бы к равномерному выцветанию в целом, а вместо этого чернила уменьшились неравномерно, гораздо больше в некоторых центральных местах, чем по краям.

На фотографии Л. К. Хэнди 1903 года не видно ни отпечатка руки, ни линий прилива, которые другие приписывают процессу копирования методом влажного переноса. Но в протоколах обследования Стаута и Эрлиха 1942 года упоминаются эти особенности, которые также хорошо видны на фотографиях, сделанных в 1940 году, а затем в 1942 году во время лечения в Форт-Ноксе.

Что-то произошло с Декларацией между 1903 и 1940 годами, что не было задокументировано или еще не раскрыто.Будущие исследования могут ответить на эти вопросы. Это похоже на головоломку, в которой некоторые части (или фотографии) отсутствуют и могут появиться.

Тем временем Декларация независимости находится в Ротонде Национального архива, сохраненная и сохранная для будущих поколений. Слова и намерение сохраняются, даже если физический объект демонстрирует эффекты «руки времени».

 

Авторы

Кэтрин Николсон была заместителем начальника отдела консервации в Национальном архиве, а Мэри Линн Ритценталер была начальником отдела консервации. Оба сейчас на пенсии, они работали в команде реставраторов, которые изучали и обрабатывали Декларацию независимости, Конституцию и Билль о правах, а также входили в группу дизайнеров нынешних корпусов.

 

Чтобы узнать больше о

 

 

Как фотография с другого конца света зажгла историю любви, охватившую весь континент

(CNN) — Это были первые месяцы пандемии Covid-19, и Реджи Ларош, застрявший в своей квартире во Флориде, изо всех сил пытается оставаться оптимистом.

Когда Ларош работал на телевидении, он объехал весь земной шар. Теперь он был прикован к тем же четырем стенам, не зная, что его ждет в будущем.

Группа была создана Барбарой Дуриау из Амстердама в марте того года, когда ограничения Covid впервые ударили по Европе.

Участникам было предложено загружать фотографии видов из своих домов, сопровождаемые кратким описанием того, что они могли видеть, где они были и как они себя чувствовали.

Когда Ларош обнаружил группу, это было похоже на проблеск света в темноте.

«Эта страница была создана, чтобы дать людям надежду», — сказал он сегодня CNN Travel. «Я обнаружил, что просматриваю все фотографии и просто на мгновение чувствую, что снова путешествую».

Когда Ларош обнаружил «Вид из моего окна», это было в мае 2020 года. У него было три месяца снимков окна, которые он мог пролистать. Он мог любоваться снежными пейзажами Швейцарии, видами с крыш домов Италии и обширными пейзажами Новой Зеландии.

Но одна фотография особенно привлекла его внимание.Недавний снимок, сделанный с парадного крыльца: голубое небо, еще голубее море в обрамлении пышной зелени.

Оно было загружено кем-то по имени Кэти Антуан, которая подписала его местоположением: Пунаауйя, Таити, Французская Полинезия. Антуан писал, что это был вид из ее домашнего офиса на остров Морреа. Она добавила, что с таким видом работать из дома не так уж и плохо.

В прошлом году Ларош провел некоторое время на Таити и влюбился в этот остров. Фотография Антуана вернула его обратно в ту поездку.

«Мне тут же вспомнилась красота этого места, люди, которых я встретил, еда и все остальное», — говорит он сейчас.

Он снова и снова возвращался к фотографии.

«Меня сразу же потянуло к этому», — говорит он.

Он был так увлечен этой сценой, что просто лайкнуть фото было недостаточно. Он составил сообщение этому незнакомцу.

«Мне очень понравилась твоя фотография», — написал он и отправил ей запрос на добавление в друзья.

Кэти Антуан опубликовала эту фотографию вида из своего окна на Таити в мае 2020 года, привлекая внимание жителя Флориды Реджи Лароша.

Предоставлено Реджи Ларош и Кэти Антуан

На другом конце света Кэти Антуан перехватила сообщение Реджи Ларош и подумала, как ответить.

Сначала подруга указала ей на «Вид из моего окна», и Антуан сразу же присоединился к группе в Facebook.

«Мне понравилась идея дать другим людям надежду и дать другим людям возможность увидеть другой взгляд, отличный от их взгляда», — говорит Антуан CNN Travel сегодня.

Ее вдохновило загрузить собственное фото, и она была рада, когда ее мнение вызвало резонанс, получив около 15 000 лайков.

Затем появилось сообщение на Facebook от Лароша.

Хотя Антуан оценил его просьбу, она ответила, что не будет добавлять его в друзья на Facebook.

«Я вежливо отказался, потому что обычно не принимаю незнакомцев», — говорит сегодня Антуан.

Но она не удалила запрос. И в последующие месяцы Facebook продолжал напоминать ей о Реджи Лароше, рассылая напоминания и предлагая его как «кого-то, кого вы, возможно, знаете».

Часто, когда Антуан получала эти уведомления, она проверяла профиль Лароша на Facebook.Его настройки означали, что она могла видеть его фотографии и сообщения, даже если они не были официально связаны.

Всякий раз, когда она видела последние обновления Антуана, она была заинтригована.

«Мне очень понравилась чувствительность фотографий, которые он размещал», — говорит она сегодня. «На самом деле многие вещи могли быть моими сообщениями».

Почти год спустя, в апреле 2021 года, Антуан с опозданием принял предложение Лароша в друзья. Уведомление Facebook снова появилось, и она решила нажать кнопку «Принять».В тот момент он уже не казался незнакомцем, как год назад.

Что касается Лароша, то Кэти Антуан и ее потрясающий таитянский вид ушли из его памяти. Когда он получил уведомление о том, что она приняла его запрос на добавление в друзья, он был сбит с толку и задался вопросом, была ли она кем-то, кого он встретил во время своей поездки на Таити в 2019 году.

Он пролистал ее страницу в поисках подсказок, потом увидел ее фотографию того вида, с горами, морем и небом. Это щелкнуло — она была женщиной из «Вид из моего окна».»

Теперь официально друзья на Facebook, Ларош и Антуан начали лайкать и комментировать посты друг друга, время от времени отправляя сообщения.

Связь с Калифорнией

Антуан прожила на Таити большую часть своей жизни, но у нее есть дом в южной Калифорнии, и с наступлением лета 2021 года путешествие из Французской Полинезии в США казалось быть на картах впервые за долгое время, поэтому Антуан начал планировать поездку в Штаты.

Она написала Ларошу и, узнав, что он будет в Лос-Анджелесе примерно в то же время, предложила встретиться, пока она там.

Ларкоэ была единственной из знакомых Антуана на Facebook, с которой она никогда не встречалась лично, и она чувствовала, что должна это исправить.

Она также думала, что будет весело завести нового друга, и, судя по их общению в социальных сетях, она была уверена, что у нее все получится с Ларошем.

Анотин и Ларош впервые встретились в отеле Manchester Grand Hyatt в заливе Сан-Диего в августе 2021 года.

Антуан говорит, что она не нервничала, так как у нее не было особых ожиданий. Ларош говорит, что у него был некоторый трепет, в основном потому, что он так привык к взаимодействию в Zoom, и идея личной встречи с кем-то новым казалась немного сюрреалистичной.

Ларош ждал в вестибюле отеля, высматривая Антуана. Когда подъехал внедорожник с тонированными стеклами, он подумал, не увидит ли он, что в отель заселится знаменитый гость.

Когда машина тронулась с места, он понял, что машина действительно высадилась из-под Антуана — с другом на буксире.

Группа поздоровалась. Антуан и Ларош говорят, что сразу почувствовали себя непринужденно.

«Мы сразу же стали лучшими друзьями», — говорит Ларош. «У нас начался разговор, я чувствовал себя с ней совершенно комфортно».

После этих первых представлений Ларош, Антуан и друг Антуана направились в центр Сан-Диего. Они проверили исторический корабль USS Midway, прежде чем вместе поужинать.

Блуждая по городу, Ларош и Антуан болтали о своей жизни и чувствовали, как их мгновенная связь укрепляется, хотя они не были уверены, куда она приведет.

«Я чувствовал, что только что встретил кого-то очень особенного», — говорит Ларош. «Но я еще не думал, что это будут отношения, я не думал об этом».

На следующий день Ларош и Антуан снова встретились — на этот раз без друга Антуана.

За мексиканской едой, а позже, когда они бродили по улицам Сан-Диего, их разговор продолжился, и их связь углубилась.

«Это было действительно потрясающее чувство человека, которого вы только что встретили, и вы чувствуете, что знаете этого человека уже давно», — говорит Антуан.

Что-то изменилось, и они оба это почувствовали.

«Я поймал себя на том, что совершенно естественно держу ее за руку, — говорит Ларош.

На следующий день Ларош должен был вылететь из Калифорнии, но отложил свой рейс. Антуан пригласил его поехать с ней в ее дом в Палм-Спрингс.

Через несколько дней Антуану снова пришлось отложить свой полет. Остаток пребывания Антуана в США они провели вместе.

«Меня влекло к нему, к его душе», — говорит сегодня Антуан.

«Это быстро, очень быстро переросло в нечто большее, чем просто дружба, потому что была душевная связь, которая была действительно удивительной.»

Когда пришло время Антуану лететь обратно на Таити, они оба знали, что сделают все возможное, чтобы снова увидеться как можно скорее.

И действительно, всего несколько недель спустя Ларош летела на Таити.

Трансформационная встреча

Реджи Ларош и Кэти Антуан теперь пара.

Предоставлено Реджи Ларош и Кэти Антуан

Прошлой осенью они провели вместе большую часть времени во Французской Полинезии, и гибкий график работы Лароша позволял ему работать оттуда.

«За такой короткий период времени произошло преображение, красота», — говорит он об их отношениях до сих пор.

Их связь, говорят они, основана на глубоком уважении друг к другу.

«Реджи — фантастический человек, он так много знает — он путешествовал по миру», — говорит Антуан.«Он очень сильный человек, но в то же время чувствительный и очень скромный».

«У меня такое ощущение, что я путешествовал по семи морям и искал с кем разделить жизнь, и вот я нашел ее, и все это время она пряталась на маленьком островке посреди южной части Тихого океана, — говорит Ларош.

Барбара Дурио, создательница «Вид из моего окна», говорит, что история Лароша и Антуана — это то, что делает группу Facebook, которую она создала, такой особенной.

Это сообщество, в настоящее время насчитывающее более двух миллионов членов, основано на «сочувствии, доброте, доброжелательности, мечте и побеге», — рассказывает она CNN Travel.

Дурио также благодарен за то, что создал что-то обнадеживающее в темное время. «Границы были закрыты, окна и мысли открыты», — так она выразилась.

В последние месяцы Дюрио самостоятельно опубликовал две книги, в которых собраны некоторые выдающиеся посты и истории из сообщества «Вид из моего окна».

Ей всегда нравилось рассматривать фотографии, говорит Дюрио, но главное, что скрывается за ними.

«Больше всего меня трогают истории, стоящие за фотографиями. Они смешные или трогательные, а от некоторых у вас мурашки по коже», — говорит она.

«За каждой фотографией стоит история обычного человека, его видение жизни. Это всего лишь маленький уголок мира одного человека, который находит свое место в большой картине, которой является планета.»

Помимо романа Лароша и Антуана, Дюрио говорит, что через группу сформировались и другие дружеские отношения и связи на разных континентах.

Ее вторая книга заканчивается историей американского участника «Вид из моего окна», который был вдохновлен на то, чтобы нарисовать вид, загруженный французом в Дордони, Франция, и летом 2021 года лично встретился с ним во время отпуска во Франции.

Дурио надеется, что больше людей в сообществе смогут встретиться, когда позволят обстоятельства, и планирует выставку «Вид из моего окна» в Брюсселе в 2022 году.

Что касается будущего Лароша и Антуана, они надеются разделить свое время между США и Таити.

На данный момент работа Лароша позволяет ему путешествовать, поэтому пара в основном проводит время вместе на Таити. В будущем они говорят, что хотели бы исследовать мир вместе.

Но вид из окна Антуана в Пунаауйе всегда будет иметь особое значение для них обоих.

В ноябре 2021 года Ларош опубликовал свою фотографию вида в группе Facebook, на этот раз с заходящим солнцем над океаном.

«Когда я был на Таити, однажды утром я выглянул и увидел тот же вид, который свел нас вместе более полутора лет назад», — говорит он сейчас. «И я просто подумал, как я счастлив, что такая простая вещь, как пост, теперь принесла мне столько радости и счастья».

Верхнее фото предоставлено Реджи Ларош и Кэти Антуан

7 инструментов, которые помогут вам создавать потрясающие коллажи в Instagram

Если вы следите за последними тенденциями в социальных сетях, скорее всего, вы сделали коллаж в Instagram.Нет, мы не говорим о бумаге, ножницах и клее. Вспомните девятку лучших в Instagram. Или мем «LinkedIn, Instagram, Facebook, Twitter».

Но бренды использовали эту искусную художественную форму не только для создания мемов. Коллажи Instagram могут объединять несколько фотографий, чтобы продемонстрировать разные ракурсы и характеристики продукта — или даже снимки до и после. Добавьте рамки и границы для подведения итогов мероприятия в стиле записок. Или соберите несколько штук для руководств по подаркам и сезонных досок настроения.

Все это и многое другое можно сделать без обрезков бумаги и суперклея. Ассортимент бесплатных приложений для создания коллажей в Instagram упрощает обрезку и укладку.

Ну что, чувствуешь себя неважно? Читайте советы, приемы и инструменты, необходимые для того, чтобы сделать коллажи частью вашей бизнес-стратегии в Instagram.

Загрузите бесплатный пакет из 72 настраиваемых шаблонов Instagram Stories прямо сейчас . Экономьте время и выглядите профессионально, стильно продвигая свой бренд.

Как сделать коллаж в Instagram

Выполните следующие действия, чтобы узнать, как сделать коллаж из постов и историй в Instagram.

Подача

Вот как сделать коллаж из поста в Instagram:

1. Загрузите и откройте Layout.
2. Нажмите на изображения, которые вы хотите добавить. Вы можете выбрать до девяти. Рядом с каждым выбранным изображением появится галочка.

3. Выберите нужный макет в верхней части экрана.
4. Нажмите на любое изображение, чтобы отредактировать его. Используйте синие ручки для изменения размера.
5. Отразите или переверните каждое изображение в соответствии с желаемым результатом.
6. Добавьте границы, если хотите.
7. Нажмите «Сохранить».
8. Поделитесь в Instagram или сохраните в фотопленку.

Совет: Instagram Layout предлагает только основные функции редактирования. Если ваши фотографии требуют доработки, сначала отредактируйте их и сохраните в фотопленку.

Истории

Вот как сделать коллаж в Instagram Stories. Язык может немного отличаться в зависимости от используемого вами устройства.

1. Откройте Instagram.
2. Коснитесь значка камеры в верхнем левом углу или проведите пальцем вправо.
3. Сделать снимок.

4. Откройте инструмент «Перо». Это значок волнистой линии, второй справа вверху.
5. Выберите цвет фона. Нажмите и удерживайте изображение, пока цвет не заполнит изображение. Хит готово.

6. Покиньте Instagram и перейдите к фотопленке.
7. Выберите фотографию, которую хотите добавить, и нажмите «Копировать».

8. Откройте Instagram и дождитесь появления Добавить стикер . Коснитесь его и поместите в нужное место.

9. Повторяйте, пока не добавите все фотографии, которые планируете включить. Добавляйте рисунки, наклейки, текст или теги.

10. Поделиться.

Все еще новичок в Instagram Stories? Вот как их использовать.

Советы по созданию коллажей в Instagram

Преобразите свою социальную игру с помощью этих советов по созданию коллажей в Instagram.

Начните с концепции

Все коллажи в Instagram должны создаваться целенаправленно. Не делайте коллажи просто так.

И они должны вписываться в ваш общий маркетинговый план в Instagram.

Прежде чем приступить к его созданию, подумайте, почему коллаж лучше, чем пост с одним изображением, карусель или другой вариант.

Ваш ответ приведет к вашей концепции коллажа. Вот несколько примеров для начала:

Использование разделенного экрана для демонстрации нескольких вариантов

Покажите новую коллекцию, модельный ряд или варианты продукции

Поощряйте обратную связь и участие

Создание пошаговых инструкций, инструкций до и после

Использование нескольких визуальных элементов для создания повествования

Выберите правильное сочетание изображений

Хороший коллаж в Instagram никогда не должен подавлять зрителя.Выбор, который вы делаете, всегда должен быть направлен на то, чтобы максимально четко передать сообщение или идею.

В некоторых случаях требуется большой объем, например, чтобы передать размер или разнообразие сообщества. В остальное время используйте изображения экономно и намеренно.

Придерживайтесь простых визуальных образов, имеющих четкую направленность. Изображения, которые слишком детализированы или уменьшены, теряют эффект при объединении с другими и уменьшении размера.

Избегайте конфликтов цветов, создав дополнительную палитру.Если это невозможно, попробуйте добавить оттенки или обработку, чтобы фотографии соответствовали друг другу.

Когда ничего не помогает или для поднятия настроения, используйте черно-белое изображение.

Освежите свои навыки работы с визуальным контентом с помощью этих 12 советов.

Создайте свой коллаж

Иногда простое сочетание изображений — это все, что вам нужно. Но бывают случаи, когда требуется еще немного «жужа». И есть несколько способов поднять свой коллаж на ступеньку выше.

Вот несколько примеров: от рамок из винтажной пленки до цветов и эффектной графики.

Рамки могут придать серии фотографий ностальгическую атмосферу или эффект фотобудки. Они также могут внести порядок и ясность в мешанину изображений.

Текстуры и формы могут добавить размерности и целостности.

Узоры могут добавить изюминку и интригу к серии изображений.

Текстовые поля могут охватывать все, от информации о продукте до положительных комментариев.

Добавить наклейки и бирки

Наклейки и теги делают ваши истории и публикации в Instagram привлекательными и привлекательными для покупок.И коллажи не исключение. В лучшем случае коллажи могут даже открыть новые способы использования этих функций.

Если на вашем коллаже несколько инфлюенсеров, партнеров или поклонников, обязательно отметьте их. Это может привлечь больше внимания к вашей публикации или кампании.

Для коллажей с руководствами по подаркам, сводками новостей или несколькими продуктами метки для покупок позволяют людям больше узнать о предмете, который привлекает их внимание. Instagram позволяет вам отмечать до пяти продуктов на пост, так что используйте его по максимуму.На данный момент в Stories можно добавить только одну наклейку продукта.

Бренды очень эффектно использовали стикеры в коллажах Instagram Story. Французский ювелирный дизайнер Луиза Дамас использует наклейку для опроса, чтобы узнать, какие украшения нравятся людям больше всего. Netflix использует его, чтобы зрители могли проголосовать за самых одетых участников The Circle .

Смешайте это с мультимедиа

коллажа Instagram могут объединять изображения, видео, музыку и текст в одном посте.

Однако сделать это хорошо может быть непросто. Посты со слишком большим количеством медиа могут показаться беспорядочными или хаотичными.

Все сводится к сильной концепции и четкому посылу.

Dove использует коллаж, чтобы разрушить стереотипы о красоте с помощью сетки меняющихся портретов. Обратите внимание, как меняется только одно изображение в каждом кадре, причем со скоростью, позволяющей зрителям воспринимать все целиком.

Серия

Coachella «вам может понравиться» сочетает визуальные эффекты с видео, чтобы предоставить снимки и звуковые фрагменты артистов, которые могут понравиться ее подписчикам.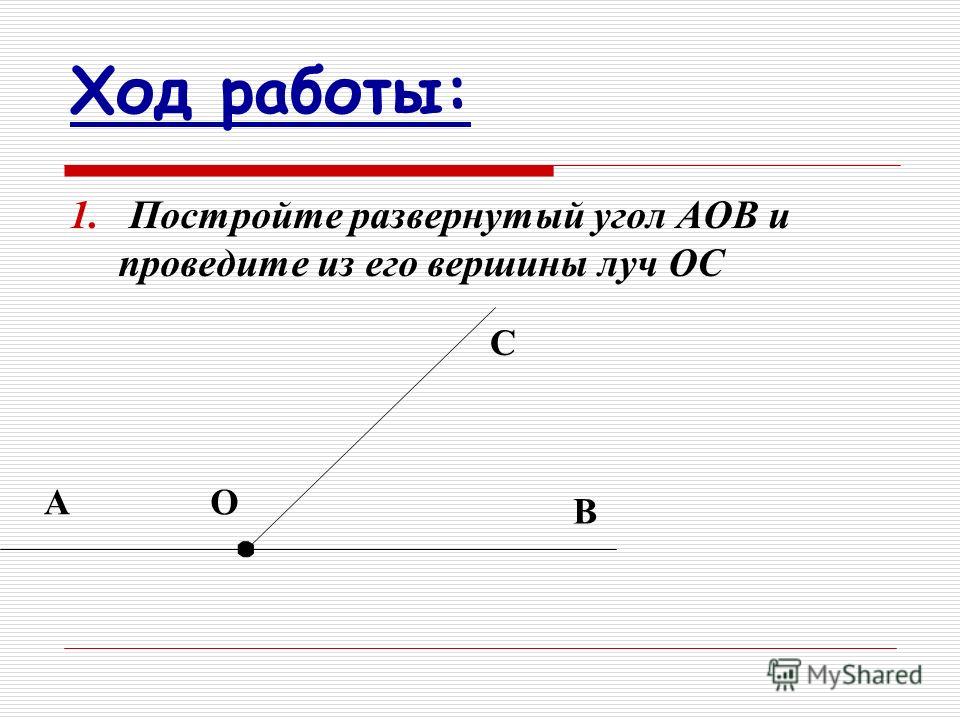 Структура кампании очень гладкая и понятная.

Попробуйте продвинутые техники коллажа

Коллажи могут быть хорошим способом втиснуть все в один пост. Но нет причин ограничивать себя одним. Превратите коллаж из Instagram в карусель с несколькими постами или историю. Или распространите его по своей ленте.

Узнайте, как из отдельных изображений сделать одно большое, и другие лайфхаки для Instagram.

Не забывайте об эстетике корма

Технически ваша лента в Instagram уже представляет собой коллаж из каждого опубликованного вами поста.Добавление поста-коллажа в микс может показаться занятным, если только вы не подходите к этому стратегически.

Убедитесь, что ваш коллаж в Instagram соответствует эстетике вашей ленты. Если вы часто используете определенные фильтры или пресеты Instagram, коллаж не должен быть исключением. Используйте его и в коллаже.

Планируйте заранее с помощью календаря контента, такого как Hootsuite Planner, чтобы вы могли увидеть, как коллаж будет выглядеть рядом с другим контентом, прежде чем публиковать.

То, что вы потратили больше времени на коллаж, не означает, что вы должны тратить меньше времени на что-то другое.Перед публикацией помните о сигналах ранжирования алгоритма Instagram.

7 приложений для создания коллажей в Instagram

Используйте эти приложения для создания коллажей в Instagram, чтобы ускорить рабочий процесс и добавить изюминку.

1. Компоновка

Как официальное приложение для создания коллажей в Instagram, Layout удовлетворит ваши основные потребности в создании коллажей.

Добавьте до девяти фотографий и расположите их в разных макетах. Сохраняйте сообщения в виде квадратов, что означает, что они хороши для сетки, но не всегда идеально подходят для коллажей Instagram Story.

Для редактирования фотографий и более красивых шаблонов ознакомьтесь с вариантами ниже.

Скачать: iOS и Android

2. Разложить

Unfold — одно из самых популярных приложений для создания коллажей в Instagram. На самом деле приложение настолько популярно, что такие бренды, как Tommy Hilfiger, даже создали на платформе фирменные шаблоны.

Доступно множество настраиваемых параметров как для постов, так и для Instagram Stories. И регулярно добавляются новые макеты для особых событий или трендов.Его можно использовать бесплатно, но ежемесячные подписчики имеют доступ к более широкому набору наклеек, шрифтов и функций.

Скачать: iOS и Android

3. Дизайнерский комплект

Набор для дизайна A Design Kit от создателей A Color Story и Filmm предлагает создателям набор и кучу бесплатных инструментов для создания коллажей в Instagram. Эти шаблоны, кисти и наклейки кажутся милыми и хитрыми, они становятся яркими и игривыми.

Этот инструмент хорош для постов и историй, с ежемесячной подпиской.

Скачать: iOS

4. Сторилюкс

Как следует из названия, это приложение для создания коллажей в Instagram специализируется на формате Story. Доступно более 570 фото- и видеошаблонов с фонами, фильтрами, брендингом и инструментами стилизации. Доступен для бесплатной или ежемесячной подписки.

Скачать: iOS

5. Моджо

Mojo позиционирует себя как редактор видеоисторий для Instagram. Ежемесячно в библиотеку из более чем 100 шаблонов добавляются новые шаблоны и шрифты.Каждый из них на 100% редактируется, поэтому вы можете брендировать и адаптировать его по своему усмотрению. Вы случайно сняли видео в пейзаже? Без проблем. У создателей Mojo есть несколько исправлений для общей проблемы с ориентацией видео.

Скачать: iOS и Android

6. SCRL

Имея доступ к более чем 30 000 фотобиблиотеке Unsplash, SCRL позволяет легко создавать слои коллажей в Instagram. Эти стоковые фотографии могут повысить ценность вашего контента без больших затрат.

Это приложение особенно хорошо подходит для панорамных каруселей.Другими словами, вы можете использовать его инструменты, чтобы развернуть коллаж из серии постов. Это популярный подход к составлению капсул гардероба, обзоров событий и концепций повествования.

Скачать: iOS

7. Магисто

Magisto — видеоредактор, позволяющий создавать видеоколлажи или слайд-шоу из фотографий. Бесплатное приложение включает в себя тематические шаблоны, доступ к музыкальной библиотеке, а также фильтры, эффекты и исправления стабилизации.

Планы

Professional и Business предлагают доступ к обширной фото- и видеобиблиотеке.

Скачать: iOS и Android

Ищете другие приложения для Instagram? Вот 17, которые выведут ваши посты на новый уровень.

Экономьте время, управляя своим присутствием в Instagram, используя Hootsuite. С единой панели управления вы можете планировать и публиковать публикации непосредственно в Instagram, привлекать аудиторию, измерять эффективность и запускать все свои другие профили в социальных сетях.