Построение функций, содержащих модуль.
Построение графика квадратичной функции, содержащий знак модуля.
Абсолютной величиной (модулем) неотрицательного числа называется само это число, абсолютной величиной отрицательного числа называется противоположное ему положительное число.
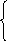 Х, если Х≥0
Х, если Х≥0
|X|=
-Х, если Х<0
График функции с модулем можно построить стандартным способом и способом преобразования симметрии относительно оси ОХ или оси ОУ.
Для построения графиков квадратичных функций, содержащих знак модуля стандартным способом, как и при решении уравнений, сначала находят корни выражений, стоящих под знаком модуля. В результате ось Ох разбивается на промежутки. Убираем знаки модуля, беря каждое выражение в каждом промежутке с определённым знаком,
которые находим методом интервалов. В каждом промежутке получается функция без знака модуля. Строим график каждой функции в каждом промежутке.
Для построения графиков функций вида у = ах2 + в|х| + с, у = |ах2 + вх + с|,
у =|ах2 + в|х| + с| воспользуемся способом симметричного отображения. Рассмотрим это на конкретных примерах.
Пример 1.
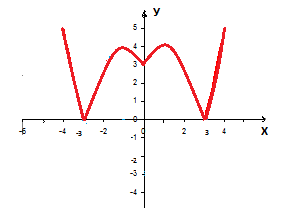
Функция у = |х2 — 2х — 3|
1 шаг.
Строим график функции y=x2-2x-3.
Вершина параболы:
хо= 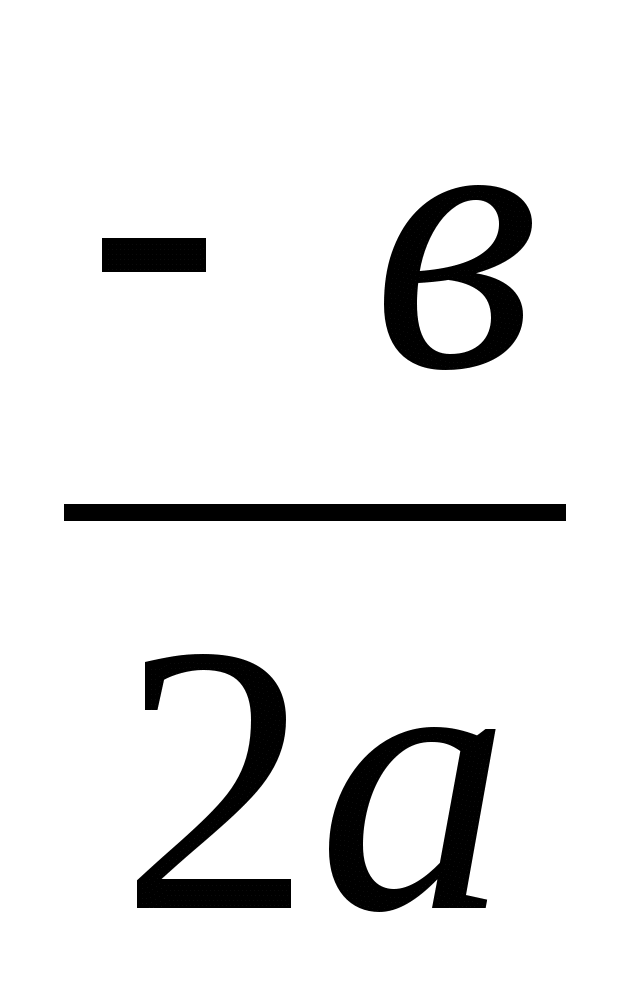 =1, уо
=1, уо
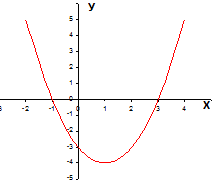 =-1, х2=3.
=-1, х2=3.2 шаг.
Часть графика, которая расположена под осью ОХ, симметрично отображаем относительно оси абсцисс.
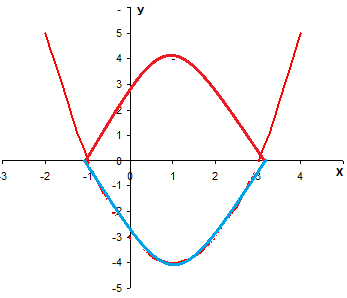
3 шаг.
Нижнюю часть графика удаляем.
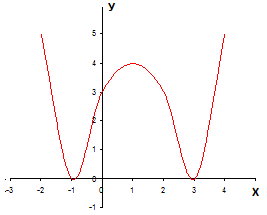
.
Пример 2.
Функция y=x2-2|x|-3
1 шаг.
Строим график функции y=x2-2x-3.
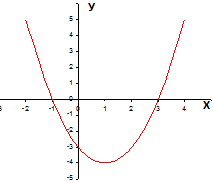
2 шаг.
Часть графика, расположенную на правой полуплоскости симметрично отображаем относительно оси ОУ.
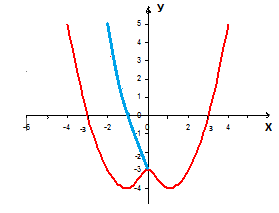
Получаем следующий график функции y=x2-2|x|-3.
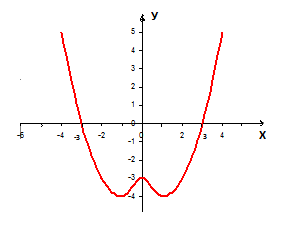
Пример 3.
Функция у =|х2 — 2|х| — с|
1 шаг.
Строим график функции y=x2-2x-3.

2 шаг.
Часть графика, расположенную на правой полуплоскости симметрично отображаем относительно оси ОУ. Это будет графиком функции y=x2-2|x|-3.

3 шаг.
Часть графика, которая расположена под осью ОХ, симметрично отображаем относительно оси абсцисс.
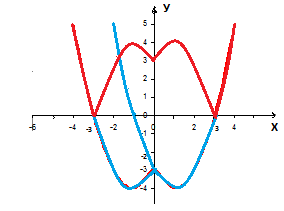
Получается график функции у =|ах2 + в|х| + с|.
.
infourok.ru
Алгоритм построения графиков функций содержащих модуль
Инфоурок › Алгебра ›Презентации›Алгоритм построения графиков функций содержащих модуль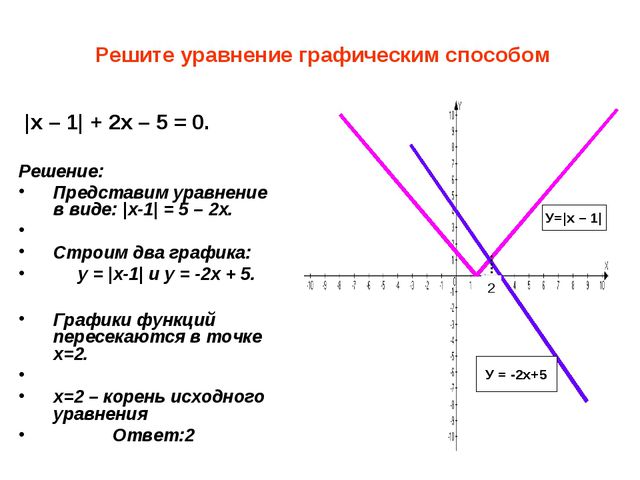
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:Решите уравнение графическим способом |x – 1| + 2x – 5 = 0. Решение: Представим уравнение в виде: |x-1| = 5 – 2x. Строим два графика: у = |x-1| и у = -2х + 5. Графики функций пересекаются в точке х=2. х=2 – корень исходного уравнения Ответ:2 У=|x – 1| У = -2х+5 2
2 слайд Описание слайда:
Описание слайда:Построение графиков вида |y| = f (x) Алгоритм построения графика: 1.Построить график функции y=f(x) для тех х из области определения, при которых f(x)≥ 0 2. Отразить полученную часть графика симметрично относительно оси абсцисс. Построить график функции |у| =1-х. Y=1- x
 Описание слайда:
Описание слайда:Построение графика функции у = f (|x|) Алгоритм построения графиков функции у = f (|x|): 1. Построить график функции f (x). 2. При х ≥ 0 график сохраняется, а при х < 0 полученная часть графика отображается симметрично относительно оси ОУ.
4 слайд Описание слайда:
Описание слайда:Построение графика функции у = f (|x|) Y=f (|x|) Y=f (x)
5 слайд Описание слайда:
Описание слайда:Построить график функции у = | x — 2 | Построение а) Строим график функции у = х -2. б) График нижней полуплоскости отображаем вверх симметрично относительно оси ОХ. Y = x — 2 Y = | x-2 |
6 слайд
Построить график функции 1.Строим график функции 2. График функции получаем из графика отображением симметрично относительно оси ОХ части графика, расположенной ниже оси ОХ.
7 слайд Описание слайда:
Описание слайда:Построить график функции у = 2|x| — 2 Построение. а) Строим график функции у = 2х – 2 для х>0. б) Достраиваем его левую часть для х<0, симметрично построенной относительно оси ОУ. Y=2x — 2 Y=2|x| — 2
8 слайд Описание слайда:
Описание слайда:Построение графиков вида |y| = |f (x)| Алгоритм построения: Строим график функции у = f (x). Часть графика f (x)< 0, симметрично отображаем относительно оси ОХ. Полученный график симметрично отражаем относительно оси ОХ. 1 способ |y| = |1-x | 2 способ Y=1-x Y=|1-x| |y|=|x-1|
9 слайд Описание слайда:
Описание слайда:Построение графика функции y=|f (x)| Алгоритм построения графиков функции y = |f(x)|: 1. Строим график функции f (x). 2. Часть графика, лежащая над осью ОХ, сохраняется, часть его, лежащая под осью ОХ, отображается симметрично относительно оси ОХ Y=f (x) Y=|f (x)| Y=|f (x)|
 Описание слайда:
Описание слайда:Построение графика функции y = |f (x)| Y= f (x) Y=| f (x) |
11 слайд Описание слайда:
Описание слайда:Построить график функции 1.Построить график функции 2. График функции .получаем из графика отражением симметрично оси ОУ части графика при х ≥ 0
12 слайд Описание слайда:
Описание слайда:Решить уравнение |x+6|=|x+2| графическим способом 1 способ. Используя стандартный алгоритм. Ответ: -2 2 способ. Решаем, опираясь на геометрические соображения. На равном расстоянии от точек -6 и 2 лежит единственная точка х =-2 Ответ: -2 Графическое решение Ответ: -2 Y=|x-2| Y=|x+6| -2

Курс профессиональной переподготовки
Учитель математики

Курс повышения квалификации
Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДВ-167843
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарийinfourok.ru
Открытый урок по теме «Показательная функция. Функционально-графические методы решений уравнений и неравенств»
Цель: рассмотреть задачи Единого государственного экзамена базового, повышенного и высокого уровня сложности с применением функционально- графических методов на примере показательной функции у = ах, а>1, а0.
Задачи урока:
- повторить свойство монотонности показательной функции;
- свойство ограниченности показательной функции;
- повторить определение абсолютной величины; работа с графиками, содержащими модуль;
- ввести понятие сложной функции; рассмотреть графики сложной функции и их область значений;
Оборудование: презентация графиков функций, подготовленная с применением графической программы “Advanced Grapher”.
Ход урока:
1. Вступительное слово учителя.
Слайд 0. Показательная функция. “Функционально — графические методы решения уравнений и неравенств”
Функционально — графический метод основан на использовании графических иллюстраций, применении свойств функции и позволяет решать многие задачи математики.
Сегодня мы рассмотрим задачи Единого государственного экзамена базового, повышенного и высокого уровня сложности с применением функционально- графических методов на примере показательной функции у = ах, а>1, а0. С помощью графической “Advanced Grapher” выполним иллюстрации ко всем задачам.
Слайд 0а. Почему так важно знать свойства показательной функции?.
- По закону показательной функции размножалось бы все живое на Земле, если бы для этого имелись благоприятные условия, т.е. не было естественных врагов и было вдоволь пищи. Доказательство тому – распространение в Австралии кроликов, которых там не было раньше. Достаточно было выпустить пару особей, как через некоторое время их потомство стало национальным бедствием.
- В природе, технике и экономике встречаются многочисленные процессы, в ходе которых значение величины меняется в одно и то же число раз, т.е. по закону показательной функции. Эти процессы называются процессами органического роста или органического затухания.
- Например, рост бактерий в идеальных условиях соответствует процессу органического роста; радиоактивный распад веществ – процессу органического затухания.
- Законам органического роста подчиняется рост вклада в Сберегательном банке, восстановление гемоглобина в крови у донора или раненого, потерявшего много крови.
2. Актуализация знаний учащихся.
Группа А.
На первом этапе урока устно по готовым чертежам повторим свойства показательной функции:
- определение по графику функции соответствующей формулы;
- свойство монотонности показательной функции;
- свойство ограниченности показательной функции;
Слайд 1. Определить вид графика (устная работа 5 минут). На рисунке изображены графики показательных функций. Соотнесите график функции с формулой.
Рисунок1.
Рисунок2.
Рисунок3.
Рисунок4.
Слайд 2. Свойство монотонности показательной функции (устная работа 2 минуты).
Назовите функцию, возрастающую (убывающую) на множестве действительных чисел. Соотнесите график с соответствующей формулой
Рисунок5.
Рисунок6.
При 1<а<0 показательная функция возрастает.
При а>0 показательная функция убывает.
Слайд 3. Свойство ограниченности показательной функции (устная работа 2 минуты).
Укажите множество значений функции.
Рисунок7.
Графические методы дают возможность решать неравенства, содержащие разные функции.
Слайд 4. Решить графически неравенство.
Что можно сказать про графики функций и график функции у=12 — 1,5х?
(График показательной функции лежит выше функции, записанной в правой части уравнения).
>12 — 1,5х
Рисунок8.
Ответ: х>2. О
Рисунок9.
Oтвет: х>0.
2. Показательная функция содержит знак модуля в показателе степени.
Группа В – это комбинированные задачи. Рассмотрим задачи, содержащие абсолютную величину (модуль).
Повторим определение модуля.
(запись на доске)
Слайд 5. Укажите множество значений функции (5 минут).
Сделать записи в тетради:
1).
2).
Графическая иллюстрация представлена на слайде 5. Объяснить, как построены графики.
Рисунок10.
Е(у)=[1;
Рисунок11.
Е(у)=(0;1]
3. Нахождение области значений сложной функции.
Слайд 6.
Достаточно непросто определять область значений сложных функций.
Определим, что такое сложная функция. Если функция f ставит в соответствие числу х число у, а функция g – числу у число z, то говорят что h есть сложная функция, составленная из функции g и f и пишут h=g(f(x)).
При этом D(h) является E(f) или его частью D(h)E(f).
Слайд 7. Используя умение строить график квадратичной функции, определите последовательно координаты вершины параболы, найдите область значений.
, — вершина параболы.
Рисунок12.
Рисунок13.
Вопрос: определите характер монотонности функции.
Показательная функция у = 16t возрастает, так как 16>1 .
При наименьшем значении показателя функции
.
Е(у)=[2;.
График иллюстрирует наш вывод.
Рисунок14.
Вопрос: определите характер монотонности функции.
Показательная функция у = убывает, так как <1.
При наименьшем значении показателя функции
. Е(у)=(0;].
График иллюстрирует наш вывод.
4. Решение графически систем уравнений, содержащих показательную функцию.
Слайд 8. Найти значение выражения х+ у,если (х;у) является решением системы уравнений.
Решение:
-параллельный перенос на 1 единицу влево.
- параллельный перенос на 2 единицы влево.
х=-1, у=1
х+ у=0.
Рисунок15.
Ответ: 0.
5. Решение уравнений, содержащих параметры.
Наиболее сложные задания содержатся в группе С.
Слайд 9. Найдите все значения р, при которых уравнение
имеет единственный корень.
Решение:
Пусть 3х=t, t>0.
3t (3t2-6t) + 9t – 5 = p.
Введем функцию f(t) = 9t3 -18t2 + 9t – 5.
Исследуем функцию с помощью производной и построим ее график.
f ‘(x) =27t2 – 36t + 9.
Найдем стационарные точки: f ‘(x)=0.
27t2 – 36t + 9 = 0.
3t2 – 4t + 1 = 0.
t1=1, t2=.
f()=9=-2+3-5=,
f(1)=9-18+9-5= — 5.
График функции f(t) = 9t3 -18t2 + 9t – 5 изображен на рисунке. Уравнение имеет 1 корень при р = -5 и р> .
Рисунок16.
Графическая иллюстрация решения выполнена с использованием программы “Advanced Grapher”.
Рисунок17.
Слайд 10.
Домашнее задание:
1).
2).
3).Найдите все значения р, при которых уравнение
имеет ровно два корня.
6. Самостоятельная работа (при наличии времени).
Решить графически неравенство.
1).. Ответ: (-;2].
2). . Ответ: (-1;0)
7. Итоги урока
По мере изучения курса алгебры постоянно возрастает применение функционально-графических методов, что позволяет быстро и красиво решать многие уравнения и неравенства Единого Государственного экзамена.
urok.1sept.ru
Графики функций, содержащих модуль

Иоганн Бернулли

Цели урока:
- общеобразовательные: обеспечить повторение, обобщение и систематизацию знаний по теме «Графики функций, содержащие знак модуля»; создать условия контроля усвоения знаний и умений.
- развивающие: способствовать формированию умений применять приёмы обобщения, сравнения, выделения главного; развитию математического кругозора, мышления, речи, внимания, памяти.
- воспитательные: содействовать воспитанию интереса к математике, активности, организованности, формировать положительную мотивацию учения, развивать учебно-познавательную деятельность, коммуникативность.


- Область определения функции y= ( x² + 3x – 4) × | x – 7 |
x – 7
a) x ≥ 0 ; б) х – любое число; в) х ≠ -7; х ≠ 7; г) х ≠ 7.

- Область определения функции y= ( x² + 3x – 4) × | x – 7 |
x – 7
a) x ≥ 0 ; б) х – любое число; в) х ≠ -7; х ≠ 7; г) х ≠ 7.

- Область определения функции y= ( x² + 3x – 4) × | x – 7 |
x – 7
a) x ≥ 0 ; б) х – любое число; в) х ≠ -7; х ≠ 7; г) х ≠ 7.
2. Функция y = x² — 10x +21 имеет нули
а) 7; 3 б) -7; 3 в) 7; -3 г) -7; -3.

- Область определения функции y= ( x² + 3x – 4) × | x – 7 |
x – 7
a) x ≥ 0 ; б) х – любое число; в) х ≠ -7; х ≠ 7; г) х ≠ 7.
2. Функция y = x² — 10x +21 имеет нули
а) 7; 3 б) -7; 3 в) 7; -3 г) -7; -3.

- Область определения функции y= ( x² + 3x – 4) × | x – 7 |
x – 7
a) x ≥ 0 ; б) х – любое число; в) х ≠ -7; х ≠ 7; г) х ≠ 7.
2. Функция y = x² — 10x +21 имеет нули
а) 7; 3 б) -7; 3 в) 7; -3 г) -7; -3.
- Вершиной параболы y= x² — 4x – 5 является точка
а) (2; 9) б) ( -2; 9) в) ( 2; -9) г) ( -2; -9).

- Область определения функции y= ( x² + 3x – 4) × | x – 7 |
x – 7
a) x ≥ 0 ; б) х – любое число; в) х ≠ -7; х ≠ 7; г) х ≠ 7.
2. Функция y = x² — 10x +21 имеет нули
а) 7; 3 б) -7; 3 в) 7; -3 г) -7; -3.
- Вершиной параболы y= x² — 4x – 5 является точка
а) (2; 9) б) ( -2; 9) в) ( 2; -9) г) ( -2; -9).

4. График функции y = |x – 3| изображён на рисунке
а) б)
в) г)

4. График функции y = |x – 3| изображён на рисунке
а) б)
в) г)

5. Упростить выражение √ х² + 8х + 16
а) упростить нельзя; б) √ (х + 4)² ; в) х + 4 г) | x + 4 | .

5. Упростить выражение √ х² + 8х + 16
а) упростить нельзя; б) √ (х + 4)² ; в) х + 4 г) | x + 4 | .

5. Упростить выражение √ х² + 8х + 16
а) упростить нельзя; б) √ (х + 4)² ; в) х + 4 г) | x + 4 | .
6. Нулями подмодульных выражений для функции
y= |3x-6| + 2|x+1| — ½ |7x+21| являются числа
а) 3; -1; 2 б) -3; -1; 2 в) -2; -½; 3 г) -3; -½; 2.

1. Устная работа.
5. Упростить выражение √ х² + 8х + 16
а) упростить нельзя; б) √ (х + 4)² ; в) х + 4 г) | x + 4 | .
6. Нулями подмодульных выражений для функции
y= |3x-6| + 2|x+1| — ½ |7x+21| являются числа
а) 3; -1; 2 б) -3; -1; 2 в) -2; -½; 3 г) -3; -½; 2.

5. Упростить выражение √ х² + 8х + 16
а) упростить нельзя; б) √ (х + 4)² ; в) х + 4 г) | x + 4 | .
6. Нулями подмодульных выражений для функции
y= |3x-6| + 2|x+1| — ½ |7x+21| являются числа
а) 3; -1; 2 б) -3; -1; 2 в) -2; -½; 3 г) -3; -½; 2.
7. Сколько точек пересечения имеют графики функций
y= x²+4x-3 и y= 9 .
а) 1; б) 3; в) ни одной; г) 2.

5. Упростить выражение √ х² + 8х + 16
а) упростить нельзя; б) √ (х + 4)² ; в) х + 4 г) | x + 4 | .
6. Нулями подмодульных выражений для функции
y= |3x-6| + 2|x+1| — ½ |7x+21| являются числа
а) 3; -1; 2 б) -3; -1; 2 в) -2; -½; 3 г) -3; -½; 2.
7. Сколько точек пересечения имеют графики функций
y= x²+4x-3 и y= 9 .
а) 1; б) 3; в) ни одной; г) 2.

5. Упростить выражение √ х² + 8х + 16
а) упростить нельзя; б) √ (х + 4)² ; в) х + 4 г) | x + 4 | .
6. Нулями подмодульных выражений для функции
y= |3x-6| + 2|x+1| — ½ |7x+21| являются числа
а) 3; -1; 2 б) -3; -1; 2 в) -2; -½; 3 г) -3; -½; 2.
7. Сколько точек пересечения имеют графики функций
y= x²+4x-3 и y= 9 .
а) 1; б) 3; в) ни одной; г) 2.
8. Множество значений функции y= 8-x² .
а) (- ∞ ; 8 ] б) (8; +∞) в) ( — ∞; 8) г) [ 8; + ∞).

5. Упростить выражение √ х² + 8х + 16
а) упростить нельзя; б) √ (х + 4)² ; в) х + 4 г) | x + 4 | .
6. Нулями подмодульных выражений для функции
y= |3x-6| + 2|x+1| — ½ |7x+21| являются числа
а) 3; -1; 2 б) -3; -1; 2 в) -2; -½; 3 г) -3; -½; 2.
7. Сколько точек пересечения имеют графики функций
y= x²+4x-3 и y= 9 .
а) 1; б) 3; в) ни одной; г) 2.
8. Множество значений функции y= 8-x² .
а) (- ∞ ; 8 ] б) (8; +∞) в) ( — ∞; 8) г) [ 8; + ∞).

9. График функции y = f (|x|) получен из y = f (x)
а) при х ≥ 0 график остаётся без изменений;
б) при х ˂ 0 полученная часть графика отображается симметрично относительно оси 0 Y .
10. График функций y = |f(x)| получен из y = f(x) c ледующим образом
а) часть графика, лежащая выше оси ОХ сохраняется;
б) часть графика, лежащая ниже оси ОХ симметрично отображается относительно оси О X .




Леонард Эйлер

Найдите корень уравнения. 2 + √ х² +2х + 1 = 3х + 1
1. Свернуть подкоренное выражение по формулам сокращённого умножения.
2. Используя свойство √ а² = | a | , преобразовать уравнение.
3. Привести уравнение к виду | f(x) | = g (x).
4 . В одной системе координат построить графики функций
y=|f (x)|, y= g(x).
5 . Найти абсциссу точки пересечения графиков.

Николай Иванович Лобачевский

X € ( -2; 4)
Y=4
при х € [ 2; +∞)



Тип рассмотренных заданий
Понял хорошо.
1. Решение уравнений.
Вызывало затруднения.
2. Решение неравенств.
Требуется доработать.
3. Исследование функций.
4. Задачи с параметрами.


multiurok.ru
Урок по теме «Построение графиков квадратичной функции с модулем»

Урок по теме «Построение графиков квадратичной функции с модулем»
Учебник А.Г.Мордкович, базовый уровень, 4 — й урок темы «Функция y = ax 2 + bx + c, ее свойства и график»
Быкасов Андрей Иванович,
учитель математики НОУ «Нефтеюганская православная гимназия», г.Нефтеюганск, Тюменская область

Тема : «Построение графиков
квадратичной функции с модулем »
Цель: обобщить знание свойств квадратичной функции и научить применять свойства квадратичной функции при построении графиков квадратичной функции с модулем
Задачи:
- Выявить степень сформированности у учащихся понятия квадратичной функции, её свойств, особенностей её графика.
- Создать условия для формирования умения анализировать, сравнивать, классифицировать графики изученных функций.
- Продолжить развитие умения построения графиков квадратичной функции с модулем , используя программу AGrapher .
- Формировать умение сотрудничать, работая в группе.
Оборудование: проектор, экран , 4 компьютера, программа AGrapher .

Этапы урока
- Организационный
- Мотивация к учебной деятельности.
- Актуализация знаний и фиксация затруднения в пробном действии (работа с графиками функций).
- Выявление места и причины затруднения.
- Построение проекта выхода из затруднения.
- Реализация построенного проекта.
- Самостоятельная работа с самопроверкой по эталону.
- Включение в систему знаний и повторение.
- Рефлексия учебной деятельности. Оценивание работы на уроке.
- Домашнее задание.

1. Организационный
На перемене дети садятся по группам. Группы формируются
на добровольной основе, консультант группы определяется
учителем. Каждой группе выдаются листы контроля
результатов деятельности.
Здравствуйте, ребята! Я рада сегодня вас видеть и очень надеюсь на совместную плодотворную работу. Сегодня мы работаем в группах. В каждой группе мною был назначен консультант, который поможет мне оценить в конце урока каждого из вас. В течение всего урока мы будем накапливать баллы: за каждый правильный, точный и логичный ответ Вы будете получать «+» в таблице, лежащей на вашем столе. Здесь мне будет нужна помощь консультантов. В конце урока мы просуммируем «+» и поставим отметки в зависимости от их количества:
более 8 «+»- «5»
6-7 «+»- «4»
4-5 «+»- «3».

2. Мотивация к учебной деятельности . Задача этапа: Создать условия для возникновения у ученика внутренней потребности включения в учебную деятельность.
Если вы хотите научиться плавать, то смело
входите в воду, а если хотите научиться
решать задачи, то решайте их!
Дьёрдь Пойя
Сегодня нам предстоит решение многих задач, вы видите, как можно научится их решению по мнению известного венгерского математика Д.Пойя. Согласны ли вы, что такой подход применим и к нашему уроку?( Да )
Для начала предлагаю вспомнить, что мы знаем о функциях.

За каждое выполненное задание, консультант выставляет «+» в лист контроля (максимум 4 балла)
3 . Актуализация знаний и фиксация затруднения в пробном действии.
1 группа
Запишите формулы и названия функций, которые вы видите на графиках. (Каждые 2 правильно записанные формулы оцениваются «+», максимум 4 балла).
Постройте графики функций:
4 группа
2 группа
Постройте графики функций:
№ 1
№ 2
№ 3
№ 4 .
№ 1
№ 2
№ 3
№ 4
3 группа
Постройте графики функций:
№ 1.
№ 2.
№ 3. №4.
2. 1Актуализация знаний и фиксация з1атруднения в пр№1обном действии.

Задание для первой группы
График №1
График №2
График №3
График №5
График №4

Задание для первой группы
График №6
График №7
График №8

Проверка
1группа
- № 1
- № 2
- № 3
- № 4
- № 5
- № 6
- № 7
- № 8
За каждое правильно выполненные 2 задания, консультант выставляет «+» в лист контроля

Проверка
График №1
График № 3
2группа
График №2
График № 4
За каждое правильно выполненное задание, консультант выставляет «+» в лист контроля

Проверка
3 группа
График №2
График №3
График №4
График №1
За каждое правильно выполненное задание, консультант выставляет «+» в лист контроля

Проверка
4 группа
График №1
График №3
График №2
График №4
За каждое правильно выполненное задание, консультант выставляет «+» в лист контроля

3 . Актуализация знаний и фиксация затруднения в пробном действии.
- Повторим определение модуля
- Как получаем из функции можно получить функцию ?
- Постройте графики функций
За каждое правильно выполненное задание, консультант выставляет «+» в лист контроля
3 . Актуализация знаний и фиксация затруднения
в пробном действии.
1 . Организовать актуализацию изученных способов действий, достаточных для построения нового знания.
2. Зафиксировать актуализированные способы действий в речи.
3. Зафиксировать актуализированные способы действий в знаках (эталонах).
Графики каких функций вам знакомы ?( линейная, прямой и обратной пропорциональности, квадратичная, у = )
Как по графику определить вид функции и её формулу? (уметь пользоваться правилами параллельных переносов вдоль осей Ох,Оу, уметь определять коэффициенты, оси симметрии и асимптоты)
Формулы для каких графиков функций вы не смогли определить? Почему?
(последние формулы видим впервые, поэтому не можем определить вид функции и как строить графики)
Давайте попробуем сформулировать цель нашего урока .
(Научиться строить графики нового вида, научиться узнавать их среди других графиков функций, описывать их свойства.)
А я добавлю к вашей цели еще одну: обобщить знание свойств квадратичной функции и научиться применять свойства квадратичной функции в построении графиков с модулем.

Тема урока
«Построение графиков
квадратичной функции с модулем»

4.Построение проекта выхода из затруднения.
- Построим графики квадратичных функций с модулем
- Выполнив практическую работу, сделаем вывод о свойствах графика
и

5. Реализация построенного проекта.
1.Организовать построение нового способа на примере, вызвавшем затруднение. 2.Организовать фиксацию нового способа действия в речи и с помощью эталона.
3. Зафиксировать преодоление возникшего ранее затруднения.
Каждой группе предлагается построить график одной функции в программе AGrapher , описать её свойства по алгоритму:
1
2



6 .Организовать фиксацию нового способа действия в речи и с помощью эталона.
а) Давайте обобщим способы построения графиков функций, в которых выражение, задающее функцию, находится под знаком модуля, в единый алгоритм (строим график функции без модуля, потом часть графика, находящаяся ниже оси Ох, отображается в верхнюю полуплоскость)
б) Давайте обобщим способы построения графиков функций, в которых аргумент находится под знаком модуля, в единый алгоритм. (строим график функции без модуля, потом часть графика, находящаяся правее оси Оу, отображается в левую полуплоскость)
На основании какого математического понятия мы получаем эти новые способы действия ? (На основании определения модуля выражения)
Сравним полученный нами алгоритм с эталоном .
За каждый правильный ответ, консультант выставляет «+» в лист контроля.

6. Алгоритм построения графика квадратичной функции вида (эталон)
1.Строим график функции у = f (х).
2.Часть графика, для которой, значения функции положительны — оставляем без изменения.
3.Часть графика, для которой, значения функции отрицательны – зеркально отображаем в верхнюю полуплоскость.

Алгоритм построения графика квадратичной функции вида (эталон)
1.Строим график функции у = f (х).
2.Часть графика, для которой, значения аргумента положительны — оставляем без изменения.
3.Часть графика, для которой, значения аргумента положительны – зеркально отображаем в левую полуплоскость.

7 . Самостоятельная работа с самопроверкой по эталону.
Каждой группе выдается задание на построение графиков функций
1 группа
2 группа
3 группа
4 группа
За правильно выполненное задание, консультант выставляет «+» в лист контроля

8. Включение в систему знаний и повторение.
Как построить график квадратичной функции с модулем .(проговаривают алгоритмы)
Графики каких функций мы можем построить с учетом нового знания, полученного сегодня на уроке? (перечисляют функции)

8. Включение в систему знаний и повторение.
Построить графики функций

8. Включение в систему знаний и повторение. (проверка)
1 . 2. 3.
4. 5.

9. Подведение итогов, рефлексия
- Просуммируем «+» и поставим отметки в зависимости от их количества:
более 8 «+» — «5»
6-7 «+» — «4»
4-5 «+» — «3».
В листе контроля укажите, как вы оцениваете свои достижения поставленных целей на этом уроке
1. Затрудняюсь в построении графика без помощи алгоритма
2. Могу построить строить графики функций с модулями
3. Я все понял и могу объяснить другим

10. Домашнее задание
1. Затрудняюсь в построении графика без помощи алгоритма
Выучить определение модуля. Построить графики функций:
2. Могу построить строить графики функций с модулями
3. Я все понял и могу объяснить другим
Самоанализ урока
Тема урока. «Построение графиков квадратичной функции с модулем».
Цель урока: обобщить знание свойств квадратичной функции и научить применять её свойства в п остроении графиков квадратичной функции с модулем.
Урок четвертый в теме «Функция y = ax 2 + bx + c , ее свойства и график».
Цель урока р
multiurok.ru