График обратной пропорциональности | Алгебра
График обратной пропорциональности — функции
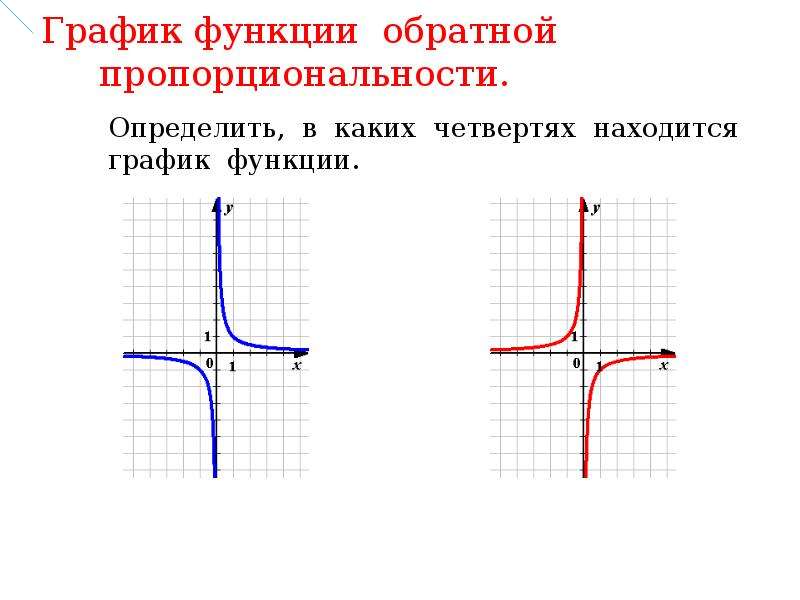
— гипербола. При k>0 ветви гиперболы расположены в I и III координатных четвертях, при k<0 — во II и IV.
Как построить график обратной пропорциональности? Для этого достаточно определить несколько точек гиперболы. Удобно брать те значения x, на которые удобно делить k.
Рассмотрим построение графика обратной пропорциональности на конкретных примерах.
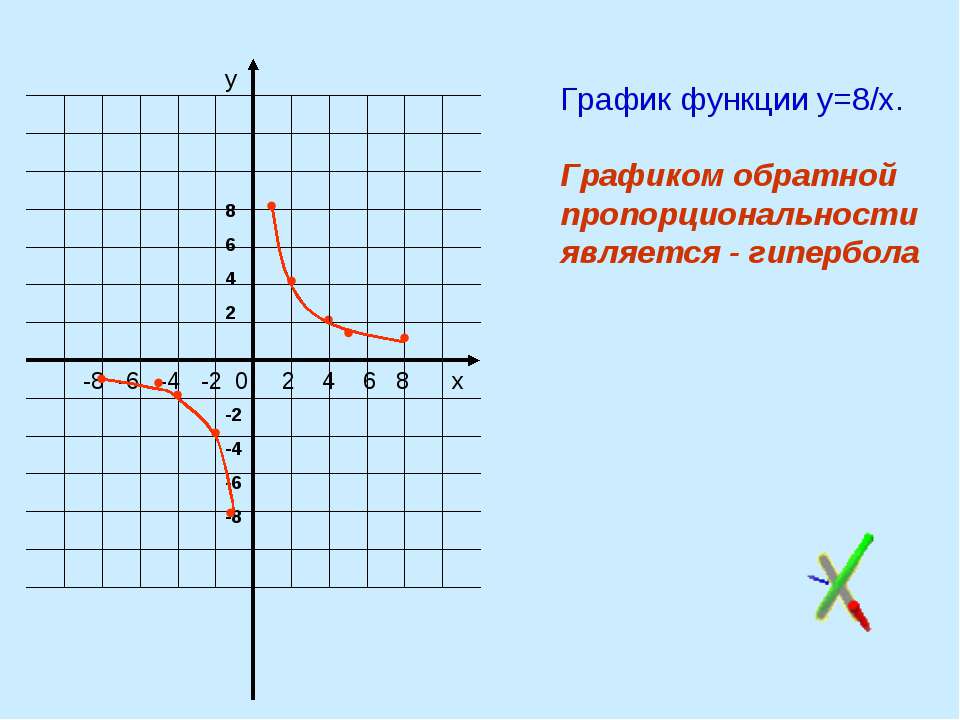
Эта функция — обратная пропорциональность. Её график — гипербола, ветви которой расположены в I и III координатных четвертях. Для построения гиперболы выберем значения x, на которые удобно делить 8: -8; -4; -2; -1; 1; 2; 4; 8. Подставляя их в формулу вместо x, находим соответствующие значения y:
Таким образом, нашли 8 точек с координатами
(-8;-1), (-4; -2), (-2; -4), (-1; -8), (1; 8), (2; 4), (4; 2) и (8; 1).
На практике эти вычисления оформляют в виде таблицы — в верхнюю строчку записывают выбранные значения x, в нижнюю — y, полученные при подстановке соответствующего значения x в формулу функции.
Полученные точки отмечаем на координатной плоскости:
Затем через эти точки проводим две ветви гиперболы:
Важно!
Оси Ox и Oy для гиперболы являются асимптотами. Это означает, что ветви гиперболы на бесконечности приближаются к осям, но никогда их не пересекут.
Для построения гиперболы можно брать только положительные значения x. Вторая ветвь гиперболы симметрична первой относительно точки O.
Эта функция — обратная пропорциональность. Её график — гипербола, ветви которой расположены во II и IV-й координатных четвертях. Для построения гиперболы составим таблицу:
Полученные точки отмечаем на координатной плоскости:
И строим график:
Функция обратной пропорциональности | Алгебра
Определение
Функция обратной пропорциональности — это функция, заданная формулой
где x — независимая переменная, k — число, отличное от нуля.
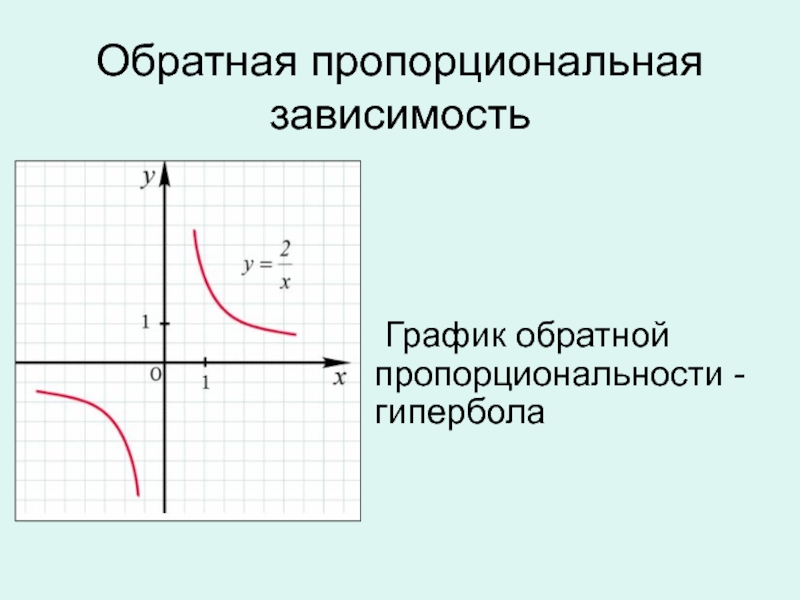
Графиком обратной пропорциональности является гипербола. Гипербола состоит из двух ветвей. (так называют две части графика).
Для построения гиперболы нужно знать несколько точек (больше точек — точнее график). Лучше выбирать те значения x, на которые удобно делить k.
Свойства функции обратной пропорциональности
1) Область определения обратной пропорциональности состоит из всех значений x, кроме нуля:
D: x∈(-∞;0) U (0;∞).
2) Область значений обратной пропорциональности — все значения y, кроме нуля:
E: y∈(-∞;0) U (0;∞).
3) Функция обратной пропорциональности не имеет нулей.
4) При k>0
ветви гиперболы расположены в I и III координатных четвертях:
Обратная пропорциональность убывает на каждом из промежутков области определения, то есть при x∈(-∞;0) U (0;∞).
Функция принимает положительные значения при x>0, или
y>0 при x∈ (0;∞).
Функция принимает отрицательные значения при x<0, или
y<0 при x∈(-∞;0).
При k<0
ветви гиперболы расположены вo II и IV координатных четвертях:
Обратная пропорциональность возрастает на каждом из промежутков области определения, то есть при x∈(-∞;0) U (0;∞).
Функция принимает положительные значения при x<0, или
y<0 при x∈(-∞;0).
Функция принимает отрицательные значения при x>0, или
y>0 при x∈ (0;∞).
Оси Ox и Oy для обратной пропорциональности являются асимптотами — прямыми, к которым ветви гиперболы неограниченно приближаются (но никогда их не достигнут).
В следующий раз на конкретных примерах рассмотрим, как строить график обратной пропорциональности.
Гипербола. Обратная пропорциональность 8 класс онлайн-подготовка на Ростелеком Лицей
114. Функция у = k/x и ее график
Обратная пропорциональность – это функциональная зависимость, при которой уменьшение либо увеличение в несколько раз независимой величины (аргумента) вызывает пропорциональное увеличение, либо уменьшение зависимой величины (функции).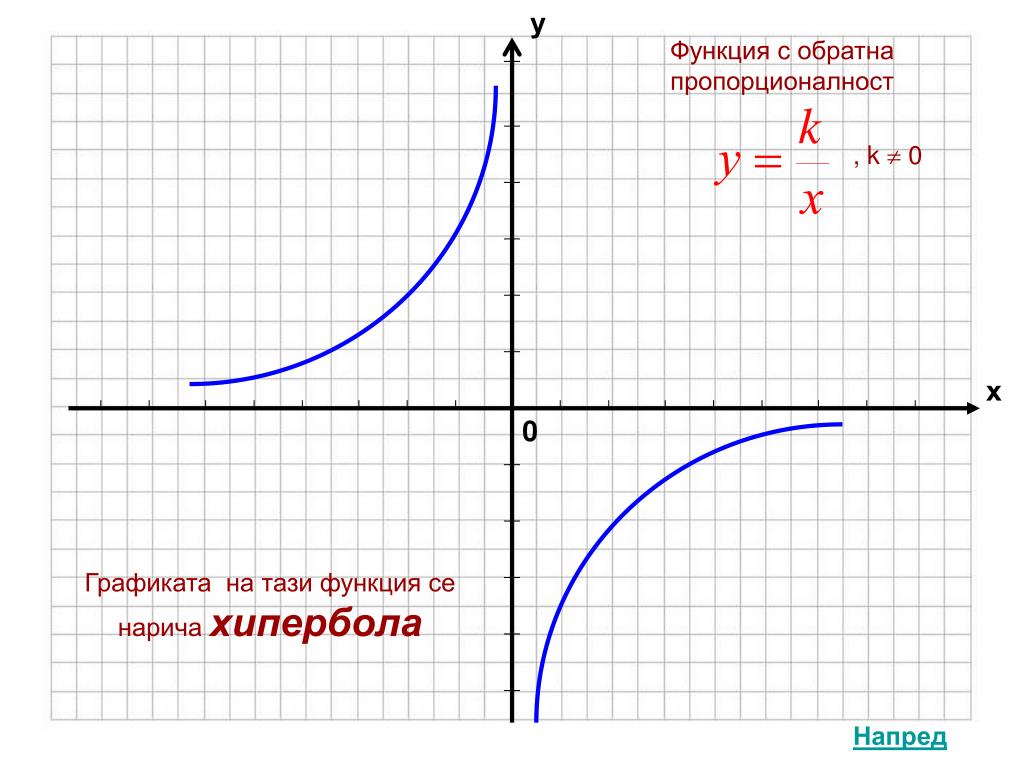
Обратной пропорциональностью называется функция, которую можно задать формулой вида y=kx, где х – независимая переменная, а k – любое число, k≠0.
Допустим, мы пришли в магазин за тетрадями. Тетради на прилавке и деньги в кошельке находятся в обратной пропорциональности. Т.е. чем больше мы купим тетрадей, тем меньше денег у нас останется.
Графиком функции является гипербола.
График функции при k>0:
Гипербола состоит из 2 частей: одна находится в I четверти, где значения X и Y положительные, а вторая часть – в III четверти, где значения X и Y отрицательные.
y(x)>0 при x∈(0;+∞)
y(x)<0 при x∈(-∞;0)
Если двигаться по одной ветви гиперболы от -∞ к 0, то мы замечаем, что функция убывает, если двигаться по другой ветви гиперболы от 0 до +∞, то мы снова видим, что функция убывает. Следовательно, функция y=kx, где k>0, убывает.
График функции при k<0:
Гипербола состоит из 2 частей: одна находится во 2 четверти, где значения X отрицательные, а значения Y положительные, а вторая часть – в 4 четверти, где значения X положительные, а значения Y отрицательные.
y(x)<0 при x∈(0;+∞)
y(x)>0 при x∈(-∞;0)
Если двигаться по одной ветви гиперболы от -∞ к 0, то мы замечаем, что функция возрастает, если двигаться по другой ветви гиперболы от 0 до +∞, то мы снова видим, что функция возрастает. Следовательно, функция y=kx, где k<0, возрастает.
Свойства функции:
-
Область определения функции:
D(f) = (-∞;0)∪(0;+∞).
-
Область значения функции:
E(f) = (-∞;0)∪(0;+∞).
-
Наибольшего и наименьшего значения функция y=kx не имеет.
-
y=kx нечетная функция, то есть график симметричен относительно начала координат (0;0).
-
Функция не ограничена.
-
Функция не пересекает координатные оси (OX и OY).
Если добавить константу а (где a любое число) в знаменатель в качестве слагаемого к X, то произойдет перемещение гиперболы по оси OX (вместе с вертикальной асимптотой).
В таком случае уравнением функции станет y=kx+a.
Если перед а стоит знак «+» (y=kx+a), a>0, то график функции передвигается по оси OX влево.
Для примера возьмем уравнение y=1x+2:
Гипербола смещена на 2 влево.
Если перед а стоит знак «–» (y=kx-a), a>0, то график функции передвигается по оси OX вправо.
Для примера возьмем уравнение y=1x-2:
Гипербола смещена на 2 вправо.
Если добавить константу b (где b любое число) к дроби в качестве слагаемого, то произойдет перемещение гиперболы по оси OY (вместе с горизонтальной асимптотой). В таком случае уравнением функции станет y=kx+b.
Если перед b стоит знак «+» (y=kx+b), b>0, то график функции передвигается по оси OY вверх.
Для примера возьмем уравнение y=1x+2:
Гипербола смещена на 2 вверх.
Если перед b стоит знак «-» (y=kx-b), b>0, то график функции передвигается по оси OY вниз.
Для примера возьмем уравнение y=1x-2
Гипербола смещена на 2 единицы вниз.
От коэффициента k зависит, как будут вести себя ветви гиперболы относительно начала координат.
Например, сравним y=10x и y=1x:
Мы видим, что график функции y=1x значительно уже графика функции y=10x.
Чем больше коэффициент k, тем больше расстояние между ветвями гиперболы.
Функция обратной пропорциональности и её график
2. Задачи, приводящие к понятию обратной пропорциональности.
Площадь прямоугольника со сторонамиx и y равна S. Выразите у через S и х.
1) Если
S 24 , то
24
у
х
3. Задачи, приводящие к понятию обратной пропорциональности.
Площадь прямоугольника со сторонами2) Если
S 6
, то
6
у
х
Как связаны между собой х и у?
4. Задачи, приводящие к понятию обратной пропорциональности.
 Пешеход путь S проходит со скоростью v
Пешеход путь S проходит со скоростью vза t часов. Выразите время пешехода
через путь и скорость.
1) Если
S 60 , то
60
t
v
5. Задачи, приводящие к понятию обратной пропорциональности.
Пешеход путь S проходит со скоростью vза t часов. Выразите время пешехода
через путь и скорость.
2) Если
S 3
, то
3
t
v
Как связаны между собой
скорость и время?
6. О п р е д е л е н и е.
Обратной пропорциональностьюназывается функция, которую
можно задавать формулой вида
где х – независимая переменная,
k – не равное нулю число.
7. Свойства функции
1х 0
Областью определения функции является
множество всех чисел, отличных от нуля.
2
k 0 у 0
Областью значений функции является
множество всех чисел, отличных от нуля.
8. График функции
Построим по точкам график функциигипербола
11. График функции
Построим по точкам график функциигипербола
14.
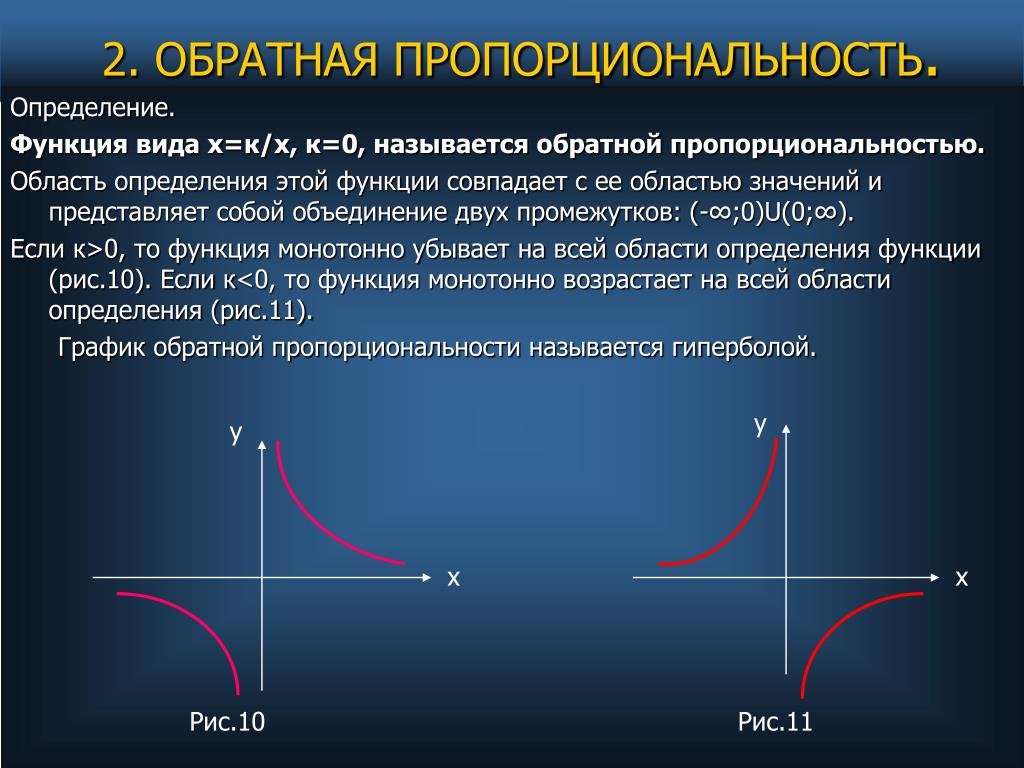 Особенности графиков. Симметричность
Особенности графиков. Симметричностьветвей графика
относительно (0; 0)
k>0
I, III четверти
15. Особенности графиков.
Симметричностьветвей графика
относительно (0; 0)
k
II, IV четверти
Задание №1
Укажите, какую из функций
можно назвать
обратной пропорциональностью:
х
у
3
3
у
х
у 3х
у х 3
у х
3
1
у
3х
Задание №2
Укажите среди графиков
гиперболу
Не верно
1
Подумай
Молодец!
2
3
Задание №3
Задайте функцию обратной
пропорциональности, если ее график
проходит через точку:
( 1; 3 )
х
у
k
3
1
k 3
Задание №3
Задайте функцию обратной
пропорциональности, если ее график
проходит через точку:
( 2; -6 )
( -12; 4 )
( 5; 0,5 )
Задание №4
Постройте график функции
Проверка
I, III четверти
Симметрично
Относительно
О (0; 0)
Задание №4
Постройте график функции
1) Значение у, соответствующее
значению х, равному 2; 4; -1; -4; -5
Проверка
х=2
у=4
х=4
у=2
х = -1 у = -8
х = -4 у = -2
х = -5 у = -1,6
Задание №4
Постройте график функции
Найдите по графику
значение у, соответствующее
значению х, равному 2; 4; -1; -4; -5
Найдите по графику:
значение х, которому соответствует
значение у, равное -4; -2; 8
Проверка
у = -4 х = -2
у = -2 х = -4
у=8
х=1
Обратная пропорциональность.
 График функции — презентация онлайн Функция
График функции — презентация онлайн Функцияk
у
x
,
её свойства и график.
Y
6
5
4
3
2
1
-5 -4 -3 -2 -1 0 1 2 3 4 5 6
-1
-2
-3
-4
-5
-6
Х
Y
6
5
4
3
2
1
-5 -4 -3 -2 -1 0 1 2 3 4 5 6
-1
-2
-3
-4
-5
-6
y=
k
x
— обратная
пропорциональность,
где k ≠ 0 – заданное число.
Графиком является гипербола
Построим график функции:
1
1
х
1 2 4 6
4
2
1
1
1
у
1
4 2
2
4
6
у
Гипербола
4
в I и III
Гипербола
3
координатных
симметрична
2
четвертях.
относительно
начала
-6
-4 -3 -2 -1 1
1
у
x
х 0
II
координат.
— — — — — — — — — — —
I
6х
0 -1 1 2 3 4
Ось х и ось у –
асимптоты
гиперболы.
-2
-3
-4
III
IV
Свойства функции У=
1.
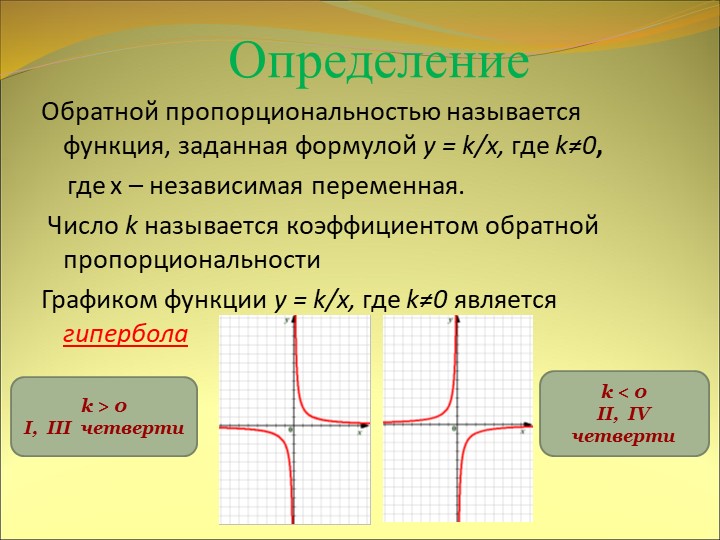
1.Область
D ( у ) ;0
к
х
0 ;
, где к>0 :
у
E ( у ) ; 0 0;
определения
2.
2.Область
значений
3. у>0, если х 0 ;
у
1
4. Функция
-3 -2 -1 0 1 2 3
убывает при
-1
х ; 0 0;
не ограничена
5. Функция
Ограниченность
ни сверху, ни снизу.
6. унаим.= НЕТ
унаиб.= НЕТ
7. Непрерывность
Претерпевает разрыв при х = 0.
х
Построим график функции:
1
1
х
1 2 4
4
2
1
1
у
4 2 1 2 4
у
Гипербола во
4
II и IV
3
координатных
2
четвертях.
11 2 3 4
-6
-4 -3 -2 -1 0
-1
-2
-3
-4
1
у
x
х 0
— — — — — -6
1
— — — — — -6
6
х
Свойства функции У=
1.
1.Область
D ( у ) ;0
к
х
0 ;
, где к
у
E ( у ) ; 0 0;
определения
2.
2.Область
значений
3.
 у>0, если х 0 ;
у>0, если х 0 ; у
1
4. Функция
-3 -2 -1 0 1 2 3
возрастает при
-1
х ; 0 0;
5. Функция
Ограниченность
не ограничена
ни сверху, ни снизу.
6. унаим.= НЕТ
унаиб.= НЕТ
7. Непрерывность
Претерпевает разрыв при х = 0.
х
Найдите
унаиб. и унаим.
2
функции У=х
на отрезке
2 ; 1
Унаиб.=-1
Унаим.=-2
у
4
3
2
1
-4 -3 -2 -1
2
У=х
01 2 3 4
-1
-2
-3
-4
х
Найдите
унаиб. и унаим.
2
функции У=х
у
4
3
2
1
на полуинтервале
1; 4
Унаиб.= 2
Унаим.=НЕТ
-4 -3 -2 -1
2
У=х
х
01 2 3 4
-1
-2
-3
-4
Найдите
унаиб. и унаим.
2
функции У=х
на луче
; 1
Унаиб.= НЕТ
Унаим.= -2
у
4
3
2
1
-4 -3 -2 -1
2
У=х
х
01 2 3 4
-1
-2
-3
-4
Найдите
унаиб.
 и унаим.
и унаим.2
функции У=х
на луче
1;
Унаиб.= 2
Унаим.= НЕТ
у
4
3
2
1
-4 -3 -2 -1
2
У=х
х
01 2 3 4
-1
-2
-3
-4
Решить графически уравнение:
3
х 2
х
1
у
Построим в одной системе
координат графики функций:
у=х-2
Х 0 2
У -2 0
3
у
х
х 1 2 3 -1 -2 -3
у 3 1,5 1 -3 -1,5 -1
4
3
2
1
3
у
х
х
-4 -3 -2 -1 0 1 2 3 4
у=х-2
-2
-3
Найдём абсциссы точек
2 пересечения
графиков
3
ОТВЕТ:
х=-1, х=3
Решить графически уравнение:
4
х 3
х
1
у
5
4
3
2
1
Построим в одной с. к.
графики функций:
4
у
х
х 1 2 4 -1 -2 -4
у -4 -2 -1 4 2 1
у=х+3
Х
У
у=х+3
-4 -3 -2 -1 0 1 2 3 4 5
-1
-2
-3
-4
4
y
х
х
0 -3
Найдём
абсциссы
точек пересечения графиков
Нет точек
пересечения
2
3 0
3 ОТВЕТ:
Нет корней
Решить графически систему уравнений:
3
у
У= х
у=3х²
1
Построим в одной с.
 к.
к.графики функций:
3
У= х
х
у
1 2 3 -1
3 1,5 1 -3
у=3х²
Х
У
0 ±1
0 3
5
4
3
2
1
у=3х²
(1;3)
3
y
х
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
-1
-2 -3
-2
-1,5 -1
-3
-4
-5
Найдём координаты точек
2 пересечения
графиков
3 ОТВЕТ (1;3)
х
Постройте график функции
-x²,если -2≤х≤1
f(x)= 1х ,если х>1
и опишите её свойства.
-x²,если -2≤х≤1
f(x)= 1х ,если х>1
у
у=-х²
Х
0
У
0
±1 ±2
-1 -4
-2 ≤ х ≤ 1
1
У= х
х 0,5 1 2 -0,5 -1 -2
у 2 1 0,5 -2 -1 -0,5
х>1
4
1
-4 -3 -2 -1 0 1 2 3
-1
-4
х
Свойства функции:
1.Область
1. D ( f ) 2 ;
определения
у
E ( f ) 4 ;1
f(x)=
4
-x²,если -2≤х≤1
1/х,если х>1
2.
2.Область
значений
3. у=0, если х= 0
у>0, если х 1;
у
х 2; 0 0;1
1
-3 -2 -1 0 1 2 3 4
-2
4.
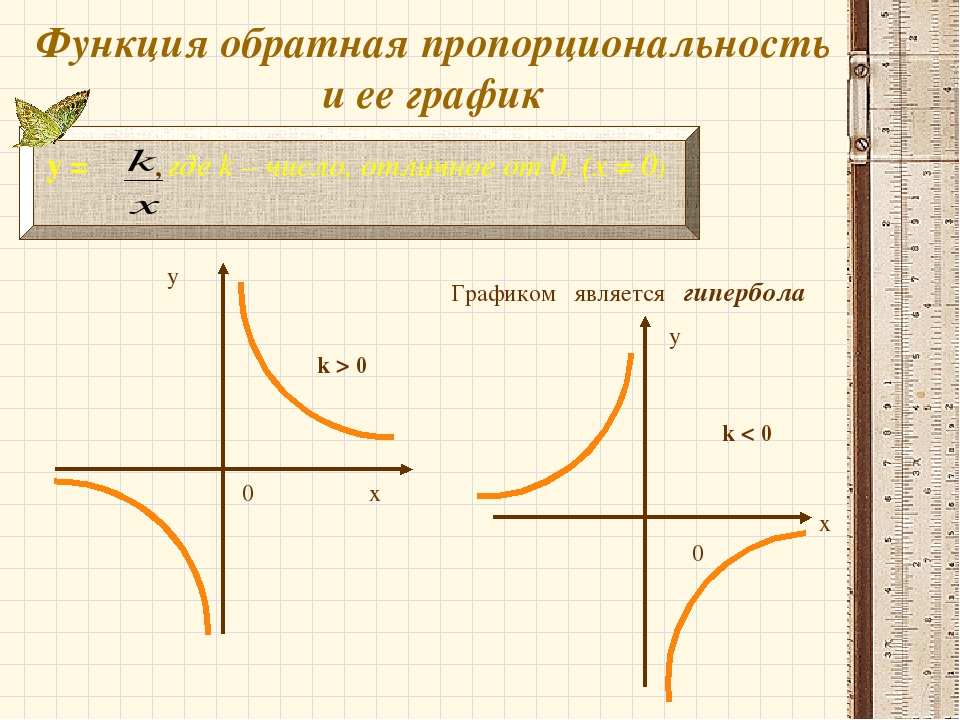 Функция убывает
Функция убываетпри х 0 ;1 1;
-4
Функция возрастает
при х 2 ; 0
ограничена сверху и снизу.
5.Функция
Ограниченность
6. унаим.= — 4
унаиб.= НЕТ
7. Непрерывность
Претерпевает разрыв при х = 1.
х
Дома: Используя презентацию или
учебник выучить свойства функции
параграф 18. Решить: № 7; 9(а).
Обратная функция график обратной функции. Функция обратной пропорциональности.
Характеристики функции k/x
График \(y =\frac{k}{x}\) приближается к оси \(x\) по мере увеличения значения \(x \), но никогда не встречается с осью \(X\). Это называется горизонтальной асимптотой графика.
Каждая часть графика также становится ближе к оси \(y\), поскольку \(x\) приближается к \(0\), но никогда не встречается с осью \(y\), поэтому нет значения для \(y\), когда \(x = 0\). Это называется вертикальной асимптотой графика. Этот тип функции называется гиперболой, где \(k-\) действительное число и \(x ≠ 0\).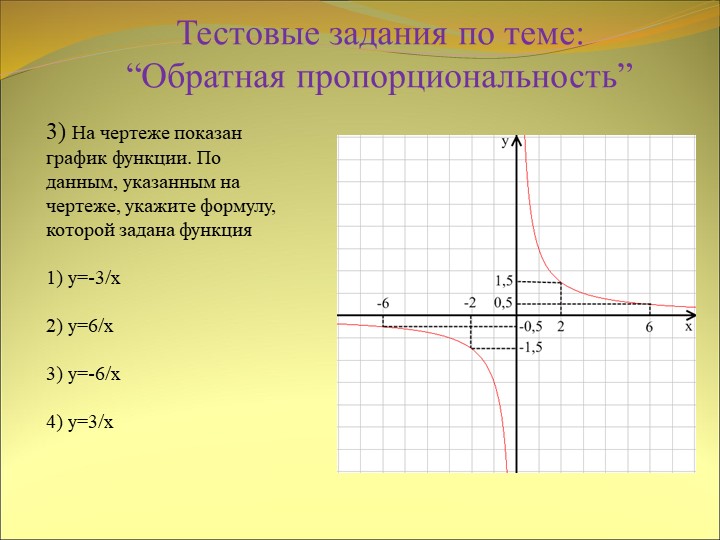
Пример 1. Постройте график функции \(y =\frac{5}{x}\).
Решение.- Выберем произвольные точки \(x \) и посчитаем соответсвующие им значения \(y\) :
- Построим точки из таблицы и плавно соединим их:
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявкуРепетитор по математике
Брестский государственный университет им. А.С. Пушкина
А.С. Пушкина
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-11 классов. Объясню простым языком даже самую сложную тему. Люблю математику и покажу как она прекрасна. Считаю, что всему можно научить, нужно лишь желание, время и преподаватель, способный заинтересовать ребенка.
Объясню простым языком даже самую сложную тему. Люблю математику и покажу как она прекрасна. Считаю, что всему можно научить, нужно лишь желание, время и преподаватель, способный заинтересовать ребенка.
Репетитор по математике
Российская таможенная академия
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 8-11 классов по обществознанию. Моя основная задача — помочь школьнику с комфортом подготовиться к сдаче выпускных экзаменов на максимальный для ученика балл. В своей деятельности использую собственные наработки, только современные и актуальные материалы. Мои выпускники являются студентами/выпускниками СПбГУ, ВШЭ, МГИМО, РГПУ им. А.И. Герцена, ВУМО, РАНХиГС, РТА и др.
Моя основная задача — помочь школьнику с комфортом подготовиться к сдаче выпускных экзаменов на максимальный для ученика балл. В своей деятельности использую собственные наработки, только современные и актуальные материалы. Мои выпускники являются студентами/выпускниками СПбГУ, ВШЭ, МГИМО, РГПУ им. А.И. Герцена, ВУМО, РАНХиГС, РТА и др.
Репетитор по математике
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-11 класса. Помогу Вам разобраться в любой интересующей теме по математике . Даже, если кажется, что какая-либо задача является совсем невыполнимой, с моей помощью она не только станет для Вас решаемой, но также весьма интересной и увлекательной! Жду Вас на занятиях!.
Помогу Вам разобраться в любой интересующей теме по математике . Даже, если кажется, что какая-либо задача является совсем невыполнимой, с моей помощью она не только станет для Вас решаемой, но также весьма интересной и увлекательной! Жду Вас на занятиях!.
Математика 10 класс
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Математика 10 класс
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Похожие статьи
Записаться на бесплатный урок
3.
 3.2 Функция, описывающая обратную пропорциональную зависимость, её график Видеоурок: Обратная пропорциональность и её график
3.2 Функция, описывающая обратную пропорциональную зависимость, её график Видеоурок: Обратная пропорциональность и её графикЛекция: Функция, описывающая обратную пропорциональную зависимость, её график
Обратная пропорциональностьКогда на физике или на другом предмете говорят об обратной пропорциональности, мы понимаем это, как рост одной величины в то время, когда вторая величина уменьшается.
Функция, которая описывает обратную пропорциональность или зависимость, имеет следующий вид:
y = k/x, стоит обратить внимание на то, что коэффициент не может быть равен нулю, иначе обратная пропорциональность превратиться в линейную зависимость.
Чем больше будет значение аргумента, тем меньше будет значение функции, и наоборот.
Давайте посмотрим внимательно, где находится аргумент. Его местонахождение говорит о том, что при рассматривании данной функции, появляются некие ограничения, а именно то, что в знаменателе не может быть нуля. Именно поэтому областью определения данной функции будет множество всех значений, кроме нуля.
Его местонахождение говорит о том, что при рассматривании данной функции, появляются некие ограничения, а именно то, что в знаменателе не может быть нуля. Именно поэтому областью определения данной функции будет множество всех значений, кроме нуля.
Отсюда следует, что функция так же не может принимать значение нуля.
График обратной функции
Для построения графика данной функции нам понадобится 5 точек для положительных «х» и «у», а также для отрицательных «х» и «у», в отличие от линейной функции.
Обратите внимание так же на то, что при положительных «х» и при положительном коэффициенте значение функции так же будет положительным числом.
Если значение «х» отрицательно, а коэффициент положительный, то функция так же будет отрицательной. Аналогичные рассуждения для отрицательного коэффициента. Отсюда можно сделать вывод, что данная функция одновременно может находиться в двух четвертях.
Обратно пропорциональная функция является симметричной относительно биссектрисы четвертей.
Итак, возьмем функцию у = 1/х.
Найдем для него координаты «х» и «у», занесем все данные в таблицу.
Расставим все полученные точки на плоскости и соединим их кривыми.
График данной функции всегда будет стремиться к нулю по оси ОХ и по оси ОУ, но так до него и не достигнет, из-за невозможности нуля в знаменателе.
Как влияет коэффициент на вид графика?
Чем больше значение коэффициента, тем дальше график находится от начала координат.
А что случится, если к дроби добавить какое-то число и в знаменателе добавить слагаемое? Все просто! Произойдет сдвиг. Если к дроби прибавить число, то произойдет сдвиг по оси ОУ:
если число отрицательное, то график сместиться на некоторое число единиц ниже по оси ОУ;
если число положительное, то график сместиться на некоторое число единиц выше по оси ОУ.
Если в знаменателе к аргументу добавить положительное число, то график сместиться по оси ОХ влево, если добавить отрицательное — то вправо.
Итак, например, имеем график вида:
Получим следующий график:
Вопрос Видео: Распознавание графиков, которые показывают обратную пропорцию
Стенограмма видео
Какой из приведенных графиков представляет обратную вариацию?
Затем у нас есть четыре графика (A), (B), (C) и (D), построенные в первом квадранте координатной плоскости. Чтобы ответить на этот вопрос, напомним себе, что мы подразумеваем под термином «обратная вариация». Предположим, у нас есть переменные 𝑦 и 𝑥. Если они обратно пропорциональны друг другу или представляют обратную вариацию, мы говорим, что 𝑦 пропорционально единице над 𝑥.Соответствующее уравнение, которое мы используем для описания этой связи: 𝑦 равно 𝑘 над 𝑥.
Теперь, конечно, 𝑦 также может быть обратно пропорционально квадрату 𝑥. В этом случае мы говорим, что 𝑦 пропорционально единице на 𝑥 в квадрате. И соответствующее уравнение 𝑦 равно 𝑘 на 𝑥 в квадрате. Это верно для 𝑦 обратно пропорционально квадратному корню из 𝑥, кубу из 𝑥 и так далее.
Это верно для 𝑦 обратно пропорционально квадратному корню из 𝑥, кубу из 𝑥 и так далее.
По сути, мы ищем график уравнения вида 𝑦 равно 𝑘 над 𝑥 в 𝑛-й степени, где 𝑛 должно быть положительным числом.Итак, есть некоторые графики, которыми можно сразу пренебречь. График (С) представляет собой прямую линию. Это означает, что его общая форма 𝑦 равно 𝑚𝑥 плюс 𝑏. Но он проходит через начало координат, точку ноль, нуль, так что, фактически, поскольку его 𝑦-пересечение равно нулю, мы можем записать его как 𝑦 равно 𝑚𝑥 или 𝑦 равно 𝑘𝑥. Это, по сути, пример двух переменных, которые прямо пропорциональны друг другу. И поэтому мы игнорируем вариант (C).
Аналогично, вариант (D) выглядит так, как будто он может быть представлен в виде 𝑦 равно 𝑘, умноженному на квадратный корень из 𝑥.И глядя на пару координат здесь, например, четыре, два и один, один, мы можем наверняка убедиться, что эти координаты удовлетворяют этому уравнению. Это пример того, что 𝑘 прямо пропорционально квадратному корню из 𝑥.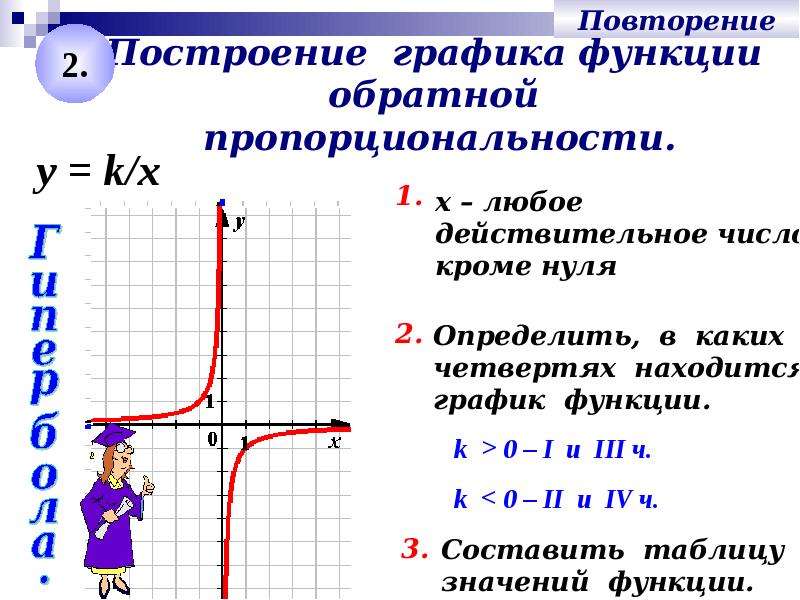 Таким образом, это не является обратной вариацией, и мы пренебрегаем (D).
Таким образом, это не является обратной вариацией, и мы пренебрегаем (D).
Аналогично, уравнение (B) может иметь вид 𝑦 равно 𝑘𝑥 в квадрате. Это, конечно, похоже на квадратное. И это отражение нашего предыдущего графика в строке 𝑦 равно 𝑥. Еще раз, это график, который представляет прямую вариацию.Его 𝑦 напрямую зависит от 𝑥 в квадрате, поэтому мы игнорируем вариант (B).
Таким образом, остается только вариант (А). И это имеет большой смысл, когда мы думаем о том, что мы знаем о графике, скажем, 𝑦 равно единице на 𝑥. Это выглядит так, и у него есть асимптоты, заданные 𝑦- и 𝑥-осями. Точно так же график 𝑦 равен единице на 𝑥 в квадрате выглядит следующим образом. На самом деле, если мы подумаем о форме кривой исключительно в первом квадранте, график 𝑦 равен 𝑘 по 𝑥 в 𝑛-й степени для положительных значений 𝑛 всегда будет иметь эту форму.Итак, ответ (А). Затем график (A) представляет обратную вариацию: 𝑦 обратно пропорциональна некоторой степени 𝑥.
Пропорциональность (математика) | Психология Вики
Оценка |
Биопсихология |
Сравнительный |
Познавательный |
Развивающие |
Язык |
Индивидуальные различия |
Личность |
Философия |
Социальные |
Методы |
Статистика |
Клинический |
Образовательные |
промышленный |
Профессиональные товары |
Мировая психология |
Статистика: Научный метод · Методы исследования · Экспериментальная конструкция · Курсы статистики бакалавриата · Статистические тесты · Теория игры · Теория принятия решений
В математике две величины называются пропорциональными , если они изменяются таким образом, что одна из величин постоянно кратна другой, или, что то же самое, если они имеют постоянное отношение.
Определение
Более формально, переменная y называется пропорциональной (или иногда прямо пропорциональной ) переменной x , если существует постоянное ненулевое число k такое, что
Отношение часто обозначается
и постоянное соотношение
называется константой пропорциональности или константой пропорциональности отношения пропорциональности.
Примеры
- Если объект движется с постоянной скоростью, то пройденное расстояние пропорционально времени, затраченному на перемещение, причем скорость является константой пропорциональности.
- Длина окружности пропорциональна ее диаметру с коэффициентом пропорциональности, равным π.
- На карте, нарисованной в масштабе, расстояние между любыми двумя точками на карте пропорционально расстоянию между двумя местоположениями, которые представляют точки, при этом константа пропорциональности является масштабом карты.

- Величина силы, действующей на определенный объект со стороны гравитации Земли на уровне моря, пропорциональна массе объекта, а гравитационная постоянная является константой пропорциональности.
Свойства
С
эквивалентно
отсюда следует, что если y пропорционально x с (ненулевой) константой пропорциональности k , то x также пропорционально y 6 k 900 37 с константой пропорциональности .
Если y пропорционально x , то график зависимости y от x будет представлять собой прямую линию, проходящую через начало координат с наклоном линии, равным константе пропорциональности.
Обратная пропорциональность
Как отмечено в приведенном выше определении, две пропорциональные переменные иногда называют прямо пропорциональными . Это сделано для того, чтобы противопоставить пропорциональность обратной пропорциональности .
Две переменные являются обратно пропорциональными (или изменяющимися обратно ), если одна из переменных прямо пропорциональна мультипликативной величине, обратной другой, или, что то же самое, если их произведение является константой.Отсюда следует, что переменная y обратно пропорциональна переменной х , если существует ненулевая константа k такая, что
По сути, концепция обратной пропорциональности означает, что по мере увеличения абсолютного значения или величины одной переменной абсолютное значение или величина другой уменьшается, так что их произведение (константа пропорциональности) всегда одинаково .
Например, время, необходимое для путешествия, обратно пропорционально скорости движения; время, необходимое для рытья ямы, (приблизительно) обратно пропорционально количеству копающих людей.
График двух переменных, изменяющихся обратно пропорционально в декартовой координатной плоскости, является гиперболой. Произведение значений X и Y каждой точки на кривой будет равно константе пропорциональности ( k ). Поскольку k никогда не может равняться нулю, график никогда не пересекает ни одну из осей.
Произведение значений X и Y каждой точки на кривой будет равно константе пропорциональности ( k ). Поскольку k никогда не может равняться нулю, график никогда не пересекает ни одну из осей.
Экспоненциальная и логарифмическая пропорциональность
Переменная y экспоненциально пропорциональна переменной x , если y прямо пропорциональна экспоненциальной функции x , то есть если существует ненулевая константа k такая, что
Аналогично, переменная y является логарифмически пропорциональной переменной x , если y прямо пропорционально логарифму x , если существует 9036 x константа, то есть k такое, что
Экспериментальное определение
Чтобы экспериментально определить, являются ли две физические величины прямо пропорциональными, необходимо выполнить несколько измерений и нанести полученные точки данных на график в декартовой системе координат.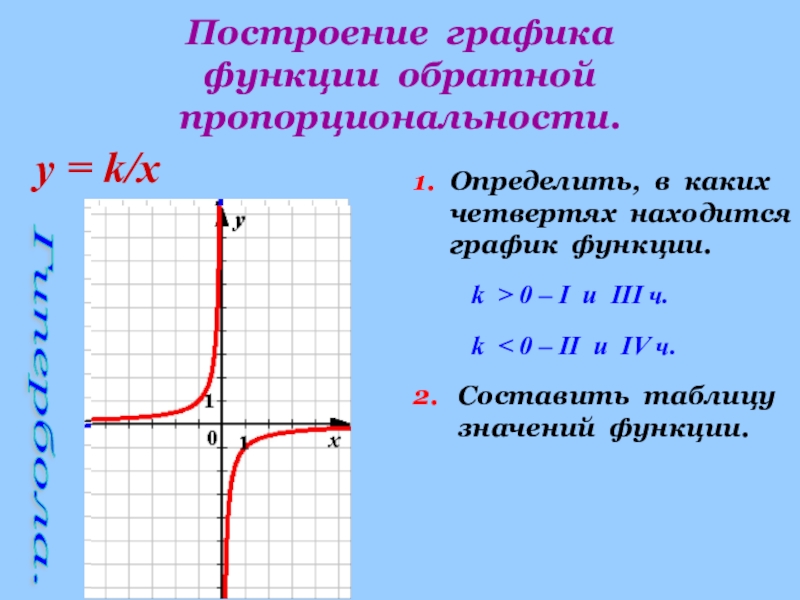 Если точки лежат на прямой линии, проходящей через начало координат (0, 0), или близко к ней, то две переменные, вероятно, пропорциональны, а константа пропорциональности определяется наклоном линии.
Если точки лежат на прямой линии, проходящей через начало координат (0, 0), или близко к ней, то две переменные, вероятно, пропорциональны, а константа пропорциональности определяется наклоном линии.
См. также
de:Proportionalität es: пропорциональный fr:Proportionalité ио: Пропорционо он: יחס ישר nl: Рехт дажередиг нет: proporsjonalitet vi: Tỉ lệ nghịch ж: 正 比
графиков | Информационные бюллетени Smore
В этой теме вы узнаете о…
- Пропорции (прямые и косвенные)
- Параболы
- Кубики
- Экспоненты
В таблице ниже приведены упражнения, которые будут рассмотрены. Темы в КРАСНОМ 5.3 работают.
Ресурсы
1. Прямо пропорциональные
Две переменные находятся в прямой зависимости друг от друга, если одна переменная постоянно кратна другой; когда одна переменная изменяется, другая изменяется на тот же коэффициент.
Если y прямо пропорционально x, , то y=kx, , где k — постоянное число
- Если x увеличивается (или уменьшается), y увеличивается (или уменьшается)
- Если x удваивается (или уменьшается вдвое), у удваивается (или уменьшается вдвое)
- Другой способ сказать, что «у прямо пропорциональна х», это y напрямую зависит от х
- График прямой пропорциональности представляет собой прямую линию, проходящую через ( 0,0) с градиентом k.
Чтобы решить задачу прямой пропорции:
- Определите две переменные, скажем, x и y, и форму уравнения пропорции, y=kx
- Подставьте значения 9024 и x x найти k, константу пропорциональности
- Переписать y=kx , используя значение k
- Подставить значение x или y в y=kx для решения задачи.
См. пример на стр. 287
2.
 Обратная пропорция Две переменные обратно пропорциональны , когда одна переменная увеличивается, а другая уменьшается на ту же величину.
Обратная пропорция Две переменные обратно пропорциональны , когда одна переменная увеличивается, а другая уменьшается на ту же величину.Если y обратно пропорционально x, то y= k/x, где k — константа (число), называемая константой пропорциональности.
- Если x увеличивается, y уменьшается.
- Если x уменьшается, y увеличивается
- Если x удваивается, y уменьшается вдвое
- Если x уменьшается вдвое, y удваивается x»
Для решения задач обратной пропорциональности:
- Определите две переменные (x и y)
- Подставьте значения x и y, чтобы найти константу пропорциональности
- Перепишите y=k/x , используя значение k
- Подставьте значение x или y в y=k/x , чтобы решить
Прочтите примеры на с.290-292
3. Графики преобразования
График преобразования используется для преобразования одних единиц измерения в другие. Например, перевод австралийских долларов в доллары США. Обычно он содержит прямую линию от начала координат.
Например, перевод австралийских долларов в доллары США. Обычно он содержит прямую линию от начала координат.См. примеры на стр. 10. 294
6.Парабола
. Уравнение с наивысшей степенью x, равной двум, называется квадратным уравнением . График квадратного уравнения обычно дает гладкую U-образную кривую, называемую параболой .- Ось симметрии — это ось Y
- Вершина или точка поворота (0,0).
См. примеры на с. 309-310
8.Кубическое уравнение
Уравнение с наивысшей степенью 3 называется кубическим уравнением . График кубического уравнения называется кубической кривой.Кубическая кривая:
- Не имеет оси симметрии
- Имеет вращательную симметрию 180 градусов относительно (0,0): если вы повернете ее вверх ногами, она отобразится сама на себя
- Если a положительна, график всегда увеличивается, кроме точки (0,0)
- Если a отрицательно, график всегда уменьшается, кроме точки (0,0).
 3), определяет, будет ли граф шире или уже.
3), определяет, будет ли граф шире или уже.
10. Гипербола y=k/x
График зависимости y=k/x, где k является постоянным, представляет собой кривую с двумя ветвями, называемую гиперболой .- График имеет две отдельные ветви в разных квадрантах
- Если k положительное, график находится в 1-м и 3-м квадрантах
- Если k отрицательное, график находится во 2-м и 4-м квадрантах
- График имеет две оси симметрии: их уравнения y=x и y=-x
- Граф имеет вращательную симметрию 180 градусов относительно (0,0).
- Чем выше значение k, тем дальше гипербола от осей x и y
- Когда x становится очень большим, y становится ближе к 0
- Когда x становится ближе к 0, y становится очень большим
- График подходит очень близко к осям x и y, но никогда не пересекает их. Оси x и y называются асимптотами , потому что график приближается к ним, но никогда не касается их.
 x, где a — положительная константа, а переменная x — степень, называется показательным уравнением .х всегда положителен.
x, где a — положительная константа, а переменная x — степень, называется показательным уравнением .х всегда положителен.
12. Круг
Читать пример 20 на с. 332
Прямая и обратная пропорция
Уважаемые ученики средней школы, сегодня мы рассмотрим тему прямой и обратной пропорции.Эта тема обычно тестируется вместе с похожими фигурами или похожими треугольниками на экзаменах по математике уровня E или N по математике. Без лишних слов, давайте начнем!
Из этой заметки вы узнаете:
1) Что означает прямо пропорциональная связь между двумя переменными?
2) Что означает обратно пропорциональная связь между двумя переменными?
3) Графики пропорциональности
1) Что означает прямо пропорциональная связь между двумя переменными?
Когда говорят, что две переменные или величины прямо пропорциональны, это в основном означает, что две переменные/величины увеличиваются или уменьшаются, чтобы сохранить соотношение постоянным. Формула прямой пропорциональности задается следующим образом:
Формула прямой пропорциональности задается следующим образом:
y ∝ x
y = kx или y / x = k , где k — константа
Некоторые реальные примеры прямо пропорциональных отношений:
1. Вы работаете неполный рабочий день, за который вам выплачивается почасовая оплата, следовательно, количество отработанных вами часов прямо пропорционально почасовой ставке, или количество отработанных часов ∝ почасовая ставка .
Например, если почасовая ставка составляет 10 долларов, вы получите 10 долларов за 1 час работы, 20 долларов за 2 часа работы, 30 долларов за 3 часа работы и т. д. и т. д.
2. Вы вышли на пробежку и бежали с постоянной скоростью 5 км/ч. Это означает, что количество часов, которые вы пробежали, прямо пропорционально пройденному расстоянию, или количество часов пробежки ∝ пройденное расстояние . Вы бы проехали 5 км за первый час, 10 км за второй час, 15 км за третий час и так далее и тому подобное.
Теперь попробуем решить задачу на прямую пропорциональность:
Джейн пытается испечь торт. Она следует рецепту, который говорит ей, что: 5 стаканов муки используются на каждые 2 стакана использованного сахара.Однако Джейн пытается испечь пирог большего размера, чем указано в рецепте, и вместо этого решила использовать 8 чашек муки. Следовательно, сколько чашек сахара должна использовать Джейн?
Ответ:
Пусть y = количество использованных чашек сахара и x = количество использованных чашек муки
y = kx
используется, следовательно:
2 = k (5)
Следовательно, k = 0,4 и y = 0,4x
Джейн хочет использовать 8 чашек муки, чтобы испечь больший пирог, следовательно:
y = 0.4 (8)
= 3,2 стакана
На 8 стаканов муки Джейн должна использовать 3 с 1/5 стакана сахара.
2) Что означает обратно пропорциональная связь между двумя переменными?
Когда говорят, что две переменные или величины обратно пропорциональны, это в основном означает, что произведение двух переменных равно константе.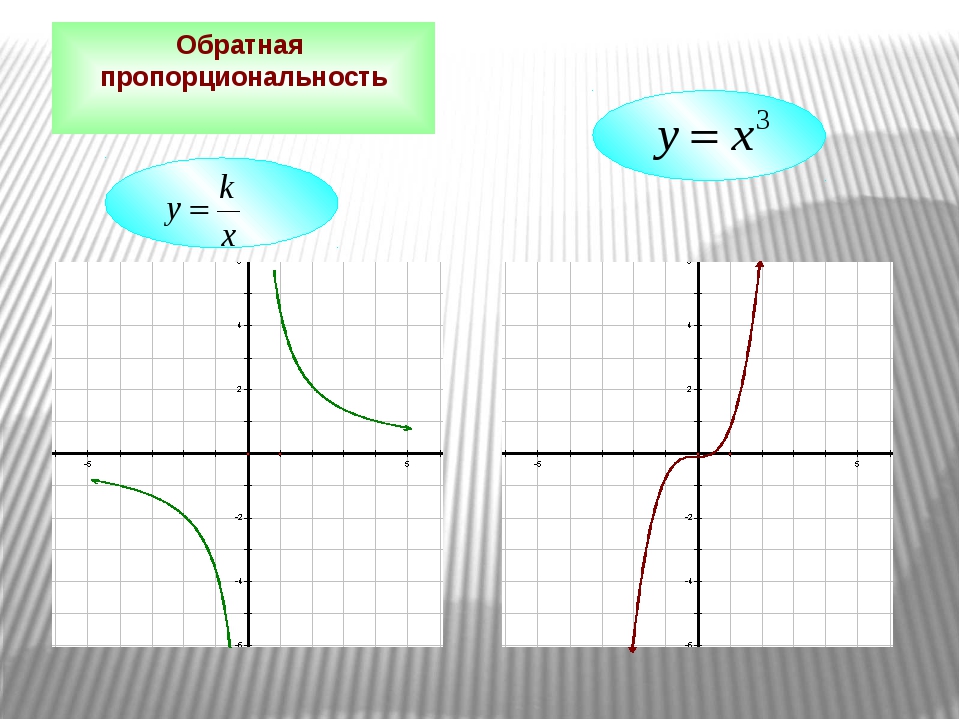 Когда одна переменная увеличивается, другая должна уменьшаться, чтобы константа оставалась действительной. Формула обратной пропорциональности задается следующим образом:
Когда одна переменная увеличивается, другая должна уменьшаться, чтобы константа оставалась действительной. Формула обратной пропорциональности задается следующим образом:
y ∝ k / x
y = k / x или yx = k , где k — константа
Некоторые реальные примеры обратно пропорциональных отношений:
1.Скорость и время в пути: чем быстрее вы едете, тем меньше времени требуется для завершения пути, а это означает, что скорость обратно пропорциональна времени в пути.
2. В теме «Идеальный газ» в химии Закон Бойля гласит, что объем идеального газа обратно пропорционален давлению газа. т.е. Объем ∝ k / Давление
Теперь попробуем решить вопрос с обратной пропорциональностью:
Ответ:
В этом вопросе мы понимаем, что количество мужчин, задействованных в ремонте дороги, обратно пропорционально количеству часов. повезли ремонтировать дорогу.
Поэтому пусть время, затраченное на ремонт дороги, будет равно t, а поскольку в вопросе также говорится, что 8 человек работают с той же скоростью, что и 5 человек, то скорость остается неизменной .
Пусть y = количество рабочих, задействованных в ремонте дороги, и x = количество часов, затраченных на ремонт дороги
yx = k
(количество рабочих) (время, затраченное на ремонт) = k
5 x 8 = k
k = 40
Следовательно, 9 xt = 40
t = 40 / 8
= 5 часов
Графики с участием пропорциональности 900 все, что вам нужно сделать, это построить графики на основе уравнений.Давайте посмотрим, как это делается:
Для прямой пропорциональности формула имеет вид: y = kx, что, если вспомнить из главы «Графики функций и графические решения», представляет собой просто прямолинейный график!
Что касается обратной пропорциональности, формула имеет вид: y = k/x, что напоминает график обратной функции!
Пришло время надеть свои мыслительные кепки и начать решать некоторые вопросы!
1. Напряжение, В вольт, в электрической цепи прямо пропорционально току, I ампер, протекающему по цепи. Когда I = 2,4, V = 90
Когда I = 2,4, V = 90
а) Выразите V через I
б) Найдите V, если I = 5,5
c) Найти I, когда V = 184,5
2. Когда фиксированный объем воды наливается в цилиндрическую банку, глубина D см воды обратно пропорциональна площади поперечного сечения A см² цилиндрической банки.
Когда A = 35, D = 140
а) Найдите формулу для A через D
б) Найти A, когда D = 150
c) Найдите D, если A = 60
3.Масса M кг твердого куба, сделанного из свинца, пропорциональна кубу длины L см ребра. Когда L = 0,4, М = 120
а) Найдите формулу для M через L
б) Найдите значение М при L = 0,7
в) Найдите значение L при М = 2450, дайте ответ, исправленный до 3-х значащих цифр.
4. Сила притяжения F ньютонов между двумя сферами обратно пропорциональна квадрату расстояния d м между центрами сфер.
При d = 1,35, F = 0,08,
а) Выразите F через d
б) Найдите F при d = 4,5
c) Найдите d, если F = 0,03, и ваш ответ будет исправлен до трех значащих цифр.
На сегодня у нас все, студенты! Math Lobby надеется, что после прочтения этой статьи и решения вопросов вы сможете получить четкое представление о концепциях прямой пропорциональности и обратной пропорциональности.
По любым вопросам пишите нам в Facebook или Instagram! И как всегда: работайте усердно, сохраняйте мотивацию, и мы желаем всем студентам успешного и приятного путешествия с Math Lobby!
Если вы хотите, чтобы получал от нас больше советов по средней математике ,
Посетите нашу страницу Facebook на www.facebook.com/mathlobbymotivation/
Посетите и ПОДПИСЫВАЙТЕСЬ на нашу страницу в Instagram по адресу https://www.instagram.com/mathlobbymotivation/
Посетите наш веб-сайт по адресу: www.mathlobby4.com .com
Свяжитесь с нами по номеру SMS/WhatsApp/Telegram или по телефону +65 96322202
*
*
*
#mathlobby #mathlobbymotivation #bestmathtuition #mathtuitionpotongpasir #mathtuitionsg #freemathresources #sgmaths #sgmathtutor #emath #amath #secschool #mathtutorsg #sgedu #nleveltuition #mathtuition #secondarymath #mathtutors #tuitionsg #singaporemath #sgtuition #sgtuition #sgtuition #sgtuition #math #математика #mathtutor #обучение #sgparents #secondaryschool
Чему равна константа К в обратной вариации? – СидмартинБио
Чему равна константа К в обратной вариации?
Основная идея обратной вариации заключается в том, что по мере увеличения одной переменной другая переменная уменьшается. Это означает, что если x увеличивается, y уменьшается, а если x уменьшается, y увеличивается. Число k является константой, поэтому во всей обратной вариационной задаче это всегда одно и то же число.
Это означает, что если x увеличивается, y уменьшается, а если x уменьшается, y увеличивается. Число k является константой, поэтому во всей обратной вариационной задаче это всегда одно и то же число.
Что такое К в пропорции?
Константа пропорциональности k определяется выражением k=y/x, где y и x — две величины, прямо пропорциональные друг другу. Как только вы узнаете константу пропорциональности, вы можете найти уравнение, представляющее прямо пропорциональную связь между x и y, а именно y = kx, с вашим конкретным k.
Какая формула для обратно пропорциональных функций?
Если две переменные обратно пропорциональны, то при увеличении одной другая уменьшается, и наоборот. Если переменная y обратно пропорциональна переменной x, то y = k/x, где k — константа пропорциональности.
Как написать уравнение обратной зависимости?
Формула обратной зависимости помогает математически представить обратно пропорциональную зависимость.Формула обратной вариации: x × y = k или y = k/x, где x и y — две переменные, а k — константа пропорциональности.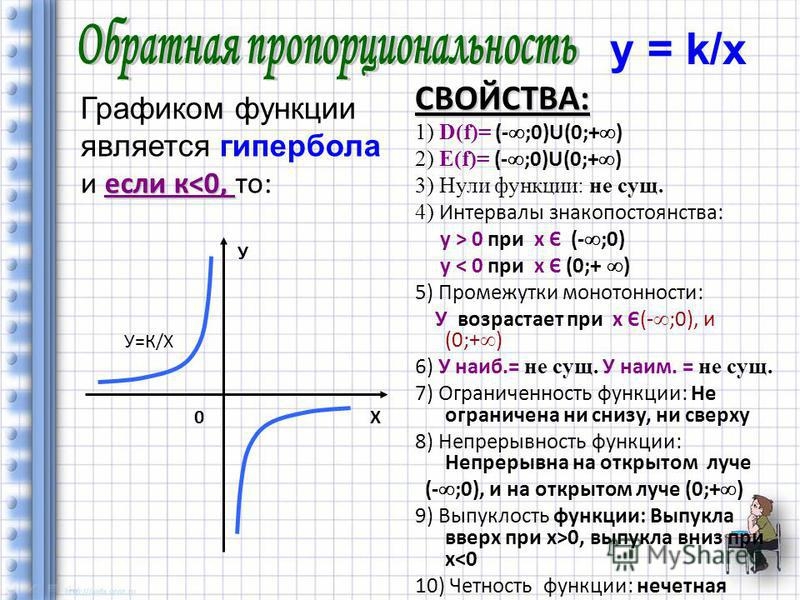
Как вы меняетесь обратно пропорционально?
Обратная вариация может быть представлена уравнением xy=k или y=kx . То есть y изменяется обратно пропорционально x, если существует некоторая ненулевая константа k такая, что xy=k или y=kx, где x≠0,y≠0 . Предположим, что y изменяется обратно пропорционально x, так что xy=3 или y=3x.
Что такое обратно пропорциональный граф?
График обратно пропорциональной зависимости отображает вертикальную асимптоту на оси y, поскольку значение y неограниченно возрастает по мере того, как x все ближе и ближе к нулю (но положительно), и неограниченно уменьшается по мере того, как x все ближе и ближе к нулю ( но отрицательно) и горизонтальная асимптота на оси абсцисс по оси у получается …
Что означает обратно пропорциональный?
Когда значение одной величины увеличивается по отношению к уменьшению другой или наоборот, говорят, что они обратно пропорциональны.Это означает, что две величины ведут себя противоположно по своей природе. Например, скорость и время обратно пропорциональны друг другу. При увеличении скорости время сокращается.
Например, скорость и время обратно пропорциональны друг другу. При увеличении скорости время сокращается.
Что такое пропорциональное и обратно пропорциональное?
Прямо пропорциональные переменные – это переменные, у которых при увеличении одной переменной увеличивается и другая. Обратно пропорциональные переменные — это переменные, в которых одна переменная уменьшается с увеличением другой переменной, а одна переменная увеличивается с уменьшением другой переменной.Это противоположно прямой пропорциональности.
Какая формула обратно пропорциональна?
Обратная вариация может быть представлена уравнением xy=k или y=kx . То есть y изменяется обратно пропорционально x, если существует некоторая ненулевая константа k такая, что xy=k или y=kx, где x≠0,y≠0 .
В каком отношении в А обратно пропорциональна В?
Обратная пропорция Две переменные a и b называются обратно пропорциональными, если; а∝1/б. В этом случае увеличение переменной b вызывает уменьшение значения переменной a. Точно так же уменьшение переменной b вызывает увеличение значения переменной a.
Точно так же уменьшение переменной b вызывает увеличение значения переменной a.
Как найти обратно пропорциональную величину К?
Метод 2) Мы также знаем, что в обратной пропорции уравнение x + y = k становится x = k/y. Таким образом, чтобы найти значение k, мы можем использовать известные значения, чтобы найти неизвестные с помощью вышеизложенного. Вы также можете использовать обратно пропорциональную формулу для решения сумм.
Какова формула обратной пропорциональности?
Формула обратно пропорциональности.Если х и у две величины, находящиеся в обратных вариациях, то. х ∝ 1/г. x = k(1/y) Где «k» — универсально положительная константа. Его также можно представить как xy = k.
Как решать пропорциональные уравнения?
Вы также можете использовать обратно пропорциональную формулу для решения сумм. Вы можете составить уравнение, используя эти четыре простых шага: Шаг 1) Сначала запишите пропорциональное отношение. Шаг 2) Второй шаг заключается в преобразовании в уравнение с использованием константы пропорциональности.
Как найти обратную вариацию X?
Значит, величины обратно пропорциональны. Обратная вариация может быть представлена уравнением x y = k или y = k x . То есть y изменяется обратно пропорционально x, если существует некоторая ненулевая константа k такая, что x y = k или y = k x , где x ≠ 0 , y ≠ 0 .
Обратная вариация — ChiliMath
Концепция обратной вариации резюмируется приведенным ниже уравнением.
Ключевые идеи обратной вариации
- Мы говорим, что y изменяется обратно пропорционально x, если y выражается как произведение некоторого постоянного числа k и обратной величины x.

- Однако значение k не может равняться нулю , т.е. k \ne 0.
- Выделив k с одной стороны, становится ясно, что k есть фиксированное произведение x и y. Это означает, что умножение x и y всегда дает постоянный результат k.
k также известен как константа вариации или константа пропорциональности.
Примеры обратной вариации
Пример 1: Укажите, изменяется ли y обратно пропорционально x в таблице ниже. Если да, напишите уравнение для обратной вариации.
Решение :
Чтобы таблица имела обратную характеристику вариации, произведение для всех пар x и y в наборе данных должно быть одинаковым.
Произведение переменных x и y постоянно для всех пар данных.Мы можем утверждать, что k = 24 есть константа вариации. Написание уравнения обратной пропорциональности,
Вот график уравнения y = {{24} \over x} с точками из таблицы.
Пример 2: Укажите, изменяется ли y обратно пропорционально x в таблице ниже. Если да, напишите уравнение для обратной вариации.
Решение :
Если данные в таблице представляют обратную вариацию, произведение x и y должно быть постоянным числом.
Очевидно, что умножение x и y дает фиксированное число. Это становится нашей постоянной вариации, таким образом, k = — 1,3. Уравнение обратной вариации записывается как
Это график y = {{ — \,3} \over x} с точками из таблицы.
Пример 3: Учитывая, что y изменяется обратно пропорционально x. Если х = — 1,2, то у = 14.
a) Напишите уравнение обратной вариации, связывающее x и y.
б) Каково значение у, когда х = 4?
Часть а) Напишите уравнение обратной вариации, связывающее x и y.
- Начните с написания общей формулы обратной вариации: y = {k \over x}.
 Это дает нам представление о том, что мы можем найти k, поскольку значения x и y заданы.
Это дает нам представление о том, что мы можем найти k, поскольку значения x и y заданы.
- Теперь мы можем написать обратное вариационное уравнение, связывающее x и y.
Часть b) Каково значение y, когда x = 4?
- Чтобы найти у, подставьте x = 4 в уравнение, найденное в части а).
Пример 4: Если y изменяется обратно пропорционально x, найдите отсутствующее значение y в
.Решение :
Используйте первую точку \left( {4, — \,2} \right)\, чтобы определить значение k по формуле y = {k \over x} .
Написание уравнения обратной вариации, связывающего x и y,
Чтобы найти отсутствующее значение y в точке \left( { — \,8,y} \right), просто подставьте значение x в формулу, найденную выше, а затем упростите.
Пример 5: Чтобы сбалансировать рычаг (качели), вес изменяется обратно пропорционально расстоянию объекта от точки опоры. Если Джон, весящий 140 фунтов, сидит в 7 футах от точки опоры, где должен сидеть его брат Лео, весящий 98 фунтов, чтобы уравновесить качели?
Если Джон, весящий 140 фунтов, сидит в 7 футах от точки опоры, где должен сидеть его брат Лео, весящий 98 фунтов, чтобы уравновесить качели?
Решение :
Важно нарисовать набросок сценария, чтобы иметь представление о том, что происходит.
Нам говорят, что вес обратно пропорционален расстоянию.Это означает, что наша формула для обратной вариации веса и расстояния:
Мы можем найти значение k, используя информацию о Джоне, потому что его вес и расстояние от точки опоры четко заданы в задаче.
Ниже приведено уравнение обратной вариации веса и расстояния.
Помните, что мы пытаемся определить, на каком расстоянии Лео, весом 98 фунтов, должен сидеть от точки опоры, чтобы уравновесить качели. Для этого подставьте вес Льва в формулу, найденную выше, и найдите «d».
Таким образом, Лео должен сесть в 10 футах от точки опоры , чтобы сбалансировать качели!
Вас также может заинтересовать:
Прямая вариация
Использование прямой и обратной вариации — Элементарная алгебра
Цели обучения
К концу этого раздела вы сможете:
- Решение задач прямой вариации
- Решить обратные вариационные задачи
Когда две величины связаны пропорцией, мы говорим, что они пропорциональны друг другу. Другой способ выразить это отношение состоит в том, чтобы говорить о вариации двух величин. В этом разделе мы обсудим прямую вариацию и обратную вариацию.
Другой способ выразить это отношение состоит в том, чтобы говорить о вариации двух величин. В этом разделе мы обсудим прямую вариацию и обратную вариацию.
Решить задачи прямого изменения
Линдси получает 15 фунтов стерлингов в час на своей работе. Если мы допустим, что s будет ее зарплатой, а ч будет количеством часов, которые она отработала, мы могли бы смоделировать эту ситуацию с помощью уравнения
Зарплата Линдси является произведением константы 15 и количества часов, которые она отработала.Мы говорим, что зарплата Линдси 90 872 напрямую зависит от количества часов, которые она отработала, — 90 225. Две переменные изменяются прямо, если одна является произведением константы, а другая.
Прямая вариация
Для любых двух переменных x и y , y напрямую зависит от x , если
Константа k называется константой вариации.
В приложениях, использующих прямую вариацию, обычно нам известны значения одной пары переменных, и нас попросят найти уравнение, связывающее x и y .Затем мы можем использовать это уравнение, чтобы найти значения y для других значений x .
Как решать задачи прямого изменения
Если y напрямую зависит от x и когда , найдите уравнение, связывающее x и y .
Если изменяется прямо как и найдите уравнение, связывающее x и y .
Если изменяется прямо как и найдите уравнение, связывающее x и y .
Мы перечислим шаги ниже.
Решите задачи прямого изменения.
- Напишите формулу прямого изменения.

- Подставить заданные значения переменных.
- Найдите константу вариации.
- Напишите уравнение, связывающее x и y.
Теперь решим несколько приложений прямой вариации.
Когда Рауль бежит на беговой дорожке в тренажерном зале, количество калорий, х , которые он сжигает, напрямую зависит от количества минут, м , в течение которых он использует беговую дорожку.Он сжег 315 калорий, когда использовал беговую дорожку в течение 18 минут.
- ⓐ Напишите уравнение, связывающее c и m .
- ⓑ Сколько калорий он сожжет, если пробежит по беговой дорожке 25 минут?
Количество сожженных калорий, c , напрямую зависит от количества времени, t, , потраченного на упражнения. Арнольд сжег 312 калорий за 65 минут тренировки.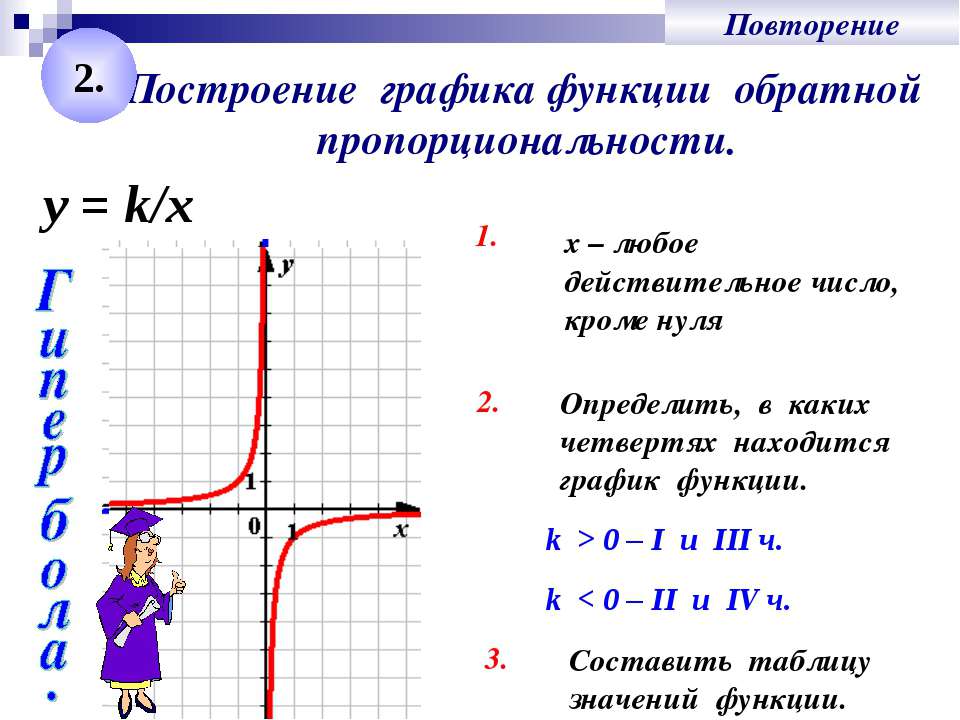
- ⓐ Напишите уравнение, связывающее c и t .
- ⓑ Сколько калорий он сожжет, если будет заниматься в течение 90 минут?
ⓐⓑ 432 калории
Расстояние, которое проходит движущееся тело, d , прямо зависит от времени, t , оно движется. Поезд проходит 100 миль за 2 часа
ⓐ Напишите уравнение, связывающее d и t .
ⓑ Сколько миль он проедет за 5 часов?
ⓐⓑ 250 миль
В предыдущем примере в задаче были названы переменные c и m .Обычно это не так. Нам нужно будет назвать переменные в следующем примере как часть решения, как мы это делаем в большинстве прикладных задач.
Количество галлонов бензина, которое использует автомобиль Юнис, напрямую зависит от количества миль, которые она проезжает. На прошлой неделе она проехала 469,8 миль и израсходовала 14,5 галлона бензина.
На прошлой неделе она проехала 469,8 миль и израсходовала 14,5 галлона бензина.
- ⓐ Напишите уравнение, связывающее количество использованных галлонов бензина с количеством пройденных миль.
- ⓑ Сколько галлонов бензина использовала бы машина Юнис, если бы она проехала 1000 миль?
Решение
ⓑ
Обратите внимание, что в этом примере единицами постоянной вариации являются галлоны на милю.В повседневной жизни мы обычно говорим о милях/галлонах.
Расстояние, которое преодолевает Брэд, напрямую зависит от времени, проведенного в пути. Брэд проехал 660 миль за 12 часов,
- ⓐ Напишите уравнение, связывающее количество пройденных миль со временем.
- ⓑ Сколько миль Брэд может пройти за 4 часа?
ⓐⓑ 220 миль
Вес жидкости прямо пропорционален ее объему. Жидкость весом 24 фунта имеет объем 4 галлона.
- ⓐ Напишите уравнение, связывающее вес с объемом.

- ⓑ Если жидкость имеет объем 13 галлонов, какова ее масса?
ⓐⓑ 78 фунтов
В некоторых случаях одна переменная зависит от квадрата другой переменной. Когда это происходит, уравнение прямой вариации имеет вид . Мы решаем эти приложения так же, как и предыдущие, подставляя заданные значения в уравнение для решения для k .
Максимальная нагрузка, которую может выдержать балка, напрямую зависит от квадрата диагонали поперечного сечения балки.Балка с диагональю 4 дюйма выдержит максимальную нагрузку 75 фунтов.
- ⓐ Напишите уравнение, связывающее максимальную нагрузку с поперечным сечением.
- ⓑ Какова максимальная нагрузка, которую может выдержать балка с диагональю 8 дюймов?
Решение
ⓑ
Расстояние, на которое падает объект, прямо пропорционально квадрату времени падения. Мяч падает на 144 фута за 3 секунды.
ⓐ Напишите уравнение, связывающее расстояние со временем.
ⓑ Как далеко упадет предмет за 4 секунды?
ⓐⓑ 256 футов
Площадь круга изменяется прямо пропорционально квадрату радиуса. Круглая пицца радиусом 6 дюймов имеет площадь 113,04 квадратных дюйма.
- ⓐ Напишите уравнение, связывающее площадь с радиусом.
- ⓑ Какова площадь пиццы радиусом 9 дюймов?
ⓐⓑ 254,34 квадратных дюйма
Решение обратных вариационных задач
Многие приложения используют две переменные, которые изменяются обратно .При увеличении одной переменной другая уменьшается. Уравнение, которое связывает их.
Обратная вариация
Для любых двух переменных x и y , y изменяется обратно пропорционально x , если
Константа k называется константой вариации.
Слово «инверсия» в инверсной вариации относится к мультипликативной инверсии. Мультипликативная инверсия x равна .
Мы решаем обратные вариационные задачи так же, как решали прямые вариационные задачи.Изменился только общий вид уравнения. Мы скопируем поле процедуры сюда и просто изменим «прямое» на «обратное».
Решить обратные вариационные задачи.
- Напишите формулу обратной вариации.
- Подставить заданные значения переменных.
- Найдите константу вариации.
- Напишите уравнение, связывающее x и y.
Если y изменяется обратно пропорционально и когда , найдите уравнение, связывающее x и y .
Расход топлива (миль на галлон) автомобиля обратно пропорционален его весу. Автомобиль, который весит 3100 фунтов, получает 26 миль на галлон на шоссе.
- ⓐ Напишите уравнение вариации.
- ⓑ Каков будет расход топлива автомобиля весом 4030 фунтов?
Решение
ⓐ
ⓑ
Стоимость автомобиля обратно пропорциональна его возрасту. Елена купила двухлетнюю машину за 20 000 фунтов стерлингов.
ⓐ Напишите уравнение вариации.
ⓑ Сколько будет стоить машина Елены, когда ей исполнится 5 лет?
ⓐⓑ ?8,000
Время, необходимое для опорожнения бассейна, обратно пропорционально скорости накачки. Люси потребовалось 2,5 часа, чтобы опорожнить свой бассейн с помощью насоса, рассчитанного на 400 галлонов в минуту.
- ⓐ Напишите уравнение вариации.
- ⓑ Сколько времени ей понадобится, чтобы опорожнить бассейн с помощью насоса, рассчитанного на 500 галлонов в минуту?
ⓐⓑ 2 часа
Частота гитарной струны обратно пропорциональна ее длине.Струна длиной 26 дюймов имеет частоту 440 колебаний в секунду.
- ⓐ Напишите уравнение вариации.
- ⓑ Сколько колебаний в секунду будет, если длину струны уменьшить до 20 дюймов, поместив палец на лад?
Решение
ⓐ
ⓑ
Количество часов, необходимое для таяния льда, обратно пропорционально температуре воздуха. Предположим, что глыба льда тает за 2 часа при температуре 65 градусов.
- ⓐ Напишите уравнение вариации.
- ⓑ За сколько часов та же глыба льда растает, если температура будет 78 градусов?
ⓐⓑ часов
Сила, необходимая для разрушения доски, обратно пропорциональна ее длине. Ричард использует давление в 24 фунта, чтобы сломать доску длиной 2 фута.
- ⓐ Напишите уравнение вариации.
- ⓑ Сколько фунтов давления необходимо, чтобы сломать доску длиной 5 футов?
ⓐⓑ 9.6 фунтов
Раздел Упражнения
Практика делает совершенным
Решение задач прямого изменения
В следующих упражнениях решите.
Если изменяется прямо как и , найдите уравнение, которое связывает .
Если изменяется прямо как и , найдите уравнение, которое связывает
Если изменяется прямо как и найдите уравнение, которое связывает
Если изменяется прямо как и , найдите уравнение, которое связывает
Сумма денег, которую зарабатывает Салли, P , напрямую зависит от количества n ожерелий, которые она продает.Когда Салли продает 15 ожерелий, она зарабатывает 150 фунтов стерлингов.
- ⓐ Напишите уравнение, связывающее P и n .
- ⓑ Сколько денег она заработает, если продаст 4 ожерелья?
ⓐⓑ
Цена, P , которую Эрик платит за бензин, напрямую зависит от количества галлонов, г , которые он покупает. Покупка 20 галлонов бензина стоит ему 50 фунтов стерлингов.
- ⓐ Напишите уравнение, связывающее P и g .
- ⓑ Сколько будет стоить Эрику 33 галлона?
Терри нужно испечь пироги для сбора средств. Количество яблок, и , прямо зависит от количества пирогов, и . Чтобы испечь два пирога, нужно девять яблок.
- ⓐ Напишите уравнение, связывающее с и с .
- ⓑ Сколько яблок нужно Терри для шести пирогов?
ⓐⓑ 27 яблок
Джозеф отправляется в путешествие.Расстояние d , которое он проходит до остановки на обед, прямо зависит от скорости, v , которую он проходит. Он может проехать 120 миль со скоростью 60 миль в час.
- ⓐ Напишите уравнение, связывающее d и v .

- ⓑ Какое расстояние он проедет, прежде чем остановиться на обед со скоростью 65 миль в час?
Цена бензина, который купил Джесси, напрямую зависит от того, сколько галлонов он купил. Он купил 10 галлонов бензина за 39 фунтов стерлингов.80.
- ⓐ Напишите уравнение, связывающее цену с количеством галлонов.
- ⓑ Сколько будет стоить Джесси 15 галлонов бензина?
ⓐⓑ
Расстояние, которое преодолевает Сара, напрямую зависит от того, как долго она едет. Она проходит 440 миль за 8 часов.
- ⓐ Напишите уравнение, связывающее расстояние с количеством часов.
- ⓑ Какое расстояние Салли может пройти за 6 часов?
Масса жидкости прямо пропорциональна ее объему.Жидкость массой 16 кг имеет объем 2 литра.
- ⓐ Напишите уравнение, связывающее массу с объемом.
- ⓑ Каков объем этой жидкости, если ее масса 128 кг?
ⓐⓑ
Длина, на которую растягивается пружина, напрямую зависит от груза, размещенного на конце пружины. Когда Сара положила 10-фунтовый арбуз на подвесные весы, пружина растянулась на 5 дюймов.
Когда Сара положила 10-фунтовый арбуз на подвесные весы, пружина растянулась на 5 дюймов.
- ⓐ Напишите уравнение, связывающее длину пружины с весом.
- ⓑ Арбуз какого веса растянет пружину на 6 дюймов?
Расстояние, на которое падает объект, прямо пропорционально квадрату времени падения. Мяч падает с высоты 45 футов за 3 секунды.
- ⓐ Напишите уравнение, связывающее расстояние со временем.
- ⓑ На какое расстояние упадет мяч через 7 секунд?
ⓐⓑ 245 футов
Максимальная нагрузка, которую может выдержать балка, напрямую зависит от квадрата диагонали поперечного сечения балки.Балка с диагональю 6 дюймов выдержит максимальную нагрузку 108 фунтов.
- ⓐ Напишите уравнение, связывающее нагрузку с диагональю поперечного сечения.
- ⓑ Какая нагрузка будет на балку с диагональю опоры 10 дюймов?
Площадь круга изменяется прямо пропорционально квадрату радиуса.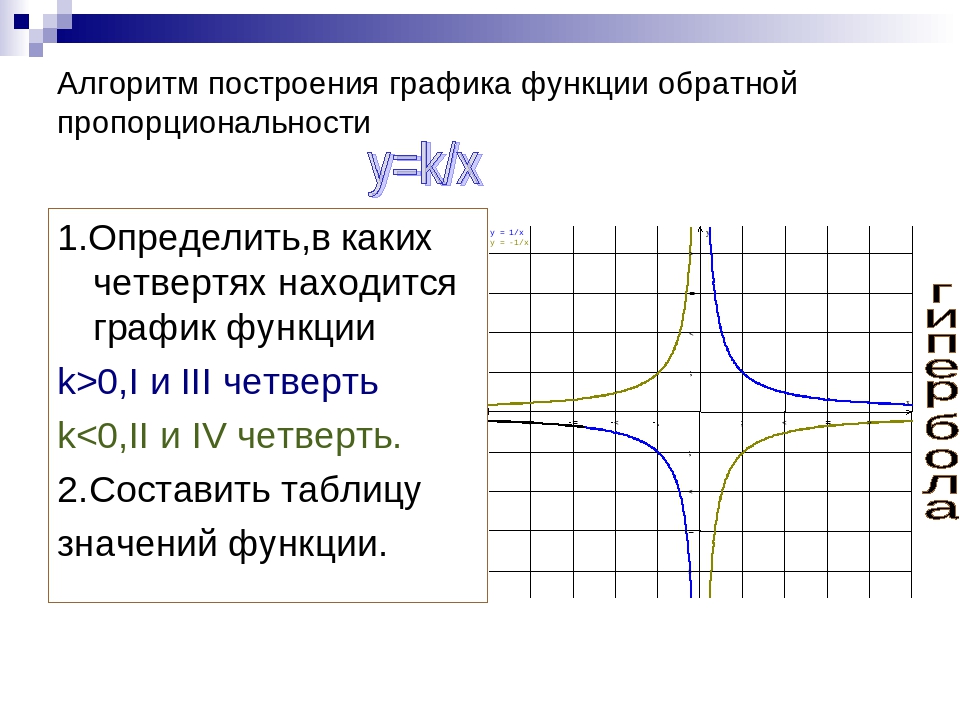 Круглая пицца радиусом 6 дюймов имеет площадь 113,04 квадратных дюйма.
Круглая пицца радиусом 6 дюймов имеет площадь 113,04 квадратных дюйма.
- ⓐ Напишите уравнение, связывающее площадь с радиусом.
- ⓑ Какова площадь личной пиццы радиусом 4 дюйма?
ⓐⓑ
Расстояние, на которое падает объект, прямо пропорционально квадрату времени падения.Мяч падает на 72 фута за 3 секунды,
- ⓐ Напишите уравнение, связывающее расстояние со временем.
- ⓑ На какое расстояние упадет мяч за 8 секунд?
Решение обратных вариационных задач
В следующих упражнениях решите.
Напишите уравнение обратной вариации для решения следующих задач.
Расход топлива (миль на галлон) автомобиля обратно пропорционален его весу.Toyota Corolla весит 2800 фунтов и расходует 33 мили на галлон на шоссе.
- ⓐ Напишите уравнение, связывающее количество миль на галлон с весом автомобиля.

- ⓑ Какой расход топлива будет у Toyota Sequoia весом 5500 фунтов?
ⓐⓑ 16,8 миль на галлон
Стоимость автомобиля обратно пропорциональна его возрасту. Джеки купила 10-летнюю машину за 2400 фунтов стерлингов.
- ⓐ Напишите уравнение, связывающее стоимость автомобиля с его возрастом.
- ⓑ Сколько будет стоить машина Джеки, когда ей исполнится 15 лет?
Время, необходимое для опорожнения резервуара, обратно пропорционально скорости откачки.Джанет потребовалось 5 часов, чтобы откачать свой затопленный подвал с помощью насоса, рассчитанного на 200 галлонов в минуту,
.- ⓐ Напишите уравнение, связывающее количество часов с производительностью насоса.
- ⓑ Сколько времени потребуется Джанет, чтобы прокачать свой подвал, если она использует насос мощностью 400 галлонов в минуту?
ⓐⓑ
Объем газа в сосуде изменяется обратно пропорционально давлению на газ. Контейнер с гелием имеет объем 370 кубических дюймов под давлением 15 фунтов на квадратный дюйм.
Контейнер с гелием имеет объем 370 кубических дюймов под давлением 15 фунтов на квадратный дюйм.
- ⓐ Напишите уравнение, связывающее объем с давлением.
- ⓑ Каков будет объем этого газа, если давление увеличить до 20 фунтов на квадратный дюйм?
На струнном инструменте длина струны изменяется обратно пропорционально частоте ее колебаний. 11-дюймовая струна на скрипке имеет частоту 400 циклов в секунду.
- ⓐ Напишите уравнение, связывающее длину струны с ее частотой.
- ⓑ Какова частота 10-дюймовой струны?
ⓐⓑ 440 циклов в секунду
Пол, дантист, определил, что количество кариеса, которое развивается во рту его пациента каждый год, изменяется обратно пропорционально количеству минут, затрачиваемых на чистку зубов каждую ночь.У его пациентки, Лори, было 4 кариеса при чистке зубов в течение 30 секунд (0,5 минуты) каждую ночь.
- ⓐ Напишите уравнение, связывающее количество кариеса со временем, затрачиваемым на чистку зубов.

- ⓑ Сколько кариесов, по мнению Пола, будет у Лори, если бы она чистила зубы по 2 минуты каждый вечер?
Количество билетов на спортивный сбор средств обратно пропорционально цене каждого билета. Брианна может купить 25 билетов по 5 евро каждый.
- ⓐ Напишите уравнение, связывающее количество билетов с ценой каждого билета.
- ⓑ Сколько билетов могла бы купить Брианна, если бы каждый билет стоил ?2,50?
ⓐⓑ 50 билетов
Закон Бойля гласит, что если температура газа остается постоянной, то давление изменяется обратно пропорционально объему газа. Брейдон, аквалангист, имеет баллон, вмещающий 6 литров воздуха под давлением 220 фунтов на квадратный дюйм.
- ⓐ Напишите уравнение, связывающее давление с объемом.
- ⓑ Если давление увеличится до 330 фунтов на квадратный дюйм, сколько воздуха сможет вместить баллон Брейдона?
Смешанная практика
Если изменяется прямо как и найдите уравнение, которое связывает
Сила, необходимая для разрушения доски, обратно пропорциональна ее длине. Если Том использует 20 фунтов давления, чтобы сломать доску длиной 1,5 фута, сколько фунтов давления ему потребуется, чтобы сломать доску длиной 6 футов?
Если Том использует 20 фунтов давления, чтобы сломать доску длиной 1,5 фута, сколько фунтов давления ему потребуется, чтобы сломать доску длиной 6 футов?
Количество часов, необходимое для таяния льда, обратно пропорционально температуре воздуха. Глыба льда тает за 2,5 часа при температуре 54 градуса. За какое время растает тот же кусок льда, если температура будет 45 градусов?
Длина растяжения пружины напрямую зависит от груза, размещенного на конце пружины.Когда Мередит поместила дыню весом 6 фунтов на подвесные весы, пружина растянулась на 2 дюйма. Насколько растянулась бы пружина, если бы мускусная дыня весила 9 фунтов?
Сумма, которую получает Джун, напрямую зависит от количества часов, которые она отработала. Когда она отработала 15 часов, ей заплатили 111 фунтов стерлингов. Сколько ей заплатят за 18 часов работы?
Расход топлива (миль на галлон) автомобиля обратно пропорционален его весу. Ford Focus весит 3000 фунтов и получает 28.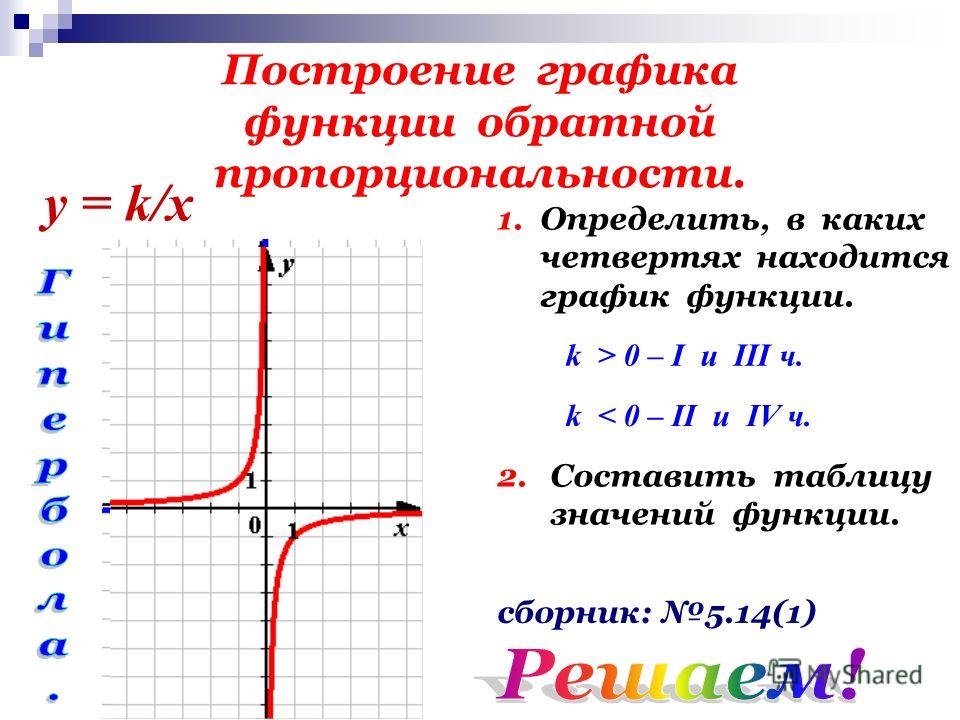 7 литров по трассе. Каким будет расход топлива для Ford Expedition, который весит 5500 фунтов? Округлите до десятых.
7 литров по трассе. Каким будет расход топлива для Ford Expedition, который весит 5500 фунтов? Округлите до десятых.
Объем газа в сосуде изменяется обратно пропорционально давлению на газ. Если емкость с аргоном имеет объем 336 кубических дюймов при давлении 2500 фунтов на квадратный дюйм, каков будет его объем, если давление уменьшится до 2000 фунтов на квадратный дюйм?
Расстояние, на которое падает объект, прямо пропорционально квадрату времени падения.Если объект упадет на 52,8 фута за 4 секунды, как далеко он упадет за 9 секунд?
Площадь поверхности колеса обозрения прямо пропорциональна квадрату его радиуса. Если площадь одной стороны колеса обозрения диаметром 150 футов составляет 70 650 квадратных футов, какова площадь одной стороны колеса обозрения диаметром 16 футов?
Математика на каждый день
Служба поездок Стоимость поездки из центра города в аэропорт, расстояние до которого составляет 14 миль, составляет 35 фунтов стерлингов.
- ⓐ Напишите уравнение, связывающее стоимость c с количеством миль м .
- ⓑ Сколько будет стоить поездка на 22 мили с этой услугой?
ⓐⓑ ?55
Дорожное путешествие Количество часов, которое требуется Джеку, чтобы добраться из Бостона в Бангор, обратно пропорционально его средней скорости движения. Когда он едет со средней скоростью 40 миль в час, ему требуется 6 часов на поездку.
- ⓐ Напишите уравнение, связывающее количество часов ч со скоростью с.
- ⓑ Сколько времени займет поездка, если его средняя скорость будет 75 миль в час?
Письменные упражнения
Своими словами объясните разницу между прямой вариацией и обратной вариацией.
Придумайте из своего жизненного опыта пример обратной вариации.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.
ⓑ Изучив контрольный список, как вы думаете, хорошо ли вы подготовились к следующей главе? Почему или почему нет?
Упражнения на обзор главы 8
Упростить рациональные выражения
Определение значений, для которых рациональное выражение не определено
В следующих упражнениях определите значения, для которых рациональное выражение не определено.
Оценка рациональных выражений
В следующих упражнениях оцените рациональные выражения для заданных значений.
Упрощение рациональных выражений
В следующих упражнениях упрощайте.
Упрощение рациональных выражений с противоположными множителями
В следующих упражнениях упрощайте.
Сложение и вычитание рациональных выражений с общим знаменателем
Сложение рациональных выражений с общим знаменателем
В следующих упражнениях доп.
Вычитание рациональных выражений с общим знаменателем
В следующих упражнениях вычтите.
Сложение и вычитание рациональных выражений, знаменатели которых противоположны
В следующих упражнениях сложите и вычтите.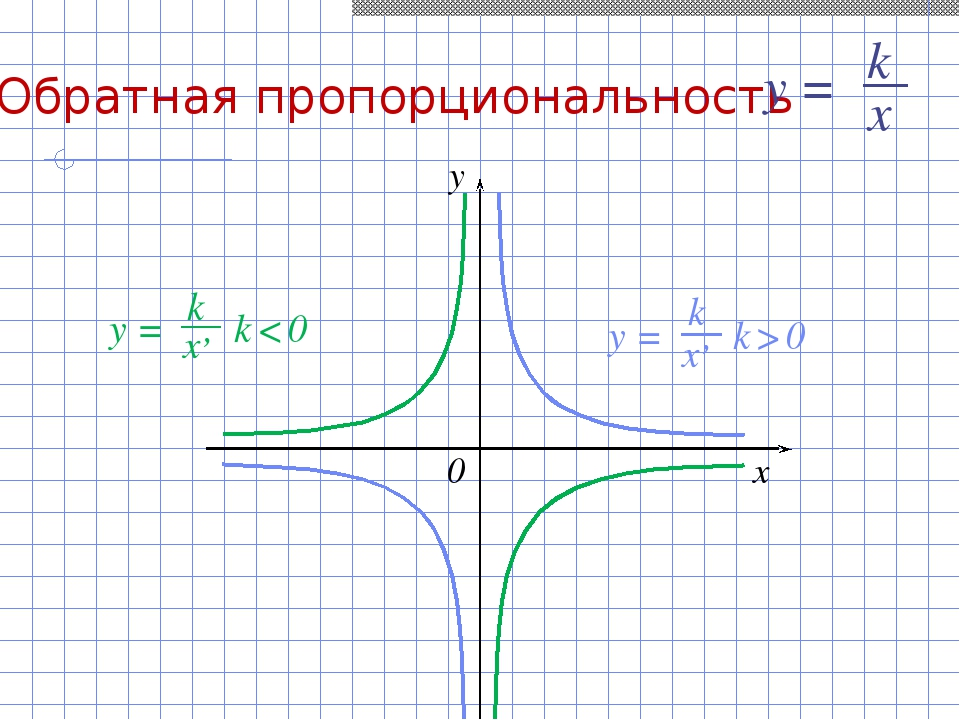
Сложение и вычитание рациональных выражений с отличающимися знаменателями
Найдите наименьший общий знаменатель рациональных выражений
В следующих упражнениях найдите ЖК-дисплей.
Найти эквивалентные рациональные выражения
В следующих упражнениях перепишите как эквивалентные рациональные выражения с заданным знаменателем.
Переписать как эквивалентные рациональные выражения со знаменателем:
Переписать как эквивалентные рациональные выражения со знаменателем:
Переписать как эквивалентные рациональные выражения со знаменателем:
Добавление рациональных выражений с разными знаменателями
В следующих упражнениях доп.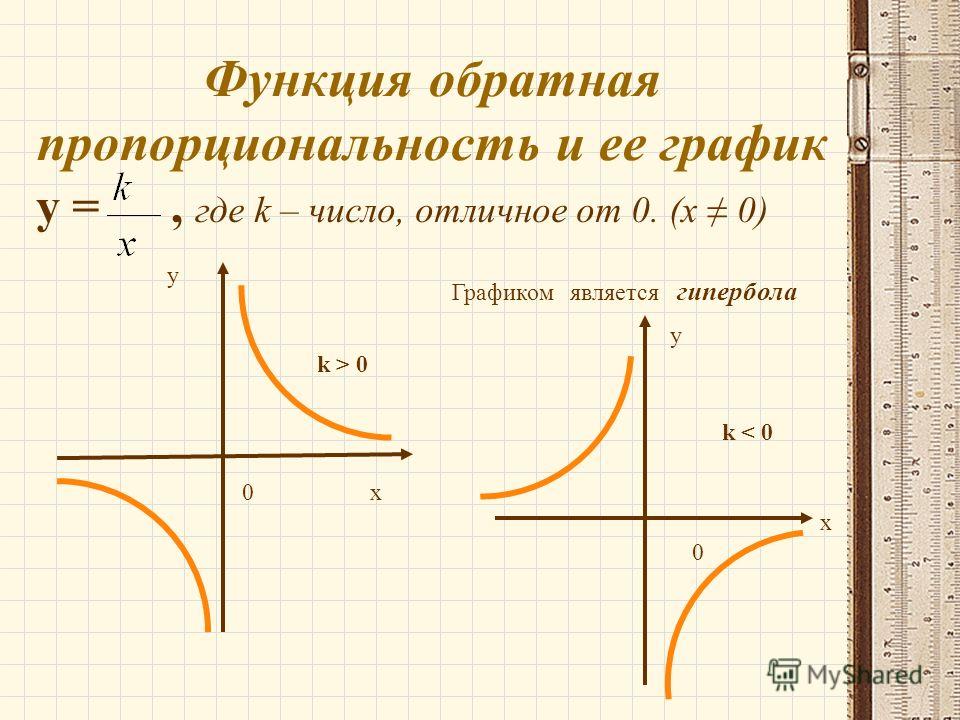
Вычитание рациональных выражений с разными знаменателями
В следующих упражнениях вычитание и сложение.
Упрощение сложных рациональных выражений
Упростите сложное рациональное выражение, записав его в виде деления
В следующих упражнениях упрощайте.
Упрощение сложного рационального выражения с помощью ЖК-дисплея
В следующих упражнениях упрощайте.
Решение рациональных уравнений
Решение рациональных уравнений
В следующих упражнениях решите.
Решение рационального уравнения для определенной переменной
В следующих упражнениях найдите указанную переменную.
Решить пропорцию и сходство приложений с похожими фигурами
Решение пропорций
В следующих упражнениях решите.
В следующих упражнениях решите пропорции.
Рэйчел выпила клубничный коктейль на 21 унцию, содержащий 739 калорий.Сколько калорий в коктейле на 32 унции?
Лео отправился в Мексику на рождественские каникулы и обменял 525 долларов на мексиканские песо. В то время по обменному курсу 1 доллар США был равен 16,25 мексиканских песо. Сколько мексиканских песо он получил за поездку?
Сколько мексиканских песо он получил за поездку?
Решайте задачи с похожими фигурами
В следующих упражнениях решите.
∆ABC похож на ∆XYZ. На рисунке даны длины двух сторон каждого треугольника.Найдите длины третьих сторон.
На карте Европы Париж, Рим и Вена образуют треугольник, стороны которого показаны на рисунке ниже. Если фактическое расстояние от Рима до Вены равно 700 милям, найдите расстояние, равное
.- ⓐ Париж в Рим
- ⓑ Париж в Вену
Рост Тони 5,75 фута. Однажды вечером его тень была 8 футов в длину. В то же время тень соседнего дерева была 32 фута в длину.Найдите высоту дерева.
Высота маяка в Пенсаколе, штат Флорида, составляет 150 футов. Стоя рядом со статуей, Натали ростом 5,5 футов отбрасывает тень длиной 1,1 фута. Какой длины будет тень маяка?
Решение задач равномерного движения и рабочих приложений
Решение задач равномерного движения
В следующих упражнениях решите.
Возвращаясь в 5 часов домой от родителей, Лиза попала в плохую погоду.Она смогла проехать 176 миль в хорошую погоду, но затем, двигаясь на 10 миль в час медленнее, проехала 81 милю в плохую погоду. С какой скоростью она ехала в плохую погоду?
Марк летит на самолете, который может пролететь 490 миль при скорости попутного ветра 20 миль в час и 350 миль при скорости попутного ветра 20 миль в час. Какова скорость самолета?
Джон может ехать на велосипеде со скоростью 8 миль в час быстрее, чем Люк может ехать на своем велосипеде. Люку требуется на 3 часа больше, чем Джону, чтобы проехать 48 миль.Как быстро Джон может ездить на велосипеде?
Марк готовился к триатлону. Он пробежал 8 километров и проехал на велосипеде 32 километра за 3 часа. Его скорость бега была на 8 километров в час меньше скорости езды на велосипеде. Какова была его скорость бега?
Рабочие приложения Solve
В следующих упражнениях решите.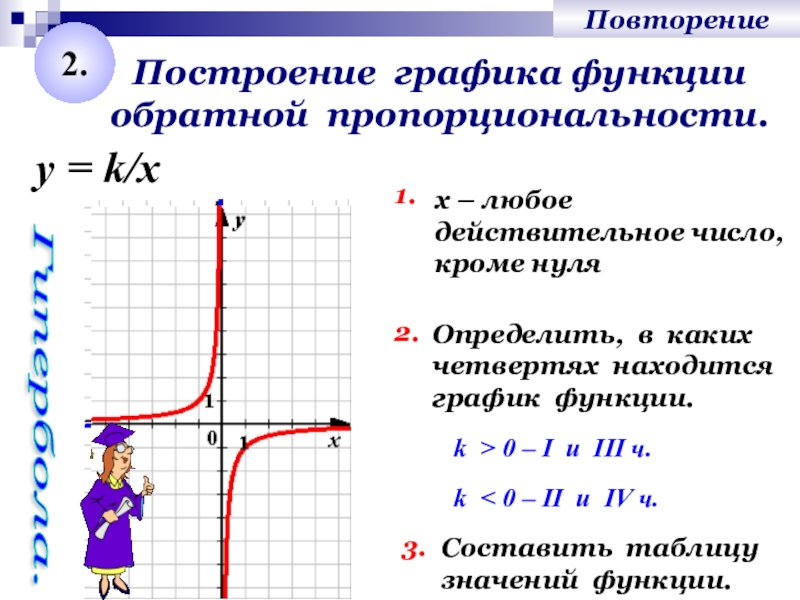
Джерри может построить комнату за 1 час, а Джейк за 4 часа. Как долго они смогут создать комнату, работая вместе?
Лизе требуется 3 часа, чтобы подстричь газон, а ее кузине Барб — 2 часа.Как долго они будут работать вместе?
Джеффри может покрасить дом за 6 дней, но если у него есть помощник, он может сделать это за 4 дня. Сколько времени понадобится помощнику, чтобы покрасить дом в одиночку?
Сью и Деб вместе пишут книгу, на которую у них уходит 90 дней. Если бы Сью работала одна, это заняло бы у нее 120 дней. Сколько времени потребуется Деб, чтобы написать книгу в одиночку?
Использование прямой и обратной вариации
Решение задач прямого изменения
В следующих упражнениях решите.
Ванесса едет к своему жениху. Расстояние, d , прямо зависит от скорости, v , которую она проезжает. Если она проедет 258 миль со скоростью 60 миль в час, как далеко она проедет со скоростью 70 миль в час?
Если она проедет 258 миль со скоростью 60 миль в час, как далеко она проедет со скоростью 70 миль в час?
Если стоимость пиццы напрямую зависит от ее диаметра, и если пицца диаметром 8 дюймов стоит 12 фунтов стерлингов, сколько будет стоить пицца диаметром 6 дюймов?
Расстояние до остановки автомобиля зависит от квадрата его скорости.Чтобы остановить автомобиль, движущийся со скоростью 50 миль в час, требуется 200 футов. Сколько футов потребуется, чтобы остановить автомобиль, движущийся со скоростью 60 миль в час?
Решение обратных вариационных задач
В следующих упражнениях решите.
Количество билетов на музыкальный сбор средств обратно пропорционально цене билетов. Если у Мадлен достаточно денег, чтобы купить 12 билетов по 6 фунтов стерлингов, сколько билетов Мадлен может позволить себе купить, если цена вырастет до 8 фунтов стерлингов?
На струнном инструменте длина струны изменяется обратно пропорционально частоте ее колебаний. Если 11-дюймовая струна на скрипке имеет частоту 360 циклов в секунду, какую частоту имеет 12-дюймовая струна?
Если 11-дюймовая струна на скрипке имеет частоту 360 циклов в секунду, какую частоту имеет 12-дюймовая струна?
Практический тест
В следующих упражнениях упрощайте.
В следующих упражнениях выполните указанную операцию и упростите.
В следующих упражнениях решите каждое уравнение.
В следующих упражнениях решите.
Рекомендуемая доза эритромицина для собак составляет 5 мг на каждый фунт веса собаки. Если Дейзи весит 25 фунтов, сколько миллиграммов эритромицина должен назначить ветеринар?
Джулия провела 4 часа в воскресенье днем, занимаясь в тренажерном зале. Она пробежала на беговой дорожке 10 миль, а затем проехала на велосипеде 20 миль. Ее скорость на велосипеде была на 5 миль в час выше, чем скорость бега на беговой дорожке. Какова была ее скорость бега?
Ее скорость на велосипеде была на 5 миль в час выше, чем скорость бега на беговой дорожке. Какова была ее скорость бега?
Курт может проехать на велосипеде 30 миль по ветру за то же время, что и 21 милю против ветра. Если скорость ветра 6 миль в час, какова скорость Курта на его велосипеде?
Аманда пробегает до парка 8 миль по одному маршруту, а затем возвращается по 14-мильному маршруту. Обратный путь занимает у нее на 1 час больше времени, чем пробежка в парке. Найдите скорость ее бега.
Опытный мойщик окон может вымыть все окна в доме Майка за 2 часа, а новичок может вымыть все окна за 7 часов. Сколько времени им потребуется, чтобы работать вместе?
Джош может расколоть грузовик с бревнами за 8 часов, но, работая с его отцом, они могут сделать это за 3 часа. Сколько времени потребуется отцу Джоша, работающему в одиночку, чтобы расколоть бревна?
Цена, которую Тайлер платит за бензин, напрямую зависит от количества галлонов, которые он покупает.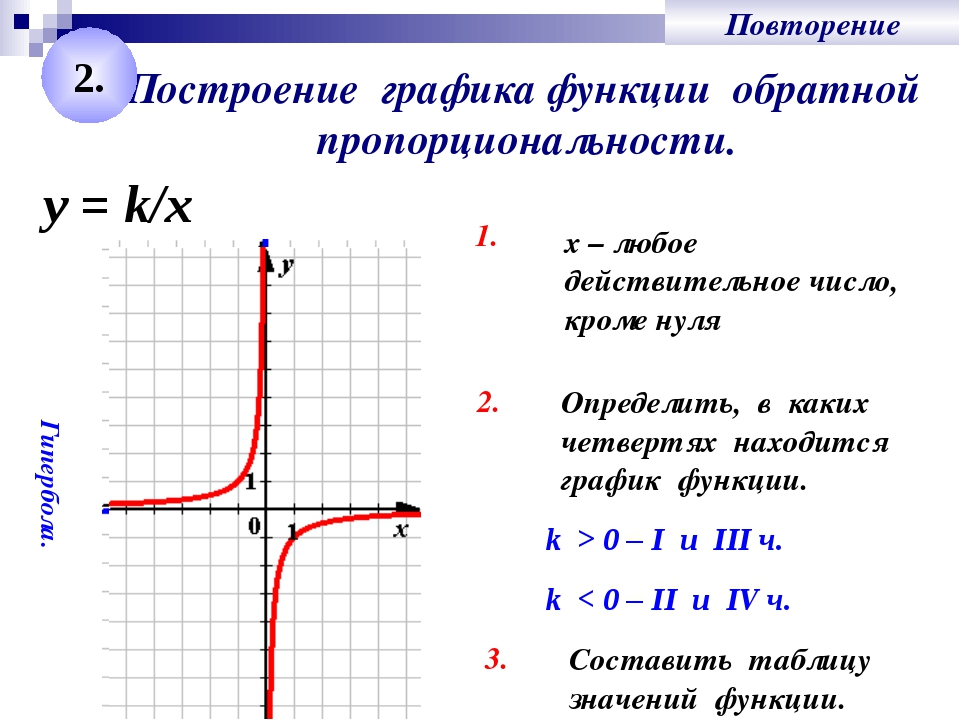 Если 24 галлона стоили ему 59,76 фунта стерлингов, сколько стоили бы 30 галлонов?
Если 24 галлона стоили ему 59,76 фунта стерлингов, сколько стоили бы 30 галлонов?
Объем газа в сосуде обратно пропорционален давлению на газ. Если контейнер с азотом имеет объем 29,5 литров при 2000 фунтов на квадратный дюйм, каков объем, если баллон имеет рейтинг 14,7 фунтов на квадратный дюйм? Округлить до ближайшего целого числа.
Города Дейтон, Колумбус и Цинциннати образуют треугольник в южном Огайо, как показано на рисунке ниже, на котором показаны расстояния между этими городами на карте в дюймах.
Фактическое расстояние от Дейтона до Цинциннати составляет 48 миль. Какое на самом деле расстояние между Дейтоном и Колумбусом?
.
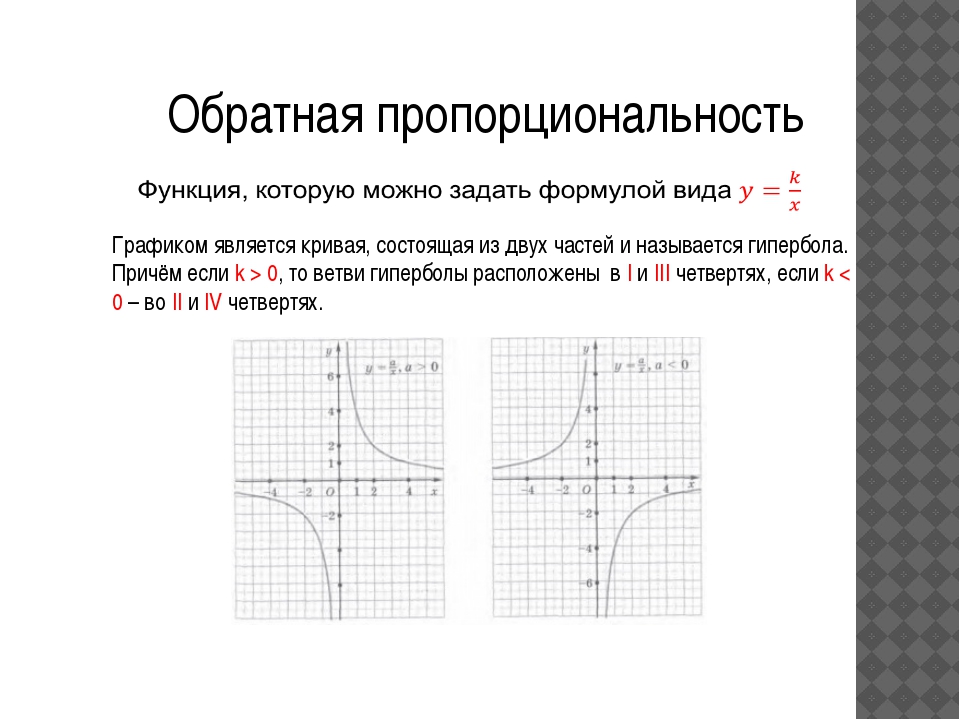
 3), определяет, будет ли граф шире или уже.
3), определяет, будет ли граф шире или уже. x, где a — положительная константа, а переменная x — степень, называется показательным уравнением .х всегда положителен.
x, где a — положительная константа, а переменная x — степень, называется показательным уравнением .х всегда положителен.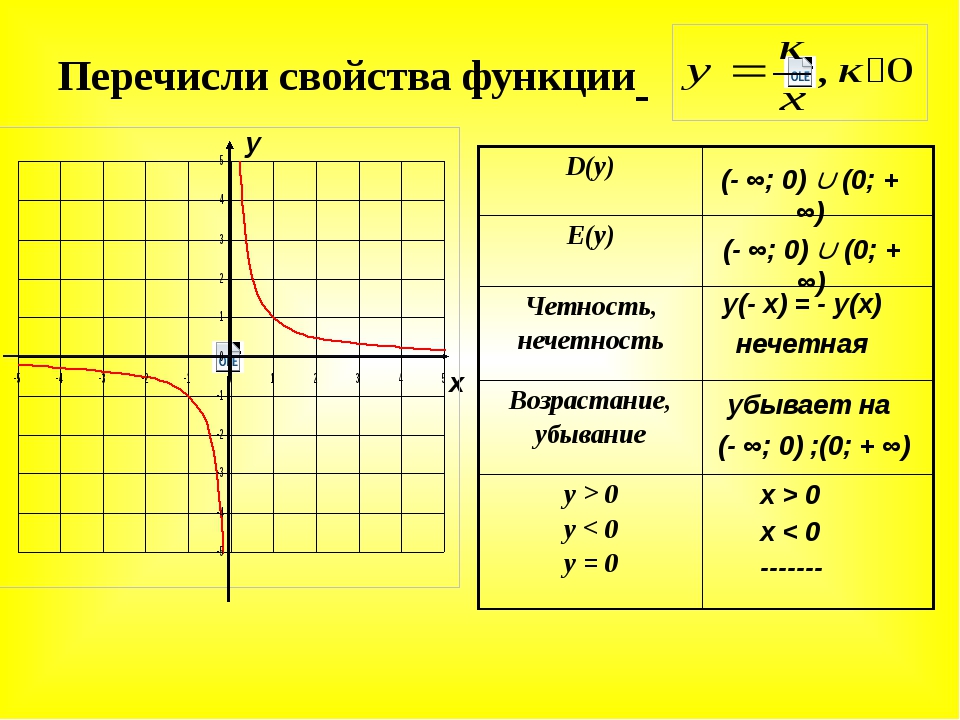
 Это дает нам представление о том, что мы можем найти k, поскольку значения x и y заданы.
Это дает нам представление о том, что мы можем найти k, поскольку значения x и y заданы.