Методическая разработка по математике (4 класс) по теме: Геометрические задачи

УПРАЖНЕНИЯ И ГОЛОВОЛОМКИ СО СПИЧКАМИ

1. «Три».

Положите пять спичек (как на рисунке).

Прибавьте к ним ещё пять спичек так, чтобы получилось три.

Если дети затрудняются с решением, то учитель подсказывает, что должно получиться слово «три».

Ответ:

2. «Сто».

Приложите к четырем спичкам пять спичек так, чтобы получилось сто.

Ответ:

3. «Весы».

Весы составлены из девяти спичек и не находятся в состоянии равновесия. Требуется переложить в них пять спичек так, чтобы весы были в равновесии.

Ответ:

4. «Два фужера».

Два фужера составлены из десяти спичек. Переложить шесть спичек так, чтобы получился дом.

Ответ:

5. «Храм».

Этот греческий храм построен из одиннадцати спичек. Требуется переложить четыре спички так, чтобы получилось пятнадцать квадратов.

Ответ:

6. «Ключ».

Из десяти спичек сделан ключ. Переложить в нём четыре спички так, чтобы получилось три квадрата.

Ответ:

7. «Три квадрата».

Построена фигура, как на рисунке ниже. Переложить в ней пять спичек так, чтобы получилось три квадрата.

Ответ:

8. Решите древнюю головоломку. Из этих фигур нужно сложить прямоугольник, у которого все стороны равны. (Это квадрат!)

Ответ:

9.  Как   из  двух  спичек   сделать   десять  и  пятьдесят,  не  ломая  их?  (,.)

Нельзя  ли  из  трёх  спичек  сделать  шесть,  девять  и  сто, не ломая их? (,,.)

Как из четырех спичек сделать двенадцать, сорок, шестьдесят и тысячу, не ломая их?
(,,,.)

10. В каждом из этих примеров есть ошибка. Чтобы её исправить, следует переложить всего по одной спичке

                (Ответ:.)

                (Ответ:.)

                (Ответ:.)

        (Ответ:.)

                (Ответ:.)

        (Ответ:.)

                (Ответ:.)

11. Разрежь фигуру.

а) Из 9 одинаковых квадратов составили фигуру. Разрежь её на три части равной площади.

б) Разрежь раскрашенную фигуру на 2 равные части так, чтобы из них можно было составить прямоугольник.

в) Разрежьте треугольник на 3 части так, чтобы из получившихся частей можно было бы сложить прямоугольник.

г) Пирог прямоугольной формы двумя разрезами раздели на 4 части так, чтобы две из них были четырехугольной формы, а две – треугольной формы.

д) Раздели прямой линией циферблат часов на 2 части так, чтобы суммы чисел в этих частях были равными.

е) Квадрат разрежь на 2 неравные части и составь из них треугольник.

Ответы:

а)

б)

в)                                         г)

д)                                         е)

12. Линии и точки.

а) На прямой поставлены 4 точки. Сколько всего получилось отрезков, концами которых являются эти точки?

Ответ: 6 отрезков.

б) Незнайка начертил 3 прямых линии. На каждой из них отметил три точки. Всего Незнайка отметил 6 точек. Покажи, как это он мог сделать.

Ответ:

в) Перечеркни 9 точек отрезками, не отрывая карандаша от бумаги.

                                Ответ:

                

13. Обведи (нарисуй) фигуры, не отрывая карандаша от бумаги и не проводя дважды по одной и той же линии.

а)                

Ответ: Сначала  проведи  диагональ,  потом обведи сам квадрат, а затем – окружность

б)         

Ответ: Сначала проведи звезду, а потом – пятиугольник.

в)

Ответ: Сначала обведи внутреннюю фигуру из двух треугольников, а потом внешний контур.

14. Разгадайте кроссворд и найдите в нем лишнее слово.

1. Что образуют два луча, выходящие из одной точки?

2. Что получим, если на некотором расстоянии друг от друга на прямой поставить две точки?

3. Родственник круга, но больше похож на яйцо птицы.

4. В нем 100 см или 10 дм.

5. Замкнутая ломаная из трех звеньев.

6. Что можно поставить на листе бумаги ручкой, чаще в конце предложения.

7. Что это за фигура: четыре стороны равны, а все углы обязательно прямые.

8. Какой линией можно соединить три точки, которые находятся не на одной прямой.

9. Как называется линия, которая образует пятиугольник.

Ответ: 1. Угол. 2. Отрезок. 3. Овал. 4. Метр. 5. Треугольник. 6. Точка. 7. Квадрат. 8. Кривая. 9. Ломаная.

15. Поверни избушку (задача со спичками).

Учитель. Чтобы получить карту сегодняшнего путешествия по сказкам, надо повернуть эту избушку на курьих ножках.

Задание: как переложить две спички, чтобы избушка повернулась другой стороной?

                                        Ответ:

16. Отгадайте кроссворды и найдите зашифрованные слова.

1. В одном метре десять ….

2. В этой единице массы измеряются вес человека.

3. В одном дециметре десять ….

4. Запись, составленная из чисел, букв и знаков арифметических действий.

5. Выполненное из прозрачного материала, с помощью которого можно измерять площадь фигуры.

Ответы: 1. Дециметр. 2. Килограмм. 3. Сантиметр. 4. Выражение. 5. Палетка.

1. Специальные знаки для записи чисел.

2. Единица длины.

3. Числа от нуля, используемые при счете.

4. Название угла меньше прямого.

5. На него нельзя делить.

6. Самая маленькая из известных вам единиц длины.

7. Самая большая единица длины.

Ответы: 1. Цифра. 2. Метр. 3. Натуральные. 4. Острый. 5. Нуль. 6. Миллиметр. 7. Километр.

Ответы:  По вертикали:  4.  Полночь.  5.  Полтинник. По горизонтали: 1. Четверть. 2. Доля. 3. Каникулы.

По горизонтали:

1. Единица длины.

2. Фамилия древнегреческого математика.

3. Наименьшее трехзначное число.

4. Однозначное число.

5. Результат сложения.

6. Прямоугольник с равными сторонами.

7. Один из компонентов деления.

8. Математическое выражение, требующее выполнения некоторых действий над числами.

9. Математический знак в виде полумесяца.

10 Упражнение, для выполнения которого необходимо думать, вычислять, записывать ответ.

По вертикали:

11. Царица наук.

Ответы: По горизонтали: 1. Метр. 2. Пифагор. 3. Сто. 4. Семь. 5. Сумма. 6. Квадрат. 7. Делитель. 8. Периметр. 9. Скобка. 10. Задача. По вертикали: 11. Математика.

По горизонтали:

2. Знак математического действия.

4. Запись из одной или нескольких цифр.

5. Часть прямой, соединяющая две точки.

7. Многоугольник.

8. Математическое действие.

9. Старинная мера длины.

По вертикали:

1. Часть прямой.

2. Геометрическая фигура.

3. Математическое действие.

6. Упражнения, выполняемые с помощью рассуждений и вычислений.

7. Число разрядов в классе.

Ответы: По горизонтали: 2. Плюс. 4. Число. 5. Отрезок. 7. Треугольник. 8. Деление. 9. Пядь. По вертикали: 1. Луч. 2. Плоскость. 3. Сложение. 6. Задачи. 7. Три.

По горизонтали:

1. Трехзначное число.

2. Старая русская единица длины.

8. Единица измерения времени.

9. Математическое действие.

10. Равенство, содержащее букву.

13. Тысячная часть числа.

14. Десятая часть основной единицы длины.

По вертикали:

2. Буква латинского алфавита.

4. Черта на шкале.

5. Неметрическая мера объема.

6. Старая русская мера массы.

7. Наименьшее натуральное число.

11. Образцовое средство измерения.

12. Объем килограмма воды.

Ответы: По горизонтали: 1. Триста. 3. Вершок. 8. Секунда. 9. Деление. 10. Уравнение. 13. Промилле. 14. Дециметр. По вертикали: 2. Игрек. 4. Штрих. 5. Баррель. 6. Фунт. 7. Единица. 11. Мера. 12 Литр.

НЕСТАНДАРТНЫЕ ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ — Студопедия.Нет

В НАЧАЛЬНОМ КУРСЕ МАТЕМАТИКИ

Шипилова А. Э. ( ФГБОУ ВО «Оренбургский государственный педагогический университет» )

Научный руководитель – Л. А. Гороховцева, канд. пед. наук, доцент

 

Включение нестандартных геометрических задач в начальный курс математики оказывает положительное влияние на развитие пространственного воображения младших школьников, которое заявлено одним из требований к результатам освоения основной образовательной программы начального общего образования Федерального государственного образовательного стандарта в области математики и информатики.

Решение таких задач способствует не только развитию пространственного, но и образного мышления детей младшего школьного возраста, которое приводит к успешному усвоению учащимися систематического курса геометрии.

Анализ методической литературы показывает, что понятие «нестандартная задача» активно используется различными авторами в русле концепции развивающего обучения младших школьников математике, так как в ходе самостоятельного творческого открытия решения таких задач учащиеся активно овладевают различными приемами умственной деятельности, расширяют свои математические знания и области их применения.

Уточним определение понятия «нестандартная геометрическая задача», включающее в себя понятие нестандартная задача, то есть задача, содержащая геометрический материал и требующая ориентации в практическом и теоретическом пространстве (как видимом, так и воображаемом), алгоритм решения которой учащимся неизвестен.

Автор А. К. Мендыгалиева выделяет следующие виды нестандартных геометрических задач в начальном курсе математики: «Геометрические головоломки, геометрия в пространстве, геометрия на клетчатой бумаге. Это такие задачи, решение которых базируется на основных понятиях планиметрии, свойствах плоских фигур и логических рассуждениях, либо практических действиях» [1, с. 688].

Нестандартные геометрические задачи мы встречаем на страницах всех учебников математики для начальных классов. Одновременно с изучением арифметического материала выстраивается система для освоения понятий геометрии, которая включает в себя задания нестандартного характера. Виды и объем представленных нестандартных геометрических задач значительно отличаются в учебниках разных авторов, что приводит к различному уровню осмысления детьми пространственных отношений окружающей действительности, а следовательно и геометрического материала в целом.  

Проблема обучения младших школьников решению нестандартных геометрических задач актуальна в методике преподавания математики в начальной школе, она также важна и с позиции расширения возможностей наглядного обучения геометрии. Как утверждает И.В. Шадрина:
«При изучении геометрии младшими школьниками недостаточно опираться только на непосредственное созерцание. Наглядное обучение геометрии в начальной школе должно обеспечить учащимся возможность оперировать предметными моделями идеальных геометрических фигур, выявлять геометрические факты методами физического эксперимента. Любое новое знание должно быть получено в процессе активных действий самого ребенка, а не ограничиваться наблюдениями за действиями других. Организованная на такой основе познавательная деятельность позволяет ему думать «руками и глазами», практически преобразуя предмет изучения

в соответствии с поставленной целью» [2, с. 142–143].

Литература

1. Мендыгалиева, А. К. Некоторые виды нестандартных задач в начальном курсе математики // Научно-методический электронный журнал «Концепт». – 2016. – Т. 17. – С. 686–690.

2. Шадрина, И. В. Обучение математике в начальных классах / И. В. Шадрина. – М. : Школьная пресса, 2003. – 144 с.

 

ЗАНЯТИЕ КАК ФОРМА ОРГАНИЗАЦИИ РЕГЛАМЕНТИРОВАННОЙ

ДЕЯТЕЛЬНОСТИ В УЧРЕЖДЕНИИ ДОШКОЛЬНОГО ОБРАЗОВАНИЯ

Шульга М. В. (УО МГПУ им. И. П. Шамякина, Мозырь)

Научный руководитель – Т. А. Пазняк, ст. преподаватель

Занятие является основной формой организации образовательного процесса в учреждении дошкольного образования

Целью нашего исследования являлось: изучение особенностей занятий как основной формы организации образовательного процесса в учреждении дошкольного образования.

Объект исследования – образовательный процесс учреждения дошкольного образования. Предметом нашего исследования является занятие.

Главными формами организации жизни в детском саду являются игра и связанные с нею формы активности, занятия, предметно-практическая деятельность. Значительное место в жизни детского сада принадлежит занятиям. Занятия должны носить развивающий характер, обеспечивать максимальную активность, самостоятельность процесса познания, способствовать формированию у воспитанников самостоятельности, способности к совместной координированной деятельности, развитию любознательности и познавательных интересов [1, с. 16]. Занятия в учреждении дошкольного образования имеют следующую структуру:

Начало занятия предполагает непосредственную организацию детей: необходимо переключить их внимание на предстоящую деятельность, вызвать интерес к ней, создать соответствующий эмоциональный настрой, раскрыть учебную задачу. Ход (процесс) занятия – это самостоятельная умственная или практическая деятельность детей, заключающаяся в усвоении знаний и умений, которые определены учебной задачей. Окончание занятия – посвящено подведению итогов и оценке результатов учебной деятельности детей. Качество полученного результата зависит от возраста и индивидуальных особенностей детей, от сложности учебной задачи. Виды занятий: 1. Комбинированное: занятие имеет определенную цель, объединенную конкретной тематикой, и может комбинировать в себе несколько задач: усвоение знаний умений и навыков, творческое применение и получение знаний. 2. Тематические: организуются, если планирование носит тематический принцип. Посвящается чаще всего таким темам, как времена года, природные явления, творчество поэтов и т. д. 3. Доминантные: отличаются от тематических тем, что имеют доминирующий вид деятельности, который является ведущим на протяжении всего занятия. 4. Интегрированные: при их проведении происходит интеграция видов деятельности. Требует логической взаимосвязи между ними. 5. Комплексное: является занятием которое предполагает организацию педагогического процесса во взаимосвязи всех его сторон . Занятие имеет три части и проводится 9–12 раз в год [2]. В зависимости от количества воспитанников на занятии: фронтальные занятия проводятся для выявления количественной и качественной оценки один раз в квартал; групповая форма организации: работа с небольшой подгруппой детей, состоящей от 3 до 8 воспитанников. Подгруппа собирается на основе личной симпатии и наличии общих интересов у детей друг к другу, личностным особенностям ребенка, но не позволяет ему взаимодействовать с другими детьми и для ребенка является дискомфортной. Индивидуальная форма организации  позволяет уделять им больше внимания. Для нее характерен ряд признаков: 1) на занятиях идет освоение детьми умений по определенному разделу обучения; 2) занятия проводятся со всеми детьми данной возрастной группы, с постоянным составом детей; 3) занятия организуются и проводятся под руководством взрослого, который определяет задачи и содержание занятия, подбирает методы и приемы, организует и направляет познавательную деятельность детей по освоению знаний, умений и навыков.

Литература

1. Житко, И. В. Планирование работы дошкольного учреждения / И. В. Житко [и др.]. – Минск, 1999. – С.16.

2. Микляева, Н. В. Дошкольная педагогика // Н. В. Микляева, Ю. В. Микляева [и др.]. – Москва : Юрайт, 2017. – 411 с.

 

Решение одной геометрической задачи несколькими способами

Решение одной геометрической задачи несколькими способами.

Автор: Бондаренко Ольга Викторовна

Введение………………………………………………………………3

1. Методы решения геометрических задач………………………5

2. Примеры решения задач данными методами…………………7

3. Решение одной геометрической задачи несколькими способами……………………………………………………10

Заключение……………………………………………………………17

Литература……………………………………………………………19

Общеизвестно, что учащиеся прочно усваивают только то, что прошло через их индивидуальные усилия. Проблема самостоятельности учащихся при обучении не является новой. Этому вопросу отводили исключительную роль ученые всех времен. Особенно четкие концепции о роли самостоятельности в приобретении знаний имеются в трудах К.Д.Ушинского, Д.И.Писарева и др. Эта проблема является актуальной и сейчас. Внимание к ней объясняется тем, что самостоятельность играет весьма важную роль не только при получении среднего образования, но и при продолжении обучения после школы , а также в дальнейшей трудовой жизни школьников.

В наше время, в условиях развития рыночной экономики, когда наблюдается небывалый рост объема информации, от каждого человека требуется высокий уровень профессионализма и такие деловые качества как предприимчивость, способность ориентироваться, быстро и безошибочно принимать решения, а это невозможно без умения работать творчески.

Математика является наиболее удобным предметом для развития творческих способностей учащихся. Этому способствует логическое построение предмета, четкая система упражнений для закрепления полученных знаний и абстрактный язык математики. Воспитание самостоятельности у учащихся постепенно в течение всего периода обучения и предусматривает способность полноценно аргументировать, выделять главное, существенное, умение рассуждать, доказывать, находить рациональные пути выполнения заданий, делать соответствующие выводы, обобщать и применять их при решение конкретных вопросов.

Сущность самостоятельной работы заключается в том, что она выполняется учеником без непосредственного участия учителя, но по его заданию и под его контролем. Существуют разные подходы к классификации самостоятельных работ . Подразделяют их на обучающие и контролирующие, творческие и репродуктивные, устные и письменные, на общие, групповые и индивидуальные, на классные и домашние.

Творческие самостоятельные работы, включающие возможность решение задач несколькими способами, составление задач и примеров самими учащимися и т.п. наиболее важны из всех видов самостоятельных работ. Они требуют от учащихся собственной инициативы, будят мысль, заставляют анализировать и осуществлять самостоятельные решения.

В своей работе я рассмотрел различные методы решения геометрических задач и применение данных методов к решению одной геометрической задачи. Во-первых, эта тема меня очень заинтересовала, когда мы проходили её на уроках геометрии, и я решил узнать больше о методах решения. Во-вторых, методы решения геометрических задач занимают особое место в математике, поскольку решение их вызывает определенные трудности у учеников и абитуриентов.

I.Методы решения геометрических задач.

Говоря о поисках решения геометрической задачи, приходится иметь ввиду, что существуют различные методы её решения. Поэтому поиски прежде всего следует направить на выбор конкретного метода. Условно можно разбить на следующие группы:

1. Традиционный метод.

Связан с использованием соотношений в треугольнике и круге, признаками равенства и подобия и др. Часто приходится проводить дополнительные построения, например, описанные окружности.

2. Метод геометрических преобразований.

Связан с применением преобразований плоскости и пространства (параллельный перенос, симметрия, гомотетия и т.п.).

3. Векторный метод.

Связан с использованием векторов, в частности скалярного и векторного произведений.

4. Тригонометрический метод.

Использует применение тригонометрии, теорем синусов и косинусов.

5. Переформулировка задачи.

Замена задачи другой, эквивалентной данной.

Перечисленные методы могут пересекаться, в одном решении может применяться несколько методов. Например, можно заменить исходную задачу другой, которую решают с помощью векторов и преобразований.

При решении геометрических задач полезно показать, что рассматриваемую задачу можно решить различными методами, и если один способ не приводит к цели или слишком громоздок, то лучше обратиться к другому. «Лучше решить одну задачу несколькими методами, чем несколько задач — одним» (Д.Пойя).

II. Примеры решения задач данными методами.

Прежде чем перейти к рассмотрению выбранной мною задачи, хотелось бы показать, как происходит поиск решения на примере, используя некоторые из вышеперечисленных методов.

З а д а ч а. Треугольники АВС и А₁В₁С₁ не имеют общих точек, кроме вершины С, и АСА₁ = ВСВ₁ = 90°, СА=СА₁, СВ=СВ₁. Доказать, что медиана СD треугольника АВС перпендикулярна прямой А₁В₁.

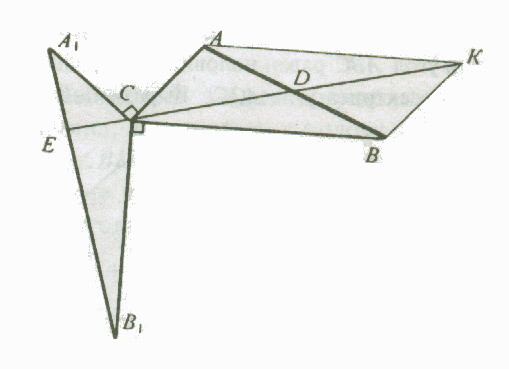
Рис.1

Заметим прежде всего те свойства фигуры, которые сразу бросаются в глаза:

1°. Треугольники АСА₁ и ВСВ₁ прямоугольные и равнобедренные.

2°. АСВ + А₁СВ₁ = 180°.

Рассмотрим различные способы использования этих свойств.

Р е ш е н и я.

1 способ. На рисунке присутствует несколько прямых углов с одной вершиной, поэтому напрашивается использование поворота на 90° вокруг точки С. Пусть при таком повороте треугольник А₁В₁С₁ переходит в треугольник А₂ВС. Тогда точки А, С и А₂ лежат на одной прямой и С – середина АА₂. Следовательно, СD есть средняя линия треугольника АВА₂ и поэтому СD А₂В. Но А₂В А₁В₁ по свойству повороту, значит, CD A₁B₁.

II способ. Воспользуемся векторным произведением векторов.

А₁В₁∙ 2CD = (СВ₁ – СА₁)(СА + СВ) = СВ₁∙СА – СА₁∙СА + СВ₁∙СВ – СА₁∙СВ = СА ∙СВ₁∙cos ACB₁ – 0 + 0 — CA∙CB∙cos A₁CB = 0, так как АСВ₁ = А₁СВ = 90° + АСВ.

Вывод: CD A₁B₁.

III способ (традиционный). Продолжим сторону АС до точки А₂ так, что АС = А₂С (рис. 1). Тогда из замеченного выше свойства 2° следует: А₂СВ = А₁СВ₁, и треугольники А₂СВ и А₁СВ₁ равны. В треугольнике АВА₂ отрезок CD – средняя линия и поэтому CD А₂В. Из равенства треугольников получаем СВМ = СВ₁М. Значит, вокруг четырехугольника МСВВ₁ можно описать окружность с диаметром ВВ_1. Отсюда угол ВМВ₁ опирается на диаметр и А₂В А₁В₁ . Следовательно, CD A₁B₁.

IV способ (традиционный). Достроим треугольник АВС до параллелограмма САКВ (рис.2).

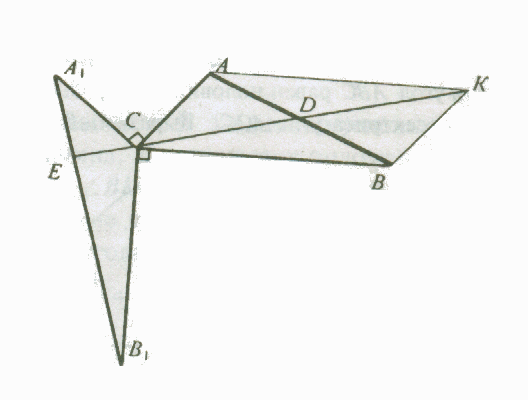
Рис.2

Тогда ∆САК = ∆А₁СВ₁ по двум сторонам и углу между ними и , следовательно, СА₁В₁ = АСК = α. Продолжим прямую СК до пересечения с отрезком А₁В₁ в точке Е. Тогда А₁СЕ = 180° — 90° — α = 90° — α, откуда следует, что А₁ЕК = 90°.

III. Решение одной геометрической задачи несколькими способами.

Ниже предлагаются девять решений одной красивой геометрической задачи. Кроме вышеперечисленных методов, здесь используются и другие, с помощью которых также можно решить рассматриваемую мною задачу.

З а д а ч а. На гипотенузе АВ прямоугольного треугольника АВС построен квадрат ABDE в той полуплоскости от прямой АВ, которой не принадлежит треугольник АВС. Найти расстояние от вершины С прямого угла до центра квадрата, если катеты ВС и АС имеют соответственно длины a и b.

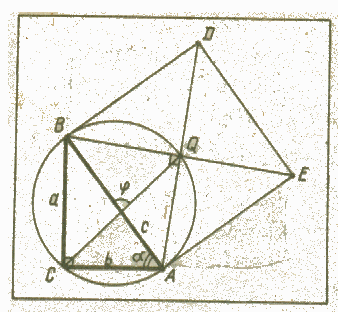
Рис.3

Решение 1 (по теореме синусов).

Пусть Q — центр построенного квадрата(рис.3). Так как угол AQB прямой, то точка Q лежит на описанной около треугольника АВС окружности. Ее диаметром служит гипотенуза АВ. Из треугольника AQC по теореме синусов имеем: СQ = АВsin(α+45°), где α – величина угла ВАС. Далее получаем:

CQ= c(sinαcos45°+cosαsin45°) = c(+) = , где с = АВ. Итак, искомое расстояние CQ равно .

Решение 2 (по теореме косинусов).

Из того же треугольника AQC по теореме косинусов находим:

CQ² = b² + AQ² – 2b∙CQcos (α+45°).

Рассмотрим треугольник AQB, который является прямоугольным и равнобедренным (BQ=QA). По теореме Пифагора находим, что AQ² = c². Тогда

CQ² = b² + c² – 2b∙∙( — ) = b² + (a² + b²) – b² + ab = (a +b)², СQ = .

Решение 3 (по теореме Птолемея).

Во вписанном в окружность четырехугольнике сумма произведений длин противоположных сторон равна произведению длин диагоналей (теорема Птолемея). Поэтому для вписанного четырехугольника AQBC имеем:

a∙AQ + b∙BQ = c∙CQ.

Но AQ = BQ = и, следовательно,

(a + b) = c∙ CQ, откуда CQ = .

Решение 4 (методом площадей).

Сумма площадей треугольников АВС и ABQ равна площади четырехугольника AQBC:

ab + AQ² = c∙CQsinφ,

где φ – величина угла между прямыми AB и CQ. Луч CQ есть биссектриса угла АСВ, так как вписанные углы ACQ и BCQ опираются на равные дуги AQ и BQ.По теореме о внешнем угле треугольника φ = α + 45°. Подставив в предыдущее равенство AQ² = (a² + b²) и sinφ = ∙ (по решению 1), получим:

ab + (a^{2 +}b²) = CQ∙(a + b) и CQ = .

Решение 5 (методом геометрических преобразований).

Выполним поворот около центра Q квадрата на 90°: В→А, А→А₁, С→С₁ (рис.4). Так как А₁АС₁ = СВА, то

САВ + ВАА₁ + А₁АС₁ = 180°,

и поэтому точки С,А,С₁ лежат на одной прямой. В треугольнике CQC₁ угол CQC₁ прямой (угол поворота), CQ = C₁Q, СС₁ = АС₁ = a+b. Следовательно, CQ = .

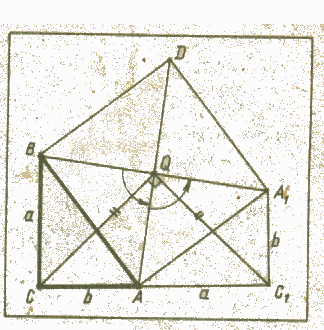
Рис.4

Решение 6 (методом координат).

Примем прямые СА и СВ за оси Ох и Оу прямоугольной декартовой системы координат. Найдем координаты х, у точки Q. Она принадлежит биссектрисе угла АСВ (по решению 4) и равноудалена от точек A(b,0) и B(0,a). Имеем систему:

х = у

(x — b)² + у² = х² + (у — а)²,

откуда 2х(b — а ) = b² – a² (подставив первое равенство во второе).

Если a ≠b, то имеем решение х = у = .

При a = b четырехугольник AQBC является квадратом и х = у =а, т.е. координаты точки Q удовлетворяют прежнему решению. По формуле расстояния между двумя точками

CQ = = = .

Решение 7 (векторное).

Положим = b и = a и выразим через эти векторы вектор (рис.3):

= = + ( + ) = + ( — ) + = ( + ) + ,

положив = αа + βb, найдем коэффициенты α и β этого разложения, используя условия ∙ = 0 и = , которые приводят к системе уравнений:

(α + β)(- ) = 0,

(α + β)² = (– )².

Поскольку = 0, то эта система эквивалентна такой:

α² — β² = 0,

α² a² + β²b^{2 = 2} + ² ,

откуда α = и β = и, следовательно,

= + , = ( + ) + ( + ) = ( + ).

Наконец, CQ² = (a+b)², CQ = .

Решение 8 (методом комплексных чисел).

Введем прямоугольную декартову систему координат так же, как при решении 6. Тогда точки А,В,С будут иметь соответственно комплексные координаты b, ai, 0, причем a = , b = . При повороте на 90° вектор переходит в вектор . Этому повороту соответствует умножение на комплексное число i. Поэтому имеем равенство: (ai — q)i = b-q, где q – комплексная координата точки Q. Отсюда q = . Находим:

CQ² = q = ∙ = (a+b)².

Решение 9 (чисто геометрическое).

Опишем около квадрата другой квадрат со стороной a+b. Тогда искомое расстояние, очевидно, равно половине диагонали большего квадрата.

Из всех представленных решений легко найти наиболее рациональные, но суждения о простоте или сложности того или иного решения задачи в значительной мере субъективно. Оно существенно зависит от подготовленности, от уровня владения методами решения задач. При недостаточных навыках решений методом геометрических преобразований, векторным или координатным методом можно сказать, что первые четыре решения и решение 9 гораздо проще остальных. Однако решения 5 и 6 для подготовленного человека представляются ничуть не сложнее. Векторный метод для решения данной задачи оказался малоэффективным – решение 7 сложнее остальных. Решение 8 с помощью комплексных чисел выглядит очень простым, но требует специальной подготовки.

В своей работе я рассмотрела различные способы решений одной геометрической задачи, используя известные методы. Анализируя все решения, я сделала для себя важные выводы. Во-первых, благодаря такой работе снимается психологический барьер перед поиском решения задачи. Ведь если знаешь, что задача имеет несколько способов решения, то смелее берешься за неё. Постепенно, решая задачу за задачей, приобретаешь некоторый опыт, что позволит развить математическое чутье. Во-вторых, подробный разбор способов решения задач является хорошим подспорьем для того, чтобы освежить в памяти пройденный материал. В-третьих, при такой работе над задачей формируется логическое мышление, развивается интуиция, систематизируются знания, расширяется общеобразовательный кругозор. В-четвертых, овладевая основными методами решения задач, составляющими важную часть многих эвристических алгоритмов, можно рационально планировать поиск решения задачи, выполнять полезные преобразования условия задачи, а также использовать известные приемы познавательной деятельности – наблюдение, сравнение, обобщение.

Все перечисленное создает условия для формирования навыков исследовательской деятельности, способствующей накоплению творческого потенциала.

Литература.

1. Л.Р. Шикова. «Исследовательская деятельность школьников в процессе решения геометрических задач». «Математика в школе.»№4, 1995.

2. Я.П.Понарин. «Задача одна – решений много». «Математика в школе» №1,1992.

3. Д.Ф.Изаак. «Поиски решения геометрической задачи». «Математика в школе»№6,1998.

4. В.А.Филимонов, Т.Н.Фисенко. «Об одном подходе к изучению геометрии в средней школе». «Математика в школе» №1,1997

5. Д.Пойя. «Как решать задачу». М.,1959.

6. Д.Пойя. «Математическое открытие». М., 1970.

7. Э.Г.Готман, З.А.Скопец. «Задача одна — решения разные».

Интересные задачи с практическим содержанием

Цель урока: научиться применять теоретические знания для решения задач с практическим содержанием, показать красоту и значимость геометрии.

ХОД УРОКА

1. Повторение теории

а) Признаки подобия треугольников.
б) Пропорциональные отрезки в круге.

2. Слово учителя о цели этого урока

Геометрия – это не просто наука о свойствах треугольников, параллелограммов, окружностей. Геометрия – это целый мир, который окружает нас с самого рождения. Ведь все, что мы видим вокруг, так или иначе относится к геометрии, ничто не ускользает от ее внимательного взгляда. Геометрия помогает человеку идти по миру с широко открытыми глазами, учит внимательно смотреть вокруг и видеть красоту обычных вещей, смотреть и думать, думать и делать выводы.

На уроке будут рассмотрены красивые задачи, решить которые, помогут знания по геометрии, которые учащиеся получили в 8 классе.

3. Выступление одного из учащихся с кратким сообщением о Конан Дойле

 

Всемирно известный писатель Артур Конан Дойль был врачом.
Но он очень хорошо, видимо, знал геометрию. В рассказе “Обряд дома Месгрейвов” он описал, как Шерлоку Холмсу нужно было определить, где будут конец тени от вяза, который срубили. Он знал высоту этого дерева ранее. Шерлок Холмс так объяснил свои действия: “… я связал вместе два удилища, что дало мне шесть футов, и мы с моим клиентом отправились к тому месту, где когда-то рос вяз. Я воткнул свой шест в землю, отметил направление тени и измерил ее. В ней было девять футов.
Дальнейшие мои вычисления были уж совсем несложны. Если палка высотой в шесть футов отбрасывает тень в девять футов, то дерево высотой в шестьдесят четыре фута отбросит тень в девяносто шесть футов, и направление той и другой, разумеется, будет совпадать”.

Задача 1. Измерение высоты дерева

Для того, чтобы измерить высоту дерева BD, приготовили прямоугольный треугольник АВ₁C₁ с углом А = 45^о и, держа его вертикально, отошли на такое расстояние, при котором, глядя вдоль гипотенузы АВ₁, увидели верхушку дерева В. Какова высота дерева, если расстояние
АС = 5,6м, а высота человека 1,7м?

Дано:

АВ₁С_1,
С = 90^о,
А = 45^о.
АС = 5,6м
h человека = 1,7м.

Найти: BD

Решение:

1) Так как А общий для обоих треугольников, а АС₁В₁ и АСВ (по условию) прямые (то есть равны по 90^о), то АС₁В₁ и АСВ – подобные (по признаку подобия о 2-х углах).
2) Тогда АВ₁C₁ = АВС = 45^о, => ВС = АС = 5,6м, но к получившейся длине мы должны еще прибавить рост человека, то есть длина дерева DB = 7,3м.

Ответ: 7,3м.

Задача 2. Неприятельская вышка

Открытый участок дороги находится на полосе АВ шириной в 50м; неприятельский наблюдательный пункт находится на верху колокольни высотой MN = 22м. Какой высоты следует сделать вертикальную маску КВ на расстоянии 500м от колокольни, чтобы закрыть дорогу от наблюдателя противника?

Дано:

AMN, АВ = 50м,
MN = 22м,
BN = 500м

Найти: КВ.

Решение:

АКВ ~ АМN (по 2-м углам: А – общий, АВК и AMN – прямые, а если треугольники подобны, то все его элементы тоже подобны. То есть, , а . Следовательно, м.

Ответ: 2 м.

Задача 3. Земля как на ладони, когда ты в небе на воздушном шаре

Как далеко видно с воздушного шара, поднявшегося на высоту 4 км над Землей (радиус Земли примерно равен 6370 км)?

Решение:

1. По теореме о касательной к окружности, касательная перпендикулярна радиусу, проведенному в точку касания, то есть OTM = 90^о.
2. MO = 6370 + 4 = 6374 км,
3. тогда по теореме Пифагора:

MT ² + OT ² = MO ²
MT ² = MO ² – OT ²

MT = 112,9 км

Ответ: 112,9 км

Задача 4. Определение расстояния до кораблей в море

Решения отдельных старинных задач практического характера могут найти применение и в настоящее время, а поэтому заслуживают внимания.
История геометрии хранит немало приемов решения задач на нахождение расстояний. Определение расстояний до кораблей, находящихся в море, – одна из таких задач, решаемая двумя способами.
Найти расстояние от точки А, находящейся на берегу до корабля

Дано:

А = 1;
В = 2;
АВ = а.

Найти: АК.

Решение:

1-й способ. Пусть корабль находится в точке К, а наблюдатель в точке А. Требуется определить расстояния КА. Построив в точке А прямой угол, необходимо отложить на берегу два равных отрезка АВ = ВС. В точке С вновь построить прямой угол, причем наблюдатель должен идти по перпендикуляру до тех пор, пока не дойдет до точки D, из которой корабль К и точка В были бы видны лежащими на одной прямой. Прямоугольный треугольники ВСD и ВАК равны, следовательно, CD = AК, а отрезок CD можно непосредственно измерить.

Второй способ, получивший название метода триангуляции, нашел применение в астрономии. С его помощью измерялись расстояния до небесных тел. Этот метод состоит из 3-х этапов:

1. Измерение углов 1 и 2 и расстояния АВ.
2. Построение А’В’К’ с углами 1 и 2 при вершинах А’ и В’ соответственно.
3. Учитывая подобие треугольников АВК, А’В’К’ и равенство , по известным длинам отрезков АВ, А’К’ и А’В’ нетрудно найти длину отрезка АК.

Задача 5. Хорды в романе

Поэт Г. Лонгфелло был еще и математиком. Наверное, поэтому яркие образы, украшающие математические понятия, которые он использовал в своем романе “Кавана”, позволяет запечатлеть некоторые теоремы и их применение. Читаем в романе Лонгфелло следующую задачу:

“Лилия, на одну пядь, поднимавшаяся над поверхностью воды, под порывом свежего ветра коснулась поверхности озера в двух локтях от прежнего места: исходя из этого требовалось определить глубину озера”. (1 пядь равна 10 дюймам, два локтя 21 дюйму)

А решается эта задача на основе теоремы: если две хорды одной окружности пересекаются, то произведение длин частей одной из них равно произведению длин частей другой.
Посмотрим на рисунок, и сразу станет ясно, как находится глубина озера (x):

21 ^. 21 = 10(x + (x +10)),
441 = 20x + 100,
x = 17,05 (дюймов).

Ответ: 17,05 дюймов.

4. Итог урока

На уроке были рассмотрены наиболее актуальные задачи, связанные с геометрическими измерениями на местности – определением высоты предмета, нахождением расстояния до недоступных предметов. Приведенные задачи имеют значительный практический интерес, закрепляют полученные знания по геометрии и могут использоваться для практических работ. Ценно то, что для их решения не требуется знаний больших, чем в объеме 8 классов.

5. Задание на дом:

№1

Гора Эльбрус (на Кавказе) поднимается над уровнем моря на 5600м. Как далеко можно видеть с вершины этой горы?

№2

М – наблюдательный пункт высотой h метров над Землей; радиус Земли R, MT = d есть наибольшее видимое расстояние. Доказать, что .

№ 3

Найти расстояние от острова, находящегося на озере, до пункта В на берегу. (Остров О принять за точку).

№ 4

Вершина горы видна из точки А под углом 3842’, а при приближении к горе на 200м вершина стала видна под углом 42. Найти высоту горы.

Список литературы:

1. Сергеев И.Н., Олехник С.Н., Гашков С.Б. “Примени математику”, М., Наука, 1989.

2. Балк М.Б., Балк Г.Д. “Математика после уроков”, М., Просвещение, 1971.

3. Четверухин Н.Ф. “Методы геометрических построений”, М., Учпедгиз, 1952.

4. Косякин А.С., Никулин А.С., Смирнов А.С. “Землеустроительные работы”, М., Недра, 1988.

5. Киселев А.П., Рыбкин Н.А. “Геометрия 7–9 планиметри. Дрофа 1995

6. Ткачев А.В.Домашняя математика 8 класс

7. Газета Математика №5 1999 г.

8. Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия.

Нестандартные геометрические задачи повышенной сложности

Урок математики в 3 классе.

Автор: Ковалевская Любовь Эдуардовна учитель начальных классов Петровская средняя школа Казахстан.

Данный урок проводится в 3 классе .

Повторение и закрепление знаний по теме»Геометрические фигуры».

Предмет: математика.

Класс:3.

Тема: Нестандартные геометрические задачи повышенной сложности.

Тип: закрепление.

Цели и задачи: формирование умения размышлять, ориентироваться в нестандартных ситуациях, осуществлять перенос знаний, обосновывать полученные выводы. Развитие логических действий, творческих способностей. Воспитание интереса, любви к математике.

Учебно- методическое обеспечение:

А.Б.Акпаева. Математика 3 класс.

Ход урока.

1.Сообщение темы (Слайд1)

Сегодня вместе со сказочными героями отправимся в путешествие по стране Геометрии.

Встреча с клубочком. Дети заблудились в лесу. (Слайд 2)

По лугу шли, клубок нашли,

За ним пошли.

Вперед, находочка, кати,

В любимый класс нас приведи!

II. Встреча с теремком (Слайд 3)

Ай, да терем, теремок!

Он не низок, невысок.

Если сможете, ребята,

Несколько задач решить,

Разрешат тогда зверята

Вас в ворота пропустить.

А задачи таковы:

1) Игра «Угадай фигуру» (Слайд 4-7)

— Расставь 8 стульев у четырех стен комнат так, чтобы у каждой стены стояло по 3 стула. Расставь 9, потом 10, потом 11 стульев.

Проверка:

(Слайд 8)

Окна в доме открываются,

Звери в окнах появляются,

В лапках держат все задачки.

У кого ответ готов

На вопрос этих жильцов?

Игра «Танграмм» (Слайд 9)

7 частей у каждого

обучающегося в конверте.

Задание: Составить фигуру журавля.

Графический диктант.

3→; 1↑; 1→; 4↓; 6 →; 1↑; 1 →; 1↓; 1 ←; 7↓; 1←; 3 ↑; 5 ←; 3↓;1←; 7 ↑; 3 ←;3↑.

(Слайд 10)

(Слайд 11)

— Найдите верные высказывания, и вы узнаете название космического корабля.

(Слайд 12)

∟С = 56⁰ – острый;

∟Т = 95⁰– прямой;

∟О = 100⁰ – тупой;

∟К = 34⁰ – тупой;

∟Ю = 90⁰ – прямой;

∟З = 3⁰ – острый.

(Союз)

Хоть и тесно нам здесь жить,

Живем мы все дружно,

Умеем дружить.

И вам всем, ребятам,

Каждый желает,

Пусть ссор и обид

Класс ваш не знает.

Вас в ворота пропускаем,

Идти прямо предлагаем,

Вот по этому пути

Должны до леса вы дойти.

(Слайд 14)

III. Встреча с Красной Шапочкой

(Слайд 15)

Тропинка «Площадь задач»

Помогите-ка, ребята,

Волка мне перехитрить.

Но для этого вам надо

Задачу для меня решить.

Площадь закрашенной фигуры вам надо найти,

Тогда до милой бабушки смогу я дойти.

Iвариант

9м

7м

3

1м

дм

II вариант

5дм

2дм

3дм

2дм

Физминутка

Луч с лучом соединили,

Вершину в точке закрепили.

Так тупой, прямой и острый

Угол нам построить просто.

Пение песенок о точке, отрезке, прямой, ломаной.

IV. Встреча с Незнайкой

(Слайд 16)

Повстречали дальше с вами

Мы Незнайку на пути.

Его вежливо спросили

Куда дальше нам идти.

Он помочь пообещал,

Но задание всем дал:

«Чтоб узнать о дальнейшем пути,

Должны вы по лесенке вверх пойти.

А там наверху в ответе примера

Указана будет дорога до сквера.

А в сквере вас ждет друг лучший мой.

Подскажет дорогу он к школе родной,

Где игры нас ждут среди лучших друзей.

Итак, смело вверх!

Ну, кто же быстрей?!

(Слайд 17)

Математическая эстафета (дети делятся на две команды)

** — 15 * = 60

84 — *6 = 4*

60 — 2* = *5

34 + 2*= *0

18 +1*= *2

*5 – 3* = 47

*5 — 1* = 57

1*+ *7 =100

Путь открыт! Вперед, ребята!

V. Встреча с Буратино (у озера) (Слайд 18)

Мог бы вам помочь, ребята,

Только злющий Карабас

Спрятал здесь, в пруду, куда-то

Ключ от двери вашей в класс.

И только лягушка-квакушка одна

Поможет достать вам ключик со дна.

Ребята, задачку скорее решите,

Лягушку с пятеркой в ответе спросите.

Она вам поможет ключик достать,

Ответы к задачке скорей написать.

Все вместе мы в школу пойдем поскорей,

Чтоб встретить там много хороших друзей.

(Слайд 19)

Задача.Ученикилесной школы – Белка, Ёж, Лиса и Заяц – начертили такие фигуры, каждый – по одной:

Лиса

Еж

Белка

Заяц

Еж не стал чертить многоугольник, Заяц не выбрал треугольник, а Лиса начертила такой прямоугольник, у которого есть свое название. Какую фигуру начертила белочка?

Наконец добрались в школу к вам

И расселись по местам.

А теперь всех, кто в пути

Дорогу нам помог найти,

Приглашаем поиграть

И вместе с нами порешать.

Школа головоломок. Обобщение.

Мой веселый звонкий мяч!

Ты куда помчался вскачь?

Сколько мячик прыгнул раз?

Кто подскажет нам сейчас?

Мяч поможет вам ответить на вопросы, решить все задачи.

Комбинации точек вы рассмотрите

С ударом мяча их соотнесите.

Учитель стучит мячом о пол, дети должны посчитать, сколько раз.

(Слайд 21)

а)б)в)

Мячик, а ну-ка, кружись, давай,

Задачки решать нам помогай!

Игра «Сосчитай треугольники».(Слайд 22)

Ч то такое треугольник,

Часто знает и дошкольник

А уж вам-то как не знать!

Но совсем другое дело-

Быстро, точно и умело

Треугольники считать.

Например, в фигуре этой

Сколько разных? Рассмотри!

Все внимательно исследуй

И по краю, и внутри!

Игра «Закономерности» (Слайд 23)

Заполни пустые клетки в четвертом квадрате, не нарушая закономерности.

Итог занятия

Закончить путешествие настала нам пора.

Настала перемена. Вы рады, дети?

Да!

(Слайд 24)

Литература:

В.Г. Житомирский, Л.Н.Шеврин. Путешествие по стране Геометрии.- 2-е изд. – М.: Педагогика, 1994.

Т.В. Жильцова, Л.А.Обухова. Поурочные разработки по наглядной геометрии: 1 — 4 класс.- М.: ВАКО, 2004.

Л.Г.Петерсон. Математика. 2 класс. Часть 3. – М.: Издательство «Ювента», 2009.

План-конспект урока по математике (2 класс) на тему: Решение нестандартных геометрических задач (конспект занятия))

Решение нестандартных геометрических задач повышенной трудности

Кружковое занятие по математике

во 2 классе разработала учитель начальных классов

МБОУ «СОШ №27 с углубленным

изучением отдельных предметов»

 г. Балаково Саратовской  области

Хохлова Татьяна Геннадьевна        

 

Тема: Решение нестандартных геометрических задач повышенной трудности.

Тип занятия: общеметодологической  направленности

Целевая  направленность занятия:

— содержательная;

— деятельностная.

Цели для учителя:

1. Развитие регулятивных УУД: управление своей деятельностью, контроль и коррекция знаний, инициативность и самостоятельность.
2. Развитие коммуникативных УУД:  формирование умения размышлять, ориентироваться в нестандартной ситуации, осуществлять перенос знаний, обосновывать полученные выводы.
3. Развитие универсальных логических действий, творческих способностей обучающихся.
4. Воспитание интереса, любви к математике.

Цели для ученика:

1.  Понимание деятельностной единицы содержания образования;

умение ее применить в учебной, предметной задаче и реальной жизненной ситуации.

Ход занятия

1. Сообщение темы (Слайд1)

1. Сегодня вместе со сказочными героями отправимся в путешествие по стране Геометрии.

Встреча с клубочком. Дети заблудились в лесу. (Слайд 2)

По лугу шли, клубок нашли,

За ним пошли.

Вперед, находочка, кати,

В любимый класс нас приведи!  

                                                             

II. Встреча с теремком   (Слайд 3)

Ай, да терем, теремок!

Он не низок, невысок.

Если сможете, ребята,

Несколько задач решить,

Разрешат тогда зверята

Вас в ворота пропустить.

А  задачи  таковы:

1) Игра «Угадай фигуру» (Слайд 4-7)                         

— Расставь 8 стульев у четырех стен комнат так, чтобы у каждой стены стояло по 3 стула. Расставь 9, потом 10, потом 11 стульев.

Проверка:

(Слайд 8)

Окна в доме открываются,

Звери в окнах появляются,

В лапках держат все задачки.

У кого ответ готов

На вопрос этих жильцов?

1. Игра «Танграмм» (Слайд 9)

7 частей у каждого

обучающегося в конверте.

Задание: Составить фигуру журавля.

2. Графический диктант. 

3→; 1↑; 1→; 4↓; 6 →; 1↑; 1 →; 1↓; 1 ←; 7↓; 1←; 3 ↑; 5 ←; 3↓;1←; 7 ↑; 3 ←;3↑.

(Слайд 10)

3. (Слайд 11)

— Найдите верные высказывания, и вы узнаете название космического корабля.

(Слайд 12)

∟С = 560 – острый;

∟Т = 950 – прямой;

∟О = 1000 – тупой;

∟К = 340 – тупой;

∟Ю = 900 – прямой;

∟З = 30 – острый.

(Союз)

(Слайд 13)

Хоть и тесно нам здесь жить,

Живем мы все дружно,

Умеем дружить.

И вам всем, ребятам,

Каждый желает,

Пусть ссор и обид

Класс ваш не знает.

Вас в ворота пропускаем,

Идти прямо предлагаем,

Вот по этому пути

Должны до леса вы дойти.

 (Слайд 14)                                                   

III. Встреча с Красной Шапочкой

(Слайд 15)                                                          

Тропинка «Площадь задач»

Помогите-ка, ребята,

Волка мне перехитрить.

Но для этого вам надо

Задачу для меня решить.

Площадь закрашенной фигуры вам надо найти,

Тогда до милой бабушки смогу я дойти.

Iвариант

               9м

                 7м

  1м

3дм  

II вариант

                 5дм

2дм

                                         3дм

2дм                    

Физминутка

Луч с лучом соединили,

Вершину в точке закрепили.

Так тупой, прямой и острый

Угол нам построить просто.

Пение песенок о точке, отрезке, прямой, ломаной.

IV. Встреча с Незнайкой

(Слайд 16)

Повстречали дальше с вами

Мы Незнайку на пути.

Его вежливо спросили

Куда дальше нам идти.

Он помочь пообещал,

Но задание всем дал:

«Чтоб узнать о дальнейшем пути,

Должны вы по лесенке вверх пойти.

А там наверху в ответе примера

Указана будет дорога до сквера.

А в сквере вас ждет друг лучший мой.

Подскажет дорогу он к школе родной,

Где игры нас ждут среди лучших друзей.

Итак, смело вверх!

Ну, кто же быстрей?!

(Слайд 17)

Математическая эстафета (дети делятся на две команды)

** — 15 * = 60

84 — *6 = 4*

34 + 2*= *0

60 — 2* = *5

*5 – 3* = 47

18 +1*= *2

1*+ *7 =100

*5 — 1* = 57

Путь открыт! Вперед, ребята!

V. Встреча с Буратино (у озера)     (Слайд 18)   

Мог бы вам помочь, ребята,

Только злющий Карабас

Спрятал здесь, в пруду, куда-то

Ключ от двери вашей в класс.

И только лягушка-квакушка одна

Поможет достать вам ключик со дна.

Ребята, задачку скорее решите,

Лягушку с пятеркой в ответе спросите.

Она вам поможет ключик достать,

Ответы к задачке скорей написать.

Все вместе мы в школу пойдем поскорей,

Чтоб встретить там много хороших друзей.

(Слайд 19)                            

Задача. Ученики лесной школы – Белка, Ёж, Лиса и Заяц – начертили такие фигуры, каждый – по одной:                                                        

Лиса

Еж

Белка

 Заяц

Еж не стал чертить многоугольник, Заяц не выбрал треугольник, а Лиса начертила такой прямоугольник, у которого есть свое название        . Какую фигуру начертила белочка?

Наконец добрались в школу к вам

И расселись по местам.

А теперь всех, кто в пути

Дорогу нам помог найти,

Приглашаем поиграть

И вместе с нами порешать.

1. Школа головоломок. Обобщение.

(Слайд 20)

Мой веселый звонкий мяч!

Ты куда помчался вскачь?

Сколько мячик прыгнул раз?

Кто подскажет нам сейчас?

1. Мяч поможет вам ответить на вопросы, решить все задачи.

Комбинации точек вы рассмотрите

С ударом мяча их соотнесите.

Учитель стучит мячом о пол, дети должны посчитать, сколько раз.

(Слайд 21)

а)                                б)                        в)

Мячик, а ну-ка, кружись, давай,

Задачки решать нам помогай!

2. Игра  «Сосчитай треугольники».        (Слайд 22)

Что такое треугольник,

Часто знает и дошкольник

А  уж вам-то как не знать!

Но совсем другое дело-

Быстро, точно и умело

Треугольники считать.

Например, в фигуре этой

Сколько разных? Рассмотри!

Все внимательно исследуй

И по краю, и внутри!

3. Игра «Закономерности» (Слайд 23)

Заполни пустые клетки в четвертом квадрате, не нарушая закономерности.

2. Итог занятия

Закончить путешествие настала нам пора.

Настала перемена. Вы рады, дети?

Да!

(Слайд 24)

Литература:

В.Г. Житомирский, Л.Н.Шеврин. Путешествие по стране Геометрии.- 2-е изд. – М.: Педагогика, 1994.

Т.В. Жильцова, Л.А.Обухова. Поурочные разработки по наглядной геометрии: 1 — 4 класс.- М.: ВАКО, 2004.

Л.Г.Петерсон. Математика. 2 класс. Часть 3. – М.: Издательство «Ювента», 2009.

Учебный курс «Решение геометрических задач» 7 класс

Рассмотрено на заседании ШМО Руководитель ШМО

______ ( Уталиева А. Н.

Протокол №1

от 27.08.2014г.

«Согласовано»

Заместитель директора по УВР

МОУ «ООШ № 2 г.Новоузенска»

__________ ( Макарова О.А.)

«____»__________2014г.

«Утверждаю»

Директор МОУ «ООШ №2 г.Новоузенска»

___________ (Бондарева И А.)

Приказ № ____

от «____»___________2014г.

Рабочая программа

учебного курса « Решение геометрических задач»

Шараповой Марии Викторовны

учителя математики

7 класс.

Рассмотрено на заседании
педагогического совета
протокол № 1

от 28.08.2014г.

2014-2015 учебный год

Пояснительная записка

Одно из труднейших звеньев учебного процесса – научить учащихся решать задачи. Геометрическая задача – это ситуация, требующая от учащихся мыслительных и практических действий. Хотя способы решения традиционных задач хорошо известны , но организация деятельности учащихся по решению задач является одним из условий обеспечения глубоких и прочных знаний у учащихся. Сегодня знания учащихся по геометрии явно демонстрируют все большую дифференциацию учащихся по качеству подготовки. Прослеживается тенденция явного роста качества подготовки сильной группы учащихся и все большее отставание от них групп учащихся с удовлетворительным и неудовлетворительным уровнем подготовки. Постепенно картина меняется в сторону количественных показателей, выделяются целые темы и элементы содержания, которые «выпадают» из поля зрения всей группы учащихся, они начинают отставать не только по качеству подготовки, но и по объему знаний.

Как правило, в образовательных учреждениях выбирается учебный план универсального образования, при котором все предметы изучаются на базовом уровне, а расширение идет за счет учебных курсов. По геометрии это означает выбор базового уровня с учебной нагрузкой в два недельных часа, что означает точное следование базовому стандарту предмета, но при этом невозможно изучить все методы решения задач, а следовательно, невозможно обеспечить формирование умения решать задачи повышенной сложности (что базовый уровень стандарта и не предусматривает). Поэтому учебные курсы по решению геометрических задач в первую очередь призваны развивать содержание базового курса геометрии, и в непрофильных классах у учащихся появляется реальная возможность при наличии данного учебного курса получить подготовку, соответствующую углубленному уровню изучения предмета .

Учебный курс «Решение нестандартных геометрических задач» рассчитан на учащихся 7 класса общеобразовательных учреждений универсального профиля, где геометрия преподается по базовому уровню. Программа составлена на основе программ:

1. учебника «Геометрия 7-9» /Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Позняк Э. Г., Юдина И. И. М.: Просвещение, 2008.

Настоящий учебный курс рассчитаны на преподавание в объеме 34 часа (1 час в неделю на 1год обучения в 7 классе). 

Цель данного курса углубить и систематизировать знания учащихся 7 класса по геометрии путем решения разнообразных задач и способствовать их профессиональному определению. 

Его основная направленность — углублению знаний по темам при изучении курса геометрии. Занятия проводится 1 час в неделю в течение 2 полугодий

Цели учебного курса: 

1. развитие познавательных интересов, интеллектуальных и творческих способностей в процессе решения геометрических задач и самостоятельного приобретения новых знаний; 
   2. совершенствование полученных в основном курсе знаний и умений; 
   3. формирование представителей о постановке, классификаций, приемах и методах решения геометрических задач. 

Задачи курса: 
1. углубление и систематизация знаний учащихся; 
2. усвоение учащимися общих алгоритмов решения задач; 
3. овладение основными методами решения задач. 
Программа элективного курса составлена с учетом государственного образовательного стандарта и содержанием основных программ курса геометрии базовой и профильной школы. Он ориентирует учителя на дальнейшее совершенствование уже усвоенных учащимися знаний и умений. 

Календарно-тематическое планирование

учебного курса «Решение геометрических задач»

7 класс

№

Тема

Дата

Примечание

план

факт

1

Первые шаги в геометрии 

2

Решение задач 

3

Пространство и его размерность 

4

Простейшие геометрические фигуры 

5

Простейшие геометрические фигуры 

6

Конструирование из «Т» 

7

Куб и его свойства 

8

Куб и его свойства 

9

Задачи на разрезание и складывание фигур 

10

 Треугольник

11

 Треугольник

12

Правильные многогранники 

13

Многогранники 

14

Геометрические головоломки 

15

Измерение длины 

16

Измерение площади и объёма 

17

Измерение площади и объёма 

18

Вычисление длины, площади и объёма 

19

Окружность

20

Окружность

21

Геометрический тренинг 

22

Геометрический тренинг 

23

Геометрический тренинг 

24

Топологические опыты 

25

Топологические опыты 

26

Топологические опыты 

27

Задачи со спичками 

28

Зашифрованная переписка 

29

Задачи, головоломки, игры 

30

Задачи, головоломки, игры 

31

Задачи, головоломки, игры 

32

Задачи, головоломки, игры 

33

Задачи, головоломки, игры 

34

Итоговое занятие

Список литературы.

1. Абдрашитов Б.М. Учитесь мыслить нестандартно: книга для учащихся.М.:Просвещение: АО «Учебная литература» 1996.

2. Козлова Е.Г. Сказки и подсказки: Задачи для математического кружка. — М.: МИРОС, 1994.-128с.

3. Кривоногов В.В. Нестандартные задания по математике: 5-11 классы.- М.:Издательство «Первое сентября» 2003.

4.Фарков А.В. .Математические олимпиады в школе. 5-11 классы

5.Шарыгин И.Ф. Математика. Задачи на смекалку.- М..: «Просвещение» 1996

6. Еженедельное учебно-методическое приложение к газете «Первое сентября» Математика

7. Научно-теоретический и методический журнал «Математика в школе».