Цилиндр. Геометрия, 11 класс: уроки, тесты, задания.

1.	Сечение цилиндра плоскостью Сложность: лёгкое	1
2.	Расчёты в осевом сечении цилиндра Сложность: лёгкое	2
3.	Площади боковой поверхности и осевого сечения цилиндра Сложность: среднее	2
4.	Радиус цилиндра Сложность: среднее	3
5.	Площадь поверхности цилиндра Сложность: среднее	4
6.	Радиус цилиндра, описанного около призмы Сложность: среднее	2
7.	Изменения площади боковой поверхности цилиндра Сложность: среднее	2
8.	Цилиндр вписан в призму Сложность: среднее	5
9.	Определение высоты цилиндра Сложность: среднее	3
10.	Площадь сечения цилиндра Сложность: среднее	4
11.	Площадь перпендикулярных сечений цилиндра Сложность: среднее	5
12.	Боковая поверхность Сложность: среднее	5
13.	Вращение прямоугольника Сложность: среднее	4
14.	Площадь сечения, параллельного оси цилиндра Сложность: среднее	5
15.	Площадь поверхности цилиндра, описанного около призмы Сложность: сложное	5

www.yaklass.ru

Урок 6. тела вращения. цилиндр — Геометрия — 11 класс

Геометрия, 11 класса

Урок №6. Тела вращения. Цилиндр

Перечень вопросов, рассматриваемых в теме:

• тело вращения;
• цилиндрическая поверхность, её образующая; цилиндр, все его элементы и сечения;
• площади поверхностей цилиндра.

Глоссарий по теме

Цилиндрическая поверхность

– это поверхность, образованная прямыми, проходящими через все точки окружности, перпендикулярными плоскости, в которой лежит эта окружность.

Эти прямые – образующие цилиндрической поверхности.

Прямая, проходящая через центр окружности, перпендикулярно к плоскости – ось цилиндрической поверхности.

Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами.

Круги – основания цилиндра; отрезки образующих, заключённые между основаниями – образующие цилиндра; образованная ими часть цилиндрической поверхности – боковая поверхность.

Ось цилиндрической поверхности называется осью цилиндра.

Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.

Сечение – изображение фигуры, образованной рассечением тела плоскостью.

Осевое сечение – вариант сечения, при котором плоскость проходит через ось тела.

Развёртка боковой поверхности цилиндра – прямоугольник, одна сторона которого равна высоте цилиндра, а другая длине окружности основания.

Основная литература:

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций: базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс.

Дополнительная литература:

Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-79.

Открытые электронные ресурсы:

Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177

Теоретический материал для самостоятельного изучения

1. Основные определения

Определение

Цилиндрической поверхностью называется поверхность, образованная прямыми, проходящими через все точки окружности, перпендикулярными плоскости, в которой лежит эта окружность (см.рис.).

Определение

Сами прямые называют образующими цилиндрической поверхности.

Определение

Прямая, проходящая через точку О, перпендикулярно к плоскости, называется осью цилиндрической поверхности.

Так как все образующие и ось перпендикулярны плоскости 𝛂, значит они параллельны друг другу (вспомнить теорему «Если две прямые перпендикулярны к плоскости, то они параллельны»).

Если построить ещё одну плоскость 𝛃, которая будет параллельна плоскости 𝛂, то отрезки образующих, заключённые между плоскостями 𝛂 и 𝛃 будут параллельны и равны друг другу (вспомнить свойство параллельных плоскостей «отрезки параллельных прямых, заключённые между параллельными плоскостями, равны»). Точки, являющиеся концами отрезков параллельных прямых и лежащие в плоскости 𝛃, дают окружность, равную окружности, лежащей в плоскости 𝛂.

Определение

Тело, ограниченное цилиндрической поверхностью и двумя кругами (границы которых есть те самые равные окружности в плоскостях 𝛂 и 𝛃) называется цилиндром.

Определение

Круги называются основаниями цилиндра, отрезки образующих, заключённые между основаниями, — образующими цилиндра, а образованная ими часть цилиндрической поверхности – боковой поверхностью цилиндра.

Определение

Ось цилиндрической поверхности называется осью цилиндра.

Определение

Длина образующей называется высотой цилиндра (все образующие равны и параллельны), а радиус основания – радиусом цилиндра.

Также цилиндр можно получить вращением прямоугольника вокруг одной из сторон. Тогда эта сторона (вокруг которой происходит вращение) будет совпадать с осью цилиндра, противоположная сторона будет образовывать боковую поверхность, а две оставшиеся стороны образуют верхнее и нижнее основания, одновременно являясь радиусами цилиндра.

2. Сечения цилиндра различными плоскостями

Пусть секущая плоскость проходит через ось цилиндра. Такое сечение называют осевым. Оно представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра.

Если секущая плоскость перпендикулярна оси цилиндра, то сечение является кругом.

Если секущая плоскость проходит параллельно оси цилиндра, но не содержит саму ось, то сечение является прямоугольником две стороны которого – образующие, а две другие – отрезки, соединяющие эти образующие в верхнем и в нижнем основании (ЗАМЕЧАНИЕ: эти отрезки меньше диаметров оснований цилиндра).

3. Основные формулы

Формула для вычисления площади боковой поверхности цилиндра: S_бок=2𝛑RL.

То есть площадь боковой поверхности равна произведению длины окружности основания цилиндра на его высоту.

Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. В виде формулы это можно записать так: S_полн=2𝛑R(R+L).

Примеры и разбор решения заданий тренировочного модуля

1. Дан цилиндр.

Выберите значение площади его боковой поверхности

1) 60π

2) 192π

3) 120π

4) 36π

Решение:

Площадь боковой поверхности вычисляется по формуле: S=2πRL.

R=6, L=10

Подставим: S=2π·6·10=120π.

Ответ: 3) 120π

2. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу 120⁰. Образующая цилиндра равна 6, расстояние от оси до секущей плоскости равно 1. Найдите площадь сечения.

Решение:

Сделаем чертеж:

По условию задачи ∟АОВ=120⁰, ВС= 6.

Расстояние от оси до секущей плоскости — отрезок ОН=1.

Найдем сторону АВ сечения.

∆ОНВ — прямоугольный.

В ∆ОНВ: ОН=1, ∟НОВ=60⁰.

НВ=ОН·tg60⁰=1·.

S_сеч=6·=18

Ответ: 18

3. Высота цилиндра на 6 больше его радиуса, площадь полной поверхности равна 144π. Найдите его образующую.

Решение:

S_полн =2πR(R+L)

По условию задачи L=R+6.

144π=2πR(R+R+6).

Получили квадратное уравнение относительно радиуса:

R²+6R-72=0

R=-12 или R=6. Так как длина радиуса не может быть отрицательной, получаем значение: R=6. Тогда образующая цилиндра равна 12.

Ответ: 12.

resh.edu.ru

Опорный конспект по геометрии на тему «Цилиндр»

Цилиндр

Опр. Цилиндром называется тело, которое состоит из двух кругов, совмещаемых

параллельным переносом и всех отрезков, соединяющих соответствующие точки

этих кругов.

Круги называют основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей этих кругов – образующими цилиндра (рис. 1)

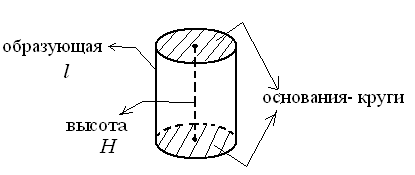
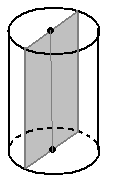
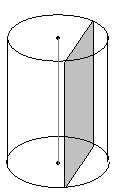
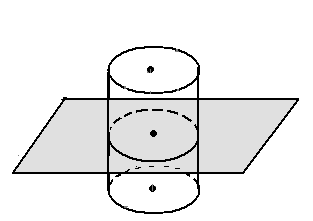
рис. 1 рис. 2 рис. 3 рис. 4

Свойства цилиндра:

1) Основания цилиндра равны и лежат в параллельных плоскостях.

2) Образующие цилиндра равны и параллельны.

Опр. Радиусом цилиндра называется радиус его основания.

Опр. Высотой цилиндра называется расстояние между плоскостями его оснований.

Опр. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.

Осевое сечение цилиндра – прямоугольник со сторонами 2R и l (в прямом цилиндре l = Н) рис. 2

Сечение цилиндра, параллельные его оси, являются прямоугольниками (рис. 3).

Сечение цилиндра плоскостью, параллельной основаниям – круг, равный основаниям (рис. 4)

Площадь поверхности цилиндра.

Боковая поверхность цилиндра составлена из образующих.

Полная поверхность цилиндра состоит из оснований и боковой поверхности.

S_полн = 2S_осн + S_бок; S_осн = П∙R²; S_бок = 2П∙R∙Н 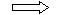S_полн = 2ПR∙(R + Н)

Практическая часть:

№1. Радиус цилиндра равен 3см, а его высота- 5см. Найдите площадь осевого сечения и площадь пол-

ной поверхности цилиндра.

№2. Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 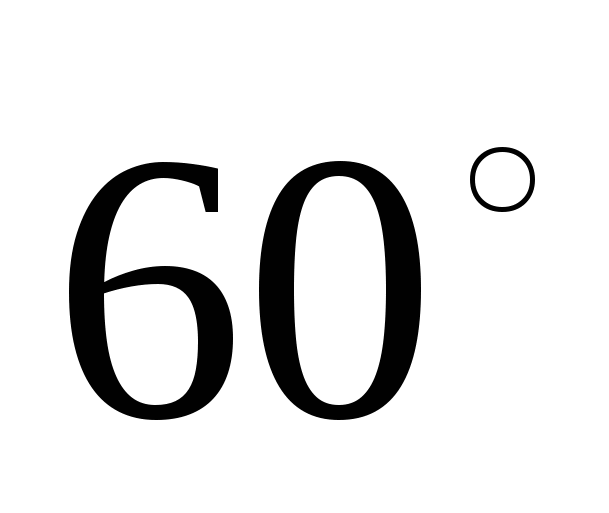и равна 20 см. Найдите площадь боковой поверхности цилиндра.

№3. Радиус цилиндра равен 2см, а его высота- 3см. Найдите диагональ осевого сечения цилиндра.

№4. Диагональ осевого сечения цилиндра, равная 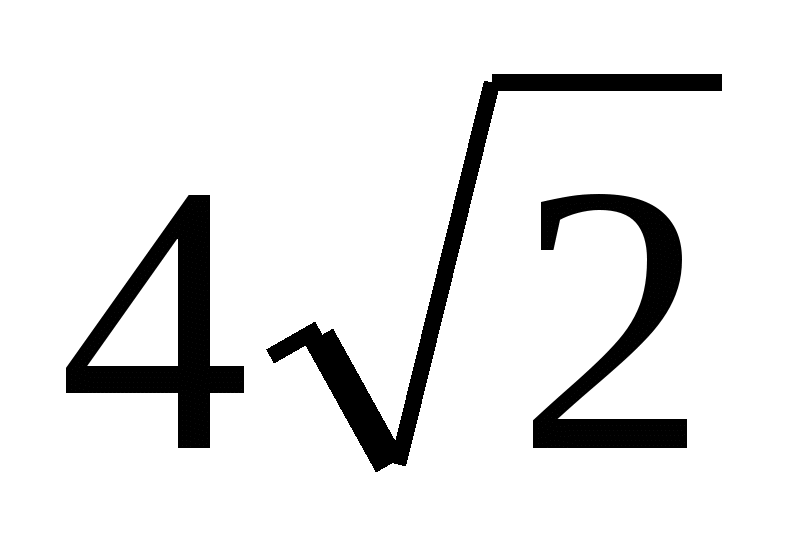, образует с плоскостью основания угол . Найдите площадь боковой поверхности цилиндра.

№5. Площадь боковой поверхности цилиндра равна 15. Найдите площадь осевого сечения.

№6. Найдите высоту цилиндра, если площадь его основания равна 1, а S _бок = .

№7. Диагональ осевого сечения цилиндра имеет длину 8см и наклонена к плоскости основания под углом 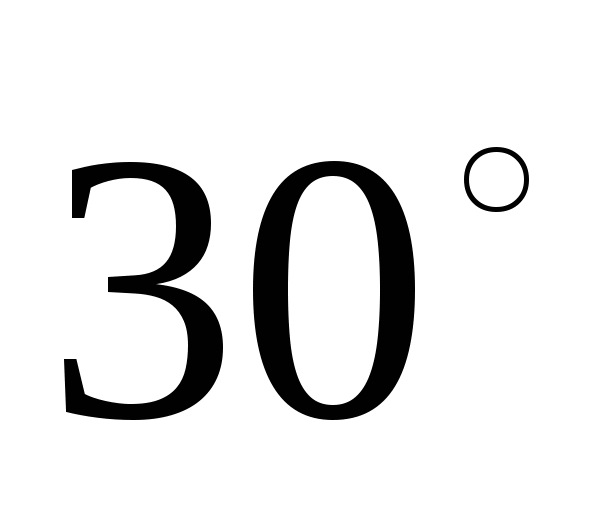. Найдите полную поверхность цилиндра.

№8.

Цилиндрическая дымовая труба с диаметром 65см имеет высоту 18м. Сколько жести нужно для её изготовления, если на заклепку уходит 10% материала?

infourok.ru

Цилиндр — методическая рекомендация. Геометрия, 11 класс.

1.	Сечение цилиндра плоскостью	1 вид — рецептивный	лёгкое	1 Б.	Сечение цилиндра плоскостью.
2.	Расчёты в осевом сечении цилиндра	1 вид — рецептивный	лёгкое	2 Б.	Осевое сечение прямоугольника, угол диагонали с основанием.
3.	Площади боковой поверхности и осевого сечения цилиндра	2 вид — интерпретация	среднее	2 Б.	Использование формулы площади боковой поверхности и осевого сечения цилиндра для расчётов.
4.	Радиус цилиндра	2 вид — интерпретация	среднее	3 Б.	Вычисление радиуса цилиндра по площади его поверхности.
5.	Площадь поверхности цилиндра	2 вид — интерпретация	среднее	4 Б.	Вычисление площади поверхности цилиндра (прикладная задача).
6.	Радиус цилиндра, описанного около призмы	2 вид — интерпретация	среднее	2 Б.	Вычисление радиуса цилиндра, описанного около треугольной призмы, основанием которой является прямоугольный треугольник.
7.	Изменения площади боковой поверхности цилиндра	2 вид — интерпретация	среднее	2 Б.	В задании нужно определить, как меняется площадь боковой поверхности цилиндра при данных изменениях радиуса и высоты.
8.	Цилиндр вписан в призму	3 вид — анализ	среднее	5 Б.	Определение боковой поверхности призмы, в которую вписан цилиндр с данной боковой поверхностью.
9.	Определение высоты цилиндра	3 вид — анализ	среднее	3 Б.	Определение высоты цилиндра с использованием данных площади осевого сечения и основания цилиндра.
10.	Площадь сечения цилиндра	3 вид — анализ	среднее	4 Б.	Определение площади сечения цилиндра плоскостью в данном расстоянии от центра основания.
11.	Площадь перпендикулярных сечений цилиндра	3 вид — анализ	среднее	5 Б.	Определение площади перпендикулярных сечений цилиндра, если дана площадь осевого сечения.
12.	Боковая поверхность	3 вид — анализ	среднее	5 Б.	Определение соотношения площадей боковой поверхности цилиндра и вписанной в цилиндр призмы.
13.	Вращение прямоугольника	3 вид — анализ	среднее	4 Б.	Определение боковых поверхностей цилиндров, если прямоугольник вращается вокруг одной и другой стороны.
14.	Площадь сечения, параллельного оси цилиндра	3 вид — анализ	среднее	5 Б.	Определение площади плоскости сечения цилиндра, которая отсекает от основания дугу данной величины.
15.	Площадь поверхности цилиндра, описанного около призмы	3 вид — анализ	сложное	5 Б.	Определение площади поверхности цилиндра, описанного около прямой призмы прямоугольного треугольника.

www.yaklass.ru

Урок геометрии по теме «Понятие цилиндра. Площадь поверхности цилиндра». 11-й класс

Цели:

• введение понятия цилиндрической поверхности, цилиндра и его элементов;
• рассмотрение различных видов сечения цилиндра плоскостью;
• выведение формул для вычисления площадей боковой и полной поверхностей цилиндра;
• подготовка учащихся к ЕГЭ;
• способствование развитию у учащихся умения самостоятельно делать выводы, применять полученные знания на практике;
• воспитание познавательного интереса к математике;
• воспитание внимательности, наблюдательности, самостоятельности, способности к коллективной работе;
• развитие пространственного мышления;
• способствование осознанию ценности коллективной мыслительной деятельности;
• формирование представление о математике, как о части общечеловеческой культуры.

Задачи:

• Познакомить учащихся с новым геометрическим телом, научить решать задачи по данной теме.
• Развивать пространственное мышление учащихся, умения анализировать и систематизировать материал.
• Воспитывать трудолюбие, графическую культуру учащихся.

Тип урока: урок изучения нового материала

Оборудование и дополнительные материалы:

• ПК.
• Мультимедийный проектор.
• Интерактивная доска.
• Презентация, см. Приложение 1.

Ход урока

1. Организационный момент. (2 минуты)

(Вход в класс по группам)

Сегодня на уроке мы продолжим знакомство со стереометрическими фигурами. А именно, дадим определение цилиндру, познакомимся с его элементами, самостоятельно выведем формулы площади поверхности цилиндра и площадь полной поверхности цилиндра и, решая задачи, увидим практическое применение полученных знаний.

Начнем наш урок с интеллектуальной разминки.

2. Интеллектуальная разминка. (7 минут)

Задача (на доске чертеж):

В прямоугольном треугольнике АВС (ÐС=90°): ÐВ=60°, АВ=20см. Найти ВС и АС. (Длину отрезка АС найти разными способами.) (можно рассмотреть решения на доске, желательно один способ от команды)

3. Объяснение материала (15 минут)

Понятие цилиндра.

Рассмотрим две параллельные плоскости α и β и окружность, с центром в точке О и радиуса r, лежащую в плоскости α.

Вопрос: В виде чего изображается окружность на плоскости?

Через каждую точку окружности проведем прямую, перпендикулярную α.

Отрезки прямых, заключенные между плоскостями α и β, образуют цилиндрическую поверхность. Сами отрезки называются образующими цилиндрической поверхности.

По построению концы образующих расположенных в α заполняют окружность L , а концы образующих в β заполняют окружность L1, с центром в точке О1– это точка пересечения прямой ОО1 с β и перпендикулярно α.

Множество концов образующих, лежащих в β, получается из окружности параллельным переносом на вектор ОО1.

Определение. Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L и L1, называется цилиндром.

Слово цилиндр пришло из греческого языка, и обозначает – “валик”, “каток”.

Построим изображение цилиндра в тетрадях: для этого необходимо построить проекции двух равных окружностей и соединить их двумя образующими.

Элементы цилиндра:

• Круги L и L1– основания цилиндра;
• цилиндрическая поверхность – боковая поверхность цилиндра;
• прямая ОО1– ось цилиндра;
• образующие цилиндрической поверхности – образующие цилиндра;
• длина образующей – высота цилиндра;
• радиус основания – радиус цилиндра.

Прямым круговым цилиндром называют цилиндр, у которого в основании лежат круги, а образующая перпендикулярна основаниям. В дальнейшем прямой круговой цилиндр будем называть просто “цилиндр”.

Существуют другие виды цилиндрических поверхностей, о них мы поговорим позже.

С данным геометрическим телом вы знакомы давно. Приведите примеры цилиндров из окружающего мира (по одному от команды).

Цилиндр можно рассматривать как тело, полученное вращением прямоугольника вокруг одной из его сторон.

Виды сечений

Рассмотрим сечения цилиндра.

На партах у вас модели цилиндров. Подумайте, как можно провести сечения, и какие геометрические фигуры получатся в результате.

Проверим ваши предположения:

1. Осевое сечение цилиндра – это сечение цилиндра плоскостью, проходящей через ось цилиндра.

Вопрос: Какая фигура получается?

Если осевое сечение цилиндра – квадрат, то цилиндр называют равносторонним.

2. Сечение, параллельное оси цилиндра.

Вопрос: Какая фигура получается?

3. Сечение плоскостью, перпендикулярной оси цилиндра

Вопрос: Какая фигура получается?

4. Сечение плоскостью, под углом к оси цилиндра

Вопрос: Какая фигура получается?

Если в основании цилиндра круг – цилиндр называется круговой. В основании цилиндра может лежать любая фигура. Образующие могут быть не перпендикулярными к основаниям. Например, наклонный круговой цилиндр.

Площадь поверхности цилиндра

Практическая работа.

Используя макеты прямого кругового цилиндра, выведите формулы площади боковой поверхности цилиндра и площади полной поверхности цилиндра, зная радиус и высоту цилиндра.

(Проверка предложенных формул по слайду)

5. Решение задач (12 минут)

Решение № 522 (рисунок цилиндра на доске)

1 ученик записывает дано, найти и решение для нахождения высоты цилиндра;

2 ученик (одновременно) записывает решение для нахождения радиуса цилиндра и его площади основания.

6. Деловая игра (7 минут)

Строители газопроводов и нефтепроводов должны соблюдать требования по эксплуатации и в целях коррозии трубы двукратно обматывают специальной пленкой.

Учащиеся разбиваются на бригады:

ГАЗПРОМ – трубоукладчики газопровода;

ТРАНСНЕФТЬ – трубоукладчики нефтепровода;

бригада ПОСТАВЩИК (ПО ОДНОМУ ЧЕЛОВЕКУ ОТ КАЖДОЙ КОМАНДЫ образуют две команды по два человека) – поставщики пленки.

Практическая задача для трубоукладчиков газопроводов.

Вычислить, какую площадь трубы необходимо обмотать пленкой, если диаметр трубы 154 см, длина 5 км. (π = 3)

Практическая задача для трубоукладчиков нефтепроводов.

Вычислить, какую площадь трубы необходимо обмотать пленкой, если диаметр трубы 76 см, длина 5 км. (π = 3)

Практическая задача для поставщиков.

Сколько рулонов изоляционной пленки необходимо поставить газовикам и сколько нефтяникам, если в рулоне 3000 м² пленки.

7. Рефлексия, домашнее задание (2 минуты)

8. Домашнее задание: п. 53-54, №№521, 523

Литература:

• Геометрия: Учеб. Для 10-11 кл. общеобразоват. учреждений / Л. С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.
• Интернет – ресурсы:
• http://www.ampravda.ru/files/articles/21124/skuikn8557v3-400.jpg
• http://www.profi-forex.org/news/entry1008084705.html
• В презентации используется видео неизвестного автора и логотипы компаний Газпром и Транснефть.

ГАЗПРОМ

Строители газопроводов и нефтепроводов должны соблюдать требования по эксплуатации и в целях коррозии трубы двукратно обматывают специальной пленкой.
Вычислить, сколько понадобится такой пленки, если необходимо двукратно обмотать трубу, диаметр которой 154 см, а длина 5 км.

ТРАНСНЕФТЬ

Строители газопроводов и нефтепроводов должны соблюдать требования по эксплуатации и в целях коррозии трубы двукратно обматывают специальной пленкой

Вычислить, сколько понадобится такой пленки, если необходимо двукратно обмотать трубу, диаметр которой 76 см, а длина 5 км.

ПОСТАВЩИК ГАЗПРОМ

Сколько рулонов изоляционной пленки необходимо поставить газовикам, если в рулоне 3000 м² пленки?

ПОСТАВЩИК ТРАНСНЕФТЬ

Сколько рулонов изоляционной пленки необходимо поставить нефтяникам, если в рулоне 3000 м² пленки?

urok.1sept.ru

Комбинации цилиндра и призмы — урок. Геометрия, 11 класс.

Цилиндр называется описанным около призмы, если многоугольники оснований призмы вписаны в окружности оснований цилиндра, а образующие цилиндра являются боковыми рёбрами призмы.

            

Цилиндр можно описать только около такой прямой призмы, около основания которой можно описать окружность.

Например, цилиндр всегда можно описать около прямой треугольной призмы, около правильной призмы.

Рисунок составляется в зависимости от содержания задания, часто достаточно рисунка основания комбинаций этих тел, т. к. высота призмы равна высоте цилиндра.

Окружность основания цилиндра описана около многоугольника основания призмы.

Радиус цилиндра — это радиус окружности, описанной около многоугольника основания призмы.

 

 

Центр окружности, описанной около треугольника, является точкой пересечения серединных перпендикуляров к сторонам треугольника.

 

 

Центр окружности, описанной около четырёхугольника, является точкой пересечения серединных перпендикуляров к сторонам четырёхугольника. Около четырёхугольника можно описать окружность, если суммы противоположных углов равны 180°.

Формулы вычисления радиуса \(R\) описанной окружности

\(a, b, c\) — стороны, \(h\) — высота, \(d\) — диагональ.

 

Правильный треугольник	\(R =\) 23h;           \(R=\) a33
Прямоугольный треугольник	\(R=\) 12 гипотенузы
Произвольный треугольник	R=abc4S;R=a2sinα
Квадрат	\(R =\) a22
Прямоугольник	\(R =\) d2
Правильный шестиугольник	\(R = a\)

Цилиндр вписан в призму, если окружности оснований цилиндра вписаны в многоугольники оснований призмы.

  

 

Цилиндр можно вписать только в такую прямую призму, в многоугольник основания которой можно вписать окружность.

Например, цилиндр всегда можно вписать в прямую треугольную призму, в правильную призму.

Рисунок создаётся в зависимости от содержания задачи, часто достаточно нарисовать основание комбинаций этих тел, т. к. высота цилиндра равна высоте призмы.

Окружность основания цилиндра вписана в многоугольник основания призмы.

Радиус цилиндра — радиус окружности, вписанной в многоугольник основания призмы.

 

Центр вписанной в треугольник окружности находится в точке пересечения биссектрис треугольника.

 

 

Центр окружности, вписанной в четырёхугольник, находится в точке пересечения биссектрис четырёхугольника. В четырёхугольник можно вписать окружность, если равны суммы длин противоположных сторон.

Формулы вычисления радиуса \(r\) вписанной окружности

Где \(h\) — высота, \(S\) — площадь, \(p\) — полупериметр, \(a\) — сторона.

 

Правильный треугольник	r=13h;r=a36
Произвольный (и прямоугольный) треугольник	\(r =\) Sp
Квадрат	\(r =\) 12\(a\)
Ромб	\(r =\) Sp или \(r =\) 12 от \(h\)
Правильный шестиугольник	\(r =\) a32

  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

www.yaklass.ru

Цилиндр

ОПРЕДЕЛЕНИЕ ЦИЛИНДРА И ЕГО ЭЛЕМЕНТОВ

Цилиндр (круговой цилиндр) – тело, которое состоит их двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.

Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, — образующими цилиндра. Эти отрезки образуют цилиндрическую поверхность, являющуюся боковой поверхностью цилиндра.

Если основаниями цилиндра не являются круги, то цилиндр может быть эллиптическим. Обычно, такие виды цилиндра в элементарной геометрии не рассматриваются.

Альтернативное определение.

Цилиндром называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя пересекающими ее параллельными плоскостями.

Полная поверхность цилиндра состоит из оснований и боковой поверхности.

Цилиндр называется прямым, если его образующие перпендикулярны к плоскости оснований.

Прямой цилиндр наглядно можно представить как тело, полученное в результате вращения прямоугольника вокруг стороны как оси.

Радиусом цилиндра называется радиус его основания.

Высотой цилиндра называется расстояние между плоскостями его оснований.

Осью цилиндра называется прямая, проходящая через центры основания. Она параллельна образующим.

Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник. Две стороны его – образующие цилиндра, а две другие – параллельные хорды оснований. Осевое сечение цилиндра – это сечение плоскостью, проходящей через его ось.

Касательной плоскостью к цилиндру называется плоскость, проходящая через образующую цилиндра и перпендикулярная плоскости осевого сечения, содержащей эту образующую.

Объем цилиндра

Объем цилиндра равен произведению площади основания на высоту Н:

Если у цилиндра известны только площадь основания и образующая, то объем такого цилиндра будет равен произведению площади основания на образующую и синус угла между основанием и образующей [2].

Для цилиндра, в основании которого лежит круг, объем цилиндра будет равен площади круга на высоту [3][4].

Площадь боковой поверхности цилиндра

Площадь боковой поверхности прямого цилиндра с радиусом R основания и высотой Н
Содержание главы:
 Соотношение объема шара и конуса | Описание курса | Задачи про цилиндр со вписанной призмой 

   

profmeter.com.ua