Цилиндр, конус, шар | ЕГЭ по математике (профильной)
Цилиндр, конус, шар
Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.
Образующие цилиндрической поверхности называются образующими цилиндра, на рисунке образующая $L$.
Цилиндр называется прямым, если его образующие перпендикулярны основаниям. Осевое сечение цилиндра — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра.
Основные понятия и свойства цилиндра:
- Основания цилиндра равны и лежат в параллельных плоскостях.
- Все образующие цилиндра параллельны и равны.
- Радиусом цилиндра называется радиус его основания ($R$).
- Высотой цилиндра называется расстояние между плоскостями оснований (в прямом цилиндре высота равна образующей).
- Осью цилиндра называется отрезок, соединяющий центры оснований ($ОО_1$).

Объем цилиндра больше объема шара в $1.5$ раза, следовательно, чтобы найти объем шара, надо объем цилиндра разделить на $1.5$.
$V_{шара}=30:1.5=20$
Ответ: $20$
Конусом (круговым конусом) называется тело, которое состоит из круга, точки, не лежащей в плоскости этого круга, и всех отрезков, соединяющих заданную точку с точками круга.
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими и обозначаются (l).
$l=SA$
Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Ось прямого конуса и его высота равны.
$SО$ — высота и ось конуса.
Свойства конуса:
- Все образующие конуса равны.
- Осевым сечением конуса является равнобедренный треугольник, основание которого равно двум радиусам, а боковые стороны равны образующим конуса.
- Если боковая поверхность конуса – полукруг, то осевым сечением является равносторонний треугольник, угол при вершине равен $60°$.
 2$
2$Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$:
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Значения тригонометрических функций некоторых углов:
$α$ $30$ $45$ $60$ $sinα$ ${1}/{2}$ ${√2}/{2}$ ${√3}/{2}$ $cosα$ ${√3}/{2}$ ${√2}/{2}$ ${1}/{2}$ $tgα$ ${√3}/{3}$ $1$ $√3$ $ctgα$ $√3$ $1$ ${√3}/{3}$ Признаки подобия треугольников:
- Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Презентация «Цилиндр» — геометрия, презентации
библиотека
материаловСодержание слайдов
Номер слайда 1
Цилиндр
Повторениеа+bab2(а+b)По какой формуле находится площадь прямоугольника?Верно!а²
Номер слайда 3
Повторение2r.
 Пr²2 Пr. По какой формуле находится площадь круга?Верно!Пr
Пr²2 Пr. По какой формуле находится площадь круга?Верно!ПrНомер слайда 4
Повторение2r2 Пr. Пr. По какой формуле находится длина окружности?Верно!2 П
Вычислить длину окружности и площадь круга, если радиус окружности равен 2,5 см.
 Повторение. С = 2 Пr = 2 П2,5 = 5 ПS=Пr² = 6,25 ПОтвет
Повторение. С = 2 Пr = 2 П2,5 = 5 ПS=Пr² = 6,25 ПОтветНомер слайда 6
Тема урока. Цилиндр
Номер слайда 7Рассмотрим произвольную плоскость α и окружность L с центром О радиуса r, лежащую в этой плоскости.
 Через каждую точку окружности проведем прямую, перпендикулярную к плоскости α. Поверхность, образованная этими прямыми, называется цилиндрической поверхностью, а сами прямые — образующими цилиндрической поверхности. Прямая, проходящая через точку О перпендикулярно к плоскости α, называется осью цилиндрической поверхности. Поскольку все образующие и ось перпендикулярны к плоскости α, то они параллельны друг другу.
Через каждую точку окружности проведем прямую, перпендикулярную к плоскости α. Поверхность, образованная этими прямыми, называется цилиндрической поверхностью, а сами прямые — образующими цилиндрической поверхности. Прямая, проходящая через точку О перпендикулярно к плоскости α, называется осью цилиндрической поверхности. Поскольку все образующие и ось перпендикулярны к плоскости α, то они параллельны друг другу.Рассмотрим теперь плоскость β, параллельную плоскости α. Отрезки образующих, заключенные между плоскостями α и β, параллельны и равны друг другу.
Номер слайда 9
По построению концы этих отрезков, расположенные в плоскости α, заполняют окружность L. Концы же, расположенные в плоскости β, заполняют окружность L1 с центром О1 радиуса r, где О1 — точка пересечения плоскости β с осью цилиндрической поверхности. Справедливость этого утверждения следует из того, что множество концов образующих, лежащих в плоскости β, получается из окружности L параллельным переносом на вектор OO1. Параллельный перенос является движением и, значит, наложением, а при наложении любая фигура переходит в равную ей фигуру.
 Следовательно, при параллельном переносе на вектор ОО1 окружность L перейдет в равную ей окружность L1 радиуса r с центром в точке О1.
Следовательно, при параллельном переносе на вектор ОО1 окружность L перейдет в равную ей окружность L1 радиуса r с центром в точке О1.Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L и L1 называется цилиндром. Круги называются основаниями цилиндра, отрезки образующих, заключенные между основаниями, — образующими цилиндра, а образованная ими часть цилиндрической поверхности — боковой поверхностью цилиндра. Ось цилиндрической поверхности называется осью цилиндра. Все образующие цилиндра параллельны и равны друг другу.
 Длина образующей называется высотой цилиндра, а радиус основания — радиусом цилиндра.
Длина образующей называется высотой цилиндра, а радиус основания — радиусом цилиндра.Номер слайда 11
Номер слайда 12
Развертка цилиндра
Номер слайда 13
Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон.
 На рисунке изображен цилиндр, полученный вращением прямоугольника АВСD вокруг стороны АВ. При этом боковая поверхность цилиндра образуется вращением стороны СD, а основания — вращением сторон ВС и АD. Поэтому цилиндр называют телом вращения.
На рисунке изображен цилиндр, полученный вращением прямоугольника АВСD вокруг стороны АВ. При этом боковая поверхность цилиндра образуется вращением стороны СD, а основания — вращением сторон ВС и АD. Поэтому цилиндр называют телом вращения.Номер слайда 14
Сечения цилиндра. Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого — образующие, а две другие — диаметры оснований цилиндра. Такое сечение называется осевым. АВСD – осевое сечение
Номер слайда 15
Сечения цилиндра.
 Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом. В самом деле, такая секущая плоскость — плоскость y на рисунке отсекает от данного цилиндра тело, также являющееся цилиндром. Его основаниями служат два круга, один из которых и есть рассматриваемое сечение.
Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом. В самом деле, такая секущая плоскость — плоскость y на рисунке отсекает от данного цилиндра тело, также являющееся цилиндром. Его основаниями служат два круга, один из которых и есть рассматриваемое сечение.Номер слайда 16
Наклонный цилиндр. Наклонный цилиндр — цилиндр, основаниями которого являются круги, но образующие цилиндра не перпендикулярны к плоскостям оснований.
Номер слайда 17
Цилиндр в архитектуре«Уолл Билдинг» в Хиро
Номер слайда 18
Цилиндр в архитектуре»Башня ветров» в Иокогаме
Номер слайда 19
Цилиндр в архитектуре.
 Цементный комбинат на окраине французской столицы
Цементный комбинат на окраине французской столицыНомер слайда 20
Цилиндр в архитектуре. В китайском городе Чунцин появилась уменьшенная версия стеклянного Apple Store из Шанхая.
Номер слайда 21
Цилиндр в архитектуре.
 Английский замок в Сандерленде украшает необычный фонтан, который создал архитектор Уильям Пай. Фонтан представляет собой прозрачный цилиндр с воронкой водоворота по середине.
Английский замок в Сандерленде украшает необычный фонтан, который создал архитектор Уильям Пай. Фонтан представляет собой прозрачный цилиндр с воронкой водоворота по середине.Номер слайда 22
Цилиндр в архитектуре. Отель Radisson Blue расположен в Берлине и знаменит своим удивительным архитектурным стилем. Здесь так же находится самый большой цилиндрический аквариум в мире.
Номер слайда 23
Площадь боковой поверхности цилиндра.
 Представим себе, что его боковую поверхность разрезали по образующей АВ и развернули таким образом, что все образующие оказались расположенными в некоторой плоскости α. В результате в плоскости α получится прямоугольник АВВ1 А1. Стороны АВ и В1 А1 прямоугольника представляют собой два края разреза боковой поверхности цилиндра по образующей АВ. Этот прямоугольник называется разверткой боковой поверхности цилиндра. Основание АА1 прямоугольника является разверткой окружности основания цилиндра, а высота АВ — образующей цилиндра, поэтому АА1 = 2πr, АВ = h, где г — радиус цилиндра, h — его высота.
Представим себе, что его боковую поверхность разрезали по образующей АВ и развернули таким образом, что все образующие оказались расположенными в некоторой плоскости α. В результате в плоскости α получится прямоугольник АВВ1 А1. Стороны АВ и В1 А1 прямоугольника представляют собой два края разреза боковой поверхности цилиндра по образующей АВ. Этот прямоугольник называется разверткой боковой поверхности цилиндра. Основание АА1 прямоугольника является разверткой окружности основания цилиндра, а высота АВ — образующей цилиндра, поэтому АА1 = 2πr, АВ = h, где г — радиус цилиндра, h — его высота.Номер слайда 24
Площадь боковой поверхности цилиндра.
 За площадь боковой поверхности цилиндра принимается площадь ее развертки. Sбок = 2 Пrh
За площадь боковой поверхности цилиндра принимается площадь ее развертки. Sбок = 2 ПrhНомер слайда 25
Площадь полной поверхности цилиндра. Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. Так как площадь каждого основания равна πr2, то для вычисления площади полной поверхности цилиндра получаем формулу:
Номер слайда 26
Решение задач.
 Задача 1. Дано: Площадь боковой поверхности цилиндра равна S. Найти: площадь осевого сечения цилиндра. Решение задачи
Задача 1. Дано: Площадь боковой поверхности цилиндра равна S. Найти: площадь осевого сечения цилиндра. Решение задачиНомер слайда 27
Решение задач. Решение: По рисунку площадь осевого сечения – это площадь прямоугольника ABCD. SABCD=AB x AD = 2rh. Sбок=2 Пrh=S (по условию)Выразим 2rh = S : ППодставим в формулу площади и получим. SABCD = S : П
Номер слайда 28
Решение задач.
 Задача 2. Сколько квадратных метров листовой жести пойдет на изготовление трубы длиной 4 м и диаметром 20 см, если на швы необходимо добавить 2,5% площади ее боковой поверхности?Решение задачи
Задача 2. Сколько квадратных метров листовой жести пойдет на изготовление трубы длиной 4 м и диаметром 20 см, если на швы необходимо добавить 2,5% площади ее боковой поверхности?Решение задачиНомер слайда 29
Дано: L=4; d=20см=0,2м. Найти: S. Решение: Воспользуемся формулой площади полной поверхности цилиндра. Радиус равен половине диаметра – 0,1м, а высота цилиндра равна длине нужной трубы – 4м. Так на швы нужно добавить 2,5% площади ее боковой поверхности, нужно найти: (S+2,5%S). Подставим вместо S формулу площади боковой поверхности, и вычислим: Ответ: 2,6 м2.

Номер слайда 30
Список источников содержания и иллюстраций. Геометрия: учеб. для 10 — 11 кл. для общеобразовательных учреждений: базовый и профильный уровни /Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – М.: «Просвещение», 2008-2014 Иллюстрации:http://d3mlntcv38ck9k.cloudfront.net/content/konspekt_image/38125/420ec120_f310_0130_97dc_22000a1d011d.jpghttp://d3mlntcv38ck9k.cloudfront.net/content/konspekt_image/38126/428c0210_f310_0130_97dd_22000a1d011d.pnghttp://doc4web.ru/uploads/files/49/48418/hello_html_7b721d81.
 pnghttps://lh5.googleusercontent.com/-KSm_ot. Ixa. W0/T06 RUh. G0kl. I/AAAAAAAAI4w/Dz. BDf. Dn. Jf. MQ/s1600/razvertka_cilindra.gifhttp://content.foto.mail.ru/mail/t.ant/_answers/i-407.jpghttps://lh6.googleusercontent.com/-Wk0 YGd. Hhpxc/T0y1_88awd. I/AAAAAAAAI5 I/s. Ut. Jc. Yo9c5 I/s1600/cilindr_vraschenie.gif
pnghttps://lh5.googleusercontent.com/-KSm_ot. Ixa. W0/T06 RUh. G0kl. I/AAAAAAAAI4w/Dz. BDf. Dn. Jf. MQ/s1600/razvertka_cilindra.gifhttp://content.foto.mail.ru/mail/t.ant/_answers/i-407.jpghttps://lh6.googleusercontent.com/-Wk0 YGd. Hhpxc/T0y1_88awd. I/AAAAAAAAI5 I/s. Ut. Jc. Yo9c5 I/s1600/cilindr_vraschenie.gifНомер слайда 31
Иллюстрации:http://d3mlntcv38ck9k.cloudfront.net/content/konspekt_image/38128/43590490_f310_0130_97df_22000a1d011d.pnghttp://d3mlntcv38ck9k.cloudfront.net/content/konspekt_image/38129/43eab530_f310_0130_97e0_22000a1d011d.
 pnghttp://studyport.ru/data/Exact_Science/te1d_36/image3872.gifhttp://d3mlntcv38ck9k.cloudfront.net/content/konspekt_image/38131/44c8a5c0_f310_0130_97e2_22000a1d011d.pnghttp://photostock.su/48398.jpeg http://savepic.su/422861.png http://ramki-kartinki.ru/_ph/27/2/686148141.jpghttp://mcocos.ru/tmp-tvbreak/img/ramka.pnghttp://vsadu.ucoz.ru/lessons/sr_group/fg08.jpghttp://konspekta.net/studopediainfo/baza2/150620514939.files/image016.jpghttp://konspekta.net/studopediainfo/baza2/150620514939.files/image023.jpg http://img.architector.ua/images/articles/fortissimo/pic_big/pic_1409049687.jpghttp://www.macdigger.ru/wp-content/uploads/2015/01/Apple-Store-interior-3.jpghttp://karaul.ru/uploads/posts/2013-04/1366273992_vodovorot002.jpghttp://lifeglobe.net/x/entry/2897/6.jpg http://comfort-montage.ru/upload/iblock/c05/c05ef35c3132c9647bf919c709a93853.jpg
pnghttp://studyport.ru/data/Exact_Science/te1d_36/image3872.gifhttp://d3mlntcv38ck9k.cloudfront.net/content/konspekt_image/38131/44c8a5c0_f310_0130_97e2_22000a1d011d.pnghttp://photostock.su/48398.jpeg http://savepic.su/422861.png http://ramki-kartinki.ru/_ph/27/2/686148141.jpghttp://mcocos.ru/tmp-tvbreak/img/ramka.pnghttp://vsadu.ucoz.ru/lessons/sr_group/fg08.jpghttp://konspekta.net/studopediainfo/baza2/150620514939.files/image016.jpghttp://konspekta.net/studopediainfo/baza2/150620514939.files/image023.jpg http://img.architector.ua/images/articles/fortissimo/pic_big/pic_1409049687.jpghttp://www.macdigger.ru/wp-content/uploads/2015/01/Apple-Store-interior-3.jpghttp://karaul.ru/uploads/posts/2013-04/1366273992_vodovorot002.jpghttp://lifeglobe.net/x/entry/2897/6.jpg http://comfort-montage.ru/upload/iblock/c05/c05ef35c3132c9647bf919c709a93853.jpgурок «Цилиндр как тело вращения»
Тема урока «Цилиндр как фигура вращения»
Цель урока: ввести понятие «цилиндр», его элементы и разновидности.

Задачи урока:
1. Образовательная
- Ввести понятие цилиндра и его видов; элементы цилиндра, сечения цилиндра.
- Вывести формулу вычисления площади боковой и полной поверхности цилиндра.
- Закрепить понятия с помощью выполнения заданий.
2. Развивающая
- Способствовать развитию умения учащихся самостоятельно формулировать цели и задачи.
- Развивать пространственное воображение.
3. Воспитывающая
- Способствовать осознанию ценности коллективной мыслительной деятельности.
-
Формировать представление о математике, как о части общечеловеческой культуры.

Тип урока: сообщение новых знаний
Формы организации деятельности учащихся: групповая, фронтальная
Ожидаемый результат:
учащиеся должны знать
- определение цилиндра;
- виды цилиндра;
- элементы цилиндра;
- разновидности сечений цилиндра;
учащиеся должны уметь:
- вычислять элементы цилиндра при решении задач;
-
находить полную, боковую поверхность цилиндра.

Оборудование и материалы: интерактивная доска, компьютер, карточки с заданиями, линейки, карандаши.
ХОД УРОКА
1. Организационный момент
Здравствуйте уважаемые коллеги, дорогие ребята. Приглашаем Вас на наш он-лайн урок.
Девизом нашего урока я выбрала японскую пословицу: ««Не стыдись спросить –
не знать еще стыднее!».
2. Постановка целей и задач урока.
Прежде всего хотелось бы определиться с темой урока. А поможет нам в этом энциклопедический словарь, в котором даётся несколько определений одного и того же понятия.
1.
 Это основная деталь поршневых машин (двигателя внутреннего сгорания, паровой
Это основная деталь поршневых машин (двигателя внутреннего сгорания, паровой
машины и т.п.).
2. Высокая твердая шляпа такой формы с небольшими полями.
3. Геометрическое тело, образованное вращением прямоугольника вокруг одной из его сторон.
Конечно же, речь идёт о цилиндре. Запишите тему нашего урока «Цилиндр как тело вращения».
Как вы думаете, какова наша цель урока? (выслушать предположения учеников).
Итак, цель нашего урока дать определение одному из тел вращения.
Задачи: рассмотреть элементы и виды цилиндров, узнать, как вычислять полную и боковую поверхности цилиндра, познакомиться с разновидностями сечений цилиндра, научиться использовать полученные знания при решении задач и упражнений.
3.
 Объяснение нового материала.
Объяснение нового материала.
Вопрос учителя: «Какие предметы из окружающей среды напоминают вам цилиндр?»
Как видите, цилиндры окружают нас повсюду поэтому так важно знать свойства этой фигуры.
Сегодня на уроке у меня есть помощницы, которые подготовили для вас небольшую информацию о цилиндре. (Презентация учениц).
Историческая справка:
С конусом и цилиндром люди знакомы с глубокой древности. В 1906 году была обнаружена книга Архимеда (287–212 гг. до н.э.) “О методе”, в которой дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед приписывает честь открытия этого принципа – Демокриту (470–380 гг. до н.э.) – древнегреческому философу-материалисту. С помощью этого принципа Демокрит получил формулу для вычисления объема пирамиды и конуса.
Много сделала для геометрии школа Платона (428–348 гг.
 до н.э.). Школе Платона с частности принадлежит: а) исследование свойств призмы, пирамиды, цилиндра и конуса; б) изучение конических сечений.
до н.э.). Школе Платона с частности принадлежит: а) исследование свойств призмы, пирамиды, цилиндра и конуса; б) изучение конических сечений.
4. Первичное закрепление материала.
1) Деление на группы
Для организации дальнейшей работы, я предлагаю вам разделиться на группы. Я раздам листочки, на которых написана часть какого-либо математического факта. Вам необходимо составить фразу, найдя пару. А затем вспомнить в каком классе вы знакомились с данным фактом.
Для учеников
сумма углов треугольника равна
вертикальные углы равны
внутренние односторонние углы
квадрат гипотенузы равен
площадь квадрата равна
апофема – это
в сумме дают 180˚
цилиндр – это
квадрату его стороны
180˚
тело вращения
сумме квадратов катетов
высота боковой грани правильной пирамиды
Формирование групп
7 класс:
Сумма углов треугольника равна 180˚.

Вертикальные углы равны.
Внутренние односторонние углы в сумме дают 180˚.
8 класс:
Квадрат гипотенузы равен сумме квадратов катетов.
Площадь квадрата равна квадрату его стороны.
10 класс:
Апофема – это высота боковой грани правильной пирамиды.
Цилиндр – это тело вращения.
2. Групповая работа
Каждой группе предлагается следующее задание:
1 группа
Разгадать кроссворд.
По горизонтали
1.
 Отрезок, соединяющий вершину цилиндра с точкой окружности основания,
Отрезок, соединяющий вершину цилиндра с точкой окружности основания,
называют…
4. Фигура, полученная в пересечении цилиндра плоскостью, называется…
цилиндра
5. Осевым сечением цилиндра является…
По вертикали
2. Какой вид не может иметь сечение цилиндра?
3. Сколько образующих можно провести в цилиндре?
5. Цилиндр может быть получен вращением…
6. Сечением цилиндра плоскостью, перпендикулярной его образующей,
является…
Ответы:
По горизонтали
1.
 Высота
Высота
4. Сечением
5. Прямоугольник
По вертикали
2. Треугольник
3. Много
5. Прямоугольника
6. Круг
2 группа . Творческое задание «Мы – поэты»
Из слов урок, цилиндр, тема, круг, сечение, плоскость, площадь придумать четверостишие.
Приветствуется творчество, находчивость.
Для оценивания работы участников 1-2 группы я предлагаю в конце вашей работы заполнить лист оценивания:
Лист оценивания группы 1
Фамилия, имя ученика
Участие в обсуждении
Участвовал в презентации работы группы
Общий балл
Оценка
Формулировал правиль-ные ответы — 2
Выдви-гал идеи, но не всегда верные — 1
В обсуждении не участвовал -0
Презенто-вал работу группы — 1
Не участво-вал в презента-ции — 0
Шкала перевода балла в оценку:
3 балла – «5», 2 балла – «4», 1 балл – «3», 0 баллов – «2»
Лист оценивания группы 2
Фамилия, имя ученика
Участие в обсуждении
Участвовал в презентации работы группы
Общий балл
Оценка
Выдви-гал интерес-ные идеи, соответствующие теме — 2
Выдви-гал идеи, но не всегда соответствующие теме — 1
В обсужде-нии не участво-вал -0
Презентовал работу групп-пы — 1
Не участво-вал в презентации — 0
Шкала перевода балла в оценку:
3 балла – «5», 2 балла – «4», 1 балл – «3», 0 баллов – «2»
3 группа
Блиц- опрос «Дальше-дальше…»
1.
 Назови элементы цилиндра (Боковая поверхность, основание, ось, радиус, образующая, высота)
Назови элементы цилиндра (Боковая поверхность, основание, ось, радиус, образующая, высота)
2. Назови вид осевого сечения цилиндра (прямоугольник, квадрат)
3. Может ли сечение цилиндра быть:
прямоугольником (да)
квадратом (да)
трапецией? (нет)
4. Какие из данных утверждений верны:
- любое сечение цилиндра плоскостью, перпендикулярной основанию есть окружность, равная окружности основания; (нет)
- любое сечение цилиндра плоскостью есть окружность, равная окружности основания; (нет)
- плоскость, перпендикулярная оси цилиндра, пересекает его по кругу, равному основанию цилиндра; (да)
- сечением цилиндра могут быть круг, прямоугольник, эллипс. (да)
Оценку даёт группа по количеству набранных звёзд.

Дополнительные вопросы стр. 36 учебника: №3, 4, 6, 8, 9, 10
3. Цилиндр катится по некоторой плоскости. Какую фигуру образует при этом ось
цилиндра?
4. Какая фигура получается в сечении цилиндра плоскостью:
а) параллельной оси цилиндра (прямоугольник, квадрат),
б) параллельной основаниям цилиндра (круг),
в) не параллельная оси цилиндра (эллипс),
г) не параллельная основаниям цилиндра? (эллипс)
6.Как должны быть расположены две равные окружности, чтобы через них можно было
провести цилиндрическую поверхность? (параллельно друг другу)
8. Можно ли вращением произвольного параллелограмма вокруг одной из его сторон
получить цилиндр? (нет).

9. Сколько существует плоскостей, рассекающих данный цилиндр:
а) на два равных цилиндра (множество, но они будут проходить через ось цилиндра перпендикулярно основанию – осевые сечения или через середину высоты, параллельно основаниям)
б) две равные фигуры (множество, будут содержать две равные хорды, лежащие соответственно в верхнем и нижнем основании).
10. Как изменится площадь боковой поверхности цилиндра, если, его:
а) высоту увеличить в два раза (увеличится в два раза),
б) радиус основания увеличить в три раза? (увеличится в три раза)
Презентация работы 1 группы. Оценка работы группы.
5. Решение задач
Устно задачи по готовым чертежам.
№ 1.
 Дан цилиндр с радиусом основания 3 м и высотой 8 м. Найдите диагональ осевого сечения цилиндра.
Дан цилиндр с радиусом основания 3 м и высотой 8 м. Найдите диагональ осевого сечения цилиндра.
По условию задачи радиус основания равен 3 м, значит диаметр AD = 6 м. Диагональ осевого сечения находится в прямоугольном треугольнике АСD и является его гипотенузой, если высота СD = 10 м, то по теореме Пифагора
АС2 = AD2 + СD2. Тогда АС = (Пифагорова тройка)
№ 2. Дан цилиндр с радиусом основания 6 см, диагональ осевого сечения равна 13 см. Найдите площадь осевого сечения цилиндра.
По условию задачи радиус основания равен 6с м, значит диаметр AD = 12 см. Диагональ осевого сечения АС = 13 см, находится в прямоугольном треугольнике АСD и является его гипотенузой.
 Найдём высоту по теореме Пифагора
Найдём высоту по теореме Пифагора
СD2 = АС2 — AD2. Тогда СD = 5 см (Пифагорова тройка).
Осевым сечением является прямоугольник АВСD, площадь которого равна произведению диаметра и высоты. Площадь осевого сечения равна 60 см2.
№3. Сколько понадобится краски, чтобы покрасить бак цилиндрической формы с диаметром основания 4 м и высотой 7 м, если на 1 кв. м расходуется 200 г краски (значение возьмите равным 3)?
По условию задачи, необходимо покрасить бак цилиндрической формы. Значит, нужно найти полную поверхность цилиндра. Если диаметр равен 4 м, а высота 3 м, то боковая поверхность равна 4·7· = 84 м2. Радиус основания равен 2 м, тогда площадь основания ·22 = 12 м2.
 Полная поверхность будет равна сумме боковой поверхности и двум площадям основания: 84 + 12 · 2 = = 84 + 24 = 108 м2. Тогда нужно будет 108 · 200 = 21 600 г =
Полная поверхность будет равна сумме боковой поверхности и двум площадям основания: 84 + 12 · 2 = = 84 + 24 = 108 м2. Тогда нужно будет 108 · 200 = 21 600 г =
= 21 кг 600 краски
6. Итог урока
а) Презентация работы 2 группы. Оценивание работы второй группы.
б) Рефлексия урока.
Перед вами на столе лежат кружочки трёх цветов. Вам необходимо выбрать цвет, соответствующий полученным знаниям на уроке.
Зелёный – тема понятна;
Жёлтый — остались вопросы;
Красный – тема не понятна.

в) Домашнее задание.
Стр. 32-36, №11-15
Ода цилиндрам!
Цилиндры вокруг окружают тебя:
Зарыты в земле глубоко,
И фокусник ловкий
Зайчонка для нас
Достал из него так легко.
Цилиндрам в быту почет и хвала,
Ну что тут еще вам сказать:
И денно, и нощно, и мощно по ним
Течет газ , тепло и вода.
Цилиндров значение так велико,
О них никогда не забудь.
О свойствах его при решенье задач
Ты помни, конечно, всегда!
Конспект урока по геометрии «Цилиндр» 11 класс
Урок по геометрии на тему: «Цилиндр».

11 класс
Цели.
Познакомить учащихся с новыми понятиями: цилиндрическая поверхность, цилиндр, основания цилиндра, образующие цилиндра. осевое сечение и сечение, перпендикулярное оси цилиндра, развертка цилиндра ; дать формулы для вычисления площади боковой и полной поверхности цилиндра .
Научить решать ключевые задачи по данной теме.
3. Формирование грамотной математической речи, умения слушать,
анализировать , строить логические цепочки, делать выводы, работать с
чертежами.
4. Формирование трудовых навыков, умения распределять своё
рабочее время на уроке, быстро, грамотно и аккуратно оформлять
записи в своих конспектах.
5. Формирование математического мировоззрения, математической
культуры, культуры речи, использование математических терминов и
символики.
6. Формирование умения чётко и ясно излагать свои мысли, обсуждать и
корректировать высказывания своих одноклассников.

7. Формирование интереса к предмету математики путём
использования формы урока беседа-лекция, использования
наглядности(моделей) и ИКТ.
Ход урока.
1 этап. Проверка Д/З, вопросы. (5мин.)
2 этап. Объяснение новой темы. (20 мин.)
Учащимся предлагается лекция с поддержкой на интерактивной доске, все необходимые записи они делают в своих конспектах .
Определение цилиндра. Сечения цилиндра.
Рассмотрим рисунок 1:
Вы видите две параллельные плоскости и и окружность L с центром O радиуса , расположенную в плоскости . Через каждую точку окружности L проведем прямую перпендикулярную к плоскости . Отрезки этих прямых, заключенные между плоскостями и , образуют цилиндрическую поверхность. Сами отрезки называются образующими цилиндрической поверхности (на рис.1 AA1, MM1 – образующие).

По построению концы образующих, расположенные в плоскости , заполняют окружность L. Концы же образующих, расположенные в плоскости , заполняют окружность L1 с центром O1 радиуса r, где O1 – точка пересечения плоскости с прямой, проходящей через точку O перпендикулярно к плоскости .
Справедливость этого утверждения следует из того, что множество концов образующих, лежащих в плоскости , получается из окружности L параллельным переносом на вектор .
Рассмотрим рисунок 2:
Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L и L1 называется цилиндром. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра. Образующие цилиндрической поверхности называются образующими цилиндра.
Все образующие параллельны и равны друг другу как отрезки параллельных прямых, заключенных между параллельными плоскостями и .
 Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.
Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.Рассмотрим рисунок 3:
Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон. На рисунке изображен цилиндр, полученный вращением прямоугольника ABCD вокруг стороны AB.
Рассмотрим рисунок 4:
Здесь представлены сечения цилиндра различными плоскостями. Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, а сечение называется осевым. Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом.
На практике нередко встречаются цилиндры более сложной формы.
Рассмотрим рисунок 5:
Здесь изображен цилиндр, в основании которого фигура, ограниченная параболой и отрезком.
Рассмотрим рисунок 6:
На нём изображен цилиндр, у которого основания – круги, но образующие не перпендикулярны основаниям.

2) Площадь поверхности цилиндра.
Рассмотрим рисунок 7:
Представим себе, что боковую поверхность цилиндра разрезали по образующей AB и развернули таким образом, чтобы все образующие лежали в некоторой плоскости . В результате в плоскости получается прямоугольник . Этот прямоугольник называется разверткой боковой поверхности цилиндра. – развертка окружности основания, поэтому . – высота цилиндра.
За площадь боковой поверхности цилиндра принимается площадь ее развертки.
Поэтому .
Площадь полной поверхности равна: .
3 этап . Решение задач. (10 мин.) (Л. С. Атанасян, Геометрия 10-11).
№522. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующей цилиндра равен . Найдите: а) высоту цилиндра; б) радиус цилиндра; в) площадь основания цилиндра.
Дано:
Найти:
а) h; б) r; в) Sосн
Решение:
а)
б)
в) .

№529. Высота цилиндра равна 8 см, радиус равен 5 см. Найдите площадь сечения цилиндра плоскостью, параллельной его оси, если расстояние между этой плоскостью и осью цилиндра равно 3 см.
Дано:
Найти:
SABCD
Решение:
.
4 этап. Подведение итогов. Выводы. Домашнее задание. (5 мин.)
Сегодня на уроке мы познакомились с новым телом в пространстве, выяснили из каких элементов оно состоит, рассмотрели различные его сечения, определили их развертку, научились вычислять площади его боковой и полной поверхностей.
На примерах решения задач посмотрели, как применять изученный материал к их решению. Научились строить чертежи цилиндра, его сечений и его развёртки.
Д/З. Атанасян Л.С. Геометрия 10-11 п.53-55; №530, 538, 546.
6
Наглядная геометрия
Предисловие главного редактора Портала Знаний:
Мы предлагаем вашему вниманию замечательную книгу Гильберта и Кон-Фоссена «Наглядная геометрия».

Самым замечательным в этой книге является то, что сложные рассуждения можно увидеть зрительно и решение сложной задачи получается непосредственно из чертежа или графика. Традиция видения решения идет от древних греков.
Такие геометрические представления очень полезны в современной аналитике.
Мы дополнили книгу несколькими задачами, позволяющими читателю поупражняться в проведении рассуждений.
Надеемся, что чтение избранных глав этой прекрасной книги доставит удовольствие читателям.
Если читатель по-настоящему увлечется геометрией, то можно познакомиться с несколькими главами из книги Евклида, отрывки из которой тоже можно найти на нашем портале.
Предисловие автораВ нашей книге это очень часто проявляется. При большом разнообразии материала было все же необходимо придать каждой отдельной главе известную законченность и в последующих главах не предполагать полного знания предыдущих; путем отдельных маленьких повторений мы надеялись достигнуть того, что каждая отдельная глава, а иногда даже отдельные разделы представляют интерес сами по себе и в отдельности доступны пониманию читателя.
 Пусть читатель прогуливается в огромном саду геометрии, в котором каждый может составить себе такой букет, какой ему нравится.
Пусть читатель прогуливается в огромном саду геометрии, в котором каждый может составить себе такой букет, какой ему нравится.Основу этой книги составили четырехчасовые лекции «Наглядной геометрии», которые я читал зимой 1920/21 г. в Геттингене и которые обработал В. Роземан. В основном содержание и построение их остались неизменными. В деталях С. Кон-Фоссен многое переработал и частично расширил.
Давид Гильберт
Геттинген, июнь 1932 г.
Глава I Простейшие кривые и поверхностиПлоские кривыеПростейшая поверхность — плоскость, простейшие кривые — плоские кривые, простейшая среди последних — прямая.
Прямую можно определить либо как кратчайший путь между двумя точками, либо как линию пересечения двух плоскостей, либо как ось вращения.
Следующей — в порядке возрастания сложности — кривой является окружность.
 Уже эта кривая послужила исходной точкой для столь многочисленных и столь глубоких исследований, что они могли бы сами по себе заполнить содержание целого курса.
Уже эта кривая послужила исходной точкой для столь многочисленных и столь глубоких исследований, что они могли бы сами по себе заполнить содержание целого курса.Мы определяем окружность как кривую, все точки которой отстоят на равном расстоянии от данной точки. Мы получаем окружность общеизвестным построением при помощи циркуля или натянутой нити.
Рис. 2.
Самое построение наглядно показывает, что окружность есть замкнутая, на всем протяжении выпуклая кривая; поэтому через каждую точку окружности можно провести определенную прямую — касательную, имеющую с окружностью только одну общую точку, точку касания, а в остальной части лежащую целиком вне окружности (рис. 1).
Радиус МВ, проведенный в точку касания , должен быть кратчайшим расстоянием от центра М круга до касательной ибо все точки последней, за исключением точки касания, лежат вне круга и, следовательно, отстоят от центра дальше, чем точка касании.

Отсюда далее следует, что этот радиус перпендикулярен к касательной. Для доказательства построим зеркальное изображение центра относительно прямой , т. е. опустим перпендикуляр из точки М на прямую и продолжим его на равное расстояние до точки ; тогда называется зеркальным изображением точки . А так как есть кратчайшее расстояние от до , то из соображений симметрии также должно быть кратчайшим расстоянием от до
Следовательно, должно быть кратчайшим расстоянием между и , и, значит, линия не может иметь излома в точке , т. е. действительно является перпендикуляром к
Само собой напрашивается обобщение построения окружности, а именно: при построении окружности с помощью нити мы брали связанную нить, закрепляли ее конец в неподвижной точке, центре круга, и, натягивая нить, вычерчивали кривую.
Если же закрепить связанную нить не в одной, а в двух точках, то мы получим кривую, похожую на окружность, называемую эллипсом.
Точки закрепления нити называются фокусами эллипса.

Рис. 2.
Рис. 3.
Построение с помощью нити показывает, что эллипс можно определить как кривую, точки которой имеют постоянную сумму расстояний от двух данных точек.
Сближая фокусы, мы получим окружность как предельный случай эллипса.
Задача от главного редактора: как вы думаете, если направить луч из центра окружности, куда он отразится, если окружность представляет собой зеркало?
Вы направляете луч из фокуса зеркального эллипса, куда отразится этот луч?
Представляя кривые зеркалами, попробуйте решить такие же задачи с другими кривыми, описанными в книге.
Всем упомянутым свойствам окружности соответствуют простые свойства эллипса.
Эллипс также замкнут, всюду выпуклый и имеет в каждой своей точке касательную, которая, за исключением точки касания, целиком лежит вне эллипса.

Радиусам окружности соответствуют в эллипсе две прямые, соединяющие точку эллипса с фокусами. Они называются радиусами-векторами точки эллипса.
Тому факту, что касательная к окружности перпендикулярна‚ радиусу в точке касания, соответствует в случае эллипса то, что касательная образует равные углы с радиусами-векторами, проведенными в точку касания.
Это утверждение означает, что на рис. 2:
Для доказательства (рис. 3) построим зеркальное изображение точки относительно касательной и обозначим его. Прямая , которая пересекается с касательной в некоторой точке, есть кратчайшее расстояние между и .
Следовательно, есть кратчайший путь от к , имеющий общую точку, с касательной, ибо для всякой иной точки касательной будет больше, чем .
С другой стороны, кратчайший путь между и , имеющий общую точку с касательной, образуют радиусы-векторы, проведенные в точку касания , ибо всякая другая точка касательной, как расположенная вне эллипса, имеет большую сумму расстояний от фокусов, чем точка эллипса; значит, точки и совпадают, а отсюда и вытекает наше утверждение, ибо и расположены симметрично относительно прямой , а есть вертикальный для .

Это свойство касательной к эллипсу находит применение в оптике, чем и объясняется название «фокусы».
Именно, если поместить источник света в одном фокусе, толучи, зеркально отраженные от эллипса, соберутся в другом фокусе.
Рис. 4.
Не так легко, как построение эллипса, хотя принципиально столь же просто, построение кривой, у которой разность расстояний ее точек от двух неподвижных точек постоянна.
Эта кривая называется гиперболой, а неподвижные точки — ее фокусами. Для каждой точки или кривой (рис. 4) должно удовлетворяться или соотношение , или .
Соответственно этому гипербола состоит из двух отдельных ветвей. Вид гиперболы наглядно показывает, что кривая эта всюду выпукла и имеет касательную во всякой точке.
Ниже (с. 17, примечание) будет показано, что и в случае гиперболы касательная к кривой имеет с этой кривой только одну общую точку – именно точку прикосновения.
 Так же, как и в случае эллипса, можно показать, что касательная к гиперболе делит пополам угол между радиусами-векторами, проведенными в точку касания (рис. 6, с. 13).
Так же, как и в случае эллипса, можно показать, что касательная к гиперболе делит пополам угол между радиусами-векторами, проведенными в точку касания (рис. 6, с. 13).Из эллипса с помощью предельного перехода можно получить новую кривую – параболу (рис. 5). Для этого оставим один фокус, например и ближайшую к нему вершину эллипса неподвижными (вершинами эллипса называются точки пересечения кривой с прямой, соединяющей ее фокусы).
Будем теперь рассматривать эллипсы, получающиеся при перенесении второго фокуса все далее от точки на продолжение прямой ; эти эллипсы стремятся к некоторой предельной кривой, которая и есть парабола.
Из самого предельного перехода можно вывести простое определение параболы.
Именно, при вычерчивании эллипса с помощью нити мы можем заметить, что если карандаш находится вблизи точки S (рис. 5), то при достаточно большом расстоянии между и отрезок нити, соединяющей карандаш с точкой , почти параллелен линии.
Следовательно, если в некоторой точке прямой восстановить перпендикуляр к , то приближенно будем иметь:
(где — основание перпендикуляра, опущенного из точки на прямую ).
 Если теперь ввести новую постоянную, равную
Если теперь ввести новую постоянную, равную( имеет постоянное значение для каждой кривой), то будем иметь:
Это соотношение будет удовлетворяться с тем большей точностью, чем расстояние , а для предельной кривой оно будет вполне точно.
Рис. 5.
Таким образом парабола есть кривая, для точек которой сумма расстояний от некоторой определенной точки и некоторой определенной прямой постоянна или (что приводит к тому же) такая кривая, точки которой отстоят на равном расстоянии от некоторой постоянной точки и некоторой постоянной прямой.
Мы получим эту последнюю прямую, если проведем прямую, параллельную и расположенную по другую сторону от точки на расстоянии, равном : она называется директрисой параболы.
Если вообразить, что парабола представляет собой отражающее зеркало, то она должна отражать все лучи, падающие параллельно , в точку ; это также следует из предельного перехода.

Мы рассмотрели семейство эллипсов, имеющих общую вершину и общий ближайший к этой вершине фокус. Теперь рассмотрим семейство всех эллипсов, имеющих общие фокусы.
Это семейство «софокусных» эллипсов покрывает плоскость однократно и непрерывно, т. е. через каждую точку плоскости проходит одна и только одна кривая семейства; действительно, каждой точке соответствует вполне определенная сумма расстояний от этой точки до фокусов, и следовательно, каждая точка принадлежит тому эллипсу, которому соответствует эта сумма расстояний 1.
Рис. 6.
Возьмем еще семейство гипербол, имеющих эти же взятые нами точки в качестве фокусов. Это семейство также покрывает плоскость однократно и непрерывно2. Так что через каждую точку плоскости проходят в точности две кривые системы, состоящей из софокусных эллипсов и гипербол (рис. 6).
В каждой точке (за исключением фокусов) касательные к проходящим через эту точку двум кривым — эллипсу и гиперболе — делят пополам угол между радиусами-векторами взятой точки и смежный с ним угол; следовательно, касательные эти взаимно перпендикулярны.

Таким образом софокусные эллипсы и гиперболы образуют два «взаимно ортогональных семейства кривых» (два семейства называются ортогональными, если каждая кривая одного семейства пересекает каждую кривую другого семейства под прямым углом; угол пересечения двух кривых определяется как угол между касательными к этим кривым, проведенными в точке пересечения).
Теперь, чтобы получить наглядное представление о нашей системе кривых (рис. 7), начнем с прямой, перпендикулярной к отрезку , проходящей через его середину, и затем рассмотрим семейство гипербол.
Мы видим, что гиперболы становятся все более сжатыми и, наконец, переходят в полупрямые, служащие продолжением отрезка вправо и влево.
При этом плоскость целиком заполняется гиперболами.
Теперь мы переходим к самому отрезку , к которому непосредственно примыкают сперва очень сжатые эллипсы, которые затем постепенно становятся все более округлыми и вместе с тем безгранично растут. Таким образом мы вторично заполняем всю плоскость.

Другой, и притом исключительно простой, пример взаимно ортогональных семейств кривых представляют концентрические окружности и прямые, проходящие через их общий центр. Эту систему можно получить из предыдущей путем предельного перехода, заставляя сближаться оба фокуса.
При этом эллипсы переходят в окружности, а гиперболы — в пары прямых. Линии уровня и линии наибольшего подъема на географических картах суть также ортогональные семейства.
Рис. 7.
Рис. 8.
Наконец, упомянем другое построение с помощью нити, приводящее к ортогональным семействам.
Возьмем конец нити, навернутой на какую-нибудь выпуклую кривую, например на окружность, и станем разматывать нить, все время натягивая ее (рис. 8). Тогда конец нити опишет «эвольвенту» окружности.
Эта кривая описывает один за другим витки вокруг окружности представляя собой, таким образом, спираль.
 Само построение наглядно показывает, что кривая перпендикулярна к одной из двух касательных к окружности, которые можно провести из какой-либо точки кривой.
Само построение наглядно показывает, что кривая перпендикулярна к одной из двух касательных к окружности, которые можно провести из какой-либо точки кривой.Все последующие витки эвольвенты также пересекают эту касательную под прямым углом, причем отрезок касательной между двумя последующими витками эвольвенты имеет постоянную длину и равен как раз длине взятой окружности.
Можно получить бесконечное множество эвольвент той же самой окружности, если при разматывании нити начать с других точек окружности.
Но все эвольвенты могут быть получены также из одной эвольвенты путем вращения ее вокруг центра окружности. Семейство эвольвент покрывает всю плоскость за исключением внутренности круга однократно и непрерывно. Оно ортогонально к семейству полупрямых, касательных к окружности, взятых в определенном направлении обхода окружности.
И вообще для любого заданного семейства прямых ортогональное семейство состоит из эвольвент.
Образующая их кривая – та, которую (как в нашем примере окружность) огибают прямые заданного семейства.

Мы вернемся еще к этому в дифференциальной геометрии (гл. IV) и кинематике (гл. V).
[1] Отрезок прямой, соединяющий оба фокуса, представляет также эллипс (особенный, выродившийся). Этот эллипс получается, если принять за значение суммы расстояний длину отрезка прямой, соединяющей фокусы.
[2] Прямая, проходящая через оба фокуса, если из неё выбросить отрезок, соединяющий фокусы, есть вырожденная гипербола, точно так же как прямая, перпендикулярная к отрезку, соединяющему фокусы, и проходящая через его середину; для этой последней разность расстояний имеет постоянное значение – нуль.
Страницы: 1 2 3 4 5 … 7 След. ВсеВ начало
Содержание портала
определение цилиндра в геометрии – тест от Skills4U
Хотите без ошибок научиться решать задачи на цилиндр за 11 класс? Интерактивный тренажер, созданный на базе интеллектуальной образовательной платформы Skills4u,поможет вам сделать это за короткое время.
 Всего несколько дней – и вы уверенно будете отвечать на вопросы по теме «Цилиндр», геометрия за 11 класс средней школы.
Всего несколько дней – и вы уверенно будете отвечать на вопросы по теме «Цилиндр», геометрия за 11 класс средней школы.Наш тест состоит всего из 10 вопросов, а, точнее, задач, которые подобраны таким образом, чтобы быстро сформировать устойчивый учебный навык вычисления объема цилиндра. Для многих тема «Цилиндр» по геометрии за 11 класс оказывается довольно сложной. Некоторые уже успели подзабыть основные формулы и даже само определение цилиндра в геометрии. Возможно, потребуется заглянуть в учебник или справочник, чтобы вспомнить теорию. А практику поможет подтянуть наш тренажер.
В каждом задании требуется вычислить объем цилиндра, но вводные условия все время разные. Если вам удастся с первого раза пройти тест по теме «Цилиндр», вы быстро вспомните все основные формулы. Ответ нужно вписать в соответствующую графу. Если вы ошиблись, система покажет верный ответ, и вы сразу поймете, почему ваши расчеты неверны. Кстати, первичное тестирование всем желающим предоставляется совершенно бесплатно.

Очень удобно, что наша платформа предлагает пройти тест по теме «Цилиндр» с ответами. Это экономит время и позволяет избежать ошибок в конце года, на итоговых контрольных и экзаменах. Да, само решение не приведено, но вы знаете, к чему стремиться. Кроме того, в качестве подсказки предлагается округлять до десятых бесконечные десятичные дроби и использовать запятую в десятичных дробях в качестве разделителя. Посмотрите, возможно, вы не учли этого важного условия.
По итогам тестирования система анализирует ваши ответы и предлагает продолжить занятия. Для того чтобы успешно пройти тест по геометрии, 11 класс, «Цилиндр», необходимо вернуться к решению задач в тот же день через несколько часов, а затем регулярно заниматься в течение следующих 4-5 дней. За это время успевает сформироваться стойкий учебный навык правильных вычислений, который не раз выручит вас на контрольной работе или на экзамене.
Итак, если вам с трудом дается тема «Цилиндр», геометрия в целом, советуем зарегистрироваться на сайте и оформить доступ к образовательной платформе Skills4u на месяц, полугодие или целый учебный год.
 Вы сможете тренировать свои умения и навыки в удобное для вас время, не прибегая к услугам репетиторов. В условиях дистанционного обучения эта услуга очень востребована.
Вы сможете тренировать свои умения и навыки в удобное для вас время, не прибегая к услугам репетиторов. В условиях дистанционного обучения эта услуга очень востребована.Цилиндры — геометрия и искусство
Дом-мастерская архитектора К.С. Мельникова
1927—1929 гг.Уникальным в доме Мельникова является уже то, что в конце 1920-х годов, когда в СССР шло сворачивание НЭПа, а по всей стране началось строительство домов-коммун, одному человеку разрешили построить частный дом в центре столицы. Конструкции стен и перекрытий дома-мастерской не только оригинальны, но и выполнены на уровне технических изобретений, несколько из которых были Мельниковым впоследствии запатентованы.
Объёмная композиция дома представляет собой два разновысоких вертикальных цилиндра одинакового диаметра, врезанных друг в друга на треть радиуса, образуя тем самым необычную форму плана в виде цифры «8», ориентированную по направлению «север — юг». Более низкий цилиндр со срезанной по вертикали южной частью завершён плоской крышей с открытой террасой. Возвышающийся над ним задний цилиндр имеет покатую кровлю, понижающуюся от центра здания к его северной части.
Возвышающийся над ним задний цилиндр имеет покатую кровлю, понижающуюся от центра здания к его северной части.
К. С. Мельников подробно обосновывает преимущества цилиндрической конструкции: «Экономия материалов: Прямая связь архитектурного изучения геометрии с экономическим эффектом. Задача состоит в том, чтобы… площадь пола была окружена минимальным периметром стен. Требуемая площадь, скажем, 1600 кв. м. Высота — величина постоянная… Возьмем параллелепипед, куб и цилиндр… Итак, по трем вариантам периметр составит соответственно 200, 160 и 140 м. Совершенно реальная экономия от формы объема».
Обращённый к Кривоарбатскому переулку главный фасад дома-мастерской имеет строго фронтальную симметричную композицию. В центре срезанной части малого цилиндра находится единственный вход в дом, по сторонам которого расположены два крупных прямоугольных окна. Основную плоскость фасада здания занимает огромное окно-экран, протянувшееся на всю высоту второго этажа.Более свободно решены фасады заднего, северного цилиндра.
 Его стены прорезаны 57 шестигранными вертикальными окнами, образующими единый орнамент со своеобразным ритмом повторяющихся элементов, расположенных пятью ярусами. Нижний ряд окон отделён более высоким отрезком глухой стены от четырёх верхних. Второй ярус соответствует второму этажу, три верхних яруса — третьему. Динамику в общую композицию северного фасада вносит необычный рисунок оконных переплётов трёх типов: один у окон первого яруса, другой во втором и четвёртом ярусах и третий — в третьем и пятом ярусах окон.
Его стены прорезаны 57 шестигранными вертикальными окнами, образующими единый орнамент со своеобразным ритмом повторяющихся элементов, расположенных пятью ярусами. Нижний ряд окон отделён более высоким отрезком глухой стены от четырёх верхних. Второй ярус соответствует второму этажу, три верхних яруса — третьему. Динамику в общую композицию северного фасада вносит необычный рисунок оконных переплётов трёх типов: один у окон первого яруса, другой во втором и четвёртом ярусах и третий — в третьем и пятом ярусах окон.
(википедия)Simple English Wikipedia, бесплатная энциклопедия
Правый круговой цилиндрЦилиндр — это одна из самых простых изогнутых трехмерных геометрических форм, поверхность которой образована точками на фиксированном расстоянии от данного линейного сегмента, известная как ось цилиндра. Форму можно представить как круговую призму. И поверхность, и твердую форму, созданную внутри, можно назвать цилиндром .
 Площадь и объем цилиндра известны с древних времен.
Площадь и объем цилиндра известны с древних времен.В дифференциальной геометрии цилиндр в более широком смысле определяется как линейчатая поверхность, охватываемая однопараметрическим семейством параллельных линий. Цилиндр, поперечное сечение которого является эллипсом, параболой или гиперболой, называется эллиптическим цилиндром , параболическим цилиндром или гиперболическим цилиндром соответственно.
Обычно цилиндр означает конечное сечение правого кругового цилиндра , т.е.е., цилиндр с образующими, перпендикулярными основанию, с закрытыми концами, образующими две круглые поверхности, как на рисунке (справа). Если цилиндр имеет радиус r и длину (высоту) h , то его объем определяется по формуле:
- V = π r 2 h
и его площадь поверхности составляет:
- площадь верха (π r 2 ) +
- площадь дна (π r 2 ) +
- площадь стороны (2π прав ).

Следовательно, без верха или низа (боковой поверхности) площадь поверхности равна:
- A = 2π rh .
Сверху и снизу площадь поверхности составляет:
- A = 2π r 2 + 2π rh = 2π r ( r + h ).
Для данного объема цилиндр с наименьшей площадью поверхности имеет h = 2 r . Для данной площади поверхности цилиндр с наибольшим объемом имеет h = 2 r , т.е.е. цилиндр помещается в куб (высота = диаметр).
Имеет правильный круговой цилиндр высотой h единиц и основание радиусом r единиц с осями координат, выбранными так, чтобы начало координат было в центре одного основания, а высота измерялась вдоль положительной оси x. Плоское сечение на расстоянии x единиц от начала координат имеет площадь A ( x ) квадратных единиц, где
- A (x) = πr2 {\ displaystyle A (x) = \ pi r ^ {2}}
или
- A (y) = πr2 {\ displaystyle A (y) = \ pi r ^ {2}}
Элемент объема, представляет собой правый цилиндр с площадью основания Aw i квадрат ед.
 и толщиной Δ i x ед.{2} \, h \,}
и толщиной Δ i x ед.{2} \, h \,}Цилиндрические секции — это точки пересечения цилиндров с плоскостями. Для правильного кругового цилиндра есть четыре возможности. Плоскость, касательная к цилиндру, пересекает цилиндр на единой прямой. При перемещении параллельно самой себе плоскость либо не пересекает цилиндр, либо пересекает его двумя параллельными линиями. Все остальные плоскости пересекают цилиндр по эллипсу или, когда они перпендикулярны оси цилиндра, по окружности.{2} = 1.}
Это уравнение для эллиптического цилиндра , обобщение обычного кругового цилиндра ( a = b ). Еще более общим является цилиндр обобщенного типа : поперечное сечение может иметь любую кривую.
Цилиндр представляет собой вырожденный квадрат , потому что по крайней мере одна из координат (в данном случае z) не появляется в уравнении.
У наклонного цилиндра верхняя и нижняя поверхности смещены друг относительно друга.
 {2} + 2ay = 0. \,} В проективной геометрии цилиндр — это просто конус, вершина которого находится на бесконечности, что визуально соответствует цилиндру в перспективе, который выглядит как конус к небу.
{2} + 2ay = 0. \,} В проективной геометрии цилиндр — это просто конус, вершина которого находится на бесконечности, что визуально соответствует цилиндру в перспективе, который выглядит как конус к небу.Simple English Wikipedia, бесплатная энциклопедия
Правый круговой цилиндрЦилиндр — это одна из самых простых изогнутых трехмерных геометрических форм, поверхность которой образована точками на фиксированном расстоянии от данного линейного сегмента, известная как ось цилиндра.Форму можно представить как круговую призму. И поверхность, и твердую форму, созданную внутри, можно назвать цилиндром . Площадь и объем цилиндра известны с древних времен.
В дифференциальной геометрии цилиндр в более широком смысле определяется как линейчатая поверхность, охватываемая однопараметрическим семейством параллельных линий. Цилиндр, поперечное сечение которого является эллипсом, параболой или гиперболой, называется эллиптическим цилиндром , параболическим цилиндром или гиперболическим цилиндром соответственно.

Обычно цилиндр означает конечное сечение правильного кругового цилиндра , т. Е. Цилиндр с образующими, перпендикулярными основаниям, с закрытыми концами, образующими две круглые поверхности, как в фигура (справа). Если цилиндр имеет радиус r и длину (высоту) h , то его объем определяется по формуле:
- V = π r 2 h
и его площадь поверхности составляет:
- площадь верха (π r 2 ) +
- площадь дна (π r 2 ) +
- площадь стороны (2π прав ).
Следовательно, без верха или низа (боковой поверхности) площадь поверхности равна:
- A = 2π rh .
Сверху и снизу площадь поверхности составляет:
- A = 2π r 2 + 2π rh = 2π r ( r + h ).
Для данного объема цилиндр с наименьшей площадью поверхности имеет h = 2 r .
 {2}}
{2}}Элемент объема, представляет собой правый цилиндр с площадью основания Aw i квадрат ед. и толщиной Δ i x ед.{2} \, h \,}
Цилиндрические секции — это точки пересечения цилиндров с плоскостями. Для правильного кругового цилиндра есть четыре возможности. Плоскость, касательная к цилиндру, пересекает цилиндр на единой прямой. При перемещении параллельно самой себе плоскость либо не пересекает цилиндр, либо пересекает его двумя параллельными линиями. Все остальные плоскости пересекают цилиндр по эллипсу или, когда они перпендикулярны оси цилиндра, по окружности.{2} = 1.}
Это уравнение для эллиптического цилиндра , обобщение обычного кругового цилиндра ( a = b ). Еще более общим является цилиндр обобщенного типа : поперечное сечение может иметь любую кривую.
Цилиндр представляет собой вырожденный квадрат , потому что по крайней мере одна из координат (в данном случае z) не появляется в уравнении.

У наклонного цилиндра верхняя и нижняя поверхности смещены друг относительно друга.{2} + 2ay = 0. \,} В проективной геометрии цилиндр — это просто конус, вершина которого находится на бесконечности, что визуально соответствует цилиндру в перспективе, который выглядит как конус к небу.
Simple English Wikipedia, бесплатная энциклопедия
Правый круговой цилиндрЦилиндр — это одна из самых простых изогнутых трехмерных геометрических форм, поверхность которой образована точками на фиксированном расстоянии от данного линейного сегмента, известная как ось цилиндра.Форму можно представить как круговую призму. И поверхность, и твердую форму, созданную внутри, можно назвать цилиндром . Площадь и объем цилиндра известны с древних времен.
В дифференциальной геометрии цилиндр в более широком смысле определяется как линейчатая поверхность, охватываемая однопараметрическим семейством параллельных линий. Цилиндр, поперечное сечение которого является эллипсом, параболой или гиперболой, называется эллиптическим цилиндром , параболическим цилиндром или гиперболическим цилиндром соответственно.

Обычно цилиндр означает конечное сечение правильного кругового цилиндра , т. Е. Цилиндр с образующими, перпендикулярными основаниям, с закрытыми концами, образующими две круглые поверхности, как в фигура (справа). Если цилиндр имеет радиус r и длину (высоту) h , то его объем определяется по формуле:
- V = π r 2 h
и его площадь поверхности составляет:
- площадь верха (π r 2 ) +
- площадь дна (π r 2 ) +
- площадь стороны (2π прав ).
Следовательно, без верха или низа (боковой поверхности) площадь поверхности равна:
- A = 2π rh .
Сверху и снизу площадь поверхности составляет:
- A = 2π r 2 + 2π rh = 2π r ( r + h ).
Для данного объема цилиндр с наименьшей площадью поверхности имеет h = 2 r .
 {2}}
{2}}Элемент объема, представляет собой правый цилиндр с площадью основания Aw i квадрат ед. и толщиной Δ i x ед.{2} \, h \,}
Цилиндрические секции — это точки пересечения цилиндров с плоскостями. Для правильного кругового цилиндра есть четыре возможности. Плоскость, касательная к цилиндру, пересекает цилиндр на единой прямой. При перемещении параллельно самой себе плоскость либо не пересекает цилиндр, либо пересекает его двумя параллельными линиями. Все остальные плоскости пересекают цилиндр по эллипсу или, когда они перпендикулярны оси цилиндра, по окружности.{2} = 1.}
Это уравнение для эллиптического цилиндра , обобщение обычного кругового цилиндра ( a = b ). Еще более общим является цилиндр обобщенного типа : поперечное сечение может иметь любую кривую.
Цилиндр представляет собой вырожденный квадрат , потому что по крайней мере одна из координат (в данном случае z) не появляется в уравнении.

У наклонного цилиндра верхняя и нижняя поверхности смещены друг относительно друга.{2} + 2ay = 0. \,} В проективной геометрии цилиндр — это просто конус, вершина которого находится на бесконечности, что визуально соответствует цилиндру в перспективе, который выглядит как конус к небу.
Определение и свойства цилиндра — Math Open Reference
Определение и свойства цилиндра — Math Open ReferenceЦилиндр — это замкнутое твердое тело, имеющее два параллельных (обычно круглых) основания, соединенных изогнутой поверхностью.
Попробуй это На рисунке ниже перетащите оранжевую точку, чтобы изменить размеры цилиндра.
Основание и сторона
Цилиндр — это геометрическое тело, которое очень часто встречается в повседневной жизни, например банка для супа. Если вы его разобьете, то обнаружите, что у него два конца, называемые базы, которые обычно имеют круглую форму. Базы всегда конгруэнтный а также параллельно друг другу.
 Если бы вы «развернули» цилиндр, вы бы обнаружили, что его сторона на самом деле представляет собой прямоугольник, когда он сплющен.
(См. Площадь цилиндра).
Если бы вы «развернули» цилиндр, вы бы обнаружили, что его сторона на самом деле представляет собой прямоугольник, когда он сплющен.
(См. Площадь цилиндра).Высота
Высота х — это перпендикулярное расстояние между основаниями.При расчете объема наклонного цилиндра важно использовать перпендикулярную высоту (или «высоту»).
Радиус
Радиус r цилиндра равен радиус базы. Если вместо этого вам дается диаметр, не забудьте уменьшить его вдвое.
Ось
Линия, соединяющая центр каждой базы.
Цилиндры правый и наклонный
Когда два основания находятся точно друг над другом, а ось расположена под прямым углом к основанию, это называется «прямым цилиндром».Если одно основание смещено в сторону, ось оказывается не под прямым углом к основанию, и в результате получается наклонный цилиндр. Основания, хотя и не непосредственно друг над другом, все же параллельны.
В апплете вверху страницы установите флажок «Разрешить наклон» и перетащите оранжевую точку в сторону, чтобы увидеть наклонный цилиндр.

Правый цилиндр Наклонный цилиндр Объем и площадь поверхности
Форма оснований
Обычно основания представляют собой круги, поэтому знакомый суп можно технически назвать «правильным круговым цилиндром».Это самый распространенный вид, и если кто-то просто говорит «цилиндр», обычно они имеют в виду именно это. Основания могут иметь практически любую изогнутую форму, но наиболее распространенной альтернативой кругу является эллипс. В этом случае форму можно было бы назвать «эллиптическим цилиндром».
Отношение к призме
Призма — это твердое тело, основания которого представляют собой многоугольники, а стороны — плоские поверхности. (См. Определение призмы). Строго говоря, цилиндр — это не призма, но он очень похож.В призме, основания которой являются правильными многоугольниками, призма начинает приближаться к цилиндру, когда количество сторон велико.

Подробнее об этом см. Связь цилиндра с призмой.
Другой способ изготовления цилиндра
Другой способ создать круговой цилиндр — это рассматривать его как локус линии, движущейся параллельно оси и на фиксированном расстоянии от нее.
Подробнее об этом см. Цилиндр как геометрическое место линии.
Связанные темы
(C) Открытый справочник по математике, 2011 г.
Все права защищены.Формула Объем цилиндра. Объясняется картинками и примерами. Формула для …
На этой странице исследуются свойства правильного кругового цилиндра. Цилиндр имеет радиус (r) и высоту (h) (см. Рисунок ниже).
Эта форма похожа на банку из-под газировки. Каждый цилиндр имеет радиус и высоту, как вы можете видеть на диаграмме ниже.
Практика Проблемы в области цилиндраЗадача 1
Каков объем цилиндра радиусом 2 и высотой 6?
Покажи ответЗадача 2
Каков объем цилиндра радиусом 3 и высотой 5?
Покажи ответЗадача 3
Какова площадь цилиндра радиусом 6 и высотой 7?
Покажи ответИспользуйте формулу площади цилиндра.

- Объем = Π * (r) 2 (h)
- Объем = * (6) 2 (7) = 252 Π
Цилиндры — промежуточная геометрия
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т.
 д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105Или заполните форму ниже:
Геометрия: Цилиндры и Конусы
Цилиндры и Конусы
В определении призмы основания должны были быть конгруэнтными многоугольниками.
 Если основания представляют собой конгруэнтные замкнутые кривые (например, окружность), то у вас цилиндр .Я нарисовал цилиндр с круглым основанием на рис. 21.4. Основание этого цилиндра — круг, поэтому у него нет вершин. Большинство цилиндров, с которыми вы сталкиваетесь, имеют круги для формы основания, и они называются круговыми цилиндрами . Но иметь круглое основание — это всего лишь вежливость. Это не требование.
Если основания представляют собой конгруэнтные замкнутые кривые (например, окружность), то у вас цилиндр .Я нарисовал цилиндр с круглым основанием на рис. 21.4. Основание этого цилиндра — круг, поэтому у него нет вершин. Большинство цилиндров, с которыми вы сталкиваетесь, имеют круги для формы основания, и они называются круговыми цилиндрами . Но иметь круглое основание — это всего лишь вежливость. Это не требование.Рисунок 21.4 Круглый цилиндр.
Когда вы думаете о цилиндре, сразу приходит на ум форма консервной банки.Эти типы цилиндров классифицируются как правильные круговые цилиндры.
Ослабление ограничений на основания призмы созданных цилиндров. Ослабление ограничений на форму основания пирамиды приведет к созданию конуса. Постройте конус так же, как вы построили пирамиду. Начните с замкнутой кривой, лежащей в плоскости, которая будет служить основанием конуса, и точкой, которая будет служить вершиной конуса.
 Конус — это твердое тело, образованное внутренней частью этой замкнутой кривой вместе с поверхностью, образованной, когда каждая точка замкнутой кривой соединяется с вершиной с использованием отрезков линии.
Конус — это твердое тело, образованное внутренней частью этой замкнутой кривой вместе с поверхностью, образованной, когда каждая точка замкнутой кривой соединяется с вершиной с использованием отрезков линии.Solid Facts
Цилиндр — это твердое тело, образованное двумя конгруэнтными замкнутыми кривыми в параллельных плоскостях вместе с поверхностью, образованной отрезками линий, соединяющими соответствующие точки двух кривых. Круглый цилиндр — это цилиндр с круглым основанием.
Конус назван по форме его основания. На рисунке 21.5 показан круговой конус. Круглые конусы делятся на две категории: правильные круговые конусы и наклонные круговые конусы.Прямой круговой конус — это круговой конус, в котором отрезок прямой, соединяющий вершину конуса с центром круглого основания, перпендикулярен плоскости основания. Наклонный круговой конус — это круговой конус, в котором отрезок прямой, соединяющий вершину конуса с центром круглого основания, не перпендикулярен плоскости основания.

Рисунок 21.5 Круглый конус.
Solid Facts
Конус — это твердое тело, образованное внутренней частью плоской замкнутой кривой вместе с поверхностью, образованной, когда каждая точка на замкнутой кривой соединяется с некопланарной точкой с помощью отрезков линии.
Основание конуса — это плоская замкнутая кривая конуса.
Вершина конуса — это некопланарная точка, которая присоединяется к каждой точке основания.
Правый круговой конус — это круговой конус, в котором отрезок прямой, соединяющий вершину конуса с центром круглого основания, перпендикулярен плоскости основания.
Наклонный круговой конус — это круговой конус, в котором отрезок прямой, соединяющий вершину конуса с центром круглого основания, не перпендикулярен плоскости основания.
Если у вас возникли проблемы с визуализацией математического описания рожка, вы можете найти его модель в своем любимом магазине мороженого.


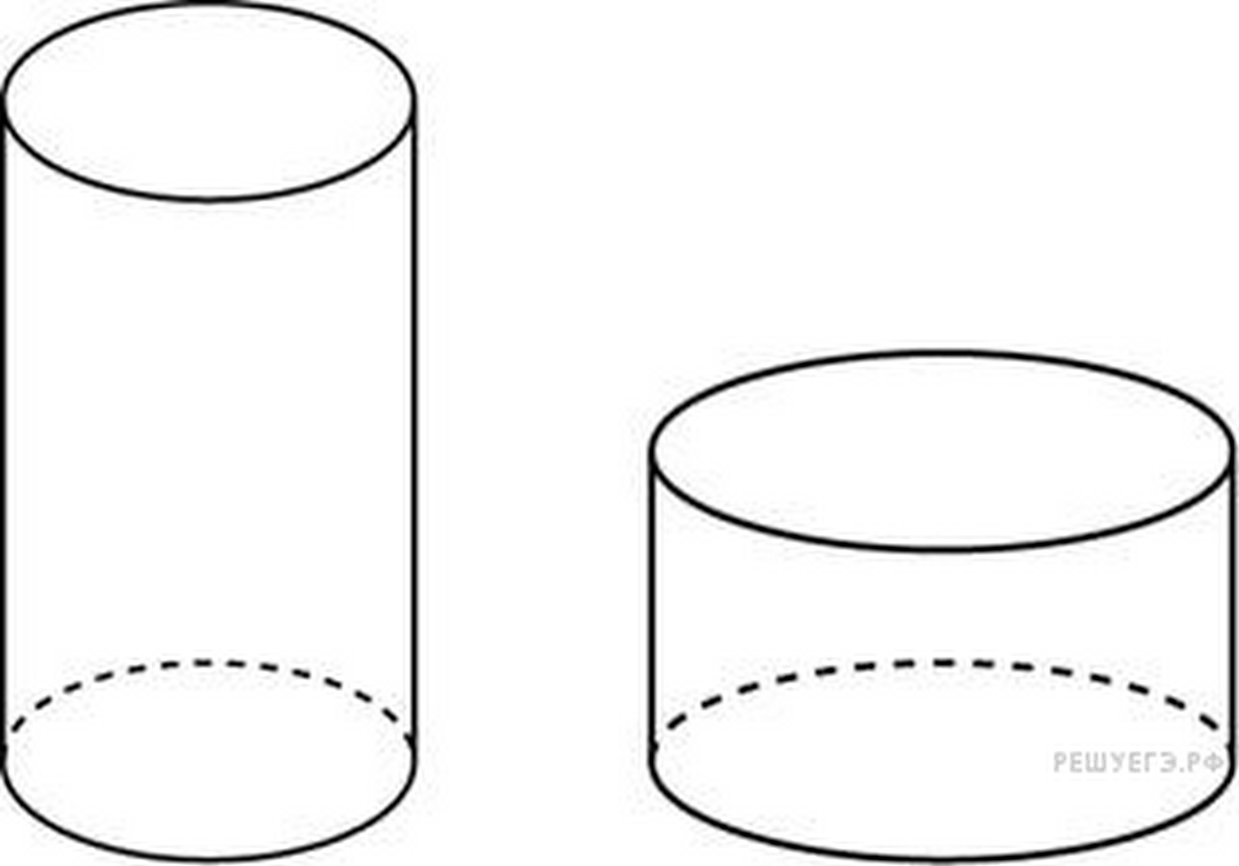 2$
2$
 Пr²2 Пr. По какой формуле находится площадь круга?Верно!Пr
Пr²2 Пr. По какой формуле находится площадь круга?Верно!Пr Повторение. С = 2 Пr = 2 П2,5 = 5 ПS=Пr² = 6,25 ПОтвет
Повторение. С = 2 Пr = 2 П2,5 = 5 ПS=Пr² = 6,25 ПОтвет Через каждую точку окружности проведем прямую, перпендикулярную к плоскости α. Поверхность, образованная этими прямыми, называется цилиндрической поверхностью, а сами прямые — образующими цилиндрической поверхности. Прямая, проходящая через точку О перпендикулярно к плоскости α, называется осью цилиндрической поверхности. Поскольку все образующие и ось перпендикулярны к плоскости α, то они параллельны друг другу.
Через каждую точку окружности проведем прямую, перпендикулярную к плоскости α. Поверхность, образованная этими прямыми, называется цилиндрической поверхностью, а сами прямые — образующими цилиндрической поверхности. Прямая, проходящая через точку О перпендикулярно к плоскости α, называется осью цилиндрической поверхности. Поскольку все образующие и ось перпендикулярны к плоскости α, то они параллельны друг другу.
 Следовательно, при параллельном переносе на вектор ОО1 окружность L перейдет в равную ей окружность L1 радиуса r с центром в точке О1.
Следовательно, при параллельном переносе на вектор ОО1 окружность L перейдет в равную ей окружность L1 радиуса r с центром в точке О1. Длина образующей называется высотой цилиндра, а радиус основания — радиусом цилиндра.
Длина образующей называется высотой цилиндра, а радиус основания — радиусом цилиндра. На рисунке изображен цилиндр, полученный вращением прямоугольника АВСD вокруг стороны АВ. При этом боковая поверхность цилиндра образуется вращением стороны СD, а основания — вращением сторон ВС и АD. Поэтому цилиндр называют телом вращения.
На рисунке изображен цилиндр, полученный вращением прямоугольника АВСD вокруг стороны АВ. При этом боковая поверхность цилиндра образуется вращением стороны СD, а основания — вращением сторон ВС и АD. Поэтому цилиндр называют телом вращения. Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом. В самом деле, такая секущая плоскость — плоскость y на рисунке отсекает от данного цилиндра тело, также являющееся цилиндром. Его основаниями служат два круга, один из которых и есть рассматриваемое сечение.
Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом. В самом деле, такая секущая плоскость — плоскость y на рисунке отсекает от данного цилиндра тело, также являющееся цилиндром. Его основаниями служат два круга, один из которых и есть рассматриваемое сечение.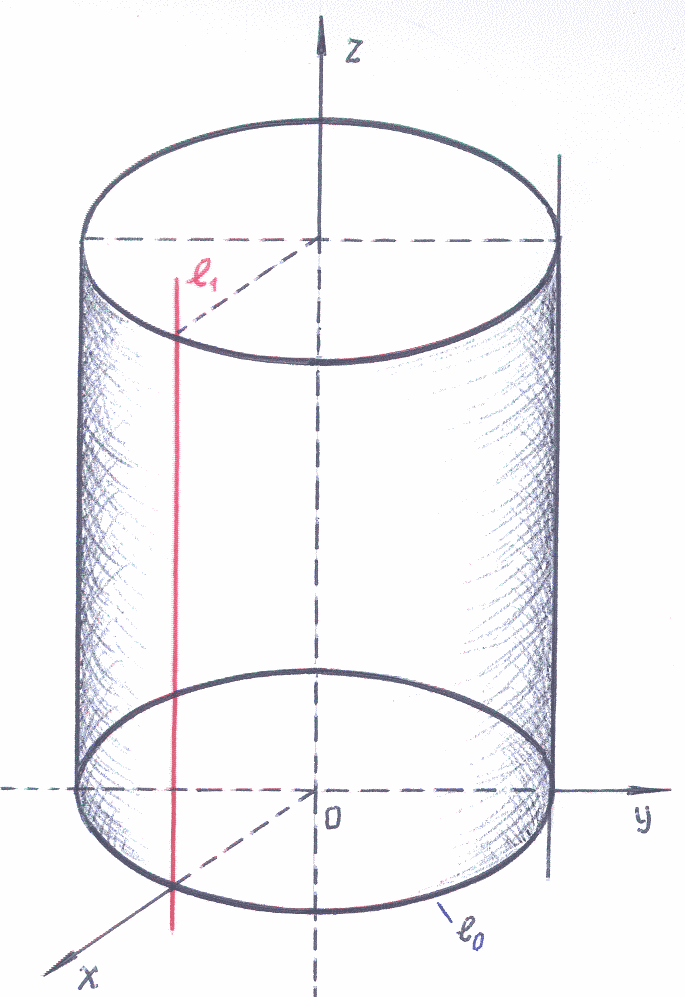 Цементный комбинат на окраине французской столицы
Цементный комбинат на окраине французской столицы Английский замок в Сандерленде украшает необычный фонтан, который создал архитектор Уильям Пай. Фонтан представляет собой прозрачный цилиндр с воронкой водоворота по середине.
Английский замок в Сандерленде украшает необычный фонтан, который создал архитектор Уильям Пай. Фонтан представляет собой прозрачный цилиндр с воронкой водоворота по середине. Представим себе, что его боковую поверхность разрезали по образующей АВ и развернули таким образом, что все образующие оказались расположенными в некоторой плоскости α. В результате в плоскости α получится прямоугольник АВВ1 А1. Стороны АВ и В1 А1 прямоугольника представляют собой два края разреза боковой поверхности цилиндра по образующей АВ. Этот прямоугольник называется разверткой боковой поверхности цилиндра. Основание АА1 прямоугольника является разверткой окружности основания цилиндра, а высота АВ — образующей цилиндра, поэтому АА1 = 2πr, АВ = h, где г — радиус цилиндра, h — его высота.
Представим себе, что его боковую поверхность разрезали по образующей АВ и развернули таким образом, что все образующие оказались расположенными в некоторой плоскости α. В результате в плоскости α получится прямоугольник АВВ1 А1. Стороны АВ и В1 А1 прямоугольника представляют собой два края разреза боковой поверхности цилиндра по образующей АВ. Этот прямоугольник называется разверткой боковой поверхности цилиндра. Основание АА1 прямоугольника является разверткой окружности основания цилиндра, а высота АВ — образующей цилиндра, поэтому АА1 = 2πr, АВ = h, где г — радиус цилиндра, h — его высота. За площадь боковой поверхности цилиндра принимается площадь ее развертки. Sбок = 2 Пrh
За площадь боковой поверхности цилиндра принимается площадь ее развертки. Sбок = 2 Пrh Задача 1. Дано: Площадь боковой поверхности цилиндра равна S. Найти: площадь осевого сечения цилиндра. Решение задачи
Задача 1. Дано: Площадь боковой поверхности цилиндра равна S. Найти: площадь осевого сечения цилиндра. Решение задачи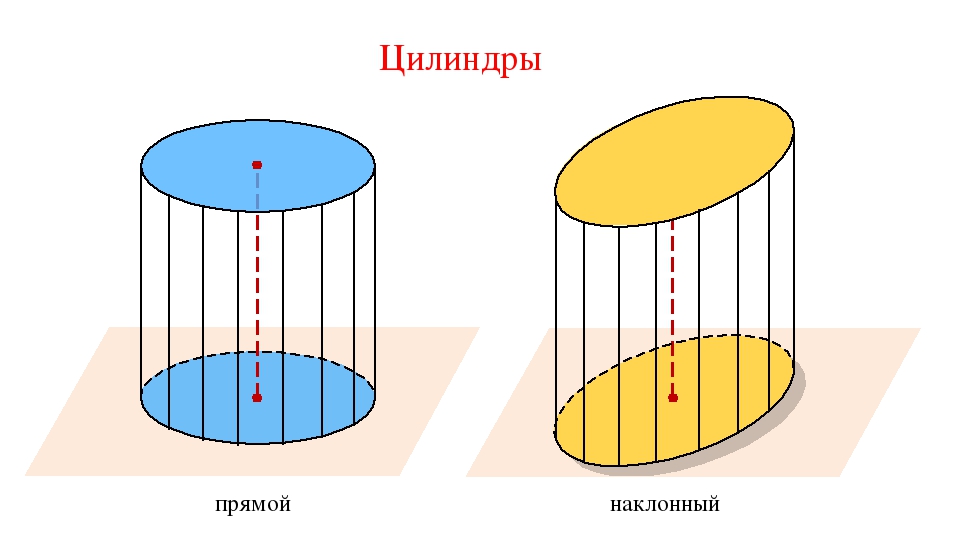 Задача 2. Сколько квадратных метров листовой жести пойдет на изготовление трубы длиной 4 м и диаметром 20 см, если на швы необходимо добавить 2,5% площади ее боковой поверхности?Решение задачи
Задача 2. Сколько квадратных метров листовой жести пойдет на изготовление трубы длиной 4 м и диаметром 20 см, если на швы необходимо добавить 2,5% площади ее боковой поверхности?Решение задачи
 pnghttps://lh5.googleusercontent.com/-KSm_ot. Ixa. W0/T06 RUh. G0kl. I/AAAAAAAAI4w/Dz. BDf. Dn. Jf. MQ/s1600/razvertka_cilindra.gifhttp://content.foto.mail.ru/mail/t.ant/_answers/i-407.jpghttps://lh6.googleusercontent.com/-Wk0 YGd. Hhpxc/T0y1_88awd. I/AAAAAAAAI5 I/s. Ut. Jc. Yo9c5 I/s1600/cilindr_vraschenie.gif
pnghttps://lh5.googleusercontent.com/-KSm_ot. Ixa. W0/T06 RUh. G0kl. I/AAAAAAAAI4w/Dz. BDf. Dn. Jf. MQ/s1600/razvertka_cilindra.gifhttp://content.foto.mail.ru/mail/t.ant/_answers/i-407.jpghttps://lh6.googleusercontent.com/-Wk0 YGd. Hhpxc/T0y1_88awd. I/AAAAAAAAI5 I/s. Ut. Jc. Yo9c5 I/s1600/cilindr_vraschenie.gif pnghttp://studyport.ru/data/Exact_Science/te1d_36/image3872.gifhttp://d3mlntcv38ck9k.cloudfront.net/content/konspekt_image/38131/44c8a5c0_f310_0130_97e2_22000a1d011d.pnghttp://photostock.su/48398.jpeg http://savepic.su/422861.png http://ramki-kartinki.ru/_ph/27/2/686148141.jpghttp://mcocos.ru/tmp-tvbreak/img/ramka.pnghttp://vsadu.ucoz.ru/lessons/sr_group/fg08.jpghttp://konspekta.net/studopediainfo/baza2/150620514939.files/image016.jpghttp://konspekta.net/studopediainfo/baza2/150620514939.files/image023.jpg http://img.architector.ua/images/articles/fortissimo/pic_big/pic_1409049687.jpghttp://www.macdigger.ru/wp-content/uploads/2015/01/Apple-Store-interior-3.jpghttp://karaul.ru/uploads/posts/2013-04/1366273992_vodovorot002.jpghttp://lifeglobe.net/x/entry/2897/6.jpg http://comfort-montage.ru/upload/iblock/c05/c05ef35c3132c9647bf919c709a93853.jpg
pnghttp://studyport.ru/data/Exact_Science/te1d_36/image3872.gifhttp://d3mlntcv38ck9k.cloudfront.net/content/konspekt_image/38131/44c8a5c0_f310_0130_97e2_22000a1d011d.pnghttp://photostock.su/48398.jpeg http://savepic.su/422861.png http://ramki-kartinki.ru/_ph/27/2/686148141.jpghttp://mcocos.ru/tmp-tvbreak/img/ramka.pnghttp://vsadu.ucoz.ru/lessons/sr_group/fg08.jpghttp://konspekta.net/studopediainfo/baza2/150620514939.files/image016.jpghttp://konspekta.net/studopediainfo/baza2/150620514939.files/image023.jpg http://img.architector.ua/images/articles/fortissimo/pic_big/pic_1409049687.jpghttp://www.macdigger.ru/wp-content/uploads/2015/01/Apple-Store-interior-3.jpghttp://karaul.ru/uploads/posts/2013-04/1366273992_vodovorot002.jpghttp://lifeglobe.net/x/entry/2897/6.jpg http://comfort-montage.ru/upload/iblock/c05/c05ef35c3132c9647bf919c709a93853.jpg

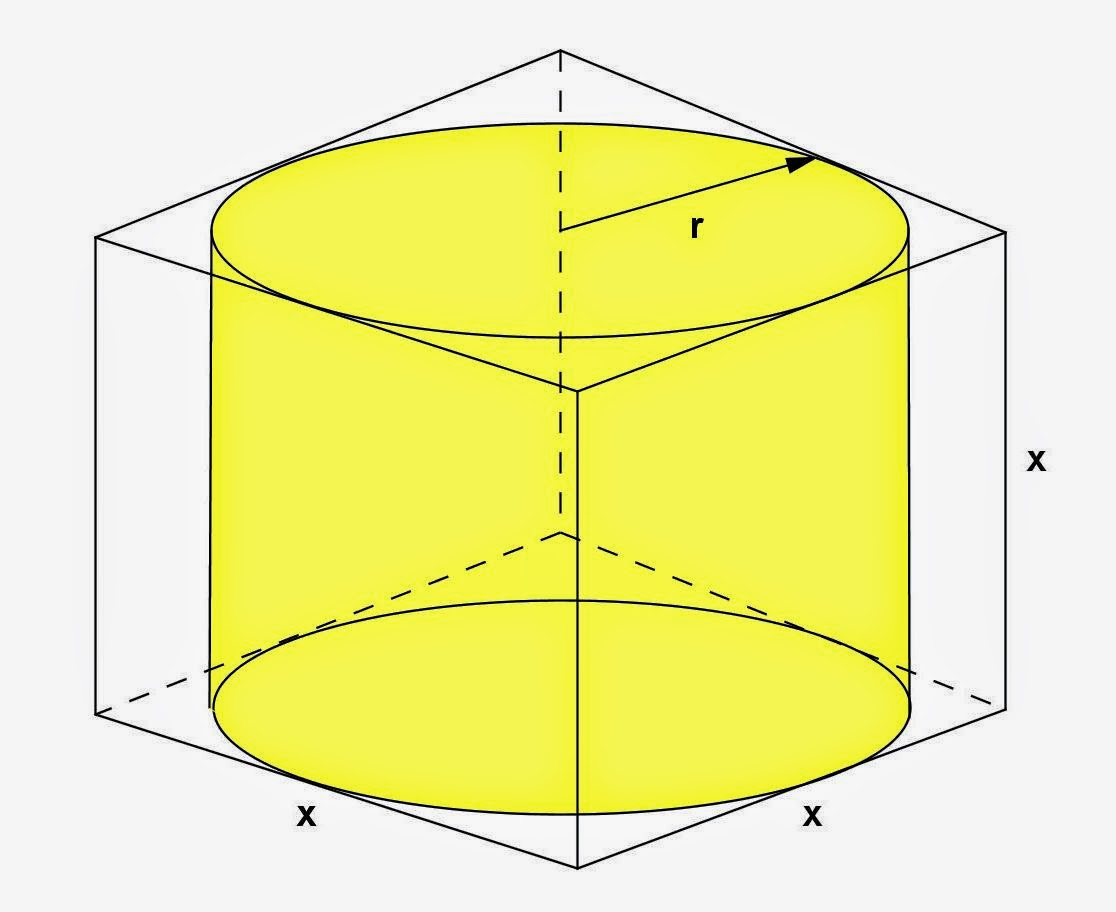
 Это основная деталь поршневых машин (двигателя внутреннего сгорания, паровой
Это основная деталь поршневых машин (двигателя внутреннего сгорания, паровой
 Объяснение нового материала.
Объяснение нового материала.
 до н.э.). Школе Платона с частности принадлежит: а) исследование свойств призмы, пирамиды, цилиндра и конуса; б) изучение конических сечений.
до н.э.). Школе Платона с частности принадлежит: а) исследование свойств призмы, пирамиды, цилиндра и конуса; б) изучение конических сечений.
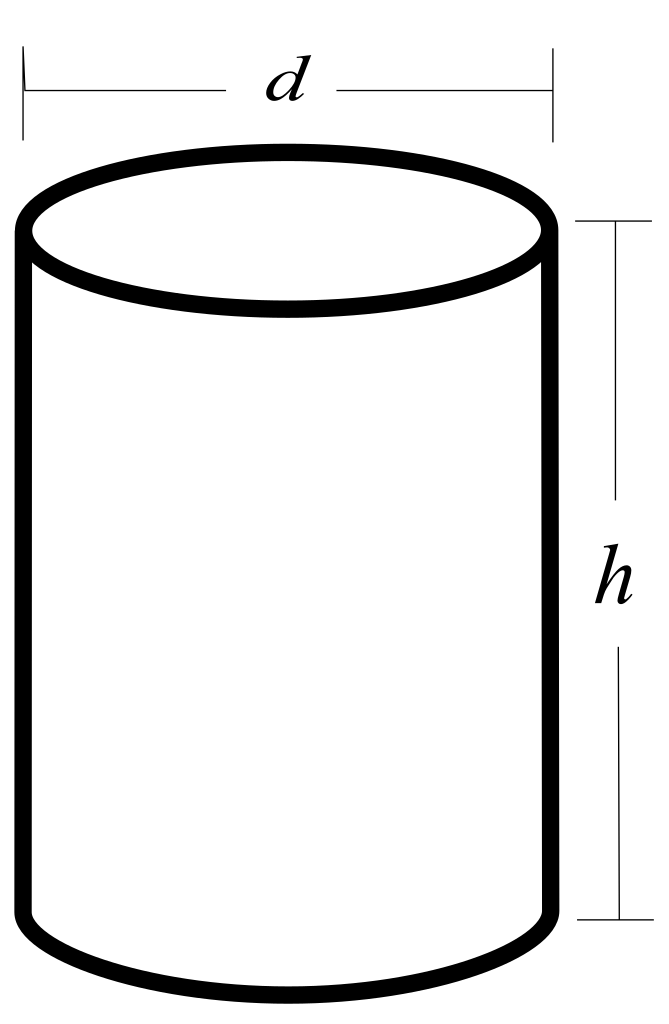
 Отрезок, соединяющий вершину цилиндра с точкой окружности основания,
Отрезок, соединяющий вершину цилиндра с точкой окружности основания,
 Высота
Высота
 Назови элементы цилиндра (Боковая поверхность, основание, ось, радиус, образующая, высота)
Назови элементы цилиндра (Боковая поверхность, основание, ось, радиус, образующая, высота)


 Дан цилиндр с радиусом основания 3 м и высотой 8 м. Найдите диагональ осевого сечения цилиндра.
Дан цилиндр с радиусом основания 3 м и высотой 8 м. Найдите диагональ осевого сечения цилиндра.
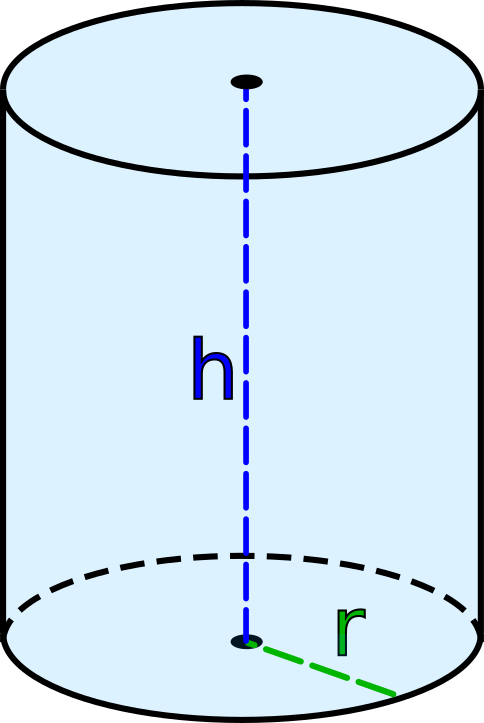 Найдём высоту по теореме Пифагора
Найдём высоту по теореме Пифагора
 Полная поверхность будет равна сумме боковой поверхности и двум площадям основания: 84 + 12 · 2 = = 84 + 24 = 108 м2. Тогда нужно будет 108 · 200 = 21 600 г =
Полная поверхность будет равна сумме боковой поверхности и двум площадям основания: 84 + 12 · 2 = = 84 + 24 = 108 м2. Тогда нужно будет 108 · 200 = 21 600 г =




 Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.
Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.


 Пусть читатель прогуливается в огромном саду геометрии, в котором каждый может составить себе такой букет, какой ему нравится.
Пусть читатель прогуливается в огромном саду геометрии, в котором каждый может составить себе такой букет, какой ему нравится.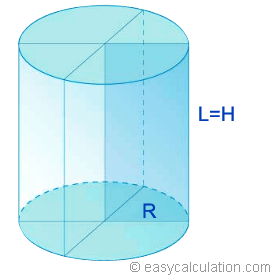 Уже эта кривая послужила исходной точкой для столь многочисленных и столь глубоких исследований, что они могли бы сами по себе заполнить содержание целого курса.
Уже эта кривая послужила исходной точкой для столь многочисленных и столь глубоких исследований, что они могли бы сами по себе заполнить содержание целого курса.
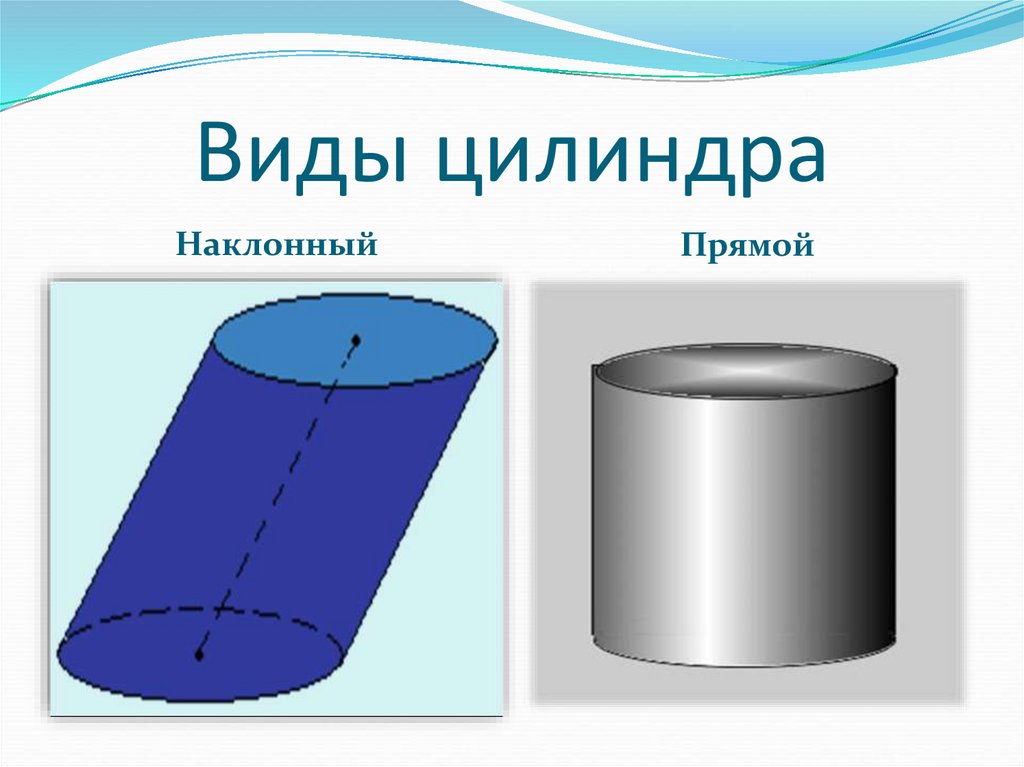


 Так же, как и в случае эллипса, можно показать, что касательная к гиперболе делит пополам угол между радиусами-векторами, проведенными в точку касания (рис. 6, с. 13).
Так же, как и в случае эллипса, можно показать, что касательная к гиперболе делит пополам угол между радиусами-векторами, проведенными в точку касания (рис. 6, с. 13). Если теперь ввести новую постоянную, равную
Если теперь ввести новую постоянную, равную


 Само построение наглядно показывает, что кривая перпендикулярна к одной из двух касательных к окружности, которые можно провести из какой-либо точки кривой.
Само построение наглядно показывает, что кривая перпендикулярна к одной из двух касательных к окружности, которые можно провести из какой-либо точки кривой.
 Всего несколько дней – и вы уверенно будете отвечать на вопросы по теме «Цилиндр», геометрия за 11 класс средней школы.
Всего несколько дней – и вы уверенно будете отвечать на вопросы по теме «Цилиндр», геометрия за 11 класс средней школы.
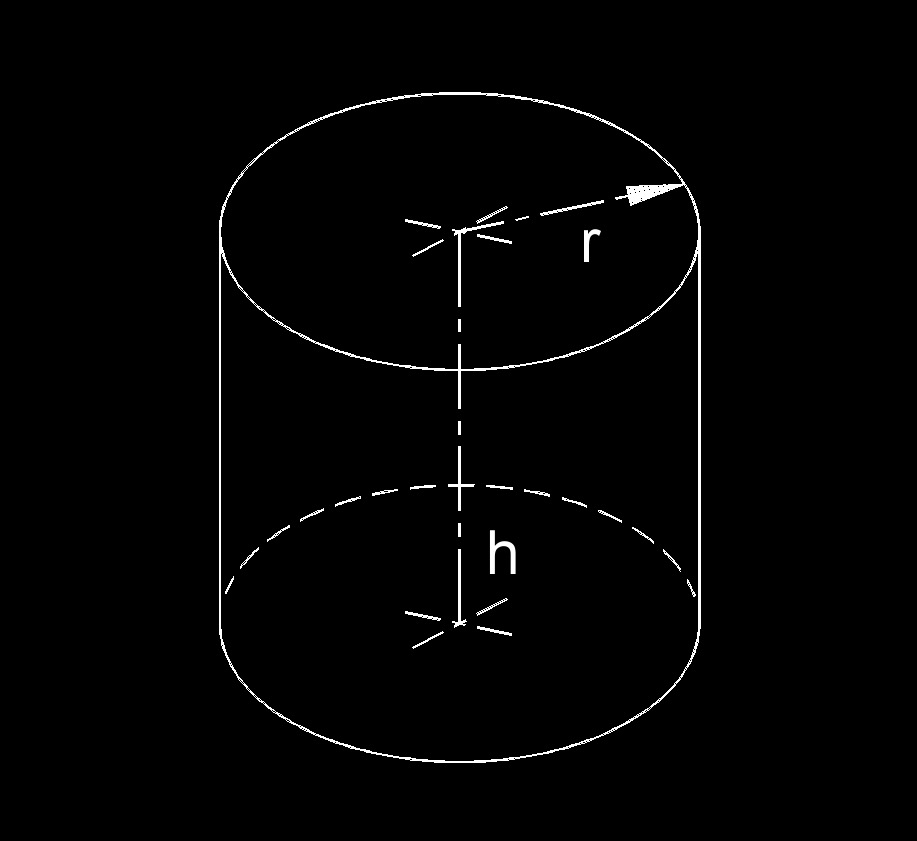 Вы сможете тренировать свои умения и навыки в удобное для вас время, не прибегая к услугам репетиторов. В условиях дистанционного обучения эта услуга очень востребована.
Вы сможете тренировать свои умения и навыки в удобное для вас время, не прибегая к услугам репетиторов. В условиях дистанционного обучения эта услуга очень востребована.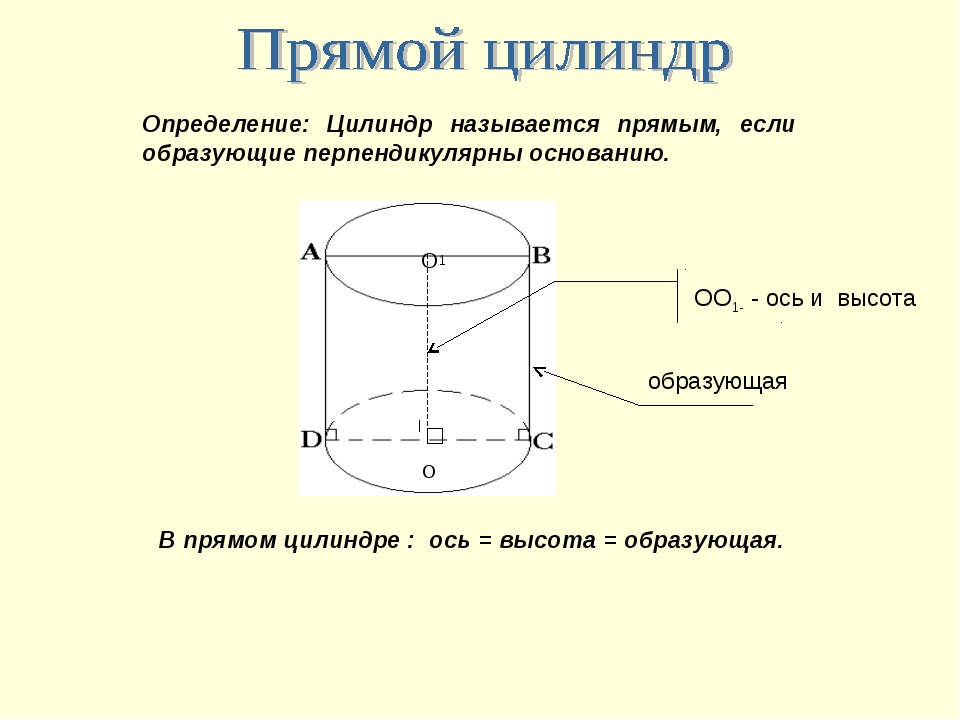 Возвышающийся над ним задний цилиндр имеет покатую кровлю, понижающуюся от центра здания к его северной части.
Возвышающийся над ним задний цилиндр имеет покатую кровлю, понижающуюся от центра здания к его северной части. Его стены прорезаны 57 шестигранными вертикальными окнами, образующими единый орнамент со своеобразным ритмом повторяющихся элементов, расположенных пятью ярусами. Нижний ряд окон отделён более высоким отрезком глухой стены от четырёх верхних. Второй ярус соответствует второму этажу, три верхних яруса — третьему. Динамику в общую композицию северного фасада вносит необычный рисунок оконных переплётов трёх типов: один у окон первого яруса, другой во втором и четвёртом ярусах и третий — в третьем и пятом ярусах окон.
Его стены прорезаны 57 шестигранными вертикальными окнами, образующими единый орнамент со своеобразным ритмом повторяющихся элементов, расположенных пятью ярусами. Нижний ряд окон отделён более высоким отрезком глухой стены от четырёх верхних. Второй ярус соответствует второму этажу, три верхних яруса — третьему. Динамику в общую композицию северного фасада вносит необычный рисунок оконных переплётов трёх типов: один у окон первого яруса, другой во втором и четвёртом ярусах и третий — в третьем и пятом ярусах окон. Площадь и объем цилиндра известны с древних времен.
Площадь и объем цилиндра известны с древних времен.
 и толщиной Δ i x ед.{2} \, h \,}
и толщиной Δ i x ед.{2} \, h \,}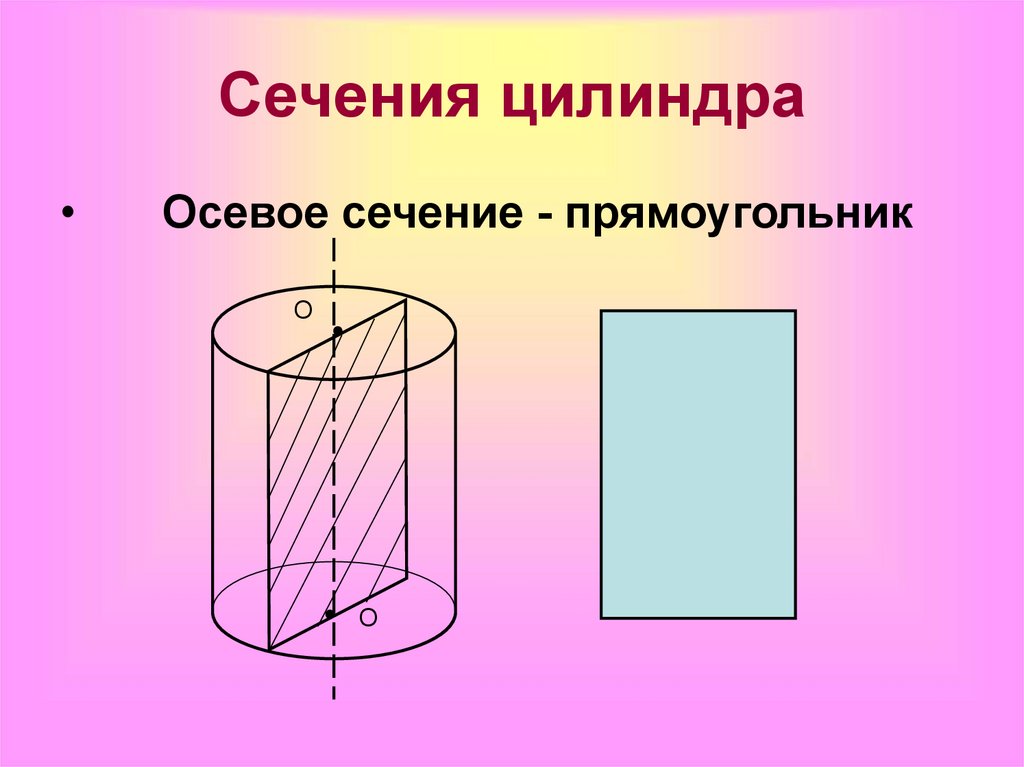 {2} + 2ay = 0. \,} В проективной геометрии цилиндр — это просто конус, вершина которого находится на бесконечности, что визуально соответствует цилиндру в перспективе, который выглядит как конус к небу.
{2} + 2ay = 0. \,} В проективной геометрии цилиндр — это просто конус, вершина которого находится на бесконечности, что визуально соответствует цилиндру в перспективе, который выглядит как конус к небу.
 {2}}
{2}}

 {2}}
{2}}
 Если бы вы «развернули» цилиндр, вы бы обнаружили, что его сторона на самом деле представляет собой прямоугольник, когда он сплющен.
(См. Площадь цилиндра).
Если бы вы «развернули» цилиндр, вы бы обнаружили, что его сторона на самом деле представляет собой прямоугольник, когда он сплющен.
(См. Площадь цилиндра).



 д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.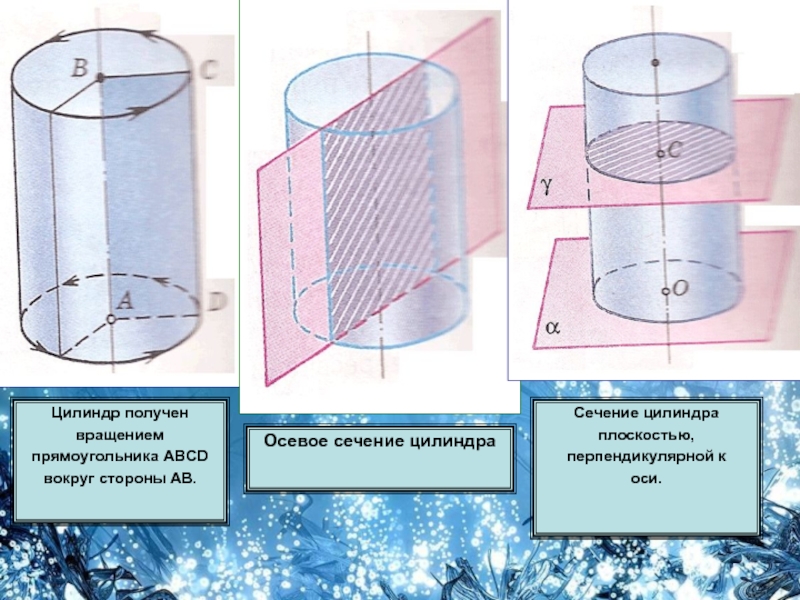 Если основания представляют собой конгруэнтные замкнутые кривые (например, окружность), то у вас цилиндр .Я нарисовал цилиндр с круглым основанием на рис. 21.4. Основание этого цилиндра — круг, поэтому у него нет вершин. Большинство цилиндров, с которыми вы сталкиваетесь, имеют круги для формы основания, и они называются круговыми цилиндрами . Но иметь круглое основание — это всего лишь вежливость. Это не требование.
Если основания представляют собой конгруэнтные замкнутые кривые (например, окружность), то у вас цилиндр .Я нарисовал цилиндр с круглым основанием на рис. 21.4. Основание этого цилиндра — круг, поэтому у него нет вершин. Большинство цилиндров, с которыми вы сталкиваетесь, имеют круги для формы основания, и они называются круговыми цилиндрами . Но иметь круглое основание — это всего лишь вежливость. Это не требование. Конус — это твердое тело, образованное внутренней частью этой замкнутой кривой вместе с поверхностью, образованной, когда каждая точка замкнутой кривой соединяется с вершиной с использованием отрезков линии.
Конус — это твердое тело, образованное внутренней частью этой замкнутой кривой вместе с поверхностью, образованной, когда каждая точка замкнутой кривой соединяется с вершиной с использованием отрезков линии.
