Все формулы для треугольника

Геометрия. Планиметрия

Формулы для произвольного треугольника

к содержанию справочника

1. Медиана треугольника.

   Обратите внимание, что медиана проведена именно к стороне .

2. Биссектриса треугольника.

   Обратите внимание, что биссектриса проведена именно к стороне

3. Теорема косинусов.

4. Теорема синусов.

   (следствие)

5. Площадь треугольника.

   (формула Герона),
   где (полупериметр)

6. Радиус вписанной окружности.

   , где

   (периметр)

7. Радиус описанной окружности.

8. Теорема Менелая.

 

Метки треугольник. Смотреть запись.

Формулы площади треугольника. Видеоурок. Геометрия 8 Класс

Площадь – одна из важных характеристик фигуры на плоскости. Можно сказать так: чем больше краски нужно для того, чтобы покрасить фигуру, тем больше ее площадь (см. рис. 1).

Рис. 1. Чем больше краски нужно для того, чтобы покрасить фигуру, тем больше ее площадь

Любое измерение – это сравнение с эталоном. Для площади в качестве эталона выбрали площадь квадрата со стороной  (она равна  кв. ед.) (см. рис. 2). Поэтому раньше вычисление площади называлось квадратурой.

Рис. 2. Площадь квадрата со стороной

 м равна

Понятно, что вычислять площадь, каждый раз разбивая фигуру на квадраты, неудобно (да и не всегда возможно). Поэтому для различных типов фигур были выведены формулы для вычисления площади (см. рис. 3).

Рис. 3. Для различных типов фигур выведены формулы для вычисления площади

Поскольку треугольник – базовая и одна из самых важных фигур, то для него было получено сразу несколько различных формул. Их основное отличие – элементы треугольника, которые в них используются.

Так, помимо «классической» формулы – через высоту и основание (см. рис. 4):

Рис. 4. Произвольный треугольник со сторонами  и высотой , проведенной к стороне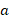

на этом уроке мы будем рассматривать:

1.                  вычисление площади треугольника по двум сторонам и углу между ними (см. рис. 5):

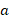Рис. 5. Произвольный треугольник со сторонами  и углом , лежащим между сторонами  и

2.                  по трем сторонам – формула Герона (см. рис. 6):

где  – полупериметр:

Рис. 6. Произвольный треугольник со сторонами

3.         с использованием радиуса  описанной окружности (см. рис. 7):

Рис. 7. Окружность радиуса  описана около произвольного треугольника со сторонами  

4.         с использованием радиуса  вписанной окружности (см. рис. 8):

где  – полупериметр:

Рис. 8. Произвольный треугольник со сторонами  описан около окружности радиуса

---

 

Единицы измерения

Обратите внимание, что в большинстве задач, с которыми вы будете сталкиваться на уроках математики, длины отрезков, площади фигур и т. д. будут даваться без единиц измерения, например: длины сторон треугольника равны . Обычно подразумевают «условные единицы». Но что это значит? Можно дать эквивалентную формулировку: длины стороны треугольника равны

,  и , где  – это сколько-то сантиметров (метров, километров, ярдов, …) (см. рис. 9).

Рис. 9. Прямоугольный треугольник со сторонами

,  и , где  – единица измерения (см, м, км, ярды и т. д.)

Тогда любая длина в рамках данной задачи будет пропорциональна этой условной единице . Например, высота такого треугольника, проведенная к гипотенузе, будет равна  усл. ед., или

 см (м, км, …) (см. рис. 10).

Рис. 10. Прямоугольный треугольник со сторонами ,  и  и высотой  см (м, км, …), проведенной к гипотенузе

Таким образом, решив задачу для условных единиц, мы можем использовать решение для любых единиц измерения, используя нужный нам

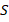. То же касается и площади  – у данного треугольника она будет равна  кв. ед., или   (, , …).

При этом надо помнить: если в условии все же указаны единицы измерения (например, все длины даны в сантиметрах), то, во-первых, надо следить, чтобы все величины при вычислениях были с одинаковыми единицами измерения (чтобы не умножить метры на сантиметры), а во-вторых, не забывать указывать получившиеся единицы для найденных величин.

---

 

Начнем изучение формул для вычисления площади треугольника с той, которую мы вывели самой первой:

Пожалуй, это наиболее часто используемая формула.

Вспомним, как мы вывели эту формулу. Вспомним, что площадь прямоугольника со сторонам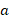и  и  равна (см. рис. 11):

Рис. 11. Прямоугольник со сторонам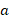и  и

Проведем диагональ, получим два прямоугольных треугольника. Они равны: катеты равны, как противоположные стороны прямоугольника (см. рис. 12). Значит, их площади одинаковы.

Рис. 12. Если провести диагональ в прямоугольнике, то получится два равных прямоугольных треугольника

Получаем, что площадь прямоугольного треугольника с катетами 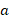 и  равна:

Для произвольного треугольника можно рассмотреть два случая. Если высота проведена из вершины острого угла (см. рис. 13), то треугольник делится на два прямоугольных, для каждого из которых верна формула площади:

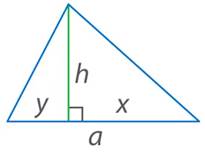
Рис. 13. Произвольный остроугольный треугольник, где проведенная к стороне 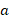 высота  делит 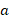 на отрезки, равные  и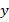

Если же высота проведена из вершины тупого угла, то она проходит вне треугольника (см. рис. 14). Тогда площадь исходного треугольника не сумма, а разность площадей двух прямоугольных:

Рис. 14. Произвольный тупоугольный треугольник, где проведенная к стороне 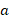 высота  проходит вне треугольника

Итак, площадь произвольного треугольника можно вычислить по формуле (см. рис. 15):

где 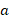 – длина любой из сторон треугольника, а  – длина высоты, проведенной к этой стороне.

Рис. 15. Произвольный треугольник с высотой , проведенной к стороне

Что нам дает эта формула?

1.                  С ее помощью можно вычислить площадь треугольника, зная длины стороны и высоты, которая к ней проведена. Например, сторона равна , высота . Площадь треугольника равна :

2.                  Два треугольника с одинаковыми основаниями и высотой имеют равные площади.

Возьмем два параллельных рельса, расстояние между которыми равно . На одном рельсе отметим отрезок длиной . На втором рельсе возьмем точку и соединим с концами отрезка. Получим треугольник (см. рис. 16). Высота его равна расстоянию между рельсами, т. е. , а основание равно . Площадь равна .

Рис. 16. На одном из параллельных рельсов, расстояние между которыми равно , отметили отрезок длиной , а на втором – взяли точку и соединили с концами отрезка

Начнем двигать точку по верхнему рельсу (см. рис. 17). Треугольник начинает растягиваться и менять форму. Но длины основания и высоты у него не меняются. Следовательно, не меняется и площадь.

Рис. 17. При движении точки по верхнему рельсу треугольник измененной формы имеет ту же площадь, т. к. длины основания и высоты остаются теми же

Этот факт мы использовали, когда доказывали, что медиана делит треугольник на два равновеликих треугольника. Действительно, у этих треугольников общая высота, а основания равны, так как основание медианы – середина стороны (см. рис. 18).

Рис. 18. Медиана делит треугольник на два равновеликих треугольника

3.                  Использовать эту формулу можно для вычисления длин сторон или высот, даже если вычислять площадь и не требуется.

 

Пример 1. В треугольнике сторона , сторона , высота . Найти высоту  (см. рис. 19).

Рис. 19. Иллюстрация к примеру 1

Решение.

Приравняем площади треугольника, вычисленные для сторон  и :

Выразим :

Ответ: .

Фактически мы здесь можем использовать не формулу для вычисления площади треугольника, а следствие из нее:

где  – высоты, проведенные к соответствующим сторонам.

 

Пример 2. В треугольнике длины сторон равны: , , . Найти высоту, проведенную к большей стороне  (см. рис. 20).

Рис. 20. Иллюстрация к примеру 2

Решение.

Заметим, что это египетский треугольник. Его стороны подчиняются соотношению:

Следовательно, по обратной теореме Пифагора, он прямоугольный (см. рис. 21). Большая сторона является гипотенузой.

Рис. 21. Иллюстрация к примеру 2

С одной стороны, площадь прямоугольного треугольника можно найти как полупроизведение катетов:

С другой – как полупроизведение гипотенузы на высоту, проведенную из прямого угла:

Приравнивая, получаем:

Ответ: .

Используем формулу  для выведения формулы площади правильного треугольника. Поскольку правильный треугольник задается одним элементом – длиной своей стороны, то логично, что и его площадь должна выражаться через сторону.

Опустим высоту  (она является биссектрисой и медианой) (см. рис. 22).

Рис. 22. Равносторонний треугольник  со стороной  и высотой , являющейся и биссектрисой, и медианой

Тогда:

Стороны треугольника | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Зная стороны треугольника, можно найти все остальные его параметры по выведенным для треугольника формулам, просто подставив их значения. Периметр треугольник будет представлять собой сумму всех его сторон, а площадь выводится по формуле Герона, как квадратный корень из произведения полупериметра на его разность с каждой стороной по очереди, и деленному на два. P=a+b+c S=√(p(p-a)(p-b)(p-c)/2)

Все углы в треугольнике, зная стороны, можно найти через теорему косинусов. (рис.75) cos⁡α=(b^2+c^2-a^2)/2bc

В произвольном треугольнике также есть три медианы m (делящие противоположную сторону пополам), три биссектрисы l (делящие угол пополам) и три высоты h (перпендикуляры из угла к стороне или ее проекции). Все их можно вычислить, имея в распоряжении значения трех сторон. Формула медианы, которая опущена на сторону c.(рис.75.1) m_c=√(2a^2+2b^2-c^2 )/2

Найти медиану, опущенную на сторону a или b, можно заменив необходимые стороны в формуле так, чтобы сторона, поделенная медианой пополам, была со знаком «–». m_a=√(2b^2+2c^2-a^2 )/2 m_b=√(2a^2+2c^2-b^2 )/2

Формула биссектрисы, которая выходит из угла γ и опущена на сторону с. (рис.75.2) l_c=√(ab(a+b+c)(a+b-c))/(a+b)

Чтобы найти биссектрисы, которые выходят из двух других углов, нужно преобразовать формулу аналогично формуле медианы, где противоположная сторона со знаком «–». l_b=√(ac(a+b+c)(a+c-b))/(a+c) l_a=√(bc(a+b+c)(b+c-a))/(b+c)

Формула высоты, которая опущена на сторону a, b или c видоизменяется таким образом, чтобы в знаменателе была нужная сторона.(рис.75.3) h_a=(2√(p(p-a)(p-b)(p-c) ))/a h_b=(2√(p(p-a)(p-b)(p-c) ))/b h_c=(2√(p(p-a)(p-b)(p-c) ))/c

Также в любом треугольнике можно провести среднюю линию, которая также как медиана обозначается буквой m, поэтому для их разделения, будем использовать заглавную M для средней линии. Средняя линия параллельна той стороне, которая выбрана основанием треугольника, и равна ее половине. Среди свойств средней линии можно отметить, что боковые стороны она делит на две равные части, поэтому если начертить все три средние линии в треугольнике, то получится еще один треугольник, подобный первому, в два раза меньше. (рис. 75.7) M_a=a/2 M_b=b/2 M_c=c/2

В каждый треугольник можно вписать окружность и описать ее вокруг него. Центр вписанной в треугольник окружности будет находиться на пересечении его биссектрис, а радиус будет опущен под прямым углом к любой стороне и его формула выводится также по Герону. (рис.75.5) r=√(((p-a)(p-b)(p-c))/p)

Центр описанной вокруг произвольного треугольника окружности находится на пересечении его медиатрисс (срединных перпендикуляров, радиус опущен в любую вершину или угол, и вычисляется по следующей формуле. (рис.75.6) R=abc/(4√(p(p-a)(p-b)(p-c)))

Теорема о площади треугольника. Формулы для нахождения площадей параллелограмма и треугольника

На этом уроке мы выведем формулу площади треугольника через синус его угла.

Сформулируем, проанализируем и докажем теорему о площади треугольника.

Теорема звучит так:

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Запишем данную теорему в стандартных для треугольника обозначениях.

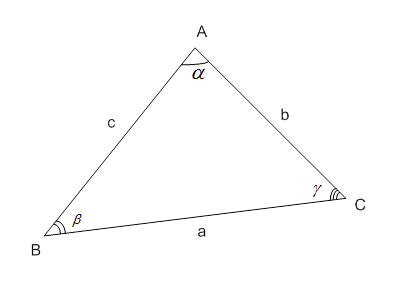
Рис. 1. Площадь треугольника

Формула площади треугольника (рис. 1) имеет такой вид:

 

Докажем данную теорему.

Дано: (рис. 2)

Доказать:

Доказательство:

Любой треугольник АВС имеет не менее двух острых углов, так как сумма углов треугольника равна 180 градусов. Пусть острыми являются угол  и угол . Тогда высота АН= находится внутри треугольника АВС, потому что иначе сумма углов в треугольнике  (рис. 2) превышала бы 180 градусов (угол  прямой, так как  – высота; а угол при вершине В тупой, так как угол  (по условию).

Рис. 2. Иллюстрация к теореме

Получили два прямоугольных треугольника общим катетом АН=. Для нахождения данного катета мы используем свойство сторон и углов прямоугольного треугольника: гипотенузу умножаем на синус противолежащего угла:     

 

Подставим данное значение в формулу площади треугольника:

 

Получаем:

 

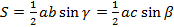
Мы доказали две формулы из трёх через острые углы . Если угол α острый, доказательство будет аналогичное. Если угол α будет прямым, доказательство очевидное (. При  высота С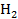= 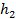находится вне треугольника АВС (рис. 3).

Рис. 3. Иллюстрация к теореме

Рассмотрим треугольник  . В нём угол 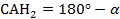. Чтобы найти катет , нужно гипотенузу умножить на синус противолежащего угла:

 

 

          

Подставляем в формулу для площади треугольника  () значение катета :

 

Мы доказали и третью формулу. Следовательно, доказали теорему.

Также эту теорему можно доказать координатным методом (рис. 4).

Дано: треугольник АВС, ,

Доказать:

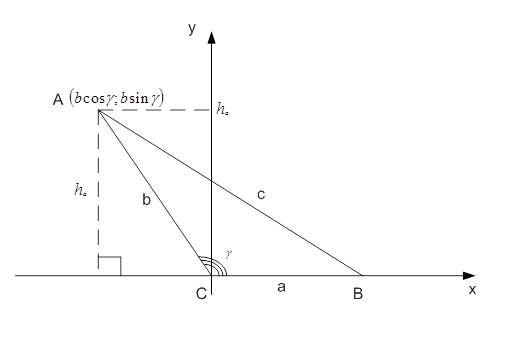
Рис. 4. Иллюстрация к теореме

Координаты вершины А определяются через длину АС=b и угол γ. В предыдущих уроках мы выяснили, что координаты точки А будут . А  – это высота , то есть ордината точки А.

   

Подставляем в формулу площади треугольника:

 

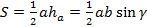
Формула доказана независимо от величины углов треугольника – за начало координат была взята точка С. Остальные 2 формулы получаются аналогично, если за начало координат взять точку А или В.

Полученные формулы можно использовать во многих задачах.

Дано: треугольник АВС, АВ= см, АС=4 см, ⦟А=(рис. 5)

Найти: площадь треугольника АВС

Решение:

Рис. 5. Иллюстрация к задаче

Для решения данной задачи воспользуемся ранее доказанной теоремой.

 

Подставляем известные значения:

 

 

Докажите, что площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.

Доказательство:

Для доказательства воспользуемся свойствами параллелограмма. Диагональ BD рассекает параллелограмм на два треугольника.  (рис. 6) по трём равным сторонам (противоположные стороны в параллелограмме равны, следовательно, АВ=CD, AD=BC. Сторона BD – общая для двух треугольников.). Отсюда следует, что площади этих двух треугольников тоже равны.

Площадь параллелограмма

 

Согласно теореме о площади треугольника

Рис. 6. Иллюстрация к задаче

 

Значит, площадь параллелограмма равна

 =

Можно рассмотреть и угол В. Он равен , следовательно, . Поэтому площадь параллелограмма можно рассчитать через :

 

Формула для площади параллелограмма доказана.

Треугольники ADB и ADC параллелограмма ABCD . Доказать, что площади этих треугольников равны.

Доказательство:

Рис. 7. Иллюстрация к задаче

Площади первого и второго треугольника есть произведение половины основания на высоту (рис. 7). Основание у них одинаковое (AD), высота, опущенное на это основание, также одинаковая, следовательно:

 

Дано:, АС15 см,

Найти: сторону АВ (рис. 8)

Решение:

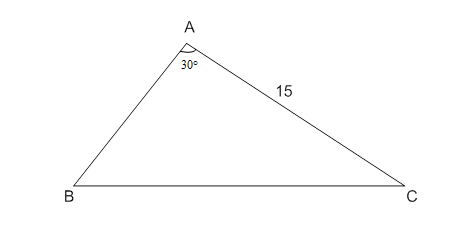
Рис. 8. Иллюстрация к задаче

Найдём сторону АВ через формулу площади треугольника

 

Подставляем известные величины:

 

 см

 

Докажите, что площадь параллелограмма равна половине произведения длин его диагоналей на синус угла между ними.

Дано: ABCD – параллелограмм (рис. 9)

Доказать:

Доказательство: первый способ:

Учтём, что угол α и угол  имеют один и тот же синус:

 

Площадь треугольника АОВ (согласно теореме о площади треугольника):

 

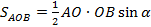
Площадь треугольника ВОС: 

Рис. 9. Иллюстрация к задаче

 

Так как синусы равны, то и . Учитывая, что , а , мы доказали, что диагонали параллелограмма делят его на 4 равновеликих треугольника.

Поэтому для нахождения площади параллелограмма достаточно найти площадь одного из треугольников и умножить на 4.

   

Так как , то

Что и требовалось доказать.

 

Рис. 10. Иллюстрация к задаче

Из точки С диагонали АС проводим прямую CР, параллельную другой диагонали (BD). Получаем параллелограмм BDPC, треугольник ABD равновелик треугольнику DCP, так как

Основания и высота у них одинаковы.

Таким образом, отнимая от параллелограмма ABCD треугольник ABD и прибавляя треугольник DCP, получаем треугольник АСР с такой же площадью, как у исходного параллелограмма. И площадь этого треугольника равна:

 

 

    

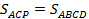Так как СРBD и  , то

  

Что и требовалось доказать.

Дано: , , высота ВН=h

Найти: площадь треугольника АВС (рис. 11)

Решение:

                                           

Рис. 11. Иллюстрация к задаче

Согласно теореме о площади треугольника

 

Выражаем АВ и ВС через h и другие известные величины. АВ является

гипотенузой в прямоугольном треугольнике АВН, поэтому:

, при  (рис. 11 а)

, при  (рис. 11 б)

Аналогично находим ВС (). В обоих случаях:

Подставляем данные значения в формулу площади треугольника:

 

На данном уроке мы доказали теорему о площади треугольника через синус его

угла и решили задачи по данной теме.

           

Список литературы

1. Атанасян Л. С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.
2. Фарков А. В. Тесты по геометрии: 9 класс. К учебнику Л. С. Атанасяна и др. – М.: Экзамен, 2010.
3. Погорелов А. В. Геометрия, уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. E-science.ru (Источник).
2. 2mb.ru (Источник).
3. Festival.1september.ru (Источник).

 

Домашнее задание

1. В треугольнике ABC AB = 1 см, BC = 2 см, , . Найдите площадь треугольника. 
2. Для определения площади треугольника АВС измерили две его стороны a и b и угол между ними γ. Вычислить площадь (a= 125 мм, b= 160 мм, γ = 52).
3. Площадь треугольника АВС равна 18. АС = ВС = 3. Найдите сторону АВ.

Формулы треугольника | Формулы с примерами

Формулы
Формула теоремы синусов

Формулы теоремы косинусов

Формула тангенсов

Формулы площади треугольника

Формула синуса половинного угла

Формула косинуса половинного угла

Формула тангенса половинного угла

Формула радиуса описанной окружности

Формула радиуса вписанной окружности треугольника

Формулы биссектрисы угла

Формулы прямоугольного треугольника

Формулы косоугольных треугольников

Формулы площади треугольника

Формулы площади треугольника

Подождите пару секунд пока подгрузятся формулы

Внимание! Десятичную дробь надо писать с точкой(.), а не с запятой!

Через основание и высоту

$$S= \frac{1}{2} ah $$ \(S\) — площадь треугольника

\(a\) — основание

\(h\) — высота

\(a =\)    \(h =\)

---

Через две стороны и угол

$$S= \frac{1}{2} ab sin \alpha $$ \(S\) — площадь треугольника

\(a\) — сторона

\(b\) — сторона

\( \alpha \) — угол между сторонами \(a\) и \(b\)

\(a =\)    \(b =\)    \( \alpha =\)

---

Формула Герона

$$S= \sqrt{p(p-a)(p-b)(p-c)} $$ \(S\) — площадь треугольника

\(a\) — сторона

\(b\) — сторона

\(c\) — сторона

\(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)

\(a =\)    \(b =\)    \(c =\)

---

Через радиус вписанной окружности

$$S= rp $$ \(S\) — площадь треугольника

\(r\) — радиус вписанной окружности

\(a\) — сторона

\(b\) — сторона

\(c\) — сторона

\(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)

\(r =\)    \(p =\)

---

Через радиус описанной окружности

\(S= \frac{abc}{4R} \)

\(S\) — площадь треугольника

\(R\) — радиус описанной окружности

\(a\) — сторона

\(b\) — сторона

\(c\) — сторона

\(a =\)   \(b =\)

\(c =\)   \(R =\)

---

Площадь прямоугольного треугольника

$$S= \frac{1}{2} ab $$ \(S\) — площадь треугольника

\(a\) — сторона

\(b\) — сторона

\(a =\)    \(b =\)

---

Площадь прямоугольного треугольника

$$S= de $$ \(S\) — площадь треугольника

\(d =\)    \(e =\)

---

Формула Герона для прямоугольного треугольника

$$ S= (p-a)(p-b) $$ \(S\) — площадь треугольника

\(a\) — сторона

\(b\) — сторона

\(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)

\(a =\)    \(b =\)    \(p =\)

---

Площадь равнобедренного треугольника

$$S= \frac{1}{2} a^2 sin \alpha$$ \(S\) — площадь треугольника

\(a\) — сторона

\(\alpha\) — угол между боковыми сторонами

\(a =\)    \( \alpha =\)

---

Площадь равнобедренного треугольника

\(a\) — сторона

\(b\) — сторона

\(\alpha\) — угол между боковыми сторонами и основанием

\(a =\)    \(b =\)    \( \alpha =\)

---

Площадь равнобедренного треугольника

$$S= \frac{b^2}{4tg \frac{ \alpha }{2}} $$ \(S\) — площадь треугольника

\(b\) — сторона

\(\alpha\) — угол между боковыми сторонами и основанием

\(b =\)    \(\alpha =\)

---

Формула Герона для равнобедренного треугольника

a =    b =

---

Площадь равностороннего треугольника

$$S= \frac{ \sqrt{3}a^2}{4} $$ \(S\) — площадь треугольника

\(a\) — сторона

\(a =\)

---

Площадь равностороннего треугольника

$$S= \frac{3 \sqrt{3}R^2}{4}$$ \(S\) — площадь треугольника

\(R\) — радиус описанной окружности

\(R =\)

---

Площадь равностороннего треугольника

$$S= 3 \sqrt{3}r^2 $$ \(S\) — площадь треугольника

\(r\) — радиус вписанной окружности

\(r =\)

---

Площадь равностороннего треугольника

$$S= \frac{h^2}{\sqrt{3}}$$ \(S\) — площадь треугольника

\(h\) — высота

\(h =\)