Решение задач. Видеоурок. Геометрия 7 Класс
На этом уроке мы будем решать задачи по пройденной теме. Вначале повторим изученный материал. Вспомним аксиому о параллельных прямых и следствие из нее. Повторим определение луча и угла и единицы измерения отрезков и углов. Вспомним определение равных геометрических фигур и то, как сравнивают и измеряют отрезки и углы. Вспомним, что такое середина отрезка и биссектриса угла, какие углы называются острыми, прямыми и тупыми. Повторим теоремы о сумме смежных углов и о равенстве вертикальных углов. Вспомним, что такое перпендикулярные прямые и теорему о том, что две перпендикулярные к третьей прямые не пересекаются. И будем решать типовые задачи на повторенный материал.
Вспомним сведения, изученные в текущей теме:
— Аксиома. Через две точки можно провести прямую, и только одну.
— Прямые на плоскости могут пересекаться, могут не иметь общих точек.
— Угол измеряется в градусах. 1 градус – это сто восьмидесятая часть от развернутого угла.
— Сумма смежных углов равна 180о.
— Вертикальные углы равны между собой.
— Прямые, пересекающиеся под углом 90о, называются перпендикулярными.
— Прямые, перпендикулярные одной прямой, не пересекаются.
Пример 1: Найти угол между биссектрисами смежных углов.
Решение:
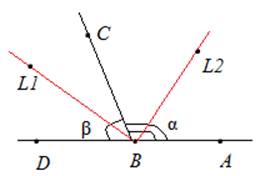
Рис. 1. Чертеж к примеру 1
Биссектриса BL1 угла ∠DBC = β делит его на два угла, градусная мера которых равна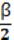 
. Необходимо найти угол ∠ L1 ВL2. Выполним сложение углов: ∠ L1 ВL2 = ∠ L1 ВС + ∠СВL2 = 
. Сумма углов α + β равна 180о, поскольку данные углы – смежные.Ответ: 90о.
Отметим, что в данной задаче нам не было известно, какие градусные меры углов ∠DBC и ∠АBC, однако мы знаем, что их сумма равна 180о.
Пример 2: Отрезок длиной 36 см поделили на 4 неравных части. Расстояние между серединами крайних частей равно 30 см. Найдите расстояние между серединами средних частей отрезка.
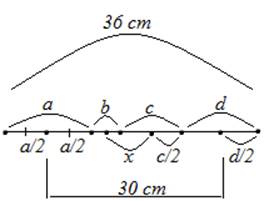
Рис. 2. Чертеж к примеру 2
Решение:
Найдем величину суммы отрезков 
Соответственно,
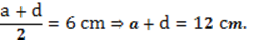
Вычислим сумму длин оставшихся отрезков: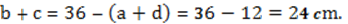 
Найдем расстояние между серединами средних частей отрезка.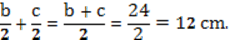 
Ответ: 12 см.
Пример 3: Отрезок длиной m разделен на три части. Найти расстояние между серединами крайних частей.
Решение:
Выполним рисунок.
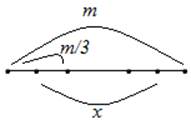&n
interneturok.ru
Простейшие задачи на построение. Видеоурок. Геометрия 7 Класс
Данный видеоурок создан специально для самостоятельного изучения темы «Простейшие задачи на построение». В ходе него учащиеся узнают о том, как решать простейшие задачи на построение, используя циркуль и линейку. Учитель объяснит материал на примере конкретных задач, а также напомнит несколько изученных ранее аксиом.
Определим, какие действия мы можем выполнять при помощи циркуля и линейки. Во-первых, с помощью линейки можно провести произвольную прямую, а также прямую, проходящую через две точки. Через две точки можно провести прямую, и при том только одну.
С помощью циркуля можно построить окружность заданного радиуса.
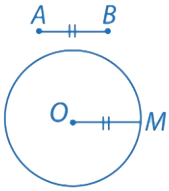
Рис. 1. Окружность и прямая
Пример 1: На заданном луче от его начала отложить отрезок, равный данному. Отрезок АВ и луч ОС даны по условию:
Рис. 2.1. Условие к примеру 1
Построение:
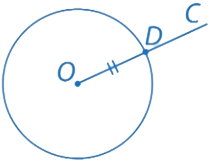
Рис. 2.2. Решение к примеру 1
Построение выполняем следующим образом: строим окружность с центром в точке О и радиусом АВ. Точка D является точкой пересечения окружности и луча. Отрезок OD – искомый, так как он равен АВ.
Построение выполнено.
Пример 2: Отложить от данного луча угол, равный данному. Заданы угол А и луч ОМ. Построить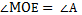 
.
Построение:
Рис. 3.1. Условие к примеру 2
1. Построить окружность Окр(А, r = AB). Точки В и С – являются точками пересечения со сторонами угла А.
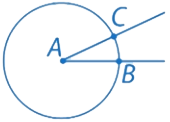
Рис. 3.2. Решение к примеру 2
2. На луче ОМ построить окружность с центром в точке О радиуса r = АВ. Получаем точку D на пересечении луча ОМ и окружности
3. Строим третью окружность с центром в точке D радиуса r = BC (где В и С точки пересечения угла А и первой окружности) и получаем точку Е на пересечении двух окружностей
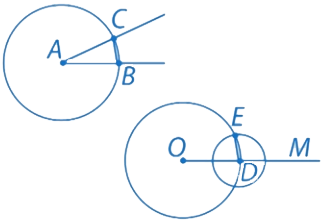
Рис. 3.3. Решение к примеру 2
4. Получаем искомый угол МОЕ = углу А
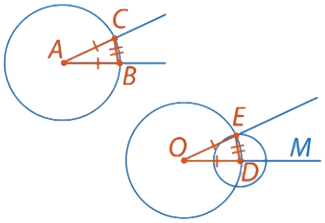
5. Угол МОЕ – искомый, так как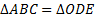 
.
Построение выполнено.
Пример 3: Построить биссектрису данного угла. Дан угол А, необходимо выполнить построение биссектрисы АЕ.
Рис. 4.1. Условие к примеру 3
Построение:
1. Построим окружность Окр(А, r = АB). Точки В и С – точки пресечения окружности со сторонами угла.
2. Выполним построение окружности Окр(В, r = CB) и окружности Окр(С, r = CB). Данные окружности пересекаются в точке Е.
3. Луч АЕ – биссектриса – искомый, так как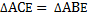 
. Из этого следует, что 
.
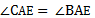Рис. 4.2. Решение к примеру 3
Построение выполнено.
Пример 4: Из точки, лежащей на данной прямой, требуется провести перпендикуляр к данной прямой.
Построение:
1. МА = МВ. Мы зафиксировали определенные равные отрезки по обе стороны от заданной точки.
2. Построим окружности Окр(А, r = АB) и Окр(В, r = АB). Эти окружности пересекаются в точках P и Q.
3. PМ – искомая прямая. Медиана РМ есть и высота в равнобедренном треугольнике РАВ.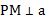 
.
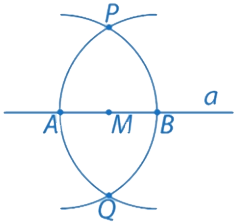
Рис. 5. Решение к примеру 4
Построение выполнено.
Пример 5
Рис. 6.1. Условие к примеру 5
Построение:
1. Построим окружности Окр(А, r = АB) и Окр(В, r = АB). Эти окружности пересекаются в точках P и Q.
2. PQ пересекает АВ в точке О, точка О – искомая, так как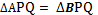 
, поэтому PQ – биссектриса в равнобедренном треугольнике РАВ. Следовательно, PQ – медиана.
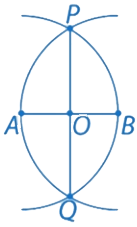
Рис. 6.2. Решение к примеру 5
Построение выполнено.
Рекомендованные ссылки на интернет-ресурсы
- Первый признак равенства треугольников (Источник).
- Справочный портал calc.ru (Источник).
Рекомендованное домашнее задание
1. № 99. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. – М.: Просвещение, 2010.
2. Увеличьте произвольный угол на 25%.
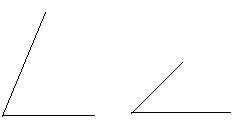
3. Постройте угол, который равен сумме (разности) двух углов, изображенных на рисунках.
4. Докажите, что если две стороны и угол, который лежит против большей из них, одного треугольника соответственно равны двум сторонам и углу, который лежит против большей стороны второго треугольника, то эти треугольники равны.
Консультация (7 класс) на тему: Как научиться решать задачи по геометрии?
Как научиться решать задачи по геометрии?
Дорогие ребята, Вы начали изучать геометрию. Это новая для вас дисциплина, и вы поначалу можете испытывать трудности в её освоении. Не пугайтесь: пройдет некоторое время, и вы научитесь с легкостью решать любые геометрические задачи. Для приобретения необходимого навыка нужно лишь приложить немного усилий. Итак, как решать задачи по геометрии?
Вам понадобится: учебник, тетрадь, ручка, карандаш, линейка, транспортир, циркуль, ластик.
Инструкция:
- Внимательно прочитайте условие задачи.
- Сделайте чертеж.
- Отметьте на чертеже то, что вам дано: длины сторон, величины углов. Если в условии задачи сказано, что какие-то отрезки равны, поставьте на них одинаковые штрихи. Равные по величине углы отмечайте одинаковыми дужками: одинарными, двойными, волнистыми. Углы разных величин выделяйте разными дужками.
- Исследуйте фигуры, представленные в задаче. Вспомните их определения и свойства.
- Определите тему, к которой относится ваша задача. Освежите в голове теоретический материал по этой теме, повторите основные теоремы.
- Рассмотрите примеры решения задач по этой теме. В задачах, приводимых в учебнике в качестве примеров, часто рассматриваются принципиальные вопросы, которые вы должны знать.
- Если вы чувствуете себя в теме достаточно уверенно, приступайте к решению задачи. Начните с того, что требуется найти или доказать. Подумайте, каким путем это можно сделать. То есть, решайте задачу «с конца».
- Если вы не видите путей решения задачи, попробуйте найти хоть что-нибудь, используя имеющиеся данные. Возможно, так к вам придет идея, как решать задачу.
Полезные советы: не увлекайтесь «устными» доказательствами. Записывайте решение задачи как можно более подробно, если не оговорено иное. Некоторые вещи могут казаться вам очевидными, но всё равно прописывайте их. Так у вас будет отрабатываться навык, вы лучше запомните идею.
Рекомендации от учителя математики Е.В.Жалыбиной
nsportal.ru
Конспект «Геометрия 7 ЗАДАЧИ на построение»
Геометрия 7 ЗАДАЧИ на построение
Ключевые задачи на построение в 7 классе: 1) построить отрезок, равный данному; 2) построить угол, равный данному; 3) построить середину данного отрезка; 4) построить биссектрису данного угла; 5) построить треугольник, равный данному, или построить треугольник по трем заданным сторонам; 6) построить треугольник по двум сторонам и углу между ними; 7) построить треугольник по стороне и двум прилежащим к ней углам; 8) построить прямую, проходящую через данную точку, не принадлежащую данной прямой и перпендикулярную прямой; 9) построить прямую, проходящую через данную точку и параллельную данной прямой; 10) построить прямоугольный треугольник по гипотенузе и острому углу; 11) построить прямоугольный треугольник по гипотенуза и катету.
«Геометрия 7 ЗАДАЧИ на построение» содержат подробное указание «что делаем», «как делаем», а также показан пример «записи построения в тетради».
РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ НА ПОСТРОЕНИЕ
Опорная задача № 1. Построить отрезок, равный данному.
Опорная задача № 2. Построить угол, равный данному.
Опорная задача № 3. Построить середину данного отрезка.
Опорная задача № 4. Построить биссектрису данного угла.
Задача № 5. Построить треугольник, равный данному, или построить треугольник по трем заданным сторонам.
Задача № 6. Построить треугольник по двум сторонам и углу между ними.
Задача № 7. Построить треугольник по стороне и двум прилежащим к ней углам.
Задача № 8. Построить прямую, проходящую через данную точку, не принадлежащую данной прямой и перпендикулярную прямой.
Задача № 9. Построить прямую, проходящую через данную точку и параллельную данной прямой.
Задача № 10. Построить прямоугольный треугольник по гипотенузе и острому углу.
Задача № 11. Построить прямоугольный треугольник по гипотенуза и катету.
Это конспект по теме «Геометрия 7 ЗАДАЧИ на построение». Выберите дальнейшие действия:
uchitel.pro
Окружность. Задачи на построение — урок. Геометрия, 7 класс.
Окружность — геометрическая фигура, состоящая из всех точек плоскости, которые находятся на заданном расстоянии от данной точки.
Эту точку называют центром окружности, а заданное расстояние — радиусом окружности.
Радиус — это отрезок, соединяющий центр окружности с любой точкой окружности. Из определения следует, что можно провести бесконечное количество радиусов, и они все имеют одинаковую длину.
Отрезок, который соединяет две точки на окружности, называют хордой.
Если хорда проходит через центр окружности, то её называют диаметром окружности.
Диаметр — самая длинная хорда.
В окружности также можно провести бесконечное количество диаметров.
Если соединить две точки окружности не отрезком, а кривой, проходящей по самой окружности, то часть окружности между двумя точками называют дугой.
Если на окружности отметить две точки, то получаются две дуги. Поэтому для названия дуги используют три латинские буквы, которые могут быть как маленькие, так и большие.
На рисунке выше можем назвать: дуга \(BDH\), дуга \(ACG\) и другие.
На рисунке ниже нарисованы: дуга \(AxB\) и дуга \(AyB\).
Часть плоскости, ограниченная окружностью, называется кругом.
Задачи на построение
В задачах, где необходимо выполнить конструкции, используются циркуль и линейка.
Очень важно запомнить, что в этих задачах линейка используется не как инструмент для измерения, а исключительно только для того, чтобы провести прямую, луч или отрезок через две данные точки, то есть, чтобы провести прямую линию. Циркуль используется для построения окружности или дуги окружности.
Рассмотрим пять основных построений, в которых используем упомянутые действия — построение прямой линии и окружности:
1. на данном луче от его начала отложить отрезок, равный данному.
2. Построение угла, равного данному.
3. Построение биссектрисы угла.
4. Построение перпендикулярных прямых.
5. Построение середины отрезка.
1. На данном луче от его начала отложить отрезок, равный данному.
См. видео.
Ясно, что таким образом мы получили отрезок, равный данному. Соответственно определению окружности, она состоит из точек, расположенных на заданном расстоянии (радиусе) от некоей точки (центра окружности).
Если центром служит начальная точка луча \(C\), радиусом — данный отрезок \(AB\), то точка пересечения окружности и луча \(D\) и есть искомая конечная точка отрезка \(CD\), равного данному отрезку \(AB\).
2. Построение угла, равного данному.
См. видео.
Докажем, что построенный угол \(ECD\) и есть тот искомый угол, равный данному углу \(AOB\).
Если мы построили окружность с центром \(C\) — начальной точкой луча и таким же радиусом, как у окружности с центром \(O\), то \(CD\) \(=\) \(OB\).
Если далее мы построили окружность с центром \(D\) и радиусом, равным отрезку \(BA\), и получили точку пересечения обеих окружностей \(E\), то \(BA\) \(=\) \(DE\).
Провели луч \(CE\). Очевидно, \(OA\) \(=\) \(CE\).
Значит, треугольники \(AOB\) и \(ECD\) равны по третьему признаку равенства треугольников, у них равны и углы, в том числе угол \(ECD\) равен углу \(AOB\).
3. Построение биссектрисы угла.
См. видео.
Чтобы доказать, что \(OC\) действительно делит угол \(AOB\) пополам, достаточно рассмотреть треугольники \(AOC\) и \(BOC\).
\(OA = OB\) как радиусы одной окружности, а \(AC = BC\), так как мы при построении выбрали одинаковые радиусы для обеих окружностей.
Сторона \(OC\) — общая.
Эти треугольники равны по третьему признаку.
Следовательно, их соответствующие углы равны.
Значит, \(AOC\) и \(BOC\) — две равные части одного угла, это означает, что луч \(OC\) делит угол пополам.
4. Построение перпендикулярных прямых.
См. видео.
Почему \(DE\) является перпендикулярной к \(BC\)?
\(AB = AC\) — так эти точки были отложены при построении.
\(BD = CD\), так как мы обе окружности построили с одинаковыми радиусами.
Значит, \(DA\) или \(EA\) — медианы, проведённые к основанию равнобедренных треугольников \(BDC\) или \(BEC\).
Медиана в равнобедренном треугольнике является также высотой, то есть перпендикулярна к основанию.
5. Построение середины отрезка.
См. видео.
Эта конструкция такая же, как в случае построения перпендикулярных прямых, и уже доказано, что \(DC\) или \(EC\) делит \(AB\) пополам, то есть \(C\) — серединная точка отрезка \(AB\).
www.yaklass.ru
Треугольники. Геометрия, 7 класс: уроки, тесты, задания.
Вход
Вход
Регистрация
Начало
Поиск по сайту
ТОПы
Учебные заведения
Предметы
Проверочные работы
Обновления
Новости
Переменка
Отправить отзыв
- Предметы
- Геометрия
- 7 класс
-
Первый признак равенства треугольников
-
Медианы, биссектрисы и высоты треугольника
-
Второй и третий признаки равенства треугольников
-
Задачи на построение
www.yaklass.ru
Задачи на сравнение и измерение отрезков и углов. Видеоурок. Геометрия 7 Класс
На этом уроке мы повторим задачи на сравнение и измерение отрезков и углов.
Следует вспомнить основные опорные факты, которые необходимо использовать при решении задач.
1) Из трёх точек на прямой одна и только одна лежит между двумя другими.
2) Каждый отрезок имеет определённую длину, больше нуля.
3) Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
4) Из начальной точки можно отложить отрезок заданной длины, причем только один.
5) Каждый угол имеет определенную градусную меру.
6) Развернутый угол равен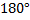 
.
7) Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
8) От любого луча в заданную плоскость можно отложить угол с заданной градусной мерой, меньший 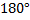, и притом лишь один.
Задача 1
Точк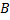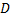и 
, 
и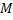 
лежат на одной прямой. 
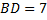cм,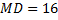 
см. Найти расстояние 
.
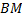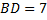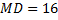Дано: см, см.
Найти:.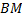
Решение
Мы знаем, что среди трёх точек, лежащих на одной прямой, существует лишь одна точка, которая лежит между двумя крайними.
Выполним пояснительный рисунок.
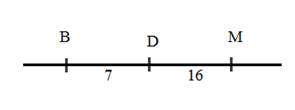
Рис. 1. Чертёж к задаче 1
1) 
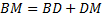
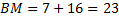
Ответ: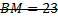
см.
Мы допустили ошибку, не рассмотрев все возможные случаи. Точка посередине не обязательно должна быть точкой 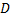. Расстояние 
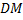мы отложили вправо, значит, мы должны отложить его влево.
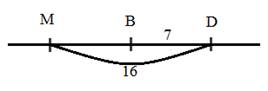
Рис. 2. Чертёж к задаче 1
Ответ оказался неверным. Рассмотрим второй случай.
2) 
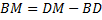
interneturok.ru