Задачи по геометрии на повторение 7 класс

Задачи по теме « Равнобедренный треугольник»

1. В треугольнике АВС углы ВАС и ВСА равны, их биссектрисы АА1 и СС1 пересекаются в точке О. Докажите, что треугольник АОС равнобедренный.

2. Найдите периметр треугольника АВС если два его угла равны, а две стороны имеют длины 40 см и 20см.

3. В треугольнике АВС угол В=120⁰ , а угол А= 30⁰ . Точка D принадлежит стороне АС, причем угол ВDС тупой. Докажите, что АВ ВD.

4.Разность длин двух сторон равнобедренного тупоугольного треугольника равна 4 см, а его периметр равен 19 см.Найдите длины сторон треугольника.

5. В равнобедренном треугольнике АВС угол В — тупой. Высота ВD равна 4 см. Найдите периметр треугольника АВС, если периметр треугольника АВD равен 12 см.

6.В треугольнике АВС внешние углы при вершинах А и С равны. Найдите длину биссектрисы ВD , если периметр треугольника АВС равен 72 см, а периметр треугольника АВD равен 48 см.

Задачи по теме « Признаки равенства треугольников»

1. На высоте АН равнобедренного треугольника с углом А=900 взята точка О. Докажите, что треугольники ВОН и НОС равны.

2. В треугольнике КМР КМ=МР. Точки А и В середины сторон KM и MP соответственно. АС и ВD перпендикулярны прямой КР. Докажите, что треугольники КАС и DВР равны.

3. Даны равносторонние треугольники АВС и А1В1С1 точки О и О1 – точки пересечения высот этих треугольников, причем ОА= О1А1 . Докажите, что треугольники АВС и А1В1С1 равны.

4. Треугольник АВС равносторонний. AC – основание. Точки К , L , М- середины сторон АВ , ВС и АС соответственно . Докажите, что треугольники АКМ и МLC равны.

5. Даны треугольники АВС , с высотой СН , и KMN с высотой NL . Причем , угол В=600, угол М=600, СН=LN и АВ=KM. Докажите , что треугольники АВС и KMN равны.

6. В равнобедренном треугольнике АВС ВК – медиана, проведенная к основанию. Точки М и N принадлежат боковым сторонам. Луч КВ – биссектриса угла МКN . Докажите, что АМ=NC.

Задачи по теме « Окружность»

1. В окружности с центром О проведены радиусы ОК , ОМ , ОN , таким образом ,что углы КОМ и МОN равны. Докажите , что треугольники КОМ и МОN равны.

2. В окружности с центром О диаметру АС перпендикулярен радиус ОВ. Докажите, что АВ=ВС.

3. В окружности с центром О проведены две непараллельные хорды КМ и РN , причем КМ= РN. Точка А – середина КМ, точка В – середина Р N . Докажите, что треугольник АОВ равнобедренный.

Задачи по теме «Смежные и вертикальные углы»

1. Один из углов, образовавшихся при пересечении двух прямых равен 480 .Найти остальные углы.

2. Дан треугольник АВС. На продолжении сторон АВ и ВС за вершину В отмечены точки К и М соответственно. Угол КВМ=300 Угол А в 3 раза больше угла С. Найти угол, смежный с углом С.

3. На окружности с центром О последовательно отмечены точки А, В, С, D, К так, что точки А и К являются концами диаметра, углы АОС и СОК равны. Угол АОВ= 300 , угол DОК=600 . Докажите, что ВD=АС.

Задачи по теме «Параллельные прямые»

1. Отрезки KM и PL –диаметры некоторой окружности. Докажите, что прямые KP и ML параллельны.

2. Точки А и С лежат по разные стороны от прямой BD . Известно, что АВ параллельна DC и AD параллельна ВС. Докажите, что угол BAD равен углу DCB, АВ=DC и AD= BC.

3. На биссектрисе CD равнобедренного треугольника АВС взята точка М. Через эту точку проведены прямые, параллельные сторонам АС и ВС и пересекающие основание АВ в точках Н и К. Докажите, что АН=КВ.

4. На сторонах MP и PN треугольника MPN взяты точки А и В соответственно. Угол PMN равен углу РАВ и равен 600, угол MNP равен 500. Найдите, чему равен угол АВN.

5. В треугольнике АВС угол А равен 300, угол С равен 1200. Докажите, что биссектриса внешнего угла при вершине С лежит на прямой, параллельной прямой АВ.

6. На одной стороне неразвернутого угла взяты точки E и F, на другой – G и H , так, чтобы EG параллельно FH , точка М принадлежит отрезку EG , угол MFE равен углу MFH, угол MHF равен MHG. Докажите, что EG= EF+GH.

Индивидуальные домашние задания по геометрии, 7 класс

I полугодие

Из опыта работы Петуховой Н.М.

Учебник: Геометрия, 7-9

Авторы: Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.,

Позняк Э.Г., Юдина И.И.

Индивидуальные домашние задания по геометрии

7 класс, I полугодие

Составленный мною дидактический материал предназначен для учащихся, плохо усваивающих учебный материал по геометрии, слабо владеющих общими учебными навыками, у которых в дополнение ко всему ещё и слабая мотивация обучения вообще. Обычно такие учащиеся не могут самостоятельно подготовиться к уроку, а часто и не стремятся этого делать, контроль со стороны родителей отсутствует. Создание индивидуальных заданий – это ещё одна попытка помочь ребёнку начать изучение нового для него предмета.

Применение карточек с индивидуальными заданиями, составленными именно для конкретного ученика, повышает мотивацию изучения материала. Получив карточку и устные рекомендации учителя , ученик всё-таки чаще настраивается на выполнение задания, начинает работать с книгой, заучивает необходимые формулировки и выполняет простейшие задания по теме. Это позволяет ему на последующих уроках активнее включаться в устную работу, лучше усваивать новый материал. Если по карточке что-то не выполнено, ребёнок обязательно подойдёт к учителю и задаст вопрос, тогда как при работе над общим домашним заданием такие дети обычно вопросов не задают.

Задания, конечно, очень просты, некоторые просто дублируют задачи учебника, в других изменены обозначения или ориентация фигур на рисунках. В первом задании карточки даётся рекомендация по изучению теоретического материала.

Если всё первое полугодие ученик занимается по карточкам, то со второго или даже раньше, он сможет выполнять те домашние задания, которые даются всему классу. Конечно, это удаётся не всегда, так как очень много и других факторов, влияющих на успешность обучения. Для многих детей индивидуальные задания оказываются существенной помощью в том плане, что они хотя бы начинают систематически уделять время самоподготовке.

В дальнейшем данный дидактический материал будет совершенствоваться по содержанию, планируется разработка таких заданий по остальным темам курса геометрии. 7 класса

Г-7ИДЗл-1 Луч и угол.

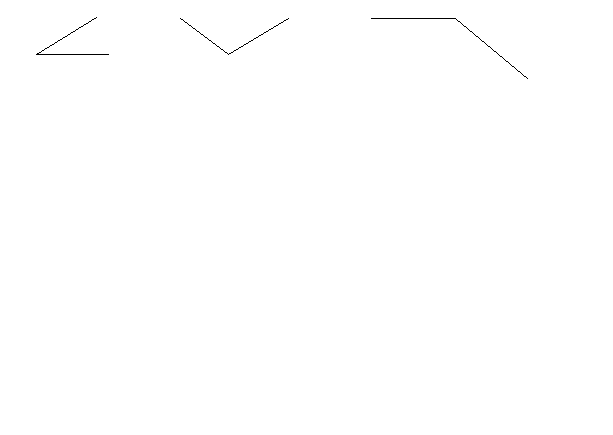№1. Прочитай п.3-4, внимательно рассмотри рисунки. Запиши углы, изображённые на рисунке:

М С D Q R

N E O

B

№2. Начерти угол ВОС. Лучом ОК раздели угол ВОС на два различных угла. Запиши эти углы.

Г-7ИДЗл-2 Сравнение отрезков и углов

№1. Прочитай п.5-6 Ответь на вопросы устно:

1) Какие фигуры называют равными? 2) Как установить, равны ли фигуры Ф

и Ф?

3) Что называется биссектрисой угла?

№2. Начерти отрезок МК и отметь его середину Е. Отметь на отрезке МК точку С так, чтобы отрезок МС был больше отрезка СК.

№3. Начерти развёрнутый угол, обозначь его буквами и запиши. Начерти биссектрису этого угла, обозначь и запиши.

Г-7 ИДЗл-3 Измерение отрезков

№1. Прочитай внимательно п. 7-8. В каких единицах и какими инструментами измеряются длины отрезков? (устно)

№2. Известно, что отрезок МК больше отрезка АС. Длины этих отрезков 3 см и 7 см. Запиши, чему равна длина каждого отрезка.

№3. Точка F лежит на отрезке АВ. При этом АF=4 см, BF=9 см. Сделай схематический рисунок к задаче. Найди длину отрезка АВ.

Г-7 ИДЗл-4 Измерение углов

№1. Прочитай п. 9-10. Ответь на вопросы устно:

1. Что такое градус? Что называют минутой? Секундой?

2. Сколько в градусе минут? В минуте секунд? Прочитай запись: 214514.

3. Какова градусная мера развёрнутого угла?

№2. АВС = 36, МКЕ = АВС. Запиши, чему равен угол МКЕ.

№3. Луч ОК выходит из вершины угла DОС (см. рисунок). DОК = 120, КОС=24.

Найдите градусную меру угла DОС. D K

Запиши решение в тетрадь, сделав рисунок.

№4. А – прямой, В – острый, С- развёрнутый,

 R – тупой. Изобрази эти углы, измерь и.

запиши их градусные меры. O C

Г-7 ИДЗл-5 Смежные и вертикальные углы

№1. Прочитай п.11. Выучи, какие углы называются смежными, какие – вертикальными.

№2. Построй смежные углы АОС и СОВ.

№3. Чему равна сумма смежных углов?

№4. Один из смежных углов равен 48. Найди другой.

№5. Что ты узнал о вертикальных углах? Построй вертикальные углы, если один из них равен 60. Найди все получившиеся на рисунке углы.

Г-7ИДЗл-6 Перпендикулярные прямые

№1. Прочитай п.12-13. Выучи ответы на вопросы:

1. Какие прямые называются перпендикулярными?

2. Что можно сказать о двух прямых, перпендикулярных третьей прямой?

3. Какими приборами измеряют прямые углы на местности?

№2. Построй прямые а, в, с, если известно, что а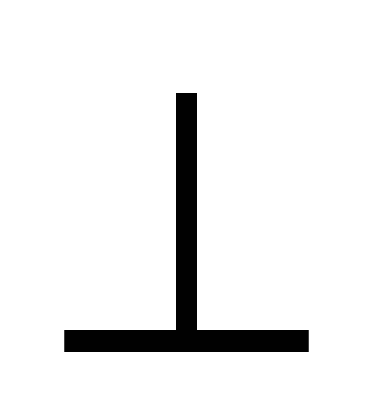в, вс.Пересекаются ли прямые а и с?

№3. Один из углов больше другого в 2 раза. Могут ли эти углы быть вертикальными? Почему?

№4. Повтори п.11.

Г-7ИДЗл-7 Подготовка к контрольной работе по теме «Начальные геометрические сведения»

№1. Ответь на вопросы для повторения к главе I на стр. 25-26 учебника, повторяя пп. 1-13.

№2. Угол 1 на рисунке равен 35.

Найди углы 2,3,4. 1 2

№ 3. Реши задачи № 75 и № 82а из учебника.

4 3

Г-7ИДЗл-8 Первый признак равенства треугольников

№1. Повтори п.14.

№2. 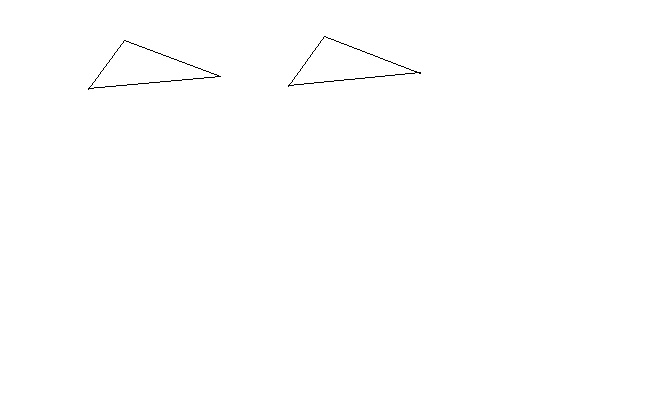Известно, что треугольники АВС и МРК равны. При этом АВ = 12см, МК = 27 см, М = 50. Найдите МР, АС, А. Запиши ответ.

В Р

А С М К

№3. Прочитай п. 15. Выучи, что называется теоремой. Выучи теорему – первый признак равенства треугольников. Запомни, что признаки равенства треугольников применяются для доказательства равенства треугольников.

№4. Реши задачу № 94, используя 1 признак равенства треугольников.

Г-7 ИДЗл-9 Перпендикуляр к прямой.

№1. Прочитай п.16. Делая рисунок в черновике, выучи, что называется перпендикуляром к прямой.

№2. Начерти прямую m. Отметь точку N, не лежащую на прямой m. Проведи из точки N перпендикуляр к прямой m. Обозначь основание перпендикуляра буквой К.

№3. Выучи теорему о существовании и единственности перпендикуляра к прямой.

Можно ли через точку N (см. № 2) провести ещё хотя бы один перпендикуляр к прямой m, отличный от NК? Ответ объясни.

№4. Посмотри на рисунке 58, как надо строить перпендикуляр к прямой. Потренируйся.

№5. Какой из отрезков на рисунке можно считать перпендикуляром к прямой а?

С

а

А В D F

Г-7ИДЗл-10 Медианы, биссектрисы и высоты треугольника

№1. Повтори, что такое середина отрезка и биссектриса угла.

№2. Прочитай п.17. Выучи, что называется медианой треугольника. Построй треугольник АВС. Проведи медиану АМ. Сделай необходимые пометки, чтобы показать, что это медиана.

В

А С

№3. Выучи, что называется биссектрисой треугольника. Проведи в треугольнике АВС биссектрису СК. Также сделай пометки на рисунке.

№4. Выучи, что называется высотой треугольника. Проведи в том же треугольнике АВС высоту ВТ. Сделай пометки.

№5. Выучи замечательные свойства медиан, биссектрис и высот треугольника.

№6.В треугольнике МКР отрезок КЕ является биссектрисой и высотой, Р = 40, К=100. Найди углы треугольника РКЕ, предварительно сделав рисунок.

Г-7ИДЗл-11 Свойство углов равнобедренного треугольника

№1. Выучи из п.18, какой треугольник называется равнобедренным. Построй равнобедренный треугольник АВС, укажи его боковые стороны и основание.

№2. Периметр равнобедренного треугольника равен 25 см, боковая сторона – 9 см. Найди основание треугольника.

№3. Выучи, какой треугольник называется равносторонним. Найди периметр равностороннего треугольника, если одна из его сторон равна 6 см.

№4. Выучи теорему о свойстве углов при основании равнобедренного треугольника. Прочитай её доказательство, стараясь понять и запомнить рассуждения. Попробуй доказать теорему самостоятельно.

№5. АС – основание равнобедренного треугольника. А = 42 . Найди С.

Г-7ИДЗл-12 Свойство биссектрисы (высоты, медианы) равнобедренного треугольника.

№1. Повтори п.18. с самого начала. Выучи новую теорему. Разбери её доказательство.

Сформулируй свойства высоты и медианы равнобедренного треугольника. Запомни их.

№2. Биссектриса ВК равнобедренного треугольника АВС, проведённая к основанию АС, равна 8 см. Боковая сторона равна 10 см. Найдите периметр треугольника ВКС, если основание равно 12 см.

№3. Повтори первый признак равенства треугольников.

Г-7 ИДЗл-13 Второй признак равенства треугольников

№1. Прочитай п.19. Выучи теорему- второй признак равенства треугольников. Попытайся понять доказательство сразу. Прочитай доказательство ещё раз внимательно. Попытайся доказать самостоятельно.

№2. Найди равные треугольники, докажи их равенство:

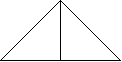
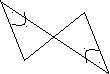Р N Q

T NT=LT

C M E K L

Г-7 ИДЗл-14 Третий признак равенства треугольников

№1. Прочитай внимательно п. 20. Выучи теорему – третий признак равенства треугольников.

№2. Докажи, что отрезок, соединяющий две противоположные вершины прямоугольника, делит его на два равных треугольника. Сделай рисунок, введи обозначения.

№3. В

АВ=ВD, АС=CD. Равны ли треугольники АВС и DВС?

C

А D

Г-7 ИДЗл-15 Окружность

№1. Найди в п. 21, что называется окружностью. Выучи это определение. Построй окружность с помощью циркуля. Обозначь центр окружности О. Проведи диаметр СК, радиус ОМ, хорду ВА. Запомни, что такое хорда, диаметр, радиус.

№2. Проведи окружность с центром О и радиусом 3 см. Выдели на окружности дугу МК.

№3. Диаметр окружности равен 16 см. Чему равен её радиус?

№4. Найди диаметр окружности, если её радиус равен 5см.

Г-7 ИДЗл-16 Построения циркулем и линейкой

№1. Прочитай п.22. Что можно делать с помощью циркуля и линейки?

№2. Начерти отрезок КЕ. Начерти луч ОС. С помощью циркуля отложи от начальной точки луча ОС отрезок, равный отрезку КЕ.

№3. Прочитай в п.23 о том, как отложить от данного луча угол, равный данному. Повтори это решение в тетради, предварительно изобразив угол А и луч ОМ.

Г-7 ИДЗл-17 Примеры задач на построение циркулем и линейкой.

№ 1. Прочитай в п.23 о том, как построить биссектрису угла. Начерти произвольный (любой) угол и построй его биссектрису по указанному в учебнике алгоритму.

№2. Найди в п.23 ответ на вопрос: какую задачу называют задачей о трисекции угла? Имеет ли эта задача решение?

№3. Найди в п.23 соответствующее объяснение и реши следующие задачи:

1. Начерти прямую а. Отметь на ней точку Е. Проведи через точку Е прямую, перпендикулярную прямой а.

2. Начерти отрезок МS. Построй середину этого отрезка – точку С.

Решение более сложных задач. Видеоурок. Геометрия 7 Класс

На этом уроке мы будем решать более сложные задачи по пройденной теме. Вначале повторим аксиому о параллельных прямых и три случая взаимного расположения прямых на плоскости. Также повторим, что такое смежные углы и теорему о сумме смежных углов, что такое вертикальные углы и теорему о равенстве вертикальных углов, что такое перпендикулярные прямые и теорему о двух перпендикулярных прямых, проведенных к третьей. После приступим к решению более сложных задач на повторенный материал.

Вспомним сведения, изученные в текущей теме:

— Аксиома. Через две точки можно провести прямую, и только одну.

— Прямые на плоскости могут пересекаться.

— Пересекающиеся прямые задают два типа углов – смежные и вертикальные.

— Теорема о сумме смежных углов. Сумма смежных углов 180^о.

— Вертикальные углы равны. Если хотя бы один из вертикальных углов 90^о, прямые перпендикулярны.

— Прямые, перпендикулярные другой прямой, не имеют общих точек.

— Прямые могут не иметь общих точек.

— Прямые могут совпадать и иметь бесконечное множество общих точек.

Аксиома гласит, что через две точки (разные точки, которые не совпадают друг с другом) можно провести прямую, и только одну. 

                                

Рис. 1. Рисунок к аксиоме о точках и прямой

Прямые на плоскости могут иметь три варианта расположения. Они могут пересекаться. В таком случае образуются смежные и вертикальные углы.

На рисунке 2 изображены 4 пары смежных углов 1 и 2, 2 и 3, 3 и 4, 4 и 1.

        

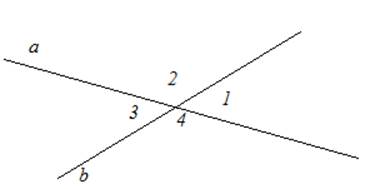
Рис. 2. Смежные и вертикальные углы

Известно, что сумма смежных углов 180^о.

Также на рисунке изображены вертикальные углы: 1 и 3, 2 и 4. Вертикальные углы равны между собой. 

Второй случай расположения прямых – прямые не имеют общих точек. В данной теме мы рассматривали этот факт в следующем контексте: прямые, перпендикулярные другой прямой, не имеют общих точек, что изображено на рисунке 3.

                                         

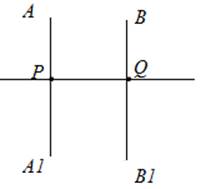
Рис. 3. Перпендикулярные прямые

Третий случай расположения прямых – они совпадают. Таким образом, они имеют бесконечное множество общих точек. По сути, это одна и та же прямая.

Вспомним определение смежных углов. Данные углы имеют общую сторону, а две другие являются продолжением другой. Вертикальные углы являются таковыми, если стороны одного угла являются продолжениями сторон для другого. Вертикальные углы равны.

Частный случай смежных и вертикальных углов – все подобные углы равны 90^о. В таком случае прямые, образующие эти прямые, называются перпендикулярными.

Рассмотрим некоторые задачи:

Пример 1: Три прямые пересекаются в одной точке. Найдите сумму углов ∠1 + ∠2 + ∠3 и  ∠4 + ∠5 + ∠6.

Решение:

                                     

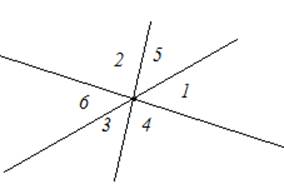
Рис. 4. Чертеж к примеру 1

∠2 = ∠4 как вертикальные. Следовательно, ∠1 + ∠2 + ∠3 = ∠1 + ∠4 + ∠3 = 180^о, так как они образуют развернутый угол. ∠5 = ∠3 как вертикальные, поэтому ∠4 + ∠5 + ∠6 = ∠4 + ∠3 + ∠6 = 180^о.

Ответ: 180^о.

Пример 2: При пересечении двух прямых образовались два угла, один из которых на 60^о больше другого. Найдите эти углы.

Решение:        

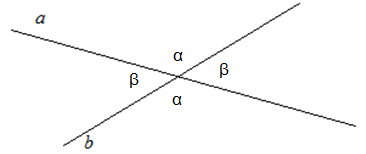
Рис. 5. Чертеж к примеру 2

Исходя из того, что сумма углов α и β равна 180^о, как смежных, а угол α на 60^о больше, чем β, составим и решим систему уравнений:

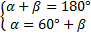
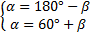
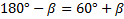
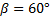
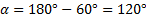
Ответ: Данные углы равны 60 ^о, 60 ^о, 120 ^о, 120 ^о.

Пример 3: Из точки О проведены лучи ОА, ОВ и ОС, причем ОВ⊥ОА. Угол, образованный биссектрисами углов ∠АОВ и ∠ВОС, равен 75^о. Найдите углы ∠АОВ, ∠ВОС и ∠АОС.

Решение:

              

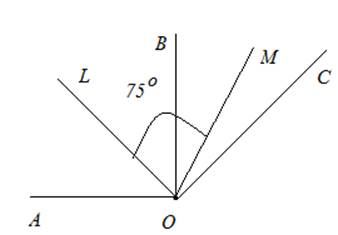
Рис. 6. Чертеж к примеру 3

Пусть угол ∠АОВ = α, тогда угол ∠LOB = ∠LOA = 45^o =  (так как LO – биссектриса). Аналогично ∠СОВ = β, тогда угол ∠МOB = ∠МOС = 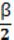. Получается, что ∠LOM = ∠LOB + ∠BOM =  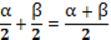= 75^o. Отсюда .

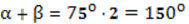∠АОС = α + β = .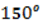

∠ВОМ = ∠ВОС = 60^о.

Ответ: 90^о, 60^о, 150^о.

Пример 4:  Из точки О проведены лучи ОА, ОВ и ОС, причем ОВ⊥ОА. Лучи ОL и ОМ – биссектрисы углов ∠АОВ и ∠ВОС. Доказать, что ∠AOС = 2∠LOM.

Решение:

                              

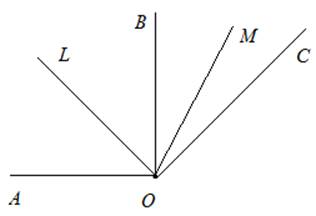
Рис. 7. Чертеж к примеру 4

Обозначим угол ∠ВОС = α, ∠АОВ = β. ∠ LOA = ∠LOВ = 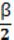 (ОL – биссектриса). ∠МОВ = ∠МОС = . ∠ LOM = ∠МОВ + ∠LOВ = . ⇒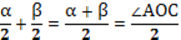

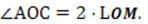
Доказано.

 

Рекомендованные ссылки на интернет-ресурсы

1. Геометрические задачи (Источник).
2. Обобщающий урок по геометрии в 7-м классе (Источник).
3. Прямая линия, отрезок (Источник).

 

Рекомендованное домашнее задание

1. № 13, 17. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А.  – М.: Просвещение, 2010.
2. В результате пересечения двух прямых образовалось 4 угла, каждый из которых меньше развернутого. Найдите эти углы, если их градусные меры относятся как 5:1.
3. Правильно ли утверждать, что перпендикуляром к прямой называется любой отрезок, перпендикулярный данной?
4. * Один из смежных углов в два раза больше разности между ними. Определите эти углы.

Практика. Решение задач. Треугольники. Видеоурок. Геометрия 7 Класс

На этом уроке мы потренируемся решать различные задачи, в которых встречаются треугольники.

Согласитесь: одно дело смотреть, как кто-то ездит на велосипеде, и совсем другое – попробовать ездить самому. Практика помогает не только закрепить умения и, если нужно, довести их до автоматизма, но и приобрести решительность в своих действиях.

Мы уже обладаем достаточно большим арсеналом геометрических инструментов – аксиом, определений, теорем. Но этими инструментами необходимо научиться пользоваться. Этим сейчас мы с вами и займемся.

 

Задачи на соотношение сторон и углов в треугольнике

Прежде чем приступить к решению задач, сделаем еще одно важное замечание: чтобы научиться ездить на коньках по кругу и не падать, достаточно сходить на каток несколько раз, а чтобы стать олимпийской чемпионкой, нужно тренироваться 6 дней в неделю. Все это применимо и к математике. Тем, кто не собирается в дальнейшем связывать свою жизнь с математикой, достаточно решать небольшое количество задач для того, чтобы отработать несложные навыки и уметь применять их на практике.

Тем же, кто захочет углубиться в изучение математики и планирует выбрать профессию, которая с ней связана, нужно решать много самых разных задач, чтобы довести некоторые навыки до автоматизма.

Задача 1

Построить треугольник с периметром 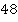 и соотношением длин сторон .

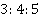Решение

Вспомним, что периметр – это сумма длин сторон треугольника.

Зная только периметр, построить треугольник не получится. Почему? Потому что с одним и тем же периметром существует бесконечное множество разных, не похожих друг на друга треугольников (см. рис. 1).

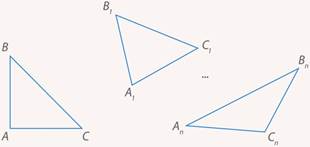
Рис. 1. Различные треугольники, имеющие один и тот же периметр

Но мы знаем соотношение сторон, т. е. его форму. Значит, сможем решить задачу. Для этого нам нужно сначала найти стороны этого треугольника.

Такую задачу мы уже много раз решали. Есть три величины, известна их сумма (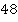) и соотношение: 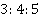. Вспомним, что если величины относятся как 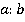, то их можно обозначить как  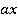и 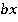. Для трех величин все аналогично: длины сторон относятся как 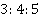, можем обозначить их как:

, ,

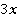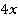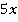
По условию их сумма (периметр) равна :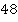

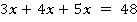
Решаем полученное уравнение:

Решение прикладных задач «Задачи с геометрическим содержанием» 7 класс

Тема: Задачи с геометрическим содержанием

Дата проведения: 14.12.2016 год

Класс: 7

Цели:

1. усилить практическую направленность изучения геометрии, конструкторские навыки

2. повышать интерес, мотивацию и, как следствие, эффективность изучения геометрии

3. учиться ведению логически строгого доказательства, формировать представления о соотношениях размеров объектов и связанных с ними геометрических величин

4. способствовать самореализации и самосовершенствованию каждого ученика

Оборудование:

1. карточки с заданиями

2. наглядные иллюстрации к задачам

3. сборники геометрических заданий

4. бумага, ножницы для практических экспериментов

Этапы занятия:

1. Организационные моменты (1 мин)

2. Разминка (5 мин)

3. Разбор интересных задач на проведение линий, разбиение фигур, перекраивания (15 мин)

4. Решение задач с геометрическим содержанием на развитие функциональной грамотности (20 мин)

5. Творческое домашнее задание (2 мин)

6. Подведение итогов занятия (2 мин)

Ход занятия:

1 этап. (Организационный)

Учитель: – Для работы разобьемся на группы, чтобы вам было интереснее работать с товарищами. Постарайтесь быть активными, полезными для своей команды. Вносите свои предложения, прислушивайтесь к мнению других.
(Класс разбивается на группы, в составе которых оказываются учащиеся с разной математической подготовкой. Это необходимо для того, чтобы каждый нашел себе применение, и «слабый» имел возможность тянуться за «сильным»)

II этап. Разминка

1. Задача «Посчитаем квадратики»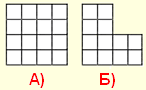

На рисунке А можно увидеть больше квадратиков, чем на рисунке Б.

На сколько?

Ответ: 30-17=13
2. Задача «Садовник»

У садовника имеется 32 м провода, которым он хочет обозначить на земле границу клумбы. Форму клумбы ему надо выбрать из следующих вариантов.

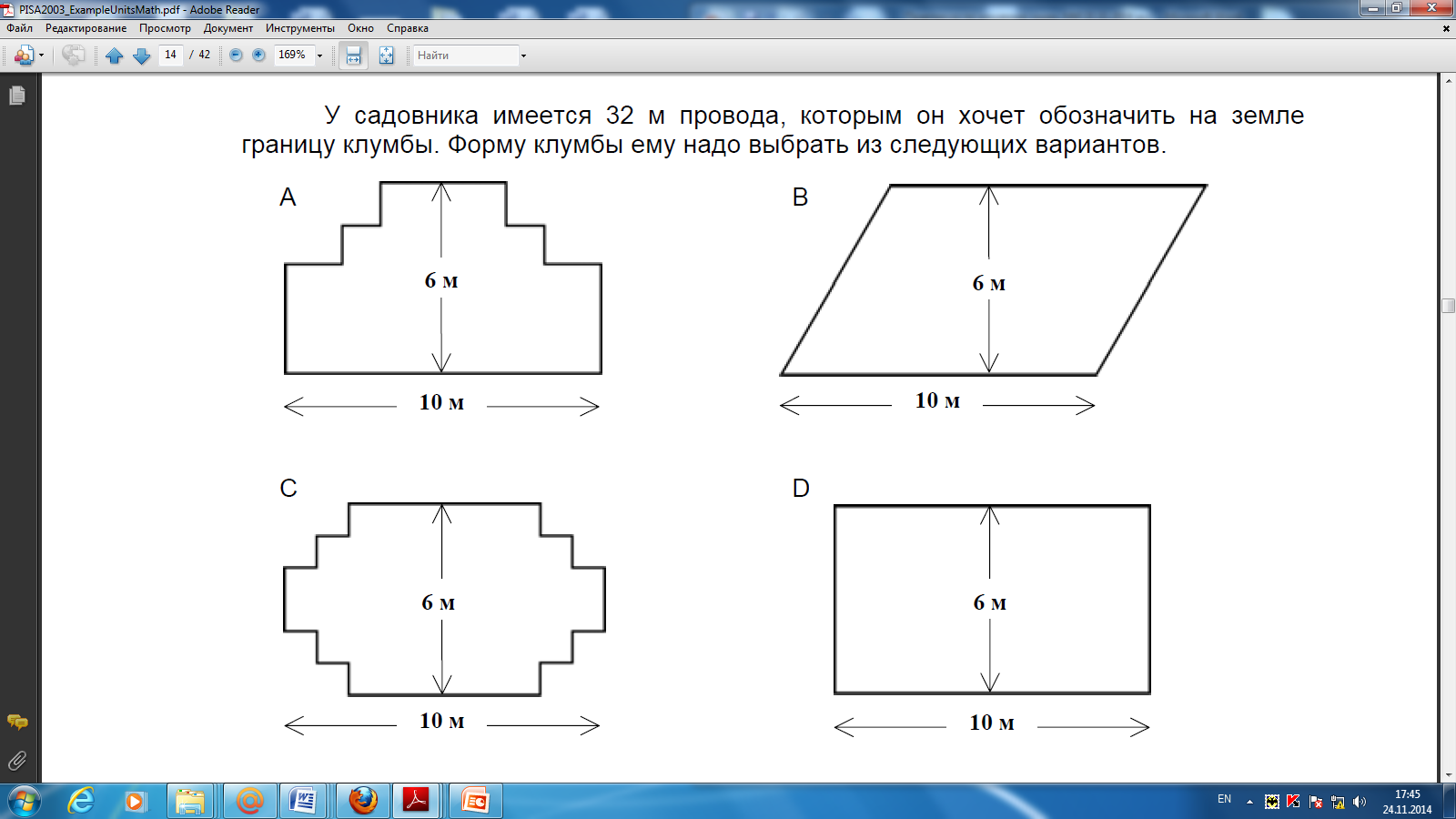
Обведите слово «Да» или «Нет» около каждой формы клумбы в зависимости от того, хватит или не хватит садовнику 32 м провода, чтобы обозначить ее границу.

Форма клуба

Хватит ли 32 м провода, чтобы обозначить границу клумбы?

Форма А

Да / Нет

Форма В

Да / Нет

Форма С

Да / Нет

Форма D

Да / Нет

Оценка выполнения:

Форма A Да.

Форма B Нет.

Форма C Да.

Форма D Да.

Задача 3. Изображенную на рисунке фигуру требуется разделить на 6 частей, проведя всего лишь 2 прямые. Как это сделать?

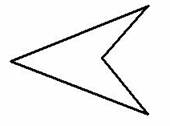
III этап. Разбор интересных задач на проведение линий, разбиение фигур, перекраивания.

Задача 4.

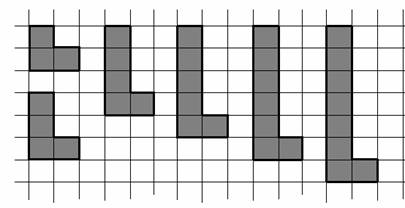
Как из набора «уголков» сложить прямоугольник?
Решение:
Подсчитаем, какую площадь займут все «уголки» 3+4+5+6+7+8=11*3=33. Значит, стороны прямоугольника могут быть равны 3 и 11. Остается заполнить прямоугольник 3*11 данными «уголками». Например, как на рисунке:

Задача 5.
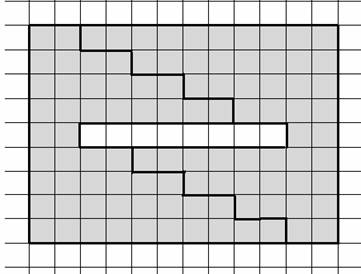
Разрежьте фигуру на две части и сложите из них квадрат.

Вопросы для обсуждения:
– Какова площадь первоначальной фигуры?
12*9-8=108-8=100
– Значит, сложив части, мы получим квадрат размером 10*10.
– На сколько нужно увеличить сторону длиной 9 клеток и на сколько уменьшить другую сторону? (на 1 и на 2)
Вариант разрезания:

Задача 6.

Мальчик укладывает книги в прямоугольную коробку. Все книги одинакового размера. Какое максимальное количество книг, которое полностью заполнит коробку?

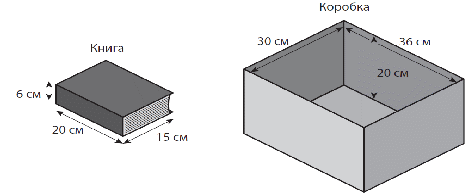
Ответ: 12

Предложенное задание соответствует учебной программе 5-7 класса теме «Объём прямоугольного параллелепипеда». Однако невысокий процент выполнения данного задания связан, возможно, с некоторыми затруднениями, которые вызывают у школьников решение задач на совместное применение двух объёмов прямоугольных параллелепипедов.

IV этап. Решение задач на развитие функциональной грамотности

Задача 7. Чему равна площадь прямоугольника, длина которого 10 см, а ширина в 2 раза меньше?

Отметь правильный ответ.

А.15 см² Б.30 см² В.50 см² Г.80 см²

Ответ: В

Комментарий. Стандартное задание на применение формулы площади прямоугольника.

Задача 8. Все стороны прямоугольника уменьшили в 2 раза. Во сколько раз уменьшилась площадь прямоугольника?
Отметь правильный ответ.
А. в 2 раза Б. в 4 раза В. в 8 раз
Г. Для ответа не хватает данных о длине сторон исходного прямоугольника

Ответ: Б

Комментарий. В этом задании отсутствие конкретных размеров прямоугольника не позволяет получить результат прямым вычислением с использованием формулы площади прямоугольника. Необходимо либо провести рассуждение общего характера, либо провести формальное преобразование буквенного выражения, либо построить графическую (геометрическую) модель. В любом случае это требует содержательного анализа предметной ситуации. Кроме того отсутствие конкретных размеров прямоугольника провоцирует некоторых детей выбрать ответ Г.

Задача 9. Известно, что площадь квадрата со стороной b в 4 раза больше площади квадрата со стороной а (см. чертеж).

Найди а

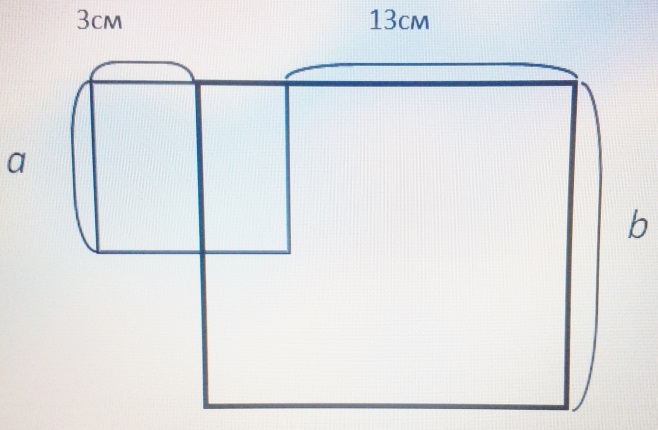
Ответ: а=в:2

Комментарий. В этом задании связь между сторонами а и в не очевидна. Чтобы её увидеть, надо преобразовать чертёж: сдвинуть маленький квадрат так, чтобы его стороны легли на стороны большого квадрата, то есть вправо.

Задача 10. Шоколад и Поварята

Пять Маленьких Поварят решили разделить между собой большую прямоугольную шоколадку.

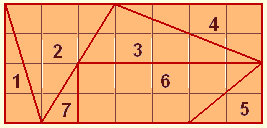
Но она упала на пол и когда они развернули ее, то увидели, что шоколадка разбилась на 7 кусков.

Николай съел самый большой кусок.
Света и Маша съели одно и тоже количество шоколада, но Света съела три куска, а Маша только один кусок.

Белла съела 1/7 часть целой шоколадки, и Катя съела все остальное.

Какой кусок шоколадки достался Кате?

Решение: Самый большой съел Николай ,№6, Далее посчитал количество полных квадратиков в плитке-28, и в каждом куске:№1=2квадр.,№2=6кв.№3=5 кв,№4=4кв,№5=2кв.,№7=1кв. Значит Белла1/7=28/7=4, Белла съела №4,Света=Маша, поэтому №1+№5+№7(5квадратиков)=№3(5квадр), Остаётся Катя съела №2.

Задача 11. Одеяло для Гулливера

Жители страны Лиллипутия сделали одеяло для Гулливера из разных кусков материала, который был у них под рукой.

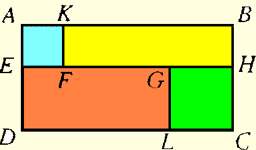
Чему равна площадь одеяла прямоугольной формы ABCD если:

• площадь куска квадратной формы AEFK — 4 единицы площади,

• площадь куска квадратной формы GHCL — 9 единиц площади,

• точки E, F, G, и H лежат на одной прямой,

• и длина отрезка FG равна 5-ти единицам длины.

Решение: раз площадь куска квадратной формы AEFK — 4 единицы площади то значит линия АК равна 2 единицам площади + и длина отрезка FG равна 5-ти единицам длины и + площадь куска квадратной формы GHCL — 9 единиц площади значит отрезок GH равен з единицы длинны итого 5+2+3=10 единиц длины зная это мы складываем отрезки АЕ ( 2 единицы длинны ) и НК ( з единицы длинны )и получаем 5 единиц длинны потом умножаем полученные числа и получаем 50 Ответ 50.

Задача 12. Геометрия на шахматной доске

У нас была квадратная доска, подобная шахматной.

На каждую клетку по краям этой доски и на каждую клетку одной из диагоналей мы поставили по одной шахматной фигуре.

Нам для этого понадобилось 64 фигуры.

Сколько пустых клеток все еще осталось на этой доске? (132; 196; 208; 225)

Решение: Взять ответы и прибавить к ним 64. Чтобы получился квадрат — надо чтобы стороны были равны. То есть количество клеток одинаково у каждой стороны. 132+64= 196, 196+64=250,208+64=272, 225+64=289. Только при количестве клеток 196 получится квадрат (стороны по 14 клеток). Значит ответ — 132

Задача 13. Посчитаем плитки

Человек прикинул в уме, что он может выложить пол комнаты, имеющей квадратную форму, квадратной плиткой, и что ему не понадобится ни одну из них разрезать.

Сначала, он положил плитки по краям комнаты, и на это у него ушло 56 плиток.

Найдите, сколько всего ему надо иметь плиток, чтобы покрыть весь пол. Чему равна сумма цифр этого числа?

Решение: 56-4=52, 52:4=13, 13+2+15, 15*15=225, 2+2+5+9. Ответ: 9.

Задача 14.

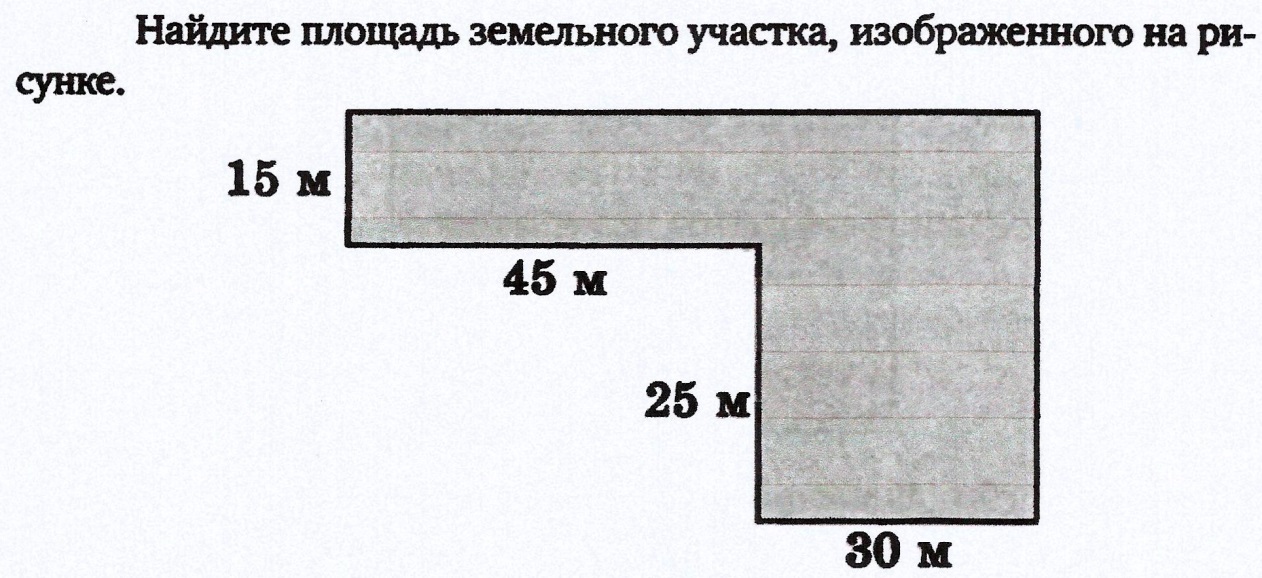
Решение:

 

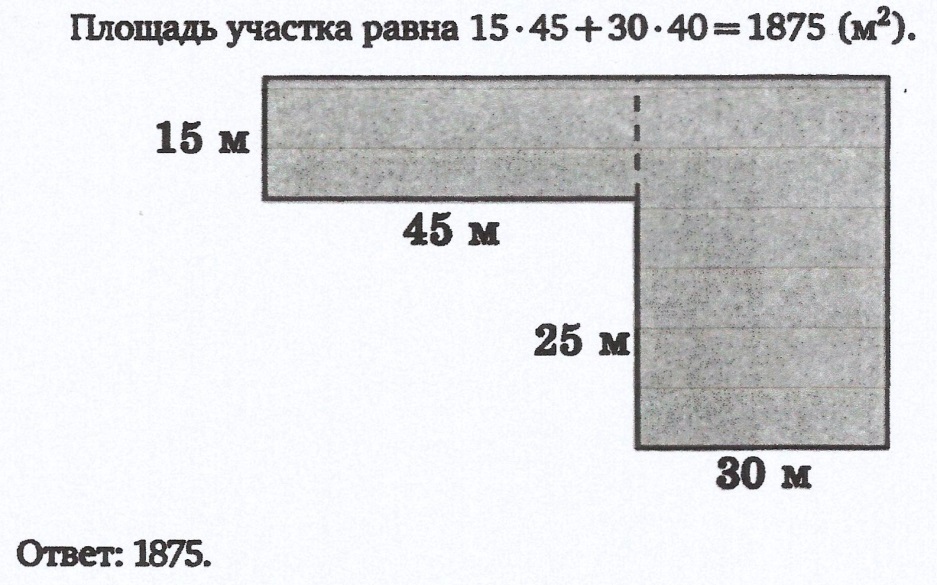
V этап. Творческое домашнее задание

На прямоугольном заводском дворе размером 150 м x 110 м, загруженном строениями, хотят разбить круглый газон радиусом 5 м. Там стоят 10 складов, размеры которых 20×20 м, 4 цеха размером 40м x 10 м и круглое бензохранилище радиуса 10 м. Докажите, что можно разбить этот газон вне зависимости от расположения строений.

VI этап. Подведение итогов занятия.

1. Узнали ли вы сегодня на занятии что-то новое? Что именно?

2. Понравилась ли вам работа в группах? Какую роль в группе играли вы? (Активно обсуждал, предлагал идеи, слушал других, старался не привлекать к себе внимания и т.п.)

3. Какие интересные элементы можно добавить в организацию занятия?

Ответы ребят помогут учителю оценить проведенное занятие, спланировать дальнейшую работу.

Задание 15, 16 (при наличии времени)

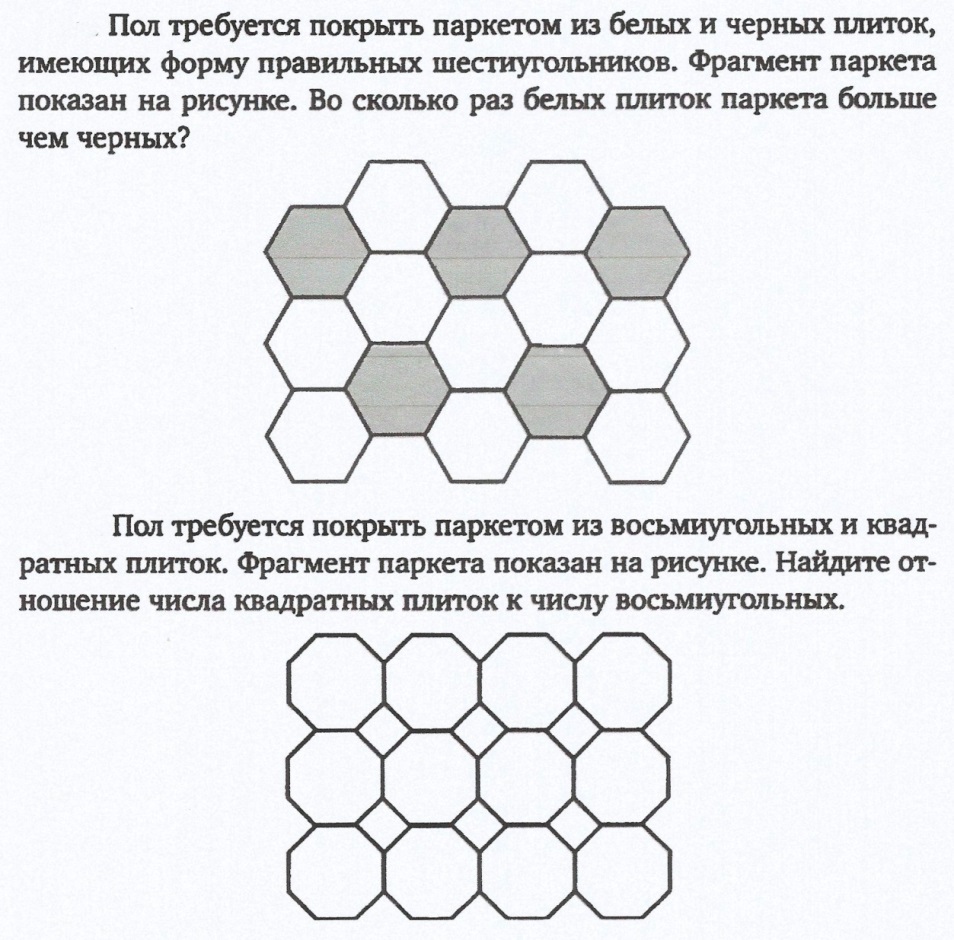
Ответ: 2. В каждой вертикальной полоске паркета на одну черную плитку приходится две белых. Таким образом, белых плиток паркета в два раза больше, чем черных.

Ответ: 1. На каждую восьмиугольную плитку приходится одна квадратная. Отношение числа квадратных плиток к числу восьмиугольных равно 1.