Тренировочные задания на решение квадратных уравнений 8 класс
Квадратные уравнения 8 класс алгебра
Учитель: Федулкина Т.А.
- Что такое квадратные уравнения. Виды уравнений.
Формула квадратного уравнения: ax2+bx+c=0,где a≠0, где x — переменная, a,b,c — числовые коэффициенты.
Пример полного квадратного уравнения:
3x2-3x+2=0
x2-16x+64=0
Решение полных квадратных уравнений сводится к нахождению дискриминанта:
Формула дискриминанта: D=b2-4aс
Если D>0, то уравнение имеет два корня и находим эти корни по формуле:
Если D=0, уравнение имеет один корень
Если D<0, уравнение не имеет вещественных корней.
№1 x2-x-6=0
Записываем сначала, чему равны числовые коэффициенты a, b и c.
a=1,b=-1,c=-6
D=b2-4ac=(-1)2-4∙1∙(-6)=1+24=25
Дискриминант больше нуля, следовательно, у нас два корня, найдем их:
Ответ: x1=3; x2=-2
№2 x2+2x+1=0
Записываем, чему равны числовые коэффициенты a,b и c.
a=1,b=2,c=1
D=b2-4ac=(2)2-4∙1∙1=4-4=0
Дискриминант равен нулю, следовательно, один корень:
x=-b/2a=-2/(2∙1)=-1
Ответ: x=-1
№3 7x2-x+2=0
Записываем, чему равны числовые коэффициенты a,b и c.
a=7,b=-1,c=2
D=b2-4ac=(-1)2-4∙7∙2=1-56=-55
Дискриминант меньше нуля, следовательно, корней нет.
Рассмотрим неполное квадратное уравнение:
ax2+bx=0, где числовой коэффициент c=0.
Пример как выглядят такие уравнения: x2-8x=0, 5x2+4x=0.
Чтобы решить такое уравнение необходимо переменную x вынести за скобки. А потом каждый множитель приравнять к нулю и решить уже простые уравнения.
ax2+bx=0 x(ax+b)=0 x1=0 x2=-b/a
№1 3x2+6x=0
Выносим переменную x за скобку,
x(3x+6)=0
Приравниваем каждый множитель к нулю,
x1=0 3x+6=0 3x=-6 x2=-2
Ответ: x1=0; x2=-2
№2 x2-x=0
Выносим переменную x за скобку,
x(x-1)=0
Приравниваем каждый множитель к нулю,
x1=0
x2=1
Ответ: x1=0; x2=1
Рассмотрим неполное квадратное уравнение:
ax2+c=0, где числовой коэффициент b=0
Чтобы решить это уравнение, нужно записать так:
x2=c/a , если число c/a будет отрицательным числом, то уравнение не имеет решения.
А если c/a положительное число, то решение выглядит таким образом: корень квадратного уравнения
№1 x2+5=0
x2=-5, видно, что -5<0, значит нет решения.
Ответ: нет решения
№2 3x2-12=0
3x2=12
x2=12/3
x2=4
x1=2
x2=-2
Ответ: x1=2; x2=-2
2) Тренировочные задания на решение квадратных уравнений 8 класс алгебра.
Задания для устного решения:
- Решите неполное квадратное уравнение:
1) | 6) | 11) | 16) |
2) | 7) | 12) | 17) |
3) | 8) | 13) | 18) |
4) | 9) | 14) | 19) |
5) | 10) | 15) | 20) |
- Решите квадратное уравнение, используя теорему Виета:
1) | 6) | 11) | 16) |
2) | 7) | 12) | 17) |
3) | 8) | 13) | 18) |
4) | 9) | 14) | 19) |
5) | 10) | 20) |
- Решите квадратное уравнение, используя формулу :
1) | 6) | 11) | 16) |
2) | 7) | 12) | 17) |
3) | 8) | 13) | 18) |
4) | 9) | 14) | 19) |
5) | 10) | 15) | 20) |
- Найдите дискриминант квадратного уравнения по формуле D= :
1) | 6) | 11) | 16) |
2) | 7) | 12) | 17) |
| 3) | 8) | 13) | 18) |
4) | 9) | 14) | 19) |
5) | 10) | 15) | 20) |
- Сколько корней имеет квадратное уравнение, если D= равно:
1) | 6) | 11) | 16) |
2) | 7) | 12) | 17) |
3) | 8) | 13) | 18) |
4) | 9) | 14) | 19) |
5) | 10) | 15) | 20) |
- Решите квадратное уравнение:
1) | 6) | 11) | 16) |
2) | 7) | 12) | 17) |
3) | 8) | 13) | 18) |
4) | 9) | 14) | 19) |
5) | 10) | 15) | 20) |
скачать файл
Дата публикации — 03.12.2017
Урок алгебры 8 класс по теме » Решение квадратных уравнений по формуле»
Северо – Казахстанская область
Айыртауский район
КГУ « Всеволодовская неполная средняя школа»
Открытый урок
алгебры«Формула корней квадратного уравнения.»
8 класс
Учитель
математики и физики
Брыкина Лариса Васильевна
2015 год
Тема: Формулы корней квадратного уравнения
Содержательная цель: повторение и закрепление умений и навыков решения квадратных уравнений .
Деятельностная цель: формировать умения сравнивать, выделять главное в изучаемом материале, обобщать, формировать навыки самостоятельной работы, коммуникативные навыки.
Задачи:
Способствовать формированию умений применять на практике полученные знания
Развивать логическое мышление, память, внимание, математическую речь
Воспитывать активность, трудолюбие, взаимоуважение
Тип урока: урок систематизации и обобщения знаний
Используемые технологии: урок построен в технологии деятельностного метода с использованием ИКТ технологий..
Методы обучения: наглядные, практические, самостоятельная работа.
Формы работы: фронтальная, индивидуальная, групповая.
Оборудование: персональные компьютеры, презентация к уроку, раздаточный материал, музыкальное сопровождение, дополнительная информация (эпиграф, словарь Ушакова), черный ящик, индивидуальные листы контроля.
Ход урока.
Организационный момент.
Добрый день! Добрый час!
Я очень рада видеть вас.
Прозвенел уже звонок
Начинается урок.
Улыбнулись, подтянулись
Друг на друга посмотрели
И тихонько дружно сели.
Мотивация к учебной деятельности. Постановка целей и задач урока.(Слайды 1-6)
На доске висят высказывания «Зри в корень», «Корень зла», «Корень учения горек, да плод его сладок»
Внимание! Черный ящик! Угадайте, что в ящике. Даю три определения этому предмету:
1. Непроизводная основа слова.
2. Число, которое после подстановки его в уравнение обращает уравнение в тождество.
3. Один из основных органов растений.
Что общего между высказываниями и предметом в черном ящике? (Речь идет о слове корень.)
С каким математическим понятием связан этот предмет. О чем пойдет речь на уроке? /об уравнениях/
«Уравнение — это золотой ключ, открывающий все математические сезамы»
С. Коваль.
Как понимаете слово сезам? В переводе с арабского —«тайна». Тайну квадратных уравнений мы продолжаем открывать и сегодня на уроке.
— Какие цели необходимо поставить перед собой? (повторить и закрепить умения решать квадратные уравнения)
— Каждый из вас имеет получить оценку за урок по результатам работы на различных этапах. Для этого у вас на партах лежат карты результативности, в которые вы будете фиксировать свои успехи. Для ответа на поставленный вопрос вы поднимаете руку и ни в коем случае не перебиваете друг друга. Желаю всем удачи.
3.Актуализация опорных знаний. Презентация
1.Разминка ( каждый правильный ответ 2 балл).(Слайды 7 -21)
(уравнение второй степени называется квадратным уравнением)
(уравнение вида ах2+bx+c=0, где а, b и с – любые действительные числа, причем а≠ 0, х – переменная, называется квадратным уравнением)
Перечислите виды квадратных уравнений. (полные, неполные, приведенные)
Какое квадратное уравнение называется приведенным? (квадратное уравнение называется приведенным если а = 1 и имеет вид х2 + рх + q = 0).
Назовите формулу для нахождений дискриминанта квадратного уравнения?
От чего зависит количество корней квадратного уравнения? (кол-во корней квадратного уравнения зависит от дискриминанта D)
Сколько корней имеет квадратное уравнение, если D больше 0? (при D > 0, уравнение имеет два корня)
Сколько корней имеет квадратное уравнение, если дискриминант меньше 0 (при D < 0, уравнение не имеет корней)
2.Тест “Виды квадратных уравнений” С помощью сигнальных карточек.
Среди данных уравнений укажите:
полные квадратные уравнения
неполные квадратные уравнения
приведенные квадратные уравнения
неквадратные уравнения
1) х4 + 5х2 +3 = 0
2) 6х2 + 9 = 0
3) х2 – 3х = 0
4) –х2 + 2х +4 = 0
5) 3х + 6х2 + 7 =0
— Молодцы. С видами квадратных уравнений мы разобрались. Кстати, а вы знаете, когда появились первые квадратные уравнения?
4.Историческая справка ( Слайды 22 -27)
Первые упоминания о способах решения уравнений, которые мы сейчас называем квадратными, относятся во второму тысячелетию до н.э.
Это эпоха расцвета Вавилона и Древнего Египта.
Квадратные уравнения впервые встречаются в работе индийского математика и астронома Ариабхатты.
Другой индийский ученый Брахмагупта (VII в) изложил общее правило решения квадратных уравнений, которое практически совпадает с современным.
В 1202 году итальянский ученый Леонардо Фибоначчи изложил формулы квадратного уравнения. И лишь в 17 веке, благодаря Ньютону, Декарту и другим ученым, эти формулы приняли современный вид. 
— Ребята, а с каким еще понятием мы постоянно сталкиваемся при решении квадратных уравнений? (С дискриминантом)
— А вот понятие Д придумал английский ученый Сильвестр, он называл себя даже “математическим Адамом” за множество придуманных терминов.
А зачем он нам нужен?(Он определяет число корней квадратного уравнения)
— Итак, давайте еще раз проговорим алгоритм решения полного квадратного уравнения.
( Слайд 28)
АЛГОРИТМ решения квадратных уравнений

Выделить в уравнении коэффициенты: a,b,c
 Вычислить дискриминант по формуле и определить количество корней:
Вычислить дискриминант по формуле и определить количество корней:
Если D<0, то уравнение не имеет действительных корней.
 Если D=0, то уравнение имеет один действительный корень и вычислить его можно по формуле.
Если D=0, то уравнение имеет один действительный корень и вычислить его можно по формуле.
Первый шаг в алгоритме решения квадратных уравнений – это правильное нахождение коэффициентов уравнения.
Решение задач.
Вариант 1
Фамилия_____Адинец Сергей_________________
Заполните таблицу.
Уравнение
Коэффициенты
а
в
с
3х2+2х+4=0
3
2
4
-3х2+7х-4=0
-3
7
-4
х2-х+1=0
1
-1
1
2х2-9=0
2
0
-9
Вариант 2
Фамилия_______Жежеря Карина_______________
Заполните таблицу.
Уравнение
Коэффициенты
а
в
с
9х2-х-8=0
9
-1
-8
-5х2+2х+3=0
-5
2
3
7х2-8х+1=0
7
-8
1
5х2-19=0
5
0
-19
Вариант 3
Фамилия______Молдагулов Руслан________________
Заполните таблицу.
Уравнение
Коэффициенты
а
в
с
2х2-3х+1=0
2
-3
1
-х2-5х-6=0
-1
-5
-6
25х2-10х+1=0
25
-10
1
2х2=0
2
0
0
Вариант 4
Фамилия_______Петраш Дмитрия_______________
Заполните таблицу.
Уравнение
Коэффициенты
а
в
с
2х2-5х+10=0
2
-5
10
-2х2-3х+1=0
-2
-3
1
х2+х+2=0
1
1
2
х2-5х=0
1
-5
0
Вариант 5
Фамилия_______Шайкеновой Алины_______________
Заполните таблицу.
Уравнение
Коэффициенты
а
в
с
2х2-3х-5=0
2
-3
-5
-х2+4х+5=0
-1
4
5
-х2+ 2х-7=
-1
2
-7
х2-16=0
1
0
-16
Проверку осуществляют приглашенные эксперты.
А для тех кто закончил работу раньше есть возможность заработать дополнительные баллы ( 2 балла), выполнив на доске задание:
Составьте квадратные уравнения, если известны их коэффициенты:
а=3, b=8, c=2;
а=1, b=0, c= -1;
а=5, b=0,5, c= -3;
Ответы: 3х2+8х+2=0
х2 -1=0
5х2+0,5х-3=0
Физминутка.
7.Закрепление пройденного материала.
— Ну что ж, приступим к практической части нашего урока.
Решение уравнений у доски и в тетради. ( Слайды 31 – 36)
Выбирают уравнение учащиеся сами по уровню сложности.
Чтобы решить уравнение,
Корни его отыскать.
Нужно немного терпения,
Ручку, перо и тетрадь.
Д=1 + 120 = 121
Х1 =(-1+11):10 = 1
Х2 =(-1-11):10 = -1,2
Д=16 + 20 = 36
Х1 =(-4+6):12= 1/6
Х2 =(-4-6):12= -5/6
D = 25 – 24= 1,
Х1 =(5+1):2= 3
Х2 =(5- 1):2= 2
D = 4 + 60 = 64,
x1 = (2+8):2=5,
x2 = (2-8):2=-3.
D = 9 – 48 = –39, корней нет;
8. Самостоятельная работа.
— Хорошо. Вместе мы поработали. Теперь посмотрим, как вы умеете работать самостоятельно. Вам предлагается трехуровневая работа.
Если вы еще не уверены в своих силах и желаете закрепить решение уравнение, то выбираете уровень А (3 балла).
Если считаете, что материал усвоен хорошо – В (6 баллов).
Ну, а если желаете испробовать свои силы на более сложных заданиях – уровень С (10 баллов) для вас.
В процессе решения я проверяю ваши работы и проставляю заработанные баллы.
Уровень А.
№1 Продолжите вычисление дискриминанта D квадратного уравнения ax2 + bx + c = 0 по формуле D = b2 — 4ac. ( 2 балла)
5х2 — 7х + 2 = 0
D = b2 — 4ac = (-7)2 – 4· 5 · 2 = …; (9)
№2. Закончите решение уравнения 3х2 — 5х – 2 = 0. ( 2 балла)
D = b2 — 4ac = (-5)2— 4· 3·(-2) = 49;
х1 = … 2 х2=…-1/3
Уровень В.
Решите уравнение:
а) 6х2 – 4х + 32 = 0; ( 4 балла) Д=16-768 = -752 – решений нет
б) х2 + 5х — 6 = 0. ( 4 балла) Д= 25 +24 = 49 х = 1 и -6
Уровень С. Решите уравнение: (3х — 1)(х + 3) = х + 5х2 ( 10 баллов)
-2х2 + 7х-3=0 Д= 49-24= 25 х =1/2 и 3
Для тех, кому трудно дается математика, предлагается карточка-информатор.
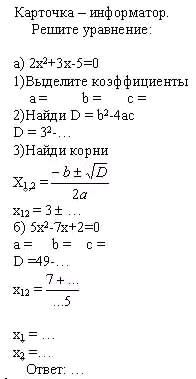
9. Рефлексия. ( Слайды 37-38)
Оцените свою работу на уроке по индивидуальному листу самоконтроля.
Листок самоконтроля: (фамилия, имя )………………………….
Количество баллов
Разминка
Тест « Виды уравнений»
Работа по карточкам «Определить коэффициенты уравнения»
Дополнительное задание
Решение уравнений
Самостоятельная работа.
Итог: (оцените свою деятельность на уроке).
Рефлексия. Как мы сегодня поработали:

Какие новые знания вы добыли?
Чему научились? Цель нашего урока достигнута?
Вы узнали универсальную формулу решения квадратных уравнений. В ее универсальности и заключалась тайна.
11.Домашнее задание. ( Слайды 39 -41)
Выучить п.7, решить №. №№136 (2,4), 137(6,8),134(2,4)
Счастливого пути в поисках новых знаний!
Вариант 1
Фамилия_____Адинец Сергей_________________
Заполните таблицу.
Уравнение
Коэффициенты
а
в
с
3х2+2х+4=0
-3х2+7х-4=0
х2-х+1=0
2х2-9=0
Вариант 2
Фамилия_______Жежеря Карина_______________
Заполните таблицу.
Уравнение
Коэффициенты
а
в
с
9х2-х-8=0
-5х2+2х+3=0
7х2-8х+1=0
5х2-19=0
Вариант 3
Фамилия______Молдагулов Руслан________________
Заполните таблицу.
Уравнение
Коэффициенты
а
в
с
2х2-3х+1=0
-х2-5х-6=0
25х2-10х+1=0
2х2=0
Вариант 4
Фамилия_______Петраш Дмитрия_______________
Заполните таблицу.
Уравнение
Коэффициенты
а
в
с
2х2-5х+10=0
-2х2-3х+1=0
х2+х+2=0
х2-5х=0
Вариант 5
Фамилия_______Шайкеновой Алины_______________
Заполните таблицу.
Уравнение
Коэффициенты
а
в
с
2х2-3х-5=0
-х2+4х+5=0
-х2+ 2х-7=
х2-16=0
Решение квадратных уравнений 8 класс
ПЛАН-КОНСПЕКТ УРОКА по математике 8 класс
«Решение квадратных уравнений»
ФИО: Толстая Дарья Александровна
Место работы: МОУ «СОШ» с. Корткерос
Должность: учитель
Предмет: математика
Класс: 8 класс
Тема и номер урока в теме: «Формулы корней квадратных уравнений»
Учебник: Алгебра А.Г. Мордкович
8. Цель урока: Организация продуктивной деятельности учащихся, направленной на достижение ими:
1) личностных результатов:
уметь слушать другого и понимать его речь;
уметь хорошо говорить и легко выражать свои мысли;
учиться применять свои знания и умения к решению новых проблем;.
Умение формулировать для себя цели
2)метапредметных результатов:
познавательной
информационно-коммуникативной
развитие умений анализировать, аргументировать сделанныйвыбор,
умение вступать в речевое общение, участвовать в диалоге;
приведение примеров, подбор аргументов, формулирование выводов;
отражение в устной и письменной форме результатов своей деятельности
рефлексивной
оценивание своих учебных достижений;
владение навыками само- и взаимоконтроля;
умение ставить личностные цели и оценивать степень их достижения.
3) предметных результатов:
распознавать линейные и квадратные уравнения;
решать квадратные уравнения;
определять наличие корней квадратных уравнений по дискриминанту;
закрепить знания учащихся по теме решения квадратных уравнений;
9.Оборудование.
УМК: Алгебра 8 класс (Мордкович)
Карточки для групповой работы.
Тип урока: урок обобщающего повторения
Формы работы учащихся: групповая, индивидуальная
Необходимое техническое оборудование: компьютер, проектор, экран.
Структура и ход урока
СТРУКТУРА И ХОД УРОКА
Ход урока
Деятельность учителя
Деятельность учеников
Виды формируемых УУД
Познавательная
Коммуникативная
Регулятивная
I. Организационно-мотивационный момент
Приветствует учащихся, проверяет готовность к уроку. Включает проектор, демонстрация презентации.
Приветствуют учителя, проверяют свою готовность к уроку .
2. Мотивация
Обратная связь на уроке осуществляется при помощи диалога учителя и ученика. Заполняем бланк ответов. За каждое верно выполненное задание или верный устный ответ на бланке, вы можете ставить 1 балл В конце урока при подведении итогов подсчитываем количество баллов и оцениваем свою работу на уроке. Учитель может добавить балл за оригинальную идею, либо другой способ решения».
Знакомятся с бланком ответов. Подписывают бланк.
3 . Постановка цели урока.
3. Актуализация знаний учащихся.
Устная работа.
Теоретическая разминка.
Продолжаем сегодня работать с квадратными уравнениями. И давайте сформулируем тему и цели нашего урока, а в этом нам поможет стихотворение.

Три ключевых слова в этом стихотворении: уравнения, решать, квадрат.
(Спрашивает несколько человек)
И так тема «решение квадратных уравнений» и цель: повторить и закрепить умение решать квадратные уравнения
В бланк ответов за каждый правильный ответ в раздел «Теоретическая разминка» ставим 1 балл.
1) из списка уравнений, убираем то, которое вы считаете лишним, ответ обоснуем

2)Закончить определение квадратного уравнения

3)Дать определение видам квадратных уравнений. И распределить уравнения по группам

4) От чего и как зависят корни уравнения?

5) Рассмотрим алгоритм решения квадратных уравнений. Формулу нахождения Д, формулы нахождения корней, в зависимости от Д

Читают стихотворение, обращают внимание на выделенные слова. Формируют тему и цель урока.

Открывают тетради, записывают число и тему урока
Работают устно. Отвечающий, ученик за каждый правильный ответ с объяснением, ставит в бланк по 1 баллу
1) из списка убирают линейное уравнение
2) ученик заканчивает определение
3) Ученик дает определения каждому виду квадратного уравнения и распределяют уравнения по колонкам
4) Рассказывает о дискриминанте
5) Рассматривают схематический алгоритм решения уравнений квадратных
Умение выделять существенную информацию из текста
Структурирование знаний;
Умение осуществлять анализ объектов с выделением существенных признаков ;
Умение осуществлять сравнение, сериацию и классификацию по заданным критериям
Осознанное построение речевого высказывания в устной форме;
Умение строить рассуждение в форме связи простых суждений об объекте, его строении, своиствах и связях
Умение формулировать личную цель
Умение формулировать собственное мнение;
Уметь строить понятные для партнера высказывания, учитывающие, что он знает и видит, а что нет;
Адекватно использовать речевые средства, строить монологическое высказывание, владеть диалоговой формой речи
Принимать и сохранять учебную задачу;
4. Решение задач
4.1. Найди ошибку
4.2. Историческая справка
1) в бланке, разделе «Найди ошибку» будем оценивать по трехбалльной системе
3- балла, если нашел ошибку и решил правильно уравнение
2- не нашел ошибку, но правильно нашел корни уравнения
1-балл, представил ответ у доски или помогал в вычислениях.
0- не участвовал в работе
У каждой группы есть карточки с решенными уравнениями. Вам необходимо проверить уравнения, если уравнение решено не верно найти ошибки и решить его


Работаем в группах. Каждой группе раздается по несколько уравнений. Решаем уравнения и на корни уравнении находим соответственную букву. В итоге у вас получается слово. После составления слова . На столе лежит информация о слове. Представитель с группы подходит и выбирает нужную информацию и представляет классу. За каждое решенное уравнение в раздел « Историческая справка» ставим по одному баллу.


1) работают и обсуждают в группах. Находят ошибки, решают уравнения и представляют его у доски.
Оценивают друг друга в группе
Работают в группах. Уравнения распределяются между участниками групп. После составления слова выбирают информацию о слове и представляют ее классу
Использование знаково-символических средств, в том числе моделей и схем для решения задач;
Осознанное построение речевого высказывания в устной и письменной форме;
Понимать возможность различных позиций других людей;
Учитывать разные мнения;
Умение формулировать собственное мнение и позицию;
Умение договариваться и приходить к общему мнению;
Уметь контролировать действия партнера;
Адекватно использовать речевые средства, строить монологическое высказывание, владеть диалоговой формой речи
Взаимодействие
сотрудничество
Принимать и сохранять учебную задачу;
5. Подведение итогов
Каждый подсчитывает общее количество баллов и оценивает себя по следующим критериям

Каждый подсчитывает общее количество баллов и оценивает себя
V. Самостоятельная работа.

На отдельных листочках выполняются задание со слайда. После листочки сдаются.
Применение полученной информации самостоятельно.
VI.
Рефлексия
Дерево возможных вариантов.
На доске изображено дерево.
На партах у учащихся карточки трех цветов. Каждый ученик прикрепляет к дереву листок таким образом:
Зелененный – «Я усвоил тему»
Желтый – «Тему усвоил не до конца»
Красный – «Тема неусвоена полностью»
оценка процесса и результатов деятельности
контроль, коррекция своей работы
№
Этап урока
Название используемых ЭОР
(с указанием порядкового номера из Таблицы 2)
Деятельность учителя
(с указанием действий с ЭОР, например, демонстрация)
Деятельность ученика
Время
(в мин.)
1.
Организационно-мотивационный момент
Презентация (созданная учителем)
Приветствует учащихся, проверяет готовность к уроку. Включает проектор, демонстрация презентации.
Обратная связь на уроке осуществляется при помощи сигнальных карточек красного и зеленого цветов. Приготовьте свои сигнальные карточки. На каждый прозвучавший ответ вы поднимаете сигнальные карточки, показывая зелёным цветом своё согласие с ответом одноклассника. В случае расхождения мнений вы показываете красную карточку, идёт обсуждение, выявляется причина разногласия.
За каждое верно выполненное задание или верный устный ответ на полях своей тетради вы можете ставить знак «+». В конце урока при подведении итогов подсчитываем количество плюсов и оцениваем свою работу на уроке. Учитель может добавить «+» за оригинальную идею, либо другой способ решения».
Постановка личностной цели.
Ребята, а задумывался ли каждый из вас над тем, с какой целью он сегодня пришел в школу? Какая цель есть у каждого из вас? Я вам помогу вам сформулировать для себя цель. Предлагаю вам выбрать свою личную цель из списка на доске. Запишите ее номер в тетради на полях. Постарайтесь работать на эту цель в течение всего урока. В конце урока мы проанализируем, смогли ли Вы ее достичь и в какой мере.
Приветствуют учителя, проверяют свою готовность к уроку и выбирают себе цели из списка на экране.

2 мин.
2 . Постановка цели урока.
Презентация (созданная учителем)
Рассмотрите уравнения, записанные на доске, и постарайтесь разбить их на группы по одному или нескольким признакам и поясните, по какому признаку или каким признакам вы их разбили на группы.

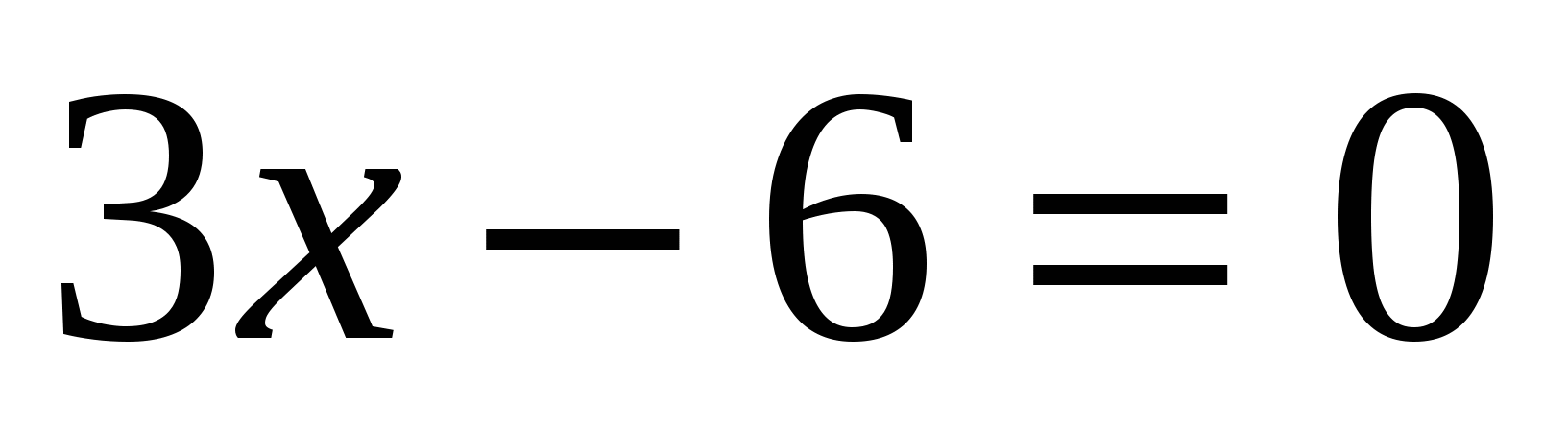

5х – 20 = 10 + 2х,
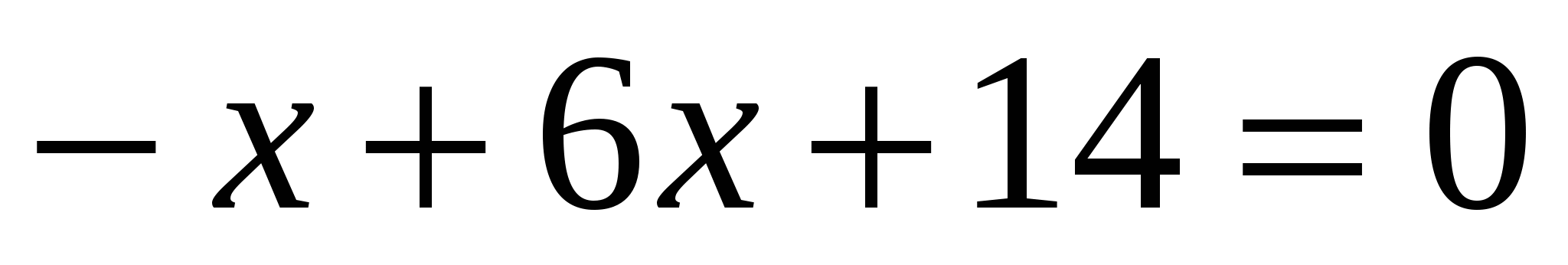
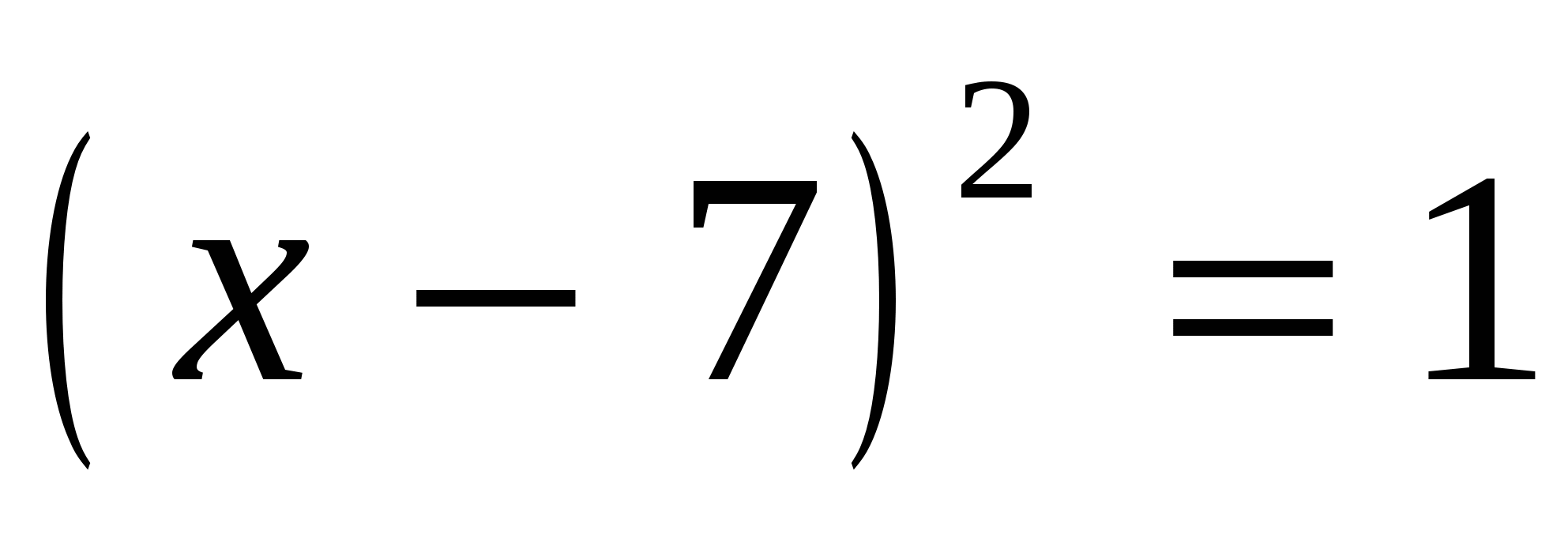
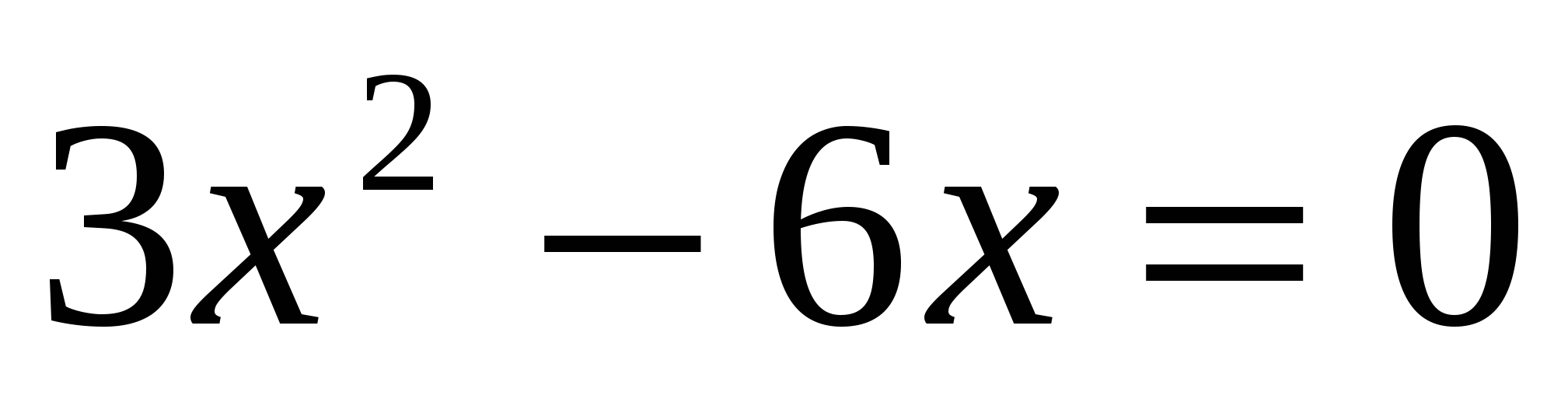
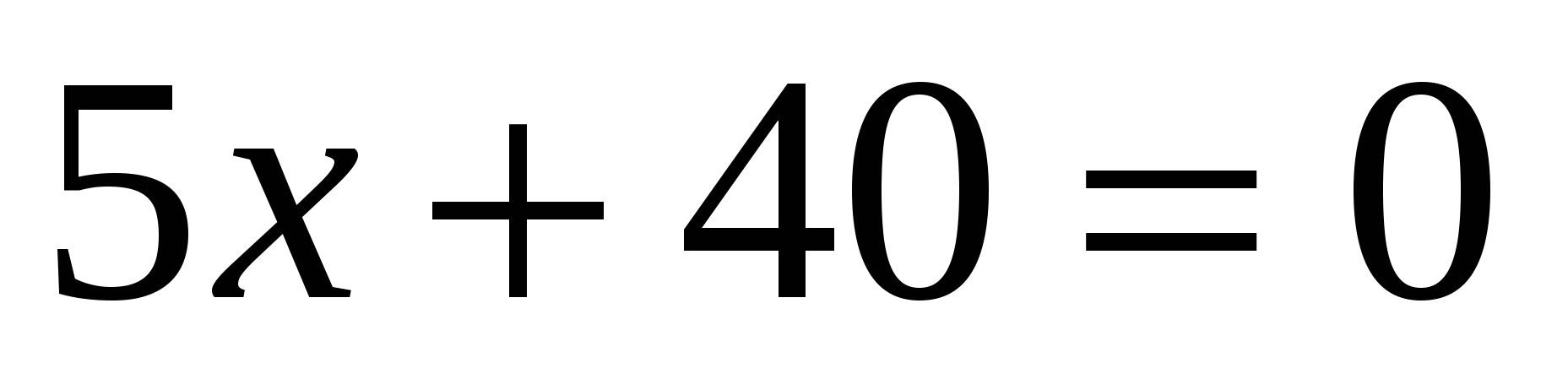
Учащиеся отвечают на вопросы и могут дать такие ответы:
данные уравнения можно разбить:
— на две группы: линейные и квадратные;
— на три группы: неизвестное в первой степени: неизвестное во второй степени и неизвестное и в первой, и во второй степени.)
3 мин.
А, как вы думаете, какая тема сегодняшнего урока? Что будет сегодня на уроке в роли «главного героя»?
(Могут быть ответы «Решение уравнений», или «Решение линейных и квадратных уравнений», или «Решение квадратных уравнений»)
Цель нашего урока:
научиться
распознавать линейные и квадратные уравнения;
решать квадратные уравнения, а также уравнения, сводящиеся к ним различными способами;
определять наличие корней квадратных уравнений по дискриминанту и коэффициентам.
Правильно! Откройте тетради запишите дату, тема урока
3. Теоретическая разминка
Решение квадратного уравнения (N 138388),
ЭОР №1
А теперь устно решите следующие задачи. И в каждой из них постарайтесь не пропустить ошибку.
Итак, в путь!
1.Сравните два утверждения «Квадратное уравнение ах2 +х-2=0 имеет корни» и «Уравнение ах2 +х-2=0 имеет корни», сделайте вывод: это одинаковые по смыслу утверждения или нет, поясните ответ.
Запускается ЭОР №1

Учащиеся отвечают на вопросы, аргументируя свое мнение.
5 мин.
Решение уравнения с квадратным корнем
(N 138298), ЭОР №2
2. Какие способы решения приведённого квадратного уравнения вы знаете?
Запускается ЭОР №2

Учащиеся отвечают на вопросы с аргументацией.
3. Всегда ли целесообразно применять формулы корней квадратного уравнения?
Учащиеся отвечают на вопрос, обосновывая свой ответ.
Формула (N 180658),
ЭОР №3
4. Назовите все возможные идеи решения уравнения:
1) 9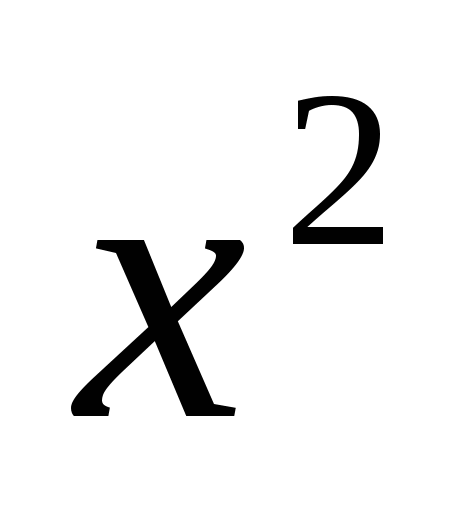 -6х+1=0
-6х+1=0
2) 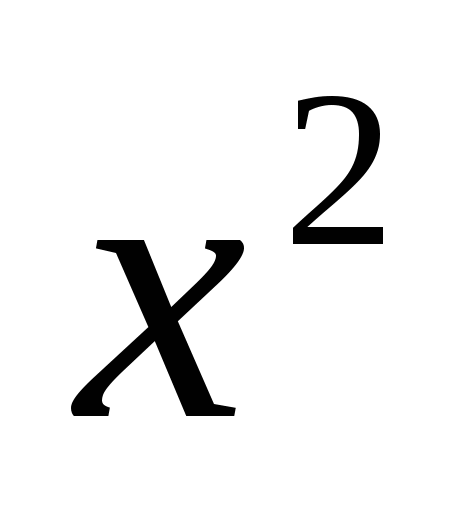 -5х+4=0
-5х+4=0
3)3х + Зх — 6х -6х +х+1=0 (линейное уравнение, известные в одну сторону, неизвестные в другую).
Запускается ЭОР №3

Оцените результат своей деятельности на этом этапе урока и на полях поставьте знак + за каждый верный ответ
Учащиеся отвечают на вопрос
(Возможные ответы: метод выделения полного квадрата, формула корней квадратного уравнения)
(метод выделения полного квадрата; формула корней квадратного уравнения; теорема, обратная теореме Виета, по свойству коэффициентов).
(линейное уравнение, известные в одну сторону, неизвестные в другую).
4. Самостоятельная работа (работа в парах)
Закрепление умений решать неполные квадратные уравнения (N 191881), Запускается ЭОР №4
Запускается ЭОР №4
(Расположен на рабочем столе каждого компьютера, оценивает программа)
Закрепление умений решать неполные квадратные уравнения
Работа в парах.
10 мин
Определение квадратного уравнения. Неполные квадратные уравнения (N 191870), ЭОР №4
Определение квадратного уравнения. Неполные квадратные уравнения
Запускается ЭОР №5
(Расположен на рабочем столе каждого компьютера, оценивает программа)
Индивидуальная работа
5. ФИЗКУЛЬТМИНУТКА
Мы видим глазами наш удивительный мир, который пронизан светом ласкового солнца. Недаром говорят, что лучше один раз увидеть, чем сто раз услышать. Наши глаза помогают нам познавать окружающий мир, учиться, выполнять различную работу. Человеку с плохим зрением труднее будет учиться, работать. Наши глаза настолько драгоценны, что мы просто обязаны их беречь. И сейчас сделаем гимнастику для глаз. Дорогие гости присоединяйтесь к нам.
Упражнения для глаз (сидя на месте):
Закрыть глаза, до лёгкого ощущения боли, сжать веки.
Глядя на стену впереди, выполнить вращения глазами, мысленно рисуя знак бесконечности ∞
Зажать правую руку в кулак так, чтобы большой палец был перпендикулярен потолку и вытянуть её перед собой. Двигая рукой влево, вправо, глазами смотреть на кончик большого пальца руки.
Смотрим вверх, вниз, не двигая головой.
Смотрим влево вправо, не двигая головой.
Вытянули голову вверх, повернули ею влево, вправо, вверх, вниз.
7-8 раз.
Закончили упражнения.
Молодцы! Отдохнули, а теперь продолжаем.
Ребята выполняют упражнения
2 мин.
6. Самостоятельная работа
Решение квадратных уравнений по формуле. К1, ЭОР №6
Квадратные уравнения встречаются не только на уроках алгебры, но и на геометрии, физике. Эти уравнения занимают одно из главных мест в математике.Вы сами определяете, выбрав одно из двух заданий.
На работу вам 7 минут, а затем обсуждаем полученные решения.
10 мин
Запускается ЭОР №6
(Расположен на рабочем столе каждого компьютера, оценивает программа)
А) Решение квадратных уравнений по формуле
Работают индивидуально
Запускается ЭОР (дополнительно)
(Расположен на рабочем столе каждого компьютера, оценивает программа)
В) Тест по теме «Квадратные уравнения»
Работают индивидуально
С) Работа в рабочей тетради.
Взаимопроверка
Работают индивидуально в рабочей тетради.
Стр.43 № 217
7. Домашнее задание.
Откройте дневники, запишите задание на дом: 378(2а), 382(б). Творческое задание (по желанию) «Квадратные уравнения, полученные в данных задачах, решите несколькими способами».
Запись домашнего задания
1 мин.
8 . Интересная задача.
ЭОР №7
Запускается ЭОР №7
Как аль-Хорезми решал квадратные уравнения

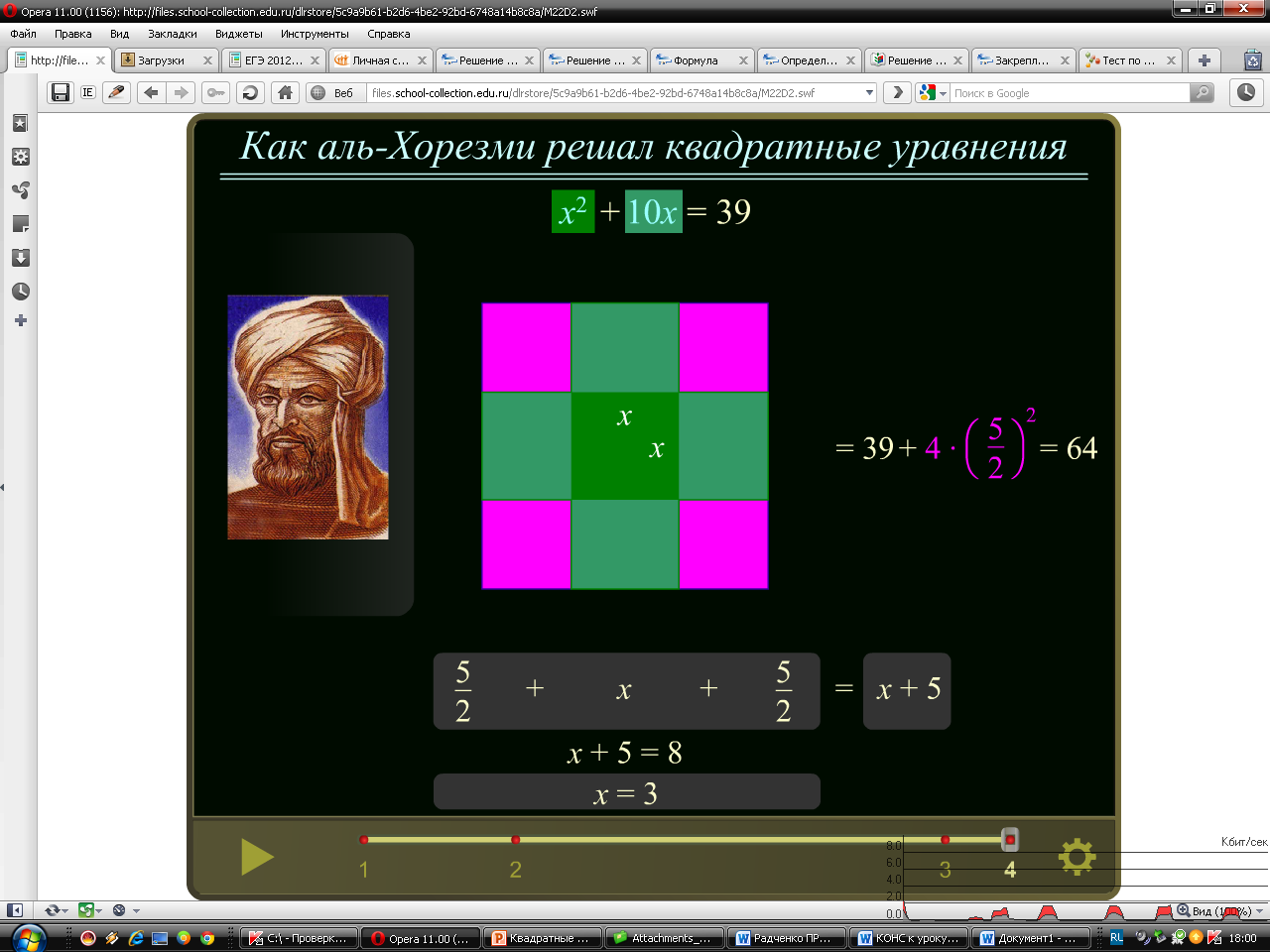
Слушают анимацию.
Записывают алгоритм.
2 мин.
9. Подведение итогов урока. Рефлексия

Анализ достижений предметных и метапредметных результатов
Вопросы к учащимся:
Что нового вы узнали сегодня на уроке? Чему научились?
Опыт использования каких «старых» знаний вам сегодня пригодился?
Что вызвало у вас удивление на уроке?Какой вид деятельности понравился вам больше всего и почему?
Как вы считаете, какой способ решения квадратных уравнений универсальный?
Молодцы! Всем вам, я думаю, хочется получить хорошую оценку
Оцените свою деятельность (в баллах и в словесной форме):
Критерии выставления отметок
«5» — 9-10 +,
«4» 7-8+,
«3»-5-6+.
Ребята подсчитывают количество «+» на полях и выставляют себе на полях в тетради отметку (положительные отметки будут выставлены в журнал).
Учащиеся отвечают на вопросы с аргументацией.
5 мин.
Анализ личностных результатов
А теперь посмотрим, достигли ли Вы своей личной цели, которую записывали в начале урока?
Покажите зеленую карточку, если вы достигли личную цель, и красную, если нет. (Ребята, может кто-то из вас открыто назовет свою цель и ответит на вопрос «достиг он ее и почему он так считает?)
Учащиеся отвечают на вопросы, аргументируя
Приложение к плану-конспекту урока
Решение квадратных уравнений
Таблица 2
ПЕРЕЧЕНЬ ИСПОЛЬЗУЕМЫХ НА ДАННОМ УРОКЕ ЭОР
№
Название ресурса
Тип, вид ресурса
Форма предъявления информации (иллюстрация, презентация, видеофрагменты, тест, модель и т.д.)
Гиперссылка на ресурс, обеспечивающий доступ к ЭОР
1
Решение квадратного уравнения
(N 138388)
ЦОР, учебные и методические материалы (УММ),
инновационный учебный материал, информационный И
Презентация, теоретический слайд.
http://www.school-collection.edu.ru/catalog/res/50170cb2-c355-422b-bf7c-5cd58b27ee9f/?interface=pupil&subject=17
2
Решение уравнения с квадратным корнем (N 138298)
ЦОР, УММ,
инновационный учебный материал, И
Презентация, теоретический слайд
http://www.school-collection.edu.ru/catalog/res/213df871-b48c-41d0-94cf-cc2c99cf8437/
3
Формула (N 180658)
ЦОР, УММ,
инновационный учебный материал, И
Презентация. Алгоритм решения квадратного уравнения. Примеры
http://www.school-collection.edu.ru/catalog/res/aa8f5cca-dd62-49df-b476-edc728d688b1/?fullView=1&from=&interface=pupil&class=50&subject=17&rubric_id[]=108459&rubric_id[]=108460&rubric_id[]=108461&rubric_id[]=108462&rubric_id[]=108348
4
Закрепление умений решать неполные квадратные уравнения (N 191881
ЦОР, УММ,
Инновацион-ный учебный материал, П
Интерактивное задание. Ресурс содержит задания на закрепление умений решать неполные квадратные уравнения
http://school149.avers-telecom.ru/catalog/res/54467594-eccb-4d4e-8039-4a73b6f69ca6/?fullView=1&from=d356d90c-9bae-4d83-99a7-c6c3c51d765c&&rubric_id%5B%5D=112697
5
Определение квадратного уравнения. Неполные квадратные уравнения
(N 191870)
ЦОР, УММ, инновационный учебный материал, практический модуль (П)
Задание, интерактивная модель.
http://school-collection.edu.ru/catalog/res/54467594-eccb-4d4e-8039-4a73b6f69ca6/?from=253f44a5-bb2a-4221-ae16-5b990bb69526&interface=pupil&class=50&subject=17
6
Решение квадратных уравнений по формуле. К1
Открытая образовательная модульная мультимедийная система (ОМС), контрольный модуль (К)
5 заданий с параметризацией.
http://fcior.edu.ru/card/14481/reshenie-kvadratnyh-uravneniy-po-formule-k1.html
7
Как аль-Хорезми решал квадратные уравнения
ЦОР, УММ, коллекции, предметные коллекции, алгебра, инновационный учебный материал, И
Анимация из 3 сцен., демонстрация
http://files.school-collection.edu.ru/dlrstore/5c9a9b61-b2d6-4be2-92bd-6748a14b8c8a/M22D2.swf
Дополнительное задание
№
Название ресурса
Тип, вид ресурса
Форма предъявления информации (иллюстрация, презентация, видеофрагменты, тест, модель и т.д.)
Гиперссылка на ресурс, обеспечивающий доступ к ЭОР
1
Тест по теме «Квадратные уравнения»
ЦОР, учебные материалы для ученика, тест
Презентация содержит контрольные вопросы по теме
http://www.openclass.ru/node/242893
«Квадратные уравнения» 8 класс
Тема урока: «Решение квадратных уравнений»
Цель урока:
закрепление темы: «Квадратное уравнение»; создание условий для осознанного и уверенного владения навыком решения квадратных уравнений, рассмотрение различных способов решения квадратных уравнений.
Образовательные задачи урока:
закрепить знания, выработать умение выбирать рациональный способ решения квадратных уравнений, расширить и углубить представления учащихся о решении уравнений,
Развивающие задачи урока:
развивать математическое мышление, память, внимание;
развивать умение анализировать, сравнивать, обобщать, классифицировать, строить умозаключения, делать выводы;
развивать коммуникативные навыки через коллективный способ Воспитательные задачи урока:
воспитывать культуру умственного труда;
воспитывать культуру коллективной работы;
воспитывать информационную культуру;
воспитывать потребность добиваться успехов в приобретении знаний;
Формы обучения:
Индивидуальная, фронтальная работа, парная работа, групповая (коллективная) деятельность.
Тип урока:
Урок закрепления изученного материала.
Оборудование:
Компьютер, мультимедийная установка, презентация, карточки.
I этап. Организационный момент.(5 мин)
Учитель: Добрый день уважаемые гости , дорогие ребята! Я рада приветствовать Вас на уроке математике.
— Давайте улыбнемся друг другу. Мысленно пожелаем успехов себе товарищам. Пусть сегодняшний урок принесет нам всем радость общения,обогатит нас полезными знаниями и умениями.
Наш урок я хочу начать притчей.
( звучит фоновая музыка)
Однажды молодой человек пришёл к мудрецу и пожаловался ему: «Каждый день по 5 раз я произношу фразу «Я принимаю радость в мою жизнь, но радости в моей жизни нет». Мудрец положил перед собой ложку, вилку и кружку и попросил: «Назови, что ты выбираешь из них».
«Ложку» , — ответил юноша.«Произнеси это слово 5 раз», — сказал мудрец.
«Я выбираю ложку», — послушно произнёс юноша 5 раз.«Вот видишь, сказал мудрец, — повторяй хоть миллион раз в день, ложка не
станет твоей. Надо протянуть руку и взять ложку».
В чем заключается смысл притчи? Чему она учит?
Учитель :Вот именно сегодня надо взять свои знания и применить их на практике,потому что на нашем уроке мы обобщим все знания и покажем все наши умения по теме : КВАДРАТНЫЕ УРАВНЕНИЯ
Эпиграфам к уроку станут слова
Каждый вид работы на уроке будет оцениваться в баллах,
которые вы будете заносить в оценочный лист (заранее положить на парты).
II этап. Проверка домашнего задания. (5 мин)
Давайте, ребята, проверим домашнее задание. Что было задано на дом?
Поисково-исследовательская работа по теме «Квадратные уравнения, как применяется на практике?!»
III этап Актуализация знаний учащихся.
Теоретический опрос ( 10 мин)
Учитель: « Теория без практики мертва, практика без теории слепа» Так давайте же проверим ваши знания! Правильный ответ оценивается в 1 балл
1.Какое уравнение называется квадратным?
(что значит решить квадратное уравнение)
2. Какое квадратное уравнение называется приведённым, а какое — неприведённым?
3. Какие ещё квадратные уравнения, кроме приведённых и неприведённых,различают?
4. Какое уравнение является полным?
5. Записать виды неполных квадратных уравнений
6. Какие методы решения квадратного уравнения вам известны?
7. Теорема Виета
(Ученики выходят к интерактивной доске)
Заполните таблицу, распределив уравнения по видам
IV этап. Работа у доски(10 мин)
Метод выделения квадрата двучлена. Вспомнить способ решения этого метода. Решить уравнение: х2 + 10х -25 = 0 (один учащийся у доски, остальные в тетради – желательно самостоятельно, затем проверяют). Давайте оценим перспективы этого метода (применим во всех квадратных уравнениях, но не всегда удобен)
С помощью формул корней квадратного уравнения. Вспомнить способ решения этого метода. Решить уравнение: 5 х2— 8 х – 4=0 (один учащийся у доски, остальные в тетради – желательно самостоятельно, затем проверяют). Давайте оценим перспективы этого метода (применим во всех квадратных уравнениях)
Метод переброски коэффициента а. Вспоминаем способ решения (Делим на а обе части уравнения и решаем по теореме, обратной теореме Виета) Решить уравнение: 5х2 +10х — 15 = 0 Учащиеся высказывают свое мнение по применению этого способа (Данный метод всегда применим, в случае удобных коэффициентов)
Следующие два метода применяются при определенных условиях. Они основаны на двух теоремах. Вспоминаем! (Если в квадратном уравнении ax2+bx+c=0 : 1. a+b+c=0 , то х1=1, х2=с/а 2. a-b+c=0, то х1=-1, х2=-с/а ) Вызывается два ученика для решения квадратных уравнений (класс решает в тетрадях с последующей проверкой) 4х2-12х+8=0 и 3х2+5х+2=0 Учащиеся высказывают свое мнение по применению этого способа (Данный метод не всегда применим, но такие уравнения решаются быстро)
V этап. Парная работа (5мин)
Учитель: Ребята, что вы видите на картинках?
( пара планет, день сменяется ночью , эо тоже как пара, цикл погоды зимы и лета) а к чему это всё?
Учитель: Мы будем работать в парах, и проверять друг друга?
(раздаю тесты)
И вот теперь вы должны проявить свои умения при решении различных квадратных уравнений, выполнив задания теста в течение 5 мин. и проверить друг друга.
1. Решить уравнение: 3х2 = 01) — 3; 2) 0; 3) 3; 4) 1.
№2. Решить уравнение: 3х2 – 3х + 4= 0
1) 4 ; 2) 3 и 4; 3) -3 и 4; 4) нет корней
№3. Решить уравнение: 3х2 – 5х + 6 =0
1) – 2 и 3; 2) 2 и — 3; 3) 2 и 3; 4) -0,25
№4. Решить уравнение: х2 – 64 = 0
1) 8 и — 8; 2) 4 и -4; 3) 2 и 32; 4) -2 и 32
Оценка теста: 1задание – 1 балл
2 задание — 2 балла
3 задание – 2 балла
4 задание – 1 балл
Ответы теста: 2431
VI этап. Физкульминутка (2 мин)
Знания — великая сила, дающая нам уверенность в будущем! Но все, же главнее здоровья ничего нет.
Поэтому берегите свое здоровье. И для сохранения нашего здоровья сделаем физминутку,чуть отдохнем
VII этап. Групповая работа(5 мин).
Ну что же, ребята отдохнули? Готовы продолжить работать дальше?
Ваша сама любимая форма работы на уроке какая ? Ну что ж приступаем тогда!
Неотъемлемая часть каждого нашего урока-групповая работа
Быстренько разделитесь на группы , оценивается в 2 балла
Решите уравнение: (3х + 4)² + (5х – 1)² = 38 + х
Вот одна из задач знаменитого индийского математика XII века Бхаскара
Обезьянок резвых стая,
Всласть поевши, развлекалась.
Их в квадрате часть восьмая,
На поляне забавлялась,
А двенадцать по лианам
Стали прыгать, повисая…
Сколько ж было обезьянок,
Ты скажи мне в этой стае?
VIII. Работа с черным ящиком (10 мин)
Попытаемся сделать математику на уроке немного более занимательной.
Вам необходимо угадать, что же находится в черном ящике.
Математика и биология
Учитель: Угадайте, что в ящике. Даю три определения этому предмету:
Основа слова.
Число, которое после постановки его в уравнение обращает уравнение в тождество.
Один из основных органов растений.
/Корень/корень имбиря.
Учитель: А вы знаете полезные свойства имбиря?
Давайте решим задачку:
Определить процент содержания спирта в настойке ,если в ней 50 граммов спирта, 250г имбиря.
Далее быстренько найдите корни квадратных уравнений:
И расположите правильно числа и получите названия растения.
x2 — 8x + 15 = 0x2 — 11x + 18 = 0
x2 — 5x — 6 = 0
x2 — 5x + 4 = 0
3
2
56
221
Р
О
З
А
Учитель: Что это за растение?
Ответ: Роза.
Учитель: Розы – самые нежные, красивые удивительные цветы, поражающие своими окрасками и ароматами, они всегда считались королевами цветов.
( звучит музыка,дарят розы)
Видите, ребята, все в этом мире взаимосвязано: математика, русский язык и биология. Мы увидели, что слово «корень» встречается на уроках биологии и математики. И не только.
И закончить сегодняшний урок хотелось бы словами великого математика У. Сойера: «Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт»
Итоги урока. Рефлексия: (2 мин)
Оценивание учащихся. Сообщение домашнего задания.
Домашнее задание: На экране: домашнее задание.
1.Запишите, пожалуйста, уравнения, которые надо решить дома.
— составить задачу, решение, которой сводилось бы к составлению квадратного уравнения,
— составить кроссворд по теме «Квадратные уравнения»
— составить презентацию по теме «Квадратные уравнения».
Урок 30. решение приведённых квадратных уравнений. теорема виета — Алгебра — 8 класс
КонспектКвадратное уравнение x2 – 6x + 8 = 0 имеет два корня, x1 = 2; x2 = 4.
x1 • x2 = 8 – равно свободному члену;
x1 + x2 = 6 – равно второму коэффициенту, взятому с противоположным знаком.
Таким свойством обладает любое приведённое квадратное уравнение, имеющее корни. Докажем это.
Рассмотрим приведённое квадратное уравнение x2 + px + q = 0.
D = p2 – 4q.
Пусть D > 0, тогда уравнение имеет два действительных различных корня: и
и  .
.
Найдём сумму и произведение корней:
Таким образом, если x1 и x2 – корни приведённого квадратного уравнения x2 + px + q = 0, то
x1 + x2 = –p;
x1 • x2 = q.
Если дискриминант приведённого квадратного уравнения будет равен 0, то условимся считать, что тогда уравнение имеет не один корень, а два совпавших корня, и поэтому доказанная теорема будет также верна.
Эта теорема называется теоремой Виета по имени французского математика Франсуа Виета.
Любое квадратное уравнение можно привести к равносильному ему приведённому квадратному уравнению, разделив обе части уравнения на первый коэффициент. Тогда при наличии действительных корней у этого уравнения и согласно теореме Виета, получим вышеприведённые равенства. Это следствие из теоремы Виета – обобщённая теорема Виета.

Используем теорему Виета для нахождения произведения и суммы корней уравнения 2x2 + 9x + 7 = 0.
D = b2 – 4ac = 92 – 4 • 2 • 7 = 25 > 0, значит, уравнение имеет 2 корня. Эти же корни имеет приведённое квадратное уравнение  .
.
По теореме Виета
На практике чаще всего используется теорема, обратная теореме Виета:
тогда y и z – корни уравнения x2 + px + q = 0.
Запишем уравнение x2 + px + q = 0 в виде x2 – (y + z)x + y • z = 0.
Проверим, что у является корнем уравнения. Подставим его вместо х:
y2 – (y + z)y + y • z = 0.
Получим 0 = 0, значит, y – корень уравнения.
Аналогично можно проверить, что и z является корнем уравнения.
С помощью теоремы, обратной теореме Виета, можно проверять, правильно ли найдены корни квадратного уравнения.
Уравнение x2 – 5x + 6 = 0 имеет два корня x1 = 2; x2 = 3. Покажем, что корни найдены верно:
x1 + x2 = 5;
x1 • x2 = 6.
Значит, по теореме, обратной теореме Виета, числа 2 и 3 являются корнями данного уравнения.
С помощью теоремы, обратной теореме Виета, также можно подбором находить корни приведённого квадратного уравнения.
x2 + 13x + 40 = 0
D = 132 – 4 • 1 • 40 = 169 – 160 = 9 > 0, значит, уравнение имеет два корня.
Подберём такие x1 и x2, чтобы 
Таким образом, по теореме, обратной теореме Виета, получим корни данного уравнения x1 = –5; x2 = –8.
Алгебра. 8 класс: учеб. для общеобразоват. организаций / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 6-е изд. – М.: Просвещение, 2017.
Статья по алгебре (8 класс) по теме: РАЗЛИЧНЫЕ СПОСОБЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ
Различные способы решения квадратных уравнений.
Содержание:
- Введение.
- Из истории квадратных уравнений.
- Способы решения квадратных уравнений.
- Решение квадратных уравнений по формуле.
- Разложение левой части уравнения на множители.
- Решение квадратных уравнений по теореме Виета.
- Метод выделения полного квадрата.
- Решение квадратных уравнений способом переброски коэффициентов.
- Свойства коэффициентов квадратного уравнения.
- Графическое решение.
- Решение с помощью линейки и циркуля.
- Номограммы в решении квадратных уравнений.
- Геометрический способ решения.
- Решение квадратных уравнений по теореме Безу.
- Решение одного уравнения всеми способами.
- Литература.
- Приложение.
Введение
Прежде чем рассмотреть способы решения квадратных уравнений, вспомним
определение: Квадратным уравнением называется уравнение вида
аx2 + bx + c = 0,
где х- переменная, а,b и с-некоторые числа, причем, а ≠ 0.
Если в квадратном уравнении ах2 + bx + c = 0 хотя бы один из коэффициентов b или с равен нулю, то такое уравнение называют неполным квадратным уравнением.
Цель работы:
Расширение и углубление знаний в области решений квадратных уравнений.
Задачи:
- Рассмотреть всевозможные способы решений квадратных уравнений.
- Научиться применять эти способы решений.
- Выявить наиболее удобные способы решений.
- Составить дидактический материал для использования разных способов решений квадратных уравнений.
Актуальность этой темы заключается в том, что при сдаче ГИА и ЕГЭ квадратные уравнения необходимо решать не только на алгебре, геометрии, но и на физике. А так как время экзамена ограничено, значит надо уметь быстро найти рациональный способ решения. Работа способствует выработке навыка решения квадратных уравнений и умению быстро находить рациональный способ решения.
Из истории квадратных уравнений.
Развитие земледелия и астрономии ставили перед учеными древности задачи, для решения которых требовалось умение решать квадратные уравнения.
Решение некоторых квадратных уравнений известно было вавилонянам около 2000 лет до н.э.. Затем решение уравнений стало под силу грекам, а за ними индейцам, которые графически научились решать некоторые виды квадратных уравнений. Но общих способов решения пока не вывели.
В III в. н.э. квадратное уравнение х2 — 20х + 96 = 0 решил древнегреческий математик Диофант без обращения к геометрии, но решение х= -2 для Диофанта не существовало, т.к. отрицательные числа древняя математика не знала.
Способы решений квадратных уравнений.
- Решение квадратных уравнений по формуле.
Вывод формулы:
Умножим обе части уравнения
ах2 + bх + с = 0, а ≠ 0,
на 4а и следовательно имеем:
4а2х2 + 4аbх + 4ас = 0.
((2ах) 2 + 2*2ах * b + b2) – b2 + 4ас = 0,
(2ах + b) 2 = b2 – 4ас,
2ах + b = ± √ b2 – 4ас
2ах = – b ± √ b2 – 4ас
Х 1,2 =
● Примеры
Решим уравнения:
а) 2×2-5x+2= 0.
а = 2, b = -5, с = 2, D = b2 – 4ас =(-5)2-4*2*2=25-16=9, D >два разных корня;
х = , х =
; х =
, х1=2 , х2 =
, х2 = 1/2
Таким образом, в случае положительного дискриминанта,
т. е. при b2 – 4ас≥0 уравнение ах2 + bх + с = 0 имеет два различных корня.
б) 4×2-12x+9 = 0,
а =4, b= — 12, с = 9. D = b2 – 4ас=144-4*4*9=0, D = 0, один корень;
х=1,5
Итак, если дискриминант равен нулю, т. е. D = b2 – 4ас= 0, то уравнение ах2 + bх + с = 0 имеет единственный корень, х =
в) 2х2 -3х + 2 = 0, а =2, b= -3, с = 2, D = b2 – 4ас= 9 – 4∙2∙2 =9 – 16 = — 7, D
Уравнение не имеет корней.
- Разложение левой части на множители.
х2 — 2х — 8 = 0. Разложим левую часть на множители:
х2 — 2х — 8 = х2 — 4х +2х -8 = х(х -4 ) + 2(х -4) = (х + 2)(х -4).
(х + 2)(х -4)=0.
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = -2, а также при х = 4.
Это означает, что число — 2 и 4 являются корнями уравнения х2 — 2х — 8 = 0.
- Решение квадратных уравнений по теореме Виета.
Знаменитый французский учёный Франсуа Виет(1540-1603)
Теорема Виета:
Сумма корней приведенного квадратного уравнения х2+ рх + q = 0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену, т.е. х1 + х2 = — р,
х1 · х2 = q.
Теорема, обратная теореме Виета. Если р, q, x1, x2 таковы, что х1 + х2 = — р,
х1 · х2 = q, то х1 и х2 – корни уравнения х2+ рх + q = 0
- Метод выделения полного квадрата.
Поясним этот метод на примере.
Решим уравнение х2 + 6х – 40 = 0
Выделим в левой части полный квадрат. Для этого запишем выражение
х2 + 6х в следующем виде: х2 + 6х = х2 + 2· х ·3.
В полученном выражении первое слагаемое – квадрат числа х, а второе – удвоенное произведение х на 3. поэтому чтобы получить полный квадрат, нужно прибавить 9, так как
х2 + 2· х ·3 + 9 = (х + 3)2 .
Преобразуем теперь левую часть уравнения х2 + 6х – 40 = 0,
прибавляя к ней и вычитая 9. Имеем: х2 + 6х – 40 = х2 + 2х ·3 + 9 – 9 – 40 = (х + 3)2 – 49.
Таким образом, данное уравнение можно записать так: (х + 3)2 –49 = 0, т.е. (х + 3)2 = 49.
Следовательно, х + 3 = 7, х1= 4, или х +3 = -7 , х2 = -10.
- Решение квадратных уравнений способом переброски коэффициентов.
Рассмотрим квадратное уравнение ах2 + bх + с = 0, а ≠ 0.
Умножая обе его части на а, получаем уравнение а2 х2 + а bх + ас = 0.
Пусть ах = у, откуда х =y/a; тогда приходим к уравнению у2 + by + ас = 0,
равносильного данному. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получаем х1 = и х2 =
. При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
● Примеры
Решим уравнение 2х2-9x+9 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение у2 – 9y +18 = 0.
Согласно теореме Виета
y1=6 x1=6/2 x1=3
y2=3 x2=3/2 x2=1,5
Ответ: 1,5;3.
- Свойства коэффициентов квадратного уравнения.
ах2 + bх + с = 0, где а ≠ 0.
1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х1 = 1, х2 = с/а.
Пример.
Решим уравнение 2013х2 –2014х + 1 = 0.
Решение. Так как а + b + с = 0 (2013 – 2014 + 1 = 0), то х1 = 1, х2 = c/a = 1/2013.
Ответ: 1; 1/2013.
2) Если a + c=b , то х1 =-1, х2 = -с/а
Решим уравнение 11×2+27x+16= 0
х1= — 1, х2 = -16/11
Ответ: х1=-1, х2 =-16/11
- Графическое решение.
Если в уравнении х2 + px + q = 0 перенести второй и третий члены в правую часть, то получим х2 = — px — q.
Построим графики зависимости у = х2 и у = — px — q.
График первой зависимости — парабола, проходящая через начало координат. График второй зависимости — прямая (рис.1). Возможны следующие случаи:
— прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
— прямая и парабола могут касаться (одна общая точка), т.е. уравнение имеет одно решение;
— прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
Рис. 3
- Решение с помощью линейки и циркуля.
- Номограммы в решении квадратных уравнений.
z2 + pz + q = 0
номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.
Криволинейная шкала номограммы построена по формулам
- Геометрический способ решения.
у2+ 6у – 16 = 0.
Решение представлено на рис.8 , где
у2 + 6у = 16, или у2+ 6у + 9 = 16 + 9.
Решение. Выражения у2 + 6у – 16 +9 – 9 = 0 – одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у1 = 2, у2 = – 8.
у2 | 3у |
3у | 9 |
Рис.8
- Решение квадратных уравнений по теореме Безу.
х²-4х+3=0
Р2(х)= х²-4х+3
α; ±1,±3.
α =1, 1-4+3=0
Разделим р(х) на (х-1)
(х²-4х+3)/(х-1)=х-3
х²-4х+3=(х-1)(х-3)
(х-1)(х-3)=0
x-1=0 или х-3=0
х=1 х=3
Ответ: x1=1, x2=3
Решение одного уравнения всеми способами.
«Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу различными способами, чем решать три-четыре различные задачи. Решая одну задачу различными способами, можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается опыт». У. У. Сойер.
1)Решение квадратного уравнения по формуле:
x2+8x-9=0
a=1 b=8 c=-9
D=b2-4ac
D=82-4*1*(-9)=64+36=100>0-действуют 2 корня
=1
= -9
Ответ:-9;1
2)Разложение левой части на множители:
а)x2+8x-9=0 б)x2+8x-9=0
x2+9x-x-9=0 x2+8x-8-1=0
x2-x+9x-9=0 x2-1+8x-8=0
x(x-1)+9(x-1)=0 (x-1)(x+1)+8(x-1)=0
(x-1)(x+9)=0 (x-1)(x+1+8)=0
x-1=0 или x+9=0 x-1=0 или x+9=0
x1=1 x2=-9 x1=1 x2=-9
Ответ:-9;1 Ответ:-9;1
3)Решение по теореме Виета.
x2+8x-9=0
x1 *x2=-9
x1+x2=-8
Методом подбора находим:
x1=-9; x2=1
Ответ:-9;1
4)Метод выделения полного квадрата:
x2+8x-9=0 x+4=±√25
x2+2*x* 4 + 42-42-9=0 x+4=±5
x2+2 x 4+16-25=0 x+4=5 или x+4=-5
(x+4)2=25 x1=1 x2=-9
Ответ: -9;1
5)Решение способом переброски коэффициентов.
Квадратное уравнение решается данным способом если a ≠1.
Поэтому х2+8х-9=0 данным способом не решается.
6)Свойства коэффициентов квадратного уравнения:
х2+8х-9=0
а=1 b=8 c=-9
a+b+c=0, тогда х1=1 х2 = -9
Ответ:-9;1
7) Графическое решение:
х2+8х-9=0
х2=-8х+9
у=х2 ; у=-8х+9
Построим графики данных функций:
у=х2- парабола с центром в точки О(0:0)
у=-8х+9- линейная функция, графиков является прямая.
x | 0 | 2 |
y | 9 | -7 |
Ответ: -9; 1. Рис.9
8)Решение уравнения с помощью циркуля и линейки.
х2+8х-9=0
Строим центр окружности:
О(; )
== -4 === -4
O(-4;-4) – центр окружности
Проводим окружность с радиусом OA
A(0;1)
Абсциссы точек пересечения окружности с осью OX Рис.10
являются корнями квадратного уравнения.
Ответ: -9; 1.
9)Геометрический способ решения.
S=x2 | S=4x |
S=4x | 16 |
а) х2+8х-9=0 x 4
х2+8х=9
х2+2*4x=9
(x+4)2=x2+8x+16
х2+8x+16=9+16
(x+4)2=25
x+4=± Рис.11
x+4=±5
x+4=5 или х+4=-5
х1=1 х2=9
Ответ:-9;1
б)х2+8х-9=0
х2+4*2х=9
х2+4*2х+4*4=(х+4)2 х2+8x+16=9+16
(x+4)2=25
x+4=±5
x=-9
x=1
Ответ:-9;1
10)Решение с помощью номограммы.
x2+8x-9=0
по т. Виета x1*x2=-9
Значит, уравнение имеет корни разных знаков. Найдём сначала положительный корень.
p=8 g=-9
x1=1 x2=-p-x1
x2=-8-1=-9
Ответ:-9;1.
11)Решение по теореме Безу.
x2+8x-9=0
Делители -9: ±1; ±3; ±9.
Найдём подбором x который является корнем x2+8x-9=0
x=1 – является корнем.
Произведём деление трёхчлена.
x2+8x-9 x-1
x2-x x+9
9x-9
9x-9
0
(х-1)*(х+9)=0
x=1 x=-9
Ответ:-9;1.
Литература:
- Алгебра. 8 класс. Учебник для общеобразовательных учреждений / Ю.Н. Макарычев, Н. Г. Миндюк, М. : просвещение, 2011
- Гусев В. А., Мордкович А. Г. Математика: Справочные материалы: Книга для учащихся. – М.: Просвещение, 1988
- Глейзер Г. И. История математики в школе. – М.: просвещение, 1982
- Брадис В. М. Четырехзначные математические таблицы для среденй школы. – м., просвещение, 1990
- Алгебра. 8 класс. Учебник (профильный) / А. Г. Мордкович, М. : мнемозина, 2011
- Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки. М., Квант, №4/72. С.34.
- Дидактические материалы по алгебре.
- Математика. ГИА – 30 вариантов / А. Л. Семенов, И. В. Ященко, М: национальное образование, 2013
Дидактический материал к работе
1. Решите квадратное уравнение, разлагая его левую часть на множители:
а) х2 – х = 0; е) х2 – 4х + 4 = 0;
б) х2 + 2х = 0; ж) х2 + 6х + 9 = 0;
в) 3 х2 – 3х = 0; з) х2 + 4х +3 = 0;
г) х2 – 81 = 0; и) х2 + 2х – 3 = 0.
д) 4 х2 – = 0;
2. Решите уравнения по формуле:
а) 2х2 – 5х + 2= 0 г) 4х2 – 12х +9 = 0
б) 6х2 + 5х + 1=0 д) 10х2 – 6х + 0,9 = 0
в) 3х2 – 7х – 1 = 0 е) 2х2 – 3х + 2 = 0
3. Не решая квадратного уравнения, определите знаки его корня:
1) х2 – 2х – 15 = 0 7) х2 – 2х + 1 = 0
2) х2 + 2х – 8 = 0 8) х2 + 4х + 4 = 0
3) х2 + 10х + 9 = 0 9) х2 – 6х + 9 = 0
4) х2 – 12х + 35 = 0 10) 4х2 + 7х – 2 = 0
5)3 х2 +1 4х + 16 = 0 11) 5х2 – 9х – 2 = 0
6) х2 – 5х + 6 = 0 12) х2 – 11х + 15 = 0
4. Решите уравнения, используя метод «переброски»:
2х2 – 9х +9 = 0 5) 3х2 + х – 4 = 0
10х2 – 11х + 3 = 0 6) 5х2 – 11х + 6 = 0
3х2 +11х +6 = 0 7) 2х2 + х – 10 = 0
4х2 +12х + 5 = 0 8) 6х2 +5х – 6 = 0
5. Решите уравнения, используя свойства коэффициентов:
5х2 – 7х + 2 = 0 5) 839х2 – 448х – 391 = 0
3х2 + 5х – 8 = 0 6) 939х2 + 978х +39 = 0
11х2 + 25х – 36 = 0 7) 313х2 + 326х + 13 = 0
11х2 + 27х +16 = 0 8) 2013х2 – 2014х + 1 = 0
6. Решите уравнения по формуле четного коэффициента:
4х2 – 36х + 77 = 0 3) 4х2 + 20х + 25 = 0
15х2 – 22х – 37 = 0 4) 9х2 – 12х + 4 = 0
7. Решите приведенные квадратные уравнения с помощью выделения квадрата двучлена:
х2 – 8х – 9 = 0 3) х2 + 18х + 81 = 0
х2 + 6х – 40 = 0 4) х2 — 56х + 64 = 0
8. Решите графически уравнения:
1) х2 – х – 6 = 0; 4) х2 – 2х – 3 = 0;
2) х2 – 4х + 4 = 0; 5) х2 + 2х – 3 = 0;
3) х2 + 4х +6 = 0; 6) 4х2 – 4х – 1 = 0.
9. Решите с помощью циркуля и линейки следующие уравнения:
1) х2 – 3х + 2 = 0; 4) 2х2 – 7х + 5 = 0;
2) х2 – 3х – 10 = 0; 5) х2 – 6х + 9 = 0;
3) х2 +4х + 3 = 0; 6) х2 +4х + 5 = 0.
10. Решите с помощью номограммы уравнения:
1) z2 – 7z + 6 = 0; 4) z2 – z – 6 = 0 ;
2) z2 + 5z + 4 = 0; 5) z2 – 11z + 18 = 0;
3) z2 – 4z + 4 = 0; 6) z2 – 2z + 3 = 0.
Урок алгебры для 8-го класса по теме «Решение задач с помощью квадратных уравнений»
Тема урока: Решение задач с помощью квадратных уравнений.
Цели урока:
- Закрепить навыки решения текстовых задач с помощью квадратных уравнений;
- Развивать у учащихся внимание при чтении условия задачи и выборе способа решения уравнения;
- Воспитание ответственности и коллективизма у учащихся.
Оборудование: мультимедийный проектор, экран, графопроектор, шесть конвертов с шестью карточками, на каждой из которых написана задача.
Структура урока:
- Организационный момент: замена тетрадей, учащиеся рассаживаются по группам: 6 групп по 5-6 человек в каждой, группы составлены разноуровневые– 3 мин.
- Мотивация учебной деятельности через осознание учащимися практической значимости применяемых знаний и умений, сообщение темы, цели и задач урока -2 мин
- Актуализация изученного материала:
- Вопросы:
- Какое уравнение называется квадратным?
- Что показывает дискриминант?
- Формулы корней квадратного уравнения?
- Задания для устного решения Презентация 1 – 7 мин:
- Решить уравнения;
- Найти натуральный корень уравнения.
- Решение задач (работа в группах):
Каждой группе предлагается конверт с 6
задачами. Набор задач у каждой группы одинаков.
Каждый ученик выбирает себе задачу и решает ее. В
первую очередь выбирать задачи № 1-5. Возможно
советоваться с ребятами из своей группы. Учитель
контролирует процесс и, в случае необходимости,
оказывает помощь – 7 мин.
От каждой группы выходят по 1 человеку (те, кто
раньше решил свою задачу) и оформляют свои
решения на доске (3 чел.), на пленках для
графопроектора (2 чел). Учитель контролирует,
чтобы задачи были различны (задачи 1-5).
Весь класс сверяет свои решения с теми, которые
представлены на доске. Те задачи, которых у
учеников нет в тетрадях, они записывают. Для
удобства текст проверяемой на доске задачи
представлен в виде слайдов Презентации
2.
В ходе проверки задач, записанных на доске,
остальные ребята, решавшие эти же задачи, вносят
свои коррективы, если необходимо. Задачу 6
проверяет учитель в тетрадях, если есть время, то
– разбор на доске. (15 мин.)
- Подведение итогов урока, обобщение и систематизация результатов выполненных заданий. (4 мин.)
- Постановка домашнего задания: № 656, 651, составить свою задачу, аналогичную одной из решенных в классе, и решить ее. (2 мин)
Задачи (в порядке разбора их у доски):
1. Несколько подруг решили обменяться фотографиями на память. Чтобы каждая девочка получила по одной фотографии каждой своей подруги, потребовалось 30 фотографий. Сколько было подруг?
Решение:
Пусть было х подруг, тогда каждая должна получить по (х – 1) фотографии. Всего фотографий было х(х – 1), что по условию задачи равно 30. Составим и решим уравнение:
х(х – 1) = 30
х2 – х – 30 = 0,
D = 1 + 120 = 121,
х = ,
х1 = – 5 – не удовлетворяет смыслу
задачи,
х2 = 6.
По смыслу ясно, что х – натуральное число, и существует только два последовательных натуральных числа, произведение которых равно 30. Итак, х = 6. 6 подруг обменивались фотографиями.
Ответ: 6 подруг.
2. Несколько приятелей решили сыграть турнир по шахматам. Кто-то из них подсчитал, что если каждый сыграет с каждым по одной партии, то всего будет сыграно 36 партий. Сколько было приятелей?
Решение:
Пусть х приятелей участвует в турнире, тогда
каждый из них сыграет (х – 1) партию, но в этом
случае партия каждой пары учтена дважды, значит
всего было сыграно х(х – 1) партий, что по условию
задачи равно 36. Составим и решим уравнение:
х(х
– 1) = 36,
х(х – 1) = 72,
х2 – х – 72 = 0,
D = 1 + 288 = 289,
х = ,
х1 = 9,
х2 = – 8 – не удовлетворяет смыслу
задачи.
Рассуждения, аналогичные задаче 1.
9 приятелей участвовало в турнире.
Ответ: 9 приятелей.
3. Задача Диофанта (III в.)
Найти два числа. Зная, что их сумма равна 20, а произведение – 96.
Решение:
Пусть х – одно из чисел, тогда второе число – (20 – х). Значит х(20 – х) – произведение этих чисел, что по условию задачи равно 96. Составим и решим уравнение:
х(20 – х) = 96,
20х – х2 – 96 = 0,
х2 – 20х + 96 = 0,
= 100 – 96 =
4,
х = 10 + 2,
х1 = 12,
х2 = 8.
12 – первое число, тогда 20 – 12 = 8 – второе число;
8 – первое число, тогда 20 – 8 = 12 второе число.
Ответ: 12 и 8.
4. Решение Диофанта (показывает учитель):
Пусть числа 10 + х и 10 – х (сумма их равна 20), тогда (10 + х)(10 – х) – их произведение, что равно 96. Имеем:
(10 + х)(10 – х) = 96,
100 – х2 = 96,
х2 = 4.
х = + 2.
В обоих случаях искомые числа 12 и 8.
Ответ: 12 и 8.
5. Задача Бхаскары, Индия, XII в.
Цветок лотоса возвышается над тихим озером на полфута. Когда порыв ветра отклонил цветок от прежнего места на 2 фута, цветок скрылся под водой. Определите глубину озера.
Решение.
Пусть глубина озера х ф., тогда длина стебля (х
+ ) ф.
Учитывая, что цветок рос вертикально, составим и
решим уравнение:
х2 + 22 = (х + )2
х2 + 4 = х2 + х +
х = 3
3 фута –
глубина озера.
Ответ: 3 ф.
6. В море встретились два корабля. Один из них шел в восточном направлении, другой – в северном. Скорость первого на 10 узлов больше, чем второго. Через 2 часа расстояние между ними оказалось равным 100 милям. Найдите скорость каждого корабля.
Решение:
Пусть х узлов – скорость второго корабля, тогда (х – 10) узлов – скорость первого корабля, за 2 часа они пройдут 2х и 2(х – 10) миль соответственно, т.к. они идут в перпендикулярных направлениях, то, используя теорему Пифагора, составим и решим уравнение:
(2х)2 + (2(х + 10))2 = 1002
4х2 + 4(х2 + 20х + 100) = 10000
2х2 + 20х + 100 = 2500
х2 + 10х + 50 – 1250 = 0
х2 + 10х – 1200 = 0
= 25 + 1200 =
1225
х = – 5 + 35
х1 = – 40 – не удовлетворяет смыслу
задачи,
х2 = 30
30 узлов – скорость корабля, идущего на север,
тогда 30 + 10 = 40 (узлов) – скорость корабля, идущего
на восток.
Ответ: 30 узлов и 40 узлов.
7. Два равных прямоугольника сложили так, что они образуют букву Т и их общей частью является меньшая сторона одного из прямоугольников. Периметр образовавшейся фигуры равен 42 м, а площадь каждого прямоугольника равна 27 м2. Найти стороны прямоугольников.
Решение.
P = 3b + 3a + (b – a) = 4b + 2a,
a = –
2b, S = ab
Пусть b см длина прямоугольника, тогда
ширина прямоугольника ( – 2b) м, т.к. P = 42 м, то
длина – (21 – 2b)м. Площадь прямоугольника b(21
– 2b), что по условию равно 27 м2.
Составим и решим уравнение.
b(21 – 2b) = 27
21b – 2b2 – 27 = 0
2b2 – 21b + 27 = 0
D = 441 – 4 * 2 * 27 = 441 – 216 = 225
b =
b1 = 9
b2 = 1
Если 9 м – длина, тогда 21 – 2 * 9 = 3(м) – ширина.
Если 1м –
длина, тогда 21 – 2 * 1 = 18(м) – ширина, что не удовлетворяет
смыслу задачи.
Ответ: 9 м и 3 м.
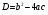 Вычислить дискриминант по формуле и определить количество корней:
Вычислить дискриминант по формуле и определить количество корней: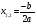 Если D=0, то уравнение имеет один действительный корень и вычислить его можно по формуле.
Если D=0, то уравнение имеет один действительный корень и вычислить его можно по формуле.