В данной публикации мы рассмотрим одну из основных теорем по геометрии 8 класса – теорему Фалеса, которая получила такое название в честь греческого математика и философа Фалеса Милетского. Также разберем пример решения задачи для закрепления изложенного материала.
Формулировка теоремы
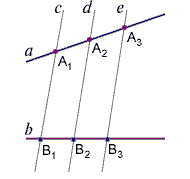
Если на одной из двух прямых отмерить равные отрезки и через их концы провести параллельные прямые, то пересекая вторую прямую они отсекут на ней равные между собой отрезки.

- A1A2 = A2A3 …
- B1B2 = B2B3 …
Примечание: Взаимное пересечение секущих не играет роли, т.е. теорема верна и для пересекающихся прямых, и для параллельных. Расположение отрезков на секущих, также, не важно.
Обобщенная формулировка
Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках*: параллельные прямые отсекают на секущих пропорциональные отрезки.
В соответствии с этим для нашего чертежа выше справедливо следующее равенство:

* т.к. равные отрезки, в т.ч., являются пропорциональными с коэффициентом пропорциональности, равным единице.
Обратная теорема Фалеса
1. Для пересекающихся секущих
Если прямые пересекают две другие прямые (параллельные или нет) и отсекают на них равные или пропорциональные отрезки, начиная от вершины, значит эти прямые являются параллельными.

Из обратной теоремы следует:

Обязательное условие: равные отрезки должны начинаться от вершины.
2. Для параллельных секущих
Отрезки на обеих секущих должны быть равны между собой. Только в этом случае теорема применима.

- a || b
- A1A2 = B1B2 = A2A3 = B2B3 …
Пример задачи
Дан отрезок AB на плоскости. Разделите его на 3 равные части.

Решение

Проведем из точки A прямую a и отметим на ней три подряд идущих равных отрезка: AC, CD и DE.
Крайнюю точку E на прямой a соединяем с точкой B на отрезке. После этого через оставшиеся точки C и D параллельно BE проведем две прямые, пересекающие отрезок AB.
Образованные таким образом точки пересечения на отрезке AB делят его на три части, равные между собой (согласно теореме Фалеса).
Теорема Фалеса
Теорема ФалесаЕсли параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
- Основная информация
- Доказательство
- Таблица доступности
Доказательство
Пусть дан угол AOB. Известно, что OA1=A1A2=A2A3=A3A4=…, A1B1∥A2B2, A2B2∥A3B3, … . Докажем, что OB1=B1B2=B2B3= … .
Предположим, что OB1≠B1B2. Пусть серединой отрезка OB2 является некоторая точка C1. Тогда отрезок A1C1-средняя линия треугольника A2OB2. Отсюда A1C1∥A2B2. Значит, через точку A1 проходит две прямые, параллельные прямой A2B
Предположим, что B1B2≠B2B3. Пусть серединой отрезка B1B3 является некоторая точка C2. Тогда отрезок A2C2-средняя линия трапеции A3A1B1B3. Отсюда A2C2∥A3B3. Значит через точку A2 проходит две прямые, параллельные прямой A3B3. Мы пришли к противоречию. Следовательно, B1B2=B2B3.
Аналогично доказывают, что B2B3=B3B4 и т.д.
Теорема доказана.
Таблица доступности
| Автор | Издательство | Местонахождение |
|---|---|---|
| Мерзляк А.Г., Полонский В.Б. | «Геометрия»; ©Вентана-Граф | 8 класс; Глава 2; §11; теор. 11.1; с.74 |
| Бутузов В.Ф. | «Геометрия»; ©Просвещение | 8 класс; Глава 5; §15; п.61; с.62 |
| Шарыгин И.Ф. | «Геометрия 7-9 класс»; ©Дрофа | Глава 6; п.6.2; теор. 6.4; с.199 |
| Погорелов А.В. | «Геометрия 7-9 класс»; ©Просвещение | §6; п.57;с.78 |
| Козлова С.А. | «Геометрия 7-9 класс»; ©Баласс | §10.5; теор.44; с.149 |
ⒸРезанов Константин
Поддержка: [email protected]
Теорема Фалеса — Википедия
Материал из Википедии — свободной энциклопедии
- Эта теорема о параллельных прямых. Смотри также Теорема Фалеса об угле, опирающемся на диаметр окружности.
Теорема Фалеса — теорема планиметрии о параллельных и секущих.
Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.
Формулировки
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
- Более общая формулировка, также называемая теорема о пропорциональных отрезках
Параллельные прямые отсекают на секущих пропорциональные отрезки:
- A 1 A 2 B 1 B 2 = A 2 A 3 B 2 B 3 = A 1 A 3 B 1 B 3 . {\displaystyle {\frac {A_{1}A_{2}}{B_{1}B_{2}}}={\frac {A_{2}A_{3}}{B_{2}B_{3}}}={\frac {A_{1}A_{3}}{B_{1}B_{3}}}.}
Замечания
- В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.
- Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.
Доказательство в случае секущих
Доказательство в случае параллельных прямых
Проведем прямую BC. Углы ABC и BCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BC, а углы ACB и CBD равны как внутренние накрест лежащие при параллельных прямых AC и BD и секущей BC. Тогда по второму признаку равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. ■
Вариации и обобщения
Обратная теорема
Если в теореме Фалеса равные отрезки начинаются от вершины (часто в школьной литературе используется такая формулировка), то обратная теорема также окажется верной. Для пересекающихся секущих она формулируется так:
Если прямые, пересекающие две другие прямые(параллельные или нет), отсекают на обеих из них равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны. |
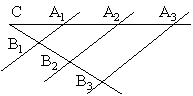 В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины
В обратной теореме Фалеса важно, что равные отрезки начинаются от вершиныТаким образом (см. рис.) из того, что C B 1 C A 1 = B 1 B 2 A 1 A 2 = … {\displaystyle {\frac {CB_{1}}{CA_{1}}}={\frac {B_{1}B_{2}}{A_{1}A_{2}}}=\ldots } , следует, что A 1 B 1 | | A 2 B 2 | | … {\displaystyle A_{1}B_{1}||A_{2}B_{2}||\ldots } .
Если секущие параллельны, то необходимо требовать равенство отрезков на обеих секущих между собой, иначе данное утверждение становится неверным (контрпример — трапеция, пересекаемая линией, проходящей через середины оснований).
Этой теоремой пользуются в навигации: столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется направление с одного судна на другое.
Лемма Соллертинского
Следующее утверждение, двойственно к лемме Соллертинского:
В случае теоремы Фалеса коникой будет бесконечно удалённая точка, соответствующая направлению параллельных прямых.
Это утверждение, в свою очередь, является предельным случаем следующего утверждения:
Пусть f {\displaystyle f} — проективное преобразование коники. Тогда огибающей множества прямых X f ( X ) {\displaystyle Xf(X)} будет коника (возможно, вырожденная). |
Теорема Фалеса в культуре
Аргентинская музыкальная группа Les Luthiers[es] представила песню, посвящённую теореме[1].
Литература
- Атанасян Л. C. и др. Геометрия 7-9. — Изд. 3-е. — М.: Просвещение, 1992.
Примечания
См. также
Главная > Образование > Математика > МАТЕМАТИКА «С НУЛЯ» (учебник) >
<< Назад | Оглавление | Далее >>
Пропорции
Равенство вида
x1 | = | y1 |
x2 | y2 |
называется пропорцией. При этом говорят, что:
x1 относится к x2 как y1 относится к y2,
или
отношение чисел x1 и x2 равно отношению чисел y1 и y2,
или же
числа x1 и x2 соотносятся так же, как числа y1 и y2,
или, наконец,
числа x1 и y1 (!) пропорциональны числам x2 и y2 (то есть числители пропорциональны знаменателям).
Входящие сюда числа x1, x2, y1 и y2 называются членами пропорции. Обычно все они положительны, но это необязательно. Предполагается, однако, что ни одно из них не равно нулю. Особого названия это равенство удостоилось по той причине, что оно часто встречается при решении разных математических задач.
Пропорции можно преобразовывать, перенося члены «с верху» одной части равенства «в низ» другой части равенства и наоборот. Эту процедуру легко обосновать следующим образом. Допустим мы хотим перенести x1 из левой части в правую. Для этого умножим обе части пропорции на 1/x1:
1 |
| x1 | = | 1 |
| y1 | . |
x1 | x2 | x1 | y2 |
В результате получаем
1 | = | y1 | , |
x2 | x1y2 |
то есть переменная x1 у нас переместилась «по диагонали сверху вниз». Перенесем теперь «влево наверх» переменную y2. Это достигается умножением на нее обеих частей данного равенства. В результате имеем
y2 | = | y1 | . |
x2 | x1 |
Мы получили новую пропорцию, которая отличается от исходной перестановкой членов, расположенных «по диагонали». Таким образом, в первоначальном равенстве
x1 | = | y1 |
x2 | y2 |
числители x1 и y1 соотносятся между собой точно так же, как и соответствующие им знаменатели x2 и y2.
Обобщенная теорема Фалеса
Теорема Фалеса, рассмотренная в прошлый раз, допускает следующее обобщение.
Пусть две произвольные прямые x и y пересекаются тремя параллельными прямыми n1, n2 и n3 в точках X1, X2, X3 и Y1, Y2, Y3, как показано на рисунке:

Тогда длины отсекаемых отрезков образуют следующую пропорцию
|Y1Y2| | = | |X1X2| | . |
|Y1Y3| | |X1X3| |
Докажем эту теорему в случае, когда отношение длин
представляет собой рациональное число, то есть может быть выражено в виде несократимой дроби
|X1X2| | = | a | , |
|X1X3| | b |
где a и b — некоторые натуральные числа, a < b. Разобьем отрезок X1X3 на b одинаковых частей. (При этом точка X2 окажется одной из точек деления.) Проведем через каждую точку деления прямые, параллельные n1, n2 и n3. (Одна из этих прямых совпадет с прямой n2.)

По теореме Фалеса (в ее первоначальном варианте), отрезок Y1Y3 также делится этими прямыми на b равных частей, из которых a частей составляют отрезок Y1Y2. Следовательно,
|Y1Y2| | = | a | = | |X1X2| | , |
|Y1Y3| | b | |X1X3| |
что и требовалось доказать. Из нашего построения следует также, что
|Y2Y3| | = | b − a | = | |X2X3| |
|
|Y1Y3| | b | |X1X3| |
и
|Y2Y3| | = | b − a | = | |X2X3| | . |
|Y1Y2| | a | |X1X2| |
Пользуясь свойствами пропорций, эти равенства можно переписать в виде одной цепочки:
|Y1Y2| | = | |Y2Y3| | = | |Y1Y3| | . |
|X1X2| | |X2X3| | |X1X3| |
Таким образом, отрезки отсекаемые на прямой y пропорциональны соответствующим отрезкам на прямой x.
Теоретически возможна также ситуация, когда отношение длин
не является рациональным числом, поскольку длины отрезков |X1X2| и |X1X3| могут, в принципе, выражаться иррациональными числами. Однако на практике такой случай никогда не встречается. Для определения длин отрезков мы всегда пользуемся каким-либо измерительным прибором (например, школьной линейкой), который выдает лишь округленные результаты в виде конечной десятичной дроби.
Важное следствие
Пусть даны несовпадающие прямые x и y, которые пересекаются в точке O, и еще — две параллельные прямые n1 и n2, которые пересекают прямую x в точках X1 и X2 и прямую y в точках Y1 и Y2, как показано на рисунке.

Введем обозначения:
x1 = |OX1|, x2 = |OX2|;
y1 = |OY1|, y2 = |OY2|;
z1 = |X1Y1|, z2 = |X2Y2|.
Тогда
x1 | = | y1 | = | z1 | . |
x2 | y2 | z2 |
Действительно, оба равенства в этой цепочке непосредственно следует из обобщенной теоремы Фалеса. Для первого равенства это ясно сразу, а для второго это становится очевидным после того, как мы через точку Y1 проведем прямую m, параллельную прямой x.

Верно и обратное утверждение. Пусть дана та же геометрическая конструкция и известно, что
x1 | = | y1 | . |
x2 | y2 |
Тогда прямые n1 и n2 параллельны. В самом деле, проведем через точку X1 вспомогательную прямую, параллельную прямой n2. По обобщенной теореме Фалеса, эта вспомогательная прямая проходит через точку Y1. Следовательно, она совпадает с прямой n1. Таким образом, прямая n1 параллельна прямой n2.
Масштаб
Выйдем на улицу, прихватив с собой лист бумаги и карандаш. Расположим наш лист горизонтально и поставим на нем приблизительно посередине точку O. Из этой точки проведем мысленно лучи в направлении различных примечательных точек на местности, расположенных в радиусе примерно ста метров, — деревьев, столбов, углов зданий и того подобного.
Допустим, у нас есть возможность измерить расстояния до этих примечательных точек. Пусть, например, расстояние до ближайшего дерева равно 10 м. Мысленно отложим от точки O в направлении этого дерева отрезок, длина которого в 1000 раз меньше данного расстояния, и отметим карандашом на бумаге положение второго его конца. Нетрудно рассчитать, что расстояние от точки O до отметки составит 10 м/1000 = 1 см.
Подобным же образом, пусть расстояние до какого-то другого примечательного объекта равно x1. Умножим это расстояние на число k, равное 1/1000. Мысленно отложим от точки O отрезок длиной x2 = kx1 вдоль луча, направленного на данный объект. В том месте на бумаге, где находится второй конец отрезка, сделаем отметку карандашом. Проделаем такую процедуру со всеми примечательными точками на местности, используя всё время одно и то же значение параметра k. Если какие-либо из этих точек соединены между собой забором или стеной или же чем-то подобным, то между соответствующими метками на бумаге также проведем линии.
В результате на нашем листе бумаги получится карта местности. В силу теоремы Фалеса и свойств пропорций, все соотношения между расстояниями на бумаге будут в точности такими же, как и в действительности. Более того, все линии на бумаге окажутся параллельны соответствующим линиям на местности. Эта параллельность, конечно, нарушится, когда мы унесем наш лист куда-нибудь в другое место, однако углы между линиями сохранятся.
Параметр k, который мы использовали в нашем построении, называется масштабным коэффициентом или просто масштабом. Разумеется, он необязательно должен быть равен 1/1000. Он может, в принципе, принимать любое значение, важно лишь, чтобы это значение оставалось всё время неизменным в процессе построения карты.
На настоящих географических картах масштаб обязательно указывается в легенде, при этом вместо дробной черты обычно используется двоеточие. Например, масштаб 1:100 000 означает, что один сантиметр на карте соответствует 100000 сантиметрам (то есть одному километру) на местности.
Технические чертежи также всегда выполняются, как говорят, в определенном масштабе. Масштаб 1:1 означает, что деталь начерчена в натуральную величину. А масштаб 10:1 говорит о том, что чертеж выполнен с десятикратным увеличением.
Замечание о параллельных прямых
Мы назвали параллельными такие несовпадающие прямые, угол между которыми равен нулю. Мы отметили, что такие прямые нигде не пересекаются. Докажем теперь, что если прямые лежат в одной плоскости и не параллельны (то есть угол между ними отличен от нуля), то тогда они обязательно где-нибудь пересекутся.
Пусть на плоскости даны две прямые — x и n. Отметим на них произвольные точки — O и Y — и проведем через эти точки третью прямую — y. Если исходить из того, что угол между прямыми x и n не равен нулю, то смежные углы должны оказаться не равны друг другу. Пусть для определенности α1 > α2, как показано на рисунке.

Проведем через точку O прямую n1, параллельную прямой n. Отметим на ней со стороны угла α1 произвольную точку N1 и проведем через эту точку прямую y1, параллельную прямой y. При этом образуется параллелограмм, обозначенный на рисунке серым фоном.

Это значит, что прямая y1 пересекает прямую n в некоторой точке, которую мы обозначим через N. Прямая x, заходя на «территорию» параллелограмма в точке O, обязательно должна где-то оттуда выйти. Она может это сделать либо через отрезок YN, либо через отрезок N1N. В первом случае сразу становится очевидно, что прямая x пересекает прямую n. Рассмотрим второй случай. Обозначим точку пересечения прямой x и отрезка N1N через X1. Проведем через нее прямую n2, параллельную прямой n. Эта прямая разбивает параллелограмм ON1NY на два новых параллелограмма и пересекает прямую y в некоторой точке Y1. Отметим на прямой x такую точку X, для которой выполняется соотношение
|OY1| | = | |OX1| | . |
|OY| | |OX| |
Проведем через точки X и Y прямую. Согласно рассмотренному выше следствию из теоремы Фалеса, эта прямая параллельна прямой n2, а значит, образует нулевой угол с прямой n. Следовательно, новая прямая совпадает с прямой n, которая, таким образом, пересекает прямую x в точке X.
Мы теперь можем утверждать, что следующие три утверждения о несовпадающих прямых a и b, лежащих в одной плоскости, означают в точности одно и то же:
(1) Угол между прямыми a и b равен нулю.
(2) Прямые a и b нигде не пересекаются.
(3) Прямые a и b параллельны.
В традиционных курсах геометрии определением параллельности прямых служит утверждение 2. Мы выбрали для этих целей утверждение 1. Ведь гораздо проще определить угол между двумя прямыми, чем удостовериться, что они нигде не пересекаются на всём своем бесконечном протяжении.
Конспект
1. Равенство вида x1/x2 = y1/y2 называется пропорцией. Числители пропорциональны знаменателям. Числитель и знаменатель одной дроби соотносятся так же, как числитель и знаменатель другой дроби. Эквивалентное равенство: x1/y1 = x2/y2.
2. Обобщенная теорема Фалеса. Пусть две произвольные прямые a и b пересекаются тремя параллельными прямыми. Тогда отрезки, отсекаемые на прямой a, пропорциональны соответствующим отрезкам, отсекаемым на прямой b.
3. Следствие 1. Пусть стороны угла с вершиной в точке O пересекаются двумя параллельными прямыми n1 и n2. Тогда отрезки, отсекаемые на прямых n1 и n2, соотносятся так же, как отрезки, отложенные на любой из сторон угла от точки O до соответствующих точек пересечения с прямыми n1 и n2.
4. Следствие 2. Пусть на сторонах угла отложены от вершины отрезки таким образом, что отрезки на одной стороне пропорциональны отрезкам на другой. Тогда прямые, проходящие через соответствующие концы этих отрезков, параллельны друг другу.
5. На карте сохраняются все соотношения между расстояниями и все углы. Отношение расстояния между некоторыми двумя точками на карте к расстоянию между соответствующими точками на местности не зависит от выбора точек и называется масштабом.
6. Если угол между двумя прямыми, лежащими в одной плоскости, не равен нулю, то такие прямые обязательно пересекаются.
Теорема Фалеса — Википедия
Материал из Википедии — свободной энциклопедии

- Эта теорема о параллельных прямых. Смотри также Теорема Фалеса об угле, опирающемся на диаметр окружности.
Теорема Фалеса — теорема планиметрии о параллельных и секущих.
Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.
Формулировки
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
- Более общая формулировка, также называемая теорема о пропорциональных отрезках
Параллельные прямые отсекают на секущих пропорциональные отрезки:
- A 1 A 2 B 1 B 2 = A 2 A 3 B 2 B 3 = A 1 A 3 B 1 B 3 . {\displaystyle {\frac {A_{1}A_{2}}{B_{1}B_{2}}}={\frac {A_{2}A_{3}}{B_{2}B_{3}}}={\frac {A_{1}A_{3}}{B_{1}B_{3}}}.}
Замечания
- В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.
- Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.
Доказательство в случае секущих
Доказательство в случае параллельных прямых
Проведем прямую BC. Углы ABC и BCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BC, а углы ACB и CBD равны как внутренние накрест лежащие при параллельных прямых AC и BD и секущей BC. Тогда по второму признаку равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. ■
Вариации и обобщения
Обратная теорема
Если в теореме Фалеса равные отрезки начинаются от вершины (часто в школьной литературе используется такая формулировка), то обратная теорема также окажется верной. Для пересекающихся секущих она формулируется так:
Если прямые, пересекающие две другие прямые(параллельные или нет), отсекают на обеих из них равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны. |
 В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины
В обратной теореме Фалеса важно, что равные отрезки начинаются от вершиныТаким образом (см. рис.) из того, что C B 1 C A 1 = B 1 B 2 A 1 A 2 = … {\displaystyle {\frac {CB_{1}}{CA_{1}}}={\frac {B_{1}B_{2}}{A_{1}A_{2}}}=\ldots } , следует, что A 1 B 1 | | A 2 B 2 | | … {\displaystyle A_{1}B_{1}||A_{2}B_{2}||\ldots } .
Если секущие параллельны, то необходимо требовать равенство отрезков на обеих секущих между собой, иначе данное утверждение становится неверным (контрпример — трапеция, пересекаемая линией, проходящей через середины оснований).
Этой теоремой пользуются в навигации: столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется направление с одного судна на другое.
Лемма Соллертинского
Следующее утверждение, двойственно к лемме Соллертинского:
В случае теоремы Фалеса коникой будет бесконечно удалённая точка, соответствующая направлению параллельных прямых.
Это утверждение, в свою очередь, является предельным случаем следующего утверждения:
Пусть f {\displaystyle f} — проективное преобразование коники. Тогда огибающей множества прямых X f ( X ) {\displaystyle Xf(X)} будет коника (возможно, вырожденная). |
Теорема Фалеса в культуре
Аргентинская музыкальная группа Les Luthiers[es] представила песню, посвящённую теореме[1].
Литература
- Атанасян Л. C. и др. Геометрия 7-9. — Изд. 3-е. — М.: Просвещение, 1992.
Примечания
См. также
«Мерзляк Геометрия 8 Глава 2»
Мерзляк Геометрия 8 Глава 2 — это краткий конспект учебника по геометрии за 8 класс (А.Г.Мерзляк и др.) в 4-х частях. Цитаты из учебника помогут учащимся, которые сдали учебник в библиотеку при переходе в старший класс, быстро освежить знания, полученные в 8 классе. Часть 2-я «Подобные треугольники».
Перейти к Главе 1 Перейти к Главе 3 Перейти к Главе 4
Глава 2. Подобие треугольников
§ 11. Теорема Фалеса. Теорема о пропорциональных отрезках.
§ 12. Подобные треугольники. Лемма о подобных треугольниках.
§ 13. Первый признак подобия треугольника. Свойство пересекающихся хорд. Свойство касательной и секущей.
Теорема Менелая.
Теорема Птолемея.
§ 14. Второй и третий признак подобия треугольника.
Прямая Эйлера.
«Мерзляк Геометрия 8 Глава 2» СОДЕРЖАНИЕ: § 11. Теорема Фалеса. Теорема о пропорциональных отрезках. § 12. Подобные треугольники. Лемма о подобных треугольниках. § 13. Первый признак подобия треугольника. Свойство пересекающихся хорд. Свойство касательной и секущей. Теорема Менелая. Теорема Птолемея. § 14. Второй и третий признак подобия треугольника. Прямая Эйлера.
Перейти к Главе 1 Перейти к Главе 3 Перейти к Главе 4
Это конспект по теме «Мерзляк Геометрия 8 Глава 2». Вернуться к Списку конспектов по геометрии

- Эта теорема о параллельных прямых. Смотри также Теорема Фалеса об угле, опирающемся на диаметр окружности.
Теорема Фалеса — теорема планиметрии о параллельных и секущих.
Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.
Формулировки
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
- Более общая формулировка, также называемая теорема о пропорциональных отрезках
Параллельные прямые отсекают на секущих пропорциональные отрезки:
- A 1 A 2 B 1 B 2 = A 2 A 3 B 2 B 3 = A 1 A 3 B 1 B 3 . {\displaystyle {\frac {A_{1}A_{2}}{B_{1}B_{2}}}={\frac {A_{2}A_{3}}{B_{2}B_{3}}}={\frac {A_{1}A_{3}}{B_{1}B_{3}}}.}
Замечания
- В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.
- Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.
Доказательство в случае секущих
Доказательство в случае параллельных прямых
Проведем прямую BC. Углы ABC и BCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BC, а углы ACB и CBD равны как внутренние накрест лежащие при параллельных прямых AC и BD и секущей BC. Тогда по второму признаку равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. ■
Вариации и обобщения
Обратная теорема
Если в теореме Фалеса равные отрезки начинаются от вершины (часто в школьной литературе используется такая формулировка), то обратная теорема также окажется верной. Для пересекающихся секущих она формулируется так:
Если прямые, пересекающие две другие прямые(параллельные или нет), отсекают на обеих из них равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны. |
 В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины
В обратной теореме Фалеса важно, что равные отрезки начинаются от вершиныТаким образом (см. рис.) из того, что C B 1 C A 1 = B 1 B 2 A 1 A 2 = … {\displaystyle {\frac {CB_{1}}{CA_{1}}}={\frac {B_{1}B_{2}}{A_{1}A_{2}}}=\ldots } , следует, что A 1 B 1 | | A 2 B 2 | | … {\displaystyle A_{1}B_{1}||A_{2}B_{2}||\ldots } .
Если секущие параллельны, то необходимо требовать равенство отрезков на обеих секущих между собой, иначе данное утверждение становится неверным (контрпример — трапеция, пересекаемая линией, проходящей через середины оснований).
Этой теоремой пользуются в навигации: столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется направление с одного судна на другое.
Лемма Соллертинского
Следующее утверждение, двойственно к лемме Соллертинского:
В случае теоремы Фалеса коникой будет бесконечно удалённая точка, соответствующая направлению параллельных прямых.
Это утверждение, в свою очередь, является предельным случаем следующего утверждения:
Пусть f {\displaystyle f} — проективное преобразование коники. Тогда огибающей множества прямых X f ( X ) {\displaystyle Xf(X)} будет коника (возможно, вырожденная). |
Теорема Фалеса в культуре
Аргентинская музыкальная группа Les Luthiers[es] представила песню, посвящённую теореме[1].
Литература
- Атанасян Л. C. и др. Геометрия 7-9. — Изд. 3-е. — М.: Просвещение, 1992.
Примечания
См. также
Фалес

| родился | Приблизительно 624 г. до н.э., Милет, Малая Азия. (Сейчас Балат, Турция) |
| Умер | Приблизительно 547 г. до н. Э. |
Фалес, по профессии инженер, был первым из Семи Мудрецов или мудрецов Древней Греции.Фалес известен как первый греческий философ, математик и ученый. Он основал геометрию линий, поэтому ему приписывают введение абстрактной геометрии.
Он был основателем Ионической школы философии в Милете, и учитель Анаксимандра. Во времена Фалеса Милет был важным греком мегаполис в Малой Азии, известный стипендией. Было основано несколько школ в Милете, привлекая ученых, философов, архитекторов и географов
Вполне возможно, что Фалесу дали кредит на открытия, которые на самом деле не были его.Он известен как теоретическим, так и практическим пониманием геометрии. Фалес признан многими источниками как тот, кто определил Созвездие Малой Медведицы и использовать его для навигации. Некоторые считают, что он написал книгу о навигации, но она так и не была найдена.
Два письма и некоторые стихи Фалеса цитируются Диогеном Лерцием в его Жизни Философов. Многое из того, что мы знаем о Фалесе как философе происходит от Аристотеля. Геродот, живший примерно через шестьдесят лет после Фалеса, также писал о нем, как и Евдем, первый крупный историк математики.Прокл, который писал примерно в 450 году нашей эры, сослался на «Историю геометрии» Евдемуса, ныне утраченную, как его источник. Фалесу приписывают введение концепций логическое доказательство абстрактных предложений.
Фалес отправился в Египет и учился у священников, где он узнал о математических инновациях и принес эти знания обратно в Грецию. Фалес также провел геометрические исследования и, используя треугольники, применил свое понимание геометрии, чтобы вычислить расстояние от берега кораблей в море. Это было особенно важно для греков, будь то корабли, чтобы торговать или сражаться.Фалес посоветовал ученику Анаксимандра, Пифагор, чтобы посетить Египет, чтобы продолжить обучение математике и философии.

Пока Фалес был в Египте, он мог определить высоту пирамиды, измерив длину ее тени, когда длина его собственной тени была равна его высоте. Фалес узнал о египетских съемщиках канатов и их методах исследования земли для фараона с помощью кольев и канатов. Границы собственности должны были восстанавливаться каждый год после затопления Нила.После того, как Фалес вернулся в Грецию около 585 г. до н.э. с заметками о том, что он узнал, и Греческие математики перевели методы канатных захватов методом канатов и кола в систему точек, линий и дуг. Они также перенесли геометрию с полей на страницу, используя два инструмента рисования — линейку для прямых линий. и компас для дуг. (См. Конструкции с компасом и линейкой). Греки назвали свои бумажные исследования «геометрией» для «измерения земли» в честь египтян, от которых пришли знания.

Фалесу приписывают следующие пять теорем геометрии:
- Круг делится пополам по диаметру.
- Углы у основания любого равнобедренного треугольника равны.
- Если две прямые пересекаются, образующиеся противоположные углы равны.
- Если один треугольник имеет два угла и одна сторона равна другому треугольнику, эти два треугольника равны во всех отношениях. (См. Congruence)
- Любой угол, вписанный в полукруг, является прямым углом.Это известно как теорема Фалеса.
Египтяне и вавилоняне, должно быть, поняли вышеупомянутые теоремы, но до Фалеса не было известно ни одного зарегистрированного доказательства. Он использовал два из своих более ранних результатов — что базовые углы равнобедренного треугольника равны, и общая сумма углов в треугольнике равняется двум прямым углам — для доказательства теоремы № 5. По словам Диогена Лерция, Когда Фалес открыл эту теорему, он пожертвовал волом!
Фалес соединял миры мифа и разума своей верой в то, что для понимания мира нужно знать его природу («физис», отсюда и современная «физика»).Он полагал, что все явления могут быть объяснены в естественных терминах, вопреки распространенному мнению в то время, что сверхъестественные силы определяли почти все. Фалес заявил, что это было «не то, что мы знаем, а то, как мы это знаем» (научный метод). Его вклад поднял измерения от практической до философской логики.
Есть много записанных рассказов о Фалесе, некоторые из которых являются бесплатными, а другие критическими:
- Геродот отметил, что Фалес предсказал солнечное затмение в 585 г. до н.э. заметный прогресс для греческой науки.Аристотель сообщил, что Фалес использовал свои навыки в распознавании погодных условий, чтобы предсказать, что в следующем сезоне урожай оливок будет обильным. Он купил все оливковые прессы в этом районе и разбогател, когда предсказание сбылось.
- Платон рассказал историю о том, как Фалес смотрит на ночное небо, не наблюдая за тем, куда он шел, и поэтому упал в канаву. Девушка-слуга, которая пришла ему на помощь, сказала ему: «Как ты ожидаешь понять, что происходит? в небе, если вы даже не видите, что у ваших ног?
Цитаты, приписанные Фалесу
- «Множество слов не является доказательством разумного ума.»
- «Надежда — хлеб бедняков».
- «Прошлое несомненно, будущее неясно».
- «Нет ничего более активного, чем мысль, потому что он путешествует по вселенной, и ничто не является более сильным, чем необходимость, для которой все должны подчиниться».
- «Познай себя».
Другие биографии на этом сайте
(C) 2011 Copyright Math Открытая ссылка.
Все права защищены
Введение:
Известный греческий математик Фалес дал важную истину, касающуюся двух равноугольных треугольников, т. Е. «Соотношение любых двух соответствующих сторон в двух равноугольных треугольниках всегда одинаково». Фалес использовал результат, названный Основной Теоремой Пропорциональности для того же самого. Прежде чем обсуждать другие критерии и теоремы о подобных треугольниках, важно понять эту очень фундаментальную теорему, связанную с треугольниками: базовая теорема пропорциональности или теорема BPT .Эта теорема является ключом к лучшему пониманию концепции подобия.
Основная теорема пропорциональности:
Основная теорема пропорциональности гласит, что «Если проведена линия , параллельная одной стороне треугольника, чтобы пересечь две другие стороны в разных точках, две другие стороны будут , разделенными в том же соотношении » .
На следующем рисунке сегмент \ (DE \) параллелен стороне \ (BC \) \ (\ Delta ABC \).Обратите внимание, как \ (DE \) делит \ (AB \) и \ (AC \) в одном и том же соотношении:
Доказательство основной теоремы о пропорциональности:
Подарено:
- \ (\ Delta ABC \)
- \ (DE \ параллель BC \)
Доказать: \ (\ frac {{AD}} {{DB}} = \ frac {{AE}} {{EC}} \)
Строительство:
- Присоединяйтесь \ (BE \) и \ (CD \)
- Draw \ (DP \ bot AC \)
- Draw \ (EQ \ bot AB \)
Доказательство: Рассмотрим \ (\ Delta AED \).Если вам нужно вычислить площадь этого треугольника, вы можете взять \ (AD \) за основу, а \ (EQ \) за высоту, чтобы:
\ [{\ rm {ar}} \ left ({\ Delta AED} \ right) = \ frac {1} {2} \ times AD \ times EQ \]
Теперь рассмотрим \ (\ Delta DEB \). Чтобы вычислить площадь этого треугольника, вы можете взять \ (DB \) за основание, а \ (EQ \) (снова) за высоту (перпендикулярно противоположной вершине \ (E \)).
Таким образом,
\ [{\ rm {ar}} \ left ({\ Delta DEB} \ right) = \ frac {1} {2} \ times DB \ times EQ \]
Далее рассмотрим соотношение этих двух областей, которые вы рассчитали:
\ [\ frac {{{\ rm {ar}} \ left ({\ Delta AED} \ right)}} {{{\ rm {ar}} \ left ({\ Delta DEB} \ right)}} = \ frac {{\ frac {1} {2} \ times AD \ times EQ}} {{\ frac {1} {2} \ times DB \ times EQ}} = \ frac {{AD}} {{DB} } \]
Точно так же вы можете оценить соотношение площадей \ (\ Delta AED \) и \ (\ Delta EDC \):
\ [\ frac {{{\ rm {ar}} \ left ({\ Delta AED} \ right)}} {{{\ rm {ar}} \ left ({\ Delta EDC} \ right)}} = \ frac {{\ frac {1} {2} \ times AE \ times DP}} {{\ frac {1} {2} \ times EC \ times DP}} = \ frac {{AE}} {{EC} } \]
Наконец, мы знаем, что «Два треугольника на одной базе и между одинаковыми параллелями равны в области ».Здесь \ (\ Delta DEB \) и \ (\ Delta EDC \) находятся на одной базе \ (DE \) и между одними и теми же параллелями — \ (DE \ parallel BC \).
\ [\ Rightarrow ar \ left ({\ Delta DEB} \ right) = ar \ left ({\ Delta EDC} \ right) \]
Учитывая вышеупомянутые результаты, мы можем отметить,
\ [{\ frac {{ar \ left ({\ Delta AED} \ right)}} {{ar \ left ({\ Delta DEB} \ right)}} = \ frac {{ar \ left ({\ Delta AED} \ right)}} {{ar \ left ({\ Delta EDC} \ right)}}} \]
\ [{\ Rightarrow \ boxed {\ frac {{AD}} {{DB}} = \ frac {{AE}} {{EC}}}} \]
Это завершает наше доказательство того факта, что \ (DE \) делит \ (AB \) и \ (AC \) в одинаковом соотношении.
Следовательно доказано.
✍Note: \ (DE \) параллельно \ (BC \) было решающим для доказательства. Без этого области \ (\ Delta DEB \) и \ (\ Delta EDC \) не были бы одинаковыми, и, следовательно, эти два отношения были бы разными.
Можно ли сказать, что обратное из основной теоремы о пропорциональности (BPT) будет иметь место? То есть, если в треугольнике отрезок прямой делит две стороны в одинаковом соотношении, будет ли он параллелен третьей стороне? Ответ да .Давайте докажем этот результат.
Конверс БПТ
Обращение к BPT гласит: «В треугольнике, если отрезок прямой пересекает две стороны и делит их в одинаковом соотношении, то он будет параллельным третьей стороне».
Доказательство обратного BPT:
Рассмотрим следующую цифру,
Это с учетом , что \ ({\ frac {{AD}} {{DB}} = \ frac {{AE}} {{EC}}} \).
Теперь предположим, что \ (DE \) не параллелен \ (BC \). Нарисуйте отрезок от \ (DF \) до \ (D \), который параллелен \ (BC \), как показано:
Используя BPT , мы видим, что \ (DF \) должно делить \ (AB \) и \ (AC \) в одинаковом соотношении. Таким образом, мы должны иметь:
\ [\ frac {{AD}} {{DB}} = \ frac {{AF}} {{FC}} \]
Но нам уже дано, что:
\ [\ frac {{AD}} {{DB}} = \ frac {{AE}} {{EC}} \]
Это означает, что:
\ [\ frac {{AE}} {{EC}} = \ frac {{AF}} {{FC}} \]
Добавление 1 к обеим сторонам, мы имеем,
\ [\ begin {align}
\ frac {{AE}} {{EC}} + 1 & = \ frac {{AF}} {{FC}} + 1 \ hfill \\
\ Rightarrow \ frac {{AE + EC}} {{EC}} & = \ frac {{AF + FC}} {{FC}} \ hfill \\
\ Rightarrow \ frac {{AC}} {{EC}} & = \ frac {{AC}} {{FC}} \ hfill \\
\ end {align} \]
\ [\ Rightarrow \ boxed {EC = FC} \]
Этого не может быть, если \ (E \) и \ (F \) — это разные точки, поэтому они должны совпадать с .Таким образом, мы можем заключить, что \ (DE \) параллельна \ (BC \), что завершает доказательство обратного к BPT.
Следовательно доказано.
Решенные примеры
Пример 1: Рассмотрим \ (\ Delta ABC \), в котором отрезок \ (DE \), параллельный \ (BC \), выводится из \ (D \) на \ (AB \) в \ (E \) на \ (AC \), как показано ниже:
Покажите, что \ (\ Delta ADE \) похож на \ (\ Delta ABC \).
Решение: Напомним, что два треугольника называются схожими, если они равны угловым (соответствующие углы равны), а соответствующие стороны пропорциональны.Очевидно, что \ (\ Delta ADE \) и \ (\ Delta ABC \) равносильны, так как:
\ (\ угол A \) = \ (\ угол A \) (общий угол)
\ (\ angle ADE \) = \ (\ angle ABC \) (соответствующие углы)
\ (\ angle AED \) = \ (\ angle ACB \) (соответствующие углы)
Теперь мы покажем, что соответствующие стороны пропорциональны. Используя BPT , мы имеем:
\ [\ begin {align} \ frac {{AD}} {{DB}} & = \ frac {{AE}} {{EC}} \\ \ Rightarrow \ quad \ frac {{DB}} {{AD }} & = \ frac {{EC}} {{AE}} \\ \ Rightarrow \ quad \ frac {{DB}} {{AD}} + 1 & = \ frac {{EC}} {{AE}} + 1 \\ \ Rightarrow \ quad \ frac {{DB + AD}} {{AD}} & = \ frac {{EC + AE}} {{AE}} \\ \ Rightarrow \ quad \ frac {{AB} } {{AD}} & = \ frac {{AC}} {{AE}} \\ \ Rightarrow \ quad \ frac {{AD}} {{AB}} & = \ frac {{AE}} {{AC }} \ end {align} \]
Таким образом, мы показали, что две пары сторон пропорциональны.Все, что остается показать, что приведенные выше соотношения также равны отношению третьей пары, то есть к \ (\ frac {{DE}} {{BC}} \).
Чтобы доказать это, проведите отрезок \ (EF \) параллельно \ (AB \), как показано:
Поскольку \ (EF \ parallel AB \), BPT говорит нам, что:
\ [\ begin {align} \ frac {{CE}} {{EA}} & = \ frac {{CF}} {{FB}} \\ \ Rightarrow \ quad \ frac {{CE}} {{EA }} + 1 & = \ frac {{CF}} {{FB}} + 1 \\ \ Rightarrow \ quad \ frac {{CE + EA}} {{EA}} & = \ frac {{CF + FB} } {{FB}} \\ \ Rightarrow \ quad \ frac {{AC}} {{AE}} & = \ frac {{BC}} {{FB}} \ end {align} \]
Но \ (BF \) равно \ (DE \) (поскольку \ (DEFB \) — параллелограмм), и поэтому:
\ [\ begin {align} \ frac {{AC}} {{AE}} & = \ frac {{BC}} {{DE}} \\ \ Rightarrow \ quad \ frac {{AE}} {{AC }} & = \ frac {{DE}} {{BC}} \ end {align} \]
Таким образом, мы наконец имеем:
\ [\ frac {{AD}} {{DB}} = \ frac {{AE}} {{AC}} = \ frac {{DE}} {{BC}} \]
Это доказывает, что все три пары сторон пропорциональны, что означает, что два треугольника похожи.
\ [\ Rightarrow \ boxed {\ Delta ADE \ sim \ Delta ABC} \]
✍Note: Результат, который мы обсудили здесь, чрезвычайно важен и будет часто использоваться, поэтому крайне важно, чтобы вы снова прошли обсуждение, если вы не полностью его поняли.
Задача: \ (E \) и \ (F \) — точки на сторонах \ (PQ \) и \ (PR \) соответственно \ (\ Delta PQR \). В следующем случае укажите, есть ли \ (EF \ параллельный QR \),
\ (PQ = 1.28 {\ text {cm}} \), \ (PR = 2,56 {\ text {cm}} \), \ (PE = 0,18 {\ text {cm}} \) и \ (PF = 0,36 {\ text { см}} \)
ipСовет: Применить обратное к BPT .
Пример 2: \ (ABCD \) — это трапеция такая, что \ (AB \ параллельный DC \). \ (E \) и \ (F \) — это точки на непараллельных сторонах \ (AD \) и \ (BC \) соответственно, такие что \ (EF \ parallel AB \), как показано ниже:
Покажите, что \ (\ frac {{AE}} {{ED}} = \ frac {{BF}} {{FC}} \).
Решение: Соедините \ (BD \) и дайте ему пересечь \ (EF \) в \ (G \), как показано ниже:
Теперь мы применим BPT дважды, один раз в \ (\ Delta ADB \) и один раз в \ (\ Delta DBC \).У нас есть:
\ [\ left \ {\ begin {align} & \ frac {{AE}} {{ED}} = \ frac {{BG}} {{GD}} \\ & \ frac {{BG}} {{ GD}} = \ frac {{BF}} {{FC}} \ end {align} \ right. \]
Ясно,
\ [\ boxed {\ frac {{AE}} {{ED}} = \ frac {{BF}} {{FC}}} \]
Задача: \ (ABCD \) — это трапеция, в которой \ (AB \ параллельный DC \) и его диагонали пересекаются друг с другом в точке \ (O \). Покажите это \ (\ frac {{AO}} {{BO}} = \ frac {{CO}} {{DO}} \).
ipСовет: Нарисуйте \ (EO \) такой, что \ (E \) является точкой на \ (AD \) и \ (EO \ параллельный AB \), затем примените BPT в \ (\ Delta DAB \) и \ (\ Delta ADC \).
Пример 3: Рассмотрим следующий рисунок:
Указано, что \ (\ frac {{CD}} {{DA}} = \ frac {{CE}} {{EB}} \) и \ (\ angle CDE \) = \ (\ angle CBA \ ). Докажите, что \ (\ Delta CAB \) равнобедренный.
Решение: Нам говорят, что \ (\ frac {{CD}} {{DA}} = \ frac {{CE}} {{EB}} \)
Итак, к обратному показателю BPT , мы можем заметить,
\ [DE \ параллельный AB \]
Таким образом,
\ [\ angle CDE = \ angle CAB {\ text {}} \ left ({{\ text {соответствующие углы}}} \ right) \]
Но также дано, что
\ [\ angle CDE = \ angle CBA \]
Что означает, что
\ [\ angle CAB = \ angle CBA \]
\ [\ Rightarrow \ boxed {CA = CB} \]
Следовательно, \ (\ Delta CAB \) составляет равнобедренных .
Задача: Используя базовую теорему о пропорциональности, докажите, что линия, проведенная через середину одной стороны треугольника, параллельной другой, делит пополам третью сторону.
ipСовет: Так как линия проходит через среднюю точку, значит, она делит сторону треугольника на равной пропорции, и эта теорема также известна как теорема о средней точке .
Доказательство теоремы Пифагора
Что такое теорема Пифагора?
Вы можете узнать все о теореме Пифагора, но вот краткое резюме:
Теорема Пифагора говорит, что, в прямоугольном треугольнике, квадрат a (который является × a, и написано a 2 ) плюс квадрат b ( b 2 ) равно квадрату с ( с 2 ):
a 2 + b 2 = c 2
Доказательство теоремы Пифагора с использованием алгебры
Мы можем показать, что a 2 + b 2 = c 2 с использованием алгебры
Посмотрите на эту диаграмму… у этого есть тот «abc» треугольник в этом (четыре из них фактически):
Площадь всей площади
Это большой квадрат, каждая сторона имеет длину a + b , поэтому общая площадь равна:
A = (a + b) (a + b)
Площадь Кусочков
Теперь давайте сложим области всех меньших частей:
Во-первых, меньший (наклонный) квадрат имеет площадь: c 2
Каждый из четырех треугольников имеет площадь: ab 2
Итак, все четыре из них вместе: 4ab 2 = 2ab
Сложение наклоненного квадрата и четырех треугольников дает: A = c 2 + 2ab
Обе области должны быть равны
Площадь большого квадрата равна площади наклонного квадрата и 4 треугольников .Это можно записать как:
(a + b) (a + b) = c 2 + 2ab
СЕЙЧАС, давайте изменим это, чтобы увидеть, можем ли мы получить теорему Пифагора:
Начните с: (a + b) (a + b) = c 2 + 2ab
Развернуть (a + b) (a + b): 2 + 2ab + b 2 = c 2 + 2ab
Отнимите «2ab» с обеих сторон: 2 + b 2 = c 2
СДЕЛАНО!
Теперь мы можем понять, почему работает теорема Пифагора… и это на самом деле доказательство теоремы Пифагора.
Это доказательство пришло из Китая более 2000 лет назад!
Есть много других доказательств теоремы Пифагора, но это работает хорошо.
,Теорема о круге — математика GCSE Редакция
Теоремы
В этом разделе объясняется теорема о круге, включая касательные, сектора, углы и доказательства.
В видео ниже показаны правила, которые необходимо помнить, чтобы выработать теоремы о круге.

Равнобедренный треугольник
Два радиуса и хорда образуют равнобедренный треугольник.
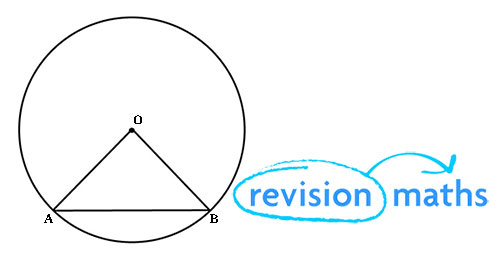
перпендикулярная хорда Bisection
Перпендикуляр от центра круга к хорде всегда будет делить аккорд на две части (разделить его на две равные длины).
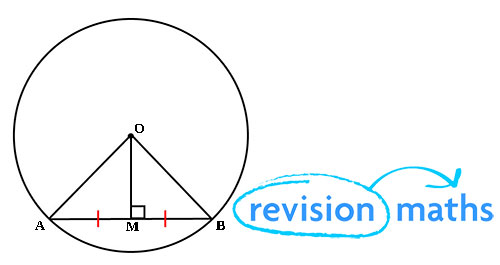
углов на одной и той же дуге
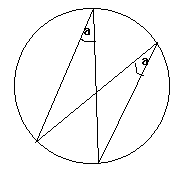
Углы, образованные из двух точек на окружности, равны другим углам в той же дуге, образованной из этих двух точек.
Угол в полукруге
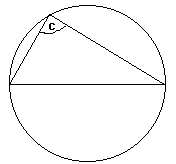
Углы, образованные линиями от концов диаметра круга к его окружности, образуют прямой угол. Итак, с — это прямой угол .
Доказательство
Мы можем разделить треугольник на две части, нарисовав линию от центра круга до точки на окружности, которой касается наш треугольник.
Мы знаем, что каждая из линий, которые являются радиусом круга (зеленые линии), имеют одинаковую длину. Поэтому каждый из двух треугольников равнобедренный и имеет пару равных углов.
Но все эти углы вместе должны составлять до 180 °, поскольку они являются углами исходного большого треугольника.
Следовательно, x + y + x + y = 180, другими словами 2 (x + y) = 180.
и т. Д. X + y = 90. Но x + y — это размер угла, который мы хотели найти.
Касательные
Касательная к окружности — это прямая линия, которая касается окружности только в одной точке (поэтому она не пересекает окружность — она просто касается ее).
Касательная к окружности образует прямой угол с радиусом окружности в точке контакта касательной.
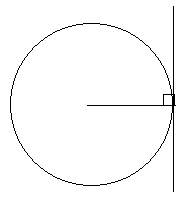
Кроме того, если две касательные нарисованы на окружности и они пересекаются, длины двух касательных (от точки, где они касаются окружности, до точки, где они пересекаются) будут одинаковыми.
Угол в центре
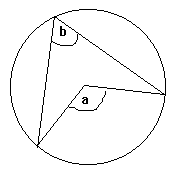
Угол, образованный в центре круга линиями, исходящими из двух точек на окружности круга, в два раза больше угла, образованного на окружности круга линиями, исходящими из тех же точек. то есть а = 2b .
Доказательство
Возможно, вам придется доказать этот факт:
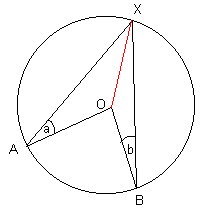
OA = OX, так как оба они равны радиусу круга.Следовательно, треугольник AOX равнобедренный и поэтому XOXA = a
Аналогично, ∠OXB = b
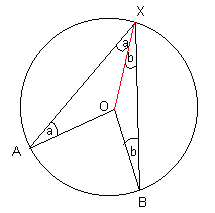
Поскольку углы в треугольнике составляют в целом 180, мы знаем, что ∠XOA = 180 — 2a
Аналогично, ∠BOX = 180 — 2b
Так как углы вокруг точки составляют в целом 360, мы имеем, что ∠AOB = 360 — ∠XOA — ∠BOX
= 360 — (180-2a) — (180-2b)
= 2a + 2b = 2 (a + b) = 2 ∠AXB
Теорема об альтернативном сегменте
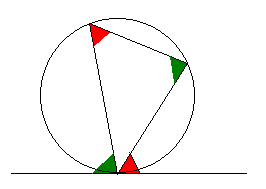
На этой диаграмме показана теорема об альтернативном сегменте .Короче говоря, красные углы равны друг другу, а зеленые углы равны друг другу.
Доказательство
Возможно, вам понадобится доказать теорему об альтернативном сегменте:
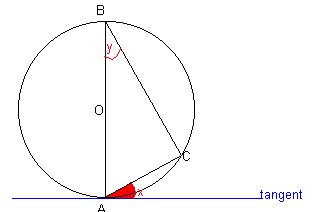
Мы используем факты о связанных углах
Касательная составляет угол 90 градусов с радиусом круга, поэтому мы знаем, что ∠OAC + x = 90.
Угол в полукруге равен 90, поэтому ∠BCA = 90.
Углы в треугольнике добавить до 180, так что ∠ВСА + ∠OAC + y = 180
Следовательно, 90 + ∠OAC + y = 180 и так ∠OAC + y = 90
Но OAC + x = 90, поэтому ∠OAC + x = ∠OAC + у
отсюда х = у
Циклические четырехугольники
Четырехсторонний четырехсторонний — это четырехугольная фигура в круге, где каждая вершина (угол) четырехугольника касается окружности круга.Противоположные углы такого четырехугольника составляют до 180 градусов.
Площадь сектора и длина дуги
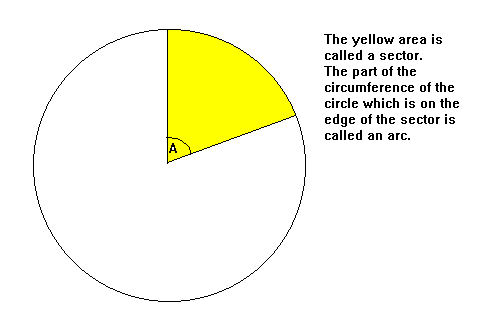
Если радиус окружности равен r,
Площадь сектора = πr 2 × A / 360
Длина дуги = 2πr × A / 360
Другими словами, площадь сектора = площадь круга × A / 360
длина дуги = окружность круга × A / 360
Для получения дополнительной информации об определениях круга нажмите здесь
,