Прямоугольный треугольник, формулы и примеры
Определение и формулы прямоугольного треугольника
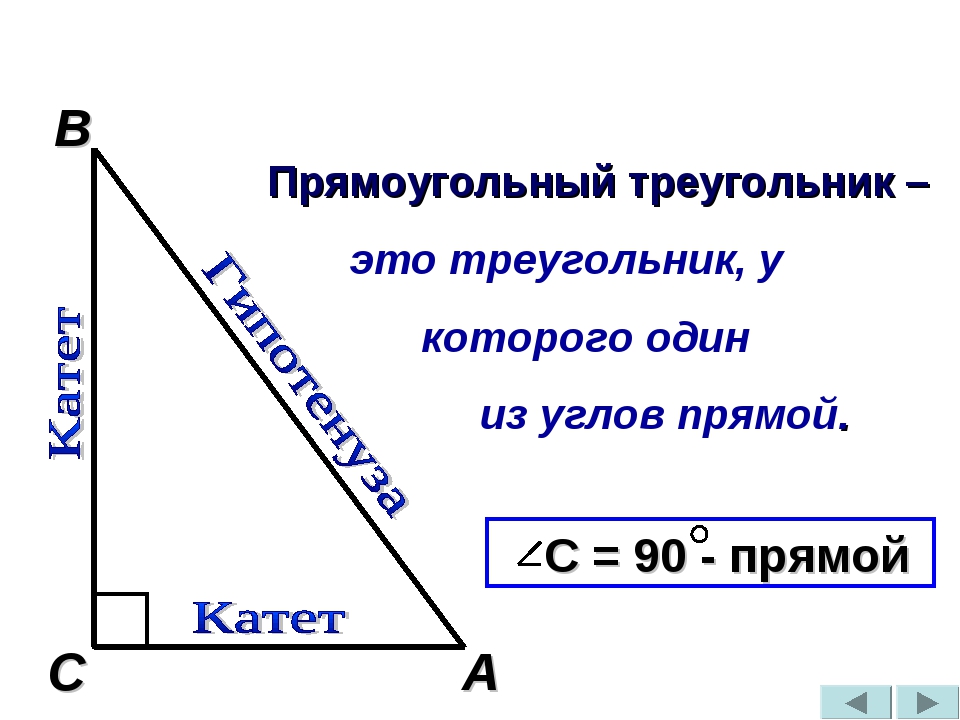
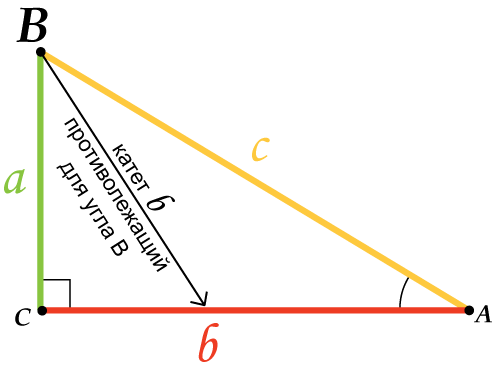
Стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла, – гипотенузой.
Для прямоугольного треугольника справедливы следующие утверждения:
Признаки равенства прямоугольных треугольников
- По двум катетам: если два катета одного прямоугольного треугольника равны катетам другого прямоугольного треугольника, то такие треугольники равны.
- По гипотенузе и катету: если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
- По стороне и острому углу: Если сторона и прилежащий к ней острый угол одного прямоугольного треугольника соответственно равны стороне и прилежащему к ней острому углу другого прямоугольного треугольника, то такие треугольники равны
Подробнее про признаки равенства треугольников читайте по ссылке.
Тригонометрические соотношения в прямоугольном треугольнике
Площадь прямоугольного треугольника равна половине произведения катетов и вычисляется по формуле
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Прямоугольный треугольник. Определения и свойства
Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).
Сторона, противоположная прямому углу, называется гипотенузой
прямоугольного треугольника.Стороны, прилежащие к прямому углу, называются катетами.
Признаки равенства прямоугольных треугольников
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны (по двум катетам).
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны (по катету и острому углу).
Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны (по гипотенузе и катету).
Свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна 90˚.
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.
3. Теорема Пифагора:
, где 
– катеты, 
– гипотенуза. Видеодоказательство
4. Площадь 
прямоугольного треугольника с катетами :
5. Высота 
прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:
6. Центр описанной окружности – есть середина гипотенузы.
7. Радиус 
описанной окружности есть половина гипотенузы :
8. Медиана, проведенная к гипотенузе, равна ее половине
9. Радиус 
вписанной окружности выражается через катеты и гипотенузу следующим образом:
Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.
И, думаю, будет полезна таблица формул для треугольника
egemaximum.ru
Все формулы для треугольника
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:
L — биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b — катеты прямоугольного треугольника
с — гипотенуза
α — угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):
Формула длины биссектрисы через гипотенузу и угол, ( L):
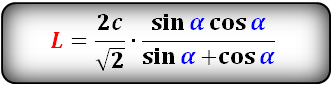
2. Найти по формулам длину биссектрисы из острого угла на катет:
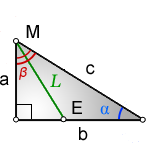
L — биссектриса, отрезок ME , исходящий из острого угла
a, b — катеты прямоугольного треугольника
с — гипотенуза
α, β — углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, ( L):
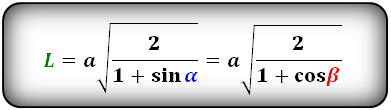
Формула длины биссектрисы через катет и гипотенузу, (L):
www-formula.ru
Все формулы прямоугольного треугольника ℹ️ определение, примеры расчетов углов, соотношение сторон, формулы нахождения площади и периметра, теорема Пифагора
Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то есть 90 градусов). Соотношения между сторонами и углами прямоугольного треугольника лежат в основе тригонометрии.
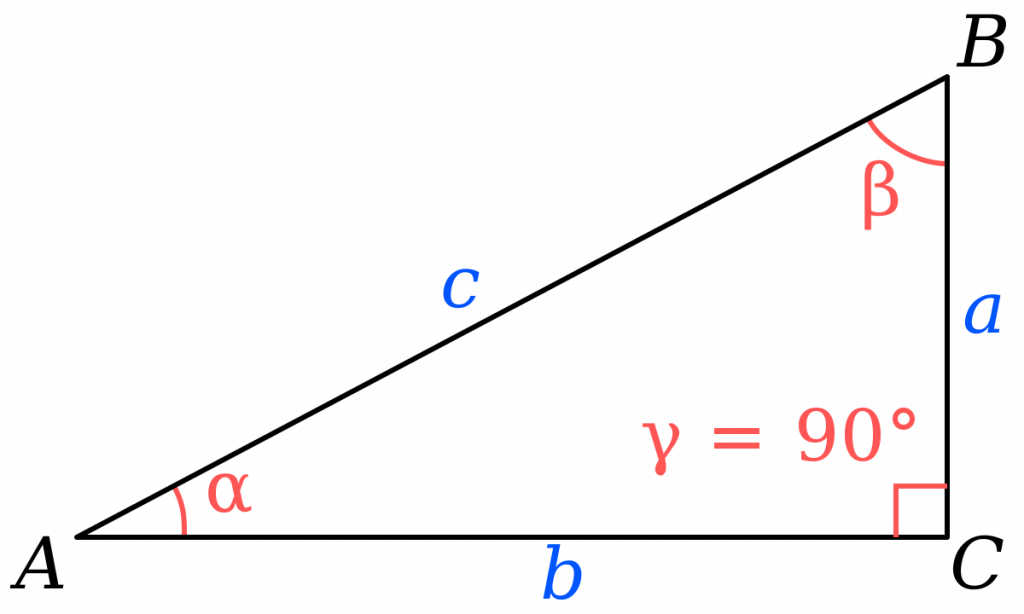
Формулы
1. Сумма острых углов прямоугольного треугольника равна 90 0: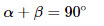
2. Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе:
3. Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе:
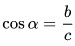
4. Тангенс острого угла равен отношению противолежащего катета к прилежащему катету:
5. Котангенс острого угла равен отношению прилежащего катета к противолежащему катету:
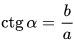
6. Секанс острого угла равен отношению гипотенузы к прилежащему катету:
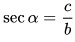
7. Косеканс острого угла равен отношению гипотенузы к противолежащему:
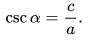
8. Катет, противолежащий углу, равен произведению гипотенузы на синус этого угла:
9. Катет, прилежащий углу, равен произведению гипотенузы на косинус этого угла:
10. Катет, противолежащий углу, равен произведению второго катета на тангенс угла:
11. Катет, прилежащий углу, равен произведению второго катета на котангенс угла:
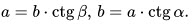
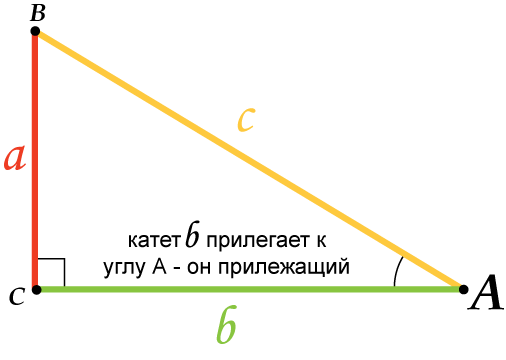
12. Гипотенуза равна отношению катета к синусу противолежащего угла, и/или частному отношению катета и косинуса прилежащего угла (угла между ними):
13. Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
14. Медианы, проведенные к катетам прямоугольного треугольника:
15. Медиана, проведенная к гипотенузе:
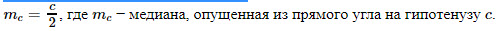
16. Радиус окружности, описанной около прямоугольного треугольника:
17. Радиус окружности, вписанной в прямоугольный треугольник:
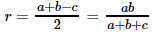
18. Площадь прямоугольного треугольника равна половине произведения катетов треугольника:
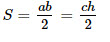
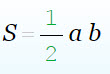
19. Периметр прямоугольного треугольника
nauka.club
Все формулы сторон прямоугольного треугольника
Как найти,
гипотенузу или катеты в прямоугольном треугольнике.
a, b — катеты
c — гипотенуза
α, β — острые углы
Формулы для катета, (a):
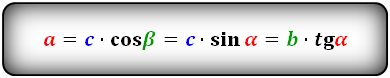
Формулы для катета, (b):
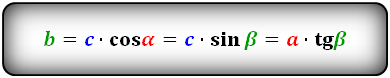
Формулы для гипотенузы, (c):
Формулы сторон по теореме Пифагора, (a,b):
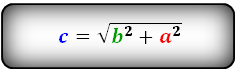
- Подробности
- Автор: Administrator
www-formula.ru
Решение прямоугольного треугольника | Формулы и расчеты онлайн
Решение прямоугольного треугольника по двум сторонам
Если даны две стороны прямоугольного треугольника, то третья сторона может быть вычислена по теореме Пифагора. Острые углы определяются по формулам тригонометрических функций острого угла — Синус угла — sin(A), Косинус угла — cos(A), Тангенс угла — tg(A), Котангенс угла — ctg(A), Секанс угла — sec(A), Косеканс угла — cosec(A).
Решение прямоугольного треугольника
Если известны катет a и гипотенуза c
Второй катет b определится по теореме Пифагора:
\[ b = \sqrt{c^2 — a^2} \]
Угол A определится по формуле синуса:
\[ \sin(A) = \frac{a}{c} \]
Поскольку сумма всех углов треугольника равна 180° то второй острый угол определится так:
\[ B = 180° — 90° — A \]
Вычислить, найти решение прямоугольного треугольника по двум сторонам (катет и гипотенуза)
Если известны катеты a и b
Гипотенуза с определится по теореме Пифагора:
\[ c = \sqrt{a^2 + b^2} \]
Угол A определится по формуле тангенса:
\[ \tg(A) = \frac{a}{b} \]
Поскольку сумма всех углов треугольника равна 180° то второй острый угол определится так:
\[ B = 180° — 90° — A \]
Вычислить, найти решение прямоугольного треугольника по двум сторонам (катет и катет)
Решение прямоугольного треугольника по стороне и острому углу
Если дан острый угол A, то B найдется по формуле:
\[ B = 90° — A \]
Стороны можно найти по следующим формулам:
\[ a = c · \sin(A) \] | \[ b = c · \cos(A) \] | \[ a = b · \tg(A) \] |
\[ b = c · \sin(B) \] | \[ a = c · \cos(B) \] | \[ b = a · \tg(B) \] |
\[ c = \frac{a}{\sin(A)} \] | \[ c = \frac{b}{\cos(A)} \] | \[ b = \frac{a}{\tg(A)} \] |
Вычислить, найти решение прямоугольного треугольника если известны катет a и противолежащий угол A
Здесь все углы мы найдем по формуле (7). Гипотенузу по формуле (14) и второй катет по формуле (16).
В помощь студенту
Решение прямоугольного треугольника |
стр. 237 |
|---|
www.fxyz.ru
Прямоугольный треугольник, формулы, задачи в общем виде
Тема этого занятия – «Прямоугольный треугольник, формулы, задачи в общем виде». Для начала дадим еще раз определение прямоугольному треугольнику, повторим основные тригонометрические функции и формулы, в которых он применяется. Решим задачи на вписанную в такие треугольники окружность и описанную вокруг них окружность.
Тема: Итоговое повторение курса геометрии за 7-9 классы
Урок: Прямоугольный треугольник, формулы, задачи в общем виде
Для начала рассмотрим задачи о вписанной и описанной окружности в прямоугольный треугольник.
Около любого треугольника можно описать окружность.
Центр описанной окружности лежит на пересечении серединных перпендикуляров треугольника.
Серединный перпендикуляр отрезка есть ГМТ (геометрическое место точек), равноудаленных от конца отрезка.
В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы.
Покажем это:
Дополним прямоугольный треугольник до прямоугольника.
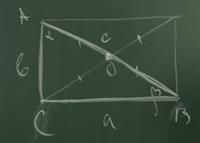
Диагонали прямоугольника точкой пересечения делятся пополам. Точка О равноудалена от концов отрезка и является точкой пересечения серединных перпендикуляров.
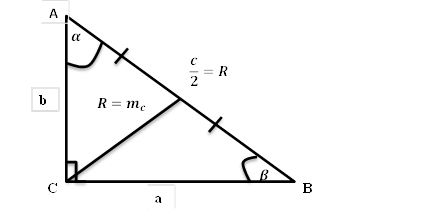
В любой треугольник можно вписать окружность.
Центр вписанной окружности лежит на пересечении биссектрис треугольника.
Точка пересечения биссектрис есть ГМТ (геометрическое место точек), равноудаленных от сторон треугольника.
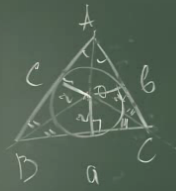
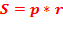
Доказательство:
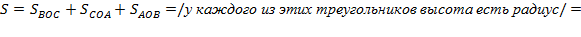
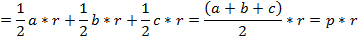
Напомним формулы для площади треугольника:
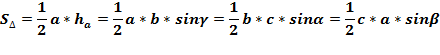
Теперь мы можем вычислить радиус вписанной окружности произвольного треугольника по формуле:
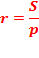
вычисляя S любым удобным способом.
Дан прямоугольный треугольник. Найти радиус вписанной окружности.
1. Проведем биссектрисы углов и получим центр вписанной окружности.
2. Из точки O центра вписанной окружности опускаем перпендикуляры на стороны и получаем точки касания M, K, L. Через них и пройдет вписанная окружность.
3. Отметим равные отрезки касательных.
Напомним: отрезки касательных, проведенных из одной точки к окружности, равны.
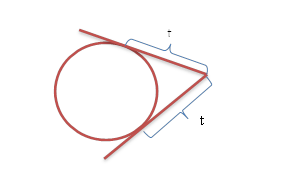
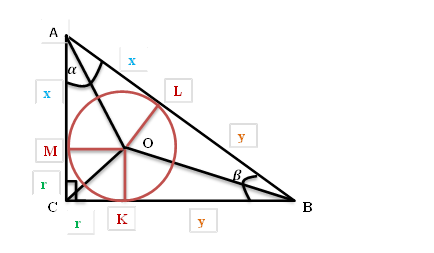
В нашем случае: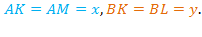 
Заметим, что CMOK – квадрат. Т.к. OM = OK = r, то и CM = CK = r.
4). Запишем связь между касательными и сторонами.
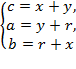
Сложим равенства:
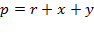
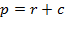
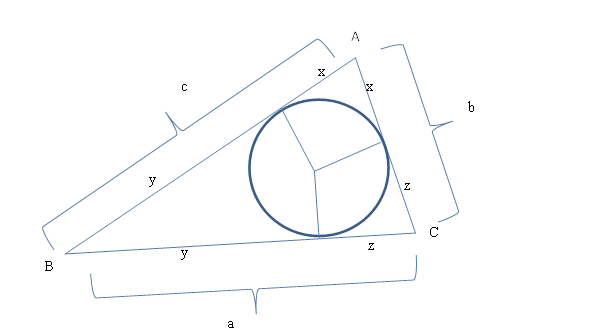
Аналогично рассуждая, получаем:
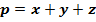
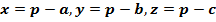
Список литературы
1. Зив Б.Г., Мейлер В.М. Геометрия. Дидактические материалы, 9 класс (Источник).
Домашнее задание
Задачи с пунктами С30, С31 (задачник Зив Б.Г.).
interneturok.ru