Прямоугольный треугольник формулы — Математическая шкатулка
Треугольник называется прямоугольным, если у него один из углов является прямым. Стороны, прилежащие к прямому углу, называются катетами, а сторона, лежащая напротив прямого угла, гипотенузой.
Прямоугольный треугольник: основные формулы
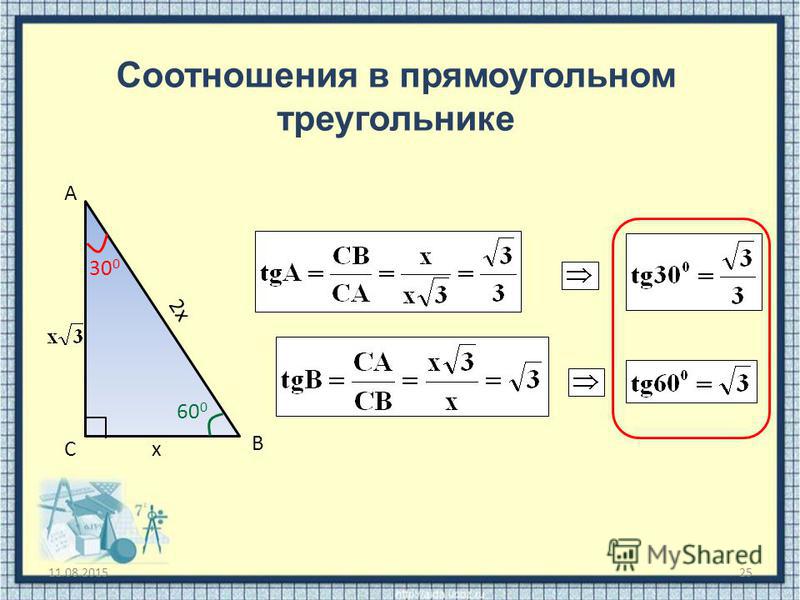
- Пусть <A = 30°. Катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы. CB = AB:2.
- Сумма острых углов прямоугольного треугольника равна 90°. <A + <B = 90°.
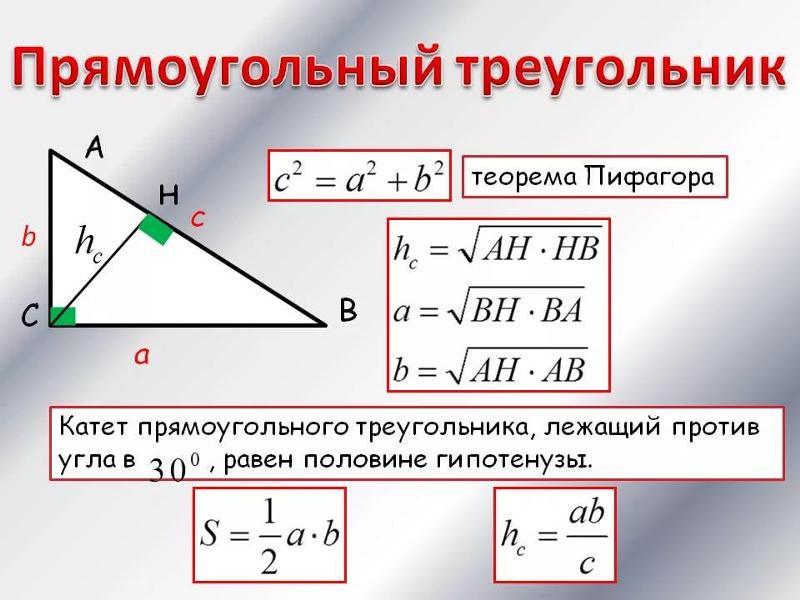
- Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. AB2 = AC2 + CB2
Прямоугольный треугольник: формулы площади и проекции
- Высота прямоугольного треугольника, проведенная к гипотенузе, равна : h = (ab):c.
- Высота прямоугольного треугольника, опущенная на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу: CH2 = AH·BH.
- Катет прямоугольного треугольника – среднее пропорциональное или среднее геометрическое между гипотенузой и проекцией этого катета на гипотенузу: CA

- Медиана, проведенная к гипотенузе прямоугольного треугольника, равна ее половине.
- Площадь прямоугольного треугольника равна половине произведения катетов. S = (ab):2.
- Площадь прямоугольного треугольника равна половине произведения гипотенузы и высоты. S = (hc):2.
Прямоугольный треугольник: формулы тригонометрия
- Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе. cosα = AC: AB.
- Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе. sinα = BC:AB.
- Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. tgα = BC:AC.
- Котангенс острого угла прямоугольного треугольника равен отношению прилежащего катета к противолежащему. ctgα = AC:BC.
- Основное тригонометрическое тождество: cos 2α + sin2α = 1.
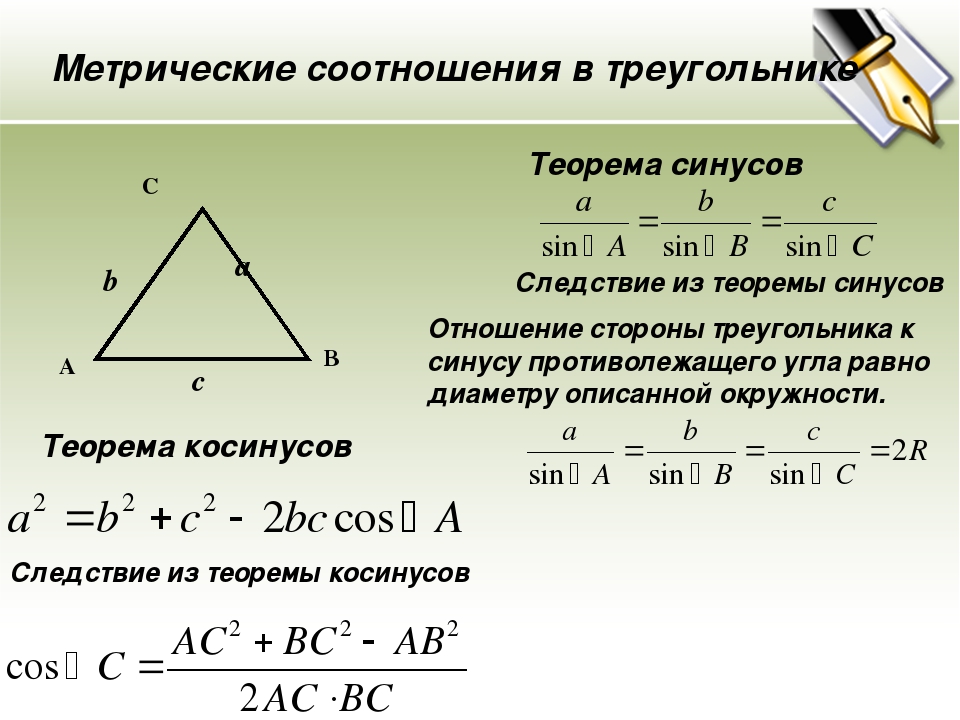
- Теорема косинусов: b2 = a2 + c2 – 2ac·cosα.

- Теорема синусов: CB :sinA = AC : sinB = AB.
Прямоугольный треугольник: формулы для описанной окружности
- Радиус описанной окружности равен половине гипотенузы : R=AB:2.
- Центр описанной окружности лежит на середине гипотенузы.
Прямоугольный треугольник: формулы для вписанной окружности
Радиус окружности, вписанной в прямоугольный треугольник, вычисляется по формуле: r = (a + b -c):2.
Рассмотрим применение тригонометрических формул прямоугольного треугольника при решении задания 6(вариант 32) из сборника для подготовки к ЕГЭ по математике профиль автора Ященко.
В треугольнике ABC угол С равен 90°, sinA = 11/14, AC =10√3. Найти АВ.
Решение:
- Применяя основное тригонометрическое тождество, найдем cosA = 5√3/14.
- По определению косинуса острого угла прямоугольного треугольника имеем: cosA = AC : AB, AB = AC : cosA = 10√3·14:5√3 = 28.
Ответ: AB = 28.
ЗАДАНИЕ 12 ЕГЭ МАТЕМАТИКА ПРОФИЛЬ( 20 ВАРИАНТ ЯЩЕНКО 2018)
Прямоугольные треугольники — урок.
 Геометрия, 7 класс.
Геометрия, 7 класс.Свойства прямоугольного треугольника
Сумма двух острых углов прямоугольного треугольника равна 90°.
Сумма углов треугольника равна 180°, а прямой угол равен 90°, поэтому сумма двух острых углов прямоугольного треугольника∡ \(1\) \(+\) ∡ \(2 =\) 90°.
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы (гипотенуза в два раза длиннее катета, лежащего против угла в \(\)30°\(\)).
Рассмотрим прямоугольный треугольник \(ABC\), в котором ∡ \(A\) — прямой, ∡ \(B =\) 30°, и значит, что ∡ \(C =\) 60°.
Докажем, что \(BC = 2 AC\).
Приложим к треугольнику \(ABC\) равный ему треугольник \(ABD\), как показано на рисунке.
Получим треугольник \(BCD\), в котором ∡ \(B =\) ∡ \(D =\) 60°, поэтому \(DC = BC\). Но \(DC = 2 AC\). Следовательно, \(BC = 2 AC\).
Справедливо и обратное суждение.
Если катет прямоугольного треугольника равен половине гипотенузы (или гипотенуза в два раза длиннее катета), то угол, лежащий против этого катета, равен 30°.
Признаки равенства прямоугольных треугольников
Основываясь на общих признаках равенства треугольников для прямоугольных треугольников можно сформулировать свои признаки равенства, потому что в прямоугольном треугольнике угол между двумя катетами — прямой, а любые два прямых угла равны.1. Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
3. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
4. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
Прямоугольный треугольник
Треугольник в геометрии представляет одну из основных фигур. Из предыдущих уроков вы знаете, что треугольник – это многоугольная фигура, которая имеет три угла и три стороны.
Треугольник называют прямоугольным, если у него есть прямой угол, который равен 90 градусов.
Прямоугольный треугольник имеет две взаимно перпендикулярные стороны, называемые катетами; третья его сторона называется гипотенузой. Гипотенуза является самой большой стороной этого треугольника.
- По свойствам перпендикуляра и наклонных гипотенуза длиннее каждого из катетов (но меньше их суммы).
- Сумма двух острых углов прямоугольного треугольника равна прямому углу.
- Две высоты прямоугольного треугольника совпадают с его катетами. Поэтому одна из четырех замечательных точек попадает в вершины прямого угла треугольника.
- Центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы.

- Медиана прямоугольного треугольника, проведенная из вершины прямоуго угла на гипотенузу, является радиусом описанной около этого треугольника окружности.
Свойства и особенности прямоугольных треугольников
I – е свойство. В прямоугольном треугольнике сумма его острых углов равна 90°. Против большей стороны треугольника лежит больший угол, а против большего угла лежит большая сторона. В прямоугольном треугольнике наибольшим углом, является прямоугольный угол. Если же в треугольнике самый большой угол имеет более 90°, то такой треугольник перестает быть прямоугольным, так как сумма всех углов превысить 180 градусов. Со всего этого следует, что гипотенуза является наибольшей стороной треугольника.
II – е свойство. Катет прямоугольного треугольника, который лежит против угла в 30 градусов, равен половине гипотенузе.
III – е свойство. Если же в прямоугольном треугольнике катет равняется половине гипотенузы, то и угол, который лежит напротив данного катета будет равен 30 градусам.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Больше интересного в телеграм @calcsboxУрок 25. прямоугольные треугольники — Геометрия — 7 класс
Геометрия
7 класс
Урок № 25
Прямоугольные треугольники
Перечень рассматриваемых вопросов:
- Виды треугольников.
- Прямоугольный треугольник.
- Свойства прямоугольного треугольника.
- Признаки равенства прямоугольных треугольников.
Тезаурус:
Остроугольный треугольник – треугольник, у которого все углы острые.
Тупоугольный треугольник – треугольник, у которого два угла острые, а третий – тупой.
Прямоугольный треугольник – треугольник, у которого один угол – прямой, т.е. равный 90°. Сторона прямоугольного треугольника, лежащая напротив прямого угла, называется гипотенузой, а две другие стороны – катетами.
Внешним углом треугольника называется угол, смежный любому углу треугольника. Его градусная мера равна сумме двух углов треугольника, не смежных с ним.
Основная литература:
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М.
 А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Давайте рассмотрим виды треугольников. Существуют следующие виды:
- Остроугольный треугольник – треугольник, у которого все углы острые.
- Тупоугольный треугольник – треугольник, у которого два угла острые, а третий – тупой.
- Прямоугольный треугольник – треугольник, у которого два угла острые, а один – прямой, т.е. равный 90°. Сторона прямоугольного треугольника, лежащая напротив прямого угла, называется гипотенузой, а две другие стороны – катетами.
Обратите внимание, на рисунке изображён треугольник АВС с прямым углом С, в прямоугольном треугольнике гипотенуза всегда является самой большой стороной.
Рассмотрим свойства прямоугольного треугольника:
- Сумма двух острых углов прямоугольного треугольника равна 90°.

Сумма всех углов треугольника равна 180°, прямой угол равен 900, следовательно, сумма двух острых углов прямоугольного треугольника равна 90°.
- Катет прямоугольного треугольника, лежащий напротив угла 300, равен половине гипотенузы.
Рассмотрим прямоугольный треугольник АВС, в котором ∠А – прямой, ∠В = 30° и, значит, ∠С = 60°.
Докажем, что FC = ½ BC
Достроим к треугольнику АВС равный ему треугольник ABD так, как у нас показано на рисунке. Получим треугольник ВСD, в котором ∠В = ∠D = 60°, поэтому DC = BC (по признаку равнобедренного треугольника). Но АС = ½ DC. Следовательно, АС = ½BC, что и требовалось доказать.
- Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
Рассмотрим прямоугольный треугольник АВС, у которого катет АС равен половине гипотенузы ВС. Докажем, что ∠ АВС = 30°.
Докажем, что ∠ АВС = 30°.
Достроим к треугольнику АВС равный ему треугольник ABD так, как у нас показано на рисунке. Получим равносторонний треугольник BCD. Углы равностороннего треугольника равны друг другу (т.к. сумма углов треугольника равна 180°, а в равностороннем треугольнике все углы равны, следовательно, 180° : 3= 60° – каждый угол равностороннего треугольника). В частности, ∠DВС = 60°. Но ∠DВС= 2∠АВС. Следовательно, ∠АВС = 30°, что и требовалось доказать.
Признаки равенства прямоугольных треугольников.
Так как в прямоугольном треугольнике угол между двумя катетами прямой, а любые два прямых угла равны, то из первого признака равенства треугольников следует:
если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
Далее из второго признака равенства треугольников следует:
если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему другого, то такие треугольники равны.
Рассмотрим ещё два признака равенства прямоугольных треугольников.
Теорема. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
Дано: ∆АВС и ∆НМХ, ∠С = ∠Х = 90°, АВ = НМ, ∠А = ∠Н.
Доказать: ∆АВС и ∆НМХ
Доказательство. Из первого свойства прямоугольных треугольников мы можем сделать вывод, что в таких треугольниках два других острых угла также равны, поэтому треугольники равны по второму признаку равенства треугольников (по стороне и двум прилежащим к ней углам). Теорема доказана.
Разбор заданий тренировочного модуля.
№ 1.Найдите острые углы прямоугольного равнобедренного треугольника.
Объяснение. Мы знаем, что сумма двух острых углов в прямоугольном треугольнике равна 90°, а в равнобедренном треугольнике углы при основании равны, следовательно, можно вычислить градусную меру острого угла прямоугольного равнобедренного треугольника: 90° : 2= 45°.
Ответ: острый угол прямоугольного равнобедренного треугольника равен 45°.
№ 2.Опираясь на рисунок, укажите, по какому признаку равны треугольники.
Варианты ответов:
- по катету и прилежащему к нему острому углу;
- по гипотенузе и прилежащему к ней острому углу;
- по катету и прямому углу;
- двум катетам.
Объяснение. На рисунке указано равенство катетов МС и ВС, углы МСН и ВСА вертикальны, значит, они равны. Следовательно, треугольники АВС и НСМ равны по катету и прилежащему к нему острому углу, подходит ответ 1.
Ответ: 1. по катету и прилежащему к нему острому углу.
Формула площади прямоугольного треугольника
В элементарной геометрии прямоугольным треугольником называется фигура, состоящая из трёх отрезков соединённых в точках, с углами два из которых острые, а один прямой (то есть равен 90°). Прямоугольный треугольник характеризуется целым рядом важных свойств, многие из которых составляют основу тригонометрии (например, соотношения между его сторонами и углами).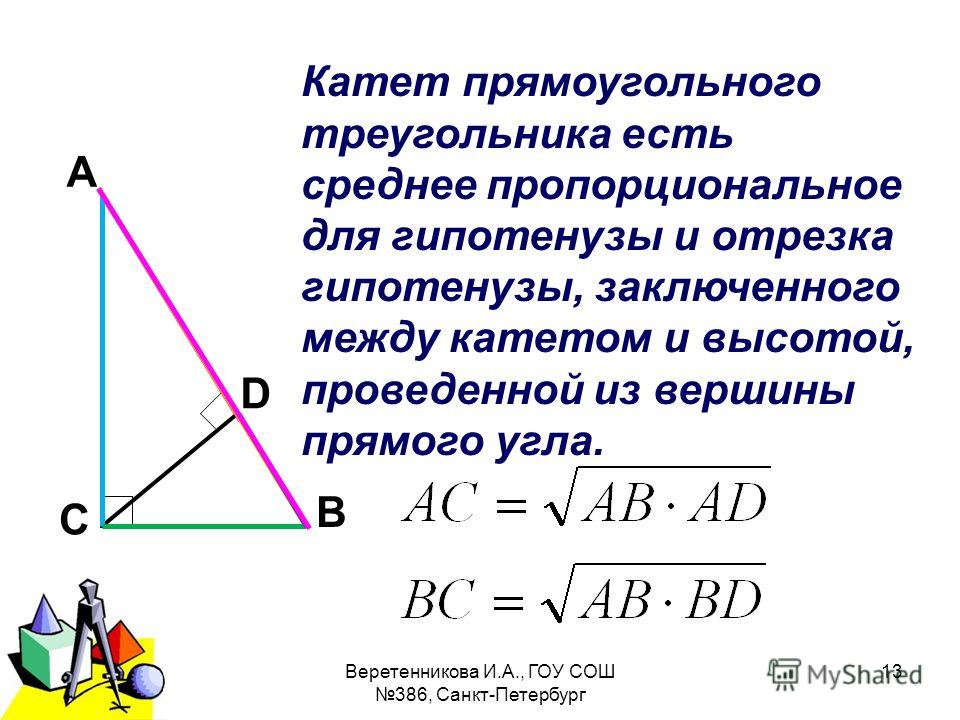 Еще со школьной скамьи все мы знаем, как вычислить площадь прямоугольного треугольника, а в повседневной жизни встречаемся с этой геометрической фигурой достаточно часто, порой даже не замечая этого. Достаточно широкое применение находит она в технике и поэтому такую задачу, как нахождение площади прямоугольного треугольника, часто приходится решать инженерам, конструкторам и архитекторам.
Еще со школьной скамьи все мы знаем, как вычислить площадь прямоугольного треугольника, а в повседневной жизни встречаемся с этой геометрической фигурой достаточно часто, порой даже не замечая этого. Достаточно широкое применение находит она в технике и поэтому такую задачу, как нахождение площади прямоугольного треугольника, часто приходится решать инженерам, конструкторам и архитекторам.
Зодчим определять эту величину требуется тогда, когда они проектируют здания с фронтонами, которые являются завершением фасадов и имеют треугольную форму ограниченную карнизом, а по бокам – скатами крыши. Нередко угол между скатами бывает прямой, и в таких случаях фронтон имеет форму прямоугольного треугольника. Определять его площадь требуется по той простой причине, что необходимо точно знать количество строительного материала, необходимого для его обустройства. Следует заметить, что фронтоны являются обязательными элементами малоэтажных строений (загородных домов, коттеджей, дач).
Нахождение площади прямоугольного треугольника
Формула расчёта площади прямоугольного треугольника
a – катет
b – катет
S – площадь прямоугольного треугольника
Форму прямоугольного треугольника имеют многие детали, из которых изготавливается современная мебель. Как известно, для того чтобы наиболее рационально использовать площадь помещений, все элементы обстановки должны размещаться в ней оптимальным образом. С пользой задействовать такие зоны, как углы, можно с помощью столов треугольной формы, столешницы которых в большинстве случаев представляют собой прямоугольные треугольники с катетами, вплотную прилегающими к стенам. При проектировании и расчете этих элементов конструкторы мебельного производства применяют формулу, по которой нахождение площади прямоугольного треугольника осуществляется на основе длины его сторон. Кроме того, им нередко приходится разрабатывать конструкции столиков, крепящихся непосредственно к стенам, в состав которых входят опорные элементы, также представляющие собой прямоугольные треугольники.
Строителям, занимающимся облицовочными работами, нередко в своей профессиональной деятельности приходится использовать керамическую плитку, имеющую форму прямоугольного треугольника с катетами одинаковой или различной длины. Им также приходится определять площадь этих элементов для того, чтобы выяснить необходимое их количество.
Форму прямоугольного треугольника имеет и такой важный и необходимый измерительный инструмент, как угольник. С его помощью производится построение и контроль прямых углов, а используется он очень широко и многими: от обычных школьников на уроках геометрии до конструкторов суперсовременной техники.
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК формулы площади, периметра, радиуса
Прямоугольный треугольник – это треугольник, у которого один из углов прямой (90°).
Другие виды треугольников:
Любой прямоугольный треугольник характеризуется катетами a и b и гипотенузой c (см. рисунок).
рисунок).
Катет – это сторона прямоугольного треугольника, образующая прямой угол с другой стороной (также катетом).
Гипотенуза – это сторона прямоугольного треугольника, лежащая напротив прямого угла.
Именно эти характеристики используются в формулах прямоугольного треугольника при вычислении площади, периметра, а также радиусов вписанной и описанной окружностей.
Формула радиуса вписанной окружности для прямоугольного треугольника
Радиус вписанной окружности r можно вычислить, зная стороны прямоугольного треугольника:
Формула радиуса описанной окружности для прямоугольного треугольника
Радиус описанной окружности R можно вычислить, зная гипотенузу прямоугольного треугольника:
Формула периметра прямоугольного треугольника
Периметр P прямоугольного треугольника можно получить, зная его стороны:
При вычислении площади прямоугольного треугольника часто требуется знать его полупериметр:
Формулы площади прямоугольного треугольника
При вычислении площади прямоугольного треугольника можно пользоваться формулами, которые применяются для вычисления площади произвольного треугольника, так как прямоугольный треугольник является частным случаем для треугольников.
Площадь прямоугольного треугольника S можно вычислить, зная его катеты a и b:
Еще одна формула позволяет вычислить площадь прямоугольного треугольника по его катетам a и b и полупериметру p (формула Герона):
S = (p – a) ⋅ (p – b)
Прямоугольный треугольник. Решения
Задачи на треугольник бывают простые, сложные и очень сложные. Если имеем прямоугольный треугольник то формулы для вычисления площади, катетов, радиусов вписанной и описанной окружности несколько упрощаются. Ниже приведены решения примеров на любой вкус, анализируйте их — возможно они помогут Вам в учебе.
Задача 1. Найдите синусы острых углов и гипотенузу прямоугольного треугольника если его катеты равны: а ) 6 см и 8 см; б) 4 см и 7 см.
Решение. Применим теорему Пифагора к заданным катетам
Для задания а) гипотенуза равна
та для б) соответственно
Синус острого угла в прямоугольном треугольнике равен отношению катета напротив угла к гипотенузе.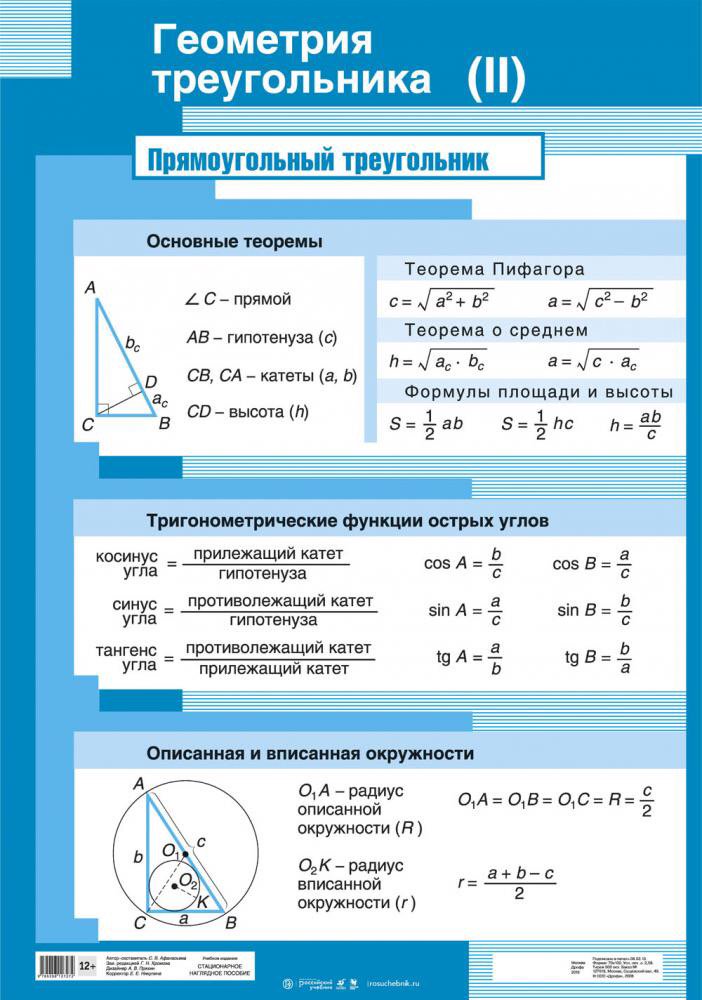
.
Рисунок с необходимыми формулами для синусов и формулой Пифагора приведен ниже
Вычисляем синусы искомых углов
а)
б)
На этом пример завершен.
————————
Задача 2. Найдите катеты прямоугольного треугольника если его гипотенуза и второй катет соответственно равны: а ) 15 см и 9 см; б) 8 см и 4 см.
Решение. На основе теоремы Пифагора получим
Подставляем значения
а)
б)
Ответ: Катеты треугольника равны 12 см и см.
————————
Задача 3. В прямоугольном треугольнике гипотенуза равна 17 см. Один из катетов на 7 см меньше гипотенузы. Определиите катеты треугольника.
Решение. Для заданного примера и подобных ему необходимо составлять уравнения. В этом примере обозначим через
x – большой катет. Тогда x-7 – меньший катет.
По формуле Пифагора имеем
Делим на два и решаем квадратное уравнение с помощью дискриминанта
Второй корень уравнения исключаем, поскольку он противоречит условию задачи.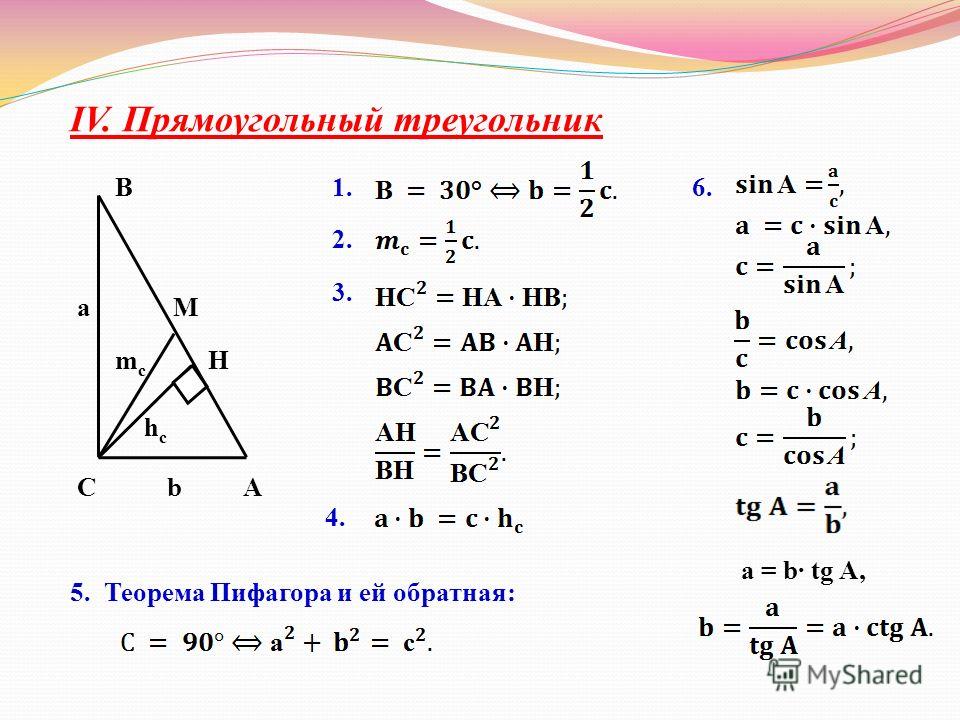 Таким образом один катет равен 15 см, а второй – 15-7=8 см.
Таким образом один катет равен 15 см, а второй – 15-7=8 см.
Ответ: Катеты прямоугольного треугольника равны 15 и 8 см.
————————
Задача 4. Вычислите длину высоты равностороннего треугольника сторона которого равна 12 см.
Решение. Если треугольник равносторонний то высота делит основание пополам. Кроме этого высота является перпендикуляром. Таким образом задача состоит в нахождении катета когда известно, что гипотенуза равна 12 см, а второй катет – 12/2=6 см.
По теореме Пифагора вычисляем
Ответ: Катет равен см.
————————
Задача 5. Сторона квадрата равна 7 см. Определите длину диагонали.
Решение. Поскольку стороны квадрата равны то нужно найти гипотенузу прямоугольного равнобедренного
треугольника с катетами длиной 7 см. Используем известную формулу Пифагора
Ответ: Диагональ квадрата равна см.
————————
Задача 6. Большая диагональ и большая основа прямоугольной трапеции равны соответственно 8 см и 6 см.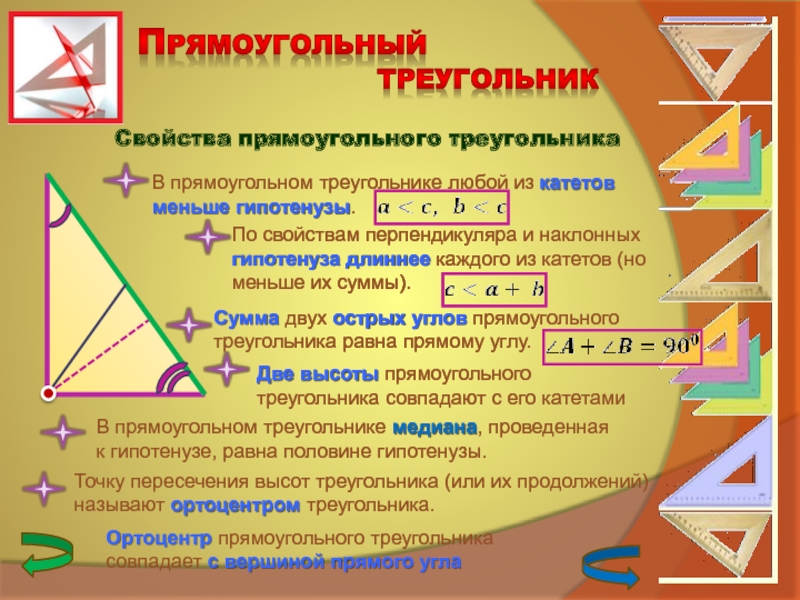 Найдите длину меньшей боковой стороны трапеции.
Найдите длину меньшей боковой стороны трапеции.
Решение. Рассмотрим вспомогательный рисунок трапеции.
По условию известна диагональ BD=8 см и AD=6 см. Катет AB прямоугольного треугольника находим по формуле
Ответ: Сторона трапеции равна см.
————————
Задача 7. В треугольнике АВС угол В = 90 градусов, ВD перпендикулярна АС, АВ = 16 см, ВС = 12 см. Найдите длину отрезка АD и тангенс угла при основании.
Решение. Рассмотрим вспомогательный рисунок к заданию.
Составим пропорции для отыскания отрезка AD
Второе уравнение построим на основе теоремы Пифагора
Думаю выше Вам все понятно. Следующим шагом подставляем DC и значение катетов в уравнение
Отрезок найдено, тангенс угла А находим по формуле
Определим длину гипотенузы — для этого найдем неизвестную часть DC
Гипотенуза равна сумме AD+DC
Вычислим тангенс угла при основании
Ответ: AD=80/7, tan(A)=0,8.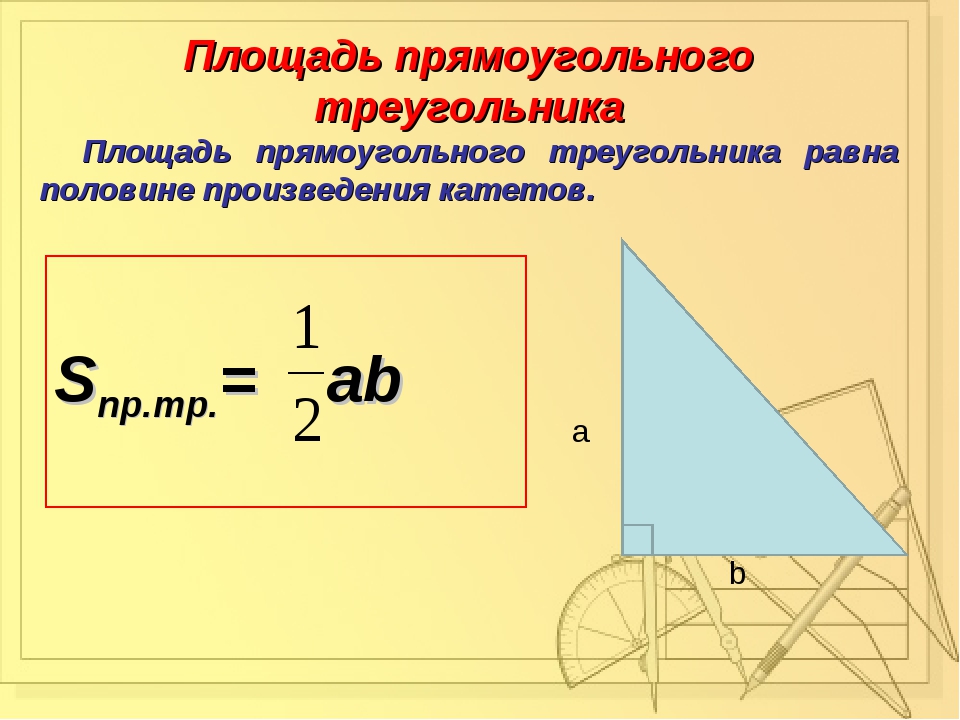
————————
Задача 8. Периметр прямоугольного треугольника равен 12 см, а один из из его катетов — 3 см. Найдите площадь
треугольника.
Решение. Данный пример на сложение уравнения с неизвестными.
Первое уравнение соответствует формуле периметра треугольника, второе — теореме Пифагора.
Обозначим b – неизвестный катет, с – гипотенуза треугольника.
Составляем систему уравнений
Имеем два уравнения с двумя неизвестными. Метод решения Вам известен: из первого уравнения выражаем одну из переменных и подставляем во второе. В результате после упрощений получим квадратное уравнение один из корней которого и будет решением. Второй получим в результате подстановки в первую зависимость системы уравнений.
У меня получилось что b=4 см, c=5 см.
Если не верите то можете пройти описанные выше процедуры.
Площадь находим как половину произведения катетов
Ответ: площадь треугольника 6 сантиметров квадратных.
————————
Задача 9. Катеты прямоугольного треугольника равны 3 см и 4 см. Найти радиус вписанной и описанной окружности.
Катеты прямоугольного треугольника равны 3 см и 4 см. Найти радиус вписанной и описанной окружности.
Решение. Радиус описанной окружности найти легче — он равен половине гипотенузы. Вычисляем ее длину по теореме Пифагора
Отсюда находим больший радиус
Радиус вписанной в прямоугольный треугольник окружности можно найти несколькими способами.
Пойдем простым и определим его на основе формулы площади треугольника
Как видите вычислить радиус вписанной окружности достаточно просто. Находим площадь треугольника
и подставляем в предыдущую формулу
Вот такой сложный на восприятие пример легко решается при знании необходимых формул.
Ответ: радиусы описанной и вписанной окружности равны 2,5 см и 1 см соответственно.
————————
Изучайте формулы основных геометрических фигур, набирайтесь опыта на практике и со временем примеры будете решать без труда. Если же не удается решить пример или задачу, или непонятно условие задачи обращайтесь к специалистам. На этом сайте и подобных интернет ресурсах Вы всегда можете решить любую сложную задачу.
На этом сайте и подобных интернет ресурсах Вы всегда можете решить любую сложную задачу.
Посмотреть материалы
Площадь круга, треугольника, квадрата, прямоугольника, параллелограмма, трапеции, эллипса и сектора
Площадь — это размер поверхности!
Узнайте больше о площади или воспользуйтесь калькулятором площади.
Пример: Какова площадь этого прямоугольника?
Формула:
Площадь = w × h
w = ширина
h = высота
Мы знаем, что w = 5 и h = 3 , поэтому:
Площадь = 5 × 3 = 15
Пример: Какова площадь этого круга?
Радиус = r = 3
| Площадь | = π × r 2 | |
| = π × 3 2 | ||
| = π × (3 × 3) | ||
= 3. 14159 … × 9 14159 … × 9 | ||
| = 28,27 (до 2 знаков после запятой) |
Пример: Какова площадь этого треугольника?
Высота = h = 12
База = b = 20
Площадь = ½ × b × h = ½ × 20 × 12 = 120
Более сложный пример:
Пример: Сэм косит траву по цене 0,10 доллара за квадратный метр
Сколько зарабатывает Сэм, обрабатывая эту область:
Разобьем область на две части:
Часть А представляет собой квадрат:
Площадь A = a 2 = 20 м × 20 м = 400 м 2
Часть B представляет собой треугольник.При взгляде сбоку он имеет основание 20 м и высоту 14 м.
Площадь B = ½b × h = ½ × 20 м × 14 м = 140 м 2
Итак, общая площадь:
Площадь = Площадь A + Площадь B = 400 м 2 + 140 м 2 = 540 м 2
Сэм зарабатывает 0,10 доллара за квадратный метр
Сэм зарабатывает = 0,10 доллара × 540 млн 2 = 54 доллара
3.
 4: Треугольники, прямоугольники и теорема Пифагора
4: Треугольники, прямоугольники и теорема ПифагораЦели обучения
К концу этого раздела вы сможете:
- Решать приложения, используя свойства треугольников
- Используйте теорему Пифагора
- Решение приложений с использованием свойств прямоугольника
Прежде чем начать, пройдите тест на готовность.
- Упростить: \ (12 (6h) \).
Если вы пропустили эту проблему, просмотрите Упражнение 1.10.1. - Длина прямоугольника на три меньше ширины. Пусть w представляет ширину. Напишите выражение для длины прямоугольника.
Если вы пропустили эту проблему, просмотрите упражнение 1.3.43. - Решите: \ (A = \ frac {1} {2} bh \) для b, когда A = 260 и h = 52.
Если вы пропустили эту проблему, просмотрите упражнение 2.6.10. - Упростить: \ (\ sqrt {144} \).
Если вы пропустили эту проблему, просмотрите Упражнение 1.9.10.
Решение приложений с использованием свойств треугольников
В этом разделе мы будем использовать некоторые общие геометрические формулы. Мы адаптируем нашу стратегию решения проблем, чтобы мы могли решать геометрические приложения. Формула геометрии назовет переменные и даст нам уравнение для решения. Кроме того, поскольку все эти приложения будут включать в себя какие-то формы, большинство людей сочтут полезным нарисовать фигуру и пометить ее с заданной информацией. Мы включим это в первый шаг стратегии решения проблем для геометрических приложений.
Мы адаптируем нашу стратегию решения проблем, чтобы мы могли решать геометрические приложения. Формула геометрии назовет переменные и даст нам уравнение для решения. Кроме того, поскольку все эти приложения будут включать в себя какие-то формы, большинство людей сочтут полезным нарисовать фигуру и пометить ее с заданной информацией. Мы включим это в первый шаг стратегии решения проблем для геометрических приложений.
РЕШЕНИЕ ГЕОМЕТРИЧЕСКИХ ПРИЛОЖЕНИЙ
- Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте фигуру и напишите на ней указанную информацию.
- Определите то, что мы ищем.
- Обозначьте то, что мы ищем, выбирая переменную для его представления.
- Переведите в уравнение, написав соответствующую формулу или модель для ситуации. Подставьте в данную информацию.
- Решите уравнение, используя хорошие методы алгебры.

- Проверьте ответ, подставив его обратно в уравнение, решенное на шаге 5, и убедившись, что он имеет смысл в контексте проблемы.
- Ответьте на вопрос полным предложением.
Мы начнем с геометрических приложений, изучив свойства треугольников. Давайте рассмотрим некоторые основные факты о треугольниках. Треугольники имеют три стороны и три внутренних угла.Обычно каждая сторона помечена строчной буквой, которая соответствует прописной букве противоположной вершины.
Множественное число слова вершина составляет вершин . У всех треугольников по три вершины . Треугольники названы по их вершинам: Треугольник на рисунке \ (\ PageIndex {1} \) называется \ (\ треугольник {ABC} \).
Рисунок \ (\ PageIndex {1} \): треугольник ABC имеет вершины \ (A \), \ (B \) и \ (C \). Длины сторон равны \ (a \), \ (b \) и \ (c \).
Три угла треугольника связаны особым образом.{\ circ} \]
- Сумма углов треугольника равна 180 °.
Периметр:
\ [P = a + b + c \]
- Периметр — это сумма длин сторон треугольника.
Площадь:
\ (A = \ frac {1} {2} bh, b = \ text {base}, h = \ text {height} \)
- Площадь треугольника равна половине основания, умноженной на высоту.
Пример \ (\ PageIndex {1} \)
Размеры двух углов треугольника — 55 и 82 градуса.Найдите размер третьего угла.
Решение

\ (\ begin {array} {rll} {55 + 82 + 43} & {\ stackrel {?} {=}} & {180} \\ {180} & {=} & {180 \ checkmark} \ конец {массив} \)
Попробовать \ (\ PageIndex {1} \)
Размеры двух углов треугольника — 31 и 128 градус. Найдите размер третьего угла.
- Ответ
21 градус
Попробовать \ (\ PageIndex {2} \)
Размеры двух углов треугольника — 49 и 75 градусов.Найдите размер третьего угла.
- Ответ
56 градусов
Пример \ (\ PageIndex {2} \)
Периметр треугольного сада составляет 24 фута. Длина двух сторон четыре фута и девять футов. Какова длина третьей стороны?
Решение
Попробовать \ (\ PageIndex {3} \)
Периметр треугольного сада составляет 48 футов. Длина двух сторон 18 футов и 22 фута.Какова длина третьей стороны?
- Ответ
8 футов
Попробовать \ (\ PageIndex {4} \)
Длина двух сторон треугольного окна составляет семь футов пять футов. Периметр 18 футов. Какова длина третьей стороны?
- Ответ
6 футов
Пример \ (\ PageIndex {3} \)
Площадь треугольного церковного окна — 90 квадратных метров.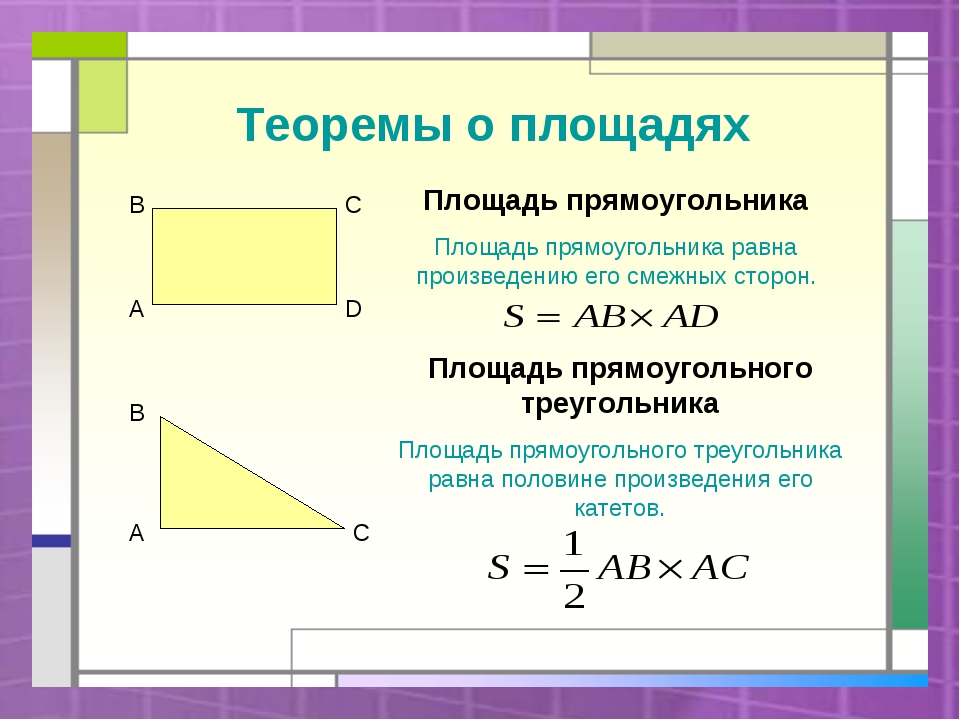 {2} \)
{2} \)
\ (12 = h \)
\ (\ begin {array} {rll} {A} & {=} & {\ frac {1} {2} bh} \\ {90} & {\ stackrel {?} {=}} & {\ frac {1} {2} \ cdot 15 \ cdot 12} \\ {90} & {=} & {90 \ checkmark} \ end {array} \)
 Ответьте на вопрос.
Ответьте на вопрос.Попробовать \ (\ PageIndex {5} \)
Площадь треугольной картины составляет 126 квадратных дюймов. База 18 дюймов. Какая высота?
- Ответ
14 дюймов
Попробовать \ (\ PageIndex {6} \)
Треугольная дверь палатки имеет площадь 15 квадратных футов. Высота пять футов.Что такое база?
- Ответ
6 футов
Свойства треугольника, которые мы использовали до сих пор, применимы ко всем треугольникам. Теперь мы рассмотрим один конкретный тип треугольника — прямоугольный треугольник. Прямоугольный треугольник имеет один угол 90 °, который мы обычно отмечаем маленьким квадратом в углу.
Рисунок \ (\ PageIndex {3} \)Определение: ПРАВЫЙ ТРЕУГОЛЬНИК
Прямоугольный треугольник имеет один угол 90 °, который часто отмечается квадратом в вершине.
Пример \ (\ PageIndex {4} \)
Один угол прямоугольного треугольника составляет 28 °. Какова мера третьего угла?
Решение
 Решите уравнение.
Решите уравнение.\ (\ begin {array} {rll} {180} & {\ stackrel {?} {=}} & {90 + 28 + 62} \\ {180} & {=} & {180 \ checkmark} \ конец {массив} \)
Попробовать \ (\ PageIndex {7} \)
Один угол прямоугольного треугольника составляет 56 °. Какова мера другого малого угла?
- Ответ
34 °
Попробовать \ (\ PageIndex {8} \)
Один угол прямоугольного треугольника составляет 45 °.Какова мера другого малого угла?
- Ответ
45 °
В примерах, которые мы видели до сих пор, мы могли нарисовать фигуру и пометить ее сразу после прочтения задачи. В следующем примере нам нужно будет определить один угол через другой. Мы будем ждать, чтобы нарисовать фигуру, пока не напишем выражения для всех искомых углов.
В следующем примере нам нужно будет определить один угол через другой. Мы будем ждать, чтобы нарисовать фигуру, пока не напишем выражения для всех искомых углов.
Пример \ (\ PageIndex {5} \)
Размер одного угла прямоугольного треугольника на 20 градусов больше, чем размер самого маленького угла.{rd} \) угол (прямой угол)
Подставить в формулу.
\ (\ begin {align *} 2a + 110 & = 180 \\ [3pt]
2a & = 70 \\ [3pt]
a & = 35 \ text {first angle} \\ [3pt]
a & + 20 \ text {второй угол} \\ [3pt]
{\ color {red} {35}} & + 20 = 55 \ end {align *} \)
И третий угол равен 90.
\ (\ begin {array} {rll} {35 + 55 + 90} & {\ stackrel {?} {=}} & {180} \\ {180} & {=} & {180 \ checkmark} \ конец {массив} \)
Попробовать \ (\ PageIndex {9} \)
Размер одного угла прямоугольного треугольника на 50 ° больше, чем размер наименьшего угла.Найдите размеры всех трех углов.
- Ответ
20 °, 70 °, 90 °
Попробовать \ (\ PageIndex {10} \)
Размер одного угла прямоугольного треугольника на 30 ° больше, чем размер самого маленького угла. Найдите размеры всех трех углов.
- Ответ
30 °, 60 °, 90 °
Используйте теорему Пифагора
Мы узнали, как соотносятся друг с другом размеры углов треугольника. Теперь мы узнаем, как длины сторон соотносятся друг с другом. Важное свойство, которое описывает взаимосвязь между длинами трех сторон прямоугольного треугольника, называется теоремой Пифагора . Эта теорема использовалась во всем мире с древних времен. Он назван в честь греческого философа и математика Пифагора, жившего около 500 г. до н.э.
Теперь мы узнаем, как длины сторон соотносятся друг с другом. Важное свойство, которое описывает взаимосвязь между длинами трех сторон прямоугольного треугольника, называется теоремой Пифагора . Эта теорема использовалась во всем мире с древних времен. Он назван в честь греческого философа и математика Пифагора, жившего около 500 г. до н.э.
Прежде чем сформулировать теорему Пифагора, нам нужно ввести некоторые термины для сторон треугольника.Помните, что прямоугольный треугольник имеет угол 90 °, отмеченный небольшим квадратом в углу. Сторона треугольника, противоположная углу 90 ° 90 °, называется гипотенузой , а каждая из других сторон называется катетами .
Рисунок \ (\ PageIndex {4} \) Теорема Пифагора говорит, как длины трех сторон прямоугольного треугольника соотносятся друг с другом. В нем говорится, что в любом прямоугольном треугольнике сумма квадратов длин двух катетов равна квадрату длины гипотенузы.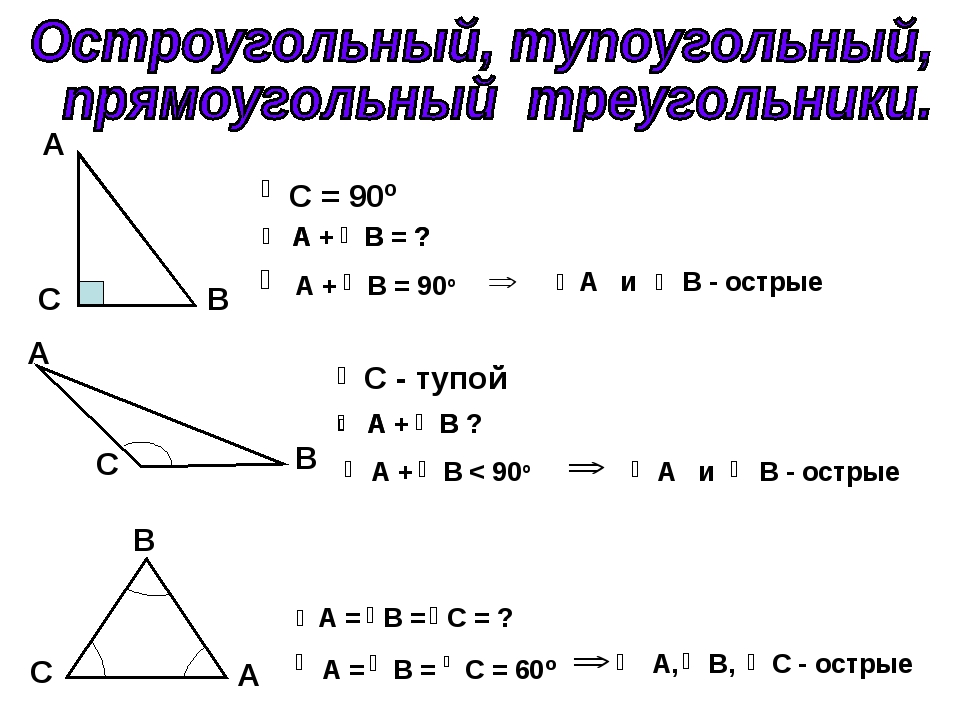 {2} \).
{2} \).
Поскольку теорема Пифагора содержит возведенные в квадрат переменные, чтобы найти длину стороны прямоугольного треугольника, нам придется использовать квадратные корни.
Пример \ (\ PageIndex {6} \)
Используйте теорему Пифагора, чтобы найти длину гипотенузы, показанной ниже.
Решение
Этикетка сторона c на рисунке.

Попробовать \ (\ PageIndex {11} \)
Используйте теорему Пифагора, чтобы найти длину гипотенузы в треугольнике, показанном ниже.
- Ответ
с = 10
Попробовать \ (\ PageIndex {12} \)
Используйте теорему Пифагора, чтобы найти длину гипотенузы в треугольнике, показанном ниже.
- Ответ
с = 13
Пример \ (\ PageIndex {7} \)
Используйте теорему Пифагора, чтобы найти длину ноги, показанной ниже.
Решение
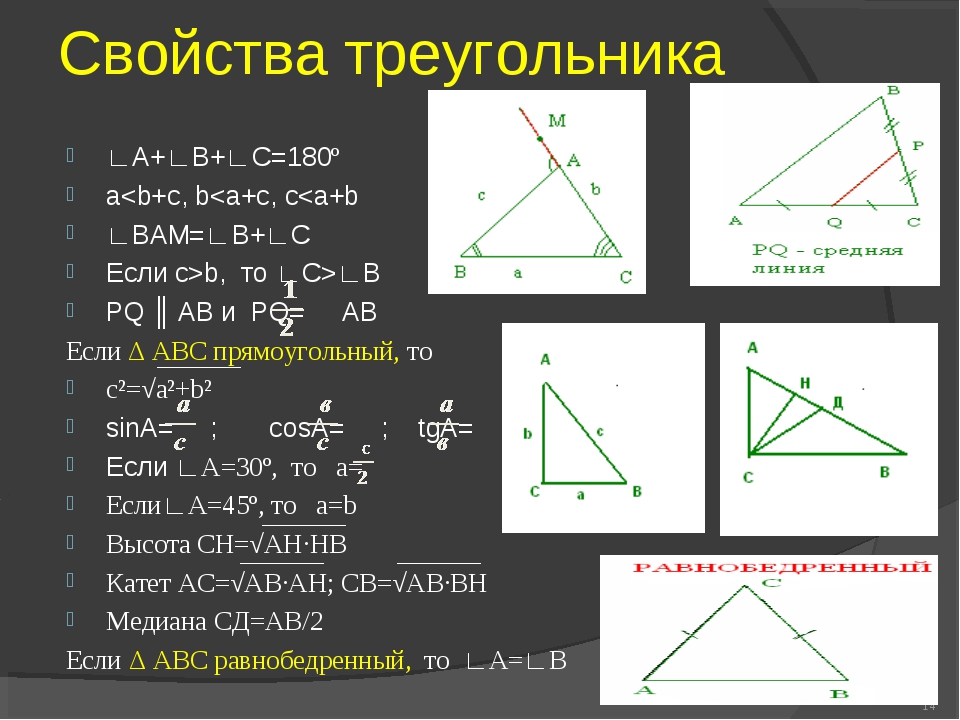
Попробовать \ (\ PageIndex {13} \)
Используйте теорему Пифагора, чтобы найти длину катета в треугольнике, показанном ниже.
- Ответ
8
Попробовать \ (\ PageIndex {14} \)
Используйте теорему Пифагора, чтобы найти длину катета в треугольнике, показанном ниже.
- Ответ
12
Пример \ (\ PageIndex {8} \)
Кельвин строит беседку и хочет укрепить каждый угол, разместив 10-дюймовый кусок дерева по диагонали, как показано выше.
Если он скрепляет деревянную балку так, чтобы концы распорки находились на одинаковом расстоянии от угла, какова длина ног прямоугольного треугольника? Примерно с точностью до десятых долей дюйма.
Решение
\ (\ begin {array} {ll} {\ textbf {Шаг 1.} \ text {Прочтите проблему.}} & {} \\\\ {\ textbf {Шаг 2} \ text {Определите, кто мы ищем.}} & {\ text {расстояние от угла, к которому должна быть прикреплена скобка}} \\ {} & {\ text {}} \\ \\ {\ textbf {Шаг 3.{2} \ text {Да.}} & {} \\\\ {\ textbf {Шаг 7. Ответьте на вопрос.}} & {\ Text {Кельвен должен закрепить каждый кусок}} \\ {} & {\ текст {дерево примерно в 7,1 дюйма от угла.}} \ end {array} \)
Попробовать \ (\ PageIndex {15} \)
Джон ставит основание 13-футовой лестницы в пяти футах от стены своего дома, как показано ниже. Как далеко до стены поднимается лестница?
- Ответ
12 футов
Попробовать \ (\ PageIndex {16} \)
Рэнди хочет прикрепить 17-футовую гирлянду огней к вершине 15-футовой мачты своей парусной лодки, как показано ниже. На каком расстоянии от основания мачты он должен прикрепить конец световой струны?
На каком расстоянии от основания мачты он должен прикрепить конец световой струны?
- Ответ
8 футов
Решение приложений с использованием свойств прямоугольника
Возможно, вы уже знакомы со свойствами прямоугольников. Прямоугольники имеют четыре стороны и четыре прямых (90 °) угла. Противоположные стороны прямоугольника имеют одинаковую длину. Мы называем одну сторону прямоугольника длиной \ (L \), а его прилегающую сторону — шириной \ (W \).
Расстояние вокруг этого прямоугольника равно \ (L + W + L + W \) или \ (2L + 2W \). Это периметр , \ (P \) прямоугольника.
\ [P = 2L + 2W \]
А как насчет области прямоугольника? Представьте себе прямоугольный коврик длиной 2 фута и шириной 3 фута. Его площадь составляет 6 квадратных футов. На рисунке шесть квадратов.
\ [\ begin {array} {l} {A = 6} \\ {A = 2 \ cdot3} \\ {A = L \ cdot W} \ end {array} \]
Площадь равна длине, умноженной на ширину. Формула площади прямоугольника
Формула площади прямоугольника
\ [A = LW. \]
СВОЙСТВА ПРЯМОУГОЛЬНИКА
Прямоугольник имеет четыре стороны и четыре прямых (90 °) угла.
Длины противоположных сторон равны.
Периметр прямоугольника равен сумме удвоенной длины и удвоенной ширины.
\ [P = 2L + 2W \]
Площадь прямоугольника равна произведению длины и ширины.
\ [A = L · W \]
Пример \ (\ PageIndex {9} \)
Длина прямоугольника 32 метра, ширина 20 метров.Какой периметр?
Решение
Нарисуйте рисунок и напишите на нем указанную информацию.

\ (P = 104 \)
\ (\ begin {array} {rcl} {P} & {\ stackrel {?} {=}} & {104} \\ {20 + 32 + 20 + 32} & {\ stackrel {?} {= }} & {104} \\ {104} & {=} & {104 \ checkmark} \ end {array} \)
Попробовать \ (\ PageIndex {17} \)
Длина прямоугольника составляет 120 ярдов, а ширина — 50 ярдов. Какой периметр?
- Ответ
340 ярдов
Попробовать \ (\ PageIndex {18} \)
Длина прямоугольника 62 фута, ширина 48 футов. Какой периметр?
Какой периметр?
- Ответ
220 футов
Пример \ (\ PageIndex {10} \)
Площадь прямоугольной комнаты составляет 168 квадратных футов.Длина 14 футов. Какая ширина?
Решение
Нарисуйте рисунок и напишите на нем указанную информацию.
 Решите уравнение.
Решите уравнение.\ (\ frac {168} {14} = \ frac {14W} {14} \)
\ (12 = Вт \)
\ (\ begin {array} {rcl} {A} & {=} & {LW} \\ {168} & {\ stackrel {?} {=}} & {14 \ cdot 12} \\ { 168} & {=} & {168 \ checkmark} \ end {array} \)
Попробовать \ (\ PageIndex {19} \)
Площадь прямоугольника составляет 598 квадратных футов. Длина 23 фута.Какая ширина?
- Ответ
26 футов
Попробовать \ (\ PageIndex {20} \)
Ширина прямоугольника 21 метр. Площадь 609 кв. Какая длина?
- Ответ
29 метров
Пример \ (\ PageIndex {11} \)
Найдите длину прямоугольника с периметром 50 дюймов и шириной 10 дюймов.
Решение
Попробовать \ (\ PageIndex {21} \)
Найдите длину прямоугольника с периметром 80 и шириной 25.
- Ответ
15
Попробовать \ (\ PageIndex {22} \)
Найдите длину прямоугольника: периметр 30 и ширина 6.
- Ответ
9
Мы решили задачи, в которых задавалась длина или ширина, а также периметр или площадь; Теперь мы научимся решать задачи, в которых ширина определяется длиной.Мы будем ждать, чтобы нарисовать фигуру, пока не напишем выражение для ширины, чтобы мы могли пометить одну сторону этим выражением.
Пример \ (\ PageIndex {12} \)
Ширина прямоугольника на два фута меньше его длины. Периметр — 52 фута. Найдите длину и ширину.
Решение
| Шаг 1. Прочтите проблему. | |
| Шаг 2. Определите , что вы ищете. | длина и ширина прямоугольника |
| Шаг 3. Имя. Выберите переменную для ее представления. Так как ширина определяется длиной, мы полагаем длину \ (L = \). Ширина на два фута меньше длины, поэтому мы принимаем ширину \ (L-2 \). | \ (P = 52 \) фут |
| Шаг 4. Переведите . | |
| Напишите соответствующую формулу.Формула периметра прямоугольника связывает всю информацию. | \ (P = 2L + 2W \) |
| Заменить в данной информации. | \ (52 = 2L + 2 (L − 2) \) |
| Шаг 5. Решите уравнение. | \ (52 = 2L + 2L − 4 \) |
| Объедините похожие термины. | \ (52 = 4L − 4 \) |
| Добавьте по 4 с каждой стороны. | \ (56 = 4 л \) |
| Разделить на 4. | \ (\ frac {56} {4} = \ frac {4L} {4} \) \ (14 = L \) Длина 14 футов. |
| Теперь нам нужно найти ширину. | Ширина равна \ (L − 2 \). Ширина 12 футов. |
| Шаг 6. Проверьте. Так как \ (14 + 12 + 14 + 12 = 52 \), это работает! | |
| Шаг 7. Ответьте на вопрос. | Длина 14 футов, ширина 12 футов. |
Попробовать \ (\ PageIndex {23} \)
Ширина прямоугольника на семь метров меньше его длины. Периметр — 58 метров. Найдите длину и ширину.
- Ответ
18 метров, 11 метров
Попробовать \ (\ PageIndex {24} \)
Длина прямоугольника на восемь футов больше ширины. Периметр — 60 футов. Найдите длину и ширину.
- Ответ
19 футов 11 футов
Пример \ (\ PageIndex {13} \)
Длина прямоугольника на четыре сантиметра больше ширины в два раза.По периметру 32 сантиметра. Найдите длину и ширину.
Решение
Попробовать \ (\ PageIndex {25} \)
Длина прямоугольника в восемь раз больше ширины в два раза. Периметр равен 64. Найдите длину и ширину.
- Ответ
24, 8
Попробовать \ (\ PageIndex {26} \)
Ширина прямоугольника в шесть раз меньше его длины в два раза. Периметр 18.Найдите длину и ширину.
- Ответ
5, 4
Пример \ (\ PageIndex {14} \)
Периметр прямоугольного бассейна составляет 150 футов. Длина на 15 футов больше ширины. Найдите длину и ширину.
Решение
Попробовать \ (\ PageIndex {27} \)
Периметр прямоугольного бассейна составляет 200 футов. Длина на 40 футов больше ширины.Найдите длину и ширину.
- Ответ
70 футов, 30 футов
Попробовать \ (\ PageIndex {28} \)
Длина прямоугольного сада на 30 ярдов больше ширины. Периметр 300 ярдов. Найдите длину и ширину.
- Ответ
90 ярдов, 60 ярдов
Ключевые понятия
- Стратегия решения проблем для геометрических приложений
- Прочтите задачу и сделайте так, чтобы все слова и идеи были понятны.Нарисуйте фигуру и напишите на ней указанную информацию.
- Определите то, что мы ищем.
- Назовите то, что мы ищем, выбрав переменную для его представления.
- Переведите в уравнение, написав соответствующую формулу или модель для ситуации. Подставьте в данную информацию.
- Решите уравнение, используя хорошие методы алгебры.
- Проверьте ответ в задаче и убедитесь, что он имеет смысл.{2} \), где \ (c \) — длина гипотенузы, а \ (a \) и \ (b \) — длины катетов.
- Свойства прямоугольников
- Прямоугольники имеют четыре стороны и четыре прямых (90 °) угла.
- Длины противоположных сторон равны.
- Периметр прямоугольника равен сумме удвоенной длины и удвоенной ширины: \ (P = 2L + 2W \).
- Площадь прямоугольника равна длине, умноженной на ширину: \ (A = LW \).
Как решать задачи геометрии с использованием прямоугольников и треугольников
o Пункт
o Строка
o Линейный сегмент
или Луч
o Угол
o Прямоугольник
o Периметр
o Площадь
o Площадь
o Треугольник
Цели
o Ознакомьтесь с некоторыми фундаментальными геометрическими фигурами
o Вычислить периметр и площадь прямоугольника
o Вывести формулу площади треугольника
Геометрия изучает точки, линии, формы, углы и отношения между ними.Мы рассмотрим некоторые простые формы, такие как треугольники и прямоугольники, и обсудим, как вычислить некоторые из их свойств.
Элементы геометрии
Прежде чем рассматривать некоторые более сложные фигуры, мы должны понять определенные термины, которые используются на протяжении всего изучения геометрии. Несколько основных геометрических понятий включают точки, линии и углы. Точка — это, по сути, местоположение — оно часто обозначается маленькой точкой, представляет собой местоположение в пространстве и не имеет длины, ширины или глубины.Ниже показаны несколько точек.
Линия в геометрии имеет большинство тех же характеристик, что и в реальной жизни (и в алгебре). Геометрическая линия прямая и бесконечно продолжается в противоположных направлениях. Если две прямые пересекаются в одной точке, то говорят, что они пересекаются на . Пример линии показан ниже; обратите внимание, что на концах линии есть стрелки, указывающие, что линия продолжается бесконечно.
Конечная часть линии называется сегментом линии . Сегменты линии имеют конечную (ограниченную) длину, в отличие от линий, длина которых бесконечна (неограничена). Линейный сегмент показан ниже; концы отрезка показаны точками.
Луч — это часть линии только с одной конечной точкой, как показано ниже. Его длина по-прежнему бесконечна, но у него есть один идентифицируемый конец.
Когда две прямые, отрезки, лучи или их комбинация пересекаются, они образуют угол . Пример угла показан ниже.
Углы могут быть измерены в градусах (°) в диапазоне от 0 ° до 360 °. Некоторые примеры угловых измерений показаны ниже.
Используя эти основные геометрические термины и фигуры, мы можем теперь перейти к изучению некоторых более сложных фигур.
Прямоугольники
Прямоугольник — особый вид замкнутой геометрической фигуры с четырьмя сторонами; ниже показан пример прямоугольника.
Прямоугольники можно описать двумя измерениями: длиной (которую мы можем назвать l ) и шириной (которую мы можем назвать w ). Противоположные стороны прямоугольника равны по длине, а все «внутренние» углы составляют 90 °; таким образом, мы можем нарисовать прямоугольник, как показано ниже.
Одной из характеристик прямоугольника, которую мы можем легко вычислить, является его периметр , который является суммой длин всех сторон. Периметр P выглядит следующим образом:
P = l + w + l + w
Мы можем упростить это выражение, преобразовав сложение похожих членов в умножение:
P = l + l + w + w
P = 2 l + 2 w
Например, рассмотрим прямоугольник ниже.
Поскольку противоположные стороны равны по длине, прямоугольник имеет две стороны длиной 6 единиц и две стороны длиной 3 единицы. Таким образом, периметр следующий:
Периметр 18 шт. (Обратите внимание, что «единицей измерения» могут быть дюймы, футы, метры или любой другой тип измерения длины. Если единица измерения указана, используйте эту конкретную единицу; в противном случае достаточно общего термина «единицы».)
Практическая задача : Вычислите периметр прямоугольника ниже. Все размеры указаны в футах.
Решение : Напомним, что противоположные стороны прямоугольника равны по длине. Таким образом, у этого прямоугольника две стороны длиной 10 футов и две стороны длиной 2 фута. Тогда периметр P будет иметь следующий вид:
В качестве альтернативы мы могли бы просто использовать полученную выше формулу.
Практическая задача : Некий прямоугольник имеет периметр 50 метров и длину 14 метров. Какая у него ширина?
Решение : Мы можем решить эту проблему, внимательно изучив представленную информацию и применив то, что мы знаем о решении уравнений. Прежде всего мы знаем, что периметр P прямоугольника подчиняется следующей формуле, где l — длина, а w — ширина.
В постановке задачи указывается периметр ( P ), а также длина ( l ). Давайте введем эти значения в приведенное выше уравнение, а затем упростим результат, насколько это возможно.
Чтобы найти ширину прямоугольника, нам нужно только решить для w , используя тот же подход, который мы использовали при решении линейных уравнений.
Таким образом, ширина прямоугольника составляет 11 метров.Давайте проверим этот результат, чтобы убедиться, что он работает. Из постановки задачи мы знаем, что длина прямоугольника 14 метров.
Итак, ответ подтверждается.
Мы также можем вычислить площадь прямоугольника, которая является мерой того, сколько места он занимает. Рассмотрим прямоугольник шириной 4 единицы и длиной 2 единицы.
Давайте разделим каждую сторону на сегменты длиной 1, как показано ниже.
Теперь, используя эти деления, мы нарисуем сетку, разделяющую прямоугольник.
Обратите внимание, что сетка разделена на меньшие области, каждая сторона которых имеет длину 1 единицу.
Каждая из этих меньших областей представляет собой квадрат (прямоугольник, длина и ширина которого равны) со сторонами длиной 1.Мы определяем одну из этих областей как 1 квадратную единицу — квадрат, размеры которого (длина и ширина) равны 1 единице. Теперь обратите внимание, что в прямоугольнике всего 8 квадратных единиц, которые разделены на два ряда по четыре или четыре ряда по два (в зависимости от того, как вы смотрите на диаграмму). Но вычислить количество объектов (в данном случае квадратных единиц) в строках и столбцах можно путем умножения: обратите внимание, что количество квадратных единиц в прямоугольнике — это просто произведение длины и ширины. Таким образом, площадь A прямоугольника длиной l и шириной w является произведением l и w:
.Эта формула применима к любому прямоугольнику, независимо от длины его сторон.(То есть длины могут быть целыми положительными числами, дробями, десятичными знаками, рациональными числами или иррациональными числами.)
Например, допустим, у нас есть прямоугольник длиной 5 дюймов и шириной 3 дюйма, как показано ниже.
Наша цель — вычислить, сколько квадратов со стороной 1 дюйм может поместиться в этот прямоугольник — в результате получится общая площадь прямоугольника. Размещая квадраты от края до края, мы можем разместить пять из них по прямоугольнику и три по прямоугольнику.
Из диаграммы видно, что в прямоугольник можно уместить 15 квадратов размером один квадратный дюйм — таким образом, прямоугольник имеет площадь 15 квадратных дюймов. Конечно, это то же самое, что указывает формула:
Практическая задача : Вычислите площадь прямоугольника шириной 32 дюйма и длиной в дюйм.
Решение : Формула площади для прямоугольника применяется независимо от используемых чисел (конечно, если они положительные). Таким образом, давайте просто воспользуемся формулой для площади A:
Треугольники
Мы также можем рассмотреть некоторые характеристики другой распространенной геометрической фигуры: треугольника. Треугольник — замкнутая геометрическая фигура с тремя сторонами; примеры треугольников показаны ниже.
Периметр треугольника рассчитывается почти так же, как и периметр прямоугольника: просто сложите длины сторон треугольника (в этом случае фигура имеет только три стороны, и все эти стороны могут быть разной длины. ). Однако вычислить площадь несколько сложнее. Для прямоугольников мы смогли увидеть площадь как простые ряды и столбцы квадратов. Из-за формы треугольника мы не можем аккуратно вписать в него квадраты.
Мы должны использовать несколько иной подход к нахождению площади треугольника. Давайте рассмотрим общий треугольник, показанный ниже; этот треугольник не имеет особо особых свойств.
Теперь давайте определим два характерных размера этого (или любого) треугольника: длину основания (которую мы назовем b ) и высоту (которую мы назовем h ).Основание — это просто длина стороны «на земле» или в нижней части рисунка. Тогда высота — это максимальное расстояние, которое треугольник достигает «над землей».
Площадь треугольника составляет А. Если бы у нас было два таких треугольника абсолютно одинаковой формы, общая площадь этих двух треугольников была бы 2 А. Давайте воспользуемся этим фактом, чтобы попытаться построить более знакомую фигуру. .
Сначала мы разрежем один из треугольников по высоте.
Обратите внимание, что оба разделенных треугольника имеют высоту h (как мы определили для исходного треугольника) и что их основания равны x и y, , где x + y равно b. Мы не знаем, что такое x и y , но, поскольку мы разрезаем треугольник, мы знаем, что сумма этих двух оснований должна равняться основанию исходного треугольника. Теперь давайте попробуем переставить части, чтобы получился прямоугольник!
Давайте теперь рассмотрим характеристики этой новой фигуры (помните, она имеет площадь 2 A, , где A, — площадь исходного треугольника).
Рисунок представляет собой прямоугольник с примечанием, что противоположные стороны равны по длине (помните, что x + y = b ). Но мы знаем, как вычислить площадь прямоугольника: это просто произведение длины и ширины (в данном случае b и h ). Однако эта общая площадь составляет удвоенных площади исходного треугольника. Таким образом, произведение b и h равно 2 A.
Изучив линейные уравнения, мы узнали, как найти определенную переменную. В этом случае мы можем выделить A , умножив обе части выражения на.
Таким образом, мы вывели формулу площади треугольника. Этот вывод, хотя и не показан в его полной математической строгости, дает правильную формулу площади для всех треугольников, а не только для указанной выше.Процесс вычисления высоты h треугольника может быть несколько сложным, но если вы знаете основание и высоту, теперь вы можете вычислить площадь треугольника.
Практическая задача : Вычислите площадь треугольника ниже.
Решение : Если мы повернем треугольник так, чтобы 10-футовая сторона оказалась внизу, мы увидим, что сегмент пунктирной линии представляет высоту треугольника.
Затем мы можем вычислить площадь треугольника, используя формулу, которую мы вывели на уроке.
Формула площади и объема для геометрических фигур
пи (π) = 3,14155 …
Формула периметра | |
| Квадрат | 4 × сторона |
| Прямоугольник | 2 × (длина + ширина) |
| Параллелограмм | 2 × (сторона1 + сторона2) |
| Треугольник | сторона1 + сторона2 + сторона3 |
| Правильный n-полигон | n × сторона |
| Трапеция | высота × (base1 + base2) / 2 |
| Trapezoid | base1 + base2 + height × [ csc (theta1) + csc (theta2)] |
| Окружность | 2 × pi × радиус |
| Эллипс | 4 × radius1 × E (k, pi / 2) E (k, pi / 2) — полный эллиптический интеграл второго рода k = (1 / radius1) × sqrt (radius1 2 — radius2 2 ) |
Формула площади | |
| Квадрат | сторона 2 |
| Прямоугольник | длина × ширина |
| Параллелограмм | основание × высота |
| Треугольник | основание × высота / 2 |
| Правильный n-многоугольник | (1/4) × n × сторона 2 × кроватка (pi / n) |
| Трапеция | высота × (base1 + base2) / 2 |
| Окружность | pi × радиус 2 |
| Эллипс | пи × радиус1 × радиус2 |
| Куб (поверхность) | 6 × сторона 2 |
| Сфера (поверхность) | 4 × пи × радиус 2 |
| Цилиндр ( вс сторона стороны) | периметр окружности × высота |
| 2 × pi × радиус × высота | |
| Цилиндр (вся поверхность) | Области верхней и нижней окружностей + Площадь стороны |
| 2 (пи × радиус 2 ) + 2 × пи × радиус × высота | |
| Конус (поверхность) | пи × радиус × сторона |
| Тор (поверхность) | пи 2 × (радиус2 2 — радиус1 2 ) |
Формула объема | |
| Куб | сторона 3 |
| Прямоугольная призма | сторона1 × сторона2 × сторона3 |
| Сфера | (4 / 3) × пи × радиус 3 |
| Эллипсоид | (4/3) × пи × радиус1 × радиус2 × радиус3 |
| Цилиндр | пи × радиус 2 × высота | Конус | (1/3) × пи × радиус 2 × высота |
| Пирамида | (1/3) × (площадь основания) × высота |
| Тор | (1/4) × pi 2 × (r1 + r2) × (r1 — r2) 2 |
Источник: Spiegel, Murray R.Математический справочник формул и таблиц.
Серия набросков Шаума по математике. McGraw-Hill Book Co., 1968.
Площадь треугольника — объяснение и примеры
В этой статье вы узнаете, площадь треугольника и определяют площадь различных типов треугольников . Площадь треугольника — это пространство внутри треугольника. Он измеряется в квадратных единицах.
Перед тем, как перейти к теме области треугольника , давайте познакомимся с такими терминами, как основание и высота треугольника.
Основание — это сторона треугольника, которая считается нижней частью, а t высота треугольника — это перпендикулярная линия, опущенная на его основание из вершины, противоположной основанию. .
На приведенном выше рисунке пунктирными линиями показаны возможные высоты ABC. Обратите внимание, что у каждого треугольника, возможно, есть три высоты или высоты.
- Высота треугольника △ ABC равна h 1 , когда основание является стороной.
- Высота треугольника △ ABC равна h3 при основании AB.
- Высота треугольника △ ABC равна h 3 при основании
- Высота треугольника △ ABC может находиться вне треугольника ( h 4 ), что составляет такая же высота h 1 .
Из иллюстраций выше мы можем сделать следующие наблюдения:
- Высота треугольника зависит от его основания.
- Перпендикуляр к основанию треугольника равен высоте треугольника.
- Высота треугольника может быть вне треугольника.
Обсудив понятие высоты и основания треугольника, давайте теперь приступим к вычислению площади треугольника.
Как найти площадь треугольника?
Площадь прямоугольника нам хорошо известна, т.е. длина * ширина . Что будет, если прямоугольник разделить пополам по диагонали (разрезать пополам)? Какая будет его зона новостей? Например, в прямоугольнике с основанием и высотой 6 единиц и 12 единиц, соответственно, площадь прямоугольника составляет 72 квадратных единицы.
Теперь, если вы разделите на две равные половины (после деления прямоугольника пополам по диагонали), площадь двух новых фигур должна составлять 36 квадратных единиц каждая. Две формы новостей представляют собой треугольники. Это означает, что если прямоугольник разрезан по диагонали на две равные половины, две новые формы образуются треугольниками, где каждый треугольник имеет площадь, равную ½ площади прямоугольника.
Площадь треугольника — это общее пространство или область, окруженная определенным треугольником.
Площадь треугольника равна произведению основания и высоты, разделенных на 2.
Стандартная единица измерения площади — квадратные метры (м 2 ).
Другие единицы включают:
- Квадратные миллиметры (мм 2 )
- Квадратные дюймы (дюйм 2 )
- Квадратные километры (км 2 )
- Квадратные ярды.
Формула площади треугольника
Общая формула для вычисления площади треугольника:
Площадь (A) = ½ (b × h) квадратных единиц, где; A — площадь, b — основание, h — высота треугольника.Треугольники могут быть разной природы, но важно отметить, что эта формула применима ко всем треугольникам. Различные типы треугольников имеют разные формулы площади.
Примечание: основание и высота должны быть в одних и тех же единицах измерения, то есть в метрах, километрах, сантиметрах и т. Д.
Площадь прямоугольного треугольника
Площадь треугольника = (½ × основание × высота) квадратных единиц.
Пример 1
Найдите площадь прямоугольного треугольника с основанием 9 м и высотой 12 м.
Решение
A = ¹ / ₂ × основание × высота
= ¹ / ₂ × 12 × 9
= 54 см²
Пример 2
Основание и высота прямоугольного треугольника равны 70 см и 8 м соответственно. Какая площадь у треугольника?
Решение
A = ½ × основание × высота
Здесь у нас 70 см и 8 м. Вы можете работать с cm или m. Давайте работать в метрах, заменив 70 см на метры.
Разделите 70 см на 100.
70/100 = 0,7 м.
⇒ A = (½ × 0,7 × 8) м 2
⇒ A = (½ x 5,6) м 2
⇒ A = 2,8 м 2
Площадь равнобедренного треугольника
An Равнобедренный треугольник — это треугольник, у которого две стороны равны, а также два угла равны. Формула площади равнобедренного треугольника:
⇒A = ½ (основание × высота).
Если высота равнобедренного треугольника не указана, для определения высоты используется следующая формула:
Высота = √ (a 2 — b 2 /4)
Где;
b = основание треугольника
a = длина стороны двух равных сторон.
Следовательно, площадь равнобедренного треугольника может быть;
⇒A = ½ [√ (a 2 — b 2 /4) × b]
Кроме того, площадь равнобедренного прямоугольного треугольника определяется по формуле:
A = ½ × a 2 , где a = длина стороны двух равных сторон
Пример 3
Вычислите площадь равнобедренного треугольника с основанием 12 мм и высотой 17 мм.
Решение
⇒ A = ½ × основание × высота
⇒ 1/2 × 12 × 17
⇒ 1/2 × 204
= 102 мм 2
Пример 4
Найдите площадь равнобедренного треугольника, длина сторон которого составляет 5 м и 9 м.
Решение
Пусть основание b = 9 м и a = 5 м.
⇒ A = ½ [√ (a 2 — b 2 /4) × b]
⇒ ½ [√ (5 2 — 9 2 /4) × 9]
= 9,81 м 2
Площадь равностороннего треугольника
Равносторонний треугольник — это треугольник, в котором три стороны равны и три внутренних угла равны. Площадь равностороннего треугольника:
A = (a 2 √3) / 4
, где a = длина сторон.
Пример 5
Вычислите площадь равностороннего треугольника со стороной 4 см.
Решение
⇒ A = (a 2 /4) √3
⇒ (4 2 /4) √3
⇒ (16/4) √3
= 4√3 см 2
Пример 6
Найдите площадь равностороннего треугольника с периметром 84 мм.
Решение
Периметр равностороннего треугольника = 3a.
⇒ 3a = 84 мм
⇒ a = 84/3
⇒ a = 28 мм
Площадь = (a 2 /4) √3
⇒ (28 2 /4) √3
= 196√3 мм 2
Площадь разностороннего треугольника
Разносторонний треугольник — это треугольник с 3 разными длинами сторон и 3 разными углами.Площадь разностороннего треугольника можно рассчитать по формуле Герона.
Формула Герона дается как;
⇒ Площадь = √ {p (p — a) (p — b) (p — c)}
, где «p» — это полупериметр, а a, b, c — длины сторон.
⇒ p = (a + b + c) / 2
Пример 7
Вычислите площадь треугольника с длинами сторон 18 мм, 20 мм и 12 мм.
Решение
⇒ p = (a + b + c) / 2
Подставьте значения a, b и c.
⇒ p = (12 + 18 + 20) / 2
⇒ p = 50/2
⇒ p = 25
⇒ Площадь = √ {p (p — a) (p — b) (p — c)}
= √ {25 x (25 — 12) x (25 — 18) x (25 — 20)}
= √ (25 x 13 x 7 x 5)
= 5√455 мм 2
Площадь треугольника — веб-формулы
Треугольник — это многоугольник с тремя сторонами, который можно разделить на следующие типы:
· Равносторонний треугольник имеет равные стороны и равные углы.
· Равнобедренный треугольник имеет две равные стороны и два равных угла.
· Разносторонний треугольник имеет три неравные стороны и три неравных угла.
· Прямоугольный треугольник имеет один прямой угол (90 °).
· Остроугольный треугольник имеет все углы менее 90 °.
· Тупоугольный треугольник имеет один угол больше 90 °.
Периметр треугольника = Сумма трех сторон.
На рисунке рядом с ΔABC периметр представляет собой сумму AB + BC + AC.
Площадь треугольника определяется как:
A = ½ × основание × высота
Любая сторона треугольника может считаться его основанием.
Тогда длина перпендикулярной линии от противоположной вершины принимается за соответствующую высоту или высоту.
На приведенном выше рисунке площадь, таким образом, дается как: ½ × AC × BD .
Дополнительные формулы для определения площади треугольника:
Площадь треугольника = √ (s (sa) (sb) (sc)) по формуле Герона (или формуле Героя), где a , b и c — длины сторон треугольника, и s = ½ ( a + b + c ) — это полупериметр треугольника.
Площадь равностороннего треугольника
A = √ (3) · ¼ · сторона, где сторона = a = b = c
Площадь равнобедренного треугольника
A = ¼ · b · √ (4a 2 — b 2 )
Площадь прямоугольного треугольника
A = ½ × Произведение сторон, содержащих прямой угол.
Если даны две стороны и угол между ними, то площадь треугольника можно определить по следующей формуле:
Площадь = ½ · a · b · sinC = ½ · b · c · sinA = ½ · a · c · sin B
Пример 1: Найдите площадь треугольника с основанием 14 см и высотой 10 см.
Решение :
b = 14 см
h = 10 см
A = ½ · 14 · 10 = 70 см 2
Пример 2: Найдите площадь треугольника, стороны и угол между которыми имеют следующие значения:
a = 5 см и b = 7 см
C = 45 o
Решение:
Площадь треугольника = ½ · a · b · sinC
Площадь = ½ × 5 × 7 × 0.707 (начиная с sin 45 ° = 0,707)
Площадь = ½ × 24,745 = 12,3725 м 2
Что такое область 2D-форм?
Что такое площадь 2D-фигур?
Площадь любой 2D-формы — это размер области, заключенной в нее. Есть несколько 2D-форм, таких как квадрат, прямоугольник, круг, ромб и треугольник. Цветная область в каждой форме представляет область соответствующей формы.
Единица площади называется квадратными. У разных форм есть разные формулы для расчета площади.Площадь квадрата и прямоугольника :
Площадь квадрата и прямоугольника равна произведению двух смежных сторон.
| 2D Форма | Формула площади | Пример |
| Квадрат | Площадь квадрата = Сторона × Сторона Площадь = S × S | Площадь = 4 × 4 = 16 кв.размеры в см |
| Прямоугольник | Площадь прямоугольника = длина × ширина = длина × ширина | Площадь = 8 × 3 = 24 кв. См |
Площадь треугольника :
Треугольники могут быть разных типов, например равносторонний треугольник, равнобедренный треугольник и прямоугольный треугольник, но формула для площади всех видов треугольников одинакова.
Площадь треугольника определяется по формуле: 1 ⁄ 2 × b × h, где основание (b) — длина любой стороны треугольника, а высота (h) — расстояние по перпендикуляру между основанием. и верхняя вершина треугольника.
Пример:
В треугольнике ABC основание составляет 6 единиц, а высота — 4 единицы.
Итак, площадь треугольника ABC = 1 ⁄ 2 × b × h
= 1 ⁄ 2 × 6 × 4
= 12 кв. Единиц
Круг :
Площадь круга вычисляется по формуле π × r 2 , где r — радиус круга, а π — константа, значение которой равно 227 или 3.14
Пример: Площадь вышеуказанного круга = π × r 2
= 3,14 × 4 2
= 3,14 × 16
= 50,24 кв. См
Ромб :
Формула для определения площади ромба: pq / 2, где p и q — две диагонали ромба.
В ромбе ABCD площадь можно вычислить следующим образом:
Площадь ромба = 1 ⁄ 2 pq
= 1 ⁄ 2 × 3 × 5
= 7,5 см кв.
Параллелограмм :
Чтобы найти площадь параллелограмма, мы используем формулу b × h, где b обозначает основание, а h обозначает высоту. Высота — это расстояние по вертикали между основанием и верхом.
Пример:
На приведенном выше рисунке площадь параллелограмма равна b × h.


 А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.