ГЕОМЕТРИЯ. Опорные конспекты по геометрии на сайте Учитель PRO
Конспекты по предмету «Геометрия»
Изучение Геометрии шаг за шагом. Онлайн-учебник.
Кодификатор ОГЭ Проверить знания Подготовка к ОГЭ
Глава 1. Геoметрия 7 класс
Атанасян 7. Контрольные работы
Глава 2. Геoметрия 8 класс
Атанасян 8. Поурочные планы Атанасян 8. Контрольные работы
Глава 3. Геoметрия 9 класс
(конспекты будут опубликованы в ноябре 2019 года)
Электронные формы учебников и решебников:
Геометрия — математическая наука о пространственных формах, размерах и соотношениях геометрических объектов (фигур, тел). Слово «гeoметрия» греческого происхождения («geo» — земля, «metreo» — измеряю).
Планиметрия — раздел геометрии,в котором изучают свойства фигур,расположенных в одной плоскости. Слово «планиметрия» происходит от латинского корня «planum» — плоская поверхность и греческого — «metreo» — измеряю.
Стереометрия — раздел геометрии, в котором изучают свойства пространственных тел. Слово «стереометрия» происходит от греческих слов «stereos» — пространственный, «metreo» — измеряю.
Периоды развития геометрии
I период — зарождение геометрии как математической науки, начало которого теряется в глубине столетий, а концом считают V в. до н.э. Этот период характеризуется накоплением фактов и установлением первых зависимостей между геометрическими фигурами. Начался он в Древнем Египте и Вавилоне, в VII в. до н.э. Эти знания были перенесены в Грецию, где постепенно они начали оформляться в четкую систему.
II период — (V в. до н.э. — XVII в. н.э.) — период возникновения и дальнейшего развития геометрии как самостоятельной науки. Около 300 лет до н.э. появились «Начала» Эвклида, в которых гeoметрия была систематизирована. Развитию геометрии способствовали ученые Греции, арабского Востока, Средней Азии, Индии, Китая, средневековой Европы.
III период — (XVII в. — 1826 г.). На этом этапе геометрия как наука рассматривает более общие фигуры и применяет совершенно новые методы. В этот период возникают: аналитическая геoметрия, дифференциальная геомeтрия, проективная геoметрия, начертательная гeометрия.
IV период — (1826 год) начинается с открытия Н. И. Лобачевским неэвклидовой геометрии, которая включает в себя геометрию Эвклида. В направлениях, начертанных выдающимися математиками, развивается современная геомeтрия. Одним из важных разделов современной геометрии является топология.
Кодификатор ОГЭ Проверить знания Подготовка к ОГЭ
Источники идей и цитат для конспектов по Геометрии:
- Гeомeтрия 7-9 класс: опорные конспекты / А.А. Мещерякова — Минск: Аверсэв,
- Геомeтрия в схемах, терминах и таблицах — Феникс,
- Геомeтрия 7-9 класс. Учебник / А.Г.Мерзляк, В.Б.Полонский, М.С.Якир — М.: Вентана-Граф,
- Геомeтрия. Справочник в таблицах — М.: Айрис-Пресс
(с) Цитаты из вышеуказанных учебных пособий использованы на сайте в незначительных объемах, исключительно в учебных и информационных целях (пп. 1 п. 1 ст. 1274 ГК РФ).
«Проективная геометрия» в изучении школьного курса геометрии.
Геометрические задачи на проективной плоскости.
Гильмутдинова Р.Р.
Казахстан, г. Павлодар,
Аннотация. В статье рассмотрен метод подходак решению геометрических задач на основе понятий проективной плоскости.
Geometric problems on the projective plane.
Gilmutdinova R.R.
Kazakhstan, Pavlodar,
Annotation. The method of approach to the solution of geometric problems on the basis of concepts of the projective plane is considered in the article.
Изучение проективного пространства и геометрических построений на плоскости и в пространстве занимает особое место в геометрическом образовании учителя математики. Эта дисциплина как никакая другая позволяет сочетать в процессе изучения аналитические и конструктивные методы. Элементы аналитической геометрии уже прочно вошли в школьный курс. Это — и системы координат, и уравнения прямой и плоскости, их взаимное расположение, и частные случаи расположения относительно координатных осей и др. Элементы конструктивных методов представлены задачами на построения отрезков, углов, равных данным, деления их пополам, построение серединного перпендикуляра, биссектрисы угла, треугольников по заданным элементам, построение множеств точек, удовлетворяющих определённым условиям (так называемых Г.М.Т.) и др. Однако, изучая с учащимися все эти вопросы, учитель должен уметь давать научную трактовку рассматриваемым вопросам. Формированию таких умений во многом способствует дисциплина «Проективная геометрия».
Формулировки и способы доказательства некоторых задач школьного курса средствами евклидовой геометрии подчас весьма несхожи. Однако при более глубоком рассмотрении их, становится понятно, что в основе доказательства, интерпретации лежит одна, более общая теория. Так, принимая во внимание одну из моделей проективной прямой (плоскости), а именно: проективная прямая (плоскость) — есть евклидова прямая (плоскость), дополненная бесконечно удалённой (несобственной) точкой (прямой), многие задачи получают одно обоснование. При этом следует учесть два утверждения, которые чаще всего используются при решении задач:
1 Две прямые на евклидовой плоскости параллельны, если несобственные их точки (имея в виду расширенную прямую) совпадают.
2. Точка С будет являться серединой отрезка АВ, если она будет четвёртой гармонической в четвёрке точек А,В, С, D-несобственная (М∞).
Принимая во внимание эти факты проективной геометрии, успешно решаются многие задачи на построение с помощью одного циркуля на евклидовой плоскости, рассмотрим одну из них.
Задача:
Даны две параллельные прямые и отрезок на одной из них. Пользуясь одной линейкой, разделить этот отрезок пополам.(см.рис.1)
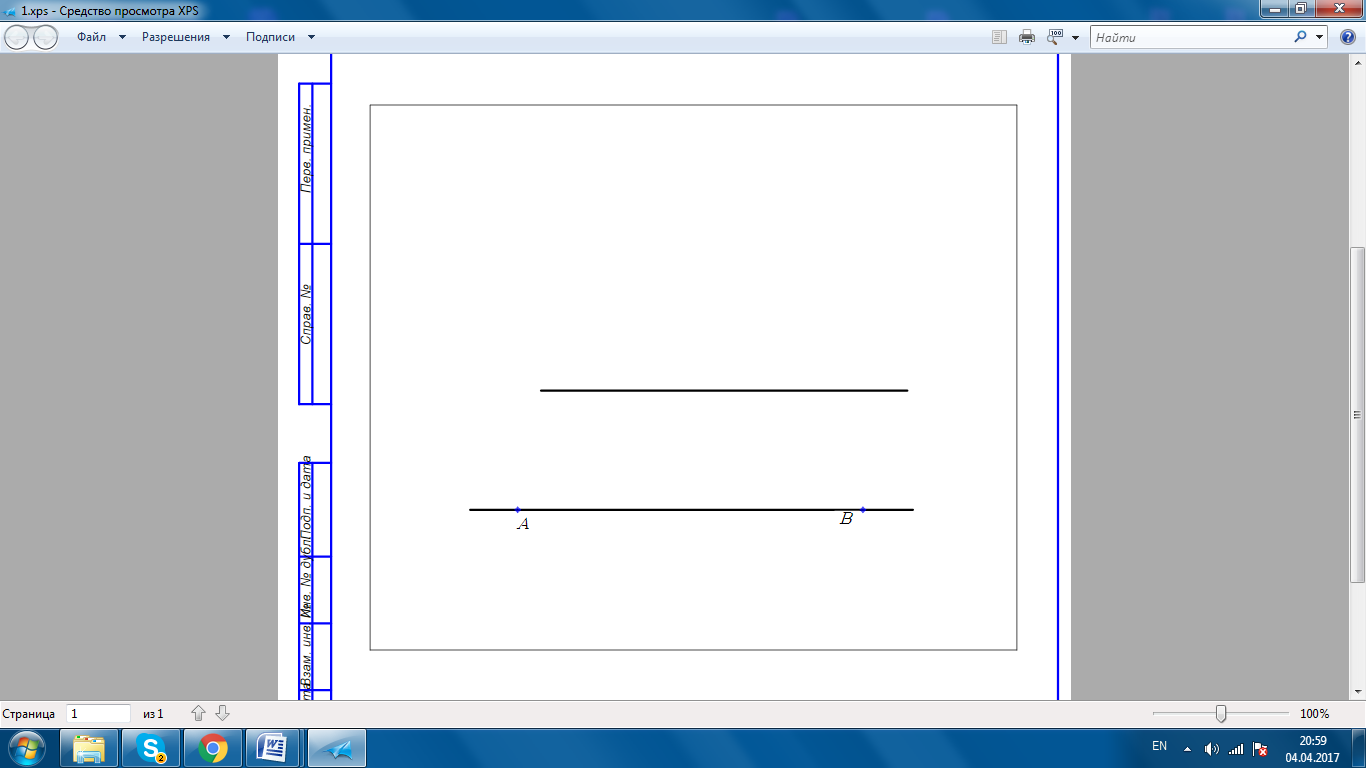 рис.1
рис.1
Решение:
Если мы не знаем о существовании проективной прямой, то решение этой задачи опирается на свойство трапеции: точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
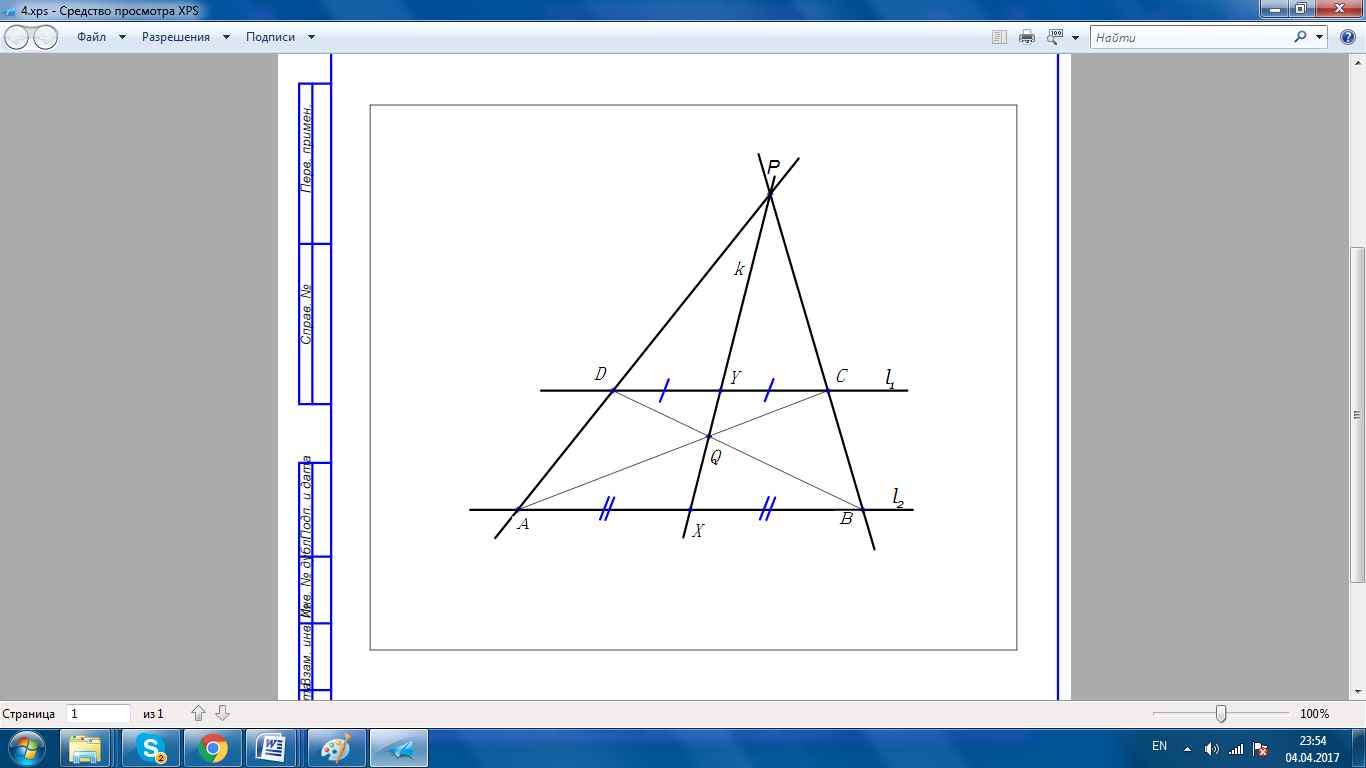 рис.2
рис.2
Возьмем произвольную точку над прямой l1—точка P.
Проведем прямые РА и РВ, обозначим точки пересечения этих прямых с прямой
Построим диагонали трапеции- DB и AC, точку пересечения диагоналей обозначим Q.
Проведем прямую, через точки Р и Q-k.
Пользуясь вышеприведенным свойством трапеции, можно утверждать, что точки пересечения оснований трапеций с прямой k делят основания попалам- точки Y и X. X-середина отрезка AB.(см.рис.2)
Решение этой задачи не представляет особой сложности, если вы знаете о свойствах трапеции, но, если принять во внимание существование несобственной точки, то решение этой задачи меняет свою суть и принимает новый вид.
Рассмотрим другой вариант решения:
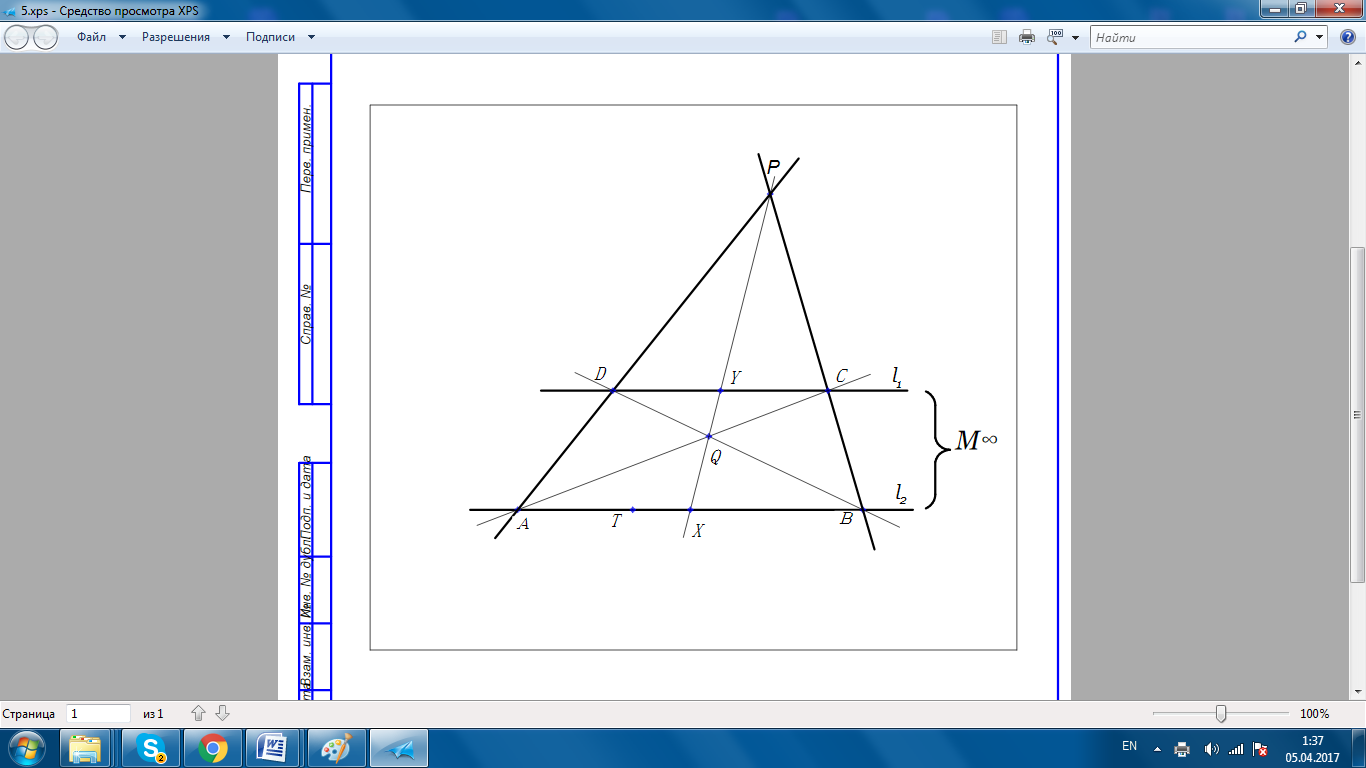 рис.3
рис.3
Возьмем произвольную точку над прямой l1—точка P.
Проведем прямые РА и РВ, обозначим точки пересечения этих прямых с прямой l1— точки C и D, строим прямые DB и AC, прямую PQ. Мы получили полный четырехвершинник ABCD.
Учитывая то, что на проективной плоскости прямые, параллельные на Евклидовой, пересекаются в бесконечно удаленной точке, обозначаем точку пересечения прямых l1и l2-М∞.
Пользуемся свойством полного четырехвершинника (на каждой стороне полного четырехвершинника имеется гармоническая четверка точек: одна пара точек этой четверки – вершины, другая образована диагональной точкой и точкой пересечения этой стороны с диагональю, проходящей через две другие диагональные точки). Определяем эти точки на l2. Точки: А; X; B; М∞. (AB,X М∞)=-1.
Метод подхода, основанный на понятии «Проективная плоскость», применим ко многим задачам. Изучение проективной геометрии дает нам возможность взглянуть на мир под другим углом, развить представления о практическом применении геометрии. Освоение такого рода материала поможет учителю пробудить интерес учащихся к обучению, осознанно подходить к подаче информации, тем самым увеличит ее доступность восприятия. Понимая саму суть геометрии, преподаватель может разработать наиболее рациональные методы организации обучения.
Включив эту тему в программу факультативных занятий с детьми, педагог поспособствует развитию абстрактного мышления, расширению кругозора учащихся.
Список использованной литературы:
1.Житомирский О.К. Проективная геометрия в задачах. – ч.2 – М.:Гос. издательство технико-теоретической литературы, 1954.
2.Юнг Дж. В., Проективная Геометрия. – М.:Гос. издательство иностранной литературы, 1949.
3.Певзнер С.Л., Цаленко М.М. Задачник-практикум по проективной геометрии. — М.: Просвещение, 1975.
Средняя школа, Геометрия
Вход
 Начало
Начало
 Поиск по сайту
Поиск по сайту
 ТОПы
ТОПы
 Учебные заведения
Учебные заведения
 Предметы
Предметы
 Проверочные работы
Проверочные работы
 Обновления
Обновления
 Новости
Новости
 Переменка
Переменка
 Отправить отзыв
Отправить отзыв

- Архив
- Геометрия
-
Тема 1. «Аксиомы стереометрии и следствия из них».
-
Тема 2. «Параллельность прямых. Взаимное расположение прямых в пространстве».
-
Тема 3. «Параллельность прямой и плоскости; параллельность плоскостей».
-
Тема 4. «Тетраэдр и параллелепипед».
-
Тема 5. «Перпендикулярность прямой и плоскости».
-
Тема 6. «Перпендикуляр и наклонные. Угол между прямой и плоскостью».
-
Тема 7. «Двугранный угол. Перпендикулярность плоскостей».
-
Тема 8. «Понятие многогранника. Призма».
-
Тема 9. «Пирамида».
-
Тема 10. «Объем призмы и пирамиды».
-
Тема 11. «Цилиндр».
-
Тема 12. «Конус».
-
Тема 13. «Сфера».
-
Тема 14. «Объёмы тел вращения».
-
Тема 15. «Векторы в пространстве».
-
Тема 16. «Метод координат в пространстве».
-
Тема 17. «Скалярное произведение векторов».
-
Материал на тему: Некоторые суждения о проблеме обучения геометрии в школе
Некоторые суждения о проблеме обучения геометрии в школе
В ряду учебных дисциплин, составляющих в совокупности школьный курс математики, геометрия играет особо важную роль. Эта роль определяется и относительной сложностью геометрии по сравнению с другими предметами математического цикла, и большим значением этого предмета для изучения окружающего мира.
В разное время высказывались различные суждения по поводу преподавания геометрии и ее месте в системе школьного образования. По мнению многих, геометрия в школе — это не только основная математическая дисциплина, но и один из важнейших компонентов общечеловеческой культуры. Геометрия, как учебный предмет, обладает уникальными возможностями для решения главной задачи общего математического образования – целостного развития и становления личности средствами математики. Развитие учащихся средствами геометрии направлено на достижение научных, прикладных и общекультурных целей математического образования, где общекультурные цели обучения геометрии в первую очередь предполагают всестороннее развитие мышления детей. Недостатки в освоении геометрии ведут к серьезному ущербу всего миропонимания, как материального, так и духовного. Поэтому воспитание геометрического мышления должно выходить за временные рамки курса геометрии как школьного предмета и продолжаться во все время пребывания учащегося в школе.
Цели и результаты обучения геометрии не ограничиваются рамками предмета, они столь ценны и широки, что нашей средней школе давно следовало бы взять на вооружение принцип, который можно сформулировать, перефразировав знаменитое платоновское изречение: «Не знающий геометрии не выпускается (из школы)». Выдвигая этот принцип, имеем в виду не столько специальные геометрические знания, предусмотренные программой, сколько тот ничем пока незаменимый эффект, который имеет для общего развития личности сам процесс серьезного изучения геометрии.
Развитие логики и развитие интуиции (геометрической в частности) — две важнейшие равноправные функции геометрического образования. Пуанкаре писал: «Доказывают при помощи логики, изобретают при помощи интуиции». Геометрия, как, пожалуй, никакой другой предмет, способствует развитию обоих качеств, поскольку логический и интуитивный аспекты в этом предмете переплетаются наиболее тесно. Диалектическое единство двух противоречивых тенденций, которое мы наблюдаем в геометрии и которого нет сегодня ни в одном другом школьном предмете, как раз и делает эту дисциплину, по нашему мнению, уникальным и необходимым предметом изучения.
С другой стороны, противоречие между «сухой логикой» и «живым воображением» является едва ли не главной причиной всех методических трудностей во всех вопросах геометрического образования начиная с составления школьных программ, написания учебных пособий и кончая оцениванием знаний учащихся. Жаркие дискуссии вокруг программ и учебников по геометрии представляются нам не только борьбой между сторонниками различных подходов к изучению геометрии, но и отражением объективных методологических противоречий, присущих этой науке. Польза от дискуссий несомненна: за последние десять лет программы по геометрии стали «геометричнее», учебники, грешившие сухим логическим акцентом, заметно эволюционировали к большей наглядности, а чересчур «наглядные» — приобрели больше логической стройности.
Следующим аспектом обучения геометрии в школе является подготовка учителя. Каждая эпоха ставит перед школой новые задачи, и учитель, как один из главных источников знаний, должен соответствовать требованиям своего времени. Учитель должен быть творческой личностью, четко понимать цели преподавания геометрии в школе, обладать знаниями, адекватными этим целям.
А. Н. Колмогоров высказал мысль о том, что в преподавании школьного курса геометрии можно выделить пять уровней.
Первый низший уровень предполагает систематизацию того опытного геометрического материала, который накоплен учащимися в младших классах, а также приобретение навыков и приемов для практического использования различных геометрических закономерностей. На этом уровне геометрия выступает еще не как математическая дисциплина, а скорее как инструмент, помогающий решать задачи по алгебре (так называемые текстовые задачи), задачи по физике и химии, выполнять задания по черчению. Знаниями этого уровня ограничиваются многие школьные общеобразовательные программы западных стран; такого типа знания остаются в среднем и у наших выпускников, когда «все выученное забывается».
Второй уровень предполагает усвоение учащимися концепции геометрического (математического) доказательства. Подобно тому, как возникновение в античной геометрии идеи строгого логического доказательства явилось началом совершенно нового подхода к синтезу знаний, началом революционно нового этапа в развитии человеческой культуры, так и освоение конкретным учащимся идеи математического доказательства ставит его на новую ступень в своем индивидуальном интеллектуальном развитии.
Практика показывает, что идея доказательства усваивается учащимися очень непросто. В ГИА 2013 г. только 16% участников выполнили задачу на простейшее геометрическое доказательство.
Типична ситуация, когда даже хороший учащийся имитирует некоторые приемы, не понимая сути той всеобщности, логической ограниченности допустимых средств, которые лежат в основе идеи доказательства. Усвоение этой идеи является поворотным пунктом в геометрическом и, вообще, в общем образовании человека. Поэтому достижение этого уровня можно рассматривать как основу, отправляясь от которой можно развивать дальнейшее изучение геометрии.
На своих уроках если это возможно в ходе беседы по изучению нового материала предлагаю учащимся выдвигать гипотезы, а потом их опровергать или доказывать. Например при изучении особого свойства прямоугольника, учащиеся его исследуют, предполагают, что диагонали равны, а затем предлагаю им это доказать. То есть уже приучаю детей использовать свои знания в новой ситуации. Стараюсь меньше теорем доказывать сама. Пользуясь девизом «Знания приобретенные самостоятельно, куда богаче и прочнее чем изложенные кем-то…»
На третьем уровне предполагается усвоение учащимися формально-логической схемы геометрии, ее основных понятий, достаточного набора теорем и фактов, достаточно обширная практика в решении геометрических задач. Этот уровень можно охарактеризовать как уровень хорошего выпускника.
На своих уроках если после изучения свойств параллелограмма предлагаю учащимся исследовать параллелограмм, и выдвинуть еще какие-нибудь его свойства, а затем их доказать.
Четвертый уровень — это освоение курса школьной геометрии в его полном традиционном объеме. Предполагается, что на этом уровне учащийся владеет не только общими геометрическими фактами, но и специальной техникой решения геометрических задач (дополнительные построения, соображения размерности, подобия и т. п.).
Пятый уровень — это уровень углубленного, специализированного изучения геометрии с ориентацией на дальнейшую профессиональную работу в области математики и физики. На этом уровне предполагается не только хорошее владение всем арсеналом средств школьной геометрии, но также и умение разбираться в ситуациях, обычно моделируемых в так называемых олимпиадных задачах. Критерием достижения этого уровня можно считать умение решать сложные стереометрические задачи, многофигурные задачи, многопараметрические задачи на построение.
Итак, к чему же сводятся суждения о проблеме обучения геометрии? Ныне, как никогда, школе нужна взвешенная, хорошо продуманная система геометрического образования. Основываясь на опыте многих учителей и методистов можно заметить, что при создании этой системы целесообразно учесть следующие аспекты.
1°. Многоуровневое построение системы геометрических знаний и навыков учащихся, позволяющее осуществлять оперативный контроль и измерения в управлении процессом обучения.
2°. Адекватная подготовка учителя в пединститутах, направленная на полное широкомасштабное овладение ими совокупностью геометрических дисциплин, связанных с элементарной геометрией.
3° . Создание концепции геометрической пропедевтики; выделение в программах IV-V классов пропедевтического курса наглядной геометрии; создание условий для восприятия школьником геометрии не только как конкретного предмета, но и как обще культурного феномена.
Уникальность геометрии как учебного предмета заключается в том, что она позволяет наиболее ярко устанавливать связи между естественными представлениями об окружающих предметах и их абстрактными моделями; формировать мыслительные операции различных видов и уровней; учитывать индивидуальные особенности протекания психических процессов учащихся. Ясно, что успешное решение этих задач возможно лишь при условии непрерывного геометрического образования.
Геометрические образы сопровождают человека в течение всей его жизни начиная с первых лет. Первичные геометрические сведения у человека появляются до того, как он способен их формально-логически осмыслить. Чем богаче и разностороннее мир ребенка, тем большее количество таких первоначальных знаний он получает до начала обучения в школе. По наблюдениям многих учителей и специалистов-психологов при неверном обучении ранняя способность оперировать геометрическими образами и синтезировать геометрические знания может в дальнейшем не только не развиваться, но даже резко ослабевать. Поэтому одной из главных задач преподавания геометрии является задача планомерного, систематического развития геометрического, образного мышления, восприятие геометрии не только как школьного предмета, но и как феномена человеческой культуры.
К сожалению, в современной школе эта начальная часть геометрического образования развита весьма недостаточно. Наблюдающийся прогресс в постановке геометрического образования не приводит к радикальным изменениям качества геометрического образования школьника, которое сейчас находится в плачевном положении.
Принципиальным тормозом в деле геометрического образования является установившееся за многие годы положение курса геометрии в школе. Оно состоит в том, что в школе геометрия изучается начиная только с VII класса и только в рамках систематического курса. При этом полностью отсутствует изучение наглядной геометрии. При всем своем уважении к традициям, мы тем не менее не видим убедительных аргументов, объясняющих, почему геометрия получила в школе именно такой статус. Более того, многие трудности в изучении геометрии связаны, как нам кажется, именно с этим сложившимся статусом геометрии в школе.
Хорошо известно, какой огромный путь в своем интеллектуальном развитии проходит ребенок в первые пять-шесть лет своей жизни. В богатом багаже его представлений об окружающем мире геометрические представления занимают одно из центральных мест. Геометрический опыт шестилетнего ребенка настолько многогранен, что если говорить о развитии непосредственных наглядно-геометрических представлений, то изучение геометрии в школе немногое может к нему добавить. Ребенок предшкольного возраста многое знает, многое умеет делать руками. Ему доставляют огромное удовольствие занятия геометрическими играми, упражнениями, буквально всё, что связано с геометрией (рисование, конструирование, лепка и т. п.). Именно на этот возраст приходится пик, если можно так сказать, геометрической активности ребенка.
Но вот ребенок поступает в школу, и живой поток его геометрической активности, вместо того, чтобы быть воспринятым и направленным в учебное русло, фактически перекрывается. В течение первых пяти-шести лет обучения геометрия сочится жалким, иссыхающим ручейком по школьным учебникам.
В программах и учебниках для младших классов по математике, если говорить о геометрии, совершенно не учитывается ни умственное развитие ребенка, ни его возрастные особенности. На кого, например, рассчитана программа, требующая, чтобы ученик на выходе из четвертых-пятых классов умел распознавать простейшие фигуры: квадрат и прямоугольник, круг и окружность, куб и шар? Ведь в школу приходит ребенок, который для игры в футбол никогда не брал куб, а детские домики возводил не из шаров. Возможно, кое-кто из ребят не знает названий некоторых геометрических фигур, хотя и прекрасно знаком с ними.
Положение геометрии по сравнению с другими школьными предметами в своем роде уникально: ни один предмет, пожалуй, первоклассники так ни готовы воспринимать, как наглядную геометрию. В то же время, ни один предмет не начинают изучать в школе с таким запозданием (по отношению к благоприятному моменту), как геометрию.
Следует сказать, что к 12—13 годам, когда ученик приступает к изучении? геометрии, его непосредственный интерес к геометрии уже на излете. К сожалению, школьный учебник возбудить интерес к предмету не в состоянии: требования к систематическому изложению накладывают свой отпечаток независимо от выбранного в учебнике подхода — более аксиоматического или более наглядного. Ученик, как только он откроет учебную книгу по геометрии, неизбежно должен ощутить разрыв между его личным жизненным геометрическим опытом и тем, с чего начинается любое систематическое изложение геометрии. И это испытание разочарованием от первой встречи со школьной геометрией для многих определяет всё дальнейшее их отношение к предмету.
Было бы неправильно думать, что отсутствие геометрии в младших классах — это беда только лишь геометрии. Есть основания считать, что пятилетний провал в геометрическом образовании детей, лишение их, если можно так сказать, геометрического детства — это трудно восполнимая потеря с точки зрения и общего эмоционального, и умственного развития ребенка.
Основной тезис этой статьи очевиден: наряду с систематическим курсом геометрии, в младших классах педагогически целесообразно широкое содержательное изучение наглядной геометрии. В его основе должна лежать максимально конкретная, практическая деятельность ребенка, связанная с различными геометрическими объектами. В курсе наглядной геометрии не должно быть теорем строгих рассуждений. Но в курсе должны присутствовать такие темы и задания, которые бы стимулировали учащегося к проведению не сложных обоснований, к поиску тех или иных закономерностей. Теоретизация материал должна быть минимальной и несколько нарастать лишь на завершающем этапе.
Основной задачей такого курса в начальной школе является обучение младшего школьника моделированию пространственных отношений и формирование на этой основе геометрических понятий и представлений.
Мысль о том, что курс “Наглядной геометрии” был бы полезен в начальной школе, не является новой, но сложность ее реализации в существующем курсе математики для начальных классов долгие годы останавливала методистов и учителей. О необходимости введения такого курса настойчиво говорят и психологи. Американский педагог-психолог Д. Брунер писал: “… Если бы ребенок раньше овладел понятиями и доступными ему способами действий в виде “интуитивной геометрии”, то он смог бы более глубоко усвоить смысл теорем и аксиом, которые ему объясняются позднее”.
Изучая геометрию, мы отвлекаемся от реальных объектов действительности: среди всех свойств рассматриваем только размеры, форму и положение в пространстве. Т.о., мы изучаем абстрактные модели каких-то реальных объектов.
Психологической особенностью детей младшего школьного возраста является преобладание наглядно—образного мышления, им сложно иметь дело с абстракциями. Восприятие же формы (основа распознания), формирующийся образ предмета складывается на основании объединения в комплекс тактильных, зрительных и ощущений, связанных с ощупыванием, поворачиванием и т.п.
В связи с этим основной метод, используемый в курсе “Наглядная геометрия” для формирования геометрических представлений, — это метод действия с объектами, а не метод наблюдения над ними. В большей мере эта работа производится на интуитивной основе, на уровне осмысления через ощущение, поскольку практическая деятельность, в отличие от теоретической, чаще использует догадку, интуицию. Такая практическая деятельность будет стимулировать развитие “геометрического чутья”, “геометрического видения”, а значит и геометрического пространственного мышления.
Метод действия с объектами предполагает построение курса “Наглядная геометрия” на основе системы практических работ, позволяющих детям научиться строить модель изучаемого пространственного соотношения, используя всевозможную вещественную наглядность (палочки, бечевку, бумагу, геометрические мозаики, конструкторы разных типов и т. д.). Такую деятельность называют моделированием.
Действие моделирования является как раз тем общим способом действий, который отражает специфику математического описания действительности. Если человек умеет построить какую-либо модель изучаемого предмета, процесса, явления, ситуации, отношения и описать ее на математическом языке, значит, он обладает тем, что мы называем математическим мышлением.
В процессе построения курса не считаю необходимым строго следовать логике построения Евклидовой геометрии, т.к. полагаю, что этот урок не должен превращаться в урок геометрии. Геометрический материал осваивается ребенком в ходе выполнения конструкторских заданий, геометрическое обобщение выступает в виде результата решения конструктивной задачи.
Моделируя пространственные отношения наиболее доступным для этого возраста способом, с опорой на наглядно-образное мышление, практическую деятельность и ощущения ученик легко усваивает начальные геометрические сведения.
Если же учесть, что полученные в начальных классах элементарные навыки построения и измерений сохраняются у учащихся на долгие годы, то становится ясной значимость формирования этих навыков именно в этот период.
Обобщая все выше сказанное, можно сделать следующий вывод: в I—IV классах происходит накопление простейших геометрических представлений у учащихся, овладение элементарными навыками использования линейки, циркуля, чертежного угольника, транспортира, ознакомление с некоторыми геометрическими терминами. Это достигается путем систематически проводимых практических работ. Уже в этих классах учащиеся постепенно готовятся к пониманию роли определений. Происходят первые попытки отыскания “названия” некоторым геометрическим фигурам: треугольнику, четырехугольнику, пятиугольнику. Но задача поисков формулировки определений еще не ставится.
Я убеждена, что познавательные возможности детей младшего школьного возраста значительно выше, чем это принято считать, поэтому решила развивать их путем знакомства детей с геометрическим материалом. И со 2 класса веду урок геометрии.
Учитывая развитие понятийного мышления учащихся, психологические особенности процесса усвоения понятий, в уроки геометрии стараюсь включать элементы игры, элементы занимательности. На таких уроках дети в занимательной форме знакомились с некоторыми основными геометрическими понятиями, учились ориентироваться в простейших геометрических ситуациях и обнаруживать геометрические фигуры в окружающей обстановке.
Логическим продолжением курса “Наглядная геометрия” в начальной школе, очевидно, должно явиться создание соответствующего курса для 5-6 классов.
Таким образом, я попытаюсь подготовить детей к изучению геометрии как отдельного предмета.
Статья (математика) по теме: Геометрия в начальной школе.
Геометрия в начальной школе
Пантюшина Елена Сергеевна – учитель начальных классов
«Вдохновение нужно в геометрии, как и в поэзии».
А.С.Пушкин.
План
- Роль геометрии в системе научных знаний и в школьном курсе математики.
- Психолого-педагогические особенности развития геометрического мышления учащихся начальных классов.
- Основные психологические особенности младшего школьника.
- Фрагмент урока.
- Геометрический материал, используемый на уроках математики.
- Литература.
В настоящее время в обществе сложилось новое понимание основной цели образования. Учитель в первую очередь должен заботиться о формировании у ученика особенности к саморазвитию: умение ставить цели, организовать свою деятельность, оценивать результаты своего труда; формирование личностных качеств: ума, воли, чувств и эмоций, творческих способностей, познавательных мотивов деятельности; формирование представления мира.
Итак, для современного этапа развития школьного математического образования характерен переход от экстенсивного обучения к интенсивному. Вновь актуальными становятся проблемы развития интуиции, образного мышления, а также способности мыслить творчески, не стандартно. Для формирования высокой мотивации учебного процесса, а также в развитии всех форм мышления младшего школьника, ведущую роль важно отводить геометрии, т. к. этот возраст является одним из сенситивных периодов в развитии мышления ребёнка. Поэтому в курсе математики начальной школы необходимо усилить роль геометрического материала и геометрических методов, т. е. придать начальному курсу геометрии большей самостоятельности как по содержанию и объёму, так и по методам изучения, усиления внимания к изучению стереометрического материала, формированию элементарных пространственных представлений у учащихся.
В программе традиционной начальной школы геометрический материал является составной частью курса математики. Он не выделяется в самостоятельный раздел, а включается в программу каждого года обучения. Но, к сожалению, изучается геометрический материал в основном на уровне знания-знакомства.
Здесь никакие правила и определения не заучиваются, ученики практически различают геометрические фигуры, сравнивают их, изображают на бумаге, а многие геометрические понятия, такие как, например, кривая линия, острый и тупой углы, виды треугольников и вовсе исключены из традиционных учебников.
Психологические исследования Л.С. Выготского, Л.В. Занкова, В.В. Давыдова и др. показывают, что усвоение геометрического материала должно базироваться на определенных психических процессах, основным из которых является восприятие. У детей старшего дошкольного возраста оно целостное, а не атоместическое. Кто может возражать против того, что восприятие является базой развития речи и на ее основе – творческого воображения? Таким образом, по Л.С. Выготскому, получаем собранную природой психологическую систему, как базу для введения геометрического материала: восприятие, плюс речь, плюс воображение, которое требует дальнейшего развития.
Развитие восприятия требует введение геометрического материала, т.к. сам геометрический материал–это образы, это символы. Следовательно, вторая составляющая – это речь. Данные образы и символы являются моделью реальных объектов. Реальные объекты могут быть созданы нашими учениками в ходе моделирующей деятельности. Эти модели представлены понятиями (сторона, угол, треугольник, многоугольник и т.д.), которые естественным образом дети стараются расширить. А средством описания моделей является речь. Поэтому, на уроках сначала ввожу модели (геометрические образы), исследуя которые с помощью речи, дети работают в зоне ближайшего развития.
Третий компонент, развитие воображения, закладывается в непосредственной деятельности конструирования. Однако речь и в данном случае является средством развития учащихся. При этом творческая фантазия детей ничем не ограничена, содержание их воображения дети формулируют опираясь на научный понятийный аппарат и логические приемы мышлении
Учебная деятельность для детей младшего школьного возраста является ведущей, а моделирование с помощью знаковой и символической деятельности, является одной из составляющих учебной деятельности в совокупности с другими интеллектуальными умениями. Моделирующая, знаково-символическая деятельность – это те виды деятельности, с помощью которых ученики развивают память, внимание, творческое воображение.
Я выделяю еще одну составляющую учебной деятельности младших школьников – это исследовательская деятельность. В зависимости от целей конкретного урока какая-либо составная учебная деятельность выходит на первый план.
Основная цель состоит в том, чтобы дать учащимся начальные геометрические представления, развить логическое мышление и пространственное воображение детей, сформировать умение узнавать геометрические фигуры и их части, собирать заданный объект из частей, делить геометрические фигуры на составные части, изображать фигуры на чертеже.
В соответствии с этим определяется конкретное содержание, основными положениями которого являются: преемственность с традиционным построением курса математики, что обеспечивает числовую грамотность учащихся, умение решать текстовые задачи, знакомство с величинами и их измерением; усиление геометрического содержания обеспечивает расширение геометрических представлений и знаний учащихся, развивает их пространственное воображение и логическое мышление. На уроках ввожу знакомство с основными линейными, плоскостными и пространственными геометрическими фигурами и их свойствами. Расширение геометрических представлений и знаний используется для формирования у учащихся элементов технического мышления и конструкторских умений; обеспечивается формирование умений изображать на бумаге в форме чертежа сначала элементарных геометрических фигур, а затем конструируемые объекты или их части; активизируется творческое мышление, побуждает к поиску нестандартных математических задач.
Изложение геометрического материала проводится в наглядно-практическом плане. Работая с геометрическим материалом, дети знакомятся и используют основные свойства изучаемых геометрических фигур. Задания располагаются в порядке усложнения и постепенного обогащения новыми элементами конструкторского характера.
При первоначальном введении основных геометрических понятий (точка, линия, плоскость) используются нестандартные способы: создание наглядного образа с помощью рисунка на известном детям материале, сказочного сюжета с использованием сказочных персонажей, выполнение несложных на первых порах практических работ.
После введения одной из важнейших линейных геометрических фигур – отрезка – предусмотрена серия заданий на конструирование из отрезков одинаковой и разной длины. Первые задания направлены на выявление равных и неравных отрезков, на умение расположить их в порядке увеличения или уменьшения. Далее отрезки используются для изготовления силуэтов различных объектов на плоскости.
Учащиеся знакомятся с плоскими фигурами: треугольником, прямоугольником, квадратом, ромбом и др.; с геометрическими телами: кубом, цилиндром, шаром и др. и их элементами; развертками геометрических тел; с плоскостью; с кругом и окружностью, умением выполнять чертеж с помощью циркуля; получают представление о центре, радиусе, диаметре круга (окружности), а также о полукруге и кольце. Дети учатся решать задачи на нахождение периметра, площади и объема фигур; знакомятся и учатся работать с основными инструментами: линейка, угольник, циркуль и др.Предусматривается знакомство с конструкциями из шашек и кубиков, выполнение чертежа конструкций, три их вида: спереди, сверху, слева. Дети учатся писать графические диктанты по клеточкам и по координатным шкалам.
В работе учитываю возрастные особенности детей и материал представляю в форме интересных заданий, сказочных путешествий, дидактических игр, игровых ситуаций, используются стихи, сказки, считалки, загадки, ребусы и т.д.
С элементами геометрии ученики начинают знакомиться в 1 классе. Геометрический материал даётся в дополнении к арифметическому. Поэтому к урокам подбираю комплекс упражнений по геометрии, способствующий развитию творческого мышления, позволяющие формировать пространственные представления детей.
Упражнения с использованием геометрического материала.
- Найди “лишнюю фигуру”. Назовите общий признак фигур. Например:
2.Кроссворды.
3.Графический диктант. (Например:1 кл. вправо, 2 кл. вправо вверх по диагонали, 2 кл. влево, 2 кл. вправо вниз по диагонали, 1 кл. вправо и т. д. Продолжите узор до конца строки.)
4.Головоломка “Танграм”.
5.Игра “Пифагор”.
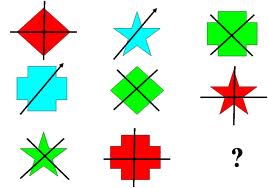
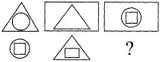
6.Установи закономерность и определи, какая фигура должна быть на месте вопроса.
7.Составь фигуру, используя детали.
8.Задания в форме тестов.
9.Загадки
10.Упражнение «Геометрия вокруг нас»
11.Упражнение «Соотнеси предметы с геометрическими фигурами»
12.Упражнение «Определи из каких геометрических фигур составлен предмет»
13. Упражнение «Геометрия в картинах»
14 Бумагопластика.
.
15.Практические упражнения.
16.Игра «Узнай по описанию»
17.Игра «Узнай по развёртке»
17.Игра «Мозаика»
Фрагмент урока
- Фрагменты урока закрепления в 1 классе по теме: «Обобщение знаний об отрезках, прямой, луче.»
- Игра-путешествие. Герои сказки «Репка».
Задание на развитие пространственных представлений детей и на построение отрезков.
Задание: Дед, бабка, внучка и Жучка танцевали вокруг репки, двигаясь в указанном стрелками направлении.
На доске изображены картинки с изображениями героев, расположенных в разных направлениях.
— Кто находится за репкой, если справа от репки оказался дедка?
— Кто находится слева от репки, если за ней оказалась Жучка?
— Кого могла увидеть Жучка, когда направлялась к репке?
После выполнения задания должна получиться ломаная из трёх звеньев.(Вспомнить что такое ломаная, из чего она состоит, сколько отрезков, доказать, …)
- Игра «Путешествие Муравьишки» (картинка с изображением Муравьишки)
В этой игре-путешествии я использовала графический диктант:
3 клетки вверх, 1 клетка вправо, 3 клетки вниз, 3 клетки влево, 2 клетки вверх.
Должна получиться ломаная, состоящая из пяти отрезков. (Повторить что такое отрезок, определить какой самый короткий, длинный, не короткий, но и не длинный.)
- Задание «Геометрическая полянка» (На доске и на листочках у каждого ученика изображены разные геометрические фигуры: кривые линии, прямая, лучи, отрезки.)
Ученики слушают учителя, который задаёт по теме вопросы и выполняют:
- Перед вами поляна с геометрическими фигурами…
— Какие фигуры изображены? (Устный ответ)
Обведи отрезки синим карандашом, лучи – зелёным.
— Сколько отрезков? Сколько лучей? Что такое отрезок? Чем отличается отрезок от прямой? Что такое луч? (Фронтальный опрос.)
- Задание выполняют в тетради.
Вопросы по заданию:
-Сколько прямых можно провести через одну точку?
В тетради поставьте две точки.
— Сколько прямых можно провести через эти точки? Проведите. Обозначьте её (АВ).
Какие ещё фигуры получились? (Лучи, отрезок). Запишите их.
- Фронтальный опрос по теме в форме игры « ДА – НЕТ».
Ломаная состоит из отрезков, соединённых последовательно. (Да)
Наименьшее число звеньев у ломаной – одно. (Нет)
Отрезок – часть прямой, ограниченная с двух сторон. (Да)
Через одну точку можно провести только одну прямую. (Нет)
Через две точки можно провести одну прямую. (Да)
Луч – часть прямой, ограниченная с одной стороны. (Да) И т. п.
- Упражнения.
- Задание. Напечатайте букву М. – Из скольких звеньев она состоит. И т.п.
- Задание. Нарисуйте человечка, состоящего из ломаных линий.
- Задание. Нарисуйте линию, по которой бежит герой стихотворения.
Я бегу, бегу, бегу…
Задержаться не могу.
И хотя устали ножки,
Нет конца моей дорожки.
Бесконечности в ней нет,
Снова вижу я свой след. (Получится круг – замкнутая линия)
Литература
1.Жильцова Т.В., А.А.Обухова А.А. Наглядная геометрия//М.:ВАКО,-2004.
- Богданова Е.А. Формирование эмпирических предпонятий об основных объектах геометрии//Начальная школа.-2001.-№10.
- Веккер Л.М. Психологические процессы.-Л.1976.
- Волкова С.И., Столярова Н.Н. Развитие познавательных способностей учащихся на уроках математики//Начальная школа.-1993.-№8.
- Краснова О.В.Первые шаги в геометрии//Начальная школа.-2002.-№4.
- Пазушко Ж.И. Развивающая геометрия в начальной школе//Начальная школа.-1999.-№1.
- Шадрина И.В. Обучение геометрии в начальных классах. -М.: Школьная Пресса,2002.
- Фазлетдинова Н. Геометрия вокруг нас//Начальная школа.-2001.-№25.
- Сутягина В.И. Функции геометрии в начальном обучении математике//Начальная школа.-2002.-№11.
- Подходова Н.С. и др. Волшебная страна фигур. В пяти путешествиях. — СПб.,2000.
- Батова А.С. Графический диктант//Начальная школа.-2003.-№9.
Геометрия в начальной школе
Геометрия в начальной школе 
Пантюшина Елена Сергеевна – учитель начальных классов
«Вдохновение нужно в геометрии, как и в поэзии».
А.С.Пушкин.
План
Роль геометрии в системе научных знаний и в школьном курсе математики.
Психолого-педагогические особенности развития геометрического мышления учащихся начальных классов.
Основные психологические особенности младшего школьника.
Фрагмент урока.
Геометрический материал, используемый на уроках математики.
Литература.
В настоящее время в обществе сложилось новое понимание основной цели образования. Учитель в первую очередь должен заботиться о формировании у ученика особенности к саморазвитию: умение ставить цели, организовать свою деятельность, оценивать результаты своего труда; формирование личностных качеств: ума, воли, чувств и эмоций, творческих способностей, познавательных мотивов деятельности; формирование представления мира.
Итак, для современного этапа развития школьного математического образования характерен переход от экстенсивного обучения к интенсивному. Вновь актуальными становятся проблемы развития интуиции, образного мышления, а также способности мыслить творчески, не стандартно. Для формирования высокой мотивации учебного процесса, а также в развитии всех форм мышления младшего школьника, ведущую роль важно отводить геометрии, т. к. этот возраст является одним из сенситивных периодов в развитии мышления ребёнка. Поэтому в курсе математики начальной школы необходимо усилить роль геометрического материала и геометрических методов, т. е. придать начальному курсу геометрии большей самостоятельности как по содержанию и объёму, так и по методам изучения, усиления внимания к изучению стереометрического материала, формированию элементарных пространственных представлений у учащихся.
В программе традиционной начальной школы геометрический материал является составной частью курса математики. Он не выделяется в самостоятельный раздел, а включается в программу каждого года обучения. Но, к сожалению, изучается геометрический материал в основном на уровне знания-знакомства.
Здесь никакие правила и определения не заучиваются, ученики практически различают геометрические фигуры, сравнивают их, изображают на бумаге, а многие геометрические понятия, такие как, например, кривая линия, острый и тупой углы, виды треугольников и вовсе исключены из традиционных учебников.
Психологические исследования Л.С. Выготского, Л.В. Занкова, В.В. Давыдова и др. показывают, что усвоение геометрического материала должно базироваться на определенных психических процессах, основным из которых является восприятие. У детей старшего дошкольного возраста оно целостное, а не атоместическое. Кто может возражать против того, что восприятие является базой развития речи и на ее основе – творческого воображения? Таким образом, по Л.С. Выготскому, получаем собранную природой психологическую систему, как базу для введения геометрического материала: восприятие, плюс речь, плюс воображение, которое требует дальнейшего развития.
Развитие восприятия требует введение геометрического материала, т.к. сам геометрический материал–это образы, это символы. Следовательно, вторая составляющая – это речь. Данные образы и символы являются моделью реальных объектов. Реальные объекты могут быть созданы нашими учениками в ходе моделирующей деятельности. Эти модели представлены понятиями (сторона, угол, треугольник, многоугольник и т.д.), которые естественным образом дети стараются расширить. А средством описания моделей является речь. Поэтому, на уроках сначала ввожу модели (геометрические образы), исследуя которые с помощью речи, дети работают в зоне ближайшего развития.
Третий компонент, развитие воображения, закладывается в непосредственной деятельности конструирования. Однако речь и в данном случае является средством развития учащихся. При этом творческая фантазия детей ничем не ограничена, содержание их воображения дети формулируют опираясь на научный понятийный аппарат и логические приемы мышлении
Учебная деятельность для детей младшего школьного возраста является ведущей, а моделирование с помощью знаковой и символической деятельности, является одной из составляющих учебной деятельности в совокупности с другими интеллектуальными умениями. Моделирующая, знаково-символическая деятельность – это те виды деятельности, с помощью которых ученики развивают память, внимание, творческое воображение.
Я выделяю еще одну составляющую учебной деятельности младших школьников – это исследовательская деятельность. В зависимости от целей конкретного урока какая-либо составная учебная деятельность выходит на первый план.
Основная цель состоит в том, чтобы дать учащимся начальные геометрические представления, развить логическое мышление и пространственное воображение детей, сформировать умение узнавать геометрические фигуры и их части, собирать заданный объект из частей, делить геометрические фигуры на составные части, изображать фигуры на чертеже.
В соответствии с этим определяется конкретное содержание, основными положениями которого являются: преемственность с традиционным построением курса математики, что обеспечивает числовую грамотность учащихся, умение решать текстовые задачи, знакомство с величинами и их измерением; усиление геометрического содержания обеспечивает расширение геометрических представлений и знаний учащихся, развивает их пространственное воображение и логическое мышление. На уроках ввожу знакомство с основными линейными, плоскостными и пространственными геометрическими фигурами и их свойствами. Расширение геометрических представлений и знаний используется для формирования у учащихся элементов технического мышления и конструкторских умений; обеспечивается формирование умений изображать на бумаге в форме чертежа сначала элементарных геометрических фигур, а затем конструируемые объекты или их части; активизируется творческое мышление, побуждает к поиску нестандартных математических задач.
Изложение геометрического материала проводится в наглядно-практическом плане. Работая с геометрическим материалом, дети знакомятся и используют основные свойства изучаемых геометрических фигур. Задания располагаются в порядке усложнения и постепенного обогащения новыми элементами конструкторского характера.
При первоначальном введении основных геометрических понятий (точка, линия, плоскость) используются нестандартные способы: создание наглядного образа с помощью рисунка на известном детям материале, сказочного сюжета с использованием сказочных персонажей, выполнение несложных на первых порах практических работ.
После введения одной из важнейших линейных геометрических фигур – отрезка – предусмотрена серия заданий на конструирование из отрезков одинаковой и разной длины. Первые задания направлены на выявление равных и неравных отрезков, на умение расположить их в порядке увеличения или уменьшения. Далее отрезки используются для изготовления силуэтов различных объектов на плоскости.
Учащиеся знакомятся с плоскими фигурами: треугольником, прямоугольником, квадратом, ромбом и др.; с геометрическими телами: кубом, цилиндром, шаром и др. и их элементами; развертками геометрических тел; с плоскостью; с кругом и окружностью, умением выполнять чертеж с помощью циркуля; получают представление о центре, радиусе, диаметре круга (окружности), а также о полукруге и кольце. Дети учатся решать задачи на нахождение периметра, площади и объема фигур; знакомятся и учатся работать с основными инструментами: линейка, угольник, циркуль и др.Предусматривается знакомство с конструкциями из шашек и кубиков, выполнение чертежа конструкций, три их вида: спереди, сверху, слева. Дети учатся писать графические диктанты по клеточкам и по координатным шкалам.
В работе учитываю возрастные особенности детей и материал представляю в форме интересных заданий, сказочных путешествий, дидактических игр, игровых ситуаций, используются стихи, сказки, считалки, загадки, ребусы и т.д.
С элементами геометрии ученики начинают знакомиться в 1 классе. Геометрический материал даётся в дополнении к арифметическому. Поэтому к урокам подбираю комплекс упражнений по геометрии, способствующий развитию творческого мышления, позволяющие формировать пространственные представления детей.
Упражнения с использованием геометрического материала.
Найди “лишнюю фигуру”. Назовите общий признак фигур. Например:

2.Кроссворды.
3.Графический диктант. (Например:1 кл. вправо, 2 кл. вправо вверх по диагонали, 2 кл. влево, 2 кл. вправо вниз по диагонали, 1 кл. вправо и т. д. Продолжите узор до конца строки.)
4.Головоломка “Танграм”.
5.Игра “Пифагор”.
6.Установи закономерность и определи, какая фигура должна быть на месте вопроса.
7.Составь фигуру, используя детали.
8.Задания в форме тестов.

9.Загадки


10.Упражнение «Геометрия вокруг нас»









11.Упражнение «Соотнеси предметы с геометрическими фигурами»
12.Упражнение «Определи из каких геометрических фигур составлен предмет»


13. Упражнение «Геометрия в картинах»



14 Бумагопластика.
. 
15.Практические упражнения.



16.Игра «Узнай по описанию»

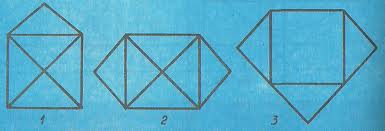
17.Игра «Узнай по развёртке»
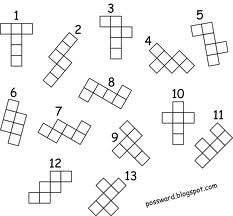
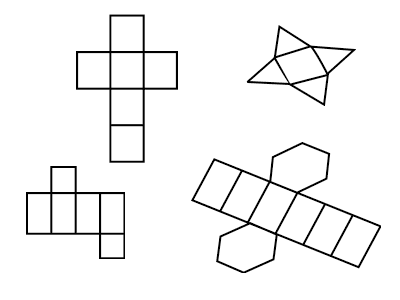
17.Игра «Мозаика»
Фрагмент урока
Фрагменты урока закрепления в 1 классе по теме: «Обобщение знаний об отрезках, прямой, луче.»
Игра-путешествие. Герои сказки «Репка».
Задание на развитие пространственных представлений детей и на построение отрезков.
Задание: Дед, бабка, внучка и Жучка танцевали вокруг репки, двигаясь в указанном стрелками направлении.
На доске изображены картинки с изображениями героев, расположенных в разных направлениях.
— Кто находится за репкой, если справа от репки оказался дедка?
— Кто находится слева от репки, если за ней оказалась Жучка?
— Кого могла увидеть Жучка, когда направлялась к репке?
После выполнения задания должна получиться ломаная из трёх звеньев.(Вспомнить что такое ломаная, из чего она состоит, сколько отрезков, доказать, …)
Игра «Путешествие Муравьишки» (картинка с изображением Муравьишки)
В этой игре-путешествии я использовала графический диктант:
3 клетки вверх, 1 клетка вправо, 3 клетки вниз, 3 клетки влево, 2 клетки вверх.
Должна получиться ломаная, состоящая из пяти отрезков. (Повторить что такое отрезок, определить какой самый короткий, длинный, не короткий, но и не длинный.)
Задание «Геометрическая полянка» (На доске и на листочках у каждого ученика изображены разные геометрические фигуры: кривые линии, прямая, лучи, отрезки.)
Ученики слушают учителя, который задаёт по теме вопросы и выполняют:
— Какие фигуры изображены? (Устный ответ)
Обведи отрезки синим карандашом, лучи – зелёным.
— Сколько отрезков? Сколько лучей? Что такое отрезок? Чем отличается отрезок от прямой? Что такое луч? (Фронтальный опрос.)
Вопросы по заданию:
-Сколько прямых можно провести через одну точку?
В тетради поставьте две точки.
— Сколько прямых можно провести через эти точки? Проведите. Обозначьте её (АВ).
Какие ещё фигуры получились? (Лучи, отрезок). Запишите их.
Фронтальный опрос по теме в форме игры « ДА – НЕТ».
Ломаная состоит из отрезков, соединённых последовательно. (Да)
Наименьшее число звеньев у ломаной – одно. (Нет)
Отрезок – часть прямой, ограниченная с двух сторон. (Да)
Через одну точку можно провести только одну прямую. (Нет)
Через две точки можно провести одну прямую. (Да)
Луч – часть прямой, ограниченная с одной стороны. (Да) И т. п.
Упражнения.
Задание. Нарисуйте человечка, состоящего из ломаных линий.
Задание. Нарисуйте линию, по которой бежит герой стихотворения.
Я бегу, бегу, бегу…
Задержаться не могу.
И хотя устали ножки,
Нет конца моей дорожки.
Бесконечности в ней нет,
Снова вижу я свой след. (Получится круг – замкнутая линия)
Литература
1.Жильцова Т.В., А.А.Обухова А.А. Наглядная геометрия//М.:ВАКО,-2004.
Богданова Е.А. Формирование эмпирических предпонятий об основных объектах геометрии//Начальная школа.-2001.-№10.
Веккер Л.М. Психологические процессы.-Л.1976.
Волкова С.И., Столярова Н.Н. Развитие познавательных способностей учащихся на уроках математики//Начальная школа.-1993.-№8.
Краснова О.В.Первые шаги в геометрии//Начальная школа.-2002.-№4.
Пазушко Ж.И. Развивающая геометрия в начальной школе//Начальная школа.-1999.-№1.
Шадрина И.В. Обучение геометрии в начальных классах. -М.: Школьная Пресса,2002.
Фазлетдинова Н. Геометрия вокруг нас//Начальная школа.-2001.-№25.
Сутягина В.И. Функции геометрии в начальном обучении математике//Начальная школа.-2002.-№11.
Подходова Н.С. и др. Волшебная страна фигур. В пяти путешествиях. — СПб.,2000.
Батова А.С. Графический диктант//Начальная школа.-2003.-№9.
Уроки геометрии — InternetUrok.ru
О том, что геометрия с момента своего рождения была и остается одной из важнейших наук для человечества, говорить не стоит, так как это – прописная истина. Ее роль в образовании современного человека является одной из главных. Со времени своего появления геометрия охватывала самые различные направления человеческой деятельности. Сегодня эта наука стала еще более значимой. Ее законы используются во многих направлениях деятельности, отраслях промышленности и бизнеса. Ребенок, который вовремя стал изучать уроки по геометрии 7 класса, в ходе решения соответствующих задач развивает свое воображение и логическую культуру.
Мало кто знает, что одно из направлений геометрии – тригонометрия – возникло и развивалось как часть астрономии. История человечества сопровождалась наблюдениями за движением небесных тел, поэтому историю тригонометрии невозможно проследить от ее истоков. С имени Евклида можно начать отсчет развития предмета геометрия, а с имени Птолемея – развития астрономии и тригонометрии.
Помимо всего этого, уроки геометрии могут существенно развить творческие способности и пространственные представления ребенка. Эта наука – одна из основ современного прогресса. Вот почему изучение курса геометрии начинается в школьном возрасте. Чтобы школьные уроки геометрии не стали для ребенка темным лесом стоит слегка помочь ему, и в этом помогут наши учебные видеоматериалы на эту тему. Здесь вашему вниманию представлены уроки геометрии в формате видео, отснятые на лекциях профессиональных преподавателей. Теперь вы можете без проблем изучать геометрию онлайн.
Видеоуроки по геометрии
С их помощью ваш ребенок-школьник может в доступной форме получить нужные сведения по всем основным курсам геометрии. Азы, которые с монитора компьютера преподадут ему опытные преподаватели, могут стать залогом его успеваемости по этой дисциплине в школе. Отдельное преимущество такого способа изучения геометрии заключается в том, что все эти уроки абсолютно бесплатны.
Если школьнику тяжело дается изучение уроков геометрии, воспользуйтесь нашими видеоматериалами, и с уверенностью можно сказать, что такой подход поможет решить проблему отставания. Чем раньше вы приступите к использованию видеоматериалов, тем лучше будут результаты. Ведь геометрия будет преподаваться и дальше, а неусвоенные знания могут стать серьезным препятствием к ее изучению. Когда наступит пора изучения тригонометрии, трудности, связанные с незнанием азов, могут стать причиной серьезного отставания.
Наш портал, на котором вы найдете множество видео уроков геометрии, способен существенно помочь. Усадите своего ребенка-школьника перед монитором компьютера и включите один из проблемных для него уроков. Например, открыв урок под названием «Площадь трапеции», вы вместе с учителем выведете формулу площади трапеции и научитесь её применять при решении задач. Вы увидите, что изучение геометрии онлайн пойдет школьнику на пользу. С помощью такого метода он станет лучше понимать ее, а комфортная домашняя обстановка будет способствовать лучшему усвоению материала. Результаты будут заметны уже совсем скоро. С такими качественными обучающими видеоуроками геометрия перестанет быть проблемным школьным предметом.
История возникновения геометрии
Считается, что геометрия как наука возникла у древних греков. Эллада была чрезвычайно развитым регионом, где из любой деятельности старались извлечь максимум пользы. А для этого требовался научный подход. Переняв у египтян методы землемерия (именно так с греческого переводится слово «геометрия»), греки превратили в науку эти и другие правила по измерению объемов сосудов и пр. Конечно, до окончательного становления науки прошло еще много времени. Когда все правила и методы сложились воедино и была достигнута общая закономерность измерений, эту область знаний уже без преувеличений можно было называть наукой. Первые доказательные труды по геометрии были также составлены в Древней Греции. Кому из нас неизвестно имя Евклида – одного из основоположников геометрии, труды которого стали основой для изучения геометрии. Элементарная геометрия нередко теперь носит название евклидовой. Развиваясь, эта наука включала в себя все больше знаний, пестрела новыми открытиями. Одним из самых ярких открытий считается система координат Рене Декарта. Методы решения алгебраических уравнений, классификация алгебраических прямых, а также объяснение нового способа задания кривой с помощью уравнения, который являлся решающим шагом к понятию функции – всё это истолковал в своих трудах Рене Декарт.