6.9.1. Решение систем линейных уравнений графическим способом
data-ad-client=»ca-pub-8602906481123293″
data-ad-slot=»2890988705″>
- Способ заключается в построении графика каждого уравнения, входящего в данную систему, в одной координатной плоскости и нахождении точки пересечения этих графиков. Координаты этой точки (x; y) и будут являться решением данной системы уравнений.
- Если прямые, являющиеся графиками уравнений системы, пересекаются, то система уравнений имеет единственное решение.
- Если прямые, являющиеся графиками уравнений системы, параллельны, то система уравнений не имеет решений.
- Если прямые, являющиеся графиками уравнений системы, совпадают, то система уравнений имеет бесконечное множество решений.
Примеры. Решить графическим способом систему уравнений.
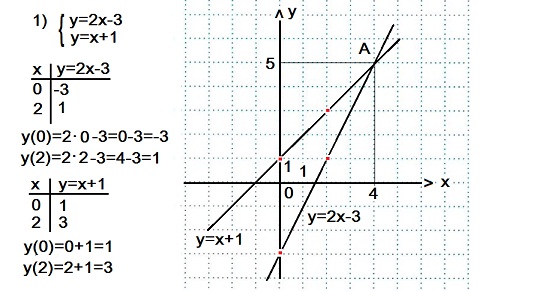 Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек. Мы составили таблицы значений х и у для каждого из уравнений системы.
Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек. Мы составили таблицы значений х и у для каждого из уравнений системы.
Прямую y=2x-3 провели через точки (0; -3) и (2; 1).
Прямую y=x+1 провели через точки (0; 1) и (2; 3).
Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.
Ответ: (4; 5).
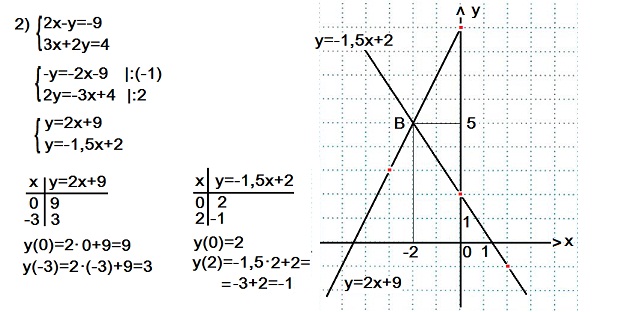 Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.
Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.
Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3). Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).
Наши прямые пересеклись в точке В(-2; 5).
Ответ: (-2; 5).
www.mathematics-repetition.com
Основные понятия. Графический метод (С.М.Слупко). Видеоурок. Алгебра 7 Класс
Мы начинаем разговор о системах линейных уравнений. Этот урок будет разделен на две части:
Обсуждение того, что такое система. Решение систем.
Начнем с первого вопроса – что такое система.
Пример:
Если сыщик знает про одного преступника, что тот высокий (см. Рис. 1), а про второго, что тот блондин (см. Рис. 2), то эти два условия не объединены в систему, они относятся к разным неизвестным, к разным преступникам.

Рис. 1. Высокие преступники

Рис. 2. Преступники-блондины
Если это информация про одного и того же преступника, то это – система. Оба условия выполняются одновременно. Одну информацию можно использовать для уточнения другой. Преступник – высокий блондин. (См. Рис. 3.)

Рис. 3. Преступник – высокий блондин
Пример:
Пусть нам известно, что дом находится на ул. Гоголя. Вариантов, где точно расположен дом, много – целая улица. (См. Рис. 4.)

Рис. 4. Улица Гоголя
Дом находится на проспекте Мира. То же самое – вариантов много. (См. Рис. 5.)
Рис. 5. Проспект Мира
Но если эта информация относится к одному и тому же дому, то сразу понятно, что дом находится на перекрестке. (См. Рис. 6.) Два условия объединены в систему.

Рис. 6. Дом находится на перекрестке
Итак, система – это объединение нескольких условий так, чтобы они выполнялись одновременно.
Решим такую задачу. Два человека вскопали огород площадью 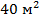 . Сколько вскопал каждый? (См. Рис. 7.)
. Сколько вскопал каждый? (См. Рис. 7.)

Рис. 7. Иллюстрация к задаче
Решение
Запишем условие уравнением: 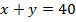 , где
, где 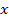 – площадь, которую вскопал первый человек,
– площадь, которую вскопал первый человек,  – площадь, которую вскопал второй человек.
– площадь, которую вскопал второй человек.
Решение такого уравнения – пара чисел. Их бесконечно много. Например, один вскопал  , другой –
, другой – 
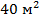 , другой – ничего. (См. Рис. 9.)
, другой – ничего. (См. Рис. 9.)
Рис. 8. Один вскопал  , другой –
, другой – 

Рис. 9. Один вскопал все 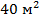
Можно изобразить каждое такое решение в виде точки на координатной плоскости. Все решения выстроятся в одну прямую. (См. Рис. 10.) Эту прямую называют графиком уравнения.
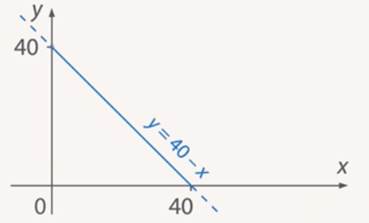
Рис. 10. График уравнения
Каждая точка этой прямой – одно частное решение уравнения. (См. Рис. 11.)
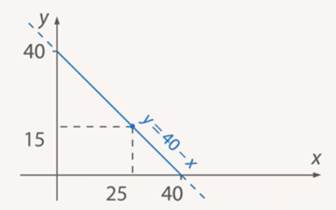
Рис. 11. Частное решение
Теперь такая задача. Два человека вскопали равные площади. Сколько вскопал каждый?
Уравнение имеет вид: 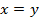 . Здесь тоже бесконечно много решений.
. Здесь тоже бесконечно много решений.
А если речь идет про один и тот же огород, про одних и тех же людей, то эти два условия выполняются одновременно. Двое вскопали огород 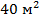
Уравнения нужно объединить в систему. Договорились обозначать это фигурной скобкой:  .
.
Второе уравнение можно переписать в стандартном виде: 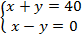 . Такая запись эквивалентна исходной.
. Такая запись эквивалентна исходной.
Здесь уже только одно решение – каждый вскопал по  .
.
Эта пара чисел является решением каждого из уравнений системы. На графике она является точкой, принадлежащей обоим графикам, то есть точкой их пересечений. (См. Рис. 12.)
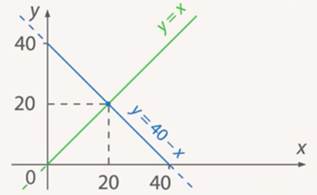
Рис. 12. Графическое решение системы
Ответ:  .
.
Система – это требование, чтобы несколько условий выполнялись одновременно: 
Простой случай системы в математике – два линейных уравнения с двумя неизвестными: 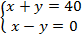 Решением системы называется общее решение для всех уравнений:
Решением системы называется общее решение для всех уравнений: 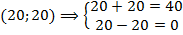
Рассмотрим систему:  .
.
Изобразим множество решений каждого уравнения – построим графики уравнений.
Первое уравнение: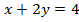 . Множество решений – прямая. Чтобы ее изобразить, нужны две любые точки, то есть два любых решения. Можно взять, например, такие решения:
. Множество решений – прямая. Чтобы ее изобразить, нужны две любые точки, то есть два любых решения. Можно взять, например, такие решения:  и
и 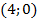 .
.
Отметим эти решения на координатной плоскости и проведем через них прямую. Мы получили все решения уравнения. (См. Рис. 13.)

Рис. 13. Решение первого уравнения
Аналогично для второго уравнения: 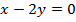 . Возьмем, например, точки
. Возьмем, например, точки 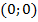 и
и 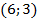 . Изобразим их на координатной плоскости и проведем через них прямую. (См. Рис. 14.)
. Изобразим их на координатной плоскости и проведем через них прямую. (См. Рис. 14.)
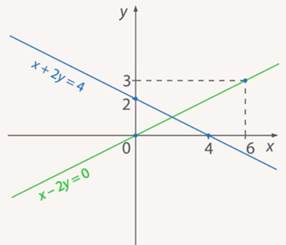
Рис. 14. Решение второго уравнения (зеленый график)
Итак, каждая прямая – это множество решений одного уравнения. Где находится точка, которая является решением обоих уравнений? Конечно, это точка пересечения прямых.
По-другому это решение можно записать в виде пары чисел, координат точки пересечения:  . (См. Рис. 15.)
. (См. Рис. 15.)
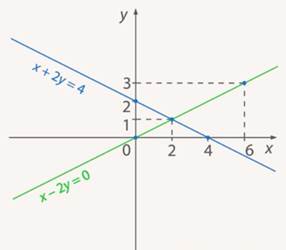
Рис. 15.  решение системы – точка пересечения графиков
решение системы – точка пересечения графиков
Решение превращает уравнение в верное числовое равенство. Проверим (вместо переменных подставим найденные значения):

Ответ:  .
.
Как записывать ответ

Ответ записывают по-разному:
Ответ: 
Ответ: 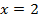 ;
; 
Ответ: 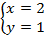
Во всех случаях понятно, о чем идет речь. Но, все-таки запись 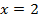 является уравнением. Решением системы является пара чисел, а не два уравнения (как во второй и третьей записях).
является уравнением. Решением системы является пара чисел, а не два уравнения (как во второй и третьей записях).
Так что формально верная запись ответа здесь только одна – в виде пары чисел  .
.
Вернемся к примеру с домом и двумя улицами: 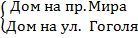 .
.
Система этих двух условий означает, что один и тот же дом находится и на одной и на другой улице. Решение системы – дом находится на перекрестке. (См. Рис. 6.)
Но что, если улицы окажутся параллельными? (См. Рис. 16.) Тогда дом никак не может быть одновременно на двух улицах. Решения у такой системы нет.
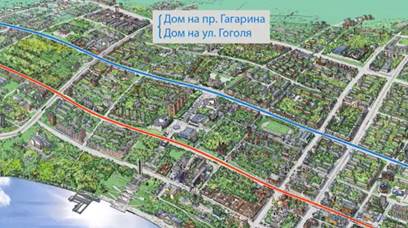
Рис. 16. Улицы параллельны
Точно такая же ситуация с системой двух уравнений.
Пример. Решить систему:  .
.
Решение
Построим графики уравнений. Возьмем по два решения для каждого из уравнений. Например, 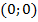 и
и  для
для  и
и 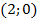 и
и 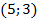 для
для 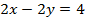 .
.
Графики параллельны. Общих точек не существует. Решения у системы нет. (См. Рис. 17.)

Рис. 17. Графики параллельны – решения у системы нет
Можно ли это было увидеть, не строя графиков? Да, можно.
Разделим обе части второго уравнения на
interneturok.ru
Графический способ решения систем уравнений
Графиками таких уравнений могут являться различные линии.

Решить систему — значит найти все её решения или доказать, что их нет.
Определение:
Решением системы называется пара значений переменных, обращающая каждое уравнение системы уравнений с двумя переменными в верное равенство.
Пример.
Нужно проверить, обращают ли пара значений уравнения системы в верные равенства.

1. Первая пара (-2, 1). Подставим их в систему:

Первое уравнение обратилось в верное равенство, а второе — нет. Значит, пара чисел (-2;1) не является решением данной системы.
2. Вторая пара (1;-2). Поставим эти значения в систему:

Получаем два верных равенства. Значит, пара чисел (1;-2) является решением данной системы.
Пример.
Решить систему двух уравнений:

Изобразим график системы:

Видим, что графики пересеклись в двух точках. Их координаты и являются решением системы. Данная система имеет два решения: (0;3) и (3;0).
Проверим, действительно ли они являются решениями. Подставим эти значения в систему:

Проверка необходима потому, что графический метод позволяет получить приближённые значения. Иногда их сложно указать точно.
Получили две пары значений: (0;3) и (3;0).
Пример.
Решить систему уравнений:

Изобразим график системы:

Точку пересечения этих графиков имеет координаты (0;1). Подставим значения в систему:

Получили верные равенства. Значит, решением данной системы является пара чисел (0;1).
Пример.
Решить систему двух уравнений:

Изобразим график системы:

Видим две точки пересечения. Их координаты трудно указать точно. Поэтому прежде чем записать ответ, полученные значения нужно подставить в систему:

Решением системы будут две пары чисел(2,5;2,5) и (6,5;6,5).
videouroki.net
Решение системы уравнений графическим методом средствами MS Excel
Цели и задачи.
- Развитие приемов умственной деятельности, формирование и развитие функционального мышления учащихся, развитие познавательных потребностей учащихся, создание условий для приобретения опыта работы учащихся в среде ИКТ.
- Достижение сознательного усвоения учебного материала учащимися, работа над повышением грамотности устной речи, правильного использования компьютерных терминов.
- Научить применять возможности MS Excel в повседневной жизни, в познавательной деятельности.
- Закрепить навыки создания таблиц и диаграмм.
- Научить решать систему уравнений графическим методом, исследовать график функции.
Оборудование урока: компьютеры, мультимедиа проектор.
Программное обеспечение: Windows XP, пакет программ MS Office 2003.
Содержание урока
Организационный момент.
Здравствуйте.
Тема нашего урока тесно связана с математикой разделы “Графики функций” и “Решение систем уравнений”. Поэтому нам понадобятся ранее полученные навыки. Но мы постараемся упростить нашу задачу с помощью применения современных вычислительных средств.
Запишите в тетради тему урока и укажите дату.
Назовите мне кого из класса сегодня нет.
Актуализация знаний.
Давайте вспомним, что такое уравнение, и как его можно решить графически.
Назовите, пожалуйста, что в математике называют уравнением, решением уравнения и системой уравнений.
(Учащиеся приводят определения)
Уравнение – это математическое выражение, содержащее неизвестную величину (переменную) и 0 с правой стороны от знака =.
Система уравнений – несколько связанных уравнений, имеющих одинаковые обозначения неизвестных величин (переменных).
Решением уравнения – называют такое значение неизвестной величины, при подстановке которого левая часть выражения принимает значение 0. И мы получаем верное равенство.
Но, с другой стороны, подобное выражение можно представить как функцию с зависимой и независимой величинами. Если мы слева от знака = поставим Y, а справа заданное выражение. Y – зависимая величина, Х – независимая величина. В этом случае Решением уравнения является точка пересечения графика функции с осью ОХ.
Постановка проблемы.
Для решения уравнения графическим методом необходимо рассчитать значения функции в ключевых точках с координатой Х (Х меняется в диапазоне допустимых значений), нанести эти точки на систему координат, построить график функции и определить координаты точки пересечения графика с осью ОХ.
Это достаточно сложная задача. Нужно достаточно много вычислений и аккуратное построение графика функции. Также мы заранее не можем сказать, из какого диапазона чисел необходимо брать значения Х.
Но эту задачу может взять на себя ЭВМ.
Мы воспользуемся возможностями программы MS Excel.
Основная часть
Давайте разобьемся на 2 группы. Сильные ученики, которые уже хорошо владеют средствами MS Excel, попытаются самостоятельно разработать таблицу. А остальные ребята будут вместе со мной последовательно выполнять действия.
Сильные ученики пересаживаются за дальние компьютеры и самостоятельно разрабатывают таблицу для решения системы уравнений. Они должны получить примерно такую картинку на экране.
С остальными мы работаем в режиме “Делай как Я”. Я демонстрирую действия на экране проектора и комментирую, вы стараетесь выполнять эти действия у себя на ЭВМ.
И так. Мы запустили программу MS Excel.
Мы хотим разработать таблицу для решения системы уравнений:
Y = x ^ 2 + 2
Y = 2 * x + 3
Нам необходимо задать диапазон изменения величины Х и рассчитать соответствующее значение Y.
Сформируем начальные данные.
В ячейку A1 запишем – нач Х =. В ячейку D1 запишем – шаг Х =. В ячейках B1, E1 их соответствующие значения – (-2,5) и 0,15.
В ячейках C4, F4 запишем общий вид наших уравнений. В строке 5 сформируем заголовки будущих таблиц значений заданных функций.
Теперь в столбиках B, E мы должны сформировать значения для величины Х. А в столбиках C, E значения величин Y. У нас должна получиться вот такая картинка. Столбики со значением величины X мы должны сформировать так, чтобы было удобно менять начальное его значение и шаг X, которые мы создали в заголовке.
Приложение 1
Приложение 2
Формулы, которые нам нужно ввести приведены на рисунке.
Заметьте, что большинство формул повторяются, и их можно ввести методом копирования.
Заполните, пожалуйста, в каждой таблице 20-25 строчек.
Символ $ в формуле обозначает, что данный адрес ячейки является абсолютным и он не будет изменяться при копировании формулы.
Проверьте, чтобы ваши расчётные данные совпадали с рисунком 2.
Нам осталось красиво оформить таблицы. Для этого нужно указать, какие границы отображать в ячейках расположения расчётных таблиц. Выделите их указателем мышки и задайте режим “Все границы”.
Теперь нам необходимо построить графики заданных функций. Для этого воспользуемся инструментом “Диаграммы”.
Выберем тип диаграммы Точечная-Сглаженная и на следующем экране укажем необходимые нам диапазоны данных, как указано на рисунке. Незабудем указать название для каждого графика. Легенду расположим снизу. А саму диаграмму “На текущем листе”, поместив её справа от расчётных таблиц.
Если вы всё сделали правильно, то у вас на экране должна получиться вот такая картинка.
У кого не получилось, давайте вместе разберёмся в ошибках и добъёмся требуемого результата.
Теперь изменяя значения в ячейках B1, D1 можно смещать графики функций вдоль оси ОХ и изменять их масштаб.
Мы видим, что одно из решений нашей системы уравнений равно -1,5.
Задание 1.
Изменяя начальное значение Х, найдите на графике второе решение системы уравнений.
Сколько у вас получилось?
Великолепно. У нас получилось. Мы легко решили такую сложную систему уравнений.
Но можно немного изменить нашу таблицу и усовершенствовать для решения множества подобных систем уравнений или для исследования графиков заданных функций.
Приложение 1
Приложение 2
Для этого нужно внести изменения в таблицу и расчётные формулы.
Можно сделать следующим образом, как показано на рисунке. Формулы в ячейках показаны на следующем рисунке.
Задание 2.
Самостоятельно внесите все необходимые изменения.
Задание 3.
Попробуйте изменять коофициенты A, B, C, D и посмотрите, как меняется форма и положение графиков соответствующих формул.
Заключительный этап урока
Ребята, как вы думаете, что удобней самостоятельно строить график функции на бумаге или поручить эту задачу ЭВМ?
А что легче для вас?
Конечно же, на данном этапе вам удобней самостоятельно на бумаге построить график функции. Но в конце урока мы получили универсальную таблицу, которая позволяет решать множество подобных заданий.
Мы ещё раз убедились, что компьютер это мощный инструмент, который позволяет не только приятно проводить время за играми, но и решать серьёзные задачи.
Надеюсь, что вам понравилось сегодняшняя работа. И вы Довольны достигнутыми результатами.
Спасибо за урок.
urok.1sept.ru