Равнобедренный, равносторонний и прямоугольный треугольники.
Просмотр содержимого документа
«Равнобедренный, равносторонний и прямоугольный треугольники.»
РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК
Равнобедренным называется треугольник, у которого две стороны равны.
Равные стороны называются боковыми, третья сторона – основанием.

ТЕОРЕМА: В равнобедренном треугольнике углы при основании равны.
ОБРАТНАЯ ТЕОРЕМА: Если в треугольнике углы при основании равны, то этот треугольник равнобедренный.
ТЕОРЕМА: В равнобедренном треугольнике медиана, проведённая к основанию, является биссектрисой и высотой.

Свойства равнобедренного треугольника
В равнобедренном треугольнике медианы, проведённые к боковым сторонам, равны.


В равнобедренном треугольнике биссектрисы, проведённые к боковым сторонам, равны.



В равнобедренном треугольнике высоты, проведённые к боковым сторонам, равны.

РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК
Равносторонним называется треугольник, у которого все стороны равны.

Свойства равностороннего треугольника
У равностороннего треугольника все углы равны 60°.

В равностороннем треугольнике медианы, проведённые из всех вершин являются биссектрисами и высотами.

Длины высот, медиан и биссектрис, проведённых к каждой из сторон равностороннего треугольника, равны.
 (рисунок сверху)
(рисунок сверху)
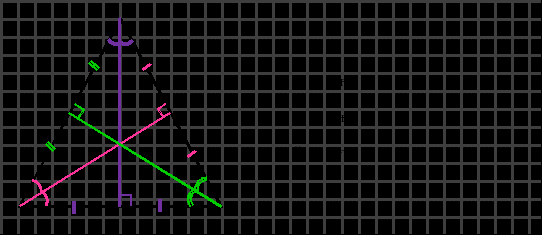
Точка пересечения высот, биссектрис и медиан называется центром равностороннего (правильного) треугольника и является центром вписанной и описанной окружностей (то есть в равностороннем треугольнике центры вписанной и описанной окружностей совпадают).

Расстояние от точки пересечения высот, биссектрис и медиан до любой вершины треугольника равно радиусу описанной окружности (рисунок сверху).
Расстояние от точки пересечения высот, биссектрис и медиан до любой стороны треугольника равно радиусу вписанной окружности (рисунок сверху).
Сумма радиусов вписанной и описанной окружностей правильного треугольника равна его высоте, медиане и биссектрисе:

Радиус описанной около равностороннего треугольника со стороной а окружности вычисляется по формуле:

Радиус вписанной в равносторонний треугольник со стороной а окружности вычисляется по формуле:

Высота равностороннего треугольника со стороной а окружности вычисляется по формуле:

Площадь равностороннего треугольника вычисляется по формулам (а – сторона треугольника,
 – высота, r – радиус вписанной окружности, R – радиус описанной окружности):
– высота, r – радиус вписанной окружности, R – радиус описанной окружности):



Прямоугольным называется треугольник, у которого один угол прямой (равен 90°).

Стороны, составляющие прямой угол называются катетами, третья сторона называется гипотенузой.
ПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
ТЕОРЕМА: Если гипотенуза и один острый угол одного прямоугольного треугольника равны соответственно гипотенузе и одному острому углу другого прямоугольного треугольника, то такие треугольники равны.

ТЕОРЕМА: Если катет и противолежащий ему угол одного прямоугольного треугольника равны соответственно катету и противолежащему углу другого прямоугольного треугольника, то такие треугольники равны.

ТЕОРЕМА: Если гипотенуза и катет одного прямоугольного треугольника равны соответственно гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
ТЕОРЕМА ПИФАГОРА: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Свойства прямоугольного треугольника
В прямоугольном треугольнике сумма двух острых углов равна 90° (рисунок сверху).
В прямоугольном треугольнике гипотенуза больше любого из катетов (рисунок сверху).
В прямоугольном треугольнике катет, противолежащий углу 30° равен половине гипотенузы.
Две высоты прямоугольного треугольника совпадают с его катетами.
Центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы.
Длина гипотенузы равна диаметру (двум радиусам) описанной окружности или радиус описанной окружности, прямоугольного треугольника, равен половине гипотенузы.
Медиана прямоугольного треугольника, проведённая из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности (AO – медиана)
Длина медианы, проведённой из вершины прямого угла (к гипотенузе), равна половине гипотенузы.
Высота прямоугольного треугольника, проведённая к гипотенузе равна произведению катетов, делённому на гипотенузу (h – высота, проведённая к гипотенузе, а – гипотенуза,
Высота прямоугольного треугольника, проведённая к гипотенузе, делит его на подобные треугольники.
Высота, проведённая к гипотенузе, — есть среднее пропорциональное между отрезками, на которые она делит гипотенузу ( т.е. между проекциями катетов на гипотенузу)
Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.
Периметр прямоугольного треугольника равен сумме двух радиусов вписанной и четырёх радиусов описанной окружностей.
Площадь прямоугольного треугольника равна половине произведения катетов.
В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ
Синусом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.
Котангенсом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему.
3
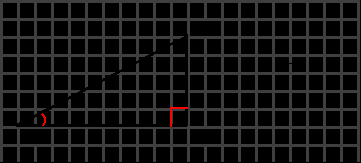
Сторона «A» и угол «α» равнобедренного треугольника
Основным элементом равнобедренного треугольника является высота, проведенная к основанию, она же медиана, она же биссектриса. Благодаря этим свойствам, она делит основание на две равные части под прямым углом, образуя прямоугольный треугольник с катетами в виде высоты и половины основания и гипотенузой, которая является боковой стороной. Поэтому, зная боковую сторону и угол α можно найти основание, высоту, и затем все остальные параметры. (рис.88.2) h_b=m_b=l_b=a sinα b=2a cosα
Периметр треугольника равен сумме двух боковых сторон и основания или удвоенного произведения боковой стороны на косинус угла. Площадь, как половина произведения основания на высоту, представлена в виде квадрата боковой стороны, умноженной на синус и косинус угла. P=2a+b=2a+2a cosα S=hb/2=(a^2 sinα)/2
Найти угол β равнобедренного треугольника через угол α можно, зная, что сумма всех углов в треугольнике равна 180 градусам. (рис.88.1) β=180°-2α
Так как высота, опущенная на основание равнобедренного треугольника, равна высоте и биссектрисе, а две боковые стороны равны между собой, следовательно оставшиеся высоты медианы и биссектрисы опущенные на них, также между собой равны. (рис.88.3, 88.4, 88.8) Вычислить медиану, биссектрису и высоту через боковую сторону и угол α можно, подставив их в соответствующие формулы. m_a=√(a^2+2b^2 )/2=√(a^2+8a^2 cos^2α )/2=(a√(1+8 cos^2α ))/2 h_a=(b√((4a^2-b^2)))/2a=(2a cosα √((4a^2-4a^2 cos^2α)))/2a=2a cosα √((1-cos^2α)) l_a=(b√(a(2a+b) ))/(a+b)=(2a cosα √(2+2 cosα ))/(1+2 cosα )
Средняя линия любого треугольника равна стороне, которой она параллельна, деленной на два. Если заменить сторону b на удвоенное произведение стороны a на косинус угла α, то данная средняя линия будет равна боковой стороне, умноженной на этот косинус. (рис.88.5) M_b=b/2=(2a cosα)/2=a cosα M_a=a/2
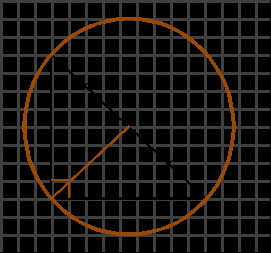
Если вписать в равнобедренный треугольник окружность, то ее радиус будет равен упрощенному радикалу, полученному из общей формулы радиуса окружности, вписанной в произвольный треугольник. Подставив в нее вместо стороны b известную боковую сторону и удвоенный косинус угла при основании, можно еще более упростить выражение. (рис.88.6) r=b/2 √((a-2b)/(a+2b))=(2a cosα)/2 √((a-2*2a cosα)/(a+2*2a cosα ))=a cosα √((1-4 cosα)/(1+4 cosα ))
Радиус окружности, описанной вокруг равнобедренного треугольника через боковую сторону и угол при основании, выглядит как отношение боковой стороны к двум квадратным корням из разности единицы и косинуса угла при основании во второй степени. (рис.88.7) R=a^2/√(4a^2-b^2 )=a^2/√(4a^2-4a^2 cos^2α )=a/(2√(1-cos^2α ))
Равнобедренный, равносторонний и прямоугольный треугольники
РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК
Равнобедренным называется треугольник, у которого две стороны равны.
Равные стороны называются боковыми, третья сторона – основанием.

ТЕОРЕМА: В равнобедренном треугольнике углы при основании равны.
ОБРАТНАЯ ТЕОРЕМА: Если в треугольнике углы при основании равны, то этот треугольник равнобедренный.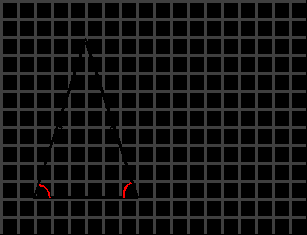
ТЕОРЕМА: В равнобедренном треугольнике медиана, проведённая к основанию, является биссектрисой и высотой.

Свойства равнобедренного треугольника
В равнобедренном треугольнике медианы, проведённые к боковым сторонам, равны.

В равнобедренном треугольнике биссектрисы, проведённые к боковым сторонам, равны.
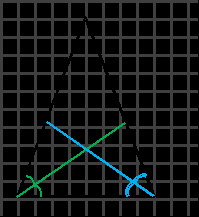

В равнобедренном треугольнике высоты, проведённые к боковым сторонам, равны.
РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК
Равносторонним называется треугольник, у которого все стороны равны.
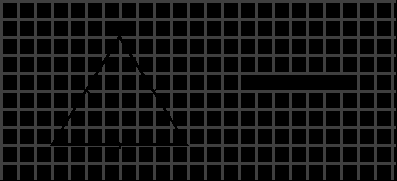
Свойства равностороннего треугольника
У равностороннего треугольника все углы равны 60°.

В равностороннем треугольнике медианы, проведённые из всех вершин являются биссектрисами и высотами.

Длины высот, медиан и биссектрис, проведённых к каждой из сторон равностороннего треугольника, равны.
(рисунок сверху)
Точка пересечения высот, биссектрис и медиан называется центром равностороннего (правильного) треугольника и является центром вписанной и описанной окружностей (то есть в равностороннем треугольнике центры вписанной и описанной окружностей совпадают).
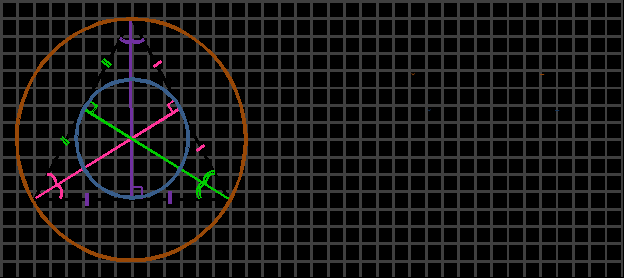
Расстояние от точки пересечения высот, биссектрис и медиан до любой вершины треугольника равно радиусу описанной окружности (рисунок сверху).
Расстояние от точки пересечения высот, биссектрис и медиан до любой стороны треугольника равно радиусу вписанной окружности (рисунок сверху).
Сумма радиусов вписанной и описанной окружностей правильного треугольника равна его высоте, медиане и биссектрисе:
Радиус описанной около равностороннего треугольника со стороной а окружности вычисляется по формуле:
Радиус вписанной в равносторонний треугольник со стороной а окружности вычисляется по формуле:
Высота равностороннего треугольника со стороной а окружности вычисляется по формуле:
Площадь равностороннего треугольника вычисляется по формулам (а – сторона треугольника, – высота, r – радиус вписанной окружности, R – радиус описанной окружности):
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Прямоугольным называется треугольник, у которого один угол прямой (равен 90°).

Стороны, составляющие прямой угол называются катетами, третья сторона называется гипотенузой.
ПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
ТЕОРЕМА: Если гипотенуза и один острый угол одного прямоугольного треугольника равны соответственно гипотенузе и одному острому углу другого прямоугольного треугольника, то такие треугольники равны.
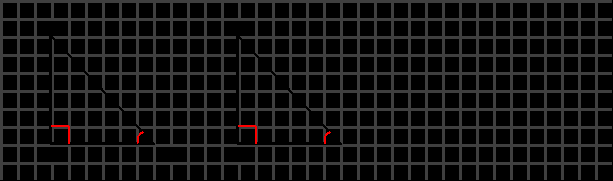
ТЕОРЕМА: Если катет и противолежащий ему угол одного прямоугольного треугольника равны соответственно катету и противолежащему углу другого прямоугольного треугольника, то такие треугольники равны.

ТЕОРЕМА: Если гипотенуза и катет одного прямоугольного треугольника равны соответственно гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
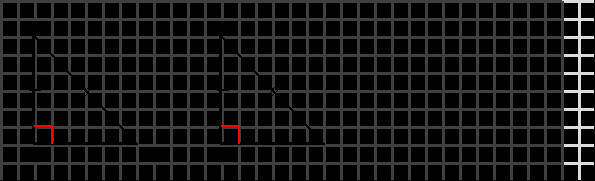
ТЕОРЕМА ПИФАГОРА: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Свойства прямоугольного треугольника
В прямоугольном треугольнике сумма двух острых углов равна 90° (рисунок сверху).
В прямоугольном треугольнике гипотенуза больше любого из катетов (рисунок сверху).
В прямоугольном треугольнике катет, противолежащий углу 30° равен половине гипотенузы.
Две высоты прямоугольного треугольника совпадают с его катетами.


Центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы.

Длина гипотенузы равна диаметру (двум радиусам) описанной окружности или радиус описанной окружности, прямоугольного треугольника, равен половине гипотенузы.
Медиана прямоугольного треугольника, проведённая из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности (AO – медиана)
Длина медианы, проведённой из вершины прямого угла (к гипотенузе), равна половине гипотенузы.
Высота прямоугольного треугольника, проведённая к гипотенузе равна произведению катетов, делённому на гипотенузу (h – высота, проведённая к гипотенузе, а – гипотенуза, b и с — катеты)
Высота прямоугольного треугольника, проведённая к гипотенузе, делит его на подобные треугольники.
Высота, проведённая к гипотенузе, — есть среднее пропорциональное между отрезками, на которые она делит гипотенузу ( т.е. между проекциями катетов на гипотенузу)
Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.
Периметр прямоугольного треугольника равен сумме двух радиусов вписанной и четырёх радиусов описанной окружностей.
Площадь прямоугольного треугольника равна половине произведения катетов.
ТРИГОНОМЕТРИЧЕСКИЕ СООТНОШЕНИЯ
В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ
Синусом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.
Котангенсом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему.
Высота треугольника — Википедия
Материал из Википедии — свободной энциклопедии
Высота в треугольниках различного типа
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону (точнее, на прямую, содержащую противоположную сторону). В зависимости от типа треугольника высота может содержаться внутри треугольника (для остроугольного треугольника), совпадать с его стороной (являться катетом прямоугольного треугольника) или проходить вне треугольника у тупоугольного треугольника.
 Высоты треугольника
Высоты треугольника- Все три высоты треугольника пересекаются в одной точке, называемой ортоцентром. Это утверждение легко доказать, используя векторное тождество, справедливое для любых точек A, B, C, E{\displaystyle A,\ B,\ C,\ E}, не обязательно даже лежащих в одной плоскости:
- EA→⋅BC→+EB→⋅CA→+EC→⋅AB→=0{\displaystyle {\overrightarrow {EA}}\cdot {\overrightarrow {BC}}+{\overrightarrow {EB}}\cdot {\overrightarrow {CA}}+{\overrightarrow {EC}}\cdot {\overrightarrow {AB}}=0}
(Для доказательства тождества следует воспользоваться формулами
- AB→=EB→−EA→,BC→=EC→−EB→,CA→=EA→−EC→{\displaystyle {\overrightarrow {AB}}={\overrightarrow {EB}}-{\overrightarrow {EA}},\,{\overrightarrow {BC}}={\overrightarrow {EC}}-{\overrightarrow {EB}},\,{\overrightarrow {CA}}={\overrightarrow {EA}}-{\overrightarrow {EC}}}
В качестве точки E следует взять пересечение двух высот треугольника.)
- Ортоцентр изогонально сопряжен центру описанной окружности.
- Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).
- Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.
- Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника. Последний треугольник называют дополнительным треугольником по отношению к первому треугольнику.
- Последнее свойство можно сформулировать так: Центр описанной около треугольника окружности служит ортоцентром дополнительного треугольника.
- Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности.
- Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
- Если О — центр описанной окружности ΔABC, то OH→=OA→+OB→+OC→{\displaystyle {\overrightarrow {OH}}={\overrightarrow {OA}}+{\overrightarrow {OB}}+{\overrightarrow {OC}}} ,
- |OH|=9R2−(a2+b2+c2){\displaystyle |OH|={\sqrt {9R^{2}-(a^{2}+b^{2}+c^{2})}}} , где R{\displaystyle R} — радиус описанной окружности; a,b,c{\displaystyle a,b,c} — длины сторон треугольника.
- Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
- Любой отрезок, проведенный из ортоцентра до пересечения с описанной окружностью всегда делится окружностью Эйлера пополам. Ортоцентр есть центр гомотетии этих двух окружностей.
- Теорема Гамильтона. Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих ту же самую окружность Эйлера (окружность девяти точек), что и исходный остроугольный треугольник.
- Следствия теоремы Гамильтона:
- Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника Гамильтона, имеющих равные радиусы описанных окружностей.
- Радиусы описанных окружностей трёх треугольников Гамильтона равны радиусу окружности, описанной около исходного остроугольного треугольника.
- В остроугольном треугольнике ортоцентр лежит внутри треугольника; в тупоугольном — вне треугольника; в прямоугольном — в вершине прямого угла.
Свойства высот равнобедренного треугольника[править | править код]
- Если в треугольнике две высоты равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса), и третья высота одновременно является медианой и биссектрисой того угла, из которого она выходит.
- Верно и обратное: в равнобедренном треугольнике две высоты равны, а третья высота одновременно является медианой и биссектрисой.
- У равностороннего треугольника все три высоты равны.
Свойства оснований высот треугольника[править | править код]
- Основания высот образуют так называемый ортотреугольник, обладающий собственными свойствами.
- Описанная около ортотреугольника окружность — окружность Эйлера. На этой окружности также лежат три середины сторон треугольника и три середины трёх отрезков, соединяющих ортоцентр с вершинами треугольника.
- Другая формулировка последнего свойства:
- Теорема Эйлера для окружности девяти точек. Основания трёх высот произвольного треугольника, середины трёх его сторон (основания его внутренних медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (на окружности девяти точек).
- Теорема. В любом треугольнике отрезок, соединяющий основания двух высот треугольника, отсекает треугольник подобный данному.
- Теорема. В треугольнике отрезок, соединяющий основания двух высот треугольника, лежащие на двух сторонах, антипараллелен третьей стороне, с которой он не имеет общих точек. Через два его конца, а также через две вершины третьей упомянутой стороны всегда можно провести окружность.
Свойства минимальной из высот треугольника[править | править код]
Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:
- Минимальная ортогональная проекция треугольника на прямые, лежащие в плоскости треугольника, имеет длину, равную наименьшей из его высот.
- Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины.
- При непрерывном движении двух точек по периметру треугольника друг навстречу другу, максимальное расстояние между ними за время движения от первой встречи до второй, не может быть меньше длины наименьшей из высот треугольника.
- Минимальная высота в треугольнике всегда проходит внутри этого треугольника.
- ha=bsinγ=csinβ,{\displaystyle h_{a}=b\sin \gamma =c\sin \beta ,}
- ha=2Sa,{\displaystyle h_{a}={\frac {2S}{a}},} где S{\displaystyle S} — площадь треугольника, a{\displaystyle a} — длина стороны треугольника, на которую опущена высота.
- ha2=12(b2+c2−12(a2+(b2−c2)2a2)){\displaystyle h_{a}^{2}={\frac {1}{2}}(b^{2}+c^{2}-{\frac {1}{2}}(a^{2}+{\frac {(b^{2}-c^{2})^{2}}{a^{2}}}))}
- ha=bc2R,{\displaystyle h_{a}={\frac {bc}{2R}},} где bc{\displaystyle bc} — произведение боковых сторон, R−{\displaystyle R-} радиус описанной окружности
- ha:hb:hc=1a:1b:1c=bc:ac:ab{\displaystyle h_{a}:h_{b}:h_{c}={\frac {1}{a}}:{\frac {1}{b}}:{\frac {1}{c}}=bc:ac:ab}
- 1ha+1hb+1hc=1r{\displaystyle {\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}={\frac {1}{r}}}, где r{\displaystyle r} — радиус вписанной окружности.
- S=1(1ha+1hb+1hc)⋅(1ha+1hb−1hc)⋅(1ha



 – высота, r – радиус вписанной окружности, R – радиус описанной окружности):
– высота, r – радиус вписанной окружности, R – радиус описанной окружности):