Графически решить систему уравнений: Система линейных уравнений. Графический способ решения

Posted on by alexxlab

Содержание

Графический способ решения систем линейных уравнений с двумя переменными.

Данная разработка предназначена для учеников 7 класса и для тех, кто, в своё время, пропустил эту тему. В теоретической части изложена суть графического способа решения систем, алгоритм этого способа, приведены примеры с графиками. В практической части содержатся задания для закрепления знаний и умений.

Просмотр содержимого документа
«Графический способ решения систем линейных уравнений с двумя переменными.»

Графический способ решения систем линейных уравнений с двумя переменными.

Приступаем к рассмотрению способов решения линейных уравнений с двумя переменными.

В школьном курсе алгебры изучаются три способа решения систем.

  1. Графический способ (с помощью графиков).

  2. Способ подстановки.

  3. Способ сложения.

Разбираем каждый из них подробно. В этой теме внимание уделено графическому способу. Название говорит само за себя: нужно строить графики. Мы уже выяснили, что линейное уравнение с двумя переменными легко преобразуется в линейную функцию путём выражения переменной у через переменную х (используя правила переноса и деления/умножения на одно и то же число). Преобразовав таким образом каждое уравнение, входящее в систему, и, построив графики, можно визуально определить решение системы, т.е. точку пересечения этих графиков. Останется только лишь как можно более точно выяснить координаты этой точки. Это и есть решение системы.

При решении системы линейных уравнений с двумя переменными графическим способом, необходимо:

  • в каждом уравнении выразить переменную у через переменную х;

  • на одной системе координат построить график каждой полученной функции;

  • найти общие точки построенных прямых;

  • определить, если это возможно, координаты общих точек прямых. Они и есть решение системы.

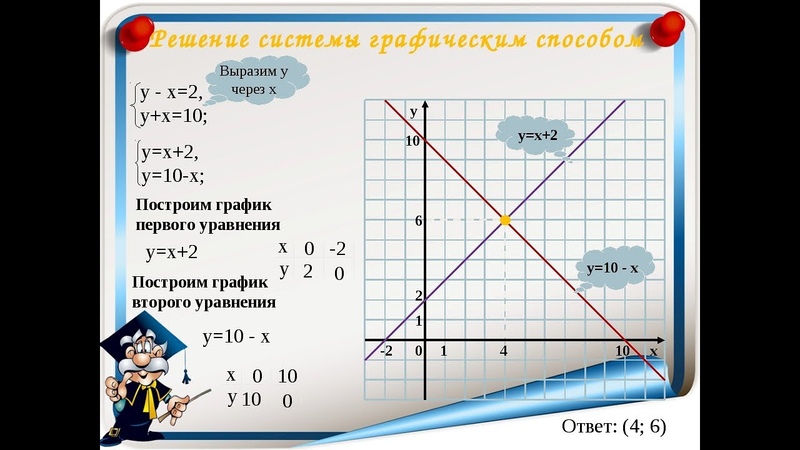
Например, решить графическим способом систему

Выразим переменную у через переменную х.

Описываем функции.

– линейная функция, графиком является прямая, проходящая через точки

– линейная функция, графиком является прямая, проходящая через точки

На одной системе координат строим графики описанных функций.

Находим координаты точки А – точки пересечения прямых. .

Значит, система имеет единственное решение

У графического способа решения систем есть существенный недостаток. Найденное решение не всегда бывает точным, т.к. на системе координат иногда невозможно выбрать такой единичный отрезок, чтобы чётко определить координаты точки пересечения. Зачастую решение является приближённым.

  1. Решить систему уравнений графическим способом:

  1. Составьте системы уравнений, графики которых изображены на рисунках, и найдите по рисунку их решения.

а) б) в)

г) д) е)

ж) з) и)

  1. Используя графический способ, определите, имеет ли решения система уравнений:

  1. Решить графически систему уравнений. Выяснить, проходит ли третья прямая через точку пересечения первых двух.

  1. Решить графически систему уравнений:

3

Графический способ решения систем уравнений (9 класс)

Класс: 9 а

Тип урока: урок нового знания

Тема урока: Графический способ решения систем уравнений

Цели урока:

— дидактические: организация деятельности учащихся по восприятию, осмыслению, первичному запоминанию и закреплению знаний по теме «Графический способ решения систем уравнений»; обобщение и углубление знаний, умений учащихся применять графические способы решения уравнений и систем уравнений и их комбинаций;

— развивающие: развитие логического мышления, культуры графического построения, наблюдательности, памяти, умения анализировать, сравнивать и делать выводы;

— воспитательные: средствами учебного занятия создать условия, способствующие формированию умения искать пути выхода из затруднения.

Планируемые результаты:

— предметные: освоение учащимися новой темы «Графический способ решения систем уравнений» и применение её при решении задач;

— метапредметные (регулятивные – Р, коммуникативные – К, познавательные – П): умение  определять понятия, создавать обобщения, устанавливать аналогии, устанавливать причинно-следственные связи, строить  логическое рассуждение, умозаключение и делать выводы;

— личностные (Л) – установление учащимися связи между целью учебной деятельности и ее мотивом.

Оборудование: мультимедийный проектор, экран, компьютер, электронные презентации для устной работы и изучения новой темы, выполненная в Microsoft Power Point,

Карта урока

Деятельность учителя

(указать цель на каждом этапе)

Деятельность учащихся

(с указанием форм деятельности)

Формируемые УУД (конкретные)

Мотивационно-ориентировочная часть

1. Мотивация к учебной деятельности

(2-3 мин)

выработка на личностно значимом уровне положительного самоопределения ученика к деятельности на уроке

Здравствуйте! Садитесь!

Французский писатель Анатоль Франс однажды заметил: «Учиться можно только весело … Чтобы переваривать знания, надо поглощать их с аппетитом». Так вот, давайте сегодня на уроке будем следовать этому совету писателя, будем активны, внимательны, будем поглощать знания с большим желанием.

Перед вами лежит листок бумаги. Обведите на нём свою руку. Продолжите предложения, характеризующие ваше эмоциональное состояние в данный момент:

Мизинец – Мне сейчас …

Безымянный – Я хочу …

Средний – Я буду…

Указательный – Чего я жду от урока…

Большой – Мне интересно …

Организация рабочего места, постановка перед собой целей

-действовать, запоминать, усваивать

К: планирование учебного сотрудничества

2. Актуализация знаний (5-7 мин) Цель: формулирование цели и темы урока

Повторение: Что называется графиком уравнения с двумя переменными?

В тетрадях записать уравнение, которое соответствует данному графику.

Слайды 3-7

Взаимопроверка: обменяться тетрадями и проверить. Слайд 8

Слай 9

Решить систему уравнений:

Уравнения какой степени входят в систему уравнений?

В 7 классе мы рассматривали системы уравнений первой степени с двумя переменными. Теперь займёмся решением систем, составленных из двух уравнений второй степени или из одного уравнения первой степени, а другого второй степени.

Вспомним, что решением системы двух уравнений с двумя переменными является пара чисел, обращающая каждое уравнение системы в верное равенство. Решить систему – значит найти все её решения или доказать, что решений нет.

Какие способы решения систем уравнений вы знаете?

Слайд 10

Тема нашего урока «Графический способ решения систем уравнений»

Перед вами стоит задача – показать свои знания и умения по решению систем уравнений с помощью графиков.

В тетрадях записывают уравнение, которое соответствует данному графику.

|

К: формулирование и обоснование собственного мнения;

П: установление причинно-следственной связи.

3. Практическая работа и фиксация затруднения в пробном действии(10-12 мин)

Цель: выдвижение гипотезы о решении системы, содержащей уравнение второй степени; актуализация мыслительных операций и познавательных процессов, достаточных для построения нового знания;

мотивация к пробному учебному действию и его самостоятельному осуществлению

Исследовательская работа построение алгоритма решения системы уравнений

Задача: В ходе работы необходимо исследовать систему, построить графики, найти точки пересечения графиков. Результатом работы должен стать алгоритм решения системы уравнений. При анализе полученных результатов, обратите внимание на следующие моменты:

Слайды 11-12

Самостоятельно решить систему уравнений:

Слайд 13

Решают систему уравнений, строят графики, находят точки пересечения, записывают ответ. Составляют алгоритм решения систем уравнений графическим способом и записывают его в тетрадь.

Алгоритм решения систем уравнений графическим способом

  1. Построить в одной системе координат графики уравнений, входящих в систему.

  2. Найти координаты точек пересечения графиков.

  3. Записать ответ.

Р:основы прогнозирования как предвидение будущих событий;

К:

учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве;

П: проведение практической работы под руководством учителя

4.

Выявление места и причин затруднения (постановка проблемы)

(5-7мин)

Цель: восстановление выполненной операции и фиксирование (вербально и знаково) место — шаг, операцию, где возникло затруднение;

соотнести свои действия с используемым способом действий (алгоритмом, понятием и т. д.) и на этой основе выявить и зафиксировать во внешней речи причину затруднения — те конкретные знания, умения или способности, которых недостает для решения исходной задачи.

При решении системы что вызвало у вас затруднение?

Слайд 14

Формулируют гипотезу:

  1. Выражение переменной у через х

  2. Нахождение значений х и у

  3. Построение графика по найденным значениям переменных

Р: целеполагание, планирование путей достижения целей;

К: работа в паре;

П: проведение практической работы

5.

Первичное закрепление знаний при решении упражнений

(3-5 мин)

Цель: организация усвоения детьми решения систем уравнений графическим способом с их проговариванием во внешней речи.

Решить систему:

Решение системы с комментированием.

Слайды 15-17

Работа с презентацией. Комментируют сколько графиков, их расположение в координатной плоскости, количество решений.

Р: целеполагание, планирование путей достижения целей;

К: учитывать разные мнения и сиремиться к координации различных позиций в сотрудничестве;

П: проведение практической работы

Операционно-познавательная часть

6.

Реализация построенного проекта (5-8 мин)

Цель: создание коммуникативного взаимодействия с целью реализации построенного проекта, направленного на приобретение недостающих знаний;

уточнение общего характера нового знания.

Разбор затруднений.

Решить самостоятельно:

Слайд 19

Слайд 20

Слайд 21

Проверка решения систем уравнений:

— что является графиками каждого уравнения

— сколько решений имеет ваша система уравнений

Работают по рядам:

1 ряд – 1 система

2 ряд – 2 система

3 ряд – 3 система

Р: умение самостоятельно контролировать своё время и управлять им;

К: работа в парах

П: построение логических рассуждений.

Рефлексивно-оценочная

7.

Включение в систему знаний и повторение (2мин)

Цель: выявление границы применимости нового знания; повторение учебного содержания, необходимого для обеспечения содержательной непрерывности.

Спрашивает:

1)какие знания предыдущих уроков алгебры сегодня вы использовали на уроке?

2) проговаривает перспективу изучения данной темы

Отвечают

Р: самостоятельно оценивать правильность своих действий

8.

Рефлексия деятельности

(2 мин)

Цель: фиксация нового содержания, изученного на уроке; оценивание собственной деятельности на уроке; выявление затруднений как направления для будущей учебной деятельности;

Вернёмся к китайской мудрости. Вернёмся к началу урока и посмотрим на ваши ладошки.

Мизинец – Мне сейчас …

Безымянный – Я хочу …

Средний – Я буду…

Указательный – Чего я жду от урока…

Большой – Мне интересно …

Обратим внимание на указательный и большой пальцы.

Оценивают

Р:выделение и осознание учащимся того что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения.

Графический метод решения уравнений: описание метода, примеры

Особенности метода

Графический метод предполагает использование графиков функций. В общем случае построение графиков функций – дело непростое. Поэтому, графический метод решения уравнения обычно применяется лишь тогда, когда функции, отвечающие частям уравнения, довольно простые в плане построения графиков, и при этом не видно другого аналитического метода решения. Это одна из особенностей графического метода решения уравнений.

Другая особенность касается получаемых по графикам результатов. Полученные по графикам результаты можно считать лишь приближенными. Дело здесь в том, что сами по себе графики функций — вещь не совсем точная (но при этом очень наглядная и во многих отношениях удобная), особенно если говорить о графиках, построенных от руки. Это следует из принципов, которыми мы руководствуемся при построении графиков функций. Что мы делаем для построения графика функции в общем случае? Проводим исследование функции, чтобы получить ряд «опорных» точек, таких как граничные точки области определения, максимумы-минимумы, точки перегиба, и понять поведение функции на всех интервалах ее области определения. После этого определяем несколько контрольных точек. Дальше переносим все определенные в ходе исследования точки на координатную плоскость и, сейчас внимание, соединяем их плавной линией в соответствии с выясненным в ходе исследования поведением функции. Эта «плавная линия» и есть график функции. О какой точности можно здесь говорить? Понятно, что она определяется точностью нашего построения.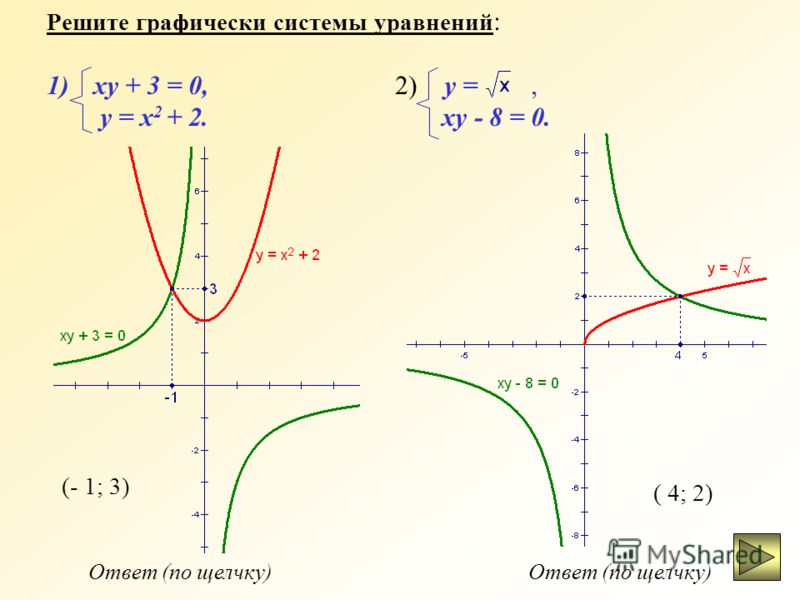

С приближенными, найденными по графикам, значениями корней уравнения можно так или иначе работать. В некоторых случаях определенные по графикам значения корней оказываются точными значениями, в чем позволяет убедиться проверка подстановкой. В других случаях есть возможность уточнить значения корней до требуемой степени точности, для этого существуют специальные методы уточнения значений корней. А вот если по графикам нет возможности определить количество корней, не говоря уже об их значении, то, почти наверняка, стоит отказываться от графического метода решения уравнения. Добавим наглядности сказанному.

Давайте посмотрим на изображенные в одной прямоугольной системе координат графики функций и y=−x2+6·x−5.

По этому чертежу сложно судить даже о количестве корней уравнения , не говоря уже про их значения с приемлемой степенью точности. Здесь можно лишь грубо сказать, что если корни есть, то их значения находятся на промежутке от нуля до трех. Такую прикидку мы даем по той причине, что графики функций в обозначенном промежутке очень близки, почти совпадают. Если есть возможность построить графики более точно в обозначенном промежутке, то это немного проясняет картину:

Сейчас мы видим три точки пересечения, даже можем приближенно указать их абсциссы: 1, 2 и 2,7. Но опять же, это не более чем приближенные результаты, нуждающиеся в проверке и строгом обосновании.

Учитывая оговоренные особенности графического метода решения уравнения, для себя можно принять следующее: к графическому методу стоит обращаться лишь тогда, когда функции, отвечающие частям уравнения, довольно простые в плане построения графиков, когда по построенным графикам можно с уверенностью указать точное количество точек их пересечения, и когда не просматривается альтернативный метод решения.

К началу страницы

Работа 3. Графическое решение уравнений и систем уравнений

Рис. 11

-5

-1

 

X

1

 

3 5

-2

 

—

 

В появившемся диалоговом окне делаем поворот по часовой стрелке. В результате получаем рис. 12.

Редактировать график можно также при помощи курсора. С этой целью необходимо подвести курсор к элементу графика, например, к стенке и нажать правую клавишу мыши. В результате появится контекстное меню, с помощью которого можно ввести нужные изменения.

8

 

 

6

 

 

4

Z

6-8

4-6

 

 

2

 

2-4

0

 

0-2

 

 

4

 

 

Y

Рис. 12

4. Отчет по работе

Распечатки диаграмм и графиков.

Литература: [3], с. 123-132.

1. Цель работы

Ознакомиться с графическими методами решения уравнений и систем уравнений.

2. Основные теоретические положения

Кроме аналитического способа решения уравнений f(x)=0 можно пользоваться и графическим способом. Графический способ наиболее эффективен для решения трансцедентных уравнений. При графическом способе

24

для уравнения строится график y=f(x) и решением уравнения является точка пересечения графика с осью у=0. Если разбить уравнение на две произвольные части, то можно для каждой части построить график. В этом случае решением уравнения будет абсцисса точки пересечения графиков для этих частей. Такой способ может использоваться и для решения систем двух линейных уравнений с двумя неизвестными.

3. Порядок выполнения работы

Задание 1. Решить графически уравнение y=cos2(πx) на интервале [0;1]. Задание 2. Решить графически уравнение х3-4х2-3х+6=0.

Задание 3. Решить графически систему уравнений y =sin x

в диапазоне

y = cos x

 

х [0;3] с шагом х=0,2.

Задание 4. Решить систему уравнений согласно индивидуальному заданию.

3.1. Выполнение задания 1.

Решить графически уравнение y=cos2(πx) на интервале [0;1] значит найти все значения х внутри данного интервала, где функция у пересекает ось Х.

 

 

3.1.1.Провести табуляцию значений х и у (см. Работу 2).

 

 

 

 

В результате получим табл. 9.

Таблица 9

 

 

 

 

 

 

 

 

3. 2

 

 

В

результате

получим

2

 

Значение х

Значение у

Значение Pi

график рис. 13. Из графика

3

 

0

=COS(A3*C$3)

3,1415

видно, что уравнение имеет

4

 

0,1

=COS(A4*C$3)

 

единственный корень. Что-

 

 

 

 

 

бы получить точное решение

5

 

0,2

=COS(A5*C$3)

 

 

 

уравнения, нужно щелкнуть

6

 

0,3

=COS(A6*C$3)

 

 

 

левой

клавишей

мыши

по

7

 

0,4

=COS(A7*C$3)

 

 

 

точке пересечения графика с

8

 

0,5

=COS(A8*C$3)

 

осью ОХ. На графике

9

 

0,6

=COS(A9*C$3)

 

появится текст (см. рис. 13).

 

 

 

 

 

Здесь Точка

“0,5”

–

10

 

0,7

=COS(A10*C$3)

 

 

 

значение х

 

 

11

 

0,8

=COS(A11*C$3)

 

 

 

 

 

Значение “4,633Е-05”≈0 –

12

 

0,9

=COS(A12*C$3)

 

 

 

значение у.

 

 

13

 

1

=COS(A13*C$3)

 

 

 

 

 

 

 

 

 

 

 

3.2. Выполнение задания 2.

 

 

 

 

 

 

Найдем графическое решение уравнения х3-4х2-3х+6=0.

 

 

 

Для этого представим его в виде

 

 

 

 

 

 

 

 

х3=4х2+3х-6

 

 

(2)

и построим на одной диаграмме графики двух функций:

 

 

 

 

 

 

у1=х3

левая часть уравнения (2) и

 

 

25

у2=4х2+3х-6 правая часть уравнения (2)

Рис. 2+3*A13-6

3.2.1. Открыть новый рабо-

чий лист (Вставка – Лист).

3.2.2. Провести табуляцию значений аргумента х и функций у1 и у2 (см. Работу 2)

В результате получим табл.10.

3.2.3. Строим график функций у1 и у1 на одной диаграмме (рис. 14). Из графиков видно, что на рассмотренном интервале функции у1 и у2 пересекаются только два раза(корни х1=-1,2 и х2=1,2).

 

 

 

 

 

26

 

20

 

 

 

 

 

 

15

 

 

 

 

 

 

10

 

 

 

 

 

у1=х^3

5

 

 

 

 

 

 

 

 

 

 

y2=4*x^2+3*x-6

0

 

 

 

 

 

 

 

 

 

 

 

-5

2

-1,2

-0,4

0,4

1,2

2

—

 

 

 

 

 

 

-10

 

 

 

 

 

 

 

 

 

 

 

Рис. 14

 

3.2.3. Для нахождения третьего корня нужно увеличить диапазон решения. Из графика видно, что при х<-2 функции у1 и у2 расходятся.

Значитрешениенужноискатьприх>2. Увеличимдиапазондох=5, т.е. х [-2;5]: а) продолжитьтабулированиеаргументахдоячейкиА20; б) скопироватьформулуизячейкиВ13 вячейкиВ14:В20; в) скопироватьформулуизячейкиС13 вячейки С14:С20;

г) построить график для этого случая. На этом графике функции у1 и у2 пересекаютсятрижды. Третийкореньх3=4,4.

3.3. Выполнение задания 3

Решить графически систему уравнений значит найти координаты точек, в которых пересекаются графики функций, входящих в систему уравнений. Практически при выполнении задания 2 мы решили систему уравнений

 

y = x

3

 

 

 

 

 

.

 

 

 

2

 

 

 

 

y =5 −5x

 

 

Для нахождения корней уравнений системы

y =sin x

y = cos x

в диапазоне х [0;3] с шагом х=0,2, следует выполнить следующие действия. 3.1.1. Добавить новый рабочий лист (Вставка – Лист).

3.2.2. Провести табулирование переменных х, y=sin x, y=cos x, аналогично Работе 2 и пп. 3.1, 3.2 данной работы:

-в ячейку А1 ввести заголовок Аргумент х, в ячейку А2 – значение 0, в ячейку А3 — значение 0,2 и провести табуляцию аргумента х в ячейках А2:А17;

-в ячейку В1 ввести заголовок y=sin(x);

-в ячейку В2 ввести формулу =SIN(A2) и скопировать ее в ячейки В3:В17;

-в ячейку С1 ввести заголовок y=cos(x);

-в ячейку С2 ввести формулу =COS(A2) и скопировать ее в ячейки C3:C17.

3.2.3. Построить график функций y=sin x, y=cos x на одной диаграмме:

27

а) выполнить команды Вставка – Диаграмма; б) в первом диалоговом окне Мастера диаграмм выберем Тип диаграммы

График, Вид — Левый верхний, Далее; в) во втором окне Мастера диаграмм на вкладке Диапазон данных

ввести:

Диапазон В2:С17

Ряды в: столбцах; Затем щелкнуть по вкладке Ряд и ввести:

Подписи оси Х А2:А17 ;

Щелкнуть по кнопке Далее; г) в третьем окне Мастера диаграмм ввести:

Название диаграммы

Система

 

 

Ось Х

Аргумент

 

 

Ось У

Значения

 

щелкнуть по кнопке Далее; д) на последнем шаге Мастера диаграмм выбрать опцию

На отдельном листе и щелкнуть Готово.

На полученном графике (рис.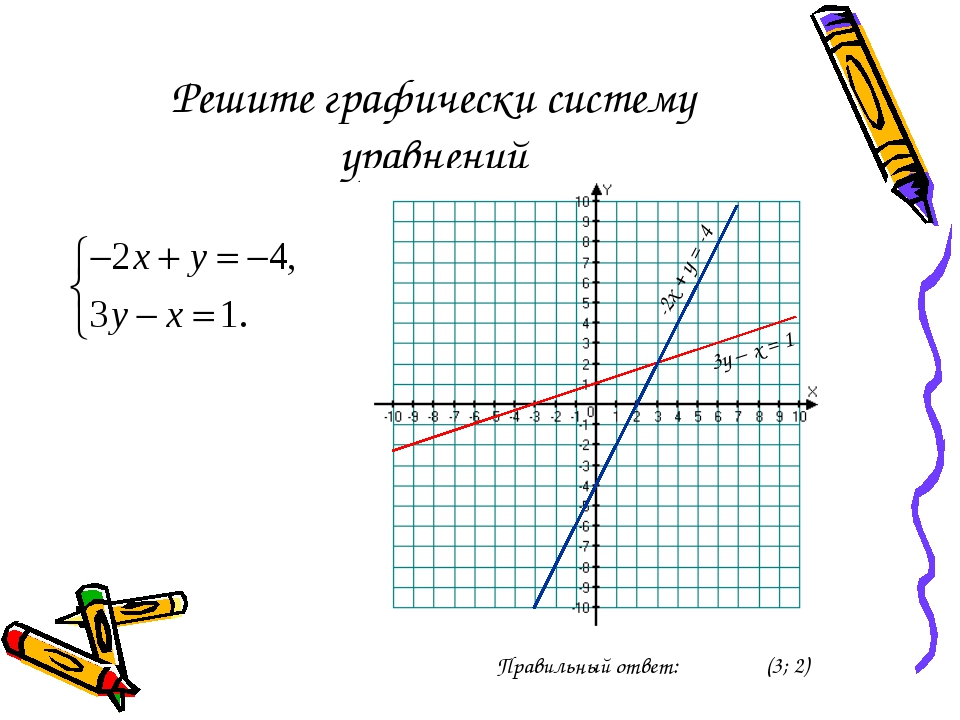 15) видно, что в указанном диапазоне система имеет единственное решение (графики имеют только одну точку пересечения).

 

 

 

 

Система

 

 

1,5

 

 

 

 

 

Значения

1

 

 

 

 

 

0,5

 

 

 

 

y=sin(x)

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

y=cos(x)

 

-0,50

 

 

 

 

 

,6

,2

,8

,4

3

 

 

 

 

-1

0

1

1

2

 

 

 

 

 

 

 

 

-1,5

 

 

 

 

 

 

 

 

Аргумент

 

Для нахождения решения:

 

Рис. 15

 

 

 

 

 

-поставить указатель мыши в точку пересечения графиков;

-щелкнуть левой клавишей мыши. Появится надпись с указанием приблизительного решения системы уравнений:

Ряд “y=cos(x)” Точка “0,8” Значение: 0,6967067

Следовательно, решением уравнения являются:

х=0,8

у=0,697.

28

3.4.Выполнение задания 4

3.4.1. Выбратьизтабл. 11 индивидуальноезаданиепоуказаниюпреподавателя 3.4.2. Добавить новый рабочий лист (Вставка – Лист).

3.4.3. Графически решить систему уравнений по индивидуальному заданию.

Таблица 11

Решить систему уравнений в указанном диапазоне с заданным шагом.

№

Система уравнений

Диапазон

Шаг изменения

варианта

изменения

Аргумента х

 

аргумента

0

y = ln x

 

х [0,2;3]

x=0,2

 

+4

 

y = −2x

 

 

1

y = 2 / x

х [0,2;3]

x=0,2

 

 

 

y = 2x

 

 

 

2

y = 2sin x

х [0;2]

x=0,1

 

 

 

y =3x

 

 

 

3

y = ex

х [0,2;3]

x=0,1

 

 

 

 

 

 

y = x / 2

 

 

 

 

2

 

 

 

 

4

 

 

 

 

+4

х [0;2]

x=0,2

 

 

 

y =

 

x

 

 

 

 

 

 

 

y =

4x

 

 

5

y = cos x

х [0,2;3]

x=0,1

 

 

 

 

 

 

y = 2x

 

 

6

y = −3x +5

х [0;2]

x=0,2

 

 

 

 

 

 

y = ln x

 

 

7

y =

3sin x

х [0;2]

x=0,1

 

 

 

 

 

 

y = e x

 

 

 

8

y = 4 − x

х [0;2]

x=0,1

 

2sin x

 

y =

 

 

9

y = ln x

х [0,2;3]

x=0,2

 

 

 

 

 

 

y = 2cos x

 

 

4. Отчет по работе

Распечатка графиков.

Литература: [3], с. 187-193.

Примеры графического решения уравнений и систем уравнений

x3 + x – 2 = 0.

Это уравнение кубическое, так как содержит неизвестное x в кубе. Такие уравнения в школьном курсе алгебры по формулам не решаются. Решим данное уравнение графически. Запишем уравнение так:

x3 = –x + 2.

Теперь построим графики функции y = x3 и y = –x + 2. Это будут кубическая парабола и прямая. Из чертежа видно, что обе линии пересекаются в одной точке, абсцисса которой равна 1. Итак, уравнение имеет один корень x = 1 (черт. 84).

Пример 2. Решить уравнение:

x3 – x2 – 2 = 0.

Решение. Запишем уравнение в виде

x3 = x2 + 2.

Построим (на миллиметровой бумаге) параболы: кубическую y = x3 и квадратную y = x2 + 2. Из чертежа 85 видим, что эти линии пересекаются в одной точке M.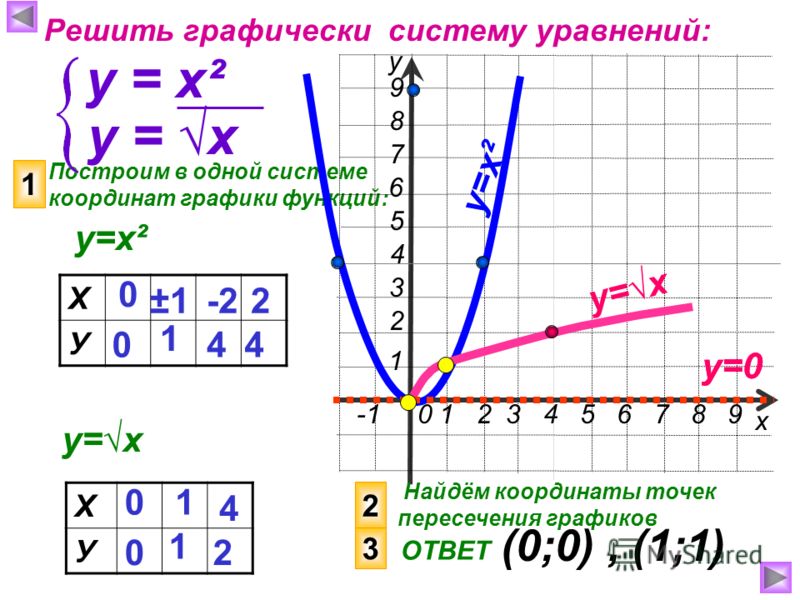 Опустив перпендикуляр из точки M на ось абсцисс, найдем приближенно корень данного уравнения: x ≈ 1,7.

В § 81 был показан графический способ решения системы уравнений первой степени с двумя неизвестными. Строились прямые — графики данных уравнений. Если эти прямые пересекались, то координаты точки пересечения и являлись решением системы.

Совершенно так же решаются графически и системы уравнений второй степени с двумя неизвестными.

Строится график каждого из уравнений системы. Если эти графики имеют одну или несколько общих точек, то координаты каждой из этих точек удовлетворяют обоим уравнениям, то есть являются решением системы. Приведем пример.

Пример 3.

Графиком первого уравнения является прямая, проходящая через точки (7; 0) и (0; 7). Графиком второго уравнения является гипербола (см. § 76).

На чертеже 86 видно, что прямая пересекает гиперболу в двух точках. Измерив их расстояние от осей, найдем решения системы:

x1 = 1; y1 = 6 и x2 = 6; y2 = 1.

Нетрудно проверить подстановкой, что мы получили два решения данной системы.

Графический способ решения систем уравнений: алгоритм и пример решения

 

Рассмотрим следующие уравнения:

1. 2*x + 3*y = 15;

2. x2 + y2 = 4;

3. x*y = -1;

4. 5*x3 + y2 = 8.

Каждое из представленных выше уравнений является уравнением с двумя переменными. Множество точек координатной плоскости, координаты которых обращают уравнение в верное числовое равенство, называется графиком уравнения с двумя неизвестными.

График уравнения с двумя переменными

Уравнения с двумя переменными имеют большое многообразие графиков. Например, для уравнения 2*x + 3*y = 15 графиком будет прямая линия, для уравнения x2 + y2 = 4 графиком будет являться окружность с радиусом 2, графиком уравнения y*x = 1 будет являться гипербола и т.д.

У целых уравнений с двумя переменными тоже существует такое понятие, как степень. Определяется эта степень, так же как для целого уравнения с одной переменной. Для этого приводят уравнение к виду, когда левая часть есть многочлен стандартного вида, а правая – нуль. Это осуществляется путем равносильных преобразований.

Графический способ решения систем уравнения

Разберемся, как решать системы уравнений, которые будут состоять из двух уравнений с двумя переменными. Рассмотрим графический способ решения таких систем.

Пример 1. Решить систему уравнений:

{ x2 + y2 = 25

{y = -x2 + 2*x + 5.

Построим графики первого и второго уравнений в одной системе координат. Графиком первого уравнения будет окружность с центром в начале координат и радиусом 5. Графиком второго уравнения будет являться парабола с ветвями, опущенными вниз.

Все точки графиков будут удовлетворять каждый своему уравнению. Нам же необходимо найти такие точки, которые будут удовлетворять как первому, так и второму уравнению. Очевидно, что это будут точки, в которых эти два графика пересекаются.

Используя наш рисунок находим приблизительные значения координат, в которых эти точки пересекаются. Получаем следующие результаты:

A(-2,2;-4,5), B(0;5), C(2,2;4,5), D(4,-3).

Значит, наша система уравнений имеет четыре решения.

x1 ≈ -2,2; y1 ≈ -4,5;

x2 ≈ 0; y2 ≈ 5;

x3 ≈ 2,2; y3 ≈ 4,5;

x4 ≈ 4,y4 ≈ -3.

Если подставить данные значения в уравнения нашей системы, то можно увидеть, что первое и третье решение являются приближенными, а второе и четвертое – точными. Графический метод часто используется, чтобы оценить количество корней и примерные их границы. Решения получаются чаще приближенными, чем точными.

Нужна помощь в учебе?



Предыдущая тема: Уравнения, приводимые к квадратным: биквадратные и рациональные
Следующая тема:&nbsp&nbsp&nbspПоследовательности: виды числовых последовательностей и примеры

Алгебра в 8 класс, урок: «Графическое решение квадратных уравнений»

Дата публикации: . 2+6x+16=0$.

3. Графическое решение системы линейных уравнений

Система уравнений `2 × 2` представляет собой набор из 2 уравнения с двумя неизвестными, которые необходимо решить одновременно (вместе), так что решения верны в оба уравнения.

Мы можем решить такую ​​систему уравнений графически . То есть рисуем график из 2-х линий и смотрим, где линии пересекаются. Точка пересечения дает нам решение.

Пример 1

Решите графически систему уравнений

2 x + 3 y = 5

x — 3 y = 7

Ответ

Рисуем 2 линии следующим образом.

2 x + 3 y = 5 зеленого цвета.

x — 3 y = 7 — пурпурный.

123456789-1-2-3-4123-1-2-3-4-5xy

`x-3y = 7`

`2x + 3y = 5`

Графики y = (-2x-5) / 3 и y = (x + 7) / 3.

Мы видим, что точка (4, −1) находится на , обе строки на график. Мы говорим, что (4, −1) — это решение для набора одновременные уравнения.

Это означает, что решения равны `x = 4`,` y = -1`.

Обратите внимание, что эти значения верны в обоих уравнениях , как показано ниже.

2 (4) + 3 (−1) = 8 — 3 = 5 [ОК]

(4) — 3 (−1) = 4 + 3 = 7 [ОК]

Итак, мы видим, что точка пересечения двух линий действительно дает нам решение для системы.

Виды решений

Система линейных уравнений 2 × 2 может иметь три возможных решения.

1. Пересечение в одной точке, поэтому только одно решение

График линейных уравнений `y = x + 3` и` y = -2x + 13`.

2. Параллельны, пересечения нет.

График линейных уравнений `y = -x + 3` и` y = -x + 7`.

3. Идентичны, поэтому пересекаются везде на линии

График линейных уравнений `x + y = 6` и` 2x + 2y = 12`.

Пример 2

Решить графически систему:

6 x — 3 y = −12

−2 x + y = 4

Ответ

Еще раз, мы наносим на график 2 линии, и точка пересечения дает решение для одновременные уравнения.

6 x — 3 y = −12 имеет x -перехват `-2`, а также y — перехват `4`.

−2 x + y = 4 имеет x -перехват `-2`, а также y — перехват `4`.

График выглядит следующим образом:

2468-2-42468xy

`6x-3y = -12`

`-2x + y = 4`

График линейных уравнений `6x-3y = -12` и` -2x + y = 4`.

Видим, что линии идентичны. Итак, решение для системы (из графика):

«все значения ( x , y ) в строке` 2x-y = -4` «.

(Обычно мы пишем уравнения в нормальной форме с положительным знаком перед членом x . )

Пример 3

Решить графически систему:

2 x — 3 y = −6

x + y = 7

Ответ

Еще раз, мы наносим на график 2 линии, и точка пересечения дает решение для одновременные уравнения.

2 x — 3 y = −6 имеет x -перехват `-3`, а также y — перехват `2`.

x + y = 7 имеет x -перехват `7` и имеет y -перехват `7`.

График выглядит следующим образом:

123456789-1-2-3-412345678910-1-2xy (3,4)

`2x — 3y = -6`

`x + y = 7`

Графики y = (2x + 6) / 3 и y = -x + 7.

Итак, мы видим, что существует одно решение для системы (из графика), и это `(3, 4)`.

Пример 4

Решить графически систему:

x — 5 y = −10

x — 5 y = 7

Ответ

Для этой системы у нас:

x — 5 y = −10 имеет x -перехват `-10`, а также y — перехват `2`.

x — 5 y = 7 имеет x -перехват `7` и имеет перехват y `-7 / 5 = -1,4`.

График выглядит следующим образом:

2468-2-4-6-8-10246-2-4xy

`x — 5y = -10`

x — 5y = 7`

График линейных уравнений x — 5 y = −10 и x — 5y = 7.

Мы видим, что нет решений для системы, так как линии параллельны.

Системы нелинейных уравнений: графические представления

Системы нелинейных уравнений:
Графические соображения (стр. 2 из 6)

Предыдущая страница проинформировала нас о взаимосвязи между решениями уравнений и точками на соответствующих графиках линий этих уравнений.Эта тема, вероятно, в последний раз упоминалась в классе, когда вы впервые узнали о построении графиков линейных уравнений, и, возможно, с тех пор о ней забыли. Но вопрос важный для решения систем уравнений. Почему? Потому что решение системы уравнений будет решением для всех уравнений в системе. Тогда это решение должно быть точкой построения всех графиков связанных линий. Но где разных линий будут иметь ту же точку на графике? Где эти линии пересекаются.

Предположим, у вас есть следующая система уравнений:

  • Решить система в виде графиков:

    Я могу изобразить каждый этих уравнений по отдельности:


    ..и каждая точка на каждый график является решением уравнения этого графика.

    Теперь посмотрим на график системы:

      л = x 2

      л = 8 x 2

    Решение для системы — любая точка, которая является решением для обоих уравнений.В другом словами, точкой решения для этой системы является любая точка, которая находится на и графики. Другими словами:

«РЕШЕНИЯ» ДЛЯ СИСТЕМ
ЯВЛЯЮТСЯ
ПЕРЕСЕЧЕНИЯМИ ЛИНИЙ

    Тогда графически решения для этой системы отмечены красным цветом на справа:

    То есть решения к этой системе относятся точки (2, 4) и (2, 4) .

Итак, когда вы пытаетесь решить систему уравнений, вы пытаетесь найти координаты точки пересечения. Copyright 2002-2011 Элизабет Стапель. Все права защищены.

Система в приведенном выше примере имела два решения, потому что график показывает два пересечения точки. В разных системах может быть разное количество решений. Например:

У системы может быть одно решение:


…лосков решений:

… или нет решений всего:

(В этой последней ситуации там, где не было решения, система уравнений называется «несовместной». )

Когда вы смотрите на график, вы можете только догадываться о приближении к решению. Если только точки решения не являются хорошими аккуратными числами (и если вы случайно знаете об этом заранее), вы не можете получить решение из изображение. Например, вы не можете сказать, какое решение к системе, изображенной справа, может быть:


… потому что у вас есть угадывать по картинке. Оказывается, решение ( x, y ) = (1 3 / 7 , 9 / 14 ), но у вас не было бы возможности узнать это по этой картинке.

Консультации: Ваш текст будет почти наверняка вы выполняете какие-нибудь упражнения «решайте с помощью графиков». Ты можно смело предположить, что для этих упражнений ответы хороши и аккуратны, потому что решения должны быть , если вы хотите иметь шанс угадывать решения по картинке.

Это «решение путем построения графика» может быть полезен тем, что помогает получить представление о том, что происходит при решении систем. Но это тоже может вводить в заблуждение в том смысле, что это означает, что все решения будут «аккуратными», когда большинство решения на самом деле довольно беспорядочные.

<< Предыдущая Вверх | 1 | 2 | 3 | 4 | 5 | 6 | Вернуться к указателю Далее >>

Цитируйте эту статью как:

Стапель, Елизавета.«Системы нелинейных уравнений: графические соображения». Purplemath .
Доступно по адресу https://www.purplemath.com/modules/syseqgen2.htm .
Дата обращения [Дата] [Месяц] 2016 г.

Графики и решения систем линейных уравнений

Результаты обучения

  • Графические системы уравнений
    • Постройте систему двух линейных уравнений
    • Постройте систему двух линейных неравенств
  • Оценить упорядоченные пары как решения для систем
    • Определить, является ли упорядоченная пара решением системы линейных уравнений
    • Определить, является ли упорядоченная пара решением системы линейных неравенств
  • Классифицируйте решения для систем
    • Определите, какой тип решения будет иметь система, на основе ее графика

Путь течения реки зависит от многих переменных, включая размер реки, количество воды в ней, какие предметы плавают в реке, идет ли дождь или нет, и так далее. Если вы хотите лучше всего описать его поток, вы должны принять во внимание эти другие переменные. В этом может помочь система линейных уравнений.

Система линейных уравнений состоит из двух или более линейных уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Вы найдете системы уравнений во всех приложениях математики. Они являются полезным инструментом для обнаружения и описания взаимосвязи поведения или процессов.Например, редко можно найти схему транспортного потока, на которую влияет только погода. Несчастные случаи, время суток и крупные спортивные соревнования — это лишь некоторые из других переменных, которые могут повлиять на транспортный поток в городе. В этом разделе мы исследуем некоторые основные принципы построения графиков и описания пересечения двух линий, составляющих систему уравнений.

Построить систему линейных уравнений

В этом разделе мы рассмотрим системы линейных уравнений и неравенств с двумя переменными. Сначала мы попрактикуемся в построении графиков двух уравнений на одном и том же наборе осей, а затем изучим различные соображения, которые необходимо учитывать при построении графиков двух линейных неравенств на одном и том же наборе осей. Для построения графика системы линейных уравнений используются те же методы, что и для построения графиков отдельных линейных уравнений. Мы можем использовать таблицы значений, уклона и интервала y или интерцептов x и y , чтобы построить обе линии на одном и том же наборе осей.

Например, рассмотрим следующую систему линейных уравнений с двумя переменными.

[латекс] \ begin {array} {r} 2x + y = -8 \\ x-y = -1 \ end {array} [/ latex]

Давайте изобразим их, используя форму пересечения наклона на одном и том же наборе осей. Помните, что форма пересечения наклона выглядит как [latex] y = mx + b [/ latex], поэтому мы захотим решить оба уравнения для [latex] y [/ latex].

Сначала найдите y в [latex] 2x + y = -8 [/ latex]

[латекс] \ begin {array} {c} 2x + y = -8 \\ y = -2x — 8 \ end {array} [/ latex]

Во-вторых, решите относительно y в [latex] x-y = -1 [/ latex]

[латекс] \ begin {array} {r} x-y = -1 \, \, \, \, \, \\ y = x + 1 \ end {array} [/ latex]

Теперь система записывается как

[латекс] \ begin {array} {c} y = -2x — 8 \\ y = x + 1 \ end {array} [/ latex]

Теперь вы можете построить оба уравнения, используя их наклоны и точки пересечения на одном и том же наборе осей, как показано на рисунке ниже. Обратите внимание на то, что графики имеют одну общую точку. Это их точка пересечения, точка, которая лежит на обеих линиях. В следующем разделе мы убедимся, что эта точка является решением системы.

В следующем примере вам будет предоставлена ​​система построения графика, состоящая из двух параллельных линий.

Пример

Постройте график системы [латекс] \ begin {array} {c} y = 2x + 1 \\ y = 2x-3 \ end {array} [/ latex], используя наклоны и пересечения линий по оси Y.

Показать решение

Сначала построим график [латекс] y = 2x + 1 [/ latex], используя наклон m = 2 и точку пересечения оси y (0,1)

Затем добавьте [латекс] y = 2x-3 [/ latex], используя наклон m = 2 и точку пересечения оси y (0, -3)

Обратите внимание на то, что это параллельные линии, и они не пересекаются.В следующем разделе мы обсудим, как не существует решений системы уравнений, представляющих собой параллельные прямые.

В следующем примере вам будет предоставлена ​​система, уравнения которой выглядят по-разному, но после построения графика оказываются той же линией.

Пример

Изобразите систему [латекс] \ begin {array} {c} y = \ frac {1} {2} x + 2 \\ 2y-x = 4 \ end {array} [/ latex], используя x — и y -перехватывает.

Показать решение

Сначала найдите точки пересечения по осям x и y [latex] y = \ frac {1} {2} x + 2 [/ latex]

Пересечение x будет иметь значение 0 для y, поэтому подставьте y = 0 в уравнение и выделите переменную x.

[латекс] \ begin {array} {c} 0 = \ frac {1} {2} x + 2 \\\ подчеркивание {\, \, \, \, \, \, \, \, — 2 \, \, \, \, \, \, — 2} \\ — 2 = \ frac {1} {2} x \\\ left (2 \ right) \ left (-2 \ right) = \ left (2 \ справа) \ frac {1} {2} x \\ — 4 = x \ end {array} [/ latex]

Х-точка пересечения [latex] y = \ frac {1} {2} x + 2 [/ latex] равна [latex] \ left (-4,0 \ right) [/ latex].

Угол пересечения по оси Y найти легче, поскольку это уравнение имеет форму пересечения с угловым коэффициентом. Y-точка пересечения равна (2,0).

Теперь мы можем построить [latex] y = \ frac {1} {2} x + 2 [/ latex], используя точки пересечения

Теперь найдите перехватчики [latex] 2y-x = 4 [/ latex]

Подставьте y = 0 в уравнение, чтобы найти точку пересечения с x.

[латекс] \ begin {array} {c} 2y-x = 4 \\ 2 \ left (0 \ right) -x = 4 \\ x = -4 \ end {array} [/ latex]

Х-точка пересечения [latex] 2y-x = 4 [/ latex] равна [latex] \ left (-4,0 \ right) [/ latex].

Теперь подставьте x = 0 в уравнение, чтобы найти точку пересечения оси y.

[латекс] \ begin {array} {c} 2y-x = 4 \\ 2y-0 = 4 \\ 2y = 4 \\ y = 2 \ end {array} [/ latex]

Y-пересечение [latex] 2y-x = 4 [/ latex] равно [latex] \ left (0,2 \ right) [/ latex].

ПОДОЖДИТЕ, это те же перехваты, что и [latex] y = \ frac {1} {2} x + 2 [/ latex]! Фактически, [latex] y = \ frac {1} {2} x + 2 [/ latex] и [latex] 2y-x = 4 [/ latex] на самом деле одно и то же уравнение, выраженное по-разному.Если бы вы записали их оба в форме пересечения наклона, вы бы увидели, что это одно и то же уравнение.

Если вы построите график, это одна и та же линия. В следующем разделе мы увидим, что системы с двумя одинаковыми уравнениями в них имеют бесконечное число решений.

Построение графика системы линейных уравнений состоит из выбора метода построения графиков, который вы хотите использовать, и построения графиков обоих уравнений на одном и том же наборе осей. Когда вы строите график системы линейных неравенств на одном и том же наборе осей, вам необходимо учесть еще несколько вещей.

Постройте систему двух неравенств

Помните из модуля по построению графиков, что график одного линейного неравенства разбивает координатную плоскость на две области. По одну сторону лежат все решения неравенства. С другой стороны, решений нет. Рассмотрим график неравенства [латекс] y <2x + 5 [/ latex].

Пунктирная линия [латекс] y = 2x + 5 [/ latex]. Каждая упорядоченная пара в заштрихованной области под линией является решением [latex] y <2x + 5 [/ latex], поскольку все точки под линией делают неравенство истинным. Если вы сомневаетесь в этом, попробуйте подставить координаты x и y точек A и B в неравенство — вы увидите, что они работают. Итак, заштрихованной областью показаны все решения этого неравенства.

Граничная линия делит координатную плоскость пополам. В этом случае он показан пунктирной линией, поскольку точки на линии не удовлетворяют неравенству. Если бы неравенство было [латекс] y \ leq2x + 5 [/ латекс], то граница была бы сплошной.

Изобразим еще одно неравенство: [latex] y> −x [/ latex].Вы можете проверить пару точек, чтобы определить, какую сторону границы нужно заштриховать. Контрольные точки M и N дают верные утверждения. Итак, заштриховываем область над линией. Линия пунктирна, поскольку точки на линии не соответствуют действительности.

Чтобы создать систему неравенств, вам нужно построить график двух или более неравенств вместе. Давайте использовать [latex] y <2x + 5 [/ latex] и [latex] y> −x [/ latex], поскольку мы уже изобразили каждый из них.

Фиолетовая область показывает, где перекрываются решения двух неравенств.Эта область является решением системы неравенств . Любая точка в этой фиолетовой области будет верна как для [latex] y> −x [/ latex], так и для [latex] y <2x + 5 [/ latex].

В следующем примере вам дана система двух неравенств, граничные линии которых параллельны друг другу.

Примеры

Изобразите систему [latex] \ begin {array} {c} y \ ge2x + 1 \\ y \ lt2x-3 \ end {array} [/ latex]

Показать решение

Границы для этой системы такие же, как и для системы уравнений из предыдущего примера:

[латекс] \ begin {array} {c} y = 2x + 1 \\ y = 2x-3 \ end {array} [/ latex]

Построение граничных линий будет аналогично, за исключением того, что неравенство [латекс] y \ lt2x-3 [/ latex] требует, чтобы мы нарисовали пунктирную линию, а неравенство [латекс] y \ ge2x + 1 [/ латекс] потребует сплошная линия.Графики будут выглядеть так:

Теперь нам нужно добавить регионы, представляющие неравенства. Для неравенства [латекс] y \ ge2x + 1 [/ latex] мы можем проверить точку по обе стороны от линии, чтобы увидеть, какую область закрасить. Давайте проверим [латекс] \ left (0,0 \ right) [/ latex], чтобы упростить задачу.

Заменить [латекс] \ left (0,0 \ right) [/ latex] на [latex] y \ ge2x + 1 [/ latex]

[латекс] \ begin {array} {c} y \ ge2x + 1 \\ 0 \ ge2 \ left (0 \ right) +1 \\ 0 \ ge {1} \ end {array} [/ latex]

Это неправда, поэтому мы знаем, что нам нужно заштриховать другую сторону граничной линии для неравенства [latex] y \ ge2x + 1 [/ latex].График теперь будет выглядеть так:

Теперь закрасим область, которая показывает решения неравенства [латекс] y \ lt2x-3 [/ latex]. Опять же, мы можем выбрать [latex] \ left (0,0 \ right) [/ latex] для тестирования, потому что это упрощает алгебру.

Заменить [латекс] \ left (0,0 \ right) [/ latex] на [latex] y \ lt2x-3 [/ latex]

[латекс] \ begin {array} {c} y \ lt2x-3 \\ 0 \ lt2 \ left (0, \ right) x-3 \\ 0 \ lt {-3} \ end {array} [/ latex ]

Это неправда, поэтому мы знаем, что нам нужно заштриховать другую сторону граничной линии для неравенства [латекс] y \ lt2x-3 [/ latex]. График теперь будет выглядеть так:

У этой системы неравенства нет общих черт.

Как бы выглядел график, если бы система выглядела так?

[латекс] \ begin {массив} {c} y \ ge2x + 1 \\ y \ gt2x-3 \ end {array} [/ latex].

Проверка точки [latex] \ left (0,0 \ right) [/ latex] вернет положительный результат для неравенства [latex] y \ gt2x-3 [/ latex], и тогда график будет выглядеть следующим образом:

Фиолетовая область — это область перекрытия обоих неравенств.

В следующем разделе мы увидим, что точки могут быть решениями систем уравнений и неравенств. Проверим алгебраически, является ли точка решением линейного уравнения или неравенства.

Определить, является ли упорядоченная пара решением системы линейных уравнений

Линии на графике выше определены как

[латекс] \ begin {массив} {r} 2x + y = -8 \\ x-y = -1 \ end {array} [/ latex].

Они пересекаются в том, что выглядит как [латекс] \ left (-3, -2 \ right) [/ latex].

Используя алгебру, мы можем проверить, что эта общая точка на самом деле [latex] \ left (-3, -2 \ right) [/ latex], а не [latex] \ left (-2.999, -1.999 \ right) [/ latex ]. Подставляя значения x и y упорядоченной пары в уравнение каждой линии, вы можете проверить, находится ли точка на обеих линиях. Если подстановка приводит к истинному утверждению, значит, вы нашли решение системы уравнений!

Поскольку решение системы должно быть решением всех уравнений в системе, вам нужно будет проверить точку в каждом уравнении.В следующем примере мы заменим -3 на x и -2 на y в каждом уравнении, чтобы проверить, действительно ли это решение.

Пример

[латекс] \ left (-3, -2 \ right) [/ latex] решение системы

[латекс] \ begin {array} {r} 2x + y = -8 \\ x-y = -1 \ end {array} [/ latex]

Показать решение Сначала проверьте [латекс] 2x + y = -8 [/ latex]:

[латекс] \ begin {массив} {r} 2 (-3) + (- 2) = -8 \\ — 8 = -8 \\\ текст {ИСТИНА} \ end {array} [/ latex]

Теперь проверьте [латекс] x-y = -1 [/ latex].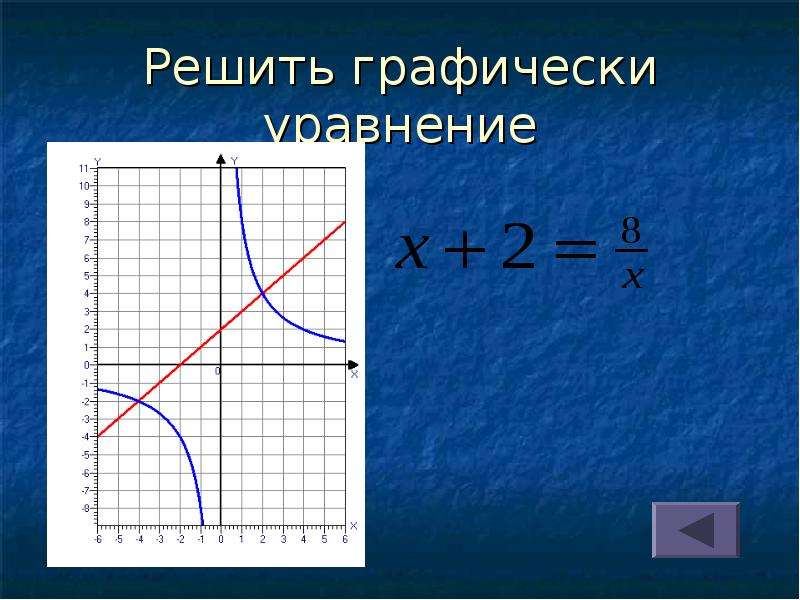

[латекс] \ begin {array} {r} (- 3) — (- 2) = -1 \\ — 1 = -1 \\\ text {TRUE} \ end {array} [/ latex]

[латекс] \ left (-3, -2 \ right) [/ latex] — это решение [latex] x-y = -1 [/ latex]

Поскольку [latex] \ left (-3, -2 \ right) [/ latex] является решением каждого из уравнений в системе, [latex] \ left (-3, -2 \ right) [/ latex] это решение системы.

Ответ

[латекс] \ left (-3, -2 \ right) [/ latex] — это решение системы.

Пример

— это (3, 9) решение системы

[латекс] \ begin {array} {r} y = 3x \\ 2x – y = 6 \ end {array} [/ latex]

Показать решение Поскольку решение системы должно быть решением всех уравнений в системе, проверьте точку в каждом уравнении.

Замените 3 на x и 9 на y в каждом уравнении.

[латекс] \ begin {array} {l} y = 3x \\ 9 = 3 \ left (3 \ right) \\\ text {TRUE} \ end {array} [/ latex]

(3, 9) представляет собой раствор [латекс] y = 3x [/ латекс].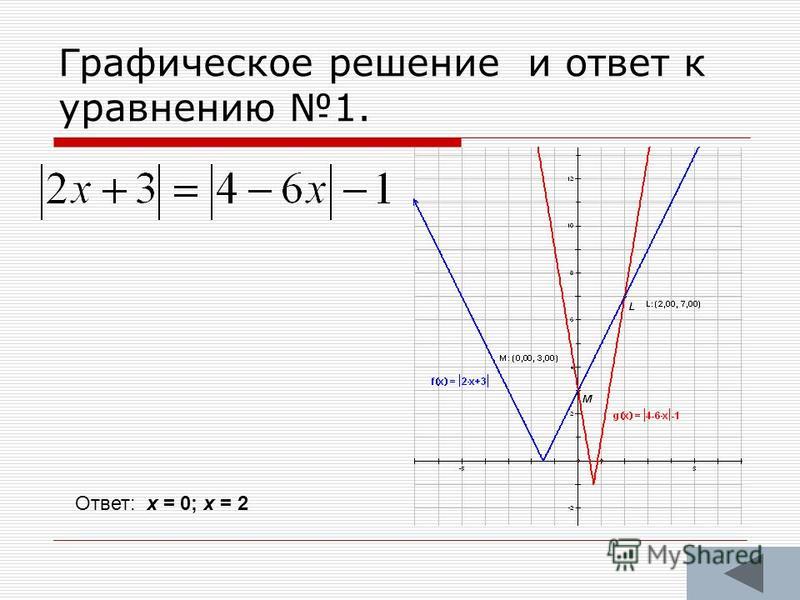

[латекс] \ begin {array} {r} 2x – y = 6 \\ 2 \ left (3 \ right) –9 = 6 \\ 6–9 = 6 \\ — 3 = 6 \ text {FALSE } \ end {array} [/ latex]

(3, 9) — это , а не раствор [латекса] 2x – y = 6 [/ латекс].

Поскольку (3, 9) не является решением одного из уравнений системы, оно не может быть решением системы.

Ответ

(3, 9) не является решением системы.

Подумай об этом

[латекс] (- 2,4) [/ латекс] решение для системы

[латекс] \ begin {array} {r} y = 2x \\ 3x + 2y = 1 \ end {array} [/ latex]

Прежде чем производить какие-либо вычисления, посмотрите на заданную точку и первое уравнение в системе. Можете ли вы предсказать ответ на вопрос, не занимаясь алгеброй?

Показать решение

Подставьте -2 вместо x и 4 вместо y в первое уравнение:

[латекс] \ begin {array} {l} y = 2x \\ 4 = 2 \ left (-2 \ right) \\ 4 = -4 \\\ text {FALSE} \ end {array} [/ latex]

Вы можете остановить тестирование, потому что точка, которая является решением системы, будет решением обоих уравнений в системе.

[latex] (- 2,4) [/ latex] НЕ является решением для системы

[латекс] \ begin {array} {r} y = 2x \\ 3x + 2y = 1 \ end {array} [/ latex]

Помните, что для решения системы уравнений значения точки должны быть решением обоих уравнений. Как только вы найдете одно уравнение, для которого точка неверна, вы определили, что оно не является решением системы.

Мы можем использовать тот же метод, чтобы определить, является ли точка решением системы линейных неравенств.

Определить, является ли упорядоченная пара решением системы линейных неравенств

На приведенном выше графике вы можете видеть, что точки B и N являются решениями для системы, потому что их координаты делают оба неравенства истинными.

Напротив, точки M и A лежат вне области решения (фиолетовый). Хотя точка M является решением неравенства [latex] y> −x [/ latex], а точка A является решением неравенства [latex] y <2x + 5 [/ latex], ни одна из точек не является решением для система . В следующем примере показано, как проверить точку, чтобы увидеть, является ли она решением системы неравенств.

Пример

Является ли точка (2, 1) решением системы [латекс] x + y> 1 [/ latex] и [latex] 2x + y <8 [/ latex]?

Показать решение Проверьте суть каждого неравенства. Замените 2 на x и 1 на y . Является ли дело решением обоих неравенств?

[латекс] \ begin {массив} {r} x + y> 1 \\ 2 + 1> 1 \\ 3> 1 \\\ text {TRUE} \ end {array} [/ latex]

(2, 1) — решение для [латекса] x + y> 1 [/ latex].

[латекс] \ begin {array} {r} 2x + y <8 \\ 2 \ left (2 \ right) +1 <8 \\ 4 + 1 <8 \\ 5 <8 \\\ text {TRUE} \ end {array} [/ latex]

(2, 1) — решение для [латекса] 2x + y <8. [/ Latex]

Поскольку (2, 1) является решением каждого неравенства, оно также является решением системы.

Ответ

Точка (2, 1) является решением системы [латекс] x + y> 1 [/ latex] и [latex] 2x + y <8 [/ latex].

Вот график системы в примере выше. Обратите внимание, что (2, 1) находится в фиолетовой области, которая является областью перекрытия для двух неравенств.

Пример

Является ли точка (2, 1) решением системы [латекс] x + y> 1 [/ latex] и [latex] 3x + y <4 [/ latex]?

Показать решение

Отметьте точку с каждым неравенством. Замените 2 на x и 1 на y . Является ли дело решением обоих неравенств?

[латекс] \ begin {массив} {r} x + y> 1 \\ 2 + 1> 1 \\ 3> 1 \\\ text {TRUE} \ end {array} [/ latex]

(2, 1) — решение для [латекса] x + y> 1 [/ latex].

[латекс] \ begin {array} {r} 3x + y <4 \\ 3 \ left (2 \ right) +1 <4 \\ 6 + 1 <4 \\ 7 <4 \\\ text {FALSE} \ end {array} [/ latex]

(2, 1) — это , а не , решение для [латекса] 3x + y <4 [/ latex].

Поскольку (2, 1) — это , а не как решение одного из неравенств, это не решение системы.

Ответ

Точка (2, 1) не является решением системы [латекс] x + y> 1 [/ latex] и [latex] 3x + y <4 [/ latex].

Вот график этой системы. Обратите внимание, что (2, 1) не находится в фиолетовой области, которая является перекрывающейся областью; это решение одного неравенства (красная область), но не решение второго неравенства (синяя область).

Как показано выше, нахождение решений системы неравенств может быть выполнено путем графического отображения каждого неравенства и определения общей для них области. Ниже приведены дополнительные примеры, показывающие весь процесс определения области решений на графике для системы двух линейных неравенств. Общие шаги описаны ниже:

  • Изобразите каждое неравенство в виде линии и определите, будет ли оно сплошным или пунктирным
  • Определите, с какой стороны каждой граничной линии представлены решения неравенства, проверив точку на каждой стороне
  • Заштрихуйте область, которая представляет решения для обоих неравенств

Пример

Закрасьте область графика, которая представляет решения для обоих неравенств. [латекс] x + y \ geq1 [/ латекс] и [латекс] y – x \ geq5 [/ латекс].

Показать решение Изобразите одно неравенство. Сначала нарисуйте граничную линию, используя таблицу значений, пересечений или любой другой метод, который вы предпочитаете. Граница для [латекса] x + y \ geq1 [/ latex] — это [латекс] x + y = 1 [/ latex] или [латекс] y = −x + 1 [/ latex]. Поскольку знак равенства стоит вместе со знаком «больше», граница будет сплошной.

Найдите упорядоченную пару по обе стороны от граничной линии. Вставьте значения x и y в неравенство [latex] x + y \ geq1 [/ latex] и посмотрите, какая упорядоченная пара дает истинное утверждение.

[латекс] \ begin {array} {r} \ text {Test} 1: \ left (−3,0 \ right) \\ x + y \ geq1 \\ — 3 + 0 \ geq1 \\ — 3 \ geq1 \\\ text {FALSE} \\\\\ text {Test} 2: \ left (4,1 \ right) \\ x + y \ geq1 \\ 4 + 1 \ geq1 \\ 5 \ geq1 \\\ текст {ИСТИНА} \ end {array} [/ latex]

Поскольку (4, 1) приводит к истинному утверждению, область, которая включает (4, 1), должна быть заштрихована.

Проделайте то же самое со вторым неравенством. Постройте граничную линию, затем проверьте точки, чтобы определить, какая область является решением неравенства. В этом случае граница [латекс] y – x = 5 \ left (\ text {или} y = x + 5 \ right) [/ latex] сплошная.Контрольная точка (−3, 0) не является решением [latex] y – x \ geq5 [/ latex], а контрольная точка (0, 6) является решением.

Ответ

Фиолетовая область на этом графике показывает набор всех решений системы.

В этом разделе мы увидели, что решения систем линейных уравнений и неравенств могут быть упорядоченными парами. В следующем разделе мы будем работать с системами, у которых нет решений или есть бесконечно много решений.

Используйте график для классификации решений по системам

Напомним, что линейное уравнение отображается в виде линии, что означает, что все точки на линии являются решениями этого линейного уравнения. Есть бесконечное количество решений. Как мы видели в предыдущем разделе, если у вас есть система линейных уравнений, пересекающихся в одной точке, эта точка является решением системы. Что произойдет, если линии никогда не пересекаются, как в случае с параллельными линиями? Как бы вы описали решения для такой системы? В этом разделе мы исследуем три возможных результата решения системы линейных уравнений.

Три возможных исхода решений систем уравнений

Напомним, что решение системы уравнений — это значение или значения, которые являются истинными для всех уравнений в системе.Есть три возможных исхода решений систем линейных уравнений. Графики уравнений внутри системы могут сказать вам, сколько решений существует для этой системы. Посмотрите на изображения ниже. На каждой показаны две линии, составляющие систему уравнений.

Одно решение Нет решений Бесконечные решения
Если графики уравнений пересекаются, то существует одно решение, истинное для обоих уравнений. Если графики уравнений не пересекаются (например, если они параллельны), то для обоих уравнений нет истинных решений. Если графики уравнений совпадают, то существует бесконечное количество решений, которые верны для обоих уравнений.
  • Одно решение: Когда система уравнений пересекается в упорядоченной паре, система имеет одно решение.
  • Бесконечные решения: Иногда два уравнения отображаются в виде одной линии, и в этом случае у нас есть бесконечное количество решений.
  • Нет Решение: Когда линии, составляющие систему, параллельны, решений нет, потому что эти две линии не имеют общих точек.

Пример

Используя график [latex] \ begin {array} {r} y = x \\ x + 2y = 6 \ end {array} [/ latex], показанный ниже, определите, сколько решений есть в системе.

Показать решение Линии пересекаются в одной точке. Таким образом, у этих двух линий есть только одна общая точка, есть только одно решение системы.
Ответ

Есть одно решение этой системы.

Пример (расширенный)

Используя график [latex] \ begin {array} {r} y = 3,5x + 0,25 \\ 14x – 4y = -4,5 \ end {array} [/ latex], показанный ниже, определите, сколько решений имеет система. .

Показать решение Линии параллельны, то есть не пересекаются. Решения по системе нет.
Ответ

Нет решений по системе.

Пример

Сколько решений имеет система [latex] \ begin {array} {r} y = 2x + 1 \\ — 4x + 2y = 2 \ end {array} [/ latex]?

Показать решение Сначала изобразите оба уравнения на одних и тех же осях.

Два уравнения изображены на одной линии. Таким образом, каждая точка на этой линии является решением системы уравнений.

Ответ

Система [latex] \ begin {array} {r} y = 2x + 1 \\ — 4x + 2y = 2 \ end {array} [/ latex] имеет бесконечное количество решений.

В следующем разделе мы изучим некоторые алгебраические методы поиска решений систем уравнений. Напомним, что линейные уравнения с одной переменной могут иметь одно решение, без решения или много решений, и мы можем проверить это алгебраически.Мы будем использовать те же идеи для алгебраической классификации решений систем с двумя переменными.

Решение систем уравнений с помощью графического представления

Чтобы исследовать такие ситуации, как ситуация с производителем скейтборда, нам необходимо признать, что мы имеем дело с более чем одной переменной и, вероятно, более чем с одним уравнением. Система линейных уравнений состоит из двух или более линейных уравнений, составленных из двух или более переменных, так что все уравнения в системе рассматриваются одновременно.Чтобы найти единственное решение системы линейных уравнений, мы должны найти числовое значение для каждой переменной в системе, которое будет удовлетворять всем уравнениям в системе одновременно. Некоторые линейные системы могут не иметь решения, а другие могут иметь бесконечное количество решений. Чтобы линейная система имела единственное решение, должно быть по крайней мере столько же уравнений, сколько переменных. Даже в этом случае это не гарантирует уникального решения.

В этом разделе мы рассмотрим системы линейных уравнений с двумя переменными, которые состоят из двух уравнений, содержащих две разные переменные.Например, рассмотрим следующую систему линейных уравнений с двумя переменными.

[латекс] \ begin {array} {c} 2x + y = \ text {} 15 \\ 3x-y = \ text {} 5 \ end {array} [/ latex]

Решение системы линейных уравнений с двумя переменными — это любая упорядоченная пара, которая удовлетворяет каждому уравнению независимо. В этом примере упорядоченная пара (4, 7) является решением системы линейных уравнений. Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям.Вскоре мы исследуем методы поиска такого решения, если оно существует.

[латекс] \ begin {array} {l} 2 \ left (4 \ right) + \ left (7 \ right) = 15 \ text {} \ text {True} \ hfill \\ 3 \ left (4 \ right ) — \ left (7 \ right) = 5 \ text {} \ text {True} \ hfill \ end {array} [/ latex]

Помимо учета количества уравнений и переменных, мы можем классифицировать системы линейных уравнений по количеству решений. Согласованная система уравнений имеет по крайней мере одно решение. Согласованной системой считается независимая система , если она имеет единственное решение, такое как пример, который мы только что исследовали.Две линии имеют разные уклоны и пересекаются в одной точке на плоскости. Согласованной системой считается зависимая система , если уравнения имеют одинаковый наклон и одинаковые точки пересечения y . Другими словами, линии совпадают, поэтому уравнения представляют одну и ту же линию. Каждая точка на линии представляет пару координат, удовлетворяющую системе. Таким образом, существует бесконечное количество решений.

Другой тип системы линейных уравнений — это несовместимая система , в которой уравнения представляют собой две параллельные линии.Линии имеют одинаковый наклон и разные точки пересечения y- . Для обеих линий нет общих точек; следовательно, у системы нет решения.

A Общее примечание: Типы линейных систем

Существует три типа систем линейных уравнений с двумя переменными и три типа решений.

  • Независимая система имеет ровно одну пару решений [латекс] \ left (x, y \ right) [/ latex]. Точка пересечения двух линий — единственное решение.
  • Несогласованная система не имеет решения. Обратите внимание, что две линии параллельны и никогда не пересекутся.
  • Зависимая система имеет бесконечно много решений. Линии совпадают. Это одна и та же линия, поэтому каждая пара координат на линии является решением обоих уравнений.

На Рисунке 2 сравниваются графические представления каждого типа системы.

Рисунок 2

Как сделать: для данной системы линейных уравнений и упорядоченной пары определите, является ли упорядоченная пара решением.

  1. Подставьте упорядоченную пару в каждое уравнение системы.
  2. Определите, являются ли истинные утверждения результатом подстановки в обоих уравнениях; в таком случае заказанная пара является решением.

Пример 1: Определение того, является ли упорядоченная пара решением системы уравнений

Определите, является ли упорядоченная пара [латекс] \ left (5,1 \ right) [/ latex] решением данной системы уравнений.

[латекс] \ begin {array} {l} x + 3y = 8 \ hfill \\ 2x — 9 = y \ hfill \ end {array} [/ latex]

Решение

Подставьте упорядоченную пару [латекс] \ left (5,1 \ right) [/ latex] в оба уравнения.

[латекс] \ begin {array} {ll} \ left (5 \ right) +3 \ left (1 \ right) = 8 \ hfill & \ hfill \\ \ text {} 8 = 8 \ hfill & \ text { True} \ hfill \\ 2 \ left (5 \ right) -9 = \ left (1 \ right) \ hfill & \ hfill \\ \ text {} \ text {1 = 1} \ hfill & \ text {True} \ hfill \ end {array} [/ latex]

Упорядоченная пара [латекс] \ left (5,1 \ right) [/ latex] удовлетворяет обоим уравнениям, поэтому это решение системы.

Анализ решения

Мы можем ясно увидеть решение, построив график каждого уравнения.Поскольку решение представляет собой упорядоченную пару, удовлетворяющую обоим уравнениям, это точка на обеих прямых и, следовательно, точка пересечения двух прямых.

Рисунок 3

Попробуй 1

Определите, является ли упорядоченная пара [латекс] \ left (8,5 \ right) [/ latex] решением следующей системы.

[латекс] \ begin {array} {c} 5x — 4y = 20 \\ 2x + 1 = 3y \ end {array} [/ latex]

Решение систем уравнений с помощью построения графиков

Существует несколько методов решения систем линейных уравнений.Для системы линейных уравнений с двумя переменными мы можем определить как тип системы, так и решение, построив систему уравнений на одном и том же наборе осей.

Пример 2: Решение системы уравнений с двумя переменными с помощью построения графика

Решите следующую систему уравнений, построив график. Определите тип системы.

[латекс] \ begin {array} {c} 2x + y = -8 \\ x-y = -1 \ end {array} [/ latex]

Решение

Решите первое уравнение для [латекс] y [/ латекс].

[латекс] \ begin {array} {c} 2x + y = -8 \\ y = -2x — 8 \ end {array} [/ latex]

Решите второе уравнение для [латекс] y [/ латекс].

[латекс] \ begin {array} {c} x-y = -1 \\ y = x + 1 \ end {array} [/ latex]

Изобразите оба уравнения на том же наборе осей, что и на рисунке 4.

Рисунок 4

Кажется, что линии пересекаются в точке [латекс] \ влево (-3, -2 \ вправо) [/ латекс]. Мы можем убедиться, что это решение системы, подставив упорядоченную пару в оба уравнения.

[латекс] \ begin {array} {ll} 2 \ left (-3 \ right) + \ left (-2 \ right) = — 8 \ hfill & \ hfill \\ \ text {} -8 = -8 \ hfill & \ text {True} \ hfill \\ \ text {} \ left (-3 \ right) — \ left (-2 \ right) = — 1 \ hfill & \ hfill \\ \ text {} -1 = — 1 \ hfill & \ text {True} \ hfill \ end {array} [/ latex]

Решением системы является упорядоченная пара [латекс] \ left (-3, -2 \ right) [/ latex], поэтому система независима.

Попробуй 2

Решите следующую систему уравнений, построив график.

[латекс] \ begin {массив} {l} \ text {} 2x — 5y = -25 \ hfill \\ -4x + 5y = 35 \ hfill \ end {array} [/ latex]

Вопросы и ответы

Можно ли использовать построение графиков, если система непоследовательна или зависима?

Да, в обоих случаях мы все еще можем построить график системы для определения типа системы и решения. Если две линии параллельны, система не имеет решения и непоследовательна. Если две линии идентичны, система имеет бесконечное количество решений и является зависимой системой.

Узнайте, как решить систему уравнений графически