§ 09. Построение графиков дробно-линейных функций

Функция вида , где и , называется Дробно-линейной. Графиком этой функции является гипербола.

Частным случаем дробно-линейной функции является функция обратной пропорциональности . График этой функции состоит из двух ветвей, симметричных относительно начала координат. При гипербола расположена в первой и третьей четвертях, при – во второй и четвертой четвертях.

Пример 11. Постройте график функции .

Решение. Выделим целую часть дроби .

Таким образом, уравнение, которым задается график функции, примет вид . График заданной функции получается из графика функции сдвигом на 2 единицы по оси OX влево, растяжением вдоль оси OY в 2 раза и сдвигом на 1,5 единицы по оси OY вверх.

Заметим, что график функции не пересекает прямые и , хотя и приближается к ним достаточно близко. Такие прямые называются Асимптотами графика функции. График дробно-линейной функции имеет две асимптоты – вертикальную и горизонтальную . Построение графика удобно начинать именно с нахождения асимптот: для нахождения вертикальной асимптоты приравниваем знаменатель дроби нулю, а для нахождения горизонтальной асимптоты выделяем целую часть дроби (рис. 34).

Построение графика произвольной дробно-линейной функции выполняется по алгоритмам, разобранным в примере 11.

Упражнения

8. Постройте графики функций:

А) ; б) ;

В) ; г) ;

Д) ; е) .

9. Постройте графики функций:

А) ; б) ;

В) ; г) ;

Д) ; е) ;

Ж) ; з) .

10. Постройте графики функций:

А) ; б) ;

В) ; г) ;

Д) ; е) .

11. Постройте графики функций:

А) ; б) ; в) ;

Г) ; д) ; е) .

< Предыдущая		Следующая >

Дробная линейная функция на занятиях с репетитором по математике

Рассмотрим вопросы методики изучения такой темы, как «построение графика дробной линейной функции». К сожалению, ее изучение удалено из базовой программы и репетитор по математике на своих занятиях не так часто ее затрагивает, как хотелось бы. Однако, математические классы еще никто не отменял, вторую часть ГИА тоже. Да и в ЕГЭ существует вероятность ее проникновения в тело задачи С5 (через параметры). Поэтому придется засучить рукава и поработать над методикой ее объяснения на уроке со средним или в меру сильным учеником. Как правило, репетитор по математике вырабатывает приемы объяснений по основным разделам школьной программы в течение первых 5 -7 лет работы. За это время через глаза и руки репетитора успевают пройти десятки учеников самых разных категорий. От запущенных и слабых от природы детей, лодырей и прогульщиков до целеустремленных талантов.

Со временем к репетитору по математике приходит мастерство объяснений сложных понятий простым языком не в ущерб математической полноте и точности. Вырабатывается индивидуальный стиль подачи материала, речи, визуального сопровождения и оформления записей. Любой опытный репетитор расскажет урок с закрытыми глазами, ибо наперед знает, какие проблемы возникают с пониманием материала и что нужно для их разрешения. Важно подобрать правильные слова и записи, примеры для начала урока, для середины и конца, а также грамотно составить упражнения для домашнего задания.

О некоторых частных приемах работы с темой пойдет речь в данной статье.

С построения каких графиков начинает репетитор по математике?

Нужно начать с определения изучаемого понятия. Напоминаю, что дробной линейной функцией называют функцию вида 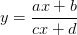. Ее построение сводится к построению самой обычной гиперболы путем известных несложных приемов преобразования графиков.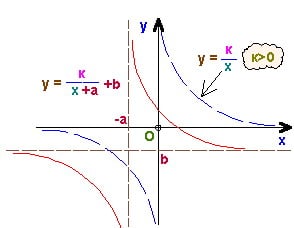

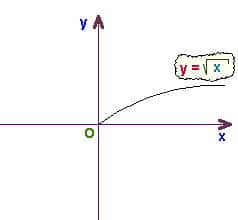На практике, несложными они оказываются только для cамого репетитора. Даже если к преподавателю приходит сильный ученик, с достаточной скоростью вычислений и преобразований, ему все равно приходится рассказывать эти приемы отдельно. Почему? В школе в 9 классе строят графики только путем сдвига и не используют методов добавления числовых множителей (методов сжатия и растяжения). Какой график используется репетитором по математике? С чего лучше начать? Вся подготовка проводится на примере самой удобной, на мой взгляд, функции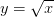 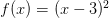. А что еще использовать? Тригонометрию в 9 классе изучают без графиков (а в переделанных учебниках под условия проведения ГИА по математике и вовсе не проходят). Квадратичная функция не имеет в данной теме такого же «методического веса», какой имеет корень. Почему? В 9 классе квадратный трехчлен изучается досконально и ученик вполне способен решать задачи на построение и без сдвигов. Форма мгновенно вызывает рефлекс к раскрытию скобок, после которого можно применить правило стандартного построения графика через вершину параболы и таблицу значений. С 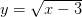такой маневр выполнить не удастся и репетитору по математике будет легче мотивировать ученика на изучение общих приемов преобразований. Использование модуля y=|x| тоже не оправдывает себя, ибо он не изучается так же плотно, как корень и школьники панически его боятся. 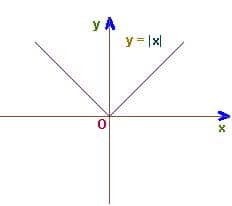К тому же, сам модуль (точнее его «навешивание») входит в число изучаемых преобразований.

Итак, репетитору не остается ничего более удобного и эффективного, как провести подготовку к преобразованиям с помощью квадратного корня. Нужна практика построений графиков примерно такого вида . Будем считать, что эта подготовка удалась на славу. Ребенок умеет сдвигать и даже сжимать/растягивать графики. Что дальше?

Далее стоит напомнить о том, как выглядит прямая пропорциональность 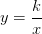и в каких четвертях располагается ее график в зависимости от знака коэффициента k.

Следующий этап – обучение выделению целой части. Пожалуй, это основная задача репетитора по математике, ибо после того, как целая часть будет выделенаона принимает на себя львиную долю всей вычислительной нагрузки на тему. Чрезвычайно важно подготовить функцию к виду, вписывающемуся в одну из стандартных схем построения. Также важно описать логику преобразований доступным понятным , а с другой стороны математически точно и стройно.

Напомню, что для построения графика 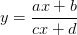необходимо преобразовать дробь к виду 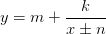. Именно к такому, а не к
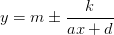, сохраняя знаменатель. Почему? Сложно выполнять преобразования того графика, который не только состоит из кусочков, но еще и имеет асимптоты. Непрерывность используется для того, чтобы соединить две-три более-менее понятно передвинутые точки одной линией. В случае разрывной функции не сразу разберешь, какие именно точки соединять. Поэтому сжимать или растягивать гиперболу – крайне неудобно. Репетитор по математике просто обязан научить школьника обходиться одними сдвигами.

Для этого помимо выделения целой части нужно еще удалить в знаменателе коэффициент c.

Выделение целой части у дроби

Как научить выделению целой части? Репетиторы по математике не всегда адекватно оценивают уровень знаний школьника и, несмотря на отсутствие в программе подробного изучения теоремы о делении многочленов с остатком, применяют правило деления уголком. Если преподаватель берется за уголочное деление, то придется потратить на его объяснение (если конечно все аккуратно обосновывать) почти половину занятия. К сожалению, не всегда это время у репетитора имеется в наличии. Лучше вообще не вспоминать ни о каких уголках.

Существует две формы работы с учеником:
1) Репетитор показывает ему готовый алгоритм на каком-нибудь примере дробной функции.
2) Преподаватель создает условия для логического поиска этого алгоритма.

Реализация второго пути мне представляется наиболее интересной для репетиторской практики и чрезвычайно полезной для развития мышления ученика. С помощью определенных намеков и указаний часто удается подвести к обнаружению некой последовательности верных шагов. В отличие от машинального выполнения кем-то составленного плана, школьник 9 класса учится самостоятельно его искать. Естественно, что все пояснения необходимо проводить на примерах. Возьмем для этого функцию 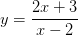и рассмотрим комментарии репетитора к логике поиска алгоритма. Репетитор по математике спрашивает: «Что мешает нам выполнить стандартное преобразование графика 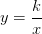, при помощи сдвига вдоль осей? Конечно же, одновременное присутствие икса и в числителе и в знаменателе. Значит необходимо удалить его из числителя. Как это сделать при помощи тождественных преобразований? Путь один – сократить дробь. Но у нас нет равных множителей (скобок). Значит нужно попытаться создать их искусственно. Но как? Не заменишь же числитель на знаменатель без всякого тождественного перехода. Попробуем преобразовать числитель, чтобы в него включалась скобка, равная знаменателю. Поставим ее туда принудительно и «обложим» коэффициентами так, чтобы при их «воздействии» на скобку, то есть при ее раскрытии и сложении подобных слагаемых, получался бы линейный многочлен 2x+3.

Репетитор по математике вставляет пропуски для коэффициентов в виде пустых прямоугольников (как это часто используют пособия для 5 – 6 классов) и ставит задачу — заполнить их числами. Подбор следует вести слева направо, начиная с первого пропуска. Ученик должен представить себе, как он будет раскрывать скобку. Так как ее раскрытия получится только одно слагаемое с иксом, то именно его коэффициент должен быть равным старшему коэффициенту в старом числителе 2х+3. Поэтому, очевидно, что в первом квадратике оказывается число 2. Он заполнен. Репетитору по математике следует взять достаточно простую дробную линейную функцию, у которой с=1. Только после этого можно переходить к разбору примеров с неприятным видом числителя и знаменателя (в том числе и с дробными коэффициентами).

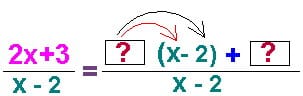
Идем дальше. Преподаватель раскрывает скобку и подписывает результат прямо над ней.

Можно заштриховать соответствующую пару множителей. К «раскрытому слагаемому», необходимо добавить такое число из второго пропуска, чтобы получить свободный коэффициент старого числителя. Очевидно, что это 7.

Итог подбора: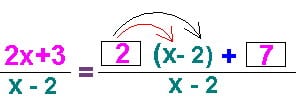

Далее дробь разбивается на сумму отдельных дробей (обычно я обвожу дроби облачком, сравнивая их расположение с крылышками бабочки). И говорю: «Разобьем дробь бабочкой». Школьники хорошо запоминают эту фразу.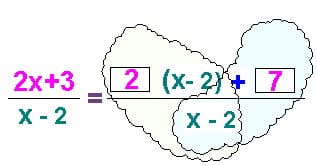

Репетитор по математике показывает весь процесс выделения целой части до вида, к которому уже можно применить алгоритм сдвига гиперболы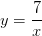

:

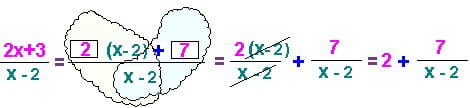
Если знаменатель имеет не равный единице старший коэффициент, то ни в коем случае не нужно его там оставлять. Это принесет и репетитору и ученику лишнюю головную боль, связанную с необходимостью проведения дополнительного преобразования, Причем самого сложного: сжатия — растяжения. Для схематического построения графика прямой пропорциональности не важен вид числителя. Главное знать его знак. Тогда к нему лучше перебросить старший коэффициент знаменателя. Например, если мы работаем с функцией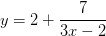

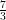, то просто вынесем 3 за скобку и «поднимем» ее в числитель, конструируя в нем дробь . Получим значительно более удобное выражение для построения: 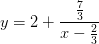Останется сдвинуть 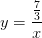на вправо и на 2 вверх.

Если между целой частью 2 и оставшейся дробью 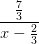возникает «минус», его тоже лучше занести в числитель. Иначе на определенном этапе построения придется дополнительно отображать гиперболу относительно оси Oy. Это только усложнит процесс.

Золотое правило репетитора по математике:
все неудобные коэффициенты, приводящие к симметриям, к сжатиям или растяжениям графика нужно перебросить в числитель.

Трудно описывать приемы работы с любой темой. Всегда остается ощущение некоторой недосказанности. Насколько удалось рассказать о дробной линейной функции — судить Вам. Присылайте Ваши комментарии и отзывы к статье (их можно написать в окошке, которое Вы видите внизу страницы). Я обязательно их опубликую.

Колпаков А.Н. Репетитор по математике Москва. Строгино. Методики для репетиторов.

Презентация на тему «Дробно-линейная функция и ее график»

1. Дробно – линейная функция и ее график.

С функцией вида y=k/x, где k≠0, ее свойствами и графиком мы уже познакомились. Обратим внимание на одну особенность этой функции. Функция y=k/x на множестве положительных чисел обладает тем свойством, что при неограниченном возрастании значений аргумента (когда x →∞) значения функций, оставаясь положительными, стремятся к нулю. При убывании положительных значений аргумента (когда x→0) значения функции неограниченно возрастают (y→∞). Аналогичная картина наблюдается и на множестве отрицательных чисел. На графике это свойство выражается в том, что точки гиперболы, по мере их удаления в бесконечность (вправо или влево, вверх или вниз) от начала координат, неограниченно приближаются к прямой: к оси x, когда |x| →∞, или к оси y, когда|x|→0. Такую прямую называют асимптотами кривой.

 

Гипербола y=k/x имеет две асимптоты: ось x и ось y.

Понятие асимптоты играет важную роль при построении графиков многих функций.

Используя известные нам преобразования графиков функций, мы можем гиперболу y=k/x перемещать в координатной плоскости вправо или влево, вверх или вниз. В результате будем получать новые графики функций.

Пример 1. Пусть y=6/x. Выполним сдвиг этой гиперболы вправо на 1,5 единицы, а затем полученный график сдвинем на 3,5 единицы вверх. При этом преобразовании сдвинутся и асимптоты гиперболы y=6/x: ось x перейдет в прямую y=3,5, ось y – в прямую y=1,5 (рис. 2).

Функцию, график которой мы построили, можно задать формулой

.

Представим выражение в правой части этой формулы в виде дроби:

Значит, на рисунке 2 изображен график функции, заданной формулой

.

У этой дроби числитель и знаменатель — линейные двучлены относительно х. Такие функции называют дробно-линейными функциями.

 

 

 

 

Вообще функцию, заданную формулой вида , где
х – переменная, а, b, c, d – заданные числа, причем с≠0 и
bc-ad≠0, называют дробно-линейной функцией.

Заметим, что требование в определении о том, что с≠0 и
bc-ad≠0, существенно. При с=0 и d≠0 или при bc-ad=0 мы получаем линейную функцию. Действительно, если с=0 и d≠0, то

.

Если же bc-ad=0, с≠0, выразив из этого равенства b через a, c и d и подставив его в формулу, получим:

.

Итак, в первом случае мы получили линейную функцию общего вида , во втором случае – константу .

Покажем теперь, как строить график дробно-линейной функции, если она задана формулой вида .

Пример 2.Построим график функции y =.

В дроби  выделим целую часть, и представим функцию в виде у = 2 — Таким образом, надо построить график функции у = 2 — . Он получается смещением гиперболы у = —  на одну единицу вправо и на две единицы вверх. График данной функции имеет вертикальную асимптоту х = 1 и горизонтальную асимптоту у = 2.

 

 

 

Пример 3.

Рассмотрим еще один способ построения графика функции у =

Для этого найдем точки пересечения графика функции с осями координат. Предположим, х=0 и определим точку пересечения с осью ординат у =  2. Теперь предположим, у = 0, получим уравнение 0 =  или 0=х+4 и найдем точку пересечения с осью абсцисс х = -4.  Построим точки А(0;2) и В(-4;0).

Определим асимптоты графика функции. Вертикальную асимптоту находим из условия, что функция не определена, т.е. х+2=0, откуда х=-2. Поведение функции при больших значениях х (|х|→∞) определяет горизонтальную асимптоту. При таких значениях х в числители дроби     можно пренебречь числом 4, в знаменателе числом 2. Тогда получаем горизонтальную асимптоту у =  =1. Построим асимптоты графика х = -2 и у = 1.

При построении графика функции учтем:

1)    Ветви графика симметричны относительно точки Е пересечения асимптот;

2)    График функции не пересекает асимптоты.

 

 

Пример 4.

  Построим график функции у = .

 

 

Раскроем знаки модуля и получим: у =,если -3≤х≤0

Построим графики полученных функций.

На промежутке(-∞;-3) гипербола у =

На промежутке [-3;0] функция определена всюду, кроме точки х = -2. При этом у = -1.

На промежутке (0;∞) гипербола у = . Учитывая выше сказанное, получаем график исходной функции.

 

 

Пример 5.

С помощью известных нам данных можно решить более сложное задание:

При каком значении параметра  а прямая  у = ах +1 касается  графика функции у =  ? Найти координаты точки касания.

Мы уже знаем, что графиком функции у =  =1 —   является гипербола с вертикальной асимптотой х=-1 и горизонтальной асимптотой у=1. Графиком функции у = ах+1 является прямая.  Координаты точки касания должны удовлетворять системе уравнений

При этом система должна иметь единственное решение.

Приравняем правые части и получим уравнение ах2+х+ах+1=х-1 или ах2+ах+2=0(а≠0).Чтобы квадратное уравнение имело один корень,  его дискриминант должен быть равен нулю, т.е. D=а2-8а=0, значит,  а=8.

Подставим значение а=8 в уравнение ах2+ах+2=0 и получим 8х2+8х+2=0. Откуда х=-0,5. Найдем соответствующее значение у = ах+1=8·(-0,5)+1=-3. Итак, координата точки касания графиков (-0,5;-3).

На графике это будет выглядеть следующим образом:

 

 

Пример 6.

В последней нашей диагностической работе по подготовке к сдаче ГИА по математике было  похожее задание :

Постройте график функции у =  и найдите все значения k, при которых прямая у = kх имеет с графиком данной функции ровно одну общую точку.

Решение:

Найдем область определения данной функции

Х2– х>0 или х(х – 1)>0

Откуда получаем x<0 и х>1.

Преобразуем функцию . Значит наша функция на своей ООФ принимает вид у=. Прямая у=kх имеет с графиком данной функции одну общую точку при k≥1.

Это задание из второй части, за правильное решение, которого можно получить максимальный балл(4 балла).

 

 

 

Пример 7.

Задача: постройте график функции у = |х|(х-4) +1 и определите, при каких значениях m прямая у = m имеет с графиком ровно три общие точки.

ООФ являются все  действительные числа.

Раскроем знак модуля: у =

 

Графиком каждой из этих функций является парабола. Поэтому найдем координаты вершины каждой.

1)    Х0= —  =  = 2

2)    У0= -3

3)    Х02= — = = 2

4)    У02=5

Значит, вершина первой параболы находится в точке с координатами (2;-3), а второй (2;5).

Проведем через точку х=2 ось симметрии. Она будет являться осью как для первой параболы, так и для второй.

Найдем нули функции, т.е. точки, в которых функция принимает значение у=0

Х2 – 4х +1 = 0, решая это уравнение находим х1=2+ и х2=2 —

-Х2 +4х+1 = 0, решая это уравнение находим х1=2+ и х2=2 —

Найдем точки пересечения графиков с осью у. Для этого подставим в нашу функцию значение х=0.

У1=1 и у2=1.

По этим характерным точкам построим график квадратичной функции. По графику видно, что прямая у=m,  имеет ровно три общие точки,  при mє (-3;1)

 

Пример 8.

Рассмотрим еще одну задачу из второй части, которая также оценивается максимальным баллом:

Найдите промежутки возрастания  и убывания функции у = 2х+3|х-1|- 4|х+2|-1 

Найдем нули функции: х-1=0, и следовательно х=1; х+2=0, и следовательно х=-2.

Раскроем знаки модуля на каждом промежутке:

1)    При х≤-2 получаем у = 2х -3(х-1) +4(х+2)-1=3х+10 – функция возрастает;

2)    При -2≤х≤1 получаем у = 2х-3(х-1) – 4(х+2) -1= -5х-6 – функция убывает;

3)    При х≥1 получаем  у = 2х+ 3(х-1) – 4(х+2) -1= х -12 – функция возрастает.

Ответ: функция возрастает на промежутках (-∞;-2] и [1;∞), функция убывает на промежутке [-2;1].

 

Ещё один приём построения графиков

График функции y=1/x можно построить несколько иначе. Нарисуем график функции у=x. Заменим каждую ординату величиной, ей обратной, и отметим соответствующие точки на рисунке. Получим график у=1/x (рис.1).

Нарисованная картина показывает, как маленькие (по абсолютной величине) ордината первого графика превращается в большие ординаты второго и, наоборот — большие ординаты первого в маленькие ординаты второго. Точки с ординатами, равными 1 (и — 1), остаются на месте.

 

 

 

Рис.1

Этот приём «деления» графиков бывает полезен всегда, когда у нас есть график у=f(x), а нам нужно понять, как ведёт себя функция y=1/f(x).

Заключение

При выполнении реферативной работы:

— уточнила свои понятия дробно-линейной  функций и выяснила, что является графиком  этой функции:

Определение 1.

Дробно-линейная функция – это функция вида , где х – переменная, a, b, c, и d – заданные числа, причем с≠0 и bc-ad≠0.

— сформировала алгоритм построения графиков этих функций;

-рассмотрела несколько методов построения графиков;

— научилась работать с дополнительной литературой и материалами, производить отбор научных сведений;

   — произвела разбор типовых заданий из второй части экзаменационных работ;

  — приобрела опыт выполнения графических работ на компьютере;

  — научилась составлять проблемно – реферативную работу.

 

 

Дробно-линейная функция. Разработки уроков

В данном уроке мы рассмотрим дробно-линейную функцию, решим задачи с использованием дробно-линейной функции, модуля, параметра.

Тема: Повторение

Урок: Дробно-линейная функция

1. Понятие и график дробно-линейной функции

Определение:

Дробно-линейной называется функция вида:

Например:

Докажем, что графиком данной дробно-линейной функции является гипербола.

Вынесем в числителе двойку за скобки, получим:

Имеем х и в числителе, и в знаменателе. Теперь преобразуем так, чтобы в числителе появилось выражение :

Теперь почленно сократим дробь:

Очевидно, что графиком данной функции является гипербола.

Можно предложить второй способ доказательства, а именно разделить в столбик числитель на знаменатель:

Получили:

2. Построение эскиза графика дробно-линейной функции

Важно уметь легко строить график дробно-линейной функции, в частности находить центр симметрии гиперболы. Решим задачу.

Пример 1 – построить эскиз графика функции:

Мы уже преобразовали данную функцию и получили:

Для построения данного графика мы не будем сдвигать оси или саму гиперболу. Мы используем стандартный метод построения графиков функции, использующий наличие интервалов знакопостоянства.

Действуем согласно алгоритму. Сначала исследуем заданную функцию.

ОДЗ:

Корни:

Таким образом, имеем три интервала знакопостоянства: на крайнем правом () функция имеет знак плюс, далее знаки чередуются, так как все корни имеют первую степень. Так, на интервале функция отрицательна, на интервале функция положительна.

Строим эскиз графика в окрестностях корней и точек разрыва ОДЗ. Имеем: поскольку в точке знак функции меняется с плюса на минус, то кривая сначала находится над осью, потом проходит через ноль и далее расположена под осью х. Когда знаменатель дроби практически равен нулю, значит, когда значение аргумента стремится тройке, значение дроби стремится к бесконечности. В данном случае, когда аргумент подходит к тройке слева функция отрицательна и стремится к минус бесконечности, справа функция положительна и выходит из плюс бесконечности.

Теперь строим эскиз графика функции в окрестностях бесконечно удаленных точек, т. е. когда аргумент стремится к плюс или минус бесконечности. Постоянными слагаемыми при этом можно пренебречь. Имеем:

Таким образом, имеем горизонтальную асимптоту и вертикальную , центр гиперболы точка (3;2). Проиллюстрируем:

Рис. 1. График гиперболы к примеру 1

3. Дробно линейная функция с модулем, ее график

Задачи с дробно-линейной функцией могут быть осложнены наличием модуля или параметра. Чтобы построить, например, график функции , необходимо следовать следующему алгоритму:

1. Построить график подмодульной функции

Предположим, получен следующий график:

Рис. 2. Иллюстрация к алгоритму

В полученном графике есть ветви, которые находятся над осью х и под осью х.

1. Наложить заданный модуль. При этом части графика, находящиеся над осью х, остаются без изменений, а те, которые находятся под осью – зеркально отображаются относительно оси х. Получим:

Рис. 3. Иллюстрация к алгоритму

Пример 2 – построить график функции:

Согласно алгоритму, сначала нужно построить график подмодульной функции, мы его уже построили (см. рисунок 1)

Далее требуется наложить на функцию модуль, при этом части графика, находящиеся над осью х, остаются без изменений, а те, которые находятся под осью – зеркально отображаются относительно оси х. Получим:

Рис. 4. График функции к примеру 2

       

4. Решение дробно-линейного уравнения с параметром

Рассмотрим следующую задачу – построить график функции . Для этого необходимо следовать следующему алгоритму:

1. Построить график подмодульной функции

Предположим, получен следующий график:

Рис. 5. Иллюстрация к алгоритму

1. Наложить заданный модуль. Чтобы понять, как это сделать, раскроем модуль.

Таким образом, для значений функции при неотрицательных значениях аргумента изменений не произойдет. Касательно второго уравнения мы знаем, что оно получается путем симметричного отображения относительно оси у. имеем график функции:

Рис. 6. Иллюстрация к алгоритму

Пример 3 – построить график функции:

Согласно алгоритму, сначала нужно построить график подмодульной функции, мы его уже построили (см. рисунок 1)

Далее требуется наложить на аргумент модуль, при этом части графика, находящиеся справа от оси у, остаются без изменений, и симметрично отображаются относительно оси у. Получим:

Рис. 7. График функции к примеру 3

Пример 4 – найти число корней уравнения с параметром:

Напомним, что решить уравнение с параметром означает перебрать все значения параметра и для каждого из них указать ответ. Действуем согласно методике. Сначала строим график функции, это мы уже сделали в предыдущем примере (см. рисунок 7). Далее необходимо рассечь график семейством прямых при различных а, найти точки пересечения и выписать ответ.

Глядя на график, выписываем ответ: при и уравнение имеет два решения; при уравнение имеет одно решение; при уравнение не имеет решений.

Рис. 8. График функции к примеру 4

Итак, мы рассмотрели дробно-линейную функцию, далее будем рассматривать функции третьей и четвертой степени.

Список рекомендованной литературы

1. Мордкович А. Г. Алгебра и начала математического анализа. М.: Мнемозина

2. Муравин Г. К., Муравина О. В. Алгебра и начала математического анализа. М.: Дрофа.

3. Колмогоров А. Н., Абрамов А. М., Дудницын Ю. П. и др. Алгебра и начала математического анализа. М.: Просвещение.

Рекомендованные ссылки на ресурсы интернет

1. Математика, которая мне нравится .

2. Егэ по математике .

3. Институт менеджмента, маркетинга и финансов .

Рекомендованное домашнее задание

1. Построить эскизы графиков функций:

2. Построить эскизы графиков функций:

3. Решить уравнение с параметром:

Внеклассный урок — Дробно-линейная функция

Дробно-линейная функция и ее график

 

                                                                                        ax + b
Дробно-линейная функция – это функция вида y = ——— ,
                                                                                         cx + d

где x – переменная, a, b, c, d – некоторые числа, причем c ≠ 0, ad – bc ≠ 0.

 

Свойства дробно-линейной функции:

1. При возрастании положительных значений аргумента значения функции убывают и стремятся к нулю, но остаются положительными. 2. При возрастании положительных значений функции значения аргумента убывают и стремятся к нулю, но остаются положительными.

 

Графиком дробно-линейной функции является гипербола, которую можно получить из гиперболы y = k/x с помощью параллельных переносов вдоль координатных осей. Для этого формулу дробно-линейной функции надо представить в следующем виде:

                 k
y = n + ———
             x – m

где n – количество единиц, на которое гипербола смещается вправо или влево,  m – количество единиц, на которое гипербола смещается вверх или вниз. При этом асимптоты гиперболы сдвигаются в прямые x = m, y = n.

Асимптота – это прямая, к которой приближаются точки кривой по мере их удаления в бесконечность (см.рисунок ниже).

Что касается параллельных переносов – см.предыдущие разделы.

 

Пример 1. Найдем асимптоты гиперболы и построим график функции:

        x + 8
y = ———
        x – 2

Решение:

                                                       k
Представим дробь в виде n + ———
                                                    x – m

 

Для этого x + 8 запишем в следующем виде: x – 2 + 10 (т.е. 8 представили в виде –2 + 10).

Получим:

 

  x + 8          x – 2 + 10          1(x – 2) + 10                 10
———  =  —————  =  ——————  =  1 + ———
  x – 2             x – 2                      x – 2                      x – 2

 

Почему выражение приняло такой вид? Ответ простой: произведите сложение (приведя оба слагаемых к общему знаменателю), и вы вернетесь к предыдущему выражению. То есть это результат преобразования заданного выражения.

 

Итак, мы получили все необходимые значения:

k = 10, m = 2, n = 1.

Таким образом, мы нашли асимптоты нашей гиперболы (исходя из того, что x = m, y = n):

x = 2, y = 1.

То есть одна асимптота гиперболы проходит параллельно оси y на расстоянии 2 единиц справа от нее, а вторая асимптота проходит параллельно оси x на расстоянии 1 единицы выше ее.

Построим график данной функции. Для этого сделаем следующее:

1) проведем в координатной плоскости пунктиром асимптоты – прямую x = 2 и прямую y = 1.

2) так как гипербола состоит из двух ветвей, то для построения этих ветвей составим две таблицы: одну для x<2, другую для x>2.

Сначала подберем значения x для первого варианта (x<2). Если x = –3, то:

                10
 y = 1 + ——— = 1 – 2 = –1
               –3 – 2

Выбираем произвольно другие значения x (например, -2, -1, 0 и 1). Вычисляем соответствующие значения y. Результаты всех полученных вычислений вписываем в таблицу:

 

Теперь составим таблицу для варианта x>2:

 

3) Далее просто составляете график функции с полученными координатами.

 
 

 

Урок-практикум по теме «Построение графика дробно-линейной функции»

Цели урока:

• закрепить умения строить график дробно-линейной функции,
• развить графические навыки учащихся.

I. Класс разбивается на группы по 4 человека так, чтобы в каждой группе был консультант и трое учащихся с разным уровнем усвоения знаний.

II. Выполнение домашней работы проверяет консультант группы.

III. Фронтальный опрос производится по вопросам:

1. Что такое дробно – линейная функция?

2. Что является графиком этой функции?

3. Какие преобразования графиков вы изучали?

4. Как определяются асимптоты?

IV. Каждая группа получает задание:

1. Определить, какая из функций является дробно – линейной (в дальнейшем ДЛФ)?

2. Выделить целую часть из ДЛФ, которую вы определили.

3. Построить график этой ДЛФ, используя соответствующую последовательность преобразований графиков.

Задание № 1 для первой группы. Задание № 1 для второй группы.

Каждая группа записывает результаты на доске и демонстрирует чертёж графика, который соответствует данной функции. (Учитель имеет ранее подготовленные чертежи этих ДЛФ).

Задание № 2. построить график ДЛФ, используя асимптоты и контрольные точки.

Задание для первой группы – это ДЛФ из задания № 1 для второй группы: у = .

Задание для второй группы – это ДЛФ задания № 1 для первой группы: у = .

Выполнив задание, каждая группа проверяет верность построения графика ДЛФ по чертежу графика на доске.

Итогом обсуждения полученных результатов является вывод:

1. График любой дробно – линейной функции есть гипербола.

2. Построить график ДЛФ можно:

1) выделяя целую часть из ДЛФ и осуществляя соответствующую последовательность преобразований графиков;

2) применяя практические приёмы построения гиперболы: использование асимптот, контрольных точек и учёт симметрии графика относительно точки пересечения асимптот.

V. Рефлексия на уроке осуществляется в ходе выполнения задания:

Установите, какой график соответствует данной функции:

Рисунок 1.

Таблица ответов.

Вариант	Задание
	1	2	3	4	5
В — 1	В	Е	D	С	А
В -2	А	С	Е	В	D

VI. Подведение итогов урока. Задание на дом.

Учитель. На уроке вы строили графики ДЛФ – параболы, применяя различные приёмы: деление многочлена на многочлен разными способами, поиск асимптот, использование контрольных точек, учёт симметрии графика. Дробно – линейная функция является рациональной и представляет собой частное двух линейных функций – многочленов первой степени.

Дома постройте графики функций, являющихся частными двух многочленов степени первой и выше первой. Это более сложные графики, но для их построения достаточно применить приёмы, с которыми вы уже знакомы.

1.

2.

3.

4.

5.

Список литературы.

1. Сикорский К. П. Дополнительные главы к курсу математики. — М.: просвещение, 1974.
2. Дворянинов С. Дробно – линейная функция в школьном курсе математики // Математика. — 2000. — № 5.
3. Самойлова В. Урок – практикум по теме “Построение графика квадратичной функции” // Математика. — 2007. — № 8.

Математика. Дробно-линейная функция. График дробно-линейной функции.

Дробно-линейная функция

Равнобочная гипербола

Исследуем функцию, заданную формулой  .

Функция строго убывает на  и на .

Доказательство. Пусть ,  и  одного знака. Тогда . 

Множество значений функции — .

Доказательство. Пусть . Тогда   принадлежит множеству значений функции.

Определение. Множество точек плоскости, которое в какой-либо системе координат является графиком функции , называется равнобочной гиперболой.

График равнобочной гиперболы приведен на рис. 29:

Рис. 29

Равнобочная гипербола  симметрична относительно начала координат.

Определение. Функция, график которой симметричен относительно начала координат, называется нечетной функцией.

Пример.  — нечетные функции.

Определение. Прямые  и  называются асимптотами равнобочной гиперболы .

Асимптоты перпендикулярны осям координат и проходят через точки на этих осях, которые не принадлежат области определения или множеству значений функции .

Преобразования системы координат

1) Изменение направления оси абсцисс

Гипербола — график функции  (рис. 30).

Рис. 30

2) Изменение масштаба

Из  получаем график функции

  

Из  получается график функции

  

Таким образом, график любой функции   является равнобочной гиперболой.

Если , нужно взять  и получить  из .

Если , нужно взять  и получить  из .

3) Сдвиг вдоль оси абсцисс

Из  получим график функции .

4) Сдвиг вдоль оси ординат

Из  получим 

  

Определение. Дробно-линейной функцией называется функция, заданная формулой

  

где .

Область определения этой функции .

Теорема. График дробно-линейной функции — равнобочная гипербола.

Доказательство. Преобразуем дробь  к виду  :

  

Нужно взять , , .

Практический прием построения графика дробно-линейной функции

1. Находится запрещенное значение .

2. Находится запрещенное значение функции. Для этого из равенства  выражается  через .

3. Наносим найденные точки на оси координат и проводим через них прямые, перпендикулярные осям — асимптоты графика.

4. Чтобы определить положение графика по отношению к асимптотам, находим одну точку графика.

5. Находим еще несколько точек и, учитывая, что гипербола симметрична относительно точки пересечения асимптот, строим ее.