Справочная таблица по теме: Квадратные уравнения
Квадратные уравнения.
Квадратным уравнением называется уравнение вида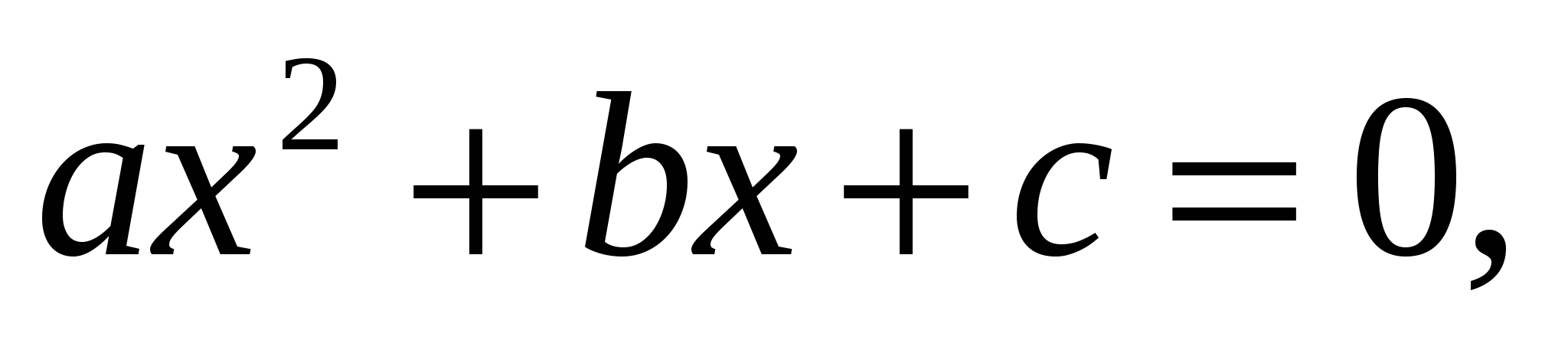 
где х – переменная, a,b,c – некоторые числа, причем а ≠ 0.
Числа a,b,c – коэффициенты квадратного уравнения.
Число а называют первым коэффициентом,
число b – вторым коэффициентом,
число с – свободным членом.
Н,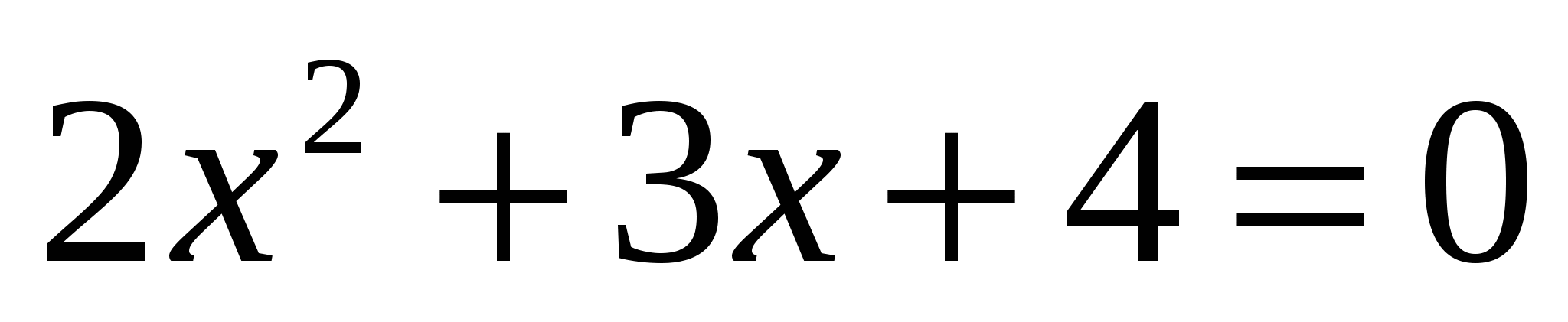 
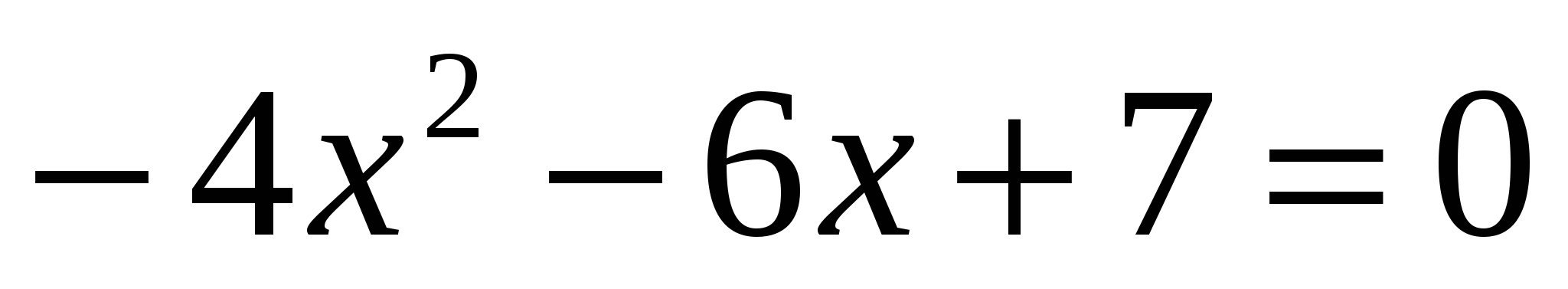
а = 2; b = 3; с = 4. а = — 4; b = — 6; с = 7.
Алгоритм решения квадратных уравнений:
вычислить дискриминант (D = b² — 4ac
и сравнить его с нулем;
а) если D > 0, то уравнение имеет два корня:
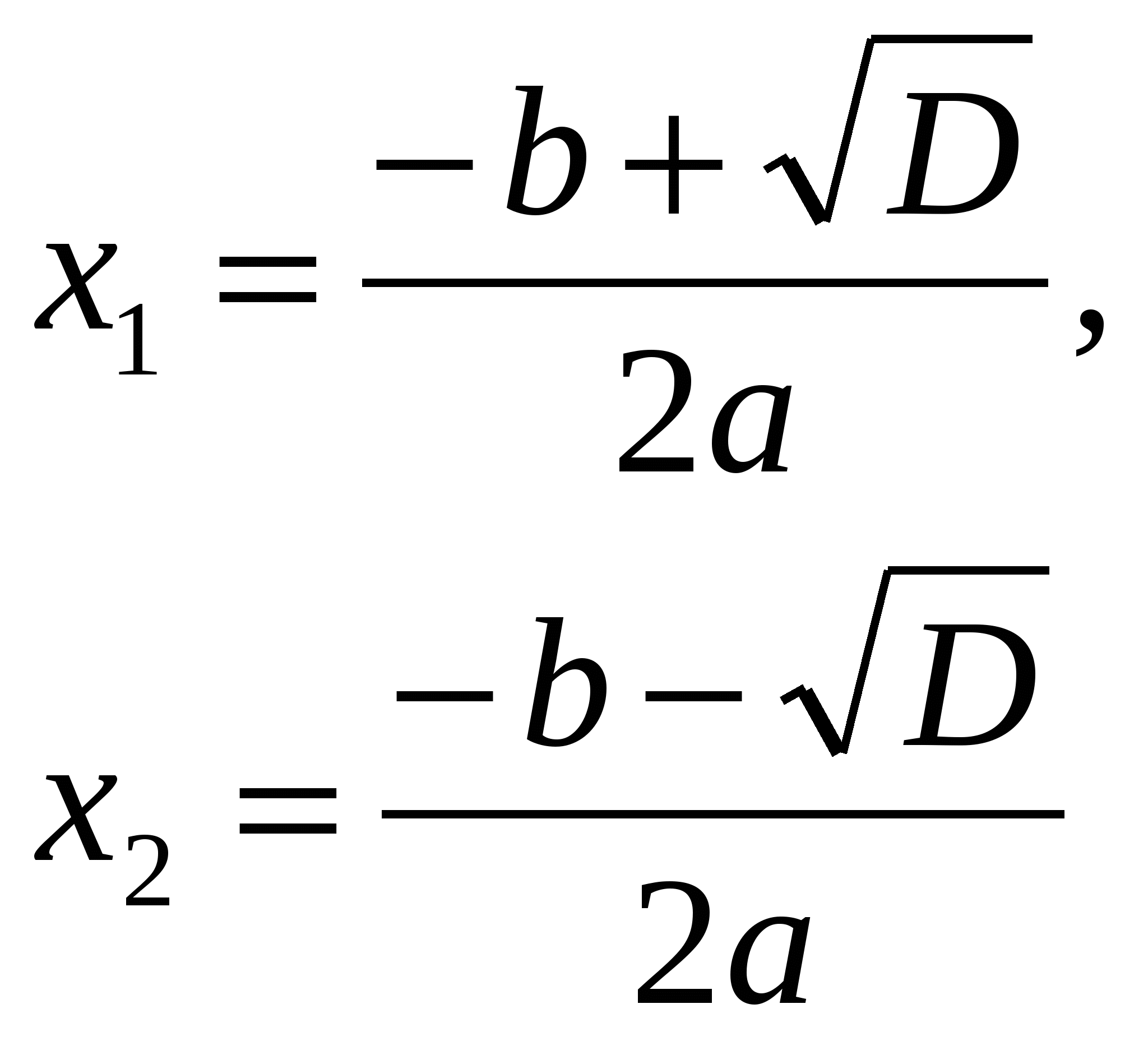
б) если D = 0, то уравнение имеет один корень: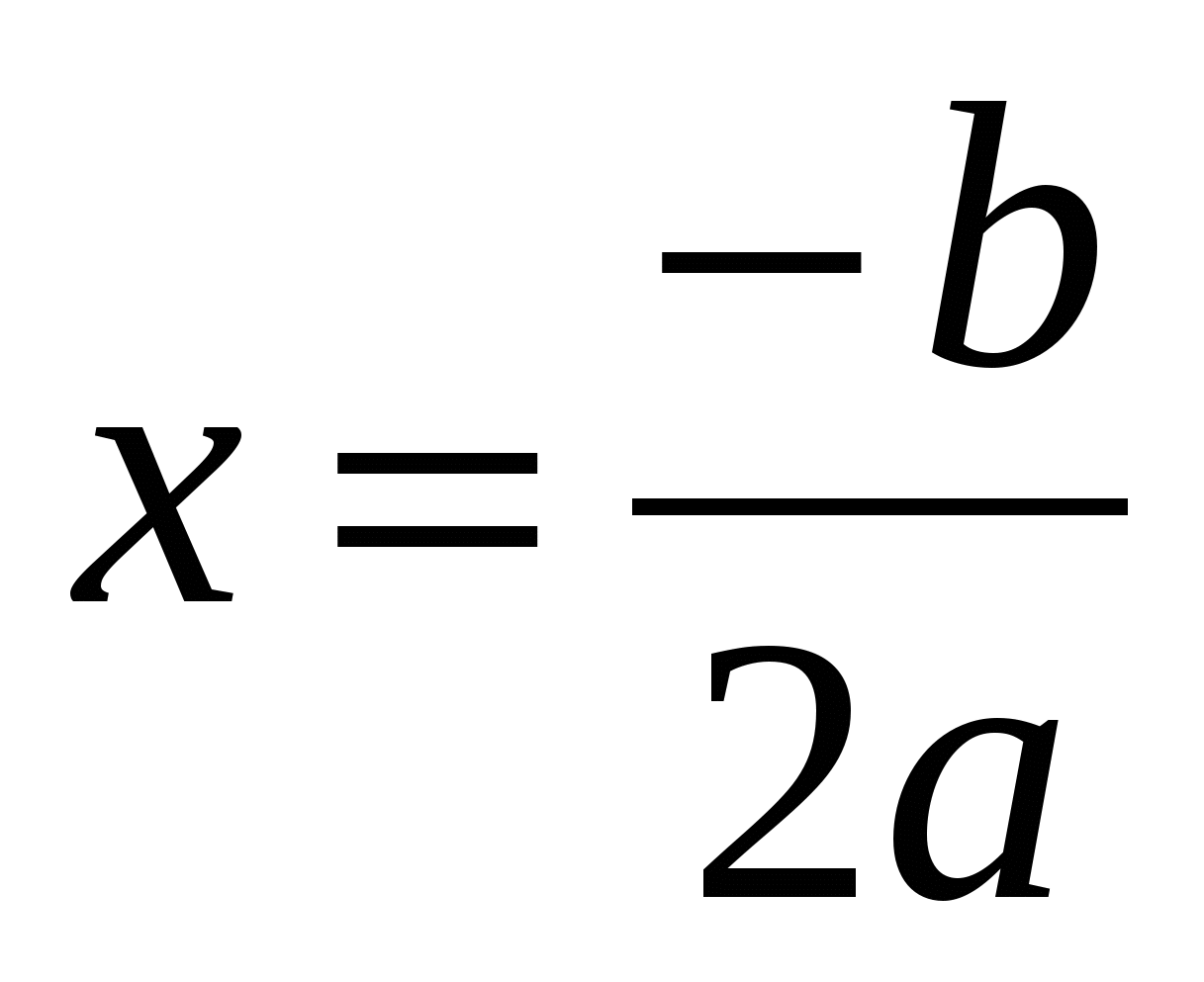 
в) если D < 0, то уравнение не имеет корней.
Решить уравнение:
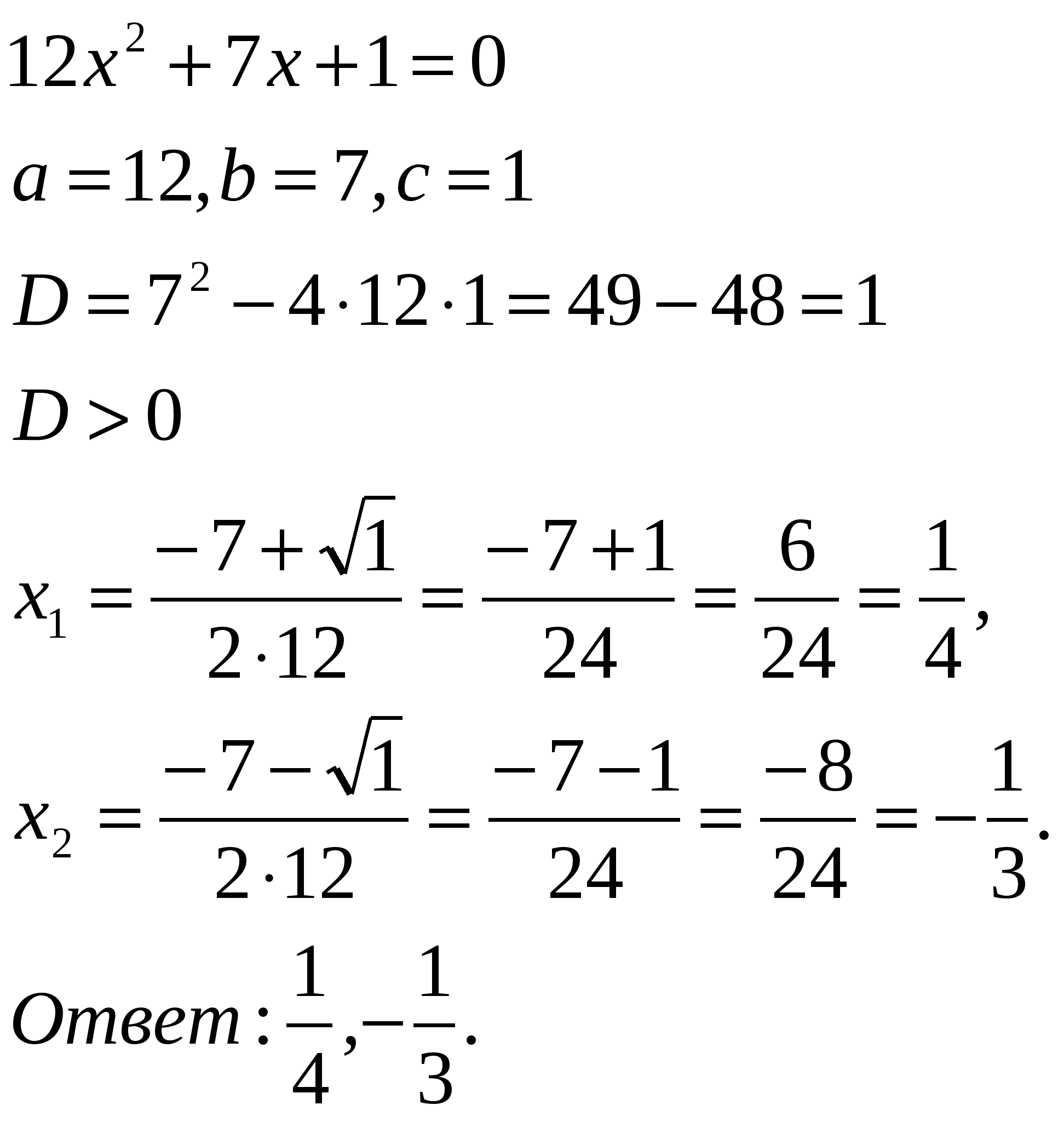
Решить уравнение:
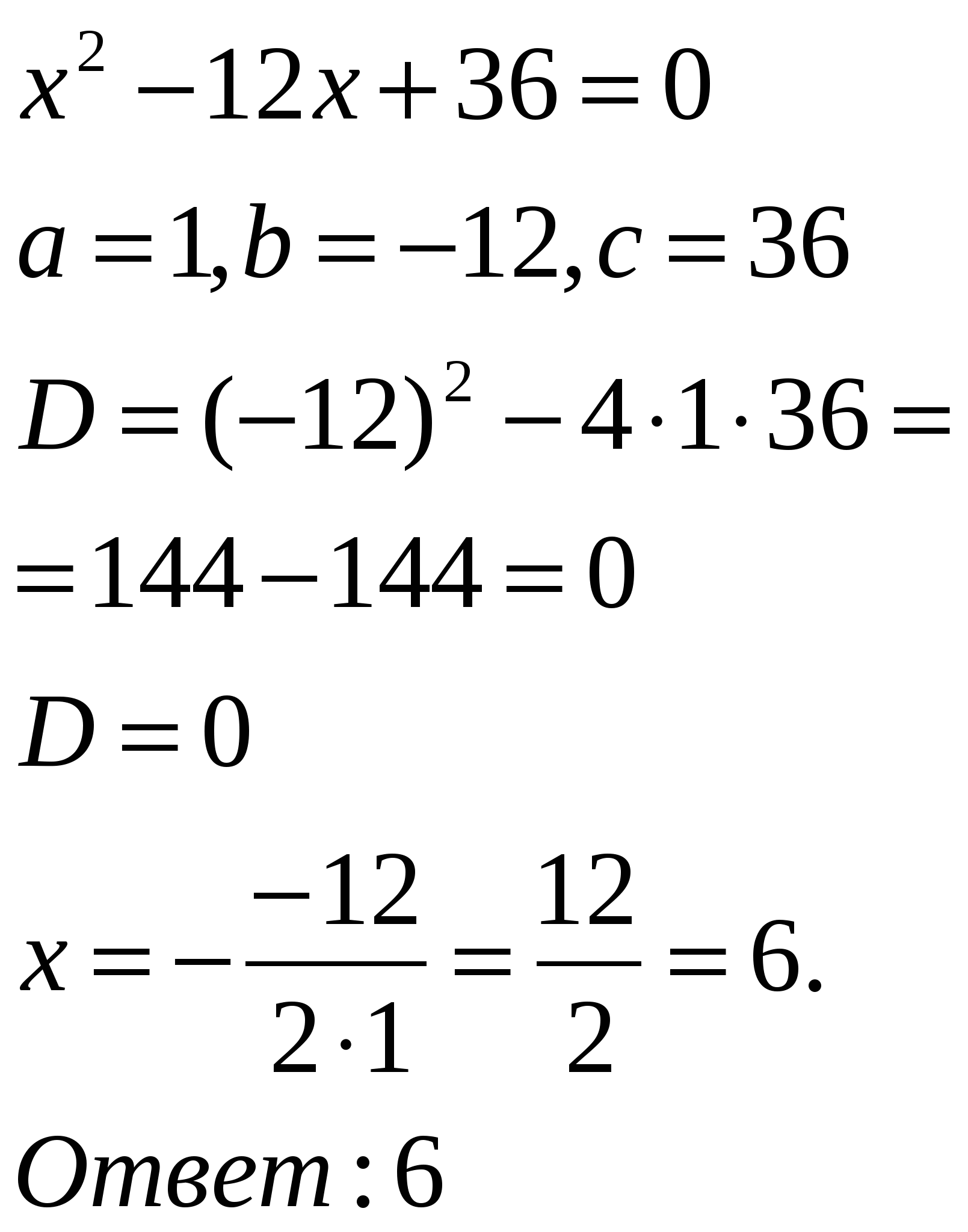
Решить уравнение:
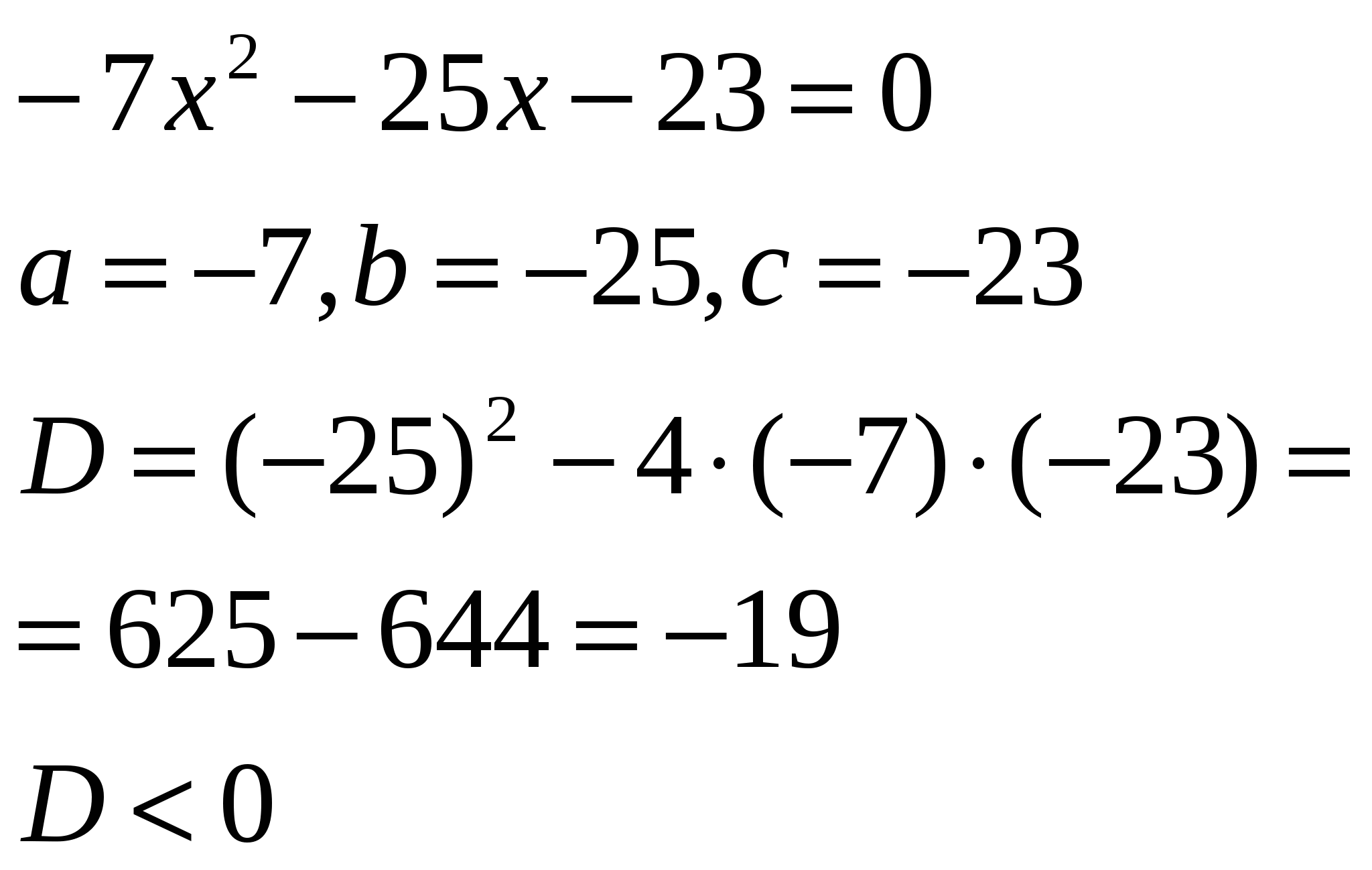
Уравнение не имеет корней.
Ответ: нет корней.
infourok.ru
Квадратное уравнение с чётным вторым коэффициентом
Если в квадратном уравнении ax2 + bx + c = 0 второй коэффициент b является чётным, то решение этого уравнения можно немного упростить. Дискриминант для такого уравнения можно вычислить по формуле D1 = k2 − ac, а корни по формулам и .
Примеры
Решим квадратное уравнение x2 + 6x − 16 = 0. В нём второй коэффициент является чётным. Чтобы воспользоваться формулами для чётного коэффициента, нужно сначала узнать чему равна переменная k.
Любое четное число n можно представить в виде произведения числа 2 и числа
n = 2k
Например, число 10 можно представить как 2 × 5.
10 = 2 × 5
В этом произведении k = 5.
Число 12 можно представить как 2 × 6.
12 = 2 × 6
В этом произведении k = 6.
Число −14 можно представить как 2 × (−7)
В этом произведении k = −7.
Как видим, сомножитель 2 не меняется. Меняется только сомножитель k.
В уравнении x2 + 6x − 16 = 0 вторым коэффициентом является число 6. Это число можно представить как 2 × 3. В этом произведении k = 3. Теперь можно воспользоваться формулами для чётного коэффициента.
Найдем дискриминант по формуле D1 = k2 − ac
D1 = k2 − ac = 32 − 1 × (−16) = 9 + 16 = 25
Теперь вычислим корни по формулам: и .
Значит корнями уравнения x2 + 6x − 16 = 0 являются числа 2 и −8.
В отличие от стандартной формулы для вычисления дискриминанта (D=b2 − 4ac), в формуле D1 = k2 − ac не нужно выполнять умножение числа 4 на ac.
И в отличие от формул и формулы и не содержат в знаменателе множитель 2 что опять же освобождает нас от дополнительных вычислений.
Пример 2. Решить квадратное уравнение 5x2 − 6x + 1=0
Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−3). То есть k = −3. Найдём дискриминант по формуле D1 = k2 − ac
D1 = k2 − ac = (−3)2 − 5 × 1 = 9 − 5 = 4
Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и
Пример 3. Решить квадратное уравнение x2 − 10x − 24 = 0
Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−5). То есть k = −5. Найдём дискриминант по формуле D1 = k2 − ac
D1 = k2 − ac = (−5)2 − 1 × (−24) = 25 + 24 = 49
Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и
Обычно для определения числа k поступают так: делят второй коэффициент на 2.
Действительно, если второй коэффициент b является чётным числом, то его можно представить как b = 2k. Чтобы из этого равенства выразить сомножитель k, нужно произведение b разделить на сомножитель 2
Например, в предыдущем примере для определения числа k можно было просто разделить второй коэффициент −10 на 2
Пример 5. Решить квадратное уравнение
Коэффициент b равен . Это выражение состоит из множителя 2 и выражения . То есть оно уже представлено в виде 2k. Получается, что
Найдём дискриминант по формуле D1 = k2 − ac
Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и
При вычислении корня уравнения получилась дробь, в которой содержится квадратный корень из числа 2. Квадратный корень из числа 2 извлекается только приближённо. Если выполнить это приближённое извлечение, а затем сложить результат с 2, и затем разделить числитель на знаменатель, то получится не очень красивый ответ.
В таких случаях ответ записывают, не выполняя приближённых вычислений. В нашем случае первый корень уравнения будет равен .
Вычислим второй корень уравнения:
Вывод формул
Давайте наглядно увидим, как появились формулы для вычисления корней квадратного уравнения с чётным вторым коэффициентом.
Рассмотрим квадратное уравнение ax2 + bx + c = 0. Допустим, что коэффициент b является чётным числом. Тогда его можно обозначить как 2k
b = 2k
Заменим в уравнении ax2 + bx + c = 0 коэффициент b на выражение 2k
ax2 + 2kx + c = 0
Теперь вычислим дискриминант по ранее известной формуле:
D = b2 − 4ac = (2k)2 − 4ac = 4k2 − 4ac
Вынесем в получившемся выражении за скобки общий множитель 4
D = b2 − 4ac = (2k)2 − 4ac =
4k2 − 4ac = 4(k2 − ac)Что можно сказать о получившемся дискриминанте? При чётном втором коэффициенте он состоит из множителя 4 и выражения k2 − ac.
В выражении 4(k2 − ac) множитель 4 постоянен. Значит знак дискриминанта зависит от выражения k2 − ac. Если это выражение меньше нуля, то и D будет меньше нуля. Если это выражение больше нуля, то и D будет больше нуля. Если это выражение равно нулю, то и D будет равно нулю.
То есть выражение k2 − ac это различитель — дискриминант. Такой дискриминант принято обозначать буквой D1
D1 = k2 − ac
Теперь посмотрим как выводятся формулы и .
В нашем уравнении ax2 + bx + c = 0 коэффициент
Но ранее было сказано, что выражение k2 − ac обозначается через D1. Тогда в наших преобразованиях следует сделать и эту замену:
Теперь вычислим квадратный корень, расположенный в числителе. Это квадратный корень из произведения — он равен произведению корней. Остальное перепишем без изменений:
Теперь в получившемся выражении вынесем за скобки общий множитель 2
Сократим получившуюся дробь на 2
Аналогично вывóдится формула для вычисления второго корня:
Задания для самостоятельного решения
Задание 1. Решить уравнение:
Решение:
Ответ: 1; 0,6
Задание 2. Решить уравнение:
Решение:
Ответ:Задание 3. Решить уравнение:
Решение:
Ответ: 1; −1,4
Задание 4. Решить уравнение:
Решение:
Ответ:Задание 5. Решить уравнение:
Решение:
Ответ:Задание 6. Решить уравнение:
Решение:
Ответ:Задание 7. Решить уравнение:
Решение:
Ответ:Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
spacemath.xyz
| Техническая информация | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Квадратные уравнения и неравенства. Алгоритмы решения квадратного уравнения и неравенства. Формулы дискриминанта и корней квадратного уравнения. Теорема Виета. Примерно 7 класс (13 лет) Поделиться:
| |||||||||||||||
dpva.ru
=0 D Нет решений | Приведенное квадратное уравнение =0 Теорема Виета: | =0 D=0 | неполное квадратное уравнение при с=0 =0 или = | Полное квадратное уравнение =0 a,b-коэффициенты с- свободный член корни при D>0 = | неполное квадратное уравнение при b=0 =0
| =0 если b-четное,то = | =0 если a+b+c=0,то =1 = | =0 если a-b+c=0,то = -1 = |
nsportal.ru
Решение квадратного уравнения в Excel
Для решения квадратного уравнения необходимо знать формулу и алгоритм нахождения квадратов уравнения
Шаг 1. Организация таблицы
На первом этапе мы организуем таблицу для ввода данных коэффициентов a,b и c.
- a называют первым или старшим коэффициентом,
- b называют вторым или коэффициентом при x,
- c называют свободным членом.
Шаг 2. Проверка равенства Дискриминанта.
Для того, чтобы вычислить корни уравнения второй степени, необходимо определить значение Дискриминанта.
Формула дискриминанта
D = b2 — 4ac
Вычисление корней уравнения второй степени происходит по формулам при условии величины Дискриминанта
| Условие | D > 0 | D = 0 | D < 0 |
| Число действительных корней | корней два | корень один | Нет решения |
| Формула | X1,2=(- b ±√ (b2 — 4 * a * c)) / (2 * a) | X1=X2=-b/(2*a) |
Шаг 3. Вычисляем корни уравнения.
После определения значения Дискриминанта используем выше приведенные формулы для нахождения корней.
Находим первый корень
Находим второй корень. Формула будет отличаться только в одном знаке.
Итог: с помощью Excel можем создать единожды таблицу и формулы для решения квадратного уравнения (уравнения второй степени) и быстро их решать.
Связанные Калькуляторы
wpcalc.com
Корни квадратного уравнения
Основные формулы
Рассмотрим квадратное уравнение:
(1) .
Корни квадратного уравнения (1) определяются по формулам:
; .
Эти формулы можно объединить так:
.
Когда корни квадратного уравнения известны, то многочлен второй степени можно представить в виде произведения сомножителей (разложить на множители):
.
Далее считаем, что – действительные числа.
Рассмотрим дискриминант квадратного уравнения:
.
Если дискриминант положителен, , то квадратное уравнение (1) имеет два различных действительных корня:
; .
Тогда разложение квадратного трехчлена на множители имеет вид:
.
Если дискриминант равен нулю, , то квадратное уравнение (1) имеет два кратных (равных) действительных корня:
.
Разложение на множители:
.
Если дискриминант отрицателен, , то квадратное уравнение (1) имеет два комплексно сопряженных корня:
;
.
Здесь – мнимая единица, ;
и – действительная и мнимая части корней:
; .
Тогда
.
Графическая интерпретация
Если построить график функции
,
который является параболой, то точки пересечения графика с осью будут корнями уравнения
.
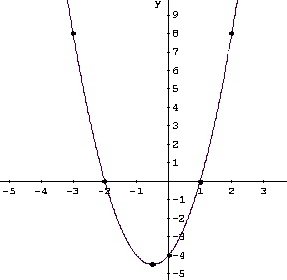
При , график пересекает ось абсцисс (ось ) в двух точках (см. рисунок ⇓).
При , график касается оси абсцисс в одной точке (см. рисунок ⇓).
При , график не пересекает ось абсцисс (см. рисунок ⇓).
Полезные формулы, связанные с квадратным уравнением
(f.1) ;
(f.2) ;
(f.3) .
Вывод формулы для корней квадратного уравнения
Выполняем преобразования и применяем формулы (f.1) и (f.3):
,
где
; .
Итак, мы получили формулу для многочлена второй степени в виде:
.
Отсюда видно, что уравнение
выполняется при
и .
То есть и являются корнями квадратного уравнения
.
Примеры определения корней квадратного уравнения
Пример 1
Найти корни квадратного уравнения:
(1.1) .
Решение
Запишем квадратное уравнение в общем виде:
.
Сравнивая с нашим уравнением (1.1), находим значения коэффициентов:
.
Находим дискриминант:
.
Поскольку дискриминант положителен, , то уравнение имеет два действительных корня:
;
;
.
Отсюда получаем разложение квадратного трехчлена на множители:
.
График функции y = 2x 2 + 7x + 3 пересекает ось абсцисс в двух точках.
Построим график функции
.
График этой функции является параболой. Она пересевает ось абсцисс (ось ) в двух точках:
и .
Эти точки являются корнями исходного уравнения (1.1).
Ответ
;
;
.
Пример 2
Найти корни квадратного уравнения:
(2.1) .
Решение
Запишем квадратное уравнение в общем виде:
.
Сравнивая с исходным уравнением (2.1), находим значения коэффициентов:
.
Находим дискриминант:
.
Поскольку дискриминант равен нулю, , то уравнение имеет два кратных (равных) корня:
;
.
Тогда разложение трехчлена на множители имеет вид:
.
График функции y = x 2 – 4x + 4 касается оси абсцисс в одной точке.
Построим график функции
.
График этой функции является параболой. Она касается оси абсцисс (ось ) в одной точке:
.
Эта точка является корнем исходного уравнения (2.1). Поскольку этот корень входит в разложение на множители два раза:
,
то такой корень принято называть кратным. То есть считают, что имеется два равных корня:
.
Ответ
;
.
Пример 3
Найти корни квадратного уравнения:
(3.1) .
Решение
Запишем квадратное уравнение в общем виде:
(1) .
Перепишем исходное уравнение (3.1):
.
Сравнивая с (1), находим значения коэффициентов:
.
Находим дискриминант:
.
Дискриминант отрицателен, . Поэтому действительных корней нет.
Можно найти комплексные корни:
;
;
.
Тогда
.
График функции не пересекает ось абсцисс. Действительных корней нет.
Построим график функции
.
График этой функции является параболой. Она не пересекает ось абсцисс (ось ). Поэтому действительных корней нет.
Ответ
Действительных корней нет. Корни комплексные:
;
;
.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Квадратные уравнения. Решение квадратных уравнений :: SYL.ru
Эта тема поначалу может показаться сложной из-за множества не самых простых формул. Мало того что сами квадратные уравнения имеют длинные записи, еще и корни находятся через дискриминант. Всего получается три новые формулы. Не очень просто запомнить. Это удается только после частого решения таких уравнений. Тогда все формулы будут вспоминаться сами собой.
Общий вид квадратного уравнения
Здесь предложена их явная запись, когда самая большая степень записана первой, и дальше — по убыванию. Часто бывают ситуации, когда слагаемые стоят вразнобой. Тогда лучше переписать уравнение в порядке убывания степени у переменной.
Введем обозначения. Они представлены в таблице ниже.
| Обозначение величины | Ее название |
| а, в, с | коэффициенты, которые являются произвольными числами |
| х | переменная |
| Д | дискриминант |
| х1, х2 | корни уравнения |
Если принять эти обозначения, все квадратные уравнения сводятся к следующей записи.
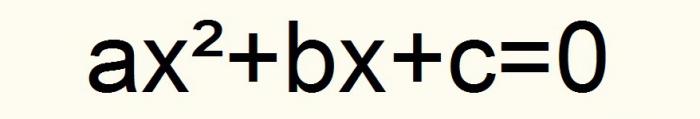
Причем коэффициент а ≠ 0. Пусть эта формула будет обозначена номером один.
Когда уравнение задано, то непонятно, сколько корней будет в ответе. Потому что всегда возможен один из трех вариантов:
- в решении будет два корня;
- ответом будет одно число;
- корней у уравнения не будет совсем.
И пока решение не доведено до конца, сложно понять, какой из вариантов выпадет в конкретном случае.
Виды записей квадратных уравнений
В задачах могут встречаться их разные записи. Не всегда они будут выглядеть как общая формула квадратного уравнения. Иногда в ней будет не хватать некоторых слагаемых. То что было записано выше — это полное уравнение. Если в нем убрать второе или третье слагаемое, то получится нечто другое. Эти записи тоже называются квадратными уравнениями, только неполными.
Причем исчезнуть могут только слагаемые у которых коэффициенты «в» и «с». Число «а» не может быть равно нулю ни при каких условиях. Потому что в этом случае формула превращается в линейное уравнение. Формулы для неполного вида уравнений будут такими:
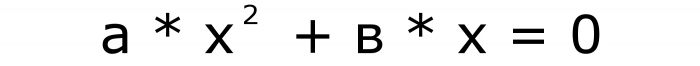
и
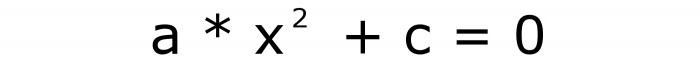
Итак, видов всего два, кроме полных, есть еще и неполные квадратные уравнения. Пусть первая формула будет иметь номер два, а вторая — три.
Дискриминант и зависимость количества корней от его значения
Это число нужно знать для того, чтобы вычислить корни уравнения. Оно может быть посчитано всегда, какой бы ни была формула квадратного уравнения. Для того чтобы вычислить дискриминант, нужно воспользоваться равенством, записанным ниже, которое будет иметь номер четыре.
После подстановки в эту формулу значений коэффициентов, можно получить числа с разными знаками. Если ответ положительный, то ответом уравнения будут два различных корня. При отрицательном числе корни квадратного уравнения будут отсутствовать. В случае его равенства нулю ответ будет один.
Как решается квадратное уравнение полного вида?
По сути, рассмотрение этого вопроса уже началось. Потому что сначала нужно найти дискриминант. После того как выяснено, что имеются корни квадратного уравнения, и известно их число, нужно воспользоваться формулами для переменных. Если корней два, то нужно применить такую формулу.
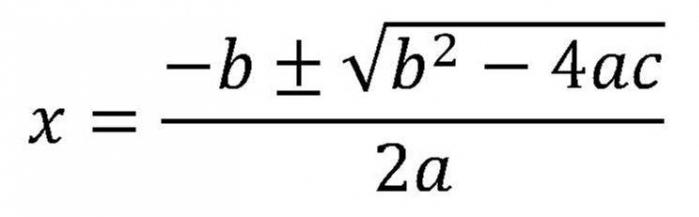
Поскольку в ней стоит знак «±», то значений будет два. Выражение под знаком квадратного корня — это дискриминант. Поэтому формулу можно переписать по-другому.
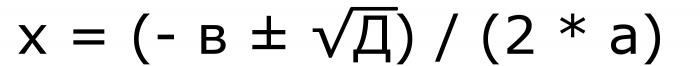
Формула номер пять. Из этой же записи видно, что если дискриминант равен нулю, то оба корня примут одинаковые значения.
Если решение квадратных уравнений еще не отработано, то лучше до того, как применять формулы дискриминанта и переменной, записать значения всех коэффициентов. Позже этот момент не будет вызывать трудностей. Но в самом начале бывает путаница.
Как решается квадратное уравнение неполного вида?
Здесь все гораздо проще. Даже нет необходимости в дополнительных формулах. И не понадобятся те, что уже были записаны для дискриминанта и неизвестной.
Сначала рассмотрим неполное уравнение под номером два. В этом равенстве полагается вынести неизвестную величину за скобку и решить линейное уравнение, которое останется в скобках. В ответе будет два корня. Первый — обязательно равен нулю, потому что имеется множитель, состоящий из самой переменной. Второй получится при решении линейного уравнения.
Неполное уравнение под номером три решается переносом числа из левой части равенства в правую. Потом нужно разделить на коэффициент, стоящий перед неизвестной. Останется только извлечь квадратный корень и не забыть записать его два раза с противоположными знаками.
Полезные советы
Далее записаны некоторые действия, помогащие научиться решать всевозможные виды равенств, которые превращаются в квадратные уравнения. Они будут способствовать тому, что ученик сможет избежать ошибок по невнимательности. Эти недочеты бывают причиной плохих оценок при изучении обширной темы «Квадратные уравнения (8 класс)». Впоследствии эти действия не нужно будет постоянно выполнять. Потому что появится устойчивый навык.
- Сначала нужно записать уравнение в стандартном виде. То есть сначала слагаемое с самой большой степенью переменной, а потом — без степени и последним — просто число.
- Если перед коэффициентом «а» появляется минус, то он может усложнить работу для начинающего изучать квадратные уравнения. От него лучше избавиться. Для этой цели все равенство нужно умножить на «-1». Это значит, что у всех слагаемых изменится знак на противоположный.
- Таким же образом рекомендуется избавляться от дробей. Просто умножить уравнение на соответствующий множитель, чтобы знаменатели сократились.
Примеры
Требуется решить следующие квадратные уравнения:
х2 − 7х = 0;
5х2 — 30 = 0;
15 − 2х − х2 = 0;
х2 + 8 + 3х = 0;
12х + х2 + 36 = 0;
(х+1)2 + х + 1 = (х+1)(х+2).
Первое уравнение: х2 − 7х = 0. Оно неполное, поэтому решается так, как было описано для формулы под номером два.
После вынесения за скобки получается: х (х — 7) = 0.
Первый корень принимает значение: х1 = 0. Второй будет найден из линейного уравнения: х — 7 = 0. Легко заметить, что х2 = 7.
Второе уравнение: 5х2 + 30 = 0. Снова неполное. Только решается оно так, как описано для третьей формулы.
После перенесения 30 в правую часть равенства: 5х2 = 30. Теперь нужно выполнить деление на 5. Получается: х2 = 6. Ответами будут числа: х1 = √6, х2 = — √6.
Третье уравнение: 15 − 2х − х2 = 0. Здесь и далее решение квадратных уравнений будет начинаться с их переписывания в стандартный вид: − х2 − 2х + 15 = 0. Теперь пришло время воспользоваться вторым полезным советом и умножить все на минус единицу. Получается х2 + 2х — 15 = 0. По четвертой формуле нужно вычислить дискриминант: Д = 22 — 4 * (- 15) = 4 + 60 = 64. Он представляет собой положительное число. Из того, что сказано выше, получается, что уравнение имеет два корня. Их нужно вычислить по пятой формуле. По ней получается, что х = (-2 ± √64) / 2 = (-2 ± 8) / 2. Тогда х1 = 3, х2 = — 5.
Четвертое уравнение х2 + 8 + 3х = 0 преобразуется в такое: х2 + 3х + 8 = 0. Его дискриминант равен такому значению: -23. Поскольку это число отрицательное, то ответом к этому заданию будет следующая запись: «Корней нет».
Пятое уравнение 12х + х2 + 36 = 0 следует переписать так: х2 + 12х + 36 = 0. После применения формулы для дискриминанта получается число ноль. Это означает, что у него будет один корень, а именно: х = -12/ (2 * 1) = -6.
Шестое уравнение (х+1)2 + х + 1 = (х+1)(х+2) требует провести преобразования, которые заключаются в том, что нужно привести подобные слагаемые, до того раскрыв скобки. На месте первой окажется такое выражение: х2 + 2х + 1. После равенства появится эта запись: х2 + 3х + 2. После того как подобные слагаемые будут сосчитаны, уравнение примет вид: х2 — х = 0. Оно превратилось в неполное. Подобное ему уже рассматривалось чуть выше. Корнями этого будут числа 0 и 1.
www.syl.ru