Функция дробная часть числа | Алгебра
Определение
Дробной частью действительного числа называется разность между этим числом и его целой частью.
Дробную часть числа x обозначают {x}.
По определению, {x}=x-[x].
Для любого x∈R 0≤{x}<1.
В частности, если n — целое число (n∈Ζ), {n}=0.
Примеры.
Вычислить дробную часть {x} числа x, если x принимает значения:
9,43; 0,3; -0,56; 12 3/7; 2/9; -4/15; 20; -11.
Решение:
{9,43}=9,43-[9,43]=9,43-9=0,43;
{0,3}=0,3-[0,3]=0,3-0=0,3;
{-0,56}=-0,56-[-0,56]=-0,56-(-1)=-0,56+1=0,44.
{20}=0;
{-11}=0.
Определение
Функцию, ставящую в соответствие каждому значению x дробную часть этого числа — число {x}, называют функцией дробной части числа и обозначают y={x}.
Функция дробная часть числа определена на множестве действительных чисел: x∈R.
Область значений функции — полуинтервал y∈[0;1).
Утверждение.
Если k∈Ζ, то {x+k}={x}.
Доказательство:
По определению дробной части числа {x+k}=x+k-[x+k].
По свойству целой части числа [x+k]=[x]+k.
Следовательно, {x+k}=x+k-[x+k]=x+k-[x]-k=x-[x]={x}.
Что и требовалось доказать.
Из утверждения следует, что на каждом промежутке вида [k; k+1), где k∈Z, график функции y={x} имеет одинаковый вид.
При k=0 x∈ [0; 1), [x]=0.
Отсюда y={x}=x-[x]=x-0=x.
То есть при x∈ [0; 1) y=x.
График функции y={x}
Стрелки на графике показывают, что правые концы отрезков не принадлежат графику.
Другой вариант показать, что левые концы отрезков принадлежат графику, а правые — не принадлежат, изобразить их, соответственно, закрашенными и выколотыми точками.
Поскольку {x+k}= {x}, функция дробная часть числа является периодической. Её период T=k — любое целое число, отличное от нуля.
Наименьший положительный период (главный период) T=1.
Целая часть — Википедия. Что такое Целая часть
 График функции «пол» (целая часть числа)
График функции «пол» (целая часть числа) 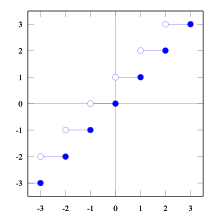 График функции «потолок»
График функции «потолок»В математике, целая часть вещественного числа x{\displaystyle x} — округление x{\displaystyle x} до ближайшего целого в меньшую сторону. Целая часть числа также называется антье (фр. entier), или пол (англ. floor). Наряду с полом существует парная функция — потолок (англ. ceiling) — округление x{\displaystyle x} до ближайшего целого в большую сторону.
Обозначения и примеры
Впервые квадратные скобки ([x]{\displaystyle [x]}) для обозначения целой части числа x{\displaystyle x} использовал Гаусс в 1808 году в своём доказательстве закона квадратичной взаимности
В современной математике используются оба обозначения[6], [x]{\displaystyle [x]} и ⌊x⌋{\displaystyle \lfloor x\rfloor }, однако существует тенденция перехода к терминологии и обозначениям Айверсона. Одна из причин этого — потенциальная неоднозначность понятия «целая часть числа»[5]. Например, целая часть числа 2,7 равна 2, но возможны два мнения на то, как определить целую часть числа −2,7. В соответствии с данным в этой статье определением [x]≡⌊x⌋=−3{\displaystyle [x]\equiv \lfloor x\rfloor =-3}, однако в некоторых калькуляторах имеется функция целой части числа INT, для отрицательных чисел определяемая как INT(-x) = -INT(x), так что INT(-2,7) = −2. В терминологии Айверсона отсутствуют возможные неоднозначности:
- ⌊2,7⌋=2,⌊−2,7⌋=−3,⌈2,7⌉=3,⌈−2,7⌉=−2{\displaystyle {\begin{matrix}\lfloor 2{,}7\rfloor =2,&\lfloor -2{,}7\rfloor =-3,\\\lceil 2{,}7\rceil =3,&\lceil -2{,}7\rceil =-2\end{matrix}}}
Определения
Функция пол ⌊⋅⌋:x↦⌊x⌋{\displaystyle \lfloor \cdot \rfloor \colon x\mapsto \lfloor x\rfloor } определяется как наибольшее целое, меньшее или равное x{\displaystyle x}:
- ⌊x⌋=max{n∈Z∣n⩽x}{\displaystyle \lfloor x\rfloor =\max\{n\in \mathbb {Z} \mid n\leqslant x\}}
Функция потолок ⌈⋅⌉:x↦⌈x⌉{\displaystyle \lceil \,\cdot \,\rceil \colon x\mapsto \lceil x\rceil } определяется как наименьшее целое, большее или равное x{\displaystyle x}:
- ⌈x⌉=min{n∈Z∣n⩾x}{\displaystyle \lceil x\rceil =\min\{n\in \mathbb {Z} \mid n\geqslant x\}}
Эти определения эквивалентны следующим неравенствам (где n — целое число):[7]
- ⌊x⌋=n⟺n⩽x<n+1⟺x−1<n⩽x⌈x⌉=n⟺n−1<x⩽n⟺x⩽n<x+1.{\displaystyle {\begin{aligned}\lfloor x\rfloor =n&\Longleftrightarrow &n\leqslant x<n+1&\Longleftrightarrow &x-1<n\leqslant x\\\lceil x\rceil =n&\Longleftrightarrow &n-1<x\leqslant n&\Longleftrightarrow &x\leqslant n<x+1.\end{aligned}}}
Свойства
В формулах, записанных ниже, буквами x{\displaystyle x} и y{\displaystyle y} обозначены вещественные числа, а буквами n{\displaystyle n} и m{\displaystyle m} — целые.
Пол и потолок как функции вещественной переменной
Функции пол и потолок отображают множество вещественных чисел в множество целых чисел:
- ⌊⋅⌋:R→Z,⌈⋅⌉:R→Z,{\displaystyle \lfloor \,\cdot \,\rfloor \colon \mathbb {R} \to \mathbb {Z} ,\quad \lceil \,\cdot \,\rceil \colon \mathbb {R} \to \mathbb {Z} ,\quad }
Пол и потолок — кусочно-постоянные функции.
Функции пол и потолок разрывны: во всех целочисленных точках терпят разрывы первого рода со скачком, равным единице.
При этом функция пол является:
Функция потолок является:
Связь функций пол и потолок
Для произвольного числа x{\displaystyle x} верно неравенство[8]
- ⌊x⌋⩽x⩽⌈x⌉{\displaystyle \lfloor x\rfloor \leqslant x\leqslant \lceil x\rceil }
Для целого x{\displaystyle x} пол и потолок совпадают:
- ⌊x⌋=x⟺x∈Z⟺⌈x⌉=x{\displaystyle \lfloor x\rfloor =x\quad \Longleftrightarrow \quad x\in \mathbb {Z} \quad \Longleftrightarrow \quad \lceil x\rceil =x}
Если x{\displaystyle x} — не целое, то значение функции потолок на единицу больше значения функции пол:
- ⌈x⌉−⌊x⌋={1,x∉Z0,x∈Z{\displaystyle \lceil x\rceil -\lfloor x\rfloor ={\begin{cases}1,&x\notin \mathbb {Z} \\0,&x\in \mathbb {Z} \end{cases}}}
Функции пол и потолок являются отражениями друг друга от обеих осей:
- ⌊−x⌋=−⌈x⌉,⌈−x⌉=−⌊x⌋{\displaystyle \lfloor -x\rfloor =-\lceil x\rceil ,\quad \lceil -x\rceil =-\lfloor x\rfloor }
Пол/потолок: неравенства
Любое неравенство между вещественным и целым числами равносильно неравенству с полом и потолком между целыми числами [7]:
- n⩽x⟺n⩽⌊x⌋x⩽n⟺⌈x⌉⩽nn<x⟺n<⌈x⌉x<n⟺⌊x⌋<n{\displaystyle {\begin{matrix}n\leqslant x&\Longleftrightarrow &n\leqslant \lfloor x\rfloor &\qquad x\leqslant n&\Longleftrightarrow &\lceil x\rceil \leqslant n\\n<x&\Longleftrightarrow &n<\lceil x\rceil &\qquad x<n&\Longleftrightarrow &\lfloor x\rfloor <n\end{matrix}}}
Два верхних неравенства являются непосредственными следствиями определений пола и потолка, а два нижние — обращение верхних от противного.
Функции пол/потолок являются монотонно возрастающими функциями:
- x⩽y⇒⌊x⌋⩽⌊y⌋,x⩽y⇒⌈x⌉⩽⌈y⌉{\displaystyle x\leqslant y\Rightarrow \lfloor x\rfloor \leqslant \lfloor y\rfloor ,\quad x\leqslant y\Rightarrow \lceil x\rceil \leqslant \lceil y\rceil }
Пол/потолок: сложение
Целочисленное слагаемое можно вносить/выносить за скобки пола/потолка [9]:
- ⌊x+n⌋=⌊x⌋+n,⌈x+n⌉=⌈x⌉+n{\displaystyle \lfloor x+n\rfloor =\lfloor x\rfloor +n,\quad \lceil x+n\rceil =\lceil x\rceil +n}
Предыдущие равенства, вообще говоря, не выполняются, если оба слагаемых — вещественные числа. Однако и в этом случае справедливы неравенства:
- ⌊x⌋+⌊y⌋⩽⌊x+y⌋⩽⌊x⌋+⌊y⌋+1,⌈x⌉+⌈y⌉−1⩽⌈x+y⌉⩽⌈x⌉+⌈y⌉{\displaystyle \lfloor x\rfloor +\lfloor y\rfloor \leqslant \lfloor x+y\rfloor \leqslant \lfloor x\rfloor +\lfloor y\rfloor +1,\quad \lceil x\rceil +\lceil y\rceil -1\leqslant \lceil x+y\rceil \leqslant \lceil x\rceil +\lceil y\rceil }
Пол/потолок под знаком функции
Имеет место следующее предложение:[10]
Пусть f(x){\displaystyle f(x)} — непрерывная монотонно возрастающая функция, определенная на некотором промежутке, обладающая свойством:
- f(x)∈Z⇒x∈Z{\displaystyle f(x)\in \mathbb {Z} \Rightarrow x\in \mathbb {Z} }
Тогда
- ⌊f(x)⌋=⌊f(⌊x⌋)⌋,⌈f(x)⌉=⌈f(⌈x⌉)⌉{\displaystyle \lfloor f(x)\rfloor =\lfloor f(\lfloor x\rfloor )\rfloor ,\quad \lceil f(x)\rceil =\lceil f(\lceil x\rceil )\rceil }
всякий раз, когда определены f(x),f(⌊x⌋),f(⌈x⌉){\displaystyle f(x),f(\lfloor x\rfloor ),f(\lceil x\rceil )}.
В частности,
- ⌊x+mn⌋=⌊⌊x⌋+mn⌋,⌈x+mn⌉=⌈⌈x⌉+mn⌉{\displaystyle \left\lfloor {\frac {x+m}{n}}\right\rfloor =\left\lfloor {\frac {\left\lfloor x\right\rfloor +m}{n}}\right\rfloor ,\quad \left\lceil {\frac {x+m}{n}}\right\rceil =\left\lceil {\frac {\left\lceil x\right\rceil +m}{n}}\right\rceil }
если m{\displaystyle m} и n{\displaystyle n} — целые числа, и n>0{\displaystyle n>0}.
Пол/потолок: суммы
Если m,n{\displaystyle m,n} — целые числа, m>0{\displaystyle m>0}, то [11]
- n=⌊nm⌋+⌊n+1m⌋+⋯+⌊n+m−1m⌋{\displaystyle n=\left\lfloor {\frac {n}{m}}\right\rfloor +\left\lfloor {\frac {n+1}{m}}\right\rfloor +\dots +\left\lfloor {\frac {n+m-1}{m}}\right\rfloor }
Вообще, если x{\displaystyle x} — произвольное вещественное число, а m{\displaystyle m} — целое положительное, то
- ⌊mx⌋=⌊x⌋+⌊x+1m⌋+⋯+⌊x+m−1m⌋{\displaystyle \lfloor mx\rfloor =\left\lfloor x\right\rfloor +\left\lfloor x+{\frac {1}{m}}\right\rfloor +\dots +\left\lfloor x+{\frac {m-1}{m}}\right\rfloor }
Имеет место более общее соотношение [12]:
- ∑0⩽k<m⌊nk+xm⌋=d⌊xd⌋+(m−1)(n−1)2+d−12,d=(m,n){\displaystyle \sum _{0\leqslant k<m}\left\lfloor {\frac {nk+x}{m}}\right\rfloor =d\left\lfloor {\frac {x}{d}}\right\rfloor +{\frac {(m-1)(n-1)}{2}}+{\frac {d-1}{2}},\quad d=(m,n)}
Так как правая часть этого равенства симметрична относительно m{\displaystyle m} и n{\displaystyle n}, то справедлив следующий закон взаимности:
- ∑0⩽k<m⌊nk+xm⌋=∑0⩽k<n⌊mk+xn⌋,m,n>0{\displaystyle \sum _{0\leqslant k<m}\left\lfloor {\frac {nk+x}{m}}\right\rfloor =\sum _{0\leqslant k<n}\left\lfloor {\frac {mk+x}{n}}\right\rfloor ,\quad m,n>0}
Разложимость в ряд
Тривиальным образом функция антье раскладывается в ряд с помощью функции Хевисайда:
- [x]=∑n=−∞+∞n(θ(x−n)−θ(x−n−1)),{\displaystyle [x]=\sum _{n=-\infty }^{+\infty }n\left(\theta (x-n)-\theta (x-n-1)\right),}
где каждое слагаемое ряда создаёт характерные «ступеньки» функции. Этот ряд сходится абсолютно, однако ошибочное преобразование его слагаемых может привести к «упрощённому» ряду
- ∑n=−∞+∞θ(x−n),{\displaystyle \sum _{n=-\infty }^{+\infty }\theta \left(x-n\right),}
который расходится.
Применение
Целочисленные функции пол/потолок находят широкое применение в дискретной математике и теории чисел. Ниже приведены некоторые примеры использования этих функций.
Количество цифр в записи числа
Количество цифр в записи целого положительного числа в позиционной системе счисления с основанием b равно [13]
- ⌊logbn⌋+1{\displaystyle \lfloor \log _{b}n\rfloor +1}
Округление
Ближайшее к x{\displaystyle x} целое число может быть определено по формуле
- (x)=⌊x+0,5⌋{\displaystyle (x)=\lfloor x+0{,}5\rfloor }
Бинарная операция mod
Операция «остаток по модулю», обозначаемая xmody{\displaystyle x{\bmod {y}}}, может быть определена с помощью функции пола следующим образом. Если x,y{\displaystyle x,y} — произвольные вещественные числа, и y≠0{\displaystyle y\neq 0}, то неполное частное от деления x{\displaystyle x} на y{\displaystyle y} равно
- ⌊x/y⌋{\displaystyle \lfloor x/y\rfloor },
а остаток
- xmody=x−y⌊x/y⌋{\displaystyle x\,{\bmod {\,}}y=x-y\lfloor x/y\rfloor }
Дробная часть
Дробная часть вещественного числа x{\displaystyle x} по определению равна
- {x}=xmod1=x−⌊x⌋{\displaystyle \{x\}=x\,{\bmod {\,}}1=x-\lfloor x\rfloor }
Количество целых точек промежутка
Требуется найти количество целых точек в замкнутом промежутке с концами α{\displaystyle \alpha } и β{\displaystyle \beta }, то есть количество целых чисел n{\displaystyle n}, удовлетворяющий неравенству
- α⩽n⩽β{\displaystyle \alpha \leqslant n\leqslant \beta }
В силу свойств пол/потолка, это неравенство равносильно
- ⌈α⌉⩽n⩽⌊β⌋{\displaystyle \lceil \alpha \rceil \leqslant n\leqslant \lfloor \beta \rfloor }.
Это есть число точек в замкнутом промежутке с концами ⌈α⌉{\displaystyle \lceil \alpha \rceil } и ⌊β⌋{\displaystyle \lfloor \beta \rfloor }, равное ⌊β⌋−⌈α⌉+1{\displaystyle \lfloor \beta \rfloor -\lceil \alpha \rceil +1}.
Аналогично можно подсчитать количество целых точек в других типах промежутков. Сводка результатов приведена ниже [14].
- #{n∈Z:α⩽n⩽β}=⌊β⌋−⌈α⌉+1{\displaystyle \#\{n\in \mathbb {Z} \colon \alpha \leqslant n\leqslant \beta \}=\lfloor \beta \rfloor -\lceil \alpha \rceil +1}
- #{n∈Z:α⩽n<β}=⌈β⌉−⌈α⌉{\displaystyle \#\{n\in \mathbb {Z} \colon \alpha \leqslant n<\beta \}=\lceil \beta \rceil -\lceil \alpha \rceil }
- #{n∈Z:α<n⩽β}=⌊β⌋−⌊α⌋{\displaystyle \#\{n\in \mathbb {Z} \colon \alpha <n\leqslant \beta \}=\lfloor \beta \rfloor -\lfloor \alpha \rfloor }
- #{n∈Z:α<n<β}=⌈β⌉−⌊α⌋−1{\displaystyle \#\{n\in \mathbb {Z} \colon \alpha <n<\beta \}=\lceil \beta \rceil -\lfloor \alpha \rfloor -1}
(Через #M{\displaystyle \#M} обозначена мощность множества M{\displaystyle M}).
Первые три результата справедливы при всех α⩽β{\displaystyle \alpha \leqslant \beta }, а четвёртый — только при α<β{\displaystyle \alpha <\beta }.
Теорема Рэлея о спектре
Пусть α{\displaystyle \alpha } и β{\displaystyle \beta } — положительные иррациональные числа, связанные соотношением [15]
- 1α+1β=1.{\displaystyle {\frac {1}{\alpha }}+{\frac {1}{\beta }}=1.}
Тогда в ряду чисел
- ⌊α⌋,⌊β⌋,⌊2α⌋,⌊2β⌋,…,⌊mα⌋,⌊mβ⌋,…{\displaystyle \lfloor \alpha \rfloor ,\lfloor \beta \rfloor ,\lfloor 2\alpha \rfloor ,\lfloor 2\beta \rfloor ,\ldots ,\lfloor m\alpha \rfloor ,\lfloor m\beta \rfloor ,\ldots }
каждое натуральное n∈N{\displaystyle n\in \mathbb {N} } встречается в точности один раз. Иными словами, последовательности
- {mα∣m∈N}{\displaystyle \{m\alpha \mid m\in \mathbb {N} \}} и {mβ∣m∈N}{\displaystyle \{m\beta \mid m\in \mathbb {N} \}},
называемые последовательностями Бетти (англ.), образуют разбиение натурального ряда.[16]
В информатике
В языках программирования
Во многих языках программирования существуют встроенные функции пола/потолка floor(), ceil().
В системах вёрстки
В TeX (и LaTeX) для символов пола/потолка ⌊{\displaystyle \lfloor }, ⌋{\displaystyle \rfloor }, ⌈{\displaystyle \lceil }, ⌉{\displaystyle \rceil } существуют специальные команды: \lfloor, \rfloor, \lceil, \rceil. Поскольку wiki использует LaTeX для набора математических формул, то и в данной статье использованы именно эти команды.
Примечания
- ↑ Lemmermeyer, pp. 10, 23.
- ↑ Обозначение Гаусса использовали Cassels, Hardy & Wright и Ribenboim. Graham, Knuth & Patashnik и Crandall & Pomerance использовали обозначение Айверсона.
- ↑ Iverson, p. 12.
- ↑ Higham, p. 25.
- ↑ 1 2 Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 88.
- ↑ Weisstein, Eric W. Floor Function (англ.) на сайте Wolfram MathWorld.
- ↑ 1 2 Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 90.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 89.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 90-91.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 93.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 108.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 112-117.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 91.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 95-96.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 99-100.
- ↑ А. Баабабов. «Пентиум» хорошо, а ум лучше // Квант. — 1999. — № 4. — С. 36-38.
См. также
Литература
- Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — М.: «Мир», 1998. — 703 с. — ISBN 5-03-001793-3.
- М. К. Потапов, В. В. Александров, П. И. Пасиченко. Алгебра и начала анализа. — АО Столетие, 1996.
Целая часть числа Википедия
График функции «пол» (целая часть числа) График функции «потолок»В математике, целая часть вещественного числа x{\displaystyle x} — округление x{\displaystyle x} до ближайшего целого в меньшую сторону. Целая часть числа также называется антье (фр. entier), или пол (англ. floor). Наряду с полом существует парная функция — потолок (англ. ceiling) — округление x{\displaystyle x} до ближайшего целого в большую сторону.
Обозначения и примеры
Впервые квадратные скобки ([x]{\displaystyle [x]}) для обозначения целой части числа x{\displaystyle x} использовал Гаусс в 1808 году в своём доказательстве закона квадратичной взаимности[1]. Это обозначение считалось стандартным[2], пока Кеннет Айверсон в своей книге «A Programming Language», опубликованной в 1962 году, не предложил[3][4][5] округление числа x{\displaystyle x} до ближайшего целого в меньшую и большую стороны называть «пол» и «потолок» x{\displaystyle x} и обозначать ⌊x⌋{\displaystyle \lfloor x\rfloor } и ⌈x⌉{\displaystyle \lceil x\rceil } соответственно.
В современной математике используются оба обозначения[6], [x]{\displaystyle [x]} и ⌊x⌋{\displaystyle \lfloor x\rfloor }, однако существует тенденция перехода к терминологии и обозначениям Айверсона. Одна из причин этого — потенциальная неоднозначность понятия «целая часть числа»[5]. Например, целая часть числа 2,7 равна 2, но возможны два мнения на то, как определить целую часть числа −2,7. В соответствии с данным в этой статье определением [x]≡⌊x⌋=−3{\displaystyle [x]\equiv \lfloor x\rfloor =-3}, однако в некоторых калькуляторах имеется функция целой части числа INT, для отрицательных чисел определяемая как INT(-x) = -INT(x), так что INT(-2,7) = −2. В терминологии Айверсона отсутствуют возможные неоднозначности:
- ⌊2,7⌋=2,⌊−2,7⌋=−3,⌈2,7⌉=3,⌈−2,7⌉=−2{\displaystyle {\begin{matrix}\lfloor 2{,}7\rfloor =2,&\lfloor -2{,}7\rfloor =-3,\\\lceil 2{,}7\rceil =3,&\lceil -2{,}7\rceil =-2\end{matrix}}}
Определения
Функция пол ⌊⋅⌋:x↦⌊x⌋{\displaystyle \lfloor \cdot \rfloor \colon x\mapsto \lfloor x\rfloor } определяется как наибольшее целое, меньшее или равное x{\displaystyle x}:
- ⌊x⌋=max{n∈Z∣n⩽x}{\displaystyle \lfloor x\rfloor =\max\{n\in \mathbb {Z} \mid n\leqslant x\}}
Функция потолок ⌈⋅⌉:x↦⌈x⌉{\displaystyle \lceil \,\cdot \,\rceil \colon x\mapsto \lceil x\rceil } определяется как наименьшее целое, большее или равное x{\displaystyle x}:
- ⌈x⌉=min{n∈Z∣n⩾x}{\displaystyle \lceil x\rceil =\min\{n\in \mathbb {Z} \mid n\geqslant x\}}
Эти определения эквивалентны следующим неравенствам (где n — целое число):[7]
- ⌊x⌋=n⟺n⩽x<n+1⟺x−1<n⩽x⌈x⌉=n⟺n−1<x⩽n⟺x⩽n<x+1.{\displaystyle {\begin{matrix}\lfloor x\rfloor =n&\Longleftrightarrow &n\leqslant x<n+1&\Longleftrightarrow &x-1<n\leqslant x\\\lceil x\rceil =n&\Longleftrightarrow &n-1<x\leqslant n&\Longleftrightarrow &x\leqslant n<x+1.\end{matrix}}}
Свойства
В формулах, записанных ниже, буквами x{\displaystyle x} и y{\displaystyle y} обозначены вещественные числа, а буквами n{\displaystyle n} и m{\displaystyle m} — целые.
Пол и потолок как функции вещественной переменной
Функции пол и потолок отображают множество вещественных чисел в множество целых чисел:
- ⌊⋅⌋:R→Z,⌈⋅⌉:R→Z,{\displaystyle \lfloor \,\cdot \,\rfloor \colon \mathbb {R} \to \mathbb {Z} ,\quad \lceil \,\cdot \,\rceil \colon \mathbb {R} \to \mathbb {Z} ,\quad }
Пол и потолок — кусочно-постоянные функции.
Функции пол и потолок разрывны: во всех целочисленных точках терпят разрывы первого рода со скачком, равным единице.
При этом функция пол является:
Функция потолок является:
Связь функций пол и потолок
Для произвольного числа x{\displaystyle x} верно неравенство[8]
- ⌊x⌋⩽x⩽⌈x⌉{\displaystyle \lfloor x\rfloor \leqslant x\leqslant \lceil x\rceil }
Для целого x{\displaystyle x} пол и потолок совпадают:
- ⌊x⌋=x⟺x∈Z⟺⌈x⌉=x{\displaystyle \lfloor x\rfloor =x\quad \Longleftrightarrow \quad x\in \mathbb {Z} \quad \Longleftrightarrow \quad \lceil x\rceil =x}
Если x{\displaystyle x} — не целое, то значение функции потолок на единицу больше значения функции пол:
- ⌈x⌉−⌊x⌋={1,x∉Z0,x∈Z{\displaystyle \lceil x\rceil -\lfloor x\rfloor ={\begin{cases}1,&x\notin \mathbb {Z} \\0,&x\in \mathbb {Z} \end{cases}}}
Функции пол и потолок являются отражениями друг друга от обеих осей:
- ⌊−x⌋=−⌈x⌉,⌈−x⌉=−⌊x⌋{\displaystyle \lfloor -x\rfloor =-\lceil x\rceil ,\quad \lceil -x\rceil =-\lfloor x\rfloor }
Пол/потолок: неравенства
Любое неравенство между вещественным и целым числами равносильно неравенству с полом и потолком между целыми числами [7]:
- n⩽x⟺n⩽⌊x⌋x⩽n⟺⌈x⌉⩽nn<x⟺n<⌈x⌉x<n⟺⌊x⌋<n{\displaystyle {\begin{matrix}n\leqslant x&\Longleftrightarrow &n\leqslant \lfloor x\rfloor &\qquad x\leqslant n&\Longleftrightarrow &\lceil x\rceil \leqslant n\\n<x&\Longleftrightarrow &n<\lceil x\rceil &\qquad x<n&\Longleftrightarrow &\lfloor x\rfloor <n\end{matrix}}}
Два верхних неравенства являются непосредственными следствиями определений пола и потолка, а два нижние — обращение верхних от противного.
Функции пол/потолок являются монотонно возрастающими функциями:
- x⩽y⇒⌊x⌋⩽⌊y⌋,x⩽y⇒⌈x⌉⩽⌈y⌉{\displaystyle x\leqslant y\Rightarrow \lfloor x\rfloor \leqslant \lfloor y\rfloor ,\quad x\leqslant y\Rightarrow \lceil x\rceil \leqslant \lceil y\rceil }
Пол/потолок: сложение
Целочисленное слагаемое можно вносить/выносить за скобки пола/потолка [9]:
- ⌊x+n⌋=⌊x⌋+n,⌈x+n⌉=⌈x⌉+n{\displaystyle \lfloor x+n\rfloor =\lfloor x\rfloor +n,\quad \lceil x+n\rceil =\lceil x\rceil +n}
Предыдущие равенства, вообще говоря, не выполняются, если оба слагаемых — вещественные числа. Однако и в этом случае справедливы неравенства:
- ⌊x⌋+⌊y⌋⩽⌊x+y⌋⩽⌊x⌋+⌊y⌋+1,⌈x⌉+⌈y⌉−1⩽⌈x+y⌉⩽⌈x⌉+⌈y⌉{\displaystyle \lfloor x\rfloor +\lfloor y\rfloor \leqslant \lfloor x+y\rfloor \leqslant \lfloor x\rfloor +\lfloor y\rfloor +1,\quad \lceil x\rceil +\lceil y\rceil -1\leqslant \lceil x+y\rceil \leqslant \lceil x\rceil +\lceil y\rceil }
Пол/потолок под знаком функции
Имеет место следующее предложение:[10]
Пусть f(x){\displaystyle f(x)} — непрерывная монотонно возрастающая функция, определенная на некотором промежутке, обладающая свойством:
- f(x)∈Z⇒x∈Z{\displaystyle f(x)\in \mathbb {Z} \Rightarrow x\in \mathbb {Z} }
Тогда
- ⌊f(x)⌋=⌊f(⌊x⌋)⌋,⌈f(x)⌉=⌈f(⌈x⌉)⌉{\displaystyle \lfloor f(x)\rfloor =\lfloor f(\lfloor x\rfloor )\rfloor ,\quad \lceil f(x)\rceil =\lceil f(\lceil x\rceil )\rceil }
всякий раз, когда определены f(x),f(⌊x⌋),f(⌈x⌉){\displaystyle f(x),f(\lfloor x\rfloor ),f(\lceil x\rceil )}.
В частности,
- ⌊x+mn⌋=⌊⌊x⌋+mn⌋,⌈x+mn⌉=⌈⌈x⌉+mn⌉{\displaystyle \left\lfloor {\frac {x+m}{n}}\right\rfloor =\left\lfloor {\frac {\left\lfloor x\right\rfloor +m}{n}}\right\rfloor ,\quad \left\lceil {\frac {x+m}{n}}\right\rceil =\left\lceil {\frac {\left\lceil x\right\rceil +m}{n}}\right\rceil }
если m{\displaystyle m} и n{\displaystyle n} — целые числа, и n>0{\displaystyle n>0}.
Пол/потолок: суммы
Если m,n{\displaystyle m,n} — целые числа, m>0{\displaystyle m>0}, то [11]
- n=⌊nm⌋+⌊n+1m⌋+⋯+⌊n+m−1m⌋{\displaystyle n=\left\lfloor {\frac {n}{m}}\right\rfloor +\left\lfloor {\frac {n+1}{m}}\right\rfloor +\dots +\left\lfloor {\frac {n+m-1}{m}}\right\rfloor }
Вообще, если x{\displaystyle x} — произвольное вещественное число, а m{\displaystyle m} — целое положительное, то
- ⌊mx⌋=⌊x⌋+⌊x+1m⌋+⋯+⌊x+m−1m⌋{\displaystyle \lfloor mx\rfloor =\left\lfloor x\right\rfloor +\left\lfloor x+{\frac {1}{m}}\right\rfloor +\dots +\left\lfloor x+{\frac {m-1}{m}}\right\rfloor }
Имеет место более общее соотношение [12]:
- ∑0⩽k<m⌊nk+xm⌋=d⌊xd⌋+(m−1)(n−1)2+d−12,d=(m,n){\displaystyle \sum _{0\leqslant k<m}\left\lfloor {\frac {nk+x}{m}}\right\rfloor =d\left\lfloor {\frac {x}{d}}\right\rfloor +{\frac {(m-1)(n-1)}{2}}+{\frac {d-1}{2}},\quad d=(m,n)}
Так как правая часть этого равенства симметрична относительно m{\displaystyle m} и n{\displaystyle n}, то справедлив следующий закон взаимности:
- ∑0⩽k<m⌊nk+xm⌋=∑0⩽k<n⌊mk+xn⌋,m,n>0{\displaystyle \sum _{0\leqslant k<m}\left\lfloor {\frac {nk+x}{m}}\right\rfloor =\sum _{0\leqslant k<n}\left\lfloor {\frac {mk+x}{n}}\right\rfloor ,\quad m,n>0}
Разложимость в ряд
Тривиальным образом функция антье раскладывается в ряд с помощью функции Хевисайда:
- [x]=∑n=−∞+∞n(θ(x−n)−θ(x−n−1)),{\displaystyle [x]=\sum _{n=-\infty }^{+\infty }n\left(\theta (x-n)-\theta (x-n-1)\right),}
где каждое слагаемое ряда создаёт характерные «ступеньки» функции. Этот ряд сходится абсолютно, однако ошибочное преобразование его слагаемых может привести к «упрощённому» ряду
- ∑n=−∞+∞θ(x−n),{\displaystyle \sum _{n=-\infty }^{+\infty }\theta \left(x-n\right),}
который расходится.
Применение
Целочисленные функции пол/потолок находят широкое применение в дискретной математике и теории чисел. Ниже приведены некоторые примеры использования этих функций.
Количество цифр в записи числа
Количество цифр в записи целого положительного числа в позиционной системе счисления с основанием b равно [13]
- ⌊logbn⌋+1{\displaystyle \lfloor \log _{b}n\rfloor +1}
Округление
Ближайшее к x{\displaystyle x} целое число может быть определено по формуле
- (x)=⌊x+0,5⌋{\displaystyle (x)=\lfloor x+0{,}5\rfloor }
Бинарная операция mod
Операция «остаток по модулю», обозначаемая xmody{\displaystyle x{\bmod {y}}}, может быть определена с помощью функции пола следующим образом. Если x,y{\displaystyle x,y} — произвольные вещественные числа, и y≠0{\displaystyle y\neq 0}, то неполное частное от деления x{\displaystyle x} на y{\displaystyle y} равно
- ⌊x/y⌋{\displaystyle \lfloor x/y\rfloor },
а остаток
- xmody=x−y⌊x/y⌋{\displaystyle x\,{\bmod {\,}}y=x-y\lfloor x/y\rfloor }
Дробная часть
Дробная часть вещественного числа x{\displaystyle x} по определению равна
- {x}=xmod1=x−⌊x⌋{\displaystyle \{x\}=x\,{\bmod {\,}}1=x-\lfloor x\rfloor }
Количество целых точек промежутка
Требуется найти количество целых точек в замкнутом промежутке с концами α{\displaystyle \alpha } и β{\displaystyle \beta }, то есть количество целых чисел n{\displaystyle n}, удовлетворяющий неравенству
- α⩽n⩽β{\displaystyle \alpha \leqslant n\leqslant \beta }
В силу свойств пол/потолка, это неравенство равносильно
- ⌈α⌉⩽n⩽⌊β⌋{\displaystyle \lceil \alpha \rceil \leqslant n\leqslant \lfloor \beta \rfloor }.
Это есть число точек в замкнутом промежутке с концами ⌈α⌉{\displaystyle \lceil \alpha \rceil } и ⌊β⌋{\displaystyle \lfloor \beta \rfloor }, равное ⌊β⌋−⌈α⌉+1{\displaystyle \lfloor \beta \rfloor -\lceil \alpha \rceil +1}.
Аналогично можно подсчитать количество целых точек в других типах промежутков. Сводка результатов приведена ниже [14].
- #{n∈Z:α⩽n⩽β}=⌊β⌋−⌈α⌉+1{\displaystyle \#\{n\in \mathbb {Z} \colon \alpha \leqslant n\leqslant \beta \}=\lfloor \beta \rfloor -\lceil \alpha \rceil +1}
- #{n∈Z:α⩽n<β}=⌈β⌉−⌈α⌉{\displaystyle \#\{n\in \mathbb {Z} \colon \alpha \leqslant n<\beta \}=\lceil \beta \rceil -\lceil \alpha \rceil }
- #{n∈Z:α<n⩽β}=⌊β⌋−⌊α⌋{\displaystyle \#\{n\in \mathbb {Z} \colon \alpha <n\leqslant \beta \}=\lfloor \beta \rfloor -\lfloor \alpha \rfloor }
- #{n∈Z:α<n<β}=⌈β⌉−⌊α⌋−1{\displaystyle \#\{n\in \mathbb {Z} \colon \alpha <n<\beta \}=\lceil \beta \rceil -\lfloor \alpha \rfloor -1}
(Через #M{\displaystyle \#M} обозначена мощность множества M{\displaystyle M}).
Первые три результата справедливы при всех α⩽β{\displaystyle \alpha \leqslant \beta }, а четвёртый — только при α<β{\displaystyle \alpha <\beta }.
Теорема Рэлея о спектре
Пусть α{\displaystyle \alpha } и β{\displaystyle \beta } — положительные иррациональные числа, связанные соотношением [15]
- 1α+1β=1.{\displaystyle {\frac {1}{\alpha }}+{\frac {1}{\beta }}=1.}
Тогда в ряду чисел
- ⌊α⌋,⌊β⌋,⌊2α⌋,⌊2β⌋,…,⌊mα⌋,⌊mβ⌋,…{\displaystyle \lfloor \alpha \rfloor ,\lfloor \beta \rfloor ,\lfloor 2\alpha \rfloor ,\lfloor 2\beta \rfloor ,\ldots ,\lfloor m\alpha \rfloor ,\lfloor m\beta \rfloor ,\ldots }
каждое натуральное n∈N{\displaystyle n\in \mathbb {N} } встречается в точности один раз. Иными словами, последовательности
- {mα∣m∈N}{\displaystyle \{m\alpha \mid m\in \mathbb {N} \}} и {mβ∣m∈N}{\displaystyle \{m\beta \mid m\in \mathbb {N} \}},
называемые последовательностями Бетти (англ.), образуют разбиение натурального ряда.[16]
В информатике
В языках программирования
Во многих языках программирования существуют встроенные функции пола/потолка floor(), ceil().
В системах вёрстки
В TeX (и LaTeX) для символов пола/потолка ⌊{\displaystyle \lfloor }, ⌋{\displaystyle \rfloor }, ⌈{\displaystyle \lceil }, ⌉{\displaystyle \rceil } существуют специальные команды: \lfloor, \rfloor, \lceil, \rceil. Поскольку wiki использует LaTeX для набора математических формул, то и в данной статье использованы именно эти команды.
Примечания
- ↑ Lemmermeyer, pp. 10, 23.
- ↑ Обозначение Гаусса использовали Cassels, Hardy & Wright и Ribenboim. Graham, Knuth & Patashnik и Crandall & Pomerance использовали обозначение Айверсона.
- ↑ Iverson, p. 12.
- ↑ Higham, p. 25.
- ↑ 1 2 Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 88.
- ↑ Weisstein, Eric W. Floor Function (англ.) на сайте Wolfram MathWorld.
- ↑ 1 2 Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 90.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 89.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 90-91.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 93.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 108.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 112-117.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 91.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 95-96.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 99-100.
- ↑ А. Баабабов. «Пентиум» хорошо, а ум лучше // Квант. — 1999. — № 4. — С. 36-38.
См. также
Литература
- Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — М.: «Мир», 1998. — 703 с. — ISBN 5-03-001793-3.
- М. К. Потапов, В. В. Александров, П. И. Пасиченко. Алгебра и начала анализа. — АО Столетие, 1996.
Функция дробная часть числа
Функция дробная часть числаФункция «Дробная часть числа», ее свойства и график
Функция дробная часть числа имеет вид y = {x}.
1. Функция имеет смысл для всех значений переменной x, что следует из определения дробной части числа. Таким образом, область определения этой функции все действительные числа
D({x}) = R.2. Функция ни четная, ни нечетная. Область определения функции симметрична относительно начала координат, но не выполняется ни условие четности ( f (-x) = f (x) ), ни условие нечетности ( f (-x) = — f (x) ).
3. Функция периодическая с наименьшим положительным периодом T = 1.
4. Функция y = {x} принимает значения на интервале [0 ; 1), что следует из определения дробной части числа, т.е.
E({x}) = [0 ; 1).5. Из предыдущего свойства следует, что функция y = {x} ограничена.
6. Функция y = {x} непрерывна на каждом интервале [n ; n+1), где n целое, в каждой точке n функция терпит разрыв первого рода. Скачок равен 1.
7. Функция y = {x} обращается в 0 при всех целых значениях x, что следует из определения функции. То есть нулями функции будут все целочисленные значения аргумента.
8. Функция y = {x} на всей области определения принимает только положительные значения.
9. Функция строго монотонно возрастающая на каждом интервале [n; n+1), где n целое число.
10. Точек экстремума функция не имеет, так как не меняет характер монотонности.
11. Учитывая свойства 6 и 9, на каждом интервале [n; n+1) функция y = {x} принимает минимальное значение в точке n.
12. График функции.
Целая часть числа — это… Что такое Целая часть числа?
- Целая часть числа
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
- Целая функция
- Целе
Смотреть что такое «Целая часть числа» в других словарях:
Целая часть числа — График целой части В математике, целая часть, антье (фр. entier) или функция «пол» (англ. floor) это функция, определённая на множестве вещественных чисел и принимающая целочисленные значения. Целая часть числа x обычно обозначается через или [x] … Википедия
ЦЕЛАЯ ЧАСТЬ — числа x (антье) (франц. entier) наибольшее целое число ?x; обозначается ЦЕЛЕ (Celje) город в Словении. Ок. 40 тыс. жителей (1990). Цинкоплавильный завод; металлообрабатывающая, химическая, деревообрабатывающая промышленность. Руины крепости 15 18 … Большой Энциклопедический словарь
Целая часть — График функции «пол» (целая часть числа) … Википедия
целая часть — числа х (антье) (франц. entier), наибольшее целое число ≤х; обозначается [х]. Так, [5,6] = 5,[ 1/2] = 1. * * * ЦЕЛАЯ ЧАСТЬ ЦЕЛАЯ ЧАСТЬ числа x (антье) (франц. entier), наибольшее целое число Јx; обозначается [x]. Так, [5,6] = 5, [ 1/2] = 1 … Энциклопедический словарь
ЦЕЛАЯ ЧАСТЬ — числа х, антье (франц. entier целый), наибольшее целое число =< х; обозначается [х]. Так, [5.6] = 5, [ 1/2] = 1 … Большой энциклопедический политехнический словарь
ЦЕЛАЯ ЧАСТЬ — числа х (антье) (франц. entier), наибольшее целое число =<х; обозначается [х]. Так, [5,6]=5,[ 1/2] = 1 … Естествознание. Энциклопедический словарь
Числа с плавающей запятой — Плавающая запятая форма представления действительных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее… … Википедия
Числа с плавающей точкой — Плавающая запятая форма представления дробных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто… … Википедия
Числа с фиксированной точкой — Число с фиксированной запятой формат представления вещественного числа в памяти ЭВМ в виде целого числа. При этом само число x и его целочисленное представление x′ связаны формулой , где z цена младшего разряда. Простейший пример арифметики с… … Википедия
Прямой код (представление числа) — Прямой код способ представления двоичных чисел с фиксированной запятой в компьютерной арифметике. Главным образом используется для записи положительных чисел. Содержание 1 Представление числа в прямом коде 1.1 Примеры … Википедия
Целая часть — это… Что такое Целая часть?
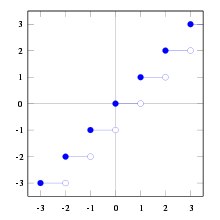 График функции «пол» (целая часть числа)
График функции «пол» (целая часть числа)  График функции «потолок»
График функции «потолок»В математике, целая часть вещественного числа — округление до ближайшего целого в меньшую сторону. Целая часть числа также называется антье (фр. entier), или пол (англ. floor). Наряду с полом существует парная функция — потолок (англ. ceiling) — округление до ближайшего целого в большую сторону.
Обозначения и примеры
Для целой части числа долгое время использовалось обозначение , введенное Гауссом[источник не указан 1264 дня]. Ни понятия функции потолок, ни специального обозначения для нее не существовало. В 1962 году Кеннет Айверсон предложил округления числа до ближайшего целого в меньшую и большую стороны называть «пол» и «потолок» и обозначать и соответственно [1].
В современной математике используются оба обозначения, и , однако существует тенденция перехода к терминологии и обозначениям Айверсона. Одна из причин этого — потенциальная неоднозначность понятия «целая часть числа»[1]. Например, целая часть числа 2,7 равна 2, но возможны два мнения на то, как определить целую часть числа −2,7. В соответствии с данным в этой статье определением , однако в некоторых калькуляторах имеется функция целой части числа INT, для отрицательных чисел определяемая как INT(-x) = -INT(x), так что INT(-2,7) = −2. В терминологии Айверсона отсутствуют возможные неоднозначности:
Определения
Функция пол определяется как наибольшее целое, меньшее или равное :
Функция потолок определяется как наименьшее целое, большее или равное :
Эти определения эквивалентны следующим неравенствам (где n — целое число) [2]:
Свойства
Везде ниже обозначают вещественные числа, а — целые.
Пол/потолок как функции вещественной переменной
Функции пол/потолок отображают множество вещественных чисел в множество целых чисел:
Пол/потолок — кусочно-постоянные функции.
Функции пол/потолок имеют разрывны во всех целочисленных точках, это разрывы первого рода со скачком, равным единице.
При этом, функция пол является:
Функция потолок является:
Связь функций пола и потолка
Для произвольного [3]
Для целого пол и потолок совпадают:
Если — не целое, то потолок ровно на единицу выше пола:
Функции пола и потолка являются отражениями друг друга от обеих осей:
Пол/потолок: неравенства
Любое неравенство между вещественным и целым числами равносильно неравенству с полом и потолком между целыми числами [2]:
Два верхних неравенства являются непосредственными следствиями определений пола и потолка, а два нижние — обращение верхних от противного.
Функции пол/потолок являются монотонно возрастающими функциями:
Пол/потолок: сложение
Целочисленное слагаемое можно вносить/выносить за скобки пола/потолка [4]:
Предыдущее равенство, вообще говоря, не выполняется, если оба слагаемых — вещественные числа. Однако и в этом случае справедливы неравенства:
Пол/потолок под знаком функции
Имеет место следующее предложение:[5]
Пусть — непрерывная монотонно возрастающая функция, определенная на некотором промежутке, обладающая свойством:
Тогда
всякий раз, когда определены .
В частности,
если и — целые числа, и .
Пол/потолок: суммы
Если — целые числа, , то [6]
Вообще, если — произвольное вещественное число, а — целое положительное, то
Имеет место более общее соотношение [7]:
Так как правая часть этого равенства симметрична относительно и , то справедлив следующий закон взаимности:
Разложимость в ряд
Тривиальным образом функция Антье раскладывается в ряд с помощью функции Хевисайда:
где каждое слагаемое ряда создаёт характерные «ступеньки» функции. Этот ряд сходится абсолютно, однако ошибочное преобразование его слагаемых может привести к «упрощённому» ряду
который расходится.
Применение
Целочисленные функции пол/потолок находят широкое применение в дискретной математике и теории чисел. Ниже приведены некоторые примеры использования этих функций.
Количество цифр в записи числа
Количество цифр в записи целого положительного числа в позиционной системе счисления с основанием b равно [8]
Округление
Ближайшее к целое число может быть определено по формуле
Бинарная операция mod
Операция «остаток по модулю», обозначаемая , может быть определена с помощью функции пола следующим образом. Если — произвольные вещественные числа, и , то неполное частное от деления на равно
- ,
а остаток
Дробная часть
Дробная часть вещественного числа по определению равна
Количество целых точек промежутка
Требуется найти количество целых точек в замкнутом промежутке с концами и , то есть количество целых чисел , удовлетворяющий неравенству
В силу свойств пол/потолка, это неравенство равносильно
- .
Это есть точек в замкнутом промежутке с концами и , равное .
Аналогично можно подсчитать количество целых точек в других типах промежутков. Сводка результатов приведена ниже [9].
(Через обозначена мощность множества ).
Первые три результата справедливы при всех , а четвертый — только при .
Теорема Рэлея о спектре
Пусть и — положительные иррациональные числа, связанные соотношением [10]
Тогда в ряду чисел
каждое натуральное встречается в точности один раз. Иными словами, последовательности
- и ,
называемые последовательностями Бетти (англ.), образуют разбиение натурального ряда.[11]
В информатике
В языках программирования
Во многих языках программирования существуют встроенные функции пола/потолка floor(), ceil().
В системах вёрстки
В TeX (и LaTeX) для символов пола/потолка , , , существуют специальные команды: \lfloor, \rfloor, \lceil, \rceil. Поскольку wiki использует LaTeX для набора математических формул, то и в данной статье использованы именно эти команды.
Примечания
- ↑ 1 2 Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 88.
- ↑ 1 2 Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 90.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 89.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 90-91.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 93.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 108.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 112-117.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 91.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 95-96.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 99-100.
- ↑ А. Баабабов «Пентиум» хорошо, а ум лучше // Квант. — 1999. — № 4. — С. 36-38.
См. также
Литература
- Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — М.: «Мир», 1998. — 703 с. — ISBN 5-03-001793-3
- М. К. Потапов, В. В. Александров, П. И. Пасиченко. Алгебра и начала анализа. — АО Столетие, 1996.
Дробная часть числа — это… Что такое Дробная часть числа?
- Дробная часть числа
Дробная часть числа — функция, определённая на вещественных числах x и равная разности между x и целой частью (антье) [x] числа x.
Дробная часть числа х обычно обозначается знаком {x}. Например:
Свойства функции
- Область определения
 .
. - Область значений
 .
. - Функция периодична с периодом T = 1
Источник
М. К. Потапов,В. В. Алескандров, П. И. Пасиченко Алгебра и начала анализа. — АО Столетие, 1996.
- Область определения
Wikimedia Foundation. 2010.
- Дробно-линейные преобразования
- Дробно-линейное отображение
Смотреть что такое «Дробная часть числа» в других словарях:
Дробная часть — числа кусочно линейная функция, определённая на вещественных числах и равная разности между и целой частью (антье) числа . Дробная часть числа х обычно обозначается знаком . Согласно определению … Википедия
ДРОБНАЯ ЧАСТЬ — числа х разность между этим числом и его целой частью ДРОБНО ЛИНЕЙНАЯ функция частное двух линейных функций, т. е. функция вида y = (ах + b)/(сх + d). Если ad bc . 0 и с . 0, график дробно линейной функции равнобочная гипербола … Большой Энциклопедический словарь
дробная часть — числа х, разность между этим числом и его целой частью [х], то есть х = х – [х]; всегда 0≤{х} … Энциклопедический словарь
ДРОБНАЯ ЧАСТЬ — числа х разность между этим числом и его целой частью: {х} = х [х]; всегда 0= < {х} < 1 … Большой энциклопедический политехнический словарь
ДРОБНАЯ ЧАСТЬ — числа х, разность между этим числом и его целой частью [х], т. е. {х} = х [х]; всегда 0 < {х} < 1 … Естествознание. Энциклопедический словарь
Целая часть числа — График целой части В математике, целая часть, антье (фр. entier) или функция «пол» (англ. floor) это функция, определённая на множестве вещественных чисел и принимающая целочисленные значения. Целая часть числа x обычно обозначается через или [x] … Википедия
Целая часть числа — см. Дробная и целая части числа … Большая советская энциклопедия
Числа с плавающей запятой — Плавающая запятая форма представления действительных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее… … Википедия
Числа с плавающей точкой — Плавающая запятая форма представления дробных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто… … Википедия
Целая часть — График функции «пол» (целая часть числа) … Википедия
 .
.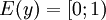 .
.