График функции дробная часть числа

Изучая алгебру 10 класса по учебнику А.Г.Мордковича и П.В. Семёнова, ученики впервые встретились с функцией целой части числа у = [х]. Некоторых она заинтересовала, но теоретических сведений, да и заданий, содержащих целую часть числа, оказалось очень мало. Чтобы поддержать интерес детей к предмету и возникла идея создания данного пособия.

Реализация программы курса рассчитана на 1 полугодие 10 класса для обучающихся физико — математического профиля.

Цель курса: расширить знания обучающихся о математических функциях и формировать умение использовать знания о функциях при решении уравнений и неравенств разной степени сложности. В представленном учебном пособии содержатся теоретические сведения справочного характера. Это сведения о функции целой части числа у = [х] и функции дробной части числа у = <х>, их графиках. Объясняются преобразования графиков, содержащих целую часть числа. Рассмотрены решения простейших уравнений и неравенств, содержащих целую или дробную частъ числа. А также методы решения квадратных, дробно — рациональных уравнений и неравенств, систем уравнений, содержащих целую или дробную часть числа.

В пособии приведены задания для самостоятельного решения.

Пособие включает в себя следующие пункты:

§1. Знакомство с функциями у = [х] и у =<х>.

§2. Уравнения, содержащие дробную или целую часть числа.

2.1 Простейшие уравнения.

2.2 Решение уравнений вида [f (х)] = g (х).

2.3 Графический способ решения уравнений.

2.4 Решение уравнений введением новой переменной.

2.5 Системы уравнений.

§3. Преобразование графиков функций, содержащих целую часть числа.

3.1 Построение графиков функций вида у = [f (х)]

3.2 Построение графиков функций вида у = f ([х]).

§4. Неравенства, содержащие целую или дробную часть числа.

§5. Целая и дробная часть числа в олимпиадных заданиях.

Ответы на задания для самостоятельного решения.

Пособие обеспечивает развитие представлений о функции и формирование прикладных навыков.

Адресовано учителям, решающим задачи профильного обучения.

Скачать:

Вложение	Размер
uchebnoe_posobie_zadachisoderzhashchie_celuyu_ili_drobnuyu_chast_chisla.doc	822.5 КБ

Предварительный просмотр:

Задачи, содержащие целую

или дробную часть числа

Вы приступаете к углубленному изучению темы «Целая и дробная части числа». Данное пособие позволит вам расширить свои знания о математических функциях при решении уравнений и неравенств разной степени сложности. В представленном пособии содержатся теоретические сведения справочного характера, объясняются преобразования графиков, содержащих целую или дробную часть числа, рассмотрены решения простейших уравнений. А также методы решения квадратных, дробно — рациональных уравнений и неравенств, систем уравнений. В пособии приведены задания для самостоятельного решения. Учебное пособие поможет вам систематизировать и обобщить полученные знания по теме «Целая и дробная части числа».

§1. Знакомство с функциями у = [х] и у=<х>………………………4

§2. Уравнения, содержащие целую или дробную часть числа…. 7

2.3 Графический способ решения уравнений………………10

1. Решение уравнений введением новой переменной……11

§3. Преобразования графиков функций, содержащих целую

1. 3.1 Построение графиков функций вида у = [f(х)]……………13
2. 3.2 Построение графиков функций вида у = f([х])……………15

§4. Неравенства, содержащие целую или дробную часть числа. 17

§5. Целая или дробная часть числа в олимпиадных заданиях…. 20

Ответы на задания для самостоятельного решения……………. 23

§1. Знакомство с функциями у = [x]

История и определение целой и дробной части числа

Понятие целой части числа было введено немецким математиком Иоганном Карлом Фридрихом Гауссом(1771—1855), автором «Трудов по теории чисел». Также Гаусс продвинул теорию специальных функций, рядов, численные методы, решение задач математической физики, создал математическую теорию потенциала.

Обозначается целая часть действительного числа x символом [x] или E(x).

Символ [x] был введён К.Гауссом в 1808 г.

Функция же целой части числа была введена Адриеном Мари Лежандром ( 1752—1833). — французским математиком. Его работа «Опыт теории чисел», которая вышла в свет в 1798 году, является фундаментальным трудом, итогом арифметических достижений XVIII века. Именно в честь него функцию y = [x] называют французским словом «Антье» (фр. «entier» -целый) обозначают E(x).

Определение: целой частью числа х называется наибольшее целое число с, не превышающее х, т.е. если [х] = с, c ≤ x

По некоторым значениям функции можно построить её график. Он выглядит следующим образом:

Свойства функции y = [x]:

1. Область определения функции y = [x] есть множество всех действительных чисел R.

2. Область значений функции y = [x] есть множество всех целых чисел Z.

3. Функция y = [x] кусочно-постоянная, неубывающая.

4. Функция общего вида.

5. Функция не периодична.

6. Функция не ограничена.

7. Функция имеет точку разрыва.

9. y 0, при х 0,при х>0.

10.Функция не имеет точек экстремума.

11. У наиб. и У наим. не существует.

Возникает вопрос: «Если есть функция целой части числа, может, есть и функция дробной части числа?»

Определение: дробная часть числа (обозначается <х>) есть разность х — [х].

Построим график функции у = <х>. Он выглядит следующим образом:

Простейшие свойства функции y = :

1. Область определения функции y = есть множество всех действительных чисел R.

2. Область значений функции y = есть полуинтервал [0;1)

3.Функция общего вида.

5.Функция не прерывна.

6.у=0, при всех целых х.

7.у>0, при всех действительных х.

8.Функция монотонно возрастает на [n; n+1)

9. Функция не имеет точек экстемума.

Представление о том, как выглядят графики функций у = [х] и у = <х>поможет выполнить и некоторые задания.

ЗАДАНИЯДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1) Построить графики функций:

2) Какими могут быть числа х и у, если:

3) Что можно сказать о величине разности х — у , если:

4) Что больше: [а] или <а>?

§2. Уравнения, содержащие целую или дробную часть числа

2.1. Простейшие уравнения

К простейшим уравнениям относятся уравнения вида [х] = а.

Уравнения такого вида решаются по определению:

Если а — дробное число, то такое уравнение не будет иметь корней.

Рассмотрим пример решения одного из таких уравнений:

[х + 1,3] = — 5. По определению такое уравнение преобразуется в неравенство:

Это и будет являться решением уравнения.

Рассмотрим ещё одно уравнение, относящееся к разряду простейших:

Для решения уравнений такого вида необходимо использовать свойство функции целого числа: Если р — целое число, то справедливо равенство

Доказательство: х = [х] +

х = k + а, где k = [х], а =

[ k + a ± p ] = [ k + a ] ± p = [х] ±p.

Решим предложенное уравнение, используя доказанное свойство: Получим [х] + 1 + [х] — 2 — [х] — 3 = 2. Приведём подобные слагаемые и получим простейшее уравнение [х] = 6. Его решением является полуинтервал х[6;7), который и будет решением данного уравнения.

Рассмотрим более сложное уравнение:

Преобразуем уравнение в неравенство: 1 ≤ х 2 -5х+6

х 2 — 5х + 6 ≥ 1 и решим её;

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

3) [x + 4] — [x + 1] = 2

2.2 Решение уравнений вида [f(x)]=g(x)

Уравнение вида [f(x)]=g(x) можно решить путем сведения их к уравнению

Рассмотрим пример 1 .

Заменим правую часть уравнения на новою переменную a и выразим отсюда x

11a = 16x + 16, 16x = 11a — 16,

Теперь решим уравнение относительно переменной а .

Раскроем знак целой части по определению и запишем с помощью системы неравенств:

Из промежутка выберем все целые значения a: 3;4;5;6;7 и проведем обратную замену:

Разделим каждое слагаемое числителя в скобке на знаменатель:

Из определения целой части числа следует, что (а+1) должно быть целым, значит и а — целое. Числа а, (а+1), (а+2) — три последовательных числа, значит одно из них обязательно делится на 2, а одно — на 3. Следовательно, произведение чисел делится нацело на 6.

То есть целое число. Значит

Решим это уравнение.

а + 1 = 0 или а 2 + 2а — 6 = 0

a = −1 ± (не являются целыми).

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ:

2.3. Графический способ решения уравнений

Решение. Решим это уравнение графически. Построим графики функций у = [х] и у = 2<х>. Найдём абсциссы точек их пересечения.

Ответ: х = 0; х = 1,5.

В некоторых случаях удобнее по графику найти ординаты точек пересечения графиков. Затем подставить полученное значение в одно из уравнений и найти искомые значения х.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

Решите уравнения графически:

10) Сколько решений имеет уравнение 2 <х>= 1 — .

2.4. Решение уравнений введением новой переменной.

Рассмотрим первый пример:

Заменим <х>на а, 0 а

а 2 — 8а + 7 = 0, которое решим по теореме, обратной теореме Виета: Полученные корни а = 7 и а = 1 . Проведем обратную замену и получим два новых уравнения: <х>= 7 и <х>= 1. Оба эти уравнения не имеют корней. Следовательно, уравнение не имеет решений.

Ответ: решений нет.

Рассмотрим ещё один случай решения уравнения введением новой

3[х] 3 + 2[х] 2 + 5[х]-10 = 0

Проведём замену [х] = а, аz. и получим новое кубическое уравнение За 3 +2а 2 +5а-10=0. Первый корень этого уравнения найдём путём подбора: а=1 — корень уравнения. Делим наше уравнение на (а-1). Получаем квадратное уравнение 3а 2 + 5а +10=0. Это уравнение имеет отрицательный дискриминант, а значит, не имеет решений. То есть, а=1 — единственный корень уравнения. Проводим обратную замену: [х]=а=1. Полученное уравнение решаем по определению целой части числа: х[1 ;2).

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ:

10) 10[х] 3 −11[х] 2 −31[х]-10 = 0

2.5. Системы уравнений.

Рассмотрим систему уравнений:

Ее можно решить либо методом сложения, либо подстановкой. Остановимся на первом способе.

После сложения двух уравнений получаем 11[x] = 11. Отсюда

[x] = 1. Подставим это значение в первое уравнение системы и получаем

[x] = 1 и [y] = 2 — решения системы. То есть x [1;2), y [2;3).

Ответ: ( x [1;2), y [2;3)).

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ:

§3. Преобразования графиков функций, содержащих целую часть числа

3.1. Построение графиков функции вида y = [f(x)]

Пусть имеется график функции у = f(х). Чтобы построить график функции у = [f(x)], поступаем следующим образом:

1. Проводим прямые у = n, n = 0; −1; +1; −2; +2; … и рассматриваем одну из полос, образованных прямыми у = n, у = n + 1.
2. Отмечаем точки пересечения прямых у = n, у = n + 1 с графиком функции у = f(х). Эти точки принадлежат графику функции у = [f(x)], так как их ординаты целые числа (на рисунке это точки А, В, С, D).

1. Для получения остальных точек графика функции у = [f(x)] в указанной полосе часть графика у = f(х), попавшую в полосу, проектируем параллельно оси Оу на прямую у = n. Поскольку любая точка М этой части графика функции у = f(х) имеет такую ординату , что n ≤ ] = n.
2. В каждой другой полосе, где имеются точки графика функции у = f(х), построение проводится аналогично.

Построим график функции у = [х]. Для этого

1. Проводим прямые у = n, n = 0; −1; +1; −2; +2; … и рассматриваем одну из полос, образованных прямыми у = n, у = n + 1.
2. Отмечаем точки пересечения прямых у = n, у = n + 1 с графиком

функции у = [х]. Эти точки принадлежат графику функции у = [х],

так как их координаты целые числа.

1. Для получения остальных точек графика функции у = [х] в указанной полосе часть графика у = х, попавшую в полосу, проецируем параллельно оси О у на прямую у = n, у = n + 1. Поскольку любая точка М этой части графика функции y = x, имеет такую ординату y 0 , что n 0 0 ] = n
2. В каждой другой полосе, где имеются точки графика функции у = х, построение проводится аналогично.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

Постройте графики функций:

1. у = ;
2. у = 2[sinx];
3. y = [3 — 1] + 3;
4. у = -[cosx] + 1;
5. y = [|x|];
6. y = [tgx];
7. y = 2[|cosx|] — 4;
8. y = 1,5[cosx] — 2;
9. y = [ctgx + 2] −1

3.2. Построение графиков функции вида y = f([x])

Пусть дан график некоторой функции у = f(х). Построение графика функции у = f([х]) осуществляется следующим образом:

1. Проводим прямые х = n, n = 0; −1; +1; −2; +2; …
2. Рассмотрим одну из полос, образованных прямыми у = n и у = n + 1. Точки А и В пересечения графика функции у = f(х) с этими прямыми принадлежат графику функции у = f([х]), так как их абсциссы — целые числа.

1. Для получения остальных точек графика функции у = f([х]) в указанной полосе часть графика функции у = f(х), попавшую в эту полосу, проектируем параллельно оси О у на прямую у = f(n).
2. В каждой другой полосе, где имеются точки графика функции у = f(х), построение ведётся аналогично.

Рассмотрим построение графика функции у = . Для этого пунктиром построим график функции у = . Далее

1. Проводим прямые х = n, n = 0; −1; +1; −2; +2; …
2. Рассмотрим одну из полос, образованных прямыми у = n и у = n + 1. Точки пересечения графика функции у = с этими прямыми принадлежат графику функции у = , так как их абсциссы — целые

3. В каждой другой полосе, где имеются точки графика функции у = , построение ведётся аналогично.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

Постройте графики функций:

§4. Неравенства, содержащие целую или дробную части числа

Назовём основными неравенствами с [х] и <х>следующие соотношения: [х] > b и <х>> b. Удобным методом их решения является графический метод. Поясним его на двух примерах.

Решение. Введём в рассмотрение две функции у = [х] и у = b и начертим их графики на одном и том же чертеже. Ясно, что тогда следует различать два случая: b — целое и b — нецелое.

Случай 1. b — целое

Из рисунка видно, что графики совпадают на [b; b + 1].

Следовательно, решением неравенства [х] ≥ b будет луч х ≥ b.

Случай 2. b — нецелое.

В этом случае графики функций у = [х] и у = b не пересекаются. Но часть графика у = [х], лежащая выше прямой, начинается в точке с координатами ([b] + 1; [b] + 1). Таким образом, решением неравенства [х] ≥ b будет луч х ≥ [b] + 1.

Остальные виды основных неравенств исследуются точно так же. Результаты этих исследований сведены ниже в таблицу.

Дробной частью действительного числа называется разность между этим числом и его целой частью.

Дробную часть числа x обозначают .

По определению, =x-[x].

Для любого x∈R 0≤

В частности, если n — целое число (n∈Ζ), =0.

Вычислить дробную часть числа x, если x принимает значения:

9,43; 0,3; −0,56; 12 3/7; 2/9; −4/15; 20; −11.

Функцию, ставящую в соответствие каждому значению x дробную часть этого числа — число , называют функцией дробной части числа и обозначают y=.

Функция дробная часть числа определена на множестве действительных чисел: x∈R.

Область значений функции — полуинтервал y∈[0;1).

По определению дробной части числа =x+k-[x+k].

По свойству целой части числа [x+k]=[x]+k.

Что и требовалось доказать.

Из утверждения следует, что на каждом промежутке вида [k; k+1), где k∈Z, график функции y= имеет одинаковый вид.

При k=0 x∈ [0; 1), [x]=0.

То есть при x∈ [0; 1) y=x.

График функции y=

Стрелки на графике показывают, что правые концы отрезков не принадлежат графику.

Другой вариант показать, что левые концы отрезков принадлежат графику, а правые — не принадлежат, изобразить их, соответственно, закрашенными и выколотыми точками.

Поскольку = , функция дробная часть числа является периодической. Её период T=k — любое целое число, отличное от нуля.

Наименьший положительный период (главный период) T=1.

Идёт приём заявок

Подать заявку

Для учеников 1-11 классов и дошкольников

Описание презентации по отдельным слайдам:

Построение графиков функций, содержащих знак целой и дробной части

Вспомним! Целой частью числа x называется наибольшее целое число n, не превышающее x Дробной частью числа называют разность между самим числом x и его целой частью:

Вычислите: [1,5] = [ 3] = [-1,3] = [-4] = < 2,37>= < 3,14>= <5>= <-2,5>= 1 3 −2 −4 0 0,14 0,37 0,5

D([x]) = R Ни четная, ни нечетная Не периодическая E ([x]) = Z Неограниченна Разрывная Нулями функции будут все значения [0;1) Принимает отрицательные значения при x 1 Неубывающая Точек экстремума нет, так как не меняет характер монотонности Не принимает наибольшего и наименьшего значений на области определения, т.к. постоянна на каждом интервале [n ; n+1) Свойства функции y=[x]

Свойства функции y= D() = R Ни четная, ни нечетная Периодическая с наименьшим положительным периодом T = 1; E() = [0,1) Ограничена Непрерывна на каждом интервале [n ; n+1), где n – целое, в каждой точке n функция терпит разрыв Нулями функции являются все целочисленные значения аргумента На всей области определения принимает только положительные значения Строго монотонно возрастающая на каждом интервале [n, n+1) Точек экстремума нет, так как не меняет характер монотонности На каждом интервале [n; n+1) функция y =принимает минимальное значение в точке n

Построение графика функции y=[f(x)] Строим прямые y=n, рассматриваем полосу y=n и y=n+1 Точки пересечения прямых y=n, y=n+1 с графиком функции y=f(x) будут принадлежать графику функции y=[f(x)], остальные точки графика y=[f(x)] в рассматриваемой полосе получим как проекцию части графика y=f(x) на прямую y=n В каждой другой полосе, где есть точки графика функции y=f(x), построение проводится аналогично y=f(x) 0 X Y 1

y=[arcsinx] X Y 0 1 y=arcsinx

Построение графика функции y=f([x]) Строим прямые x=n и рассматриваем одну из полос, образованную линиями x=n, x=n+1 Точки пересечения графика функции y=f(x) с прямыми y=n принадлежат графику функции y=f([x]), поскольку их абсциссы — целые числа; другие точки графика функции y=f([x]) в рассматриваемой полосе получим как проекцию части графика функции y=f(x), которая находится в этой полосе, на прямую y=f(n) В каждой другой полосе, где есть точки графика функции y=f(x), построение производится аналогично 0 1 y=f(x) Y X

Построение графика функции y= Cтроим прямые y=n В точках пересечения этих прямых с графиком функции y=f(x) проводят прямые, параллельные оси ординат. Значения функции y= попадают в образованные прямоугольники. Части графика функции y=f(x), которые попали в эти прямоугольники и располагаются в верхней полуплоскости, опускают вниз на расстояние n. Части графика функции, попавшие в нижнюю полуплоскость переносят вверх на расстояние |n|+1 y=f(x) X Y 1 0

Построение графика функции y=f() Легко заметить, что такие функции периодичны с периодом T=1, и на отрезке [0; 1] f()=f(x). Отсюда следует способ построения графика функции y=f(): строят график функции y=f(x) на [0; 1) продолжают этот график, учитывая свойство периодичности функции y=f() X 0 1 Y y=f(x)

Самостоятельно! Построить графики вида y=f([x]), y=[f(x)], y=f(), y=, где f(x)=cosx f(x)=sinx

• Мехоношина Елена ВалентиновнаНаписать 2669 02.10.2016

Номер материала: ДБ-231317

Не нашли то что искали?

Вам будут интересны эти курсы:

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение редакции может не совпадать с точкой зрения авторов.

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Метки:  

НАШ САЙТ РЕКОМЕНДУЕТ:

Графики и множества на плоскости — Построение графиков целой и дробной части числа — ЗФТШ, МФТИ

Рассмотрим интересный вид кусочно-заданных функций.

Определение. Целой частью [x][x] числа xx называется наибольшее целое число, не превосходящее xx.

Например, [1]=1[1] = 1, [0.7]=0[0.7] = 0, а [−0.7]=−1[−0.7] = −1. Функцию f(x)=[x]f(x) = [x] легко можно задать на промежутках между парами соседних целых чисел:

[x] = n при n ≤ x < n + 1 для всякого фиксированного целого числа n. Поэтому график этой функции имеет следующий вид (рис. 16).

Рассмотрим более трудный пример.

Построить график функции f(x)=[2x+3,5]f(x) = [2x + 3,5].

Ясно, что [2x+3,5]=[2x+0,5]+3[2x + 3,5]= [2x + 0,5] + 3. Далее,

из определения целой части числа следует такое представление:

[2x+3,5]=[2x + 3,5] ={[2x]+3,если n2≤x<n2+14,[2x]+4,если n2+14≤x<n+12\{\begin{array}{lc}&[2x] + 3, если\ {{n}\over{2}} ≤ x < {{n}\over{2}} + {{1}\over{4}},\\&[2x] + 4, если\ {{n}\over{2}} + {{1}\over{4}} ≤ x < {{n + 1}\over{2}}\end{array}

для всякого целого nn (рис. 17).

Рассмотрим ещё такой пример.

Изобразим на координатной плоскости xOyxOy множество точек (x,y)(x,y), для которых [x]=[y][x] = [y].

Ясно, что [x]=[y][x] = [y] означает, что для некоторого целого n верны неравенства n≤x<n+1n ≤ x < n + 1 и n≤y<n+1n ≤ y < n + 1. Набор всех таких точек будет объединением квадратиков так, как показано на рисунке. Жирные участки границ входят в график, а пунктирные и выколотые точки – нет (рис. 18).

С целой частью числа тесно связана такая кусочно-линейная функция.

Определение. Дробной частью {x}\{x\}\ числа xx называется число x=x−[x]{x} = x − [x].

К примеру, {1}=0\{1\} = 0, {0.7}=0.7\{0.7\} = 0.7, а {−0.7}=0.3\{−0.7\} = 0.3.

Построим график функции f(x)={x}f(x) = \{x\}. Ясно, что

f(x)=x−[x]=x−nf(x) = x − [x] = x − n при n≤x<n+1n ≤ x < n + 1 (рис. 19).

Дробная часть — это… Что такое Дробная часть?

ДРОБНАЯ ЧАСТЬ — числа х разность между этим числом и его целой частью ДРОБНО ЛИНЕЙНАЯ функция частное двух линейных функций, т. е. функция вида y = (ах + b)/(сх + d). Если ad bc . 0 и с . 0, график дробно линейной функции равнобочная гипербола …   Большой Энциклопедический словарь

дробная часть — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN fractional part …   Справочник технического переводчика

дробная часть — числа х, разность между этим числом и его целой частью [х], то есть х = х – [х]; всегда 0≤{х} …   Энциклопедический словарь

ДРОБНАЯ ЧАСТЬ — числа х разность между этим числом и его целой частью: {х} = х [х]; всегда 0= < {х} < 1 …   Большой энциклопедический политехнический словарь

ДРОБНАЯ ЧАСТЬ — числа х, разность между этим числом и его целой частью [х], т. е. {х} = х [х]; всегда 0 < {х} < 1 …   Естествознание. Энциклопедический словарь

дробная часть печатного листа — Часть печатного листа, содержащая меньшее количество страниц, чем основные тетради издания. Дробная часть возникает в случаях, когда объем издания не укладывается в целое количество печатных листов. [http://ofyug.ru/useful/abc/347] Тематики… …   Справочник технического переводчика

Дробная часть числа — Дробная часть числа  функция, определённая на вещественных числах x и равная разности между x и целой частью (антье) [x] числа x. Дробная часть числа х обычно обозначается знаком {x}. Например …   Википедия

дробная часть печатного листа — Часть печатного листа, содержащая меньшее количество страниц, чем основные тетради издания. Дробная часть возникает в случаях, когда объем издания не укладывается в целое количество печатных листов …   Краткий толковый словарь по полиграфии

Дробная часть печатного листа — часть, доля (половина, четверть, восьмая) печатного листа, содержащая меньшее число страниц, чем основные тетради издания. Д. ч. п. л. возникает в тех случаях, когда объем издания не укладывается в целое число печатных листов. Д. ч. п. л.… …   Реклама и полиграфия

Дробная часть печатного листа — половина, четверть, восьмая доля печ. л., которая образуется, когда объем издания не укладывается в целое число физ. печ. л. Д. ч. п. л. усложняет производственный процесс: приходится изготовлять несколько печ. форм дробной части листа столько,… …   Издательский словарь-справочник

Дробная часть числа Википедия

График функции y(x) = {x}.

Дробная часть числа — кусочно-линейная функция, определённая на вещественных числах x{\displaystyle x} и равная разности между x{\displaystyle x} и целой частью (антье) ⌊x⌋{\displaystyle \lfloor x\rfloor } числа x{\displaystyle x}.

Дробная часть числа х обычно обозначается знаком {x}{\displaystyle \{x\}}. Согласно определению, {x}=x−⌊x⌋{\displaystyle \{x\}=x-\lfloor x\rfloor }.

Примеры

• {1,23}=1,23−1=0,23{\displaystyle \;\{1,23\}=1,23-1=0,23}
• {−1,23}=−1,23−(−2)=0,77{\displaystyle \;\{-1,23\}=-1,23-(-2)=0,77}
• {113}=113−3=23{\displaystyle \left\{{\tfrac {11}{3}}\right\}={\tfrac {11}{3}}-3={\tfrac {2}{3}}}
• {−113}=−113−(−4)=13{\displaystyle \left\{-{\tfrac {11}{3}}\right\}=-{\tfrac {11}{3}}-(-4)={\tfrac {1}{3}}}

Свойства функции {x}

• Область определения R{\displaystyle \mathbb {R} }.
• Область значений [0;1){\displaystyle \left[0;1\right)}.
• Функция периодична с периодом 1{\displaystyle 1}.

См. также

Источник

М. К. Потапов,В. В. Александров, П. И. Пасиченко. Алгебра и начала анализа. — АО Столетие, 1996.

Дробная часть Википедия

График функции y(x) = {x}.

Дробная часть числа — кусочно-линейная функция, определённая на вещественных числах x{\displaystyle x} и равная разности между x{\displaystyle x} и целой частью (антье) ⌊x⌋{\displaystyle \lfloor x\rfloor } числа x{\displaystyle x}.

Дробная часть числа х обычно обозначается знаком {x}{\displaystyle \{x\}}. Согласно определению, {x}=x−⌊x⌋{\displaystyle \{x\}=x-\lfloor x\rfloor }.

Примеры[ | ]

• {1,23}=1,23−1=0,23{\displaystyle \;\{1,23\}=1,23-1=0,23}
• {−1,23}=−1,23−(−2)=0,77{\displaystyle \;\{-1,23\}=-1,23-(-2)=0,77}
• {113}=113−3=23{\displaystyle \left\{{\tfrac {11}{3}}\right\}={\tfrac {11}{3}}-3={\tfrac {2}{3}}}
• {−113}=−113−(−4)=13{\displaystyle \left\{-{\tfrac {11}{3}}\right\}=-{\tfrac {11}{3}}-(-4)={\tfrac {1}{3}}}

Свойства функции {x}[ | ]

• Область определения

Дробная часть числа — это… Что такое Дробная часть числа?



Дробная часть числа

Дробная часть числа — функция, определённая на вещественных числах x и равная разности между x и целой частью (антье) [x] числа x.

Дробная часть числа х обычно обозначается знаком {x}. Например:

Свойства функции

• Область определения .
• Область значений .
• Функция периодична с периодом T = 1

Источник

М. К. Потапов,В. В. Алескандров, П. И. Пасиченко Алгебра и начала анализа. — АО Столетие, 1996.

Wikimedia Foundation. 2010.

• Дробно-линейные преобразования
• Дробно-линейное отображение

Смотреть что такое «Дробная часть числа» в других словарях:

• Дробная часть — числа  кусочно линейная функция, определённая на вещественных числах и равная разности между и целой частью (антье) числа . Дробная часть числа х обычно обозначается знаком . Согласно определению …   Википедия

• ДРОБНАЯ ЧАСТЬ — числа х разность между этим числом и его целой частью ДРОБНО ЛИНЕЙНАЯ функция частное двух линейных функций, т. е. функция вида y = (ах + b)/(сх + d). Если ad bc . 0 и с . 0, график дробно линейной функции равнобочная гипербола …   Большой Энциклопедический словарь

• дробная часть — числа х, разность между этим числом и его целой частью [х], то есть х = х – [х]; всегда 0≤{х} …   Энциклопедический словарь

• ДРОБНАЯ ЧАСТЬ — числа х разность между этим числом и его целой частью: {х} = х [х]; всегда 0= < {х} < 1 …   Большой энциклопедический политехнический словарь

• ДРОБНАЯ ЧАСТЬ — числа х, разность между этим числом и его целой частью [х], т. е. {х} = х [х]; всегда 0 < {х} < 1 …   Естествознание. Энциклопедический словарь

• Целая часть числа — График целой части В математике, целая часть, антье (фр. entier) или функция «пол» (англ. floor) это функция, определённая на множестве вещественных чисел и принимающая целочисленные значения. Целая часть числа x обычно обозначается через или [x] …   Википедия

• Целая часть числа —         см. Дробная и целая части числа …   Большая советская энциклопедия

• Числа с плавающей запятой — Плавающая запятая  форма представления действительных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее… …   Википедия

• Числа с плавающей точкой — Плавающая запятая форма представления дробных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто… …   Википедия

• Целая часть — График функции «пол» (целая часть числа) …   Википедия

Дробная часть числа — это… Что такое Дробная часть числа?



Дробная часть числа

Дробная часть числа — функция, определённая на вещественных числах x и равная разности между x и целой частью (антье) [x] числа x.

Дробная часть числа х обычно обозначается знаком {x}. Например:

Свойства функции

• Область определения .
• Область значений .
• Функция периодична с периодом T = 1

Источник

М. К. Потапов,В. В. Алескандров, П. И. Пасиченко Алгебра и начала анализа. — АО Столетие, 1996.

Wikimedia Foundation. 2010.

• Дробно-линейные преобразования
• Дробно-линейное отображение

Смотреть что такое «Дробная часть числа» в других словарях:

• Дробная часть — числа  кусочно линейная функция, определённая на вещественных числах и равная разности между и целой частью (антье) числа . Дробная часть числа х обычно обозначается знаком . Согласно определению …   Википедия

• ДРОБНАЯ ЧАСТЬ — числа х разность между этим числом и его целой частью ДРОБНО ЛИНЕЙНАЯ функция частное двух линейных функций, т. е. функция вида y = (ах + b)/(сх + d). Если ad bc . 0 и с . 0, график дробно линейной функции равнобочная гипербола …   Большой Энциклопедический словарь

• дробная часть — числа х, разность между этим числом и его целой частью [х], то есть х = х – [х]; всегда 0≤{х} …   Энциклопедический словарь

• ДРОБНАЯ ЧАСТЬ — числа х разность между этим числом и его целой частью: {х} = х [х]; всегда 0= < {х} < 1 …   Большой энциклопедический политехнический словарь

• ДРОБНАЯ ЧАСТЬ — числа х, разность между этим числом и его целой частью [х], т. е. {х} = х [х]; всегда 0 < {х} < 1 …   Естествознание. Энциклопедический словарь

• Целая часть числа — График целой части В математике, целая часть, антье (фр. entier) или функция «пол» (англ. floor) это функция, определённая на множестве вещественных чисел и принимающая целочисленные значения. Целая часть числа x обычно обозначается через или [x] …   Википедия

• Целая часть числа —         см. Дробная и целая части числа …   Большая советская энциклопедия

• Числа с плавающей запятой — Плавающая запятая  форма представления действительных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее… …   Википедия

• Числа с плавающей точкой — Плавающая запятая форма представления дробных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто… …   Википедия

• Целая часть — График функции «пол» (целая часть числа) …   Википедия
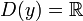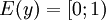