Графики функций и их производных.

ИССЛЕДОВАНИЕ ФУНКЦИИ ПРИ ПОМОЩИ ПРОИЗВОДНОЙ
возрастание
убывание
функции.

Алгоритм нахождения промежутков возрастания (убывания) функции
1. Находим область определения функции
2.Находим производную функции
3.Находим точки, в которых f’(x) =0
или f’(x) не существует
4.Отмечаем эти точки на числовой прямой
и определяем знаки производной
на полученных промежутках
5.Делаем выводы о промежутках
возрастания и убывания

Исследование
по формуле
по графику
 0, значит, функция возрастает. Если f / (x) значит, функция убывает. «
0, значит, функция возрастает. Если f / (x) значит, функция убывает. «
Признаки:
Если f / (x) 0,
значит, функция возрастает.
Если f / (x)
значит, функция убывает.

По формуле функции

Практикум:
Найдите промежутки возрастания
(убывания) функции.
Задания:

1 вариант
D(f)
2 вариант
f ‘ (x)
f ‘ (x) = 0
(не существует)
Знаки
Промежутки возрастания
производной
Промежутки убывания

1 вариант
D(f)
2 вариант
f ‘ (x)
R
f ‘ (x) = 0
R
(не существует)
Знаки
-1; 1
1
Промежутки возрастания
производной
-1; 1
Промежутки убывания
—
—
—
-1
+
+
+
-1
1

Графики.
Графики
функций
Графики
производных

График
функции
Если функция возрастает ,
то производная
положительна
y
4
2
1
-1
0
x
Если функция убывает ,
то производная
отрицательна

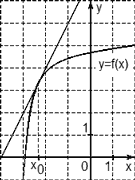
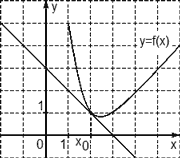
В7(ЕГЭ) На рисунке изображен график функции у = f(x) и касательная к этому графику. Определите знак производной в точке касания.

В7 (ЕГЭ) На рисунке изображен график функции у = f(x) и касательная к этому графику.

В7 .егэ . На рисунке изображен график функции , определенной на интервале (-9;8). Определите количество целых точек, в которых производная функции положительна .

В7 (егэ). На рисунке изображен график функции , определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна
.
- В7(егэ). На рисунке изображен график функции , определенной на интервале (−5; 5). Определите количество целых точек, в которых производная функции отрицательна.

Задание 7 № 6871.На рисунке изображен график функции ,
 0, значит, функция возрастает. Признаки: Если f / (x) значит, функция убывает. «
0, значит, функция возрастает. Признаки: Если f / (x) значит, функция убывает. «
Графики производных
Задания В7 (ЕГЭ)
Если f / (x) 0,
значит, функция возрастает.
Признаки:
Если f / (x)
значит, функция убывает.
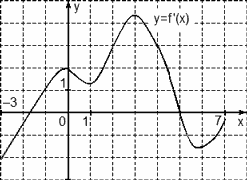
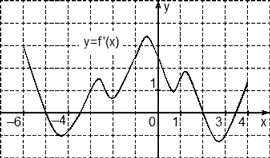
 0, значит, функция возрастает. На рисунке изображен график y=f'(x) — производной функции f(x) , определенной на интервале (-6;8) . Найдите количество промежутков возрастания функции f(x) . График производной «
0, значит, функция возрастает. На рисунке изображен график y=f'(x) — производной функции f(x) , определенной на интервале (-6;8) . Найдите количество промежутков возрастания функции f(x) . График производной «
Если f / (x) 0,
значит, функция возрастает.
На рисунке изображен график y=f'(x) — производной функции f(x) , определенной на интервале (-6;8) . Найдите количество промежутков возрастания функции f(x) .
График производной

Функция задана на отрезке. На рисунке изображен график ее производной.
- Укажите количество
промежутков
возрастания функции.
у
y=f ‘(x)
1
0
b
1
х
а

На рисунке изображен график y=f'(x) — производной функции f(x) , определенной на интервале (-8;6) . Найдите количество промежутков убывания функции f(x).
Если f / (x)
значит, функция убывает.

Функция задана на отрезке. На рисунке изображен график ее производной.
у
- Укажите количество
промежутков
убывания функции
y=f ‘(x)
1
0
b
1
х
а

На рисунке изображен график производной функции f(x),
определенной на интервале (a;b). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
у
y=f ‘(x)
1
b
0
а
1
х
(1)

На рисунке изображен график производной функции f(x),
определенной на интервале (a;b). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
у
y=f ‘(x)
1
b
0
а
1
х
(2)
![Задание 7 .На рисунке изображен график производной функции , определенной на интервале (-6;6) . В какой точке отрезка[-5;-1] функция принимает наибольшее значение.](/800/600/https/fsd.multiurok.ru/html/2018/09/10/s_5b963fd147fc2/img23.jpg)
Задание 7 .На рисунке изображен график производной функции , определенной на интервале (-6;6) . В какой точке отрезка[-5;-1] функция принимает наибольшее значение.

Задание 7 .На рисунке изображен график производной функции , определенной на интервале (-6;6) . Найдите промежутки возрастания функции . В ответе укажите сумму целых точек, входящих в эти промежутки.

Задание 7.На рисунке изображен график производной функции, определенной на интервале (-9;2). Найдите промежутки убывания функции . В ответе укажите сумму целых точек, входящих в эти промежутки.

На рисунке изображен график производной функции , определенной на интервале .Найдите промежутки возрастания функции . В ответе укажите длину наибольшего из них.

Домашнее задание:
Составить подборку однотипных заданий В7 из сборника егэ, прорешать.

Спасибо
за урок!
23
multiurok.ru
Применение производной к построению графиков функции
Если на некотором промежутке график функции представляет собой непрерывную линию, иными словами, такую линию, которую можно провести без карандаша от листа бумаги, то такая функция называется непрерывной на этом промежутке. Существуют также функции, которые непрерывными не являются. В качестве примера рассмотрим график функции, которая на промежутках [a; c] и [с; b] непрерывна, но в точке
х = с разрывна и поэтому на всем отрезке [a; b] не является непрерывной. Все функции, изучаемые нами в школьном курсе математики, – это функции непрерывные на каждом промежутке, на котором они определены.
 Отметим, что если на некотором промежутке функция имеет производную, то на этом промежутке она непрерывна.
Отметим, что если на некотором промежутке функция имеет производную, то на этом промежутке она непрерывна.
Обратное утверждение является неверным. Функция, которая непрерывна на промежутке, может не иметь производной в некоторых точках этого промежутка. Например, функция
у = |log 2 x| непрерывна на промежутке х > 0, но в точке х = 1 не имеет производной, в силу того что в этой точке график функции касательной не имеет.
Рассмотрим построение графиков с помощью производной.
Задача 1.
Построить график функции f(x) = x3 – 2x2 + x.
Решение.
1) Эта функция определена при всех х € R.
2) Найдем промежутки монотонности рассматриваемой функции и ее точки экстремума с помощью производной. Производная равна f ‘(x) = 3x2 – 4x + 1. Найдем стационарные точки:
3x2 – 4x + 1 = 0, откуда х1 = 1/3, х2 = 1.
Для определения знака производной разложим квадратные трехчлен 3x2 – 4x + 1 на множители:
f ‘(x) = 3(х – 1/3)(х – 1). Следовательно, на промежутках х < 1/3 и х > 1 производная положительна; значит, функция возрастает на этих промежутках.
Производная отрицательна при 1/3 < х < 1; следовательно, функция убывает на этом интервале.
Точка х1 = 1/3 является точкой максимума, так как справа от этой точки функция убывает, а слева – возрастает. В этой точке значение функции равно f (1/3) = (1/3)3 – 2(1/3)2 + 1/3 = 4/27.
Точкой минимума является точка х2 = 1, так как слева от этой точки функция убывает, а справа возрастает; ее значение в этой точке минимума равняется f (1) = 0.
3) При построение графика обычно находят точки пересечения графика с осями координат. Так как f(0) = 0, то график проходит через начало координат. Решая уравнение f(0) = 0, находим точки пересечения графика с осью абсцисс:
x3 – 2x2 + x = 0, х(x2 – 2х + 1) = 0, х(х – 1) 2 = 0, откуда х = 0, х = 1.
4) Для более точного построение графика найдем значения функции еще в двух точках: f(-1/2) = -9/8, f(2) = 2.
5) Используя результаты исследования (пункты 1 – 4), строим график функции у = x3 – 2x2 + x.
Для построения графика функции обычно сначала исследуют свойства этой функции с помощью ее производной по схеме, аналогичной схеме при решении задачи 1.
Таким образом, при исследовании свойств функции необходимо найти:
1) область ее определения;
2) производную;
3) стационарные точки;
4) промежутки возрастания и убывания;
5) точки экстремума и значения функции в этих точках.
Результаты исследования удобно записывать в виде таблицы. Затем, используя таблицу, строят график функции. Для более точного построения графика обычно находят точки его пересечения с осями координат и – при необходимости – еще несколько точек графика.
Если же мы сталкиваемся с четной или нечетной функцией, то для  построения ее графика достаточно исследовать свойства и построить ее график при х > 0, а затем отразить его симметрично относительно оси ординат (начала координат). Например, анализируя функцию f(x) = х + 4/х, мы приходим к выводу о том, что данная функция нечетная: f(-x) = -х + 4/(-х) = -(х + 4/х) = -f(x). Выполнив все пункты плана, строим график функции при х > 0, а график этой функции при х < 0 получаем посредством симметричного отражения графика при х > 0 относительно начала координат.
построения ее графика достаточно исследовать свойства и построить ее график при х > 0, а затем отразить его симметрично относительно оси ординат (начала координат). Например, анализируя функцию f(x) = х + 4/х, мы приходим к выводу о том, что данная функция нечетная: f(-x) = -х + 4/(-х) = -(х + 4/х) = -f(x). Выполнив все пункты плана, строим график функции при х > 0, а график этой функции при х < 0 получаем посредством симметричного отражения графика при х > 0 относительно начала координат.
Для краткости решения задач на построение графиков функции большую часть рассуждений проводят устно.
Также отметим, что при решении некоторых задач мы можем столкнуться с необходимостью исследования функции не на всей области определения, а только на некотором промежутке, например, если нужно построить график, скажем, функции f(x) = 1 + 2x2 – x4 на отрезке [-1; 2].
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Связь графиков функции и производной — Студопедия.Нет
Производная характеризует скорость изменения функции Если функция возрастает – производная положительна (касательная наклонена вправо) Если функция убывает – производная отрицательна (касательная наклонена влево) Если функция имеет максимум или минимум, либо «точку перегиба» — производная равна нулю (касательная лежит горизонтально) Чем больше скорость возрастания (или убывания) функции, тем больше по модулю производная, и тем круче (ближе к вертикали) наклон касательной В точках А и D функция возрастает – производная положительна. В точке А наклон касательной круче, значит, и производная больше, чем в точке D. В точках В и С функция убывает – производная отрицательны. В точке В функция наклон касательной круче, значит, производная меньше, чем в точке C (ПО МОДУЛЮ – больше)
Геометрический смысл производной
Производная – это тангенс угла наклона касательной (или угловой коэффициент касательной)
| Как найти угловой коэффициент касательной (или производную) | Пример: На рисунке изображены график функции  и касательная к нему в точке с абсциссой и касательная к нему в точке с абсциссой  . Найдите значение производной функции . Найдите значение производной функции  в точке в точке  . .
| 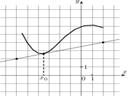 | ||
1. Найти точки на линии касательной, которые точно попадают в пересечение клеточек (обычно на рисунке эти точки отмечены). 2. Через одну из точек провести горизонтальную линию, через другую – вертикальную. Получится треугольник. 3. Сосчитать (в клеточках) длины вертикальной и горизонтальной сторон треугольника. Разделить длину вертикалной стороны на длину горизонтальной 4. Если наклон касательной вправо («подъем») – ставим знак «плюс», если наклон влево («спуск») – ставим знак «минус» |
| |||
Ответ: Значение производной в точке х0 равно 0,25 | ||||
Нахождение точек, где касательная параллельна прямой
Если требуется определить точки, где касательная параллельна прямой  , то надо искать точки, где производная равна k (числу перед иксом). А если касательная должна быть параллельна прямой
, то надо искать точки, где производная равна k (числу перед иксом). А если касательная должна быть параллельна прямой 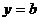 (или оси абсцисс), то производная должна быть равна 0)
(или оси абсцисс), то производная должна быть равна 0)
| Пример: Дан график производной функции f(x). Указать количество точек, в которых касательная к графику функции y=f(x) параллельна прямой y=x Решение: для прямой y=x угловой коэффициент равен 1, значит, производная должна быть равна 1. Таких точек на графике две. | 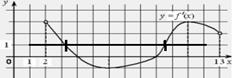 |
Физический смысл производной
- Если функцией является перемещение тела, то произвозная от этой функции – скорость
- Если функцией является скорость, то производная от этой функции – ускорение
Пример: Материальная точка движется по закону  . Найти мгновенную скорость в момент
. Найти мгновенную скорость в момент 
Скорость v – производная от перемещения s:  . При t=5
. При t=5 
Связь графиков функции и производной
| Производная | Функция | Касательная к графику функции |
| Положительна | Возрастает | Наклонена вправо (острый угол с осью Х) |
| Отрицательна | Убывает | Наклонена влево (тупой угол с осью Х) |
| Равна нулю (с вариантами) | Стационарная точка | Горизонтальна (параллельна оси Х) |
| =0, меняет знак с мИнуса на плюс | Минимум (экстремум) | |
| =0, меняет знак с плюСа на минус | МакСимум (экстремум) | |
| =0, но знак не меняет | Точка перегиба |
studopedia.net
График функции по графику производной
По графику производной y= f ‘ (x) можно не только исследовать поведение функции y=f(x) , но и попытаться построить ее график.
Поскольку для одной функции первообразных существует бесконечное множество, график функции по графику производной можно построить лишь схематично: точки экстремума и промежутки возрастания и убывания функции определить можно, а нули функции и экстремумы — нет.
Дан график производной: y= f ‘ (x):
Построить график функции y=f(x).
Решение:
Точки x=x2, x=x3, x=x4, в которых производная y= f ‘ (x) обращается в нуль — это точки экстремума функции y=f(x).
В точках x=x2 и x=x4 производная меняет знак с «-«на «+», поэтому x2 и x=x4 — точки минимума функции y=f(x).
В точке x=x3 производная меняет знак с «+» на «-«, поэтому x=x3 — точка максимума функции.
На промежутках [x1;x2] и [x3;x4] f ‘ (x)<0, поэтому y=f(x) на этих промежутках убывает.
На промежутках [x2;x3] и [x4;x5] f ‘ (x)>0, поэтому для y=f(x) они являются промежутками возрастания.
Сказать что-то более определенное о нулях и других значениях функции y=f(x) не получится. Данный эскиз графика y=f(x) — один из множества графиков первообразных для функции y= f ‘ (x). Другие могут быть получены из него параллельным переносом вдоль оси oy.
Если график производной y= f ‘ (x) представляет собой прямую, параллельную оси ox (y=b, где b- число),, то функция y=f(x) — линейная. Она является возрастающей, если b>0, убывающей, если b<0, и постоянной, если b=0.
www.uznateshe.ru
Графики функций и их производных.

ИССЛЕДОВАНИЕ ФУНКЦИИ ПРИ ПОМОЩИ ПРОИЗВОДНОЙ
возрастание
убывание
функции.

Алгоритм нахождения промежутков возрастания (убывания) функции
1. Находим область определения функции
2.Находим производную функции
3.Находим точки, в которых f’(x) =0
или f’(x) не существует
4.Отмечаем эти точки на числовой прямой
и определяем знаки производной
на полученных промежутках
5.Делаем выводы о промежутках
возрастания и убывания

Исследование
по формуле
по графику
 0, значит, функция возрастает. Если f / (x) значит, функция убывает. «
0, значит, функция возрастает. Если f / (x) значит, функция убывает. «
Признаки:
Если f / (x) 0,
значит, функция возрастает.
Если f / (x)
значит, функция убывает.

По формуле функции

Практикум:
Найдите промежутки возрастания
(убывания) функции.
Задания:

1 вариант
D(f)
2 вариант
f ‘ (x)
f ‘ (x) = 0
(не существует)
Знаки
Промежутки возрастания
производной
Промежутки убывания

1 вариант
D(f)
2 вариант
f ‘ (x)
R
f ‘ (x) = 0
R
(не существует)
Знаки
-1; 1
1
Промежутки возрастания
производной
-1; 1
Промежутки убывания
—
—
—
-1
+
+
+
-1
1

Графики.
Графики
функций
Графики
производных

График
функции
Если функция возрастает ,
то производная
положительна
y
4
2
1
-1
0
x
Если функция убывает ,
то производная
отрицательна

В7(ЕГЭ) На рисунке изображен график функции у = f(x) и касательная к этому графику. Определите знак производной в точке касания.

В7 (ЕГЭ) На рисунке изображен график функции у = f(x) и касательная к этому графику. Определите знак производной в точке касания.

В7 .егэ . На рисунке изображен график функции , определенной на интервале (-9;8). Определите количество целых точек, в которых производная функции положительна .

В7 (егэ). На рисунке изображен график функции , определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна .

- В7(егэ). На рисунке изображен график функции , определенной на интервале (−5; 5). Определите количество целых точек, в которых производная функции отрицательна.

Задание 7 № 6871.На рисунке изображен график функции , определенной на интервале (-1;12) .Определите количество целых точек, в которых производная функции отрицательна.
 0, значит, функция возрастает. Признаки: Если f / (x) значит, функция убывает. «
0, значит, функция возрастает. Признаки: Если f / (x) значит, функция убывает. «
Графики производных
Задания В7 (ЕГЭ)
Если f / (x) 0,
значит, функция возрастает.
Признаки:
Если f / (x)
значит, функция убывает.
 0, значит, функция возрастает. На рисунке изображен график y=f'(x) — производной функции f(x) , определенной на интервале (-6;8) . Найдите количество промежутков возрастания функции f(x) . График производной «
0, значит, функция возрастает. На рисунке изображен график y=f'(x) — производной функции f(x) , определенной на интервале (-6;8) . Найдите количество промежутков возрастания функции f(x) . График производной «
Если f / (x) 0,
значит, функция возрастает.
На рисунке изображен график y=f'(x) — производной функции f(x) , определенной на интервале (-6;8) . Найдите количество промежутков возрастания функции f(x) .
График производной

Функция задана на отрезке. На рисунке изображен график ее производной.
- Укажите количество
промежутков
возрастания функции.
у
y=f ‘(x)
1
0
b
1
х
а

На рисунке изображен график y=f'(x) — производной функции f(x) , определенной на интервале (-8;6) . Найдите количество промежутков убывания функции f(x).
Если f / (x)
значит, функция убывает.

Функция задана на отрезке. На рисунке изображен график ее производной.
у
- Укажите количество
промежутков
убывания функции
y=f ‘(x)
1
0
b
1
х
а

На рисунке изображен график производной функции f(x),
определенной на интервале (a;b). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
у
y=f ‘(x)
1
b
0
а
1
х
(1)

На рисунке изображен график производной функции f(x),
определенной на интервале (a;b). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
у
y=f ‘(x)
1
b
0
а
1
х
(2)
![Задание 7 .На рисунке изображен график производной функции , определенной на интервале (-6;6) . В какой точке отрезка[-5;-1] функция принимает наибольшее значение.](/800/600/https/fsd.multiurok.ru/html/2018/09/10/s_5b963fd147fc2/img23.jpg)
Задание 7 .На рисунке изображен график производной функции , определенной на интервале (-6;6) . В какой точке отрезка[-5;-1] функция принимает наибольшее значение.

Задание 7 .На рисунке изображен график производной функции , определенной на интервале (-6;6) . Найдите промежутки возрастания функции . В ответе укажите сумму целых точек, входящих в эти промежутки.

Задание 7.На рисунке изображен график производной функции, определенной на интервале (-9;2). Найдите промежутки убывания функции . В ответе укажите сумму целых точек, входящих в эти промежутки.

На рисунке изображен график производной функции , определенной на интервале .Найдите промежутки возрастания функции . В ответе укажите длину наибольшего из них.

Домашнее задание:
Составить подборку однотипных заданий В7 из сборника егэ, прорешать.

Спасибо
за урок!
23
multiurok.ru
Задача 7 — геометрический смысл производной
В задаче B9 дается график функции или производной, по которому требуется определить одну из следующих величин:
- Значение производной в некоторой точке x0,
- Точки максимума или минимума (точки экстремума),
- Интервалы возрастания и убывания функции (интервалы монотонности).
Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.
Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.
Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.
Вычисление значения производной. Метод двух точек
Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x0, и требуется найти значение производной в этой точке, применяется следующий алгоритм:
- Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x1; y1) и B (x2; y2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
- Зная координаты, легко вычислить приращение аргумента Δx = x2 − x1 и приращение функции Δy = y2 − y1.
- Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.
Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x2 − x1 = −1 − (−3) = 2; Δy = y2 − y1 = 6 − 2 = 4.
Найдем значение производной: D = Δy/Δx = 4/2 = 2.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x2 − x1 = 3 − 0 = 3; Δy = y2 − y1 = 0 − 3 = −3.
Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x2 − x1 = 5 − 0 = 5; Δy = y2 − y1 = 2 − 2 = 0.
Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.
Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.
Вычисление точек максимума и минимума
Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:
- Точка x0 называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≥ f(x).
- Точка x0 называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≤ f(x).
Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:
- Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
- Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x0 известно, что f’(x0) ≠ 0, то возможны лишь два варианта: f’(x0) ≥ 0 или f’(x0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
- Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.
Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:
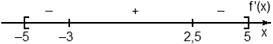
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:

Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:

На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.
Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.
Нахождение интервалов возрастания и убывания функции
В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:
- Функция f(x) называется возрастающей на отрезке [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≤ f(x2). Другими словами, чем больше значение аргумента, тем больше значение функции.
- Функция f(x) называется убывающей на отрезке [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≥ f(x2). Т.е. большему значению аргумента соответствует меньшее значение функции.
Сформулируем достаточные условия возрастания и убывания:
- Для того чтобы непрерывная функция f(x) возрастала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
- Для того чтобы непрерывная функция f(x) убывала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.
Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:
- Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
- Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
- Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.
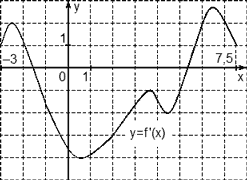
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:

Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:

Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l1 = − 6 − (−8) = 2;
l2 = 2 − (−3) = 5.
Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l2 = 5.
Смотрите также:
- Задача 7: касательная к графику функции

- Задача 7: касательная к графику функции — 2

- Пробный ЕГЭ-2011 по математике, вариант №4

- Пробный ЕГЭ 2012. Вариант 1 (без логарифмов)

- Так сокращать дроби нельзя!

- Быстрое возведение чисел в квадрат без калькулятора

www.berdov.com
Урок «График функции и её производная»
МБОУ «Дружногорская средняя общеобразовательная школа»
Урок алгебры в 11 классе по теме «График функции и её производной»
Автор урока учитель математики Ананьева Ольга Викторовна
Цели урока
Образовательные Установление связи свойств функции и её производной, исследование зависимостей между графиком функции и графиком её производной, обобщение приёмов исследования функций. создание условий необходимости самообразования и самостоятельности мышления.
Развивающие формирование познавательных мотивов и интересов, умений и навыков взаимодействия и общения, навыков индивидуального и совместного принятия решений. Обучение коллективной мыслительной и практической работе.
Воспитательные создание условий необходимости самообразования и самостоятельного и системного мышления.
Место урока Урок проводится как обобщающий исследование функции с помощью производной и для практической подготовки к итоговой аттестации.
Тип урока Урок применения знаний и умений
Оборудование: интернет-подключение, проектор, экран.
1. Организационный момент. (2 мин) На доске запись темы урока, На экране таблица:
Функция
Обозначение
Её производная
Зависимость у от х, функция
У = f (x)
У/ = f / (x)
Функция является постоянной
У = const
y/ = 0
Функция возрастает
y ↑
y/ > 0
Функция убывает
y ↓
y/ < 0
Функция имеет максимум в точке х0
max y
Производная в точке хо обращается в нуль
Функция имеет минимум в точке х0
min y
Производная в точке хо обращается в нуль
Функция в точке х = x1 имеет разрыв
Х1 – особая точка
y/ (х1) — не существует
Функция в точке х = x1 имеет излом
Х1 – особая точка
y/ (х1) — не существует
Функция в точке х1 имеет вертикальную касательную
Х1 – особая точка
y/ (х1) — не существует
2. Повторение (10 мин)
. По готовым чертежам
1. На рисунке изображен график функции 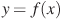 , определенной на интервале
, определенной на интервале 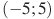 . Определите количество целых точек, в которых производная функции
. Определите количество целых точек, в которых производная функции 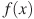 отрицательна.
отрицательна.
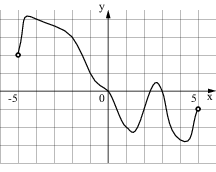
2. На рисунке изображен график функции 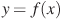 , определенной на интервале
, определенной на интервале 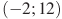 . Найдите сумму точек экстремума функции
. Найдите сумму точек экстремума функции 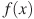 .
.

3. На рисунке изображен график функции 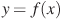 , определенной на интервале
, определенной на интервале 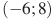 . Определите количество целых точек, в которых производная функции положительна.
. Определите количество целых точек, в которых производная функции положительна.

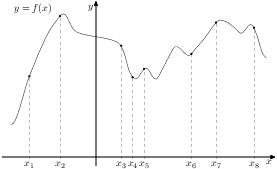
4. На рисунке изображён график функции 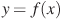 и восемь точек на оси абсцисс: ,
и восемь точек на оси абсцисс: , 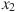 ,
, 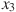 ,
,  ,
, 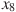 . В скольких из этих точек производная функции
. В скольких из этих точек производная функции 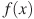 положительна?
положительна?
5. На рисунке изображён график функции 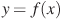 и двенадцать точек на оси абсцисс: ,
и двенадцать точек на оси абсцисс: , 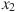 ,
, 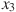 ,
,  ,
, 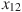 . В скольких из этих точек производная функции
. В скольких из этих точек производная функции 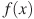 отрицательна?
отрицательна?
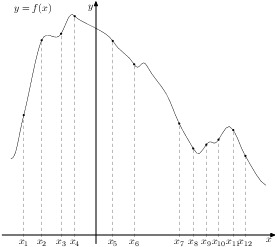
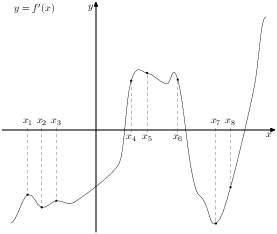
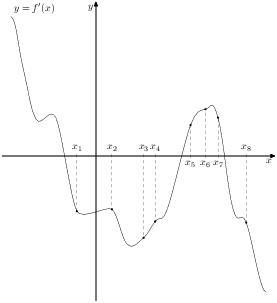
6. На рисунке изображён график  производной функции
производной функции 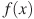 и восемь точек на оси абсцисс: ,
и восемь точек на оси абсцисс: , 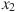 ,
, 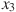 ,
,  ,
, 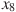 . В скольких из этих точек функция
. В скольких из этих точек функция 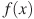 возрастает?
возрастает?
3. Основной материал урока
* Учитель Обратите внимание на вопрос в задаче № 6. По графику производной найти количество точек, в которых функция возрастает. Значит, надо вспомнить
4. На рисунке изображён график  производной функции
производной функции 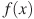 и восемь точек на оси абсцисс: ,
и восемь точек на оси абсцисс: , 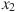 ,
, 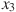 ,
,  ,
, 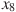 . В скольких из этих точек функция
. В скольких из этих точек функция 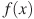 убывает?
убывает?
5.
infourok.ru
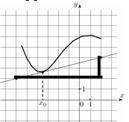
 Здесь «подъем», знак «плюс».
Здесь «подъем», знак «плюс».