Вычитание дробей | Формулы с примерами

Вычитание дробей

С одинаковыми знаменателями

Определение
Что бы найти разность дробей с одинаковыми знаменателями, нужно просто вычесть их числители. Знаменатель останется прежним.

Наглядный пример
Найдем, во сколько раз каждый знаменатель меньше общего
и умножим каждую дробь на это число.

Пример 1131 —  431 = 11 — 431 = 7  31;

92 —  3

2 = 9 — 32 = 62 =  3;1

186 —  126 = 18 — 126 = 66 =  1.1

С разными знаменателями

Определение
Чтобы вычесть дроби с разными знаменателями, надо привести их к общему знаменателю.

Порядок действий

1. Преобразуем смешанную дробь в неправильную;
2. Найдем общий знаменатель;
3. Приведем дроби к общему знаменателю;
4. Выполним действия с числителями;
5. Приведем получившуюся неправильную дробь к смешанной.

Пример
1417 —  23 =  4251 —  3451 =  8  51;

2119 —  12 =  2238 —  1938 =  3  38;

3223 —  43 =  9669 —  9269 =  4  69.

Сложение и вычитание дробей | Cubens

Сложение дробей

Сложение дробей с одинаковыми знаменателями

Чтобы добавить две дроби с одинаковыми знаменателями, нужно добавить их числители, а знаменатели оставить без изменений:

Примеры сложения дробей с одинаковыми знаменателями

Пример 1: Добавить две дроби с равными знаменателями:

и

Ответ:

Пример 2: Добавить две дроби с равными знаменателями: и

Ответ:

Сложение дробей с разными знаменателями

Чтобы добавить две дроби с разными знаменателями, нужно:

Примеры сложения дробей с разными знаменателями

Пример 3: Добавить две дроби с разными знаменателями: и

 

Ответ:

Пример 4: Добавить две дроби с разными знаменателями: и

Ответ:

Сложение смешанных чисел

Чтобы добавить два смешанных числа, нужно:

Примеры сложения смешанных чисел

Пример 5: Добавить два смешанных числа: и

Ответ:

Вычитание дробей

Вычитание дробей с одинаковыми знаменателями

Чтобы вычесть две дроби с одинаковыми знаменателями, нужно вычесть из числителя первой дроби числитель второй, а знаменатель оставить без изменений:

 

Примеры вычитания дробей с одинаковыми знаменателями

Пример 1: Вычесть две дроби с равными знаменателями: и

 

Ответ:

Вычитание дробей с разными знаменателями

Чтобы вычесть две дроби с разными знаменателями, нужно:

Примеры вычитания дробей с разными знаменателями

Пример 2: Вычесть две дроби с разными знаменателями: и

Ответ:

Вычитание смешанных чисел

Чтобы вычесть два смешанных числа, нужно:

• привести дробные части этих чисел к наименьшему общему знаменателю;
• если дробная часть уменьшаемого меньше дробной части вычитателя, превратить ее в неправильную дробь, уменьшил на единицу, целую часть;
• отдельно выполнить вычитание целых частей и отдельно дробных частей;
• сократить полученную дробь.

Примеры вычитания смешанных чисел

Пример 5: Добавить два смешанных числа: и

Ответ:

Сложение и вычитание десятичных дробей

Сложение и вычитание десятичных дробей выполняется поразрядно. Удобно это выполнять в столбик.

Подробная информация и примеры решения на сложение и вычитание десятичных дробей читайте здесь

Доли и дроби. Арифметические действия с дробями. Сокращение дроби. Умножение и деление дроби на натуральное число. Умножение и деление дробей. Сложение и вычитание дробей с различными знаменателями.

	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа.  / / Доли и дроби. Арифметические действия с дробями. Сокращение дроби. Умножение и деление дроби на натуральное число. Умножение и деление дробей. Сложение и вычитание дробей с различными знаменателями. Поделиться:    Доли и дроби. Арифметические действия с дробями. Сокращение дроби. Умножение и деление дроби на натуральное число. Умножение и деление дробей. Сложение и вычитание дробей с различными знаменателями. Дробь: это одна или несколько долей целого Знаменатель дроби (то, что записывется под чертой): это число долей, на которое делилось целое Числитель дроби (то, что записывется над чертой): это сколько таких долей было взято

Сложение и вычитание десятичных дробей

Правило сложения и вычитания десятичных дробей

Правило
1. Подписать одну дробь под другую таким образом, чтобы запятая
одной десятичной дроби оказалась под другой, т.е. что бы цифры
одноименных разрядов были точно друг под другом;

2. Сложить (или вычесть) дроби поразрядно, начиная с младшего разряда;

3. В полученном результате поставить запятую под запятыми обеих дробей.

Пример
+12, 73311, 25523, 988                          —27, 95712, 12615, 831

+21, 27713, 11234, 289                          —37, 99323, 44114, 582

+37, 21611, 32348, 539                          —77, 29253, 13024, 162

Правило сложения

Правило
! При сложении применяется правило добавлять единицу к старшему
разряду (1), если сумма цифр в данном разряде больше 9. Пример
+  74, 5131  37, 231101, 744

+  95, 5531  27, 441122, 994

+  64, 4181  59, 231123, 649

Правило вычитания

Правило
! При вычитании применяется правило занимать единицу у старшего разряда (пример 1).

! При вычитании количество цифр в дробной части предварительно уравнивают с помощью нулей (пример 2).

Пример
—122, 43•  41, 22  81, 21                          —46, 300•   • •14, 45731, 843

—153, 64•  82, 13  71, 51                          —67, 400•   • •25, 67941, 721

—204, 75•  72, 61132, 12                          —93, 700•   • •71, 92321, 777

Сложение и вычитание дробей с разными знаменателями

Складывать и вычитать дроби с разными знаменателями можно только тогда, когда в процессе вычисления дроби приведены к одному общему знаменателю.

Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, являющихся знаменателями заданных дробей.

К числителям заданных дробей нужно поставить дополнительные множители, равные отношению НОК и соответствующего знаменателя.

Числители заданных дробей умножаются на свои дополнительные множители, получаются числители дробей с единым общим знаменателем. Знаки действий («+» или «-») в записи дробей, приводимых к общему знаменателю, сохраняются перед каждой дробью. У дробей с общим знаменателем знаки действий сохраняются перед каждым приведенным числителем.

Только теперь можно сложить или вычесть числители и подписать под результатом общий знаменатель.

Внимание! Если в результирующей дроби у числителя и знаменателя есть общие множители, то дробь надо сократить. Неправильную дробь желательно перевести в смешанную дробь. Оставить результат сложения или вычитания, не сократив дробь, где это возможно, — это неоконченное решение примера!

Сложение и вычитание дробей с разными знаменателями. Правило. Чтобы сложить или вычесть дроби с разными знаменателями, нужно их сначала привести к наименьшему общему знаменателю, а потом производить действия сложения или вычитания как с дробями с одинаковыми знаменателями.

Порядок действий при сложении и вычитании дробей с разными знаменателями

1. найти НОК всех знаменателей;
2. проставить к каждой дроби дополнительные множители;
3. умножить каждый числитель на дополнительный множитель;
4. полученные произведения взять числителями, подписав под каждой дробью общий знаменатель;
5. произвести сложение или вычитание числителей дробей, подписав под суммой или разностью общий знаменатель.

Так же производится сложение и вычитание дробей при наличии в числителе букв.

Например:

Запись опубликована в рубрике Математика с метками вычитание, дробь, знаменатель, сложение. Добавьте в закладки постоянную ссылку.

Калькулятор для сложения дробей онлайн

Рассмотрим разные варианты:

а) сложение с одинаковыми знаменателями.
При выполнении действия сложения дробей, имеющих одинаковые знаменатели, нужно сложить числители исходных дробей, при этом знаменатель оставить прежний, равный знаменателю обеих дробей:

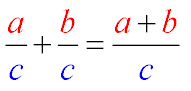
а — величина числителя 1-й дроби;
b — величина второго числителя;
с — знаменатель дробей.

б) сложение с разными знаменателями.
Чтобы выполнить действие сложения дробей с разными знаменателями, следует:
1. привести дроби к одному общему знаменателю, рассчитав наименьшее общее кратное;
2. сложить дроби, как в случае с дробями с одинаковые знаменатели, т. е числители дробей складываются, а знаменатель — без изменений.
3. если у вновь полученной дроби имеются общие множители, ее надо сократить. В противном случае пример считается неоконченным;
4. неправильную дробь следует преобразовать в смешанную.

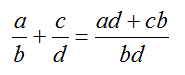
в) дроби и целого числа.
Для сложения дроби и целого числа необходимо:
1. целое число преобразовать в дробь со знаменателем которой будет 1;
2. приводим к общему знаменателю;
3. складываем дроби;
4. вновь полученную дробь, если возможно, сокращаем;
5. если в результате сложения имеем неправильную дробь, выделяем целую часть.

г) сложение смешанных дробей.
Чтобы выполнить это действие, необходимо:
1. отдельно произвести сложение целых частей;
2. отдельно — дробных частей, приведя их в случае необходимости к НОК;
3. если в дробной части вышла неправильная дробь, требуется выделить из нее целую часть и сложить с полученной целой частью.

Сложение смешанных дробей можно выразить формулой:

А, В — целые части дробей;
а, b — числители дробных частей;
с — знаменатель дроби.

С помощью онлайн калькулятора можно легко и быстро осуществить все необходимые расчеты.

Калькулятор для сложения дробей онлайн