Функция целая часть числа | Алгебра
Определение
Целой частью действительного числа x (x∈R) называется наибольшее целое число, не превосходящее x.
Целую часть числа x обозначают символом [x].
[x] читают «антье от x».
Обозначение [x] в 1808 году ввёл К. Гаусс.
В частности, если n — целое число (n∈Z), то [n]=n.
Примеры.
Вычислить целую часть числа:
7,8; 0,12; -0,7; -4,92; 15 2/3; 5/7; -3/11; 8; -50.
Решение:
Фактически вычисление целой части числа x представляет собой округление до ближайшего к числу x целого числа в меньшую сторону (то есть округление с недостатком).
[7,8]=7;
[0,12]=0;
[ -0,7]= -1;
[-4,92]= -5;
[8]=8;
[-50]= -50.
Определение
Функцию, ставящую в соответствие каждому значению x его целую часть — число [x], называют целой частью числа x и обозначают y=[x] .
Функция целая часть числа определена для любого действительного x (x∈R).
Область значений функции y=[x] — множество целых чисел (y∈Z).
Утверждение.
Для любого k∈Ζ [x+k]=[x]+k.
Доказательство:
Пусть [x]=m.
По определению целой части числа
m≤x<m+1,
m+k≤x+k<(m+k)+1.
Отсюда [x+k]=m+k=[x]+k.
Что и требовалось доказать.
График функции y=[x]
Стрелки на графике показывают, что правые концы отрезков не принадлежат графику.
Другой вариант показать, что левые концы отрезков принадлежат графику, а правые — не принадлежат, выделить их, соответственно, закрашенными и выколотыми точками:
Как решить уравнение с целой частью числа?
Простейшее уравнение [x]=a имеет решения только при целых значениях a. Если a∉Ζ, уравнение не имеет решений.
При a∈Ζ решения уравнения [x]=a удовлетворяют условию a≤x<a+1.
Примеры.
1) [x]=7
7≤x<7+1, то есть 7≤x<8.
Ответ запишем в виде числового промежутка (в данном случае, полуинтервала).
Ответ: x∈[7;8).
2) [x]=3,2.
Это уравнение не имеет решений, так как 3,2∉Ζ.
3) [7,2-0,5x]= -3
-3≤7,2-0,5x<-3+1
-3≤7,2-0,5x<-2.
Прибавим почленно к каждой части неравенства -7,2. Знаки неравенства при этом не изменятся:
-3-7,2≤-0,5x<-2-7,2
-10,2≤-0,5x<-9,2.
Умножим каждую часть неравенства на -2. При умножении на отрицательное число знаки неравенства меняются на противоположные:
20,4≥x>18,4
18,4<x≤20,4.
Ответ: x∈(18,4; 20,4].
4)2x-3[x]=9.
Выразим целую часть числа числа [x]:
Отсюда
Таким образом, x∈[-9;-6) и
На промежутке [-9;-6) [x] принимает три значения.
1. При x∈[-9;-8) [x]= -9.
Подставив в равенство (*) [x]= -9, найдём x:
Так как -9∈[-9;-8), то x= -9 — корень уравнения.
2. При x∈[-8;-7) [x]= -8, откуда
-7,5∈[-8;-7), поэтому x= -7,5 — корень уравнения.
3. При x∈[-7;-6) [x]= -7, и
-6∉[-7;-6), значит x= -6 не является корнем уравнения.
Ответ: -9; -7,5.
www.algebraclass.ru
Функция «Целая часть числа» ее свойства и график
Функция «Целая часть числа» ее свойства и графикФункция «Целая часть числа», ее свойства и график
Функция целая часть числа имеет вид y = [x].
1. Функция имеет смысл для всех значений переменной x, что следует из определения целой части числа и свойств числовых множеств (непрерывности множества действительных чисел, дискретности множества целых чисел и бесконечности обоих множеств). Следовательно, ее областью определения является все множество действительных чисел
D([x]) = R.2. Функция ни четная, ни нечетная. Область определения функции симметрична относительно начала координат, но если [x] = a, то [-x] = -(a+1), т.е. не выполняется ни условие четности ( f (-x) = f (x) ), ни условие нечетности ( f (-x) = — f (x) ).
3. Функция y = [x] не периодическая.
4. Множество значений функции y = [x], это множество целых чисел (по определению целой части числа)
E ([x]) = Z .5. Функция неограничена, так как множество значений функции все целые числа, множество целых чисел неограничено.
6. Функция разрывна. Все целые значения x точки разрыва первого рода с конечным скачком равным 1. В каждой точке разрыва имеется
7. Функция принимает значение 0 для всех x, принадлежащих интервалу [0;1), что следует из определения целой части числа. Следовательно, нулями функции будут все значения этого интервала.
8. Учитывая свойства целой части числа функция y = [x] принимает отрицательные значения при x меньших нуля, и положительные значения при x больших 1.
9. Функция y = [x] кусочно — постоянная и неубывающая.
10. Точек экстремума функция не имеет, так как не меняет характер монотонности.
11. Так как функция y = [x] постоянна на каждом интервале [n ; n+1), она не принимает наибольшего и наименьшего значений на области определения.
12. График функции.
kus-lin.narod.ru
Функция [X] (целая часть X)
Функция
[x]
равна наибольшему целому числу,
превосходящемуx (x – любое действительное число). Например: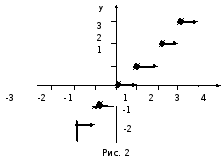
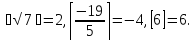
Функция [x] имеет «точки разрыва»: при целых значениях x она «изменяется скачком».
На рис.2 дан график этой функции, причем левый конец каждого из горизонтальных отрезков принадлежит графику (жирные точки), а правый – не принадлежит.
Попробуйте
доказать,
что если каноническое разложение числа n!
есть 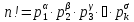
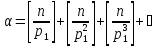
Аналогичные
формулы имеют место для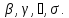
Зная
это, легко определить, например, сколькими
нулями оканчивается число 100! Действительно,
пусть 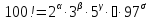 .
Тогда
.
Тогда
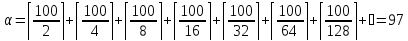 и
и 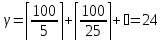 .
.
Следовательно,
100! Делится на 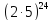 ,
т.е. оканчивается двадцатью четырьмя
нулями.
,
т.е. оканчивается двадцатью четырьмя
нулями.
Фигуры из кусочков квадрата
К числу полезных и увлекательных развлечений относится составление фигур из семи кусочков квадрата, разрезанного в соответствии с рис.3, (а), причем при составлении заданных фигур должны быть использованы все семь кусочков, и они должны налегать, даже частично, друг на друга.
На рис. 4 приведены симметричные фигуры1. Попробуйте сложить эти фигуры из частей квадрата, изображенного на рис. 3, (а).
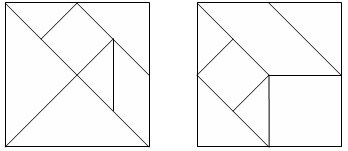
(а) (b)
Рис.3
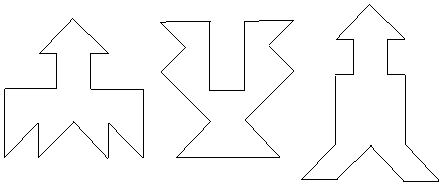
Рис. 4
Из этих же чертежей можно складывать и многие другие фигуры (например, изображения различных предметов, животных и т.п.).
Менее распространенным вариантом игры является составление фигур из кусочков квадрата, изображенного на рис. 3, (b).
Магические квадраты
Магические квадрат «n2-квадратом» назовем квадрат, разделенный на
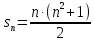
Если одинаковы лишь суммы чисел, стоящих в любом горизонтальном и вертикальном ряду, то квадрат называется полумагическим.
16 | 3 | 2 | 13 |
5 | 10 | 11 | 8 |
9 | 6 | 7 | 12 |
4 | 15 | 14 | 1 |
Магический 42 –квадрат назван именем Дюрера, математика и художника XVIвека, изображавшего квадрат на известной картине «Меланхолия».
Кстати, два нижних средних числа этого квадрата образуют число 1514-дату создания картины.
Существует лишь восемь девятиклеточных магических квадратов. Два из них, являющиеся зеркальным изображением друг друга, приведены на рисунке; остальные шесть могут быть получены из этих квадратов вращение их вокруг центра на 90°, 180°, 270°
2. Нетрудно полностью исследовать вопрос о магических квадратов при n=3
Действительно,S3 = 15 , и существует лишь восемь способов представления числа 15 в виде суммы различных чисел (от единицы до девяти):
15=1+5+9=1+6+8=2+4+9=2+5+8=2+6+7=3+4+8=3+5+7=4+5+6
Заметим, что каждое из чисел 1, 3, 7, 9 входит в две, а каждое из чисел 2, 4, 6, 8 – в три указанные суммы и лишь число 5 входит в четыре суммы. С другой стороны, из восьми трехклеточных рядов: трех горизонтальных, трех вертикальных и двух диагональных – через каждую из угловых клеток квадрата проходит по три, через центральную клетку по четыре и через каждую из остальных клеток по два ряда. Следовательно, число 5 должно обязательно стоять в центральной клетке, числа 2, 4, 6, 8 – в угловых клетках, а числа 1, 3, 7, 9 – в остальных клетках квадрата.
studfile.net
Целая часть числа Википедия
 График функции «пол» (целая часть числа)
График функции «пол» (целая часть числа) 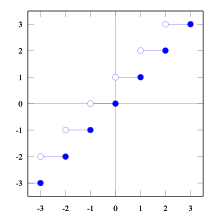 График функции «потолок»
График функции «потолок»В математике, целая часть вещественного числа x{\displaystyle x} — округление x{\displaystyle x} до ближайшего целого в меньшую сторону. Целая часть числа также называется антье (фр. entier), или пол (англ. floor). Наряду с полом существует парная функция — потолок (англ. ceiling) — округление x{\displaystyle x} до ближайшего целого в большую сторону.
Содержание
- 1 Обозначения и примеры
- 2 Определения
- 3 Свойства
- 3.1 Пол и потолок как функции вещественной переменной
- 3.2 Связь функций пол и потолок
- 3.3 Пол/потолок: неравенства
- 3.4 Пол/потолок: сложение
- 3.5 Пол/потолок под знаком функции
- 3.6 Пол/потолок: суммы
- 3.7 Разложимость в ряд
- 4 Применение
- 4.1 Количество цифр в записи числа
- 4.2 Округление
- 4.3 Бинарная операция mod
- 4.4 Дробная часть
- 4.5 Количество целых точек промежутка
- 4.6 Теорема Рэлея о спектре
- 5 В информатике
- 5.1 В языках программирования
- 5.2 В системах вёрстки
- 6 Примечания
- 7 См. также
- 8 Литература
Обозначения и примеры[ | ]
Впервые квадратные скобки ([x]{\displaystyle [x]}) для обозначения целой части числа x{\displaystyle x} использовал Гаусс в 1808 году в своём доказательстве закона квадратичной взаимности[1]. Это обозначение считалось стандартным[2], пока
ru-wiki.ru
Целая часть Википедия
 График функции «пол» (целая часть числа)
График функции «пол» (целая часть числа)  График функции «потолок»
График функции «потолок»В математике, целая часть вещественного числа x{\displaystyle x} — округление x{\displaystyle x} до ближайшего целого в меньшую сторону. Целая часть числа также называется антье (фр. entier), или пол (англ. floor). Наряду с полом существует парная функция — потолок (англ. ceiling) — округление x{\displaystyle x} до ближайшего целого в большую сторону.
Содержание
- 1 Обозначения и примеры
- 2 Определения
- 3 Свойства
- 3.1 Пол и потолок как функции вещественной переменной
- 3.2 Связь функций пол и потолок
- 3.3 Пол/потолок: неравенства
- 3.4 Пол/потолок: сложение
- 3.5 Пол/потолок под знаком функции
- 3.6 Пол/потолок: суммы
- 3.7 Разложимость в ряд
- 4 Применение
- 4.1 Количество цифр в записи числа
- 4.2 Округление
- 4.3 Бинарная операция mod
- 4.4 Дробная часть
- 4.5 Количество целых точек промежутка
- 4.6 Теорема Рэлея о спектре
- 5 В информатике
- 5.1 В языках программирования
- 5.2 В системах вёрстки
- 6 Примечания
- 7 См. также
- 8 Литература
Обозначения и примеры[ | ]
Впервые квадратные скобки ([x]{\displaystyle [x]}) для обозначения целой части числа x{\displaystyle x} использовал Гаусс в 1808 году в своём доказательстве закона квадратичной взаимности[1]. Это обозначение считалось стандартным[2], пока Кеннет Айверсон в
ru-wiki.ru
Целая часть числа — это… Что такое Целая часть числа?
- Целая часть числа
-

График целой части
В математике, целая часть, антье (фр. entier) или функция «пол» (англ. floor) — это функция, определённая на множестве вещественных чисел и принимающая целочисленные значения. Целая часть числа x обычно обозначается через
 или [x] и определяется как наибольшее целое число, не превосходящее x:
или [x] и определяется как наибольшее целое число, не превосходящее x:Примеры
Свойства
- Целая часть x всегда удовлетворяет неравенству:
 .
.
Нули функции
В промежутке [0;1) значение функции равно нулю.
См. также
Литература
- М. К. Потапов, В. В. Александров, П. И. Пасиченко. Алгебра и начала анализа. — АО Столетие, 1996.
Wikimedia Foundation. 2010.
- Целан П.
- Целе (графство)
Смотреть что такое «Целая часть числа» в других словарях:
Целая часть числа — см. Дробная и целая части числа … Большая советская энциклопедия
ЦЕЛАЯ ЧАСТЬ — числа x (антье) (франц. entier) наибольшее целое число ?x; обозначается ЦЕЛЕ (Celje) город в Словении. Ок. 40 тыс. жителей (1990). Цинкоплавильный завод; металлообрабатывающая, химическая, деревообрабатывающая промышленность. Руины крепости 15 18 … Большой Энциклопедический словарь
Целая часть — График функции «пол» (целая часть числа) … Википедия
целая часть — числа х (антье) (франц. entier), наибольшее целое число ≤х; обозначается [х]. Так, [5,6] = 5,[ 1/2] = 1. * * * ЦЕЛАЯ ЧАСТЬ ЦЕЛАЯ ЧАСТЬ числа x (антье) (франц. entier), наибольшее целое число Јx; обозначается [x]. Так, [5,6] = 5, [ 1/2] = 1 … Энциклопедический словарь
ЦЕЛАЯ ЧАСТЬ — числа х, антье (франц. entier целый), наибольшее целое число =< х; обозначается [х]. Так, [5.6] = 5, [ 1/2] = 1 … Большой энциклопедический политехнический словарь
ЦЕЛАЯ ЧАСТЬ — числа х (антье) (франц. entier), наибольшее целое число =<х; обозначается [х]. Так, [5,6]=5,[ 1/2] = 1 … Естествознание. Энциклопедический словарь
Числа с плавающей запятой — Плавающая запятая форма представления действительных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее… … Википедия
Числа с плавающей точкой — Плавающая запятая форма представления дробных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто… … Википедия
Числа с фиксированной точкой — Число с фиксированной запятой формат представления вещественного числа в памяти ЭВМ в виде целого числа. При этом само число x и его целочисленное представление x′ связаны формулой , где z цена младшего разряда. Простейший пример арифметики с… … Википедия
Прямой код (представление числа) — Прямой код способ представления двоичных чисел с фиксированной запятой в компьютерной арифметике. Главным образом используется для записи положительных чисел. Содержание 1 Представление числа в прямом коде 1.1 Примеры … Википедия
dic.academic.ru
Целая часть — это… Что такое Целая часть?
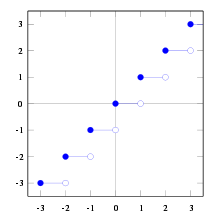 График функции «пол» (целая часть числа)
График функции «пол» (целая часть числа) 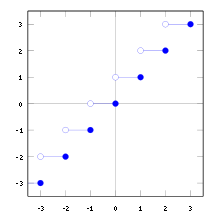 График функции «потолок»
График функции «потолок»В математике, целая часть вещественного числа — округление до ближайшего целого в меньшую сторону. Целая часть числа также называется антье (фр. entier), или пол (англ. floor). Наряду с полом существует парная функция — потолок (англ. ceiling) — округление до ближайшего целого в большую сторону.
Обозначения и примеры
Для целой части числа долгое время использовалось обозначение , введенное Гауссом[источник не указан 1264 дня]. Ни понятия функции потолок, ни специального обозначения для нее не существовало. В 1962 году Кеннет Айверсон предложил округления числа до ближайшего целого в меньшую и большую стороны называть «пол» и «потолок» и обозначать и соответственно [1].
В современной математике используются оба обозначения, и , однако существует тенденция перехода к терминологии и обозначениям Айверсона. Одна из причин этого — потенциальная неоднозначность понятия «целая часть числа»[1]. Например, целая часть числа 2,7 равна 2, но возможны два мнения на то, как определить целую часть числа −2,7. В соответствии с данным в этой статье определением , однако в некоторых калькуляторах имеется функция целой части числа INT, для отрицательных чисел определяемая как INT(-x) = -INT(x), так что INT(-2,7) = −2. В терминологии Айверсона отсутствуют возможные неоднозначности:
Определения
Функция пол определяется как наибольшее целое, меньшее или равное :
Функция потолок определяется как наименьшее целое, большее или равное :
Эти определения эквивалентны следующим неравенствам (где n — целое число) [2]:
Свойства
Везде ниже обозначают вещественные числа, а — целые.
Пол/потолок как функции вещественной переменной
Функции пол/потолок отображают множество вещественных чисел в множество целых чисел:
Пол/потолок — кусочно-постоянные функции.
Функции пол/потолок имеют разрывны во всех целочисленных точках, это разрывы первого рода со скачком, равным единице.
При этом, функция пол является:
Функция потолок является:
Связь функций пола и потолка
Для произвольного [3]
Для целого пол и потолок совпадают:
Если — не целое, то потолок ровно на единицу выше пола:
Функции пола и потолка являются отражениями друг друга от обеих осей:
Пол/потолок: неравенства
Любое неравенство между вещественным и целым числами равносильно неравенству с полом и потолком между целыми числами [2]:
Два верхних неравенства являются непосредственными следствиями определений пола и потолка, а два нижние — обращение верхних от противного.
Функции пол/потолок являются монотонно возрастающими функциями:
Пол/потолок: сложение
Целочисленное слагаемое можно вносить/выносить за скобки пола/потолка [4]:
Предыдущее равенство, вообще говоря, не выполняется, если оба слагаемых — вещественные числа. Однако и в этом случае справедливы неравенства:
Пол/потолок под знаком функции
Имеет место следующее предложение:[5]
Пусть — непрерывная монотонно возрастающая функция, определенная на некотором промежутке, обладающая свойством:
Тогда
всякий раз, когда определены .
В частности,
если и — целые числа, и .
Пол/потолок: суммы
Если — целые числа, , то [6]
Вообще, если — произвольное вещественное число, а — целое положительное, то
Имеет место более общее соотношение [7]:
Так как правая часть этого равенства симметрична относительно и , то справедлив следующий закон взаимности:
Разложимость в ряд
Тривиальным образом функция Антье раскладывается в ряд с помощью функции Хевисайда:
где каждое слагаемое ряда создаёт характерные «ступеньки» функции. Этот ряд сходится абсолютно, однако ошибочное преобразование его слагаемых может привести к «упрощённому» ряду
который расходится.
Применение
Целочисленные функции пол/потолок находят широкое применение в дискретной математике и теории чисел. Ниже приведены некоторые примеры использования этих функций.
Количество цифр в записи числа
Количество цифр в записи целого положительного числа в позиционной системе счисления с основанием b равно [8]
Округление
Ближайшее к целое число может быть определено по формуле
Бинарная операция mod
Операция «остаток по модулю», обозначаемая , может быть определена с помощью функции пола следующим образом. Если — произвольные вещественные числа, и , то неполное частное от деления на равно
- ,
а остаток
Дробная часть
Дробная часть вещественного числа по определению равна
Количество целых точек промежутка
Требуется найти количество целых точек в замкнутом промежутке с концами и , то есть количество целых чисел , удовлетворяющий неравенству
В силу свойств пол/потолка, это неравенство равносильно
- .
Это есть точек в замкнутом промежутке с концами и , равное .
Аналогично можно подсчитать количество целых точек в других типах промежутков. Сводка результатов приведена ниже [9].
(Через обозначена мощность множества ).
Первые три результата справедливы при всех , а четвертый — только при .
Теорема Рэлея о спектре
Пусть и — положительные иррациональные числа, связанные соотношением [10]
Тогда в ряду чисел
каждое натуральное встречается в точности один раз. Иными словами, последовательности
- и ,
называемые последовательностями Бетти (англ.), образуют разбиение натурального ряда.[11]
В информатике
В языках программирования
Во многих языках программирования существуют встроенные функции пола/потолка floor(), ceil().
В системах вёрстки
В TeX (и LaTeX) для символов пола/потолка , , , существуют специальные команды: \lfloor, \rfloor, \lceil, \rceil. Поскольку wiki использует LaTeX для набора математических формул, то и в данной статье использованы именно эти команды.
Примечания
- ↑ 1 2 Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 88.
- ↑ 1 2 Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 90.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 89.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 90-91.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 93.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 108.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 112-117.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 91.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 95-96.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 99-100.
- ↑ А. Баабабов «Пентиум» хорошо, а ум лучше // Квант. — 1999. — № 4. — С. 36-38.
См. также
Литература
- Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — М.: «Мир», 1998. — 703 с. — ISBN 5-03-001793-3
- М. К. Потапов, В. В. Александров, П. И. Пасиченко. Алгебра и начала анализа. — АО Столетие, 1996.
biograf.academic.ru
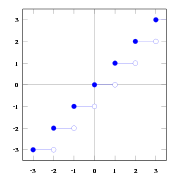
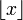 или [x] и определяется как наибольшее целое число, не превосходящее x:
или [x] и определяется как наибольшее целое число, не превосходящее x: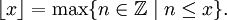
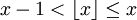 .
.