Центр тяжести и центр инерции. Условия равновесия твердого тела

Произвольные системы точек под действием внешних сил двигаются и меняют свою форму (деформируются). Существуют абсолютно твёрдые тела, то есть тела, размер и форму которых считают неизменными (размером деформации пренебрегают). Прикладывая силы к совокупности точек абсолютно твёрдого тела, можно привести его в движение и (или) к вращению.

Суммой сил, действующих на абсолютно твёрдое тело, называется такая сила, которая вызывает такое же движение этого тела, как и действующие на него силы.

Когда сумма действующих на тело сил равна нулю, центр масс этого тела находится в состоянии равномерного прямолинейного движения, то есть существует такая система инерциального отсчёта, в которой центр масс этого тела покоится (первое условие равновесия абсолютно твёрдого тела). Однако тело может вращаться относительно этого центра масс (см. рис. 1).

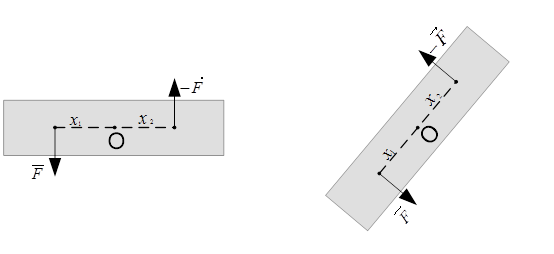
Рис. 1. Вращение абсолютно твёрдого тела при нулевом значении суммы действующих сил

Отсутствие вращательного движения тела обеспечит нулевое значение суммы моментов действующих на него сил (второе условие равновесия абсолютно твёрдого тела). При этом точка, от которой отсчитываются моменты, является произвольной.

Модуль момента силы равен произведению плеча силы (кратчайшее расстояние от точки, от которой отсчитываются моменты, до линии действия силы) на саму силу. То есть, если выбрать точку O как точку, от которой отсчитываются моменты на рис. 1, то момент силы 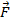 равен произведению плеча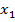

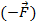 на эту силу, и он направлен против часовой стрелки; момент силы  – произведение плеча  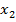на эту силу, и он также направлен против часовой стрелки. Следовательно, в данном случае, сумма моментов этих сил отлична от нуля.

Если направить силу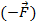

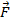 в противоположную сторону (см. рис. 2), тогда её момент направлен по часовой стрелке, а сумма моментов сил  и 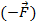 может быть равна нулю.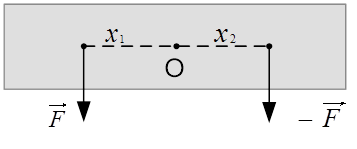

Рис. 2. Силы, действующие на твёрдое тело

Чтобы вычислить суммарную силу или суммарный момент сил, действующих на абсолютное твёрдое тело, необходимо уметь складывать силы, приложенные к разным точкам этого тела. Для этого необходимо помнить тот факт, что силу можно переносить вдоль направления её действия, так как при этом не меняется её величина и момент. Следовательно, силу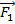

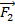 , приложенную к точке A, и силу , приложенную к точке B (см. рис. 3), переносим вдоль направления действия до тех пор, пока эти силы не окажутся в одной точке (если эти силы не параллельны). В этой точке (D) складываем векторы сил по правилу параллелограмма. Суммарная сила будет направлена вдоль диагонали этого параллелограмма, и эту силу можно продлить до пересечения с точкой (C) данного твёрдого тела.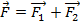

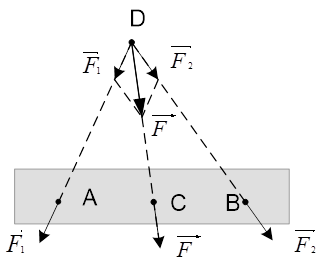
Рис. 3. Сложение векторов сил

Суммарная сила (F) должна быть не только равной по величине сумме параллельных сил (их можно складывать по абсолютной величине, так как они направлены одинаково), но и иметь такой же момент относительно любой точки, как и исходные силы (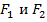). Для этого необходимо найти такую точку, относительно которой суммарный момент сил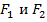

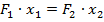 равен нулю, то есть . И приложить в этой точке суммарную силу  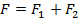(см. рис 4). Из выражения  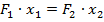находим координату точки. Это и будет точка приложения суммарной силы.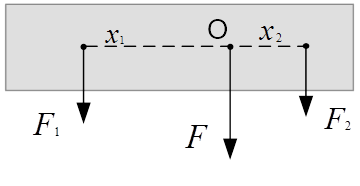

Рис. 4. Сложение параллельных сил

Определение точки приложения суммарной силы позволяет установить центр тяжести твёрдого тела.

Центр тяжести – точка приложения суммарной силы тяжести, действующей на разные материальные точки, составляющие данную систему.

Для определения точки, к которой прикладывается суммарная сила тяжести, необходимо тело, изображённое на рис. 4, повернуть на произвольный угол. При этом изменится направление действия сил 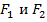 (но они останутся параллельными), направление действия силы F. Пересечение линий действия суммарной силы F до и после изменения положения тела укажет искомую точку – центр тяжести (т. O) (см. рис. 5).

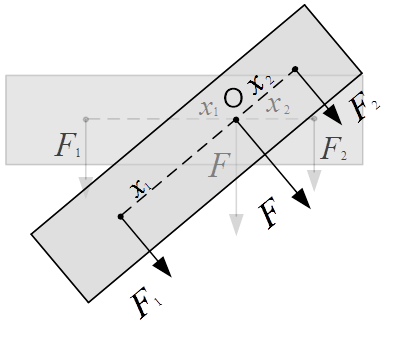
Рис. 5. Определение точки приложения суммарной силы тяжести

Как известно из прошлых уроков, центр масс (центр инерции) – такая точка, которая удовлетворяет соотношению: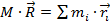

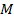, где  – масса системы,  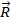– радиус вектор системы,  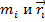– масса и радиус вектор i-й материальной точки.

Если выбрать начало отсчёта в точке центра масс, то в левой части равенства будет ноль: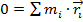

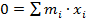. Так как это векторное равенство, то его можно спроецировать на любое направление, например, на ось X: ,  где x – расстояние от центра масс до материальной точки вдоль оси X.

Умножим полученное равенство на ускорение свободного падения (g): 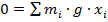, где

 – сила тяжести, действующая на материальную точку.

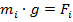
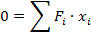
Следовательно, мы получили формулу, из которой видно, что сумма сил, умноженных на плечо, равна нулю, что является условием центра тяжести. Таким образом, центр масс совпадает с центром тяжести.

Равновесие твёрдого тела может быть устойчивым или неустойчивым.

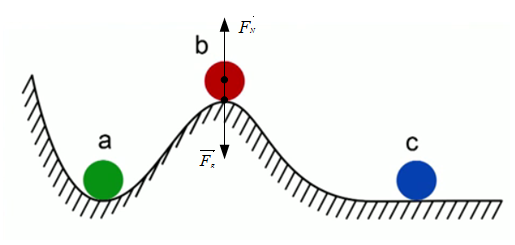
Рис. 6. Положения равновесия

На рис. 6 изображён шарик b, который лежит на горке. Сумма действующих на него сил равна нулю, если центр тяжести находится на одной вертикальной линии с точкой опоры (сила реакции опоры (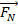

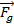) действует снизу вверх, сила тяжести (), приложенная к центру шарика, действует сверху вниз, их сумма и сумма их моментов равна нулю). Но, если этот шарик вывести из положения равновесия, он скатится. Такое положения равновесия называется неустойчивым.

Положение шарика c так же почти неустойчиво, так как любое безконечно малое воздействие на него может привести к сдвигу в любую сторону. Такое положение равновесия называется безразличным.

Шарик a находится в устойчивом положении равновесия, так как при его смещении от положения равновесия возникают силы, возвращающие в исходное положение.

Устойчивое равновесие твёрдого тела – это такое равновесие, при котором сумма сил, действующих на тело, и их моментов равна нулю, и при выводе этого тела из положения равновесия возникают силы или моменты сил, которые возвращают или поворачивают его в положение равновесия.

 

Домашнее задание

1. Что называется моментом силы?
2. Какие условия необходимы и достаточны для равновесия твердого тела?
3. Упражнение 10 (1, 2, 4), стр. 144; Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10 (см. список рекомендованной литературы).

 

Список рекомендованной литературы

1. Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10. – М.: Просвещение, 2008.
2. А.П. Рымкевич. Физика. Задачник 10-11. – М.: Дрофа, 2006.
3. О.Я. Савченко. Задачи по физике – М.: Наука, 1988.
4. А.В. Пёрышкин, В.В. Крауклис. Курс физики т. 1. – М.: Гос. уч.-пед. изд. мин. просвещения РСФСР, 1957.

 

Рекомендованные ссылки на ресурсы сети Интернет

1. Technoclub.info (Источник).
2. Schools.keldysh.ru (Источник).
3. Physics.ru (Источник).

interneturok.ru

17. Условия равновесия твердого тела. Виды равновесия

Как было указано в предыдущем разделе, твердое тело является механической системой с шестью степенями свободы. Для описания его движения требуется шесть независимых числовых уравнений. Вместо них можно взять два независимых векторных уравнения. Таковыми являются уравнение движения центра масс

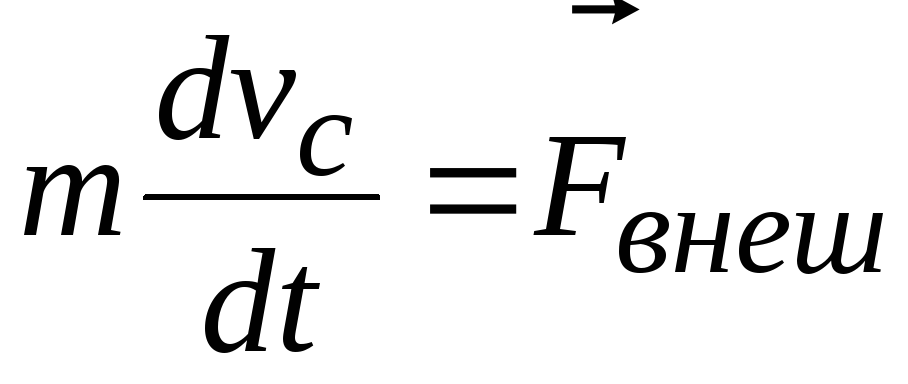(7.38)

и уравнение моментов

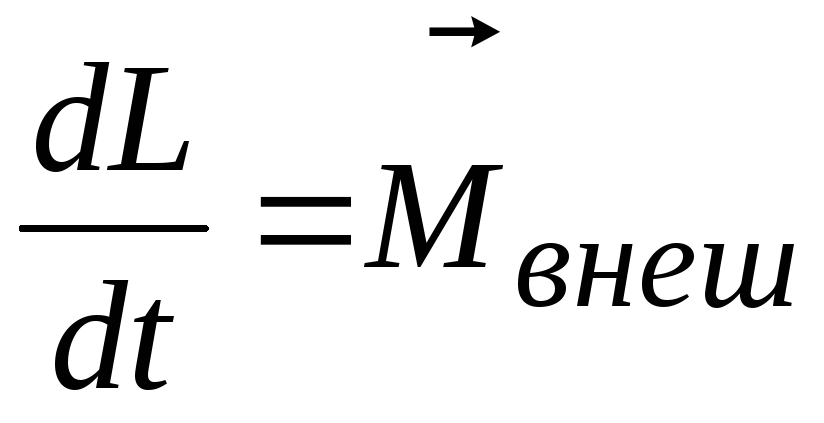(7.39)

Если твердое тело покоится, то уравнения (7.38) и (7.39) переходят в уравнения

(7.40)

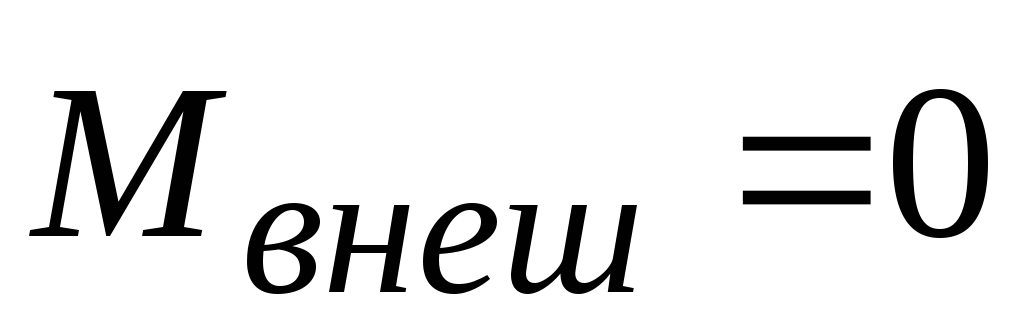(7.41)

В этих формулах 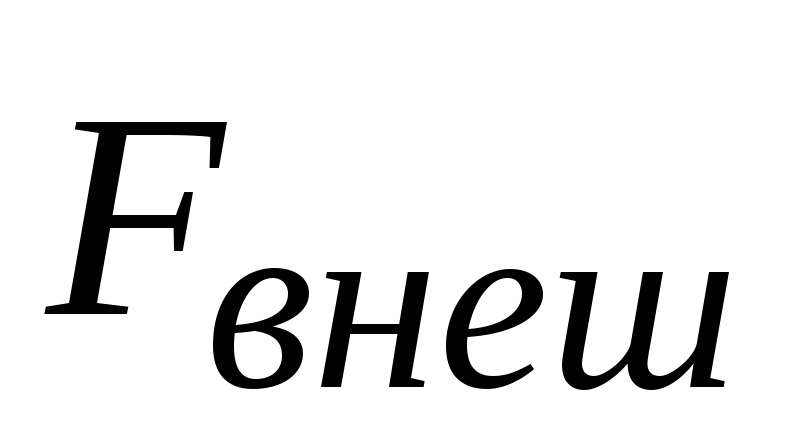– результирующая внешних сил, 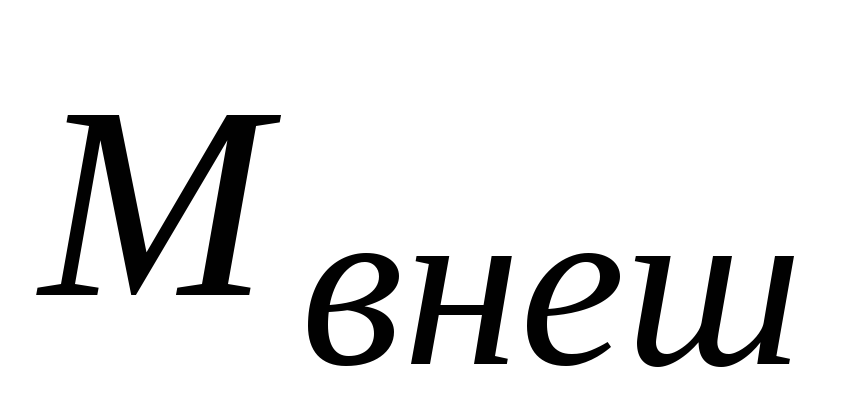– сумма моментов этих сил относительно оси вращения. Таким образом, равновесие имеет место в том случае, когда результирующая внешних сил и сумма моментов относительно оси вращения равны нулю.

Это – необходимые условия равновесия твердого тела. Но они не являются достаточными. При их выполнении центр масс может еще двигаться прямолинейно и равномерно с произвольной скоростью, а само тело может вращаться с сохранением вращательного импульса. Так как при равновесии 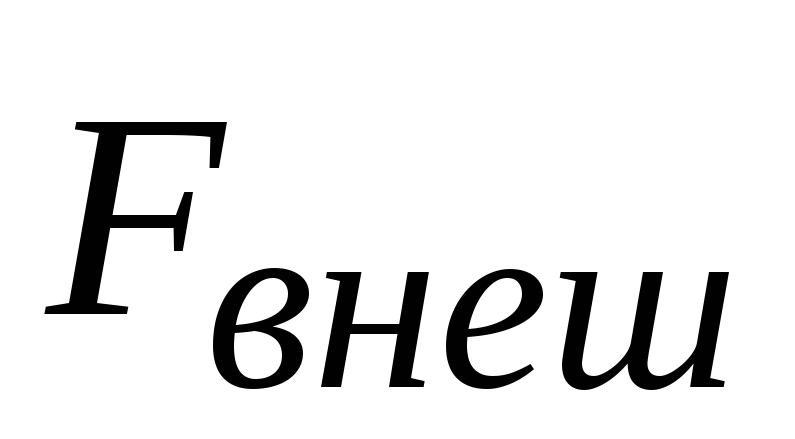равна нулю, то момент этих сил 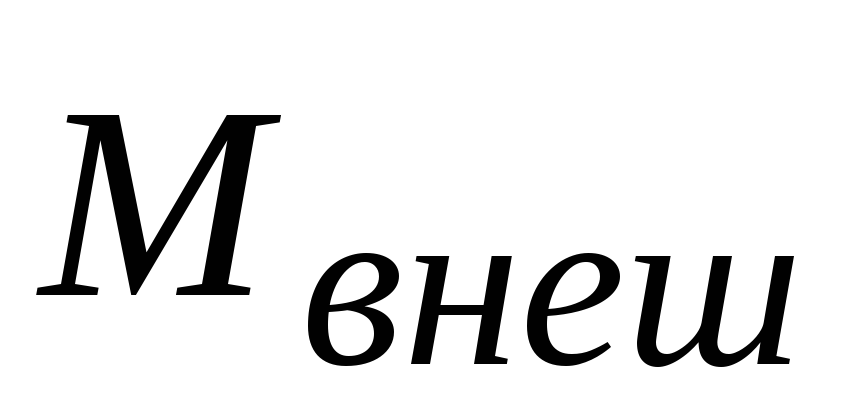в состоянии равновесия не зависит от положения неподвижного начала О, относительно которого он берется. Поэтому при решении любой задачи на равновесие твердого тела начало О можно выбирать произвольно.

Различают устойчивое и неустойчивое равновесия. Как показывает связь силы с потенциальной энергией, при равенстве нулю результирующих внешних сил в состоянии равновесия все производные потенциальной энергии по координатам должны обращаться в нуль. Отсюда следует, что для равновесия необходимо, чтобы потенциальная энергия была стационарна. Стационарность означает, что при всяком выводе системы из состояния равновесия, когда координаты материальных точек получают бесконечно малые приращения, функция потенциальной энергии остается почти постоянной. Точнее, приращения потенциальной функции при таких приращениях координат являются бесконечно малыми более высокого порядка, чем приращения самих координат. В частности, система будет находиться в равновесии, если потенциальная энергия экстремальна, т.е. минимальна или максимальна.

Если потенциальная энергия минимальна, то равновесие будет устойчивым. Диссипативные силы делают равновесие еще более устойчивым. Если потенциальная энергия максимальна, равновесие тела неустойчиво.

Эти выводы остаются справедливыми и для систем, свобода перемещения которых ограничена наложенными связями. Надо только потребовать, чтобы связи были идеальными, т.е. такими, которые не производят работы при любых возможных перемещениях системы. Примером может служить идеально гладкий шарик, надетый на идеально твердую и гладкую спицу, которая задает направление возможного перемещения шарика. Сила, действующая на шарик со стороны спицы, перпендикулярна направлению возможного перемещения и работы не производит.

18. Центр тяжести

На каждую точку частицы твердого тела действует сила тяготения Земли. Все силы тяготения параллельны друг другу, если размеры тела невелики относительно радиуса Земли, и имеют равнодействующую. Оказывается, как бы ни повернули твердое тело, эта равнодействующая будет проходить через одну точку, неизменно связанную с телом. Эта точка называется центром тяжести тела.

Если укрепить тело в точке центра тяжести, то оно будет находиться в равновесии при любом положении тела. Следовательно, сумма моментов сил тяжести всех частиц тела относительно любой горизонтальной оси, проходящей через центр тяжести, равна нулю. Подвешенное так тело после поворота вокруг любой оси, проходящей через центр тяжести, будет оставаться в равновесии, так как равнодействующая сил тяжести проходит через точку закрепления.

Центр масс твердого тела совпадает с его центром тяжести. Поэтому вместо терминов “центр масс” и “центр инерции” употребляют также термин “центр тяжести”. Следовательно, координаты центра тяжести можно найти по формуле, справедливой для радиуса-вектора центра масс, о которой мы говорили в разделе “Центр масс системы материальных точек”. Положение центра тяжести можно вычислить также по формулам (7.40) и (7.41).

Центр тяжести можно определить и экспериментально.

studfile.net

Момент силы. Условия равновесия твердого тела

Данная тема посвящена моменту силы и условиям равновесия твердого тела.

Известно, что основным признаком взаимодействия тел в динамике является возникновение ускорений. Однако часто бывает нужно знать, при каких условиях тело, на которое действует несколько сил, не движется с ускорением, а покоится или же движется равномерно и прямолинейно.

Раздел механики, в котором изучаются условия равновесия материальной точки и абсолютно твердого тела, называется статикой.

Абсолютно твердое тело — это тело, размеры и форму которого можно считать неизменной.

Все опытные факты убеждают в том, что любое тело покоится или движется равномерно и прямолинейно, если равнодействующая всех сил, действующих на него, равна нулю.

Таким образом первое условие равновесия звучит так: векторная сумма приложенных к телу сил должна быть равна нулю.

Из этого условия следует, что и сумма проекций всех сил на любое направление тоже должна быть равна нулю.

Фактически последние три равенства эквивалентны одному векторному равенству, но с их помощью достаточно просто решать задачи, поскольку проекции сил — это скалярные величины.

В повседневной жизни приходится часто сталкиваться с телами, которые не могут двигаться поступательно, но могут вращаться вокруг оси. Примерами таких тел могут служить двери и окна, качели, колеса машин и так далее.

Рассмотрим однородное тело в форме диска, которое может свободно вращаться вокруг закрепленной оси, проходящей через его центр.

Если к этому телу приложить силу в некоторой точке А, находящейся под осью вращения, то диск останется в равновесии. Действительно, в этом случае в диске возникнет сила упругости со стороны оси вращения, которая и будет компенсировать воздействие внешней силы.

Если подвесить тело в точке B, находящейся выше или ниже точки «А», то равновесие тоже не нарушится. Отсюда можно сделать вывод, что точку приложения силы можно переносить вдоль линии ее действия. При этом, как видно из рисунка, внешняя сила и сила упругости лежат на одной прямой.

Если же прямая, на которой лежит вектор внешней силы, не проходит через ось вращения, то эта сила не может быть скомпенсирована действием силы упругости оси, и тело начнет поворачивается.

А что произойдет, если к диску приложить не одну, а несколько сил, направленные в разные стороны, например, так, как это показано на рисунке?

Сила F₁ будет стремиться повернуть тело по ходу часовой стрелки, а сила F₂ — против хода часовой стрелки. Так вот, в зависимости от соотношения модулей действующих сил и кратчайших расстояний от оси вращения до линии действия сил, тело повернется в ту или иную сторону.

Если же отношение действующих сил обратно пропорционально этим кратчайшим расстояниям, то тело будет находиться в равновесии.

Данная формула известна из курса физики 7 класса, как условие равновесия рычага.

Кратчайшее расстояние от оси вращения до линии действия силы называется плечом силы. А произведение модуля силы на ее плечо называется моментом силы.

Из определения момента силы следует, что единицей его измерения в системе СИ является

Исходя из условия равновесия рычага и определения момента силы, можно сформулировать второе условие равновесия тел. И так, тело находится в равновесии, если алгебраическая сумма моментов всех сил, приложенных к телу, относительно любой оси равна нулю.

Данное условие равновесия является следствием одной из теорем механики — теоремы Вариньона.

Следует напомнить о том, что при использовании правила моментов необходимо учитывать знаки действующих сил. Так обычно считают, что момент силы, которая вызывает вращение тела по ходу часовой стрелки, положителен. И наоборот, если сила пытается повернуть тело против хода часовой стрелки, то момент этой силы считают отрицательным. Однако можно считать и наоборот.

В механике часто возникает необходимость ответить на вопрос: в каких случаях тело может сколь угодно долго оставаться в покое, если оно находилось в покое в начальный момент? Естественно, что должны выполняться условия равновесия. Но практически не во всяком положении равновесия, тело, находящееся в начальный момент в покое, будет оставаться в покое и в последующие моменты времени. Дело в том, что в реальных условиях, помимо учитываемых сил (сила тяжести, сила реакции подвеса или опоры, силы трения и так далее), тело испытывает и не учитываемые случайные воздействия. Это могут быть, например, небольшие сотрясения, колебания воздуха и тому подобное. Под действием таких сил тело хотя бы немного, но будет отклоняться от положения равновесия, а в этом случае дальнейшее поведение тела может быть различным.

Поэтому, для того, чтобы судить о поведении тела в реальных условиях необходимо уметь оценивать равновесие. Различают три вида равновесия — это устойчивое равновесие, неустойчивое равновесие и равновесие безразличное.

Равновесие тела называют устойчивым, если при отклонении тела от положения равновесия возникают силы, возвращающие тело в положение равновесия.

Примером устойчивого равновесия может служить шарик, находящийся на вогнутой поверхности. Если отклонить шарик от положения равновесия, то спустя некоторое временя он вернется в первоначальное положение. Это объясняется тем, что равнодействующая сила в любой точке траектории шарика (за исключением исходной) направлена к положению равновесия.

В устойчивом положении равновесия центр тяжести тела занимает наинизшее из всех близких положений. Тогда очевидно, что такое равновесие тела связано с минимумом его потенциальной энергии.

Если же равнодействующая сила не возвращает тело в первоначальное положение равновесия, а вызывает его дальнейшее отклонение от него, то такое равновесие называется неустойчивым.

В таком положении, например, находится шарик на выпуклой подставке. При отклонении равнодействующая сила направлена от положения равновесия. В положении неустойчивого равновесия высота центра тяжести тела максимальна. Следовательно, такое равновесие связано с максимумом потенциальной энергии тела.

Если смещения тела в любом направлении не вызывает изменение действующих на него сил (то есть равнодействующая всех сил, приложенных к телу, остается равной нулю), то такое положение равновесия называется безразличным.

В таком положении находится шарик на горизонтальной плоскости. Безразличное равновесие связано с неизменной потенциальной энергией, а высота центра тяжести тела одинакова во всех достаточно близких положениях.

Другим примером равновесий может быть равновесие тела, имеющего ось вращения. В качестве примера рассмотрим однородное тело прямоугольной формы (например, линейку), которое может вращаться вокруг оси, проходящей через точку О.

Линейка будет находиться в устойчивом равновесии, если ее центр тяжести (точка C) находится ниже оси вращения (то есть ниже точки O). При отклонении от положения равновесия возникает момент силы тяжести, который возвращает линейку в положение равновесия. Очевидно, что в отклоненном положении потенциальная энергия линейки больше, чем в положении равновесия. Таким образом, тело, имеющее ось вращения, будет находиться и устойчивом равновесии, если центр тяжести тела находится на вертикальной прямой, проходящей через ось вращения, ниже оси вращения.

Если же центр тяжести находится на вертикальной прямой, проходящей через ось вращения, расположен выше оси вращения, то равновесие будет неустойчивым. В этом случае при отклонении момент силы тяжести отклоняет тело еще дальше от первоначального положения равновесия. При этом потенциальная энергия тела уменьшается.

Если центр тяжести тела и ось вращения будут совпадать, то при любом положении тела момент силы тяжести равен нулю, поскольку равно нулю плечо этой силы. Иными словами, мы с вами будем наблюдать безразличное равновесие. Что касается потенциальной энергии тела, то она будет оставаться неизменной.

     

Рассмотрим теперь условия устойчивости тела, опирающегося не на одну точку, как в ранее рассмотренных случаях, а на несколько точек (например, стол) или имеющее площадь опоры (например, ящик). В этих случаях для устойчивого равновесия тела необходимо, чтобы вертикаль, проведенная через центр тяжести, проходила внутри площади опоры тела, то есть внутри контура, образованного линиями, соединяющими точки опоры, или внутри площадки, на которую опирается тело.

Если наклонять стол или ящик, то их центр тяжести будет подниматься. Но момент силы тяжести относительно оси вращения будет стремиться вернуть его в первоначальное положение до тех пор, пока линия действия силы тяжести проходит через площадь опоры.

Однако, если их наклонить так, что линия действия силы тяжести выйдет за пределы площади опоры, то тела опрокинутся вследствие действия момента силы тяжести. Очевидно, что имеется предельный угол наклона, то есть угол между прямой, соединяющей центр тяжести тела и крайнюю точку соприкосновения площади опоры с горизонтальной плоскостью, после которого первоначальное равновесие уже не восстанавливается и тело опрокидывается. Этот предельный угол будет тем меньше, чем выше расположен центр тяжести тела при данной площади опоры.

Основные выводы:

Рассмотрены два условия равновесия тел и основные виды равновесия.

videouroki.net

1.3. Условия равновесия твердого тела

Для равновесия тела, находящегося под действием произвольной системы сил и пар сил, необходимо и достаточно, чтобыглавный вектори главный моментэтой системы относительно любой точки равнялись нулю.Главнымвекторомназывают геометрическую сумму всех сил системы, аглавным моментомотносительно точки – геометрическую сумму моментов всех сил относительно этой точки.

В общем случае условия равновесия в векторной форме имеют вид:

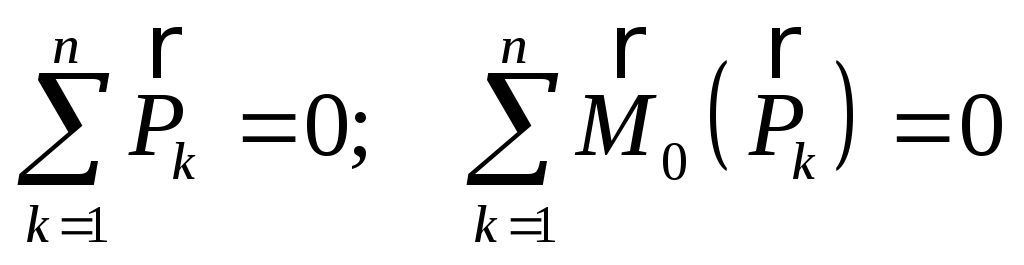. (1.1)

Проецируя векторные равенства (12.1) на координатные оси, получим аналитические условия равновесия:

;

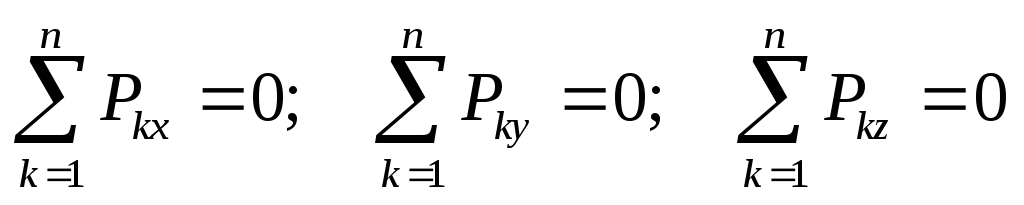(1.2)

.

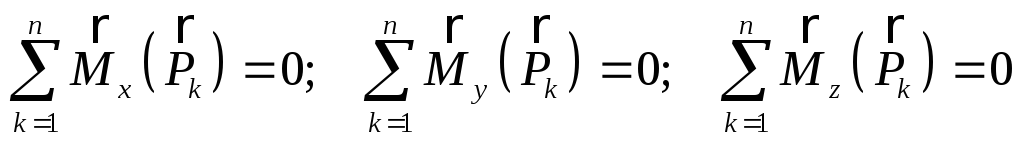Таким образом, для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из трех координатных осей и сумма моментов их относительно каждой из этих осей были равны нулю.

При рассмотрении частных случае, когда система сил, действующих на тело, не является произвольной пространственной, условия равновесия записывают с учетом специфики данной системы сил.

Задачи статики на равновесие тела под действием различных систем сил следует решать в предлагаемой последовательности:

1) выбрать объект равновесия;

2) изобразить все активные силы, действующие на объект равновесия;

3) отбросить связи, наложенные на объект равновесия, и заменить их действие реакциями, соответствующими типам связей;

4) записать для полученной системы сил систему уравнений равновесия, решить эту систему и определить искомые величины.

Примечания:

■ в качестве объекта (объектов) равновесия может быть выбрана материальная точка, тело или совокупность связанных между собой тел таким образом, чтобы к этому объекту (объектам) были приложены все искомые силы или их часть;

■ если из уравнения равновесия невозможно однозначно определить все искомые силы или иные неизвестные параметры, то задача является статически неопределеннойи решать ее в рамках статики нельзя. При этом возможны следующие случаи: число неизвестных больше числа уравнений статики, матрица системы уравнений при равенстве числа неизвестных числу уравнений – особенная (вырожденная), число неизвестных меньше числа уравнений. В последнем случае объект может находиться в равновесии только при условиях, налагаемых на активные силы.

1.4. Центр параллельных сил. Центр тяжести

В статике доказывают, что если система параллельных сил имеет равнодействующую, то существует точка, притом только одна, через которую проходит ее линия действия. Эту точку называютцентром параллельных сил. Центр параллельных сил обладает одним важным свойством – если все силы повернуть относительно параллельных осей, проходящих через точки их приложения на один и тот же угол, то равнодействующая системы этих сил повернется на тот же угол относительно аналогичной оси, проходящей через центр параллельных сил.

Рассмотрим тело произвольной формы, находящееся в поле сил тяжести Земли. При этом на каждый элементарный объем рассматриваемого тела действует сила тяжести

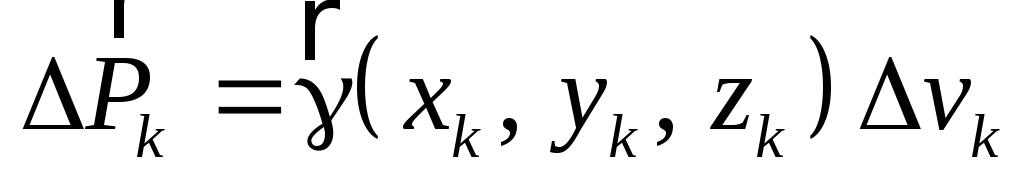, (1.3)

где 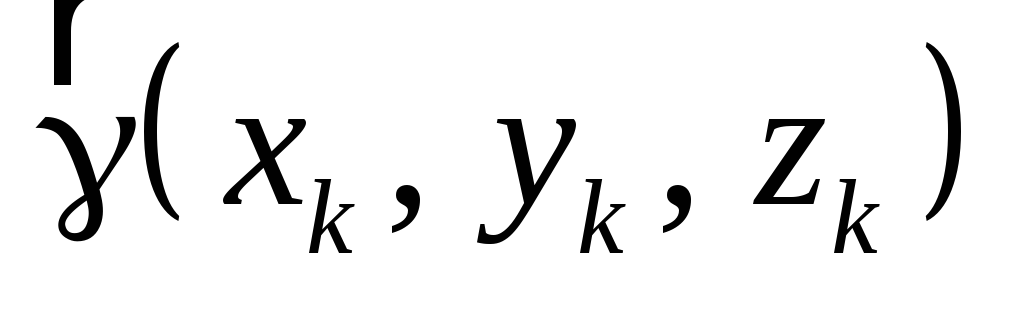– удельный вес элемента объема,

.

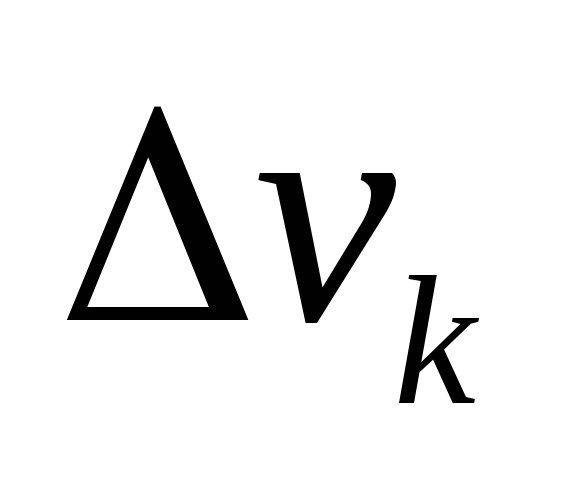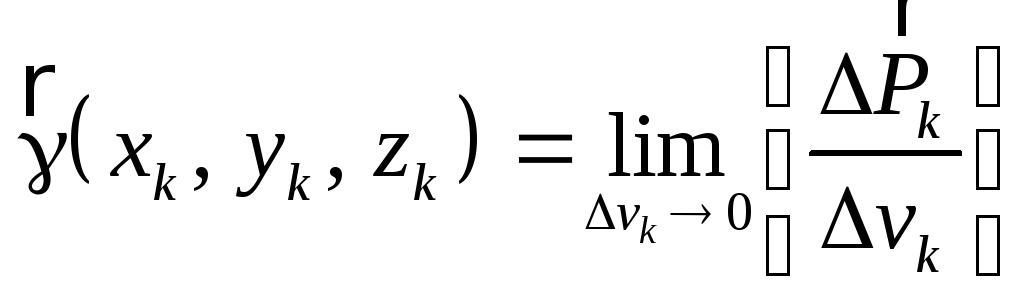Когда тело однородно, 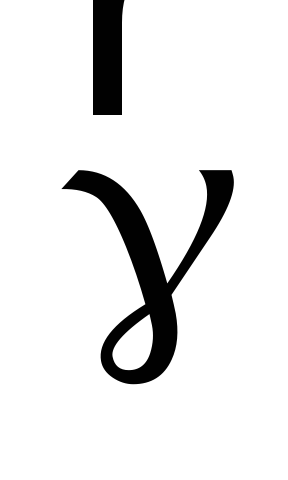не зависит от координат.

Силы тяжести, действующие на каждый элементарный объем тела, направлены к центру Земли. Если размерами тела по отношению к размерам Земли пренебречь, то систему сил тяжести можно считать системой параллельных сил, направленных в одну сторону. Такая система всегда имеет равнодействующую, а, следовательно, и центр параллельных сил.

Центр системы сил тяжести, действующих на тело со стороны Земли, называют центром тяжести тела. Если тело рассматривается в системе отсчета с центром в точкеО и с координатными осямиx,y,z(рис. 1.8), то радиус-вектор центра тяжести и его координаты определяют по формуле:

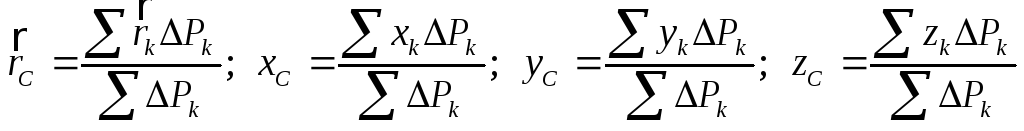. (1.4)

Здесь 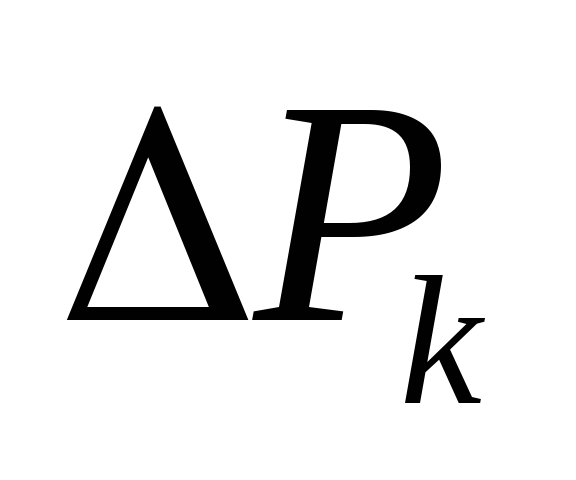– модуль силы тяжести, действующей на элементарный объем.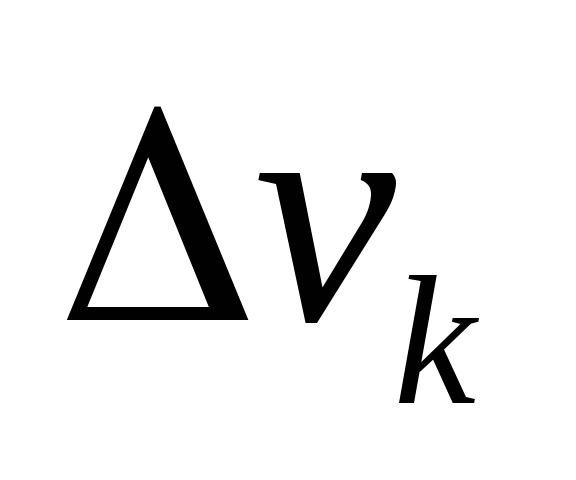

Центр тяжести не изменяет своего положения по отношению к телу при любой его ориентации относительно Земли. Центр тяжести – геометрическая точка, которая может не принадлежать телу, но обязательно с ним жестко связана. Если тело однородно, т.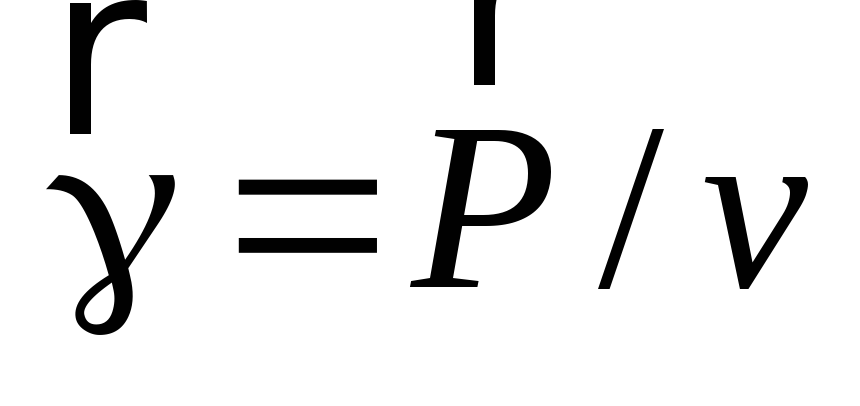е. , где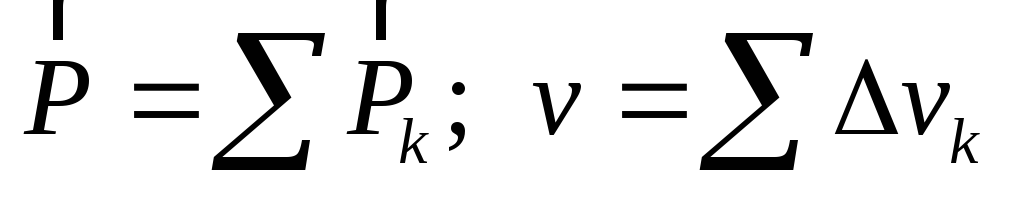, то вместо понятия центр тяжести можно использовать центр тяжести объема, занимаемого телом. Аналогично, если однородное тело представляет собой тонкую пластинку или оболочку постоянной толщины, либо тонкий криволинейный стержень постоянной толщины, то центр тяжести такого тела называютцентром тяжести поверхностиилилинии.

Формулы, по которым определяют координаты центров тяжести однородных тел, имеют следующий вид:

– центр тяжести объема

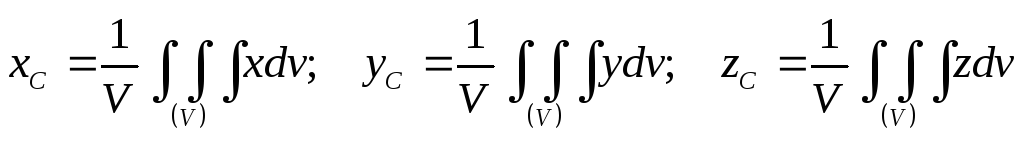; (1.5)

– центр тяжести поверхности

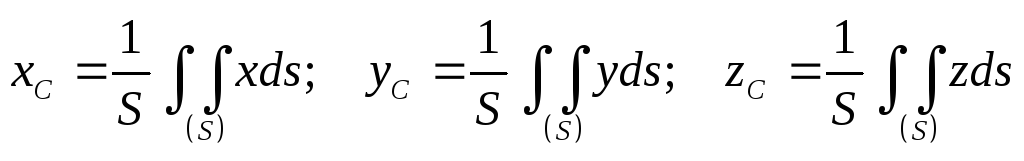; (1.6)

– центр тяжести линии

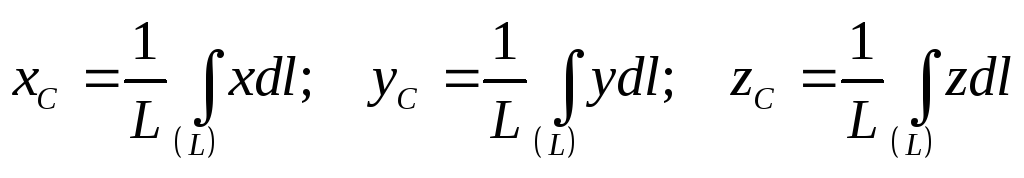, (1.7)

где соответственно величины: V– объема тел;S– площади поверхности тела;L– длины тела, по которым берут интегралы.

Для нахождения центров тяжести тел используют непосредственно приведенные формулы, а также правила симметрии и методы разбиения сложных тел на более простые, для которых легче определить положения их центров тяжести. В отдельных случаях положения центров тяжести тел находят экспериментальным путем.

1.5.Сухое трение. Законы Кулона

Понятия сухого трения вводятся в теоретическую механику из физики. Реальные тела не являются идеально гладкими и абсолютно твердыми. Поэтому при попытке перемещать или катить одно тело по поверхности другого возникают, кроме сил взаимодействия, направленных по общей нормали к соприкасающимся поверхностям в месте их контакта, силы и пары сил, которые препятствуют скольжению и качению. Эти силы называют соответственно силами трения скольженияи силами трения качения. Трение называютсухим, если между взаимодействующими твердыми телами отсутствует смазочный материал.

Многие задачи статики не могут быть решены без учета сил трения. Так, например, без этих сил невозможно равновесие твердого тела на наклонной плоскости. Всем известен факт буксования колес автомобиля на скользкой дороге, так что само движение в большинстве случаев обусловлено силами трения. Трение скольжения и трение качения учитывают в статике посредством эмпирических (опытных) данных, которые называют законами Кулона.

При попытке качения одного тела по поверхности другого сопротивление качению оказывает пара сил, называемая моментом сил трения качения. Сформулируем законы Кулона для трения качения. Направление момента сил трения качения противоположно тому направлению, в котором активные силы стремятся катить тело. Величина момента трения качения находится в интервале 0 ≤М_тр≤М_тр.пр. Ее определяют формулой

М_тр.пр= δN,

где δ – коэффициент трения качения, имеющий размерность длины;N– нормальное давление. Экспериментально установлено, что величина δ зависит от материалов тел и радиуса катящегося тела. Значения δ можно найти в справочниках.

Отличительной особенностью задач статики при наличии сил трения является то, что, когда сила трения F_трили момент сил тренияМ_трменьше предельных значений, реакции связей, включающие силу и момент сил трения, определяют из уравнений равновесия, как обычно. Если же силы трения достигают предельных значений, то их находят с помощью коэффициентов трения и вводят как известные величины. При этом, однако, тело не находится в равновесии и применение уравнений статики ко всему телу становится неправомерным. Для установления равновесия тел при наличии трения уравнения равновесия дополняют соответствующими неравенствами, которые требуют, чтобы сила трения скольжения или момент сил трения качения не превосходили предельных значений.

Вопросы для самоконтроля

1. Что изучают в разделе статика курса теоретической механики?

2. Что называют абсолютно твердым телом?

3. Как определяют понятия силы и системы сил в статике?

4. Какие соотношения существуют между силами и системами сил? Приведите классификацию сил.

5. На каких аксиомах базируются теоретические положения статики?

6. Какое тело называют несвободным?

7. Как определяют понятия связей и их реакций?

8. Какие основные связи могут быть наложены на абсолютно твердое тело? Какие реакции возникают в этих связях?

9. Как формулируют условия равновесия абсолютно твердого тела в векторной и аналитической формах?

10. Какова последовательность решения задачи об определении реакций связей?

11. Какие условия должны выполняться для разрешимости системы уравнений равновесия абсолютно твердого тела?

12. Как определяют радиус-вектор и координаты центра тяжести тела?

13. Каким образом в статике учитывают действие сил сухого трения на твердое тело?

14. В чем заключаются особенности решения задач статики при наличии сил трения?

studfile.net

1.3. Условия равновесия твердого тела

Для равновесия тела, находящегося под действием произвольной системы сил и пар сил, необходимо и достаточно, чтобыглавный вектори главный моментэтой системы относительно любой точки равнялись нулю.Главнымвекторомназывают геометрическую сумму всех сил системы, аглавным моментомотносительно точки – геометрическую сумму моментов всех сил относительно этой точки.

В общем случае условия равновесия в векторной форме имеют вид:

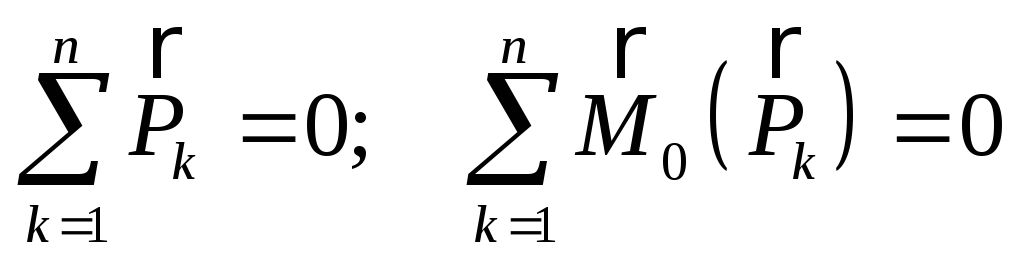. (1.1)

Проецируя векторные равенства (12.1) на координатные оси, получим аналитические условия равновесия:

;

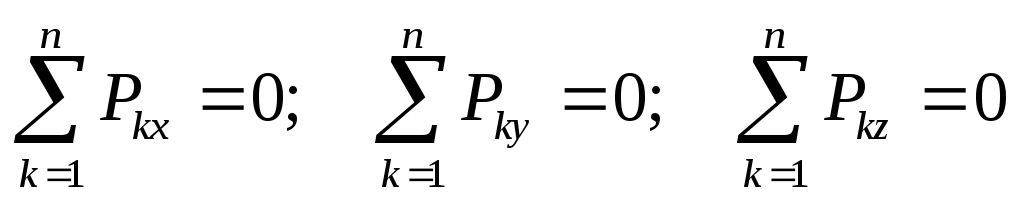(1.2)

.

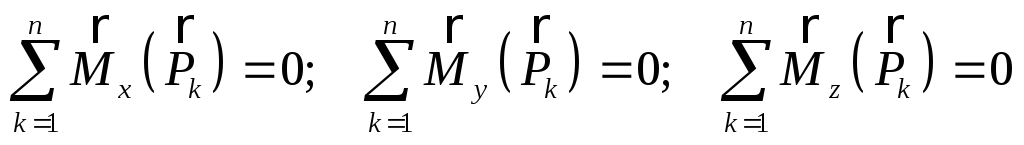Таким образом, для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из трех координатных осей и сумма моментов их относительно каждой из этих осей были равны нулю.

При рассмотрении частных случае, когда система сил, действующих на тело, не является произвольной пространственной, условия равновесия записывают с учетом специфики данной системы сил.

Задачи статики на равновесие тела под действием различных систем сил следует решать в предлагаемой последовательности:

1) выбрать объект равновесия;

2) изобразить все активные силы, действующие на объект равновесия;

3) отбросить связи, наложенные на объект равновесия, и заменить их действие реакциями, соответствующими типам связей;

4) записать для полученной системы сил систему уравнений равновесия, решить эту систему и определить искомые величины.

Примечания:

■ в качестве объекта (объектов) равновесия может быть выбрана материальная точка, тело или совокупность связанных между собой тел таким образом, чтобы к этому объекту (объектам) были приложены все искомые силы или их часть;

■ если из уравнения равновесия невозможно однозначно определить все искомые силы или иные неизвестные параметры, то задача является статически неопределеннойи решать ее в рамках статики нельзя. При этом возможны следующие случаи: число неизвестных больше числа уравнений статики, матрица системы уравнений при равенстве числа неизвестных числу уравнений – особенная (вырожденная), число неизвестных меньше числа уравнений. В последнем случае объект может находиться в равновесии только при условиях, налагаемых на активные силы.

1.4. Центр параллельных сил. Центр тяжести

В статике доказывают, что если система параллельных сил имеет равнодействующую, то существует точка, притом только одна, через которую проходит ее линия действия. Эту точку называютцентром параллельных сил. Центр параллельных сил обладает одним важным свойством – если все силы повернуть относительно параллельных осей, проходящих через точки их приложения на один и тот же угол, то равнодействующая системы этих сил повернется на тот же угол относительно аналогичной оси, проходящей через центр параллельных сил.

Рассмотрим тело произвольной формы, находящееся в поле сил тяжести Земли. При этом на каждый элементарный объем рассматриваемого тела действует сила тяжести

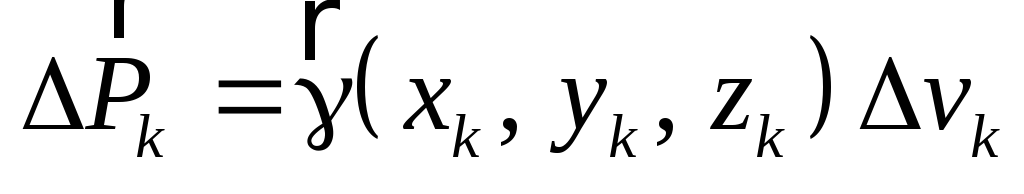, (1.3)

где 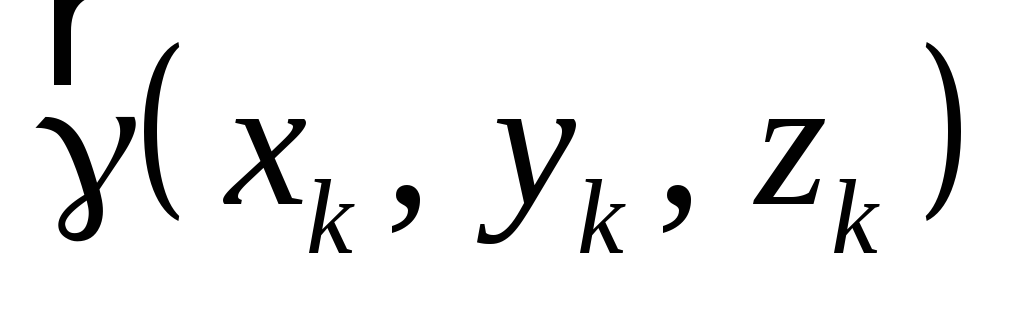– удельный вес элемента объема,

.

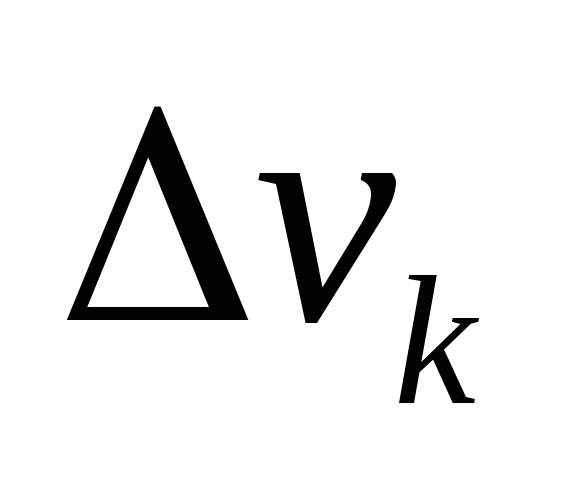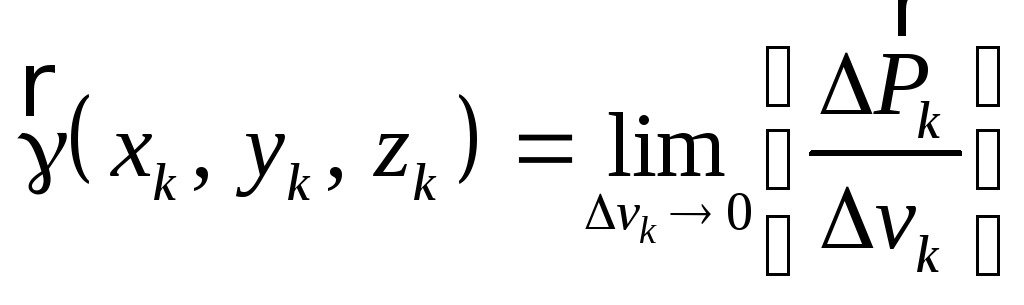Когда тело однородно, 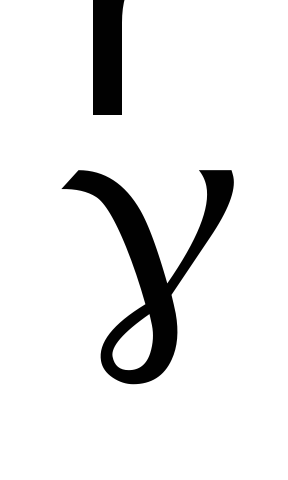не зависит от координат.

Силы тяжести, действующие на каждый элементарный объем тела, направлены к центру Земли. Если размерами тела по отношению к размерам Земли пренебречь, то систему сил тяжести можно считать системой параллельных сил, направленных в одну сторону. Такая система всегда имеет равнодействующую, а, следовательно, и центр параллельных сил.

Центр системы сил тяжести, действующих на тело со стороны Земли, называют центром тяжести тела. Если тело рассматривается в системе отсчета с центром в точкеО и с координатными осямиx,y,z(рис. 1.8), то радиус-вектор центра тяжести и его координаты определяют по формуле:

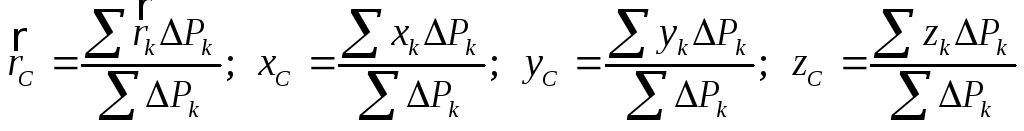. (1.4)

Здесь 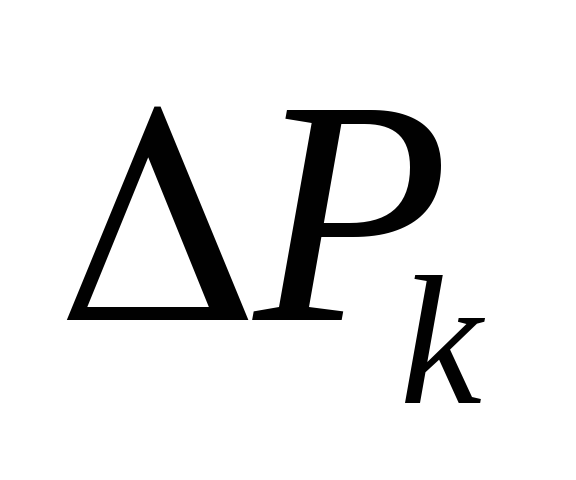– модуль силы тяжести, действующей на элементарный объем.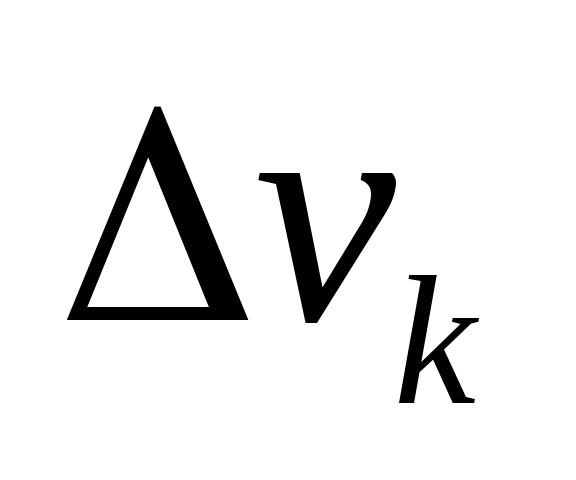

Центр тяжести не изменяет своего положения по отношению к телу при любой его ориентации относительно Земли. Центр тяжести – геометрическая точка, которая может не принадлежать телу, но обязательно с ним жестко связана. Если тело однородно, т.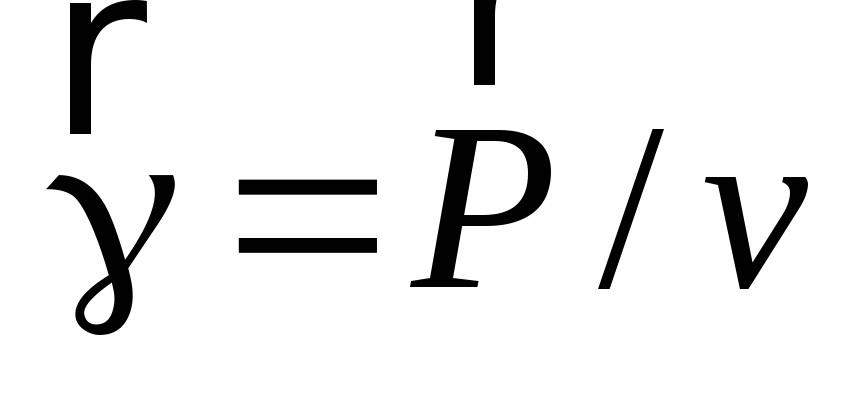е. , где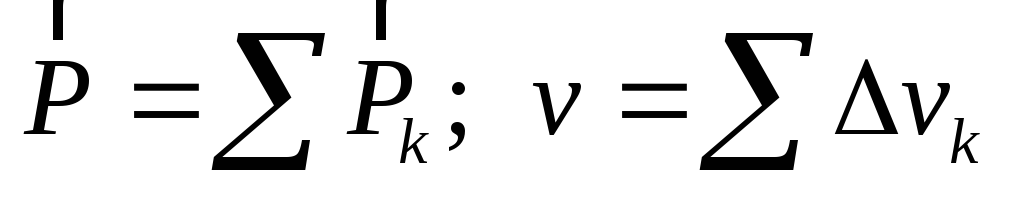, то вместо понятия центр тяжести можно использовать центр тяжести объема, занимаемого телом. Аналогично, если однородное тело представляет собой тонкую пластинку или оболочку постоянной толщины, либо тонкий криволинейный стержень постоянной толщины, то центр тяжести такого тела называютцентром тяжести поверхностиилилинии.

Формулы, по которым определяют координаты центров тяжести однородных тел, имеют следующий вид:

– центр тяжести объема

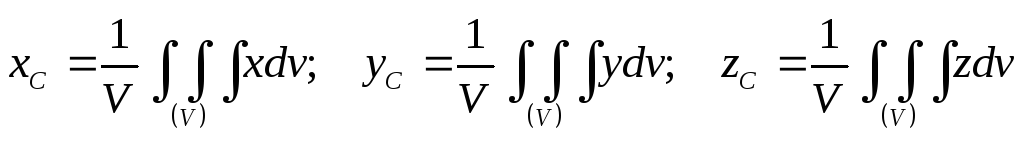; (1.5)

– центр тяжести поверхности

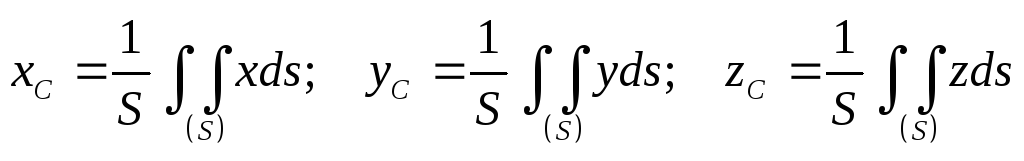; (1.6)

– центр тяжести линии

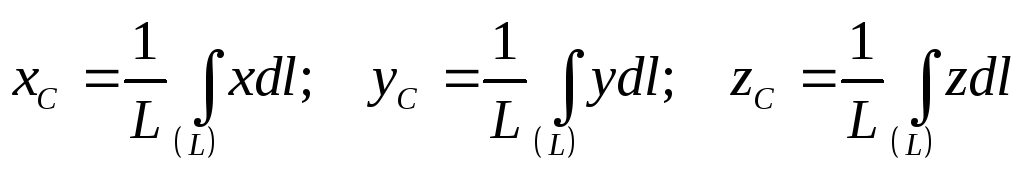, (1.7)

где соответственно величины: V– объема тел;S– площади поверхности тела;L– длины тела, по которым берут интегралы.

Для нахождения центров тяжести тел используют непосредственно приведенные формулы, а также правила симметрии и методы разбиения сложных тел на более простые, для которых легче определить положения их центров тяжести. В отдельных случаях положения центров тяжести тел находят экспериментальным путем.

1.5.Сухое трение. Законы Кулона

Понятия сухого трения вводятся в теоретическую механику из физики. Реальные тела не являются идеально гладкими и абсолютно твердыми. Поэтому при попытке перемещать или катить одно тело по поверхности другого возникают, кроме сил взаимодействия, направленных по общей нормали к соприкасающимся поверхностям в месте их контакта, силы и пары сил, которые препятствуют скольжению и качению. Эти силы называют соответственно силами трения скольженияи силами трения качения. Трение называютсухим, если между взаимодействующими твердыми телами отсутствует смазочный материал.

Многие задачи статики не могут быть решены без учета сил трения. Так, например, без этих сил невозможно равновесие твердого тела на наклонной плоскости. Всем известен факт буксования колес автомобиля на скользкой дороге, так что само движение в большинстве случаев обусловлено силами трения. Трение скольжения и трение качения учитывают в статике посредством эмпирических (опытных) данных, которые называют законами Кулона.

При попытке качения одного тела по поверхности другого сопротивление качению оказывает пара сил, называемая моментом сил трения качения. Сформулируем законы Кулона для трения качения. Направление момента сил трения качения противоположно тому направлению, в котором активные силы стремятся катить тело. Величина момента трения качения находится в интервале 0 ≤М_тр≤М_тр.пр. Ее определяют формулой

М_тр.пр= δN,

где δ – коэффициент трения качения, имеющий размерность длины;N– нормальное давление. Экспериментально установлено, что величина δ зависит от материалов тел и радиуса катящегося тела. Значения δ можно найти в справочниках.

Отличительной особенностью задач статики при наличии сил трения является то, что, когда сила трения F_трили момент сил тренияМ_трменьше предельных значений, реакции связей, включающие силу и момент сил трения, определяют из уравнений равновесия, как обычно. Если же силы трения достигают предельных значений, то их находят с помощью коэффициентов трения и вводят как известные величины. При этом, однако, тело не находится в равновесии и применение уравнений статики ко всему телу становится неправомерным. Для установления равновесия тел при наличии трения уравнения равновесия дополняют соответствующими неравенствами, которые требуют, чтобы сила трения скольжения или момент сил трения качения не превосходили предельных значений.

Вопросы для самоконтроля

1. Что изучают в разделе статика курса теоретической механики?

2. Что называют абсолютно твердым телом?

3. Как определяют понятия силы и системы сил в статике?

4. Какие соотношения существуют между силами и системами сил? Приведите классификацию сил.

5. На каких аксиомах базируются теоретические положения статики?

6. Какое тело называют несвободным?

7. Как определяют понятия связей и их реакций?

8. Какие основные связи могут быть наложены на абсолютно твердое тело? Какие реакции возникают в этих связях?

9. Как формулируют условия равновесия абсолютно твердого тела в векторной и аналитической формах?

10. Какова последовательность решения задачи об определении реакций связей?

11. Какие условия должны выполняться для разрешимости системы уравнений равновесия абсолютно твердого тела?

12. Как определяют радиус-вектор и координаты центра тяжести тела?

13. Каким образом в статике учитывают действие сил сухого трения на твердое тело?

14. В чем заключаются особенности решения задач статики при наличии сил трения?

studfile.net

Условия равновесия твердых тел

На прошлом уроке мы уже выяснили, что для равновесия необходимо, чтобы сумма всех внешних и внутренних сил, приложенных к телу, была равна нулю.

Но сумма всех внутренних сил любого тела равна нулю, исходя из третьего закона Ньютона. Поэтому, первое условие равновесия таково: сумма всех внешних сил, действующих на тело, должна быть равна нулю:

Самой очевидной внешней силой является сила тяжести, которая действует на все тела, находящиеся на Земле. Но эту силу, как мы помним, могут уравновешивать другие внешние силы. В этих случаях, возникает равновесие твердых тел.

Однако, даже если сумма всех внешних сил, действующих на тело, равна нулю — этого еще не достаточно, чтобы утверждать, что тело находится в равновесии. Дело в том, что тело может вращаться. Скажем, вы можете приложить к противоположным краям линейки силы, равные по модулю и противоположные по направлению. В этом случае, равнодействующая этих сил будет равна нулю. Несмотря на это, линейка начнет вращаться.

Значит, нужно найти еще одно условие, равновесия тела. Проведем простой опыт: попытайтесь положить линейку на ластик, так, чтоб ни один из краёв линейки не касался стола. Вам удастся сделать это только тогда, когда ластик будет точно посередине линейки. Теперь, давайте разберемся, почему так происходит. На каждый конец линейки действует сила тяжести. Кроме того, на ту часть линейки, которая соприкасается с ластиком, действует реакция опоры. Очевидно, что сила тяжести, действующая на оба конца линейки, не меняется из-за того, что вы двигаете линейку.

Значит, играет роль расстояние от каждого из концов до точки приложения силы реакции опоры.

Рассмотрим случай очень маленького отклонения линейки от положения равновесия. В этом случае, линейка повернётся на очень малый угол α.

Если линейка пришла в движение, значит, увеличилась её кинетическая энергия. А для того, чтобы изменить кинетическую энергию, необходимо совершить работу. Давайте подсчитаем работу сил:

Работа силы, как мы помним, равна произведению модулей силы, перемещения, и косинуса угла между их направлениями:

Формально, в описанной ситуации концы линейки будут двигаться криволинейно. Но мы оговорили в самом начале, что угол поворота очень маленький, поэтому, перемещения концов линейки можно считать прямолинейными. В этом случае:

Очевидно, что ось вращения проходит через середину линейки. Плечо силы — это кратчайшее расстояние от оси вращения до линии действия силы. Произведения силы на её плечо, называется моментом силы.

Исходя из этого, мы можем сформулировать второе условие равновесия тел: сумма моментов внешних сил, действующих на тело относительно оси вращения, должна быть равна нулю:

Условимся считать момент силы положительным, если эта сила стремится повернуть тело против часовой стрелки. И наоборот, момент силы будем считать отрицательным, если эта сила стремится повернуть тело по часовой стрелке.

Итак, для того, чтобы твердое тело находилось в равновесии, сумма внешних сил должна быть равна нулю и сумма моментов внешних сил должна быть равна нулю:

 

 Например, качаясь на качелях, можно найти положение равновесия. Если оба человека обладают одной и той же массой, то самое простое — это сесть обоим на самый край. Если же массы не равны, то человек с наименьшей массой должен сесть на самый край, а второй человек должен подсаживаться все ближе и ближе к оси вращения (то есть к середине качели).

В какой-то момент, расстояние от второго человека до середины качели будет меньше, чем расстояние от первого человека до середины качели, ровно во столько раз, во сколько масса второго человека, больше, чем масса первого человека. Это и будет означать, что сумма моментов внешних сил равна нулю, поэтому, качели окажутся в равновесии.

Вы знаете, что качаясь на таких качелях, нужно постоянно отталкиваться от земли.

Давайте разберемся, что происходит в этот момент. Обозначим на рисунке силы, действующие на каждого человека. Будем считать, что и тот, и другой человек сидит на краю качели, то есть расстояние от каждого из них до середины качели одинаково. Итак, представим, что один край качели, на котором сидит человек, обладающий большей массой, только что опустился. Качели не сдвинутся с места до тех пор, пока человек не оттолкнется от земли. Дело в том, что момент М₁ > M₂. Действительно, поскольку расстояние d₁ = d₂, момент силы будет больше при большей силе. Чтобы начать качаться, нужно сделать так, чтобы момент M₁ стал меньше M₂. То есть, в нашем случае, нужно сделать силу F₁ меньше, чем F₂.

На первый взгляд, это кажется невозможным, поскольку изменить силу тяжести можно только изменив массу. Но, мы имеем дело не с силой тяжести, а с весом. Вспомните, ведь именно вес определяется как сила, действующая на опору. До тех пор, пока человек не предпринимает никаких действий, сила тяжести уравновешивается реакцией опоры. То есть, в данном случае, вес равен силе тяжести. Рассмотрим теперь, что произойдет, если человек, оттолкнётся от земли. Мышцы ног приложат некоторую силу, направленную вертикально вниз, к поверхности земли. При этом по третьему закону Ньютона, поверхность земли подействует на человека с силой, равной по модулю, но противоположной по направлению. То есть, эта сила будет направлена вертикально вверх. Тогда, по второму закону Ньютона, сила тяжести будет равна сумме силы реакции опоры и силы, с которой человек оттолкнётся от земли. Таким образом, вес человека (равный реакции опоры N₁) будет равен разности между силой тяжести и силой F. Теперь, если выражение F₁ – F₂ меньше, чем F₂, то качели начнут двигаться. Как правило, достаточно приложить сравнительно небольшую силу, поскольку чаще всего, на таких качелях качаются люди с приблизительно одинаковой массой. Однако, очевидно, что человек, обладающий меньшей массой, должен будет прикладывать бо́льшую силу, чтобы нормально качаться. Или же, человек, обладающий большей массой, должен будет пододвинуться поближе к середине качели.

Все выше сказанное, скорее всего, знал каждый из вас. Теперь же, вы можете описать это с точки зрения физики и объяснить, почему так происходит.

Пример решения задачи.

Задача. На двух веревках подвешен груз, так, как показано на рисунке. Если масса груза 20 кг, то каковы силы натяжения веревок?

videouroki.net

Урок 14. статика. равновесие абсолютно твердых тел — Физика — 10 класс

Физика, 10 класс

Урок 14. Статика. Равновесие абсолютно твёрдых тел

Перечень вопросов, рассматриваемых на уроке:

1.Условия равновесия тела

2.Момент силы

3.Плечо силы

4. Центр тяжести

Глоссарий по теме

Статика – раздел механики, в котором изучается равновесие абсолютно твердых тел, называется статикой

Абсолютно твердое тело – модельное понятие классической механики, обозначающее совокупность точек, расстояния между текущими положениями которых не изменяются.

Центр тяжести – центром тяжести тела называют точку, через которую при любом положении тела в пространстве проходит равнодействующая сил тяжести, действующих на все частицы тела.

Плечо силы — это длина перпендикуляра, опущенного от оси вращения на линию действия силы.

Момент силы — это физическая величина, равная произведению модуля силы на ее плечо.

Устойчивое равновесие — это равновесие, при котором тело, выведенное из состояния устойчивого равновесия, стремится вернуться в начальное положение.

Неустойчивое равновесие — это равновесие, при котором тело, выведенное из положения равновесия и предоставленное самому себе, будет еще больше отклоняться от положения равновесия.

Безразличное равновесие системы — равновесие, при котором после устранения причин, вызвавших малые отклонения, система остается в покое в этом отклоненном состоянии

Основная и дополнительная литература по теме урока:

Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017.– С. 165 – 169.

Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2009.

Степанова Г.Н. Сборник задач по физике. 10-11 класс. — М.: Просвещение. 1999 г. С.48- 50.

Теоретический материал для самостоятельного изучения

Равновесие – это состояние покоя, т.е. если тело покоится относительно инерциальной системы отсчета, то говорят, что оно находится в равновесии. Вопросы равновесия интересуют строителей, альпинистов, артистов цирка и многих-многих других людей. Любому человеку приходилось сталкиваться с проблемой сохранения равновесия. Почему одни тела, выведенные из состояния равновесия, падают, а другие – нет? Выясним, при каком условии тело будет находиться в состоянии равновесия.

Раздел механики, в котором изучается равновесие абсолютно твердых тел, называется статикой. Статика является частным случаем динамики. В статике твердое тело рассматривается как абсолютно твердое, т.е. недеформируемое тело. Это означает, что деформация так мала, что её можно не учитывать.

Центр тяжести существует у любого тела. Эта точка может находиться и вне тела. Как же подвесить или подпереть тело, чтобы оно находилось в равновесии.

Подобную задачу в свое время решил Архимед. Им же были введены понятие плеча силы и момента силы.

Плечо силы — это длина перпендикуляра, опущенного от оси вращения на линию действия силы.

Момент силы — это физическая величина, равная произведению модуля силы на ее плечо.

После своих исследований Архимед сформулировал условие равновесия рычага и вывел формулу:

Это правило является следствием 2-го закона Ньютона.

Первое условие равновесия

Для равновесия тела необходимо, чтобы сумма всех сил, приложенных к телу была равна нулю.

формула должна быть в векторном виде и стоять знак суммы

Второе условие равновесия

При равновесии твердого тела сумма моментов вcех внешних сил, действующих на него относительно любой оси, равна нулю.

Не менее важен случай, когда тело имеет площадь опоры. Тело, имеющее площадь опоры, находится в равновесии, когда вертикальная прямая, проходящая через центр тяжести тела, не выходит за пределы площади опоры этого тела. Известно, что в городе Пизе в Италии существует наклонная башня. Несмотря на то, что башня наклонена, она не опрокидывается, хотя ее часто называют падающей. Очевидно, что при том наклоне, которого башня достигла к настоящему времени, вертикаль, проведенная из центра тяжести башни, все еще проходит внутри ее площади опоры.

В практике большую роль играет не только выполнение условия равновесия тел, но и качественная характеристика равновесия, называемая устойчивостью.

Различают 3 вида равновесия: устойчивое, неустойчивое, безразличное.

Если при отклонении тела от положения равновесия, возникают силы или моменты сил, стремящиеся вернуть тело в положение равновесия, то такое равновесие называется устойчивым.

Неустойчивое равновесие — это противоположный случай. При отклонении тела от положения равновесия, возникают силы или моменты сил, которые стремятся увеличить это отклонение.

Наконец, если при малом отклонении от положения равновесия тело все равно остается в равновесии, то такое равновесие называется безразличным.

Чаще всего необходимо, чтобы равновесие было устойчивым. Когда равновесие нарушается, то сооружение становится опасным, если его размеры велики.

Примеры и разбор решения заданий

1. Чему равен момент силы тяжести груза массой 40 кг, подвешенного на кронштейне АВС, относительно оси, проходящей через точку В, если АВ=0,5 м и угол α=45⁰

Решение:

Момент силы – это величина равная произведению модуля силы на её плечо.

Сначала найдём плечо силы, для этого нам надо опустить перпендикуляр из точки опоры на линию действия силы. Плечо силы тяжести равно расстоянию АС. Так как угол равен 45°, то мы видим, что АС=АВ

Модуль силы тяжести находим по формуле:

После подстановки числовых значений величин мы получим:

F=40×9,8 =400 Н, М= 400 ×0,5=200 Н м.

Ответ: М=200 Н м.

2. Приложив вертикальную силу F, груз массой М — 100 кг удерживают на месте с помощью рычага (см. рис.). Рычаг состоит из шарнира без трения и однородного массивного стержня длиной L=8 м. Расстояние от оси шарнира до точки подвеса груза равно b=2 м. Чему равен модуль силы F, если масса рычага равна 40 кг.

Решение:

По условию задачи рычаг находится в равновесии. Напишем второе условие равновесия для рычага:

.

После подстановки числовых значений величин получим

F= (100×9,8 ×2 + 0,5×40×9,8×8)/8=450 Н

Ответ: 450 Н.

resh.edu.ru