Построение графика квадратичной функций: алгоритм и примеры 9 класс онлайн-подготовка на Ростелеком Лицей
Тема 5.
Построение графика квадратичной функции с помощью преобразований.
Рассмотрим частные случаи
y = ax2 + n и y = a(x – m)2.
В одной системе координат построим графики функцийy=12×2 и y=12×2+5.
Составим таблицу значений функции: y=12×2
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
4,5 |
2 |
0,5 |
0 |
0,5 |
2 |
4,5 |
Чтобы получить таблицу значений для функции y=12×2+5 для тех же значений аргумента, необходимо к найденным значениям функции y=12×2 прибавить 5.
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
9,5 |
7 |
5,5 |
5 |
5,5 |
7 |
9,5 |
Получается, что каждую точку второго графика можно получить из некоторой точки первого графика с помощью параллельного переноса на 5 единиц вверх вдоль оси y.
График функции y=12×2+5 – парабола, полученная в результате сдвига вверх графика функции y=12×2.
График функции y = ax2 + n – парабола, которую можно получить из графика функции y = ax2 с помощью параллельного переноса вдоль оси y на n единиц вверх, если n > 0 или на – n единиц вниз, если n
В одной системе координат построим графики функций y=12×2 и y=12x-52. Составим таблицы значений для этих функций.
y=12×2
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
4,5 |
2 |
0,5 |
0 |
0,5 |
2 |
4,5 |
y=12x-52
|
x |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
y |
4,5 |
2 |
0,5 |
0 |
0,5 |
2 |
4,5 |
Значит, если переместить каждую точку графика y=12×2 вправо на 5 единиц, то получим соответствующую точку графика функции y=12x-52.
График функции y=12x-52 – парабола, полученная y=12x-52 в результате сдвига вправо графика функции y=12×2.
График функции y = a(x — m)2 – парабола, которую можно получить из графика функции y = ax2 с помощью параллельного переноса вдоль оси x на на m единиц вправо, если m > 0 или на – m единиц влево, если m
Полученные выводы позволяют понять, что представляет собой график функции y = a(x — m)2. Например, график функции y=12x-52+3 можно получить из графика функции y=12×2 с помощью двух параллельных переносов – сдвига вдоль оси x на 5 единиц вправо и вдоль оси y

Таким образом, график функции y = a(x — m)2 можно получить из параболы y = ax2 с помощью двух параллельных переносов: сдвига вдоль x на m единиц вправо, если m > 0 или на – m единиц влево, если m n единиц вверх, если n > 0 или на – n единиц вниз, если n
Заметим, что данные преобразования можно производить в любом порядке: сначала выполнить параллельный перенос вдоль оси x, а затем вдоль оси y или наоборот.
Преобразования, которые мы рассмотрели применимы для любых функций.
Рассмотрим пример.
Построим график функции y = x2 — 4 x двумя способами: с помощью преобразований, которые мы сегодня рассмотрели и с помощью таблицы значений функции.
Для того, чтобы построить график функции с помощью преобразований, необходимо его представить в виде y = a(x — m)2. Для этого надо выделить полный квадрат. Итак, в нашу функцию y = x2 — 4x добавим 4 и вычтем 4. Получим:
Для этого надо выделить полный квадрат. Итак, в нашу функцию y = x2 — 4x добавим 4 и вычтем 4. Получим:
y=x2-4x+4-4=x-22-4
График данной функции можно получить из графика функции y = x2 с помощью двух параллельных переносов: сдвига вдоль оси x на 2 единицы вправо, и сдвига вдоль оси y на 4 единицы вниз.
Чтобы построить график функции вторым способом, составим таблицу ее значений. Возьми нечетное количество точек, например, пять и семь. В центре поставь координаты вершины параболы.
xв=-b2a=—42∙1=2
yв=22-4∙2=-4
График квадратичной функции симметричен относительно прямой, параллельной оси y, проходящей через вершину параболы. В данном случае прямая x = 2 является осью симметрии.
|
x |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
y |
5 |
0 |
-3 |
-4 |
-3 |
0 |
5 |
Построение графика квадратичной функции
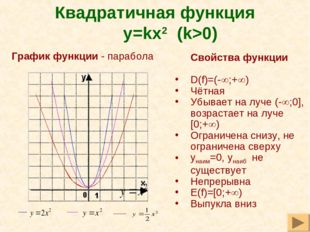
Графиком
любой квадратичной функции является парабола. У каждой параболы есть вершина, при изображении графика важно знать её
координаты. Вершина параболы имеет
координаты (m,n).
У каждой параболы есть вершина, при изображении графика важно знать её
координаты. Вершина параболы имеет
координаты (m,n).
Определите координаты вершин для парабол:
Определим координаты вершины параболы, которая является графиком квадратичной функции записанной в виде .
Преобразуем квадратный трёхчлен, выделим из него квадрат двучлена:
Второе слагаемое представим в виде удвоенного произведения:
Выделим квадрат суммы:
После сокращения получаем:
Отсюда запишем, что:
Вывод.
Графиком функции
является
парабола, которую можно получить из
параболы с помощью двух параллельных переносов: сдвига относительно оси x и сдвига относительно оси y. Данная парабола имеет вершину с
координатами (m,n), где ,
.
Осью симметрии является прямая x=m.
Пример.
Найти координаты вершины параболы .
Вершина будет иметь координаты (m,n), каждую из которых можно получить по формуле. Подставим коэффициенты квадратичной функции в формулу и найдём эти значения:
Вершина параболы имеет координаты (-2,-5).
Воспользуемся наиболее простым способом: сначала найдём m вершины по формуле. И учитывая, что вершина принадлежит графику функции, подставим m вместо аргумента в функцию:
Получили вершину, которая имеет координаты (-2,-5).
Алгоритм построения графика квадратичной функции:
1. Определить направление ветвей парабола. Если a>0, то ветви направлены вверх, если a<0, то — вниз.
2.
Найти
координаты вершины параболы и отметить её на координатной плоскости. Применив
формулу ,
найдём абсциссу вершины параболы, и, подставив это значение в формулу, задающую
функцию, найдем ординату этой точки.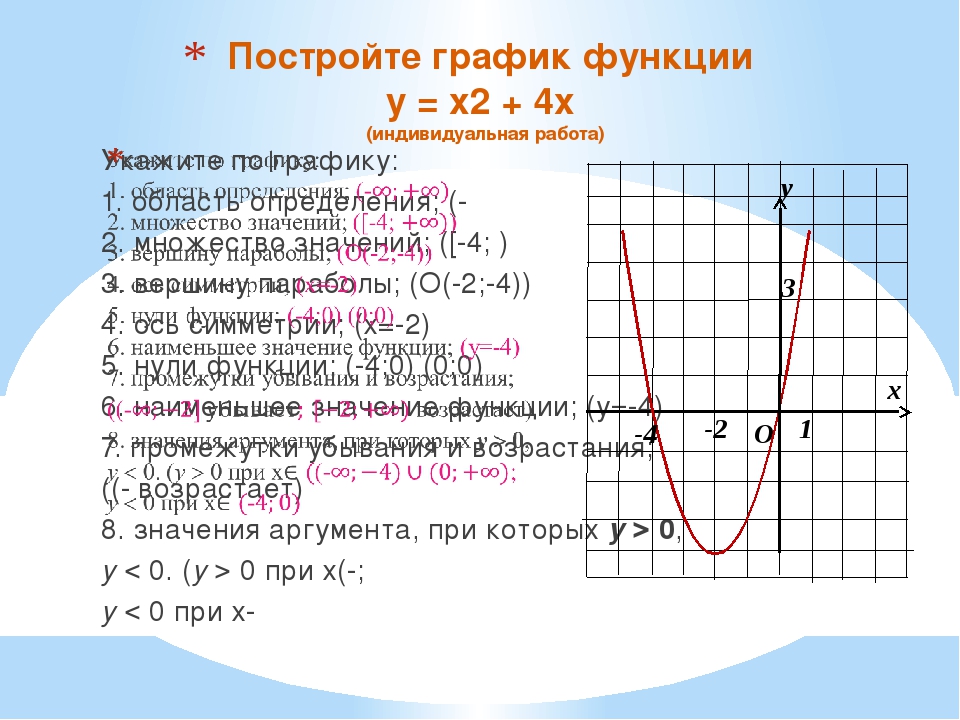
3. Определить ось симметрии x=m.
4. Построить ещё несколько точек принадлежащих параболе, составив таблицу значений функции с учётом оси симметрии.
5. Соединить отмеченные точки плавной линией.
Пример.
Изобразить график функции .
1. Определим направление ветвей параболы:
2. Найдём координаты вершины:
Получили вершину с координатами (-2, -3).
3. Определим ось симметрии:
4. Составим таблицу значений:
Выбранные значения симметричны относительно оси симметрии.
5. Отметим и соединим полученные точки на координатной плоскости:
Получили параболу, которая является графиком функции.
Пример.
Изобразить
график функции и
описать её свойства.
Изобразим график функции:
1. Определим направление ветвей параболы:
2. Найдём координаты вершины параболы:
Вершина имеет координаты (-2,-4).
3. Определим ось симметрии:
4. Составим таблицу значения функции:
5. Соединив эти точки, получаем:
Определим свойства функции.
Областью определения и областью значений являются:
Определим нули функции:
Перечислим промежутки знакопостоянства функции:
Опишем промежутки монотонности:
Свойства функции, для 9 класса по алгебре
Дата публикации: .
Ребята, мы продолжаем изучать числовые функции. Сегодня мы остановимся на такой теме, как свойства функции. Функции обладают многими свойствами. Вспомните, какие свойства мы с вами совсем недавно изучили. Правильно, область определения и область значений, они являются одними из ключевых свойств. Никогда не забывайте про них и помните, что функция всегда обладает этими свойствами.
Функции обладают многими свойствами. Вспомните, какие свойства мы с вами совсем недавно изучили. Правильно, область определения и область значений, они являются одними из ключевых свойств. Никогда не забывайте про них и помните, что функция всегда обладает этими свойствами.
В этом разделе, мы с вами определим некоторые свойства функций. Порядок, в котором мы будем их определять, рекомендую соблюдать и при решении задач.
Возрастание и убывание функции
Первое свойство, которое мы определим, это возрастание и убывание функции.
Функция называется возрастающей на множестве Х⊂D(f), если для любых х1 и х2, таких, что х1 < x2 — выполняется неравенство f(x1) < f(x2). То есть большему значению аргумента, соответствует большее значение функции.Функция называется убывающей на множестве Х⊂D(f), если для любых х1 и х2, таких, что х1 < x2 — выполняется неравенство f(x1)>f(x2). То есть большему значению аргумента, соответствует меньшее значение функции.
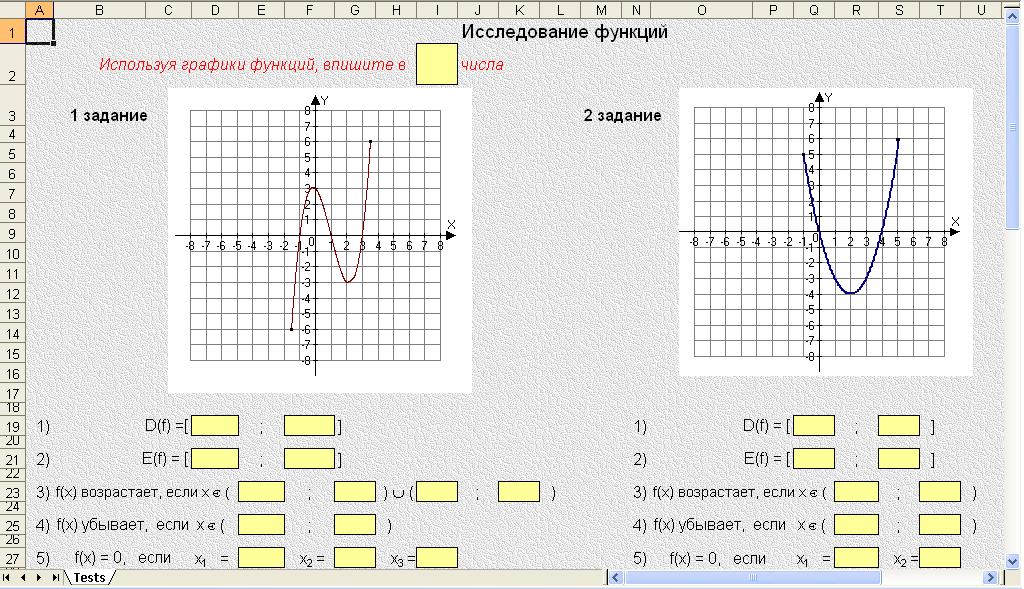
Понятия «возрастание» и «убывание» функции очень легко понять, если внимательно посмотреть на графики функции. Для возрастающей функции: мы как бы поднимаемся в горку, для убывающей соответственно — спускаемся. Общий вид возрастающих и убывающих функции представлен на графиках ниже.
Возрастание и убывание функции в общем случае называется монотонностью. То есть, наша задача -это найти промежутки убывания и возрастания функции. В общем случае это формулируется так: найти промежутки монотонности или исследовать функцию на монотонность.
Пример
Исследовать на монотонность функцию $y=3x+2$.Решение: Проверим функцию для любых х1 и х2 и пусть х1 < x2.
$f(x1)=3×1+2$
$f(x2)=3×2+2$
Поскольку, х1< x2, то f(x1) < f(x2), т. е. большему значению аргумента, соответствует большее значение функции.
Ограниченность функции
Функцию $y=f(x)$ называют ограниченной снизу на множестве Х⊂D(f), если существует такое число а, что для любых хϵХ выполняется неравенство f(x) < a. 2}≤4$, но это значит ограниченность сверху.
2}≤4$, но это значит ограниченность сверху.
Ответ: наша функция ограниченна двумя прямыми $у=0$ и $у=4$.Наибольшее и наименьшее значение
Наименьшим значение функции y= f(x) на множестве Х⊂D(f), называется некоторое число m, такое, что:
a) Существует некоторое х0, что $f(x0)=m$.
б) Для любого хϵХ, выполняется $f(x)≥f(x0)$.
Наибольшим значение функции y=f(x) на множестве Х⊂D(f), называется некоторое число m, такое что:
a) Существует некоторое х0, что $f(x0)=m$.
б) Для любого хϵХ, выполняется $f(x)≤f(x0)$.
Наибольшее и наименьшее значение принято обозначать yнаиб. и yнаим..
Понятия ограниченности и наибольшего с наименьшим значением функции тесно связаны. Выполняются следующие утверждения:
а) Если существует наименьшее значение у функции, то она ограничена снизу.
б) Если существует наибольшее значение у функции, то она ограничена сверху.
в) Если функция не ограничена сверху, то наибольшего значения не существует. 2+16x≥0$. Найдем корни квадратного трехчлена $(2х+1)(2х-9)≥0$. При $х=-0,5$ и $х=4,5$ функция обращается в ноль, во всех остальных точках она больше нуля. Тогда, по определению, наименьшее значению функции равно нулю.
2+16x≥0$. Найдем корни квадратного трехчлена $(2х+1)(2х-9)≥0$. При $х=-0,5$ и $х=4,5$ функция обращается в ноль, во всех остальных точках она больше нуля. Тогда, по определению, наименьшее значению функции равно нулю.
Ответ: yнаиб.=5 и yнаим.=0.
Ребята мы с вами еще изучали понятия выпуклости функции. При решении некоторых задач, нам это свойство может понадобиться. Это свойство, также легко определяется с помощью графиков.
Функция выпукла вниз, если любые две точки графика исходной функции соединить, и график функции окажется ниже линии соединения точек.
Функция выпукла вверх, если любые две точки графика исходной функции соединить, и график функции окажется выше линии соединения точек.
Функция непрерывна, если график нашей функции не имеет разрывов, например, как график функции выше.
Если требуются найти свойства функции, то последовательность поиска свойств такова:
а) Область определения.
б) Монотонность. 2$,
2$,
в) $y=\frac{4}{x}$.
Проверочная работа по теме «Графики функций», 9 класс
Проверочная работа по теме «Функции и графики»,вариант 1.
1. Установите соответствие между графиками функций и формулами, которые их задают.
1) 2) 3) 4)
2.На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) f( −2) = f(2)
2) f(x)>0 при x<−4 и при x>2
3) Наименьшее значение функции равно −9
3.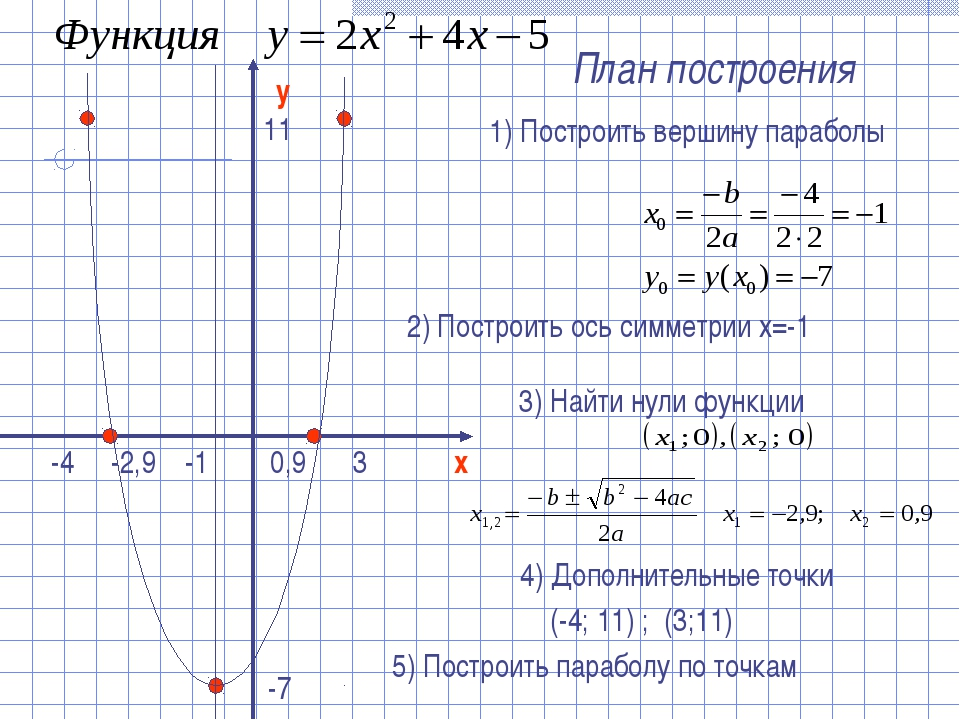 Установите соответствие между функциями и их графиками.
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) Б) В)
ГРАФИКИ
4. Найдите значение по графику функции изображенному на рисунке.
5. На рисунках изображены графики функций вида . Установите соответствие между знаками коэффициентов и и графиками функций.
КОЭФФИЦИЕНТЫ
А) Б) В)
ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер.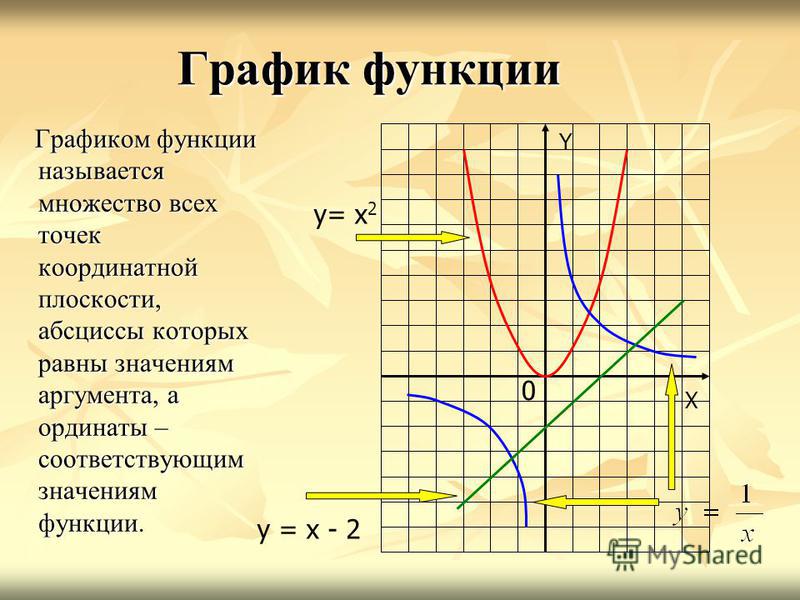
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
6. На рисунке изображён график функции Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
|
УТВЕРЖДЕНИЯ |
|
ПРОМЕЖУТКИ |
|
А) Функция возрастает на промежутке Б) Функция убывает на промежутке |
|
1) [0; 3] 2) [− 1; 1] 3) [2; 4] 4) [1; 4] |
7. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
КОЭФФИЦИЕНТЫ
А) Б) В)
ГРАФИКИ
8. Построить график функции и определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
9. Постройте график функции и определите, при каких значениях прямая имеет c графиком ровно одну общую точку.
10. Найдите область определения функции
А) б) y=
Проверочная работа по теме «Функции и графики»,вариант 2.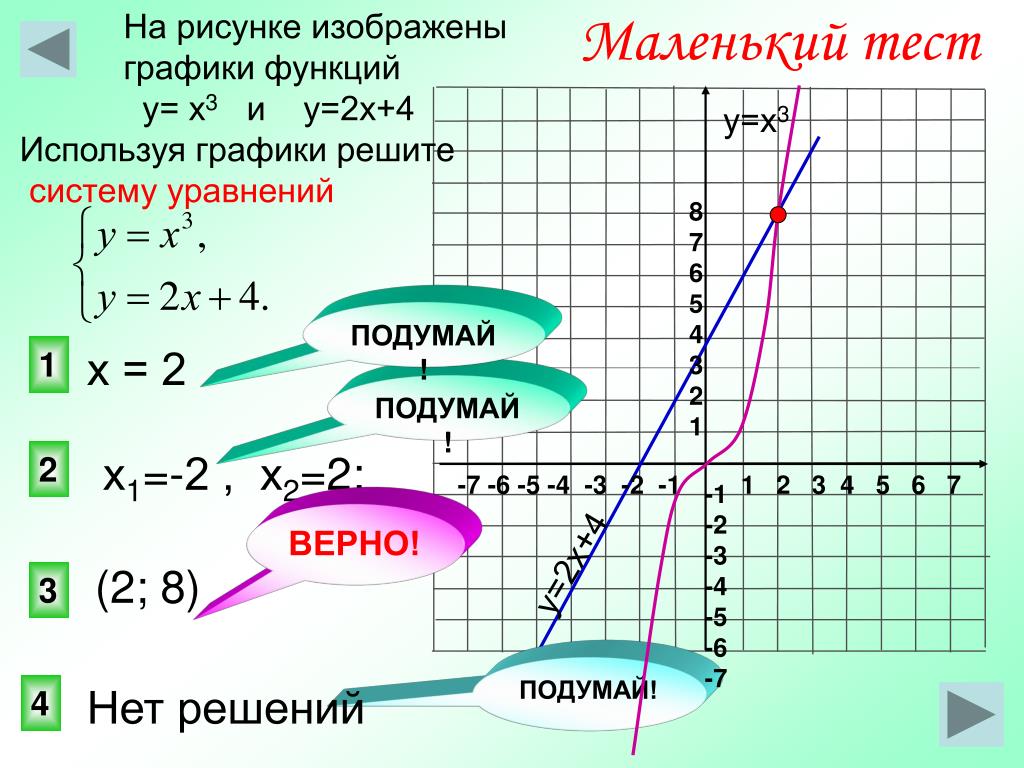
1. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
КОЭФФИЦИЕНТЫ
А) Б) В)
ГРАФИКИ
2.
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция убывает на промежутке [−1; +∞).
2) f(−3)<f(0).
3) f(x)<0 при −4<x<2.
3. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
Графики
Коэффициенты
|
1) k < 0, b < 0 |
2) k < 0, b>0 |
3) k > 0, b>0 |
4) k > 0, b<0 |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
4. На рисунке изображён график функции y = ax2 + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются.
На рисунке изображён график функции y = ax2 + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются.
|
УТВЕРЖДЕНИЯ |
|
ПРОМЕЖУТКИ |
|
А) функция возрастает на промежутке Б) функция убывает на промежутке |
|
1) [1;3] 2) [0;2] 3) [2;4] 4) [-2;3] |
5. Установите соответствие между графиками функций и формулами, которые их задают.
Установите соответствие между графиками функций и формулами, которые их задают.
1) 2) 3)
4)
6. Найдите значение по графику функции изображенному на рисунке.
7. На одном из рисунков изображен график функции Укажите номер этого рисунка.
8. Постройте график функции Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
9.
Постройте график функции
и определите, при каких значениях прямая не имеет с графиком ни одной общей точки.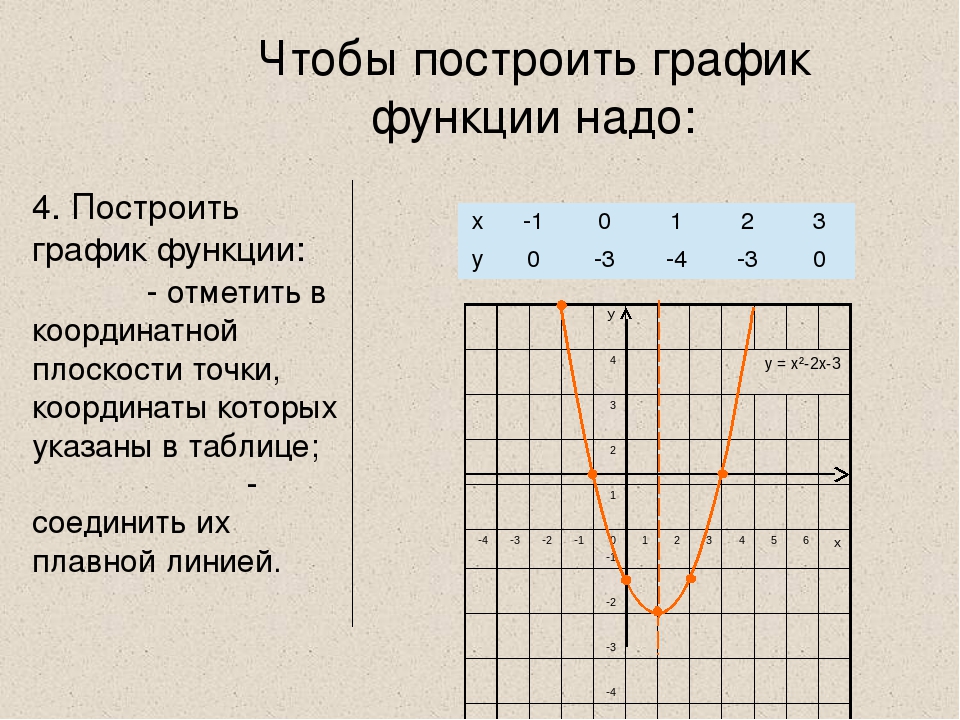
10. Найдите область определения функции
А) б)y=
Открытый урок по алгебре 9 класс. Тема: «Построение графика квадратичной функции»
Открытый урок по алгебре 9 класс.
Учитель Абаскулиева Г.С.
Тема: «Построение графика квадратичной функции»
5.10.18г.
Цели урока:
— знать определение квадратичной функции, алгоритм построения графика квадратичной функции;
— уметь находить координаты вершины параболы, дополнительные точки, строить параболу;
— воспитывать внимательность, самостоятельность, навыки работы с чертежными принадлежностями, культуру чертежа.
Оборудование: мультимедийный проектор, индивидуальные карточки.
Ход урока.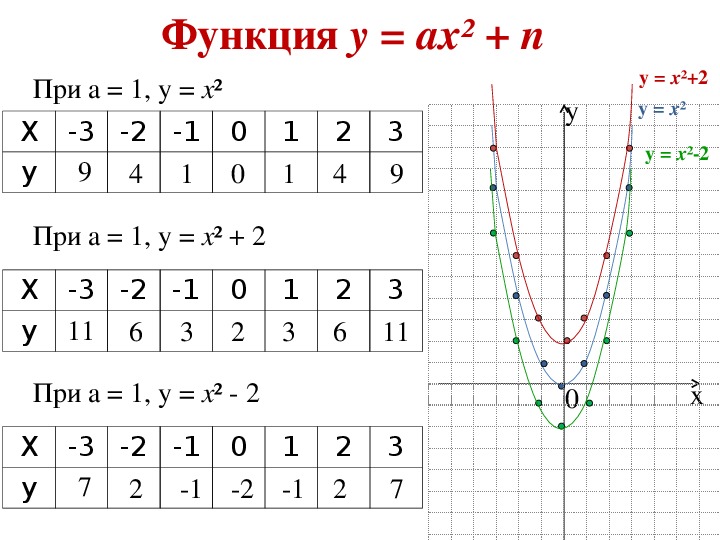
I. Организационный момент.
На прошлом уроке мы рассмотрели различные преобразования параболы. Как вы думаете, какая цель у нас сегодня?
II. Проверка домашнего задания. (№108, 110(в, г), 111, 113). Собрать тетради.
III. Актуализация знаний. ( Фронтальный опрос. Одновременно несколько учащихся работают по индивидуальным карточкам: определить направление ветвей параболы и найти координаты вершины параболы).
1. Функция какого вида называется квадратичной?(
2. Что является графиком квадратичной функции? (парабола)
3. Сколько точек необходимо для построения параболы? (минимум 5)
4. От чего зависит направление ветвей параболы? (а>0 ветви вверх, a<0 ветви вниз)
5. Как получается график ?
6. Как получается график ?
7. Дайте название функции и скажите, что является графиком этой функции:
у = 2х -5 , у = 8 + 6х, у = 2х2 – 5, у = ,
у = — х, у = -3х2, у = (х – 2)2, у = -3(х + 1)2 – 4
6.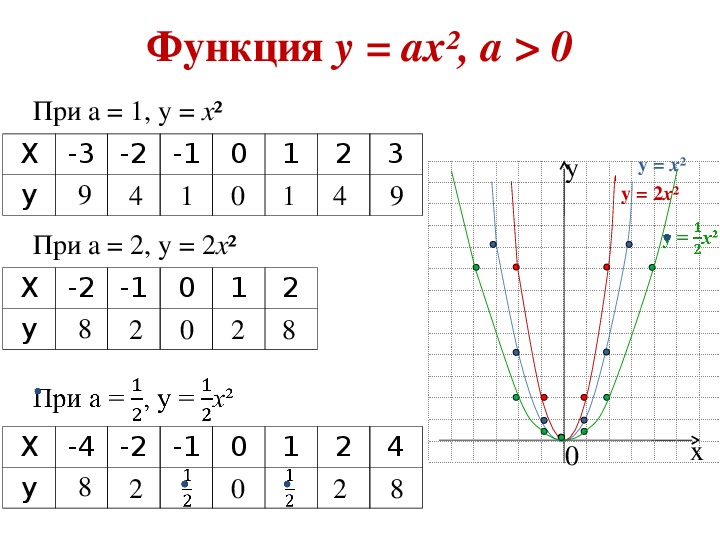 Определите, график какой
функции изображен на рисунке и назовите промежутки возрастания и убывания
функции, нули.
Определите, график какой
функции изображен на рисунке и назовите промежутки возрастания и убывания
функции, нули.
Рис. 1
А. у = — (х-3)2+ 1 Б. у = (х+3)2-1 В. у = (х-1)2+3
IV. Изучение нового материала.
Квадратичной функцией называется функция, которую можно задать формулой вида y=ax²+bx+c, где х — независимая переменная, a, b и с -некоторые числа (причём а≠0).
Графиком квадратичной функции является парабола, ветви которой направлены вверх(если а>0) или вниз (если а<0).
Чтобы построить график функции есть два способа:
1 способ.
1) Выделить квадрат двучлена из квадратного трехчлена в виде
2) Построить график с помощью двух параллельных переносов.
2 способ.
1) Найти координаты вершины параболы А(m;n) по формулам: ;
n = у(m) т.е. подставить найденное значение абсциссы m в формулу, которой задана функция и вычислить значение.
2) Прямая
x=m является осью симметрии параболы.3) Заполнить таблицу значений функции: в таблице расположить вершину в середине таблицы и взять соседние симметричные значения х.
4) Построить график функции: — отметить в координатной плоскости точки, координаты которых указаны в таблице; — соединить их плавной линией.
Построим график функции по алгоритму
у = х²-2х-1; n=1-2-1=-2 Вершина параболы (1;-2). Прямая х=1 ось симметрии праболы. Ветви параболы направлены вверх, т.к. a=1>0 Симметрично строим левую сторону параболы. |
V. Физминутка.
1. Повороты головы вправо- влево, вверх- вниз, показываем смещение вершины параболы
у = -х2+ 3 у = -(х – 2)2 у = -х2+ 6
у = = х2— 5 у = (х + 1)2 у = -х2 – 8
2. Движения руками вверх-
вниз, показываем направление ветвей параболы.
Движения руками вверх-
вниз, показываем направление ветвей параболы.
у = -х2+ 3 у = -(х – 2)2 + 2 у = -х2+ 6
у = = х2— 5 у = (х + 1)2— 5 у = -х2 – 8
VI. Решение упражнений.
№ 121 (найти координаты вершины параболы)
№122 (построить график, выяснить свойства функции)
VII. Подведение итогов:
Ответьте на вопросы. Верно ли, что:
1. Вершина параболы находится по формулам ….
2. При а >0 ветви параболы направлены …
3. При а <0 ветви параболы направлены …
4. Как называют точки пересечения параболы с осью Ох?
Домашнее задание:№123, №124.
Программа элективного курса по математике «Функции.
 Графики элементарных функций»; 9 класс — Планирование — Математика, алгебра, геометрия
Графики элементарных функций»; 9 класс — Планирование — Математика, алгебра, геометрияПрограмма элективного курса
по математике
для учащихся 9 классов
«Функции. Графики элементарных функций».
Составитель:
учитель математики
Чистоусова Елена Николаевна
МБОУ СОШ №21 города Ставрополя
Пояснительная записка
Элективный
курс по предпрофильной подготовке
учащихся 9 класса посвящен одному из
основных понятий современной математики —
функциональной зависимости.
Он позволит углубить и систематизировать
знания учащихся по изучению способов
задания функций, их свойств и графиков,
а также раскроет перед школьниками
новые знания об обратных функциях,
свойствах взаимно обратных функций,
выходящие за рамки школьной программы. Понятие функциональной зависимости,
являясь одним из центральных в математике,
пронизывает все ее приложения, оно, как
ни одно другое, приучает воспринимать
величины в их постоянной изменчивости,
во взаимной связи.
Понятие функциональной зависимости,
являясь одним из центральных в математике,
пронизывает все ее приложения, оно, как
ни одно другое, приучает воспринимать
величины в их постоянной изменчивости,
во взаимной связи.
Изучение поведения функций и построение их графиков являются важным разделом школьного курса. Иногда график является единственно возможным способом задания функции. Свободное владение техникой построения графиков часто помогает решать сложные задачи. Кроме того, умение строить графики функций представляет большой интерес для самих учащихся.
В курсе заложена возможность дифференцированного обучения, как путем использования задач различного уровня сложности, так и на основе различной степени самостоятельности осваивания нового материала. Следовательно, программа применима для самых разных групп школьников.
На
изучение всего курса отводится 17 часов,
по окончании предусмотрено зачетное
мероприятие на 1 час.
Цель курса: расширить и систематизировать знания учащихся, связанных с понятием функции, графика функции; применением этих понятий в жизни и на практике.
Задачи курса:
ознакомить учащихся с понятием функции, ее свойств и графика функции;
овладение способами построения графиков функций на всей области определения и на заданном промежутке;
ознакомление учащихся с возможностями и основными приемами работы с программой для построения графиков функций;
умение использовать свойства функции при решении задач;
определение свойств функции по графику и по аналитическому заданию;
научить строить графики, содержащие модуль;
развивать интеллектуальные способности учащихся;
формировать качества мышления, характерные для математической деятельности и необходимые для продуктивной жизни в обществе;
формирование творческого и абстрактного мышления;
формировать познавательную активность к изучению математики;
овладение
терминологией.
Ожидаемые результаты
Учащиеся должны знать:
понятие функции как математической модели, описывающей разнообразие реальных зависимостей;
Учащиеся должны уметь:
определять значение функции по значению аргумента при различных способах задания функции;
находить значение аргумента по значению функции, заданной графиком или таблицей;
строить графики изученных функций, выполнять преобразования графиков;
описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшее и наименьшее значения;
решать уравнения, системы уравнений, используя свойства функций и их графиков;
исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций;
строить графики многочленов и простейших рациональных функций с использованием программы графопостроитель;
использовать для приближённого решения уравнений и систем уравнений графический метод;
Учебно-тематический план курса
№ п/п | Наименование разделов и тем | Количество часов | Метод обучения | Форма контроля |
1. | Понятия функции и графика: зависимость; график функции; способы задания функции. | 2 | Лекция, беседа, объяснение. Применение ИКТ. | Устный опрос. |
2. | Виды функций: линейная функция; обратная пропорциональность; функция ;квадратичная функция. | 4 | Лекция, беседа, объяснение. Выполнение тренировочных упражнений. | Проверка самостотельно решенных задач. |
3. | Преобразование графиков: перенос вдоль оси ординат; перенос вдоль оси абсцисс; сжатие (растяжение) вдоль оси ординат; сжатие
(растяжение) вдоль оси абсцисс. | 4 | Лекция, решение практических задач. Применение ИКТ. | Практическая работа. |
4. | Действия над функциями: сумма (разность) функций; произведение функций; частное двух функций. | 4 | Лекция, беседа, объяснение. Выполнение тренировочных упражнений. | Проверочная работа. |
5. | Функции, содержащие операцию взятия модуля. | 2 | Лекция,
беседа, объяснение. Выполнение
тренировочных упражнений. | Тестирование. |
6. | Итоговая диагностика | 1 | Зачёт. | |
10 | Итого: | 17 |
Литература
Галицкий М.Л, Гольдман А.М., Звавич Л.И. Сборник задач по алгебре. Учебное пособие для 8 – 9 классов с углубленным изучением математики. – 7-е изд. – М. Просвещение, 2001.
Гельфанд И.М., Глаголева Е.Г., Шноль Э.Э. Функции и графики (основные приемы). – 6-е изд., испр. – М.: МЦНМО,2004.
Глаголева Е.Г.,
Серебренникова Л.Г. Метод координат:
Ч. 1: Прямая и плоскость: Учебное пособие
для учащихся ОЛ ВЗМШ при МГУ. – М., 2002.
1: Прямая и плоскость: Учебное пособие
для учащихся ОЛ ВЗМШ при МГУ. – М., 2002.
Данкова И.Н., Бондаренко Т.Е., Емелина Л.Л. и др. Предпрофильная подготовка учащихся в классе по математике: Общие положения, структура портфолио, программы курсов, сценарии занятий. – М.: «5 за знания», 2006.
Депман И.Я., Виленкин Н.Я. За страницами учебника математики: Пособие для учащихся 5 – 6 кл. сред. шк. – М.: Просвещение, 1989.
Доброва О.Н. Задания по алгебре и математическому анализу: Пособие для учащихся 9 – 11 кл. общеобразоват. учреждений. – М.: Просвещение, 1996.
Дорофеев Г.В., Бунимович Е.А., Кузнецова Л.В., Мишаева, С.С., Суворова С.Б., Мищенко Т.М., Рослова Л.О. Курс по выбору для 9 класса. Избранные вопросы математики. Математика в школе, № 10, 2003.
Дорофеев Г.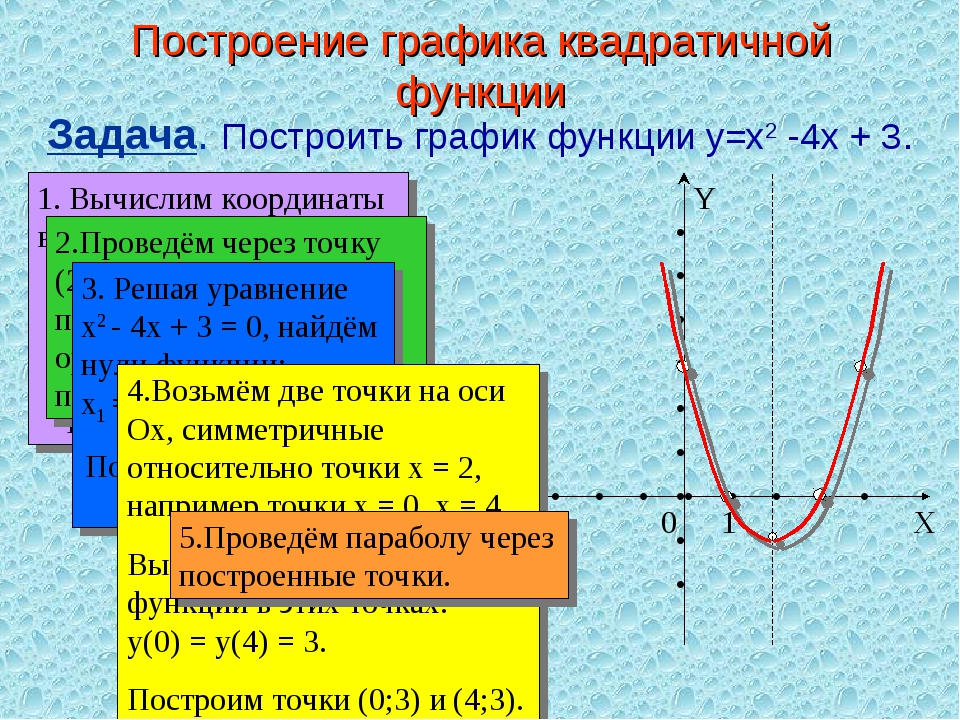 В.,
Муравин Г.К., Седова Е.А. Математика. 11 кл. Подготовка к
письменному экзамену за курс средней
школы. Решение задач с методическими
комментариями. – М.: Дрофа, 2000.
В.,
Муравин Г.К., Седова Е.А. Математика. 11 кл. Подготовка к
письменному экзамену за курс средней
школы. Решение задач с методическими
комментариями. – М.: Дрофа, 2000.
Крамор В.С. Повторяем и систематизируем школьный курс геометрии. – М.: Просвещение, 1992.
Кудрявцев С. В. и др. Дидактические материалы по алгебре для 7 класса: Пособие для учителя. С. В. Кудрявцев, Ю. Н. Макарычев, Е. М. Сорокина. 3-е изд., перераб. – М.: Просвещение, 1986.
Пичурин Л.Ф. За страницами учебника алгебры: Кн. для учащихся 7 – 9 классов общеобраз. учрежд. – 2-е изд., дораб. – М.: Просвещение, 1999.
Савин А.П. . Энциклопедический словарь юного математика.– М.: Педагогика, 1985.
Урок алгебры в 9-м классе «Квадратичная функция. Ее свойства и график»
Цели – обобщить и систематизировать знания учащихся о квадратичной функции: повторить изученные приемы исследования свойств функции, методы построения графиков; закрепить и упрочить умения и навыки учащихся по данной теме, показать ее прикладной характер, ориентировать на использование полученных знаний при дальнейшем изучении математики.
План урока:
- Разминка.
- Фронтальная работа по построению графика квадратичной функции и исследованию ее свойств.
- Работа в группах по построению графика квадратичной функции с модулем.
- Решение задачи, носящей прикладной характер, с применением свойств квадратичной функции.
- Тест, контролирующий знания учащихся по теме.
Ход урока
Учитель: Ребята, сегодня мы с вами продолжаем вести разговор об одном из важных разделов математики – функциональной зависимости. Прежде всего вспомним определение функции.
Ученик: Функция – это такая зависимость переменной у от переменной х, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной.
Учитель: Какую функцию называют квадратичной? Что является ее графиком?
Ученик: Квадратичной функцией называется функция. которую можнозадать формулой вида y = ax2 + bx + c, где x – независимая переменная, a, b и с – некоторые числа, причем а 0. График – парабола.
которую можнозадать формулой вида y = ax2 + bx + c, где x – независимая переменная, a, b и с – некоторые числа, причем а 0. График – парабола.
Учитель: С какими способами построения графиков квадратичной функции мы познакомились?
Ученик:
- способ выделения полного квадрата и дальнейшего построения с использованием искусственных преобразований;
- построение графика на основании специального исследования квадратного трехчлена.
Учитель: Повторим некоторые этапы построения графиков квадратичной функции при выполнении теста – разминки.
I. Разминка (ученики устно отвечают на вопросы теста, подготовленного на карточки или слайды). В это время предложить трем ученикам самостоятельно решить на доске задачи.
Тест:
- Какому графику соответствует функция, заданная формулой y = x2 – 2? (Рисунок 1)
Рисунок 1
- На каком из рисунков изображен график функции (Рисунок 2)
Рисунок 2
- Функция задана формулой .
 На каком из рисунков изображен ее график? (Рисунок 3)
На каком из рисунков изображен ее график? (Рисунок 3)
Рисунок 3
- Функция задана формулой . Каковы координаты вершины параболы?
a (2; – 7).
b (– 2; 24).
c (2; 25). - Каково наибольшее значение функции, заданной формулой ?
a 5.
b 7.
c –7.
Ответы: 1b; 2c; 3b; 4a; 5b.
Индивидуальные задания на доске:
1. Параболу у = 2х2 сдвинули влево на 3 единицы и вниз на 5 единиц. Задайте формулой функцию, график которой получился в результате таких преобразований.
Решение: у = 2(х + 3)2 – 5.
2. Найдите область значений функции у = х2 – 2х.
Решение:Функция ограничена снизу, у0 ===1, E(f) = (2; +)
3. Постройте график функции у = (3 – x)(х+ 1).
Постройте график функции у = (3 – x)(х+ 1).
Решение: у = — х2 + 2х +3. Нули функции: х1 = – 1 ; х2 = 3. =
(3 – 1)(1 + 1) = 4. (1; 4) – вершина параболы, ветви вниз.
II. Фронтальная работа.
Задание классу (ученик у доски):
Постройте график функции у = — х2+ 6х – 5.
По графику проведите исследование свойств функции.
Индивидуальные задания на карточках:
1. Определите, при каких значениях с наименьшее значение функции у = 2х2 + 16х + с равно 2.
Решение:
; ; .
2. Определите, при каких значениях b и c вершиной параболы у = х2 + bx + c является точка А(–2; –1).
Решение: ; –2 = ; b = 4. ; ; ; .
III. Работа в группах.
Задание группам:
Построить график функции y = |x2 – 4x + 3|. Какие виды преобразований необходимо выполнить, чтобы получить данный график из графика функции y = x2.
Решение:
Виды преобразований:
- смещение вправо на 2 единицы;
- смещение вниз на 1 единицу;
- симметрия относительно оси Ох отрицательной части графика.
Дополнительно: Построить график функции у = 3х2 + 6|х| + 6.
Индивидуальные задания на карточках (ученики выполняют на доске, объясняют решение классу после работы по группам):
1. Найти наибольшее значение функции у = — 1,5(х – 1)2на отрезке [0; 2]
Решение: х0 = 1 [0; 2], функция ограничена сверху, унаиб = у(1) = 0.
2. Найти наименьшее значение функции у = 2(х +3)2 на отрезке [– 4; 1]
Решение: х0 = -3 [– 4; 1], Функция ограничена снизу, унаим = у(-3) = 0.
3. По графику у = ах2 + bx + c определите знаки чисел a, b, c. (рисунок 4)
Решение:
- ветви вниз a < 0
- > 0, a < 0 b > 0
- при x = 0 y = c > 0
Рисунок 4
IV. Решение задачи с практическим содержанием на применение свойств квадратичной функции. (Ученик у доски)
Требуется оградить прямоугольную площадку, примыкающую к стене. Забор должен иметь длину 60 м. Какой должна быть длина и ширина площадки, чтобы площадь ее была бы наибольшей?
Решение:
Пусть х м – ширина площадки, тогда длина ее будет равна (60 – 2х) м, а площадь составит у = х(60 – 2х) м2 . Выделим полный квадрат:
Выделим полный квадрат:
у = -2(х2 – 30х) = -2(х2 – 30х + 225 – 225)= -2(х – 15)2 + 450.
При х = 15 унаиб = 450. Ширина – 15 м, длина – 30 м.
V. Тест.
Вариант I
- Какая линия является графиком функции у = – (х – 3)2 + 2?
А. Прямая, проходящая через начало координат.
Б. Прямая, не проходящая через начало координат.
В. Парабола.
Г. Гипербола. - График функции у = 2(х + 2)2получается из графика функции у =2х2сдвигом на две единицы:
А. Вправо.
Б. Влево.
В. Вверх.
Г. Вниз. - Найдите наименьшее значение функции у = 3(х – 2)2на отрезке [–2; 5].
А. 0.
Б. –12.
В. 12.
Г. 27. - Какая из перечисленных функций является ограниченной сверху?
А. у = 2х2 – 5х + 3.
Б. у = 3х2 – 1.
В. у = -3х2 + х + 1.
Г. у = . - Уравнение оси симметрии параболы у = –3х2 + 5х + 1 имеет вид:
А. .
Б. .
В. .
Г. .
Вариант II
- Какая линия является графиком функции у = – (х + 2)2 — 4?
А. Прямая, проходящая через начало координат.
Б. Прямая, не проходящая через начало координат.
В. Парабола.
Г. Гипербола. - График функции у = 3х2 – 2 получается из графика функции у =3х2сдвигом на две единицы:
А. Вправо.
Вправо.
Б. Влево.
В. Вверх.
Г. Вниз. - Найдите наименьшее значение функции у = 3(х + 2)2на отрезке [–2; 1].
А. 0.
Б. –12.
В. 12.
Г. 27. - Какая из перечисленных функций является ограниченной снизу?
А. у = –2х2 – 5х + 3.
Б. у = 3х2 – 1.
В. у = -3х2 + х + 1.
Г. у = . - Уравнение оси симметрии параболы у = 2х2 – 7х + 1 имеет вид:
А. .
Б. .
В. .
Г. .
Ответы:
- Вариант I: Г Б Г Б В
- Вариант II: Б А А В В
VI. Итоги урока.
VII. Домашнее задание.
Домашняя контрольная работа
Вариант I
- Разложите на множители квадратные трехчлены:
а) х2 – 12х + 35;
б) 7у2+ 19у — 6 - Постройте график функции у = х2 – 6х + 5.
 Найдите с помощью графика:
Найдите с помощью графика:
а) нули функции;
б) промежутки знакопостоянства;
в) промежуток, в котором функция возрастает. - Найдите наименьшее значение квадратного трехчлена х2 – 8х + 7
- Сократите дробь:
- Найдите промежутки монотонности функции y = x2 – 5|x| +4.
Вариант II
- Разложите на множители квадратные трехчлены:
а) х2 – 18х + 45;
б) 9у2+ 25у — 6 - Постройте график функции у = х2 – 8х + 13. Найдите с помощью графика:
а) нули функции;
б) промежутки знакопостоянства;
в) промежуток, в котором функция убывает. - Найдите наименьшее значение квадратного трехчлена –х2 + 6х — 4
- Сократите дробь:
- Найдите промежутки монотонности функции y = x2 – 6|x| +5.

Математические навыки в девятом классе
Хотите помочь своему девятикласснику освоить математику? Вот некоторые из навыков, которые ваш ребенок будет осваивать в классе.
Алгебра
Обзор
У учащихся старших классов математические навыки и знания распределяются не по классам, а по понятиям. В алгебре учащиеся работают с созданием и чтением выражений, рациональных чисел и полиномов, а также с правилами алгебраических обозначений. Они применяют эти навыки и понимание для решения реальных проблем.
Понимание уравнений
Понимать уравнение как математическое утверждение, в котором буквы используются для представления неизвестных чисел (например, 2x-6y+z=14 ) и которое является утверждением равенства между двумя выражениями («это равно тому» ). Объясните каждый шаг решения простого уравнения и приведите практические аргументы для обоснования метода решения. Нанесите эти уравнения на координатные оси с метками и шкалами.
Переписывание выражений
Определение способов перезаписи структуры выражения.
Решения уравнений
Поймите, что некоторые уравнения не имеют решений в данной системе счисления, но имеют решение в большей системе. Например, решение x + 1 = 0 — это целое, а не целое число; решение 2x + 1 = 0 является рациональным числом, а не целым числом; решения x² – 2 = 0 являются действительными числами, а не рациональными числами; а решения x² + 2 = 0 — это комплексные числа, а не действительные числа.
Многочлены
Сложение, вычитание и умножение многочленов (выражения с несколькими членами, такие как 5xy² + 2xy — 7 ). Понимать взаимосвязь между нулями и множителями многочленов.
Полиномиальные тождества
Используйте полиномиальные тождества для решения реальных задач.
Пример:
Прямоугольный сад имеет длину x + 2 фута и ширину x + 8 футов. Каким должно быть x, чтобы площадь сада составляла 91 кв.футов?
Каким должно быть x, чтобы площадь сада составляла 91 кв.футов?
Уравнения с одной переменной
Создавайте уравнения и неравенства с одной переменной и используйте их для решения задач, включая средневзвешенные значения, расчет ипотечных и процентных ставок и скорость перемещения.
Пример:
Самолет вылетает из аэропорта Чикаго О’Хара, двигаясь на восток со скоростью 580 миль в час. В это же время из О’Хара вылетает еще один самолет, направляясь на запад и двигаясь со скоростью 530 миль в час. Через сколько часов два самолета будут на расстоянии 1000 миль друг от друга?
Графики
Представление, интерпретация и решение уравнений и неравенств на графиках, построенных в координатной плоскости, и использование технологий для построения графиков функций и составления таблиц значений.
Геометрия
Обзор
Для учащихся старших классов математические навыки и понимание организованы не по классам, а по понятиям. В геометрии студенты работают в основном с плоской или евклидовой геометрией (с координатами и без них). Учащиеся опираются на понятия геометрии, полученные в 8-м классе, используя более точные определения и разрабатывают тщательные доказательства теорем (утверждений, истинность которых можно доказать).
В геометрии студенты работают в основном с плоской или евклидовой геометрией (с координатами и без них). Учащиеся опираются на понятия геометрии, полученные в 8-м классе, используя более точные определения и разрабатывают тщательные доказательства теорем (утверждений, истинность которых можно доказать).
Преобразование
Понимание геометрического преобразования (перемещение фигуры так, чтобы она находилась в другом положении, но с тем же размером, площадью, углами и длинами) – особенно жесткие движения: перемещения, повороты, отражения и их комбинации – включая углы, окружности, перпендикулярные прямые, параллельные прямые и отрезки прямых.
Геометрические теоремы
Понимать и доказывать геометрические теоремы о прямых и углах, треугольниках, параллелограммах и окружностях. Например, теорема Пифагора, теорема о пересечении прямых, теорема о внешнем угле.
Тригонометрия
Понимать тригонометрию как измерение треугольников (и окружностей, таких как орбиты). Применение тригонометрии к обычным треугольникам. Задайте тригонометрические отношения синуса, косинуса и тангенса.
Применение тригонометрии к обычным треугольникам. Задайте тригонометрические отношения синуса, косинуса и тангенса.
Алгебраические рассуждения
Понимать и использовать алгебраические рассуждения для доказательства геометрических теорем.
Формулы объема
Объясните формулы объема и используйте их для решения задач.
Пример:
Каков объем цилиндра высотой 10 м и радиусом 9 м? (Используйте π = 3,14)
Реальные ситуации
Применение геометрических концепций для моделирования реальных ситуаций.
- Используйте измерения и свойства геометрических фигур для описания объектов — например, смоделируйте ствол дерева или туловище человека в виде цилиндра.
- Применять концепции плотности на основе площади и объема, например, человек на квадратную милю, БТЕ на кубический фут.
- Проектируйте объекты или конструкции, удовлетворяющие определенным физическим ограничениям или минимизирующие затраты.

Числа
Обзор
Для старшеклассников математические навыки и понимание организованы не по классам, а по понятиям. В числе и количестве учащиеся расширяют свое понимание числа до мнимых чисел и комплексных чисел и работают с различными единицами измерения в моделировании.Акцент делается на использовании чисел — в расчетах, уравнениях и измерениях — для решения реальных задач, в том числе тех, которые учащиеся определяют количественно и определяют сами.
Рациональные и иррациональные числа
Поймите и объясните, почему:
- сумма двух рациональных чисел рациональна (сумма может быть записана в виде дроби или десятичной дроби)
- сумма рационального числа и иррационального числа равна иррациональный (сумма не может быть записана в виде дроби; записывается в десятичной форме, неповторяющаяся и бесконечная)
Интерпретация и преобразование единиц
Последовательно выбирать и интерпретировать единицы в формулах; масштабировать чертежи и рисунки на графиках, дисплеях данных и картах. Преобразование скоростей и измерений (граммы в сантиграммы, дюймы в футы, метры в километры, мили в километры, квадратные дюймы в квадратные футы и т. д.).
Преобразование скоростей и измерений (граммы в сантиграммы, дюймы в футы, метры в километры, мили в километры, квадратные дюймы в квадратные футы и т. д.).
Реальные проблемы
Использование единиц измерения в моделировании для решения реальных задач, например: ускорение, конвертация валюты, доход на душу населения, статистика безопасности, заболеваемость, средние показатели и т. д.)
Комплекс числа
Поймите, что комплексные числа образованы действительными числами и мнимыми числами – мнимыми числами, которые при возведении в квадрат дают отрицательный результат: i² = -1 .Используйте соотношение i² = -1 для сложения, вычитания и умножения комплексных чисел.
Понимание векторов
Понимать вектор как величину, которая имеет как величину (длину), так и направление. Сложите и вычтите векторы.
Скорость
Решите задачи, связанные со скоростью и другими величинами, представленными векторами.
Пример:
- Дрю выходит из дома на утреннюю прогулку. Он идет 13,5 км на юг и 5,5 км на запад.Какова его скорость относительно брата, который все еще спит дома в постели?
- Джек отжимается. Что требует меньшей мышечной силы – если его руки на расстоянии 0,25 м друг от друга, или его руки на расстоянии 0,5 м друг от друга?
Советы, которые помогут вашему девятикласснику на уроке математики, можно найти на нашей странице с советами по математике для девятиклассников.
Ресурсы Parent Toolkit были разработаны NBC News Learn с помощью профильных экспертов и приведены в соответствие с Common Core State Standards.
Функции и графики
М. Борн
В реальном мире очень часто одна величина зависит от другой величины.
Например, если вы работаете в заведении быстрого питания, размер вашей заработной платы зависит от количества отработанных часов. Или количество бетона, которое вам нужно заказать при строительстве здания, будет зависеть от высоты здания.
Декартова плоскость
Эта глава посвящена функциям (так мы выражаем отношения между величинами) и их графикам .
График функции действительно полезен, если мы пытаемся смоделировать реальную проблему.(«Моделирование» — это процесс нахождения соотношений между величинами.)
Иногда мы можем не знать выражения для функции, но знаем некоторые значения (возможно, из эксперимента). График может дать нам хорошее представление о том, какую функцию можно применить к ситуации для решения проблемы.
В этой главе
Обзор функций
1. Введение в функции — определение функции, обозначения функций и примеры
2. Функции из вербальных утверждений — преобразование словесных задач в функции
Графики функций
3.Прямоугольные координаты — система, которую мы используем для построения графиков наших функций
4. График функции — примеры и приложение
График функции — примеры и приложение
Домен и диапазон функции — значения `x` и `y`, которые может принимать функция
5. Построение графиков с помощью системы компьютерной алгебры — некоторые мысли об использовании компьютеров для построения графиков функций
6. Графики функций, определяемые таблицами данных — часто у нас нет алгебраического выражения для функции, только таблицы
7. Непрерывные и разрывные функции — разница становится важной в более поздней математике
8.Функции разделения — они имеют разные выражения для разных значений независимой переменной
.9. Четные и нечетные функции — они полезны в более сложной математике
Давайте теперь узнаем об определении функции и ее обозначении.
функций в реальном мире
Когда мы знакомим студентов с функциями, мы обычно воплощаем концепцию в жизнь через идею функциональных машин. Но функции действительно начнут оживать, когда наши ученики найдут применение функциям в реальном мире.
ФУНКЦИОНАЛЬНЫЕ МАШИНЫ
Студенты легко усваивают идею функциональной машины: поступает ввод; что-то происходит с ним внутри машины; выходит выход. Вводится другой вход; выходит другой выход. Что происходит внутри машины? Если мы знаем правило (или правила) работы машины и входные данные, мы можем предсказать результат. Если мы знаем правило(я) и выход, мы можем определить вход. Мы также можем представить, как машина спрашивает: «Каково мое правило?» Если мы изучим входы и выходы, мы сможем выяснить правило или правила загадочной функции.
Мы можем сделать эту метафору еще более конкретной, установив большую картонную коробку с входными и выходными отверстиями. Один ученик сидит внутри функциональной машины с загадочным правилом функции. Пока другие учащиеся по очереди вводят числа в машину, учащийся внутри коробки отправляет выходные числа через выходную щель. После двух или более входов и выходов класс обычно может понять правило загадочной функции.
«Правило функции: Умножь на 3!»
Варианты расширения действия включают:
- Найдите составную функцию (включающую 2 или более функциональных правил).

- Включить дроби, десятичные числа и/или отрицательные числа.
- Учитель или учащиеся могут создавать машины функций электронных таблиц, используя функцию формулы.
- Учащиеся могут создавать таблицы функций для решения своих одноклассников с одним или двумя правилами загадочной функции.
ОНЛАЙН ФУНКЦИОНАЛЬНЫЕ МАШИНЫ
Многие замечательные онлайновые функциональные машины развивают ту же концепцию. Учащиеся могут работать индивидуально, в парах или в классе, чтобы решить головоломки функциональных машин.
- Функциональный автомат для математической игровой площадки
Этот автомат для угадывания правил функций-загадок позволяет пользователю контролировать максимальное количество вводимых данных с возможностью ручного или компьютерного ввода и 1 или 2 функциональными правилами. Требуется пять входов/выходов, прежде чем он позволит пользователю угадать правило(я) функции.
- Три функциональных автомата на сайте Shodor Interactivate включают помощь и уроки для учащихся и учителей:
- Лаборатория учителей Анненберга Шаблоны в математике: загадочная операция
Эта сложная функциональная машина принимает пользовательский ввод для двух переменных и производит результат. После изучения ряда пар входных и выходных данных пользователь пытается сделать вывод и применить операцию-загадку, чтобы предсказать результат для пары сгенерированных машиной входных данных. Пример операции-загадки в этой машине: a * (b 1).
После изучения ряда пар входных и выходных данных пользователь пытается сделать вывод и применить операцию-загадку, чтобы предсказать результат для пары сгенерированных машиной входных данных. Пример операции-загадки в этой машине: a * (b 1).
ФУНКЦИИ В РЕАЛЬНОМ МИРЕ
Стандарт NCTM 2 для шаблонов, функций и алгебры требует, чтобы учащиеся:
- понимать различные типы паттернов и функциональных взаимосвязей;
- использовать символические формы для представления и анализа математических ситуаций и структур;
- используют математические модели и анализируют изменения как в реальном, так и в абстрактном контексте.
Обзор стандартов для 3–5 классов предполагает понимание того, что «в «реальном мире» функции являются математическим представлением многих ситуаций ввода-вывода».
По мере того, как мы указываем на функции и используем их в реальных условиях, мы можем попросить наших студентов быть внимательными к другим ситуациям ввода-вывода в реальном мире. Вы можете использовать следующие примеры:
Вы можете использовать следующие примеры:
- Автомат с газировкой, закусками или штампами
Пользователь кладет деньги, нажимает определенную кнопку, и определенный предмет падает в выходной слот.(Правило функции — цена продукта. Ввод — это деньги, объединенные с выбранной кнопкой. Выход — товар, иногда доставляемый вместе с монетами в качестве сдачи, если пользователь ввел больше денег, чем требуется по правилу функции.) - Размер:
- Â Термометр
Большинство термометров имеют шкалу Цельсия и Фаренгейта. Студенты могут изучать термометр как таблицу ввода/вывода.Учащиеся, имеющие опыт вывода правил составных функций, могут сравнить две шкалы (отметив, например, что 0°C = 32°F и 32°C = 50°F) и вычислить правило таинственной функции: формула перевода из одной шкалы в другую. - Длина окружности является функцией диаметра.

Учащиеся могут измерить диаметр и окружность нескольких круглых контейнеров или крышек и записать эти данные в таблицу. Если диаметр является входом, а окружность — выходом, каково правило функции?
Когда они делят длину окружности каждого сосуда на его диаметр, чтобы найти это правило, они должны заметить постоянное отношение — грубое приближение числа Пи.
- Длина руки зависит от высоты.
- Â Термометр
- Мили на галлон
Эффективность автомобиля в милях на галлон бензина является функцией. Если автомобиль обычно получает 20 миль на галлон, и если вы вводите 10 галлонов бензина, он сможет проехать примерно 200 миль. Эффективность автомобиля может зависеть от конструкции автомобиля (включая вес, шины и аэродинамику), скорости, температуры внутри и снаружи автомобиля и других факторов.
- Основы экономики и денежной математики:
- Недельная заработная плата зависит от почасовой ставки оплаты и количества отработанных часов.

- Сложные проценты являются функцией первоначальных инвестиций, процентной ставки и времени.
- Спрос и предложение: по мере роста цены спрос падает.
- Недельная заработная плата зависит от почасовой ставки оплаты и количества отработанных часов.
- Тени
Длина тени зависит от ее высоты и времени суток.Тени можно использовать для определения высоты больших объектов, таких как деревья или здания; то же функциональное правило (соотношение), по которому мы сравниваем длину вертикальной линейки с ее тенью, поможет нам найти неизвестный вход (высоту большого объекта), когда мы измеряем его тень.
- Геометрические узоры
- Многогранники
Изучая взаимосвязь между количеством граней, ребер и вершин различных многогранников, смогут ли учащиеся открыть правило Эйлера? F + V = E + 2 (Число граней плюс количество вершин равно количеству ребер плюс 2.) Например:Количество сторон
на каждую сторонулиц
ребра
вершин
тетраэдр
3
4
6
4
шестигранник
3
6
9
5
октаэдр
3
8
12
6
декаэдр
3
10
15
7
икосаэдр
3
20
30
12
куб
4
6
12
8
додекаэдр
5
12
30
20
- Маршрутные поезда
Учащиеся могут расположить несколько блоков шаблона в простом дизайне, дать ему имя, найти периметр дизайна (считая стандартное ребро за одну единицу), а затем сделать серию из 2 или 3 повторений этого дизайна и найти периметр.# «кошачьих голов»
периметр
1
7
2
12
3
17
 поезда по мере его роста.Когда они составляют таблицу данных, могут ли они найти правило или правила функции, описывающие взаимосвязь между количеством повторений и периметром поезда?
поезда по мере его роста.Когда они составляют таблицу данных, могут ли они найти правило или правила функции, описывающие взаимосвязь между количеством повторений и периметром поезда?Правило функции: x5+2 (или 5n+2).
- Геометрические узоры окружающего нас мира
Вы или ваши ученики можете сфотографировать архитектурные детали с повторяющимися узорами и составить таблицу для анализа каждого узора. Например, в показанной здесь кирпичной стене, если каждый кирпич имеет размеры 2 x 8 дюймов, каков периметр ряда кирпичей, расположенных в виде ступенек? Какое функциональное правило описывает эту связь?Количество кирпичей
периметр
1
20
2
32
3
44
Правило функции: x6 + 4 (или 6n + 4).
Как насчет узоров на напольной или настенной плитке? Каково отношение одного цвета к другому цвету? Сколько плиток каждого цвета нам нужно купить, чтобы выложить плиткой комнату заданного размера? Что, если бы мы захотели включить границу заданного цвета? Некоторые из мозаичных полов в Библиотеке Конгресса в Вашингтоне, округ Колумбия, являются великолепными (и сложными) примерами для изучения.
Щелкните здесь, чтобы просмотреть изображения ниже в полном размере.
В большинстве примеров в этой статье используются таблицы данных для анализа функций, но, конечно же, графики являются еще одним эффективным средством представления ситуаций ввода-вывода, включая изменения во времени (независимо от того, является ли скорость изменения постоянной или переменной).
По мере того, как учащиеся начнут использовать функции в реальном мире, будет открываться все больше и больше возможностей, и концепция и значение функций будут действительно воплощаться в жизнь.

ДОПОЛНИТЕЛЬНЫЙ РЕСУРС
Learning Math: Patterns, Functions, and Algebra
Национальный совет учителей математики. (1998). Принципы и стандарты школьной математики. Рестон, Вирджиния: NCTM
Компания Annenberg Media подготовила прекрасную коллекцию бесплатных потоковых онлайн-видео по запросу для учителей 8-х классов. Темы этой серии включают: алгебраическое мышление, закономерности в контексте, функции и алгоритмы. , пропорциональные рассуждения, линейные функции и наклон, решение уравнений, нелинейные функции и занятия в классе.Об авторе
Венди Петти — создатель отмеченного наградами веб-сайта Math Cats, автор книги «Изучение математики с помощью MicroWorlds EX » и частый докладчик на региональных и национальных конференциях по математике и технологиям. Она преподает математику в 4 и 5 классах Вашингтонской международной школы.
Она преподает математику в 4 и 5 классах Вашингтонской международной школы.Статья Венди Петти
Copyright © 2020 Education World
- Многогранники
График экспоненциальных функций
Простая экспоненциальная функция для построения графика: у знак равно 2 Икс .
| Икс | − 3 | − 2 | − 1 | 0 | 1 | 2 | 3 |
| у знак равно 2 Икс | 1 8 | 1 4 | 1 2 | 1 | 2 | 4 | 8 |
Обратите внимание, что на графике есть
Икс
-ось как
асимптота
слева и очень быстро увеличивается справа.
Изменение база изменяет форму графика.
Замена Икс с участием − Икс отражает график через у -ось; замена у с участием − у отражает его через Икс -ось.
Замена Икс с участием Икс + час переводит график час единицы влево.
Замена у с участием у − к (что равносильно добавлению к вправо) переводит график к единиц вверх.
IF.3.7 — Графические функции, выраженные символически и показывающие ключевые особенности графа, вручную в простых случаях и с использованием технологий в более сложных случаях. Графики линейных и квадратичных функций и отображение точек пересечения, максимумов и минимумов.
 Графический квадратный корень, кубический корень и кусочно-определенные функции, включая ступенчатые функции и функции абсолютного значения. Графические полиномиальные функции, идентифицирующие нули, когда доступны подходящие факторизации, и показывающие конечное поведение. Графические рациональные функции, определяющие нули и асимптоты, когда доступны подходящие факторизации, и показывающие конечное поведение. Графические экспоненциальные и логарифмические функции, показывающие точки пересечения и конечное поведение, и тригонометрические функции, отображающие период, среднюю линию и амплитуду, а также использующие фазовый сдвиг. Нахождение парабол через две точки:
Графический квадратный корень, кубический корень и кусочно-определенные функции, включая ступенчатые функции и функции абсолютного значения. Графические полиномиальные функции, идентифицирующие нули, когда доступны подходящие факторизации, и показывающие конечное поведение. Графические рациональные функции, определяющие нули и асимптоты, когда доступны подходящие факторизации, и показывающие конечное поведение. Графические экспоненциальные и логарифмические функции, показывающие точки пересечения и конечное поведение, и тригонометрические функции, отображающие период, среднюю линию и амплитуду, а также использующие фазовый сдвиг. Нахождение парабол через две точки: В этом задании на решение задач учащимся предлагается найти все квадратичные функции, описываемые данным уравнением и координатами, и описать, как графики этих функций связаны друг с другом.
Тип: Задача решения проблем
Графики квадратичных функций:Учащиеся сравнивают графики различных квадратичных функций, а затем составляют собственные уравнения, удовлетворяющие заданным условиям.
Это исследование можно провести в классе в начале раздела по рисованию парабол. Студенты должны быть знакомы с перехватами и должны знать, что такое вершина. Он эффективен после того, как учащиеся изобразили параболы в виде вершин (y=a(x–h) 2 +k), но еще не изучили графические изображения других форм.
Тип: Задача решения проблем
Графики силовых функций: Это задание требует, чтобы учащиеся узнали графики различных (положительных) степеней x.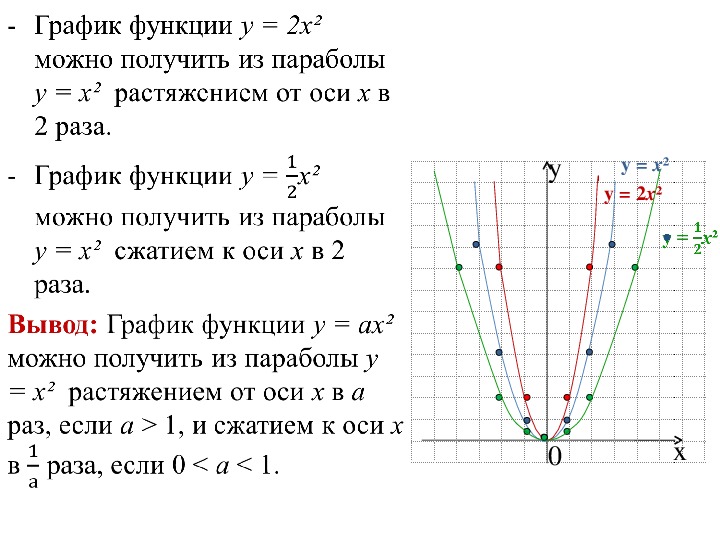
Тип: Задача решения проблем
Ползунок наклона:В этом упражнении учащиеся настраивают ползунки, которые настраивают коэффициенты и константы линейной функции, и исследуют, как их изменения влияют на график.Уравнение линии может быть в форме пересечения наклона или в стандартной форме. Это задание позволяет учащимся исследовать линейные уравнения, наклоны и точки пересечения с осью Y, а также их визуальное представление на графике. Это задание включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с апплетом Java.
Тип: виртуальный манипулятор
Графические уравнения с использованием перехватов: Этот ресурс предоставляет линейные функции в стандартной форме и предлагает пользователю изобразить их в виде графика, используя точки пересечения на интерактивном графике под задачей. Обеспечивается немедленная обратная связь, а при неправильных ответах тщательно моделируется каждый шаг решения.
Обеспечивается немедленная обратная связь, а при неправильных ответах тщательно моделируется каждый шаг решения.
Тип: виртуальный манипулятор
Графические линии:Позволяет учащимся получить доступ к декартовой системе координат, в которой линейные уравнения могут быть построены в виде графиков, а также можно наблюдать детали линии и наклона.
Тип: виртуальный манипулятор
Флаер с данными: С помощью этого виртуального манипулятора учащиеся могут построить график функции и набора упорядоченных пар на одной координатной плоскости. Константы, коэффициенты и показатели степени можно регулировать с помощью ползунков, поэтому учащийся может изучить влияние на график изменения параметров функции.Студенты также могут исследовать отклонение данных от функции. Это задание включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с апплетом Java.
Константы, коэффициенты и показатели степени можно регулировать с помощью ползунков, поэтому учащийся может изучить влияние на график изменения параметров функции.Студенты также могут исследовать отклонение данных от функции. Это задание включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с апплетом Java.
Тип: виртуальный манипулятор
Функциональный флаер: В этом онлайн-инструменте учащиеся вводят функцию для создания графика, где константы, коэффициенты и показатели степени можно регулировать с помощью ползунков.Этот инструмент позволяет учащимся изучать графики функций и то, как корректировка чисел в функции влияет на график. Используя вкладки в верхней части страницы, вы также можете получить доступ к дополнительным материалам, включая справочную информацию по затронутым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с java-апплетом.
Используя вкладки в верхней части страницы, вы также можете получить доступ к дополнительным материалам, включая справочную информацию по затронутым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с java-апплетом.
Тип: виртуальный манипулятор
Подгонка кривой:С помощью мыши учащиеся будут перетаскивать точки данных (с их планками погрешностей) и мгновенно наблюдать за формированием наиболее подходящей полиномиальной кривой.Студенты могут выбрать тип подгонки: линейный, квадратичный, кубический или квартичный. Можно отобразить наилучшую посадку или регулируемую посадку.
Тип: виртуальный манипулятор
Уравнение Граф: Этот интерактивный симулятор исследует построение графиков линейных и квадратных уравнений.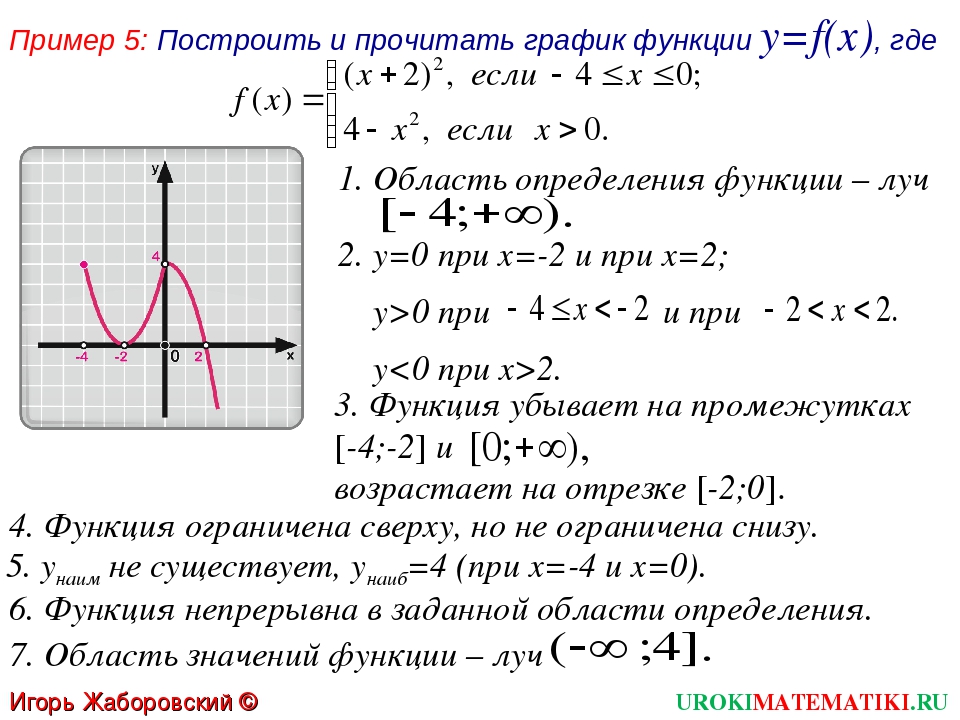 Пользователям предоставляется возможность определять и изменять коэффициенты и константы, чтобы наблюдать результирующие изменения на графике (графиках).
Пользователям предоставляется возможность определять и изменять коэффициенты и константы, чтобы наблюдать результирующие изменения на графике (графиках).
Тип: виртуальный манипулятор
3.1 Функции и обозначение функций — College Algebra
Цели обучения
В этом разделе вы:
- Определить, представляет ли отношение функцию.
- Найти значение функции.
- Определить, является ли функция взаимно однозначной.
- Используйте тест вертикальной линии для определения функций.
- График функций, перечисленных в библиотеке функций.
Реактивный лайнер меняет высоту по мере увеличения расстояния от начальной точки полета. Вес растущего ребенка со временем увеличивается. В каждом случае одна величина зависит от другой. Между двумя величинами существует взаимосвязь, которую мы можем описать, проанализировать и использовать для прогнозирования. В этом разделе мы проанализируем такие отношения.
В этом разделе мы проанализируем такие отношения.
Определение того, представляет ли отношение функцию
Отношение представляет собой набор упорядоченных пар. Набор первых компонентов каждой упорядоченной пары называется доменом , а набор вторых компонентов каждой упорядоченной пары называется диапазоном . Рассмотрим следующий набор упорядоченных пар. Первые числа в каждой паре — это первые пять натуральных чисел. Второе число в каждой паре вдвое больше первого.
{(1,2),(2,4),(3,6),(4,8),(5,10)}{(1,2),(2,4),(3,6), (4,8),(5,10)}Домен {1,2,3,4,5}.{1,2,3,4,5}. Диапазон: {2,4,6,8,10}.{2,4,6,8,10}.
Обратите внимание, что каждое значение в домене также известно как входное значение или независимая переменная, и часто обозначается строчной буквой x.x. Каждое значение в диапазоне также известно как выходное значение или зависимая переменная и часто обозначается строчной буквой yy.
Функция ff — это отношение, которое присваивает одно значение в диапазоне каждому значению в домене . Другими словами, значения x не повторяются. В нашем примере, который связывает первые пять натуральных чисел с числами, удвоенными их значениями, это отношение является функцией, поскольку каждый элемент в области значений {1,2,3,4,5},{1,2,3,4,5 }, сочетается ровно с одним элементом в диапазоне {2,4,6,8,10}.{2,4,6,8,10}.
Теперь рассмотрим множество упорядоченных пар, связывающих термины «четный» и «нечетный» с первыми пятью натуральными числами. Это выглядело бы как
{(нечетное,1),(четное,2),(нечетное,3),(четное,4),(нечетное,5)}{(нечетное,1),(четное,2),(нечетное,3), (четный,4),(нечетный,5)} Обратите внимание, что каждый элемент в домене {четный,нечетный}{четный,нечетный}
это , а не в паре ровно с одним элементом в диапазоне {1,2,3,4,5}.{1,2,3,4,5}.
Например, термин «нечетный» соответствует трем значениям из диапазона {1,3,5}{1,3,5}. а термин «четный» соответствует двум значениям из диапазона {2,4}.{2,4}.
Это нарушает определение функции, поэтому это отношение не является функцией.
а термин «четный» соответствует двум значениям из диапазона {2,4}.{2,4}.
Это нарушает определение функции, поэтому это отношение не является функцией.
На рис. 1 сравниваются отношения, которые являются функциями и не функциями.
Рисунок 1 (а) Это отношение является функцией, поскольку каждый вход связан с одним выходом. Обратите внимание, что ввод qq и rr оба дают вывод n.n. б) Это отношение также является функцией.В этом случае каждый вход связан с одним выходом. (c) Это отношение не является функцией, поскольку вход qq связан с двумя разными выходами.Функция
Функция — это отношение, в котором каждое возможное входное значение приводит ровно к одному выходному значению. Мы говорим, что «выход есть функция входа».
Входные значения составляют домен, а выходные значения составляют диапазон.
Как
Учитывая связь между двумя величинами, определите, является ли связь функцией.
- Определите входные значения.
- Определите выходные значения.
- Если каждое входное значение приводит только к одному выходному значению, классифицируйте отношение как функцию. Если какое-либо входное значение приводит к двум или более выходам, не классифицируйте отношение как функцию.
Пример 1
Определение того, являются ли прейскуранты меню функциями
Меню кофейни, показанное ниже, состоит из позиций и их цен.
ⓐ Зависит ли цена от товара?
ⓑ Является ли товар функцией цены?
Решение
ⓐ Начнем с рассмотрения ввода как пунктов меню.Тогда выходные значения являются ценами.
Каждый пункт в меню имеет только одну цену, поэтому цена зависит от пункта.
ⓑ Два блюда в меню имеют одинаковую цену. Если мы считаем, что цены являются входными значениями, а товары — выходными, то одно и то же входное значение может иметь более одного связанного с ним выхода. См. изображение ниже.
См. изображение ниже.
Следовательно, товар не зависит от цены.
Пример 2
Определение того, являются ли правила оценки класса функциями
В конкретном математическом классе общая оценка в процентах соответствует среднему баллу.Является ли средний балл успеваемости функцией процентной оценки? Является ли процентная оценка функцией среднего балла? В таблице 1 показано возможное правило выставления оценок.
| Процентное содержание | 0–56 | 57–61 | 62–66 | 67–71 | 72–77 | 78–86 | 87–91 | 92–100 |
| Средний балл | 0,0 | 1,0 | 1. 5 5 | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 |
Таблица 1
Решение
Для любого процента полученной оценки существует соответствующий средний балл, поэтому средний балл является функцией процента оценки. Другими словами, если мы вводим процентную оценку, на выходе получается определенный средний балл.
В данной системе оценивания существует диапазон процентных оценок, соответствующих одному и тому же среднему баллу.Например, учащиеся, получившие средний балл 3,0, могут иметь различные процентные оценки от 78 до 86. Таким образом, процентная оценка не является функцией среднего балла.
Попробуйте #1
В таблице 2 перечислены пять величайших бейсболистов всех времен в порядке их ранга.
| Игрок | Ранг |
|---|---|
| Бэйб Рут | 1 |
| Вилли Мейс | 2 |
| Тай Кобб | 3 |
| Уолтер Джонсон | 4 |
| Хэнк Аарон | 5 |
Таблица 2
- ⓐЗависит ли ранг от имени игрока?
- ⓑ Является ли имя игрока функцией ранга?
Использование обозначения функций
Как только мы определили, что отношение является функцией, нам нужно отобразить и определить функциональные отношения, чтобы мы могли понять и использовать их, а иногда также чтобы мы могли запрограммировать их в компьютеры. Существуют различные способы представления функций. Стандартная нотация функций — это одно из представлений, упрощающее работу с функциями.
Существуют различные способы представления функций. Стандартная нотация функций — это одно из представлений, упрощающее работу с функциями.
Чтобы представить «рост является функцией возраста», мы начнем с определения описательных переменных hh для высоты и аа для возраста. Буквы f,g,f,g и hh часто используются для обозначения функций точно так же, как мы используем x,y,x,y и zz для представления чисел и A,B,A,B, и CC для представления наборов.
его имя мы называем функцией f; рост есть функция возраста.h=f(a)Мы используем круглые скобки, чтобы указать вход функции. f(a) Мы называем функцию f; выражение читается как «f of a». Его f of a Мы называем функцию f; высота — это функция возраста. f(a) Мы называем функцию f; выражение читается как «fof a». Помните, мы можем использовать любую букву для названия функции; обозначение h(a)h(a) показывает нам, что hh зависит от п. в. Чтобы получить результат, необходимо подставить значение aa в функцию hh. Скобки указывают на то, что в функцию вводится возраст; они не указывают на умножение.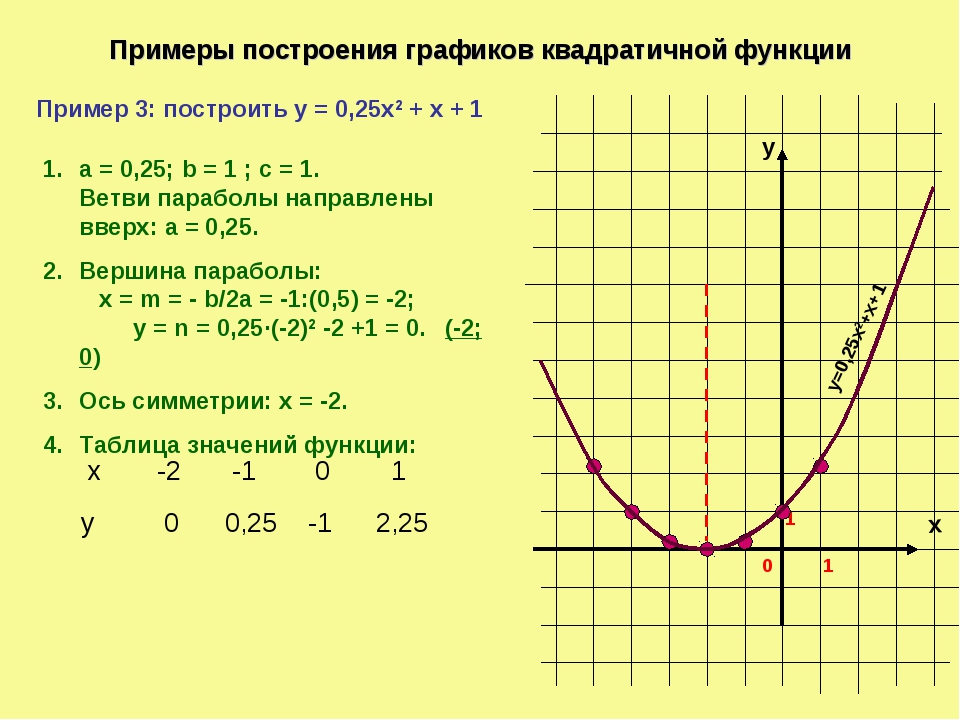
Мы также можем задать алгебраическое выражение в качестве входных данных для функции. Например, f(a+b)f(a+b) означает «сначала добавить a и b , и результатом будет вход для функции f ». Операции должны выполняться в таком порядке, чтобы получить правильный результат.
Обозначение функции
Обозначение y=f(x)y=f(x) определяет функцию с именем f.f. Это читается как «y«y есть функция x.x». Буква xx представляет входное значение или независимую переменную.Буква y, y, или f(x),f(x) представляет выходное значение или зависимую переменную.
Пример 3
Использование обозначения функций для дней в месяце
Используйте нотацию функции для представления функции, входными данными которой является название месяца, а выходными данными — количество дней в этом месяце. Предположим, что домен не включает високосные годы.
Решение
Количество дней в месяце зависит от названия месяца, поэтому, если мы назовем функцию f,f, мы напишем days=f(month)days=f(month) или d=f(m).д=f(м). Название месяца является входом для «правила», которое связывает определенное число (выход) с каждым входом.
Рисунок 2
Например, f(март)=31,f(март)=31, потому что в марте 31 день. Обозначение d=f(m)d=f(m) напоминает нам, что количество дней, dd (выход), зависит от названия месяца, mm (вход).
Анализ
Обратите внимание, что входные данные функции не обязательно должны быть числами; входными данными функции могут быть имена людей, метки геометрических объектов или любой другой элемент, определяющий какой-либо вывод.Однако большинство функций, с которыми мы будем работать в этой книге, будут иметь числа в качестве входных и выходных данных.
Пример 4
Интерпретация обозначения функций
Функция N=f(y)N=f(y) дает количество полицейских, N,N, в городе в году y. y. Что представляет собой f(2005)=300f(2005)=300?
y. Что представляет собой f(2005)=300f(2005)=300?
Решение
Когда мы читаем f(2005)=300,f(2005)=300, мы видим, что входной год — 2005. Выходное значение, количество полицейских (N),(N), равно 300.Помните, N=f(y).N=f(y). Утверждение f(2005)=300f(2005)=300 говорит нам о том, что в 2005 году в городе было 300 полицейских.
Попробуйте #2
Используйте функциональную запись, чтобы выразить вес свиньи в фунтах как функцию ее возраста в днях d.d.
Вопросы и ответы
Вместо обозначения, такого как y=f(x),y=f(x), могли бы мы использовать тот же символ для вывода, что и для функции, например y=y(x),y=y(x ), что означает « х является функцией х ?»
Да, это часто делается, особенно по прикладным предметам, использующим высшую математику, таким как физика и инженерия. Однако при изучении самой математики нам нравится сохранять различие между такими функциями, как f,f, которые являются правилом или процедурой, и выходными данными yy, которые мы получаем, применяя ff к конкретным входным данным x.x. Вот почему мы обычно используем такие обозначения, как y=f(x),P=W(d),y=f(x),P=W(d) и так далее.
Однако при изучении самой математики нам нравится сохранять различие между такими функциями, как f,f, которые являются правилом или процедурой, и выходными данными yy, которые мы получаем, применяя ff к конкретным входным данным x.x. Вот почему мы обычно используем такие обозначения, как y=f(x),P=W(d),y=f(x),P=W(d) и так далее.
Представление функций с помощью таблиц
Обычный метод представления функций — в форме таблицы. В строках или столбцах таблицы отображаются соответствующие входные и выходные значения. В некоторых случаях эти значения представляют все, что мы знаем об отношениях; в других случаях в таблице представлены несколько избранных примеров из более полных взаимосвязей.
В таблице 3 перечислены входные числа для каждого месяца (январь = 1, февраль = 2 и т. д.) и выходное значение количества дней в этом месяце. Эта информация представляет собой все, что мы знаем о месяцах и днях для данного года (это не високосный год). Обратите внимание, что в этой таблице мы определяем функцию числа дней в месяце ff, где D=f(m)D=f(m) идентифицирует месяцы целым числом, а не именем.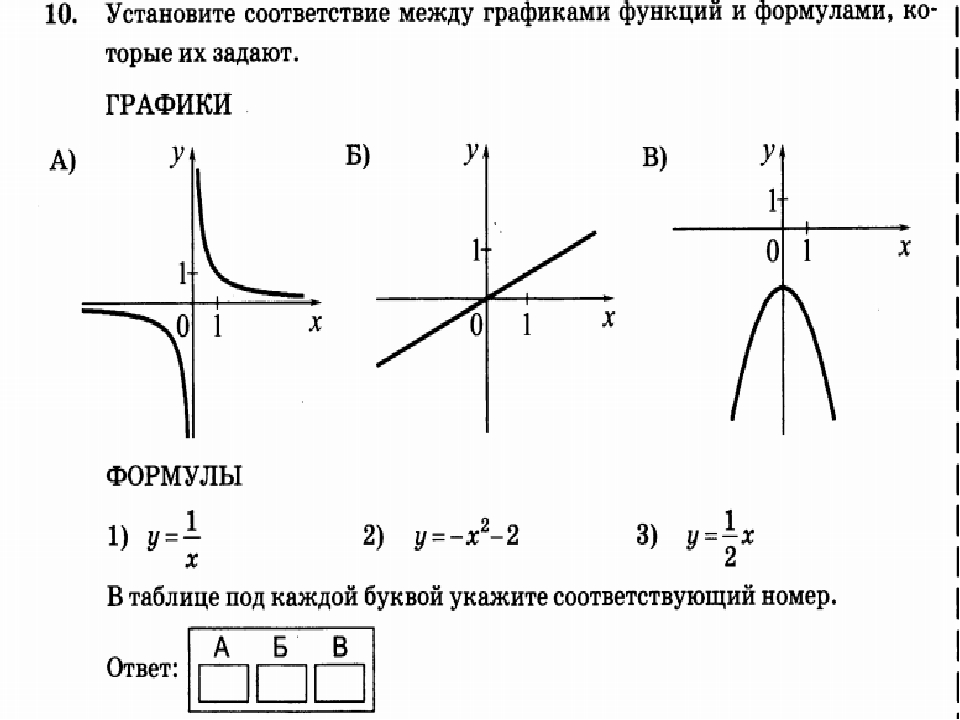
| Номер месяца, мм (ввод) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Дней в месяце, ДД (выход) | 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
Таблица 3
Таблица 4 определяет функцию Q=g(n). Q=g(n). Помните, это обозначение говорит нам, что gg — это имя функции, которая принимает входные данные nn и дает выходные данные Q .Q .
Q=g(n). Помните, это обозначение говорит нам, что gg — это имя функции, которая принимает входные данные nn и дает выходные данные Q .Q .
| нн | 1 | 2 | 3 | 4 | 5 |
| 8 | 6 | 7 | 6 | 8 |
Таблица 4
Таблица 5 показывает возраст детей в годах и их соответствующий рост.В этой таблице представлены лишь некоторые из имеющихся данных о росте и возрасте детей. Мы сразу видим, что эта таблица не представляет собой функцию, потому что одно и то же входное значение, 5 лет, имеет два разных выходных значения, 40 дюймов и 42 дюйма
| Возраст в годах, аа (ввод) | 5 | 5 | 6 | 7 | 8 | 9 | 10 |
| Высота в дюймах, ч/ч (вывод) | 40 | 42 | 44 | 47 | 50 | 52 | 54 |
Таблица 5
Как сделать
Имея таблицу входных и выходных значений, определите, представляет ли таблица функцию.
- Определите входные и выходные значения.
- Проверьте, связано ли каждое входное значение только с одним выходным значением. Если это так, таблица представляет собой функцию.
Пример 5
Идентификация таблиц, представляющих функции
Какая таблица, Таблица 6, Таблица 7 или Таблица 8 представляет функцию (если есть)?
| Вход | Выход |
|---|---|
| –3 | 5 |
| 0 | 1 |
| 4 | 5 |
Таблица 7
Решение
Таблица 6 и Таблица 7 определяют функции. В обоих случаях каждое входное значение соответствует ровно одному выходному значению. Таблица 8 не определяет функцию, поскольку входное значение 5 соответствует двум различным выходным значениям.
В обоих случаях каждое входное значение соответствует ровно одному выходному значению. Таблица 8 не определяет функцию, поскольку входное значение 5 соответствует двум различным выходным значениям.
Когда таблица представляет функцию, соответствующие входные и выходные значения также могут быть указаны с использованием обозначения функции.
Функция, представленная в Таблице 6, может быть представлена записью
f(2)=1,f(5)=3 и f(8)=6f(2)=1,f(5)=3 и f(8)=6Аналогично, операторы
g(-3)=5,g(0)=1 и g(4)=5g(-3)=5,g(0)=1 и g(4)=5представляют функцию в таблице 7. .
Таблица 8 не может быть выражена подобным образом, потому что она не представляет функцию.
Попробуйте #3
Представляет ли таблица 9 функцию?
| Вход | Выход |
|---|---|
| 1 | 10 |
| 2 | 100 |
| 3 | 1000 |
Таблица 9
Поиск входных и выходных значений функции
Когда мы знаем входное значение и хотим определить соответствующее выходное значение для функции, мы оцениваем функцию. Вычисление всегда будет давать один результат, потому что каждое входное значение функции соответствует ровно одному выходному значению.
Вычисление всегда будет давать один результат, потому что каждое входное значение функции соответствует ровно одному выходному значению.
Когда мы знаем выходное значение и хотим определить входные значения, которые дадут это выходное значение, мы устанавливаем выход равным формуле функции и решаем для входа. Решение может дать более одного решения, потому что разные входные значения могут дать одно и то же выходное значение.
Вычисление функций в алгебраических формах
Когда у нас есть функция в форме формулы, обычно несложно вычислить функцию.Например, функция f(x)=5−3x2f(x)=5−3×2 может быть вычислена путем возведения входного значения в квадрат, умножения на 3 и последующего вычитания произведения из 5.
Как
Дана формула функции, вычислить.
- Замените входную переменную в формуле предоставленным значением.

- Вычислите результат.
Пример 6
Вычисление функций при определенных значениях
Вычислить f(x)=x2+3x−4f(x)=x2+3x−4 по адресу:
- ⓐ 22
- ⓑ аа
- ⓒ а+ха+ч
- ⓓ Теперь оцените f(a+h)−f(a)hf(a+h)−f(a)h
Решение
Заменить хх в функции с каждым указанным значением.
- ⓐ Поскольку входным значением является число 2, мы можем использовать простую алгебру для упрощения. f(2)=22+3(2)−4=4+6−4=6f(2)=22+3(2)−4=4+6−4=6
- ⓑ В данном случае входное значение представляет собой букву, поэтому мы не можем еще больше упростить ответ. f(a)=a2+3a−4f(a)=a2+3a−4
- При входном значении a+h,a+h мы должны использовать распределительное свойство. f(a+h)=(a+h)2+3(a+h)−4=a2+2ah+h3+3a+3h−4f(a+h)=(a+h)2+3(a +h)−4=a2+2ah+h3+3a+3h−4
- ⓒ В этом случае мы применяем входные значения к функции более одного раза, а затем выполняем алгебраические операции над результатом.
 Мы уже нашли это
f(a+h)=a2+2ah+h3+3a+3h−4f(a+h)=a2+2ah+h3+3a+3h−4
Мы уже нашли это
f(a+h)=a2+2ah+h3+3a+3h−4f(a+h)=a2+2ah+h3+3a+3h−4и мы знаем что
f(a)=a2+3a−4f(a)=a2+3a−4Теперь объединим результаты и упростим.
f(a+h)−f(a)h=(a2+2ah+h3+3a+3h−4)−(a2+3a−4)h = 2ah+h3+3hh =h(2a+h+3) hВычтите h. =2a+h+3Simplify.f(a+h)−f(a)h=(a2+2ah+h3+3a+3h−4)−(a2+3a−4)h =2ah+h3+3hh =h (2a+h+3)hВычтите h. =2a+h+3Упрощение.
Пример 7
Оценка функций
Учитывая функцию h(p)=p2+2p,h(p)=p2+2p, вычислить h(4).h(4).
Решение
Чтобы вычислить h(4),h(4), мы подставляем значение 4 для входной переменной pp в данной функции.
h(p)=p2+2ph(4)=(4)2+2(4) =16+8 =24h(p)=p2+2ph(4)=(4)2+2(4) =16+ 8 =24Следовательно, при входе 4 на выходе 24.
Попробуйте #4
Учитывая функцию g(m)=m−4,g(m)=m−4, вычислить g(5).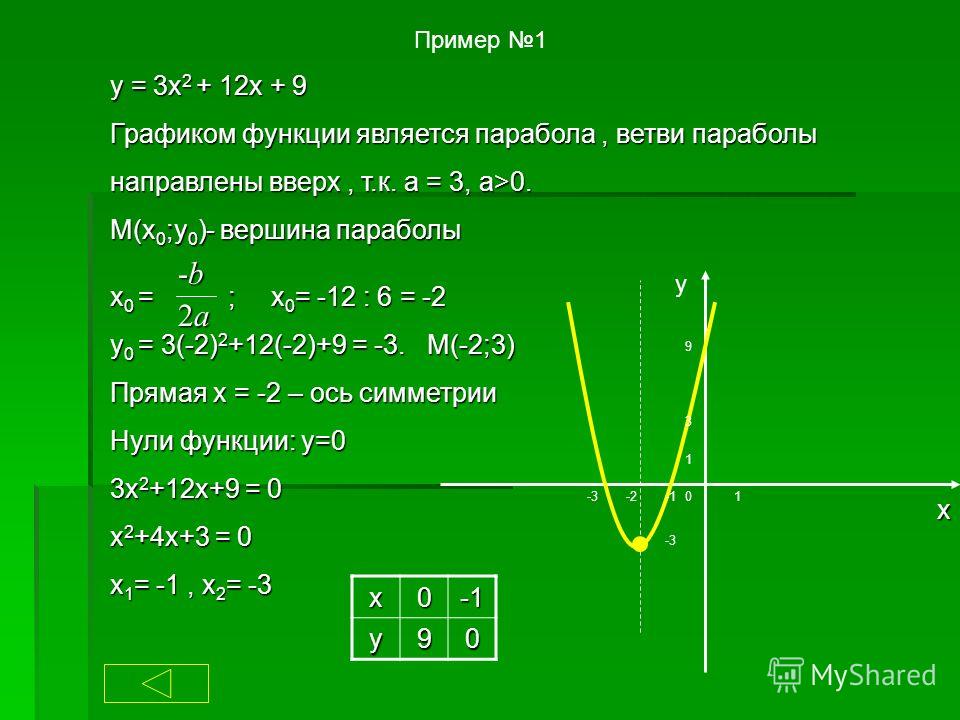 г(5).
г(5).
Пример 8
Решение функций
Учитывая функцию h(p)=p2+2p,h(p)=p2+2p, найти h(p)=3.h(p)=3.
Решение
h(p)=3 p2+2p=3Подставить исходную функцию h(p)=p2+2p.p2+2p−3=0Вычесть 3 с каждой стороны.(p+3)(p−1)=0Множитель. h(p)=3 p2+2p=3Подставить исходную функцию h(p)=p2+2p.p2+2p−3=0Вычесть 3 с каждой стороны.(p+3)(p−1)=0Множитель.Если (p+3)(p−1)=0,(p+3)(p−1)=0, либо (p+3)=0(p+3)=0, либо (p−1)= 0(p−1)=0 (или оба равны 0).Мы установим каждый фактор равным 0 и найдем pp в каждом случае.
(p+3)=0,p=-3(p-1)=0,p=1(p+3)=0,p=-3(p-1)=0,p=1Это дает нам два решения. Выход h(p)=3h(p)=3, когда на входе либо p=1p=1, либо p=-3.p=-3. Мы также можем проверить с помощью графика, как на рисунке 3. График подтверждает, что h(1)=h(-3)=3h(1)=h(-3)=3 и h(4)=24.h(4) =24.
Рисунок 3
Попробуйте #5
Учитывая функцию g(m)=m−4,g(m)=m−4, решить g(m)=2. g(m)=2.
g(m)=2.
Вычисление функций, выраженных в формулах
Некоторые функции определяются математическими правилами или процедурами, выраженными в форме уравнения.Если возможно выразить выход функции с помощью формулы, включающей входную величину, то мы можем определить функцию в алгебраической форме. Например, уравнение 2n+6p=122n+6p=12 выражает функциональную связь между nn и с.п. Мы можем переписать его, чтобы решить, является ли pp функцией n.n.
Как
Дана функция в виде уравнения, напишите ее алгебраическую формулу.
- Решите уравнение, чтобы изолировать выходную переменную с одной стороны от знака равенства, а с другой стороны как выражение, включающее только входную переменную.
- Используйте все обычные алгебраические методы решения уравнений, такие как прибавление или вычитание одной и той же величины из обеих частей или умножение или деление обеих частей уравнения на одну и ту же величину.

Пример 9
Нахождение уравнения функции
Выразите отношение 2n+6p=122n+6p=12 в виде функции p=f(n),p=f(n), если возможно.
Решение
Чтобы выразить отношение в этой форме, нам нужно иметь возможность записать отношение, где pp является функцией n,n, что означает запись в виде p=[expressioninvolvingn].p=[выражение, включающееn].
2n+6p=126p=12−2nВычесть 2n из обеих сторон.p=12−2n6Разделить обе стороны на 6 и упростить.p=126−2n6p=2−13n2n+6p=126p=12−2nВычесть 2n из обеих сторон.p=12− 2n6Разделите обе части на 6 и упростите.p=126−2n6p=2−13nСледовательно, pp как функция nn записывается как
р=f(n)=2−13np=f(n)=2−13nАнализ
Важно отметить, что не каждое отношение, выраженное уравнением, можно также выразить в виде функции с помощью формулы.
Пример 10
Выражение уравнения окружности в виде функции
Представляет ли уравнение x2+y2=1×2+y2=1 функцию с xx на входе и yy на выходе? Если это так, выразите отношение как функцию y=f(x).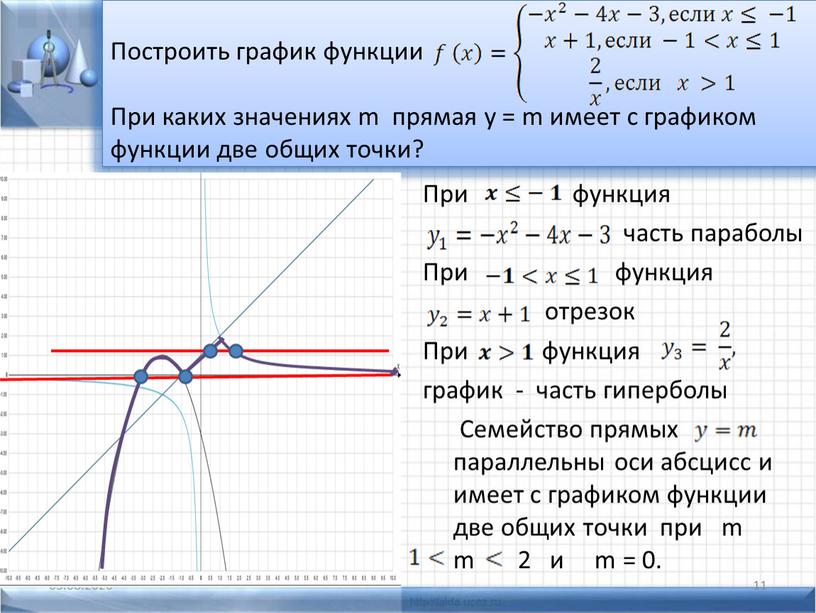 у=е(х).
у=е(х).
Решение
Сначала мы вычитаем x2x2 с обеих сторон.
Теперь попробуем найти yy в этом уравнении.
y=±1−x2=+1−x2and−1−x2y=±1−x2=+1−x2and−1−x2Мы получаем два выхода, соответствующие одному и тому же входу, поэтому эту связь нельзя представить в виде одной функции у=е(х).у=е(х).
Попробуйте #6
Если x−8y3=0,x−8y3=0, выразить yy как функцию x.x.
Вопросы и ответы
Существуют ли отношения, выраженные уравнением, которые представляют функцию, но которые все еще не могут быть представлены алгебраической формулой?
Да, такое может быть.Например, при заданном уравнении x=y+2y,x=y+2y, если мы хотим выразить yy как функцию x,x, не существует простой алгебраической формулы, включающей только xx, равное y.y. Однако каждый xx определяет уникальное значение y, y, и существуют математические процедуры, с помощью которых yy можно найти с любой желаемой точностью.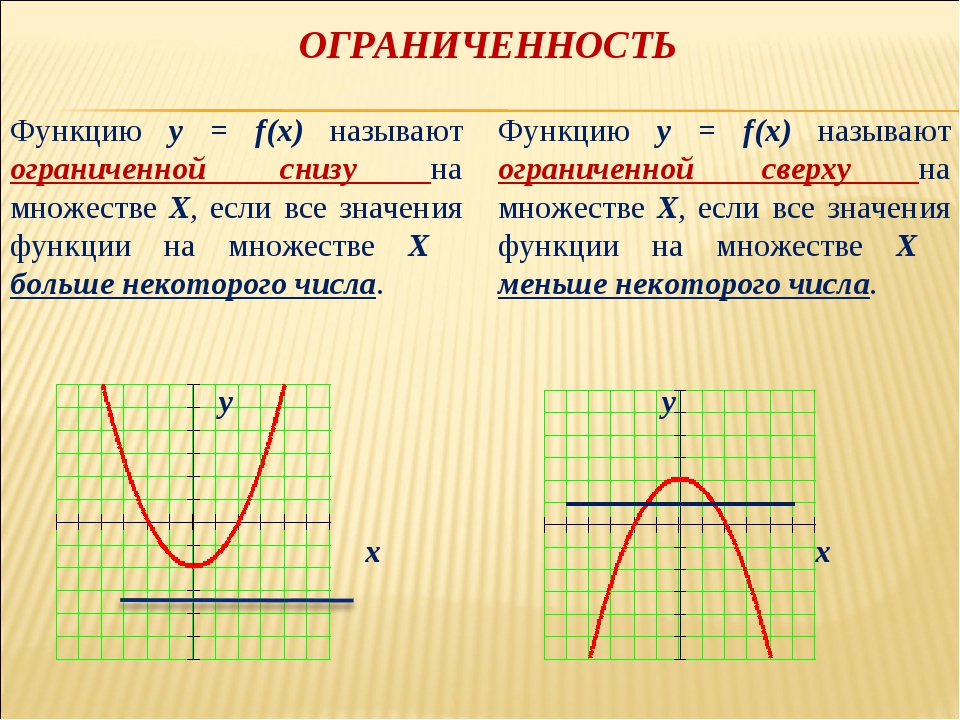 В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для yy как функции x,x, даже если формулу нельзя записать явно.
В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для yy как функции x,x, даже если формулу нельзя записать явно.
Вычисление функции, заданной в табличной форме
Как мы видели выше, мы можем представлять функции в виде таблиц.И наоборот, мы можем использовать информацию в таблицах для написания функций, и мы можем оценивать функции, используя таблицы. Например, насколько хорошо наши питомцы помнят приятные воспоминания, которыми мы делимся с ними? Существует городская легенда, что у золотой рыбки память 3 секунды, но это всего лишь миф. Золотая рыбка может помнить до 3 месяцев, а бета-рыбка имеет память до 5 месяцев. И если память щенка не превышает 30 секунд, то взрослая собака может помнить 5 минут. Это мизер по сравнению с кошкой, память которой длится 16 часов.
Функцию, связывающую тип питомца с длительностью его памяти, легче визуализировать с помощью таблицы. См. Таблицу 10.
| Домашнее животное | Объем памяти в часах |
|---|---|
| Щенок | 0,008 |
| Взрослая собака | 0,083 |
| Кат | 16 |
| Золотая рыбка | 2160 |
| Бета-рыба | 3600 |
Таблица 10
Иногда вычисление функции в форме таблицы может оказаться более полезным, чем использование уравнений.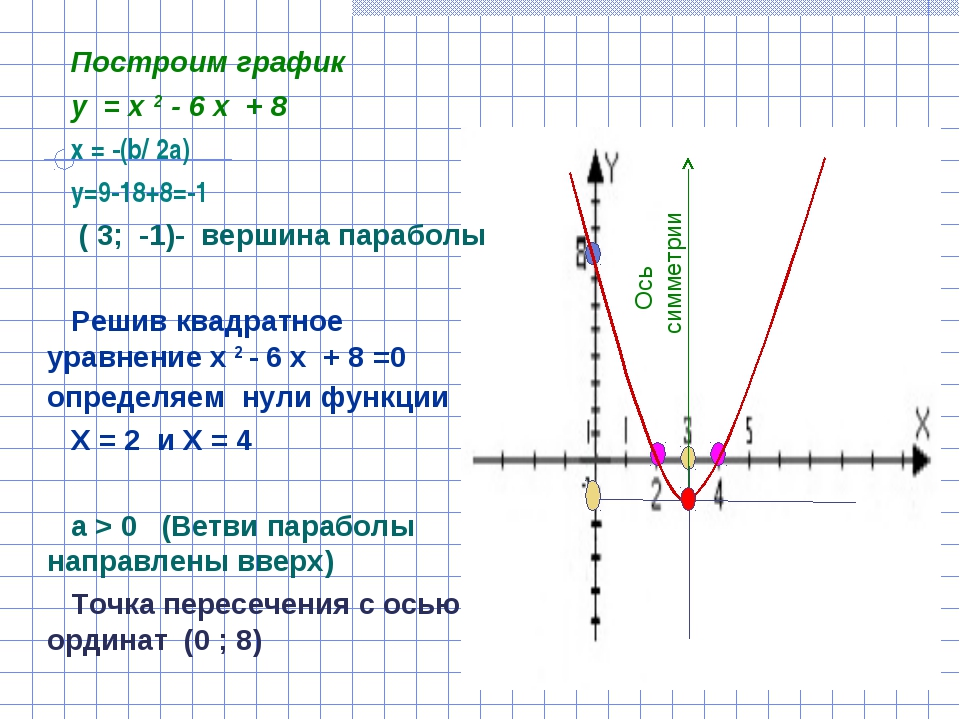 Здесь назовем функцию П.П.
Домен функции — это тип питомца, а диапазон — действительное число, представляющее количество часов, в течение которых сохраняется память питомца. Мы можем оценить функцию PP по входному значению «золотая рыбка». Мы бы написали P(золотая рыбка)=2160.P(золотая рыбка)=2160. Обратите внимание, что для вычисления функции в форме таблицы мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции PP кажется идеально подходящей для этой функции, в большей степени, чем ее запись в форме абзаца или функции.
Здесь назовем функцию П.П.
Домен функции — это тип питомца, а диапазон — действительное число, представляющее количество часов, в течение которых сохраняется память питомца. Мы можем оценить функцию PP по входному значению «золотая рыбка». Мы бы написали P(золотая рыбка)=2160.P(золотая рыбка)=2160. Обратите внимание, что для вычисления функции в форме таблицы мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции PP кажется идеально подходящей для этой функции, в большей степени, чем ее запись в форме абзаца или функции.
Как
Для функции, представленной в виде таблицы, определите конкретные выходные и входные значения.
- Найдите заданный вход в строке (или столбце) входных значений.
- Идентифицируйте соответствующее выходное значение в паре с этим входным значением.
- Найдите указанные выходные значения в строке (или столбце) выходных значений, отмечая каждый раз, когда это выходное значение появляется.

- Определите входное значение(я), соответствующее данному выходному значению.
Пример 11
Вычисление и решение табличной функции
Использование таблицы 11,
ⓐ Оценить g(3).g(3).
ⓑ Решить g(n)=6.g(n)=6.
| нн | 1 | 2 | 3 | 4 | 5 |
| г(н)г(н) | 8 | 6 | 7 | 6 | 8 |
Таблица 11
Решение
ⓐ Оценка g(3)g(3) означает определение выходного значения функции gg для входного значения n=3. п=3. Выходное значение таблицы, соответствующее n=3n=3, равно 7, поэтому g(3)=7.g(3)=7.
п=3. Выходное значение таблицы, соответствующее n=3n=3, равно 7, поэтому g(3)=7.g(3)=7.
ⓑ Решение g(n)=6g(n)=6 означает определение входных значений n,n, которые дают выходное значение 6. В таблице 11 показаны два решения: 22 и 4.4.
| нн | 1 | 2 | 3 | 4 | 5 |
| г(н)г(н) | 8 | 6 | 7 | 6 | 8 |
Когда мы вводим 2 в функцию g,g, наш выход равен 6.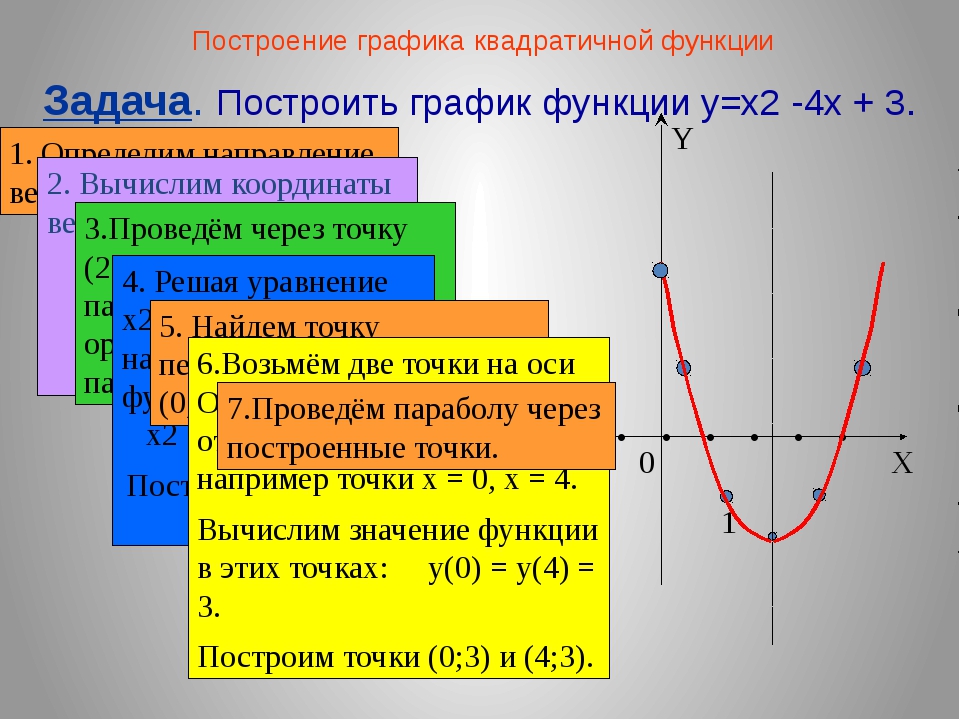 Когда мы вводим 4 в функцию g,g, наш вывод также равен 6.
Когда мы вводим 4 в функцию g,g, наш вывод также равен 6.
Поиск значений функции на графике
Вычисление функции с помощью графика также требует нахождения соответствующего выходного значения для заданного входного значения, только в этом случае мы находим выходное значение, глядя на график. Решение функционального уравнения с использованием графика требует нахождения всех экземпляров заданного выходного значения на графике и наблюдения за соответствующим входным значением (значениями).
Пример 12
Чтение значений функции из графика
Учитывая график на рисунке 4,
ⓐ Оценить f(2).ф(2).
ⓑ Решить f(x)=4.f(x)=4.
Рисунок 4
Решение
ⓐ Чтобы вычислить f(2),f(2), найдите точку на кривой, где x=2,x=2, затем считайте y -координату этой точки. Точка имеет координаты (2,1),(2,1), поэтому f(2)=1. f(2)=1. См. рис. 5.
f(2)=1. См. рис. 5.
Рисунок 5
ⓑ Чтобы решить f(x)=4,f(x)=4, находим выходное значение 44 по вертикальной оси. Двигаясь горизонтально вдоль линии y=4,y=4, находим две точки кривой с выходным значением 4:4: (−1,4)(−1,4) и (3,4).(3,4). Эти точки представляют два решения f(x)=4:f(x)=4: −1−1 или 3.3. Это означает, что f(-1)=4f(-1)=4 и f(3)=4,f(3)=4, или, когда вход равен -1-1 или 3,3, выход равен 4,4. См. рис. 6.
Рисунок 6
Определение того, является ли функция взаимно однозначной
Некоторые функции имеют заданное выходное значение, которое соответствует двум или более входным значениям. Например, на биржевой диаграмме, показанной на рисунке в начале этой главы, цена акции составляла 1000 долларов в пять разных дат, а это означает, что было пять различных входных значений, которые все привели к одному и тому же выходному значению в 1000 долларов.
Однако некоторые функции имеют только одно входное значение для каждого выходного значения, а также имеют только один выход для каждого входа. Мы называем эти функции однозначными функциями. В качестве примера рассмотрим школу, в которой используются только буквенные оценки и десятичные эквиваленты, как указано в таблице 12.
Мы называем эти функции однозначными функциями. В качестве примера рассмотрим школу, в которой используются только буквенные оценки и десятичные эквиваленты, как указано в таблице 12.
| Буквенный класс | Средний балл |
|---|---|
| А | 4,0 |
| Б | 3.0 |
| С | 2,0 |
| Д | 1,0 |
Таблица 12
Эта система оценок представляет собой функцию «один к одному», поскольку каждая введенная буква дает один конкретный средний балл успеваемости, а каждая средняя оценка соответствует одной введенной букве.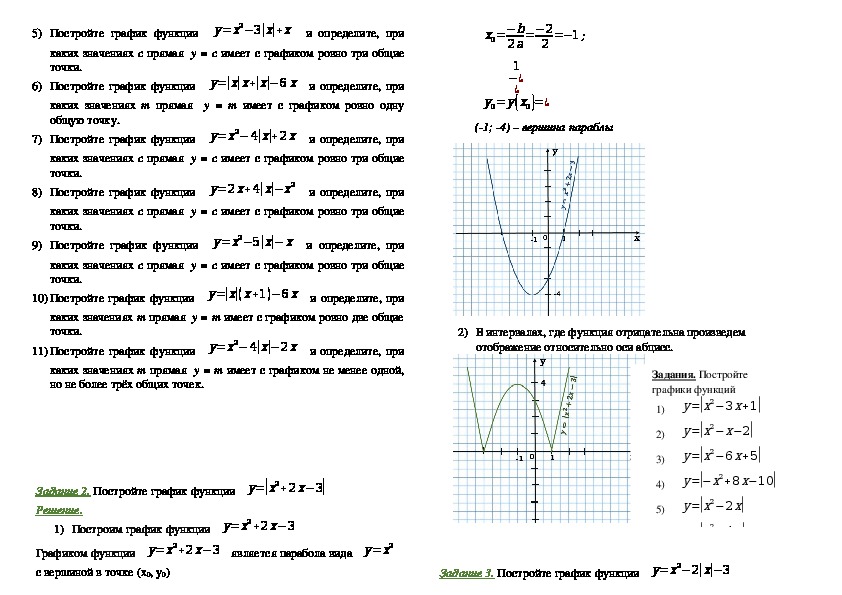
Чтобы наглядно представить эту концепцию, давайте еще раз взглянем на две простые функции, изображенные на рис. 1 (a) и рис. 1 (b) .Функция в части (a) показывает отношение, которое не является взаимно-однозначным, поскольку входные данные qq и rr оба дают выходные данные n.n. Функция в части (b) показывает взаимосвязь, которая является взаимно однозначной функцией, поскольку каждый вход связан с одним выходом.
Функция «один к одному»
Функция «один к одному» — это функция, в которой каждое выходное значение соответствует ровно одному входному значению.
Пример 13
Определение того, является ли отношение взаимно-однозначной функцией
Является ли площадь круга функцией его радиуса? Если да, то функция один к одному?
Решение
Круг радиуса rr имеет уникальную меру площади A=πr2,A=πr2, поэтому для любого входа r,r есть только один выход A. A. Площадь является функцией радиуса r.r.
A. Площадь является функцией радиуса r.r.
Если функция является однозначной, выходное значение, площадь, должно соответствовать уникальному входному значению, радиусу. Любая мера площади AA задается формулой A=πr2.A=πr2. Поскольку площади и радиусы — положительные числа, существует ровно одно решение: Aπ.Aπ. Таким образом, площадь круга является взаимно однозначной функцией радиуса круга.
Попробуйте #9
- ⓐ Зависит ли баланс от номера банковского счета?
- ⓑ Является ли номер банковского счета функцией баланса?
- ⓒ Является ли баланс однозначной функцией номера банковского счета?
Попробуйте #10
Оценить следующее:
- ⓐ Если каждый процентный балл, полученный за курс, переводится в одну буквенную оценку, является ли буквенный балл функцией процентного балла?
- ⓑ Если да, то является ли функция взаимно однозначной?
Использование теста вертикальной линии
Как мы видели в некоторых примерах выше, мы можем представить функцию с помощью графика. Графики отображают большое количество пар вход-выход на небольшом пространстве. Визуальная информация, которую они предоставляют, часто облегчает понимание отношений. По соглашению графики обычно строятся с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.
Графики отображают большое количество пар вход-выход на небольшом пространстве. Визуальная информация, которую они предоставляют, часто облегчает понимание отношений. По соглашению графики обычно строятся с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.
Наиболее распространенные графики называют входное значение xx и выходное значение y,y, и мы говорим, что yy является функцией x,x, или y=f(x)y=f(x), когда функция называется f.f. График функции представляет собой набор всех точек (x,y)(x,y) на плоскости, удовлетворяющих уравнению y=f(x).у=е(х). Если функция определена только для нескольких входных значений, то график функции представляет собой всего несколько точек, где x -координата каждой точки является входным значением, а y -координата каждой точки является соответствующее выходное значение. Например, черные точки на графике на рис. 7 говорят нам о том, что f(0)=2f(0)=2 и f(6)=1. f(6)=1. Однако множество всех точек (x,y)(x,y), удовлетворяющих y=f(x)y=f(x), является кривой. Показанная кривая включает в себя (0,2)(0,2) и (6,1)(6,1), поскольку кривая проходит через эти точки.
f(6)=1. Однако множество всех точек (x,y)(x,y), удовлетворяющих y=f(x)y=f(x), является кривой. Показанная кривая включает в себя (0,2)(0,2) и (6,1)(6,1), поскольку кривая проходит через эти точки.
Рисунок 7
Проверка вертикальной линии может использоваться для определения того, представляет ли график функцию. Если мы можем нарисовать любую вертикальную линию, которая пересекает график более одного раза, то график , а не определяет функцию, потому что функция имеет только одно выходное значение для каждого входного значения. См. рис. 8.
Рисунок 8
Как
Имея график, используйте тест вертикальной линии, чтобы определить, представляет ли график функцию.
- Изучите график, чтобы увидеть, пересекает ли какая-либо вертикальная линия кривую более одного раза.
- Если такая линия есть, определите, что график не представляет функцию.

Пример 14
Применение теста вертикальной линии
Какой из графиков на рисунке 9 представляет(ют) функцию y=f(x)?y=f(x)?
Рисунок 9
Решение
Если любая вертикальная линия пересекает график более одного раза, отношение, представленное графиком, не является функцией.Обратите внимание, что любая вертикальная линия будет проходить только через одну точку двух графиков, показанных в частях (а) и (б) рисунка 9. Отсюда мы можем сделать вывод, что эти два графика представляют функции. Третий график не представляет функцию, поскольку при максимальном количестве значений x вертикальная линия пересекает график более чем в одной точке, как показано на рисунке 10.
Рисунок 10
Попробуйте #11
Представляет ли график на рисунке 11 функцию?
Рисунок 11
Использование теста горизонтальной линии
После того, как мы определили, что график определяет функцию, простой способ определить, является ли она взаимно однозначной функцией, — использовать тест горизонтальной линии. Проведите горизонтальные линии через график. Если любая горизонтальная линия пересекает график более одного раза, то график не представляет однозначной функции.
Проведите горизонтальные линии через график. Если любая горизонтальная линия пересекает график более одного раза, то график не представляет однозначной функции.
Как
Имея график функции, используйте тест горизонтальной линии, чтобы определить, представляет ли график функцию взаимно однозначного соответствия.
- Изучите график, чтобы увидеть, пересекает ли какая-либо горизонтальная линия кривую более одного раза.
- Если такая строка есть, определить, что функция не является однозначной.
Пример 15
Применение теста горизонтальной линии
Рассмотрим функции, показанные на рисунке 9 (a) и рисунке 9 (b) . Является ли какая-либо из функций взаимно однозначной?
Решение
Функция на рисунке 9 (a) не является однозначной. Горизонтальная линия, показанная на рисунке 12, пересекает график функции в двух точках (и мы даже можем найти горизонтальные линии, пересекающие его в трех точках).)
Горизонтальная линия, показанная на рисунке 12, пересекает график функции в двух точках (и мы даже можем найти горизонтальные линии, пересекающие его в трех точках).)
Рисунок 12
Функция на рисунке 9 (b) является однозначной. Любая горизонтальная линия пересекает диагональную линию не более одного раза.
Попробуйте #12
Является ли график, показанный на рис. 9, взаимно однозначным?
Идентификация функций Basic Toolkit
В этом тексте мы будем изучать функции — формы их графиков, их уникальные характеристики, их алгебраические формулы и способы решения задач с ними. При обучении чтению мы начинаем с алфавита.При обучении арифметике мы начинаем с чисел. При работе с функциями также полезно иметь базовый набор элементов стандартного блока. Мы называем их «инструментальными функциями», которые образуют набор основных именованных функций, для которых мы знаем график, формулу и специальные свойства.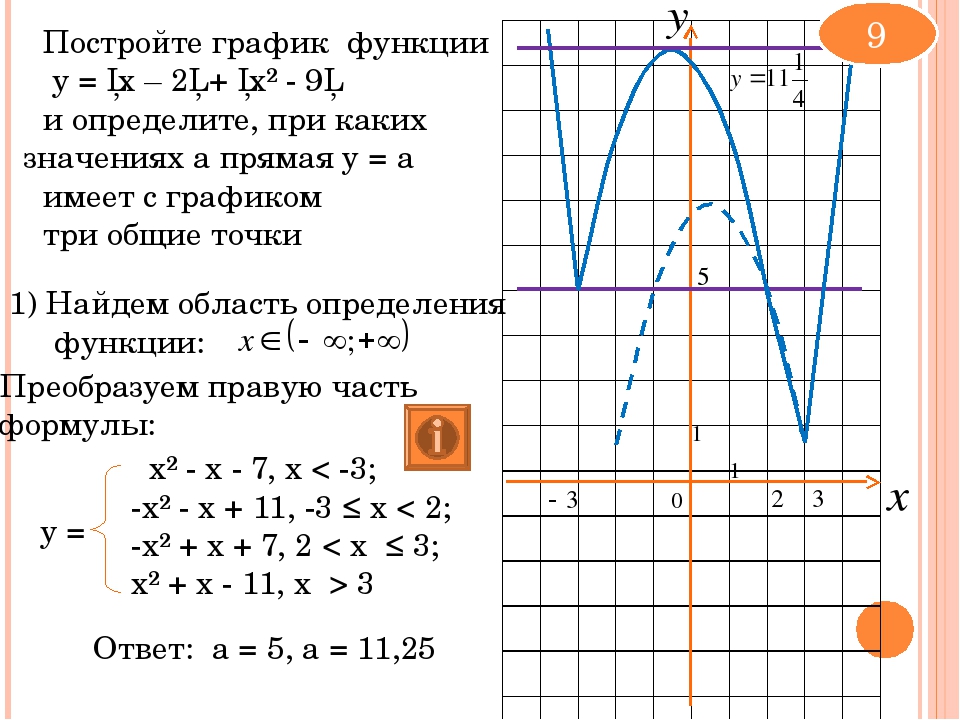 Некоторые из этих функций запрограммированы на отдельные кнопки на многих калькуляторах. Для этих определений мы будем использовать xx в качестве входной переменной и y=f(x)y=f(x) в качестве выходной переменной.
Некоторые из этих функций запрограммированы на отдельные кнопки на многих калькуляторах. Для этих определений мы будем использовать xx в качестве входной переменной и y=f(x)y=f(x) в качестве выходной переменной.
Мы будем часто встречаться с этими инструментальными функциями, комбинациями инструментальных функций, их графиками и преобразованиями в этой книге.Будет очень полезно, если мы сможем быстро распознать эти функции инструментария и их функции по имени, формуле, графику и основным свойствам таблицы. Графики и примерные табличные значения прилагаются к каждой функции, показанной в Таблице 13. 1.
В чем разница между отношением и функцией?
2.В чем разница между вводом и выводом функции?
3.Почему тест вертикальной линии говорит нам, представляет ли график отношения функцию?
4.Как определить, является ли отношение однозначной функцией?
5.Почему тест горизонтальной линии говорит нам, является ли график функции взаимно однозначным?
Алгебраический
В следующих упражнениях определите, представляет ли отношение функцию.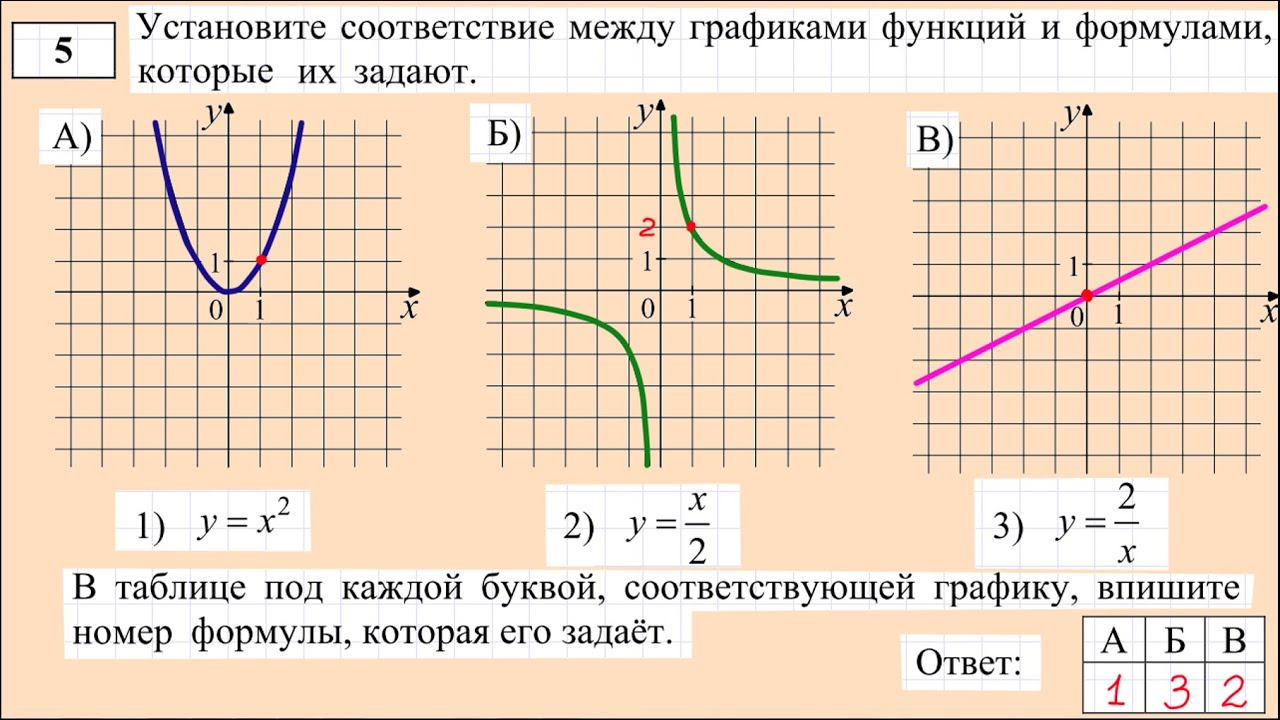
{(а,б),(в,г),(а,в)}{(а,б),(в,г),(а,в)}
7.{(а,б),(б,в),(в,в)}{(а,б),(б,в),(в,в)}
В следующих упражнениях определите, представляет ли отношение yy как функцию x.Икс.
В следующих упражнениях оцените f(−3),f(2),f(−a),−f(a),f(a+h).f(−3),f(2),f( −a),−f(a),f(a+h).
28.f(x)=−5×2+2x−1f(x)=−5×2+2x−1
30.f(x)=6x−15x+2f(x)=6x−15x+2
31.f(x)=|x−1|−|x+1|f(x)=|x−1|−|x+1|
32.Учитывая функцию g(x)=5−x2,g(x)=5−x2, вычислить g(x+h)−g(x)h,h≠0.g(x+h)−g(x )ч,ч≠0.
33.Учитывая функцию g(x)=x2+2x,g(x)=x2+2x, вычислить g(x)−g(a)x−a,x≠ag(x)−g(a)x−a ,х≠а.
34.Учитывая функцию k(t)=2t−1:k(t)=2t−1:
- ⓐ Вычислить k(2).k(2).
- ⓑ Решите k(t)=7.k(t)=7.
Учитывая функцию f(x)=8−3x:f(x)=8−3x:
- ⓐ Вычислить f(−2).f(−2).
- ⓑ Решить f(x)=−1.f(x)=−1.
Учитывая функцию p(c)=c2+c:p(c)=c2+c:
- ⓐ Оценить p(−3).
 p(−3).
p(−3). - ⓑ Решить p(c)=2.p(c)=2.
Учитывая функцию f(x)=x2−3x:f(x)=x2−3x:
- ⓐ Оценить f(5).ф(5).
- ⓑ Решить f(x)=4.f(x)=4.
Учитывая функцию f(x)=x+2:f(x)=x+2:
- ⓐ Вычислить f(7).f(7).
- ⓑ Решить f(x)=4.f(x)=4.
Рассмотрим соотношение 3r+2t=18,3r+2t=18.
- ⓐ Запишите зависимость в виде функции r=f(t).r=f(t).
- ⓑ Вычислить f(−3).f(−3).
- ⓒ Решите f(t)=2.f(t)=2.
Графический
В следующих упражнениях используйте тест вертикальной линии, чтобы определить, какие графики показывают отношения, которые являются функциями.
40. 42. 44. 46. 48. 50. 52.Учитывая следующий график,
- ⓐ Вычислить f(−1).f(−1).
- ⓑ Найдите f(x)=3.f(x)=3.
Учитывая следующий график,
- ⓐ Вычислить f(0).
 f(0).
f(0). - ⓑ Найдите f(x)=−3.f(x)=−3.
Учитывая следующий график,
- ⓐ Вычислите f(4).f(4).
- ⓑ Найдите f(x)=1.f(x)=1.
В следующих упражнениях определите, является ли данный график однозначной функцией.
56. 58.Числовой
В следующих упражнениях определите, представляет ли отношение функцию.
60.{(−1,−1),(−2,−2),(−3,−3)}{(−1,−1),(−2,−2),(−3,−3) }
61.{(3,4),(4,5),(5,6)}{(3,4),(4,5),(5,6)}
62.{(2,5),(7,11),(15,8),(7,9)}{(2,5),(7,11),(15,8),(7,9) }
Для следующих упражнений определите, представляет ли отношение, представленное в виде таблицы, yy как функцию x.x.
В следующих упражнениях используйте функцию ff, представленную в таблице ниже.
| хх | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| ф(х)ф(х) | 74 | 28 | 1 | 53 | 56 | 3 | 36 | 45 | 14 | 47 |
Таблица 14
В следующих упражнениях оцените функцию ff при значениях f(−2),f(−1),f(0),f(1),f(−2),f(−1),f(0 ),f(1) и f(2).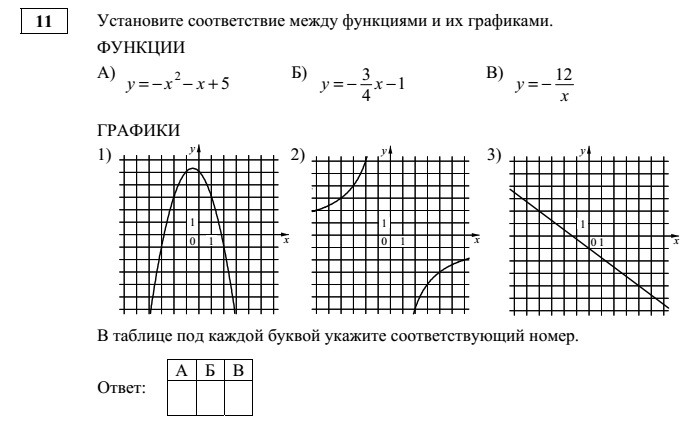 ф(2).
ф(2).
f(x)=8×2−7x+3f(x)=8×2−7x+3
72.f(x)=x−2x+3f(x)=x−2x+3
Для следующих упражнений оцените выражения, заданные функциями f,g,f,g и h:h:
f(x)=3x−2f(x)=3x−2
г(х)=5-х2г(х)=5-х2
h(x)=-2×2+3x-1h(x)=-2×2+3x-1
3f(1)−4g(−2)3f(1)−4g(−2)
75.е(73)−h(−2)f(73)−h(−2)
Технология
Для следующих упражнений постройте график y=x2y=x2 в заданной области.Определить соответствующий диапазон. Покажите каждый график.
Для следующих упражнений постройте график y=x3y=x3 в заданной области. Определить соответствующий диапазон. Покажите каждый график.
Для следующих упражнений постройте график y=xy=x в заданной области. Определить соответствующий диапазон. Покажите каждый график.
Для следующих упражнений постройте график y=x3y=x3 в заданной области. Определить соответствующий диапазон. Покажите каждый график.
85.[-0,001,0,001][-0,001,0,001]
86.
[−1000 1000][−1000 1000]
87.[−1 000 000, 1 000 000] [−1 000 000, 1 000 000]
Реальные приложения
88.Количество мусора, G,G, производимого городом с населением pp, равно G=f(p).G=f(p). GG измеряется в тоннах в неделю, а pp измеряется в тысячах человек.
- ⓐ В городе Тола с населением 40 000 человек каждую неделю производится 13 тонн мусора. Выразите эту информацию через функцию f.f.
- ⓑ Объясните смысл утверждения f(5)=2.f(5)=2.
Количество кубических ярдов земли, D,D, необходимое для покрытия сада площадью aa квадратных футов, равно D=g(a).D=g(a).
- ⓐ Для сада площадью 5000 футов 2 требуется 50 ярдов 3 земли. Выразите эту информацию через функцию g.g.
- ⓑ Объясните смысл утверждения g(100)=1.g(100)=1.
Пусть f(t)f(t) будет числом уток в озере через tt лет после 1990 года. Объясните значение каждого утверждения:
- ⓐ f(5)=30f(5)=30
- ⓑ е(10)=40f(10)=40

Пусть h(t)h(t) будет высотой ракеты над землей в футах через tt секунд после запуска. Объясните значение каждого утверждения:
- ⓐ ч(1)=200ч(1)=200
- ⓑ ч(2)=350ч(2)=350
Покажите, что функция f(x)=3(x−5)2+7f(x)=3(x−5)2+7 является , а не взаимно однозначной.
Функции и обозначения функций — Алгебра и тригонометрия
Цели обучения
В этом разделе вы:
- Определить, представляет ли отношение функцию.
- Найти значение функции.
- Определить, является ли функция взаимно однозначной.
- Используйте тест вертикальной линии для определения функций.
- График функций, перечисленных в библиотеке функций.
Реактивный лайнер меняет высоту по мере увеличения расстояния от начальной точки полета. Вес растущего ребенка со временем увеличивается. В каждом случае одна величина зависит от другой. Между двумя величинами существует взаимосвязь, которую мы можем описать, проанализировать и использовать для прогнозирования. В этом разделе мы проанализируем такие отношения.
В этом разделе мы проанализируем такие отношения.
Определение того, представляет ли отношение функцию
Отношение представляет собой набор упорядоченных пар. Набор, состоящий из первых компонентов каждой упорядоченной пары, называется доменом , а набор, состоящий из вторых компонентов каждой упорядоченной пары, называется диапазоном . Рассмотрим следующий набор упорядоченных пар. Первые числа в каждой паре — это первые пять натуральных чисел. Второе число в каждой паре вдвое больше первого.
Домен
Диапазон
Обратите внимание, что каждое значение в домене также известно как входное значение или независимая переменная и часто помечается строчной буквой Каждое значение в диапазоне также известно как выходное значение или зависимая переменная, и часто обозначается строчной буквой
Функция — это отношение, которое присваивает один элемент в диапазоне каждому элементу в домене .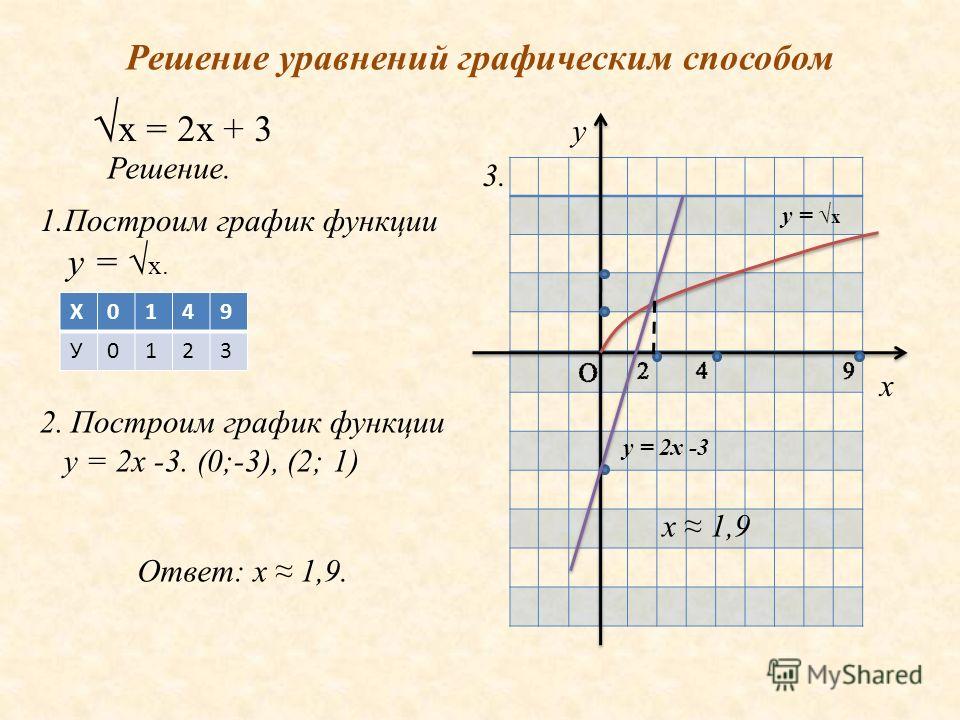 Другими словами, значения x не повторяются.В нашем примере, который связывает первые пять натуральных чисел с числами, удвоенными их значениями, это отношение является функцией, поскольку каждый элемент в домене связан ровно с одним элементом в диапазоне
Другими словами, значения x не повторяются.В нашем примере, который связывает первые пять натуральных чисел с числами, удвоенными их значениями, это отношение является функцией, поскольку каждый элемент в домене связан ровно с одним элементом в диапазоне
Теперь рассмотрим множество упорядоченных пар, связывающих термины «четный» и «нечетный» с первыми пятью натуральными числами. Это будет выглядеть как
Обратите внимание, что каждый элемент в домене
равен , а не в паре ровно с одним элементом в диапазоне
. Например, термин «нечетный» соответствует трем значениям из домена
, а термин «четный» соответствует двум. значения из диапазона,
Это нарушает определение функции, поэтому это отношение не является функцией.
(рисунок) сравнивает отношения, которые являются функциями, а не функциями.
Функция
Функция — это отношение, в котором каждое возможное входное значение приводит ровно к одному выходному значению. Мы говорим, что «выход есть функция входа».
Мы говорим, что «выход есть функция входа».
Входные значения составляют домен, а выходные значения составляют диапазон.
Как
Учитывая связь между двумя величинами, определите, является ли связь функцией.
- Определите входные значения.
- Определите выходные значения.
- Если каждое входное значение приводит только к одному выходному значению, классифицируйте отношение как функцию. Если какое-либо входное значение приводит к двум или более выходам, не классифицируйте отношение как функцию.
Определение того, являются ли прайс-листы меню функциями
Меню кофейни, показанное на (Рисунок), состоит из позиций и их цен.
- Является ли цена функцией товара?
- Является ли предмет функцией цены?
[reveal-answer q=»855295″]Показать решение[/reveal-answer]
[hidden-answer a=»855295″]
- Начнем с рассмотрения ввода как элементов меню.
 Тогда выходные значения являются ценами.
Тогда выходные значения являются ценами.Каждый пункт в меню имеет только одну цену, поэтому цена зависит от пункта.
- Два блюда в меню имеют одинаковую цену. Если мы считаем, что цены являются входными значениями, а товары — выходными, то одно и то же входное значение может иметь более одного связанного с ним выхода.См. (Рисунок). Рисунок 3.
Таким образом, пункт не зависит от цены.
[/скрытый ответ]
Определение того, являются ли правила оценки класса функциями
В конкретном математическом классе общая оценка в процентах соответствует среднему баллу. Является ли средний балл функцией процентной оценки? Является ли процентная оценка функцией среднего балла? (Рисунок) показывает возможное правило для присвоения оценок.
[скрытый ответ = ”fs-id1165135424616″]
Для любого процента полученной оценки существует соответствующий средний балл, поэтому средний балл является функцией процентной оценки. Другими словами, если мы вводим процентную оценку, на выходе получается определенный средний балл.
В данной системе оценивания существует диапазон процентных оценок, соответствующих одному и тому же среднему баллу. Например, учащиеся, получившие средний балл 3,0, могут иметь различные процентные оценки от 78 до 86. Таким образом, процентная оценка не является функцией среднего балла.
Например, учащиеся, получившие средний балл 3,0, могут иметь различные процентные оценки от 78 до 86. Таким образом, процентная оценка не является функцией среднего балла.
[/скрытый ответ]
Попробуйте
(Рисунок) перечисляет пять величайших бейсболистов всех времен в порядке их ранга.
| Игрок | Ранг |
|---|---|
| Бэйб Рут | 1 |
| Вилли Мейс | 2 |
| Тай Кобб | 3 |
| Уолтер Джонсон | 4 |
| Хэнк Аарон | 5 |
- Зависит ли ранг от имени игрока?
- Является ли имя игрока функцией ранга?
[скрытый ответ = ”fs-id1165137724415″]
а. да; б. да. (Примечание: если бы два игрока разделили, скажем, 4-е место, то имя не зависело бы от ранга.)
да; б. да. (Примечание: если бы два игрока разделили, скажем, 4-е место, то имя не зависело бы от ранга.)
[/скрытый ответ]
Представление функций с помощью таблиц
Обычный метод представления функций — в виде таблицы. В строках или столбцах таблицы отображаются соответствующие входные и выходные значения. В некоторых случаях эти значения представляют все, что мы знаем об отношениях; в других случаях в таблице представлены несколько избранных примеров из более полных взаимосвязей.
(рисунок) перечисляет входное число каждого месяца (январь = 1, февраль = 2 и т. д.) и выходное значение количества дней в этом месяце. Эта информация представляет собой все, что мы знаем о месяцах и днях для данного года (это не високосный год). Обратите внимание, что в этой таблице мы определяем функцию дней в месяце, в которой месяцы идентифицируются целым числом, а не именем.
(рисунок) определяет функцию Помните, это обозначение говорит нам, что это имя функции, которая принимает входные данные и дает выходные данные
(рисунок) отображает возраст детей в годах и их соответствующий рост.В этой таблице представлены лишь некоторые из имеющихся данных о росте и возрасте детей. Мы сразу видим, что эта таблица не представляет собой функцию, потому что одно и то же входное значение, 5 лет, имеет два разных выходных значения, 40 дюймов и 42 дюйма
| Возраст в годах,(ввод) | 5 | 5 | 6 | 7 | 8 | 9 | 10 |
| Высота в дюймах (выход) | 40 | 42 | 44 | 47 | 50 | 52 | 54 |
Как
Имея таблицу входных и выходных значений, определите, представляет ли таблица функцию.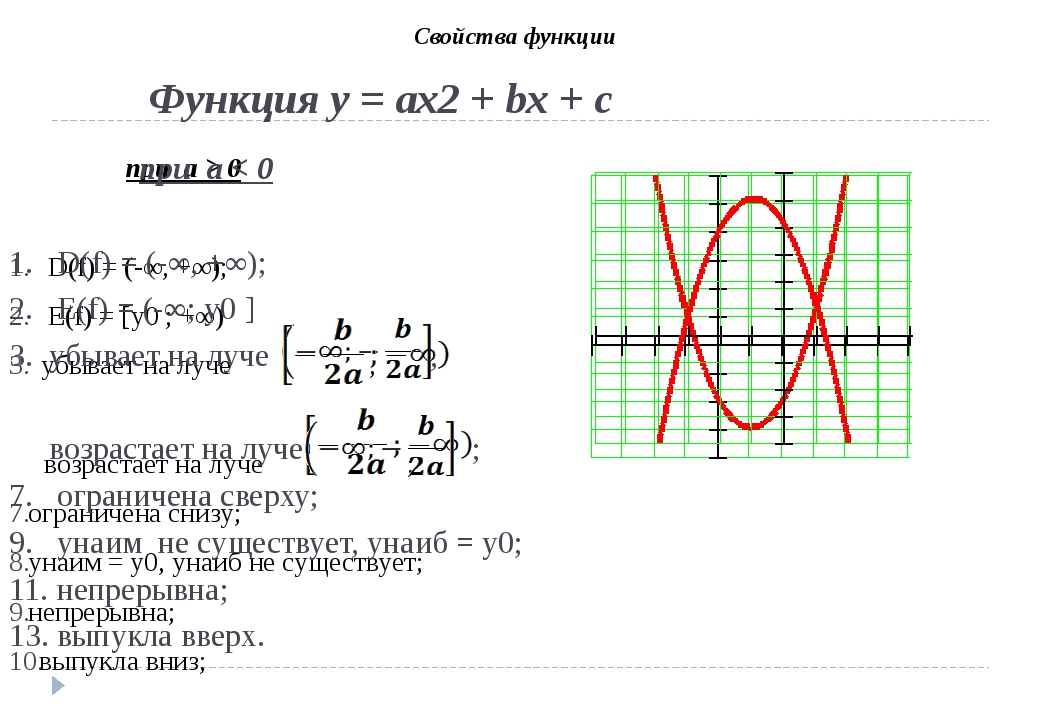
- Определите входные и выходные значения.
- Проверьте, связано ли каждое входное значение только с одним выходным значением. Если это так, таблица представляет собой функцию.
Идентификация таблиц, представляющих функции
Какая таблица (Рисунок), (Рисунок) или (Рисунок) представляет функцию (если есть)?
| Вход | Выход |
|---|---|
| –3 | 5 |
| 0 | 1 |
| 4 | 5 |
[скрытый ответ = ”fs-id1165137665675″]
(рисунок) и (рисунок) определяют функции.В обоих случаях каждое входное значение соответствует ровно одному выходному значению. (Рисунок) не определяет функцию, поскольку входное значение 5 соответствует двум различным выходным значениям.
(Рисунок) не определяет функцию, поскольку входное значение 5 соответствует двум различным выходным значениям.
Когда таблица представляет функцию, соответствующие входные и выходные значения также могут быть указаны с использованием обозначения функции.
Функция, представленная (Рисунок), может быть представлена записью
Аналогично, операторы
представляют функцию на (рис.).
(рисунок) нельзя выразить подобным образом, потому что он не представляет функцию.[/скрытый ответ]
Попробуйте
Представляет ли (Рисунок) функцию?
| Вход | Выход |
|---|---|
| 1 | 10 |
| 2 | 100 |
| 3 | 1000 |
[скрытый ответ = ”fs-id1165135322022″]
да
[/скрытый ответ]
Поиск входных и выходных значений функции
Когда мы знаем входное значение и хотим определить соответствующее выходное значение для функции, мы оцениваем функцию. Вычисление всегда будет давать один результат, потому что каждое входное значение функции соответствует ровно одному выходному значению.
Вычисление всегда будет давать один результат, потому что каждое входное значение функции соответствует ровно одному выходному значению.
Когда мы знаем выходное значение и хотим определить входные значения, которые дадут это выходное значение, мы устанавливаем выход равным формуле функции и решаем для входа. Решение может дать более одного решения, потому что разные входные значения могут дать одно и то же выходное значение.
Вычисление функций в алгебраических формах
Когда у нас есть функция в форме формулы, обычно несложно вычислить функцию.Например, функцию можно вычислить, возведя входное значение в квадрат, умножив его на 3 и затем вычтя произведение из 5.
Как
Дана формула функции, вычислить.
- Замените входную переменную в формуле предоставленным значением.
- Вычислите результат.
Попробуйте
Учитывая функцию оценки
[reveal-answer q=»fs-id1165137441862″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165137441862″]
[/скрытый ответ]
Решающие функции
Учитывая функцию решить для
Попробуйте
Учитывая функцию решить
[reveal-answer q=»fs-id1165135664055″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165135664055″]
[/скрытый ответ]
Вычисление функции, заданной в табличной форме
Как мы видели выше, мы можем представлять функции в виде таблиц.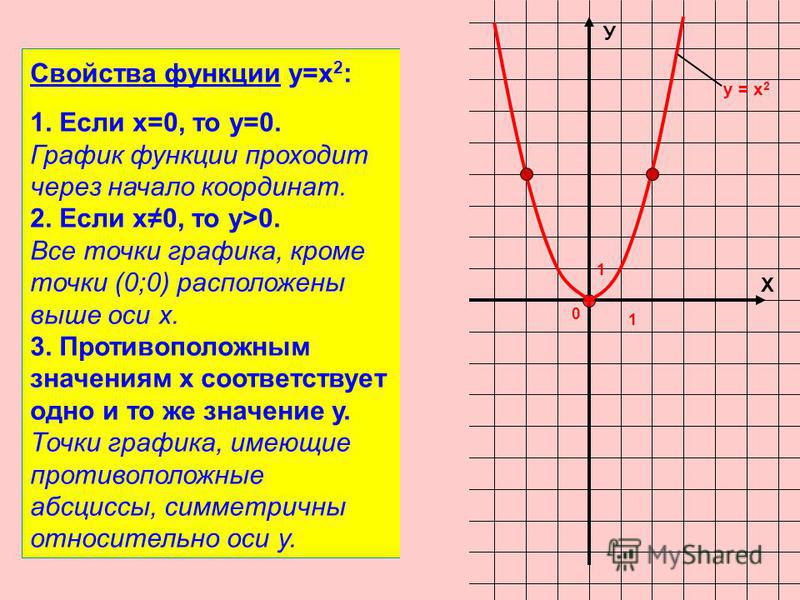 И наоборот, мы можем использовать информацию в таблицах для написания функций, и мы можем оценивать функции, используя таблицы. Например, насколько хорошо наши питомцы помнят приятные воспоминания, которыми мы делимся с ними? Существует городская легенда, что у золотой рыбки память 3 секунды, но это всего лишь миф. Золотая рыбка может помнить до 3 месяцев, а бета-рыбка имеет память до 5 месяцев. И если память щенка не превышает 30 секунд, то взрослая собака может помнить 5 минут. Это мизер по сравнению с кошкой, память которой длится 16 часов.
И наоборот, мы можем использовать информацию в таблицах для написания функций, и мы можем оценивать функции, используя таблицы. Например, насколько хорошо наши питомцы помнят приятные воспоминания, которыми мы делимся с ними? Существует городская легенда, что у золотой рыбки память 3 секунды, но это всего лишь миф. Золотая рыбка может помнить до 3 месяцев, а бета-рыбка имеет память до 5 месяцев. И если память щенка не превышает 30 секунд, то взрослая собака может помнить 5 минут. Это мизер по сравнению с кошкой, память которой длится 16 часов.
Функцию, связывающую тип питомца с длительностью его памяти, легче визуализировать с помощью таблицы. См. (Рисунок).
| Домашнее животное | Объем памяти в часах |
|---|---|
| Щенок | 0,008 |
| Взрослая собака | 0,083 |
| Кат | 16 |
| Золотая рыбка | 2160 |
| Бета-рыба | 3600 |
Иногда вычисление функции в виде таблицы может оказаться более полезным, чем использование уравнений.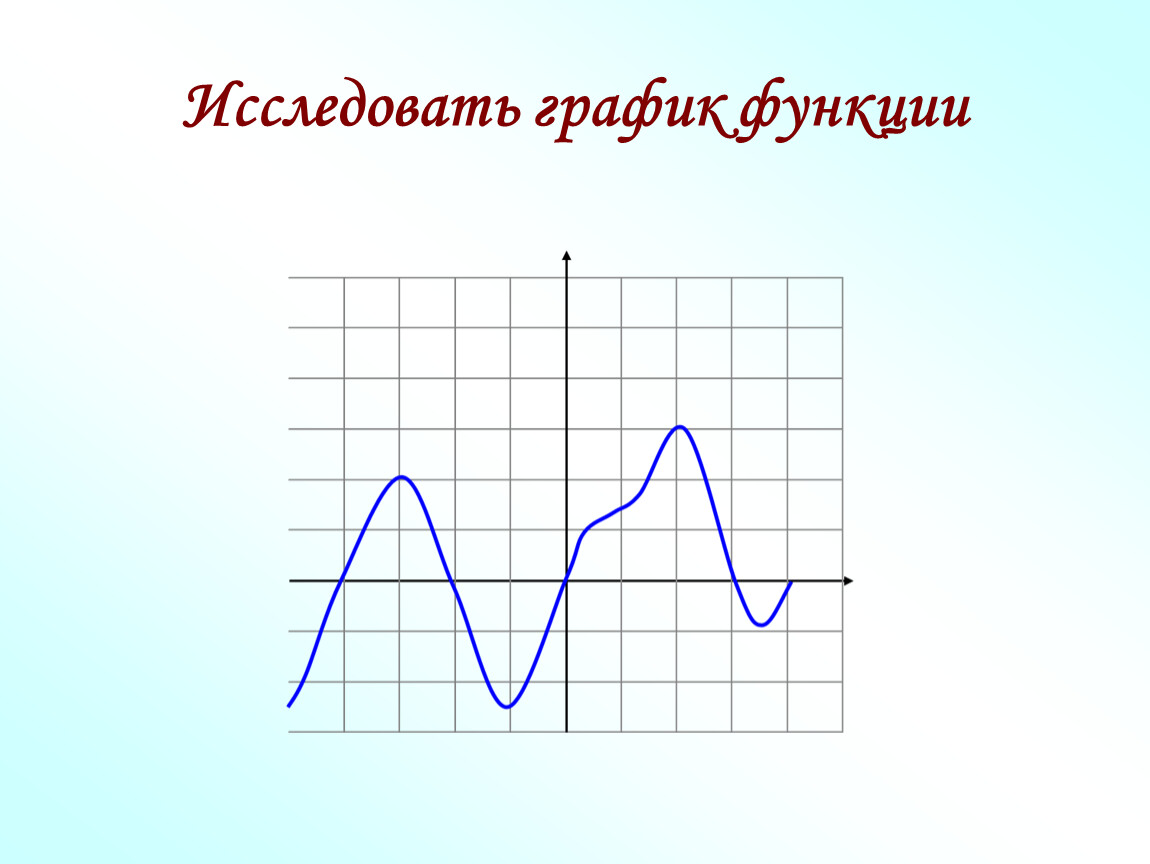 Здесь давайте вызовем функцию
Здесь давайте вызовем функцию
. Областью определения функции является тип питомца, а диапазон — действительное число, представляющее количество часов, в течение которых сохраняется память питомца. Мы можем оценить функцию по входному значению «золотая рыбка». Мы бы написали Обратите внимание, что для оценки функции в форме таблицы мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функций кажется идеально подходящей для этой функции, в большей степени, чем ее запись в форме абзаца или функции.
Как
Для функции, представленной в виде таблицы, определите конкретные выходные и входные значения.
- Найдите заданный вход в строке (или столбце) входных значений.
- Идентифицируйте соответствующее выходное значение в паре с этим входным значением.
- Найдите указанные выходные значения в строке (или столбце) выходных значений, отмечая каждый раз, когда это выходное значение появляется.

- Определите входное значение(я), соответствующее данному выходному значению.
Оценка и решение табличной функции
Использование (Рисунок),
- Оценка
- Решить
| 1 | 2 | 3 | 4 | 5 | |
| 8 | 6 | 7 | 6 | 8 |
Попробуйте
[reveal-answer q=»fs-id1165137423936″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165137423936″]
[/скрытый ответ]
Определение того, является ли функция взаимно однозначной
Некоторые функции имеют заданное выходное значение, которое соответствует двум или более входным значениям. Например, на биржевой диаграмме, показанной на (рисунке) в начале этой главы, цена акции составляла 1000 долларов в пять разных дат, а это означает, что было пять различных входных значений, которые все привели к одному и тому же выходному значению в 1000 долларов.
Например, на биржевой диаграмме, показанной на (рисунке) в начале этой главы, цена акции составляла 1000 долларов в пять разных дат, а это означает, что было пять различных входных значений, которые все привели к одному и тому же выходному значению в 1000 долларов.
Однако некоторые функции имеют только одно входное значение для каждого выходного значения, а также имеют только один выход для каждого входа. Мы называем эти функции однозначными функциями. В качестве примера рассмотрим школу, в которой используются только буквенные оценки и десятичные эквиваленты, как показано на (рис.).
| Буквенный класс | Средний балл |
|---|---|
| А | 4,0 |
| Б | 3,0 |
| С | 2,0 |
| Д | 1,0 |
Эта система оценок представляет собой функцию «один к одному», поскольку каждая введенная буква дает один конкретный средний балл успеваемости, а каждая средняя оценка соответствует одной введенной букве.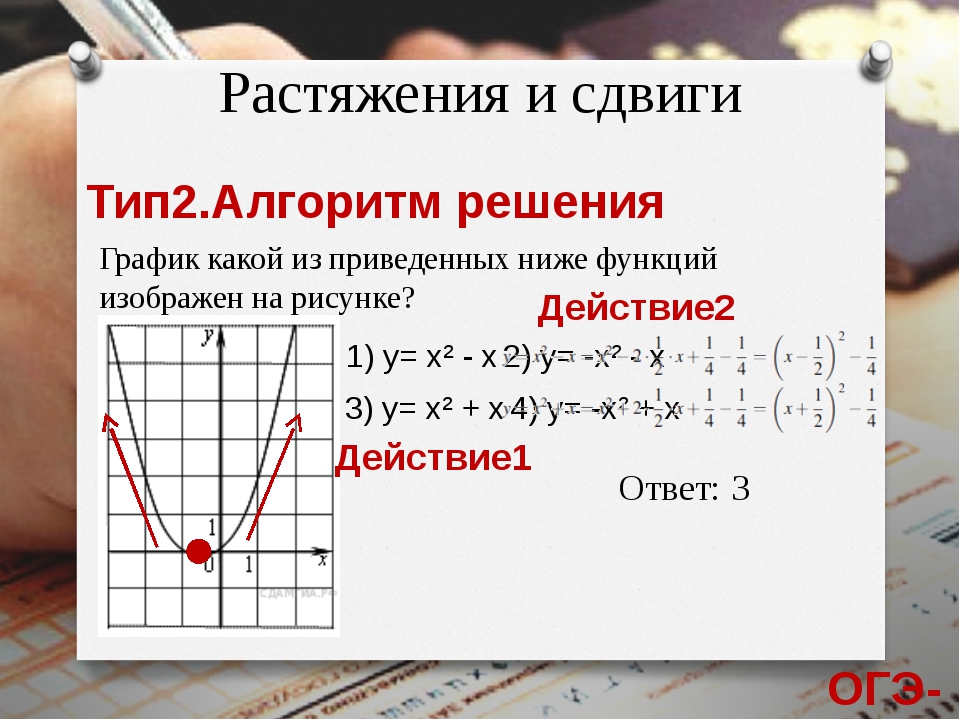
Чтобы визуализировать эту концепцию, давайте еще раз посмотрим на две простые функции, показанные на (Рисунок) (a) и (Рисунок) (b) . Функция в части (а) показывает взаимосвязь, которая не является взаимно однозначной функцией, поскольку входные данные и оба дают выходные данные Функция в части (б) демонстрирует взаимосвязь, которая является взаимно однозначной функцией, поскольку каждый вход связан с одним вывод.
Функция «один к одному»
Функция «один к одному» — это функция, в которой каждое выходное значение соответствует ровно одному входному значению.Повторяющихся значений x или y нет.
Определение того, является ли отношение взаимно-однозначной функцией
Является ли площадь круга функцией его радиуса? Если да, то функция один к одному?
Попробуйте
- Является ли баланс функцией номера банковского счета?
- Является ли номер банковского счета функцией баланса?
- Является ли баланс однозначной функцией номера банковского счета?
[скрытый ответ = ”fs-id1165137456018″]
а.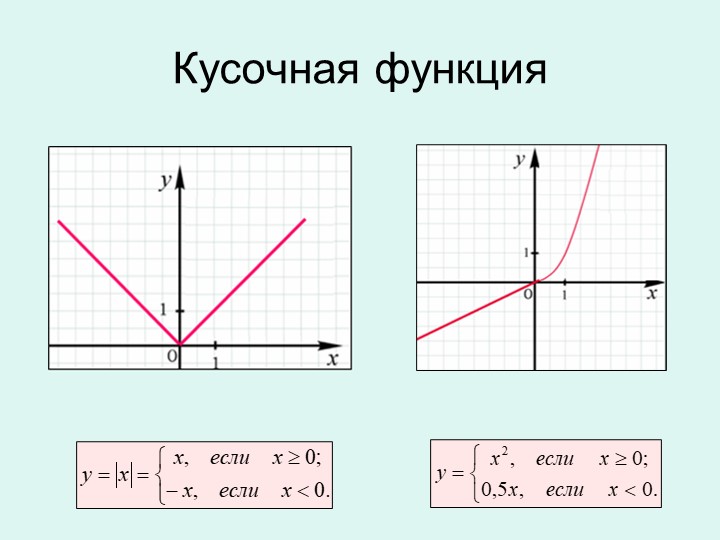 да, потому что каждый банковский счет имеет единственный баланс в любой момент времени; б. нет, так как баланс на нескольких банковских счетах может быть одинаковым; в. нет, потому что один и тот же выход может соответствовать более чем одному входу.
да, потому что каждый банковский счет имеет единственный баланс в любой момент времени; б. нет, так как баланс на нескольких банковских счетах может быть одинаковым; в. нет, потому что один и тот же выход может соответствовать более чем одному входу.
[/скрытый ответ]
Попробуйте
- Если каждый процент оценки, полученной за курс, переводится в одну буквенную оценку, является ли буквенная оценка функцией процентной оценки?
- Если да, то является ли функция взаимно однозначной?
[скрытый ответ = ”fs-id1165137655289″]
- Да, буквенная оценка зависит от процентной оценки;
- Нет, не один к одному.Мы можем получить 100 различных процентных чисел, но только около пяти возможных буквенных оценок, поэтому не может быть только одного процентного числа, соответствующего каждой буквенной оценке.
[/скрытый ответ]
Использование теста вертикальной линии
Как мы видели в некоторых примерах выше, мы можем представить функцию с помощью графика. Графики отображают большое количество пар вход-выход на небольшом пространстве. Визуальная информация, которую они предоставляют, часто облегчает понимание отношений.По соглашению графики обычно строятся с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.
Графики отображают большое количество пар вход-выход на небольшом пространстве. Визуальная информация, которую они предоставляют, часто облегчает понимание отношений.По соглашению графики обычно строятся с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.
Наиболее распространенные графики называют входное значение и выходное значение, и мы говорим, что это функция или, когда функция названа График функции представляет собой набор всех точек на плоскости, которые удовлетворяют уравнению. Если функция определена только для нескольких входных значений, то график функции состоит всего из нескольких точек, где x -координата каждой точки является входным значением, а y -координата каждой точки является соответствующим выходным значением.Например, черные точки на графике (рисунок) говорят нам о том, что множество точек, удовлетворяющих условию, представляет собой кривую. Показанная кривая включает и потому, что кривая проходит через эти точки.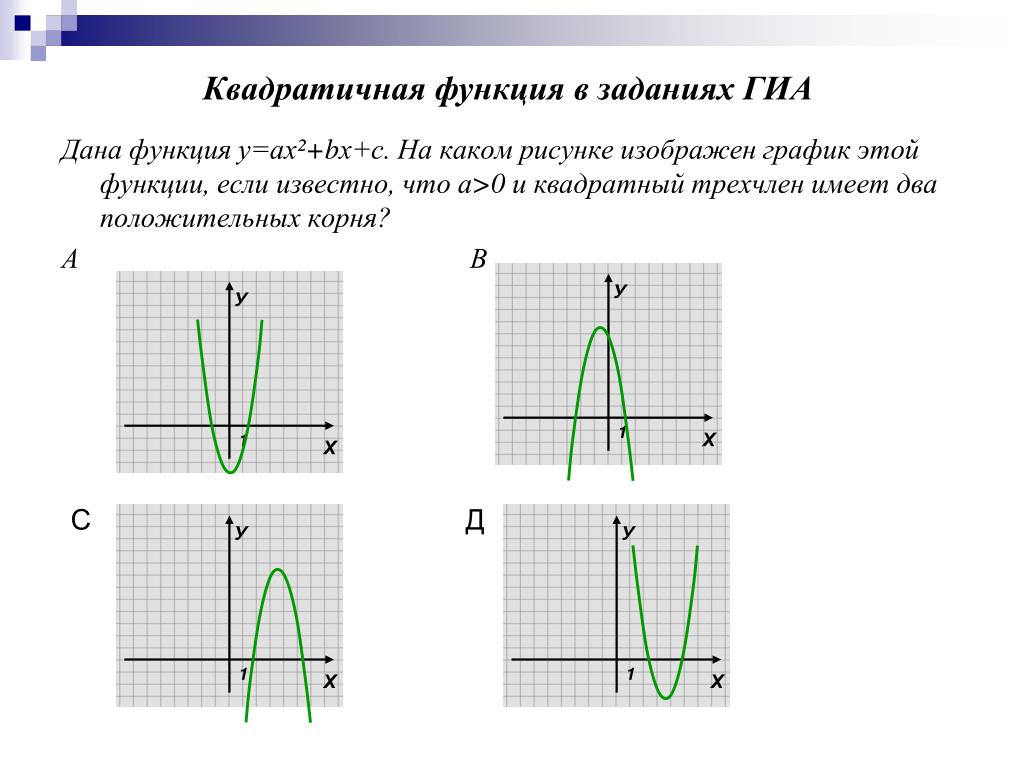
Проверка вертикальной линии может использоваться для определения того, представляет ли график функцию. Если мы можем нарисовать любую вертикальную линию, которая пересекает график более одного раза, то график , а не определяет функцию, потому что функция имеет только одно выходное значение для каждого входного значения.См. (Рисунок).
Рисунок 9.Как
Имея график, используйте тест вертикальной линии, чтобы определить, представляет ли график функцию.
- Изучите график, чтобы увидеть, пересекает ли какая-либо вертикальная линия кривую более одного раза.
- Если такая линия есть, определите, что график не представляет функцию.
Применение теста вертикальной линии
Какой из графиков на (рисунке) представляет(ют) функцию
Рисунок 10. [reveal-answer q=»fs-id11651351″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id11651351
«]
Если любая вертикальная линия пересекает график более одного раза, отношение, представленное графиком, не является функцией. Обратите внимание, что любая вертикальная линия будет проходить только через одну точку из двух графиков, показанных в частях (a) и (b) (Рисунок). Отсюда можно сделать вывод, что эти два графика представляют собой функции. Третий график не представляет функцию, поскольку при максимальном количестве значений x вертикальная линия пересекает график более чем в одной точке, как показано на (рис.).
Обратите внимание, что любая вертикальная линия будет проходить только через одну точку из двух графиков, показанных в частях (a) и (b) (Рисунок). Отсюда можно сделать вывод, что эти два графика представляют собой функции. Третий график не представляет функцию, поскольку при максимальном количестве значений x вертикальная линия пересекает график более чем в одной точке, как показано на (рис.).
[/hidden-answer]
Попробуйте
Представляет ли график на (рисунке) функцию?
Рисунок 12. [reveal-answer q=»fs-id1165134258608″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165134258608″]
да
[/скрытый ответ]
Использование теста горизонтальной линии
После того, как мы определили, что график определяет функцию, простой способ определить, является ли она взаимно однозначной функцией, — использовать тест горизонтальной линии.Проведите горизонтальные линии через график.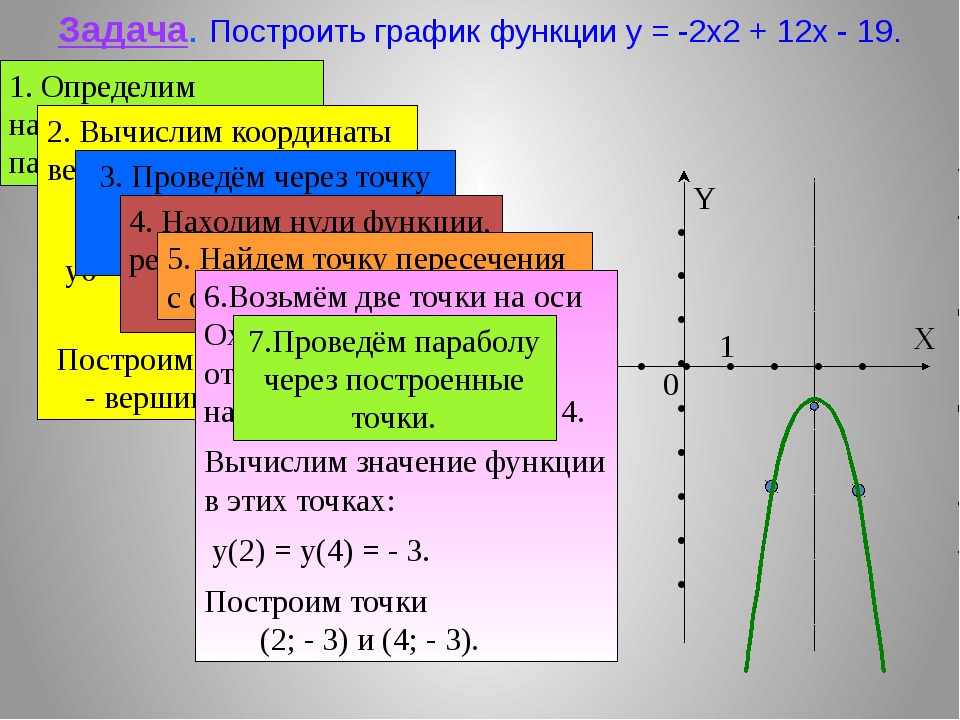 Если любая горизонтальная линия пересекает график более одного раза, то график не представляет однозначной функции.
Если любая горизонтальная линия пересекает график более одного раза, то график не представляет однозначной функции.
Как
Имея график функции, используйте тест горизонтальной линии, чтобы определить, представляет ли график функцию взаимно однозначного соответствия.
- Изучите график, чтобы увидеть, пересекает ли какая-либо горизонтальная линия кривую более одного раза.
- Если такая строка есть, определить, что функция не является однозначной.
Применение теста горизонтальной линии
Рассмотрим функции, показанные на (Рисунок) (a) и (Рисунок) (b) . Является ли какая-либо из функций взаимно однозначной?
[reveal-answer q=»fs-id1165135521259″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165135521259″]
Функция на (рис.) (a) не является однозначной. Горизонтальная линия, показанная на (Рисунок), пересекает график функции в двух точках (и мы даже можем найти горизонтальные линии, которые пересекают его в трех точках. )
)
Функция на (Рисунок) (b) является однозначной. Любая горизонтальная линия пересекает диагональную линию не более одного раза.[/hidden-answer]
Попробуйте
Соответствует ли график, показанный на (Рисунок), один к одному?
[reveal-answer q=»fs-id1165135255384″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165135255384″]
Нет, потому что он не проходит тест горизонтальной линии.
[/скрытый ответ]
Определение основных функций инструментария
В этом тексте мы будем изучать функции — формы их графиков, их уникальные характеристики, их алгебраические формулы и способы решения с ними задач.При обучении чтению мы начинаем с алфавита. При обучении арифметике мы начинаем с чисел. При работе с функциями также полезно иметь базовый набор элементов стандартного блока. Мы называем их «инструментальными функциями», которые образуют набор основных именованных функций, для которых мы знаем график, формулу и специальные свойства. Некоторые из этих функций запрограммированы на отдельные кнопки на многих калькуляторах. Для этих определений мы будем использовать как входную переменную, так и выходную переменную.
Некоторые из этих функций запрограммированы на отдельные кнопки на многих калькуляторах. Для этих определений мы будем использовать как входную переменную, так и выходную переменную.
Мы будем часто встречаться с этими инструментальными функциями, комбинациями инструментальных функций, их графиками и преобразованиями в этой книге. Будет очень полезно, если мы сможем быстро распознать эти функции инструментария и их функции по имени, формуле, графику и основным свойствам таблицы. Графики и примерные табличные значения прилагаются к каждой функции, показанной на (рис.).
Ключевые понятия
- Отношение представляет собой набор упорядоченных пар. Функция — это особый тип отношения, в котором каждое значение домена или входные данные приводят ровно к одному значению диапазона или выходным данным.См. (Рисунок) и (Рисунок).
- Обозначение функции — это сокращенный метод для связи ввода с выводом в форме См. (Рисунок) и (Рисунок).
- В табличной форме функция может быть представлена строками или столбцами, которые относятся к входным и выходным значениям.
 См. (Рисунок).
См. (Рисунок). - Чтобы оценить функцию, мы определяем выходное значение для соответствующего входного значения. Алгебраические формы функции можно вычислить, заменив входную переменную заданным значением. См. (Рисунок) и (Рисунок).
- Чтобы найти определенное значение функции, мы определяем входные значения, которые дают определенное выходное значение. См. (Рисунок).
- Алгебраическую форму функции можно записать из уравнения. См. (Рисунок) и (Рисунок).
- Входные и выходные значения функции можно определить по таблице. См. (Рисунок).
- Связывание входных значений с выходными значениями на графике — это еще один способ оценки функции. См. (Рисунок).
- Функция является однозначной, если каждое выходное значение соответствует только одному входному значению.См. (Рисунок).
- График представляет собой функцию, если любая вертикальная линия, проведенная на графике, пересекает график не более чем в одной точке. См. (Рисунок).
- График взаимно однозначной функции проходит тест горизонтальной линии.
 См. (Рисунок).
См. (Рисунок).
Раздел Упражнения
Устный
В чем разница между отношением и функцией?
[reveal-answer q=»fs-id1165137667225″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165137667225″]
Отношение представляет собой набор упорядоченных пар.Функция — это особый вид отношения, в котором никакие две упорядоченные пары не имеют одинаковых первых координат.
[/скрытый ответ]
В чем разница между вводом и выводом функции?
Почему тест вертикальной линии говорит нам, представляет ли график отношения функцию?
[reveal-answer q=»fs-id1165134118515″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165134118515″]
Когда вертикальная линия пересекает график отношения более одного раза, это означает, что для данного входа существует более одного выхода.При любом конкретном входном значении может быть только один выход, если отношение должно быть функцией.
[/скрытый ответ]
Как определить, является ли отношение однозначной функцией?
Почему тест горизонтальной линии говорит нам, является ли график функции взаимно однозначным?
[reveal-answer q=»fs-id1165137679053″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165137679053″]
Когда горизонтальная линия пересекает график функции более одного раза, это означает, что для данного выхода имеется более одного входа. Функция является однозначной, если каждый выход соответствует только одному входу.
Функция является однозначной, если каждый выход соответствует только одному входу.
[/скрытый ответ]
Алгебраический
В следующих упражнениях определите, представляет ли отношение функцию.
[reveal-answer q=»fs-id1165135318977″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165135318977″]
функция
[/скрытый ответ]
Для следующих упражнений определите, представляет ли отношение функцию
[reveal-answer q=»fs-id1165137942475″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165137942475″]
функция
[/скрытый ответ]
[reveal-answer q=»fs-id1165135675187″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165135675187″]
функция
[/скрытый ответ]
[reveal-answer q=»fs-id1165137679348″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165137679348″]
функция
[/скрытый ответ]
[reveal-answer q=»fs-id1165135581209″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165135581209″]
функция
[/скрытый ответ]
[reveal-answer q=»fs-id1165134042765″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165134042765″]
функция
[/скрытый ответ]
[reveal-answer q=»fs-id1165135434851″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165135434851″]
функция
[/скрытый ответ]
[reveal-answer q=»fs-id1165137849364″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165137849364″]
функция
[/скрытый ответ]
[reveal-answer q=»fs-id1165135527680″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165135527680″]
функция
[/скрытый ответ]
[reveal-answer q=»fs-id1165137629243″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165137629243″]
не функция
[/скрытый ответ]
Для следующих упражнений оцените функцию при указанных значениях
[reveal-answer q=»fs-id1165137409631″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165137409631″]
[/скрытый ответ]
[reveal-answer q=»fs-id1165134151868″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165134151868″]
[латекс]\sqrt{2-a-h}+5[/латекс]
[/скрытый ответ]
[reveal-answer q=»fs-id1165135357153″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165135357153″]
[/скрытый ответ]
Учитывая функции упрощения
Учитывая функции упрощения
[reveal-answer q=»fs-id1165134284461″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165134284461″]
[/скрытый ответ]
Учитывая функцию
- Оценка
- Решить
Учитывая функцию
- Оценка
- Решить
Учитывая функцию
- Оценка
- Решить
Графический
В следующих упражнениях используйте тест вертикальной линии, чтобы определить, какие графики показывают отношения, которые являются функциями.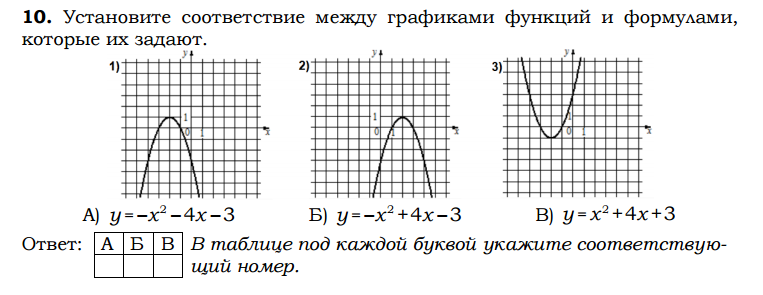
[скрытый ответ = ”fs-id1165135332505″]
не функция
[/скрытый ответ]
[reveal-answer q=»fs-id1165137597406″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165137597406″]
функция
[/скрытый ответ]
[reveal-answer q=»fs-id1165137399700″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165137399700″]
функция
[/скрытый ответ]
[reveal-answer q=»fs-id11651351«]Показать решение[/reveal-answer][скрытый ответ = ”fs-id11651351″]
функция
[/скрытый ответ]
[reveal-answer q=»fs-id11651379″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137
9″]
функция
[/скрытый ответ]
[reveal-answer q=»fs-id1165134240963″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165134240963″]
функция
[/скрытый ответ]
Учитывая следующий график,
- Оценка
- Найдите
Учитывая следующий график,
- Оценка
- Найдите
В следующих упражнениях определите, является ли данный график однозначной функцией.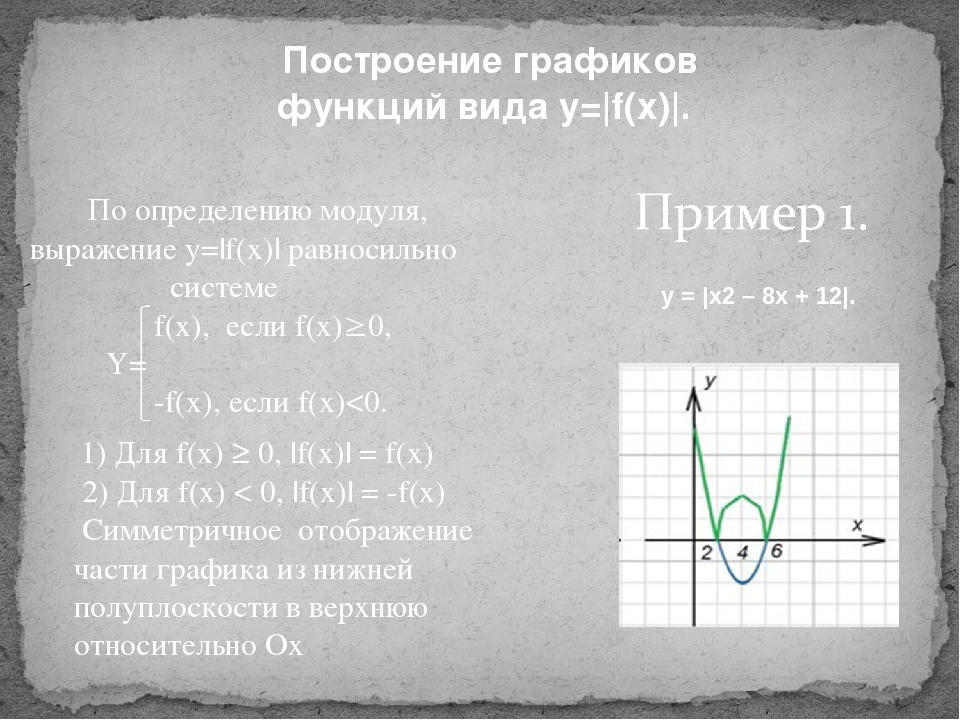
[скрытый ответ = ”fs-id1165133085670″]
не является функцией, поэтому это также не функция один к одному
[/скрытый ответ]
[reveal-answer q=»fs-id1165137583859″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165137583859″]
Функция «один к одному»
[/скрытый ответ]
[reveal-answer q=»fs-id1165135342197″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165135342197″] Функция
, но не один к одному
[/скрытый ответ]
Цифровой
В следующих упражнениях определите, представляет ли отношение функцию.
[reveal-answer q=»fs-id1165135381334″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165135381334″]
функция
[/скрытый ответ]
Для следующих упражнений определите, представляет ли отношение, представленное в виде таблицы, функцию
[скрытый ответ = ”fs-id1165137771736″]
функция
[/скрытый ответ]
| 5 | 10 | 15 | |
| 3 | 8 | 8 |
| 5 | 10 | 10 | |
| 3 | 8 | 14 |
[скрытый ответ = ”fs-id1165135641696″]
не функция
[/скрытый ответ]
Для следующих упражнений используйте функцию, представленную на (Рисунок).
| 0 | 74 |
| 1 | 28 |
| 2 | 1 |
| 3 | 53 |
| 4 | 56 |
| 5 | 3 |
| 6 | 36 |
| 7 | 45 |
| 8 | 14 |
| 9 | 47 |
Оценка
Решить
[reveal-answer q=»fs-id1165137832462″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165137832462″]
[/скрытый ответ]
Для следующих упражнений оцените функцию по значениям и
[reveal-answer q=»fs-id11651351[скрытый ответ = ”fs-id11651351
[/скрытый ответ]
[reveal-answer q=»fs-id1165137755505″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165137755505″]
[/скрытый ответ]
[reveal-answer q=»fs-id1165137770304″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165137770304″]
[/скрытый ответ]
Для следующих упражнений оцените выражения, заданные функции и
[reveal-answer q=»fs-id1165134373506″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165134373506″]
20
[/скрытый ответ]
Технология
Для следующих упражнений используйте графическое изображение в данном смотровом окне.Определите соответствующий диапазон для каждого окна просмотра. Покажите каждый график.
[reveal-answer q=»fs-id1165137809996″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165137809996″]
[/скрытый ответ]
Для следующих упражнений используйте графическое изображение в данном смотровом окне. Определите соответствующий диапазон для каждого окна просмотра. Покажите каждый график.
[reveal-answer q=»fs-id1165135634141″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165135634141″]
[/скрытый ответ]
[reveal-answer q=»fs-id1165137833875″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165137833875″]
[/скрытый ответ]
Для следующих упражнений используйте графическое изображение в данном смотровом окне.Определите соответствующий диапазон для каждого окна просмотра. Покажите каждый график.
[reveal-answer q=»fs-id1165135344910″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165135344910″]
[/скрытый ответ]
Для следующих упражнений постройте график в заданном окне просмотра. Определите соответствующий диапазон для каждого окна просмотра. Покажите каждый график.
[reveal-answer q=»fs-id1165137- 4″]Показать решение[/reveal-answer]
- http://www.baseball-almanac.com/legendary/lisn100.shtml. По состоянию на 24 марта 2014 г.
- зависимая переменная
- выходная переменная
- домен
- набор всех возможных входных значений для отношения
- функция
- отношение, в котором каждое входное значение дает уникальное выходное значение
- тест горизонтальной линии
- метод проверки того, является ли функция взаимно однозначной, путем определения того, пересекает ли какая-либо горизонтальная линия график более одного раза
- независимая переменная
- входная переменная
- ввод
- каждый объект или значение в домене, которое связано с другим объектом или значением отношением, известным как функция
- Функция «один к одному»
- функция, для которой каждое значение вывода связано с уникальным входным значением
- выход
- каждый объект или значение в диапазоне, который создается при вводе входного значения в функцию
- диапазон
- набор выходных значений, которые являются результатом входных значений в отношении
- отношение
- комплект заказанных пар
- проверка вертикальной линии
- метод проверки того, представляет ли график функцию, путем определения того, пересекает ли график вертикальная линия не более одного раза
[скрытый ответ = ”fs-id1165137
- 4″]
[/скрытый ответ]
[reveal-answer q=»fs-id1165137686659″]Показать решение[/reveal-answer][скрытый ответ = ”fs-id1165137686659″]
[/скрытый ответ]
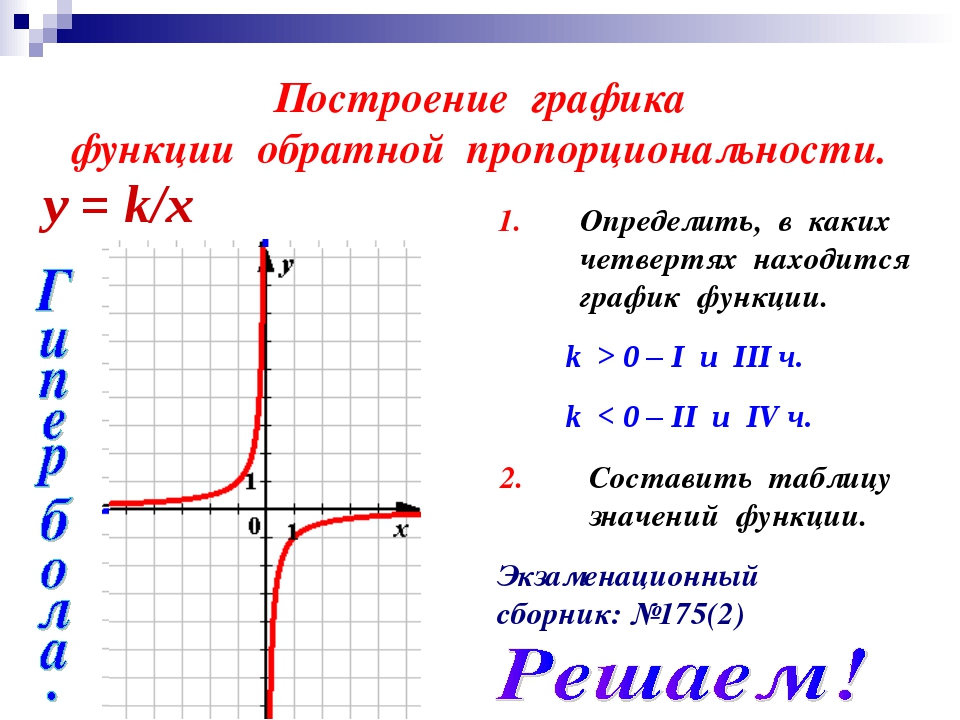


 На каком из рисунков изображен ее график? (Рисунок 3)
На каком из рисунков изображен ее график? (Рисунок 3)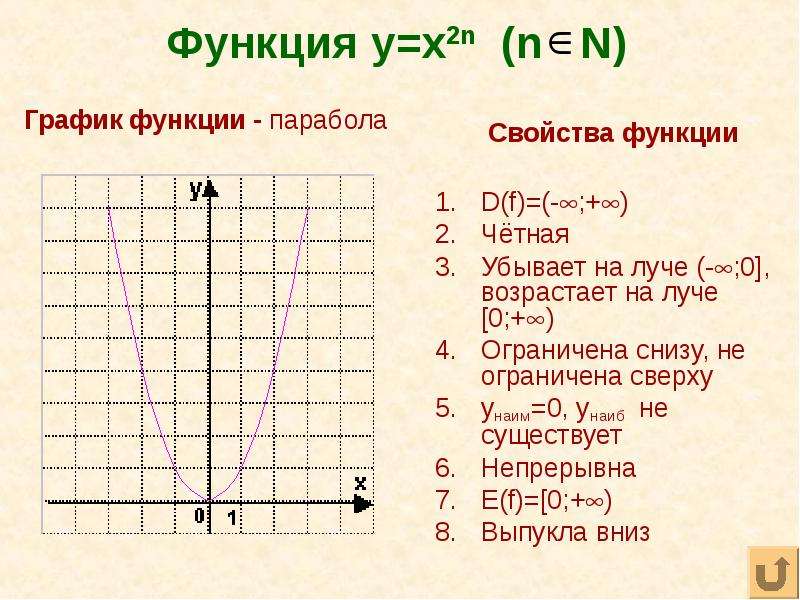
 Вправо.
Вправо. 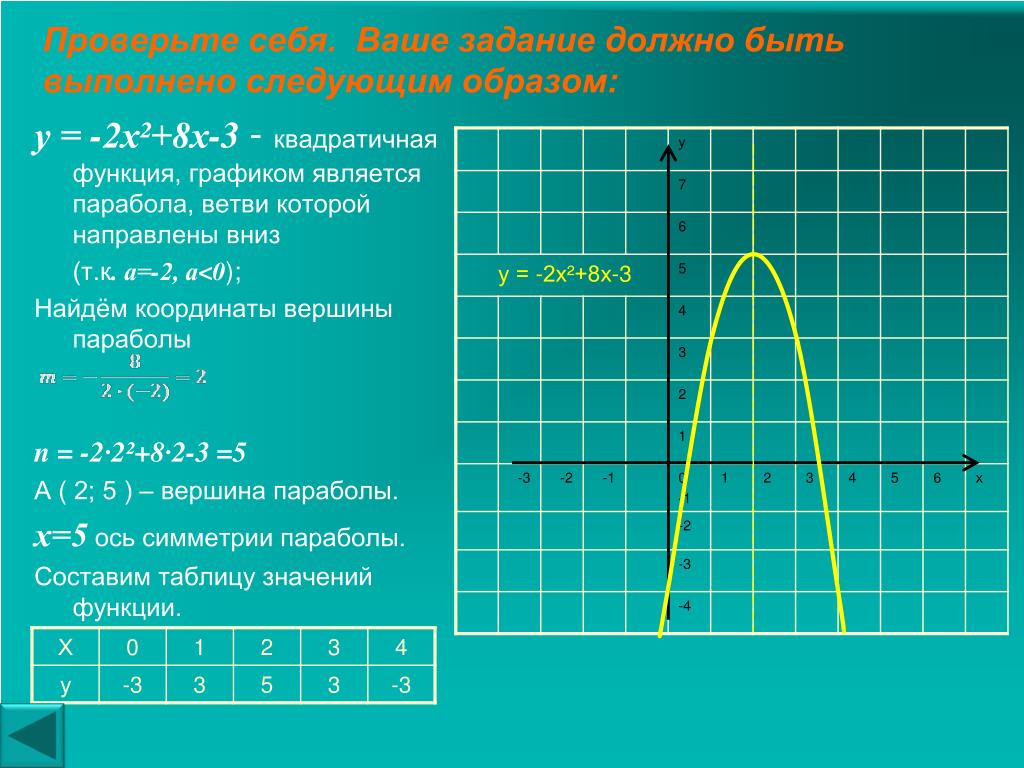 Найдите с помощью графика:
Найдите с помощью графика:


 После изучения ряда пар входных и выходных данных пользователь пытается сделать вывод и применить операцию-загадку, чтобы предсказать результат для пары сгенерированных машиной входных данных. Пример операции-загадки в этой машине: a * (b 1).
После изучения ряда пар входных и выходных данных пользователь пытается сделать вывод и применить операцию-загадку, чтобы предсказать результат для пары сгенерированных машиной входных данных. Пример операции-загадки в этой машине: a * (b 1).
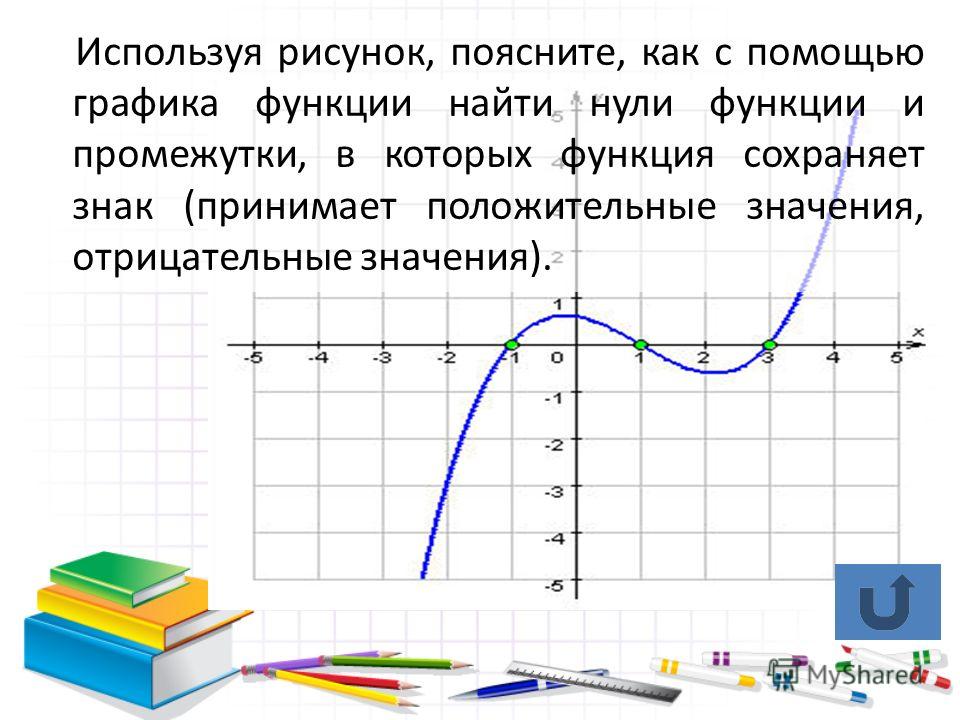
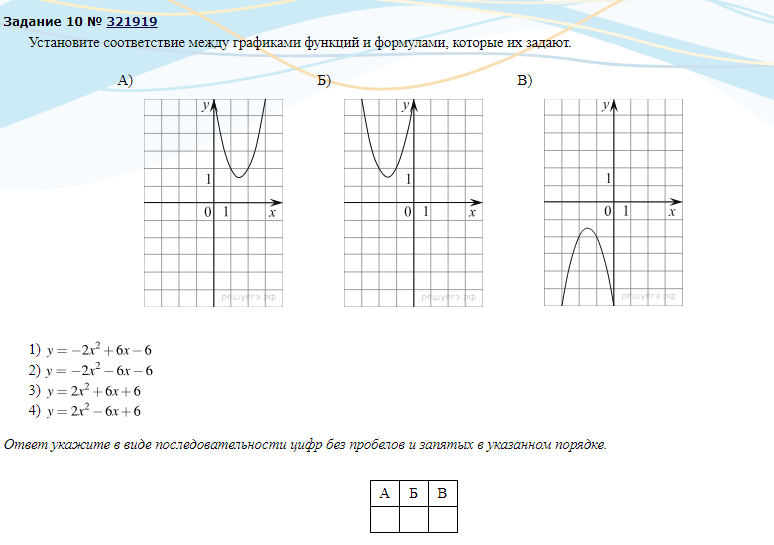 поезда по мере его роста.Когда они составляют таблицу данных, могут ли они найти правило или правила функции, описывающие взаимосвязь между количеством повторений и периметром поезда?
поезда по мере его роста.Когда они составляют таблицу данных, могут ли они найти правило или правила функции, описывающие взаимосвязь между количеством повторений и периметром поезда?

 Она преподает математику в 4 и 5 классах Вашингтонской международной школы.
Она преподает математику в 4 и 5 классах Вашингтонской международной школы.
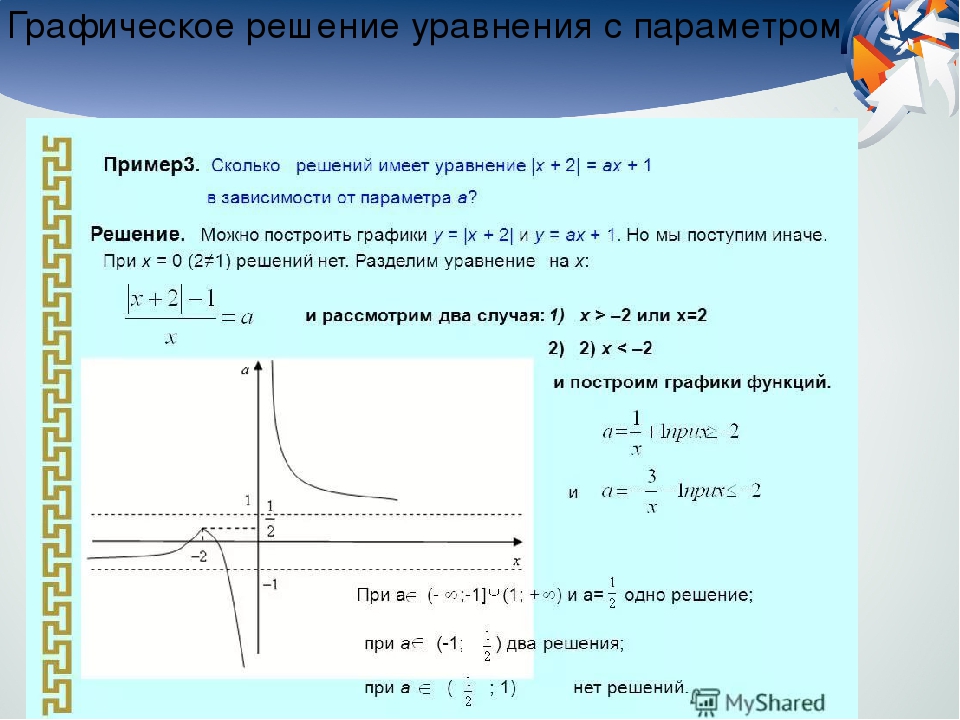 Мы уже нашли это
f(a+h)=a2+2ah+h3+3a+3h−4f(a+h)=a2+2ah+h3+3a+3h−4
Мы уже нашли это
f(a+h)=a2+2ah+h3+3a+3h−4f(a+h)=a2+2ah+h3+3a+3h−4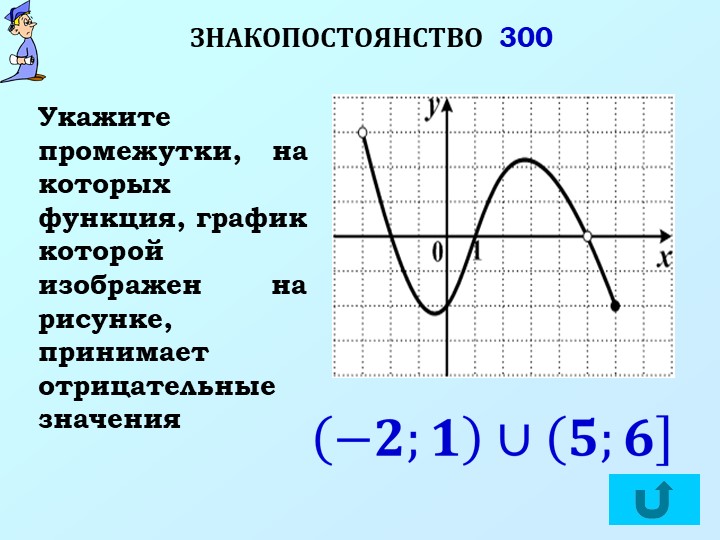


 p(−3).
p(−3).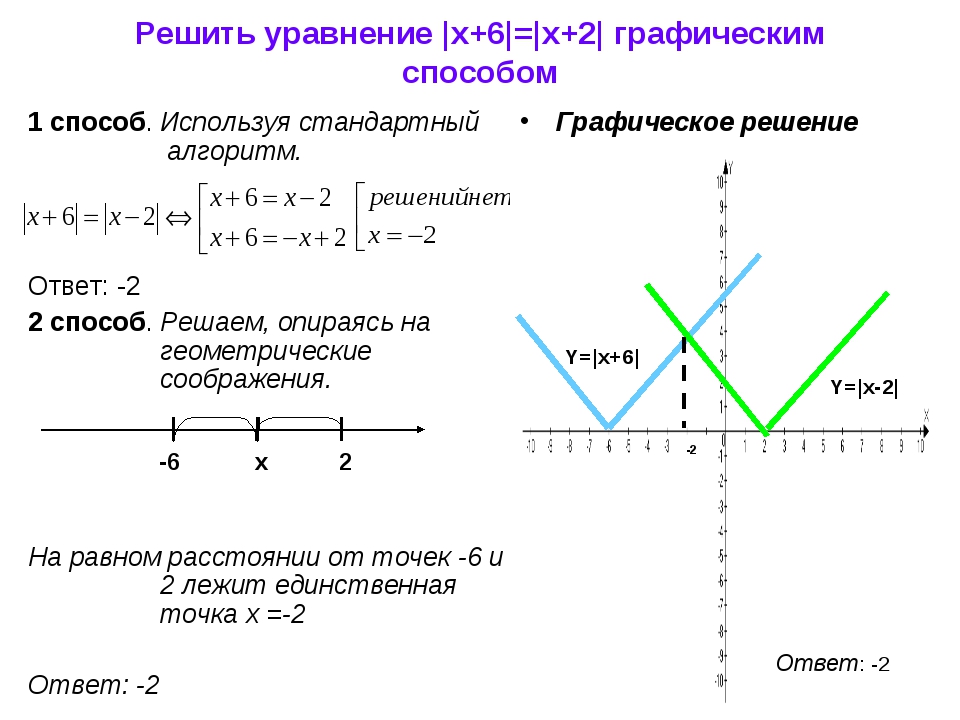 f(0).
f(0). Тогда выходные значения являются ценами.
Тогда выходные значения являются ценами.
 См. (Рисунок).
См. (Рисунок). См. (Рисунок).
См. (Рисунок).