Координаты вектора в прямоугольной системе координат: Вектор в системе координат — урок. Геометрия, 9 класс. — Детская игровая комната «Волшебный лес»

Posted on 29.06.197207.01.2022 by alexxlab

Содержание

Вектор в системе координат — урок. Геометрия, 9 класс.

Вспомним, что при умножении вектора на число k≠0 мы получаем два коллинеарных (параллельных) вектора, которые или сонаправлены, если k>0, или противоположно направлены, если k<0. Длины векторов различаются \(k\) раз.

Справедливо и обратное суждение.

Если ненулевые векторы коллинеарны, то обязательно можно найти число k≠0 так, что b→=k⋅a→.

Для неколлинеарных векторов справедливо суждение, что каждый вектор на плоскости можно представить в виде c→=k⋅a→+m⋅b→. Говорят, что вектор c→ разложен по векторам a→ и b→, а числа \(k\) и \(m\) называют коэффициентами разложения.

Это справедливо для любого вектора на плоскости, причём коэффициенты определяются единственным образом.

Выберем два не коллинеарных вектора на осях системы координат. Пусть длина каждого из них будет равна единичному отрезку в этой системе координат. Эти векторы называют координатными векторами и обозначают i→ и j→.

Если от начала координат отложить вектор a→, то его можно разложить по векторам i→ и j→ следующим образом: a→=3⋅i→+2⋅j→.

В этом разложении коэффициенты координатных векторов называют координатами вектора a→.

Это записывают как a→3;2.

Любой вектор, который равен с вектором a→, можно переместить и отложить от начала координат. Следовательно, можем сделать вывод.

Равные векторы имеют равные координаты.

Но в то же время в координатной системе можно переместить векторы i→ и j→, таким образом определить координаты векторов независимо от их места расположения в координатной системе.

Легко понять, что разница между абсциссами (координатами x) конечной и начальной точки вектора и есть абсцисса вектора, а разница между ординатами (координатами y) конечной и начальной точки вектора есть ордината вектора.

Связь между координатами противоположных векторов следует из того, что, если умножить вектор на \(-1\), результатом будет противоположный вектор.

У противоположных векторов противоположные координаты.

Важно понять ещё несколько интересных связей между координатами векторов одинаковой длины.

Координаты точки и вектора — урок. Геометрия, 11 класс.

Координаты точки

Три попарно перпендикулярные прямые с выбранными направлениями и единицей измерения образуют систему координат в пространстве. Точка пересечения всех прямых является началом системы координат.

Оси координат \(Ox\), \(Oy\) и \(Oz\) называются соответственно: \(Ox\) — ось абсцисс, \(Oy\) — ось ординат, \(Oz\) — ось аппликат.

Через две пересекающиеся прямые можно провести плоскость. Получаем три координатные плоскости: \((Oxy)\), \((Oyz)\) и \((Oxz)\).

Положение точки \(A\) в пространстве определяется тремя координатами: \(x\), \(y\) и \(z\).

Координата \(x\) называется абсциссой точки \(A\), координата \(y\) — ординатой точки \(A\), координата \(z\) — аппликатой точки \(A\).

Записываются так: \(A(x; y; z)\).

Если точка находится на оси \(Ox\), то её координаты \(X(x; 0; 0)\).

Если точка находится на оси \(Oy\), то её координаты \(Y(0; y; 0)\).

Если точка находится на оси \(Oz\), то её координаты \(Z(0; 0; z)\).

Если точка находится в плоскости \(Oxy\), то её координаты A1x;y;0.

Если точка находится в плоскости \(Oyz\), то её координаты A20;y;z.

Если точка находится в плоскости \(Oxz\), то её координаты A3x;0;z.

Координаты вектора

Если в системе координат от начальной точки отложить единичные векторы i→, j→ и k→, то можно определить прямоугольный базис. Любой вектор можно разложить по единичным векторам и представить в виде OA→=x⋅i→+y⋅j→+z⋅k→.

Коэффициенты \(x\), \(y\) и \(z\) определяются одним-единственным образом и называются координатами вектора.

Записываются так: OA→x;y;z.

Рассмотрим правила о том, как с помощью координат записать:

— координаты суммы векторов, если даны координаты векторов:

a→x1;y1;z1, b→x2;y2;z2, a→+b→x1+x2;y1+y2;z1+z2;

— координаты разности векторов, если даны координаты векторов:
a→−b→x1−x2;y1−y2;z1−z2;

— координаты произведения вектора на число, если даны координаты вектора:

n⋅a→n⋅x1;n⋅y1;n⋅z1;

— длину вектора:

a→=x12+y12+z12;

— координаты вектора, если даны координаты начальной и конечной точек вектора:

AxA;yA;zA, BxB;yB;zB, AB→xB−xA;yB−yA;zB−zA;

— расстояние между двумя точками, если даны координаты точек:

AB→=AB=xB−xA2+yB−yA2+zB−zA2;

— координаты серединной точки отрезка, если даны координаты начальной и конечной точек отрезка:

xC=xA+xB2;yC=yA+yB2;zC=zA+zB2.

Прямоугольная система координат в пространстве — Математика

Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление (оно обозначается стрелкой) и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве.
Прямые с выбранными на них направлениями называются осями координат, а их общая точка — началом координат. Она обозначается обычно буквой О.
Оси координат обозначаются так: Ох, Оу, Оz — и имеют названия: ось абсцисс, ось ординат, ось аппликат. Вся система координат обозначается Охуz.
Плоскости, проходящие соответственно через оси координат Ох и Оу, Оу и Оz, Оz и Ох, называются координатными плоскостями и обозначаются Оху, Оуz, Оzх.
Точка О разделяет каждую из осей координат на два луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч отрицательной полуосью.

В прямоугольной системе координат каждой точке А пространства сопоставляется тройка чисел, которые называются ее
координатами. Они определяются аналогично координатам точек на плоскости.

Проведем через точку А три плоскости, перпендикулярные к осям координат, и обозначим через А₁, А₂ и А_3.Точки пересечения этих плоскостей соответственно с осями абсцисс, ординат и аппликат. Первая координата точки А (она называется абсциссой и обозначается обычно буквой х) определяется так: х = ОА₁, если А₁точка положительной полуоси: х = — ОА₁, если А₁ точка отрицательной полуоси: х = 0, если А₁ совпадает с точкой О. Аналогично с помощью точки А₂определяется вторая координата (ордината) y точки А, а с помощью точки А₃ третья координата (аппликата) z точки А.

Координаты точки А записываются в скобках после обозначения точки: А (х; у; z), причем первой указывают абсциссу, второй ординату, третьей — аппликату.

Если точка А (х; у; z) лежит на координатной плоскости или на оси координат, то некоторые ее координаты равны нулю.

Примеры решения заданий

Пример 2.

Задания по теме: «Прямоугольная система координат в пространстве»
Задание № 1
Скачай задание из Приложений к странице. Распечатай, выполни предложенные задания, отсканируй и отошли учителю

Задание № 2
Скачай задание из Приложений к странице. Распечатай, выполни предложенные задания, отсканируй и отошли учителю

Задание № 3
Скачай задание из Приложений к странице. Распечатай, выполни предложенные задания, отсканируй и отошли учителю

Прямоугольная система координат. Координаты вектора

1.

Прямоугольная система координат в пространстве Если через точку
пространства проведены три
попарно перпендикулярные
прямые, на каждой из них
выбрано направление и
выбрана единица измерения
отрезков, то говорят, что
задана прямоугольная
система координат в
пространстве
Прямые с выбранными на них
направлениями называются осями
координат, а их общая точка —
началом координат. Она
обозначается обычно буквой О.
Оси координат имеют следующие
обозначения и названия:
Ох — ось абсцисс,
Оу — ось ординат,
Оz — ось аппликат.
Вся система координат обозначается
Охуz.
Плоскости, проходящие соответственно
через оси координат
Ох и Оу, Оу и Оz, Оz и Ох,
называются
координатными плоскостями
и обозначаются Оху, Оуz, Оzх.
Точка О разделяет
каждую из осей
координат на два луча.
Луч, направление

которого совпадает с
направлением оси,
называется
положительной
полуосью, а другой
луч отрицательной
полуосью.

В прямоугольной
системе координат
каждой точке М
пространства
сопоставляется
тройка чисел,
которые
называются ее
координатами.
У точки М(x;y;z)
первая координата x- абсцисса
вторая координата y- ордината
третья координата z- аппликата.
Если точка М(x;y;z) лежит на координатной
плоскости или на оси координат , то
некоторые её координаты равны 0.
На рисунке
изображены
семь точек
А (9; 5; 10),
В (4; —3; 6),
С (9; 0; 0),
D (4; 0; 5),
Е (0; 3; 0),
F (0; 0; -3),
O (0;0;0)-начало
координат

9. Координаты вектора

Зададим в пространстве
прямоугольную систему
координат Oxyz.
На каждой из положительных
полуосей отложим от начала

координат единичный вектор
(длина равна 1).
Векторы
координатные векторы .
Координатные векторы
не компланарны.

11. Любой вектор можно разложить по координатным векторам, т.

2\), откуда получаем требуемое равенство.

Утверждение

Если в прямоугольной системе координат точка \(M\) – середина отрезка \(PQ\), где \(P(x_1;y_1), \ Q(x_2;y_2)\), то

\[M\left(\dfrac{x_1 + x_2}{2}; \dfrac{y_1 + y_2}{2}\right)\]

Доказательство

Пусть \(M(a;b)\).

1) Пусть \(PQ\parallel Oy \Rightarrow x_1=x_2=a\). Значит, \(a=\dfrac{x_1+x_2}2=\dfrac{a+a}2\) – верно.

Т.к. \(PM=MQ\), следовательно, \(|y_2-b|=|y_1-b| \Rightarrow y_2-b=y_1-b\) или \(y_2-b=b-y_1\), что равносильно \(y_2=y_1\) или \(b=\dfrac{y_1+y_2}2\). Первое равенство невозможно (т.к. тогда точки \(P\) и \(Q\) совпадают).

2) Случай \(PQ\parallel Ox \Rightarrow y_1=y_2=b\) доказывается аналогично.

3) \(x_1\ne x_2, y_1\ne y_2\).

Тогда \(Ma=b\) – средняя линия трапеции \(x_1PQx_2\), следовательно, равна полусумме оснований, то есть \(b=\dfrac{y_1+y_2}2\).

Аналогично \(a=\dfrac{x_1+x_2}2\).

\[{\Large{\text{Векторы на координатной плоскости}}}\]

Лемма

Если векторы \(\overrightarrow a\) и \(\overrightarrow b\) коллинеарны, то существует такое число \(\lambda\ne 0\), что \(\overrightarrow a=\lambda\overrightarrow b\).

Доказательство

1) Если \(\overrightarrow a\uparrow \uparrow \overrightarrow b\).

Рассмотрим вектор \(\dfrac1{|\overrightarrow a|}\overrightarrow a\). Данный вектор сонавправлен с \(\overrightarrow a\), а его длина равна \(1\). Тогда вектор \(\dfrac{|\overrightarrow b|}{|\overrightarrow a|}\overrightarrow a\) также сонаправлен с \(\overrightarrow a\), но его длина равна \(|\overrightarrow b|\). То есть равен вектору \(\overrightarrow b\).

2) Если \(\overrightarrow a\uparrow \downarrow \overrightarrow b\).

Аналогично доказывается, что \(\overrightarrow b=-\dfrac{|\overrightarrow b|}{|\overrightarrow a|}\overrightarrow a\).

Определение

Если вектор \(\overrightarrow p\) представлен как линейная комбинация двух векторов: \(\overrightarrow p=\alpha\overrightarrow a+\beta \overrightarrow b\), то говорят, что вектор \(\overrightarrow p\) разложен по векторам \(\overrightarrow a\) и \(\overrightarrow b\).

\(\alpha, \beta\) – коэффициенты разложения.

Пусть векторы \(\overrightarrow i\), \(\overrightarrow j\) – векторы, длины которых равны \(1\), а направление совпадает с направлением осей \(Ox\) и \(Oy\) соответственно. Такие векторы называются

единичными векторами.

Тогда если \(\overrightarrow p=a\overrightarrow i+b\overrightarrow j\), то \(\{a;b\}\) – координаты вектора \(\overrightarrow p\).

Свойства координат вектора

1. Равные векторы имеют равные координаты.

2. Координаты суммы векторов равны сумме координат каждого вектора: если \(\overrightarrow a\{x_1;y_1\}, \ \overrightarrow b\{x_2;y_2\}\), то \(\overrightarrow a+\overrightarrow b=\{x_1+x_2;y_1+y_2\}\).

3. Каждая координата произведения вектора на число равна произведению соответствующей координаты данного вектора на это число: \(\overrightarrow a\{x;y\}, \ \lambda \) – число, то \(\lambda\overrightarrow a\{\lambda x;\lambda y\}\). 2}\).

\[{\Large{\text{Скалярное произведение векторов}}}\]

Определение

Пусть от одной точки отложены два вектора \(\overrightarrow {AB}\) и \(\overrightarrow {AC}\). Тогда угол между этими векторами – это угол \(\angle BAC\), не превышающий развернутого угла.

Скалярное произведение векторов \(\overrightarrow a\) и \(\overrightarrow b\) – это число, равное произведению длин этих векторов на косинус угла между ними.
Обозначение: \(\overrightarrow a\cdot \overrightarrow b\) или \((\overrightarrow a, \overrightarrow b)\). \[(\overrightarrow a, \overrightarrow b)=|\overrightarrow a|\cdot |\overrightarrow b|\cdot \cos\widehat{(\overrightarrow a, \overrightarrow b)}\]

Следствия

1. Если ненулевые векторы взаимно перпендикулярны, то косинус угла между ними равен нулю, следовательно, и их скалярное произведение равно нулю.

2. Если угол между ненулевыми векторами острый, то скалярное произведение положительно. 2=0 \Leftrightarrow |\overrightarrow a|=0\).

2. Переместительный закон: \(\overrightarrow a\cdot \overrightarrow b=\overrightarrow b\cdot \overrightarrow a\).

3. Распределительный закон: \(\overrightarrow a \cdot (\overrightarrow b+\overrightarrow c)=\overrightarrow a\cdot \overrightarrow b+\overrightarrow a\cdot \overrightarrow c\).

4. Сочетательный закон: \((\lambda\overrightarrow a)\cdot \overrightarrow b=\lambda (\overrightarrow a\cdot \overrightarrow b)\).

Лекция 7 декартова система координат

Тема 3. Прямоугольная система координат.

Лекция 7. Декартова система координат.

Основные вопросы

1. Проекция вектора на ось.

2. Теоремы о проекциях.

3. Декартова система координат в пространстве.

4. Координаты точки и вектора в прямоугольной системе координат.

1. Проекция вектора на ось

Осью называется прямая, направление которой задано единичным векто-ром . Пусть даны вектор и ось ℓ (рис. 2.1). Опустим из точек А и В перпендикуляры на ось ℓ и обозначим их основания соответственно через А₁ и В₁ .

Определение 1. Вектор , началом которого служит проек-ция начала вектора , а концом – проекция его конца на прямую ℓ , называется проекцией вектора на прямую ℓ (рис. 2.1).

Рис. 2.1. Проекция вектора на прямую и ось

Определение 2. Проекцией вектора на ось ℓ называется число , обоз-начаемое , где знак «+» берется в случае, когда направление вектора совпадает с направ-лением оси ℓ , а знак «-» , когда их направления противоположны.

Углом вектора (или равного с ним ) с осьюℓ называется углом φ , на который нужно повернуть кратчайшим образом ось ℓ около точки А₁ до совме-щения ее с вектором . Произвольный вектор об-разует с осью угол φ, меняющийся от 0 до π .

2. Теорема о проекциях.

Теорема 1. Проекция вектора на ось равна длине вектора, умноженной

на косинус угла между вектором и осью.

Теорема 2. При умножении вектора на число λ его проекция на ось умножается на то же число.

. (1)

Теорема 3. Проекция суммы векторов на ось равна сумме их проекций на ту же ось.

Из теорем 2 и 3 следует, что линейные операции над векторами приво-дят к соответствующим операциям над проекциями этих векторов на произвольную ось.

3. Декартова система координат в пространстве.

Определение 3. Декартовой системой координат в пространстве назы-вается совокупность точки 0 и базиса .

При этом различают аффинную и прямоугольную систему декартовых координат (Рене Декарт (1596-1650) – французский математик и философ).

В случае аффинной системы декартовых координат базисные векторы имеют произвольные направления, оставаясь некомпланарными.

При изучении последующих вопросов при решении задач векторной алгебры и аналитической геометрии будем пользоваться декартовой системой координат , когда базисные векторы попарно перпендикулярны и имеют длину, равную единице.

Базис, состоящий из взаимно перпендикулярных единичных векторов, называется ортонормированным базисом. Векторы ортонормированного ба-зиса в пространстве называются ортами и обозначаются , а на плос-кости – через . Это, так называемый, декартов базис .

Декартова система координат с ортонормированным базисом называется прямоугольной системой координат, которая может быть правой или левой (в дальнейшем будем использовать правую систему координат) (рис. 2.4). Обоз-начается обычно : 0xyz Z

M(x,y,z)

M₁

α β y Y

Рис.2.4. Правая прямоугольная система координат в пространстве

Точка 0 – начало координат. Ось 0Х – ось абсцисс, ось 0У – ось ординат, а ось 0Z – ось аппликат (различают их положительные и отрицательные по-луоси). Плоскости х0У, х0Z и У0Z называются координатными плоскостями.

4. Координаты точки и вектора.

Возьмем произвольную точку М пространства, она определит некоторый вектор . Вектор, начало которого совпадает с началом координат, а конец – с точкой М , называется радиус-вектором точки М по отношению к точке 0.

Известно, что любой вектор может быть разложен по базису выбранной системы координат, т.е. вектор однозначно представляется в виде:

Где X,Y,Z – координаты вектора , а — ортонормированный базис (X— абсцисса,Y – ордината, Z — аппликата ).

Иначе говоря, точке М сопоставляется упорядоченная тройка чисел, ко-торые являются координатами ее радиус-вектора боль-шие буквы. Наоборот, каждой упорядоченной тройке чисел х,у,z однозначно составляется точка пространства М(х,у,z) – малые буквы.

Определение 4. Координаты радиус-вектора точки М по отношению к

началу координат называются координатами точки М в выбранной системе координат. Точка М пространства обозначается : М(X,Y,Z) .

Отметим, что вектор является диагональю прямоугольного паралле-лепипеда. Вполне очевидно, что длина этой диагонали, а значит и модуль вектора определяется по следующей формуле

(3)

Если предположить, что вектор ₁ единичный, т.е. , и учесть, что его проекция на любую ось (0х,0у,0z) будет равна косинусу угла между вектором ₁ и соответствующей осью, то вектор ₁ раскладывается в декартовом базисе в виде , где — углы между вектором ₁ (а равно и ) и соответствующими осями координат 0х,0у,0z .

Следовательно, единичный вектор в координатах запишем так: (4)

Определение 5. Косинусы углов любого вектора с осями координат 0Х,0У,0Z называются направляющими косинусами этого вектора, которые определяют направление век-тора в пространстве.

Поскольку мы рассматриваем свободные векторы (т.е. такие векторы, которые без изменения длины и направления могут быть перенесены в лю-бую точку пространства, и в частности в начало координат), то любой век-тор, заданный в координатном пространстве 0х,у,z, может быть представлен в виде: (5)

Такое представление вектора называется его разложением по осям координат , или разложением по ортам .

Здесь X,Y,Z – проекции вектора на соответствующие оси координат (их чаще называют координатами вектора ; — орты этих осей). Так как с другой стороны

т.к. , то

(6)

Возводя в квадрат левую и правую части равенства (6) получим

(7) т.е. сумма квадратов направляющих косинусов любого вектора равна единице.

Пример 1. Найти длину вектора и его направля-ющие косинусы.

Решение . 1)

2) .

8

8. Декартова прямоугольная система координат в пространстве.

Три взаимно перпендикулярные оси в пространстве (координатные оси) с общим началом О и одинаковой масштабной единицей образуют декартову прямоугольную (кратко — прямоугольную) систему координат в пространстве. Оси упорядочены, т.е. указано, какая из осей считается первой (она называется осью абсцисс и обозначается Ох), какая — второй (ось ординат Оу) и какая -третьей (ось аппликат Oz).

Различают правую и левую системы декартовых прямоугольных координат (рис. 36, соответственно а, б). В этой книге принята правая система координат (будем называть ее основной.

Орты осей Ox, Oy, Oz обозначают соответственно . Так как векторы компланарны, то они образуют базис (см.п. 6), который называется декартовым прямоугольным базисом.

В силу результатов п. 6 каждый вектор может быть, и притом единственным способом, разложен по декартовому прямоугольному базису , т.е. для каждого вектора найдется, и притом единственная, тройка чисел , такая что справедливо равенство

Числа называются декартовыми прямоугольными( или прямоугольными) координатами вектора .

Рис.36

Запись ( ) означает, что вектор : имеет декартовы прямоугольные координаты

Выясним геометрический смысл чисел . Используя теоремы 2 и 1 о проекциях (см. п. 7), имеем

Аналогично .

Следовательно, числа в формуле (7) являются проекциями вектора на координатные оси Ox, Oy,Oz соответственно.

Если М — произвольная точка в пространстве, то радиусом-вектором точки М назовем вектор , имеющий своим началом

начало О заданной системы координат, а концом эту точку.

Определение. Декартовыми прямоугольными координатами точки М называются проекции ее радиуса-вектора на соответствующие координатные оси; проекция на первую координатную ось называется абсциссой точки М, на вторую — , на третью — аппликатой :

x = , у = , z = . Символ М(х; у; z) означает, что точка М имеет координаты х, у, z.

Координатные плоскости (плоскости, проходящие через пары координатных осей) делят все пространство на восемь частей, называемых октантами, которые нумеруются следующим образом: октант, лежащий над первой четвертью плоскости хОу, — I; лежащий под ней — V; соответственно октанты, лежащие над и под второй четвертью плоскости хОу, — II и VI; над и под третьей четвертью — III и VII; над и под четвертой четвертью — IV и VIII.

Каждому октанту соответствует определенная комбинация знаков координат:

Отметим, что каждой точке пространства соответствует одна упорядоченная тройка действительных чисел (х; у; z) (ее координат). Верно и обратное: каждой упорядоченной тройке действительных чисел (х; у; z) соответствует одна точка пространства. Это означает, что в пространстве положение произвольной точки М полностью определяется ее координатами х; у; z. имеем = (Если точка М лежит в плоскости хОу, то = )

Пусть заданы две точки М₁(х₁; у₁; z₁) и М₂(х₂; у₂; z₂).

Рассмотрим вектор .

Имеем = (рис. 37). Отсюда в силу теоремы 2 (см. п.6) получаем ( х₂— х₁; у₂— у₁; z₂—_{z₁ ).}

Итак, чтобы найти координаты некоторого вектора, достаточно из координат его конца вычесть одноименные координаты его начала.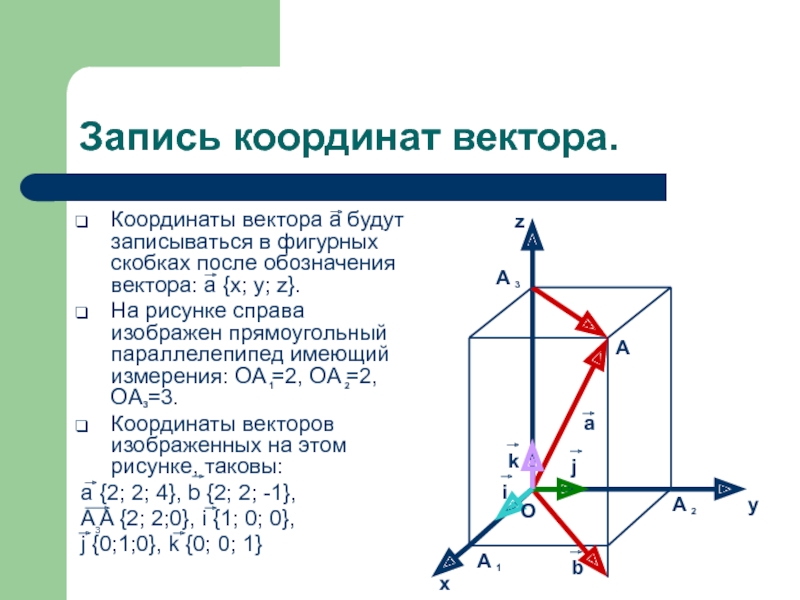

Пусть два ненулевых вектора

коллинеарны. В этом случае (см. п. 2) = ( — скаляр), что в силу следствия 2 из п. 7 равносильно трем равенствам

Это есть условие коллинеарности векторов.

Таким образом, векторы коллинеарны тогда и только тогда, когда их одноименные координаты пропорциональны.

Примечание. В равенстве (8) некоторые из знаменателей могут оказаться равными нулю. Напомним, что всякую пропорцию

понимаем в смысле равенства ad = be.

Так, например, равенства

Означают, что

Понятие вектора | Линейные операции над векторами | Понятие линейной зависимости векторов|

Линейная зависимость векторов на плоскости | Линейная зависимость векторов в пространстве

Базис на плоскости и в пространстве | Проекция вектора на ось и ее свойства | Декартова прямоугольная система координат в пространстве| Цилиндрические и сферические координаты| Главная

Прямоугольная система координат

Последующее обсуждение ограничено векторами в двумерной координатной плоскости, хотя концепции могут быть расширены и на более высокие измерения.

Если вектор сдвинут так, что его начальная точка находится в начале прямоугольной координатной плоскости, говорят, что он находится в стандартной позиции . Если вектор равен вектору и имеет начальную точку в начале координат, говорят, что он является стандартным вектором для . Другие названия стандартного вектора включают радиус-вектор и вектор положения (рис. 1).

Рисунок 1
Векторы, нарисованные на плоскости.

Вектор — это стандартный вектор для всех векторов на плоскости с тем же направлением и величиной, что и . Чтобы найти стандартный вектор для геометрического вектора в координатной плоскости, необходимо найти только координаты точки P , поскольку точка 0 находится в начале координат. Если координаты точки A ( x _A, y _A ) и координаты пункта B ( x _b, y _b), затем координаты точки P:

Пример 1: Если конечные точки вектора имеют координаты A (−2, −7) и B (3, 2), то каковы координаты точки P , которая является стандартным вектором и = (см. рис. 2)?

Рисунок 2
Рисунок для примера 1.

Если координаты точки P равны ( x , y ),

Алгебраический вектор — это упорядоченная пара действительных чисел.Алгебраический вектор, соответствующий стандартному геометрическому вектору, обозначается как ⟨ a, b ⟩, если конечная точка P имеет координаты (a, b) . Числа a и b называются компонентами вектора ⟨ a, b ⟩ (см. рис. 3 ).

Рисунок 3
Компоненты вектора.

Если a, b, c и d — все действительные числа такие, что a = c и b = d , то вектор v ⟨ a вектор u = ⟨ c, d ⟩ считаются равными.То есть алгебраические векторы с равными соответствующими компонентами равны. Если обе компоненты вектора равны нулю, говорят, что вектор является нулевым вектором . Величина вектора v = ⟨a, b⟩ равна .

Пример 2: Какова величина вектора u = ⟨3, −5⟩?

Сложение векторов определяется как сложение соответствующих компонентов векторов, то есть, если v = ⟨ a, b ⟩ и u = ⟨c, d⟩ , то v + + = ⟨a + c, b + d⟩ (рис. 4 ).

Рисунок 4
Добавление вектора.

Скалярное умножение определяется как умножение каждого компонента на константу, то есть, если v = ⟨a, b⟩ и q является константой, то q v

6 =

6 , b⟩ = ⟨qa, qb⟩ .

Пример 3: Если v = ⟨8, −2⟩ и w = ⟨3, 7⟩, то найти 5 v −2 w .

Единичный вектор — это вектор, величина которого равна 1. Единичный вектор v с тем же направлением, что и ненулевой вектор u , можно найти следующим образом:

Пример 4 : Найдите единичный вектор v с тем же направлением, что и вектор u , учитывая, что u = ⟨7, − 1⟩.

Два специальных единичных вектора, i = ⟨1, 0⟩ и j = ⟨0, 1⟩, могут использоваться для выражения любого вектора v = ⟨a, b⟩ .

Пример 5: Запишите u = ⟨5, 3⟩ с точки зрения единичных векторов i и j (рис. 5).

Рисунок 5
Чертеж для примера 5.

Векторы обладают алгебраическими свойствами, аналогичными свойствам действительных чисел (таблица 1).

Пример 6: Найти 4 u + 5 v , если u = 7 I — 3 J и V = -2 I + 5 J .

даны два вектора, u = ⟨a, b⟩ = a i I + B J и V = ⟨C, D⟩ = C I + d j , скалярное произведение , записанное как u · v , является скалярной величиной u ˙ v = ac + b ac + b Если u, v и w — векторы, а q — действительное число, то скалярные произведения обладают следующими свойствами:

Последнее свойство, u ˙ v = | и | | против | cos α можно использовать для нахождения угла между двумя ненулевыми векторами u и v . Если два вектора перпендикулярны друг другу и образуют угол 90°, говорят, что они ортогональны . Поскольку cos 90° = 0, скалярное произведение любых двух ортогональных векторов равно 0,

.
Пример 7: Учитывая, что u = ⟨ 5 , −3⟩ и u = ⟨6, 10⟩, покажите, что u и v являются ортогональными произведениями dot . u и v равно нулю.
Пример 8: Чему равен угол между u = ⟨5, −2⟩ и v = ⟨6, 11⟩?
Говорят, что объект находится в состоянии статического равновесия , если сумма всех векторов сил, действующих на объект, равна нулю.
Пример 9: Канатоходец весом 150 фунтов стоит ближе к одному концу веревки, чем к другому. Веревка меньшей длины отклоняется от горизонтали на 5°. Более длинная веревка отклоняется на 3°. Чему равно натяжение каждой части веревки?
Нарисуйте диаграмму силы со всеми тремя векторами силы в стандартном положении (рис. 6).
Рисунок 6
Рисунок для примера 9.
Сумма векторов силы должна быть равна нулю для каждого компонента.
Для компонента i : − | u |cos 5° + | против | cos 3° = 0
Для компонента j : | и | sin5° + |v| косинус 3 ° — 150 =
Решите эти два уравнения для | и | и | против |:
Подстановка значений синусов и косинусов:
Умножьте первое уравнение на 0,0872, а второе на 0,9962:
Сложите два уравнения и решите | против |:
Подставить и решить | и |:
2.4: Системы координат и компоненты вектора (часть 1)
Цели обучения
Описывать векторы в двух и трех измерениях с точки зрения их компонентов, используя единичные векторы вдоль осей.
Различать векторные компоненты вектора и скалярные компоненты вектора.
Объясните, как величина вектора определяется через компоненты вектора.
Определите угол направления вектора на плоскости.
Объясните связь между полярными координатами и декартовыми координатами на плоскости.
Векторы обычно описываются с точки зрения их компонентов в системе координат. Даже в повседневной жизни мы естественным образом пользуемся понятием ортогональных проекций в прямоугольной системе координат. Например, если вы спросите у кого-нибудь направление к определенному месту, вам, скорее всего, скажут пройти 40 км на восток и 30 км на север, чем 50 км в направлении 37° к северу от востока.
В прямоугольной (декартовой) системе координат xy на плоскости точка на плоскости описывается парой координат (x, y). Аналогичным образом вектор \(\vec{A}\) на плоскости описывается парой своих векторных координат. Координата x вектора \(\vec{A}\) называется его x-компонентой, а y-координата вектора \(\vec{A}\) называется его y-компонентой. Компонента x вектора — это вектор, обозначаемый \(\vec{A}_{x}\). Компонента вектора y — это вектор, обозначаемый \(\vec{A}_{y}\).В декартовой системе компоненты вектора x и y вектора являются ортогональными проекциями этого вектора на оси \(x\) и \(y\) соответственно. Таким образом, следуя правилу параллелограмма для сложения векторов, каждый вектор на декартовой плоскости может быть выражен как векторная сумма его векторных компонентов:
\[ \vec{A} = \vec{A}_{x} + \vec{A}_{y} \ldotp \label{2.10}\]
Как показано на рисунке \(\PageIndex{1}\), вектор \(\vec{A}\) является диагональю прямоугольника, где x-компонента \(\vec{A}_{x}\) равна сторона, параллельная оси x, и компонент y \(\vec{A}_{y}\) является стороной, параллельной оси y.Компонента вектора \(\vec{A}_{x}\) ортогональна компоненте вектора \(\vec{A}_{y}\).
Рисунок \(\PageIndex{1}\): Вектор \(\vec{A}\) на плоскости в декартовой системе координат представляет собой векторную сумму своих векторных x- и y-компонент.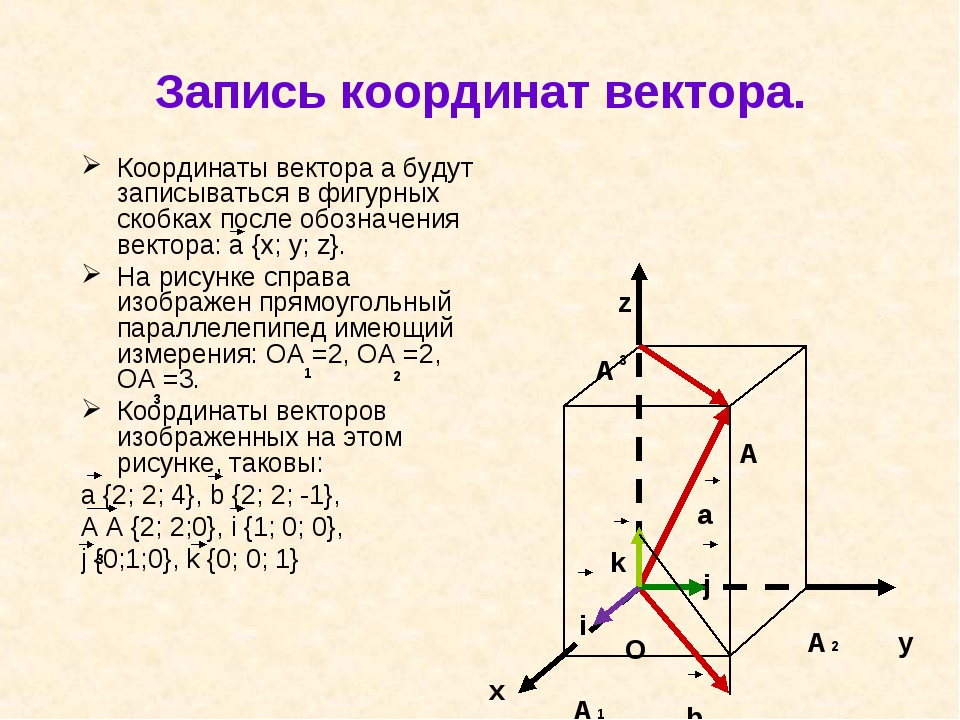 Компонента x-вектора \(\vec{A}_{x}\) является ортогональной проекцией вектора \(\vec{A}\) на ось x. Компонента вектора y \(\vec{A}_{y}\) является ортогональной проекцией вектора \(\vec{A}\) на ось y. Числа A _x и A _y, на которые умножаются единичные векторы, являются скалярными компонентами вектора.
Обычно принято обозначать положительное направление по оси x единичным вектором \(\hat{i}\), а положительное направление по оси y — единичным вектором \(\hat{j}\). Единичные векторы осей \(\hat{i}\) и \(\hat{j}\) определяют два ортогональных направления на плоскости. Как показано на рисунке \(\PageIndex{1}\), компоненты вектора x и y теперь можно записать в единицах векторов осей:
\[ \begin{cases} \vec{A}_{x} = A_{x} \hat{i} \\ \vec{A}_{y} = A_{y} \hat{j} \end {случаи} \метка{2.11}\]
Векторы \(\vec{A}_{x}\) и \(\vec{A}_{y}\), определяемые уравнением 2.11, являются векторными компонентами вектора \(\vec{A}\). Числа A _x и A _y, которые определяют компоненты вектора в уравнении \ref{2. 11}, являются скалярными компонентами вектора \(\vec{A}\). Комбинируя уравнение \ref{2.10} с уравнением \ref{2.11}, мы получаем компонентную форму вектора :
\[\vec{A} = A_{x} \hat{i} + A_{y} \hat{j} \ldotp \label{2.12}\]
Если мы знаем координаты \(b(x_b, y_b)\) начальной точки вектора (где b означает «начало») и координаты e(x _e, y _e) конца точки вектора (где e означает «конец»), мы можем получить скалярные компоненты вектора, просто вычитая координаты исходной точки из координат конечной точки:
\[ \begin{cases} A_{x} = x_{e} — x_{b} \\ A_{y} = y_{e} — y_{b} \ldotp \end{cases} \label{2.13}\]
Пример \(\PageIndex{1}\): смещение указателя мыши
Указатель мыши на мониторе компьютера в исходном положении находится в точке (6,0 см, 1,6 см) относительно нижнего левого угла. Если вы переместите указатель на значок, расположенный в точке (2,0 см, 4,5 см), каков будет вектор смещения указателя?
Стратегия
Начало системы координат xy — нижний левый угол монитора компьютера. Таким образом, единичный вектор \(\hat{i}\) на оси x указывает горизонтально вправо, а единичный вектор \(\hat{j}\) на оси y указывает вертикально вверх. Начало вектора смещения расположено в точке b(6.0, 1.6), а конец вектора смещения расположен в точке e(2.0, 4.5). Подставьте координаты этих точек в уравнение \ref{2.13}, чтобы найти скалярные компоненты D _x и D _y вектора смещения \(\vec{D}\). Наконец, подставьте координаты в уравнение \ref{2.12} для записи вектора смещения в виде компонент вектора.
Раствор
Отождествляем x _b = 6,0, x _e = 2,0, y _b = 1,6 и y _e = 4,5, где физическая единица равна 1 см. Скалярные x- и y-компоненты вектора смещения равны
.
\[D_{x} = x_{e} — x_{b} = (2,0 — 6,0)\; см = -4,0\; см,\]
\[D_{y} = y_{e} — y_{b} = (4,5 — 1,6)\; см = + 2,9\; см \ldotp\]
Форма векторной составляющей вектора смещения:
\[\vec{D} = D_{x}\; \шляпа{я} + D_{у}\; \шляпа{j} = (-4. 0\; см)\; \шляпа{i} + (2,9\; см)\; \шляпа{j} = (-4.0\; \шляпа{i} + 2.9\; \шляпа{j})\; см \ldotp \label{2.14}\]
Это решение показано на рисунке \(\PageIndex{2}\).
Рисунок \(\PageIndex{2}\): График вектора смещения. Вектор указывает от начальной точки \(b\) до конечной точки \(e\).
Значение
Обратите внимание, что физическая единица измерения — здесь 1 см — может быть помещена либо с каждым компонентом непосредственно перед единичным вектором, либо глобально для обоих компонентов, как в уравнении \ref{2.14}. Часто последний способ удобнее, потому что он проще.
Компонента вектора x \(\vec{D}_{x}\) = −4,0 \(\hat{i}\) = 4,0(\(- \hat{i}\)) вектора смещения имеет величина |\(\vec{D}_{x}\)| = |− 4,0||\(\шляпа{i}\)| = 4,0, потому что модуль единичного вектора равен |\(\hat{i}\)| = 1. Обратите внимание также, что направление x-компоненты равно \(− \hat{i}\), что антипараллельно направлению +x-оси; следовательно, вектор x-компоненты \(\vec{D}_{x}\) указывает налево, как показано на рисунке \(\PageIndex{2}\). Скалярная x-компонента вектора \(\vec{D}\) равна D _x = −4,0. Аналогично, векторная y-компонента \(\vec{D}_{y}\) = \(+ 2,9 \hat{j}\) вектора смещения имеет величину |\(\vec{D}_{y} \)| = |2.9||\(\шляпа{j}\)| = 2,9, потому что модуль единичного вектора равен |\(\hat{j}\)| = 1. Направление компонента y равно \(+ \hat{j}\), которое параллельно направлению оси +y. Следовательно, вектор y-компоненты \(\vec{D}_{y}\) направлен вверх, как показано на рисунке \(\PageIndex{2}\). Скалярная y-компонента вектора \(\vec{D}\) равна D _y = + 2.9. Вектор смещения \(\vec{D}\) является равнодействующей двух его компонент вектора.
Форма векторной составляющей вектора смещения Уравнение \ref{2.14} говорит нам, что указатель мыши переместился на мониторе на 4,0 см влево и на 2,9 см вверх от своего начального положения.
Упражнение 2.4
Голубая муха приземляется на лист миллиметровой бумаги в точке, расположенной на 10,0 см правее его левого края и на 8,0 см выше его нижнего края, и медленно движется к точке, расположенной под номером 5. 0 см от левого края и 5,0 см от нижнего края. Выберите прямоугольную систему координат с началом в левом нижнем углу листа и найдите вектор смещения мухи. Проиллюстрируйте свое решение графиком.
Когда мы знаем скалярные компоненты A _x и A _y вектора \(\vec{A}\), мы можем найти его величину A и его направляющий угол \(\theta_{A}\). Угол направления — или, для краткости, направление — это угол, который образует вектор с положительным направлением на оси x.{-1} \left(\dfrac{A_{y}}{A_{x}}\right) \ldotp \label{2.16}\]
Рисунок \(\PageIndex{3}\): Для вектора \(\vec{A}\) его величина A и его направляющий угол \(\theta_{A}\) связаны с величинами его скалярных компонентов, поскольку A , A _x и A _y образуют прямоугольный треугольник.
Когда вектор лежит либо в первом квадранте, либо в четвертом квадранте, где компонент A _x положителен (рисунок \(\PageIndex{4}\)), угол \(\theta\) в уравнении \ref{ 2. 16}) идентичен дирекционному углу \(\theta_{A}\).Для векторов в четвертом квадранте угол \(\theta\) отрицателен, что означает, что для этих векторов направляющий угол \(\theta_{A}\) измеряется по часовой стрелке от положительной оси x. Точно так же для векторов во втором квадранте угол \(\theta\) отрицателен. Когда вектор лежит во втором или третьем квадранте, где компонент A _x отрицателен, угол направления равен \(\theta_{A}\) = \(\theta\) + 180° (рис. \(\PageIndex {4}\)).
Рисунок \(\PageIndex{4}\): Скалярные компоненты вектора могут быть положительными или отрицательными.Векторы в первом квадранте (I) имеют обе скалярные компоненты положительные, а векторы в третьем квадранте имеют обе скалярные компоненты отрицательные. Для векторов в квадрантах II и III угол направления вектора равен \(\theta_{A}\) = \(\theta\) + 180°.
Пример \(\PageIndex{2}\): величина и направление вектора смещения
Вы перемещаете указатель мыши на мониторе из исходного положения в точке (6,0 см, 1,6 см) к значку, расположенному в точке (2,0 см, 4,5 см). Каковы величина и направление вектора смещения указателя?
Стратегия
В примере \(\PageIndex{1}\) мы нашли вектор смещения \(\vec{D}\) указателя мыши (см. уравнение \ref{2.{о} \ldotp\]
Упражнение 2.5
Если вектор смещения синей мухи, идущей по листу миллиметровой бумаги, равен \(\vec{D} = (−5,00\; \hat{i} − 3,00\; \hat{j})\) см, найти его величину и направление.
Во многих приложениях величины и направления векторных величин известны, и нам нужно найти равнодействующую многих векторов. Например, представьте, что 400 автомобилей движутся по мосту Золотые Ворота в Сан-Франциско при сильном ветре. Каждая машина дает мосту разные толчки в разных направлениях, и мы хотели бы знать, насколько большим может быть результирующий толчок.У нас уже есть некоторый опыт геометрического построения векторных сумм, поэтому мы знаем, что задача нахождения равнодействующей путем рисования векторов и измерения их длин и углов может довольно быстро стать неразрешимой, что приведет к огромным ошибкам. Подобного беспокойства не возникает, когда мы используем аналитические методы. Самый первый шаг в аналитическом подходе состоит в том, чтобы найти компоненты вектора, когда известны направление и величина вектора.
Вернемся к прямоугольному треугольнику на рисунке \(\PageIndex{3}\).Отношение примыкающей стороны A _x к гипотенузе A есть функция косинуса направляющего угла \(\theta_{A}\), A _x/A = cos \(\theta_{A}\), и отношение противоположной стороны A _y к гипотенузе A является синусоидальной функцией \(\theta_{A}\), A _y /A = sin \(\theta_{A}\). Когда величина A и направление \(\theta_{A}\) известны, мы можем решить эти соотношения для скалярных компонентов:
\[\begin{cases} A_{x} = A \cos \theta_{A} \\ A_{y} = A \sin \theta_{A} \ldotp \end{cases} \label{2.17}\]
При расчете компонентов вектора по уравнению \ref{2.17} необходимо соблюдать осторожность при выборе угла. Угол направления \(\theta\) _A вектора — это угол, измеренный против часовой стрелки от положительного направления по оси x к вектору. Измерение по часовой стрелке дает отрицательный угол.
Пример \(\PageIndex{3}\): компоненты векторов смещения
Группа спасения пропавшего ребенка следует за поисковой собакой по кличке Солдат. Десантник много бродит и делает много пробных обнюхиваний по разным тропам.Солдат в конце концов находит ребенка, и у истории счастливый конец, но его перемещения на разных ногах кажутся действительно запутанными. На одной из ног он проходит 200,0 м на юго-восток, затем бежит на север около 300,0 м. На третьем этапе он внимательно исследует запахи на протяжении 50,0 м в направлении 30° к западу от севера. На четвертом этапе Trooper идет прямо на юг на 80,0 м, улавливает свежий запах и поворачивает на 23° к западу от юга на 150,0 м. Найдите скалярные компоненты векторов смещения Десантника и его векторов смещения в форме векторных компонент для каждой ноги.
Стратегия
Давайте примем прямоугольную систему координат с положительной осью x в направлении географического востока с положительным направлением y, указывающим на географический север. В явном виде единичный вектор \(\hat{i}\) оси x указывает на восток, а единичный вектор \(\hat{j}\) оси y указывает на север. Десантник делает пять ног, поэтому есть пять векторов смещения. Мы начинаем с определения их величин и углов направления, затем используем уравнение \ref{2.17}, чтобы найти скалярные компоненты перемещений и Уравнение \ref{2.12} для векторов перемещений.
Раствор
На первом участке величина смещения L ₁ = 200,0 м, направление юго-восточное. В качестве дирекционного угла \(\theta_{1}\) мы можем взять либо 45°, измеренные по часовой стрелке с востока, либо 45° + 270°, измеренные против часовой стрелки с востока. При первом выборе \(\theta_{1}\) = −45°. При втором выборе \(\theta_{1}\) = + 315°.{о} = -138,1\; м,\]
\[\vec{L}_{5} = L_{5x}\; \шляпа{я} + L_{5у}\; \шляпа{j} = (-58,6\; \шляпа{i} — 138,1\; \шляпа{j})\; м \ldotp\]
Упражнение 2.6
Если Солдат перед отдыхом пробежит 20 м на запад, каков вектор его перемещения?
Авторы и авторство
Сэмюэля Дж. Линга (Государственный университет Трумэна), Джеффа Санни (Университет Лойолы Мэримаунт) и Билла Мёбса с многими соавторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Прямоугольная система координат
Точка, которая делит пополам отрезок, образованный двумя точками (x1, y1) и (x2, y2), называется средней точкой. Учитывая две точки, (x1, y1) и (x2, y2), середина — это упорядоченная пара, заданная формулой (x1+x22, y1+y22). и определяется по следующей формуле:
Средняя точка представляет собой упорядоченную пару, образованную путем нахождения среднего значения x и среднего значения y заданных точек.
Пример 8: Вычислите среднюю точку между (−1, −2) и (7, 4).
Решение: Сначала вычислите среднее значение x и y заданных точек.
Затем сформируйте среднюю точку в виде упорядоченной пары, используя усредненные координаты.
Чтобы убедиться, что это действительно средняя точка, вычислите расстояние между двумя заданными точками и убедитесь, что результат равен сумме двух равных расстояний от конечных точек до этой средней точки.Эта проверка предоставляется читателю в качестве упражнения.
Попробуйте! Найдите среднюю точку между (−6, 5) и (6, −11).
Тематические упражнения
Часть A: заказанные пары
Придайте координаты пунктов A , B , C , D и E .
1.
2.
3.
4.
5.
6.
Постройте график заданного набора упорядоченных пар.
7. {(−4, 5), (−1, 1), (−3, −2), (5, −1)}
8.{(−15, −10), (−5, 10), (15, 10), (5, −10)}
9. {(−2, 5), (10, 0), (2, −5), (6, −10)}
10. {(−8, 3), (−4, 6), (0, −6), (6, 9)}
11. {(−10, 5), (20, −10), (30, 15), (50, 0)}
12. {(−53, −12),(−13, 12),(23, −1),(53, 1)}
13. {(−35, −43),(25, 43),(1, −23),(0, 1)}
14. {(−3,5, 0), (−1,5, 2), (0, 1,5), (2,5, −1,5)}
15. {(−0,8, 0,2), (−0,2, −0,4), (0, −1), (0,6, −0,4)}
16. {(−1,2, −1,2), (−0,3, −0,3), (0, 0), (0,6, 0,6), (1,2, 1,2)}
Укажите квадрант, в котором находится данная точка.
17. (−3, 2)
18. (5, 7)
19. (−12, −15)
20. (7, −8)
21. (−3,8, 4,6)
22. (17.3, 1.9)
23. (−18, −58)
24.(34, −14)
25. х>0 и у<0
26. х<0 и у<0
27. х<0 и у>0
28. х>0 и у>0
Средняя цена галлона обычного неэтилированного бензина в городах США представлена на следующем линейном графике. Используя график, ответьте на следующие вопросы.
Источник: Бюро трудовой статистики.
29. Какова была средняя цена галлона неэтилированного бензина в 2004 г.?
30. Какова была средняя цена галлона неэтилированного бензина в 1976 г.?
31. В какие годы средняя цена галлона неэтилированного бензина составляла 1,20 доллара США?
32. Как выросла цена галлона бензина с 1980 по 2008 год?
33. На сколько процентов увеличилась цена галлона неэтилированного бензина с 1976 по 1980 год?
34. На сколько процентов увеличилась цена галлона неэтилированного бензина с 2000 по 2008 год?
Средняя цена на белую муку общего назначения в городах США с 1980 по 2008 год представлена на следующем линейном графике. Используйте график, чтобы ответить на следующие вопросы.
Источник: Бюро трудовой статистики.
35. Какова была средняя цена фунта муки в/с в 2000 г.?
36.Какова была средняя цена фунта муки в/с в 2008 г.?
37. В каком году средняя цена муки составляла 0,25 доллара за фунт?
38. В какие годы средняя цена муки составляла 0,20 доллара за фунт?
39. На сколько процентов увеличилось количество муки с 2000 по 2008 год?
40. На сколько процентов увеличилось количество муки с 1992 по 2000 год?
Используя следующие данные, постройте линейный график.
41. Доля выпускников средней школы, поступивших в колледж.
Год Процент
1969 36%
1979 40%
1989 47%
1999 42%
Источник: Сборник статистики образования.
42. Среднесуточная температура в градусах Фаренгейта в мае.
Экзамен Температура
8:00 60
12:00 72
16:00 75
20:00 67
00:00 60
4:00 55
Вычислите площадь фигуры, образованной путем соединения следующего набора вершин.
43. {(0, 0), (0, 3), (5, 0), (5, 3)}
44. {(−1, −1), (−1, 1), (1, −1), (1, 1)}
45. {(−2, −1), (−2, 3), (5, 3), (5, −1)}
46. {(−5, −4), (−5, 5), (3, 5), (3, −4)}
47. {(0, 0), (4, 0), (2, 2)}
48. {(−2, −2), (2, −2), (0, 2)}
49. {(0, 0), (0, 6), (3, 4)}
50. {(−2, 0), (5, 0), (3, −3)}
Часть B: Формула расстояния
Вычислить расстояние между заданными двумя точками.
51. (−5, 3) и (−1, 6)
52. (6, -2) и (-2, 4)
53. (0, 0) и (5, 12)
54. (−6, −8) и (0, 0)
55. (−7, 8) и (5, –1)
56. (-1, -2) и (9, 22)
57. (−1, 2) и (–7/2, −4)
58. (−12, 13) и (52, −113)
59. (−13, 23) и (1, −13)
60. (12, −34) и (32, 14)
61.(1, 2) и (4, 3)
62. (2, –4) и (–3, –2)
63. (−1, 5) и (1, −3)
64. (1, -7) и (5, -1)
65. (-7, -3) и (-1, 6)
66. (0, 1) и (1, 0)
67. (−0,2, −0,2) и (1,8, 1,8)
68. (1.2, –3.3) и (2.2, –1.7)
Для каждой задачи покажите, что три точки образуют прямоугольный треугольник.
69.(−3, −2), (0, −2) и (0, 4)
70. (7, 12), (7, –13) и (–5, –4)
71. (−1,4, 0,2), (1, 2) и (1, −3)
72. (2, -1), (-1, 2) и (6, 3)
73. (-5, 2), (-1, -2) и (-2, 5)
74. (1, -2), (2, 3) и (-3, 4)
Равнобедренные треугольники имеют две катеты одинаковой длины. Для каждой задачи покажите, что следующие точки образуют равнобедренный треугольник.
75. (1, 6), (−1, 1) и (3, 1)
76. (−6, −2), (−3, −5) и (−9, −5)
77. (−3, 0), (0, 3) и (3, 0)
78. (0, −1), (0, 1) и (1, 0)
Вычислите площадь и периметр треугольников, образованных следующим набором вершин.
79. {(−4, −5), (−4, 3), (2, 3)}
80. {(−1, 1), (3, 1), (3, −2)}
81. {(−3, 1), (−3, 5), (1, 5)}
82.{(−3, −1), (−3, 7), (1, −1)}
Часть C: Формула средней точки
Найдите среднюю точку между данными двумя точками.
83. (-1, 6) и (-7, -2)
84. (8, 0) и (4, −3)
85. (−10, 0) и (10, 0)
86. (-3, -6) и (-3, 6)
87. (−10, 5) и (14, −5)
88. (0, 1) и (2, 2)
89. (5, -3) и (4, -5)
90.(0, 0) и (1, 1)
91. (-1, -1) и (4, 4)
92. (3, -5) и (3, 5)
93. (−12, −13) и (32, 73)
94. (34, −23) и (18, −12)
95. (53, 14) и (−16, −32)
96. (−15, −52) и (710, −14)
97. Дан прямоугольный треугольник, образованный вершинами (0, 0), (6, 0) и (6, 8). Покажите, что середины сторон образуют прямоугольный треугольник.
98. Дан равнобедренный треугольник, образованный вершинами (−10, −12), (0, 12) и (10, −12), покажите, что середины сторон также образуют равнобедренный треугольник.
99. Вычислите площадь треугольника, образованного вершинами (−4, −3), (−1, 1) и (2, −3). (Подсказка: вершины образуют равнобедренный треугольник.)
100. Вычислите площадь треугольника, образованного вершинами (−2, 1), (4, 1) и (1, −5).
Часть D: Темы на доске обсуждений
101.Исследуйте и обсуждайте жизнь и вклад Рене Декарта в математику.
102. Исследуйте и обсудите историю прямоугольного треугольника и теоремы Пифагора.
103. Что такое тройка Пифагора? Приведите несколько примеров.
104. Объясните, почему нельзя использовать линейку для расчета расстояния на графике.
105. Как разделить отрезок пополам, используя только циркуль и линейку?
Прямоугольная система координат — обзор
4.4.2 РЕАЛИЗАЦИЯ YEE FDTD
Используя прямоугольную систему координат ( x, y, z ) и предполагая, что параметры материала μ, ε и σ не зависят от времени, уравнения Максвелла можно записать в виде
(4.144)∂Hx∂t=1µ∂Ey∂z−∂Ez∂y
(4.145)∂Hy∂t=1µ∂Ez∂x−∂Ex∂z
(4.146)∂Hz∂t=1µ∂ Ex∂y−∂Ey∂x
(4.147)∂Ex∂t=1ε∂Hz∂y−∂Hy∂z−σEx
(4.148)∂Ey∂t=1ε∂Hx∂z−∂Hz∂x −σEy
(4.149)∂Ez∂t=1ε∂Hy∂x−∂Hx∂y−σEz.
Следуя формулировке Йи, точка в пространстве в кубической решетке может быть обозначена как
(4. 150)ijk=iδ,jδ,kδ
, а функция пространства и времени как
(4.151)Fnijk=iδx,jδy , KΔZ, NΔT,
, где δ = Δx = Δy = Δz = Δz — это приращение пространства (иногда обозначено как δ x , δ y , δ Z ), DT — приращение времени (или ∆ t ), а i, j, k, n — целые числа.Йи использовал центрированные конечно-разностные выражения для производных по пространству и времени, которые имеют второй порядок точности в δ и δt соответственно:
(4.152a)∂Fnijk∂x=Fni+12,j,k−Fni −12,j,kδx+Oδx2
(4.152b)∂Fnijk∂t=Fn+1/2ijk−Fn−1/2ijkδt+Oδt2.
Выражения, аналогичные выражению (4.152a), можно записать для производных по координатам y и z . Чтобы вычислить все пространственные производные в уравнениях (4.144)–(4.149), используя точность уравнения (4.152а), Йи расположил компоненты E и H относительно элементарной ячейки решетки, показанной на рисунке 4. 37. Для достижения точности уравнения (4.152b) E и H оцениваются через чередующиеся половинные временные интервалы.
Для непроницаемых сред для получения хороших результатов достаточно фиксированного шага по времени и фиксированного приращения по пространству. Для таких проблем количество Δt / δ ( I, J, K ) δ ( δ = Δx , Δy , Δz ) постоянна для всех ( I, j, k ) в решетке.Тогда систему уравнений Йи можно упростить. Тафлов и Умашанкар в процессе упрощения уравнений Йи определили следующие константы:
где Δ относится к Δx, Δy , или Δz для расчета E _x , E E _Z , соответственно, и M — это целое число который обозначает конкретную среду диэлектрика или проводимости в моделируемом пространстве.Определим также вектор пропорциональности
(4.153)E˜=RbE.
Используя эти упрощения, Тафлов и Умашанкар переформулировали разностные уравнения Йи. Для кубических ячеек ( δx = δy = δz = δ ) реализация Йи дает
(4.154a)Hxn+1/2i,j+12,k+12=Hxn−1/2i,j+12,k+ 12+E˜yni,j+12,k+1−E˜yni,j+12,k+E˜zni,j,k+12−E˜zni,j+1,k+12
(4.154b )Hyn+1/2i+12,j,k+12=Hyn−1/2i+12,j,k+12+E˜zni+1,j,k+12−E˜zni,j,k+12 +E˜xni+12,j,k−E˜xni+12,j,k+1
(4.154c)Hzn+1/2i,j+12,k+12=Hzn+1/2i+12, j+12,k+E˜xni+12,j+1,k−E˜xni+12,j,k+E˜yni,j+12,k−E˜yni+1,j+12,k
m=НОСИТЕЛЬ (i+1/2, j, k)
(4.154d)E˜xn+1i+12,j,k=CamE˜xni+12,j,k+CbmHzn+1/2i+12,j+12,k−Hzn+1/2i+12,j−12, k+Hyn+1/2i+12,j,k−12−Hyn+1/2i+12,j,k+12
m=MEDIA(i, j, +1/2, k)
(4,154 д)E˜yn+1i,j+12,k=CamE˜zni,j,k+12+CbmHxn+1/2i,j+12,k+12−Hxn+1/2i,j+12,k− 12+Hzn+1/2i−12,j+12,k−Hzn+1/2i+12,j+12,k
m=НОСИТЕЛЬ (i, j, k+1/2)
(4.154f )E˜zn+1i,j,k+12=CamE˜zni,j,k+12+CbmHyn+1/2i+12,j,k+12−Hyn+1/2i−12,j,k+12 +Hxn+1/2i,j−12,k+12−Hxn+1/2i,j+12,k+12.
Необходимо сохранить массив MEDIA.Массив задает целое число типа среды диэлектрика и проводимости в местоположении каждой компоненты поля E .
Предыдущая перестановка уравнения Йи устраняет три умножения, необходимые для вычисления H _x , H _y и H _z . Это также устраняет необходимость в компьютерном хранении массивов ε и σ . С помощью уравнения (4.154a) значение компонента поля в любой точке решетки зависит только от его предыдущего значения и от предыдущего значения компонентов других векторов поля в соседних точках.
Выбор δ и δt определяется необходимостью точности и устойчивости алгоритма . Для обеспечения точности δ должно быть мало по сравнению с длиной волны, обычно δ ≤ λ /10. Чтобы приближение кубической решетки к поверхности моделируемой структуры не было слишком грубым, δ должно быть небольшим по отношению к общему размеру структуры. Устойчивость обеспечивается, если δt выбрать так, чтобы выполнялось неравенство
(4. 155)δ≤1Cmax1δx2+1δy2+1δy2,
где C _max — максимальная фазовая скорость волны в рамках модели [57].
Решетка Йи имеет тот недостаток, что уравнения закручивания Максвелла, определенные выше, могут вызвать дисперсию . Дисперсия возникает, когда фазовая скорость изменяется относительно модовой длины волны. В алгоритме Йи дисперсия также зависит от направления распространения и дискретизации решетки. Дисперсия может вызвать искажение импульса, искусственную анизотропию и псевдорефракцию.Эта тема хорошо описана Тафлоувом и Умашанкаром в [59]. Анализ в [59] показывает, что численная дисперсия в трехмерном случае может быть представлена как , — x, y, z компонентов волнового числа k ; ω – угловая частота; c – скорость света в однородной среде.
В числовом пределе δt, δx, δy, и δz , стремящихся к нулю, уравнение (4.156a) сводится к
(4.156b)ω2c2=kx2+ky2+kz2,
, что является соотношение для плоской волны в сплошной среде без потерь. Это дает обоснование тому, что уменьшение размера ячейки в FDTD дает лучший контроль над модальным распределением фазовой скорости, чтобы минимизировать дисперсию. Численная дисперсия имеет решающее значение при использовании сетки с переменными ячейками и использовании импульсов конечной длительности.Переменные сетки могут вызывать отражение и преломление в числовых режимах на границах ячеек разного размера. Это искажение модальной фазовой скорости приводит к термину дисперсия. Импульсы конечной длительности имеют высокочастотные компоненты, которые распространяются в сетке FDTD медленнее, чем более низкочастотные компоненты. Это вызывает расширение импульсов конечной длительности, что может вызвать звон. Эту проблему можно свести к минимуму, вычислив преобразование Фурье импульса и выбрав размер сетки таким образом, чтобы основные компоненты спектра разрешались как минимум с 10 ячейками на длину волны.
Прямоугольные координаты — MATLAB & Simulink
Прямоугольные координаты
Определения координат
Построить прямоугольную или декартову систему координат для трехмерное пространство путем указания трех взаимно ортогональных координат оси. На следующем рисунке показана одна из возможных спецификаций координатные оси.
Прямоугольные координаты определяют положение в пространстве в данной система координат как упорядоченная тройка действительных чисел ( x , y , z ), относительно начала координат (0,0,0).Соображения по выбору происхождения обсуждаются в Глобальной и Локальной системах координат.
Вы можете рассматривать тройку как точку в пространстве или эквивалентно как вектор в трехмерном евклидовом пространстве. Рассматривается как вектор пространстве координатные оси являются базисными векторами, и вектор дает направление к точке пространства от начала координат. Каждый вектор в пространство однозначно определяется линейной комбинацией базиса векторы. Самый распространенный набор базисных векторов для трехмерных Евклидово пространство — стандартные базисные векторы единицы:
{[1 0 0],[0 1 0],[0 0 1]}
Обозначение для векторов и точек
В программном обеспечении Phased Array System Toolbox™ вы задаете оба координатные оси и точки как векторы-столбцы.
Примечание
В этом программном обеспечении все векторы координат являются векторами-столбцами. Для удобства в документации векторы-столбцы представлены в формат [ x y z ] без транспонирования.
Как векторное обозначение [ x y z ], так и точка обозначение ( x , y , z ) используются взаимозаменяемо. Интерпретация вектора-столбца как вектор или точка зависит от контекста. Если вектор-столбец задает оси системы координат или направление, это вектор.Если вектор-столбец задает координаты, это точка.
Ортогональный базис и евклидова норма
Любые три линейно независимых вектора определяют базис для трехмерного космос. Однако это программное обеспечение предполагает, что используемые вами базисные векторы являются ортогональными.
Стандартной мерой расстояния в космосе является l ² норма, или евклидова норма. Евклидова норма вектора [ x y z ] определяется как:
Евклидова норма дает длину вектора, измеренную от начало как гипотенуза прямоугольного треугольника. Расстояние между два вектора [ x ₀ y ₀ z ₀ ] и [ x ₁ y ₁ z ₁ ] это:
(x0−x1)2+(y0−y1)2+(z0−z1)2
Ориентация координатных осей
Дан ортонормированный набор базисных векторов, представляющих координату оси, существует несколько способов ориентации осей. Следующий рисунок иллюстрирует одну такую ориентацию, называемую правой координатой . система.Стрелки на осях координат указывают положительные направления.
Если взять правую руку и направить ее вдоль положительной оси x с ладонью, обращенной к положительной оси y , и вытяните Ваш большой палец указывает положительное направление оси z .
Вращения и матрицы вращения
При преобразовании векторов в трехмерном пространстве часто встречаются матрицы вращения. Матрицы вращения используются в двух смыслах: их можно использовать для поворота вектора в новый положение или их можно использовать для поворота базы координат (или системы координат) в новую один. В этом случае вектор остается в покое, но его компоненты в новом базисе будут отличается от исходной базы. В евклидовом пространстве есть три основных вращения: по одному вокруг осей x, y и z. Каждое вращение определяется углом вращение. Угол поворота определяется как положительный для поворота, который против часовой стрелки, если смотреть наблюдателем, смотрящим вдоль оси вращения в сторону источник. Любое произвольное вращение может быть составлено из комбинации этих трех (теорема Эйлера о вращении) .Например, вы можете повернуть вектор в в любом направлении, используя последовательность из трех вращений: v′=Av=Rz(γ)Ry(β)Rx(α)v.
Матрицы вращения, которые вращают вектор вокруг x, y, и оси z задаются следующим образом:
Вращение против часовой стрелки вокруг оси x
Rx(α)=[1000cosα−sinα0sinαcosα]
Вращение против часовой стрелки вокруг оси Y
Ry(β)=[cosβ0sinβ010−sinβ0cosβ]
Вращение против часовой стрелки вокруг оси Z
Rz(γ)=[cosγ−sinγ0sinγcosγ0001]
Следующие три рисунка показывают, как выглядят положительные вращения например, для каждой оси вращения:
Для любого вращения существует обратное вращение, удовлетворяющее A−1A=1. Например, обратная матрица вращения по оси X получается как изменение знака угла:
Rx−1(α)=Rx(−α)=[1000cosαsinα0−sinαcosα]=Rx′(α)
Этот пример иллюстрирует основное свойство: обратную матрицу вращения является транспонированием оригинала. Матрицы вращения удовлетворяют A’A = 1 , и следовательно, det(A) = 1 . При поворотах длины векторов сохраняются как а также углы между векторами.
Мы можем думать о вращениях по-другому.Рассмотрим исходный набор базисных векторов i,j,k и поверните их все, используя матрицу вращения A . Этот создает новый набор базисных векторов i ‘, j, ‘k’, связанных с исходным соотношением:
Используя транспонирование, вы можете записать новые базисные векторы в виде линейного комбинаций старых базисных векторов:
Теперь любой вектор можно представить в виде линейной комбинации любого набора базисных векторов:
v=vxi+vyj+vzk=v′xi′+v′yj′+v′zk′
Используя алгебраические операции, можно вывести преобразование компоненты для фиксированного вектора, когда базис (или система координат) вращается. Этот Преобразование использует транспонирование матрицы вращения.
[v′xv′yv′z]=A−1[vxvyvz]=A′[vxvyvz]
На следующем рисунке показано, как вектор преобразуется в координату система вращается вокруг оси x. На следующем рисунке показано, как это преобразование может быть реализовано. интерпретируется как поворот вектора в противоположную сторону направление.
См. также
Система векторных координат — Listenlights
Для точного описания вектора необходимо указать некоторые конкретные длины, направления, углы, проекции или компоненты.Для этого есть три простых метода и около восьми или десяти других методов, полезных в особых случаях.
Мы будем использовать только три простых метода, и самым простым из них является декартова или прямоугольная система координат.
Декартова или прямоугольная система координат
В декартовой системе координат мы устанавливаем три координатные оси под прямым углом друг к другу и называем их осями x, y и z. Обычно выбирают правовинтовую систему координат, в которой поворот (на меньший угол) оси x относительно оси y заставит правосторонний винт двигаться в направлении оси z. Если используется правая рука, то большой, указательный и средний пальцы могут быть идентифицированы соответственно как оси x, y и z.
На рис. 1.а показана правая декартова система координат.
Рисунок 1. Декартова система координат
Точка находится по заданным координатам x, y и z.Это, соответственно, расстояния от начала координат до пересечения перпендикуляра, опущенного из точки на оси x, y и z.
На рис. 1.b показаны точки P и Q с координатами (1, 2, 3) и (2, -2, 1) соответственно.
Таким образом, точка P расположена в общей точке пересечения плоскостей x = 1, y = 2 и z = 3, а точка Q расположена на пересечении плоскостей x = 2, y = -2, z = 1.
Если мы визуализируем три плоскости, пересекающиеся в общей точке P с координатами x, y и z, мы можем увеличить каждое значение координаты на дифференциальную величину и получить три слегка смещенные плоскости, пересекающиеся в точке P ^t , чьи координаты равны x + dx, y + dy и z + dz.
Шесть плоскостей определяют прямоугольный параллелепипед, объем которого равен
Поверхности имеют дифференциальных площадей dS dxdy, dydz и dzdx .
КОМПОНЕНТЫ ВЕКТОРОВ И ЕДИНИЧНЫЕ ВЕКТОРЫ
Для описания вектора в декартовой системе координат,
Давайте сначала рассмотрим вектор r , простирающийся наружу от начала координат.
Логический способ определить этот вектор — задать три вектора-компонента, лежащие вдоль трех осей координат, векторная сумма которых должна быть заданным вектором.Если векторами-компонентами вектора r являются x, y и z, то r = x + y + z.
Векторы компонентов показаны на рис. 2.a.
Рисунок 2. Компоненты вектора
Вместо одного вектора у нас теперь три, но это шаг вперед, потому что три вектора имеют очень простую природу; каждый всегда направлен вдоль одной из осей координат.
Другими словами, составные векторы имеют величины, которые зависят от данного вектора (например, r выше), но каждый из них имеет известное и постоянное направление. Это предполагает использование единичных векторов, имеющих по определению единичную величину и направленных по осям координат в сторону возрастания значений координат.
Таким образом, a _x , a _y и a _z являются единичными векторами в декартовой системе координат.
Они направлены вдоль осей x, y и z соответственно, как показано на рис. 2.b.
Если компонентный вектор y имеет две единицы по величине и направлен в сторону увеличения значения y, мы должны написать
Вектор r _P, указывающий из начала координат в точку P (1, 2, 3), записывается как
Вектор из P в Q можно получить, применив правило сложения векторов.Это правило показывает, что вектор из начала координат в P плюс вектор из P в Q равен вектору из начала координат в Q.
Следовательно, искомый вектор из P (1, 2, 3) в Q (2, -2, 1) равен
R _PQ = r _Q – r _P = (2 – 1)a _x + (-2 – 2)a _y + (1 – 3)a _z2 = a х – 4а _у – 2а _г
На рис.2.в.
Любой вектор B тогда может быть описан как
КРУГЛЫЕ ЦИЛИНДРИЧЕСКИЕ КООРДИНАТЫ
Декартова система координат обычно является той, в которой учащиеся предпочитают работать со всеми задачами. Это часто требует от студента гораздо больше работы, потому что многие задачи обладают типом симметрии, который требует более логического решения.
Круговая цилиндрическая система координат представляет собой трехмерную версию полярных координат аналитической геометрии.
В двумерных полярных координатах точка была расположена на плоскости, задав ее расстояние p от начала координат и угол Φ между линией от точки до начала координат и произвольной радиальной линией, принятый как Φ = O
Трехмерная система координат, круговые цилиндрические координаты, получается путем указания расстояния z точки от произвольной базовой плоскости z = O, перпендикулярной линии ρ = O
Любую точку можно рассматривать как пересечение трех взаимно перпендикулярных поверхностей.
Этими поверхностями являются круговой цилиндр ( ρ = постоянная), плоскость ( Φ = постоянная) и другая плоскость (z = постоянная). Это соответствует расположению точки в декартовой системе координат на пересечении трех плоскостей (x = константа, y = константа и z = константа).
Три поверхности круговых цилиндрических координат показаны на рис. 3.а. Обратите внимание, что через любую точку можно пройти три таких поверхности, если только она не лежит на оси z, и в этом случае достаточно одной плоскости.
Рис. 3. Цилиндрическая система координат
Также должны быть определены три единичных вектора, но мы больше не можем направлять их вдоль координатных осей, поскольку такие оси существуют только в декартовых координатах. Вместо этого мы берем более широкий взгляд на единичные векторы в декартовых координатах и понимаем, что они направлены в сторону увеличения значений координат и перпендикулярны поверхности, на которой это значение координат является постоянным (т. е. единичный вектор a _x нормальен к плоскость x = постоянная и указывает на большие значения x).
Соответствующим образом теперь мы можем определить три единичных вектора в цилиндрических координатах: a _ρ , a _Φ и a _z .
Единичный вектор a _ρ в точке P(ρ ₁ , Φ ₁ , z ₁ ) направлен радиально наружу, перпендикулярно цилиндрической поверхности ρ = ρ ₁ . Он лежит в плоскостях Φ = Φ ₁ и z = z ₁ . Единичный вектор a _Φ нормальен к плоскости Φ = Φ ₁ , указывает в сторону возрастания Φ, лежит в плоскости z = z ₁ и касается цилиндрической поверхности ρ = ρ ₁ .Единичный вектор a _z совпадает с единичным вектором a _z декартовой системы координат.
На рис. 3.b показаны три вектора в цилиндрических координатах. В декартовых координатах единичные векторы не являются функциями координат. Однако два единичных вектора в цилиндрических координатах, а _ρ и _Φ , изменяются в зависимости от координаты Φ, поскольку их направления меняются. Таким образом, при интегрировании или дифференцировании по Ф _ρ и _Φ нельзя рассматривать как константы.
Единичные векторы снова взаимно перпендикулярны, поскольку каждый из них нормальен к одной из трех взаимно перпендикулярных поверхностей, и мы можем определить правостороннюю цилиндрическую систему координат как такую, в которой Φ = a _z , или (для тех, у кого гибкие пальцы) как тот, в котором большой, указательный и средний пальцы указывают в сторону увеличения ρ , Φ , и з соответственно.
Дифференциальный объемный элемент в цилиндрических координатах может быть получен путем увеличения ρ , ρ , Φ , а Z по дифференциальному приращениям D ρ , D Φ и DZ.
Два цилиндра радиуса ρ и ρ + dρ, две радиальные плоскости под углами Φ и Φ + dΦ и две горизонтальные плоскости под углами z и z + dz теперь заключают в себе небольшой объем, как показано на рис.3.в, имеющий форму усеченного клина.
Поскольку элемент объема становится очень маленьким, его форма приближается к прямоугольному параллелепипеду со сторонами длиной dρ, pdΦ и dz.
Обратите внимание, что dρ и dz являются размерными длинами, а dΦ — нет; ρdΦ — длина.
Поверхности имеют участки ρ d ρ d Φ , D ρ DZ и ρ D Φ DZ и объем становится ρ d ρ d Φdz.
Рисунок 4. Преобразование цилиндрических координат в декартовы координаты
Переменные прямоугольной и цилиндрической систем координат легко связаны между собой. Ссылаясь на рис. 4, мы видим, что
х = ρ cos Φ
у = ρ sin Φ
г = г
СФЕРИЧЕСКАЯ СИСТЕМА КООРДИНАТ
У нас нет двумерной системы координат, которая помогла бы нам понять трехмерную сферическую систему координат, в отличие от круговой цилиндрической системы координат.В некоторых отношениях мы можем опираться на наше знание системы широты и долготы для определения местоположения места на поверхности земли, но обычно мы рассматриваем только точки на поверхности, а не те, что ниже или выше земли.
Начнем с построения сферической системы координат по трем декартовым осям (рис. 5.а). Сначала определим расстояние от начала координат до любой точки как r.
Рис. 5. Сферическая система координат
Поверхность r = константа является сферой.
Вторая координата — это угол e между осью z и линией, проведенной из начала координат в рассматриваемую точку.
Поверхность e=constant представляет собой конус, а две поверхности, конус и сфера, всюду перпендикулярны вдоль их пересечения, которое представляет собой окружность радиуса r sin e. Координата e соответствует широте, за исключением того, что широта отсчитывается от экватора, а e отсчитывается от Северного полюса.
Третья координата Φ также является углом и в точности совпадает с углом Φ цилиндрических координат.Это угол между осью x и проекцией на плоскость z = O линии, проведенной из начала координат в точку. Он соответствует углу долготы, но угол Φ увеличивается к востоку. Поверхность Φ=constant представляет собой плоскость, проходящую через линию e=O (или ось z).
Мы снова должны рассматривать любую точку как пересечение трех взаимно перпендикулярных поверхностей — сферы, конуса и плоскости, каждая из которых ориентирована описанным выше образом. Три поверхности показаны на рис.5.б.
В любой точке снова могут быть определены три единичных вектора.
Каждый единичный вектор перпендикулярен одной из трех взаимно перпендикулярных поверхностей и ориентирован в том направлении, в котором увеличивается координата.
Единичный вектор a _r направлен радиально наружу, нормально к сфере r = постоянная, и лежит в конусе e = постоянная и плоскости Φ = постоянная.
Единичный вектор a _e нормальен к конической поверхности, лежит в плоскости и касается сферы.Она направлена вдоль линии долготы и указывает на юг.
Третий единичный вектор a _Φ такой же, как и в цилиндрических координатах, является нормальным к плоскости и касается как конуса, так и сферы. Он направлен на восток.
Три единичных вектора показаны на рис. 5.c.
Они, конечно, взаимно перпендикулярны, и правосторонняя система координат определяется тем, что _r x a _e = a _Φ .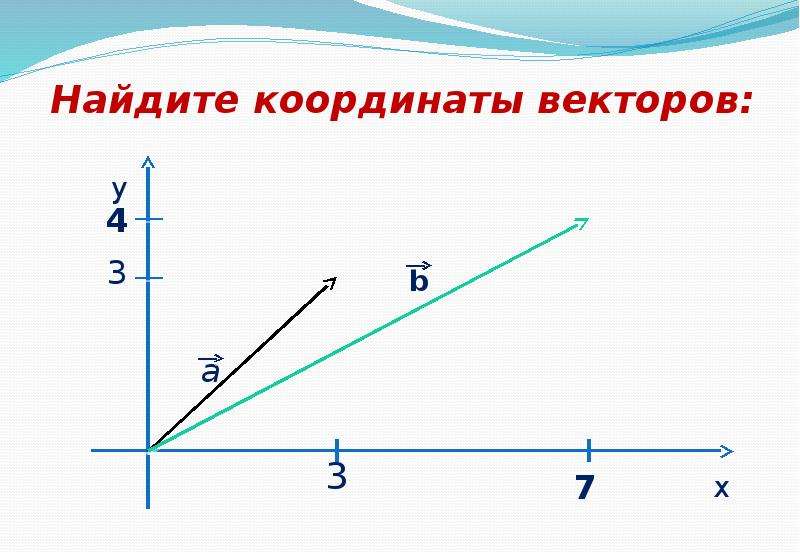 Наша система правосторонняя, как видно из рис.5.c покажет при применении определения перекрестного произведения. Правило правой руки служит для идентификации большого, указательного и среднего пальцев с направлением увеличения r, e и Φ соответственно. (Обратите внимание, что отождествление в цилиндрических координатах было с ρ, Φ и z, а в декартовых координатах с x, y и z).
Элемент дифференциального объема может быть построен в сферических координатах путем увеличения r, e и Φ на dr, de и d Φ , , как показано на рис.5.д.
Расстояние между двумя сферическими поверхностями радиуса r и r + dr равно dr; расстояние между двумя конусами, имеющими образующие углы е и е + дэ, составляет rдэ; а расстояние между двумя радиальными плоскостями под углами Φ и Φ + dΦ оказывается равным r sin edΦ после нескольких минут тригонометрических размышлений.
Поверхности имеют площади r dr de, r sin e dr d Φ и r ² sin e de d Φ , а объем r ^{9 9 2 .} Φ .
Каталожные номера
[1] «Инженерная электромагнетика, шестое издание» Уильяма Х. Хейта-младшего. Джон А. Бак
векторов
векторов
Векторы
В физике количественные модели разрабатываются на основе измерений. Их необходимо проверить, сделав дополнительные измерения. Измерения производятся в стандартных приращениях, называемых единицами. Без единиц а измерение бессмысленно.
Некоторые величины полностью определяются величиной, т. е. количество и соответствующие единицы измерения.
Действительное число само по себе называется скалярные, и такие величины называются скалярными величинами . Символы, обозначающие эти скалярные величины, нормальные буквы.
Примеры скалярных величин:
температура (T) T = 10 ^o C
временной интервал (t) t = 5 с
масса (m) m = 3 кг
Другие величины определяются величиной и направлением. От направление, мы имеем в виду направление в пространстве.
Такие количества называются векторных величин . Символы, обозначающие эти векторные величины выделены жирным шрифтом или обычными буквами со стрелками выше.
Примеры векторных величин:
перемещение ( d ) d = 10 м к северу
скорость ( v ) v = 3 м/с на восток
сила ( F ) F = 9 Н до
Для однозначного указания векторных величин нам нужен опорная точка и опорные линии , т.е.е. нам нужно система координат .
Декартова координата система является наиболее часто используемой системой координат. В два измерения, эта система состоит из пары линий на плоской поверхность или плоскость, пересекающиеся под прямым углом. Линии назвал осей и точку, в которой они пересекаются, называется началом . Оси обычно проводят горизонтально и вертикально и относят к в качестве осей x и y соответственно.
Точка на плоскости с координаты (a, b) — это единицы справа от оси y и единицы b вверх. от оси x, если a и b положительные числа.
Если a и b равны оба отрицательных числа, точка находится на единицу слева от оси Y и b единиц вниз от оси x.
На рисунке справа точка P ₁ имеет координаты (3, 4), а точка P ₂ имеет координаты (-1, -3).
В трехмерных декартовых координатах добавляется ось z, так что есть три оси, перпендикулярные друг другу.
В полярных координатах системе , каждой точке плоскости присваиваются координаты (r, φ) относительно фиксированная линия в плоскости называется осью и точка на этой линии, называемая полюсом . Для точки на плоскости координата r представляет собой расстояние от указывают на полюс, а координата φ представляет собой угол против часовой стрелки между осью и линией, соединяющей начало координат с точкой.
Координата r всегда положительна, а диапазон φ составляет от 0 до 2π (360 ^o ). Уметь преобразовывать декартовы координаты в полярные и наоборот наоборот, пусть ось полярной системы координат совпадает с ось x декартовой системы координат и полюс совпадают с источник.
На рисунке справа точка P ₁ имеет полярные координаты (r ₁ , φ ₁ ) = (5, 53,1 ^o ), а точка P ₂ имеет полярные координаты (r ₂ , φ ₂ ) = (3.16, 251,6 ^или).
Уравнения преобразования:
x = r cosφ, y = r sinφ.
r = (x ² + y ² ) ^½ , φ = загар ^-1 (г/х).
Цилиндрические координаты и сферические координаты два разных расширения полярных координат до трех измерений.
Как только мы выбрали систему координат, физический векторная величина в двух измерениях может быть представлена парой числа.
Если взять декартовы координаты, то числа будут проекциями вектора на оси декартова координата система.
Вектор и на рисунке справа имеют x-компоненту a ₁ и y-компонента a ₂ .
Его длина или величина равна a = (a ₁ ² + a ₂ ² ) ^½ . Это следует из Теорема Пифагора.
Полярный угол a , т.е.е. угол a образует с ось x — это φ.
Проблема:
Вектор A лежит в плоскости xy.
(a) Для каких ориентаций Оба прямоугольных компонента числа будут отрицательными?
(b) Для чего ориентации будут ли его компоненты иметь противоположные знаки?
Решение:
Рассуждение:
На плоскости (в двух измерениях) мы можем указать направление вектора с помощью установив систему координат и задав угол φ, который вектор образует с положительная ось x.Положительный φ — это угол, измеренный против часовой стрелки от положительной оси x.
Детали расчета:
(a) X-компонента A равна A _x = А cosφ а y-компонента A равна A _y = A sinφ. (А — величина вектора.) Если A _x и A _y отрицательные, мы нужно, чтобы cosφ и sinφ были отрицательными. φ должен лежать между 180 и 270 градусов.
(b) Чтобы A _x и A _y имели противоположные знаки, φ должен лежать от 90 до 180 градусов или от 270 до 360 градусов.
Примечание. Величина вектора говорит о его длине. это число (с единицами). Если вектор является вектором скорости, то его величина имеет единицы скорости (м/с), если это вектор смещения, то его величина имеет единицы расстояния (м) и др.
Направление в двух измерениях, то есть в плоскости, — это угол, который образует вектор. с осью x, измеренной против часовой стрелки от направления x.
Вам нужна система координат (система отсчета), прежде чем вы зададите направление.
Добавление векторов
Чтобы добавить физические векторы, они должны быть одинаковые единицы измерения. Чтобы найти сумму двух физических векторные величины с теми же единицами алгебраически , складываем x, y и z-компоненты отдельных векторов.
Пример:
Пусть вектор v ₁ имеет компоненты (3, 4) и вектор v ₂ имеют компоненты (2, -3).
Пусть v = v ₁ + v ₂ — сумма двух векторов.
Затем компоненты v равно (3+2, 4+(-3) = (5, 1)).
Величина вектора v равна v = (25 + 1) ^½ = 5,1,
а угол v , образуемый с осью x, равен φ = tan ^-1 (1/5) = 0,197 рад = 11,3 ^o .
Чтобы вычесть вектор v ₂ из вектора v ₁ мы вычитаем компоненты вектора v ₂ из компоненты вектора v ₁ .
Пример:
Пусть вектор v ₁ имеет компоненты (3, 4) и вектор v ₂ имеют компоненты (2, -3).
Пусть v = v ₁ — v ₂ — разность двух векторы.
Тогда компоненты v равны (3-2, 4-(-3) = (1, 7).
Величина вектора v равна v = (1 + 49) ^½ = 7.1
а угол v , образуемый с осью x, равен φ = tan ^-1 (7/1) = 1,429 рад = 81,9 ^о .
Графическое представление векторной величины в виде направленной линии сегмент. Чтобы найти сумму двух физических векторных величин с те же единицы графически выстраиваем стрелки, хвост к кончику. Сумма — это стрелка, проведенная от хвоста первого вектора к кончику последнего вектора. Чтобы вычесть вектор v ₂ из вектор v ₁ инвертируем вектор v ₂ и добавляем его в вектор v ₁ .
Пусть A — произвольный вектор. Вектор — A имеет одинаковой длины и направлены в противоположную сторону. Вычитание вектора A из другого вектора означает добавление вектор — A к другому вектору.
Пример:
Вектор смещения
Пусть d представляет вектор смещения из точки A с координатами (x ₁ , y ₁ ) = (-4, -1) до точки B с координатами (x ₂ , y ₂ ) = (3, 4).
Вектор смещения – это разница между векторами положения А и Б , д = Б — А .
Его компоненты
d _x = (x ₂ — x ₁ ) = 3 — (-4) = 7, d _y = (у ₂ — у ₁ ) = 4 — (-1) = 5.
Вектор смещения d имеет модуль d = (49 + 25) ^½ = 8,6.
Угол d , образуемый с осью x, равен φ = tan ^-1 (5/7) = 0.62 рад = 35,5 ^o .
Сводка:
Ссылка: Урок 1: Векторы — Основы и операции
Пожалуйста, изучите этот материал из «Кабинета физики».
Векторы и направление
Вектор Дополнение
Результат
Векторные компоненты
Разрешение вектора
Задачи относительной скорости и речного судна
.