| 1. |
Вспомогательная система координат
Сложность: лёгкое |
1 |
| 2. |
Параллельный перенос графика функции
Сложность: лёгкое |
2 |
3.
|
Направление сдвига графика функции
Сложность: лёгкое |
2 |
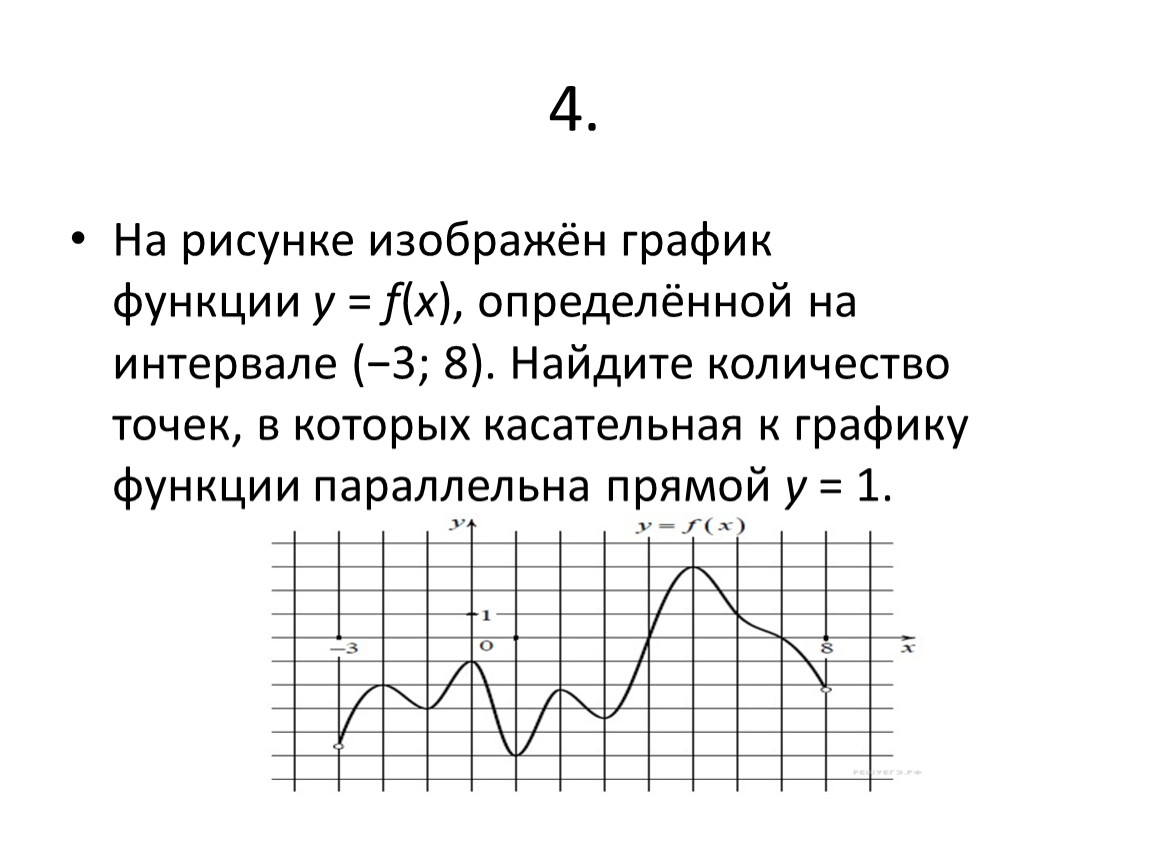
| 4. |
Формула функции
Сложность: среднее |
2 |
5.
|
Сложность: среднее |
2 |
| 6. |
Значение функции
Сложность: среднее |
2 |
7.
|
Построение графика квадратичной функции вида y = (x + a)² + b
Сложность: среднее |
3 |
| 8. |
Метод выделения полного квадрата
Сложность: сложное |
3 |
9.
|
Функции
Сложность: сложное |
3 |
| 10. |
Графическое решение системы уравнений
Сложность: сложное |
3 |
Графиком линейной функции является прямая линия. Чтобы построить график функции, нам нужны координаты двух точек, принадлежащих графику функции. Чтобы их найти, нужно взять два значения х, подставить их в уравнение функции, и по ним вычислить соответствующие значения y. Пример: В уравнении функции y=kx+b коэффициент k отвечает за наклон графика функции: если k>0, то график наклонен вправо если k<0, то график наклонен влево Коэффициент b отвечает за сдвиг графика вдоль оси OY: если b>0, то график функции y=kx+b получается из графика функцииy=kx сдвигом на b единиц вверх вдоль оси OY если b<0, то график функции y=kx+b получается из графика функции y=kx сдвигом на b единиц вниз вдоль оси OY Заметим, что во всех этих функциях коэффициент k больше нуля, и все графики функций наклонены вправо. Во всех функциях b=3 — и мы видим, что все графики пересекают ось OY в точке (0;3) На этот раз во всех функциях коэффициент k меньше нуля, и все графики функций наклонены влево. Заметим, что чем больше |k|, тем круче идет прямая. Коэффициент b тот же, b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3) Теперь во всех уравнениях функций коэффициенты k равны. И мы получили три параллельные прямые. Но коэффициенты b различны, и эти графики пересекают ось OY в различных точках: График функции y=2x+3 (b=3) пересекает ось OY в точке (0;3) График функции y=2x (b=0) пересекает ось OY в точке (0;0) — начале координат. График функции y=2x-2 (b=-2) пересекает ось OY в точке (0;-2) Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции y=kx+b. Если k<0 и b>0, то график функции y=kx+b имеет вид: Если k>0и b>0, то график функции y=kx+b имеет вид:Если k>0 и b<0, то график функции y=kx+b имеет вид: Если k<0 и b<0, то график функции y=kx+b имеет вид: Если k=0 , то функция y=kx+b превращается в функцию y=b и ее график имеет вид: Ординаты всех точек графика функции y=b равны b Если b=0, то график функции y=kx проходит через начало координат: Это график прямой пропорциональности. Отдельно отмечу график уравнения x=a. График этого уравнения представляет собой прямую линию, параллельную оси OY все точки которой имеют абсциссу x=a. Например, график уравнения x=3 выглядит так: Внимание! Уравнение x=a не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции. Условие параллельности двух прямых: График функции y=k_1{x}+b_1 параллелен графику функции y=k_2{x}+b_2, если k_1=k_2 Условие перпендикулярности двух прямых: График функции y=k_1{x}+b_1 перпендикулярен графику функции y=k_2{x}+b_2, если k_1*k_2=-1 или k_1=-1/{k_2} Точки пересечения графика функции y=kx+b с осями координат. С осью ОY. Абсцисса любой точки, принадлежащей оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY нужно в уравнение функции вместо х подставить ноль. |
Построение графиков функций геометрическими методами / math5school.ru
График функции y=f(x)+a
График функции y=f(x–a)
График функции y=kf(x), k>0
График функции y=f(kx), k>0
График функции y=–f(x)
График функции y=f(–x)
График функции y=|f(x)|
График функции y=f(|x|)
График функции
y=f(x)+aСпособ построения: параллельный перенос графика функции y=f(x) вдоль оси Oy на а единиц вверх, если a>0, и на |a| единиц вниз, если a<0.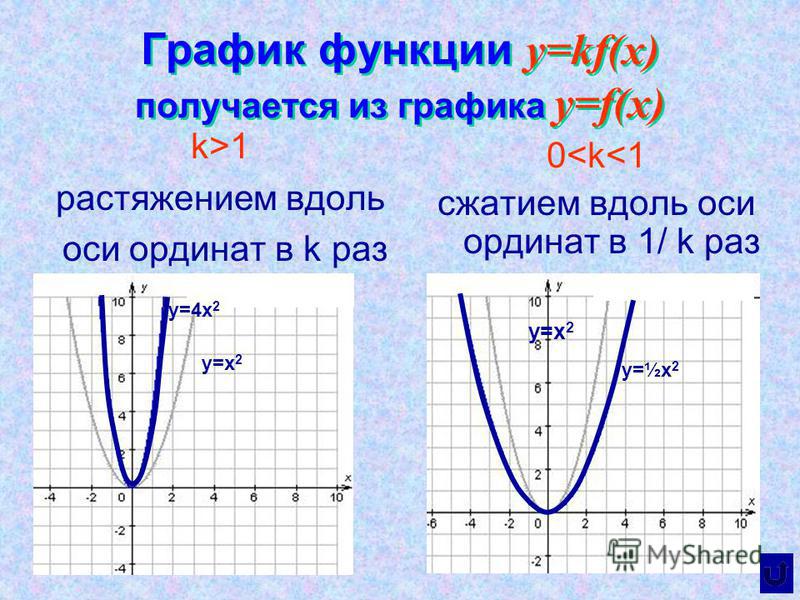
График функции
y=f(x–a)Способ построения: параллельный перенос графика функции y=f(x) вдоль оси Ox на а единиц вправо, если a>0, и на |a| единиц влево, если a<0.
График функции
y=kf(x), k>0Способ построения: растяжение графика функции y=f(x) вдоль оси Oy относительно оси Ox в k раз, если k>1, и сжатие в 1/k раз, если 0<k<1.
График функции
y=f(kx), k>0Способ построения: сжатие графика функции y=f(x) вдоль оси Ox относительно оси Oy в k раз, если k>1, и растяжение в 1/k раз, если 0<k<1.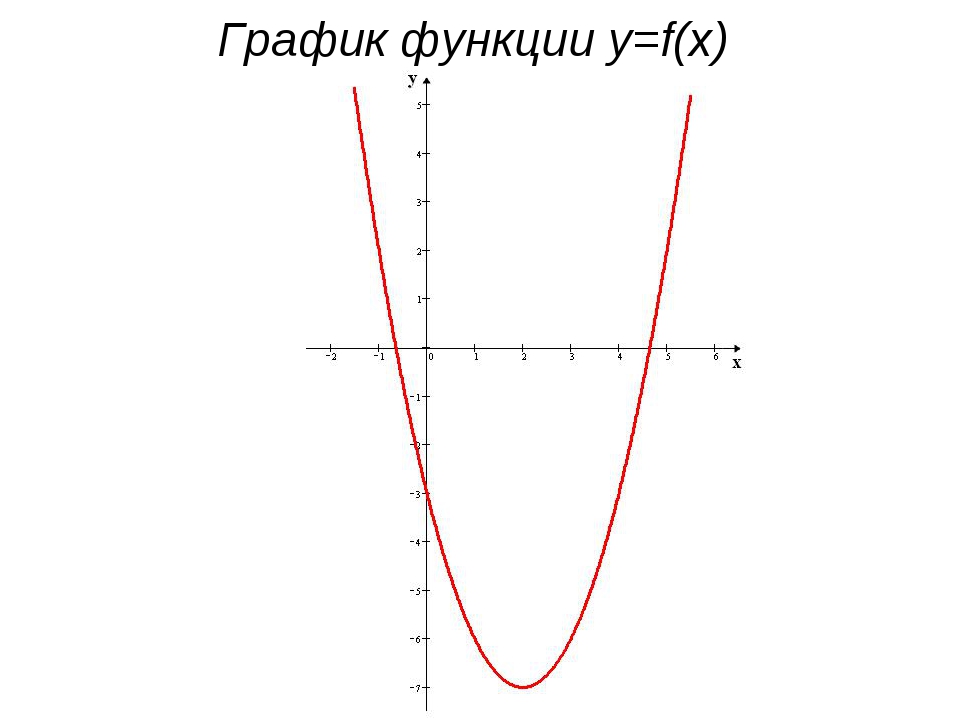
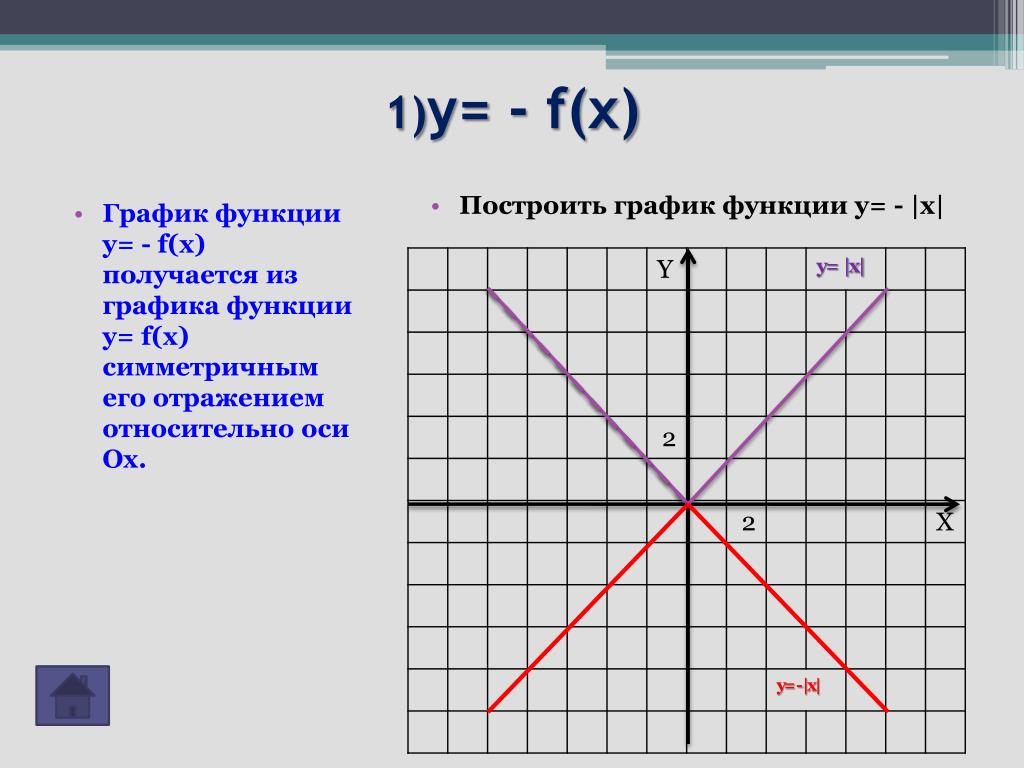
График функции
y=–f(x)Способ построения: симметричное отражение графика функции y=f(x) относительно оси Ox.
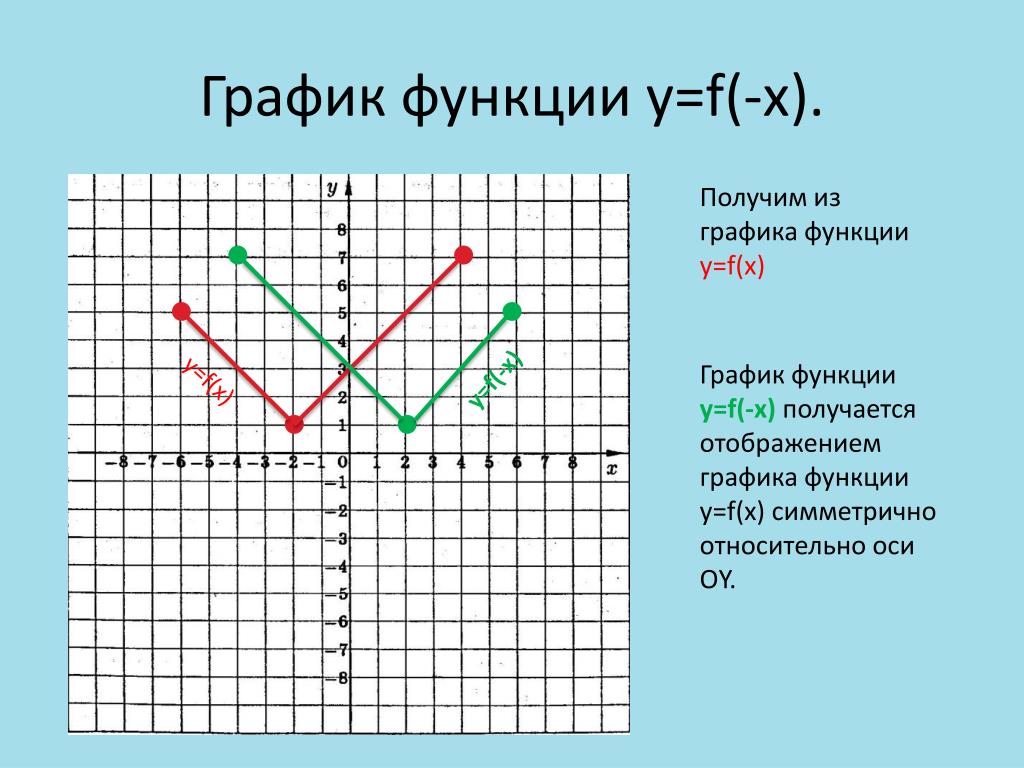
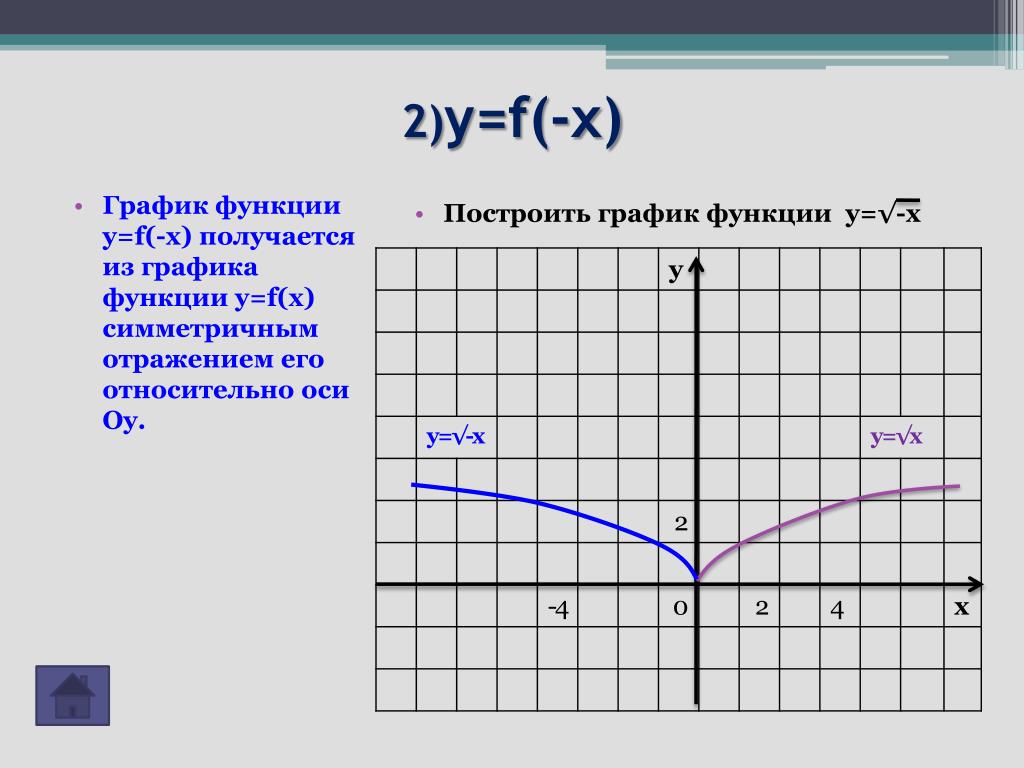
График функции
y=f(–x)Способ построения: симметричное отражение графика функции y=f(x) относительно оси Oy.
График функции
y=|f(x)|Способ построения: часть графика функции y=f(x), расположенная ниже оси Ox, симметрично отражается относительно этой оси, остальная его часть остаётся без изменения.
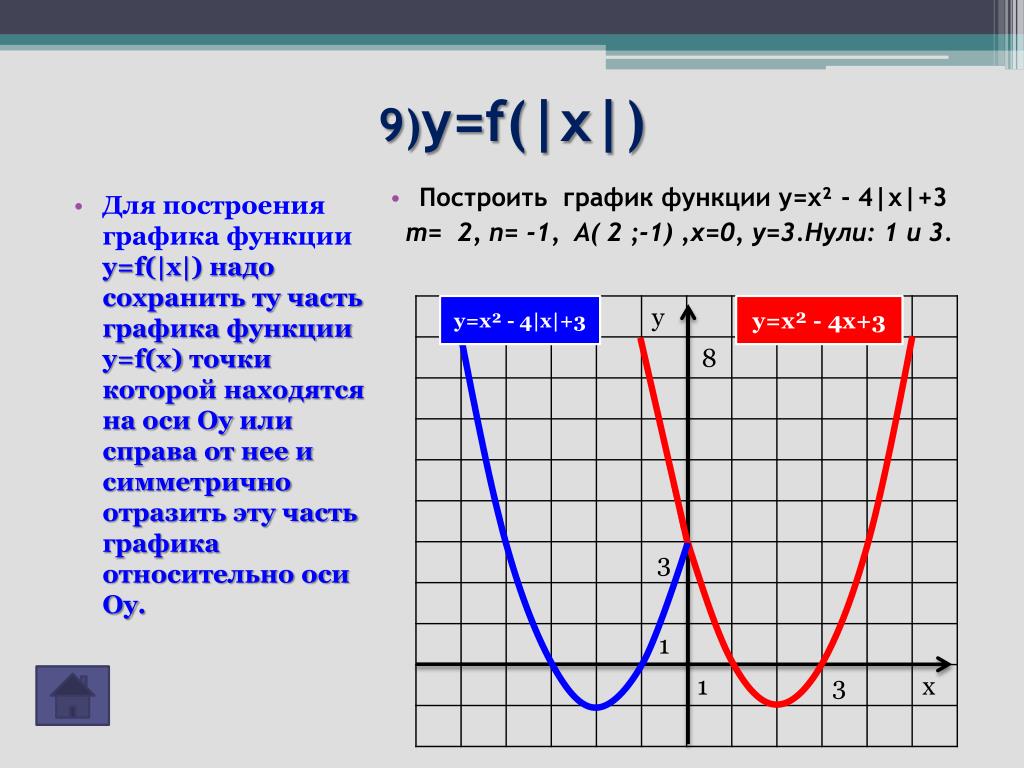
График функции
y=f(|x|)Способ построения: часть графика функции y=f(x), расположенная правее оси Oy и на ней, остаётся без изменения, а остальная его часть заменяется симметричным отображением относительно оси Oy части графика, расположенной правее оси Oy.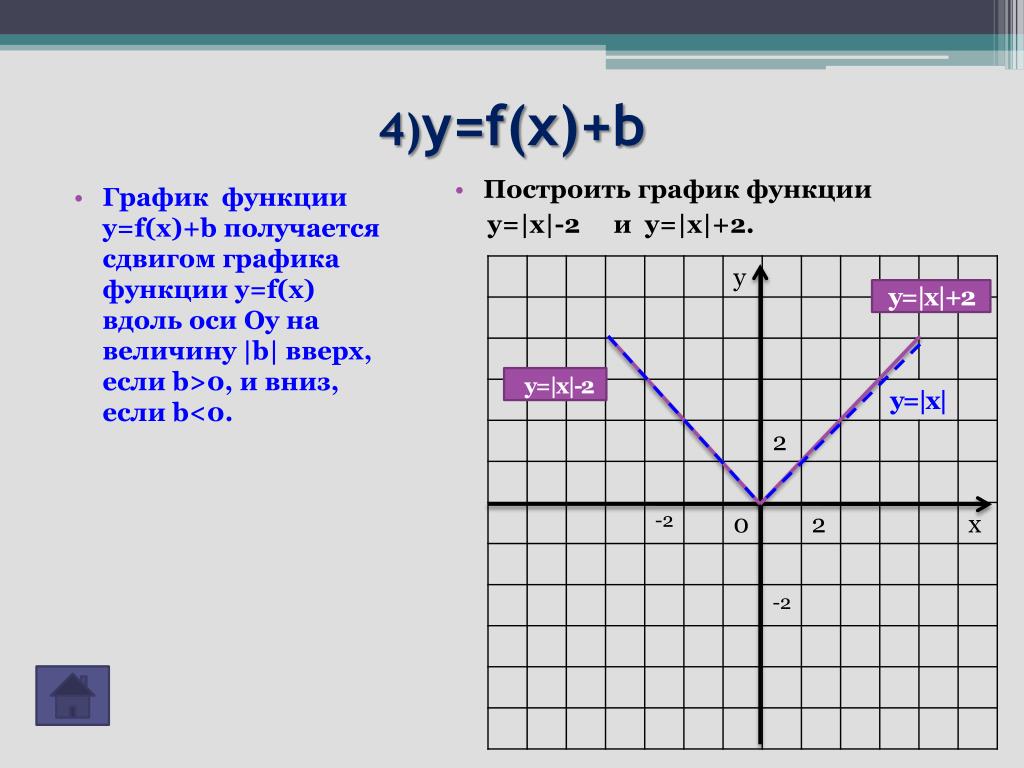
Смотрите также:
Таблицы чисел
Алгебраические тождества
Степени
Арифметический корень n-й степени
Логарифмы
Графики элементарных функций
Тригонометрия
Таблицы значений тригонометрических функций
Треугольники
Четырёхугольники
Многоугольники
Окружность
Площади геометрических фигур
Прямые и плоскости
Многогранники
Тела вращения
Открытая Математика. Функции и Графики. Параллельный перенос
Пусть имеется график функции y = f (x). Зададимся целью построить график функции y = f1 (x), где f1 (x) = f (x) + B. Ясно, что области определения этих функций совпадают. Пусть A (x0; y0) – точка на графике функции y = f (x). Соответствующая ей точка A′ (x0; y1) с той же абсциссой имеет координаты A′ (x0; y0 + B).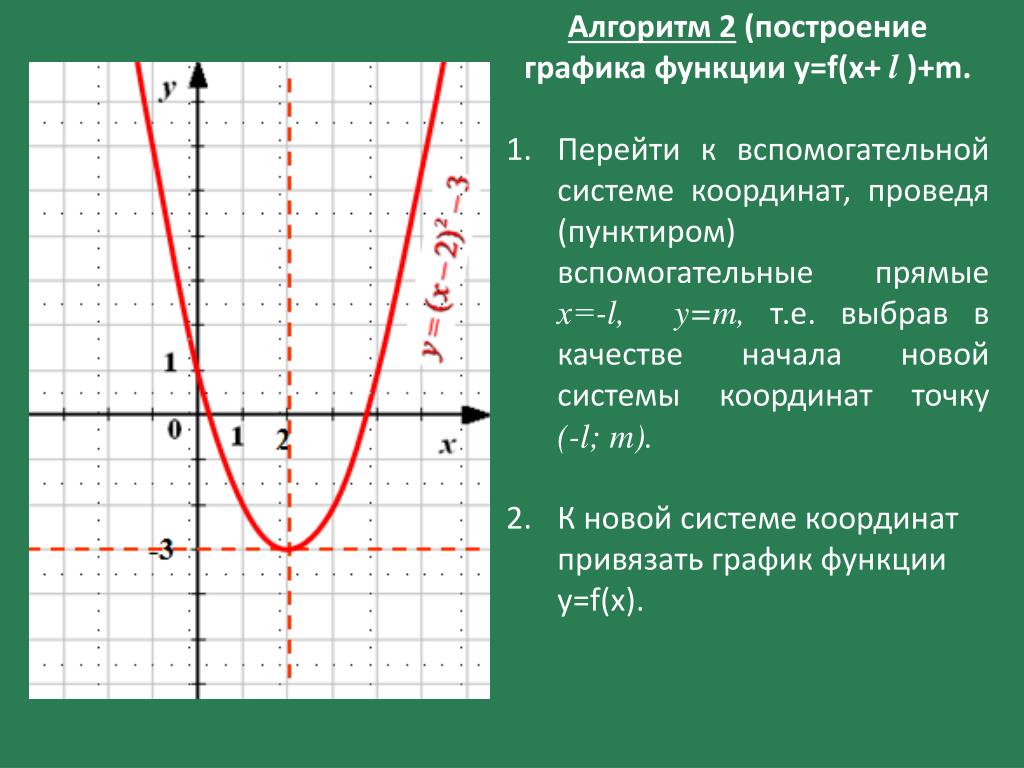 Точка A′ получается из точки A сдвигом на B вертикально вверх, если B > 0, и на |B| вниз, если B < 0. Обобщая это рассуждение на все точки, приходим к выводу, что график функции y = f (x) + B получается из графика функции y = f (x) параллельным переносом вдоль оси OY на B вверх, если B > 0, и на |B| вниз, если B < 0.
Точка A′ получается из точки A сдвигом на B вертикально вверх, если B > 0, и на |B| вниз, если B < 0. Обобщая это рассуждение на все точки, приходим к выводу, что график функции y = f (x) + B получается из графика функции y = f (x) параллельным переносом вдоль оси OY на B вверх, если B > 0, и на |B| вниз, если B < 0.
Алгебраически для каждой точки графика это можно записать системой {x′=x,y′=y+B, где x и y – координаты какой-либо точки старого графика, x′ и y′ – соответствующей ей точки нового.
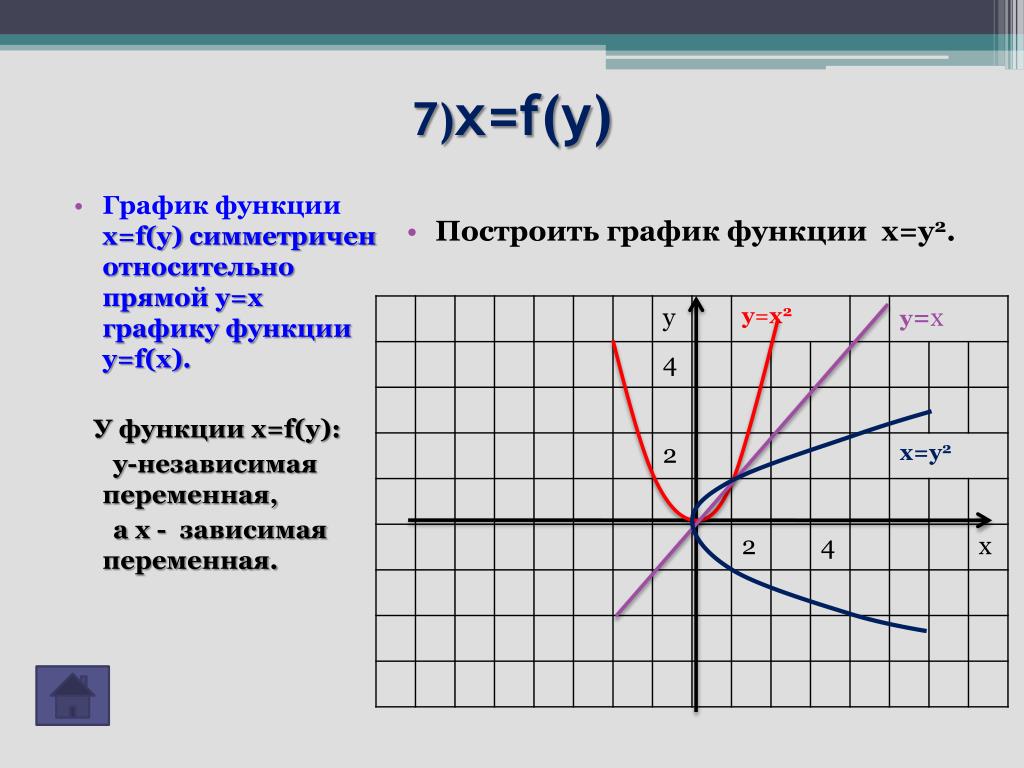
Аналогичным образом можно построить график функции y = f (x – b). Точка A′ (x′; y′) нового графика имеет такую же ординату, как и точка A (x; y), если x′ = x + b. Таким образом, чтобы построить точку A′, нужно сместить точку A вправо, если b > 0, и влево, если b < 0. 2
2
Найдём связь между графиками функций и .
Для этого изобразим в одной координатной плоскости графики функций , , .
Составим таблицы значений для функций:
Видно, что график функции можно получить из графика в квадрате параллельным переносом относительно оси х вправо на 6 единиц, m=6. А график функции параллельным переносом влево на 6 единиц, m=-6.
Определение:
График функции является параболой, которую можно получить из графика функции с помощью параллельного переноса вдоль оси х на m единиц вправо, если m>0, и на —m единиц влево, если m<0.
Пример.
Изобразить
графики функций вида ,
пользуясь уже известными определениями.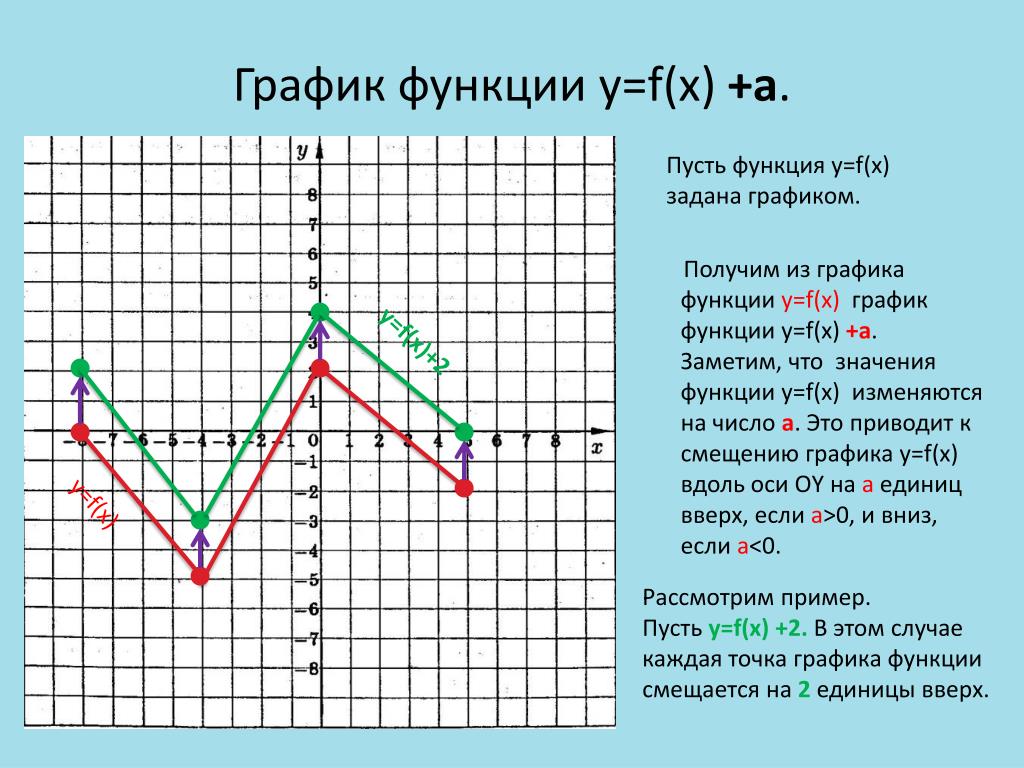
Используя шаблон , изобразим графики функции .
Сначала рассмотрим шаблон. Не трудно составить таблицу значений этой функции:
Получаем параболу.
Взглянем на формулу, которой задана функция . Это функция вида , в данном случае m=-4. Получить график этой функции можно с помощью параллельного переноса параболы относительно оси х на 4 единицы влево.
Получили график функции . Вершина данной параболы имеет координаты (-4,0).
Заметим, что вершина параболы будет иметь координаты (m,0).
Определение:
Функция вида – это парабола, которую можно получить из графика функции в квадрате с помощью двух параллельных переносов:
1. вдоль оси y на n единиц вверх, если n>0, и на —n единиц вниз, если n<0;
2. вдоль
оси x
на m
единиц вправо, если m>0,
и на —m
единиц влево, если m<0.
вдоль
оси x
на m
единиц вправо, если m>0,
и на —m
единиц влево, если m<0.
Параллельные переносы можно производить в любом порядке.
Вершина этой параболы будет иметь координаты (m,n).
Пример.
С помощью шаблона параболы изобразить график функции .
На рисунке видно, что m=-4, сдвигаем точки шаблона на 4 единицы влево и n=-3, сдвигаем полученный график на 3 единицы вниз. Получили график функции . Вершина имеет координаты (-4,-3).
Как построить график функции в Excel – База знаний Timeweb Community
График функции – графическое представление математического выражения, показывающее его решение. Для построения обычно используются линейные графики с точками, с чем прекрасно справляется Microsoft Excel. Кроме того, в нем еще можно выполнить автоматические расчеты, быстро подставив нужные значения. 2, заменив номер ячейки.
2, заменив номер ячейки.
Теперь достаточно зажать левую кнопку мыши на нижней точки готовой ячейки и растянуть таблицу, чтобы формула автоматически подставилась в остальные ячейки, и вы могли сразу ознакомиться с результатом.
Перейдите на вкладку вставки и выберите раздел с рекомендуемыми диаграммами.
В списке отыщите точечную диаграмму, которая подойдет для составления подходящего графика.
Вставьте ее в таблицу и ознакомьтесь с результатом. На следующем скриншоте вы видите параболу и значения X, при которых она получилась правильной (такую часто показывают в примерах на математике).
Всего 7 простых шагов потребовалось для достижения желаемого результата. Вы можете подставлять свои значения в таблицу и изменять их в любое время, следя за тем, как перестраивается график функций.
График функции y=sin(x)
y=sin(x) – вторая функция, которую мы возьмем за пример.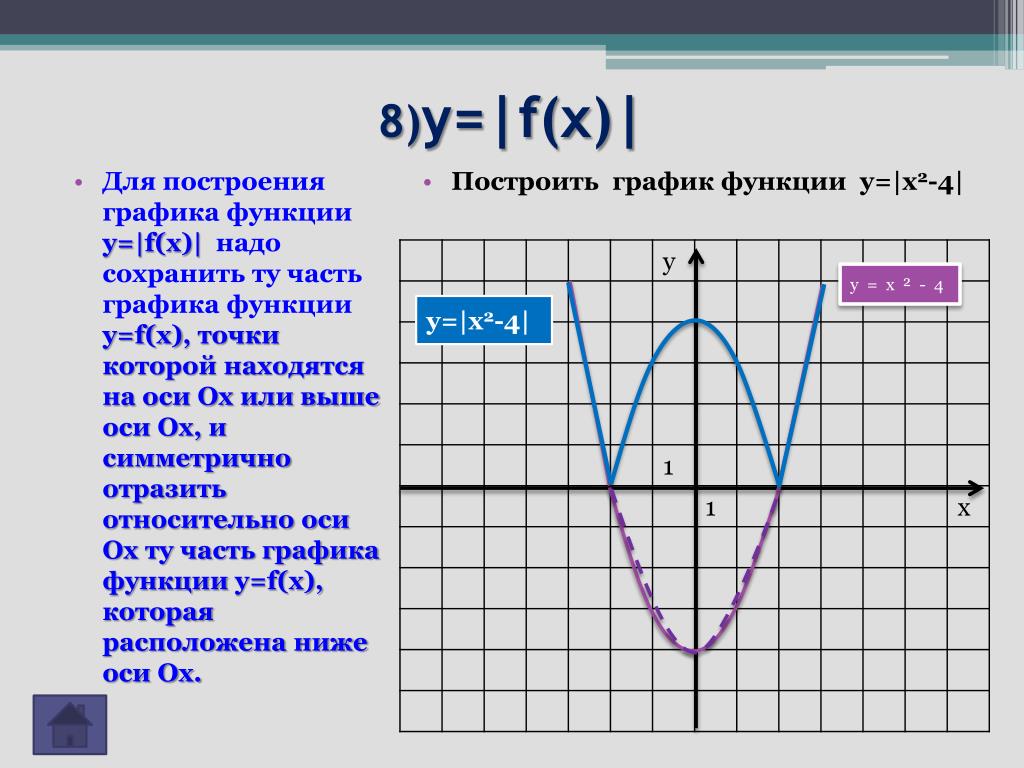 Может показаться, что ее составление осуществляется сложнее, хотя на самом деле это не так. Дело в том, что Excel сам посчитает значения, а вам останется только задать известные числа и вставить простой линейный график для вывода результатов на экран.
Может показаться, что ее составление осуществляется сложнее, хотя на самом деле это не так. Дело в том, что Excel сам посчитает значения, а вам останется только задать известные числа и вставить простой линейный график для вывода результатов на экран.
-
Если вам будет проще, впишите в отдельную клетку функцию, укажите интервал и шаг. Так вы не запутаетесь при дальнейшем заполнении ячеек.
-
Добавьте два столбца, в которые будут вписаны значения каждой оси. Это нужно не только для обозначения чисел, но и для их вычисления при помощи функций программы.
-
Начните вписывать значения X с необходимым интервалом и шагом. Кстати, вы можете заполнить всего несколько полей, а затем растянуть клетки таким же образом, как было показано в предыдущем примере, чтобы они подставились автоматически до конца вашего интервала.
-
Теперь более сложное, но не страшное действие – определение значения Y.
 Понятно, что он равняется синусу X, значит, нужно вписать функцию =SIN(A1), где вместо A1 используйте нужную ячейку, а затем растяните функцию на оставшийся интервал.
Понятно, что он равняется синусу X, значит, нужно вписать функцию =SIN(A1), где вместо A1 используйте нужную ячейку, а затем растяните функцию на оставшийся интервал. -
На следующем скриншоте вы видите результат заполнения таблицы. Используйте округление для удаления лишних знаков после запятой.
-
Вставьте обычную линейчатую диаграмму и ознакомьтесь с результатом.
На примере этих двух функций уже можно понять, как работает построение графиков в Экселе. При использовании других функций просто учитывайте особенности заполнения ячеек и не забывайте о том, что вам не нужно ничего считать, поскольку Excel все сделает за вас после указания необходимой формулы.
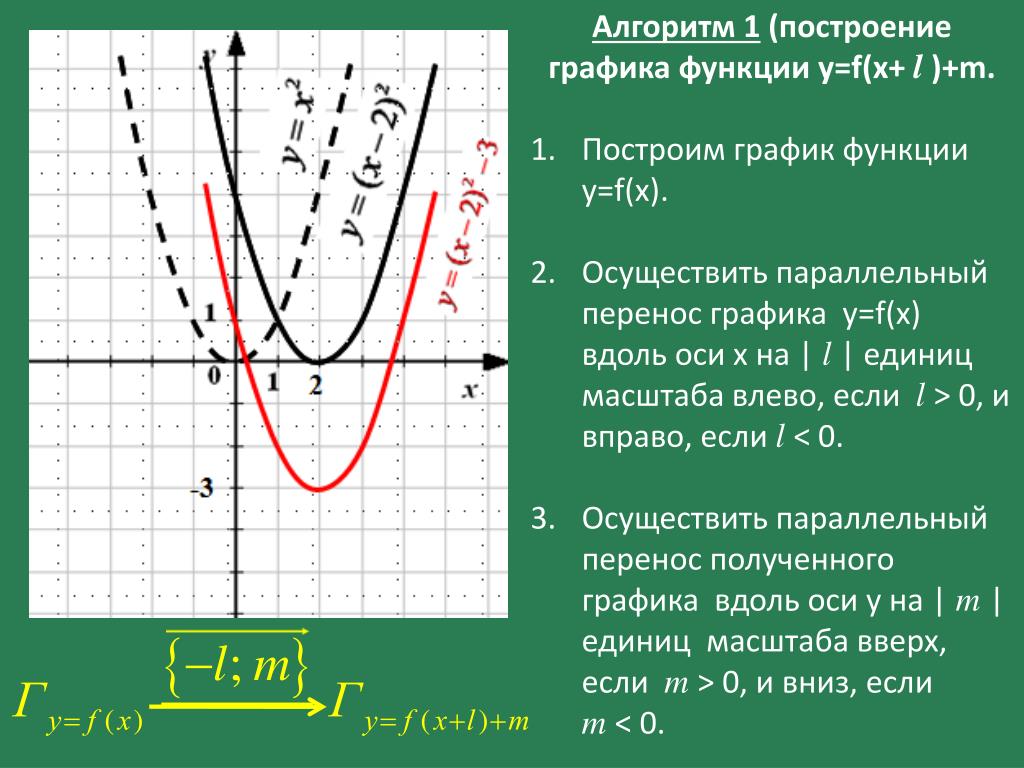
Как построить график функции y = f (x+l) и y = f (x)+m, если известен график функции y = f(x). 8-й класс
Цели:
- повторить правила построения и свойства графиков функций у = x2, , , у =| x |;
- выяснить правила построения графиков функций у = f (x + l) и у = f (x) + m;
- развить умение строить графики функций;
- развивать познавательную активность учащихся.

Оборудование: интерактивная доска, проектор, презентация к уроку.
ХОД УРОКА
1. Организационный момент
2. Устная работа (Приложение. Слайды 2-8.)
Задание: Графики каких функций
изображены на рисунках? (у = x2, у = – x2,
, , ,
, у =| x |, у =
– | x |).
Для каждой из функций сформулировать ее свойства
и правила построения графика функции.
3. Изучение нового материала (Приложение)
На координатной плоскости в тетрадях учащиеся по точкам строят графики функций у = x2 и у = x2 +1. Учащиеся самостоятельно приходят к выводу о сдвиге параболы (параллельном переносе) на 1 единицу вверх. (Слайд 10.)
На координатной плоскости в тетрадях учащиеся
по точкам строят графики функций у = x2
и у = x2– 1. Учащиеся
самостоятельно приходят к выводу о сдвиге
параболы (параллельном переносе) на 1 единицу
вниз. (Слайд 11.)
Учащиеся
самостоятельно приходят к выводу о сдвиге
параболы (параллельном переносе) на 1 единицу
вниз. (Слайд 11.)
На координатной плоскости в тетрадях учащиеся по точкам строят графики функций у = x2 и у = (x – 1)2. Учащиеся самостоятельно приходят к выводу о сдвиге параболы (параллельном переносе) на 1 единицу вправо. (Слайд 12.)
На координатной плоскости в тетрадях учащиеся по точкам строят графики функций у = x2 и у = (x + 1)2. Учащиеся самостоятельно приходят к выводу о сдвиге параболы (параллельном переносе) на 1 единицу влево. (Слайд 13.)
С помощью учителя учащиеся формулируют правило
построения графика функции у = f (x + l) и
графика функции у = f (x) + m с помощью
сдвига графика функции у = f (x).
(Слайды 14-18. Анимация сдвигов графиков на
слайдах помогает лучшему восприятию правила.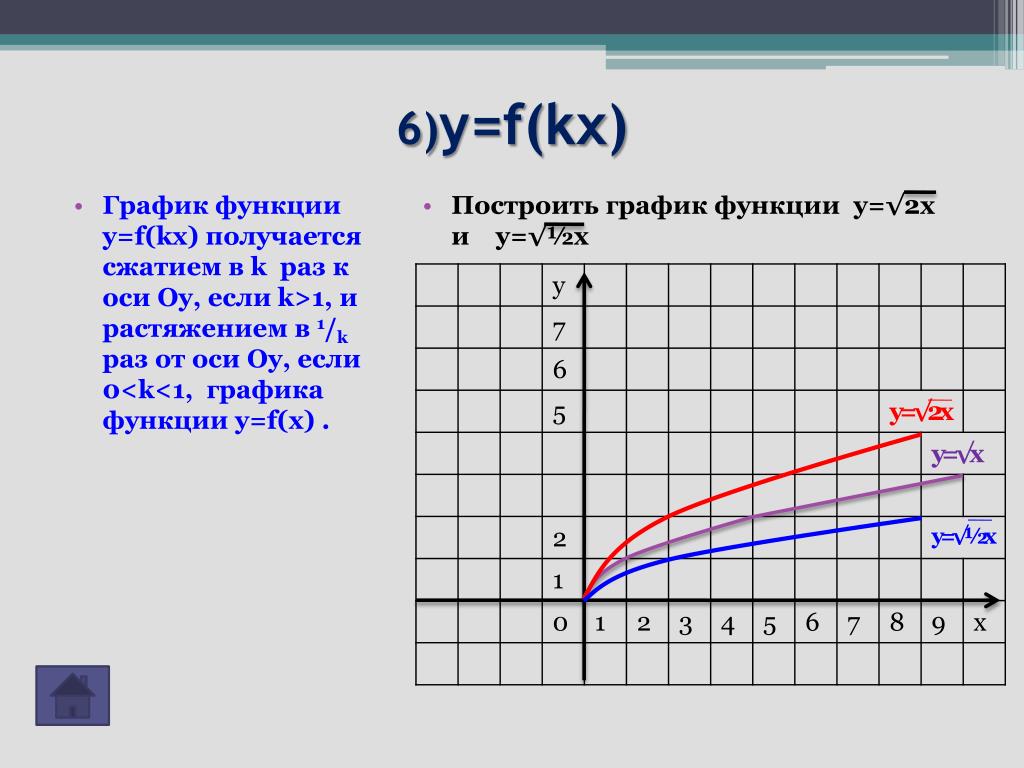 )
)
Затем рассматривается вариант построения графика функции у = f (x + l) и графика функции у = f (x) + m с помощью сдвига графика функции у = f (x), если известен график функции у = f (x) с помощью сдвига осей координат. (Слайды 19-23. Анимация сдвигов осей координат на слайдах помогает лучшему восприятию правила построения графиков.)
Правила построения графиков функций у = f (x + l) и у = f (x) + m записываются в тетрадь.
4. Закрепление материала
№ 19.6, № 20.6, № 19.11(в), № 19.12(в), № 19.13(в), № 19.14(в), № 20.11(в), № 20.12(в), № 20.13(в), № 20.14(в).
5. Домашнее задание
Параграф 19, 20 учебника, № 19.5, № 20.5, № 19.11–19.14(а), № 20.11–20.14(а).
6. Подведение итогов урока
Отражение y = f (-x) — Концепт
Существуют различные типы преобразований и их графики, один из которых является математическим отражением по оси y.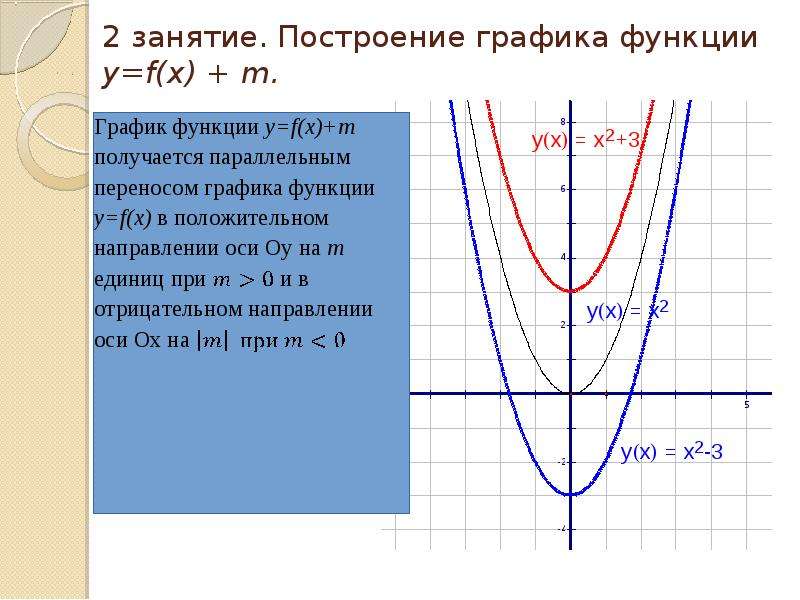 Если мы получим ту же функцию из математического отражения , это будет симметричная функция, в частности четная. Математическое отражение переворачивает график по оси y и имеет форму y = f (-x). Другие важные преобразования включают вертикальные сдвиги, горизонтальные сдвиги и горизонтальное сжатие.
Если мы получим ту же функцию из математического отражения , это будет симметричная функция, в частности четная. Математическое отражение переворачивает график по оси y и имеет форму y = f (-x). Другие важные преобразования включают вертикальные сдвиги, горизонтальные сдвиги и горизонтальное сжатие.
Поговорим об отражениях. Теперь вспомним, как отразить график y = f x по оси x. Все, что вам нужно сделать, это поставить знак минус перед f или x, верно? Y = -f of x переворачивает график по оси x. Но как отразить его по оси Y? Что ж, вместо того, чтобы переворачивать значения y, вы хотите перевернуть значения x. Таким образом, вы заменяете x на минус x, и это отразит график по оси y.
Итак, давайте рассмотрим пример y = 2 с отрицательным x. Это отражение какой родительской функции? Ну, это y равно x, верно? Это будет отражение y, равного x. Теперь, чтобы увидеть это, давайте нарисуем их вместе.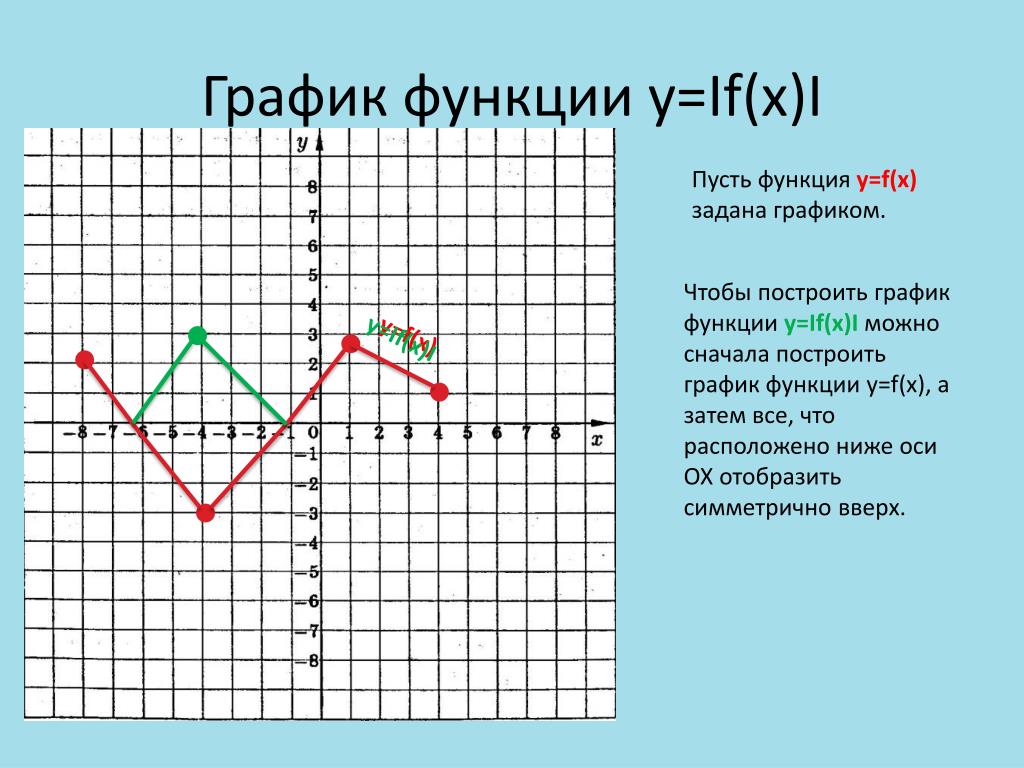 Итак, я хочу, чтобы график y был равен 2, а x, а y равен y, равен 2, вместе с -x. Мы называем y равным 2, так как x — это одна из наших родительских функций, которая имеет такую форму, как восходящая плавная кривая, проходящая через точку 0 1, и у нее есть горизонтальная асимптота на оси x y = 0.
Итак, я хочу, чтобы график y был равен 2, а x, а y равен y, равен 2, вместе с -x. Мы называем y равным 2, так как x — это одна из наших родительских функций, которая имеет такую форму, как восходящая плавная кривая, проходящая через точку 0 1, и у нее есть горизонтальная асимптота на оси x y = 0.
Нарисуем несколько точек. У нас есть u и 2 на u. Я собираюсь изменить переменные, чтобы упростить преобразование, и я собираюсь выбрать простые значения u, такие как -1 0 и 1, чтобы оценить 2 для u. 2 к отрицательному 1 — половина, 2 к 0 — 1, 2 к 1 — 2. Так что это хорошо и легко, а затем, чтобы сделать преобразование, я собираюсь сделать замену переменных -x = u . Итак, если я позволю u равняться -x и x = -u, и все, что мне нужно сделать, это изменить знак этих значений. Таким образом, -1 становится 1, 0 остается неизменным, а 1 становится -1.Но если -x = u, тогда на самом деле у меня здесь просто значения от 2 до u, поэтому эти значения просто копируются. Итак, я просто собираюсь построить график этих двух функций. Первые 2 на х. -1 половина, 0 1 и 1 2, и у меня есть узнаваемые 2 на графике x, который выглядит так.
Первые 2 на х. -1 половина, 0 1 и 1 2, и у меня есть узнаваемые 2 на графике x, который выглядит так.
А что насчет y равно 2 до -x? Разрешите выбрать другой цвет. У меня одна запятая на половину, у меня 0 1, поэтому проходит через эту точку и -1 2. Итак, это будет выглядеть так. Итак, как и было предсказано, это отражение, это отражение нашего родительского графа, y равняется 2 x.Это y равно 2 отрицательному x.
Просто помните, каждый раз, когда вы берете функцию и заменяете ее x на -x, вы отражаете график вокруг оси y. И это все.
Преобразование функции
Если вы начнете с простой родительской функции у знак равно ж ( Икс ) и его графика, некоторые модификации функции приведут к легко предсказуемым изменениям на графике.
Например:
Горизонтальный сдвиг
- Замена
ж
(
Икс
)
с участием
ж
(
Икс
—
б
)
приводит к смещению графика
б
единиц вправо.

\
- Замена ж ( Икс ) с участием ж ( Икс + б ) приводит к смещению графика б единиц слева.
Вертикальный сдвиг
- Замена ж ( Икс ) с участием ж ( Икс ) + c приводит к смещению графика c единиц вверх.
- Замена ж ( Икс ) с участием ж ( Икс ) — c приводит к смещению графика c единиц вниз.
Отражение
- Замена
Икс
с участием
—
Икс
приводит к тому, что график отображается на
у
-ось.

- Замена ж ( Икс ) с участием — ж ( Икс ) приводит к тому, что график отображается на Икс -ось.
Горизонтальное растяжение / сжатие
- Замена Икс с участием п Икс приводит к горизонтальному сжатию с коэффициентом п .
- Замена Икс с участием Икс п приводит к горизонтальному растяжению с коэффициентом п .
Вертикальное растяжение / сжатие
- Замена
ж
(
Икс
)
с участием
п
ж
(
Икс
)
приводит к вертикальному растяжению с коэффициентом
п
.

- Замена ж ( Икс ) с участием ж ( Икс ) п приводит к вертикальному сжатию с коэффициентом п .
Преобразования функций
Начнем с функции, в данном случае это f (x) = x 2 , но это может быть что угодно:
f (х) = х 2
Вот несколько простых вещей, которые мы можем сделать, чтобы переместить или масштабировать его на графике:
Мы можем переместить его вверх или вниз, добавив константу к значению y:
г (x) = x 2 + C
Примечание: чтобы переместить линию вниз на , мы используем отрицательное значение для C.
- C> 0 перемещает вверх
- C <0 перемещает его вниз
Мы можем переместить его влево или вправо, добавив константу к значению x:
г (x) = (x + C) 2
Добавление C перемещает функцию на влево на (отрицательное направление).
Почему? Что ж, представьте, что вы унаследуете состояние, когда вам будет лет = 25 лет.Если вы измените это значение на (возраст + 4) = 25 , вы получите его, когда вам исполнится 21 год. Добавление 4 сделало это раньше.
- C> 0 перемещает влево
- C <0 перемещает вправо
НО мы должны добавить C везде, где x появляется в функции (мы заменяем x + C на x).
Пример: функция v (x) = x
3 — x 2 + 4xЧтобы переместить пробелы C влево, добавьте C к x везде, где появляется x :
w (x) = (x + C) 3 — (x + C) 2 + 4 (x + C)
Простой способ запомнить, что происходит с графиком, когда мы добавляем константу:
добавить к y перейти high
добавить к x для перехода слева
Мы можем растянуть или сжать его в направлении y, умножив всю функцию на константу.
г (x) = 0,35 (x 2 )
- C> 1 растягивает
- 0
Мы можем растянуть или сжать его в направлении x, умножив x на константу.
г (x) = (2x) 2
- C> 1 сжимает
- 0
Обратите внимание, что (в отличие от направления y) большие значения вызывают большее сжатие .
Мы можем перевернуть его вверх дном, умножив всю функцию на −1:
г (x) = — (x 2 )
Это также называется отражением относительно оси x (ось, где y = 0)
Мы можем комбинировать отрицательное значение с масштабированием:
Пример: умножение на −2 перевернет его вверх ногами И растянет в направлении y.
Мы можем перевернуть его влево-вправо, умножив значение x на -1:
gif»>г (x) = (−x) 2
Он действительно переворачивает его влево и вправо! Но вы этого не видите, потому что x 2 симметрично относительно оси y.Итак, вот еще один пример с использованием √ (x):
г (х) = √ (−x)
Это также называется отражением относительно оси y (ось, где x = 0)
Сводка
| y = f (x) + C |
|
| y = f (x + C) |
|
| y = Cf (x) |
|
| y = f (Cx) |
|
| у = -f (х) | |
| y = f (−x) |
Примеры
Пример: функция g (x) = 1 / x
Вот что мы можем сделать:
Перемещение на 2 деления вверх: h (x) = 1 / x + 2
Перемещение на 3 деления вниз: h (x) = 1 / x — 3
Переместимся на 4 пробела вправо: h (x) = 1 / (x − 4) графикПеремещение на 5 делений влево: h (x) = 1 / (x + 5)
Растянуть на 2 по оси Y: h (x) = 2 / x
Сжать на 3 в направлении x: h (x) = 1 / (3x)
Переверните вверх дном: h (x) = −1 / x
Пример: функция v (x) = x
3 — 4xВот что мы можем сделать:
Перемещение на 2 места вверх: w (x) = x 3 — 4x + 2
Перемещение на 3 деления вниз: w (x) = x 3 — 4x — 3
Переместиться на 4 пробела вправо: w (x) = (x − 4) 3 — 4 (x − 4)
Переместите 5 пробелов влево: w (x) = (x + 5) 3 -4 (x + 5) график Растяните его на 2 по оси Y: w (x) = 2 (x 3 — 4x)
= 2x 3 — 8x
Сжать на 3 в направлении x: w (x) = (3x) 3 — 4 (3x)
= 27x 3 — 12x
Переверните вверх дном: w (x) = −x 3 + 4x
Все в одном.
 ..!
..!Мы можем выполнить все преобразования за один раз , используя это:
а — вертикальное растяжение / сжатие
- | а | > 1 растяжка
- | а | <1 компресс
- a <0 переворачивает график вверх ногами
б — растяжение / сжатие по горизонтали
- | b | > 1 компресс
- | b | <1 растяжка
- b <0 переворачивает график влево-вправо
c — горизонтальный сдвиг
- c <0 сдвиг вправо
- c> 0 сдвиг влево
d — вертикальный сдвиг
- d> 0 сдвигается вверх
- d <0 смещается вниз
Пример: 2√ (x + 1) +1
а = 2, с = 1, д = 1
Итак, берется функция квадратного корня, а затем
- Растягивает на 2 по оси Y
- Сдвигает влево на 1 и
- Поднимает 1
Поиграйте с этим графиком
преобразований
преобразований| Преобразования | Щелкните здесь, чтобы открыть связанный рабочий лист Mathcad: |
Один простой способ создать новую функцию из старой — добавить регулируемый параметр a . Мы называем эти модификации преобразованиями данного правила.
Мы называем эти модификации преобразованиями данного правила.
Предположим, нам дана функция f правилом y = f (x), которое описывается словесно, алгебраически, графически или численно. Есть несколько очевидных способов изменить правило, добавив регулируемый параметр a :
|
|
|
|
Эти базовые преобразования позволяют «преобразовать функцию в форму». Если вы начинаете с «известной» функции приблизительно правильного формы , преобразования — по отдельности или в комбинации — добавляют настраиваемые параметры, которые позволяют вам точно настроить форму, если необходимо, чтобы соответствовать конкретной ситуации моделирования.
Если вы начинаете с «известной» функции приблизительно правильного формы , преобразования — по отдельности или в комбинации — добавляют настраиваемые параметры, которые позволяют вам точно настроить форму, если необходимо, чтобы соответствовать конкретной ситуации моделирования.
Как отразить график по оси Y
Прежде чем мы перейдем к отражениям по оси Y, убедитесь, что вы освежили свою память о том, как выполнять простой вертикальный и горизонтальный перенос.
Отражение по оси Y
Одно из самых простых преобразований, которое можно выполнить с помощью простых функций, — это его отражение по оси Y или другой вертикальной оси. В потенциальном тестовом вопросе это можно сформулировать по-разному, поэтому убедитесь, что вы понимаете следующие термины как еще один способ сказать «выполнить отражение по оси Y»:
• График y = f (−x) y = f (-x) y = f (−x)
• График f (−x) f (-x) f (−x)
• f (−x) f (-x) f (−x) отражение
• Или просто: f (−x) f (-x) f (−x)
Чтобы сделать это, процесс чрезвычайно прост: для любой функции, какой бы сложной она ни была, просто выберите легко определяемые координаты, разделите координату x на (-1), а затем заново постройте график. эти координаты.Вот и все!
эти координаты.Вот и все!
Лучший способ попрактиковаться в рисовании отражений по оси Y — это выполнить пример задачи:
Пример:
Учитывая график y = f (x) y = f (x) y = f (x), как показано, эскиз y = f (−x) y = f (-x) y = f (−x).
Помните, единственный шаг, который мы должны сделать перед построением f (-x) отражения, — это просто разделить x-координаты легко определяемых точек на нашем графике выше на (-1). Когда мы говорим «легко определяемые точки», это означает просто точки, для которых вы знаете значения x и y , точно .Не выбирайте точки, в которых вам нужно оценить значения, так как это излишне усложняет задачу. Ниже приведены несколько изображений, которые помогут вам наглядно представить, как решить эту проблему.
Шаг 1. Знайте, что мы отражаемся поперек оси Y
Шаг 2: Определите точки, которые легко определить
Шаг 3. Разделите эти точки на (-1) и нанесите новые точки
Чтобы получить визуальный инструмент, который поможет вам в вашей практике и проверить свои ответы, перейдите по этой фантастической ссылке здесь.
Как найти ось симметрии
В некоторых случаях вам будет предложено выполнить вертикальное отражение по оси симметрии, которая не является осью Y. Но прежде чем мы перейдем к решению этой проблемы, важно знать, что мы подразумеваем под «осью симметрии». Ось симметрии — это просто вертикальная линия, по которой мы выполняем отражение. Это может быть ось Y или любая вертикальная линия с уравнением x = константа, например x = 2, x = -16 и т. Д.
Нахождение оси симметрии, как и построение самих отражений, также является простым процессом.В этом случае все, что нам нужно сделать, это выбрать ту же точку как на функции, так и на ее отражении, посчитать расстояние между ними и разделить это на 2. Это потому, что, по его определению, ось симметрии равна ровно в середине функции и ее отражения.
Лучший способ попрактиковаться в нахождении оси симметрии — это решить задачу-пример:
Пример:
Найдите ось симметрии для двух функций, показанных на изображении ниже.
Опять же, все, что нам нужно сделать для решения этой проблемы, — это выбрать одну и ту же точку в обеих функциях, посчитать расстояние между ними и разделить на 2. Давайте выберем исходную точку для этих функций, так как это самый простой вариант. с участием.
Теперь, посчитав расстояние между этими двумя точками, вы должны получить ответ 8 единиц. Последний шаг — разделить это значение на 2, что даст нам x = 4 в качестве нашей оси симметрии! Давайте посмотрим, как бы это выглядело, если бы там была настоящая строка:
Вот и все! Для дальнейшего изучения преобразований функций по отношению к тригонометрическим функциям см. Наши уроки о преобразованиях тригонометрических графиков и о том, как найти тригонометрические функции по графикам.
Что на самом деле означает y = f (x)?
Привет, Джон,
Я считаю, что иногда полезно думать о функции как о машине, когда вы вводите число в качестве входных данных для машины и получаете число в качестве выходных данных.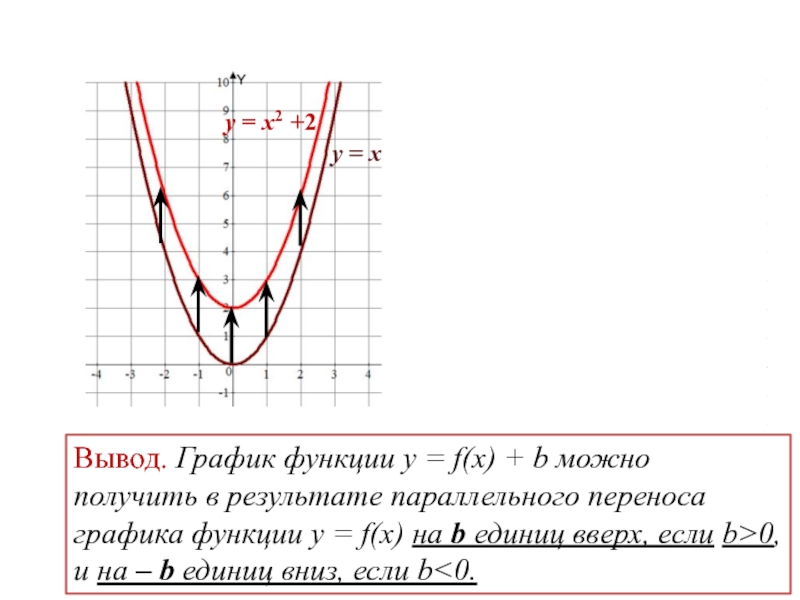 Имя функции $ f, $ вход $ x $ и выход $ f (x), $ read «$ f $ of $ x». $ Выход $ f (x) $ иногда получает дополнительное имя $ y $ на $ y = f (x). $
Имя функции $ f, $ вход $ x $ и выход $ f (x), $ read «$ f $ of $ x». $ Выход $ f (x) $ иногда получает дополнительное имя $ y $ на $ y = f (x). $
На ум приходит функция вычисления квадратного корня на вашем калькуляторе. Имя функции — $ \ sqrt {\; \;} $, и мы обычно пишем функцию как $ f (x) = \ sqrt {x}.2 — 4 = 9 — 4 = 5. $ Чтобы построить график этой функции, я бы начал с выбора некоторых значений $ x $, и, поскольку у меня есть возможность выбирать, я бы выбрал значения, которые упрощают арифметику. Например, $ x = 0, x = 1, x = -1 $ и так далее. Я собираюсь отслеживать, что я делаю, с помощью таблицы.
x | y = f (x) |
|---|---|
0 | -4 |
1 | -3 |
-1 | -3 |
2 | 0 |
3 | 5 |
Добавьте еще несколько строк в таблицу, выбрав собственные значения $ x.
 Причем, чем больше значение k, тем круче идет прямая.
Причем, чем больше значение k, тем круче идет прямая.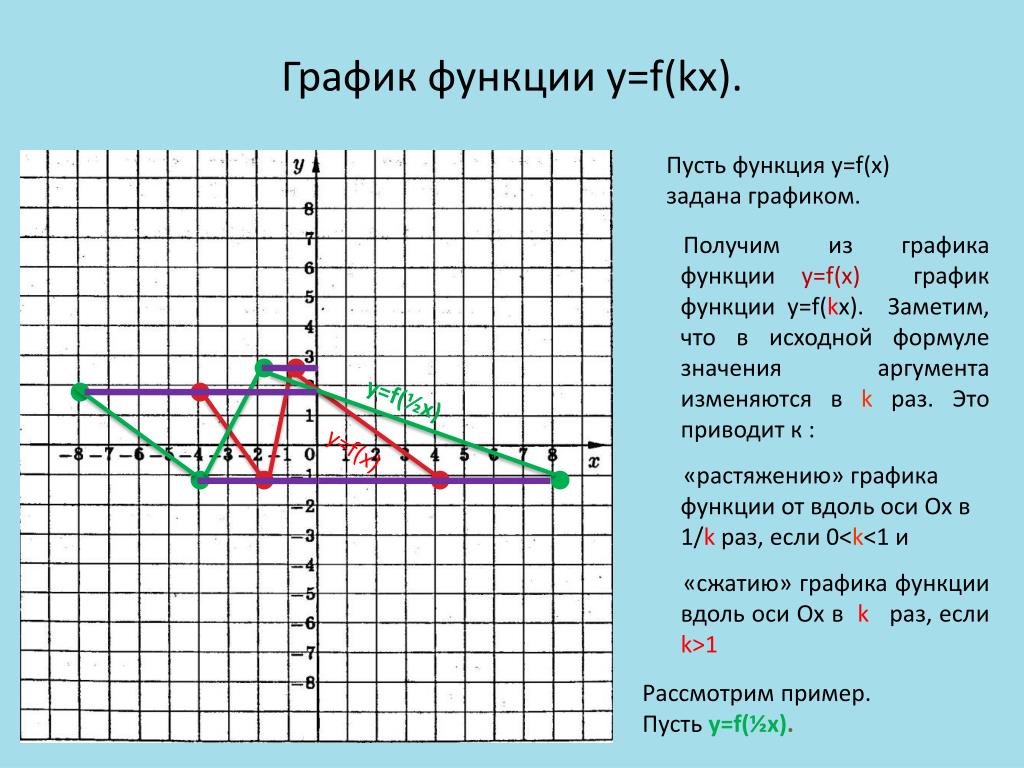
 Понятно, что он равняется синусу X, значит, нужно вписать функцию =SIN(A1), где вместо A1 используйте нужную ячейку, а затем растяните функцию на оставшийся интервал.
Понятно, что он равняется синусу X, значит, нужно вписать функцию =SIN(A1), где вместо A1 используйте нужную ячейку, а затем растяните функцию на оставшийся интервал.



 Они растягивают по горизонтали ( a a
Они растягивают по горизонтали ( a a