График функции y x 2 4: Постройте график функции y = x^2-4

Posted on by alexxlab
{2}} — \frac{4}{x + 2} = 0$$
Решаем это уравнение
Корни этого ур-ния
$$x_{1} = — \frac{4}{3} + \frac{4}{9 \sqrt[3]{\frac{2 \sqrt{105}}{9} + \frac{62}{27}}} + \sqrt[3]{\frac{2 \sqrt{105}}{9} + \frac{62}{27}}$$
Зн. экстремумы в точках:
                                                                                                                     /           ________________                          \ 
                                                                                                                     |          /          _____                           | 
                                                                                                                     |  4      /  62   2*\/ 105                4           | 
                                                                                                                   4*|- - + 3 /   -- + ---------  + -----------------------| 
                                                                                                                     |  3   \/    27       9               ________________| 
                                                                                                               2     |                                    /          _____ | 
            ________________                            /           ________________                          \      |                                   /  62   2*\/ 105  | 
           /          _____                             |          /          _____                           |      |                              9*3 /   -- + --------- | 
   4      /  62   2*\/ 105                4             |  4      /  62   2*\/ 105                4           |      \                                \/    27       9     / 
(- - + 3 /   -- + ---------  + -----------------------, |- - + 3 /   -- + ---------  + -----------------------|  - ---------------------------------------------------------)
   3   \/    27       9               ________________  |  3   \/    27       9               ________________|                ________________                              
                                     /          _____   |                                    /          _____ |               /          _____                               
                                    /  62   2*\/ 105    |                                   /  62   2*\/ 105  |       2      /  62   2*\/ 105                4               
                               9*3 /   -- + ---------   |                              9*3 /   -- + --------- |       - + 3 /   -- + ---------  + -----------------------    
                                 \/    27       9       \                                \/    27       9     /       3   \/    27       9               ________________    
                                                                                                                                                        /          _____     
                                                                                                                                                       /  62   2*\/ 105      
                                                                                                                                                  9*3 /   -- + ---------     
                                                                                                                                                    \/    27       9

Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимумы функции в точках:
$$x_{1} = — \frac{4}{3} + \frac{4}{9 \sqrt[3]{\frac{2 \sqrt{105}}{9} + \frac{62}{27}}} + \sqrt[3]{\frac{2 \sqrt{105}}{9} + \frac{62}{27}}$$
Максимумов у функции нет

Убывает на промежутках

[-4/3 + 4/(9*(2*sqrt(105)/9 + 62/27)**(1/3)) + (2*sqrt(105)/9 + 62/27)**(1/3), oo)

Возрастает на промежутках
(-oo, -4/3 + 4/(9*(2*sqrt(105)/9 + 62/27)**(1/3)) + (2*sqrt(105)/9 + 62/27)**(1/3)]

Содержание

«График квадратичной функции».

9-й класс

Цель урока:

  1. научить изображать схематически графики функций y = ax2 + n и y = a(x-m)2;
  2. уметь указывать на рисунке соответствующую формулу для графика функций;
  3. строить с помощью шаблона параболы графики функций.

Задачи урока:

Образовательные:

  • расширить сведения о свойствах квадратичной функции;
  • ознакомить учащихся с графиками частных видов квадратичной;
  • научить строить и выполнять преобразования графиков квадратичной функции.

Развивающие:

  • развитие у учащихся аналитического мышления;
  • развитие речи (расширение математического словаря).

Воспитательные:

  • привитие практических умений и навыков по построению графиков;
  • воспитание познавательной активности;
  • воспитание ответственности;
  • воспитание культуры диалога.

Тип урока: формирование новых знаний и умений.

План урока:

  1. Организационный момент.
  2. Устная работа.
  3. Изучение нового материала.
  4. Тренировочные упражнения.
  5. Самостоятельная работа.
  6. Итог урока.
  7. Сообщение домашнего задания.

Ход урока

I. Организационный момент

II. Устная работа
  • Дайте определение функции.
  • Какая функция называется квадратичной? Приведите примеры.
  • Что представляет собой график функции y = ax2?
  • В каких четвертях расположен график функции y = ax2 при а>0 и при а< 0?

III. Изучение нового материала

Пример 1

Построим графики функций y = x2 и y = — x2.

X -3 -2 -1 0 1 2 3
Y = x2 9 4
1		 0 1 4 9
Y = -x2 -9 -4 -1 0 -1 -4 -9

При любом значении х значения функций y = x2 и y = — x2 являются противоположными числами, значит соответствующие точки графиков симметричны относительно оси х (см. рис.1).


рис. 1

Вывод: График функции y= — ax2 можно получить из графика функции y = ax2 c помощью симметрии относительно оси х.

Пример 2

Построим графики функций y = x2 и y = x2 + 2.

Составим таблицу значений этих функций при одних и тех же значениях аргумента.

X -3 -2 -1 0 1 2 3
y=x2 9 4
1		 0 1 4 9
y=x2+ 2 11 6 3 2 3 6 11

Эта таблица подсказывает, что каждой точке (x0;y0) графика функции y = x2 соответствует точка (xo;y0+2) графика функции y = x2 + 2. Следовательно, график функции y = x2 + 2 получен в результате параллельного переноса графика функции y = x

2 на две единицы вверх (см. рис. 2).


рис 2.

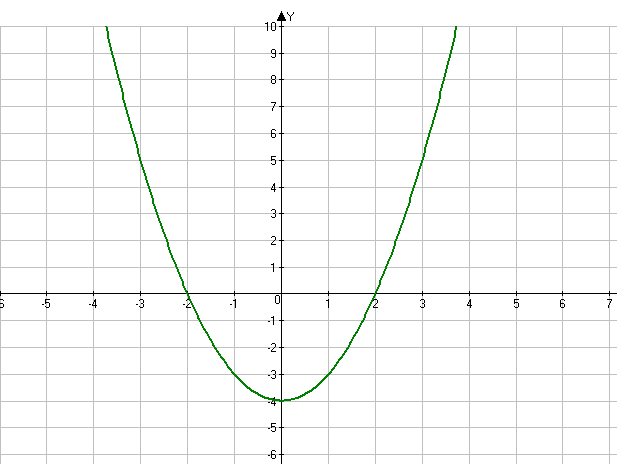
Аналогично график функции y = x2 — 4 можно получить в результате параллельного переноса графика функции y = x2 на 4 единицы вниз (см. рис.3).


рис. 3

Вывод: График функции y= ax2 + n можно получить в результате параллельного переноса графика функции y = ax2 на n единиц вверх, если n > 0 и на — n единиц вниз, если n <0.

Пример 3. Построим графики функций y = (x + 2)2 и y = (x — 2)2.

x -4 -3 -2 -1 0
1		 2 3 4
y=x2 16 9 4 1 0 1 4 9 16
y=(x+ 2)2 4 1 0 1 4 9 16 25 36
y= (x-2)2 36 25 16 9 4 1 0 1 4

По таблице видим, что график функции y=(x+2)2 получен в результате параллельного графика функции y = x2 на две единицы влево; график функции y=(x-2)2 получен в результате переноса на две единицы вправо (см. рис. 4 и рис. 5).


рис. 4


рис. 5

Вывод: График функции y=а(х-m)2 можно получить в результате параллельного переноса графика функции y = ax2 на m единиц влево, если — m < 0 и на m единиц вправо, если m > 0.

Пример 4. Построим график функции y = (x -1)2 +3.

Решение:

Построим шаблон графика функции y = x2.

Параллельно перенесем график функции y=x2 на 1 единицу вправо. Получим график функции y = (x-1)2.

Параллельно перенесем график функции y= (x-1)2 на 3 единицы вверх. Получим график функции y = (x-1)2 +3 (см. рис. 6).


рис. 6

IV. Тренировочные упражнения

1. График какой функции получим, если график функции y = x2 параллельно перенесем:

  1. на 6 единиц вверх;
  2. на 9 единиц вправо;
  3. на 12 единиц вниз;
  4. на 7 единиц влево;
  5. на 2 единицы вправо и на 3 единицы вниз;
  6. на 1 единицу влево и на 1 единицу вверх?

2. Задайте формулами вида y = ax2 + n, y = a(x — m)2 , y = a(x — m)2 + n функции, графики которых изображены на рисунках: 


рис. 7


рис. 8


рис. 9


рис. 10


рис. 11


рис. 12

V. Самостоятельная работа с последующей проверкой

(Учащимся раздаются карточки с индивидуальными заданиями).

Вариант 1

1. Используя шаблон параболы y = x2 постройте график функции:

а) y = x2 – 4;

б) y = (x-3)2;

в) y = -x2 +3;

г) y = (x + 3)2 – 3

д) y = — (x + 1)2 + 2;

2. Дополнительное задание: изобразите схематически график функции: y=¼(x — 2)2 – 3.

Вариант 2

1. Используя шаблон параболы y = x2 постройте график функции:

а) y = x2 – 3;

б) y = (x+1)2;

в) y = — x2 + 2;

г) y = — (x — 1)2 + 3;

д) y = — (x + 2)2 + 4.

2. Дополнительное задание: изобразите схематически график функции: y= -¼(x + )2+3.

VI. Итог урока

Ответьте на вопросы:

  • Как можно получить график функции y = ax2 + n, используя график функции y = ax2?
  • Как можно получить график функции y = a(x — m)2, используя график функции y = ax2?
  • Как можно получить график функции y = a(x — m)2 + n, используя график функции y = ax2?

VII. Задание на дом

Учебник «Алгебра 9» , авторы Ю.Н. Макарычев и др.

П. 6 №№ 107,108,110, на повторение № 119.

Функция y=ax^2, её график и свойства

Будьте внимательны! У Вас есть 10 минут на прохождение теста. Система оценивания — 5 балльная. Разбалловка теста — 3,4,5 баллов, в зависимости от сложности вопроса. Порядок заданий и вариантов ответов в тесте случайный. С допущенными ошибками и верными ответами можно будет ознакомиться после прохождения теста. Удачи!

Список вопросов теста

Вопрос 1

Функцию вида y=ax2+bx+c называют … .

Варианты ответов
  • линейной
  • квадратичной
  • кубической
Вопрос 2

Из приведённых ниже функций выберите квадратичные.

Варианты ответов
  • y=7x+5

  • y=3x2-2x+1

  • y=12x2-1

  • y=8x3-x+3

Вопрос 3

Запишите название графика квадратичной функции.

Вопрос 4

Сколько нулей функции может иметь квадратичная функция?

Варианты ответов
Вопрос 5

Направление ветвей параболы зависит от коэффициента . .. .

Варианты ответов
Вопрос 6

Выберите те функции, графиками которых является парабола с ветвями направленными вниз.

Варианты ответов

  • y=x2-x3

  • y=3-2x2

  • y=-x2+x-1

  • y=x2+4x+4

Вопрос 7

График функции y=ax2 всегда проходит через точку с координатами . .. .

Варианты ответов
  • (0;0)
  • (1;1)
  • (-1;1)
  • (1;-1)
  • (-1;-1)
Вопрос 8

По графику определите знак старшего коэффициента квадратичной функции. (в ответ запишите только знак + или -)

 

Вопрос 9

Выберите точки, принадлежащие графику функции y=3x2.

Варианты ответов
  • A(2;9)
  • B(-2;12)
  • C(2;12)
  • D(0;3)
  • E(5;13)
Вопрос 10

Установите соответствие между функцией и её нулями.

Варианты ответов

  • y=x2-1

  • y=3x2

  • y=4-x2

  • y=3x2+7

2-4?

Глоримар М.

спросил • 15.12.20

Более

График будет отражен по оси X, а затем сдвинут вниз на 4 единицы.

Все еще ищете помощи? Получите правильный ответ быстро.

ИЛИ
Найдите онлайн-репетитора сейчас

Выберите эксперта и познакомьтесь онлайн. Никаких пакетов или подписок, платите только за необходимое время.

¢ € £ ¥ ‰ µ · • § ¶ SS ‹ › « » < > ≤ ≥ — — ¯ ‾ ¤ ¦ ¨ ¡ ¿ ˆ ˜ ° — ± ÷ ⁄ × ƒ ∫ ∑ ∞ √ ∼ ≅ ≈ ≠ ≡ ∈ ∉ ∋ ∏ ∧ ∨ ¬ ∩ ∪ ∂ ∀ ∃ ∅ ∇ * ∝ ∠ ´ ¸ ª º † ‡ А А Â Ã Ä Å Æ Ç È Э Ê Ë Я Я Я Я Ð Ñ Ò Ó Ô Õ Ö Ø О Š Ù Ú Û Ü Ý Ÿ Þ à á â г ä å æ ç è э э ë я я я я ð ñ ò о ô х ö ø œ š ù ú û ü ý þ ÿ А В Γ Δ Е Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Р Σ Τ Υ Φ Χ Ψ Ω α β γ дельта ε ζ η θ ι κ λ μ ν ξ ο π ρ ς σ τ υ φ х ψ ω ℵ ϖ ℜ ϒ ℘ ℑ ← ↑ → ↓ ↔ ↵ ⇐ ⇑ ⇒ ⇓ ⇔ ∴ ⊂ ⊃ ⊄ ⊆ ⊇ ⊕ ⊗ ⊥ ⋅ ⌈ ⌉ ⌊ ⌋ 〈 〉 ◊

Линейные уравнения в координатной плоскости (Алгебра 1, Визуализация линейных функций) — Mathplanet

Линейное уравнение — это уравнение с двумя переменными, график которого представляет собой линию. График линейного уравнения представляет собой набор точек на координатной плоскости, все из которых являются решениями уравнения. Если все переменные представляют действительные числа, можно построить уравнение, нанеся достаточное количество точек для распознавания шаблона, а затем соединив точки, чтобы включить все точки.

Если вы хотите построить график линейного уравнения, у вас должно быть как минимум две точки, но обычно рекомендуется использовать более двух точек. При выборе очков старайтесь включать как положительные, так и отрицательные значения, а также ноль.

Пример

Привить функцию y = x + 2

Начните с выбора нескольких значений x, например. -2, -1, 0, 1 и 2 и вычислить соответствующие значения y.

Х Y = х + 2 Заказанная пара
-2 -2 + 2 = 0 (-2, 0)
-1 -1 + 2 = 1 (-1, 1)
0 0 + 2 = 2 (0, 2)
1 1 + 2 = 3 (1, 3)
2 2 + 2 = 4 (2, 4)

Теперь вы можете просто нанести пять упорядоченных пар на координатную плоскость

На данный момент это пример дискретной функции.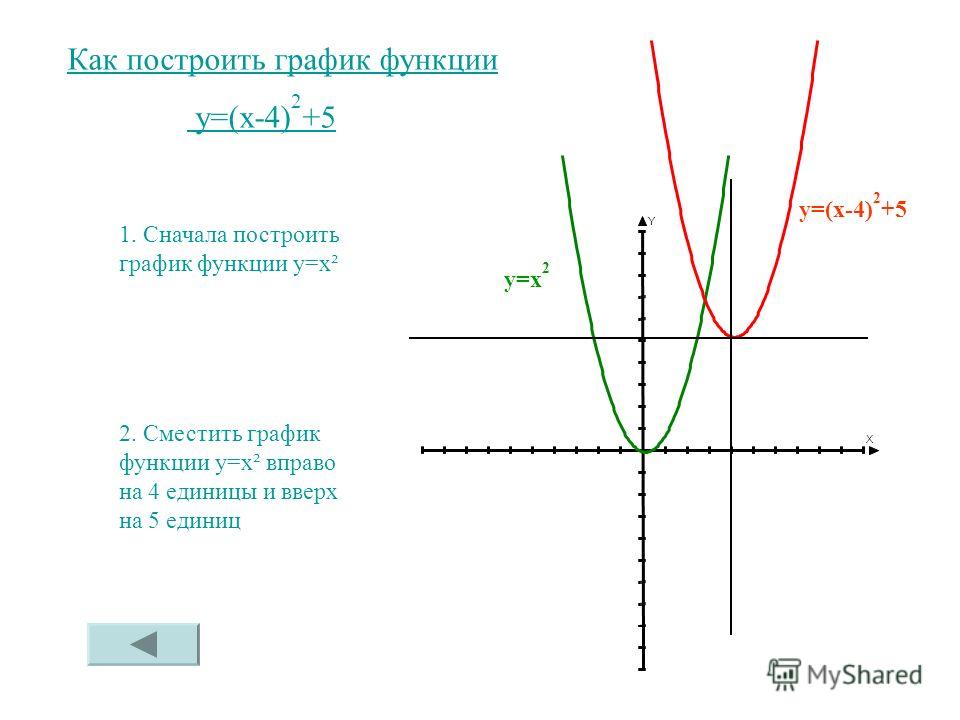 Дискретная функция состоит из изолированных точек.

Проведя линию через все точки и продолжая линию в обоих направлениях, мы получим противоположность дискретной функции, непрерывную функцию, которая имеет непрерывный график.

Если вы хотите использовать только две точки для определения линии, вы можете использовать две точки, где график пересекает оси. Точка пересечения графика с осью x называется точкой пересечения графика с осью y, а точка пересечения графика с осью y называется точкой пересечения графика с осью y.Пересечение x находится путем нахождения значения x, когда y = 0, (x, 0), а пересечение y находится путем нахождения значения y, когда x = 0, (0, y).

Стандартная форма линейного уравнения

$$Ax+By = C,\: \: A,B\neq 0$$

Прежде чем построить линейное уравнение в его стандартной форме, сначала нужно решить уравнение относительно y.

$$2y-4x=8$$

$$2y-4x\, {\color{green} {+\, 4x}}=8\, {\color{green} {+\, 4x}}$$

$$2г=4x+8$$

$$\frac{2y}{{\color{green} 2}}=\frac{4x}{{\color{green} 2}}+\frac{8}{{\color{green} 2}} $$

$$y=2x+4$$

Отсюда вы можете построить уравнение, как мы сделали в примере выше.

График y = a представляет собой горизонтальную линию, где линия проходит через точку (0, a)

Принимая во внимание, что график x = a представляет собой вертикальную линию, проходящую через точку (a, 0)

Видеоурок

Нарисуйте график линейного уравнения y =3x — 2

1.3 Функции

Функция $y=f(x)$ есть правило для определения $y$, когда нам дано значение $x$.Например, правило $y=f(x)=2x+1$ — функция. Любая линия $y=mx+b$ называется линейной функцией. График функции выглядит как кривая выше (или ниже) оси $x$, где для любого значения $x$ правило $y=f(x)$ говорит нам, как далеко можно подняться выше (или ниже) Ось $x$, чтобы достичь кривой.

Функции могут быть определены различными способами: алгебраической формулой или несколькими алгебраические формулы, графиком или экспериментально установленной таблицей значений. (В последнем случае таблица дает набор точек на плоскости, которые мы могли бы затем интерполируйте плавной кривой, если это имеет смысл.2$ $y=f(x) = \sqrt{x}$ $y=f(x)=\frac{1}{x}$

Рисунок 1.3.1. Некоторые графики.

Например, функция квадратного корня $y=f(x)=\sqrt{x}$ является правилом в котором говорится, что для заданного значения $x$ нужно взять неотрицательное число, квадрат равен $x$. Это правило имеет смысл только в том случае, если $x$ положительно или равно нулю. Мы говорим, что область определения этой функции равна $x\ge 0$, или, более формально, $\{x\in\R\mid x\ge 0\}$. Поочередно, мы можно использовать интервальную нотацию и написать, что домен равен $[0,\infty)$.(В записи интервала квадратные скобки означают, что конечная точка включены, а скобки означают, что конечная точка не включена.) Тот факт, что областью определения $y=\sqrt{x}$ является $[0,\infty)$, означает, что в график этой функции (см. рис. 1.3.1) у нас есть точки $(x,y)$ только над $x$-значениями в правой части $x$-ось.

Другой пример функции, областью определения которой является не вся ось $x$. есть: $y=f(x)=1/x$, обратная функция. Мы не можем заменить $x=0$ в этой формуле.Однако функция имеет смысл для любого ненулевого $x$, поэтому мы берем домен следующим образом: $\{x\in\R\mid x\ne 0\}$. График этой функции нет точек $(x,y)$ с $x=0$. Как $х$ приближается к 0 с любой стороны, график уходит в бесконечность. Назовем вертикальную линию $x=0$ асимптотой .

Подводя итог, можно выделить две причины, по которым некоторые значения $x$ исключаются из область определения функции заключаются в том, что (i) мы не можем делить на ноль и (ii) мы не можем извлечь квадратный корень из отрицательного числа.2$ это все $\R$. Но в контексте задачи-рассказа о нахождении площадей квадратов мы ограничиваем область определения положительными значениями $x$, потому что квадрат с отрицательной или нулевой стороной не имеет смысла.

В задаче чистой математики мы обычно берем в качестве предметной области все значения $x$, при которых формулы могут быть вычислены. Но в проблема с историей могут быть дополнительные ограничения на домен потому что только определенные значения $x$ представляют интерес или имеют практическое значение. смысл.

В задаче на историю часто используются буквы, отличные от $x$ и $y$.3$. Кроме того, могут использоваться буквы, отличные от $f$. Например, если $y$ равно скорость чего-либо в момент времени $t$, мы можем написать $y=v(t)$ с буква $v$ (вместо $f$), обозначающая функцию скорости (и $t$ играет роль $x$).

Буква, играющая роль $x$, называется независимым переменная , а буква, играющая роль $y$, называется зависимая переменная (поскольку ее значение «зависит от» значения независимого Переменная).В задачах истории, когда один должен перевести с английского языка на математический, решающим шагом является определить, какие буквы обозначают переменные. Если только слова и нет буквы даны, то мы должны решить, какие буквы использовать. Немного буквы традиционные. Например, почти всегда $t$ означает время.

Пример 1.3.1. Ящик с открытым верхом сделан из $a\times b$ прямоугольного куска картона, вырезав квадрат со стороной $x$ из каждого из четырех углы, а затем загибаем стороны вверх и герметизируем их воздуховодом Лента.Найдите формулу зависимости объема $V$ ящика от $x$ и найти область определения этой функции.

Получившийся ящик будет иметь высоту $x$ и прямоугольное основание размеры $a-2x$ на $b-2x$. Таким образом, $$ V=f(x)=x(a-2x)(b-2x). $$ Здесь $a$ и $b$ — константы, а $V$ — переменная, зависящая от на $x$, т. е. $V$ играет роль $y$.

Эта формула имеет математический смысл для любых $x$, но в истории проблемный домен гораздо меньше. Во-первых, $x$ должно быть положительный.2

Функция не всегда должна быть задана одной формулой, поскольку мы уже видели (в проблеме подоходного налога, например). Предположим, что $y=v(t)$ — функция скорости автомобиля который выходит из состояния покоя (нулевой скорости) в момент времени $t=0$; тогда неуклонно увеличивает скорость до 20 м/с, на это требуется 10 секунд. это; затем движется с постоянной скоростью 20 м/сек в течение 15 секунд; и наконец, применяет тормоза, чтобы неуклонно снижать скорость до 0, что занимает 5 секунды, чтобы сделать это. Формула для $y=v(t)$ различна в каждом из три временных интервала: сначала $y=2x$, затем $y=20$, затем $y=-4x+120$.График этой функции показан на рисунке 1.3.3.

Рисунок 1.3.3. Функция скорости.

Вообще не все функции задаются формулами. Функция может быть определяется экспериментально установленной таблицей значений или описание, отличное от формулы. Например, население $y$ США является функцией времени $t$: мы можем написать $y=f(t)$. Этот — совершенно хорошая функция — мы могли бы изобразить ее (с точностью до присутствует), если бы у нас были данные для различных $t$ — но мы не можем найти алгебраическая формула для него. 2-9)/(x-3)& $x\neq 3$\cr 6& если $x=3$.\cr}$ (отвечать)

Пример 1.3.13 Предположим, что $f(x) = 3x-9$ и $\ds g(x) = \sqrt{x}$. Что область композиции $(g\circ f)(x)$? (Напомним, что композиция определяется как $(g\circ f)(x) = g(f(x))$.) Что такое домен $(f\circ g)(x)$? (отвечать)

Пример 1.3.14 Фермер хочет построить забор вдоль реки. У него есть 500 футов ограждения и хочет обнести прямоугольный загон на трех стороны (с рекой, обеспечивающей четвертую сторону).Если $x$ является длину стороны, перпендикулярной реке, определите площадь ручка как функция $x$. Какова область определения этой функции? (отвечать)

Пример 1.3.15 Банка в форме цилиндра должна быть изготовлена ​​с общей из 100 квадратных сантиметров материала сбоку, сверху и снизу; производитель хочет, чтобы банка вмещала максимально возможную объем. Запишите объем как функцию радиуса $r$ банки; найти область определения функции. (отвечать)

Пример 1. 3.16 Банка в форме цилиндра должна быть сделана для хранения объем один литр (1000 кубических сантиметров). Производитель хочет использовать как можно меньше материала для банки. Напишите площадь поверхности банки (сумма верха, дна и боковых сторон) в зависимости от радиус $r$ банки; найти область определения функции. (отвечать)

Страница не найдена | ZNNHS

Страница не найдена | ЗННХС | Официальный сайт

Этот веб-сайт соответствует Руководству по обеспечению доступности веб-контента (WCAG 2.0) в качестве стандарта доступности для всех связанных с ним веб-разработок и услуг. WCAG 2.0 также является международным стандартом ISO 40500. Это подтверждает, что он является стабильным техническим стандартом, на который можно ссылаться. WCAG 2.0 содержит 12 руководств, организованных по 4 принципам: Воспринимаемый, Удобный, Понимаемый и Надежный (сокращенно POUR). Для каждого руководства есть проверяемые критерии успеха. Соответствие этим критериям измеряется тремя уровнями: A, AA или AAA. Руководство по пониманию и внедрению рекомендаций по обеспечению доступности веб-контента 2.0 доступен по адресу: https://www.w3.org/TR/UNDERSTANDING-WCAG20/ Специальные возможности Комбинация клавиш быстрого доступа Комбинация клавиш, используемая для каждого браузера. Chrome для Linux нажмите (Alt+Shift+shortcut_key) Chrome для Windows нажмите (Alt+shortcut_key) Для Firefox нажмите (Alt+Shift+shortcut_key) Для Internet Explorer нажмите (Alt+Shift+shortcut_key), затем нажмите (ввод) В Mac OS нажмите (Ctrl+Opt+shortcut_key) Заявление о специальных возможностях (комбинация + 0): страница заявления, на которой будут показаны доступные ключи специальных возможностей.Домашняя страница (комбинация + H): ключ доступа для перенаправления на домашнюю страницу. Основной контент (комбинация + R): ярлык для просмотра раздела контента текущей страницы. Часто задаваемые вопросы (комбинация + Q): Ярлык для страницы часто задаваемых вопросов. Контакт (комбинация + C): ярлык для контактной страницы или формы запросов. Обратная связь (комбинация + K): ярлык для страницы обратной связи. Карта сайта (комбинация + M): Ярлык для раздела карты сайта (футера агентства) на странице. Поиск (Комбинация + S): Ярлык для страницы поиска. Нажмите клавишу esc или нажмите кнопку закрытия, чтобы закрыть это диалоговое окно.×

Возможно, запрошенная вами страница была перемещена в новое место или удалена с сайта.
Вернитесь на ДОМАШНЮЮ СТРАНИЦУ или найдите то, что вы ищете, в поле поиска ниже.

ЦЕНТРАЛЬНЫЙ ПОМЕЩЕНИЕ:   

PSLV: квадратичные функции EGS

 

Для следующих квадратичных функций определите следующее:

  1. Домен
  2. Диапазон
  3. Координата вершины
  4. Уравнение оси симметрии
  5. y-точка пересечения
  6. х-перехват
0 0 2] 

f (х) = (х – 5) 2 – 4

  1. Домен: ( – ∞, ∞ )
  2. Диапазон: [ – 4, ∞ )
  3. Вершина: ( h, k ) = ( 5 , k ) = ( 5 , – 4 ) x 1 ось 90
    4. A оси A = 5
  4. y-отрезок: пусть x = 0

    5. г = ( 0 – 5 ) 2 – 4

    у = ( – 5 ) 2 – 4

    г = 25 – 4

    г = 21

  5. x-пересечение: Пусть y = 0

    6. 0 = ( х – 5 ) 2 – 4

    4 = ( х – 5 ) 2

    ±√ 4  = х – 5

    ± 2 = х – 5

    5 ± 2 = х

    х = {3, 7}

0 0 4] 

f (х) = – 3 ( х – 2 ) 2 + 1

  1. Домен: ( – ∞, ∞ )
  2. Диапазон: ( – ∞, 1 ]
  3. Вершина: ( h , k ) = ( 2 , k ) = ( 2 , k ) 2
  4. y-пересечение: Пусть x = 0

    5. у = – 3 ( 0 – 2 ) 2 + 1

    у = – 3 ( – 2 ) 2 + 1

    у = – 3 · 4 + 1

    г = – 12 + 1

    г = – 11

  5. x-пересечение: Пусть y = 0

    6. 0 = – 3 ( х – 2 ) 2 +1

    3 ( х – 2 ) 2 = 1


    х – 2 = ± 1
    ––––
    √ 3 

    х = ± 1
    ––––
    √ 3     		  + 2

    х = ± 1
    ––––
    √ 3     		  + 2 √ 3
    ––––––
    √ 3

    х = 2 ± √ 3 
    –––––––
    3
10]

Нарисуйте следующее в той же системе координат.

  1. у = х 2
  2. у = х 2 – 2
  3. у = х 2 + 2
  4. Чем этот график отличается от графика y = x 2 ?

График y = x 2 – 2 и y = x 2 + 2 отличаются от графика y = x 2
в том, что график y = x 2 – 2 сдвинут вниз на 2 единицы
, а график y = x 2 + 2 сдвинут вверх на 2 единицы.

 

Нарисуйте график следующих квадратичных функций. Дайте следующее:

  1. Вершина
  2. Ось симметрии
  3. Домен
  4. Диапазон
  5. Интервал домена, для которого функция возрастает
  6. Интервал домена, для которого функция убывает
0 0 14] 

f (х) = (х + 4) 2

  1. Vertex: (- 4, 0) (- 4, 0)
  2. Ось симметрии: x = — 4
  3. Домен: (- ∞, ∞)
  4. Диапазон: [0, ∞)
  5. Интервал области, для которой функция возрастает: ( – 4, ∞ )
  6. Интервал области, для которой функция убывает: ( – ∞ – 4 )
0 0 16] 

f (х) = (х – 5) 2 – 4

  1. Вершина: (5, — 4) (5, — 4)
  2. Ось симметрии: x = 5 x = 5
  3. Домен: (- ∞, ∞)
  4. Диапазон: [- 4, ∞)
  5. Интервал области, для которой функция возрастает: ( 5, ∞ )
  6. Интервал области, для которой функция убывает: ( – ∞ 5 )
0 0 18] 

f (х) = – 3 ( х – 2 ) 2 + 1

  1. Вершина: (2, 1) (2, 1)
  2. Ось симметрии: x = 2 x = 2
  3. Домен: (- ∞, ∞)
  4. Диапазон: (- ∞, 1]
  5. Интервал область, для которой функция возрастает: ( – ∞, 2 )
  6. Интервал области, для которой функция убывает: ( 2, ∞ )
 

Нарисуйте график следующих квадратичных функций. Дайте следующее:

  1. Вершина
  2. Ось симметрии
  3. Домен
  4. Диапазон
  5. Интервал домена, для которого функция возрастает
  6. Интервал домена, для которого функция убывает
0 0 20] 

f (х) = х 2 + 6 х + 5

f (х) = ( x 2 + 6 x + [ 6
–
2		 ] 2  –  [ 6
–
2		 ] 2 )  + 5

f (x) = ( x 2 + 6 x + 3 2 – 3 2 ) + 5

f (х) = ( х 2 + 6 х + 3 2 ) – 3 2 + 5

f (х) = (х + 3) 2 – 9 + 5

f (х) = (х + 3) 2 – 4

f (х) = (х – [ – 3 ] ) 2 – 4

  1. Vertex: (- 3, — 4) (- 3, — 4)
  2. Ось симметрии: x = — 3
  3. Домен: (- ∞, ∞)
  4. Диапазон: [- 4, ∞)
  5. Интервал области, для которой функция возрастает: ( – 3, – ∞ )
  6. Интервал области, для которой функция убывает: ( – ∞, – 3 )
0 0 22] 

f (х) = 2 х 2 – 4 х + 5

90 529 x 90 530
f (х) = ( 2 x 2 –  4 · 2
––––
2		 )  + 5

90 529 x 90 530
f (х) = 2  ( x 2 –  4
–
2		 )  + 5

f (х) = 2 ( х 2 – 2 х ) + 5

f (х) = 2  ( x 2 – 2 x + [ 2
––
2		 ] 2  –  [ 2
––
2		 ] 2 )  + 5

f (х) = 2 ( х 2 – 2 х + 1 – 1 ) + 5

f (х) = 2 ( х 2 – 2 х + 1 ) – 2 + 5

f (х) = 2 ( х – 1 ) 2 + 3

  1. Vertex: (1, 3) (1, 3)
  2. Ось симметрии: x = 1 x = 1
  3. Домен: (- ∞, ∞)
  4. Диапазон: [3, ∞)
  5. Интервал домена для которого функция возрастает: ( 1, ∞ )
  6. Интервал области, для которой функция убывает: ( – ∞, 1 )
0 0 24] 

f (х) = – 3 х 2 + 24 х – 46

90 529 x 90 530
f (х) = ( – 3 x 2 + 24 · 3
–––––
3		 ) – 46

90 529 x 90 530
f (х) = – 3  ( x 2 –  24
–––
3		 ) – 46

f (х) = – 3 ( х 2 – 8 х ) – 46

f (х) = – 3  ( x 2 – 8 x + [ 8
–
2		 ] 2  –  [ 8
–
2		 ] 2 ) – 46

f (x) = – 3 ( x 2 – 8 x + 4 2 – 4 2 ) – 46

f (х) = – 3 ( х 2 – 8 х + 16 – 16 ) – 46

f (х) = – 3 ( х 2 – 8 х + 16 ) + 48 – 46

f (х) = – 3 ( х – 4 ) 2 + 2

  1. Vertex: (4, 2) (4, 2)
  2. Ось симметрии: x = 4 x = 4
  3. Домен: (- ∞, ∞)
  4. Диапазон: (- ∞, 2]
  5. Интервал область, для которой функция возрастает: ( – ∞, 4 )
  6. Интервал области, для которой функция убывает: ( 4, ∞ )
0
26]
f (х) = 2
–
3		 х 2 – 8
–
3		 х + 5
––
3

90 529 x 90 530
f (х) = ( 2
–
3		 х 2 – 8 · 2 · 3
–––––––
3 · 2 · 3		 )  +  5
––
3

90 529 x 90 530
f (х) = 2
–
3		 ( х 2 – 8 · 3
–––––
3 · 2		 )  +  5
––
3

90 529 x 90 530
f (х) = 2
–
3		 ( х 2 – 24
–––
6		 )  +  5
––
3

f (х) = 2
–
3		 ( х 2 – 4 х )  +  5
––
3

f (х) = 2
–
3		 ( х 2 – 4 х + [ 4
–
2		 ] 2  –  [ 4
–
2		 ] 2 )  +  5
––
3

f (х) = 2
–
3		 (  х 2 – 4 х + 2 2 – 2 2 )  +  5
––
3

f (х) = 2
–
3		 ( х 2 – 4 х + 4 – 4 )  +  5
––
3

f (х) = 2
–
3		 ( х 2 – 4 х + 4 ) –  8
–
3		  +  5
––
3

f (х) = 2
–
3		 ( х – 2 ) 2  –  3
–
3

f (х) = 2
–
3		 ( х – 2 ) 2  – 1
  1. Vertex: (2, — 1) (2, — 1)
  2. Ось симметрии: x = 2 ,
  3. Домен: (- ∞, ∞)
  4. Диапазон: [- 1, ∞)
  5. Интервал области, для которой функция возрастает: ( 2, ∞ )
  6. Интервал области, для которой функция убывает: ( – ∞, 2 )
  Найдите точки пересечения x и y следующих квадратичных функций.
0 0 20] 

f (х) = х 2 + 6 х + 5

  1. y-точка: f ( 0 ) = 5
  2. x-точка:

    3. b 2 – 4ac = 6 2 – 4 · 1 · 5 = 36 – 20 = 16 > 0

    х = – б ± √ б 2 – 4ас
    ––––––––––––––
    2а    		  =  – 6 ± √ 16 
    –––––––––
    2 · 1    		  =  – 6 ± 4
    ––––––
    2

    x 1 = – 6 + 4
    ––––––
    2    		  =  – 2
    ––––
    2    		  = – 1

    x 2 = – 6 – 4
    ––––––
    2    		  =  – 10
    ––––
    2    		  = – 5
0 0 22] 

f (х) = 2 х 2 – 4 х + 5

  1. y-точка: f ( 0 ) = 5
  2. x-точка:

    3. б 2 – 4ас = ( – 4 ) 2 – 4 · 2 · 5 = 16 – 40 = – 24 < 0

    Следовательно, реальных пересечений по оси x нет.

0 0 24] 

f (х) = – 3 х 2 + 24 х – 46

  1. y-точка: f ( 0 ) = – 46
  2. x-точка:

    3. б 2 – 4ас = 24 2 – 4 · (– 3) · (– 46 ) = 576 – 552 = 24 > 0

    х = – б ± √ б 2 – 4ас
    ––––––––––––––
    2а    		  =  – 24 ± √ 24
    ––––––––––
    2 · ( – 3 )    		 ≈  – 24 ± 4.8990
    –––––––––––
    – 6

    x 1 ≈  – 24 + 4.8990
    ––––––––––––
    – 6    		  =  – 19.1010
    –––––––––
    – 6    		 ≈ 3,1835

    x 2 ≈  – 24 – 4.8990
    ––––––––––––
    – 6    		  =  – 28. 8990
    –––––––––
    – 6    		 ≈ 4,8165
0
26]
f (х) = 2
–
3		 х 2 – 8
–
3		 х + 5
––
3

  1. x-пересечение:
    2. b 2 – 4ac = ( –  8
    –
    3    		 ) 2 – 4 ·  2
    –
    3    		  ·  5
    ––
    3    		  =  64
    ––
    9    		 –  40
    ––
    9    		  =  24
    –
    9    		  =  8
    –
    3    		 ≈ 2.6667 > 0

    х = – б ± √ б 2 – 4ас
    ––––––––––––––
    2а    		 ≈  – ( – 2,6667 ) ± √ 2,6667
    –––––––––––––––––––––
    2 ( 0,6667 )    		 ≈  2. 6667 ± 1,6330
    ––––––––––––––
    1,3334

    x 1 ≈  2,6667 + 1,6330
    ––––––––––––––
    1,3334    		  =  4,2779
    ––––––
    1,3334    		 ≈ 3,2246

    x 2 ≈  2,6667 – 1,6330
    ––––––––––––––
    1,3334    		  =  1.0337
    ––––––
    1.3334    		 ≈ 0,7752
  Решите следующие проблемы.
48.

СУММА И ПРОИЗВЕДЕНИЕ ДВУХ ЧИСЕЛ:
Найдите два числа, сумма которых равна 32 , а произведение которых равно максимально возможному значению.

Пусть x будет одним из чисел, а 32 – x будет другим числом.

f (x) = x ( 32 – x ) = 32 x – x 2 = – x 2 + 32 = – ( x 2 – 32 x )

Завершение квадрата,

f (х) = – ( х 2 – 32 х + 256 ) + 256

f (х) = – ( х – 16 ) 2 + 256

Следовательно, максимум приходится на x = 16 и на x = 32 – x = 32 – 16 = 16 .

50.

Доход чартерной автобусной компании зависит от количества непроданных мест.
Если выручка в долларах, R (x) , определяется как R (x) = – x 2 + 50 x + 5000
, где x — количество непроданных мест.
Найдите количество непроданных мест, приносящих максимальный доход.
Каков максимальный доход?

R (х) = – х 2 + 50 х + 5000

Завершение квадрата,

R (x) = – ( x 2 – 50 x + 625 ) + 5000 + 625 = – ( x – 25 ) 2 + 5625

Следовательно, количество непроданных мест x = 25 .

Максимальный доход $5625 .

52.

Объект, брошенный вверх с уровня земли, имеет начальную скорость 32 фута в секунду .
Его высота в футах после t секунд равна с (t) = – 16 t 2 + 32 t .
Найдите количество секунд, которое потребуется, чтобы достичь максимальной высоты.
Какова максимальная высота?

s (t) = – 16 t 2 + 32 t = – 16 ( t 2 – 2 t )

Завершение квадрата,

s (t) = – 16 ( t 2 – 2 t + 1 ) + 16 = – 16 ( t – 1 ) 2 + 16

Следовательно, объект достигнет максимальной высоты за x = 1 секунду .

Максимальная высота — это значение функции в вершине 16 футов .

54.

Камень брошен прямо вверх с уровня земли с начальной скоростью 90 футов в секунду .

  1. Укажите функцию, описывающую высоту скалы во времени t .
  2. Определите время, когда камень достигает максимальной высоты в футах.
  3. В течение какого интервала времени камень будет находиться на высоте более 120 футов над уровнем земли?
  4. Через сколько секунд он вернется на землю?
  1. Дано ч 0 = 0 и v 0 = 90

    2. h (t) = – 16 t 2 + v 0 t + h 0

    ч (т) = – 16 т 2 + 90 т + 0 = – 16 т 2 + 90 т

  2. Нам нужно найти координаты вершины параболы, используя вершинную формулу
    с a = – 16 и b = 90 .
    3. т = –  б
    –––
    2 а    		  = –  90
    ––––––––
    2 (– 16 )    		  =  90
    –––
    32    		  =  45
    –––
    16    		  = 2,8125 с

    ч (2,8125) = – 16 ( 2,8125 ) 2 + 90 ( 2.8125) + 0 = – 16 (7,9102) = – 126,5625 + 253,125 = 126,5625

    Следовательно, вершина равна ( 2. 8125, 126.5625 ) .

    Поскольку a = – 16 < 0 означает, что парабола направлена ​​вниз, то эта вершина является точкой максимума.

    Таким образом, максимальная высота составляет 126,5625 футов .

    Камень достигает максимальной высоты 2,8125 секунды .

  3. Нам нужно решить неравенство

    4. – 16 т 2 + 90 т > 120

    – 16 т 2 + 90 т – 120 > 0

    2 ( – 8 т 2 + 45 т – 60 > 0 )

    – 8 т 2 + 45 т – 60 > 0

    Используя квадратичную формулу:

    т = – б ± √ б 2 – 4ас
    ––––––––––––––
    2а

    т = – ( 45 ) ± √ 45 2 – 4 ( – 8 ) ( – 60 )
    –––––––––––––––––––––––––––
    2 (- 8 )

    т = – 45 ± √ 2025 – 1920 гг.
    ––––––––––––––––––
    –16

    т = – 45 ± √ 105
    –––––––––––
    –16

    т ≈  – 45 ± 10. 2470
    ––––––––––––
    –16

    т ≈  – 45 + 10.2470
    ––––––––––––
    –16    		  =  – 34.7530
    –––––––––
    –16    		 ≈ 2,1721

    т ≈  – 45 – 10.2470
    ––––––––––––
    –16    		  =  – 55.2470
    –––––––––
    –16    		 ≈ 3,4529

    Эти значения t дают три интервала:

    Интервал т ч (т)
    (-∞, 2,1721) 0 0 
    ( 2,1721 , 3,4529 ) 3 126 
    ( 3.4529, ∞) 4 104 

    ч (т) = – 16 т 2 + 90 т

    ч (0) = – 16 · 0 2 + 90 · 0 = 0 < 120

    ч (3) = – 16 · 3 2 + 90 · 3 = – 16 · 9 + 270 = – 144 + 270 = 126 > 120

    ч (4) = – 16 · 4 2 + 90 · 4 = – 16 · 16 + 360 = – 256 + 360 = 104 < 120

    Следовательно, скала будет находиться на высоте более 120 футов над уровнем земли между 2. 17 сек и 3,45 сек .

  4. Решите h (t) = 0 , чтобы найти, сколько времени понадобится камню, чтобы вернуться на уровень земли.

    5. ч (т) = – 16 т 2 + 90 т = 0

    – 2 т ( 8 т – 45 ) = 0

    8 т = 45

    т = 45 ⁄ 8 = 5,625

    Следовательно, потребуется 5.625 секунд 90 142, чтобы камень вернулся на землю.

Квадратика

Квадраты – это многочлены второй степени.

Они бывают разных форм, но всегда имеют квадратный член.

Примеры

Квадратное выражение :  

     

Квадратное уравнение: 

      

Квадратичная функция:  

  

Квадратичный график: 

Квадратное неравенство:    

Квадратное отображение:       

Квадратичные графики

   Квадратичные графы имеют характерную U-образную форму
называется параболой.

  Положительные параболы smile :

у = топор 2

Отрицательные параболы хмурятся!

у = — топор 2

Рисование парабол вида y = ax

2

Выберите значения для x и поместите их в таблицу.

Вычислите соответствующее для y .

Нанесите эти точки и соедините их плавной кривой.

Пример 

Заполните таблицу значений для
уравнение           y = x 2

Нанесение этих точек на график и их объединение плавной кривой дает

Обратите внимание на симметричность графика!

Пример

Заполните таблицу значений для
уравнение           y = -5x 2

Нанесение этих точек на график и их объединение плавной кривой дает

Опять же, обратите внимание на симметричность графика!

Работа в обратном направлении

Пример

Найдите уравнение следующей параболы
вида y = ax 2

График имеет вид y = ax 2
Данная координата ( 2, 1 )
Итак, x = 2 и y = 1 лежат на кривой

.

Подставить и решить

Параболы вида y = a(x-b)

2

Пример 

Заполните таблицу значений для
уравнение y= (x-2) 2

Нанесение этих точек на график и их соединение плавной кривой дает



На этот раз график симметричен при x=2

Точка поворота (2,0)

Ось симметрии b
в уравнении   y = a(x-b) 2

Пример

Найдите уравнение следующей параболы
вида y = a(x-b) 2

График имеет вид y = a(x-b) 2
Данная координата ( 2, 3 )
Итак, x = 2 и y = 3 лежат на кривой
. Подставить и решить

Параболы вида y = a(x-b)

2 + c

Пример 

Заполните таблицу значений уравнения
у= -2(х+3) 2 + 2

Обратите внимание, что ось симметрии x = — 3

Работа в обратном направлении

Пример

Найдите уравнение следующей параболы
вида y = a(x-b) 2 + c

График имеет вид y = a(x-b) 2 + c

Данная координата (-3, -2)
Итак, x = -3 и y = -2 лежат на кривой

.


Судя по графику, b = -2, так как это ось симметрии.

Замените x=-3, y=-2 и b=-2

Точка (-2,-5) также находится на кривой.

Так что с = -5

Подставить в -2 = a +c

Подстановка a, b и c в исходное уравнение
у = а(х-б) 2 + с

Ось симметрии

Это квадратное число в форме полного квадрата.

Завершение квадрата

Параболы вида y = ax

2 + bx + c

Пример 

Заполнить таблицу значений
для уравнения y= 2x 2 +3x — 2


Поворотные моменты

Положительные параболы имеют минимальную точку поворота.

Пример

Найдите точку поворота квадратного числа

у = х 2 + 3х + 2

Точка поворота находится на оси симметрии.

Отрицательные параболы имеют максимальную точку поворота.

Корни

Корень уравнения — это значение, которое удовлетворяет
уравнение, когда его выражение равно нулю.

Например,  0 = x 2 +2x -3

Максимально возможное количество корней
совпадает со степенью многочлена,
поэтому квадратное число может иметь не более двух корней.
Не все квадратные уравнения имеют корни.

Чтобы найти корни квадратного числа,
Нарисуйте график и посмотрите, где он пересекает ось x.

или

Установить y = 0 и разложить на множители (если возможно)

Пример

Судя по графику, уравнение y = x 2 + 2x –3 имеет корни
х = -3 и х = 1

Это то же самое, что установить y равным нулю и разложить на множители: —

        

Любая скобка может равняться 0, поэтому необходимо учитывать обе скобки:

Электронная таблица Excel

Рисование парабол

Начертить график
y = ax 2 + bx + c 
                          

  • Определить форму как U ( a > 0) или ∩ ( a < 0)
  • Найдите корни уравнения.

     (ах 2 + Ьх + с = 0)

  • Отметьте корни на вашей оси.
  • Отметьте точку (0,c) на вашей оси.
  • Найдите ось симметрии.

( ½ пути между корнями)

  • Используйте это значение x, чтобы найти точку поворота.
  • Соедините значения плавной кривой.

Пример    

   Эскиз  y = x 2 — 2x — 3

Это будет U-образная форма, так как a = 1

Отрежет ось Y в точке (0,-3)

  

Пример  

  Эскиз  y = 3-2x-x 2

                       

   Это будет форма ∩, так как a = -1

Отрежет ось Y в точке (0,3)

Квадратные уравнения

Стандартная форма Квадратные уравнения имеют вид

Чтобы найти решение квадратного уравнения:

Перепишите выражение в стандартной квадратичной форме

Факторизируйте, если можете:

{Не забывайте искать общие множители и разность двух квадратов}

Используйте квадратичные формулы

 Примеры

Решите 3x — 6x 2 = 0

Решить 49 — 9x 2 = 0

Решите 15x 2 — x — 6= 0

Решите 15x 2 — x +1= 7

Факторизация квадратичных чисел             

Квадратичная формула

 Если квадратное число не факторизуется,

попробуйте квадратичную формулу:

Пример

Решить 2 + 4x -5x 2 = 0

Дайте ответ как сурд.

Пример

Найдите корни 2 + 4x -5x 2

Дайте правильный ответ с точностью до двух знаков после запятой.

     Не все квадратичные уравнения разлагаются на множители  

Дискриминант

     

Примеры

    
Дискриминант
б 2 – 4ас
= 3 2 — 4x1x4
= 9 – 16
= — 7

б 2 – 4ас < 0
Нет настоящих корней

б 2 – 4ас
= 3 2 — 4x1x(-2)
= 9 +8
= 17

б 2 – 4ас > 0
Два разных реальных корня

б 2 – 4ас
= 6 2 — 4x1x9
= 36 – 36
= 0

б 2 – 4ас = 0
Корни равны и действительны

Работа в обратном направлении

Пример

Корни ( x – 1)( x + k) = -4  равны.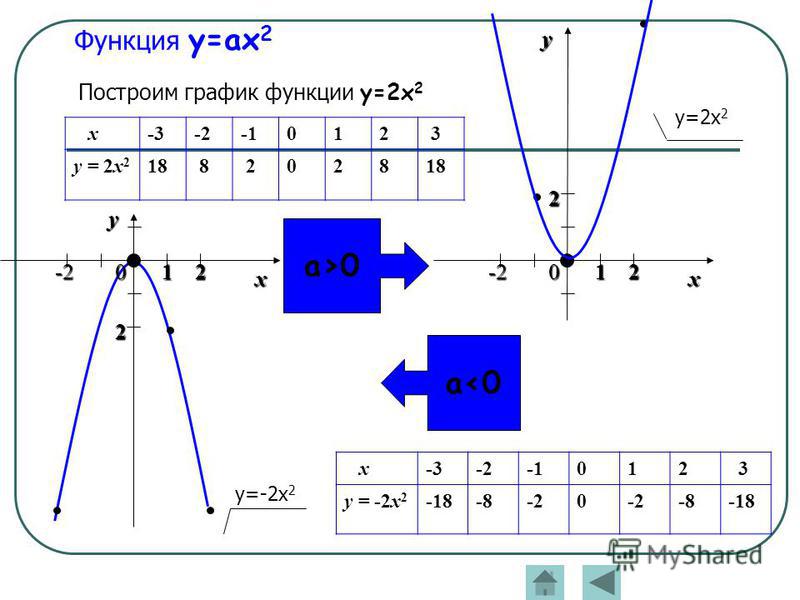
Найдите значения k.

Сначала умножьте скобки

      

Касание

 Касательная к кривой соприкасается с кривой только в одной точке.
Чтобы проверить касание, установите две функции равными друг другу
и найти полученный дискриминант.

Если     b 2 – 4ac > 0   , линия пересекается в двух различных точках.
Это не касательная.

Если    b 2 – 4ac < 0   , линия не касается кривой.
Это не касательная.

Если     b 2 – 4ac = 0   , линия касается кривой только в одной точке.
Это касательная.

Примеры

© Александр Форрест

поверхностей, часть 2

поверхностей, часть 2

Поверхности и контурные графики

Часть 2: Квадратные поверхности

Квадратные поверхности — это графики квадратных уравнений с тремя декартовыми переменными. в космосе.Подобно графикам квадратичных уравнений на плоскости, их формы зависят от знаки различных коэффициентов в их квадратных уравнениях.

Сферы и эллипсоиды

сфера является графом уравнение формы для некоторого действительного числа p . Радиус сферы равен p (см. рисунок ниже). Эллипсоиды представляют собой графики уравнений вида x 2  +  by 2  + c z 2  =  p p 9 где a , b и c  все положительные. Особенно, сфера — это особый эллипсоид, для которого a , b и c все равны.

  1. Постройте график x 2 + y 2 + z 2 = 4 на вашем листе в декартовых координатах.Затем выберите другие коэффициенты в уравнении и постройте несферический эллипсоид.
  2. Какие кривые вы найдете, когда вы пересекают сферу плоскостью, перпендикулярной одной из осей координат? Что вы нашли для эллипсоида?

Параболоиды

Поверхности, пересечения которых с плоскости, перпендикулярные любым двум координатным осям, являются параболами в тех самолеты называются параболоидами . Пример показан на рисунке ниже — это график z = x 2  + y 2 .

  1. Создайте свой собственный участок этой поверхности на листе и поверните график, чтобы увидеть его с разных точек зрения. Следуйте предложениям в рабочем листе. Какие бывают пересечения ул. поверхность с плоскостями вида z = c , для некоторой постоянной с ?
  2. Покажите, что пересечения эта поверхность с плоскостями, перпендикулярными осям x- и y- являются параболами.[Подсказка: установите либо y = c , либо x = c . для некоторой константы c .]
  3. Измените уравнение на z  = 3 x 2  + y 2 , и снова сюжет. Как изменится поверхность? В частности, что происходит с кривые пересечения с горизонтальными плоскостями.

поверхность на следующем рисунке представляет собой график z   = x 2  — y 2 . В этом случае пересечения с плоскостями, перпендикулярными х- и y- оси по-прежнему являются параболами, но два набора парабол различаются по форме. направление, в котором они указывают. По причинам, которые мы увидим, эта поверхность называется гиперболический параболоид — и по понятным причинам его также называют «седловидная поверхность».

  1. Сделайте свой собственный сюжет этой гиперболы параболоида на листе и поворачивайте график, чтобы увидеть его с разных точек зрения.Следуйте предложениям в рабочем листе. Какие бывают пересечения ул. поверхность с плоскостями вида z = c , для некоторой постоянной с ? Объясните обе части имени.

Гиперболоиды

Гиперболоиды — это поверхности в трехмерном пространстве аналогично гиперболам на плоскости. Их определение характерно то, что их пересечения с плоскостями, перпендикулярными какому-либо две оси координат являются гиперболами. Есть два типа гиперболоидов — первый тип иллюстрируется графиком x 2 + y 2 — z 2 = 1, что показано на рисунке ниже. Как показано на рисунке справа, эта форма очень похожа на форму, обычно используемую для атомных электростанций градирни. (Источник: Агентство по охране окружающей среды Ответ на инцидент в Три-Майл-Айленде.)

Эта поверхность называется гиперболоидом . одного листа , потому что это все «связано» в одно целое.(Мы будем займитесь другим делом.)

  1. Создайте свой собственный участок этой поверхности на листе и поверните график, чтобы увидеть его с разных точек зрения. Следуйте предложениям в рабочем листе. Какие бывают пересечения ул. поверхность с плоскостями вида z = c , для некоторой постоянной с ?
  2. Покажите, что пересечения эта поверхность с плоскостями, перпендикулярными осям x- и y- являются гиперболами. [Подсказка: установите либо y = c , либо x = c . для некоторой константы c .]

Другой тип — гиперболоид . из двух листов , что иллюстрируется графиком x 2 — y 2 — z 2 = 1, показано ниже.

  1. Сделайте свой собственный участок этой поверхности на листе и поверните график, чтобы увидеть его с разных точек зрения.Следуйте предложениям в рабочем листе. Какие бывают пересечения ул. поверхность с плоскостями вида z = c , для некоторой постоянной с ?
  2. Покажите, что пересечения эти две поверхности с соответствующими координатными плоскостями являются гиперболами.

В каждом из этих примеров пересечения поверхности с семейством плоскостей многое говорит нам о структуре поверхности.Мы вернемся к этой теме в части 6. когда мы смотрим на контурные линии.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *