Линейная функция 7 класс онлайн-подготовка на Ростелеком Лицей
Линейная функция и ее график
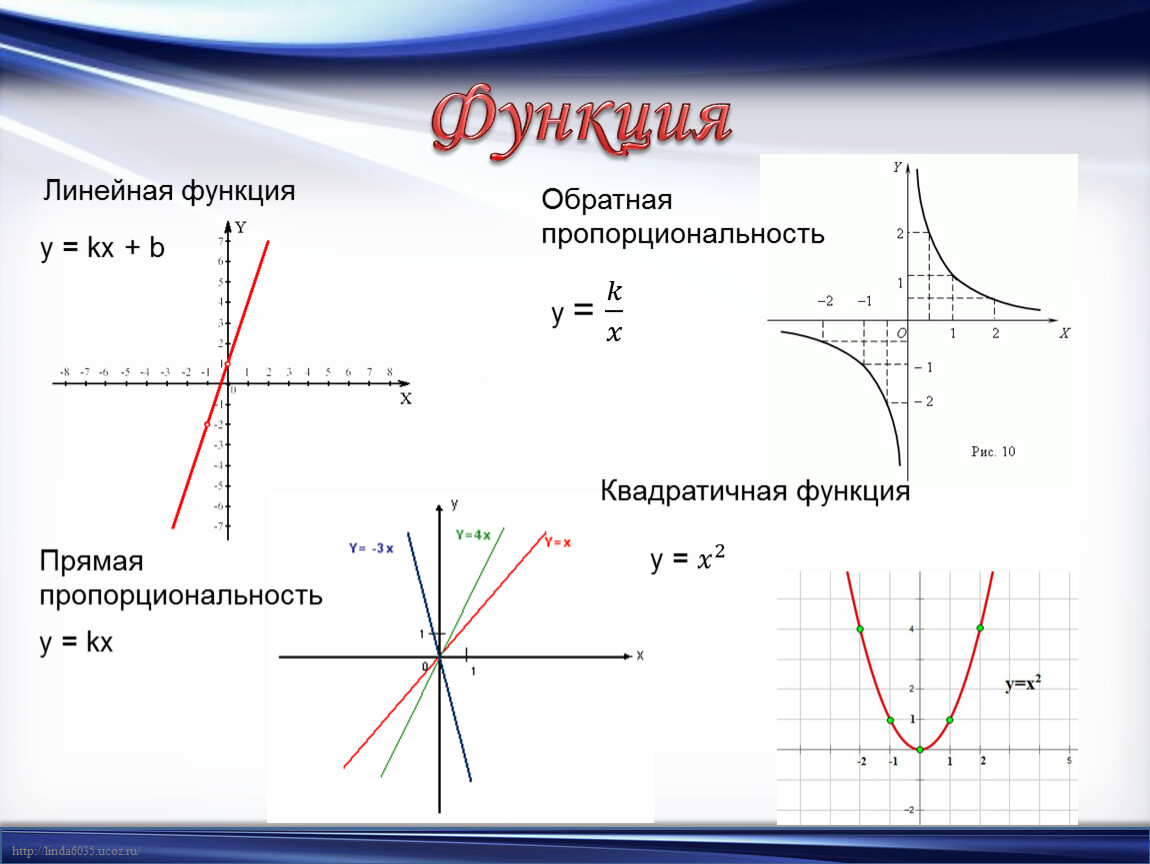
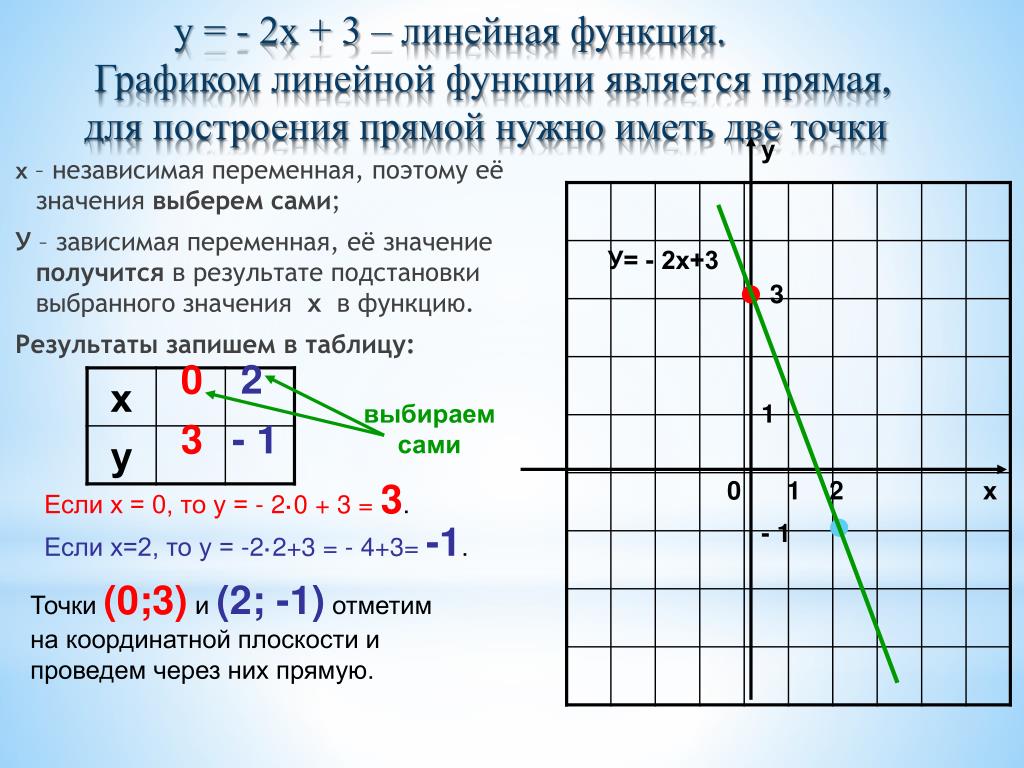
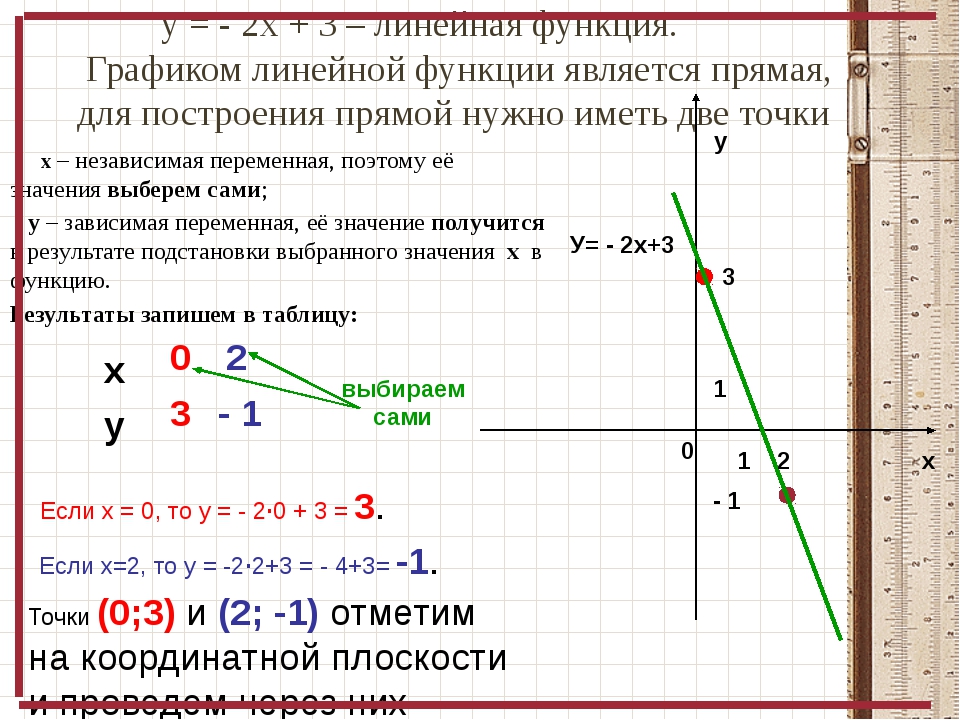
Линейная функция – это функция вида y = kx+b, где х – независимая переменная, k и b – некоторые числа.
Нетрудно заметить, что прямая пропорциональность – частный случай линейной функции. При b = 0 линейная функция принимает вид y = kx, а это и есть прямая пропорциональность.
Рассмотрим две функции: y=4x+3 и y=4x и построим их графики.
|
х |
-2 |
-1 |
0 |
1 |
2 |
|
у=4х |
-8 |
-4 |
0 |
4 |
|
|
у=4х+3 |
-5 |
-1 |
3 |
7 |
11 |
Мы видим, что график функции y = 4x+3 представляет собой прямую, параллельную графику функции у = 4х.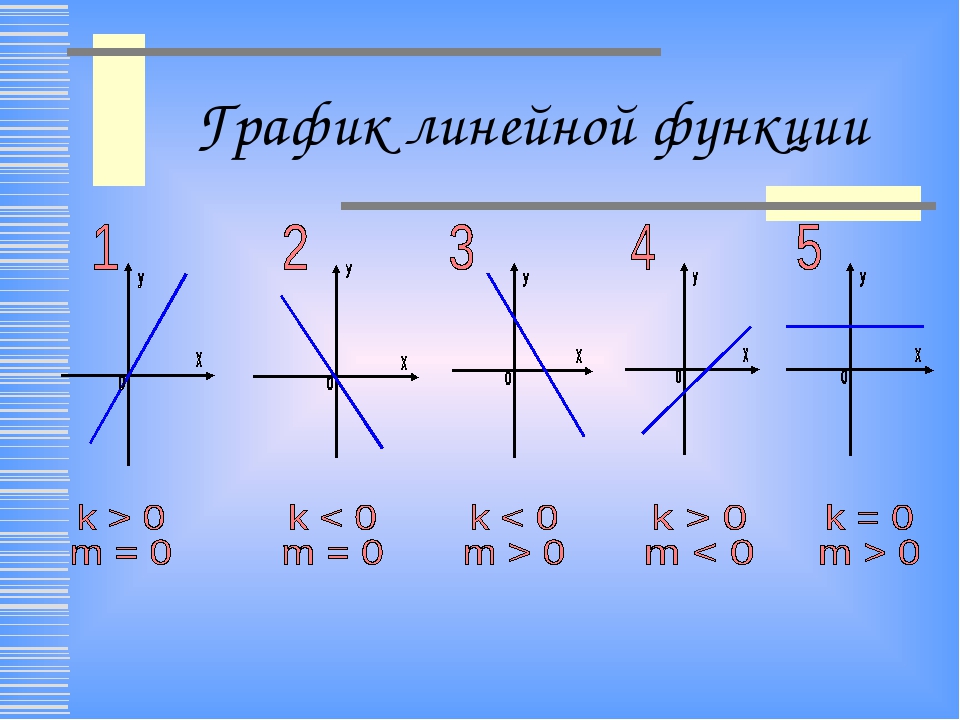 Прямая смещена на 3 единицы вверх.
Прямая смещена на 3 единицы вверх.
Таким образом, график функции у = kx+b, где k ≠ 0 – это прямая, параллельная прямой у = kx.
Для построения прямой нам достаточно знать координаты двух точек. Пусть это будут точки пересечения графика с осями координат.
То есть таблица для построения графика функции y=4x+3 будет иметь вид:
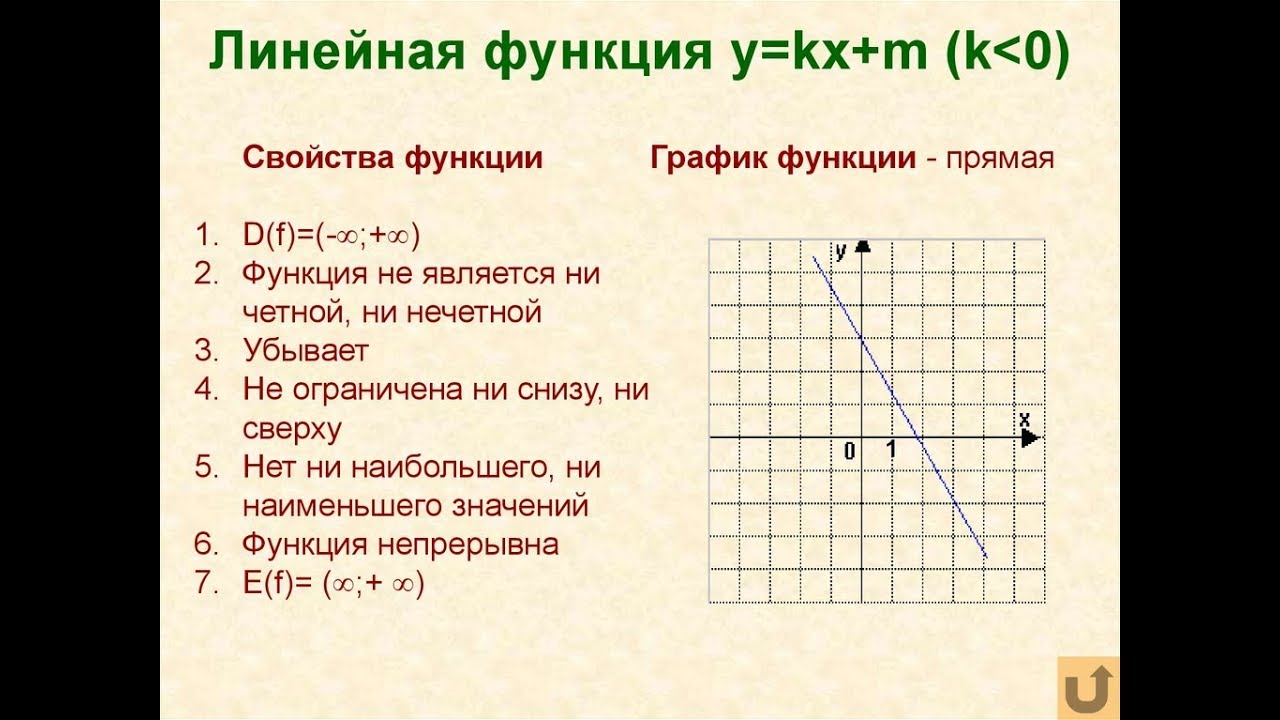
Так же, как и в случае с прямой пропорциональностью, при k>0 функция возрастает, а при k<0 – функция убывает.
Число b, как мы отметили выше, обозначает, на сколько график функции смещен вверх или вниз относительно начала координат.
Если угловые коэффициенты прямых, являющихся графиками линейных функций, одинаковые, то прямые параллельны.
Если k = 0, то линейная функция приобретает вид y = b. Это прямая, параллельная оси х и проходящая через точку (0, b).
Например, построим график прямой у=5.
Область определения линейной функции такая же, как и у прямой пропорциональности – вся числовая прямая D(y) = (- ∞;∞). Область значений Е(у) = (- ∞;∞).
Область значений Е(у) = (- ∞;∞).
Линейная функция
Функция называется
линейной, если ее можно записать в виде \(y=kx+b\), где \(k\) и \(b\) -некоторые числа.Примеры:
|
\(y=\frac{1}{3}x-5\) |
\(k=\frac{1}{3}\), \(b=-5\) |
|
|
\(y=2x\) |
\(k=2\), \(b=0\) |
|
|
\(y=8\) |
\(k=0\), \(b=8\) |
Функция не всегда сразу задана в виде \(y=kx+b\), иногда такой вид получится только после преобразований. Например, \(y=6(x-1)+10x\) — это линейная функция, потому что если раскрыть скобки и привести подобные слагаемые мы получим \(y=16x-6\).
Например, \(y=6(x-1)+10x\) — это линейная функция, потому что если раскрыть скобки и привести подобные слагаемые мы получим \(y=16x-6\).
График линейной функции всегда представляет собой прямую линию – отсюда и название: «линейная функция».
Чтобы в этом убедиться построим графики функций \(y=2x\), \(y=\frac{1}{3}x-5\), \(y=8\).
Если вы вдруг забыли, как строить графики, можете прочитать об этом здесь.
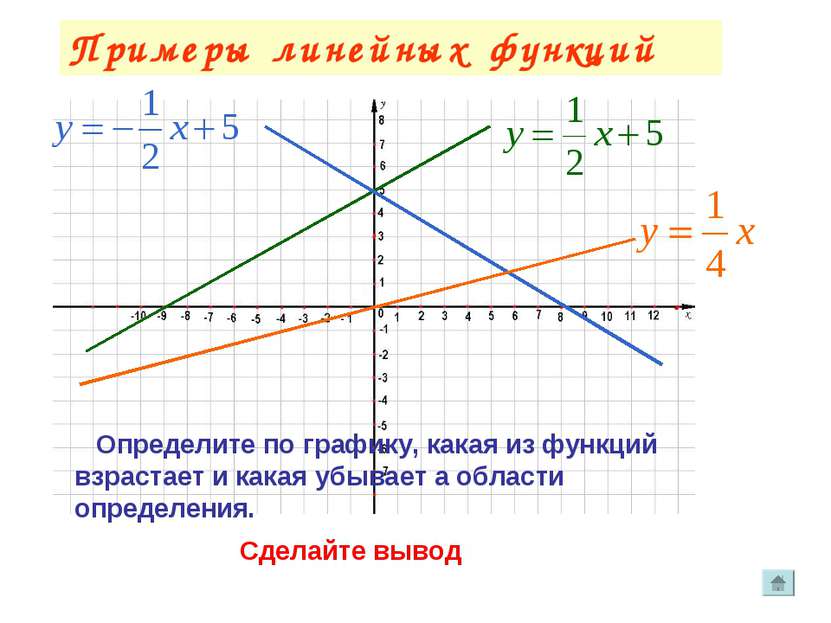
Как меняется график при разных \(k\)?
Чтобы определить, как влияет на график коэффициент \(k\), построим несколько функций разными \(k\): \(\frac{1}{3}\),\(-\frac{1}{3}\),\(2\),\(-2\) и \(0\). При этом во всех функциях сделаем \(b\) одинаковым (равным нулю), чтобы убрать его влияние.
То есть, построим графики для функций: \(y=\frac{1}{3}x\), \(y=-\frac{1}{3}x\), \(y=2x\), \(y=-2x\), \(y=0\).
Заметьте, что при \(k=2\) и \(\frac{1}{3}\) — функция возрастает, а при \(k=-2\) и \(-\frac{1}{3}\) — убывает. На самом деле:
На самом деле:
При любом \(k>0\) функция возрастает и при любом \(k<0\) — убывает. Когда же \(k=0\) — она не возрастает и не убывает, а идет параллельна оси \(x\) (или совпадает с ней).
Так же можно заметить, чем больше модуль \(k\), тем «круче» график.
Как по графику определить коэффициент k?
- Сначала определим, возрастает или убывает функция. Если возрастает – знак коэффициента \(k\) плюс, если убывает – минус.
- Дальше надо построить на прямой прямоугольный треугольник, так чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Примерно вот так:
Чтобы определить значение \(k\) по модулю (то есть, без учета знака), надо вертикальную сторону треугольника поделить на горизонтальную. Можно использовать правило для запоминания: «стоячий бьет лежачего». В данных случаях \(|k|=\frac{AC}{BC}\). То есть на первом графике \(k=2\),а на втором \(k=-\frac{1}{4}\).
То есть на первом графике \(k=2\),а на втором \(k=-\frac{1}{4}\).
Как меняется график при разных значениях \(b\)?
Чтобы определить, как \(b\) влияет на график, построим несколько функций с разными \(b\): \(6\), \(2\), \(0\), \(-3\) и \(-8\). При этом \(k\) пусть во всех функциях будет равен \(2\).
Не сложно заметить, что прямая либо поднимается на \(b\) (если \(b>0\)) либо опускается на \(|b|\) если
(\(b<0\)).
Как по графику функции определить значение \(b\)?
Очень просто — прямая пересекает ось \(y\) всегда в точке \(b\). Вы можете это увидеть на предыдущем графике.
Пример (ОГЭ): На рисунке изображены графики функций вида \(y=kx+b\). Установите соответствие между графиками функций и знаками коэффициентов \(k\) и \(b\).
A. B.C.
Коэффициенты
| 1) \(k>0\),\(b>0\) | 2) \(k<0\), \(b>0\) | 3) \(k<0\), \(b<0\) | 4) \(k>0\), \(b<0\) |
Решение:
А.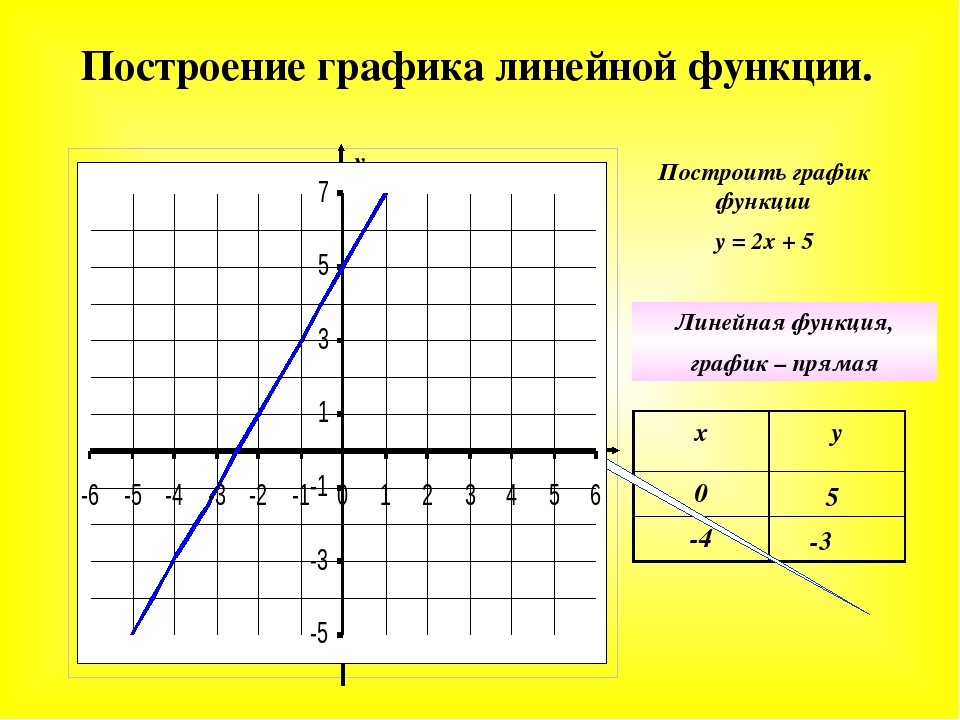
B. — функция возрастает — \(k>0\). Точка пересечения оси \(y\) и прямой находится выше нуля, значит \(b>0\). Подходит вариант под цифрой 1).
C. – функция убывает — \(k<0\). Точка пересечения оси \(y\) и прямой находится ниже нуля, значит \(b<0\). Подходит вариант под цифрой 3).
Ответ: 213.
«Читерский» способ строить график линейной функции
Можно конечно строить график линейной функции по точкам, как описано здесь, но можно и быстрее, буквально в три шага:-
Отмечаем точку \(b\) на оси игреков.
-
От неё идем вправо на количество клеточек равное знаменателю \(k\), и вверх на количество клеточек равное числителю \(k\) (если \(k>0\)) или вниз на тоже количество (если \(k<0\)).
-
Проводим через эти две точки прямую.

Пример: Построить график функции \(y=3x+1\).
|
Шаг 1. \(b=1\), поэтому отмечаем точку с этим значением на оси \(y\)
|
Шаг 2. \(k=3\), а тройка это тоже самое, что \(\frac{3}{1}\). При этом \(k>0\). Поэтому идем вправо на единицу и вверх на \(3\). Ставим точку. |
Шаг 3. Проводим через эти две точки прямую. |
Пример: Построить график функции \(y=-\frac{1}{4} x-3\).
|
Шаг 1. \(b=-3\) отмечаем точку с этим значением на оси \(y\).
|
Шаг 2. \(k=-\frac{1}{4}\), \(k<0\), числитель \(1\), знаменатель \(4\). Значит, идем вправо на \(4\) и вниз на единицу. |
Шаг 3. Проводим через эти две точки прямую. |
Немного потренируйтесь и вы сами поймете, какой это классный способ строить линейную функцию.
Abitur
Линейная функция и ее график Область определения и область значений функции.
Определение 1: Область определения функции — это множество всех значений Х, для которых функция имеет смысл.
Определение 2: Область значений функции — это множество всех значений Y, которые принимает функция.
Определение линейной функции.
Определение 3: Функция вида y=kx+b, где k, b — любые числа, называется линейной функцией.
Графиком линейной функции является прямая.
Исследование линейной функции.
Приведем схему исследование линейной функции:
1) Возрастающая функция или убывающая.
2) Точки пересечения линейной функции с осями координат.
3) Промежутки на которых функция 0.
Решение примеров.
1. Исследуйте функцию и постройте ее график:
| a). |
| 1). | Функция убывающая, так как коэффициент при x меньше нуля |
2). |
Найдем точку пересечения с осью Х: |
| Т. е. функция пересекает ось Х в точке с координатами |
| 3). | Найдем точку пересечения с осью Y: |
| Т. е. функция пересекает ось Х в точке с координатами (0;2) |
| 4). | Построим через 2 найденные точки | и (0:2) график функции: |
Задания.
1. Исследуйте функцию и постройте ее график:
| d). | e). |
Линейная функция в Excel — Офис Ассист
Электронные таблицы MS Excel.
 Построение графиков
Построение графиков- Злыдова Ирина Леонидовна, учитель информатики
Разделы: Информатика
Цели:
Оборудование: доска, ПК, карточки с заданием практической работы.
Организационный момент (постановка целей).
Начинаем наш урок информатики. Сегодня у нас практическое занятие на тему: «MS Excel. Построение графиков», на котором мы будем строить графики функций и траекторию движения тел. А именно, рассмотрим задачу на построение графика линейной и квадратичной функций и задачу по физике на тему: «Криволинейное движение тел».
Актуализация знаний.
Скажите, что мы научились выполнять в программе MS Excel.
Фронтальный опрос:
Как составить последовательность чисел в отдельных ячейках? (Чтобы создать возрастающую последовательность с постоянным шагом, следует ввести в две соседние ячейки первые два значения последовательности. Excel использует эти два значения для определения шага и исходного значения последовательности. Затем, выделить эти две ячейки и перетащить маркер заполнения вниз (курсор при этом приобретает форму плюса).
Excel использует эти два значения для определения шага и исходного значения последовательности. Затем, выделить эти две ячейки и перетащить маркер заполнения вниз (курсор при этом приобретает форму плюса).
Как ввести формулу в ячейку? (Формулу можно ввести в строке формул или в ячейке. Все формулы в Excel должны начинаться со знака равенства и не должны содержать пробелов. После завершения ввода формулы следует нажать клавишу Enter или щелкнуть по кнопке в строке формул.)
Как скопировать формулу в другие ячейки? (Для этого необходимо выделить ячейку и перетащить маркер заполнения вниз, курсор при этом приобретает форму плюса.)
Для записи формулы мы используем ссылки. А какие виды ссылок вы знаете? Приведите примеры. (Ссылки бывают относительные, абсолютные и смешанные. Ссылка $A$1 абсолютной. Ссылка A3 или B5 являются относительными.)
Назовите отличие относительной и абсолютной ссылок. (При копировании адрес относительной ячейки меняется в соответствии с новым положением ячейки, адрес абсолютной ячейки не изменяется. )
)
Формирование УН:
На прошлом уроке мы научились строить графики и диаграммы, редактировать их. А сейчас с помощью графиков найдем точку пересечения двух функций. Но сначала вспомним, какие функции являются линейными и квадратичными?
(Ответы учащихся).
Итак, линейную функцию можно записать в виде y=ax+b, где a и b — некоторые числа, а? 0. Квадратичная функция записывается в виде y=ax2+bx+c, где a, b, с — некоторые числа, а? 0.
Частный вид квадратичной функции y=x2.
Задача 1. Даны две функции y=x2 и y=ax+b. В формуле значения a и b задайте самостоятельно. Постройте графики этих функций и найдите точки пересечения графиков, если таковы имеются.
Рисунок 1.
Физкультминутка. Гимнастика для глаз.
Задача 2. Один мяч подбросили вертикально вверх с высоты 10 м. Второй мяч подбросили с земли со скоростью 10 м/с. Как будет изменяться значение высоты с изменением времени, если высота вычисляется по формуле: h=h0+v0t-gt2/2, где h0 — начальная высота, v0 — начальная скорость, g — ускорение свободного падения.
Рисунок 2.
Ответьте на вопросы:
Найдите, на какую максимальную высоту подбросили второй мяч?
Через сколько секунд два мяча будут на одной высоте и какое значение этой высоты?
Подберите свои начальные условия для задачи и постройте траектории движения тел при новых условиях.
Рефлексия и итог урока:
Сохраните свои работы.
Подведем итог.
Какие необходимы исходные данные для того, чтобы построить график функции в электронных таблицах?
Как осуществить быстрый переход от относительной ссылки к абсолютной или смешанным ссылкам. (Нажатием на клавишу F4).
Домашнее задание.
Повторить основные понятия темы: «Принцип адресации в электронных таблицах MS Excel».
|
График линейной функции — презентация онлайн
1. Исследование графика линейной функции.
7 класс2. Вспомним …
• Какая функция называется линейной?• Что является графиком линейной функции?
Как построить график?
• Что значит «точка принадлежит графику»?
• Для данных функций определите коэффициент
k и число в
y=5x+4 y= 7,6+2x y= 4x y= -6 — 0,5x
y= -5x
y= -2
3. Наблюдение 1
• Рассмотрим функцию y=kx+b такую, чтоk 0 , b=0.
Вид: y=kx
• В одной системе координат построить
графики данных функций:
y=3x
y=x
y=-7x
х
х
х
у
у
у
Каждый график строим соответствующим
цветом
4.
 Вывод: График линейной функции вида у=kх проходит
Вывод: График линейной функции вида у=kх проходитчерез начало координат.
у
y=-7x
y=3x
y=x
х
Вывод:
График линейной функции вида y = kx + b
пересекает ось ОY в точке (0;b).
6. Наблюдение 2
• Рассмотрим функцию y=kx+b, где k=0.Вид: y=b
• В одной системе координат построить графики
функций:
y=4 y=-3 y=0
Каждый график строим соответствующим цветом
7. Вывод:
График линейной функции вида y = bпроходит параллельно оси ОХ и пересекает ось ОY
в точке (0;b).
у
y=4
y=0
х
y=-3
8. Наблюдение 3
• В одной системе координатпостроить графики функций:
Y=2x
Y=2x+3
Y=2x-4
х
0
х
0
х
0
у
0
у
3
у
-4
• Каждый график строим
соответствующим цветом
9. Вывод:
Графики линейных функций вида y=kx+b параллельны,если коэффициенты при х одинаковы.
у=2x
у
у=2x-4
у=2x+3
х
10.
 Наблюдение 4 • В одной системе координат
Наблюдение 4 • В одной системе координатпостроим графики функций:
y=3x+4
х
у
Y= -2x+4
х
у
• Графики строим соответствующим
цветом
11. Вывод:
Графики двух линейных функций вида y=kx+bпересекаются, если коэффициенты при х –
различны.
у
х
12. Наблюдение 5
• В одной системе координат построимграфики функций:
y=0,5x-2
y=-2x-4
х
0
4
y=4x-1
у
0
-2
у
у
х
х
0
1
y=-0,25x-3
х
у
0
-4
13. Что получилось?
y=0,5x-2Что получилось?
y=-2x-4
х
0
4
х
0
-2
у
-2
0
у
-4
0
y=4x-1
y=-2x-4
y=0,5x-2
y=-0,25x-3
14. Вывод:
Графики двух линейных функций вида y=kx+bвзаимно перпендикулярны,
если произведение коэффициентов при х равно « -1».
15. Вывод:
Если k>0 , то уголнаклона графика
к оси ОX острый.
Функция возрастает.
• Если k
наклона графика
к оси ОX тупой.
• Функция убывает.
у
у
х
Поэтому коэффициент k называют угловым
коэффициентом прямой –
графика функции y=kx+ b.
х
16. Вывод:
Линейныеуравнения
Вывод:
Алгебраическое
условие
y = к1х+b1
к1 = к2 , b1 ≠ b2
y = к2х+b2
к1 = к2, b1= b2
Геометрический
вывод
Прямые
параллельны
Прямые
совпадают
к1 ≠ к2
Прямые
пересекаются
к1 к2 = -1
Прямые
перпендикулярны
17. Вывод:
kb
b >0
b
b =0
k>0
k
k=0
18. Подумай …
Задание 1Даны функции:
y=0,8x+2
y=4/5x-19
1)
2)
y=15-1,5x
y=1,5x-15
y=-3/2x+6
y=0,8x
Назовите те из них, графики которых
параллельны, пересекаются.
Назовите для каждой функции точку
пересечения графика с осью ОY.
19. Задание 2 По данным рисунка определить какой график соответствует каждой из данных функций:
А) y= -3xБ) y= -x-10
В) y=2x
Г) y=1,5x+4
Д) y= -8
20.
 Проверь себя … Дана функция y = 4x + 5
Проверь себя … Дана функция y = 4x + 5Задайте формулой:
▪функцию, график которой будет параллелен
графику данной линейной функции;
▪функцию, график которой будет параллелен
графику данной линейной функции и проходить через начало координат;
▪ функцию, график которой будет пересекать перпендикулярно
график данной линейной функции;
▪функцию, график которой будет пересекать
график данной линейной функции в точке (0;5) и будет параллелен оси Х.
21. Выполни дома …
• Прочитать § 32, учить конспект• Упражнения
607 (6)
608 (2)
609 (2)
611
22. Спасибо за урок ! До свидания!
Экспоненциальный | Используется, когда предпочтение увеличивается с увеличением входных значений и предпочтение растет тем быстрее, чем больше становятся входные значения. |
Гауссово | Используется, когда наивысшее предпочтение отдаётся определенному входному значению, с предпочтениями, уменьшающимися по мере удаления входных значений от данного значения. |
Большой | Используется для указания того, что большие входные значения имеют более высокое предпочтение. |
Линейный | Изменяет масштаб входных значений с использованием линейной функции. |
Логарифм | Используется, когда предпочтение для низких входных значений быстро увеличивается с увеличением входных значений и, затем, предпочтение сужается с дальнейшим увеличением входных значений. |
Логистическое снижение | Используется, когда малые входные значения являются более предпочтительными. По мере увеличения входных значений, предпочтения быстро возрастают, пока не будут сужены при больших входных значениях. |
Логистический рост | Используется, когда большие входные значения являются более предпочтительными. По мере увеличения значений, предпочтения быстро увеличиваются, пока не будут сужены при больших входных значениях. |
MSLarge | Изменяет масштаб входных данных на основе среднего и стандартного отклонения, где большие значения во входном растре имеют более высокое предпочтение. |
MSSmall | Изменяет масштаб входных данных на основе среднего и стандартного отклонения, где меньшие значения во входном растре имеют более высокое предпочтение. |
Ближайший объект | Используется, когда более предпочтительны значения очень близкие к середине. |
Степень | Используется, когда предпочтение для входных значений быстро увеличивается с увеличением входных значений. |
Небольшие | Используется для указания того, что меньшие значения входного растра имеют более высокое предпочтение. |
Симметричный линейный | Используется, когда определенное входное значение является наиболее предпочтительным, с предпочтениями, линейно уменьшающимися по мере удаления входных значений от точки. |
Линейные графики и графики стеблей и листьев (алгебра 2, уравнения и неравенства) — Mathplanet
Большинство людей знакомы с гистограммами, линейными и круговыми диаграммами. Здесь мы объясним два типа графиков, которые используются для визуализации данных.
Линейный график — это график, показывающий частоту данных вдоль числовой линии. Лучше всего использовать линейный график при сравнении менее 25 чисел. Это быстрый и простой способ организации данных.
Пример
Следующие числа являются результатом теста, пройденного классом из 24 учеников:
$16, 14, 17, 11, 14, 19, 11, 17, 12, 21, 22, 18, 11, 16, 15, 14, 18, 12, 13, 16, 17, 15, 13, 17$ $
Чтобы построить линейный график из наших данных, мы определяем шкалу, которая включает все данные в соответствующих интервалах. Затем мы наносим каждое число, используя X или другие метки, чтобы показать частоту:
Затем мы наносим каждое число, используя X или другие метки, чтобы показать частоту:
$$\;\, \, \, \;\, \, \, \;\, \, \, \;\, \, \, \;\, \, \, \;\, \, \ , \;\, \, \, \;\, \, \, \;\, \, \, \, \;\, \, \, X\\ X\;\, \, \, \;\ , \, \, \;\, \, \, \;\, \, \, \;\, \, \, ИКС\;\, \, \, \;\, \, \, \;\, \, \, X\;\, \, \, X\\ X\;\, \, \, X\;\, \, \, X\;\, \, \, X\;\, \, \, X\;\, \, \, X\;\, \, \, X\;\, \, \, X\\ X\;\, \, \, X\;\, \, \, X\;\, \, \, X\;\, \, \, X\;\, \, \, X\;\, \, \, X\;\, \, \, X\;\, \, \, X\;\, \, \, \;\,\: \: \: \, \, X \, \,\: \: X\\ ———— ——————-\\11\, \, \, \,12\, \, \, \,13\, \, \, 14\, \ , \, 15\, \, \, \: 16\, \, \, 17\, \, \, \: 18\, \, \, 19\, \, \, \, \, 20\, \ , \, 21\, \, \, 22\, \, \, 23\\$
Диаграмма «стебель-листья» в статистике — это устройство для представления количественных данных в графическом формате, похожем на гистограмму, помогающее визуализировать форму распределения.
Основа обычно состоит из цифр наибольшего общего разряда каждого элемента данных, в то время как листья содержат другие цифры каждого элемента данных.
Пример
Возвращаемся к результату из прошлого примера:
16, 14, 17, 11, 14, 19, 11, 17, 12, 21, 22, 18, 11, 16, 15, 14, 18, 12, 13, 16, 17, 15, 13, 17
Сначала мы сортируем результаты в порядке возрастания:
11, 11, 11, 12, 12, 13, 13, 14, 14, 14, 15, 15, 16, 16, 16, 17, 17, 17, 17, 18, 18, 19, 21, 22
Затем мы строим график стебля и листьев:
$$Стебель\средний лист\\ 1\,\; \; \; \; \; \; \середина 1\;1\; 1\; 2\; 2\; 3\; 3\; 4\; 4\; 4\; 5\; 5\; 6\; 6\; 6\; 7\; 7\; 7\; 7\; 8\; 8\; 9\; \\2\,\; \; \; \; \; \, \середина 1\; 2$$
Основа находится в левой колонке и содержит наши цифры десятков.Лист, найденный в правой колонке, показывает все цифры единиц для каждой из десятков и двадцаток. Чтобы определить наши исходные значения, мы просто соединяем наши цифры десятков с нашими цифрами единиц.
Видеоурок
Построить диаграмму «стебли и листья» из следующих данных: 6, 6, 7, 8, 9, 13, 16, 19, 21, 25, 26
youtube.com/embed/V8tnFezkdS8?fs=1&hl=sv_SE&rel=0″ allowfullscreen=»»/>
линейных графиков — Базовые графики R — Понятные руководства — Wiki
Ранее мы описали основы программирования R и предоставили краткие руководства по импорту данных в R .
Здесь мы опишем, как создать линейных графиков в R. Функцию график () или линий () можно использовать для создания линейного графика.
Упрощенный формат графика () и строк () выглядит следующим образом.
сюжет(х, у, тип = "л", лти = 1)
линии (х, у, тип = "л", lty = 1) - x, y : векторы координат точек для соединения
- тип : символ, указывающий тип построения.Допустимые значения:
- «p» для точек
- «л» для линий
- «b» для точек и линий
- «c» для пустых точек, соединенных линиями
- «o» для точек и линий с наложением
- «s» и «s» для ступенек
- «n» не создает ни точек, ни линий
- lty : типы линий.
 Типы линий могут быть указаны как целое число (0=пустое, 1=сплошное (по умолчанию), 2=штриховое, 3=пунктирное, 4=точка-тире, 5=длинное тире, 6=двойное тире) или как одна из строк символов «пусто». », «сплошной», «пунктирный», «точечный», «точечный», «длинный тире» или «двойной тире», где «пробел» использует «невидимые линии» (т.д., не рисует их).
Типы линий могут быть указаны как целое число (0=пустое, 1=сплошное (по умолчанию), 2=штриховое, 3=пунктирное, 4=точка-тире, 5=длинное тире, 6=двойное тире) или как одна из строк символов «пусто». », «сплошной», «пунктирный», «точечный», «точечный», «длинный тире» или «двойной тире», где «пробел» использует «невидимые линии» (т.д., не рисует их).
# Создать несколько переменных
х Мы построим график с двумя линиями: линий (x, y1) и линий (x, y2).
Обратите внимание, что функция строк () не может сама по себе построить график. Однако его можно использовать для добавления строк () на существующий график. Это означает, что сначала вы должны использовать функцию plot () для создания пустого графика, а затем использовать функцию lines () для добавления линий.
# Создайте базовый график ступеней лестницы
сюжет (х, у1, тип = "S")
# Показать и точки, и линию
сюжет (x, y1, тип = "b", pch = 19,
col = "красный", xlab = "x", ylab = "y") # Создать первую строку
сюжет (x, y1, тип = "b", кадр = FALSE, pch = 19,
col = "красный", xlab = "x", ylab = "y")
# Добавляем вторую строку
линии (x, y2, pch = 18, col = "синий", type = "b", lty = 2)
# Добавляем легенду к сюжету
легенда("сверху слева", legend=c("Строка 1", "Строка 2"),
col=c("красный", "синий"), lty = 1:2, cex=0. 8)
8) Этот анализ был выполнен с использованием статистического программного обеспечения R (версия 3.2.4).
Понравилась эта статья? Я был бы очень признателен, если бы вы помогли его распространению, отправив его по электронной почте другу или поделившись им в Twitter, Facebook или Linked In.Подарите мне немного любви с помощью кнопок «Нравится» ниже… Спасибо и, пожалуйста, не забудьте поделиться и прокомментировать ниже!!
Avez vous aimé c этой статьей? Je vous serais très reconnaissant si vous aidiez à sa диффузия en l’envoyant par courriel à un ami ou en le partageant sur Twitter, Facebook или Linked In.Montrez-moi un peu d’amour avec les like ci-dessous … Merci et n’oubliez pas, s’il vous plaît, de partager et de commenter ci-dessous!
Линейный график — определение и простые шаги для его создания
Определения статистики > Линейный график
В комплекте:
Линейный график показывает, как меняются значения. Например, вы можете построить график того, как ваш ребенок растет с течением времени. Линейные графики также можно использовать, чтобы показать, как изменяются функции. Функция — это просто уравнение, которое дает вам уникальный результат для каждого входа.Например, y = – 4/5x + 3 является функцией, потому что вы получите уникальное значение для y, если подставите любое число вместо x.
Например, вы можете построить график того, как ваш ребенок растет с течением времени. Линейные графики также можно использовать, чтобы показать, как изменяются функции. Функция — это просто уравнение, которое дает вам уникальный результат для каждого входа.Например, y = – 4/5x + 3 является функцией, потому что вы получите уникальное значение для y, если подставите любое число вместо x.
Чаще всего на линейном графике можно найти данные о том, как что-то меняется с течением времени . Линейный график, показывающий изменения во времени, иногда называют временным графиком.
График Доу-Джонса из Wall Street Journal показывает, как фондовый рынок меняется с течением времени.
Линейные графики имеют горизонтальную ось (ось X) и вертикальную ось (ось Y).В большинстве случаев время откладывается по горизонтальной оси.
Зачем использовать один?
Характеристики линейного графика делают его полезным в некоторых ситуациях. Вы бы использовали линейный график, если:
- У вас есть функция .
 Линейные графики хорошо отображают определенные значения данных, а это означает, что если у вас есть одна переменная (x), вы можете легко найти другую (y).
Линейные графики хорошо отображают определенные значения данных, а это означает, что если у вас есть одна переменная (x), вы можете легко найти другую (y). - Вы хотите показать тренды. Например, как со временем меняются ваши инвестиции или как со временем выросли цены на продукты питания.
- Вы хотите делать прогнозы. Линейный график можно экстраполировать за пределы имеющихся данных. Они позволяют вам делать прогнозы о результатах данных.
Части линейного графика.
| Название | Сообщает вам, о чем график. |
| Этикетки осей | Сообщает вам, какие данные находятся на каждой оси. |
| Масштаб оси | Показывает, сколько или сколько данных находится на каждой оси. |
| Точки | Дайте вам конкретную точку данных на линейном графике со значениями x и y. |
| Линии | Дает вам оценку значений между точками для дискретных функций (дискретные функции состоят из точек данных). В непрерывных функциях строка дает вам 90 223 фактических 90 224 данных, а не оценку. В непрерывных функциях строка дает вам 90 223 фактических 90 224 данных, а не оценку. |
Линейные графики очень легко рисовать на миллиметровой бумаге.
Первый шаг: нарисуйте линию для оси X и оси Y.
Второй шаг: добавьте метки оси и масштаб оси.
Третий шаг: после этого отметьте точки данных.
Четвертый шаг: Затем проведите линию через точки данных.
Пятый шаг: Наконец, добавьте заголовок диаграммы.
Проблемы с линейными графиками.
Линейные графики могут вводить в заблуждение. Например, на этом графике показаны данные о продажах за 4 дня. Что с этим не так?
График вводит в заблуждение из-за неравномерного масштаба по оси Y. Создается впечатление, что между 1 и 2 днями (8) произошел огромный скачок продаж, хотя на самом деле между 3 и 4 днями (11) скачок был еще больше.
А как насчет этого реального графика температур в Нью-Хейвене, Коннектикут? Это ясно показывает, что происходит глобальное потепление.
Изображение: Йельский университет
Присмотритесь, и вы увидите, что температуры показаны только для первой половины года. Это обычная тактика для введения зрителей в заблуждение.
Должен ли линейный график начинаться с начала координат?
График, начинающийся с нуля, легче понять и прочитать. Однако, в отличие от гистограмм, для линейных графиков не существует установленного правила, согласно которому вы должны начинать с исходной точки.С учетом сказанного, если вы решите начать с числа, отличного от нуля, будьте осторожны, чтобы не преувеличить бессмысленные небольшие различия (см. некоторые примеры вводящих в заблуждение графиков), например, этот из Fox News:
.Этот график преднамеренно начат с 8%, чтобы очень небольшая разница (0,2%) выглядела большой. Источник изображения: http://cloudfront.mediamatters.org
После этого скачок на 0,2% может иметь большое значение в некоторых обстоятельствах, например, при росте числа излечимых заболеваний. В общем, вы можете запускать оси в любом месте по вашему выбору; Только будьте осторожны, чтобы не ввести читателя в заблуждение.
В общем, вы можете запускать оси в любом месте по вашему выбору; Только будьте осторожны, чтобы не ввести читателя в заблуждение.
Посмотрите видео по шагам:
Видео не видно? Кликните сюда. ————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в этой области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице Facebook .
Начало работы с анализом изображений
Анализ изображений
Построение линейных графиков
Перейти к содержанию Приборная доскаАвторизоваться
Приборная панель
Календарь
Входящие
История
Помощь
- Мой Dashboard
- Анализ изображений
- Страницы
- Построение линейных графиков
- Главная
- Программа
- Модули
- Задания
- NameCoach
- Библиотеки CU Boulder
- Zoom
Сюжетная линия в R (8 примеров)
В этом руководстве по R вы узнаете, как рисовать линейные графики .
В статье восемь примеров построения линий. Если быть более точным, статья выглядит следующим образом:
Приступим…
Создание примера данных
В примерах этого руководства по R мы будем использовать следующие данные примера:
x <- 1:10 # Создать пример данных y1 <- c(3, 1, 5, 2, 3, 8, 4, 7, 6, 9) |
x <- 1:10 # Создать пример данных у1 <- с(3, 1, 5, 2, 3, 8, 4, 7, 6, 9)
Наши данные состоят из двух числовых векторов x и y1.Вектор x содержит последовательность от 1 до 10, y1 содержит несколько случайных числовых значений.
Пример 1: Базовое создание линейного графика в R
Если мы хотим нарисовать простой линейный график в R, мы можем использовать функцию plot с типом спецификации = «l». Взгляните на следующий код R:
plot(x, y1, type = "l") # Базовый линейный график в R |
plot(x, y1, type = "l") # Базовый линейный график в R
Рисунок 1: Базовый линейный график в R.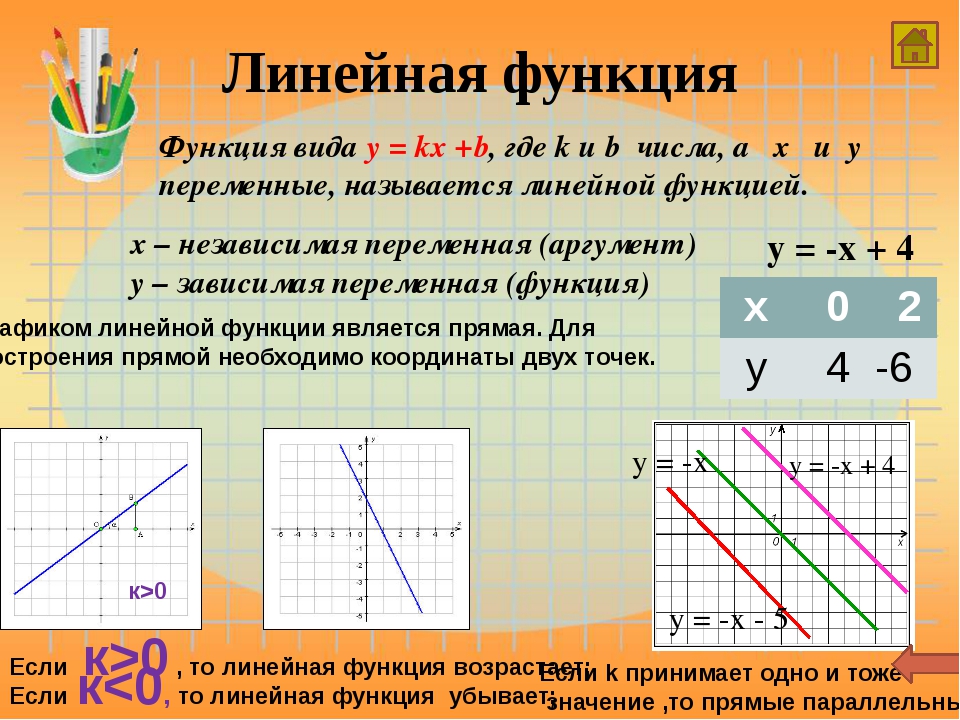
На рис. 1 показаны выходные данные предыдущего синтаксиса R: линейная диаграмма с одной черной линией.
На Рисунке 1 также видно, что наш линейный график относительно прост. В следующих примерах я объясню, как изменить различные параметры этого графика. Так что продолжайте читать!
Пример 2. Добавление основного заголовка и изменение меток осей
В примере 2 вы узнаете, как изменить основной заголовок и метки осей нашего графика с помощью аргументов main, xlab и ylab функции plot:
plot(x, y1, type = "l", # Изменить основной заголовок и метки осей
main = "Это мой линейный график",
xlab = "Мои X-значения",
ylab = "Мои значения Y") |
plot(x, y1, type = "l", # Изменить основной заголовок и метки осей main = "Это мой линейный график", xlab = "Мои X-значения", ylab = "Мои значения Y")
Рис.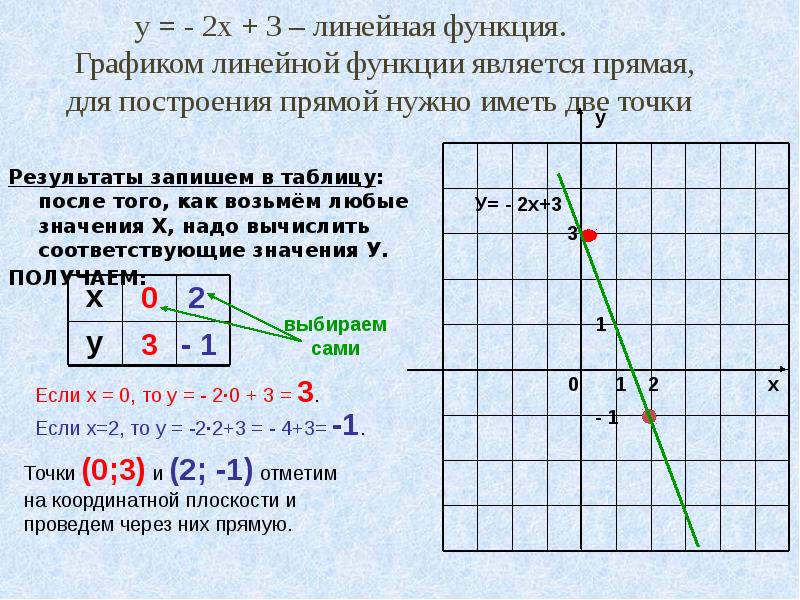 2. Основное название руководства и метки осей.
2. Основное название руководства и метки осей.
Взгляните на рисунок 2. Наш новый график имеет основной заголовок «Это мой линейный график», метку по оси X «Мои значения X» и метку по оси Y «Мои значения Y».
Пример 3: изменение цвета линии
Мы также можем настроить цвет нашей линии, используя аргумент col команды plot:
plot(x, y1, type = "l", # Изменить цвет линии
col = "pink") |
plot(x, y1, type = "l", # Изменить цвет линии col = "розовый")
Рис. 3: Измененный цвет линейного графика.
Обратите внимание, что вы можете использовать любой шестнадцатеричный код цвета или предопределенные цвета в R, чтобы изменить цвет вашей графики.
Пример 4: изменение толщины линии
Мы можем увеличить или уменьшить толщину линий линейного изображения с помощью параметра lwd следующим образом:
plot(x, y1, type = "l", # Изменить толщину линии
lwd = 10) |
plot(x, y1, type = "l", # Изменить толщину линии лвд = 10)
Рис.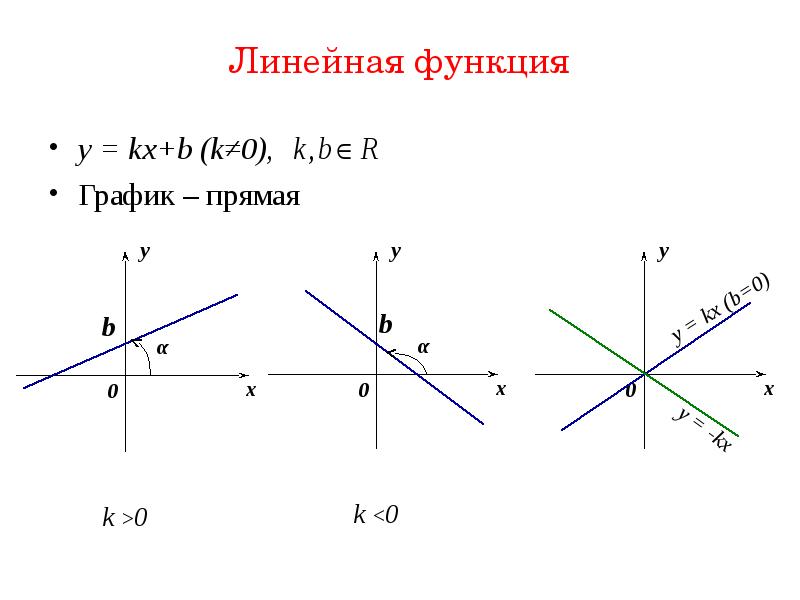 4. Толщина линий, определяемая пользователем.
4. Толщина линий, определяемая пользователем.
В этом примере мы использовали lwd, равное 10. При увеличении этого числа толщина линии увеличивается, а при уменьшении этого числа линия становится тоньше. Обратите внимание, что толщина линии также может быть изменена при экспорте изображения на компьютер.
Пример 5: добавление точек к линейному графику
Можно добавить точки, чтобы еще лучше визуализировать базовые данные нашего линейного графика. Нам просто нужно заменить тип нашего графика с «l» на «b»:
plot(x, y1, type = "b") # Добавляем символы к точкам |
plot(x, y1, type = "b") # Добавляем символы к точкам
Рисунок 5: Различные типы линейных графиков.
Пример 6. Нанесение нескольких линий на один график
В этом примере я хочу показать вам, как построить несколько линий на графике в R. Во-первых, нам нужно создать дополнительные переменные для нашего графика:
Во-первых, нам нужно создать дополнительные переменные для нашего графика:
y2 <- c(5, 1, 4, 6, 2, 3, 7, 8, 2, 8) # Создать дополнительные данные примера y3 <- c(3, 3, 3, 3, 4, 4, 5, 5, 7, 7) |
y2 <- c(5, 1, 4, 6, 2, 3, 7, 8 , 2, 8) # Создать дополнительные данные примера у3 <- с(3, 3, 3, 3, 4, 4, 5, 5, 7, 7)
Теперь мы можем использовать функцию линий, чтобы добавить эти новые данные в нашу ранее созданную линейную диаграмму:
plot(x, y1, type = "l") # Нарисовать первую строку lines(x, y2, type = "l", col = "red") # Добавляем вторую строку lines(x, y3, type = "l", col = "green") # Добавить третью строку |
plot(x, y1, type = "l") # Нарисовать первую строку lines(x, y2, type = "l", col = "red") # Добавляем вторую строку lines(x, y3, type = "l", col = "green") # Добавляем третью строку
Кроме того, мы можем добавить легенду к нашей картинке, чтобы визуализировать, какой цвет относится к какой из различных переменных.
legend("topleft", # Добавить легенду к графику
легенда = c("Строка y1", "Строка y2", "Строка y3"),
col = c("черный", "красный", "зеленый"),
lty = 1) |
legend("topleft", # Добавить легенду к графику легенда = c("Строка y1", "Строка y2", "Строка y3"), col = c("черный", "красный", "зеленый"), лты = 1)
Рис. 6. Нарисуйте несколько линий на одном графике.
На рис. 6 показаны выходные данные кода R из примера 6. Мы создали график с несколькими линиями, разными цветами для каждой линии и легендой, представляющей разные линии.
Пример 7: разные символы точек для каждой линии
Как и в примере 6, мы можем назначить разные точечные символы каждой из наших линий, указав тип = «b». С помощью аргумента pch мы можем указать разные символы точек для каждой строки.
plot(x, y1, type = "b", pch = 16) # Изменить тип символа линии (x, y2, type = "b", col = "red", pch = 15) lines(x, y3, type = "b", col = "green", pch = 8) |
plot(x, y1, type = "b", pch = 16) # Изменить тип символа линии (x, y2, type = "b", col = "red", pch = 15) линии (x, y3, type = "b", col = "green", pch = 8)
Нам также необходимо учитывать эти различные точечные символы в легенде нашего графика:
legend("topleft", # Добавить легенду к графику
легенда = c("Строка y1", "Строка y2", "Строка y3"),
col = c("черный", "красный", "зеленый"),
pch = c(16, 15, 8)) |
legend("topleft", # Добавить легенду к графику легенда = c("Строка y1", "Строка y2", "Строка y3"), col = c("черный", "красный", "зеленый"), рч = с(16, 15, 8))
Рис.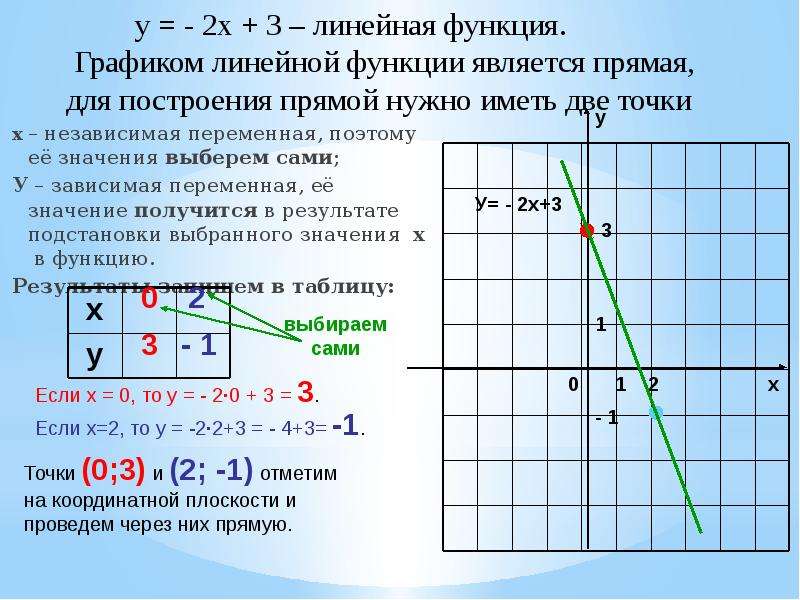 7: Изменение символов pch линейного графика.
7: Изменение символов pch линейного графика.
Пример 8: линейный график в ggplot2 (функция geom_line)
До сих пор мы использовали только функции базовой установки языка программирования R. Однако существует множество доступных пакетов, предоставляющих функции для рисования линейных диаграмм.
Одним из самых мощных пакетов для создания графики является пакет ggplot2. Мы можем установить и загрузить пакет ggplot2 с помощью следующих двух строк кода R:
установка.пакеты("ggplot2") # Установить и загрузить ggplot2
library("ggplot2") |
install.packages("ggplot2") # Установить и загрузить ggplot2 библиотека ("ggplot2")
Кроме того, нам нужно хранить наши данные во фрейме данных, поскольку пакет ggplot2 обычно основан на фреймах данных:
data <- data.frame(x = rep(1:10, 3), # Создать фрейм данных
у = с(у1, у2, у3),
строка = с(реп("у1", 10),
повтор ("у2", 10),
Реп ("у3", 10)))
head(data) # Напечатать первые 6 строк
# х у линия
# 1 3 у1
# 2 1 у1
# 3 5 у1
# 4 2 у1
# 5 3 у1
# 6 8 y1 |
данные <- данные.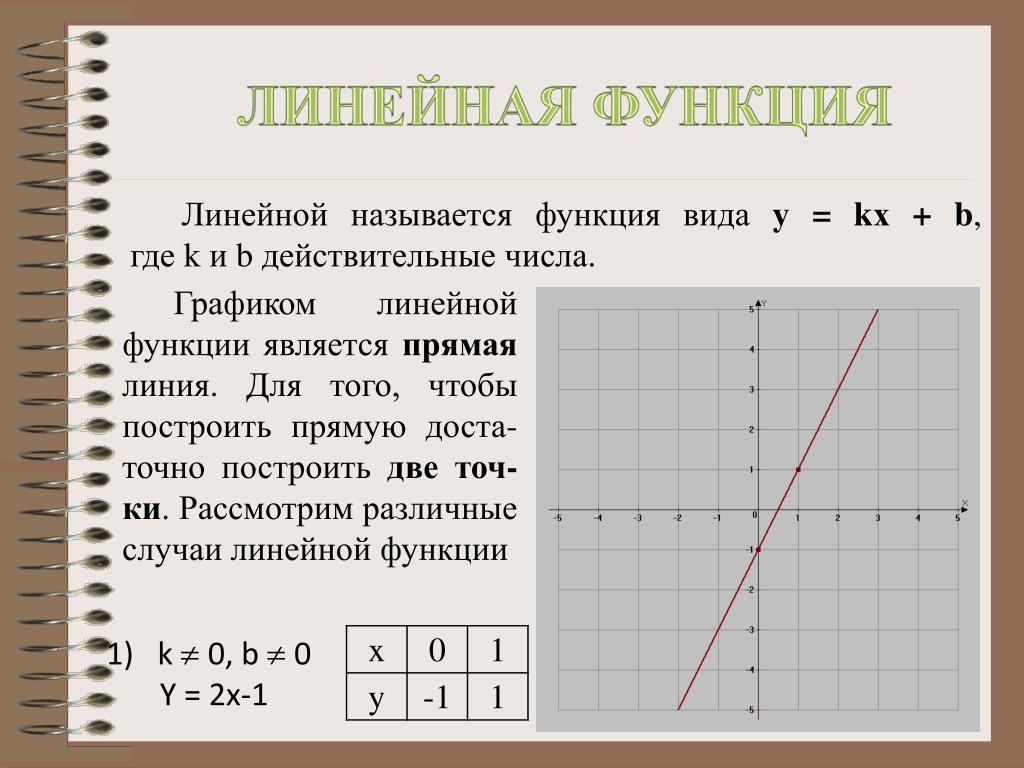 frame(x = rep(1:10, 3), # Создать фрейм данных
у = с(у1, у2, у3),
строка = с(реп("у1", 10),
повтор ("у2", 10),
Реп ("у3", 10)))
head(data) # Напечатать первые 6 строк
# х у линия
# 1 3 у1
# 2 1 у1
# 3 5 у1
# 4 2 у1
# 5 3 у1
# 6 8 у1
frame(x = rep(1:10, 3), # Создать фрейм данных
у = с(у1, у2, у3),
строка = с(реп("у1", 10),
повтор ("у2", 10),
Реп ("у3", 10)))
head(data) # Напечатать первые 6 строк
# х у линия
# 1 3 у1
# 2 1 у1
# 3 5 у1
# 4 2 у1
# 5 3 у1
# 6 8 у1
Консоль RStudio показывает, как структурированы наши новые данные.Наш фрейм данных содержит три столбца и 30 строк. Первый столбец содержит наши значения x (т. е. от 1 до 10), второй столбец состоит из значений наших трех переменных, а третий столбец указывает, какой переменной принадлежат значения строки.
Теперь мы можем применить функцию ggplot в сочетании с функцией geom_line для рисования линейного графика с помощью пакета ggplot2:
ggplot(data, aes(x = x, y = y, col = line)) + # Нарисовать линейный график с помощью ggplot2 geom_line() |
ggplot(data, aes(x = x, y = y, col = line)) + # Нарисовать линейный график с помощью ggplot2 геометрическая_линия()
Рис.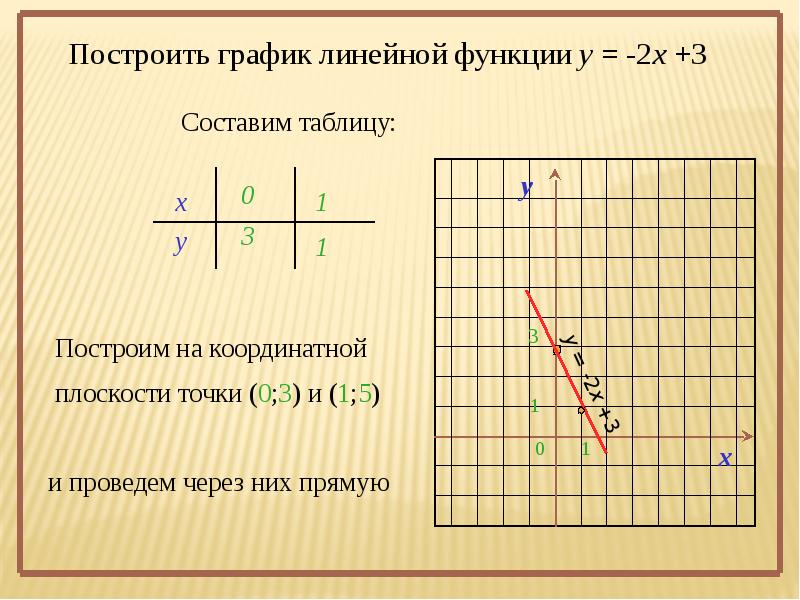 8. Создание линейной диаграммы с помощью пакета ggplot2.
8. Создание линейной диаграммы с помощью пакета ggplot2.
На рис. 8 показано, как выглядит линейный график ggplot2. Разумеется, пакет ggplot2 также предоставляет множество опций для модификации линейной графики в R.
.
Видео, дополнительные ресурсы и резюме
Вам нужна дополнительная информация о синтаксисе программирования R в этой статье? Тогда вы можете посмотреть следующее видео моего канала YouTube. Я объясняю содержание этой статьи в видео.
Видео YouTube скоро будет добавлено.
Кроме того, вы можете ознакомиться с некоторыми из соответствующих учебных пособий на этом веб-сайте.
В этом руководстве вы узнали, как построить линии между точками на языке программирования R. Если у вас есть дополнительные вопросы, не стесняйтесь, дайте мне знать в разделе комментариев.
/* Добавьте свои собственные переопределения стиля формы MailChimp в таблицу стилей вашего сайта или в этот блок стилей.
Мы рекомендуем переместить этот блок и предыдущую ссылку CSS в HEAD вашего HTML-файла.*/
]]>
ЛИНЕЙНЫХ ГРАФИК в R 📈 [С функциями графика и матплота]
ГрафикLines, также известный как линейная диаграмма или линейный график, отображает упорядоченные точки данных, соединенные прямыми сегментами. В этом руководстве вы узнаете, как строить линейные графики в базе R, используя функции plot, lines, matplot, matlines и кривой, а также как изменить стиль результирующих графиков.
Рисование линейной диаграммы в R с функцией построения графика
Линейный график можно создать в базе R с помощью функции построения графика.Учтите, что у вас есть данные, отображаемые в таблице ниже:
Вы можете построить предыдущие данные, используя три различных метода: указание двух векторов, передача данных в виде фрейма данных или с помощью формулы. Обратите внимание, что мы установили type = "l" , чтобы соединить точки данных прямыми сегментами.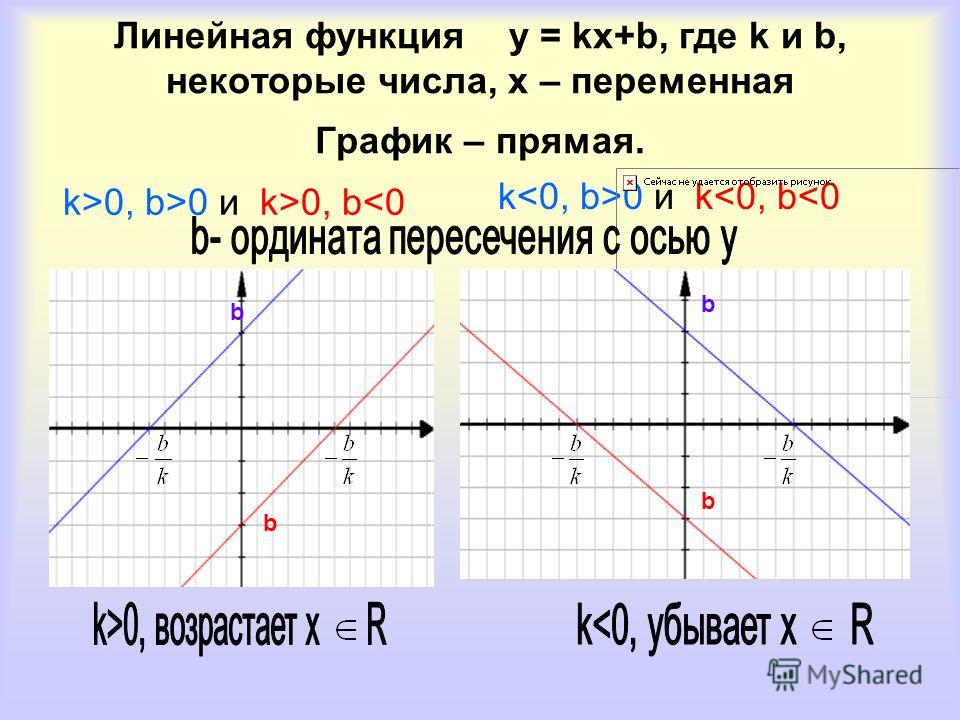
# Данные
х <- с (1, 2, 3, 4, 5)
у <- с(200, 300, 600, 700, 500)
# Векторы
график (х, у, тип = "л")
# Фрейм данных
plot(data.frame(x, y), type = "l") # Эквивалент
# Формула
plot(y ~ x, type = "l") # Эквивалент Стиль линейных графиков в R можно настроить с помощью аргументов функции.Например, цвет и ширину линии можно изменить с помощью аргументов col и lwd соответственно.
сюжет(х, у, тип = "л",
col = "голубой", # Цвет
lwd = 5) # Ширина линии Типы линейных графиков
Помимо type = "l" , в базе R доступны еще три типа линейных графиков. Установка type = "s" создаст линейный график лестницы, type = "b" создаст линейный график с сегментами и точками и type = "o" также будет отображать сегменты и точки, но с перекрытием линии.
пар(mfrow = c(1, 3))
график (x, y, тип = "s", основной = 'тип = "s"')
график (x, y, тип = "b", основной = 'тип = "b"')
график (х, у, тип = "о", основной = 'тип = "о"')
номинал (mfrow = с (1, 1)) Кроме того, существует шесть различных типов линий, которые можно указать с помощью аргумента lty , от 1 до 6:
пар(mfrow = c(2, 3))
график (x, y, тип = "l", lwd = 2, lty = 1, main = "lty = 1")
график (x, y, тип = "l", lwd = 2, lty = 2, main = "lty = 2")
график (x, y, тип = "l", lwd = 2, lty = 3, main = "lty = 3")
график (x, y, тип = "l", lwd = 2, lty = 4, main = "lty = 4")
график (x, y, тип = "l", lwd = 2, lty = 5, основной = "lty = 5")
график (x, y, тип = "l", lwd = 2, lty = 6, main = "lty = 6")
номинал (mfrow = с (1, 1)) Вы также можете настроить символ, используемый, когда тип = "b" или тип = "o" . Эти символы, также известные как символы pch, можно выбрать с помощью аргумента
Эти символы, также известные как символы pch, можно выбрать с помощью аргумента pch , который принимает значения от 0 (квадрат) до 25. Дополнительную информацию см. в разделе символы pch. Вот некоторые из доступных символов:
Цвет символа можно указать с помощью аргумента col , который также изменит цвет линии.
plot(x, y, type = "b", cex = 2, pch = 21, bg = "синий", col = "красный") Символы с 21 по 25 могут быть указаны с фоновым цветом (отличным от границы), используя аргумент bg . Однако вы также можете добавить точки отдельно, используя функцию точек . Такой подход позволит настроить все цвета по желанию.
plot(x, y, type = "l", col = "красный")
# Добавление очков
точки(x, y, # Координаты
pch = 21, # Символ
cex = 2, # Размер символа
bg = "green", # Цвет фона символа
col = "blue", # Цвет границы символа
lwd = 3) # Ширина границы символа Обратите внимание, что аргумент pch также позволяет вводить символы, но только один. В следующем примере мы передаем первые пять букв алфавита.
В следующем примере мы передаем первые пять букв алфавита.
сюжет(х, у, тип = "б",
pch = БУКВЫ[1:5], # Буквы как символы
cex = 2, # Размер символов
col = 1:5, # цвета pch
xlim = c(0, 6), # ограничения по оси X
ylim = c(150, 750)) # Пределы оси Y Добавление текста на график
Если вам нужно сделать некоторые аннотации к диаграмме, вы можете использовать функцию text , у которой первый аргумент - координата X, второй - координата Y и третий - аннотация.
сюжет(х, у, тип = "л")
текст(x = 3, y = 650, "Пользовательская аннотация") Вы также можете указать метку для каждой точки, передав вектор меток.
labels <- c("Текст 1", "Текст 2", "Текст 3", "Текст 4", "Текст 5")
сюжет (х, у, тип = "л",
xlim = c(0.5, 5.5), # ограничение по оси X
ylim = c(150, 750)) # Ограничение по оси Y
text(x = x, y = y, labels, col = "красный") Функция кривой
В предыдущем разделе мы рассмотрели, как создать линейный график из двух векторов, но в некоторых сценариях вам потребуется создать линейный график функции. 3),
main = "функция кривой")
3),
main = "функция кривой")
Линейный график в R с несколькими линиями
Если у вас есть другие переменные, вы можете добавить их на тот же график с помощью функции строк .Например, если у вас есть другая переменная с именем y2 , вы можете создать линейный график с двумя переменными со следующим кодом R:
# Больше данных
у2 <- с(300, 400, 450, 400, 250)
# Первая строка
график (х, у, тип = "л")
# Вторая линия
lines(x, y2, type = "l", col = 2) # Те же значения X Обратите внимание, что функция строк предназначена не для создания графика сама по себе, а для добавления нового слоя поверх уже созданного графика.
Функции matplot и matlines
Лучшим подходом при работе с несколькими переменными внутри фрейма данных или матрицы является функция matplot .Учитывая, что у вас есть следующие многомерные нормальные данные:
# install. packages("МАССА")
library(MASS) # Для функции mvrnorm
set.seed(1)
# Многомерные нормальные данные
означает <- rep (0, 5)
дисперсии <- матрица (1:25, ncol = 5)
data <- data.frame(mvrnorm(n = 10, mu = означает, Sigma = дисперсия))
# Первые шесть строк
голова(данные)
packages("МАССА")
library(MASS) # Для функции mvrnorm
set.seed(1)
# Многомерные нормальные данные
означает <- rep (0, 5)
дисперсии <- матрица (1:25, ncol = 5)
data <- data.frame(mvrnorm(n = 10, mu = означает, Sigma = дисперсия))
# Первые шесть строк
голова(данные) Х1 Х2 Х3 Х4 Х5
1 0,92 -1,5584821 1,6540593 2,65356974 4,6452049
2 -0.1720333 -1,4431276 -0,8738552 -0,06321522 -0,8601666
3 0,6801899 2,2411593 3,7697473 3,34137647 3,4009497
4 -1,8517645 0,4274748 -3,5673172 -8,44912188 -9,2588224
5 -0,1966158 -1,7617016 -3,0887668 -0,01224664 -0,9830791
6 0,7674637 2,1241256 2,49 3,68081631 3,8373183
Вы можете построить все столбцы сразу с помощью функции:
# Отображение всех столбцов одновременно
matplot (данные, тип = "l", main = "функция matplot") Эквивалентно функции строк , matlines позволяет добавлять новые строки к существующему графику. Например, вы можете построить первые три столбца фрейма данных с помощью функции
Например, вы можете построить первые три столбца фрейма данных с помощью функции matplot , а затем добавить последние два с помощью matlines .
# Три первых столбца фрейма данных
данные1 <- данные[, 1:3]
# Построить сразу три столбца
matplot (данные1, тип = "l", lty = 1,
ylab = "данные",
ylim = c(min(data), max(data))) # Пределы по оси Y # Два последних столбца фрейма данных
данные2 <- данные[, 4:5]
# Добавляем данные к предыдущему графику
matlines(data2, type = "l", lty = 1, col = 4:5) Линейная диаграмма с категориальными данными
Помимо создания линейных диаграмм с числовыми данными, их также можно создавать с категориальной переменной.Рассмотрим следующие образцы данных:
# Данные
данные <- data.frame(group = as.factor(c("Группа 1", "Группа 2", "Группа 3")),
переменная1 = с(1, 3, 2),
переменная2 = с(2, 1,5, 1,75))
голова(данные) группа вар1 вар2
1 Группа 1 1 2,00
2 Группа 2 3 1,50
3 Группа 3 2 1,75 Если вы хотите отобразить данные в виде линейного графика в R, вы можете преобразовать факторную переменную в числовую с помощью функции is. и создать график.Вы можете установить факторную переменную на оси X или на оси Y: numeric
numeric
пар(mfrow = c(1, 2))
#-----------------
# Группы по оси X
#-----------------
график (как. числовой (группа данных $), данные $ var1, тип = "l",
ylab = "Значение", xlab = "Группа",
хахт = "н")
# Вторая переменная
строки (as.numeric (data $ group), data $ var2, col = 2)
# Имена групп
ось (1, метки = as.character (data $ group), at = as.numeric (data $ group))
#-----------------
# Группы по оси Y
#-----------------
график (данные $ var1, как.числовой (группа данных $), тип = "l",
ylab = "Группа", xlab = "Значение",
якст = "н")
# Вторая переменная
строки (данные $ var2, as.numeric (группа данных $), столбец = 2)
# Имена групп
ось (2, метки = as.character (data $ group), at = as.numeric (data $ group))
номинал (mfrow = с (1, 1)) Легенда линейной диаграммы
Функция легенды позволяет добавлять легенды на базовые графики R. 2, тип = "л",
столбец = 2,
axes = FALSE, # Нет осей
bty = "n", # Без поля
xlab = "", ylab = "") # Новая ось
ось(4)
mtext("Строка 2", сторона = 4, строка = 3, столбец = 2)
2, тип = "л",
столбец = 2,
axes = FALSE, # Нет осей
bty = "n", # Без поля
xlab = "", ylab = "") # Новая ось
ось(4)
mtext("Строка 2", сторона = 4, строка = 3, столбец = 2)
Line Charts
Импорт графиков.graph_objects как идут импортировать numpy как np title = 'Основной источник новостей' labels = ['Телевидение', 'Газета', 'Интернет', 'Радио'] цвета = ['rgb(67,67,67)', 'rgb(115,115,115)', 'rgb(49,130,189)', 'rgb(189,189,189)'] mode_size = [8, 8, 12, 8] размер_линии = [2, 2, 4, 2] x_data = np.vstack((np.arange(2001, 2014)),)*4) y_data = np.массив([ [74, 82, 80, 74, 73, 72, 74, 70, 70, 66, 66, 69], [45, 42, 50, 46, 36, 36, 34, 35, 32, 31, 31, 28], [13, 14, 20, 24, 20, 24, 24, 40, 35, 41, 43, 50], [18, 21, 18, 21, 16, 14, 13, 18, 17, 16, 19, 23], ]) рис = идти.Фигура() для я в диапазоне (0, 4): fig.add_trace(go.Scatter(x=x_data[i], y=y_data[i], mode='lines', имя=метки[я], линия = dict (цвет = цвета [я], ширина = размер_линии [я]), connectgaps=Верно, )) # конечные точки fig.add_trace(go.Scatter( х=[x_data[i][0], x_data[i][-1]], y=[y_data[i][0], y_data[i][-1]], режим = 'маркеры', маркер = dict (цвет = цвета [i], размер = mode_size [i]) )) fig.update_layout( ось = дикт( шоулайн = Верно, шоугрид=ложь, showticklabels=Верно, цвет линии='rgb(204, 204, 204)', ширина линии=2, тики='снаружи', тикфонт = дикт( семья = 'Ариал', размер=12, цвет = 'rgb (82, 82, 82)', ), ), ось = дикт ( шоугрид=ложь, нулевая линия = ложь, шоулайн=ложь, showticklabels = Ложь, ), авторазмер=ложь, маржа = дикт( авторазвертывание=ложь, л=100, г=20, т=110, ), showlegend=ложь, plot_bgcolor = 'белый' ) аннотации = [] # Добавление меток для y_trace, label, color in zip (y_data, labels, colors): # маркировка левой_стороны графика аннотации.добавить (dict (xref = 'бумага', x = 0,05, y = y_trace [0], xanchor='правый', yanchor='средний', текст = метка + '{}%'.
format (y_trace [0]), шрифт = dict (семья = 'Arial', размер=16), showarrow=ложь)) # маркировка правой_стороны графика annotations.append(dict(xref='бумага', x=0,95, y=y_trace[11], xanchor='левый', yanchor='средний', текст='{}%'.формат (y_trace[11]), шрифт = dict (семья = 'Arial', размер=16), showarrow=ложь)) # Заголовок annotations.append(dict(xref='бумага', yref='бумага', x=0.0, y=1.05, xanchor='левый', yanchor='нижний', text='Основной источник новостей', шрифт = dict (семья = 'Arial', размер=30, цвет = 'rgb (37,37,37)'), showarrow=ложь)) # Источник аннотации.

 Линейная функция. Первый урок
Линейная функция. Первый урок ..
.. 

 ..
.. 



 Типы линий могут быть указаны как целое число (0=пустое, 1=сплошное (по умолчанию), 2=штриховое, 3=пунктирное, 4=точка-тире, 5=длинное тире, 6=двойное тире) или как одна из строк символов «пусто». », «сплошной», «пунктирный», «точечный», «точечный», «длинный тире» или «двойной тире», где «пробел» использует «невидимые линии» (т.д., не рисует их).
Типы линий могут быть указаны как целое число (0=пустое, 1=сплошное (по умолчанию), 2=штриховое, 3=пунктирное, 4=точка-тире, 5=длинное тире, 6=двойное тире) или как одна из строк символов «пусто». », «сплошной», «пунктирный», «точечный», «точечный», «длинный тире» или «двойной тире», где «пробел» использует «невидимые линии» (т.д., не рисует их). 8)
8)  Линейные графики хорошо отображают определенные значения данных, а это означает, что если у вас есть одна переменная (x), вы можете легко найти другую (y).
Линейные графики хорошо отображают определенные значения данных, а это означает, что если у вас есть одна переменная (x), вы можете легко найти другую (y). packages("МАССА")
library(MASS) # Для функции mvrnorm
set.seed(1)
# Многомерные нормальные данные
означает <- rep (0, 5)
дисперсии <- матрица (1:25, ncol = 5)
data <- data.frame(mvrnorm(n = 10, mu = означает, Sigma = дисперсия))
# Первые шесть строк
голова(данные)
packages("МАССА")
library(MASS) # Для функции mvrnorm
set.seed(1)
# Многомерные нормальные данные
означает <- rep (0, 5)
дисперсии <- матрица (1:25, ncol = 5)
data <- data.frame(mvrnorm(n = 10, mu = означает, Sigma = дисперсия))
# Первые шесть строк
голова(данные)  add_trace(go.Scatter(
х=[x_data[i][0], x_data[i][-1]],
y=[y_data[i][0], y_data[i][-1]],
режим = 'маркеры',
маркер = dict (цвет = цвета [i], размер = mode_size [i])
)) fig.update_layout(
ось = дикт(
шоулайн = Верно,
шоугрид=ложь,
showticklabels=Верно,
цвет линии='rgb(204, 204, 204)',
ширина линии=2,
тики='снаружи',
тикфонт = дикт(
семья = 'Ариал',
размер=12,
цвет = 'rgb (82, 82, 82)',
),
),
ось = дикт (
шоугрид=ложь,
нулевая линия = ложь,
шоулайн=ложь,
showticklabels = Ложь,
),
авторазмер=ложь,
маржа = дикт(
авторазвертывание=ложь,
л=100,
г=20,
т=110,
),
showlegend=ложь,
plot_bgcolor = 'белый'
) аннотации = [] # Добавление меток
для y_trace, label, color in zip (y_data, labels, colors):
# маркировка левой_стороны графика
аннотации.добавить (dict (xref = 'бумага', x = 0,05, y = y_trace [0],
xanchor='правый', yanchor='средний',
текст = метка + '{}%'.
add_trace(go.Scatter(
х=[x_data[i][0], x_data[i][-1]],
y=[y_data[i][0], y_data[i][-1]],
режим = 'маркеры',
маркер = dict (цвет = цвета [i], размер = mode_size [i])
)) fig.update_layout(
ось = дикт(
шоулайн = Верно,
шоугрид=ложь,
showticklabels=Верно,
цвет линии='rgb(204, 204, 204)',
ширина линии=2,
тики='снаружи',
тикфонт = дикт(
семья = 'Ариал',
размер=12,
цвет = 'rgb (82, 82, 82)',
),
),
ось = дикт (
шоугрид=ложь,
нулевая линия = ложь,
шоулайн=ложь,
showticklabels = Ложь,
),
авторазмер=ложь,
маржа = дикт(
авторазвертывание=ложь,
л=100,
г=20,
т=110,
),
showlegend=ложь,
plot_bgcolor = 'белый'
) аннотации = [] # Добавление меток
для y_trace, label, color in zip (y_data, labels, colors):
# маркировка левой_стороны графика
аннотации.добавить (dict (xref = 'бумага', x = 0,05, y = y_trace [0],
xanchor='правый', yanchor='средний',
текст = метка + '{}%'. format (y_trace [0]),
шрифт = dict (семья = 'Arial',
размер=16),
showarrow=ложь))
# маркировка правой_стороны графика
annotations.append(dict(xref='бумага', x=0,95, y=y_trace[11],
xanchor='левый', yanchor='средний',
текст='{}%'.формат (y_trace[11]),
шрифт = dict (семья = 'Arial',
размер=16),
showarrow=ложь))
# Заголовок
annotations.append(dict(xref='бумага', yref='бумага', x=0.0, y=1.05,
xanchor='левый', yanchor='нижний',
text='Основной источник новостей',
шрифт = dict (семья = 'Arial',
размер=30,
цвет = 'rgb (37,37,37)'),
showarrow=ложь))
# Источник
аннотации.
format (y_trace [0]),
шрифт = dict (семья = 'Arial',
размер=16),
showarrow=ложь))
# маркировка правой_стороны графика
annotations.append(dict(xref='бумага', x=0,95, y=y_trace[11],
xanchor='левый', yanchor='средний',
текст='{}%'.формат (y_trace[11]),
шрифт = dict (семья = 'Arial',
размер=16),
showarrow=ложь))
# Заголовок
annotations.append(dict(xref='бумага', yref='бумага', x=0.0, y=1.05,
xanchor='левый', yanchor='нижний',
text='Основной источник новостей',
шрифт = dict (семья = 'Arial',
размер=30,
цвет = 'rgb (37,37,37)'),
showarrow=ложь))
# Источник
аннотации.