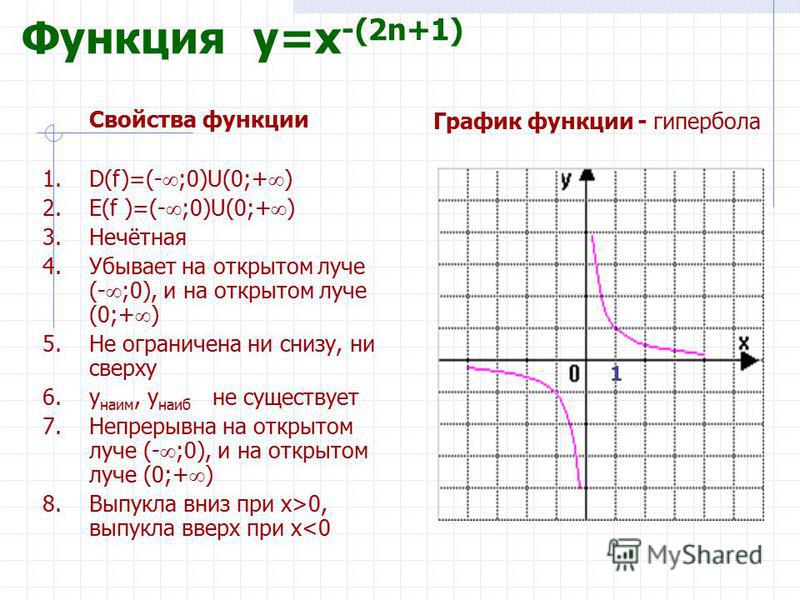
9
6,25
4
2,25
1
0,25
0
0,25
1
2,25
4
6,25
9
Отметим полученные точки на координатной плоскости и соединим их кривой:
Полученный график называют параболой. Точка (0;0) — это вершина параболы. Вершина делит график на левую и правую части, которые называют ветвями параболы.
Свойства параболы y=x²
1. Область определения $x \in (- \infty;+ \infty)$ — все действительные числа.
2. Область значений $y \in [0;+ \infty)$ — все неотрицательные действительные числа.
3. Функция убывает при $x \lt 0$, функция возрастает при $x \gt 0$.
4. Наименьшее значение функции y = 0 — в вершине параболы при x = 0. Вершина параболы совпадает с началом координат.
5. Все точки на ветвях параболы лежат выше оси абсцисс, для них $y \gt 0$.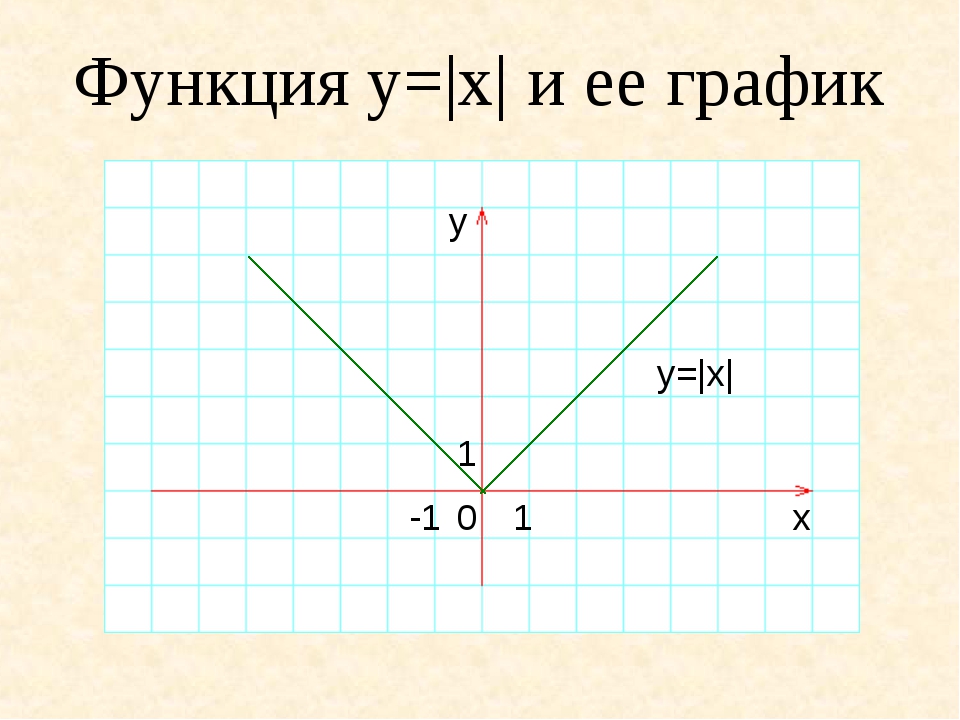
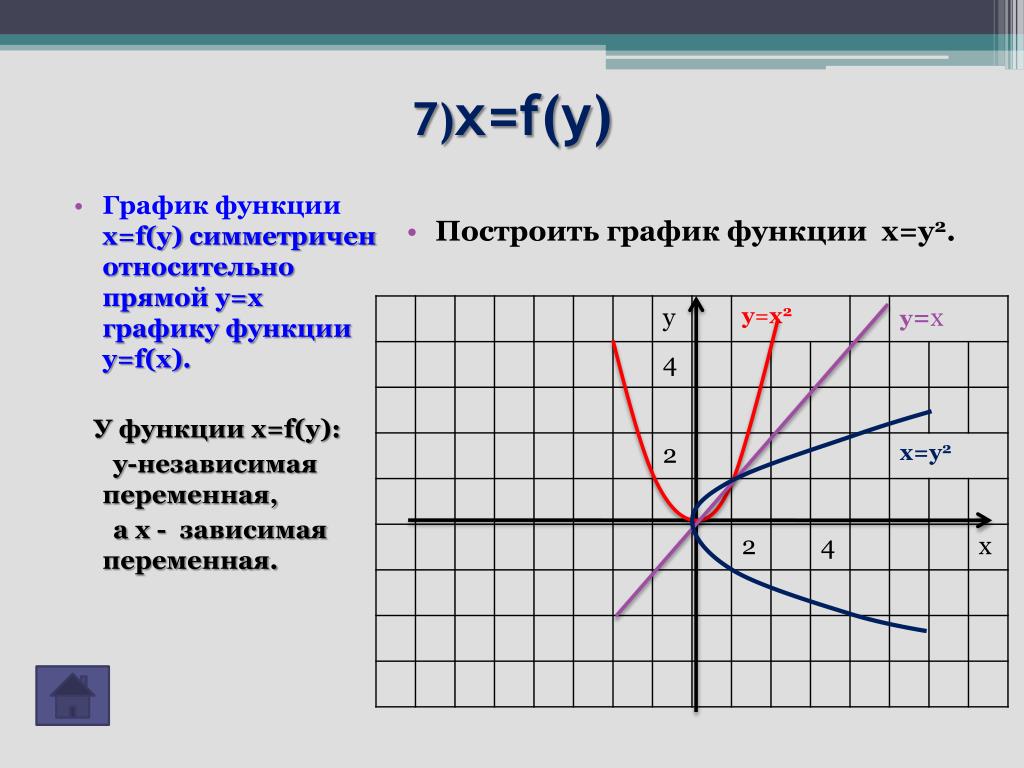
График функции y=f(x)+b | Алгебра
График функции y=f(x)+b (b>0) можно получить из графика функции y=f(x) с помощью параллельного переноса (сдвига) вдоль оси Oy на b единиц вверх.
При таком преобразовании каждая точка (x; y) графика функции y=f(x) переходит в точку (x; y+b) графика функции y=f(x)+b (то есть абсцисса (координата x) каждой точки остается без изменения, а ордината (координата y ) увеличивается на b.
Один из вариантов преобразования — осуществить параллельный перенос начала отсчёта, точки O(0;0), в точку O1(0;b) и построить график y=f(x) с началом отсчёта от точки O1.
Примеры.
1) График функции y=x²+3 может быть получен из графика функции y=x² с помощью параллельного переноса вдоль оси Oy на 3 единицы вверх.
Строим параболу y=x². Затем переносим каждую из основных точек на 3 единицы вверх.
y=x²+3 из y=x²
Можно перенести только вершину параболы, точку (0; 0), на 3 единицы вверх, в точку (0; 3), и от новой вершины строить параболу y=x² (1 единица вправо, 1 — вверх; 1 единица влево, 1 — вверх; 2 единицы вправо, 2 — вверх и т. д.). (Фактически, в этом случае осуществляется параллельный перенос начала отсчёта из точки O(0; 0) в точку O1(0; 3), и строится график y=x² с новым началом отсчёта от точки O1).
д.). (Фактически, в этом случае осуществляется параллельный перенос начала отсчёта из точки O(0; 0) в точку O1(0; 3), и строится график y=x² с новым началом отсчёта от точки O1).
1) График функции y=x³+2 может быть получен из графика функции y=x³ с помощью параллельного переноса вдоль оси Oy на 2 единицы вверх.
Можно обойтись без построения начального графика y=x³, достаточно обозначить его основные точки, и выполнить параллельный перенос каждой из них на 2 единицы вверх.
y=x³+2 из y=x³
3) График функции y=√x+4 может быть получен из графика функции y=√x параллельным переносом на 4 единицы вверх вдоль оси Oy.
Строим график функции y=√x по основным точкам. Затем переносим каждую из этих точек вверх на 4 единицы.
Через полученные точки проводим ветвь параболы:
В следующих раз рассмотрим рассмотрим построение графиков вида y=f(x)-b.
Преобразование графиков позволяет на основе графиков элементарных функций получать графики сложных функций. 2 , её свойства и график» ( 7 класс)
2 , её свойства и график» ( 7 класс)
Тест по теме «Функция , её свойства и график».
Вариант 1.
1.Из представленных ниже функций выберите квадратичную.
А) Б) В) Г)
2.Соедините график с соответствующим ему уравнением.
А) Б) В) Г) 2х
3. Определите какая из точек принадлежит графику функции .
А) ( 2;-4) Б) (-5;25) В) (9;3) Г) (4;8)
4. Определите наибольшее и наименьшее значение функции на полуинтервале .
А) 4, Б) 4,
В) нет, Г) нет,
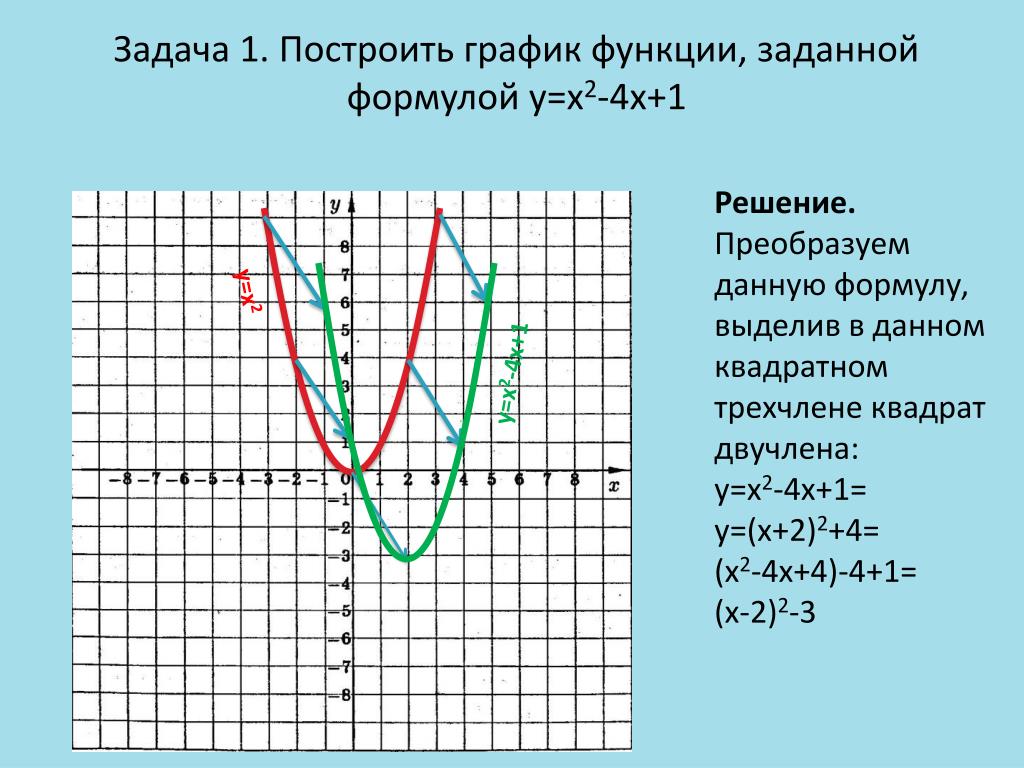
5. Определите на каком шаге допущена ошибка, исправьте её. Дана функция
1 шаг: при значении аргумента равном 4, значение функции равно 16;
2 шаг: при значении аргумента равном -3, значение функции равно -9;
3 шаг: при значении функции равном -4, значение аргумента равно 2 или -2.
6. Оцените предложенное решение в соответствии с предложенными критериями, обоснуйте свой ответ.
Постройте график функции: = =х – 2
У = х – 2 – линейная функция, график прямая.
7. Дана функция y = f(x), где f(x) = . Укажите, где вычисления выполнены не верно. Исправьте ошибку.А) f(-6) = 36 Б) 2f(3а) = 18 В) f(-4) + 7 = 23 Г) 3f(2а) + 2= 38
8. Составьте план графического решения уравнения .
Тест по теме «Функция , её свойства и график».
Вариант 2.
1.Из представленных ниже функций выберите квадратичную.
А) Б) В) Г)
2.Соедините график с соответствующим ему уравнением.
А) Б) В) Г) 2х
3. Определите какая из точек принадлежит графику функции .
А) ( 3;-9) Б) (25;5) В) (-6;36) Г) (4;8)
4. Определите наибольшее и наименьшее значение функции на полуинтервале .
А) нет, Б) 4,
В) 4, Г) нет,
5. Определите на каком шаге допущена ошибка, исправьте её.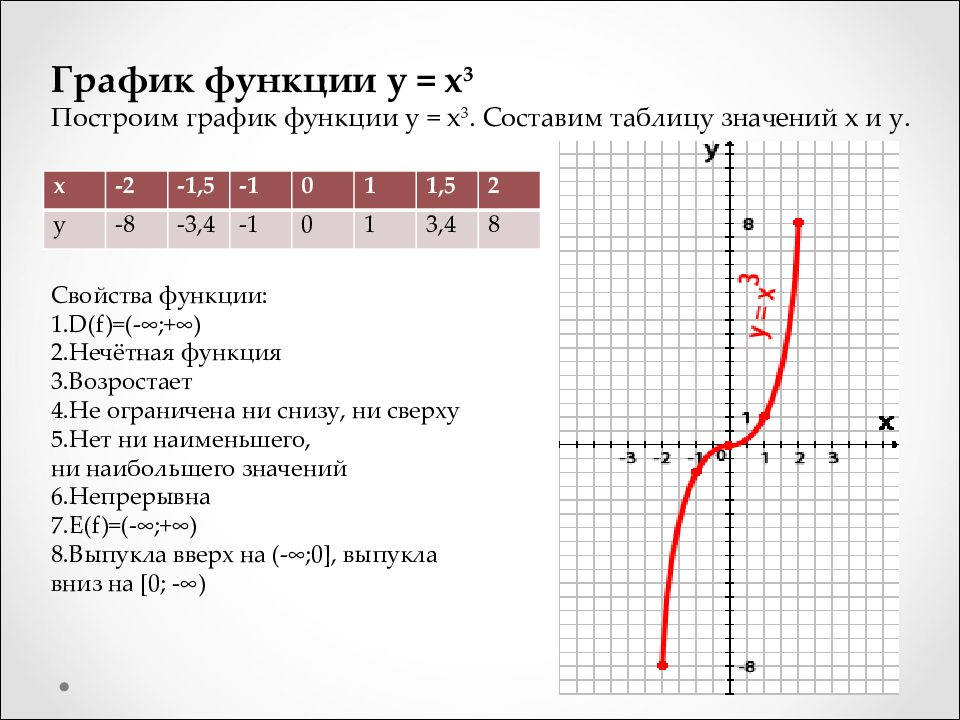 Дана функция
Дана функция
1 шаг: при значении аргумента равном 4, значение функции равно -16;
2 шаг: при значении аргумента равном 5, значение функции равно 25;
3 шаг: при значении функции равном -9, значение аргумента равно 3 или -3.
6. Оцените предложенное решение в соответствии с предложенными критериями, обоснуйте свой ответ.
Постройте график функции: = =х – 2
У = х – 2 – линейная функция, график прямая.
7. Дана функция y = f(x), где f(x) = . Укажите, где вычисления выполнены не верно. Исправьтеошибку.
А) 3f(2а) + 2= 38Б) 2f(3а) = 18 В) f(-4) + 7 = 23 Г) f(-6) = 36
8. Составьте план графического решения уравнения .
Ответы.
Вариант 1.
В
–
Б
В
1 шаг
1 балл. Ошибка в таблице значений, но с этой ошибкой решение доведено до конца, построен график.
Г
1.
 Перенести
Перенести
2. Разделить уравнение на две функции и у = 6+х
3. Построить график функции
4. Построить график функции у = 6+х в той же системе координат
5. Отметить точки пересечения графиков функций
6. Записать в ответ абсциссы точек пересечения.
( Возможен более подробный, либо более короткий план. Главное чтоб был верным).
Вариант 2.
А
–
В
А
2 шаг
2 балла. Все преобразования выполнены верно, верно построен график.
А
1. Перенести х из левой части в правую
2. Разделить уравнение на две функции и у = 6+х
3. Построить график функции
4. Построить график функции у = 6+х в той же системе координат
5. Отметить точки пересечения графиков функций
6. Записать в ответ абсциссы точек пересечения.
( Возможен более подробный, либо более короткий план. Главное чтоб был верным).
Построение графика функции онлайн | umath.ru
- Обязательно писать все знаки умножения
- Десятичные дроби нужно разделять точкой
- Список функций и констант смотрите ниже
Как пользоваться программой:
- Можно строить графики сразу нескольких функций. Для этого просто разделяйте функции точкой с запятой (;).
- Масштаб изменяется с помощью кнопок «+» и «−». Кнопка «100%» меняет масштаб на стандартный.
- Положение экрана можно менять, перетаскивая его мышью, а можно стрелками на панели слева.
- Кнопка «·» в центре джойстика переносит начало координат в центр экрана.
- Кнопка «↺» изменяет масштаб на стандартный и переносит начало координат в центр.
- В форме под графиком можно выбрать точку, которую нужно расположить в центре экрана.
Режимы
Обычный.
Параметрический. Этот режим предназначен для построения графиков кривых, заданных параметрически, то есть в виде
Этот режим предназначен для построения графиков кривых, заданных параметрически, то есть в виде
Полярные координаты. Режим позволяет построить график кривой, заданной в полярной системе координат, то есть уравнением где — радиальная координата, а — полярная координата.
Список констант
| Константа | Описание |
|---|---|
pi | Число =3,14159... |
e | Число Эйлера =2,71828... |
Список функций
| Функция | Описание |
|---|---|
+ − * / | Сложение, вычитание, умножение, деление |
( ) | Группирующие скобки |
abs() или | | | Модуль числа. Выражение abs(x) эквивалентно |x|. 3 дают 3 дают x в третьей
степени |
sqrt() | Квадратный корень |
sin() | Синус |
cos() | Косинус |
tg() | Тангенс |
ctg() | Котангенс |
arcsin() | Арксинус |
arccos() | Арккосинус |
arctg() | Арктангенс |
arcctg() | Арккотангенс |
ln() | Натуральный логарифм числа |
lg() | Десятичный логарифм числа |
log(a, b) | Логарифм числа a |
exp() | Степень числа e |
sh() | Гиперболический синус |
ch() | Гиперболический косинус |
th() | Гиперболический тангенс |
cth() | Гиперболический котангенс |
График функции
Графиком функции называется множество точек плоскости таких, что абсциссы и ординаты
этих точек удовлетворяют уравнению .
Программа создана для школьников и студентов и позволяет строить графики функций онлайн. Во многих браузерах (например, Google Chrome) картинку с графиком функции можно сохранить на компьютер.
Пожалуйста, все предложения и замечания по работе программы пишите в комментариях.
Кроме того мы планируем создать библиотеку функций с интересными и забавными графиками. Если вы открыли функцию с таким графиком, то обязательно напишите об этом в комментариях! Ваше открытие будет опубликовано и станет носить ваше имя ;).
Постройте график функции и найдите значение k
Постройте график функции y=|x-3|-|x+3| и найдите значение k, при которых прямая y=kx имеет с графиком данной функции ровно одну общую точку.
Решение:
Разберем как строить график с модулем.
y=|x-3|-|x+3|
Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3
У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).
y=—(x-3)-(—(x+3))=-х+3+х+3=6
На интервале (-∞;-3) получился график линейной функции (прямой) у=6
2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.
y=—(x-3)-(+(x+3))=-х+3-х-3=-2x
На интервале (-3;3) получился график линейной функции (прямой) у=-2х
3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
х=5
x-3=5-3=2 и x+3=5+3=8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).
y=+(x-3)-(+(x+3))=х-3-х-3=-6
На интервале (3;+∞) получился график линейной функции (прямой) у=-6
4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.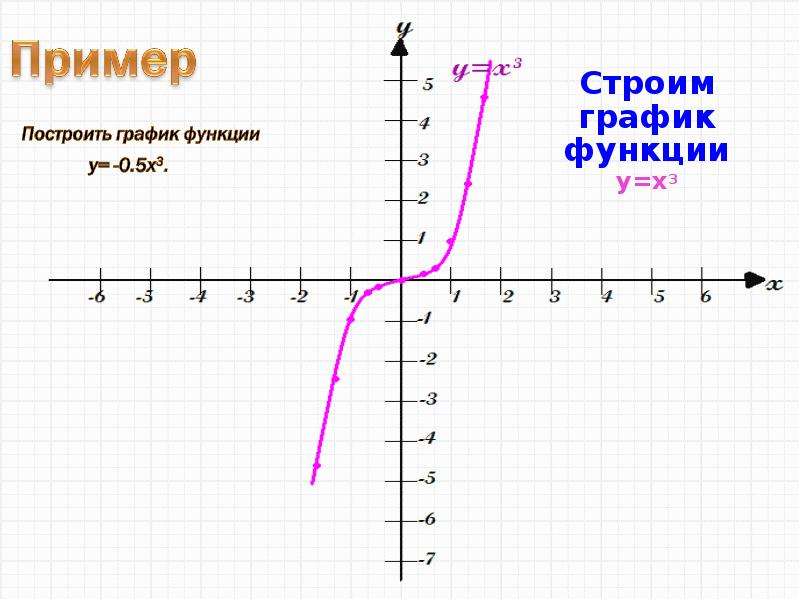
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.
5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.
Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.
Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.
Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.Этот вариант нам не подходит.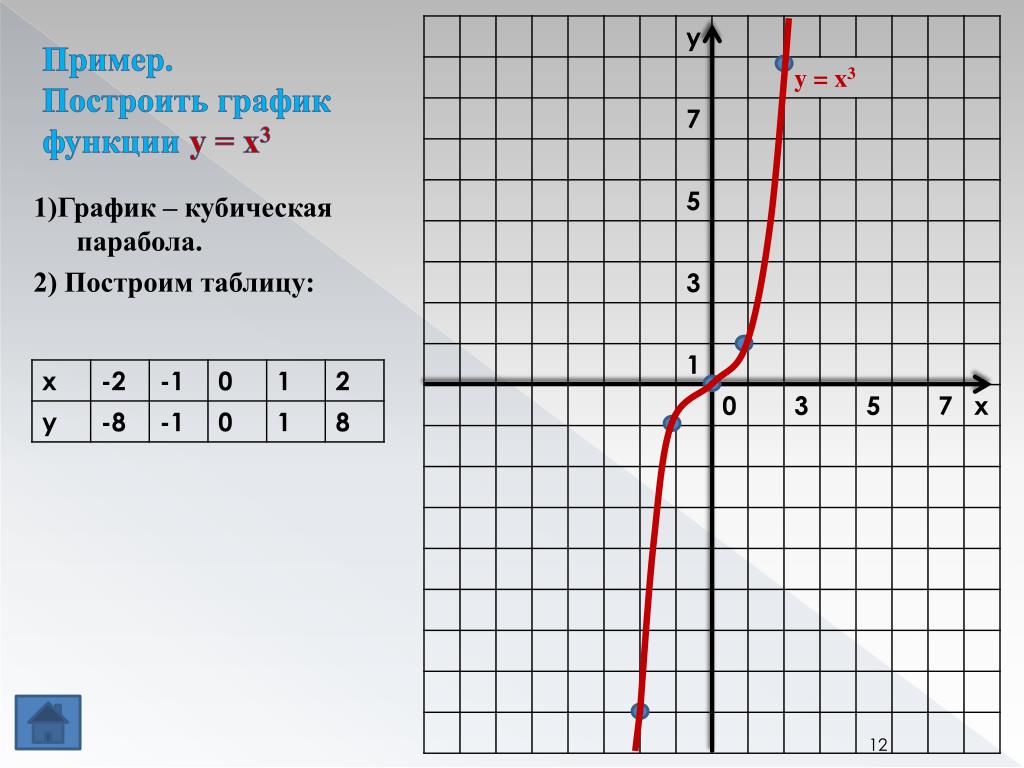
Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.
Ответ: при k принадлежащей интервалу (-∞;-2)U[0;+∞) прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
График линейных функций | Колледж алгебры
В «Линейных функциях» мы увидели, что график линейной функции представляет собой прямую линию. Мы также смогли увидеть точки функции, а также начальное значение на графике. Таким образом, построив графики двух функций, мы сможем легче сравнивать их характеристики.
Есть три основных метода построения графиков линейных функций. Первый заключается в нанесении точек, а затем в проведении линии через точки. Второй — с использованием точки пересечения и наклона y-.И третий — с помощью преобразований функции идентичности [латекс] f \ left (x \ right) = x [/ latex].
Построение графика функции по точкам
Чтобы найти точки функции, мы можем выбрать входные значения, оценить функцию по этим входным значениям и вычислить выходные значения. Входные значения и соответствующие выходные значения образуют пары координат. Затем мы наносим пары координат на сетку. В общем, мы должны оценивать функцию как минимум на двух входах, чтобы найти как минимум две точки на графике.Например, учитывая функцию [latex] f \ left (x \ right) = 2x [/ latex], мы могли бы использовать входные значения 1 и 2. Оценка функции для входного значения 1 дает выходное значение 2 , который представлен точкой (1, 2). Оценка функции для входного значения 2 дает выходное значение 4, которое представлено точкой (2, 4). Часто рекомендуется выбирать три точки, потому что, если все три точки не попадают на одну линию, мы знаем, что допустили ошибку.
Оценка функции для входного значения 2 дает выходное значение 4, которое представлено точкой (2, 4). Часто рекомендуется выбирать три точки, потому что, если все три точки не попадают на одну линию, мы знаем, что допустили ошибку.
Как сделать: для данной линейной функции построить график с помощью точек.
- Выберите минимум два входных значения.
- Оценить функцию для каждого входного значения.
- Используйте полученные выходные значения для определения пар координат.
- Нанесите пары координат на сетку.
- Проведите линию через точки.
Пример 1: Построение графика по точкам
График [латекс] f \ left (x \ right) = — \ frac {2} {3} x + 5 [/ latex] путем нанесения точек.
Решение
Начните с выбора входных значений.Эта функция включает дробь со знаменателем 3, поэтому давайте выберем в качестве входных значений числа, кратные 3. Мы выберем 0, 3 и 6.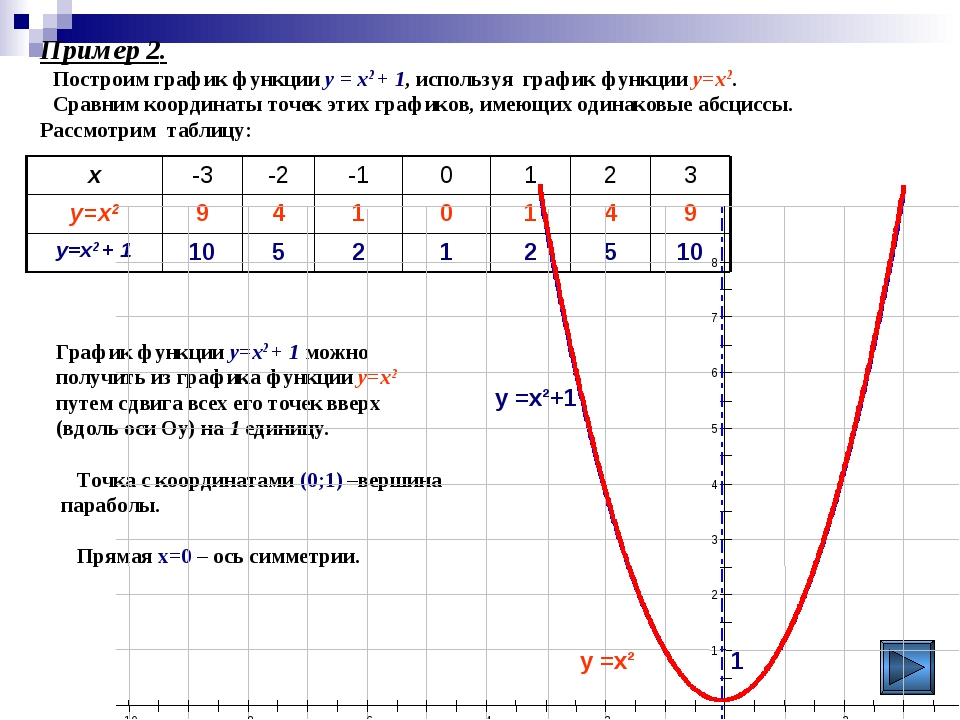
Оцените функцию для каждого входного значения и используйте выходное значение для определения пар координат.
[латекс] \ begin {case} x = 0 & & f \ left (0 \ right) = — \ frac {2} {3} \ left (0 \ right) + 5 = 5 \ Rightarrow \ left (0,5 \ right) \\ x = 3 & & f \ left (3 \ right) = — \ frac {2} {3} \ left (3 \ right) + 5 = 3 \ Rightarrow \ left (3,3 \ right) \ \ x = 6 & & f \ left (6 \ right) = — \ frac {2} {3} \ left (6 \ right) + 5 = 1 \ Rightarrow \ left (6,1 \ right) \ end {case} [/ латекс]
Постройте пары координат и проведите линию через точки.На рисунке 1 показан график функции [латекс] f \ left (x \ right) = — \ frac {2} {3} x + 5 [/ latex].
Рисунок 1
Попробуй 1
График [латекс] f \ left (x \ right) = — \ frac {3} {4} x + 6 [/ latex] путем нанесения точек.
Решение
Построение линейной функции с использованием точки пересечения
y- и наклона Другой способ построения графиков линейных функций — использование конкретных характеристик функции, а не построение точек.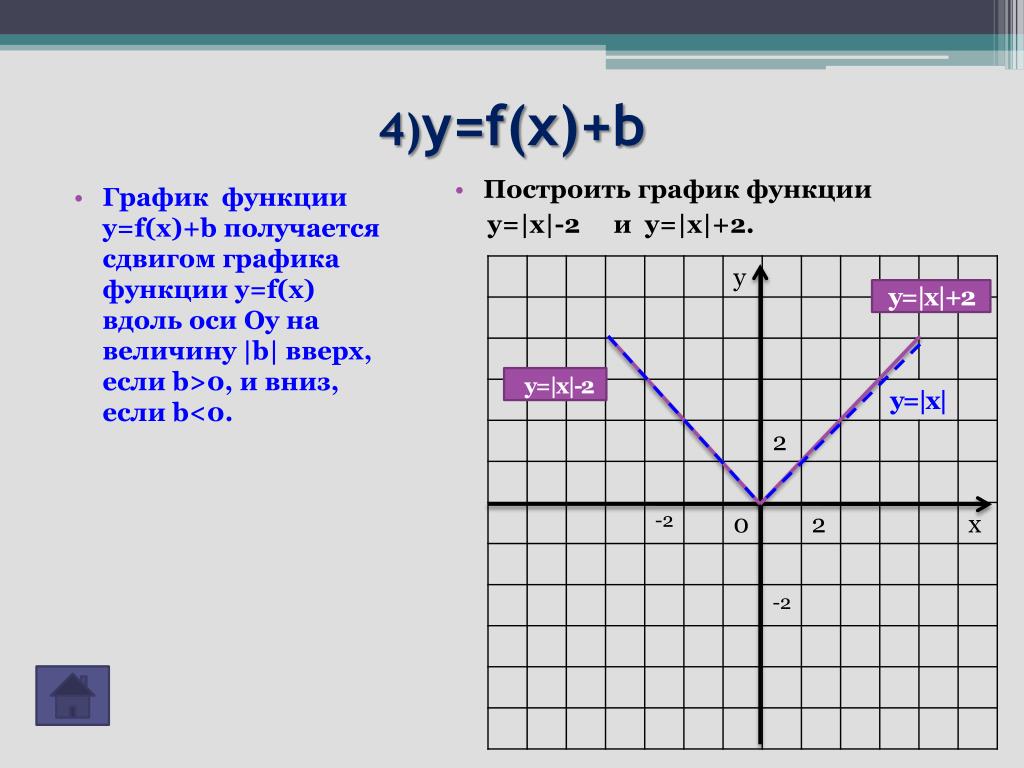 Первой характеристикой является точка пересечения y-, которая является точкой, в которой входное значение равно нулю.Чтобы найти точку пересечения y- , мы можем установить x = 0 в уравнении.
Первой характеристикой является точка пересечения y-, которая является точкой, в которой входное значение равно нулю.Чтобы найти точку пересечения y- , мы можем установить x = 0 в уравнении.
Другой характеристикой линейной функции является ее уклон м , который является мерой ее крутизны. Напомним, что наклон — это скорость изменения функции. Наклон функции равен отношению изменения выходов к изменению входов. Другой способ думать о наклоне — это разделить разницу по вертикали, или подъем, на разницу по горизонтали, или бег.Мы столкнулись как с точкой пересечения y-, так и с наклоном в линейных функциях.
Рассмотрим следующую функцию.
[латекс] f \ left (x \ right) = \ frac {1} {2} x + 1 [/ latex]
Уклон [латекс] \ frac {1} {2} [/ latex]. Поскольку наклон положительный, мы знаем, что график будет наклоняться вверх слева направо.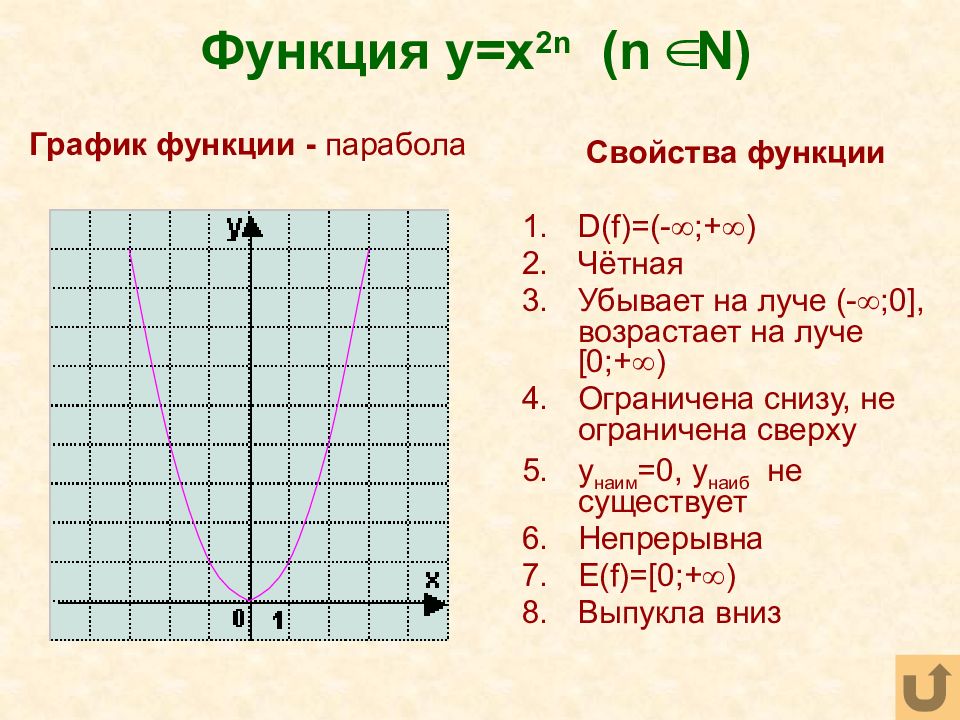 Пересечение y- — это точка на графике, когда x = 0. График пересекает ось y в точке (0, 1). Теперь мы знаем наклон и точку пересечения и .Мы можем начать построение графика с построения точки (0, 1). Мы знаем, что уклон возрастает над пробегом, [latex] m = \ frac {\ text {rise}} {\ text {run}} [/ latex]. В нашем примере у нас есть [latex] m = \ frac {1} {2} [/ latex], что означает, что подъем равен 1, а диапазон равен 2. Итак, начиная с нашего интервала y (0, 1 ), мы можем подняться на 1 и затем пробежать 2 или пробежать 2 и затем подняться на 1. Мы повторяем, пока не получим несколько точек, а затем проводим линию через точки, как показано на рисунке 2.
Пересечение y- — это точка на графике, когда x = 0. График пересекает ось y в точке (0, 1). Теперь мы знаем наклон и точку пересечения и .Мы можем начать построение графика с построения точки (0, 1). Мы знаем, что уклон возрастает над пробегом, [latex] m = \ frac {\ text {rise}} {\ text {run}} [/ latex]. В нашем примере у нас есть [latex] m = \ frac {1} {2} [/ latex], что означает, что подъем равен 1, а диапазон равен 2. Итак, начиная с нашего интервала y (0, 1 ), мы можем подняться на 1 и затем пробежать 2 или пробежать 2 и затем подняться на 1. Мы повторяем, пока не получим несколько точек, а затем проводим линию через точки, как показано на рисунке 2.
Рисунок 2
Общее примечание: графическая интерпретация линейной функции
В уравнении [латекс] f \ left (x \ right) = mx + b [/ latex]
- b — пересечение графика y и указывает точку (0, b ), в которой график пересекает ось y .

- м — наклон линии, обозначающий вертикальное смещение (подъем) и горизонтальное смещение (пробег) между каждой последовательной парой точек. Напомним формулу уклона:
[латекс] m = \ frac {\ text {изменение на выходе (подъем)}} {\ text {изменение на входе (запуск)}} = \ frac {\ Delta y} {\ Delta x} = \ frac { {y} _ {2} — {y} _ {1}} {{x} _ {2} — {x} _ {1}} [/ latex]
Вопросы и ответы
Все ли линейные функции имеют точки пересечения и ?
Да.Все линейные функции пересекают ось Y и, следовательно, имеют точки пересечения по оси Y. (Примечание: Вертикальная линия, параллельная оси Y, не имеет точки пересечения оси Y, но это не функция. )
Практическое руководство. Имея уравнение для линейной функции, постройте график функции, используя точку пересечения
y и наклон.- Оцените функцию при нулевом входном значении, чтобы найти точку пересечения y-.

- Определите наклон как скорость изменения входного значения.
- Постройте точку, представленную отрезком y- .
- Используйте [latex] \ frac {\ text {rise}} {\ text {run}} [/ latex], чтобы определить еще как минимум две точки на линии.
- Нарисуйте линию, проходящую через точки.
Пример 2: Построение графика с использованием точки пересечения
y- и наклонаГрафик [латекс] f \ left (x \ right) = — \ frac {2} {3} x + 5 [/ latex] с использованием точки пересечения и наклона y- .
Решение
Оцените функцию при x = 0, чтобы найти точку пересечения y-.Выходное значение при x = 0 равно 5, поэтому график пересечет ось y в точке (0, 5).
Согласно уравнению для функции, наклон линии равен [латекс] — \ frac {2} {3} [/ latex]. Это говорит нам о том, что для каждого вертикального уменьшения «подъема» на –2 единицы «пробег» увеличивается на 3 единицы в горизонтальном направлении. Теперь мы можем построить график функции, сначала построив точку пересечения и на рисунке 3. От начального значения (0, 5) мы переместимся на 2 единицы вниз и на 3 единицы вправо.Мы можем продлить линию влево и вправо, повторяя, а затем провести линию через точки.
Это говорит нам о том, что для каждого вертикального уменьшения «подъема» на –2 единицы «пробег» увеличивается на 3 единицы в горизонтальном направлении. Теперь мы можем построить график функции, сначала построив точку пересечения и на рисунке 3. От начального значения (0, 5) мы переместимся на 2 единицы вниз и на 3 единицы вправо.Мы можем продлить линию влево и вправо, повторяя, а затем провести линию через точки.
Рисунок 3
Попробуй 2
Найдите точку на графике, который мы нарисовали в примере 2, с отрицательным значением x .
Решение
Построение линейной функции с помощью преобразований
Другой вариант построения графиков — использовать преобразования функции идентичности [latex] f \ left (x \ right) = x [/ latex].Функция может быть преобразована сдвигом вверх, вниз, влево или вправо. Функция также может быть преобразована с помощью отражения, растяжения или сжатия.
Функция также может быть преобразована с помощью отражения, растяжения или сжатия.
Вертикальное растяжение или сжатие
В уравнении [латекс] f \ left (x \ right) = mx [/ latex] м действует как вертикальное растяжение или сжатие функции идентичности. Когда значение м отрицательное, также наблюдается вертикальное отражение графика. Обратите внимание на рис. 4, что умножение уравнения [латекс] f \ left (x \ right) = x [/ latex] на м растягивает график f на коэффициент м единиц, если м > 1 и сжимает график f на коэффициент м единиц, если 0 < м <1.Это означает, что чем больше абсолютное значение м , тем круче уклон.
Рис. 4. Вертикальные растяжения, сжатия и отражения на функции [латекс] f \ left (x \ right) = x [/ latex].
Вертикальный сдвиг
В [latex] f \ left (x \ right) = mx + b [/ latex], b действует как вертикальный сдвиг , перемещая график вверх и вниз, не влияя на наклон линии. Обратите внимание на рис. 5, что добавление значения b к уравнению [латекс] f \ left (x \ right) = x [/ latex] сдвигает график f на b единиц вверх, если b положительный и | b | единиц вниз, если значение b отрицательное.
Обратите внимание на рис. 5, что добавление значения b к уравнению [латекс] f \ left (x \ right) = x [/ latex] сдвигает график f на b единиц вверх, если b положительный и | b | единиц вниз, если значение b отрицательное.
Рис. 5. На этом графике показаны вертикальные сдвиги функции [латекс] f \ влево (x \ вправо) = x [/ latex].
Использование вертикального растяжения или сжатия вместе с вертикальным сдвигом — еще один способ определения различных типов линейных функций. Хотя это может быть не самый простой способ построить график функций такого типа, все же важно практиковать каждый метод.
Практическое руководство. Учитывая уравнение линейной функции, используйте преобразования, чтобы построить график линейной функции в форме [латекс] f \ left (x \ right) = mx + b [/ latex].
- График [латекс] f \ left (x \ right) = x [/ latex].

- Растянуть или сжать график по вертикали в м .
- Сдвинуть график вверх или вниз b единиц.
Пример 3: Построение графиков с использованием преобразований
График [латекс] f \ left (x \ right) = \ frac {1} {2} x — 3 [/ latex] с использованием преобразований.
Решение
Уравнение для функции показывает, что [latex] m = \ frac {1} {2} [/ latex], поэтому функция идентичности сжимается по вертикали с помощью [latex] \ frac {1} {2} [/ latex].Уравнение для функции также показывает, что b = –3, поэтому тождественная функция сдвинута вниз на 3 единицы по вертикали. Сначала изобразите функцию идентичности и покажите вертикальное сжатие.
Рис. 6. Функция, y = x , сжатая с коэффициентом [latex] \ frac {1} {2} [/ latex].
Тогда покажите вертикальный сдвиг.
Рис. 7. Функция [latex] y = \ frac {1} {2} x [/ latex] смещена на 3 единицы вниз.
Попробовать 3
График [латекс] f \ left (x \ right) = 4 + 2x [/ latex], с использованием преобразований.
Решение
Вопросы и ответы
Можно ли в примере 3 нарисовать график, изменив порядок преобразований на противоположный?
Нет. Порядок преобразований соответствует порядку операций. Когда функция оценивается на заданном входе, соответствующий выход вычисляется в соответствии с порядком операций. Вот почему мы сначала выполнили сжатие.Например, следуя порядку: пусть ввод будет 2.
[латекс] \ begin {case} f \ text {(2)} = \ frac {\ text {1}} {\ text {2}} \ text {(2)} — \ text {3} \ hfill \ \ = \ text {1} — \ text {3} \ hfill \\ = — \ text {2} \ hfill \ end {case} [/ latex]
Графики
Экспоненциальные функции: примеры (стр. Разделы: Вводные концепции, пошаговые инструкции по построению графиков, Работал примеров Это может показаться немного сложнее построить график, потому что почти все мои значения и будут десятичные приближения.Но если я округлюсь до разумного числа десятичных знаков (один или два, как правило, подходят для построение графиков), то этот график будет довольно простым. Мне просто нужно сделать уверен, что я нарисовал красивый аккуратный график с последовательным масштабом на моем топоры. Если степень в экспоненте
не линейный (например, « x «),
но вместо этого является квадратичным (например, «2 x 2 «)
или что-то еще, тогда график может выглядеть иначе.
Это действительно полезный функция (называемая «функцией гиперболического синуса»), но вы вероятно, не увижу его снова до исчисления.В любом случае я подсчитываю очки и участок, как обычно: Иногда вы увидите
более сложные экспоненциальные функции, подобные этим. На рассмотрение: некоторые из них различные вариации одной и той же базовой экспоненциальной функции с соответствующий график под каждым уравнением. Обратите внимание, что даже если график перемещен влево или вправо, вверх или вниз, или перевернут вверх ногами, он все еще отображает ту же кривую. Убедитесь, что вы знакомы с этой формой!
|
Построение функции y = f (x) в Python (с Matplotlib)
В нашем предыдущем уроке мы узнали, как построить прямую линию или линейные уравнения типа $ y = mx + c $.2 здесь у = х ** 2 # установка осей в центре fig = plt.figure () ax = fig.add_subplot (1, 1, 1) ax.spines [‘влево’]. set_position (‘центр’) ax.spines [‘дно’]. set_position (‘ноль’) ax.spines [‘правильно’]. set_color (‘нет’) ax.spines [‘вверху’]. set_color (‘нет’) ax.xaxis.set_ticks_position (‘снизу’) ax.yaxis.set_ticks_position (‘влево’) # построить функцию plt.plot (x, y, ‘r’) # показать сюжет plt.show ()
Кубическое уравнение
Затем мы построим простейшую кубическую функцию $ y = x ^ {3} $.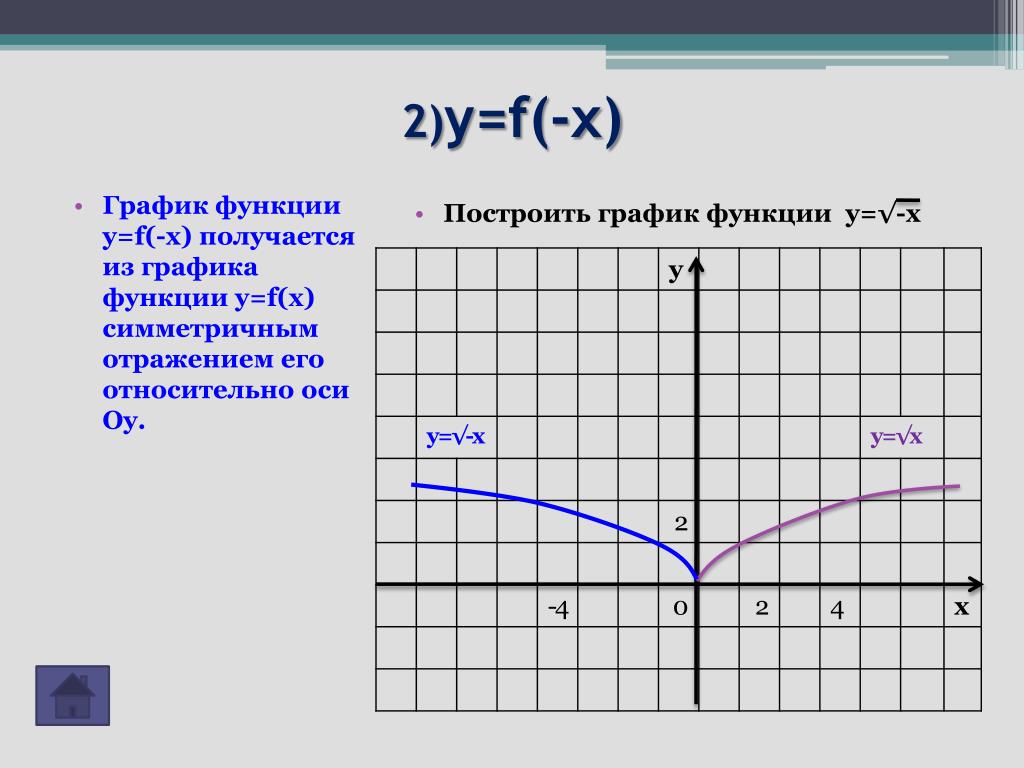 3 здесь
у = х ** 3 # установка осей в центре
fig = plt.figure ()
ax = fig.add_subplot (1, 1, 1)
ax.spines [‘влево’]. set_position (‘центр’)
ax.spines [‘дно’]. set_position (‘центр’)
ax.spines [‘правильно’]. set_color (‘нет’)
ax.spines [‘вверху’]. set_color (‘нет’)
ax.xaxis.set_ticks_position (‘снизу’)
ax.yaxis.set_ticks_position (‘влево’) # построить функцию
plt.plot (x, y, ‘g’) # показать сюжет
plt.show ()
3 здесь
у = х ** 3 # установка осей в центре
fig = plt.figure ()
ax = fig.add_subplot (1, 1, 1)
ax.spines [‘влево’]. set_position (‘центр’)
ax.spines [‘дно’]. set_position (‘центр’)
ax.spines [‘правильно’]. set_color (‘нет’)
ax.spines [‘вверху’]. set_color (‘нет’)
ax.xaxis.set_ticks_position (‘снизу’)
ax.yaxis.set_ticks_position (‘влево’) # построить функцию
plt.plot (x, y, ‘g’) # показать сюжет
plt.show ()
Тригонометрические функции
Здесь мы строим тригонометрическую функцию $ y = \ text {sin} (x) $ для значений $ x $ между $ — \ pi $ и $ \ pi $.У метода linspace () интервал установлен от $ — \ pi $ до $ \ pi $.
импортировать matplotlib.pyplot как plt
импортировать numpy как np
# 100 чисел с линейным интервалом
х = np.linspace (-np.pi, np.pi, 100)
# функция, которая здесь y = sin (x)
у = np.sin (х)
# установка осей в центре
fig = plt.figure ()
ax = fig.add_subplot (1, 1, 1)
ax.spines ['влево']. set_position ('центр')
ax.spines ['дно']. set_position ('центр')
топор.шипы ['право']. set_color ('нет')
ax.spines ['вверху']. set_color ('нет')
ax.xaxis.set_ticks_position ('снизу')
ax.yaxis.set_ticks_position ('влево')
# построить функцию
plt.plot (x, y, 'b')
# показать сюжет
plt.show ()
set_position ('центр')
ax.spines ['дно']. set_position ('центр')
топор.шипы ['право']. set_color ('нет')
ax.spines ['вверху']. set_color ('нет')
ax.xaxis.set_ticks_position ('снизу')
ax.yaxis.set_ticks_position ('влево')
# построить функцию
plt.plot (x, y, 'b')
# показать сюжет
plt.show ()
Построим его вместе с еще двумя функциями, $ y = 2 \ text {sin} (x) $ и $ y = 3 \ text {sin} (x) $. На этот раз мы помечаем функции.
import matplotlib.pyplot как plt
импортировать numpy как np
# 100 чисел с линейным интервалом
х = np.linspace (-np.pi, np.pi, 100)
# функция, которая здесь y = sin (x)
у = np.sin (х)
# установка осей в центре
fig = plt.figure ()
ax = fig.add_subplot (1, 1, 1)
ax.spines ['влево']. set_position ('центр')
ax.spines ['дно']. set_position ('центр')
ax.spines ['правильно']. set_color ('нет')
ax.spines ['вверху']. set_color ('нет')
ax.xaxis.set_ticks_position ('снизу')
топор.yaxis.set_ticks_position ('влево')
# построить график функций
plt. plot (x, y, 'b', label = 'y = sin (x)')
plt.plot (x, 2 * y, 'c', label = 'y = 2sin (x)')
plt.plot (x, 3 * y, 'r', label = 'y = 3sin (x)')
plt.legend (loc = 'верхний левый')
# показать сюжет
plt.show ()
plot (x, y, 'b', label = 'y = sin (x)')
plt.plot (x, 2 * y, 'c', label = 'y = 2sin (x)')
plt.plot (x, 3 * y, 'r', label = 'y = 3sin (x)')
plt.legend (loc = 'верхний левый')
# показать сюжет
plt.show ()
И здесь мы строим вместе как $ y = \ text {sin} (x) $, так и $ y = \ text {cos} (x) $ на одном интервале от $ — \ pi $ до $ \ pi $.
import matplotlib.pyplot как plt
импортировать numpy как np
# 100 чисел с линейным интервалом
х = np.linspace (-np.pi, np.pi, 100)
# здесь функции y = sin (x) и z = cos (x)
у = np.sin (х)
z = np.cos (х)
# установка осей в центре
fig = plt.figure ()
ax = fig.add_subplot (1, 1, 1)
ax.spines ['влево']. set_position ('центр')
ax.spines ['дно']. set_position ('центр')
ax.spines ['правильно']. set_color ('нет')
ax.spines ['вверху']. set_color ('нет')
ax.xaxis.Икс')
plt.legend (loc = 'верхний левый')
# показать сюжет
plt.show ()
Нахождение x-точек пересечения функции
Для графика любой функции пересечение по оси x — это просто точка или точки, в которых график пересекает ось x. Может быть только одна такая точка, может не быть такой точки или много, что означает, что функция может иметь несколько точек пересечения по оси x. Как вы увидите ниже, мы можем использовать график или простое правило алгебры, чтобы найти точки пересечения по x или x любой функции.Вы также можете прокрутить вниз до примера видео ниже.
Может быть только одна такая точка, может не быть такой точки или много, что означает, что функция может иметь несколько точек пересечения по оси x. Как вы увидите ниже, мы можем использовать график или простое правило алгебры, чтобы найти точки пересечения по x или x любой функции.Вы также можете прокрутить вниз до примера видео ниже.
Содержание
- Использование графика для поиска пересечений по оси x
- Использование алгебры для поиска пересечений по оси x
- Пример видео (в том числе при отсутствии x-перехватчиков)
- Дополнительная литература
объявление
Нахождение пересечений по оси x или x с помощью графика
Как упоминалось выше, функции могут иметь одно, ноль или даже множество x-точек пересечения. Их можно найти, посмотрев, где график функции пересекает ось x, которая является горизонтальной осью в плоскости координат xy.Вы можете увидеть это на графике ниже. Эта функция имеет единственную точку пересечения по оси x.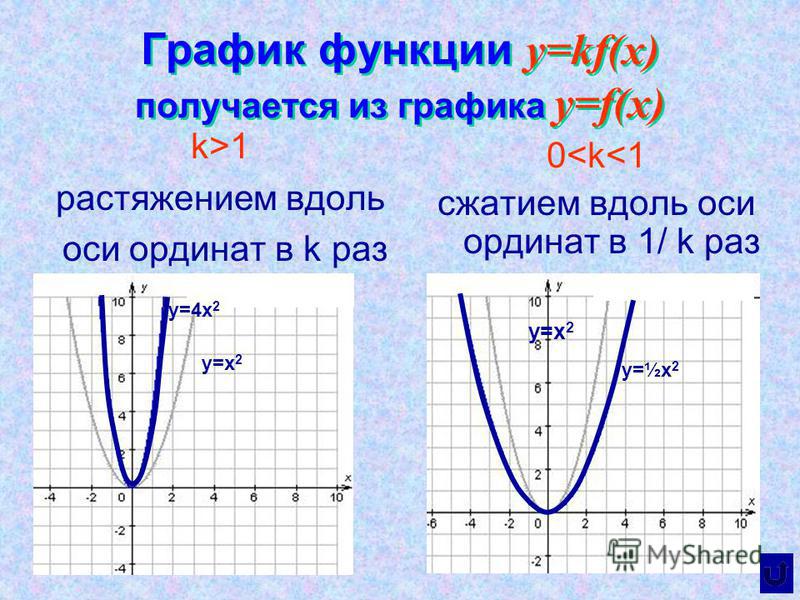
На графике ниже функция имеет два пересечения по оси x. Обратите внимание, что форма точки всегда \ ((c, 0) \) для некоторого числа \ (c \).
Наконец, на следующем графике показана функция без пересечений по оси x. Вы можете видеть это, потому что он ни в какой точке не пересекает ось абсцисс.
Более подробное обсуждение этих идей можно увидеть здесь: Нули многочлена.
Нахождение точки пересечения по оси x или точки пересечения с использованием алгебры
Общее правило для поиска точки пересечения по оси x или точки пересечения любой функции состоит в том, чтобы положить \ (y = 0 \) и решить относительно \ (x \). Это может быть несколько легко или действительно сложно, в зависимости от функции. Давайте рассмотрим несколько примеров, чтобы понять, почему это так.
Пример
Найдите точку пересечения x функции: \ (y = 3x — 9 \)
Решение
Пусть \ (y = 0 \) и решит относительно \ (x \).
\ (\ begin {align} 0 & = 3x — 9 \\ -3x & = -9 \\ x & = 3 \ end {align} \)
Ответ: Следовательно, пересечение по оси x равно 3.2 + 2x — 8 \\ 0 & = (x + 4) (x — 2) \\ x & = -4, 2 \ end {align} \)
Ответ: Эта функция имеет два пересечения по оси x: –4 и 2. Они расположены в \ ((- 4, 0) \) и \ ((2, 0) \).
Для более сложных уравнений часто бывает полезен графический калькулятор, по крайней мере, для оценки местоположения любых точек пересечения.
объявление
Видео примеры
В следующем видео вы можете увидеть, как найти точки пересечения по оси x трех различных функций.Это также включает в себя пример, в котором нет x-перехватов.
Продолжайте изучение графиков
Вы можете продолжить изучение графиков в следующих статьях.
Подпишитесь на нашу рассылку новостей!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.
Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!
СвязанныеГрафики смещения, отражения и растяжения
1.5 — Графики смещения, отражения и растяженияОпределения
- Абсцисса
- Координата x
- Ордината
- Координата Y
- Сдвиг
- Перевод, в котором размер и форма графика функции не изменены, но расположение графика.
- Масштаб
- Перевод, в котором размер и форма графика функции изменены.
- Отражение
- Перевод, в котором график функции отражается относительно оси.
Общие функции
Отчасти красота математики в том, что почти все основано на чем-то другом, и если
вы можете понять основы, а затем применить новые элементы к старым. Это способность
что делает возможным понимание математики. Если бы вы запомнили каждый кусок
математика, представленная вам без связи с другими частями, вы 1) станете
разочарован в математике и 2) не очень понимаю математику.
Это способность
что делает возможным понимание математики. Если бы вы запомнили каждый кусок
математика, представленная вам без связи с другими частями, вы 1) станете
разочарован в математике и 2) не очень понимаю математику.
Есть несколько основных графиков, которые мы видели раньше.Применяя переводы к этим основным графов, мы можем получить новые графы, которые по-прежнему обладают всеми свойствами старых. От понимая основные графики и то, как к ним применяются переводы, мы узнаем каждый новый график как небольшая вариация старого, а не как совершенно другой график, как у нас никогда раньше не видел. Понимание этих переводов позволит нам быстро распознать и нарисуйте новую функцию, не прибегая к построению точек.
Это общие функции, графики которых вы должны знать сейчас:
- Постоянная функция: y = c
- Линейная функция: y = x
- Квадратичная функция: y = x 2
- Кубическая функция: y = x 3
- Функция абсолютного значения: y = | x |
- Функция квадратного корня: y = sqrt (x)
- Наибольшая целочисленная функция: y = int (x) говорилось в предыдущем разделе.

Постоянная функция | Линейная функция | Квадратичная функция |
Кубическая функция | Функция абсолютного значения | Функция квадратного корня |
В вашем тексте линейная функция называется функцией тождества, а квадратичная функция — возведением в квадрат. функция.
Переводы
Есть два типа переводов, которые мы можем сделать с графиком функции. Они меняются и масштабирование. Если считать отражения, их три, но отражения — это всего лишь частный случай второй перевод.
Смена
Сдвиг — это жесткий перевод, поскольку он не меняет форму или размер графика
функция. Все, что будет делать сдвиг, — это изменить положение графика. Вертикальный сдвиг
добавляет / вычитает константу к / из каждой координаты y, оставляя координату x неизменной.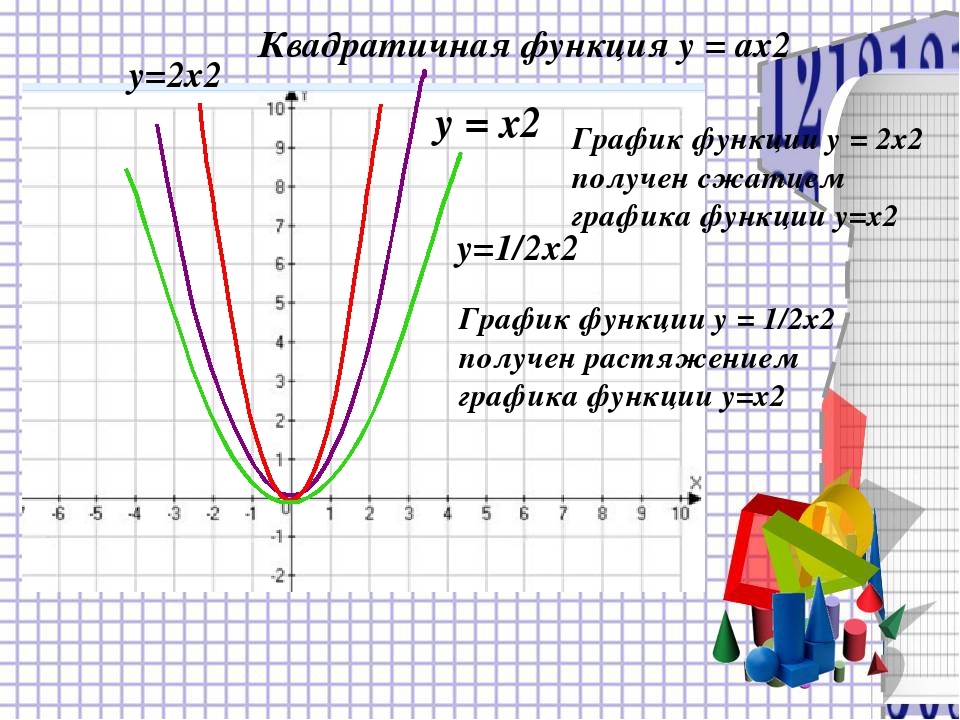 Горизонтальный сдвиг добавляет / вычитает константу к / из каждой координаты x, оставляя координату y неизменной. Вертикальные и горизонтальные сдвиги можно объединить в одно выражение.
Горизонтальный сдвиг добавляет / вычитает константу к / из каждой координаты x, оставляя координату y неизменной. Вертикальные и горизонтальные сдвиги можно объединить в одно выражение.
Сдвиги добавляются / вычитаются из компонентов x или f (x). Если константа сгруппирована с x, тогда это горизонтальный сдвиг, иначе это вертикальный сдвиг.
Весы (растяжение / сжатие)
Масштаб — это нежесткий перевод, поскольку он изменяет форму и размер графика функция.Масштаб будет умножать / делить координаты, и это изменит внешний вид, а также Местоположение. Вертикальное масштабирование умножает / делит каждую координату y на константу, оставляя координата x не изменилась. Горизонтальное масштабирование умножает / делит каждую координату x на константа, оставляя координату y неизменной. Вертикальные и горизонтальные масштабы могут быть объединены в одно выражение.
Коэффициенты масштабирования умножаются / делятся на компоненты x или f (x). Если константа сгруппирована
с x, тогда это горизонтальное масштабирование, в противном случае это вертикальное масштабирование.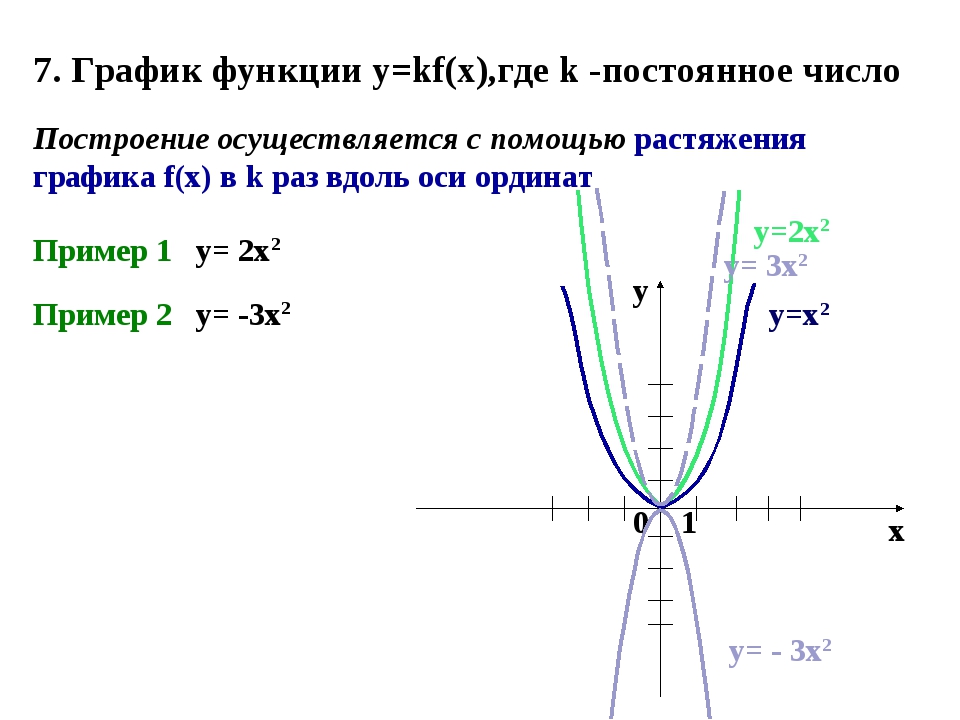
Отражения
Функция может быть отражена вокруг оси умножением на отрицательную единицу. Чтобы отразить ось Y, умножьте каждый x на -1, чтобы получить -x. Чтобы отразить ось x, умножьте f (x) на -1, чтобы получить -f (x).
Собираем все вместе
Рассмотрим основной график функции: y = f (x)
Все переводы могут быть выражены в форме:
y = a * f [b (x-c)] + d
| Вертикальный | Горизонтальный | |
|---|---|---|
| Масштаб | б | |
| Сдвиг | д | с |
| действует нормально | действует наоборот |
отступление
Понимание представленных здесь концепций является фундаментальным для понимания полиномиального и рационального
функции (ch 3) и особенно конические секции (ch 8). Это также будет играть очень большую роль в
Тригонометрия (Математика 117) и Исчисление (Математика 121, 122, 221 или 190).
Это также будет играть очень большую роль в
Тригонометрия (Математика 117) и Исчисление (Математика 121, 122, 221 или 190).
Ранее в тексте (раздел 1.2, задачи 61-64) упоминалась серия задач, которые писали уравнение линии как:
х / а + у / б = 1
Где a — точка пересечения по оси x, а b — точка пересечения по оси Y линии. «А» может действительно быть подумал о том, как далеко идти по оси x (масштабирование по оси x), и буква «b» могла думать как далеко идти в направлении «y» (масштабирование по оси y).Итак, «а» и «б» есть на самом деле множители (даже если они появляются внизу). Что они умножение это 1 который находится с правой стороны. x + y = 1 будет иметь точки пересечения с координатами x и y 1.
Хорошо. Рассмотрим уравнение: y = f (x)
Это самый простой график функции. Но преобразования могут применимо и к нему. Его можно записать в формате, показанном ниже.
В этом формате «a» — вертикальный множитель, а «b» — горизонтальный. множитель.Мы знаем, что «a» влияет на y, потому что он сгруппирован с
y и «b» влияет на
x, потому что он сгруппирован с x.
множитель.Мы знаем, что «a» влияет на y, потому что он сгруппирован с
y и «b» влияет на
x, потому что он сгруппирован с x.
Буквы «d» и «c» — вертикальные и горизонтальные. сдвигов соответственно. Мы знаем, что это сдвиги, потому что они вычитаются из переменной скорее чем быть разделенными на переменные, что сделало бы их масштабными.
В этом формате все изменения кажутся противоположными ожидаемым. Если у вас есть выражение (y-2) / 3, это вертикальный сдвиг на 2 вправо (хотя в нем указано y минус 2), и это вертикальное растяжение на 3 (хотя там указано, что y делится на 3).Важно понимать, что в этом формат, когда константы сгруппированы с переменной, на которую они влияют, перевод является противоположное (обратное) тому, что думает большинство людей.
Однако этот формат не подходит для создания эскизов с помощью технологий,
потому что нам нравится писать функции как y =, а не (y-c) / d =.
Итак, если вы возьмете обозначение выше и решите его относительно y, вы получите обозначение ниже, которое
похоже, но не совсем в нашем базовом состоянии формы, приведенном выше.
y = a * f ((x-c) / b) + d
Обратите внимание, что для определения y вам нужно было инвертировать константы «a» и «d».Вместо деления на «а» вы теперь умножаете на «а». Ну, раньше будь то ты в любом случае пришлось применить обратную константу. Когда было сказано «разделить на», ты знал это Это означало «умножать каждый y на «. Когда говорилось» вычесть d «, вы знали, что вам действительно нужно» добавить d «. У вас есть обратное уже было применено, так что больше не делайте этого! С константами, влияющими на y, поскольку они были перемещены на другую сторону, принимайте их за чистую монету. Если там написано «умножить на 2», делайте это, а не разделить на 2.
Однако константы, влияющие на x, не изменились. Они по-прежнему противоположны
какими, по вашему мнению, они должны быть. И, что еще хуже, «x разделенное b» на самом деле означает
умножение каждой координаты x на «b» было перевернуто и записано как «b умножить на x», так что это действительно
означает разделить каждый x на «b». «X минус c» на самом деле означает прибавление c к каждой координате x.
«X минус c» на самом деле означает прибавление c к каждой координате x.
Итак, окончательная форма (для технологии) такая же, как указано выше:
y = a * f [b (x-c)] + d
Хорошо, конец отступления.
Нормальное и обратное поведение
Вы заметите, что в таблице указано, что вертикальный перевод нормальный, а горизонтальный — нормальный. переводы инвертированы. Объяснение причин читайте в отступлении выше. Концепции в действительно важны для понимания многих графиков.
Примеры
- y = f (x)
- Нет перевода
- у = е (х + 2)
- +2 сгруппирован с x, поэтому это горизонтальный перевод.Поскольку он добавлен к x, а не умноженному на x, это сдвиг, а не масштаб. Поскольку там написано плюс и горизонтальные изменения инвертированы, фактический перевод заключается в перемещении всего график слева на две единицы или «вычтите два из каждой координаты x», оставив только координаты y.
- у = е (х) +2
- +2 не сгруппирован с x, поэтому это вертикальный перевод.
 Поскольку он добавлен,
это не умножение, а сдвиг, а не масштаб.Так как там написано плюс и вертикальный
изменения действуют так, как выглядят, фактический перевод заключается в перемещении всего графа на два
единиц вверх или «прибавьте два к каждой координате y», не трогая координаты x.
Поскольку он добавлен,
это не умножение, а сдвиг, а не масштаб.Так как там написано плюс и вертикальный
изменения действуют так, как выглядят, фактический перевод заключается в перемещении всего графа на два
единиц вверх или «прибавьте два к каждой координате y», не трогая координаты x. - y = f (x-3) +5
- На этот раз имеется сдвиг по горизонтали на три вправо и сдвиг по вертикали на пять вверх. Так перевод будет заключаться в перемещении всего графика вправо на три и пять вверх или «добавить три для каждой координаты x и пять для каждой координаты y «
- у = 3f (х)
- 3 умножается, поэтому это масштабирование, а не сдвиг.3 не сгруппированы с x, так что это вертикальное масштабирование. Вертикальные изменения происходят так, как вы думаете. должно быть, поэтому в результате мы «умножим каждую координату y на три», оставив только координаты x.
- у = -f (х)
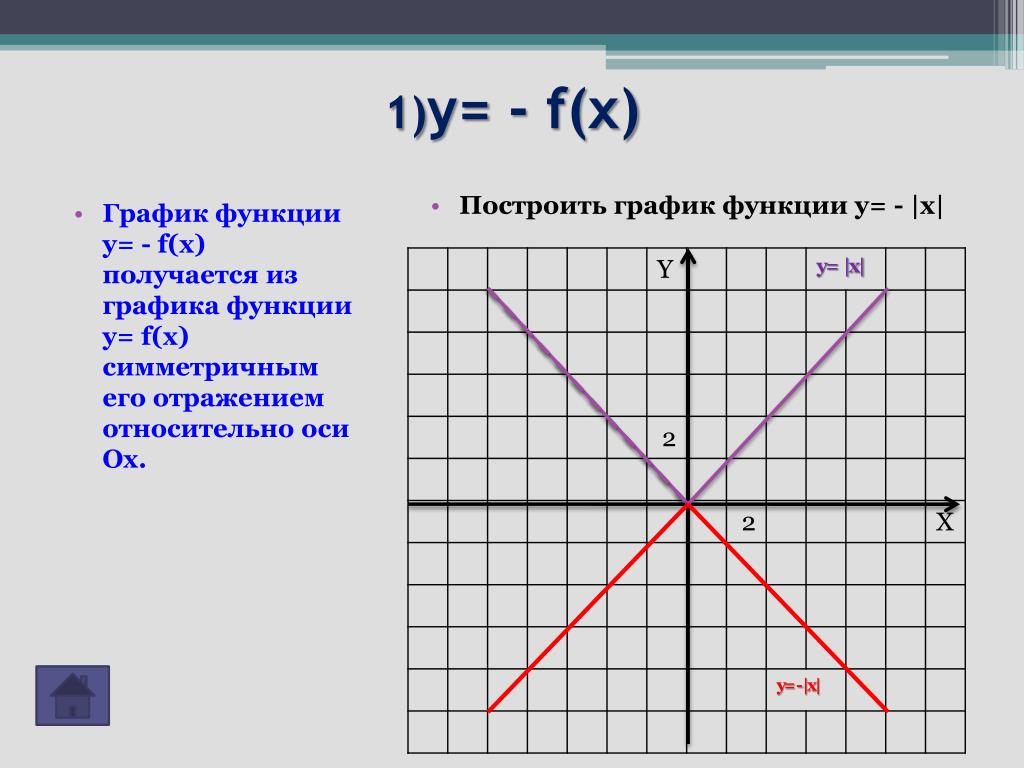
- Y нужно умножить на -1. Это заставляет перенос «отражаться относительно оси x», оставляя только координаты x.

- y = f (2x)
- 2 умножается, а не складывается, поэтому это масштабирование, а не сдвиг.2 — это сгруппированы с x, поэтому это горизонтальное масштабирование. Горизонтальные изменения противоположны чем они кажутся, вместо того, чтобы умножать каждую координату x на два, перевод заключается в «делении каждой координаты x на два», оставляя координаты y без изменений.
- y = f (-x)
- Х нужно умножить на -1. Это заставляет перемещение «отражаться относительно оси y», оставляя только координаты y.
- y = 1/2 f (x / 3)
- Перевод здесь будет таков: «умножить каждую координату y на 1/2 и умножить каждую координату x на 3 дюйма.
- у = 2f (х) +5
- Здесь может быть некоторая двусмысленность. Вы добавляете пять к каждой координате Y, а затем
умножьте на два «или вы» умножаете каждую координату y на два, а затем складываете пять «?
Вот где приходит мой предыдущий комментарий о математике, основанной на самой себе.
 играть. Существует порядок операций, который гласит, что умножение и деление
выполняется перед сложением и вычитанием. Если вы помните это, то решение
легкий. Правильное преобразование — «умножить каждую координату y на два, а затем
добавьте пять дюймов, не трогая координаты x.
играть. Существует порядок операций, который гласит, что умножение и деление
выполняется перед сложением и вычитанием. Если вы помните это, то решение
легкий. Правильное преобразование — «умножить каждую координату y на два, а затем
добавьте пять дюймов, не трогая координаты x. - y = f (2x-3)
- Теперь, когда порядок операций четко определен, двусмысленность здесь нужно сделать сначала снимается. Ответ не в том, чтобы «делить каждую координату x на два. и добавьте три «, как и следовало ожидать. Причина в том, что проблема , а не , записанная в стандартная форма. Стандартная форма — y = f [b (x-c)]. При написании в стандартной форме это проблема становится y = f [2 (x-3/2)]. Это означает, что правильный перевод: «разделить каждую координату x на два и добавить три половины», оставляя координаты y неизменными.
- у = 3f (х-2)
- Перевод здесь означает «умножить каждую координату y на три и добавить два к каждой координате x». В качестве альтернативы вы можете изменить порядок.
 Изменения x или y
можно сделать независимо друг от друга, но при наличии масштабов и сдвигов на одинаковые
переменной, важно сначала выполнить масштабирование, а затем — сдвиг.
Изменения x или y
можно сделать независимо друг от друга, но при наличии масштабов и сдвигов на одинаковые
переменной, важно сначала выполнить масштабирование, а затем — сдвиг.
Переводы и влияние на домен и диапазон
Любой горизонтальный перевод повлияет на домен и оставит диапазон неизменным.Любая вертикаль перевод повлияет на диапазон и оставит домен без изменений.
Примените тот же перевод к домену или диапазону, который вы применяете к x-координатам или y-координатам. Это работает, потому что область может быть записана в обозначении интервала как интервал между двумя координатами x. То же самое для диапазона как интервал между двумя координатами y.
Помните, что в следующей таблице домен и диапазон даны в виде интервалов. Если ты Если вы не знакомы с обозначением интервалов, обратитесь к главе о предварительных требованиях.Первая строка — это формулировка определения и должна использоваться для определения остальных ответов.
| График | Перевод | Домен | Диапазон |
|---|---|---|---|
| y = f (x) | нет | (-2,5) | [4,8] |
| y = f (x-2) | правый 2 | (0,7) | [4,8] |
| y = f (x) -2 | вниз 2 | (-2,5) | [2,6] |
| y = 3f (x) | умножить каждый y на 3 | (-2,5) | [12,24] |
| y = f (3x) | делим каждый x на 3 | (-2 / 3,5 / 3) | [4,8] |
| y = 2f (x-3) -5 | умножьте каждый y на 2 и вычтите 5; прибавьте 3 к каждому x | (1,8) | [3,11] |
| y = -f (x) | отразить относительно оси x | (-2,5) | [-8, -4] |
| y = 1 / f (x) | — величина, обратная каждому y | .(-2,5) | [1 / 8,1 / 4] |
Обратите внимание на последние два, что порядок в диапазоне изменился.Это потому, что в интервале обозначение, меньшее число всегда идет первым.
Действительно хорошие вещи
Понимание переводов также может помочь при поиске домена и диапазона функции. Допустим, ваша проблема — найти домен и диапазон функции y = 2-sqrt (x-3).
Начните с того, что вы знаете. Вы знаете, что основная функция — это sqrt (x), и вы знаете домен и диапазон sqrt (x) равны [0, + бесконечность). Вы знаете это, потому что знаете эти шесть общие функции на лицевой обложке вашего текста, которые будут использоваться в качестве строительных блоков для других функций.
| Функция | Перевод | Домен | Диапазон | |
|---|---|---|---|---|
| Начать с чего ты знаешь | y = sqrt (x) | Нет | [0, + бесконечность) | [0, + бесконечность) |
| Примените переводы | y = -sqrt (x) | Отражение относительно оси x | [0, + бесконечность) | (-infinity, 0] |
| y = 2-sqrt (x) | Добавьте 2 к каждой ординате | [0, + бесконечность) | (-бесконечность, 2] | |
| y = 2-sqrt (x-3) | Добавьте 3 к каждой абсциссе | [3, + бесконечность) | (-бесконечность, 2] |
Итак, для функции y = 2-sqrt (x-3) домен равен x≥3, а диапазон — y≤2.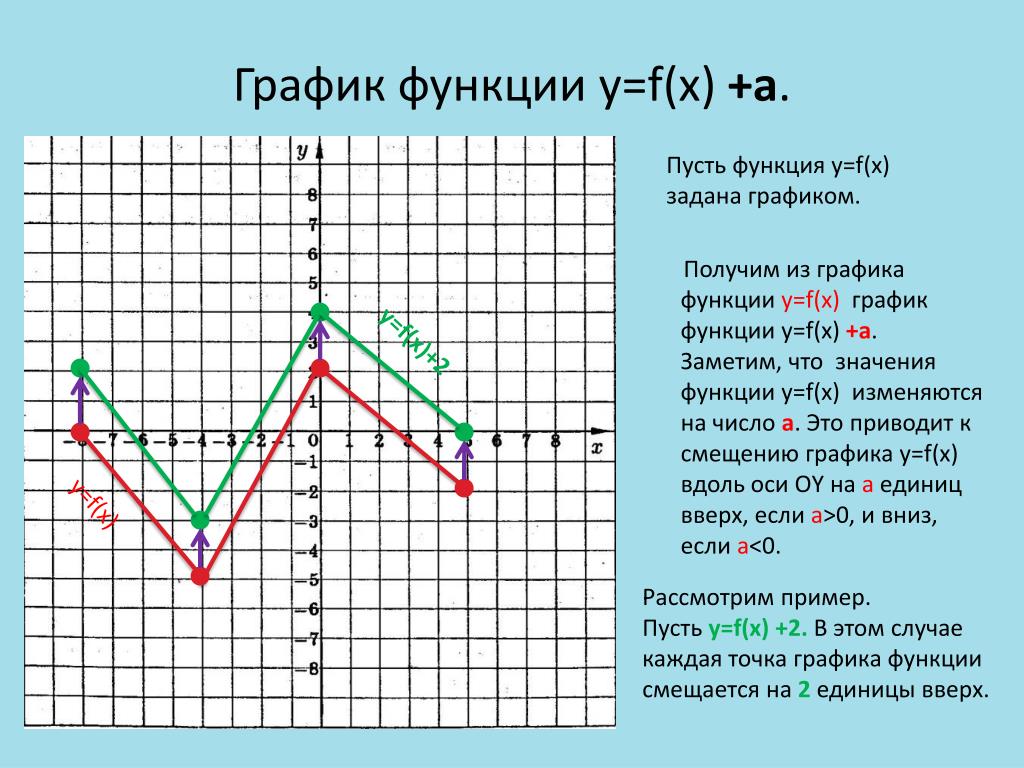
И лучшая часть в том, что вы это поняли! Вы не только поняли это, но вы были в состоянии сделать это без построения графика на калькуляторе.
Нет ничего плохого в том, чтобы построить график, чтобы увидеть, что происходит, но вы должны уметь понять, что происходит без графика, потому что мы узнали, что график калькулятор не всегда точно показывает, что происходит. Это инструмент, который поможет вам понять и понимание, а не инструмент для его замены.
Я хочу, чтобы все вы «поняли» именно эту связность математики. Все подходит вместе так красиво.
графических функций — График и производная от y = x
графическая функция — График и производная от y = x — Mathematics Stack ExchangeСеть обмена стеков
Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.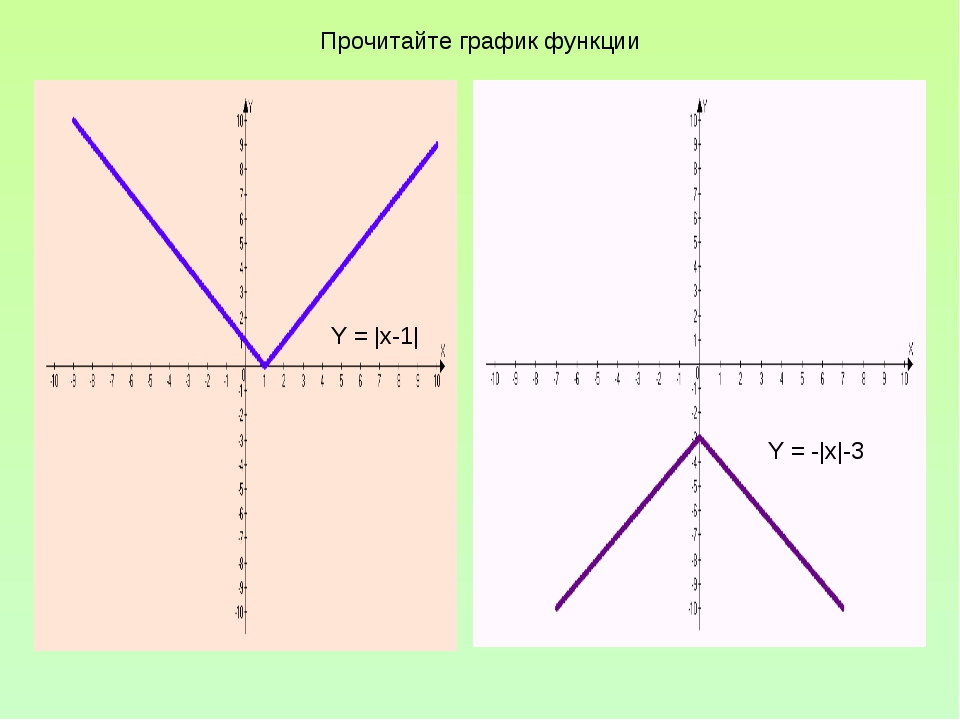
- 0
- +0
- Авторизоваться Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 283 раза
$ \ begingroup $ Мне трудно понять, почему график $ y = x $ отличается от графика $ y = \ sqrt {x ^ 2} $. Разве оба уравнения не являются одинаковыми после упрощения второго? И разве производные каждого из них не одинаковы?
Разве оба уравнения не являются одинаковыми после упрощения второго? И разве производные каждого из них не одинаковы?
Создан 18 окт.
Боб Боб16322 золотых знака33 серебряных знака1111 бронзовых знаков
$ \ endgroup $ 2 $ \ begingroup $Это другое.2} = | x | $$, который отличается от $ y = x $ Производная $ y = x $ равна $ y = 1 $, а производная $ y = | x | $ равна $ y = 1 $ для $ x> 0 $ и $ y = -1 $ для $ x <0 $
Создан 18 окт. 2} = \ sqrt {1} = \ pm1
\ end {align}
$
2} = \ sqrt {1} = \ pm1
\ end {align}
$
У каждого корня есть два решения: например, $ \ sqrt {a} = \ pm a $ $ 2 \ cdot 2 = -2 \ cdot -2 = 4 $
Поскольку функция может иметь только один $ y $ на каждые $ x $, одно решение (отрицательное) должно быть опущено.2} $, это будет выглядеть как $ y = x $ и $ y = -x $ вместе.
Создан 18 окт.
Фритьоф11111 серебряный знак55 бронзовых знаков
$ \ endgroup $ 1 $ \ begingroup $ Если $ 0 \ le a $, то $ \ sqrt {a} $ определяется как неотрицательное число, квадрат которого равен $ a $, поэтому $ \ sqrt {a} \ ge 0 $, что бы ни случилось. 2 = 4
$$
вы извлекаете квадратный корень с обеих сторон и в итоге получаете
$$
\ верт х \ верт = 2
$$
и есть два числа, которые находятся на расстоянии два от $ 0 $. Итак, вы получаете
$$
х = \ pm 2.
$$
ОП уже принял ответ, я просто попытался дать более «алгебраическую» точку зрения на смесь.
2 = 4
$$
вы извлекаете квадратный корень с обеих сторон и в итоге получаете
$$
\ верт х \ верт = 2
$$
и есть два числа, которые находятся на расстоянии два от $ 0 $. Итак, вы получаете
$$
х = \ pm 2.
$$
ОП уже принял ответ, я просто попытался дать более «алгебраическую» точку зрения на смесь.
Создан 02 окт.
Vinyl_cape_jawaVinyl_cape_jawa4,62677 золотых знаков2020 серебряных знаков4040 бронзовых знаков
$ \ endgroup $ Mathematics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.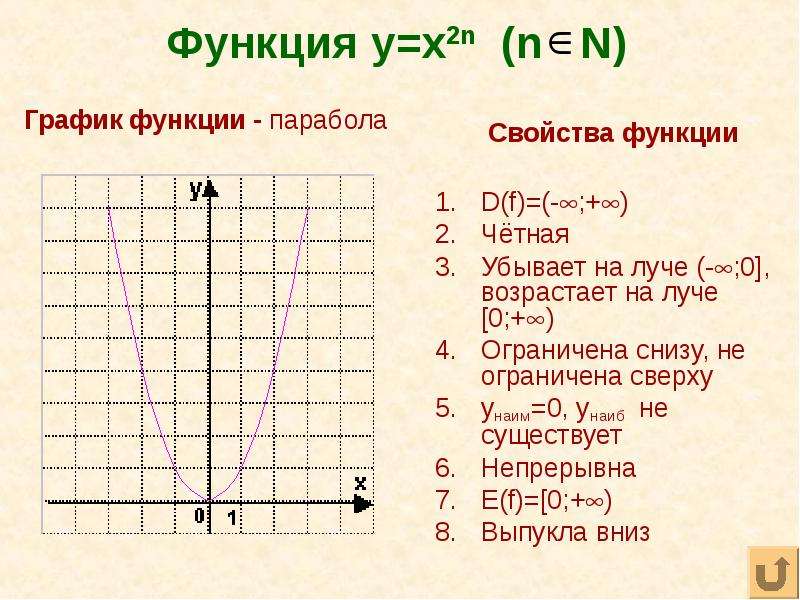
Принимать все файлы cookie Настроить параметры
График параболы — Темы в предварительном исчислении
5
Постоянная функция
Функция идентичности
Функция абсолютного значения
y = x 2 : парабола
Функция квадратного корня
Кубическая функция
Обратная функция
СЛЕДУЮЩИЕ ГРАФИКИ, которые встречаются в аналитической геометрии и исчислении.Учащийся должен уметь рисовать их и узнавать их исключительно по форме. Наносить точки не обязательно.
Постоянная функция
Вот график y = f ( x ) = 3. Это прямая линия, параллельная оси x .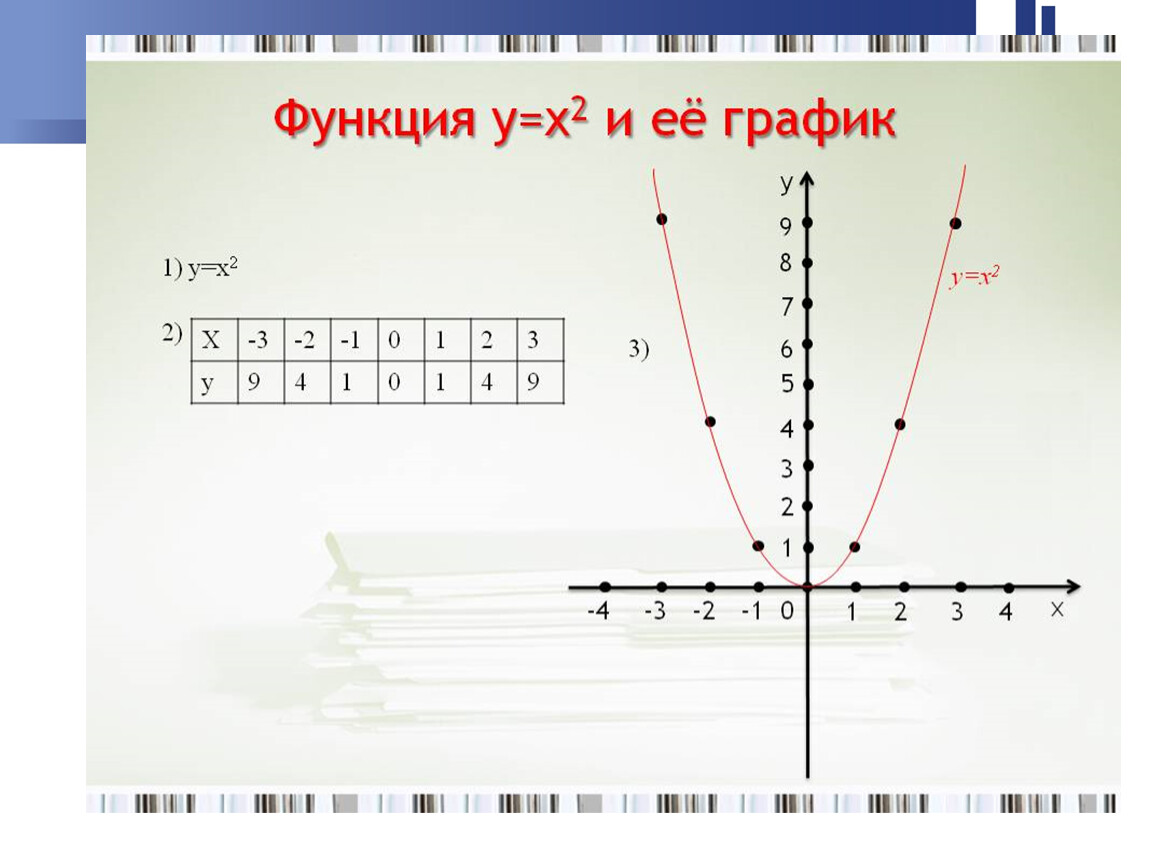 Она называется постоянной функцией, потому что каждому значению x соответствует одно и то же значение y : 3.
Она называется постоянной функцией, потому что каждому значению x соответствует одно и то же значение y : 3.
Является ли постоянная функция однозначной? Да, это так, потому что каждому значению x соответствует одно и только одно значение y . 3.
Постоянная функция имеет вид
y = c ,
, где c — константа, то есть число.
Функция идентичности и функция абсолютного значения
y = x называется функцией идентичности, потому что значение y идентично значению x .Координатные пары ( x , x ).
В функции абсолютного значения отрицательных значений из y в функции идентичности отражаются в положительную сторону. Для, | — x | = | x | = х . Координатные пары равны ( x , | x |).
Пример.
a) Какова область действия функции идентичности?
Нет естественного ограничения на значения x . Следовательно, область, в которой «живет» функция, включает каждое действительное число.
Следовательно, область, в которой «живет» функция, включает каждое действительное число.
−x
Прежде всего обратите внимание, что бесконечность «» — это не число и не место. Это слово вместе с символом мы используем для обозначения: не существует ограничений на значения x , которые мы могли бы назвать.
Обратите внимание, что мы пишем « x меньше ». Равно до бесконечности не имеет смысла.
б) Каков диапазон функции идентичности?
Диапазон — это те значения y , которые соответствуют значениям в домене.Изучение графика покажет, что и также будут принимать все действительные значения.
–лет
Парабола и функция квадратного корня
В параболе y = x 2 , координаты пары ( x , x 2 ). Мы видим, что на графике есть следующие точки: (1, 1), (−1, 1), (2, 4), (−2, 4) и так далее.
График функции квадратного корня связан с y = x 2 .Это его обратное. Координатные пары равны ( x ,). Например, (1, 1), (4, 2), (9, 3) и так далее.
Обратите внимание, что функция квадратного корня определена только для неотрицательных значений x . Ибо квадратный корень отрицательного числа не является действительным.
Также символ относится к одному неотрицательному числу, называемому главным квадратным корнем. (См. Урок 26 Алгебры, Пример 2.) y =, следовательно, функция.
Проблема 1.Какова область определения функции y = x 2 и каков ее диапазон?
Эта функция определена для всех значений x : −∞ x
Что касается диапазона, то самое низкое значение y равно 0. И нет ограничения на самое высокое значение. 0 ≤ ярдов ∞.
Проблема 2. Какова область определения функции квадратного корня и каков ее диапазон?
Функция квадратного корня определена только для неотрицательных значений x .Домен: x ≥ 0.
Что касается диапазона, то самое низкое значение y равно 0. И нет ограничения на самое высокое значение. 0 ≤ ярдов
Кубическая функция
Кубическая функция: y = x 3 . Когда x отрицательно, y отрицательно: Нечетные степени отрицательного числа отрицательны.
Проблема 3.Какова область определения кубической функции и каков ее диапазон?
Домен: −∞ x
Диапазон: −∞ y
Обратная функция
Когда x — очень большое положительное число — в крайнем правом углу оси x — его обратное число является очень маленьким положительным числом. График очень близок к оси x .
Когда x — очень маленькое положительное число , близкое к x = 0, обратная величина — очень большое положительное число.
Подобные свойства сохраняются, когда x отрицательно.
 Перенести
Перенести 

 4 из 4)
4 из 4)  Также, если есть
если в функции больше одного экспоненциального члена, график может выглядеть иначе.
Ниже приведены несколько примеров, чтобы показать вам, как они работают.
Также, если есть
если в функции больше одного экспоненциального члена, график может выглядеть иначе.
Ниже приведены несколько примеров, чтобы показать вам, как они работают.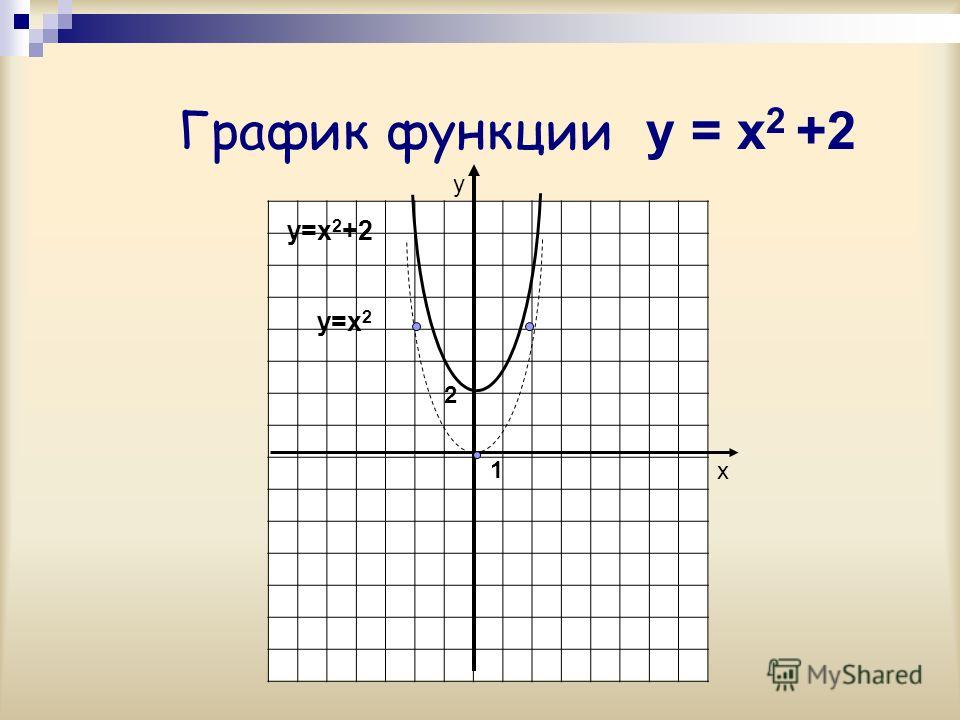 Больной
присоединяйтесь к набранным мною пунктам и убедитесь, что я не забываю рисовать
график в виде кривой линии:
Больной
присоединяйтесь к набранным мною пунктам и убедитесь, что я не забываю рисовать
график в виде кривой линии: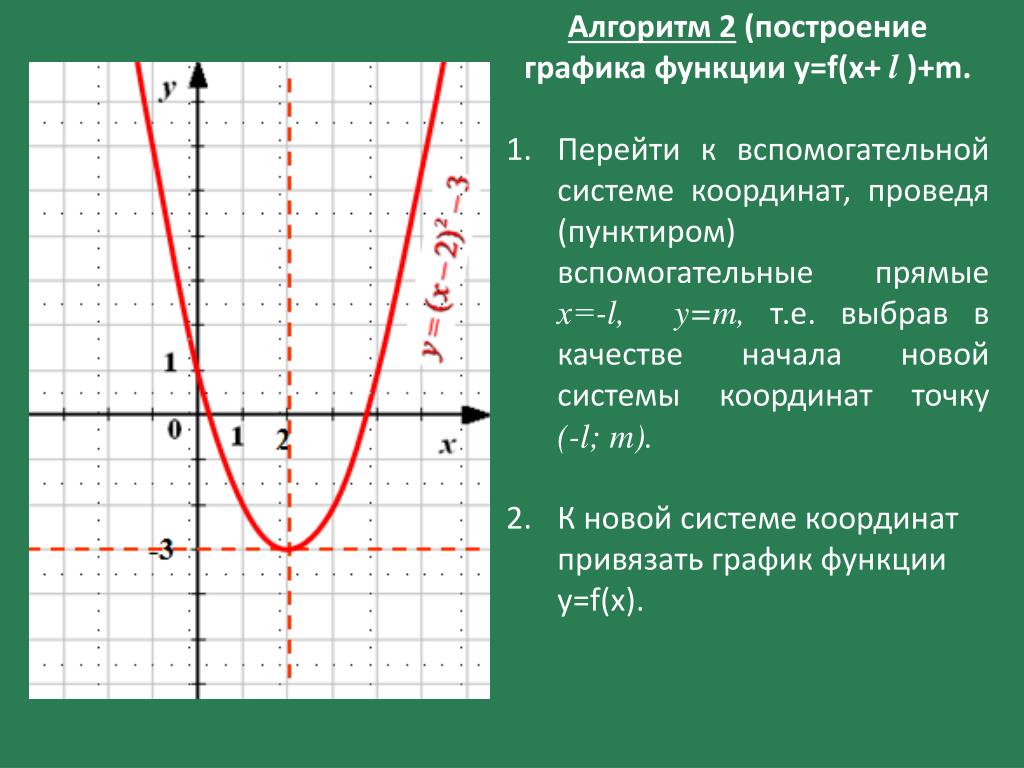 На этом этапе в
ваша математическая карьера, скорее всего, вы будете в основном иметь дело
со стандартной экспоненциальной формой. Так что убедитесь, что вам удобно
с его общей формой и поведением.
На этом этапе в
ваша математическая карьера, скорее всего, вы будете в основном иметь дело
со стандартной экспоненциальной формой. Так что убедитесь, что вам удобно
с его общей формой и поведением. «Графические экспоненциальные функции: примеры». Purplemath .
Доступно по номеру
«Графические экспоненциальные функции: примеры». Purplemath .
Доступно по номеру  set_position ('центр')
ax.spines ['дно']. set_position ('центр')
топор.шипы ['право']. set_color ('нет')
ax.spines ['вверху']. set_color ('нет')
ax.xaxis.set_ticks_position ('снизу')
ax.yaxis.set_ticks_position ('влево')
# построить функцию
plt.plot (x, y, 'b')
# показать сюжет
plt.show ()
set_position ('центр')
ax.spines ['дно']. set_position ('центр')
топор.шипы ['право']. set_color ('нет')
ax.spines ['вверху']. set_color ('нет')
ax.xaxis.set_ticks_position ('снизу')
ax.yaxis.set_ticks_position ('влево')
# построить функцию
plt.plot (x, y, 'b')
# показать сюжет
plt.show ()
 plot (x, y, 'b', label = 'y = sin (x)')
plt.plot (x, 2 * y, 'c', label = 'y = 2sin (x)')
plt.plot (x, 3 * y, 'r', label = 'y = 3sin (x)')
plt.legend (loc = 'верхний левый')
# показать сюжет
plt.show ()
plot (x, y, 'b', label = 'y = sin (x)')
plt.plot (x, 2 * y, 'c', label = 'y = 2sin (x)')
plt.plot (x, 3 * y, 'r', label = 'y = 3sin (x)')
plt.legend (loc = 'верхний левый')
# показать сюжет
plt.show ()

 Поскольку он добавлен,
это не умножение, а сдвиг, а не масштаб.Так как там написано плюс и вертикальный
изменения действуют так, как выглядят, фактический перевод заключается в перемещении всего графа на два
единиц вверх или «прибавьте два к каждой координате y», не трогая координаты x.
Поскольку он добавлен,
это не умножение, а сдвиг, а не масштаб.Так как там написано плюс и вертикальный
изменения действуют так, как выглядят, фактический перевод заключается в перемещении всего графа на два
единиц вверх или «прибавьте два к каждой координате y», не трогая координаты x.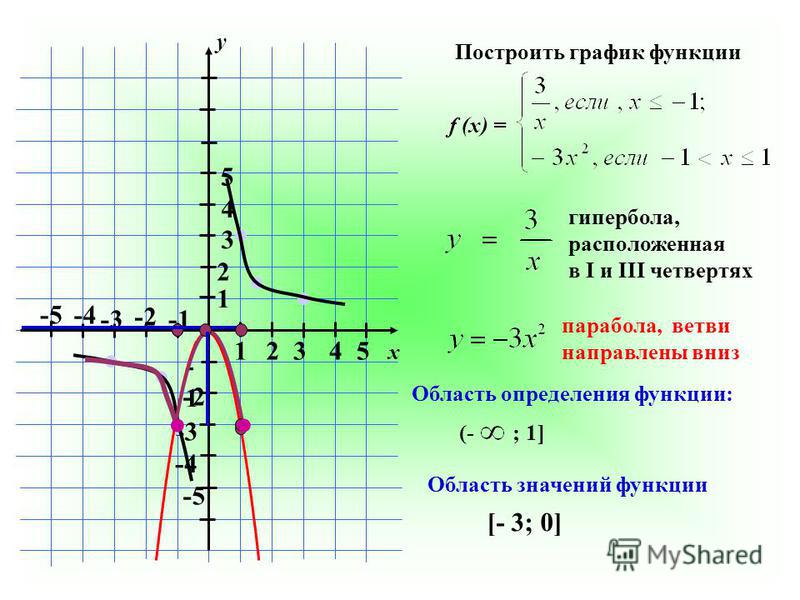
 играть. Существует порядок операций, который гласит, что умножение и деление
выполняется перед сложением и вычитанием. Если вы помните это, то решение
легкий. Правильное преобразование — «умножить каждую координату y на два, а затем
добавьте пять дюймов, не трогая координаты x.
играть. Существует порядок операций, который гласит, что умножение и деление
выполняется перед сложением и вычитанием. Если вы помните это, то решение
легкий. Правильное преобразование — «умножить каждую координату y на два, а затем
добавьте пять дюймов, не трогая координаты x. Изменения x или y
можно сделать независимо друг от друга, но при наличии масштабов и сдвигов на одинаковые
переменной, важно сначала выполнить масштабирование, а затем — сдвиг.
Изменения x или y
можно сделать независимо друг от друга, но при наличии масштабов и сдвигов на одинаковые
переменной, важно сначала выполнить масштабирование, а затем — сдвиг.