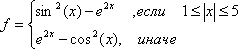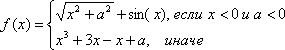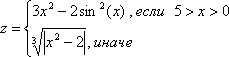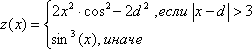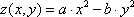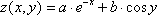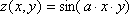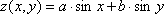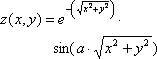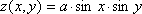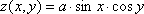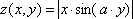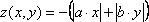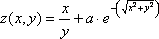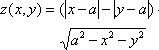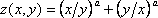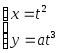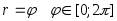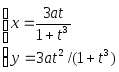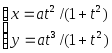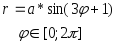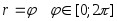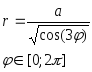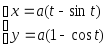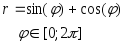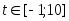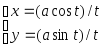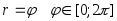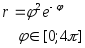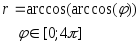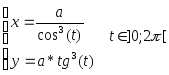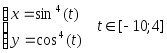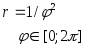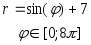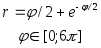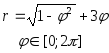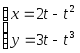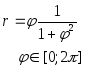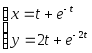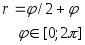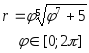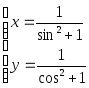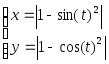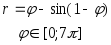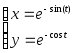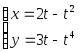График кусочной функции – Кусочные функции. Как построить график кусочной функции — Детская игровая комната «Волшебный лес»

Posted on 05.12.201822.12.2019 by alexxlab

Содержание

Кусочно-заданная функция

Реальные процессы, происходящие в природе, можно описать с помощью функций. Так, можно выделить два основных типа течения процессов, противоположных друг другу – это постепенное или непрерывное и скачкообразное (примером может служить падение мяча и его отскок). Но если есть разрывные процессы, то существуют и специальные средства для их описания. С этой целью вводятся в обращение функции, имеющие разрывы, скачки, то есть на различных участках числовой прямой функция ведет себя по разным законам и, соответственно, задается разными формулами. Вводятся понятия точек разрыва, устранимого разрыва.

Наверняка вам уже встречались функции, заданные несколькими формулами, в зависимости от значений аргумента, например:

y = {x – 3, при x > -3;
{-(x – 3), при x < -3.

Такие функции называются кусочными или кусочно-заданными. Участки числовой прямой с различными формулами задания, назовем

составляющими область определения. Объединение всех составляющих является областью определения кусочной функции. Те точки, которые делят область определения функции на составляющие, называются граничными точками. Формулы, определяющие кусочную функцию на каждой составляющей области определения, называются входящими функциями. Графики кусочно-заданных функций получаются в результате объединения частей графиков, построенных на каждом из промежутков разбиения.

Упражнения.

Построить графики кусочных функций:

1) {-3, при -4 ≤ x < 0,
f(x) = {0, при x = 0,
{1, при 0 < x ≤ 5.

График первой функции – прямая, проходящая через точку y = -3. Она берет свое начало в точке с координатами (-4; -3), идет параллельно оси абсцисс до точки с координатами (0; -3). График второй функции – точка с координатами (0; 0). Третий график аналогичен первому – это прямая, проходящая через точку y = 1, но уже на участке от 0 до 5 по оси Ох.

Ответ: рисунок 1.

2) {3, если x ≤ -4,
f(x) = {|x² – 4|x| + 3|, если -4 < x ≤ 4,
{3 – (x – 4)², если x > 4.

Рассмотрим отдельно каждую функцию и построим ее график.

Так, f(x) = 3 – прямая, параллельная оси Ох, но изображать ее нужно только на участке, где x ≤ -4.

График функции f(x) = |x² – 4|x| + 3| может быть получен из параболы y = x² – 4x + 3. Построив ее график, часть рисунка, которая лежит над осью Ox, необходимо оставить без изменений, а часть, которая лежит под осью абсцисс, симметрично отобразить относительно оси Ox. Затем симметрично отобразить часть графика, где
x ≥ 0 относительно оси Oy для отрицательных x. Полученный в результате всех преобразований график оставляем только на участке от -4 до 4 по оси абсцисс.

График третьей функции – парабола, ветви которой направлены вниз, а вершина находится в точке с координатами (4; 3). Чертеж изображаем только на участке, где x > 4.

Ответ: рисунок 2.

3) {8 – (x + 6)², если x ≤ -6,
f(x) = {|x² – 6|x| + 8|, если -6 ≤ x < 5,
{3, если x ≥ 5.

Построение предлагаемой кусочной-заданной функции аналогично предыдущему пункту. Здесь графики первых двух функций получаются из преобразований параболы, а график третьей – прямая, параллельная Ох.

Ответ: рисунок 3.

4) Построить график функции y = x – |x| + (x – 1 – |x|/x)² .

Решение. Область определения данной функции – все действительные числа, кроме нуля. Раскроем модуль. Для этого рассмотрим два случая:

1) При x > 0 получим y = x – x + (x – 1 – 1)² = (x – 2)².

2) При x < 0 получим y = x + x + (x – 1 + 1)² = 2x + x².

Таким образом, перед нами кусочно-заданная функция:

y = {(x – 2)², при x > 0;
{ x²+ 2x, при x < 0.

Графики обоих функций – параболы, ветви которых направлены вверх.

Ответ: рисунок 4.

5) Построить график функции y = (x + |x|/x – 1)² .

Решение.

Легко видеть, что областью определения функции являются все действительные числа, кроме нуля. После раскрытия модуля получим кусочно-заданную функцию:

1) При x > 0 получим y = (x + 1 – 1)² = x².

2) При x < 0 получим y = (x – 1 – 1)² = (x – 2)².

Перепишем.

y = {x², при x > 0;
{(x – 2)², при x < 0.

Графики этих функций – параболы.

Ответ: рисунок 5.

6) Существует ли функция, график которой на координатной плоскости имеет общую точку с любой прямой?

Решение.

Да, существует.

Примером может быть функция f(x) = x³. Действительно, с вертикальной прямой х = а график кубической параболы пересекается в точке (а; а³). Пусть теперь прямая задана уравнением y = kx + b. Тогда уравнение
x³ – kx – b = 0 имеет действительный корень х₀ (так как многочлен нечетной степени всегда имеет хотя бы один действительный корень). Следовательно, график функции пересекается с прямой y = kx + b, например, в точке (х₀; х₀³

blog.tutoronline.ru

Как построить график кусочной функции

☰

Кусочные функции — это функции, заданные разными формулами на разных числовых промежутках. Например,

Такая запись обозначает, что значение функции вычисляется по формуле √x, когда x больше или равен нулю. Когда же x меньше нуля, то значение функции определяется по формуле –x². Например, если x = 4, то f(x) = 2, т. к. в данном случае используется формула извлечения корня. Если же x = –4, то f(x) = –16, т. к. в этом случае используется формула –x² (сначала возводим в квадрат, потом учитываем минус).

Чтобы построить график такой кусочной функции, сначала строятся графики двух разных функций не зависимо от значения x (т. е. на всей числовой прямой аргумента). После этого от полученных графиков берутся только те части, которые принадлежат соответствующим диапазонам x. Эти части графиков объединяются в один. Понятно, что в простых случаях чертить можно сразу части графиков, опустив предварительную прорисовку их «полных» вариантов.

Для приведенного выше примера для формулы y = √x получим такой график:

Здесь x в принципе не может принимать отрицательных значений (т. е. подкоренное выражение в данном случае не может быть отрицательным). Поэтому в график кусочной функции уйдет весь график уравнения y = √x.

Построим график функции f(x) = –x². Получим перевернутую параболу:

В данном случае в кусочную функции мы возьмем только ту часть параболы, для которой x принадлежит промежутку (–∞; 0). В результате получится такой график кусочной функции:

Рассмотрим другой пример:

Графиком функции f(x) = (0.6x – 0.5)² – 1.7 будет видоизмененная парабола. Графиком f(x) = 0.5x + 1 является прямая:

В кусочной функции x может принимать значения в ограниченных промежутках: от 1 до 5 и от –5 до 0. Ее график будет состоять из двух отдельных частей. Одну часть берем на промежутке [1; 5] от параболы, другую — на промежутке [–5; 0] от прямой:

scienceland.info

Методическое пособие «Построение кусочно-заданных функций»

li{counter-increment:lst-ctn-kix_list_1-7}#doc6977624 ol.lst-kix_list_2-8.start{counter-reset:lst-ctn-kix_list_2-8 0}#doc6977624 .lst-kix_list_2-6>li{counter-increment:lst-ctn-kix_list_2-6}#doc6977624 .lst-kix_list_2-8>li:before{content:»» counter(lst-ctn-kix_list_2-8,lower-roman) «. «}#doc6977624 .lst-kix_list_1-1>li:before{content:»» counter(lst-ctn-kix_list_1-1,lower-latin) «. «}#doc6977624 ol.lst-kix_list_2-0{list-style-type:none}#doc6977624 .lst-kix_list_1-1>li{counter-increment:lst-ctn-kix_list_1-1}#doc6977624 ol.lst-kix_list_2-0.start{counter-reset:lst-ctn-kix_list_2-0 0}#doc6977624 ol.lst-kix_list_2-1{list-style-type:none}#doc6977624 ol.lst-kix_list_2-2{list-style-type:none}#doc6977624 ol.lst-kix_list_2-3{list-style-type:none}#doc6977624 ol.lst-kix_list_2-4{list-style-type:none}#doc6977624 ol.lst-kix_list_2-5{list-style-type:none}#doc6977624 .lst-kix_list_2-0>li:before{content:»» counter(lst-ctn-kix_list_2-0,decimal) «) «}#doc6977624 ol.lst-kix_list_1-2.start{counter-reset:lst-ctn-kix_list_1-2 0}#doc6977624 .lst-kix_list_1-2>li:before{content:»» counter(lst-ctn-kix_list_1-2,lower-roman) «. «}#doc6977624 .lst-kix_list_2-8>li{counter-increment:lst-ctn-kix_list_2-8}#doc6977624 .lst-kix_list_1-5>li:before{content:»» counter(lst-ctn-kix_list_1-5,lower-roman) «. «}#doc6977624 .lst-kix_list_2-3>li{counter-increment:lst-ctn-kix_list_2-3}#doc6977624 .lst-kix_list_1-8>li{counter-increment:lst-ctn-kix_list_1-8}#doc6977624 ol.lst-kix_list_1-7.start{counter-reset:lst-ctn-kix_list_1-7 0}#doc6977624 ol.lst-kix_list_2-7{list-style-type:none}#doc6977624 ol.lst-kix_list_2-6{list-style-type:none}#doc6977624 .lst-kix_list_2-3>li:before{content:»» counter(lst-ctn-kix_list_2-3,decimal) «. «}#doc6977624 .lst-kix_list_2-4>li:before{content:»» counter(lst-ctn-kix_list_2-4,lower-latin) «. «}#doc6977624 ol.lst-kix_list_2-8{list-style-type:none}#doc6977624 ol.lst-kix_list_1-5.start{counter-reset:lst-ctn-kix_list_1-5 0}#doc6977624 .lst-kix_list_1-4>li:before{content:»» counter(lst-ctn-kix_list_1-4,lower-latin) «. «}#doc6977624 ol.lst-kix_list_2-4.start{counter-reset:lst-ctn-kix_list_2-4 0}#doc6977624 ol.lst-kix_list_1-1.start{counter-reset:lst-ctn-kix_list_1-1 0}#doc6977624 .lst-kix_list_2-1>li{counter-increment:lst-ctn-kix_list_2-1}#doc6977624 .lst-kix_list_2-0>li{counter-increment:lst-ctn-kix_list_2-0}#doc6977624 ol.lst-kix_list_1-0.start{counter-reset:lst-ctn-kix_list_1-0 0}#doc6977624 ol.lst-kix_list_2-3.start{counter-reset:lst-ctn-kix_list_2-3 0}#doc6977624 .lst-kix_list_1-5>li{counter-increment:lst-ctn-kix_list_1-5}#doc6977624 .lst-kix_list_2-5>li:before{content:»» counter(lst-ctn-kix_list_2-5,lower-roman) «. «}#doc6977624 .lst-kix_list_1-0>li:before{content:»» counter(lst-ctn-kix_list_1-0,decimal) «. «}#doc6977624 .lst-kix_list_2-4>li{counter-increment:lst-ctn-kix_list_2-4}#doc6977624 .lst-kix_list_2-7>li:before{content:»» counter(lst-ctn-kix_list_2-7,lower-latin) «. «}#doc6977624 .lst-kix_list_1-8>li:before{content:»» counter(lst-ctn-kix_list_1-8,lower-roman) «. «}#doc6977624 .lst-kix_list_1-6>li{counter-increment:lst-ctn-kix_list_1-6}#doc6977624 .lst-kix_list_2-5>li{counter-increment:lst-ctn-kix_list_2-5}#doc6977624 ol.lst-kix_list_1-6.start{counter-reset:lst-ctn-kix_list_1-6 0}#doc6977624 ol.lst-kix_list_2-2.start{counter-reset:lst-ctn-kix_list_2-2 0}#doc6977624 .lst-kix_list_1-3>li:before{content:»» counter(lst-ctn-kix_list_1-3,decimal) «. «}#doc6977624 .lst-kix_list_1-0>li{counter-increment:lst-ctn-kix_list_1-0}#doc6977624 ol.lst-kix_list_2-7.start{counter-reset:lst-ctn-kix_list_2-7 0}#doc6977624 ol.lst-kix_list_2-1.start{counter-reset:lst-ctn-kix_list_2-1 0}#doc6977624 ol.lst-kix_list_1-3.start{counter-reset:lst-ctn-kix_list_1-3 0}#doc6977624 .lst-kix_list_1-3>li{counter-increment:lst-ctn-kix_list_1-3}#doc6977624 .lst-kix_list_2-7>li{counter-increment:lst-ctn-kix_list_2-7}#doc6977624 ol.lst-kix_list_2-6.start{counter-reset:lst-ctn-kix_list_2-6 0}#doc6977624 .lst-kix_list_1-2>li{counter-increment:lst-ctn-kix_list_1-2}#doc6977624 ol.lst-kix_list_2-5.start{counter-reset:lst-ctn-kix_list_2-5 0}#doc6977624 ol.lst-kix_list_1-7{list-style-type:none}#doc6977624 ol.lst-kix_list_1-8{list-style-type:none}#doc6977624 .lst-kix_list_1-6>li:before{content:»» counter(lst-ctn-kix_list_1-6,decimal) «. «}#doc6977624 .lst-kix_list_2-6>li:before{content:»» counter(lst-ctn-kix_list_2-6,decimal) «. «}#doc6977624 .lst-kix_list_1-4>li{counter-increment:lst-ctn-kix_list_1-4}#doc6977624 .lst-kix_list_2-2>li:before{content:»» counter(lst-ctn-kix_list_2-2,lower-roman) «. «}#doc6977624 .lst-kix_list_1-7>li:before{content:»» counter(lst-ctn-kix_list_1-7,lower-latin) «. «}#doc6977624 ol.lst-kix_list_1-8.start{counter-reset:lst-ctn-kix_list_1-8 0}#doc6977624 ol.lst-kix_list_1-4.start{counter-reset:lst-ctn-kix_list_1-4 0}#doc6977624 ol.lst-kix_list_1-2{list-style-type:none}#doc6977624 ol.lst-kix_list_1-1{list-style-type:none}#doc6977624 .lst-kix_list_2-1>li:before{content:»» counter(lst-ctn-kix_list_2-1,lower-latin) «. «}#doc6977624 ol.lst-kix_list_1-0{list-style-type:none}#doc6977624 .lst-kix_list_2-2>li{counter-increment:lst-ctn-kix_list_2-2}#doc6977624 ol.lst-kix_list_1-6{list-style-type:none}#doc6977624 ol.lst-kix_list_1-5{list-style-type:none}#doc6977624 ol.lst-kix_list_1-4{list-style-type:none}#doc6977624 ol.lst-kix_list_1-3{list-style-type:none}#doc6977624 ol{margin:0;padding:0}#doc6977624 .c10{border-bottom-width:1pt;border-top-style:solid;width:32.8pt;border-right-style:solid;padding:0pt 5.4pt 0pt 5.4pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}#doc6977624 .c4{border-bottom-width:1pt;border-top-style:solid;width:35.3pt;border-right-style:solid;padding:0pt 5.4pt 0pt 5.4pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}#doc6977624 .c19{border-bottom-width:1pt;border-top-style:solid;width:33.2pt;border-right-style:solid;padding:0pt 5.4pt 0pt 5.4pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}#doc6977624 .c9{border-bottom-width:1pt;border-top-style:solid;width:30pt;border-right-style:solid;padding:0pt 5.4pt 0pt 5.4pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}#doc6977624 .c2{line-height:1.0;padding-top:0pt;widows:2;orphans:2;height:11pt;text-align:center;direction:ltr;padding-bottom:0pt}#doc6977624 .c1{line-height:1.0;padding-top:0pt;widows:2;orphans:2;text-align:left;direction:ltr;padding-bottom:0pt}#doc6977624 .c13{line-height:1.5;padding-top:0pt;widows:2;orphans:2;text-align:center;direction:ltr;padding-bottom:0pt}#doc6977624 .c12{line-height:1.5;padding-top:0pt;widows:2;orphans:2;text-align:justify;direction:ltr;padding-bottom:0pt}#doc6977624 .c3{line-height:1.0;padding-top:0pt;widows:2;orphans:2;height:11pt;direction:ltr;padding-bottom:0pt}#doc6977624 .c6{line-height:1.0;padding-top:0pt;widows:2;orphans:2;direction:ltr;padding-bottom:0pt}#doc6977624 .c26{vertical-align:sub;font-size:12pt;font-family:»Times New Roman»;font-weight:bold}#doc6977624 .c0{vertical-align:baseline;font-size:12pt;font-family:»Times New Roman»;font-weight:normal}#doc6977624 .c25{vertical-align:baseline;font-size:14pt;font-family:»Times New Roman»;font-weight:normal}#doc6977624 .c11{vertical-align:super;font-size:12pt;font-family:»Times New Roman»;font-weight:normal}#doc6977624 .c22{vertical-align:super;font-size:12pt;font-family:»Times New Roman»;font-weight:bold}#doc6977624 .c27{vertical-align:baseline;font-size:24pt;font-family:»Times New Roman»;font-weight:normal}#doc6977624 .c32{vertical-align:baseline;font-size:9pt;font-family:»Times New Roman»;font-weight:normal}#doc6977624 .c20{vertical-align:baseline;font-size:12pt;font-family:»Noto Symbol»;font-weight:normal}#doc6977624 .c28{vertical-align:sub;font-size:12pt;font-family:»Times New Roman»;font-weight:normal}#doc6977624 .c7{vertical-align:baseline;font-size:12pt;font-family:»Times New Roman»;font-weight:bold}#doc6977624 .c35{vertical-align:baseline;font-size:20pt;font-family:»Times New Roman»;font-weight:normal}#doc6977624 .c5{color:#000000;font-style:normal;text-decoration:none}#doc6977624 .c14{margin-right:auto;border-collapse:collapse;margin-left:54pt}#doc6977624 .c18{margin-right:auto;border-collapse:collapse;margin-left:-5.4pt}#doc6977624 .c15{padding-left:0pt;text-align:justify;margin-left:36pt}#doc6977624 .c33{max-width:786pt;background-color:#ffffff;padding:28.4pt 25.9pt 27pt 30pt}#doc6977624 .c36{padding-left:0pt;margin-left:36pt}#doc6977624 .c23{margin:0;padding:0}#doc6977624 .c17{text-indent:54pt;margin-left:-54pt}#doc6977624 .c29{text-align:justify}#doc6977624 .c8{height:0pt}#doc6977624 .c16{text-align:center}#doc6977624 .c21{height:11pt}#doc6977624 .c30{font-style:normal}#doc6977624 .c31{font-style:italic}#doc6977624 .c24{text-decoration:underline}#doc6977624 .c34{margin-left:18pt}#doc6977624 .title{widows:2;padding-top:24pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:36pt;font-family:»Arial»;font-weight:bold;padding-bottom:6pt;page-break-after:avoid}#doc6977624 .subtitle{widows:2;padding-top:18pt;line-height:1.15;orphans:2;text-align:left;color:#666666;font-style:italic;font-size:24pt;font-family:»Georgia»;padding-bottom:4pt;page-break-after:avoid}#doc6977624 li{color:#000000;font-size:11pt;font-family:»Arial»}#doc6977624 p{color:#000000;font-size:11pt;margin:0;font-family:»Arial»}#doc6977624 h2{widows:2;padding-top:24pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:24pt;font-family:»Arial»;font-weight:bold;padding-bottom:6pt;page-break-after:avoid}#doc6977624 h3{widows:2;padding-top:18pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:18pt;font-family:»Arial»;font-weight:bold;padding-bottom:4pt;page-break-after:avoid}#doc6977624 h4{widows:2;padding-top:14pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:14pt;font-family:»Arial»;font-weight:bold;padding-bottom:4pt;page-break-after:avoid}#doc6977624 h5{widows:2;padding-top:12pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:12pt;font-family:»Arial»;font-weight:bold;padding-bottom:2pt;page-break-after:avoid}#doc6977624 h5{widows:2;padding-top:11pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:11pt;font-family:»Arial»;font-weight:bold;padding-bottom:2pt;page-break-after:avoid}#doc6977624 h6{widows:2;padding-top:10pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:10pt;font-family:»Arial»;font-weight:bold;padding-bottom:2pt;page-break-after:avoid}#doc6977624 ]]>

Б-Толкай 2013

ГБОУ СОШ с.Большой-Толкай

Методическое пособие по теме

«Построение кусочно-заданных функций

Составила ученица 9 класса

Кизельбашева Валентина.

Понятие о кусочных функциях. На различных участках числовой прямой функция может быть задана разными формулами. Например: y=f(x), где

f(x)= х2, -3х-2

2х+8, -20

Такие функции назовём кусочными. Участки числовой прямой, которые различаются формулами задания, назовём составляющими область определения, а их объединение, является областью определения кусочной функции. Точки, которые делят область определения на составляющие, называются граничными точками. Выражения, определяющие кусочную функцию на каждой составляющей области определения, называется входящими функциями.

Наличие таких свойств как чётность, нечётность, нули функции, промежутки знакопостоянства, монотонность, ограниченность у кусочных функций устанавливается согласно общепринятым определениям, с учётом особенностей составляющих области определения и входящих функций.

Для того чтобы вычислить значение кусочной функции в заданной точке, необходимо, во-первых, определить, какой составляющей области определения принадлежит эта точка, а, во-вторых, найти значение входящей функции на этой составляющей.

Ответы:

1)Функция убывает на промежутке [-2; +∞).

2)Функция возрастает на промежутках (-∞; -2] и [0; 2].

3)f(x)≥0, если х=0 и |х|≥ 3⅓;

4)у > 0, если х

5)Прямая y=m имеет с графиком две общие точки при m=3 и m=-1;

6)Прямая y=m имеет с графиком одну общую точку при m=-2 и m>1.

Задания для самостоятельной работы:

1)Постройте график функции y=f(x), где

x-1, если х

f(x)=

-1/2x+3, если x ≥ -2.

Укажите промежуток, на котором функция убывает.

2)Постройте график функции у=f(x), где

1/4х2-1, если -2≤ х ≤ 2

f(x)= 2-х, если х > 2

х+2, если х

Укажите промежутки возрастания функции.

3)Постройте график функции у=f(x), где

-х2, если -2≤ х ≤ 2

f(x)= 3х-10, если х > 2

-3x-10, если х

При каких значениях х значения функции у= f(x) неотрицательны?

4)Постройте график функции у= f(x),где

(х+1)2, если х

f(x)=

1-х2, если х ≥0.

При каких значениях х выполняется неравенство у > 0?

5)Постройте график функции у= f(x),где

х2-4х-1, если х ≥ 4

f(x)=

-х2+4х-1, если х

При каких значениях m прямая y=m имеет с графиком этой функции две общие точки?

6)Постройте график функции у= f(x),где

4/х, если х ≤ -2

f(x)= х, если -2

х2-4х+4, если х > 1.

При каких значениях m прямая y=m имеет с графиком этой функции одну общую точку?

Чтобы построить график кусочной функции, нужно:

Построить в одной системе координат графики входящих функций,
Провести прямые x=a, x=a, x=a, где a-граничные точки,
На каждой составляющей области определения (a, a), где i=1…n выбрать тот график, который соответствует входящей функции на этой составляющей.
Выяснить значение функции в граничных точках.

Если каждая входящая кусочной функции является линейной, то будем называть её кусочно-линейной функцией.

f(x)= х2, -3х-2

2х+8, -20

Построение:

у=х2
-3х-2
Выделить часть графика 1.
У=2х+8
-20
Выделить часть графика 2.

Рассмотрим построение графиков кусочных функций.

Постройте график функции y=f(x), где

f(x)= -1/2х+3, если х2

х-4 ,х>2

Укажите промежуток, в котором функция убывает.

Построим в одной системе координат графики функций у=1/2х+3, если х2 и у=х-4 ,х>2

Графиками обеих функций являются прямые. Для построения достаточно двух точек.

у=1/2х+3, х2

х	2	4
у	2	1

у=х-4 ,х>2

Ответ: Функция убывает на промежутке (-;2]

Постройте график функции y=f(x), где

2-2×2, если 2

f(x)= x-1, если x>1

-x-1, если x

Укажите промежутки возрастания функции.

Первым графиком функции является парабола, ветви направлены вниз. Построим график функции на отрезке [-2;2]

Второй график у= х-1 –прямая.

Третий график тоже прямая у=-х-1

Ответ: Функция возрастает на промежутках[-1;0]

и [1;)

Постройте график функции у=f(x), где

х2-1, если х0

f(x)= (x-1)2 ,если х>0

При каких значениях х выполняется неравенство у0

1)Первым графиком является парабола. Построим её часть (х0) путем сдвига вниз на 1 графика у= х2.

Вторым графиком является тоже парабола. Построим её часть (х>0)путем сдвига вдоль оси ох вправо на 1 графика у= х2.

Ответ: при у>0, x1

Постройте график функции у=f(x), где

-х2-4х-3, если x-1

f(x)= x+1, если -11

2/x, если х>1

При каких значениях m прямая у=m имеет с графиком этой функции две общие точки.

Построим в одной системе координат графики функций.

1) Первым графиком функции является часть параболы, ветви направлены

вниз. Найдём вершину параболы по формуле х=-b/2a

х=-(-4)/(-1·2)=-2, то у=-(-2)2-4·(-2)-3=1.Итак, вершина параболы

в точке с координатой (-2;1).

Найдём точки пересечения с осью OX;

у=0. -х2-4х-3=0

х1=-3

х2=-1

Точки пересечения с осью OX: (-3;0) и (-1;0).

Найдём точки пересечения с осью Oу:

х=0

у=-(0)2-4·0-3=3

Точки пересечения с осью OX: (0;3).

Найдём дополнительные точки

2) Второй график у= х+1 –прямая.

Построим часть прямой

3)Третьим графиком является гипербола.

Построим часть гиперболы при х>1

Ответ: прямая у=m имеет с графиком этой функции две общие точкипри m=0 и 1

Постройте график функции у=f(x), где

f(x)= -х2, если |х|1

x2-1если |х| >1

Укажите промежутки возрастания функции.

Раскрывая знак модуля данную систему можно записать в следующем виде:

f(x)= -х2, если -1х1

x2-1если , х >1

Графиками данных функций является парабола. Построим первый график.

у=-х2 ,если -1х1

x2-1если , х >1

х	1	2	3	4	-1	-2	-3	-4
у	0	3	8	15	0	3	8	15

Ответ: функция возрастает на промежутках(- ;-1] и [0;1]

Постройте график функции у=f(x), где

х2-4х+4, если x>1

f(x)= x, если -21

4/x, если х-2

При каких значениях m прямая у=m имеет с графиком этой функции одну общую точку?

Построим в одной системе координат графики функций.

1) Первым графиком функции является часть параболы, ветви направлены

вверх. Найдём вершину параболы по формуле х=-b/2a

х=-(-4)/2·1=2

у=22-4·2+4=0

Итак, вершина параболы

в точке с координатой (2;0).

Найдём точки пересечения с осью OX;

у=0

х2-4х+4=(х-2)2 ; х=0

Точки пересечения с осью OX: (0;2).

Найдём точки пересечения с осью Oу: х=0

у=02-4·0+4=4

Точки пересечения с осью OX: (0;4).

Найдём дополнительные точки

2) Второй график у= х –прямая, проходящая через начало координат.

Часть прямой, находящийся в 1 и 3 четверти.

3)Третьим графиком у=4/x, является гипербола, которая находится в 3 четверти.

Построим часть гиперболы при х-2

Ответ: прямая у=m имеет с графиком одну общую точку при m=-2 и m>1

Постройте график функции у=. При каких значениях х выполняется неравенство у3?

Область определения данной функции D(у)=(-;0)(0;2) (2;+).

Разложим числитель и знаменатель на множители дроби вынесением общего множителя за скобки. Дальше числитель разложим на множители по формуле

ax2+bx+c=a(x-x1)(x-x2)

Преобразуем дробь: у====-х-1

у=-х-1-линейная функция, графиком является прямая, рисунок 1

рис.1

Для того , чтобы ответить на вопрос

рассмотрим рисунок 2

Рис.2

Ответ: неравенство у3 выполняется при

-4х2.

Найдите все значения к, при которых прямая у=кх пересекает в трёх точках ломанную, заданную условием:

2х+4, если х

у= -2, если-33

2х-8,если х>3

Прямая y= kx пересекает в трех

различных точках эту ломаную, если ее угловой

коэффициент больше углового коэффициента

прямой, проходящей через точку –(3; -2), и

меньше углового коэффициента прямой,

парал. прямым у=2х+4 ,у=2х-8 .

Найдем угловой коэффициент прямой,

проходящей через точку (-3;-2)

-2=-3к, к=2/3

Угловой коэффициент k прямой, парал.

Прямой у=2х+8 , равен 2.

Ответ: прямая имеет с ломанной три общие точки при 2/3

nsportal.ru

Кусочные функции. Графики кусочно-линейных функций

y = {x – 3, при x > -3;
{-(x – 3), при x

Такие функции называются кусочными или кусочно-заданными . Участки числовой прямой с различными формулами задания, назовем составляющими область определения. Объединение всех составляющих является областью определения кусочной функции. Те точки, которые делят область определения функции на составляющие, называются граничными точками . Формулы, определяющие кусочную функцию на каждой составляющей области определения, называются входящими функциями . Графики кусочно-заданных функций получаются в результате объединения частей графиков, построенных на каждом из промежутков разбиения.

Упражнения.

Построить графики кусочных функций:

1) {-3, при -4 ≤ x f(x) = {0, при x = 0,
{1, при 0

Ответ: рисунок 1.

2) {3, если x ≤ -4,
f(x) = {|x 2 – 4|x| + 3|, если -4 {3 – (x – 4) 2 , если x > 4.

Рассмотрим отдельно каждую функцию и построим ее график.

Так, f(x) = 3 – прямая, параллельная оси Ох, но изображать ее нужно только на участке, где x ≤ -4.

График функции f(x) = |x 2 – 4|x| + 3| может быть получен из параболы y = x 2 – 4x + 3. Построив ее график, часть рисунка, которая лежит над осью Ox, необходимо оставить без изменений, а часть, которая лежит под осью абсцисс, симметрично отобразить относительно оси Ox. Затем симметрично отобразить часть графика, где

x ≥ 0 относительно оси Oy для отрицательных x. Полученный в результате всех преобразований график оставляем только на участке от -4 до 4 по оси абсцисс.

Ответ: рисунок 2.

3) {8 – (x + 6) 2 , если x ≤ -6,
f(x) = {|x 2 – 6|x| + 8|, если -6 ≤ x {3, если x ≥ 5.

Ответ: рисунок 3.

4) Построить график функции y = x – |x| + (x – 1 – |x|/x) 2 .

1) При x > 0 получим y = x – x + (x – 1 – 1) 2 = (x – 2) 2 .

2) При x

Таким образом, перед нами кусочно-заданная функция:

y = {(x – 2) 2 , при x > 0;
{ x 2 + 2x, при x

Графики обоих функций – параболы, ветви которых направлены вверх.

Ответ: рисунок 4.

5) Построить график функции y = (x + |x|/x – 1) 2 .

Решение.

1) При x > 0 получим y = (x + 1 – 1) 2 = x 2 .

2) При x

Перепишем.

y = {x 2 , при x > 0;
{(x – 2) 2 , при x

Графики этих функций – параболы.

Ответ: рисунок 5.

6) Существует ли функция, график которой на координатной плоскости имеет общую точку с любой прямой?

Решение.

Да, существует.

Примером может быть функция f(x) = x 3 . Действительно, с вертикальной прямой х = а график кубической параболы пересекается в точке (а; а 3). Пусть теперь прямая задана уравнением y = kx + b. Тогда уравнение
x 3 – kx – b = 0 имеет действительный корень х 0 (так как многочлен нечетной степени всегда имеет хотя бы один действительный корень). Следовательно, график функции пересекается с прямой y = kx + b, например, в точке (х 0 ; х 0 3).

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Непр

store-e.ru

Материал для подготовки к ЕГЭ (ГИА) по алгебре (9 класс) на тему: Методическое пособие «Построение кусочно заданных функций»

Методическое пособие по теме

«Построение кусочно-заданных функций»

f(x)= х2, -3х-2

2х+8, -20

Ответы:

1)Функция убывает на промежутке [-2; +∞).

2)Функция возрастает на промежутках (-∞; -2] и [0; 2].

3)f(x)≥0, если х=0 и |х|≥ 3⅓;

4)у > 0, если х

5)Прямая y=m имеет с графиком две общие точки при m=3 и m=-1;

6)Прямая y=m имеет с графиком одну общую точку при m=-2 и m>1.

Задания для самостоятельной работы:

1)Постройте график функции y=f(x), где

x-1, если х

f(x)=

-1/2x+3, если x ≥ -2.

Укажите промежуток, на котором функция убывает.

2)Постройте график функции у=f(x), где

1/4х2-1, если -2≤ х ≤ 2

f(x)= 2-х, если х > 2

х+2, если х

Укажите промежутки возрастания функции.

3)Постройте график функции у=f(x), где

-х2, если -2≤ х ≤ 2

f(x)= 3х-10, если х > 2

-3x-10, если х

При каких значениях х значения функции у= f(x) неотрицательны?

4)Постройте график функции у= f(x),где

(х+1)2, если х

f(x)=

1-х2, если х ≥0.

При каких значениях х выполняется неравенство у > 0?

5)Постройте график функции у= f(x),где

х2-4х-1, если х ≥ 4

f(x)=

-х2+4х-1, если х

При каких значениях m прямая y=m имеет с графиком этой функции две общие точки?

6)Постройте график функции у= f(x),где

4/х, если х ≤ -2

f(x)= х, если -2

х2-4х+4, если х > 1.

При каких значениях m прямая y=m имеет с графиком этой функции одну общую точку?

Чтобы построить график кусочной функции, нужно:

Построить в одной системе координат графики входящих функций,
Провести прямые x=a, x=a, x=a, где a-граничные точки,
На каждой составляющей области определения (a, a), где i=1…n выбрать тот график, который соответствует входящей функции на этой составляющей.
Выяснить значение функции в граничных точках.

Если каждая входящая кусочной функции является линейной, то будем называть её кусочно-линейной функцией.

f(x)= х2, -3х-2

2х+8, -20

Построение:

у=х2
-3х-2
Выделить часть графика 1.
У=2х+8
-20
Выделить часть графика 2.

Рассмотрим построение графиков кусочных функций.

Постройте график функции y=f(x), где

f(x)= -1/2х+3, если х2

х-4 ,х>2

Укажите промежуток, в котором функция убывает.

Построим в одной системе координат графики функций у=1/2х+3, если х2 и у=х-4 ,х>2

Графиками обеих функций являются прямые. Для построения достаточно двух точек.

у=1/2х+3, х2

х	2	4
у	2	1

у=х-4 ,х>2

Ответ: Функция убывает на промежутке (-;2]

Постройте график функции y=f(x), где

2-2×2, если 2

f(x)= x-1, если x>1

-x-1, если x

Укажите промежутки возрастания функции.

Первым графиком функции является парабола, ветви направлены вниз. Построим график функции на отрезке [-2;2]

Второй график у= х-1 –прямая.

Третий график тоже прямая у=-х-1

Ответ: Функция возрастает на промежутках[-1;0]

и [1;)

Постройте график функции у=f(x), где

х2-1, если х0

f(x)= (x-1)2 ,если х>0

При каких значениях х выполняется неравенство у0

1)Первым графиком является парабола. Построим её часть (х0) путем сдвига вниз на 1 графика у= х2.

Ответ: при у>0, x1

Постройте график функции у=f(x), где

-х2-4х-3, если x-1

f(x)= x+1, если -11

2/x, если х>1

При каких значениях m прямая у=m имеет с графиком этой функции две общие точки.

Построим в одной системе координат графики функций.

1) Первым графиком функции является часть параболы, ветви направлены

вниз. Найдём вершину параболы по формуле х=-b/2a

х=-(-4)/(-1·2)=-2, то у=-(-2)2-4·(-2)-3=1.Итак, вершина параболы

в точке с координатой (-2;1).

Найдём точки пересечения с осью OX;

у=0. -х2-4х-3=0

х1=-3

х2=-1

Точки пересечения с осью OX: (-3;0) и (-1;0).

Найдём точки пересечения с осью Oу:

х=0

у=-(0)2-4·0-3=3

Точки пересечения с осью OX: (0;3).

Найдём дополнительные точки

2) Второй график у= х+1 –прямая.

Построим часть прямой

3)Третьим графиком является гипербола.

Построим часть гиперболы при х>1

Ответ: прямая у=m имеет с графиком этой функции две общие точкипри m=0 и 1

Постройте график функции у=f(x), где

f(x)= -х2, если |х|1

x2-1если |х| >1

Укажите промежутки возрастания функции.

Раскрывая знак модуля данную систему можно записать в следующем виде:

f(x)= -х2, если -1х1

x2-1если , х >1

Графиками данных функций является парабола. Построим первый график.

у=-х2 ,если -1х1

x2-1если , х >1

х	1	2	3	4	-1	-2	-3	-4
у	0	3	8	15	0	3	8	15

Ответ: функция возрастает на промежутках(- ;-1] и [0;1]

Постройте график функции у=f(x), где

х2-4х+4, если x>1

f(x)= x, если -21

4/x, если х-2

При каких значениях m прямая у=m имеет с графиком этой функции одну общую точку?

Построим в одной системе координат графики функций.

1) Первым графиком функции является часть параболы, ветви направлены

вверх. Найдём вершину параболы по формуле х=-b/2a

х=-(-4)/2·1=2

у=22-4·2+4=0

Итак, вершина параболы

в точке с координатой (2;0).

Найдём точки пересечения с осью OX;

у=0

х2-4х+4=(х-2)2 ; х=0

Точки пересечения с осью OX: (0;2).

Найдём точки пересечения с осью Oу: х=0

у=02-4·0+4=4

Точки пересечения с осью OX: (0;4).

Найдём дополнительные точки

2) Второй график у= х –прямая, проходящая через начало координат.

Часть прямой, находящийся в 1 и 3 четверти.

3)Третьим графиком у=4/x, является гипербола, которая находится в 3 четверти.

Построим часть гиперболы при х-2

Ответ: прямая у=m имеет с графиком одну общую точку при m=-2 и m>1

Постройте график функции у=. При каких значениях х выполняется неравенство у3?

Область определения данной функции D(у)=(-;0)(0;2) (2;+).

ax2+bx+c=a(x-x1)(x-x2)

Преобразуем дробь: у====-х-1

у=-х-1-линейная функция, графиком является прямая, рисунок 1

рис.1

Для того , чтобы ответить на вопрос

рассмотрим рисунок 2

Рис.2

Ответ: неравенство у3 выполняется при

-4х2.

Найдите все значения к, при которых прямая у=кх пересекает в трёх точках ломанную, заданную условием:

2х+4, если х

у= -2, если-33

2х-8,если х>3

Прямая y= kx пересекает в трех

различных точках эту ломаную, если ее угловой

коэффициент больше углового коэффициента

прямой, проходящей через точку –(3; -2), и

меньше углового коэффициента прямой,

парал. прямым у=2х+4 ,у=2х-8 .

Найдем угловой коэффициент прямой,

проходящей через точку (-3;-2)

-2=-3к, к=2/3

Угловой коэффициент k прямой, парал.

Прямой у=2х+8 , равен 2.

Ответ: прямая имеет с ломанной три общие точки при 2/3

nsportal.ru

Задание по Excel № 2 » Построение графика кусочной функции»

Построить график кусочной функции на участке [a;b] с шагом 0,5.

№ Вар	Функция	[a;b]
1.		[-7;7]
2.		[-7;7]
3.		[-5;5]
4.		[-5;5]
5.
6.		[-7;7]
7.		[-10;10]
8.		[-10;10]
9.		[-4;10] a-коэф-т
10.		[-10;10]
11.		[-5;8] с-коэф-т
12.		[-4;4] a-коэф-т
13.		[-4;4]
14.		[-10;10] с-коэф-т
15.		[-10;10] d-коэф-т
16.		[-7;7]
17.		[-7;7]
18.		[-30;30]
19		[-30;30]
20.
21.		[-10;10]
22.	<	[-3;3]
23.		[-10;10]
24.		[-10;10]
25.		[-5;6] a-коэф-т
26.		[-5;5] b-коэф-т
27.		[-10;10]
28.		[-8;8] d-коэф-т
29.		[-5;6] a-коэф-т
30.		[-7;7] d-коэф-т

Задание по Excel № 3 «Построение трехмерной поверхности»

Получить матрицу значений функции в виде двумерной таблицы. Для этого задать изменение двух аргументов функции в виде числовых рядов, расположенных под прямым углом друг к другу. Вычислить значение функции для каждой пары аргументов. Шаг 0,1
x\y
-4
-3.5
-3
….
0
0.5

1

Z(x,y)

1.5

…
Внимание! Формула для вычисления значения функции должна быть набрана один раз, затем скопирована.
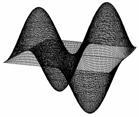
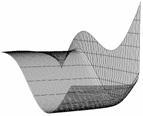
Выполнить построение трехмерной поверхности. Сравнить получившийся результат с образцом.

№	Уравнение и диапазон аргументов	Вид графика	№	Уравнение и диапазон аргументов	Вид графика
1	x=[-5;5] y=[-5;5] a=2 b=7		8	x=[-2;2] y=[—2×p ; 2×p] a=2
2	x=[-5;5] y=[-5;5] a=2 b=5		9	x=[-1;1] y=[—2×p ; 2×p] a=10 b=2
3	x=[-5 ; 5] y=[-2 ; 2] a=1.5 b=0.5		10	x=[—p ; p] y=[—p ; p] a=2
4	x=[-5;5] y=[-5;5] a=0.7		11	x=[—p ; p] y=[—p ; p] a=0.5
5	x=[—2×p ; 2×p] y=[—2×p ; 2×p] a=2 b=5		12	x=[—p ; p] y=[—p ; p] a=4
6	x=[—p ; p] y=[—p ; p] a=3		13	x=[-2;2] y=[-2;2] a=0.5
7	x=[ —p ; p] y=[ —p ; p] a=3		14	x=[-2;2] y=[-2;2] a=2
15	x=[-2;2] y=[-2;2] a=2		22	x=[0.01 ; 2×p] y=[0.01 ; 2×p] a=200
16	x=[-5;5] y=[-5;5] a=2 b=1		23	x=[0.01 ; 2×p] y=[0.01 ; p] a=200
17	x=[-5;5] y=[-5;5] a=0.3		24	x=[-3’3] y=[-1;6] a=50
18	x=[-5;5] y=[-5;5] a=0.3		25	x=[-3;3] y=[-3;3] a=0.5
19	x=[-5;5] y=[-5;5] a=5		26	x=[-3;3] y=[-3;3] a=2 b=3
20	x=[-5;5] y=[-5;5] a=0.1			x=[—p/2 + 0.05] ; p/2 — 0.05] y=[—p/2 + 0.05] ; p/2 — 0.05] a=0.1 b=2
21	x[0.1;1] y[0.1;1] a=0.1		28	x[—p/4 + 0.05] ; p/4 — 0.05] y[—p/4 + 0.05] ; p/4 — 0.05] a=2 b=1

Задание №1 по MathCAD «Двумерные графики, заданные в параметрическом виде, и графики, заданные в полярных координатах»

Задание:

1. Построить два графика;

2. Вывести таблицу значений функции, заданной в параметрическом виде;

3. При сдаче работы уметь:

 перевести полярные координаты в декартовы;

 отобразить несколько зависимостей на одном графике.

Указания к работе:

1. Для построения XY-графика, заданного в параметрическом виде необходимо:

 указать диапазон и шаг изменения параметра в виде 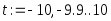. Знак «:=» вводится с помощью английского знака «:». Символ «..» вводится с помощью символа «;»

№ Вар	Функция, заданная в параметрическом виде	Функция, заданная в полярных координатах
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
26
27
28
29

 задать зависимость ;

 “Graph”à “Create XY-Plot”.

2. В полярной системе координат каждая точка задается углом и радиусом определенной длины. Длина радиуса находится в определенной зависимости от полярного угла. Для построения графика, заданного в полярных координатах необходимо:

 указать диапазон и шаг изменения полярного угла в радианах , например ;

 задать зависимость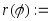

 “Graph”à “Create Polar Plot”.

studfile.net

Построение кусочной функции / Geogebra в SMART Notebook / EdGuru.RU

Сегодня мы рассмотрим построение кусочных функций в режиме Алгебра и графики виджета Geogebra.
Нам необходимо построить графики следующих функций:

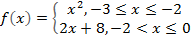
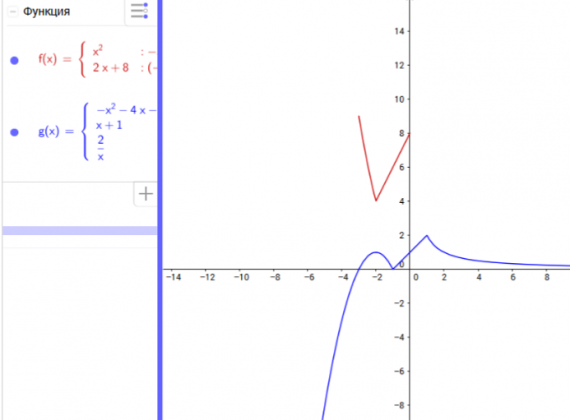
Способ 1.
Нажмите на знак плюса в строке ввода Алгебраического вида, появится всплывающее меню с пунктами: Piecewise function, Матрица, Параметрическая кривая.
Piecewise function – это и есть кусочная функция. Выбрав этот пункт, в окне алгебраического вида отобразится формула
Исправьте содержимое формулы согласно заданию.
Подсказка: Для того, чтобы увеличить количество интервалов для задания кусочной функции, нажмите на знак +, расположенный рядом с кнопкой удаления объекта

Способ 2.
Другой способ задания кусочной функции — это ввод команды с условным оператором. Рассмотрим несколько примеров.
Команда function [ 2x-1, 0, 3 ] – задаст функцию 2x-1 на промежутке от 0 до 3. Таким образом, вы можете задавать каждый участок, но график не будет объединен в единое целое. Иногда так удобно делать, если вы хотите, например, окрасить различные части графика в разные цвета.
Команда f(x) = if [ x>=3, 2x-16 ] – задаст функцию 2x-16 на промежутке от (3;+∞).
Команда f(x) = if [ -1<x<3, x^2+1, x-1 ] – задаст функцию x2+1 на промежутке от -1 до 3, на всей остальной числовой прямой будет построен график функции x-1. Таким образом, синтаксис условного оператора:
if [ условие, если верно, иначе ]
В качестве параметра иначе может выступать еще один оператор условия.
Таким образом, для задания функции g(x) из задания требуется написать команду:
g(x) = if [ x<=-1, -x^2-4x-3, if [ -1<x<=1, x+1, 2/x ] ].

edguru.ru

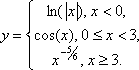
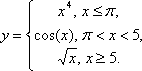
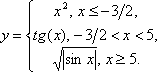
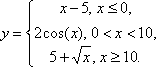
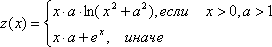
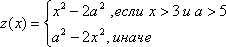
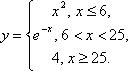
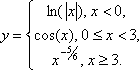
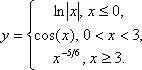
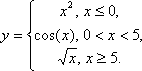
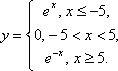
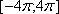
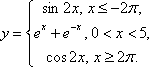x\y	-4	-3.5	-3	….	0
0.5
1		Z(x,y)
1.5
…

Кусочно-заданная функция

Как построить график кусочной функции

Методическое пособие «Построение кусочно-заданных функций»

Кусочные функции. Графики кусочно-линейных функций

Материал для подготовки к ЕГЭ (ГИА) по алгебре (9 класс) на тему: Методическое пособие «Построение кусочно заданных функций»

Задание по Excel № 2 » Построение графика кусочной функции»

Задание по Excel № 3 «Построение трехмерной поверхности»

Построение кусочной функции / Geogebra в SMART Notebook / EdGuru.RU

Добавить комментарий Отменить ответ