3х-4=х помогите решить !!!!!!!!! — Школьные Знания.com
ПОМОГИТЕ СРОЧНОООООООООО!!!!!
задача росписайте ришение срочно
Помогите решить задачу:Фигурные коньки стоят 2500 р. В период зимней распродажи цена на коньки уменьшилась на 20%, но к следующей зиме цена увеличилас … ь на 750 р. по сравнению с ценой в период распродажи. На сколько процентов выросла цена на коньки в период распродажи, по сравнению с ценой в период распродажи?
1)а15 a1=6 d=8 2)а1=-7 а34=6,2
задача прошу сделайте росписывайте решение
По асфальтовій дорозі автомобіль їхав 2 години зі швидкістю 80км/год , по ґрунтовій дорозі він їхав 4 години зі швидкістю 50км/год. Знайди середню шви … дкість автомобіля. * Срочно пжжж даю 40 балов!!!!!!
Проведіть пряму АВ і позначте точку M, яка їй не належить.Користуючись косинцем, проведіть через точку М пряму КМ,перпендикулярну до прямої АВ.Проведі … ть пряму АВ і позначте точку M, яка їй не належить.Користуючись косинцем, проведіть через точку М пряму КМ,перпендикулярну до прямої АВ.помагите пожалуйста отдам 20 балов пожалуйста срочно надо
Проблемы, связанные с освоением природных ресурсовПроанализируй предложенную ситуацию, определи способ решения проблемы, которая связана сдобычей поле … зных ископаемых.При добыче бокситов в Северном Казахстане образуются вскрышные породы, в которых содержатсякварцевый песок, глина и мел. Эти вскрышные породы образуют промышленные отходы, а эти отходы можноиспользовать для производства стекла и строительных материалов.
СПОСОБЫ ЗАДАНИЯ ЗАВИСИМОСТЕЙ МЕЖДУ ВЕЛИЧИНАМИ: АНАЛИТИЧЕСКИЙ (С ПОМОЩЬЮ ФОРМУЛЫ), ТАБЛИЧНЫЙ, ГРАФИЧЕСКИЙ. УРОК 2 УРОК ВИДЕОКОНФЕРЕНЦИЯ Открыть чат Спо … собы задания зависимостей между величинами: аналитический (с помощью формулы), табличный, графический. Урок 2 Заполни таблицу. x 3 4 6 y 10,4 13 Запиши формулой зависимость значения y от значения x.
Допоможіть із задачею. довжини сторін трикутника виражаються трьома послідовними натуральними числами.
Решаем это уравнение
Корни этого ур-ния
$$x_{1} = — \frac{1}{3} \sqrt[3]{27 \sqrt{15} + 108} — \frac{3}{\sqrt[3]{27 \sqrt{15} + 108}}$$
Зн. экстремумы в точках:
_________________ _________________
3 / ____ 3 / ____
3 \/ 108 + 27*\/ 15 4 3 3 \/ 108 + 27*\/ 15
(- -------------------- - --------------------, - ------------------------------------------------ - -------------------- + --------------------------------------------- - --------------------)
_________________ 3 2 _________________ _________________ 3
3 / ____ / _________________\ 3 / ____ 3 / ____
\/ 108 + 27*\/ 15 | 3 / ____ | \/ 108 + 27*\/ 15 3 \/ 108 + 27*\/ 15
| 3 \/ 108 + 27*\/ 15 | - -------------------- - --------------------
|- -------------------- - --------------------| _________________ 3
| _________________ 3 | 3 / ____
| 3 / ____ | \/ 108 + 27*\/ 15
\ \/ 108 + 27*\/ 15 / Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимумов у функции нет
Максимумы функции в точках:
$$x_{1} = — \frac{1}{3} \sqrt[3]{27 \sqrt{15} + 108} — \frac{3}{\sqrt[3]{27 \sqrt{15} + 108}}$$
(-oo, -(27*sqrt(15) + 108)**(1/3)/3 - 3/(27*sqrt(15) + 108)**(1/3)]
Возрастает на промежутках
[-(27*sqrt(15) + 108)**(1/3)/3 - 3/(27*sqrt(15) + 108)**(1/3), oo)
Кабель оптический ДПС-П-12У (3х4)-7кН ( 130905-00178 )
Кабель оптический ДПС-П-12У (3х4)-7кН ( 130905-00178 )Загрузка данных
Все цены на сайте являются актуальными на текущий день
Номенклатурный номер: 130905-00178 Скопировано в буфер обменаОписание
Задать вопрос Предназначены для прокладки в грунтах всех групп, в кабельной канализации, трубах, блоках, тоннелях, коллекторах, по мостам и эстакадам, внутри зданий при наличии особо высоких требований по механической устойчивости.
Конструктивно представляет собой повив оптических модулей вокруг стеклопластикового прутка, покрытый промежуточной полиэтиленовой оболочкой, броней из стальных оцинкованных проволок и наружной оболочкой из полиэтилена средней плотности. Свободное пространство в оптических модулях, в сердечнике кабеля, а также в бронепокрове заполнено гидрофобным гелем.
Устаревший номенклатурный №: 130905-01823
Маркировка
Сопутствующие товары
130103-00071 08/04/2021Наличие
-
МО Домодедово:
590
Москва:
0
Новосибирск:
26
Екатеринбург:
466
Прогноз:
неск.
 дней *
дней *
Наличие
МО Домодедово:
951
Москва:
0
Новосибирск:
0
Екатеринбург:
485
Прогноз:
неск.
 дней *
дней *
Аналоги
130905-00280 08/04/2021Центральный склад: 142001, г.Домодедово, ул.Промышленная д.13, Режим работы: Понедельник-Пятница: с 8:00 до 19:00 (суббота, воскресенье выходной)
Склад ЖБИ: 115088, г.Москва, ул. Южнопортовая д.7А, Режим работы: Понедельник-Пятница: с 8:00 до 17:00 (суббота, воскресенье выходной)
Срок поставки: Срок поставки между складами с момента подтверждения оплаты может варьироваться от 2 до 3 дней.
Прогнозируемый срок поставки не учитывает сезонность, загруженность производства и заказываемое количество. Данный срок носит информационный характер и является средним значением выполнения заказов на данное изделие за последние 12 месяцев.
Важно: Точный срок поставки согласовывается в спецификации.
Региональный склад: 630110, г.Новосибирск, ул. Богдана Хмельницкого, 93 ст.6, Режим работы: Понедельник-Пятница: с 8:00 до 17:00 (суббота, воскресенье выходной). Тел.: +7 (383) 312-04-34
Региональный склад: 620034, г.Екатеринбург, ул. Елизаветинское шоссе, 39, Режим работы: Понедельник-Пятница: с 8:00 до 17:00 (суббота, воскресенье выходной). Тел.: +7 (343) 302-54-34
Провод ПВС 3х4 Автопровод ГОСТ ПВС 3х4 АП
Провод ПВС 3х4 мм2, гибкий, многожильный. Автопровод
Провод с медной многопроволочной жилой с изоляцией из ПВХ-пластиката, в оболочке из такого же материала. Предназначен для присоединения к сети бытовых электрических приборов различного назначения.
- Рассчитан на использование в сетях переменного напряжения (до 380В).
- Применяется при изготовлении удлинителей
- Изготовлен с соблюдением ГОСТ
- Производитель — Щучинский завод «Автопровод» (Белоруссия)
Расшифровка обозначения
Первая цифра обозначает количество жил, вторая — сечение токопроводящей жилы, в мм2. Таким образом, провод ПВС 3х4 имеет 3 токопроводящие жилы по 4 мм2
Выбор сечения в зависимости от силы тока
|
Сечение жилы, мм |
0,5 |
0,75 |
1,0 |
1,5 |
2,5 |
4,0 |
6,0 |
10,0 |
16,0 |
|
Номинальный ток, А, (не более) |
2,5 |
6,0 |
10,0 |
16,0 |
25,0 |
32,0 |
40,0 |
50,0 |
60,0 |
Продажа кабеля ПВС в нарезку
Кабель и провод можно купить в нарезку в любом количестве. Чтобы сделать заказ — введите желаемое количество метров («метр» равнозначно «шт.») и нажмите кнопку «В корзину».
Чтобы сделать заказ — введите желаемое количество метров («метр» равнозначно «шт.») и нажмите кнопку «В корзину».
Оптовая закупка
Для оптовых закупок отправьте заявку через форму обратной связи (выберите в теме «Оптовые поставки, запрос цен, условий сотрудничества»). Можете приложить файлы в формате Word, Excel.
Характеристики
|
Марка |
ПВС |
|
Материал проводника |
Медь (Cu) без покрытия |
|
Количество основных жил |
3 |
|
Номинальное сечение основных жил |
4 мм² |
|
Класс проводника |
5 (многопроволочная гибкая жила) |
|
Изоляция жилы |
Поливинилхлорид (ПВХ) |
|
Маркировка жил |
Цвет |
|
Защитный проводник |
Да |
|
Материал внешней оболочки |
Поливинилхлорид (ПВХ) |
|
Цвет внешней. оболочки |
Белый |
|
Исполнение |
Круглый |
|
Максимальная температура проводника |
70 °C |
|
Рабочая температураи |
-25 … +40 °C |
|
Номинальное напряжение U (линейное) |
380 В |
Завод «Автопровод»
Щучинский завод «Автопровод», основанный 1958 году, начал свою деятельность с производства автомобильного провода.
В настоящее время завод производит более 250 видов кабельной продукции с алюминиевыми и медными жилами. Вся продукция имеет сертификат качества и соответствует необходимым требованиям безопасности (в том числе и пожарной). Высокий уровень качества подтверждается неизменным спросом.
Предприятие входит в число ведущих поставщиков соединительных шнуров и проводов, используемых в машиностроительной промышленности (БелАЗ, Лидсельмаш, МАЗ, Гомсельмаш и пр.).
Провод ПВС 3х4 Автопровод ГОСТ
Изображения и характеристики данного товара, в том числе цвет, могут отличаться от реального внешнего вида.
Комплектация и габариты товара могут быть изменены производителем без предварительного уведомления.
Описание на данной странице не является публичной офертой.
Провод ПВС 3х4 Автопровод ГОСТ — цена, фото, технические характеристики. Для того, чтобы купить Провод ПВС 3х4 Автопровод ГОСТ в интернет-магазине prestig.ru, нажмите кнопку «В КОРЗИНУ» и оформите заказ, это займет не больше 3 минут. Для того чтобы купить Провод ПВС 3х4 Автопровод ГОСТ оптом, свяжитесь с нашим оптовым отделом по телефону +7 (495) 664-64-28
Решите Свойства прямой y-3 = x-4 Tiger Algebra Solver
Переставьте:
Переставьте уравнение, вычтя то, что находится справа от знака равенства, из обеих частей уравнения:
y-3- (x-4) = 0
Шаг 1:
Уравнение прямой линии
1.1 Решите y-x + 1 = 0
Тигр распознает, что здесь есть уравнение прямой линии. Такое уравнение обычно записывается y = mx + b («y = mx + c» в Великобритании).
«y = mx + b» — это формула прямой линии, проведенной в декартовой системе координат, в которой «y» — вертикальная ось, а «x» — горизонтальная ось.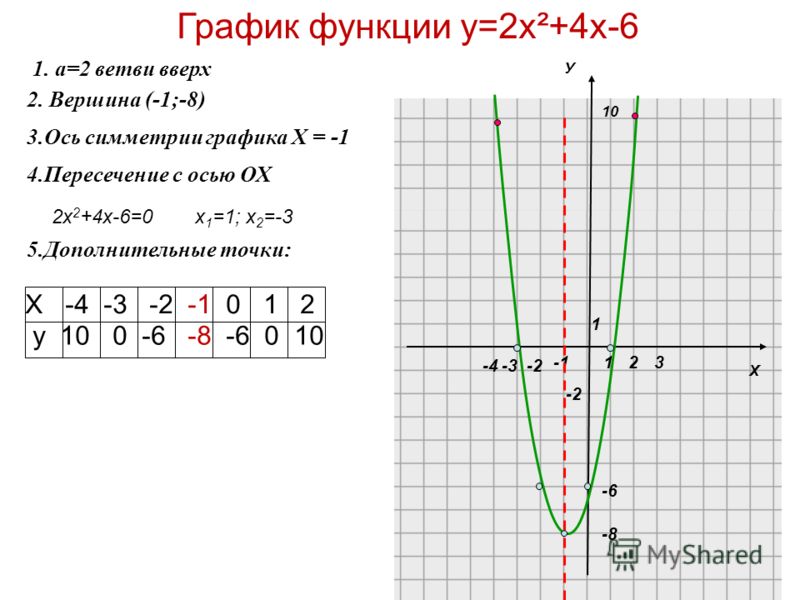
В этой формуле:
y указывает нам, как далеко идет линия.
x сообщает нам, как далеко вдоль
м находится наклон или градиент, т.е. насколько крутой является линия.
b является точкой пересечения Y, т.е. Ось Y
Пересечения по осям X и Y и наклон называются свойствами линии. Теперь мы построим график линии y-x + 1 = 0 и вычислим ее свойства
График прямой линии:
Вычислите точку пересечения оси Y:
Обратите внимание, что когда x = 0, значение y равно -1 / 1, поэтому эта линия «разрезает» ось y при y = -1.00000
Y-Intercept = -1/1 = -1.00000
Вычислите X-Intercept:
Когда y = 0, значение x равно 1/1 Наша линия, таким образом, «разрезает» ось x на x = 1.00000
x-intercept = 1/1 = 1.00000
Расчет наклона:
Наклон определяется как изменение y, деленное на изменение x. Отметим, что для x = 0 значение y равно -1,000, а для x = 2,000 значение y равно 1.000. Итак, при изменении x на 2.000 (изменение x иногда называют «RUN») мы получаем изменение на 1.000 — (-1,000) = 2,000 в y. (Изменение y иногда называют «ПОДЪЕМ», а наклон равен m = ПОДЪЕМ / РАБОТА)
Наклон = 2.000 / 2.000 = 1.000
Геометрическая фигура: прямая линия
- Наклон = 2.000 / 2.000 = 1.000
- пересечение по оси x = 1/1 = 1.00000
- пересечение по оси y = -1/1 = -1,00000
Графическое отображение линейных уравнений: другие примеры
Purplemath
Во всех предыдущих упражнениях, которые мы сделали, уравнения, которые нам давали, были решены для одной из переменных, обычно y .Однако иногда нам дают уравнения, которые не решены. В таком случае обычно проще всего сначала заняться алгеброй, чтобы решить уравнение (обычно для « y =»), чтобы упростить нашу жизнь. (Возможно, вы видели, что это называется «решение буквальных уравнений».) Необязательно, чтобы мы сначала занимались алгеброй, но мы можем сначала решить уравнение, а затем просто вставить-н-пыхтеть, или мы можем вставить уравнение как дано а затем выполните решение для каждого значения подключаемого модуля. Первое обычно позволяет сэкономить время по сравнению со вторым.
(Возможно, вы видели, что это называется «решение буквальных уравнений».) Необязательно, чтобы мы сначала занимались алгеброй, но мы можем сначала решить уравнение, а затем просто вставить-н-пыхтеть, или мы можем вставить уравнение как дано а затем выполните решение для каждого значения подключаемого модуля. Первое обычно позволяет сэкономить время по сравнению со вторым.
MathHelp.com
Для этого примера проще всего сначала решить для « y =».Это особенно верно, если я использую графический калькулятор для заполнения своей T-диаграммы, потому что графические калькуляторы могут обрабатывать линейные уравнения только в том случае, если они имеют форму « y =». Итак, чтобы облегчить себе задачу, я сначала решу это уравнение алгебраически.
Для этого я вычту 12 в левую часть и добавлю –3 y в правую часть. Затем я разделю на 3 и упрощу. Наконец, я переставлю уравнение (поменяв местами стороны), чтобы слева было и , где, как я привык, было:
4 x — 12 = 3 y
4 x — 12 = 3 y
(4 x ) / 3 — (12) / 3 = (3 y ) / 3
(4/3) x — 4 = y
y = (4/3) x — 4
Итак, я на самом деле изображаю это уравнение:
Поскольку я собираюсь умножить свои значения x на дробь, проще всего будет выбрать значения x , кратные 3, так что знаменатель сократится.
Вот мой Т-график …
… а вот мой график:
Сначала я решу уравнение для « y =»
.Итак, после того, как стороны поменяли местами, чтобы привести вещи в обычный формат, мое уравнение:
Хорошо, поэтому вычисление точек графика для этого будет беспорядочным, что со всеми дробями.Я сделаю все, что в моих силах, для Т-диаграммы, помня, что я просто сделаю все, что в моих силах, когда я пойду на график своих точек:
Из этих точек я рисую свой график:
Обратите внимание, что этот график должен быть больше (с точки зрения минимального и максимального значений оси), чем то, что я нарисовал ранее. Это потому, что точки были «беспорядочными», поэтому мне нужно было больше очков, и мне нужно было, чтобы эти точки были дальше друг от друга, чтобы убедиться, что моя линия верна.Это пример графика, на который стоит потратить дополнительное время и быть осторожным!
Редко можно встретить упражнения по построению графиков с десятичными знаками. Преобразование в дроби может быть полезным, поскольку вы сможете увидеть, какие виды значений x могут быть более полезными.
Десятичная дробь 0,4 совпадает с дробью
4/10 = 2/5. Таким образом, я могу рассматривать это уравнение как следующее:Это говорит мне о том, что выбор значений x , кратных 5, с большей вероятностью даст мне хорошие, аккуратные сюжетные точки.Вот мой Т-график:
Даже если я пропущу несколько точек на концах (что, думаю, я и сделаю), это будет широкий график, по крайней мере, с точки зрения масштаба.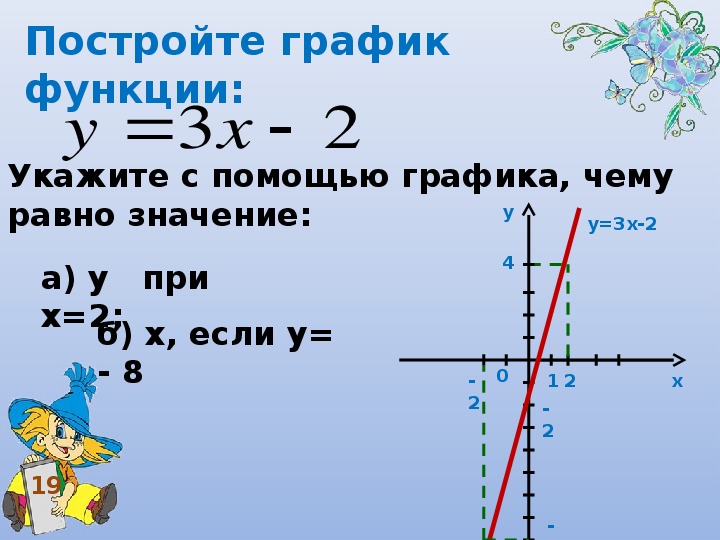
Между прочим, существуют и другие методы построения графиков прямых линий, такие как построение графиков на основе пересечений или построение графиков на основе пересечения y и наклона. Вы должны ожидать, что от вас потребуется возможность использовать любой метод, который был (или будет) представлен в вашем классе.
URL: https://www.purplemath.com/modules/graphlin4.htm
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в поиске графика прямой линии из таблицы значений. Затем нажмите кнопку и выберите «Использовать таблицу значений для построения графика уравнения» во всплывающем окне, чтобы сравнить свой ответ с ответом Mathway. (Если вы выбрали значения x , кратные 5, значения вашей таблицы почти наверняка будут «лучше» для построения графика, чем значения Mathway.Но ваша линия должна быть такой же, как у них.)
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
Нахождение точек пересечения по оси X и пересечения по оси Y | Колледж алгебры
точки пересечения графика — это точки, в которых график пересекает оси. Пересечение x- — это точка, в которой график пересекает ось x-.На данный момент координата y- равна нулю. Пересечение y- — это точка, в которой график пересекает ось y-. На данный момент координата x — равна нулю.
Чтобы определить точку пересечения x- , мы устанавливаем y равным нулю и решаем для x . Точно так же, чтобы определить точку пересечения y-, мы устанавливаем x равным нулю и решаем для y . Например, давайте найдем точки пересечения уравнения [латекс] y = 3x — 1 [/ latex].
Точно так же, чтобы определить точку пересечения y-, мы устанавливаем x равным нулю и решаем для y . Например, давайте найдем точки пересечения уравнения [латекс] y = 3x — 1 [/ latex].
Чтобы найти точку пересечения x- , установите [latex] y = 0 [/ latex].
[латекс] \ begin {array} {ll} y = 3x — 1 \ hfill & \ hfill \\ 0 = 3x — 1 \ hfill & \ hfill \\ 1 = 3x \ hfill & \ hfill \\ \ frac {1 } {3} = x \ hfill & \ hfill \\ \ left (\ frac {1} {3}, 0 \ right) \ hfill & x \ text {-intercept} \ hfill \ end {array} [/ latex]
Чтобы найти точку пересечения y- , установите [latex] x = 0 [/ latex].
[латекс] \ begin {array} {l} y = 3x — 1 \ hfill \\ y = 3 \ left (0 \ right) -1 \ hfill \\ y = -1 \ hfill \\ \ left (0, -1 \ right) y \ text {-intercept} \ hfill \ end {array} [/ latex]
Мы можем подтвердить, что наши результаты имеют смысл, наблюдая за графиком уравнения, показанным на рисунке 10.Обратите внимание, что график пересекает оси там, где мы и предполагали.
Рисунок 12
Как: по уравнению найти точки пересечения.
- Найдите точку пересечения x , задав [latex] y = 0 [/ latex] и решив для [latex] x [/ latex].
- Найдите точку пересечения y- , установив [latex] x = 0 [/ latex] и решив для [latex] y [/ latex].
Пример 4: Нахождение точек пересечения данного уравнения
Найдите точки пересечения уравнения [латекс] y = -3x — 4 [/ latex].Затем нарисуйте график, используя только точки пересечения.
Решение
Установите [latex] y = 0 [/ latex], чтобы найти точку пересечения x —.
[латекс] \ begin {array} {l} y = -3x — 4 \ hfill \\ 0 = -3x — 4 \ hfill \\ 4 = -3x \ hfill \\ — \ frac {4} {3} = x \ hfill \\ \ left (- \ frac {4} {3}, 0 \ right) x \ text {-intercept} \ hfill \ end {array} [/ latex]
Установите [latex] x = 0 [/ latex], чтобы найти точку пересечения y- .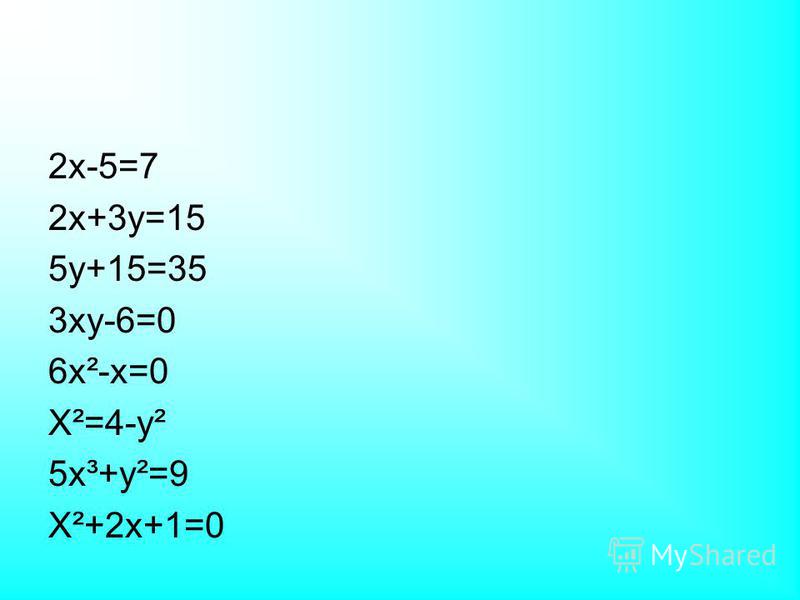
[латекс] \ begin {array} {l} y = -3x — 4 \ hfill \\ y = -3 \ left (0 \ right) -4 \ hfill \\ y = -4 \ hfill \\ \ left ( 0, -4 \ right) y \ text {-intercept} \ hfill \ end {array} [/ latex]
Постройте обе точки и проведите через них линию, как показано на рисунке 11.
Рисунок 13
Попробуй 1
Найдите точки пересечения уравнения и нарисуйте график: [latex] y = — \ frac {3} {4} x + 3 [/ latex].
Решение
Линейные уравнения и функции: функции и их графики Учебное пособие
Функции и их графики
Функция, функция, какова ваша функция? Вы личный тренер, известный шпион, ограничитель дверей или что-то совсем другое? Думаем, последний.
Функция принимает некоторые входные данные, обычно называемые x , в уравнение, f ( x ). Затем x проходит через уравнение, и в конце мы получаем некоторый результат, обычно известный как y . Обратите внимание, что y и f ( x ) на самом деле одно и то же. Может быть, и — знаменитый шпион?
Мы называем x независимой переменной и y зависимой переменной .Итак, x — это хорошая работа, а x все еще живет дома. Все возможные значения x- — это область , а все возможные значения y- — это диапазон .
Пример задачи
Найдите область и диапазон y = 3 x — 4, где 0 ≤ x <4.
Если бы нам просто дали уравнение, y = 3 x — 4, не говоря больше ни о чем, мы бы сказали, что домен — это все действительные числа.При этом не учитываются воображаемые, фальшивые, бредовые и позерские числа.
Однако в данном случае мы не можем выбрать x , которые нам нравятся под солнцем. Проблема говорит, что 0 ≤ x <4. Это означает, что наш домен ограничен всеми действительными числами от 0 до 4, включая 0, но не 4 (из-за линии под голодным ртом Пакмана).
Это означает, что наш домен ограничен всеми действительными числами от 0 до 4, включая 0, но не 4 (из-за линии под голодным ртом Пакмана).
А теперь ассортимент. Диапазон всех возможных значений: и . В нашем уравнении y = 3 x -4, значения y- — это то, что мы получаем, когда вставляем известные нам значения x- .Давайте составим таблицу, чтобы уточнить диапазон.
Диапазон этой функции: -4 ≤ y <8. Обратите внимание, что y меньше 8, потому что x не может равняться 4, поэтому y также никогда не может быть равно 8 в точности.
В этом случае диапазон легкий; мы могли бы посмотреть на наименьшее и наибольшее значения x , и они дают нам наименьшее и наибольшее значения y . Что, если бы у нас было что-то вроде y = — x 2 , с -2 < x <2?
Здесь, если мы просто подключим x = -2 и 2, мы получим y = -4 для них обоих.Однако мы знаем, что y не просто остаются на -4 все время. Мы должны проверить x = 0, чтобы найти, что y = 0, что дает нам диапазон -4 < y <0. Каждый раз, когда график может качаться или опускаться, проверьте различные числа, чтобы найти правильный диапазон.
Теперь поговорим на секунду о функциях построения графиков. Собственно, давайте поговорим и построим график одновременно. Только не проси нас тоже жевать жвачку.
Пример задачи
График y = 3 x — 4, где 0 ≤ x <4.
Ой, это снова ты. Вы собираетесь повторить вещь , не так ли?
Ничего страшного, потому что это означает, что мы уже проделали большую работу. Мы знаем домен и диапазон, и мы отметили несколько моментов.
Начните с рисования координатной плоскости . Ось x замерзает на спине, лежа, в то время как ось y стоит по стойке смирно. Они встречаются посередине в исходной точке .Не пытайтесь слишком сильно визуализировать это; на самом деле это не так больно, как кажется. Мы надеемся.
Они встречаются посередине в исходной точке .Не пытайтесь слишком сильно визуализировать это; на самом деле это не так больно, как кажется. Мы надеемся.
Мы используем числа на осях, чтобы построить точки и линию. Мы делаем заказанных пары , которые выглядят так: ( x , y ). А x всегда вызывает дробовик, так что y никогда не попадает первым.
Начиная с начала координат (0, 0), положительные значения x перемещаются вправо, а положительные значения y перемещаются вверх. Переместите оба числа вместе, чтобы построить каждую точку из нашей таблицы.
Видите, как красиво они выстраиваются? Почему они не могли так красиво выглядеть на школьных фотографиях? Что ж, проведем через них черту, пока они сидят неподвижно.
У нас здесь ограниченная область, поэтому мы рисуем только линию, где функция действительно существует. Несуществующие линии на удивление легко нарисовать, так что будьте начеку.
Вертикальность
В функциях есть кое-что очень важное. Фактически, это настолько важно, что мы собираемся поместить его в отдельную строку:
На каждые x есть только один y .Другими словами, каждый вход имеет только один выход. Один x входит, один y уходит.
Если уравнение нарушает этот принцип, это не функция. К счастью, нам не нужно подключаться и проверять каждое значение x- , чтобы увидеть, не совпадают ли какие-либо из них со значением y- . Это было бы утомительно и ужасно. Вместо этого мы можем использовать тест вертикальной линии . Какое имя, а?
Возьмем, к примеру, эти графики. Это именно то, на что похоже: рисование вертикальных линий поверх графика.Если какая-либо вертикальная линия может проходить через график более одного раза, тогда уравнение — это , а не как функция.
См. ? Мы можем сразу сказать, что является функцией, а что нет. И обратите внимание, что второй график посередине имеет одинаковое значение y- для двух разных значений x- (например, при y = 0). Это полностью разрешено. Мы просто не можем иметь одно и то же значение x- для нескольких значений y- , как на первом и третьем графиках.
? Мы можем сразу сказать, что является функцией, а что нет. И обратите внимание, что второй график посередине имеет одинаковое значение y- для двух разных значений x- (например, при y = 0). Это полностью разрешено. Мы просто не можем иметь одно и то же значение x- для нескольких значений y- , как на первом и третьем графиках.
С этого момента мы будем иметь дело с линейными уравнениями, которые легко классифицировать как линейные функции (ох, заголовок). Это вертикальная линия? Если нет, то да, Вирджиния, это функция.
Обратная функция — объяснение и примеры
Что такое обратная функция?
В математике обратная функция — это функция, отменяющая действие другой функции.
Например, , сложение и умножение являются инверсией соответственно вычитания и деления.
Обратную функцию можно рассматривать как отображение исходной функции по линии y = x. Проще говоря, обратная функция получается заменой (x, y) исходной функции на (y, x).
Мы используем символ f — 1 для обозначения обратной функции. Например, если f (x) и g (x) противоположны друг другу, то мы можем символически представить это утверждение как:
g (x) = f — 1 (x) или f (x) = g −1 (x)
Одна вещь, которую следует отметить относительно обратной функции, заключается в том, что обратная функция не совпадает с ее обратной величиной, т.е.е., f — 1 (x) ≠ 1 / f (x). В этой статье мы обсудим, как найти обратную функцию.
Поскольку не все функции имеют инверсию, важно проверить, есть ли у функции инверсия, прежде чем приступать к определению инверсии.
Мы проверяем, есть ли у функции инверсия, чтобы не тратить время на поиск чего-то, чего не существует.
Индивидуальные функции
Итак, как мы можем доказать, что данная функция имеет обратную? Функции, у которых есть обратные, называются взаимно однозначными функциями.
Функция называется взаимно однозначной, если для каждого числа y в диапазоне f существует ровно одно число x в области определения f такое, что f (x) = y.
Другими словами, область определения и диапазон однозначной функции имеют следующие отношения:
- Область f -1 = Диапазон f.
- Диапазон f -1 = Область f.
Например, чтобы проверить, является ли функция f (x) = 3x + 5 взаимно однозначной, заданной функцией f (a) = 3a + 5 и f (b) = 3b + 5.
3a + 5 = 3b + 5
⟹ 3a = 3b
⟹ a = b.
Следовательно, f (x) является взаимно однозначной функцией, поскольку a = b.
Рассмотрим другой случай, когда функция f задается формулой f = {(7, 3), (8, –5), (–2, 11), (–6, 4)}. Эта функция взаимно однозначна, потому что ни одно из ее значений y не встречается более одного раза.
А как насчет этой другой функции h = {(–3, 8), (–11, –9), (5, 4), (6, –9)}? Функция h не является взаимно однозначной, потому что значение y, равное –9, встречается более одного раза.
Вы также можете графически проверить взаимно однозначную функцию, проведя вертикальную и горизонтальную линии через график функции. Функция взаимно однозначна, если и горизонтальная, и вертикальная линии проходят через график один раз.
Как найти обратную функцию?
Нахождение обратной функции — простой процесс, хотя нам действительно нужно быть осторожными с парой шагов. В этой статье мы будем предполагать, что все функции, с которыми мы будем иметь дело, относятся друг к другу.
Вот процедура нахождения обратной функции f (x):
- Заменить обозначение функции f (x) на y.
- Поменять местами x на y и наоборот.
- Начиная с шага 2, решите уравнение относительно y. Будьте осторожны с этим шагом.
- Наконец, измените y на f −1 (x). Это обратная функция.
- Вы можете проверить свой ответ, проверив, верны ли следующие два утверждения:
⟹ (f ∘ f −1 ) (x) = x
⟹ (f −1 ∘ f) (x) = x
Давайте рассмотрим пару примеров.
Пример 1
Дана функция f (x) = 3x — 2, найдите обратную ей функцию.
Решение
f (x) = 3x — 2
Замените f (x) на y.
⟹ y = 3x — 2
Поменять местами x на y
⟹ x = 3y — 2
Решить относительно y
x + 2 = 3y
Разделим на 3, чтобы получить;
1/3 (x + 2) = y
x / 3 + 2/3 = y
Наконец, заменим y на f −1 (x).
f −1 (x) = x / 3 + 2/3
Проверить (f ∘ f −1 ) (x) = x
(f f −1 ) (x) = f [f −1 (x)]
= f (x / 3 + 2/3)
⟹ 3 (x / 3 + 2/3) — 2
⟹ x + 2 — 2
= x
Следовательно, f −1 (x) = x / 3 + 2/3 — правильный ответ.
Пример 2
Учитывая f (x) = 2x + 3, найти f −1 (x).
Решение
f (x) = y = 2x + 3
2x + 3 = y
Поменять местами x и y
⟹2y + 3 = x
Теперь решите относительно y
⟹2y = x — 3
⟹ y = x / 2 — 3/2
Наконец, заменим y на f −1 (x)
⟹ f −1 (x) = (x– 3) / 2
Пример 3
Задайте функцию f (x) = log 10 (x), найдите f −1 (x).
Решение
f (x) = log₁₀ (x)
Заменено f (x) на y
⟹ y = log 10 (x) ⟹ 10 y = x
Теперь замените x на y получить;
⟹ y = 10 x
Наконец, заменим y на f −1 (x).
f -1 (x) = 10 x
Следовательно, обратное значение f (x) = log 10 (x) равно f -1 (x) = 10 x
Пример 4
Найдите обратную функцию следующей функции g (x) = (x + 4) / (2x -5)
Решение
g (x) = (x + 4) / ( 2x -5) ⟹ y = (x + 4) / (2x -5)
Обменять y на x и наоборот
y = (x + 4) / (2x -5) ⟹ x = (y + 4) / (2y -5)
⟹ x (2y − 5) = y + 4
⟹ 2xy — 5x = y + 4
⟹ 2xy — y = 4 + 5x
⟹ (2x — 1) y = 4 + 5x
Разделите обе части уравнения на (2x — 1).
⟹ y = (4 + 5x) / (2x — 1)
Заменить y на g — 1 (x)
= g — 1 (x) = (4 + 5x) / (2x — 1)
Доказательство:
(g ∘ g −1 ) (x) = g [g −1 (x)]
= g [(4 + 5x) / (2x — 1)]
= [(4 + 5x) / (2x — 1) + 4] / [2 (4 + 5x) / (2x — 1) — 5]
Умножьте числитель и знаменатель на (2x — 1).
⟹ (2x — 1) [(4 + 5x) / (2x — 1) + 4] / [2 (4 + 5x) / (2x — 1) — 5] (2x — 1).
⟹ [4 + 5x + 4 (2x — 1)] / [2 (4 + 5x) — 5 (2x — 1)]
⟹ [4 + 5x + 8x − 4] / [8 + 10x — 10x + 5]
⟹13x / 13 = x
Следовательно, g — 1 (x) = (4 + 5x) / (2x — 1)
Пример 5
Определите обратное для следующего function f (x) = 2x — 5
Решение
Замените f (x) на y.
f (x) = 2x — 5⟹ y = 2x — 5
Поменяйте местами x и y, чтобы получить;
⟹ x = 2y — 5
Изолировать переменную y.
2y = x + 5
⟹ y = x / 2 + 5/2
Измените y обратно на f –1 (x).
⟹ f –1 (x) = (x + 5) / 2
Пример 6
Найдите функцию, обратную h (x) = (x — 2) 3 .
Решение
Измените h (x) на y, чтобы получить;
h (x) = (x — 2) 3 ⟹ y = (x — 2) 3
Поменять местами x и y
⟹ x = (y — 2) 3
Изолировать y.
y 3 = x + 2 3
Найдите кубический корень из обеих частей уравнения.
3 √y 3 = 3 √x 3 + 3 √2 3
y = 3 √ (2 3 ) + 2
Заменить y — 1 (x)
h — 1 (x) = 3 √ (2 3 ) + 2
Пример 7
Найдите значение, обратное h (x) = ( 4x + 3) / (2x + 5)
Решение
Замените h (x) на y.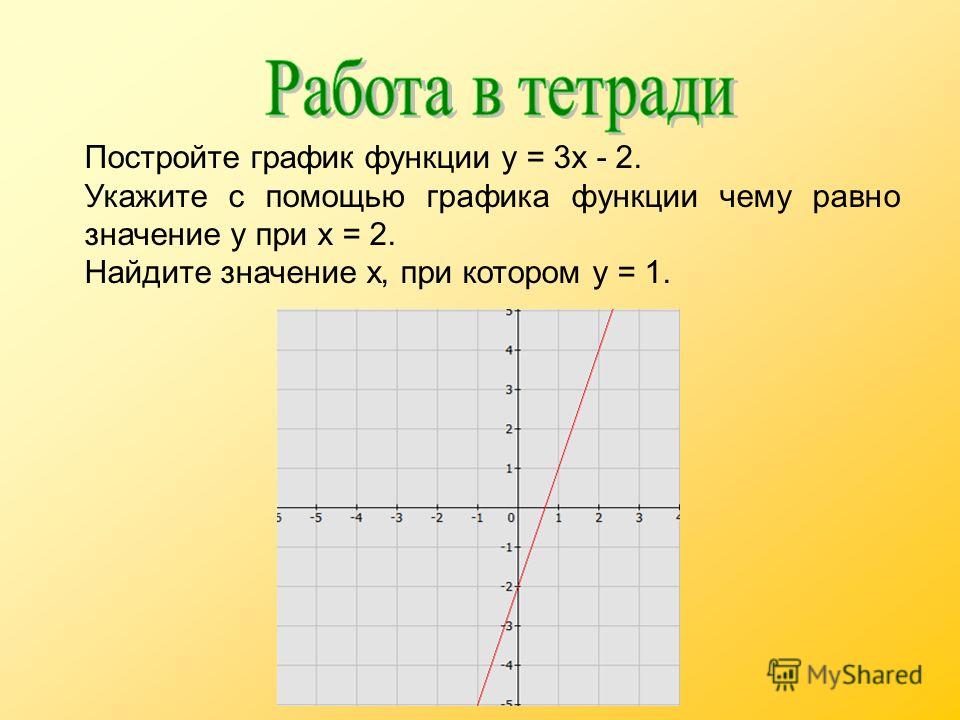
h (x) = (4x + 3) / (2x + 5) ⟹ y = (4x + 3) / (2x + 5)
Поменять местами x и y.
⟹ х = (4у + 3) / (2у + 5).
Решите относительно y в приведенном выше уравнении следующим образом:
⟹ x = (4y + 3) / (2y + 5)
Умножьте обе стороны на (2y + 5)
⟹ x (2y + 5) = 4y + 3
Распределить x
⟹ 2xy + 5x = 4y + 3
Изолировать y.
⟹ 2xy — 4y = 3 — 5x
⟹ y (2x — 4) = 3 — 5x
Разделим на 2x — 4, чтобы получить;
⟹ y = (3 — 5x) / (2x — 4)
Наконец, замените y на h -1 (x).
⟹ h — 1 (x) = (3 — 5x) / (2x — 4)
Практические вопросыНайдите обратное значение следующих функций:
- g (x) = (2x — 5) / 3.
- h (x) = –3x + 11.
- г (x) = — (x + 2) 2 — 1.
- г (x) = (5/6) x — 3/4
- f (x) = 3 x — 2.
- h (x) = x 2 + 1.
- g (x) = 2 (x — 3) 2 — 5
- f (x) = x 2 / (x 2 + 1)
- h (x) = √x — 3.
- f (x) = (x — 2) 5 + 3
- f (x) = 2 x 3 -1
- f (x) = x 2 — 4 x + 5
- г (x) = 5 √ (2x + 11)
- h (x) = 4x / (5 — x)
Функции — Алгебра — Математика A-Level Revision
В этом разделе рассматриваются функции в рамках более широкой темы «Алгебра».
Функцию можно рассматривать как правило, которое берет каждый элемент x набора и присваивает ему то же самое значение y , известное на его изображении.
x → Функция → y
Буква f, g или h часто используется для обозначения функции. Функция, которая возводит число в квадрат и добавляет 3, может быть записана как f (x) = x 2 + 5 . Это же понятие можно использовать, чтобы показать, как функция влияет на определенные значения.
Это же понятие можно использовать, чтобы показать, как функция влияет на определенные значения.
Пример
f (4) = 4 2 + 5 = 21, f (-10) = (-10) 2 +5 = 105 или, альтернативно, f : x → x 2 + 5 .
Фраза «y является функцией x» означает, что значение y зависит от значения x, поэтому:
- y можно записать через x (например, y = 3x).
- Если f (x) = 3x, а y является функцией x (т.е. y = f (x)), то значение y, когда x равно 4, равно f (4), которое находится путем замены x «s на 4. «с.
Пример
Если f (x) = 3x + 4, найти f (5) и f (x + 1).
f (5) = 3 (5) + 4 = 19
f (x + 1) = 3 (x + 1) + 4 = 3x + 7
Домен и диапазон
Область функции — это набор значений, которые вам разрешено вводить в функцию (то есть все значения, которые может принимать x).Диапазон функции — это набор всех значений, которые функция может принимать, другими словами, все возможные значения y, когда y = f (x). Итак, если y = x 2 , мы можем выбрать в качестве домена все действительные числа. Диапазон — это все действительные числа, большие (или равные) нулю, поскольку, если y = x 2 , y не может быть отрицательным.
Индивидуальные встречи
Мы говорим, что функция является взаимно однозначной , если для каждой точки y в диапазоне функции существует только одно значение x такое, что y = f (x).f (x) = x 2 не один к одному, потому что, например, есть два значения x, такие что f (x) = 4 (а именно –2 и 2). На графике функция взаимно однозначна, если любая горизонтальная линия разрезает график только один раз.
Составные функции
fg означает выполнение функции g, затем функции f. Иногда fg записывается как fog
Иногда fg записывается как fog
Пример
Если f (x) = x 2 и g (x) = x — 1, то
gf (x) = g (x 2 ) = x 2 — 1
fg (x) = f (x — 1) = (х — 1) 2
Как видите, fg не обязательно равно gf
Обратная функция
Обратной функцией является функция, которая обращает эффект исходной функции.Например, y = 2x, обратное y = ½ x.
Чтобы найти обратную функцию, поменяйте местами x «s и y» s и сделайте y предметом формулы.
Пример
Найдите обратное к f (x) = 2x + 1
Пусть y = f (x), поэтому y = 2x + 1
поменяет местами x «s и y» s:
x = 2y + 1
Сделайте y объектом формулы:
2y = x — 1, поэтому y = ½ (x — 1)
Следовательно, f -1 (x) = ½ (x — 1)
f -1 (x) — стандартное обозначение, обратное к f (x).Обратное считается существующим тогда и только тогда, когда существует функция f -1 с ff -1 (x) = f -1 f (x) = x
.Обратите внимание, что график f -1 будет отражением f на линии y = x.
Это видео объясняет больше об обратной функции
Графики
Функции можно изобразить. Функция является непрерывной , если ее график не имеет разрывов. Пример прерывного графа — y = 1 / x, поскольку граф нельзя нарисовать, не отрывая карандаш от бумаги:
Функция периодическая , если ее график повторяется через регулярные интервалы, этот интервал называется периодом.
Функция равна даже , если она не изменяется при замене x на -x. График такой функции будет симметричным по оси ординат. Даже функции, которые являются полиномами, имеют четные степени (например, y = x²).
Функция нечетная , если знак функции изменяется при замене x на -x. График функции будет иметь симметрию вращения относительно начала координат (например, y = x³).
Функция модуля
Модуль числа — это величина этого числа.Например, модуль -1 (| -1 |) равен 1. Модуль x, | x |, равен x для значений x, которые положительны, и -x для значений x, которые отрицательны. Итак, график y = | x | y = x для всех положительных значений x и y = -x для всех отрицательных значений x:
Преобразование графиков
Если y = f (x), график y = f (x) + c (где c — константа) будет графиком y = f (x), сдвинутым на c единиц вверх (в направлении y- ось).
Если y = f (x), график y = f (x + c) будет графиком y = f (x), сдвинутым на c единиц влево.
Если y = f (x), график y = f (x — c) будет графиком y = f (x), сдвинутым на c единиц вправо.
Если y = f (x), график y = af (x) представляет собой отрезок графика y = f (x), масштабный коэффициент (1 / a), параллельный оси x. [Масштабный коэффициент 1 / a означает, что «растяжение» фактически приводит к сжатию графика, если a — число больше 1]
Пример
График y = | x — 1 | будет таким же, как на приведенном выше графике, но со смещением на одну единицу вправо (так, чтобы точка V ударилась о ось x на 1, а не на 0).
Объем твердого тела революции: диски и шайбы
Если область на плоскости вращается вокруг линии в той же плоскости, полученный объект называется телом вращения.
Например, сплошной правильный круговой цилиндр можно создать, вращая прямоугольник. Точно так же твердый сферический шар можно создать, вращая полудиск.
Линия, вокруг которой мы вращаем фигуру, называется осью вращения.
Дисковый метод
Дисковый метод используется, когда мы вращаем одиночную кривую \ (y = f \ left (x \ right) \) вокруг оси \ (x- \) (или \ (y- \)). {\ frac {2} {3}}} = 1 \) вокруг своей оси симметрия.2} \) и ось \ (x — \) вокруг оси \ (y — \).
{\ frac {2} {3}}} = 1 \) вокруг своей оси симметрия.2} \) и ось \ (x — \) вокруг оси \ (y — \).
Пример 9
Найдите объем твердого тела, полученный вращением равностороннего треугольника со стороной \ (a \) вокруг одной из его сторон.Пример 10
Одна арка циклоиды \ (x = \ theta — \ sin \ theta, \) \ (y = 1 — \ cos \ theta \) вращается вокруг своего основания. Вычислите объем тела, ограниченного данной поверхностью.Пример 1.
Дисковым методом вычислить объем правого кругового конуса высотой \ (H \) и радиусом основания \ (R.1} = {8 \ pi \ left [{\ left ({1 — \ frac {1} {3}} \ right) — \ left ({- 1 + \ frac {1} {3}} \ right)} \ right]} = {8 \ pi \ cdot \ frac {4} {3}} = {\ frac {{32 \ pi}} {3}} \]Пример 5.
Симметричный параболический сегмент с основанием \ (a \) и высотой \ (h \) вращается вокруг основания. Вычислите объем полученного твердого тела вращения («лимон» Кавальери).Решение.
Квадратичная функция определяется уравнением \ (y = kx \ left ({a — x} \ right), \), где коэффициент \ (k \) может быть найден из условия \ (y \ left (\ large {{\ frac {a} {2}}} \ normalsize \ right) = h.2}}} {4}}} = {\ frac {{\ sqrt 3 a}} {2}.} \]
Итак, вершины \ (A, \) \ (B, \) \ (C \) имеют следующие координаты:
\ [{A \ left ({0, \ frac {a} {2}} \ right), \;} \ kern0pt {B \ left ({\ frac {{\ sqrt 3 a}} {2}, 0 } \ right), \;} \ kern0pt {C \ left ({0, — \ frac {a} {2}} \ right).} \]
Найдите уравнение прямой \ (AB \), используя двухточечную форму:
\ [{\ frac {{x — {x_A}}} {{{x_B} — {x_A}}} = \ frac {{y — {y_A}}} {{{y_B} — {y_A}}}, } \; \; \ Rightarrow {\ frac {{x — 0}} {{\ frac {{\ sqrt 3 a}} {2} — 0}} = \ frac {{y — \ frac {a} {2}}} {{ 0 — \ frac {a} {2}}},} \; \; \ Rightarrow {\ frac {x} {{\ sqrt 3}} = \ frac {{y — \ frac {a} {2}}} {{- 1}},} \; \; \ Rightarrow {x = \ гидроразрыв {{a \ sqrt 3}} {2} — \ sqrt 3 г.2}.} \]
.
 дней *
дней * дней *
дней *