Аналогично рассматриваем способ построения графика функции y = |x + 1| (слайд 7)

Сравнивая графики и уравнения функций (слайд 8-9),

делаем вывод о том, как можно построить график функции y = |x + a| — b смещением графика функции y = |x| (слайд 10-11)

Строим в тетрадях графики функций y = |x-3| + 3, y = |x – 3| — 2, y = |x+2| — 5, y = |x + 3| + 2 и проверяем себя при помощи слайда 12

Далее учащиеся должны на основе рисунка, представленного на слайде 13, задать функцию уравнением:

При построении графиков очень важно научить ребят анализировать область определения и множество значений функции и “переносить” указанные множества на координатную плоскость.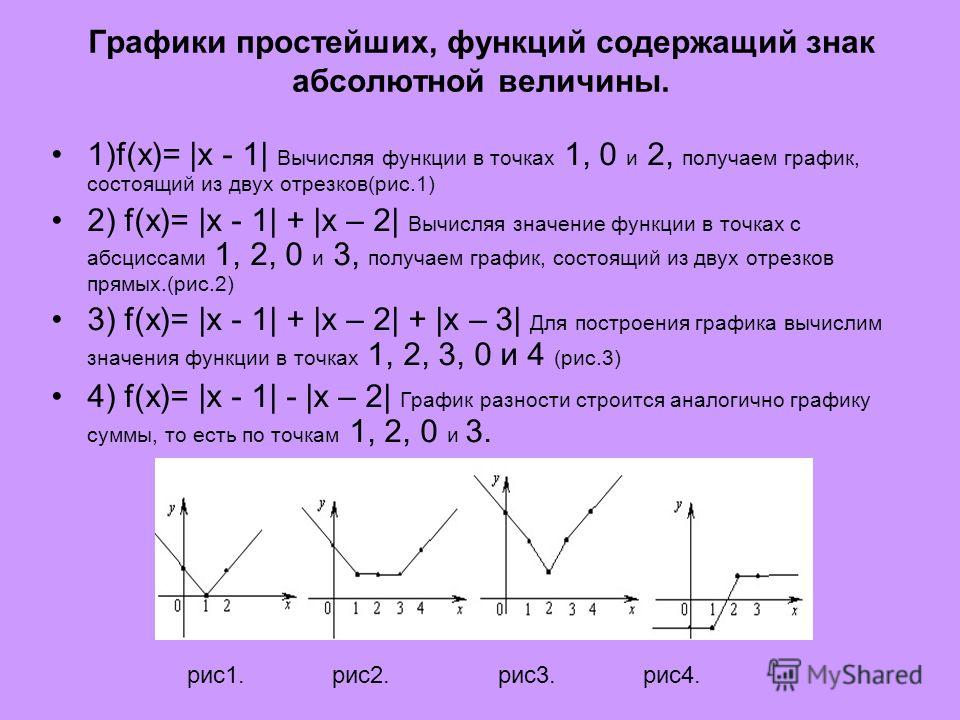

Заполняем таблицу (слайд 12):

	D(y)	E (y)
y = |x|
y = |x – 3|
y = |x – 3| +2
y = — |x|
y = |x + 2| -5
y = — |x +2| -5

И рассматриваем, как множества значений можно определить на основе графиков (слайд 15)

Учащимся предлагается определить D (y) и E(y) по рисунку (слайд 16):

Ученики самостоятельно придумывают уравнение функции по заданным D(y) и E(y) (слайд 17):

Анализируя графики и уравнения (слайд 18), ученики делают вывод о том, как влияет знак минуса перед модульными скобками на график.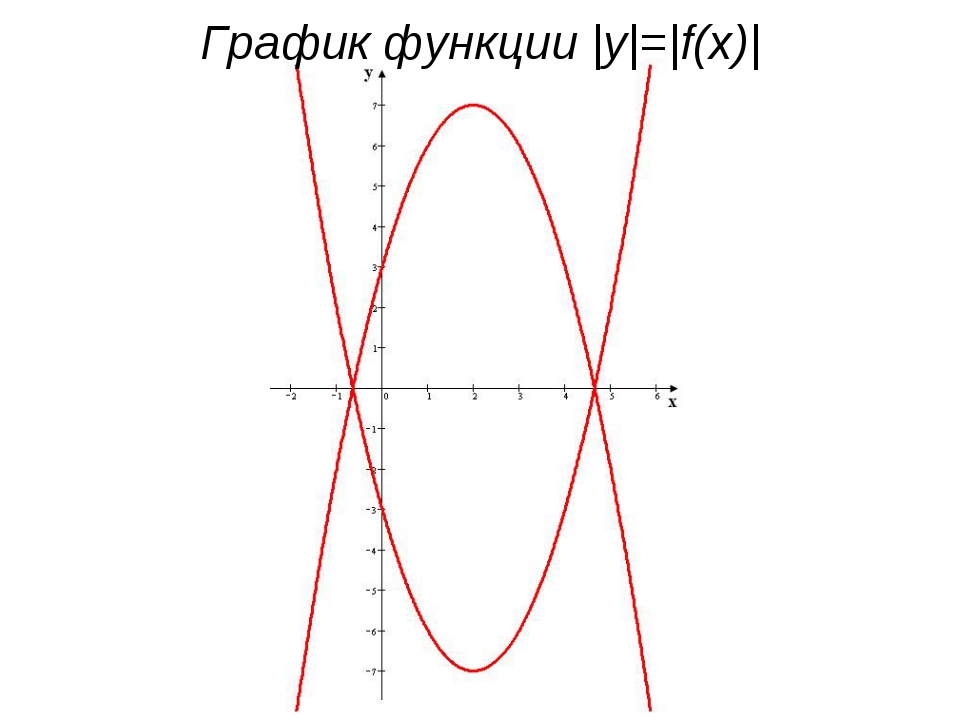 И самостоятельно задают уравнение по графикам, представленным на слайде 19.

Ход урока № 2

Устно проговариваем уравнения функций по графикам (слайд 20):

Аналогично схеме предыдущего урока (слайд 21-27) ученики знакомятся с тем, каким образом влияет коэффициент перед аргументом функции на график. В результате они должны научиться описывать уравнением следующие графики:

Для закрепления полученных знаний, в тетрадях в одной системе координат ребята строят следующие графики:

y = |0,5x| при -3 < x< 3;

y = 3 при -1 < x< 1;

y = -|x + 3| + 6 при -4 < x < -2;

y = -|x — 3| + 6 при 2 < x < 4;

y = |x + 3| + 4 при -4 < x < -2;

y = |x — 3| + 4 при 2 < x ? 4;

y = -|0,5x – 1,5| + 7 при -5 < x < -1;

y = -|0,5x + 1,5| + 7 при 1 < x < 5.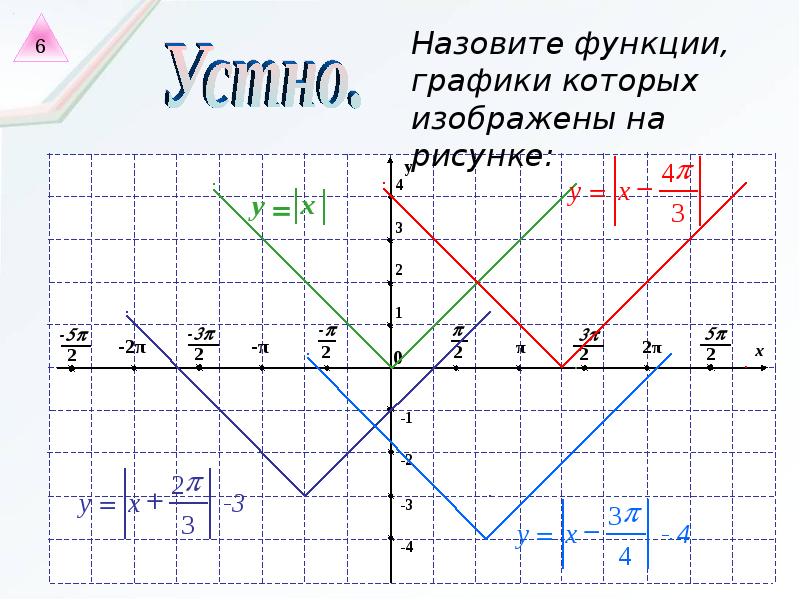

Проверяют себя по слайду 29:

Домашнее задание: придумать картину, состоящую из отрезков прямых, и описать ее при помощи уравнений функций.

Ход урока № 3

Построим графики функций y = |3x| — 3 и y = |3x – 3|. Как в каждом случае связаны y(x) и y(-x)?

Наличие условия y(x) = y(-x) означает симметрию относительно …?

Приведите примеры уравнений функции, графики которых будут симметричны относительно оси ординат

Если в модульные скобки заключается переменная y, то мы получаем условие |y| = |-y|. Какую симметрию задает это условие?

y = 3x – 3, |y| = 3x – 3, |y| = |3x| — 3, |y| = |3x – 3| путем преобразований симметрии.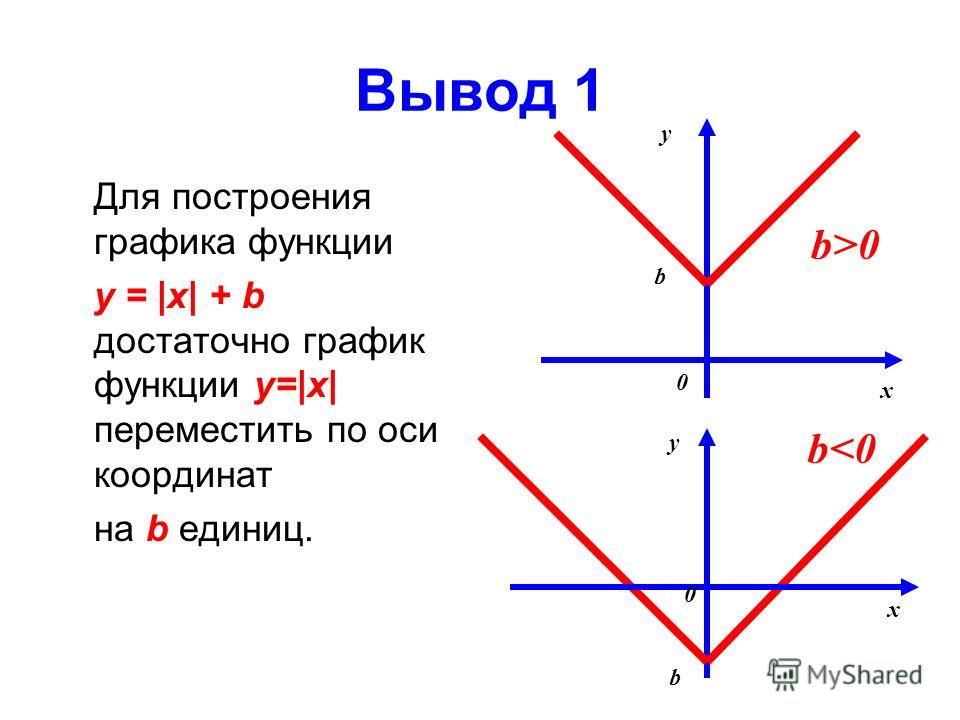

Выводим и запоминаем три правила:

Распределите, к какому типу из трех (y = f(|x|, |y| = f(x), y = |f(x)|), можно отнести каждое уравнение:

|y| = 2 – x, y = |3x — 4|, |x| + |y| = 2, |y| = 3x – 4, y = |3|x| — 4|, y = |3x| — 4, |y| = |3|x| — 4|, |y| = |3x – 4|.

Проверяем себя (слайд 35)

Строим последовательную цепочку графиков (тонкими линиями в тетрадях):

1) y = 3x – 4, y = |3x – 4|, y

2) y = 3x – 4, y = 3|x| — 4, y = |3|x| — 4|

Рассматриваем способ построения графика соответствия |x| + |y| = 2.

Самостоятельно строим график |x| — |y| = 2 и проверяем себя по слайду 39.

Домашнее задание: придумать пять уравнений соответствий с модулем, в которых встречаются все случаи, рассмотренные на уроке, и построить графики.

Постройте график функции и найдите значение k

Постройте график функции y=|x-3|-|x+3| и найдите значение k, при которых прямая y=kx имеет с графиком данной функции ровно одну общую точку.

Решение:

Разберем как строить график с модулем.

y=|x-3|-|x+3|

У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.

1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1

У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).

y=—(x-3)-(—(x+3))=-х+3+х+3=6

На интервале (-∞;-3) получился график линейной функции (прямой) у=6

2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3

У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.

y=—(x-3)-(+(x+3))=-х+3-х-3=-2x

На интервале (-3;3) получился график линейной функции (прямой) у=-2х

3. Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.

х=5
x-3=5-3=2 и x+3=5+3=8

У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).

y=+(x-3)-(+(x+3))=х-3-х-3=-6

На интервале (3;+∞) получился график линейной функции (прямой) у=-6

4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.

5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.

Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.

Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.

Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.Этот вариант нам не подходит.

Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.

Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.

Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно. Этот вариант нам подходит.

Ответ: при k принадлежащей интервалу (-∞;-2)U[0;+∞) прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Графики функций и поверхностей в Python Питон Matplotlib

Построение графиков с помощью модуля Matplotlib в Python Питон.

В этом уроке мы разберём, как строить графики функций с помощью модуля Matplotlib в Python Питон.
Matplotlib это библиотека для Python, предназначенная для визуализации данных. В данном уроке мы разберём построение графиков функций в Питон на плоскости и построение поверхности в трёхмерном пространстве. Зачастую, именно Matplotlib используется в научных исследованиях и конференциях для демонстрации полученных данных.
Для построения графиков нужно импортировать модуль Pyplot. Pyplot это модуль для работы с графиками в Питоне. Pyplot это набор команд, созданных для построения графиков функций и уравнений. Для удобного построения графиков так же нужно использовать библиотеку NumPy.
Matplotlib, как и NumPy, встроен в среду разработки Spyder, поэтому их можно импортировать без предварительной установки.
import numpy as np
import matplotlib.pyplot as plt
as np и as plt означает, что когда мы будем вызывать функции и процедуры из модулей, вместо названия модулей мы будем использовать np и plt.
Для построения графика функции в Python нужно задать саму функцию. Её можно задать с помощью лямбда-функции. Лямбда-функция — это краткий способ записи обычной функции в одну строчку. В этом уроке мы рассмотрим построение синусоиды на Питоне. Синусоида задаётся функцией f(x) = sin(x).
y = lambda x: np.sin(x)
y это обозначение функции (для её вызова мы будем использовать y(x)), lambda это ключевое слово, обозначающее начало задания лямбда-функции, x это аргумент, использующийся в функции, после двоеточия задаётся функция. Так как в стандартном Python нет функции, возвращающей синус x, мы его задаём с помощью NumPy, его мы импортировали под именем np.
Все действия в Pyplot производятся на рисунках. Для построения графика функции в Python нужно сначала задать сетку координат. Сетка координат в python задается с помощью команды  plt.subplots().
fig = plt.subplots()
Мы должны определить область значений, на которой мы будем строить график функции в Питоне. Это делается с помощью linspace.
x = np.linspace(-3, 3, 100)
linspace создаёт массив с нижней границей -3 и верхней границей 3, в созданном массиве будет 100 элементов. Чем больше будет последнее число, тем больше значений функции будет рассчитываться, тем точнее будет отображаться график в Python.
После того, как мы создали систему координат, область построения, мы можем построить график в Питон. Для построения графика фуекции в Python нужно использовать команду plt.plot(x, y(x)), где x это аргумент, y(x) это функция от x, заданная с помощью лямбда-выражения.
plt.plot(x, y(x))
После того, как мы построили  график в Python, нужно показать его на рисунке. Для этого используется plt.show().
Полный код программы на python для рисования графика функции
# импортируем модули
import numpy as np
import matplotlib.pyplot as plt
# функция
y = lambda x: np.sin(x)
# создаём рисунок с координатную плоскость
fig = plt.subplots()
# создаём область, в которой будет
# — отображаться график
x = np.linspace(-3, 3,100)
# значения x, которые будут отображены
# количество элементов в созданном массиве
# — качество прорисовки графика 
# рисуем график
plt. plot(x, y(x))
# показываем график
plt.show()

Получим график синусоиды в python в отдельном окне

Отображение нескольких графиков на одном рисунке в Python

В одной области в python можно отобразить графики нескольких функций. Добавим aeyrwb. y=x  и нарисуем ее совместно с синусоидой.
Для этого введем еще одну функцию с помощью lambda
y1=lambda x: x
Построим график этой функции
plt.plot(x,y1(x))
В итоге программа в Python для построения графиков двух функций в одном окне

# импортируем модули
import numpy as np
import matplotlib.pyplot as plt
# функция
y = lambda x: np.sin(x)
y1=lambda x: x
# создаём рисунок с координатную плоскость
fig = plt.subplots()
# создаём область, в которой будет
# — отображаться график
x = np.linspace(-3, 3,100)
# значения x, которые будут отображены
# количество элементов в созданном массиве
# — качество прорисовки графика 
# рисуем график
plt. 2
от двух аргументов. Аргументы x и y, функция z.
f = lambda x, y: x ** 2 — y ** 2
Чтобы начать рисовать трехмерные поверхности в Python нужно сначал задать область построения с помощью функции  plt.figure принимает параметр figsize(x, y), где x и y – ширина и высота рисунка в дюймах. Создадим рисунок в Python размером 12×6 дюймов для отображения графиков
fig = plt.figure(figsize = (12, 6))
В построенной области мы создадим рисунок, в котором будут отображено трёхмерное пространство с координатными осями и сама поверхность. В Питоне для этого используется fig.add_subplot(). 
ax = fig.add_subplot(1, 1, 1, projection = ‘3d’)
Функция в Python fig.add_subplot() разбивает область построения на клетки и задает в какой клетке рисовать трехмерный график. Так команда ax = fig.add_subplot(1, 1, 1, projection = ‘3d’) разбивает область построения на две клтки и в первую клетку будет отображаться трехмерный гарфик, благодаря аргументу projection = ‘3d’ 
Введём области отображения функции для каждого аргумента в Питон.
xval = np.linspace(-5, 5, 100)
yval = np.linspace(-5, 5, 100)
Нужно создать поверхность, которая будет отображаться на рисунке в Python. Для этого используется
surf = ax.plot_surface(x, y, z, rstride = 4, cstride = 4, cmap = cm.plasma)
Где x и y это принимаемые аргументы, z это получаемая функция, rstride и cstride отвечает за шаг прорисовки поверхности в Питон, чем меньше будут эти значения, тем более плавно будет выглядеть градиент на поверхности. С помощью cmap.plasma поверхность будет отображаться с цветовой схемой plasma. Например, существуют цветовые схемы, такие как viridis и magma. Полный список цветовых схем есть на сайте Matplotlib.
Пример программы на Python построение поверхности в трёхмерном пространстве# импортируем модули
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
from matplotlib import cm
import matplotlib.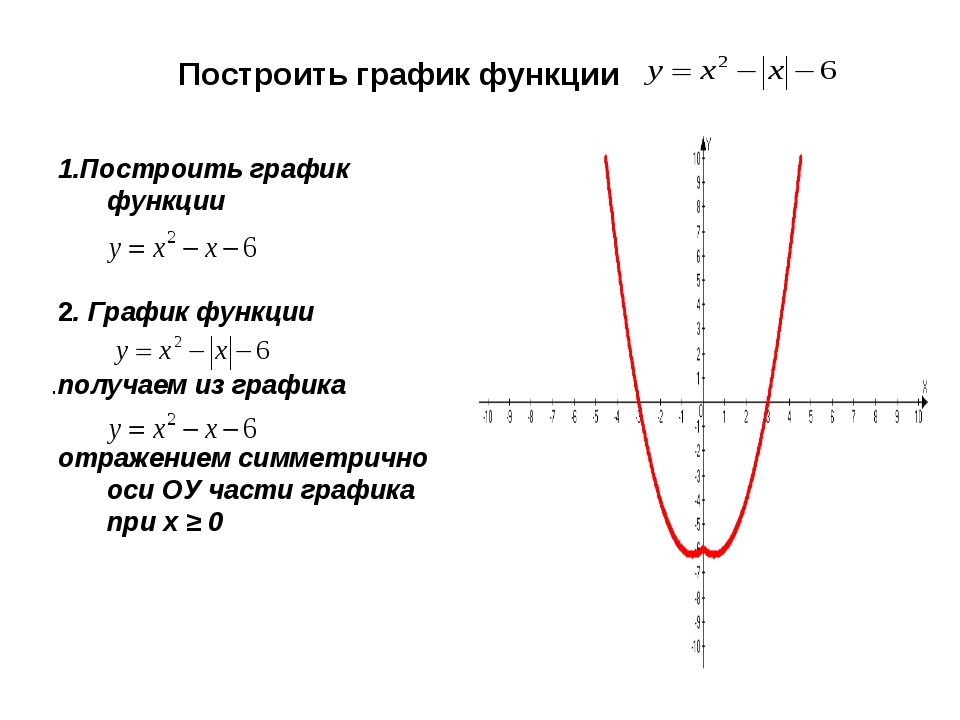 pyplot as plt
# уравнение поверхности
f = lambda x, y: x ** 2 — y ** 2
# создаём полотно для рисунка
fig = plt.figure(figsize = (10, 10))
# создаём рисунок пространства с поверхностью
ax = fig.add_subplot(1, 1, 1, projection = ‘3d’)
# размечаем границы осей для аргументов
xval = np.linspace(-4, 4, 100)
yval = np.linspace(-4, 4, 100)
# создаём массив с xval столбцами и yval строками
# — в этом массиве будут храниться значения z
x, y = np.meshgrid(xval, yval)
# приравниваем z к функции от x и y 
z = f(x, y)
# создаём поверхность
surf = ax.plot_surface(
# отмечаем аргументы и уравнение поверхности
x, y, z, 
# шаг прорисовки сетки
# — чем меньше значение, тем плавнее
# — будет градиент на поверхности
rstride = 10,
cstride = 10,
# цветовая схема plasma
cmap = cm. plasma)

Получим график трехмерной поверхности в цветовой гамме в специальном окне

Изменим параметры построения трехмерной поверхности, уменьшим размер сетик, сделаем поверхность более плавной и точной для этого уменьшаем параметры и сменим цветовую гамму на viridis

rstride = 2,
cstride = 2,
cmap = cm.viridis)

Получим график трехмерной поверхности в Python более точный и в другой цветовой гамме

Вернуться к содержанию курса python Следующая тема Классы в Питон

Поделиться:

Построение графиков, содержащих выражение под знаком модуля

1. Построение графиков, содержащих выражения под знаком модуля

2. Частный случай (под знаком модуля одно выражение и нет слагаемых без модуля)

3. Построить график функции:

4.

5. Построить график функции:

6. Построить график функции:

7.

8. a) у=|х — 1|+|2 — х| +2

9. b) y=|3х|-3х; c) y=|х-3|+|1-х|+4;

10. d) y=|5-х|-|2-х|-3; e) y=7-|х-1|+|х+5|;

11.

12. l) y=| х-2|+|3+ х|-3

13.

14. Занимательная графика

Построение графика функции онлайн | umath.ru

• Обязательно писать все знаки умножения
• Десятичные дроби нужно разделять точкой
• Список функций и констант смотрите ниже

Как пользоваться программой:

• Можно строить графики сразу нескольких функций. Для этого просто разделяйте функции точкой с запятой (;).
• Масштаб изменяется с помощью кнопок «+» и «−». Кнопка «100%» меняет масштаб на стандартный.
• Положение экрана можно менять, перетаскивая его мышью, а можно стрелками на панели слева.
• Кнопка «·» в центре джойстика переносит начало координат в центр экрана.
• Кнопка «↺» изменяет масштаб на стандартный и переносит начало координат в центр.
• В форме под графиком можно выбрать точку, которую нужно расположить в центре экрана.

Режимы

Обычный. В этом режиме можно строить графики функций, заданных уравнением

Параметрический. Этот режим предназначен для построения графиков кривых, заданных параметрически, то есть в виде

Полярные координаты. Режим позволяет построить график кривой, заданной в полярной системе координат, то есть уравнением где — радиальная координата, а — полярная координата.

Список констант

Константа	Описание
pi	Число =3,14159. 3 дают x в третьей степени
sqrt()	Квадратный корень
sin()	Синус
cos()	Косинус
tg()	Тангенс
ctg()	Котангенс
arcsin()	Арксинус
arccos()	Арккосинус
arctg()	Арктангенс
arcctg()	Арккотангенс
ln()	Натуральный логарифм числа
lg()	Десятичный логарифм числа
log(a, b)	Логарифм числа b по основанию a
exp()	Степень числа e
sh()	Гиперболический синус
ch()	Гиперболический косинус
th()	Гиперболический тангенс
cth()	Гиперболический котангенс

График функции

Графиком функции называется множество точек плоскости таких, что абсциссы и ординаты этих точек удовлетворяют уравнению .

Программа создана для школьников и студентов и позволяет строить графики функций онлайн. Во многих браузерах (например, Google Chrome) картинку с графиком функции можно сохранить на компьютер.

Пожалуйста, все предложения и замечания по работе программы пишите в комментариях.

Кроме того мы планируем создать библиотеку функций с интересными и забавными графиками. Если вы открыли функцию с таким графиком, то обязательно напишите об этом в комментариях! Ваше открытие будет опубликовано и станет носить ваше имя ;).

Часть 2 ГИА по математике. Задача с параметром

Произведем разбор задачи 23 из модуля “Алгебра”, которая предлагалась на Тренировочной работе № 1 в формате ГИА 1 октября 2013 года.

Постройте график функции y =|x −1| − |x +1| + x и найдите все значения k , при которых прямая y = kx имеет с графиком данной функции ровно одну общую точку.

При построении графика заданной функции вам будет полезно заглянуть сюда.  И само собой, необходимо знать, что такое модуль.

Мы знаем, что при раскрытии модуля следует учитывать знак подмодульного выражения. Знак подмодульного  выражения может смениться только в нуле. Поэтому, первое, что делаем – находим нули модулей.

Нуль первого модуля – 1, второго – -1.

Эти значения разбивают  ось на три области:

Так вот в крайней левой области и в средней знак первого подмодульного выражения – “–”, в оставшейся – “+”.

А знак второго подмодульного выражения – “–” в крайней левой области, “+” – в оставшихся.

Итак, перед нами кусочно-заданная функция:

Переходим к координатной плоскости, наносим три области, с которыми работаем:

Строим график функции:

Теперь вводим прямую . Эта прямая проходит через начало координат. В зависимости от коэффициента  она имеет разные углы наклона к оси .

Вы можете посмотреть мини-ролик про график прямой пропорциональности здесь.

Становится ясно, что если график прямой  располагается в зоне, помеченной сиреневым цветом (граница левая – открытая), то основной график и прямая будут иметь только одну общую точку (начало координат).

Если чуть подробнее, – то правая граница зоны – прямая , так как она параллельна прямой . Выходить правее этой границы нельзя, иначе будет более одного пересечения основного графика и прямой .

Левую границу зоны брать нельзя. В противном случае у нас будет бесконечно много решений (за счет совпадения отдельных участков графиков). Левая, открытая, граница зоны соответствует .

И, надо понимать, что прямая  никогда не займет положение оси ординат. Ось ординат является своебразным “переходом” в .

Итак, U.

Ответ:  U.

Графические функции абсолютных значений | Purplemath

Purplemath

Принятие абсолютного значения отрицательного числа делает его положительным. По этой причине графики функций абсолютных значений имеют тенденцию не совсем походить на графики линейных функций, которые вы уже изучили. Однако из-за того, как ведут себя абсолютные значения, важно включать отрицательные входные данные в вашу Т-диаграмму при построении графиков функций абсолютных значений.Если вы не выберете значения x , которые поместят отрицательные значения внутри абсолютного значения, вы обычно будете вводить себя в заблуждение относительно того, как выглядит график.

Например, предположим, что ваш класс проходит следующую викторину:

MathHelp.com

Один из других учеников делает то, что обычно делает: он выбирает только положительные значения x для своей Т-диаграммы:

Затем он наносит на график свои очки:

Эти очки хороши, насколько они идут, но их недостаточно; они не дают точного представления о том, как должен выглядеть график. В частности, они не включают никаких «минусовых» входов, поэтому легко забыть, что эти столбцы абсолютных значений означают что-то . В результате ученик забывает учесть эти столбцы и рисует ошибочный график:

НЕПРАВИЛЬНЫЙ ОТВЕТ!

Аааааа … он просто завалил викторину.

Но вы более осторожны.Вы помните, что графики абсолютных значений включают абсолютные значения, и что абсолютные значения влияют на «минусовые» входные данные. Итак, вы выбираете значения x , которые ставят «минус» внутри абсолютного значения, и выбираете еще несколько точек. Ваш T-график выглядит примерно так:

Затем вы наносите свои очки:

. .. и, наконец, вы соединяете точки:

У вас есть правильный график:

Правильный ответ!

Ааааанд… вы только что успешно прошли викторину. Хорошая работа!

Хотя графики абсолютных значений имеют тенденцию выглядеть так, как показано выше, с «локтем» посередине, это не всегда так. Однако, если вы видите график с таким изгибом, вы должны ожидать, что уравнение графика, вероятно, включает в себя абсолютное значение. Во всех случаях вам следует позаботиться о том, чтобы вы выбрали хороший диапазон значений x , потому что три значения x , расположенные рядом друг с другом, почти наверняка не дадут вам достаточно информации, чтобы нарисовать достоверное изображение.

Примечание. Полоски абсолютных значений позволяют оценивать введенные значения как всегда неотрицательные (то есть положительные или нулевые). В результате «V» на приведенном выше графике возникла там, где знак внутри был равен нулю. Когда x было меньше –2, выражение x + 2 было меньше нуля, и столбцы абсолютных значений перевернули эти «минусовые» значения из-под оси x вверх. Когда x равняется –2, аргумент (то есть выражение внутри столбцов) равен нулю.Для всех значений x справа от –2 аргумент был положительным, поэтому столбцы абсолютных значений ничего не меняли.

Другими словами, графически столбцы абсолютных значений занимают этот график:

… и перевернул «минус» (зеленый на графике) снизу оси x на верхнюю. Замечание, где аргумент столбцов абсолютного значения будет равен нулю, может быть полезным для проверки правильности построения графика.

Эта функция почти такая же, как и предыдущая.

Однако аргумент предыдущего выражения абсолютного значения был x + 2. В этом случае только x находится внутри столбцов абсолютного значения. Этот аргумент будет равен нулю, когда x = 0, поэтому я должен ожидать увидеть локоть в этой области. Кроме того, поскольку «плюс два» находится за пределами столбцов абсолютных значений, я ожидаю, что мой график будет выглядеть как обычный график абсолютных значений (представляющий собой букву «V» с коленом в начале координат), но смещенный вверх на две единицы. .

Сначала я заполню свою Т-диаграмму, выбирая по ходу несколько отрицательных значений x :

Затем нарисую точки и заполню график:

Партнер

Поскольку столбцы абсолютных значений всегда показывают неотрицательные значения, может возникнуть соблазн предположить, что графики абсолютных значений не могут опускаться ниже оси x . Но могут:

• График

  y = — | x + 2 |

Эта функция является своего рода противоположностью первой функции (выше), потому что в выражении абсолютного значения в правой части уравнения стоит «минус». Из-за этого «минуса» все положительные значения, предоставленные столбцами абсолютных значений, будут переключены на отрицательные значения.Другими словами, я должен ожидать, что этот график будет иметь изгиб в точке (–2, 0), как и первый график выше, но остальная часть графика будет перевернута вверх дном, чтобы оказаться ниже оси x .

Сначала я заполню свою Т-диаграмму:

Затем делаю свой график:

Также не предполагайте, что какой-либо график абсолютных значений всегда будет находиться только на одной стороне оси x . Графики могут пересекаться:

• График

  y = — | x | + 2

Моя Т-диаграмма:

… и мой график:

URL: https: // www.х

Управление настройками файлов cookie

Вы можете управлять своими предпочтениями в отношении того, как мы используем файлы cookie для сбора и использования информации, пока вы находитесь на веб-сайтах TI, изменяя статус этих категорий.

Категория	Описание	Разрешить
Аналитические и рабочие файлы cookie	Эти файлы cookie, включая файлы cookie из Google Analytics, позволяют нам распознавать и подсчитывать количество посетителей на сайтах TI и видеть, как посетители перемещаются по нашим сайтам. Это помогает нам улучшить работу сайтов TI (например, облегчая вам поиск информации на сайте).
Рекламные и маркетинговые файлы cookie	Эти файлы cookie позволяют размещать рекламу на основе интересов на сайтах TI и сторонних веб-сайтах с использованием информации, которую вы предоставляете нам при взаимодействии с нашими сайтами. Объявления на основе интересов отображаются для вас на основе файлов cookie, связанных с вашими действиями в Интернете, такими как просмотр продуктов на наших сайтах.Мы также можем передавать эту информацию третьим лицам для этих целей. Эти файлы cookie помогают нам адаптировать рекламные объявления в соответствии с вашими интересами, управлять частотой, с которой вы видите рекламу, и понимать эффективность нашей рекламы.
Функциональные файлы cookie	Эти файлы cookie помогают идентифицировать вас и хранить ваши действия и информацию об учетной записи, чтобы предоставлять расширенные функциональные возможности, в том числе более персонализированный и актуальный опыт на наших сайтах. Если вы не разрешите использование этих файлов cookie, некоторые или все функции и услуги сайта могут работать некорректно. Если вы не разрешите использование этих файлов cookie, некоторые или все функции и услуги сайта могут работать некорректно.
Файлы cookie социальных сетей	Эти файлы cookie позволяют идентифицировать пользователей и контент, подключенный к онлайн-социальным сетям, таким как Facebook, Twitter и другим платформам социальных сетей, и помогают TI улучшить охват социальных сетей.
Строго необходимо	Эти файлы cookie необходимы для работы сайтов TI или для выполнения ваших запросов (например, для отслеживания того, какие товары вы поместили в корзину на сайте TI.com, для доступа к защищенным областям сайта TI или для управления настроенными вами настройки файлов cookie).	Всегда на связи

Графики объектов Python — объект 3.

objgraph — это модуль, который позволяет визуально исследовать графы объектов Python.

Вам понадобится graphviz, если вы хотите рисовать красивые графики.

Я рекомендую xdot для интерактивного использования. pip install xdot должно хватить; objgraph автоматически найдет его в вашем PATH .

Быстрый старт

Попробуйте это в оболочке Python:

 >>> x = []
>>> y = [x, [x], dict (x = x)]
>>> импортировать объект
>>> объект.show_refs ([y], filename = 'sample-graph.png')
График записан в .... точку (... узлы)
Изображение создано как sample-graph.png
 

(если вы установили xdot , опустите аргумент имени файла, чтобы получить интерактивный просмотрщик.)

Вы должны увидеть такой график:

Если вы предпочитаете обрабатывать собственный вывод файла, вы можете предоставить объект файла для выводит параметр из show_refs и show_backrefs вместо имя файла. Содержимое этого файла будет содержать источник графика в формате DOT.

Обратные ссылки

Теперь попробуйте

 >>> objgraph.show_backrefs ([x], filename = 'sample-backref-graph.png')
...
График записан в .... точку (8 узлов)
Изображение создано как sample-backref-graph.png
 

, и вы увидите

Пример утечки памяти

Первоначальная цель objgraph заключалась в том, чтобы помочь мне найти утечки памяти. Идея заключалась в том, чтобы выбрать в памяти объект, которого здесь не должно быть. посмотрите, какие ссылки поддерживают его.

Чтобы получить быстрый обзор объектов в памяти, используйте образно названный show_most_common_types () :

 >>> objgraph.show_most_common_types ()
кортеж 5224
функция 1329
wrapper_descriptor 967
дикт 790
builtin_function_or_method 658
method_descriptor 340
weakref 322
список 168
member_descriptor 167
тип 163
 

Но это ищем иголку в большом стоге сена.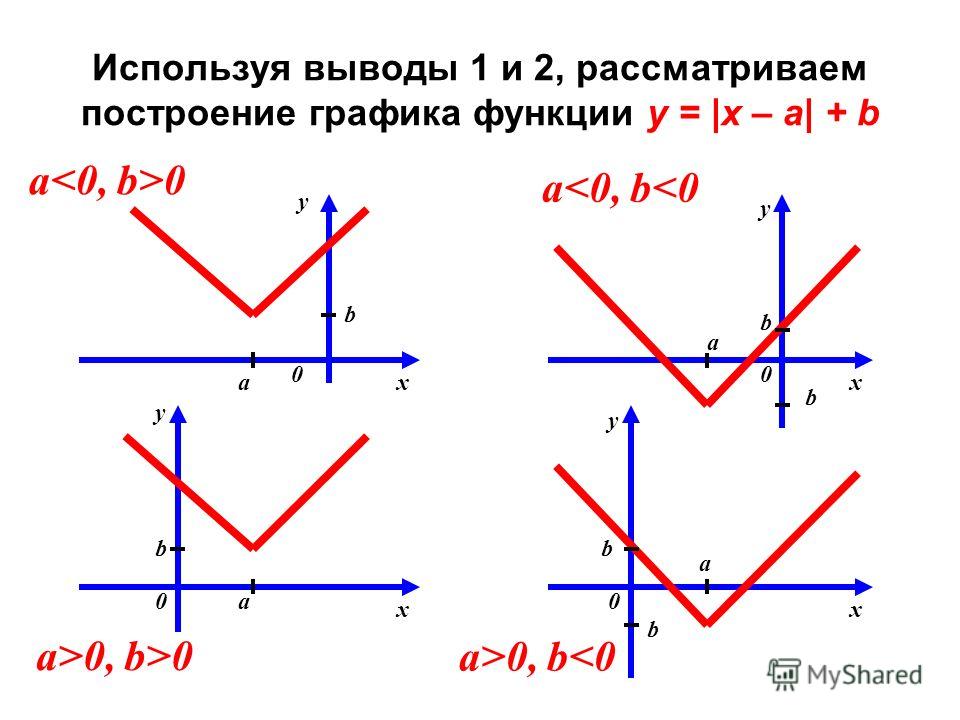 Можем ли мы ограничить наш стог сена объектам, которые были созданы недавно? Возможно.

Давайте определим функцию, которая «утекает» память

 >>> класс MyBigFatObject (объект):
...     проходить
...
>>> def computate_something (_cache = {}):
... _cache [42] = dict (foo = MyBigFatObject (),
... bar = MyBigFatObject ())
... # очень явная и легко обнаруживаемая "утечка", ну да ладно
... x = MyBigFatObject () # этот не протекает
 

Мы делаем снимок всех подсчетов объектов, которые были живы до мы вызываем нашу функцию

 >>> объект.show_growth (лимит = 3)
кортеж 5228 +5228
функция 1330 +1330
wrapper_descriptor 967 +967
 

и посмотрите, что изменится после того, как мы назовем его

 >>> computate_something ()
>>> objgraph.show_growth ()
MyBigFatObject 2 +2
дикт 797 +1
 

Легко увидеть, что появилось экземпляров MyBigFatObject, и были не освобожден. Я могу выбрать один из них наугад и проследить цепочку ссылок вернуться к одному из корней сборщика мусора.

Для простоты предположим, что все корни являются модулями. objgraph предоставляет функцию is_proper_module () для проверки этого. Если у вас есть примеры, где это неправда, я хотел бы услышать о них (хотя см. Ошибки подсчета ссылок).

 >>> импорт случайный
>>> objgraph.show_chain (
... objgraph.find_backref_chain (
... random.choice (objgraph.by_type ('MyBigFatObject')),
... objgraph.is_proper_module),
... filename = 'chain.png')
График записан в ... точку (13 узлов)
Изображение создано как chain.png
 

Возможно, удивительно найти linecache в конце этой цепочки (видимо, doctest monkey-patches it), но важные вещи — computate_something () и его словарь кеша — там.

Есть и другие инструменты, которые, возможно, лучше подходят для поиска утечек памяти: громоздкий Бульдозер.

Ошибки подсчета ссылок

Ошибки в подсчете ссылок на уровне C могут оставлять в памяти объекты, которые не на них указывают любые другие предметы. Вы можете найти их, позвонив get_leaking_objects () , но вам придется отфильтровать допустимый сборщик мусора корней от них, а всего лот из них:

 >>> корни = objgraph.get_leaking_objects ()
>>> len (корни)
4621
 

 >>> objgraph.show_most_common_types (объекты = корни)
...
кортеж 4333
дикт 171
список 74
instancemethod 4
листитератор 2
MemoryError 1
Sub 1
RuntimeError 1
Param 1
Добавить 1
 

 >>> объект.show_refs (корни [: 3], refcounts = True, filename = 'root.png')
...
График записан в ... точку (19 узлов)
Изображение создано как root.png
 

Больше примеров, которые также можно использовать как тесты

История

Я разработал набор функций, которые в конечном итоге превратились в objgraph, когда я искал утечки памяти в программе Python. Вся история — с иллюстрированные примеры — есть в этой серии сообщений блога:

А вот журнал изменений

График функции модуля

В этом уроке мы научимся строить графики таких функций, как | x — 4 |, | x + 1 |, | 2x — 1 | и т.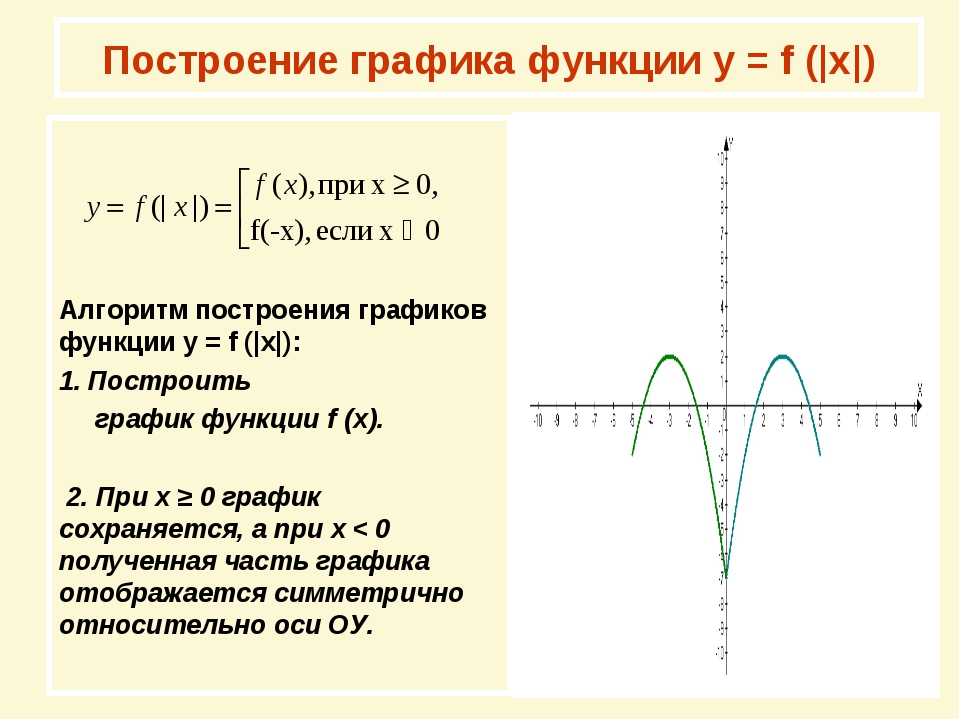 Д.

Для их построения мы снова воспользуемся определением, как и для | x |. Начнем с первого.

\ (| x — 4 | = \ left \ {\ begin {matrix}
x, & когда \ x \ ge4 \\
-x, & когда \ x <4
\ end {matrix} \ right. \)

Это означает, что для построения графика y = | x — 4 | мы должны построить график

y = x — 4, когда x ≥ 4

y = 4 — x, когда x <4

То есть для x ≥ 4 мы нарисуем линию, наклон которой равен 1, а пересечение оси y равно –4.Для x <4 мы нарисуем линию с наклоном –1 и пересечением по оси y 4.

А вот как бы выглядел график.

Это похоже на график | x |, но «сдвинут» вправо.

Попробуем второй. Вернемся к определению.

\ (| x + 1 | = \ left \ {\ begin {matrix}
x + 1, & когда \ x \ ge-1 \\
-x-1, & когда \ x <-1
\ end {matrix } \ right. \)

Это означает, что для построения графика y = | x + 1 | мы должны построить график

y = x + 1, когда x ≥ –1

y = –x — 1, когда x <–1

А вот как бы выглядел график.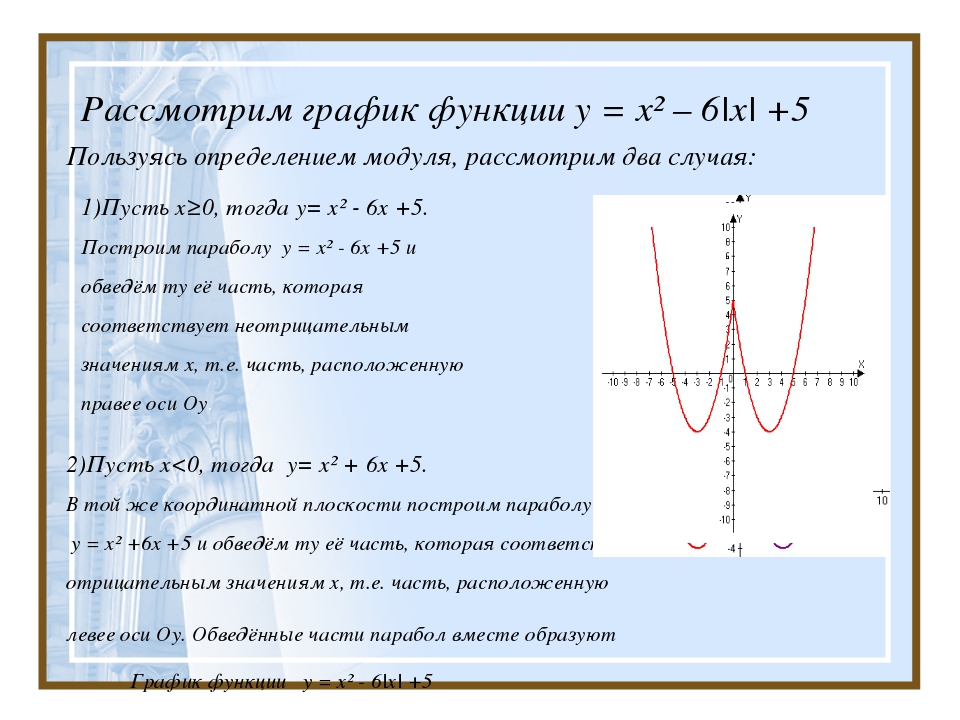

Еще раз, аналогично графику | x |, но со смещением влево.

Вы видите закономерность? Можете ли вы построить график | x — 2 | и | x + 3 |?

Вот они.

| x — 2 |

| x + 3 |

Если вы не можете понять, почему графики должны выглядеть так, попробуйте следовать определению, как в первых двух случаях.

Возьмем последний пример, | 2x — 1 |.

\ (| 2x — 1 | = \ left \ {\ begin {matrix}
2x-1, & когда \ x \ ge1 / 2 \\
-2x + 1, & когда \ x <1/2
\ end { матрица} \ right. \)

Это означает, что для построения графика y = | 2x — 1 | мы должны построить график

y = 2x — 1, когда x ≥ 1/2

y = –2x + 1, когда x <1/2

А вот как бы выглядел график.

А вот апплет, который показывает график y = | ax + b |.

Перетащите ползунки, чтобы изменить значения a и b, и посмотрите, как изменится график.На что обратить внимание

• график всегда имеет V-образную форму
• график всегда лежит выше оси X (кроме одной точки)
• крутизна «V» контролируется
• расположение вершины контролируется b (и a)

Вот и все на этом уроке.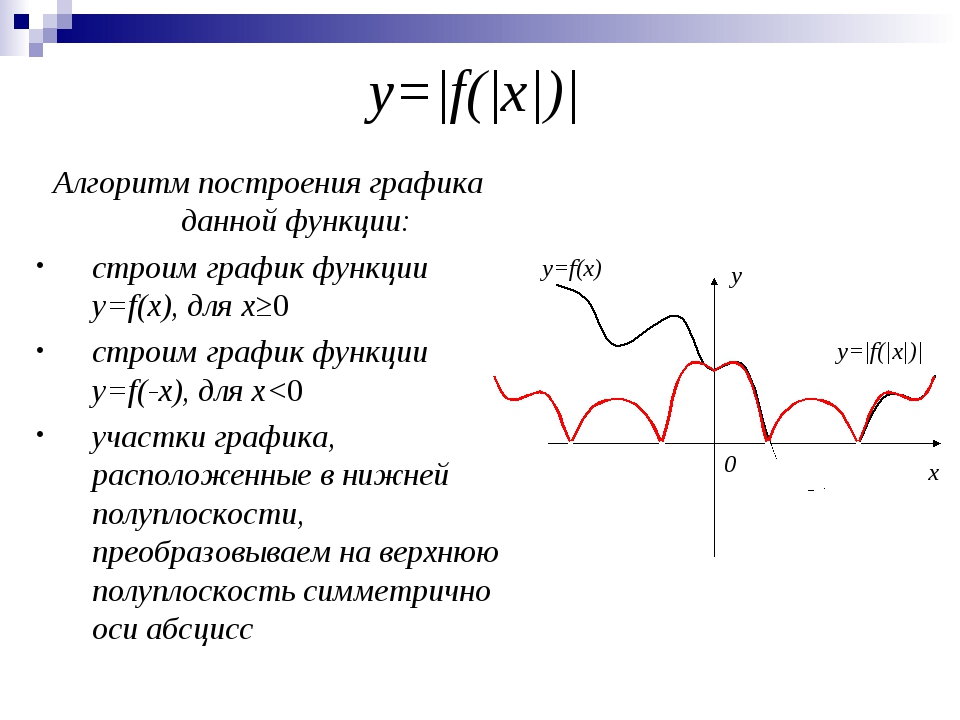 В ближайшее время мы будем использовать эти графики для решения уравнений и неравенств. Это будет весело!

графических объектов | Python | Участок

Что такое объекты графика? ¶

Фигуры, созданные, обработанные и визуализированные библиотекой Python plotly, представлены древовидными структурами данных, которые автоматически сериализуются в JSON для визуализации с помощью Plotly.js библиотека JavaScript. Эти деревья состоят из именованных узлов, называемых «атрибутами», а их структура определяется схемой рисунка Plotly.js, которая доступна в машиночитаемой форме. Модуль plotly.graph_objects (обычно импортируемый как go ) содержит автоматически сгенерированную иерархию классов Python, которые представляют нелистовые узлы в этой схеме рисунка. Термин «объекты графа» относится к экземплярам этих классов.

Основные классы, определенные в графически.Модуль graph_objects — это Figure и ipywidgets -совместимый вариант, называемый FigureWidget , которые оба представляют собой целые фигуры. Экземпляры этих классов имеют множество удобных методов для Python-манипулирования их атрибутами (например, .update_layout () или .add_trace () , которые все принимают нотацию «магического подчеркивания»), а также их рендеринга (например, .show () ) и экспорт их в различные форматы (например, .to_json () или .write_image () или .write_html () ).

Примечание: функции в Plotly Express, который является рекомендуемой точкой входа в библиотеку plotly , все построены поверх графических объектов и все возвращают экземпляры plotly.graph_objects.Figure .

Каждый атрибут фигуры, не являющийся листом, представлен экземпляром класса в иерархии plotly.graph_objects . Например, фигура fig может иметь атрибут layout.поле , которое содержит атрибуты t , l , b и r , которые являются листьями дерева: у них нет дочерних элементов. Поле в fig.layout является объектом класса plotly.graph_objects.Layout , а fig.layout.margin является объектом класса plotly.graph_objects.layout.Margin , который представляет узел поля , и он имеет поля t , l , b и r , содержащие значения соответствующих конечных узлов.Обратите внимание, что указание всех этих значений может быть выполнено без создания промежуточных объектов с использованием нотации «магического подчеркивания»: go.Figure (layout_margin = dict (t = 10, b = 10, r = 10, l = 10)) .

Объекты, содержащиеся в списке, который является значением атрибута data , называются «трассировками» и могут относиться к одному из более чем 40 возможных типов, каждый из которых имеет соответствующий класс в plotly.graph_objects . Например, трассировки типа scatter представлены экземплярами класса графически. Граф_объекты.Разброс . Это означает, что фигура, построенная как go.Figure (data = [go.Scatter (x = [1,2], y = [3,4)]), будет иметь представление JSON {"data": [{ «тип»: «разброс», «х»: [1,2], «у»: [3,4]}]} .

Графические объекты по сравнению со словарями¶

Графические объекты имеют несколько преимуществ по сравнению с простыми словарями Python:

1. Графические объекты обеспечивают точную проверку данных. Если вы укажете недопустимое имя свойства или недопустимое значение свойства в качестве ключа к объекту графика, возникнет исключение с полезным сообщением об ошибке, описывающим проблему.Это не тот случай, если вы используете простые словари и списки Python для построения ваших фигур.
2. Объекты Graph содержат описания каждого допустимого свойства в виде строк документации Python с полной справкой по API. Вы можете использовать эти строки документации в среде разработки по вашему выбору, чтобы узнать о доступных свойствах, в качестве альтернативы просмотру онлайн-полной справки.
3. К свойствам графических объектов можно получить доступ как с помощью поиска по ключу в словарном стиле (например, fig ["layout"] ), так и с помощью доступа к свойствам в стиле класса (e.грамм. рис. Макет ).
Объекты
4. Graph поддерживают вспомогательные функции более высокого уровня для обновления уже построенных фигур ( .update_layout () , .add_trace () и т. Д.).
5. Конструкторы объектов Graph и методы обновления принимают «магические символы подчеркивания» (например, go.Figure (layout_title_text = "The Title") , а не dict (layout = dict (title = dict (text = "The Title"))) ) для более компактного кода.
6. Объекты Graph поддерживают присоединенный рендеринг (.show () ) и функции экспорта ( .write_image () ), которые автоматически вызывают соответствующие функции из модуля plotly.io .

Когда использовать объекты графика напрямую¶

Рекомендуемый способ создания фигур — использование функций в модуле plotly. express, вместе известных как Plotly Express, которые все возвращают экземпляры plotly.graph_objects.Figure , поэтому каждая фигура созданный с помощью библиотеки plotly, фактически использует графические объекты под капотом, если только они не созданы вручную из словарей.

Тем не менее, некоторые виды фигур еще невозможно создать с помощью Plotly Express, например фигуры, использующие определенные типы трехмерных трасс, такие как сетка или изоповерхность . Кроме того, некоторые фигуры сложно создавать, начиная с фигуры, созданной с помощью Plotly Express, например фигуры с подзаголовками разных типов, двухосные графики или фасеточные графики с несколькими различными типами трасс. Чтобы построить такие фигуры, может быть проще начать с пустого сюжетно.graph_objects. Изобразите объект (или объект, сконфигурированный с подзаголовками с помощью функции make_subplots ()) и постепенно добавляйте трассировки и обновляйте атрибуты, как указано выше. На каждой странице документации plotly вверху отображается опция Plotly Express, если существует функция Plotly Express для создания рассматриваемого типа диаграммы, а затем версия графических объектов ниже.

Обратите внимание, что цифры, созданные Plotly Express в одном вызове функции , легко настроить во время создания и манипулировать после создания с помощью методов update_ * и add_ * .Фигуры, создаваемые Plotly Express, всегда можно построить с нуля, используя графические объекты, но этот подход обычно требует 5–100 строк кода, а не 1 строк. Вот простой пример того, как создать один и тот же объект-фигуру из одних и тех же данных, один раз с помощью Plotly Express и один раз без него. Данные в этом примере представлены в «длинной форме», но Plotly Express также принимает данные в «широкой форме», и экономия количества строк от Plotly Express по объектам графиков сопоставима. Более сложные фигуры, такие как солнечные лучи, параллельные координаты, графики фасетов или анимация, требуют гораздо большего количества строк кода графических объектов для конкретных фигур, тогда как переключение с одного представления на другое с помощью Plotly Express обычно включает изменение всего нескольких символов.

Графика: общие параметры графиков | Модули обучения Stata

В этом модуле показаны примеры различных видов графиков, которые могут быть создается с помощью команды graph twoway . Это проиллюстрировано отображением команды и получившийся граф. Для получения дополнительной информации см. Руководство по Stata Graphics доступны через Интернет и из Stata, набрав help graph и в особенно раздел о двухстороннем Диаграммы рассеяния.

  график двухстороннего разброса, чтения, записи, ///
  title («Точечная диаграмма чтения и письма»)  

  график двухстороннего разброса, чтения, записи, ///
  title ("Точечная диаграмма чтения и письма", ///
  цвет (черный) позиция (11))  

  график двухстороннего разброса, чтения, записи, ///
  title ("Точечная диаграмма чтения и письма", ///
  размер (средний) позиция (5) кольцо (0))  

  график двухстороннего разброса, чтения, записи, ///
  title ("Точечная диаграмма чтения и письма", ///
         коробка bcolor (голубой) blcolor (пурпурный) bmargin (средний))  

  график двухстороннего разброса, чтения, записи, ///
  title ("Точечная диаграмма чтения и письма" ///
  «Выборка 200 студентов», разрыв строки (3))  

  график двухстороннего разброса, чтения, записи, ///
  title ("Точечная диаграмма чтения и письма") ///
  subtitle («Выборка из 200 студентов») ///
  примечание (данные для средней школы и не только) ///
  caption (с www.ats.ucla.edu)  

  график двухстороннего разброса, чтения, записи, ///
  title ("Точечная диаграмма чтения и письма") ///
  subtitle («Выборка из 200 студентов») ///
  примечание (High School and Beyond Data, size (medium) position (5)) ///
  caption (С сайта www.ats.ucla.edu, размер (vsmall), позиция (5))  

  двухсторонний разброс, чтение, запись, ///
  ytitle (Оценка по письменному тесту) ///
  xtitle (Оценка по тесту по чтению)  

  двухсторонний разброс, чтение, запись, ///
  title ("Точечная диаграмма чтения и письма") ///
  subtitle («Выборка из 200 студентов») ///
  примечание (High School and Beyond Data, size (medium) position (5)) ///
  caption (с www.ats.ucla.edu, size (vsmall) position (5)) ///
  ytitle (Оценка по письменному тесту) ///
  xtitle (Оценка по тесту по чтению)  

  двухсторонний разброс, чтение, запись, ysize (2) xsize (4)  

  график двухсторонний разброс чтение запись, масштаб (1,5)  

  график двухстороннего разброса, чтения, записи, ///
  title ("Точечная диаграмма чтения и письма") ///
  graphregion (цвет (песок)) plotregion (fcolor (серый))  

  график двухстороннего разброса, чтения, записи, ///
  title ("Точечная диаграмма чтения и письма") ///
  graphregion (fcolor (красный) ifcolor (песок)) ///
  plotregion (fcolor (синий) ifcolor (серый))  

  график двухстороннего разброса, чтения, записи, ///
  title ("Точечная диаграмма чтения и письма") ///
  graphregion (fcolor (красный) lcolor (желтый) lwidth (толстый) ///
              ifcolor (песок) ilcolor (оранжевый) ilwidth (толстый)) ///
  plotregion (fcolor (синий) lcolor (зеленый) lwidth (толстый) ///
              ifcolor (серый) ilcolor (фиолетовый) ilwidth (толстый))  

r — Почему Shiny не отображает график в виде графика после преобразования в модульную структуру?

Хорошо, после просмотра видео Гаррета я полностью поглощен преобразованием функций моего приложения в модули.Но я понятия не имею, что происходит с этим приложением. Он работал отлично до преобразования в модули. С пользовательским интерфейсом все в порядке, с серверной тоже все в порядке, так как она не дает сбоев. Он просто ничего не показывает на выходе в Tab1. Что происходит?

callModules.R

  # МОДУЛЬ 1 UI
fotoModuleUI = function (id) {
  нс <- NS (идентификатор)
  
  tagList (
    sliderInput (ns ("fotoperiodo"), step = 0.1, post = 'horas de luz',
                    "Фотопериодо для флоры:",
                    мин = 11.0,
                    макс = 13,0,
                    значение = 12),
    
    sliderInput (ns ("широта"), шаг = 0,01, post = 'градусы',
                    "Широта:",
                    мин = -50,
                    макс = 50,
                    значение = -23),
    
    selectInput (ns ('choiceaxis'), 'Порт данных Mostrar:',
                    choices = c ('Данные', 'Цикло'), selected = 'Цикло'),
    
    actionButton (ns ('but1'), label = 'Processar'),
    
    FluidRow (
      столбец (3,
             plotlyOutput ('graph2.p ', width =' auto ', height =' auto ')) #,
      # столбец (3, textOutput ("info.graph2"))
      )
    )
  }
  
# МОДУЛЬ 1 СЕРВЕР
fotoModule = function (ввод, вывод, сеанс) {
  
  r.values ​​= reactiveValues ​​()
  
  наблюдать({
    req (input $ but1) # должен щелкнуть
    ### calcFotoperiodo () - это внешняя функция, вызываемая с помощью source () в приложении.
    mydata = calcFotoperiodo (изолировать (входная $ широта), outputForm = 'день', fotoperiodo = изолировать (входная $ fotoperiodo))
    d.period = calcFotoperiodo (изолировать (входная $ широта), outputForm = 'период', fotoperiodo = изолировать (входная $ fotoperiodo))
    
    р.values ​​$ mydata = mydata # фрейм данных
    r.values ​​$ d.period = d.period # кадр данных
    
    xaxis = реактивный (переключатель (
      input $ choiceaxis,
      Data = as.Date (r.values ​​$ mydata $ dias.ano), # vetor com dias do ano
      Ciclo = r.values ​​$ mydata $ cum # vetor com dias do ciclo
    ))
    
    r.values ​​$ xaxis = xaxis ()
    r.values ​​$ choiceaxis = input $ choiceaxis
    r.values ​​$ latitude = ввод $ широта
    r.values ​​$ fotoperiodo = input $ fotoperiodo
    r.values ​​$ floracao.I = if (input $ choiceaxis == 'Data') r.значения $ d.period $ Data.Floracao.I else r.values ​​$ d.period $ Floracao.Ti
    r.values ​​$ floracao.F = if (input $ choiceaxis == 'Data') r.values ​​$ d.period $ Data.Floracao.F else r.values ​​$ d.period $ Floracao.Tf
  })
  
  output $ graph2.p = renderPlotly ({
    req (введите $ but1)
    
    x = r.values ​​$ xaxis # vetor. vai ser uma data se input $ choiceaxis = Data, ou o dia do ciclo se for = Ciclo
    y = r.values ​​$ mydata $ duracao.dia
    
    dataplot = data.frame (x = x, y = y)
    
    range.xaxis = c (min (график данных $ x), max (график данных $ x) + 1)
    
    hoje = как.Дата (сегодня ())
    today = if (input $ choiceaxis == 'Data') hoje else r.values ​​$ mydata $ cum [which (r.values ​​$ mydata $ dias.ano == hoje)]
    
    plot_ly (график данных)%>%
      add_lines (
        х = х,
        у = у,
        name = 'Variação do Fotoperíodo',
        color = I («коричневый»)
      )%>%
      add_lines (
        х = х,
        y = r.values ​​$ fotoperiodo,
        color = I ('серый'),
        type = 'а',
        name = 'Fotoperíodo de Florção'
      )%>%
      add_lines (
        x = x [r.values ​​$ mydata $ Vegetativo == T],
        у = г.значения $ fotoperiodo,
        color = I ('зеленый'),
        type = 'а',
        name = 'Fase Vegetativa'
      )%>%
      add_lines (
        x = x [r.values ​​$ mydata $ floracao == T],
        y = r.values ​​$ fotoperiodo,
        color = I ('фиолетовый'),
        type = 'а',
        name = 'Fase replictiva'
      )%>%
      
      add_markers (
        x = r.values ​​$ floracao.I,
        y = r.values ​​$ fotoperiodo,
        name = 'Início da Floração',
        color = I ('красный'),
        символ = I ('круг-точка'),
        size = 30
      )%>%
      add_markers (
        х = р.значения $ floracao.F,
        y = r.values ​​$ fotoperiodo,
        name = 'Фим да Флорасао',
        color = I ('синий'),
        символ = I ('алмаз'),
        size = 30
      )%>%
      add_markers (
        x = сегодня,
        y = r.values ​​$ fotoperiodo,
        name = 'Hoje',
        color = I ('черный'),
        символ = I ('крест'),
        size = 30
      )%>%
      
      plotly :: layout (
        xaxis = список (
          title = if (введите $ choiceaxis == 'Data')
            'Данные'
          еще
            "Dias do ciclo",
          диапазон = диапазон.xaxis
        ),
        yaxis = list (title = "Fotoperíodo", range = c (6, 18)),
        title = paste ('Variação do Fotoperíodo na latitude', введите $ latitude)
      )%>%
      config (редактируемый = F)
  })
}

  

Прил. Р.

  # Загрузить модули ####
источник ('callModules.R')
источник ('calcFotoperiodo.R')

# UI ####
ui <- fluidPage (
  titlePanel ('Заголовок здесь'),
  жидкость = T, разборная = T,
  theme = shinythemes :: shinytheme ('супергерой'),
  tabsetPanel (
    id = 'tab1',
    ##### Вкладка 1 ####
    tabPanel (
      title = 'Анализа фотопериодо',
      fotoModuleUI ('tab1'), # вывод модуля
      div (), hr (),
      теги $ text ('ADINC.'),
      теги $ img (
        высота = 30,
        width = 30,
        src = 'leaf.png',
        смещение = 8)
    ),
    ##### Вкладка 2 ####
      tabPanel (
        title = 'Анализа Климатика',
        fotoModuleUI ('tab2') # вывод модуля
        )
    ),
  )

# СЕРВЕР ####

server <- функция (ввод, вывод, сеанс) {
  # Вкладка 1
  callModule (fotoModule, 'tab1')
}

# Запускаем приложение
shinyApp (пользовательский интерфейс = пользовательский интерфейс, сервер = сервер)
  

Информация о сеансе

R версия 4.0.2 (22.06.2020) Платформа: x86_64-w64-mingw32 / x64 (64-разрядная) Работает под: Windows 10 x64 (сборка 17134)