Показательные неравенства — как решать? Примеры, методы решения и свойства
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение показательных неравенств
Показательными считаются неравенства, которые включают в себя показательную функцию. Другими словами, это неравенства с переменной в показателе степени: af(x) > ag(x), af(x) < ag(x). Из них показательно-степенными неравенствами являются те, в которых есть переменные и в показателе степени, и в основании. |
Для изучения этой темы стоит повторить:
И, конечно, для решения тригонометрических и логарифмических показательных неравенств также придется вспомнить формулы соответствующих разделов алгебры.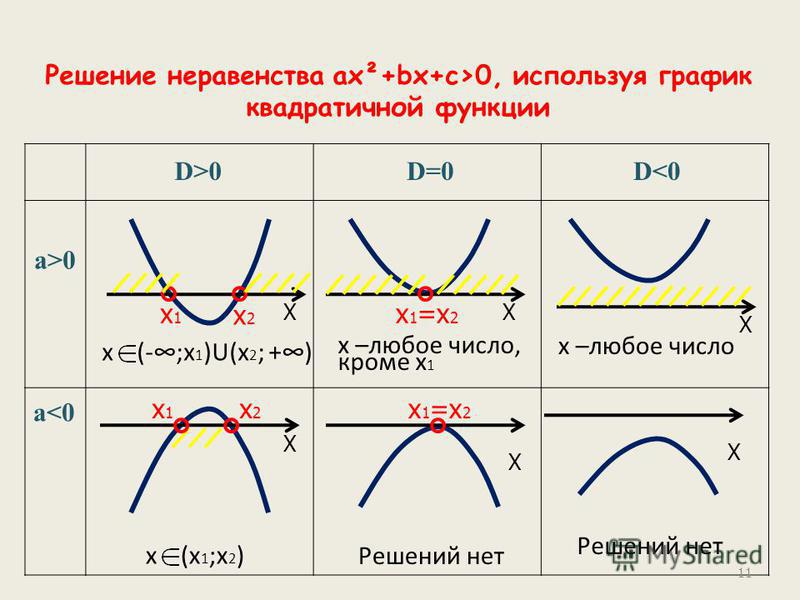
Если все это еще свежо в памяти, давайте приступим. Как и к показательным уравнениям, к неравенствам стоит подходить, помня о свойствах показательной функции. Напомним, что она выглядит так: y = ax, где a > 0 и a ≠ 1. Два графика ниже дают представление о том, на что похожа такая функция, когда основание степени а больше и меньше единицы. Наверняка вы уже догадались, каково главное свойство этой функции. Да, она монотонна.
При этом заметьте — значения а всегда больше нуля. На практике в этом несложно убедиться, если возводить какое-либо число во всевозможные степени, включая отрицательные. Например: 2-2 = 4, 2-4 = 1/16 и т. д. Значение функции будет уменьшаться, но никогда не достигнет нуля.
Для любых а и х верно неравенство ax > 0, т. е. показательная функция не принимает отрицательных значений.
Запишем следствие монотонности показательной функции в виде формул:
- af(x) > ag(x) <-> f(x) > g (x), когда функция возрастает, т.
 е. а > 1;
е. а > 1; - af(x) > ag(x) <-> f(x) < g (x), когда функция убывает, т. е. 0 < а < 1.
На этом свойстве показательных неравенств так или иначе основываются все методы решения, и сейчас мы разберемся, как им пользоваться.
Как решать показательные неравенства
Как мы уже говорили, для успешного освоения этой темы нужно хорошенько повторить все, что касается показательных уравнений. Способы решения показательных неравенств выглядят примерно так же — мы будем пытаться упростить выражение, получить одинаковые степени или одинаковые основания, по возможности свести все к квадратному или рациональному уравнению. Но есть и свои тонкости…
Допустим, у нас есть простейшее показательное неравенство:
3х > 9
Если вы помните, как решались показательные уравнения, не придется долго думать, что делать с таким неравенством — приведем его к одинаковому основанию:
3х > 32
х > 2
Казалось бы, все логично, но всегда ли можно смело вычеркивать одинаковые основания степеней? А что, если вместо 3 у нас основание степени будет 0,5? Посмотрим:
0,5х > 0,52
Проверим, верно ли в таком случае х > 2.
0,52 = 0,25;
0,53 = 0, 125 и т. д.
Как видите, на самом деле в этом случае х < 2. Неудивительно, если вспомнить, о чем мы писали в самом начале, когда рисовали графики возрастающей и убывающей показательной функции.
Если а > 1, то ax > an <-> a > n, и при решении неравенства можно просто убрать одинаковые основания степени. Если 0 < а < 1, то ax > an <-> a < n, т. е. одинаковые основания по-прежнему можно убрать, но при этом необходимо поменять знак неравенства. Если a = 1, то решений нет, т. к. единица в любой степени равна сама себе. |
Наконец, если рассмотреть случай, когда а < 0, получится неопределенность. Допустим:
(-3)х > 9
(-3)х > 32
Логичное, на первый взгляд, предположение, что х > 2, не выдержит проверки, потому что:
х = 3 -> (-3)
х = 4 -> (-3)4 = 81
х = 5 -> (-3)5 = -243
Если продолжить этот ряд, знаки будут чередоваться, и наш корень будет попеременно то меньше, то больше 2.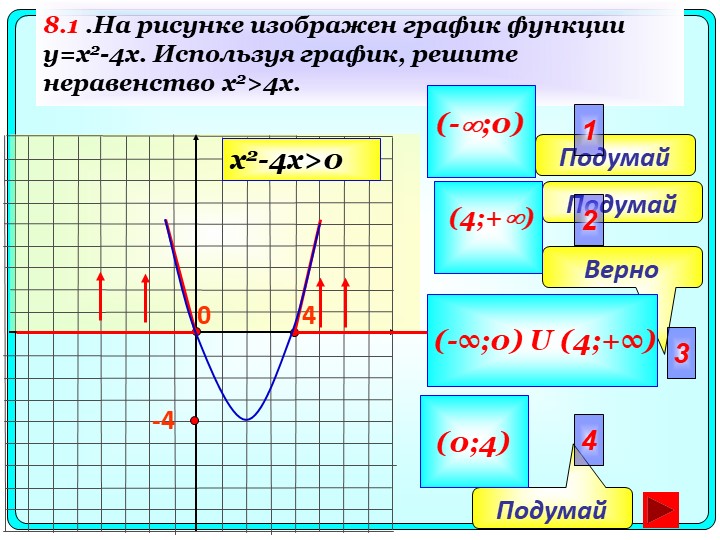 Поэтому для ясности всегда предполагается, что основание степени — положительное число.
Поэтому для ясности всегда предполагается, что основание степени — положительное число.
Это были общие правила, а сейчас рассмотрим разные виды показательных неравенств и примеры с решениями.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Показательные неравенства, сводящиеся к простейшим
Решая показательные уравнения, вы наверняка первым делом исследовали их на возможность приведения к одинаковым основаниям или одинаковым степенным функциям. Так вот, с неравенствами можно делать то же самое! Помните лишь о смене знака, если основание степени меньше единицы. И да пребудет с вами сила. 😎
Попробуем на примере несложного показательного неравенства с разными основаниями.
Пример 1
3х < 243
3х < 35
Поскольку 3 больше 1, знак не меняем:
х < 5
Ответ: х (5; +∞).
Пример 2
(1/2)х > √8
(1/2)х > 23/2
(1/2)х > (1/2)-3/2
х < -3/2, обратите внимание — мы поменяли знак, поскольку 1/2 < 1.
Ответ: х ∈ (-∞; -3/2).
Показательные неравенства, сводящиеся к квадратным
Снова давайте вспомним, как аналогичный метод применялся к показательным уравнениям. Если все переменные имели общий множитель, его можно было обозначить новой переменной — в итоге у нас, как правило, получалось квадратное уравнение. Нужно было лишь найти дискриминант и произвести обратную замену. И снова алгоритм решения показательных неравенств будет совершенно таким же.
Пример 1
9х + 27 < 12 × 3х
Наименьший общий множитель в данном случае будет 3х, обозначим его новой переменной у и перенесем все слагаемые в левую сторону.
9х + 27 < 12 × 3х
(3х)2— 12 × 3х + 27 < 0
3х = у
y2 — 12y + 27 < 0
3 < y < 9
Пришло время выполнить обратную замену.
3 < 3х < 9
31 < 3х < 32
Поскольку 3 > 1, мы не меняем знак.
1 < х < 2
Ответ: х ∈ (1;2).
Пример 2
2sin2x — 5 sinx + 2 < 0Это более сложное показательное неравенство, но и в нем можно угадать скрытое уравнение квадратичной функции — достаточно заменить sinx на новую переменную.
sinx = y
2y2— 5y + 2 < 0
y = 2
y = 1/2
1/2 < y < 2
Произведем обратную замену:
1/2 < sinx < 2
Поскольку sinx и так меньше 1, а значит, точно меньше 2, мы можем отбросить правую часть неравенства и сосредоточиться только на левой.
1/2 < sinx
Воспользуемся формулой х c (arcsina + 2πn; π — arcsina + 2πn), n ∈ z
х c (arcsin 1/2 + 2πn; π — arcsin 1/2 + 2πn), n ∈ z
х c (π/6 + 2πn; π — π/6 + 2πn), n ∈ z
х c (π/6 + 2πn; 5π/6 + 2πn), n ∈ z
Ответ: х ∈ (π/6 + 2πn; 5π/6 + 2πn), n ∈ z
Показательные неравенства, сводящиеся к рациональным
Как вы, наверное, помните из предыдущего курса алгебры, рациональные показательные неравенства — это такие, в которых левая и правая часть представляют собой дробно-рациональные функции. Метод их решения таков: нужно перенести все в левую часть, чтобы в правой остался лишь ноль, и привести к общему знаменателю. Далее решаем уравнение, отмечаем все корни на оси и применяем метод интервалов (если забыли, что это такое — повторите).
Важно помнить: если в числителе и знаменателе встретятся одинаковые множители с переменной, сокращать их нельзя.
Пример 1
Преобразуем неравенство указанным выше способом:
(обратите внимание, мы избавились от минуса в числителе и поменяли знак неравенства).
Поскольку выражение 2х + 2 в любом случае будет больше нуля, мы можем смело его исключить из неравенства.
(2х— 2) × (2х— 1/2) × (2х— 3) > 0
1/2 < 2х < 2
2х > 3
и
-1 < х < 1
х > log23
Ответ: х ∈ (-1;1) U (log23; +∞)
Пример 2
Обозначим 3х через новую переменную y:
3х = y, при условии что 3х > 0.
Применим метод интервалов и получим:
y c (1/3; 3)
Вернем на место нашу старую переменную:
3-1 < 3х <= 3
Поскольку 3 больше 1, знаки не меняем:
-1 < х <= 1
Ответ: х ∈ (-1;1).
Однородные показательные неравенства
Однородными называются такие показательные неравенства, где в каждом слагаемом сумма степеней одинакова. |
Иногда такие выражения бывают очень длинными и запутанными, но не стоит этого пугаться. Практически все неравенства с однородными показательными функциями решаются по одному принципу: стараемся упростить выражение, разделив его на одночлен, а затем при необходимости делаем замену переменных.
Пример 1
4х — 2 × 52х — 2х × 5х > 0
2 × 2х — 2 × 52х — 2х × 5х > 0
В левой части неравенства мы видим однородные функции относительно 2х и 5х. Следовательно, можно разделить обе части на 22х или 52х. Выберем 52х, т. е. 25х. В итоге у нас получится:
Если обозначить (2/5)х новой переменной y, получим квадратное неравенство:
y2— y — 2 > 0
y1 > 2
y2 < -1
Исходя из этого, у нас образуется следующее неравенство:
Поскольку 2/5 меньше 1, функция убывающая и мы должны поменять знак:
х < log2/52
Ответ: х ∈ (-∞; log2/52).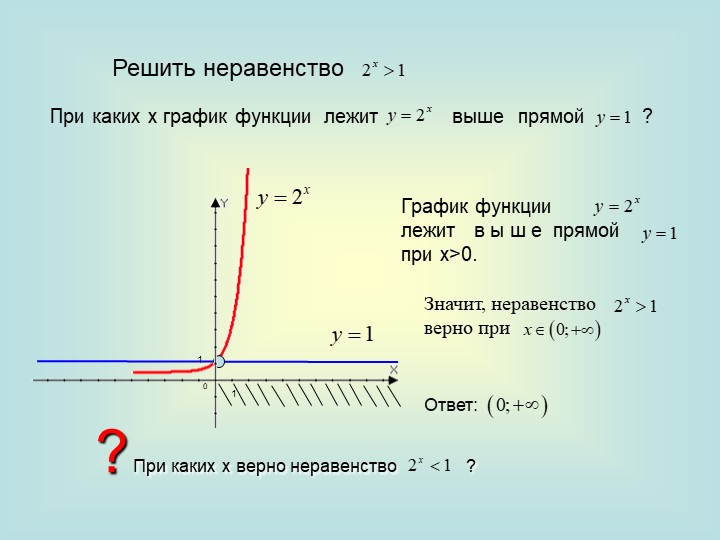
Пример 2
Но где здесь одинаковая сумма степеней? Сейчас будет:
Ответ: х ∈ (-∞; +∞) / (-2; 3)
Неравенства, решаемые графическим методом
Этот метод решения показательных неравенств — самый наглядный, и для многих он может показаться самым простым. Нужно лишь построить графики функций, заданных в левой и правой части выражения, а затем посмотреть, в какой точке они пересекаются. Если бы мы имели дело с уравнением, эта точка стала бы корнем.
Но поскольку мы рассматриваем неравенства, нужно будет выделить искомую область. Для неравенства f(x) > g(x) это будет та область, где график функции f(x) находится выше.
Пример 1
2х <= 3-х
Итак, нам нужны графики двух функций: 2х и 3 — х, а также точка их пересечения.
Очевидно, что точкой пересечения является х = 1, при этом график функции 2х ниже в области от -∞ до 1.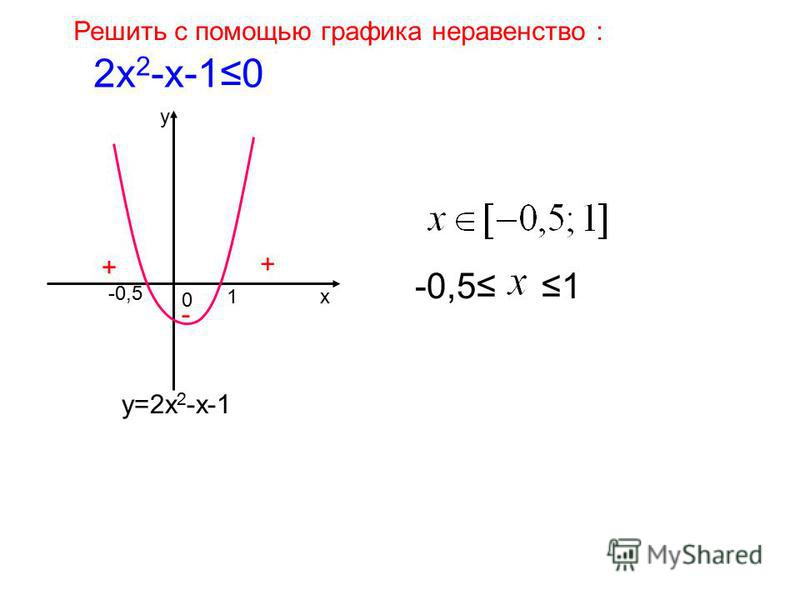
Ответ: х ∈ (-∞; 1).
Пример 2
(1/2)х > х + 3
Начертим графики этих двух функций, чтобы найти точку пересечения.
Искомой точкой будет х = -1, а областью, где функция (1/2)х находится выше — диапазон от -∞ до -1.
Ответ: х ∈ (-∞; — 1).
Решение Неравенств через Метод Интервалов
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение квадратного неравенства
Неравенство — алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.
Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.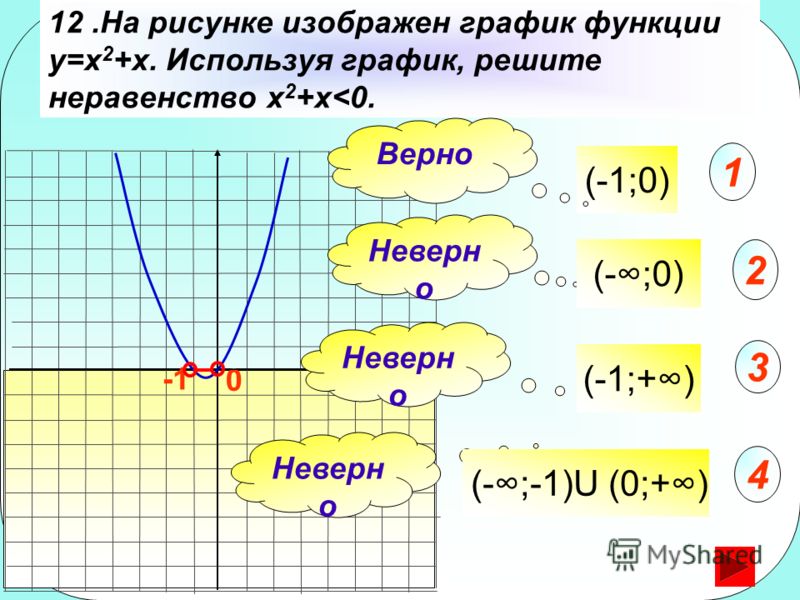 2 + bx + c меньше нуля — это числовой промежуток, где парабола лежит ниже оси ОХ.
2 + bx + c меньше нуля — это числовой промежуток, где парабола лежит ниже оси ОХ.
Если квадратное неравенство нестрогое, то корни входят в числовой промежуток. А если строгое — не входят.
Обучение на курсах по математике в онлайн-школе Skysmart сделает сложные темы понятными, а высокий балл на экзаменах — достижимым!
Решение неравенства методом интервалов
Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.
Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, <, ≤, ≥.
Сейчас мы узнаем про интервалы в контексте решения квадратных неравенств.
Интервал — это некий промежуток числовой прямой, то есть все возможные числа, заключенные между двумя числами — концами интервала. Представить эти промежутки не так просто, поэтому интервалы принято рисовать.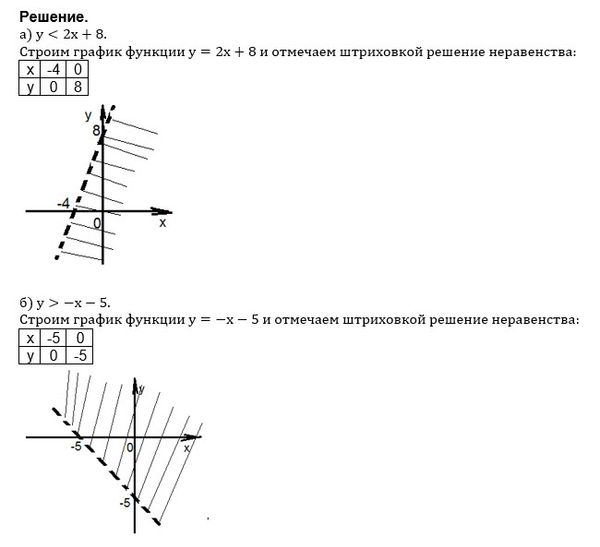 2 + bx + c из левой части квадратного неравенства.
2 + bx + c из левой части квадратного неравенства.
Если неравенство строгое, нужно отметить корни пустыми (выколотыми) точками. Если нестрогое — обычными точками. Именно эти точки разбивают координатную ось на промежутки.
Если неравенство со знаком < или ≤, то наносим штриховку над промежутками со знаком −.
В результате получаем геометрический образ некоторого числового множества — это и есть решение неравенства.
Либо вместо штриховки можно нарисовать «арки» для интервалов. Справа налево, начиная с +, проставить чередуя знаки + и −. 2 есть отрицательное число -4, и свободный член -7 тоже отрицателен.
2 есть отрицательное число -4, и свободный член -7 тоже отрицателен.
- Когда квадратный трехчлен при D > 0 имеет два корня, то знаки его значений на промежутках чередуются. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.
- Если квадратный трехчлен при D = 0 имеет один корень, то этот корень разбивает числовую ось на два промежутка, а знаки над ними будут одинаковыми. Это значит, что достаточно определить знак над одним из них и над другим поставить такой же. При этом получится, либо +, +, либо −, −.
- Когда квадратный трехчлен корней не имеет (D < 0), то знаки его значений на всей числовой прямой совпадают как со знаком старшего коэффициента a, так и со знаком свободного члена c.
Теперь мы знаем пошаговый алгоритм.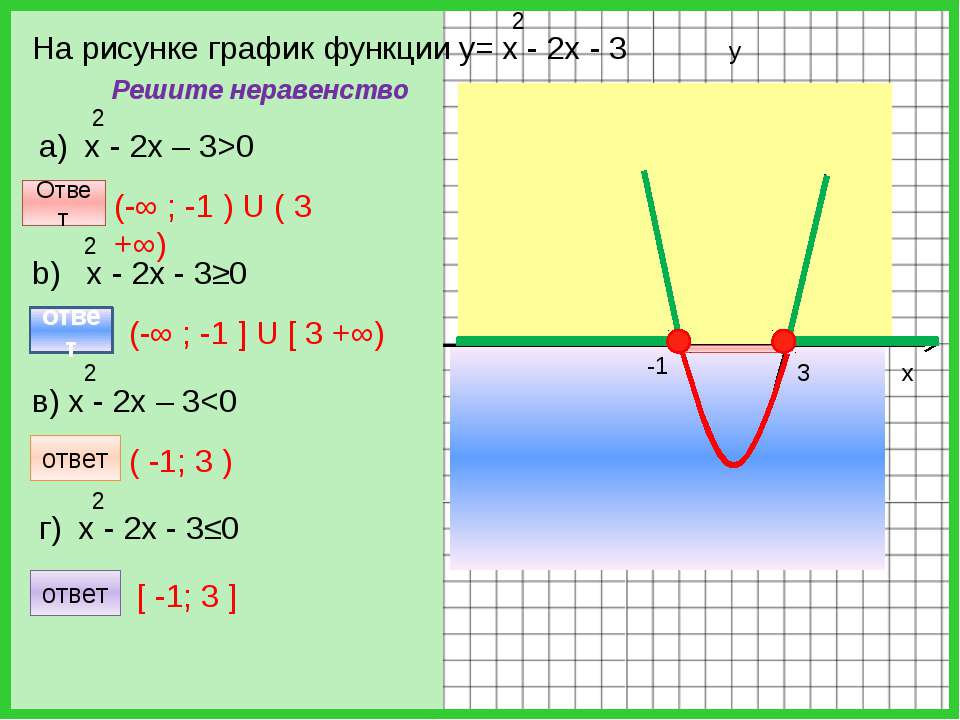 2 — 5x + 6 ≥ 0.
2 — 5x + 6 ≥ 0.
Как решаем:
- Разложим квадратный трехчлен на множители.
Неравенство примет вид:
(х — 3) * (х — 2) ≥ 0
- Проанализируем два сомножителя:
Первый: х — 3. Этот сомножитель может поменять знак при х = 3, значит при х < 0 это выражение отрицательно: х — 3 < 0, а при х > 0 принимает положительные значения: х — 3 > 0.
Второй: х — 2. Для этого сомножителя такая «знаковая» точка: х = 2.
Вывод: знак произведения (х — 3) * (х — 2) меняется только при переходе переменной через значения х = 3 и х = 2.
В этом весь смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.
- Построим чертеж.
- Рассмотрим интервалы в том же порядке, как пишем и читаем: слева направо.
х < 0 — на этом интервале ситуация не изменяется, значит, для того, чтобы определить ситуацию, можно взять любое значение из этого интервала и подставить его в произведение.
 Например: х = -1. Подставляем:
Например: х = -1. Подставляем:(-1 — 3) * (-1 — 2) = -4 * (-3) = 12
12 > 0
Вывод: при х < 0 верно неравенство (х — 3) * (х — 2) > 0.
Отобразим эти данные на чертеже:
2 < x < 3 — на этом интервале ситуация не меняется, значит, для того, чтобы определить ситуацию нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 2,5.
Подставляем:
- (2,5 — 3) (2,5 — 2) = -0,5 * 0,5 = — 0,25 < 0
Вывод: при 2 < x < 3 верно неравенство (х — 3) * (х — 2) < 0. Отметим на чертеже:
х > 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.
Подставляем:
- (25 — 3) (25 — 2) = 22*23 = 506 > 0
Вывод: при х > 3 верно неравенство (х — 3) * (х — 2) > 0. Внесем эти данные в чертеж.
- Исходное неравенство: (х — 3) * (х — 2) ≥ 0.

Если (х — 3) * (х — 2) > 0:
(x — 3) * (x + 3/2) > 0.
Если (х — 3) (х — 2) = 0 — при х1 = 3, х2 = 2.
Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.
Ответ: х ≤ 0, х ≥ 3.
Пример 2. Применить метод интервалов для решения неравенства х2+4х+3 < 0.
Как решить неравенство методом интервалов нам уже известно. Поэтому можем оформить решение кратко:
Ответ: -3 < x < -2.
Пример 3. Выполнить решение квадратного неравенства методом интервалов:
Как решаем:
- Находим корни квадратного трехчлена, который находится в левой части:
- Так как мы решаем строгое неравенство, то на координатной прямой изображаем выколотую точку с координатой 7:
- Теперь определим знаки на двух полученных промежутках (−∞, 7) и (7, +∞).
Это легко сделать, потому что дискриминант квадратного трехчлена равен нулю, а старший коэффициент со знаком минус.
 2-x-3<0
2-x-3<0тож самое.ищем корни
D=1-4*4*(-3)=49
Х1 и х2=1+ или — корень из 49 все делим на 2
х1=(1-7)\2=-3
х2=(1+7)\2=4
раскладываем на множители:4(х+3)(х-4)<0
отмечаем на числовой прямой числа -3 и 4
Ответ:(-3;4)
Дан график функции
y=x²-4x
Используя график, решите неравенство x²>4x
Решение: x² > 4x
x² — 4x > 0
Значит нас интересуют такие значения х, при которых функция положительна.
Смотрим на график, данная функция положительна на двух интервалах:
( — бесконечность; 0 ) и ( 4 ; + бесконечность)ОТВЕТ:
( — бесконечность; 0 ) V ( 4 ; + бесконечность) ,На рисунке изображен график функции
y= x² — x — 6
Используя график, решите неравенство
x² — x — 6 > 0
Решение: Если решать это задание, используя график, то решением неравенства будет та часть параболы, где ветви параболы выше оси OX. 2
2
Решение: Решение ниже в приложении, где из рисунка видно, что
Ответе:
$$ 0Построим график уравнения .
Видим, что координатная плоскость оказалась разбита на 2 области, внутри ромба и вне его. Видим, что, например, точка (3,-1) принадлежит внутренней области.
 Подставим ее координаты в неравенство.
Убеждаемся, что неравенство в данной
точке выполнено. Значит, все точки этой
области удовлетворяют неравенству.
Для проверки подставим и точку из
внешней области в неравенство. Например,
это точка (0, 8). При данных значениях
переменных неравенство обращается в
неверное числовое неравенство, а,
значит, никакая точка из внешней области
не удовлетворяет неравенству. Окончательно
получаем, что решением неравенства
является «внутренность» ромба .
Показываем это штриховкой.
Подставим ее координаты в неравенство.
Убеждаемся, что неравенство в данной
точке выполнено. Значит, все точки этой
области удовлетворяют неравенству.
Для проверки подставим и точку из
внешней области в неравенство. Например,
это точка (0, 8). При данных значениях
переменных неравенство обращается в
неверное числовое неравенство, а,
значит, никакая точка из внешней области
не удовлетворяет неравенству. Окончательно
получаем, что решением неравенства
является «внутренность» ромба .
Показываем это штриховкой.Теперь надо ответить на второй вопрос задачи. Проводя горизонтальные прямые при различных значениях а, видим, что данное неравенство имеет хотя бы одно решение при .
- Больше или равно → \ ge
- Меньше или равно → \ le
- Используйте пунктирную или пунктирную линию , если у вас есть символы строгого неравенства:> и <.
- Используйте сплошную линию , если у вас есть нестрогие символы неравенства, например \ ge и \ le. Эти символы имеют компонент «равно».
- Заштрихуйте верхнюю сторону границы, если у вас есть символы неравенства> или \ ge.
- Заштрихуйте нижнюю сторону границы, если у вас есть символы неравенства <или \ le.
- Выберите контрольную точку , расположенную в заштрихованной области. Точка имеет вид \ color {blue} \ left ({x, y} \ right).
- Подставьте значения \ color {blue} x и \ color {blue} y, взятые из контрольной точки, в исходное неравенство, затем упростите.
- Если неравенство оказывается верным утверждением, это означает, что ваш график неравенства абсолютно верен! В противном случае перепроверьте свою работу, потому что, возможно, вы закрасили не ту область.
- График не всегда представляет собой сплошную линию . Если символ неравенства в утверждении — либо, то линия на графике неравенства будет пунктирной, а не сплошной, чтобы указать, что точки вдоль линии не являются решениями неравенства.Однако, если символ неравенства — или, линия будет сплошной, как вы привыкли.
- Решение не просто линия, а целая область графика .
 Линии (сплошные или пунктирные) разделяют координатную плоскость на две части, вроде того, как забор разделяет участок земли. Все точки на одной стороне линии сделают неравенство истинным, а все точки на другой стороне — нет. Вы указываете область решений, слегка заштриховывая ее на своем графике.
Линии (сплошные или пунктирные) разделяют координатную плоскость на две части, вроде того, как забор разделяет участок земли. Все точки на одной стороне линии сделают неравенство истинным, а все точки на другой стороне — нет. Вы указываете область решений, слегка заштриховывая ее на своем графике. - Линейные неравенства с двумя переменными имеют бесконечно много упорядоченных парных решений, которые можно изобразить штриховкой в соответствующей половине прямоугольной координатной плоскости.
- Чтобы изобразить набор решений линейного неравенства с двумя переменными, сначала изобразите границу пунктирной или сплошной линией в зависимости от неравенства.
 Если дано строгое неравенство, используйте пунктирную линию для границы. Если дано инклюзивное неравенство, используйте сплошную линию. Затем выберите контрольную точку не на границе. Если контрольная точка устраняет неравенство, закрасьте область, которая ее содержит; в противном случае заштрихуйте противоположную сторону.
Если дано строгое неравенство, используйте пунктирную линию для границы. Если дано инклюзивное неравенство, используйте сплошную линию. Затем выберите контрольную точку не на границе. Если контрольная точка устраняет неравенство, закрасьте область, которая ее содержит; в противном случае заштрихуйте противоположную сторону. - При построении графиков наборов решений линейных неравенств рекомендуется проверять значения внутри и вне набора решений в качестве проверки.
| 1 | Оценить с использованием заданного значения | квадратный корень 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | y=x+4 | |
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень 1 | |
| 69 | Упростить | квадратный корень 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
Решение квадратных неравенств через графики
Речь идет о выражениях, где а ≠ 0 и выражение: ax2 + bx + c больше, либо меньше нуля.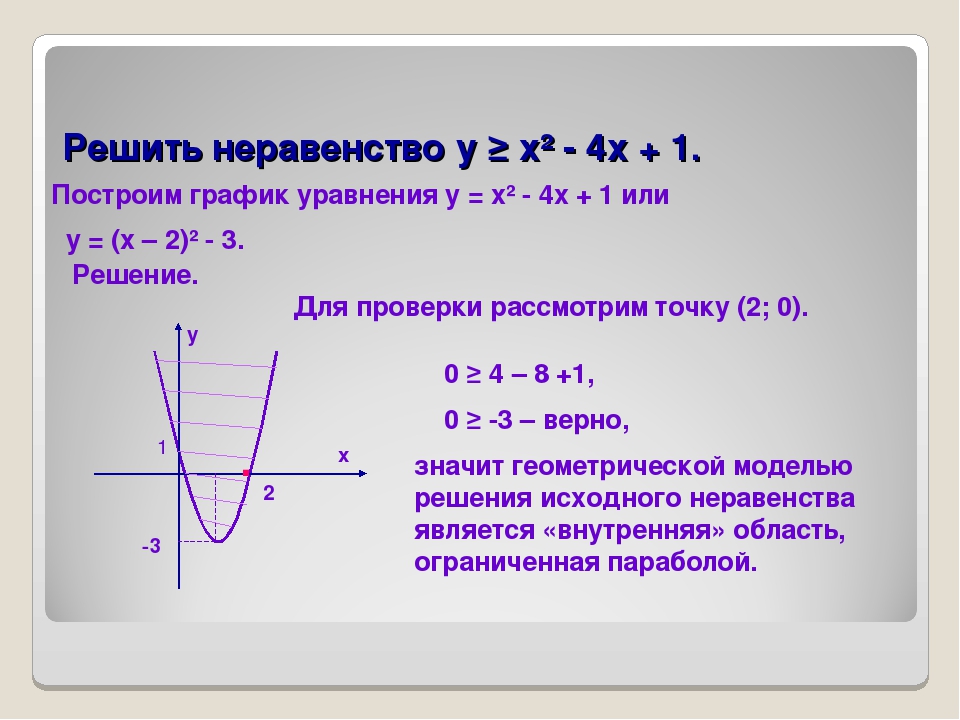
Полезный лайфхак: если «а» отрицательное, то удобнее умножить обе части неравенства на «-1», чтобы в дальнейшем проще работать с параболой, в которой ветви направлены вверх.
Пример: неравенство: x2 — 2x — 8 < 0
Найдем ось симметрии:
x = — b / 2a = — (-2) / 2*1 = 1
И определи точку вершины, подставив «x» в уравнение: 1*1 — 2*1 — 8 = -9
Соответственно, точка (1; -9) — это вершина параболы.
Т.к. a > 0 ветви направлены вверх.
Точки пересечения параболы с осью абсцисс определим через дискриминант:
D = (-2)*(-2) — 4*1*(-8) = 36
x1,2 = (2 ± 6) / 2
x1,2 = -2; 4
Можно рисовать график, причем, точно нарисовав только три точки: вершину и пересечение с абсциссой, дальнейшую красоту не так важно наводить:
Поскольку мы ищем значения y < 0, значит, на графике смотрим, что лежит ниже оси абсцисс. А это часть параболы при значениях x от -2 до 4, это и будет решением нашего неравенства.
x ∈ (-2; 4)
Обратите внимание, что мы ставим круглые скобки, так как по условиям у нас указано < , а не ≤.
Если бы у нас был наоборот знак больше, то мы бы взяли промежутки
(-∞; -2) (4; +∞) , а если знак ≥, то (-∞; -2] [4; +∞)
Для проверки вы всегда можете также подставлять в неравенство значения «x» и смотреть полученные значения.
Например, здесь, подставив 3, получаем: 32 — 2*3 — 8 < 0
9 — 6 — 8 < 0
-5 < 0 то, что нужно.
Или, подставив, 5: 52 — 2*5 — 8 < 0
25 — 10 — 8 < 0
7 < 0 и это уже неподходящее нам по условию значение.
Все квадратные неравенства можно легко решать по этой табличке графическим методом:
Если вам встречается задание с модулем x:
x2 + 2|x| — 4 < 24
То вы строите два графика:
x2 + 2*(-x) — 4 < 24
x2 + 2*(x) — 4 < 24
И смотрите все нужные точки.
youtube.com/embed/jq7G19g_5q0?rel=0&start=17″ frameborder=»0″ allowfullscreen=»»/>
Редактировать этот урок и/или добавить задание Добавить свой урок и/или заданиеДобавить интересную новость
Графики уравнений — Документ
Помощь для выполнения домашнего задания.
Графики уравнений:
1. — прямая. Соответственно, решением неравенства , является полуплоскость, лежащая ниже или выше этой прямой.
2. — гипербола, т.к. отсюда . Эта гипербола делит плоскость на 3 (!!!) области, поэтому знак неравенства надо проверять в каждой из них.
3. — «лежачая парабола», т.е. парабола, повернутая на 90 по часовой стрелке. Делит плоскость на 2 части (внутри параболы и вне ее.)
4. — окружность с центром в начале координат, радиуса R (где R>0). Решением неравенства является круг (т.е. вся область, лежащая внутри окружности, вместе с границей), а неравенства — область вне круга.
5. — при а > 0 – квадрат с вершинами в
точках (а;0), (0; а), (-а; 0), (0; -а). Соответственно,
решением неравенства
является
область внутри квадрата, а неравенства — область вне квадрата.
Соответственно,
решением неравенства
является
область внутри квадрата, а неравенства — область вне квадрата.
Преобразования графиков:
1. Чтобы построить график уравнения f(x-a; y-b)=0, надо сначала построить график уравнения f(x; y)=0, а затем сместить его на а единиц по оси Ох, и на b единиц по оси Оy.
2. Чтобы построить график уравнения , надо выполнить симметрию графика уравнения f(x; y)=0 относительно оси Оy (не забыв при этом стереть часть исходного графика, лежащую левее оси Оy).
3. Чтобы построить график уравнения , надо выполнить симметрию графика уравнения f(x; y)=0 относительно оси Ох (не забыв при этом стереть часть исходного графика, лежащую ниже оси Ох).
4. Соответственно, чтобы построить
график уравнения
,
надо сначала построить график уравнения
f(x; y)=0 (т.е.
убрать все модули) в первой четверти,
а затем выполнить симметрию этого
графика относительно всех осей.
Неравенства с двумя переменными.
Чаще всего для решения используют «метод областей». То есть сначала в неравенстве заменяют знак неравенства на знак «=» и изображают полученный график на координатной плоскости. Затем «методом пробной точки» проверяют знак неравенства в каждой из образовавшихся областей.
Кроме этого, отдельно можно рассмотреть неравенства вида и . Для их решения сначала строят график функции . Тогда решением первого неравенства будут точки, лежащие ниже этого графика, а решением второго, соответственно, точки, лежащие выше.
Можно еще выделить неравенства вида . (Знак неравенства может быть и другим). Чтобы его решить, нужно сплошной линией изобразить график уравнения и пунктирной линией — график уравнения и проверить знак неравенства в каждой получившейся области(выбрав любую точку из каждой области).
Пример 1.
№ 9.20 (г)
Изобразите
решение неравенства и определите все значения а, при которых
данное неравенство имеет хотя бы одно
решение.
Решение.
Данное неравенство равносильно следующему: .
Для этого сначала построим график уравнения .
а) В свою очередь, для построения этого графика воспользуемся правилом 4 преобразования графиков. Здесь f(x; a) = 5x + 2a . Графиком этого уравнения является прямая, пересекающая оси координат в точках (2, 0 ) и (0, 5). Т.к. мы рассматриваем случай без модулей (т.е. x и y ), то возьмем только часть этой прямой, лежащую в первой четверти.
б) чтобы построить график уравнения , выполним симметрию полученного отрезка относительно всех координатных осей и начала координат. Получим ромб с «центром» в начале координат.
б) Теперь сместим этот график на 3 единицы вправо и на 1 единицу вниз.
Получили график уравнения
Ответ: данное неравенство имеет решение при
Пример 2. Изобразить на координатной плоскости множество точек, удовлетворяющих неравенству .
Решение
1.
Построим линии, ограничивающие график
неравенства.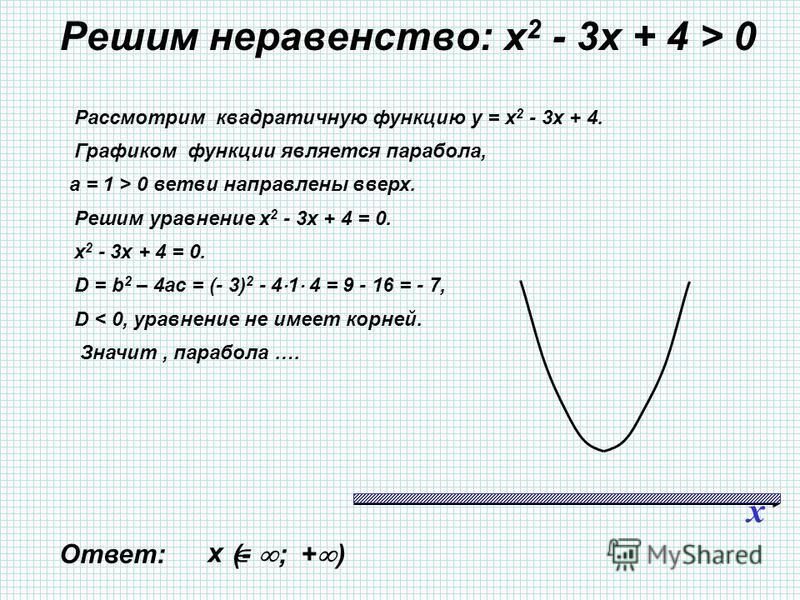 Это будут линии, которые
являются изображением множеств тех
точек, в которых числитель и знаменатель
обращаются в 0. Т.е. построим графики
уравнений
Это будут линии, которые
являются изображением множеств тех
точек, в которых числитель и знаменатель
обращаются в 0. Т.е. построим графики
уравнений
(А)
и (Б)
А) Графиком данного уравнения является окружность с центром в точке (2, -3) и радиусом, равным 4 – изображается сплошной линией, т.к. неравенство нестрогое.
Б) График этого уравнения – «лежачая парабола», опущенная на 1 единицу вниз – изображается пунктирной линией в силу область определения неравенства.
2. Пусть , . Тогда наше неравенство принимает вид .
Окружность и парабола разбивают координатную плоскость на 4 области.
Заметим, что область внутри окружности соответствует неравенству , т.е. . Область вне окружности – неравенству , т.е. .
Аналогично, область «внутри», или правее параболы соответствует неравенству или , а область «вне», или левее параболы – неравенству или .
3.
Выясним, какой знак принимает дробь в каждой из областей.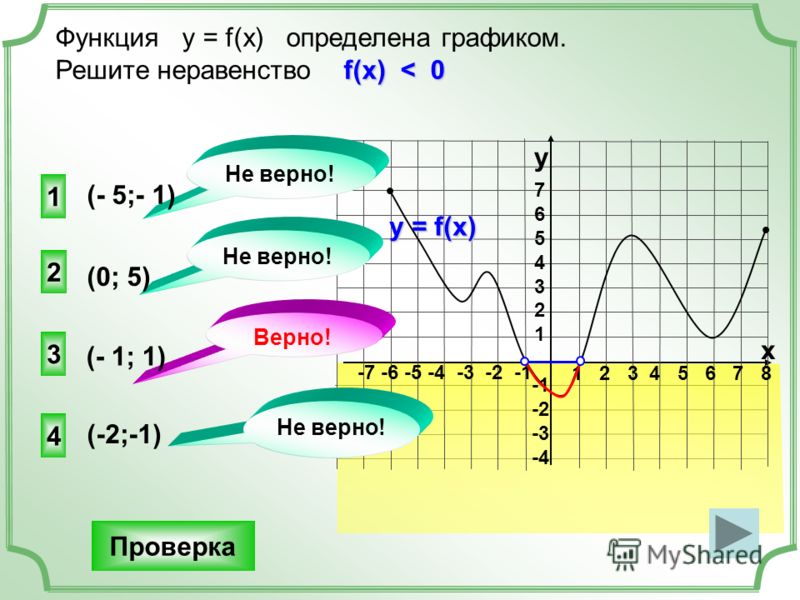
Точки, принадлежащие области I, лежат внутри параболы, но вне круга, значит, для этих точек выполняется и . Значит, для всех этих точек выполняется , и область I является решением неравенства.
В области II , но , значит, и неравенство здесь не выполняется.
В области III и , тогда . Значит, область III тоже входит в решение неравенства.
И, наконец, в области IV и , т.е. дробь неположительна и неравенство не выполнено.
Таким образом, решением неравенства является объединение областей I и III.
Уравнения и неравенства — определение и вычисление с примерами решения
Содержание:
Уравнения и неравенства
О появлении посторонних корней и потере решений уравненийВы знаете, что далеко не каждое преобразование уравнения сохраняет неизменным множество его корней. В одном случае это множество может сузиться, то есть корни будут потеряны, в другом — расшириться, то есть появятся посторонние корни.
Приведем несколько примеров.
При переходе от уравнения
Возведение обеих частей уравнения в квадрат приводит к появлению постороннего корня
Заменяя уравнение уравнением получаем посторонний корень
Метод решения уравнения, при котором данное уравнение заменяют на уравнение-следствие, а затем полученные корни подвергают проверке, называют методом следствий. Его применяют тогда, когда выполнить проверку несложно.
Однако так бывает не всегда. Например, число является корнем уравнения но чтобы в этом убедиться, надо провести довольно большую вычислительную работу.
Для подобных ситуаций возможен другой путь решения — метод равносильных преобразований. С этим методом вы ознакомились в 10 классе.
Подчеркнем, что, применяя как метод следствий, так и метод равносильных преобразований, важно знать причины потери корней и появления посторонних корней. Рассмотрим некоторые из этих причин.
Изменение области определения уравнения
Вне области определения уравнения корней нет (рис.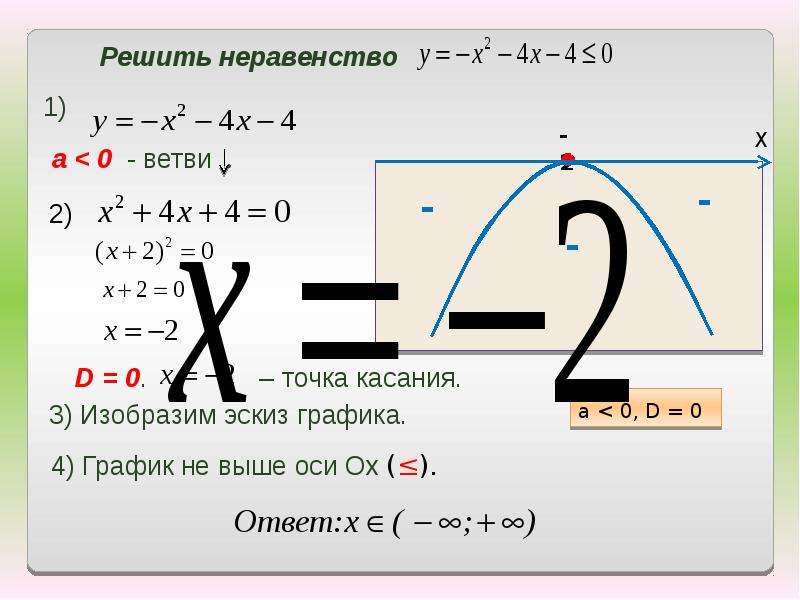 32.1). Поэтому преобразование уравнения, при котором расширяется область его определения, может привести к появлению посторонних корней.
32.1). Поэтому преобразование уравнения, при котором расширяется область его определения, может привести к появлению посторонних корней.
Например, областью определения уравнения является множество Пользуясь определением логарифма, получаем уравнение , областью определения которого является множество Расширение области определения исходного уравнения привело к появлению постороннего корня
Пример:
Решите уравнение
Решение:
Если дробь в левой части данного уравнения сократить на то получим уравнение При таком преобразовании область определения исходного уравнения расширяется на множество чисел, которые являются корнями уравнения Поэтому на самом деле данное в условии уравнение равносильно системе
Найдем корни уравнения системы. Имеем:
Поскольку то получаем Отсюда Осталось заметить, что при значение выражения отлично от нуля.
Ответ:
Если расширение области определения уравнения может привести к появлению посторонних корней, то ее сужение — возможная причина потери корней.
Например, областью определения уравнения является множество а областью определения уравнения является множество Множество содержит корень первого уравнения. Поэтому при переходе от уравнения к уравнению этот корень потерян.
Часто причиной изменения множества корней уравнения является применение равенств, правая и левая части которых имеют разные области определения.
Приведем примеры таких равенств:
В каждом из этих равенств область определения выражения, стоящего в правой части, является подмножеством области определения выражения, стоящего в левой части. Поэтому применение этих равенств слева направо может привести к потере корней, а справа налево — к появлению посторонних корней.
Пример:
Решите уравнение
Решение:
Областью определения данного уравнения является множество Очевидно, число 1 является корнем данного уравнения.
Однако применение формулы приводит к уравнению
область определения которого — множество Поэтому число 1 не является корнем полученного уравнения, то есть такой переход ведет к потере этого корня.
Решим данное уравнение методом равносильных переходов.
Данное в условии уравнение равносильно системе
Отсюда
Ответ:
Умножение обеих частей уравнения на выражение, содержащее переменнуюИногда бывает целесообразным умножить обе части уравнения на некоторое выражение. Рассмотрим последствия такого преобразования. Перейдем от уравнения
к уравнению
При таком переходе множество корней уравнения может измениться под влиянием двух факторов: области определения функции и множества корней уравнения Например, если обе части уравнения умножить
на выражение и перейти к уравнению то тем самым теряем корень Если же обе части этого уравнения умножить на то теряем корень и одновременно получаем посторонний корень
Следовательно, если при решении уравнения возникла потребность умножить обе его части на выражение то надо учитывать как область определения этого выражения, так и множество корней уравнения
Пример:
Решите уравнение
Решение:
Умножим обе части данного уравнения на выражение Поскольку то получим:
Это преобразование не изменяет области определения исходного уравнения. Появление же посторонних корней возможно за счет корней уравнения Следовательно, полученное уравнение — следствие уравнения, данного в условии.
Появление же посторонних корней возможно за счет корней уравнения Следовательно, полученное уравнение — следствие уравнения, данного в условии.
Уравнение равносильно совокупности
Решим второе уравнение совокупности. Его следствием будет уравнение Отсюда
Осталось выполнить проверку. Легко убедиться, что число 2 является корнем данного в условии уравнения, а число 0 — нет.
Ответ:
Переход от уравнения f (x) = g (x) к уравнению φ (f (x)) = φ (g (x))Переход от уравнения к уравнению
Почему уравнения
равносильны, а уравнения
не являются равносильными?
Дело в том, что свойства функции отличаются от свойств функции
Если определенная на функция обратима, то равенство выполняется тогда и только тогда, когда Поэтому в этом случае уравнения и равносильны.
Если же определенная на функция не является обратимой, то из равенства не обязательно следует, что Поэтому уравнение является следствием уравнения
Так, уравнения равносильны, потому что функция обратима. Поскольку функция не является обратимой, то уравнения не являются равносильными.
Поскольку функция не является обратимой, то уравнения не являются равносильными.
Вы знаете, что возведение обеих частей уравнения в четную степень приводит к уравнению-следствию, а возведение в нечетную степень — к равносильному уравнению.
Это связано с тем, что функция не является обратимой, а функция обратимая.
Функция обратима на множестве
В 10 классе вы пользовались этим фактом в виде такой теоремы.
Теорема 32.1. Если для любого выполняются неравенства то уравнения равносильны на множестве
Эту теорему вы использовали при решении иррациональных уравнений.
Рассмотрим пример, в котором появление постороннего корня связано с необратимостью функции
Пример:
Решите уравнение
Решение:
Поскольку определенная на функция не является обратимой, то уравнение следствие данного. Поэтому решение уравнения должно завершиться проверкой корней.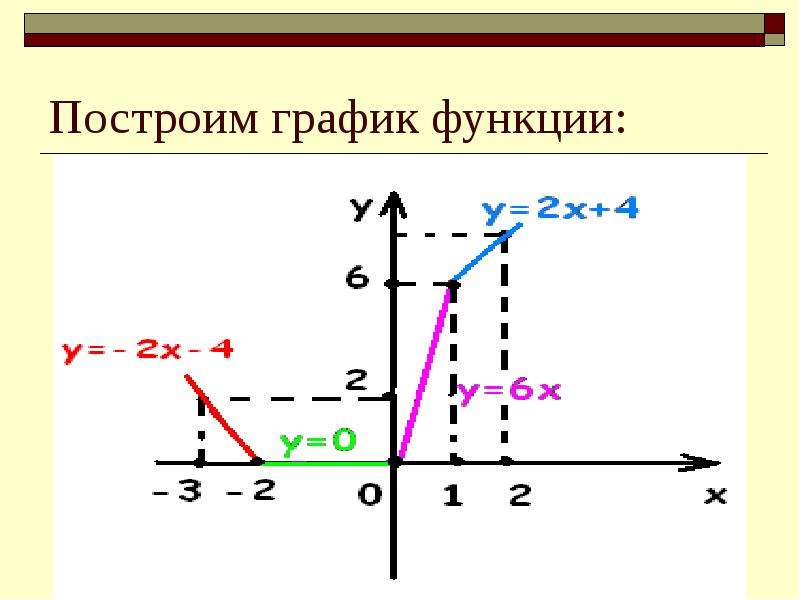 Следовательно, можно не бояться далее переходить к новым уравнениям-следствиям.
Следовательно, можно не бояться далее переходить к новым уравнениям-следствиям.
Напомним, что имеют место равенства
и Поэтому можно записать:
Ответ:
Далее имеем:
Проверим полученные корни.
При имеем:
Следовательно, число корень исходного уравнения.
При имеем:
Следовательно, число не является корнем исходного уравнения.
Ответ:
Основные методы решения уравненийВ таблице приведены схемы решения некоторых типовых уравнений.
Часто решение уравнений сводится к решению типовых уравнений, приведенных в таблице. Это иллюстрируют упражнения №№ 33.1, 33.2. К тем уравнениям, которые не сводятся к типовым, применяют специальные методы и приемы. Рассмотрим некоторые из них.
Метод разложения на множителиХорошо, если удается левую часть уравнения представить в виде произведения нескольких выражений. Как правило, этот шаг полезен, поскольку позволяет вместо данного уравнения решить совокупность более простых уравнений.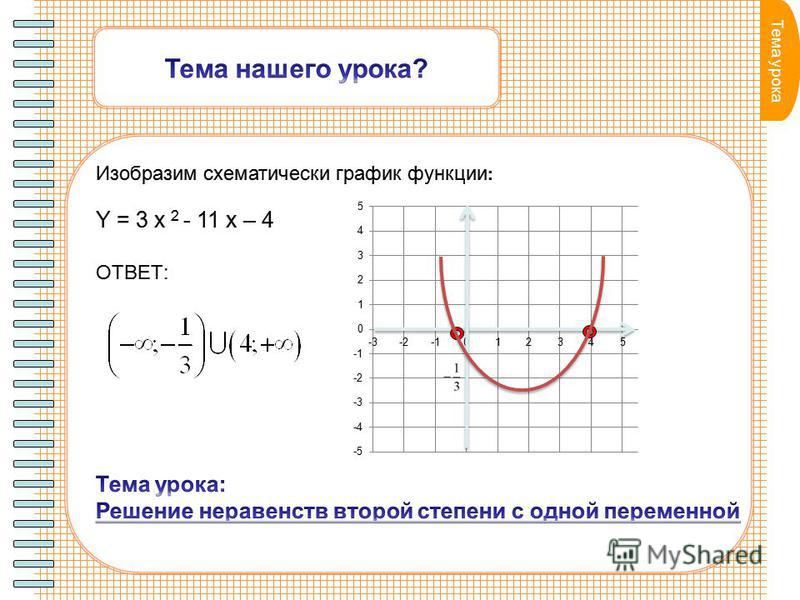
Рассмотрим примеры.
Пример:
Решите уравнение
Решение:
Очевидно, что число 1 является корнем данного уравнения. Тогда левую часть уравнения можно представить в виде произведения где квадратный трехчлен. Для нахождения разделим «уголком» многочлен на двучлен
Получили, что
Имеем:
Это уравнение равносильно совокупности
Отсюда
Ответ:
Пример:
Решите уравнение
Решение:
Имеем:
Ошибочным было бы считать, что это уравнение равносильно совокупности
Действительно, корень второго уравнения совокупности не входит в область определения исходного уравнения. На самом деле исходное уравнение равносильно системе
Отсюда
Ответ:
Метод замены переменнойПример:
Решите уравнение
Решение:
Преобразуем данное уравнение так:
Сделав замену получаем уравнение
Отсюда
Ответ:
Пример:
Решите уравнение
Решение:
Поскольку число 0 не является корнем данного уравнения, то, разделив числитель и знаменатель каждой из дробей левой части уравнения на получаем уравнение, равносильное данному:
Сделаем замену Тогда
Имеем:
Ответ:
Пример:
Решите уравнение
Решение:
Пусть Тогда
Отсюда
Исходное уравнение принимает вид
Отсюда
Получаем, что исходное уравнение равносильно совокупности
Отсюда
Поскольку то получаем
Отсюда
Пример:
Решите уравнение
Решение:
Пусть Тогда
Теперь можно записать:
Ответ:
Применение свойств функций
Поиск области определения функции может быть ключом к решению уравнения
Пример:
Решите уравнение
Решение:
Применение любых приемов, связанных с преобразованием левой части данного уравнения, вряд ли приведет к успеху.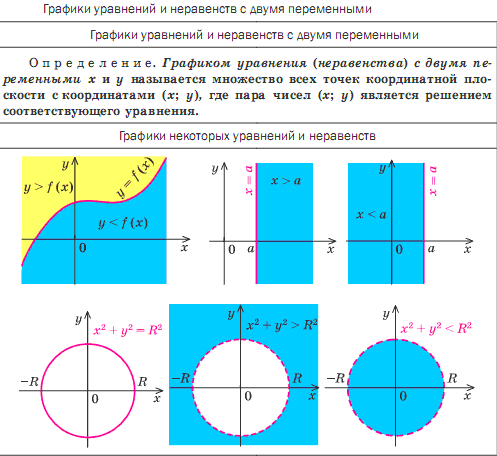 Вместе с тем нахождение области определения уравнения — путь вполне естественный.
Вместе с тем нахождение области определения уравнения — путь вполне естественный.
Имеем:
Решив эту систему, получим, что областью определения рассматриваемого уравнения является двухэлементное множество Проверка показывает, что число 1 не подходит, а число 3 является корнем исходного уравнения.
Ответ:
Пусть функции и таковы, что для любого выполняются неравенства и где некоторое число. Тогда уравнение равносильно системе
С помощью этих очевидных соображений можно решить целый ряд уравнений.
Пример:
Решите уравнение
Решение:
Поскольку
Отсюда В то же время
Поэтому исходное уравнение равносильно системе
Отсюда
Ответ:
Вы знаете, что если функция является возрастающей (убывающей), то уравнение имеет не более одного корня. Если удается корень угадать, то решение такого уравнения завершено.
Пример:
Решите уравнение
Решение:
Рассмотрим функцию
Имеем: Поскольку для любого выполняется неравенство то функция возрастает на Следовательно, уравнение имеет не более одного корня. Очевидно, что число 0 является корнем данного уравнения.
Очевидно, что число 0 является корнем данного уравнения.
Ответ:
Пример:
Решите уравнение
Решение:
Рассмотрим функцию
Легко определить, что
Каждая из функций и является возрастающей на Следовательно, функция также возрастает на
Очевидно, что число является корнем исходного уравнения. Этот корень единственный.
Ответ:
Основные методы решения неравенствВ таблице приведены схемы решения некоторых типовых неравенств.
Часто решение неравенств сводится к решению типовых неравенств, приведенных в таблице. Это иллюстрируют упражнения №№ 34.1-34.10. К тем неравенствам, которые не сводятся к типовым, применяют специальные методы и приемы. Рассмотрим некоторые из них.
Метод равносильных преобразованийПример:
Решите неравенство
Решение:
Заметим, что ошибочными являются следующие соображения: «Поскольку при выполняется неравенство то исходное неравенство равносильно системе Отсюда Несложно увидеть, что при таком «решении» теряется решение
Правильным решением данного неравенства является, например, переход к совокупности:
Решением уравнения совокупности являются числа 2 и 3, множеством решений неравенства — промежуток
Ответ:
Пример:
Решите неравенство
Решение:
Сразу возводить обе части неравенства в квадрат не является рациональным шагом, поскольку этот переход требует учитывать такое дополнительное условие:
Данное в условии неравенство целесообразно записать так:
Поскольку обе части последнего неравенства могут принимать только неотрицательные значения, то можно перейти к равносильному неравенству:
Далее получаем:
Отсюда
Ответ:
Метод интерваловПусть нули функции и ее точки разрыва разбивают область определения функции на некоторые промежутки (рис. 34.1). Тогда из следствия из теоремы Больцано-Коши (см. пункт 5) следует, что эти промежутки являются промежутками знакопостоянства функции. Определить знак функции на каждом из таких промежутков можно с помощью «пробных точек».
34.1). Тогда из следствия из теоремы Больцано-Коши (см. пункт 5) следует, что эти промежутки являются промежутками знакопостоянства функции. Определить знак функции на каждом из таких промежутков можно с помощью «пробных точек».
Эти соображения являются основой для решения широкого класса неравенств.
Пример:
Решите неравенство
Решение:
Рассмотрим функцию
Имеем: Найдем нули функции Для этого решим уравнение
Сделаем замену: Имеем:
Отсюда Получаем систему:
Отсюда
Эта система имеет три решения:
Теперь можно записать: Отсюда
Поскольку функция непрерывна, то ее нули, то есть числа 1, 2, 10, разбивают ее область определения на промежутки знакопостоянства:
Имеем:
Знаки функции на промежутках знакопостоянства показаны на рисунке 34.2. Ответ:
Применение свойств функцийПри решении примера 3 было использовано такое свойство функции, как непрерывность. Нередко ключом к решению могут быть и другие свойства функций: периодичность, четность (нечетность), возрастание (убывание), наибольшее и наименьшее значения функции и т. д.
Нередко ключом к решению могут быть и другие свойства функций: периодичность, четность (нечетность), возрастание (убывание), наибольшее и наименьшее значения функции и т. д.
Например, если и то множеством решений каждого из неравенств и является множество (рис. 34.3).
Еще один пример: если функция возрастает на промежутке и то множеством решений неравенства является промежуток (рис. 34.4). Рассмотрим примеры, иллюстрирующие вышесказанное.
Пример:
Решите неравенство
Решение:
Рассмотрим функцию
Имеем:
Решив уравнение получим
Сравнивая числа приходим к выводу, что
Тогда неравенство выполняется для всех
Ответ:
Пример:
Решите неравенство
Решение:
Областью определения данного неравенства является промежуток
Поскольку то
При получаем, что Тогда
Имеем: и Отсюда для всех выполняется неравенство
Ответ:
Пример:
Решите неравенство
Решение:
Рассмотрим функцию
Легко показать, что эта функция возрастает на Очевидно, что Тогда множеством решений неравенства является промежуток
Ответ:
—10клас
Графики уравнений и неравенств с двумя переменнымиПостроение графиков функции вида
Если нам известны графики функций и , то эскиз графика функции можно построить так: изобразить водной системе координат графики функций и , а потом построить искомый график по точкам, выполняя для каждого значения (из области определения функции) необходимые операции с отрезками, изображающими соответствующие ординаты и .
Аналогично можно построить и схематические графики функций
и
Пример:
Постройте график функции
Комментарий:
Построим в одной системе координат графики функций-слагаемых: и (на рисунке они показаны соответственно зеленой и синими линиями). Для каждого значения (кроме , которое не принадлежит области определения заданной функции) справа от оси прибавляем соответствующие отрезки — значения функций и (обе функции имеют одинаковые знаки), слева от оси — вычитаем (функции имеют противоположные знаки). На рисунке розовой линией изображен график функции
2. Графики уравнений и неравенств с двумя переменными
Определение: Графиком уравнения (неравенства) с двумя переменными и называется множество всех точек координатной плоскости с координатами , где пара чисел является решением соответствующего уравнения.
Графики некоторых уравнений и неравенств
3.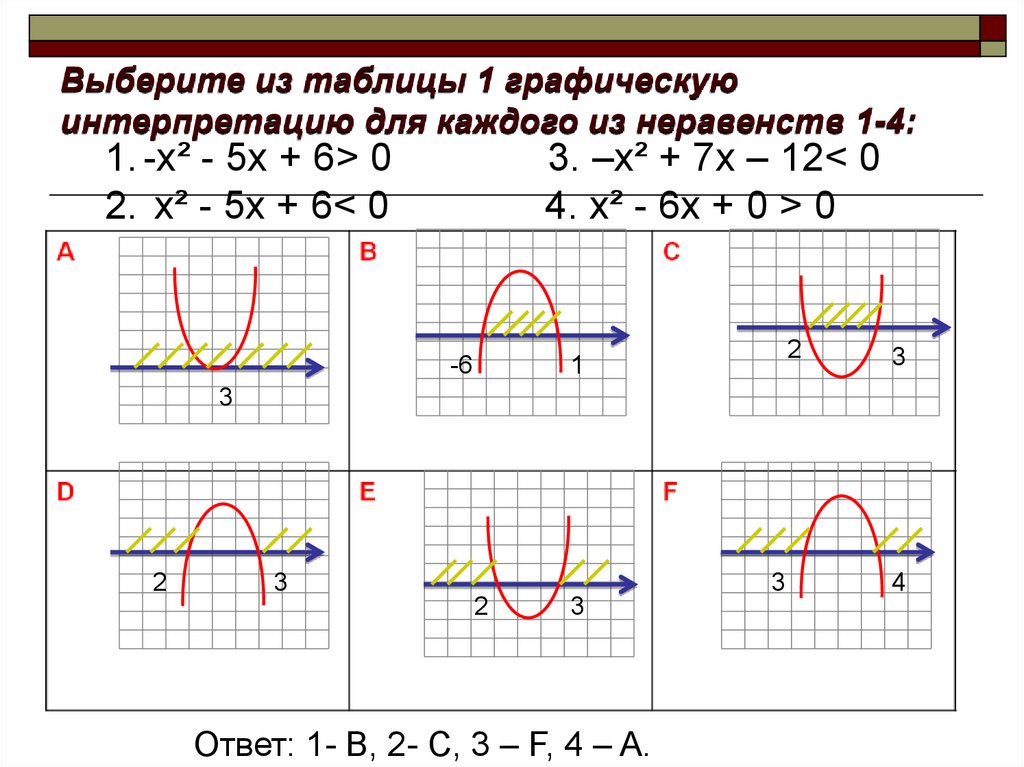 Геометрические преобразования графика уравнения
Геометрические преобразования графика уравнения
Преобразование
Параллельный перенос графика уравнения на вектор
Часть графика уравнения справа от оси (и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси .
Часть графика уравнения выше оси (и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси .
Объяснение и обоснование:
Построение графиков функции вида y=f(x)+g(x)
Построение графиков функций вида .
Если известны графики функций и , то можно построить ориентировочный вид графика функции , или , или . Для этого достаточно изобразить в одной системе координат f М
графики функций и , а потом построить искомый график по точкам, выполняя для каждого значения (из области определения заданной функции) необходимые операции над отрезками (или над длинами этих отрезков), которые изображают соответствующие ординаты функций и .
Пример построения графика функции вида приведен
в таблице 13, а графика функции вида далее в задаче 1 (в последнем случае удобно строить графики функций и не в одной системе координат, а в разных, расположенных так, чтобы их оси ординат находились на одной прямой).
Заметим, что такой способ построения графика функции не всегда дает возможность определить все характерные особенности поведения графика (часто это можно сделать только в результате специального исследования функции, которое будет рассмотрено в учебнике для 11 класса), но во многих случаях приведенный способ позволяет получить определенное представление о виде графика заданной функции.
Графики уравнений и неравенств с двумя переменнымиС понятием графика уравнения с двумя переменными вы ознакомились в курсе алгебры. Аналогично вводится и понятие графика неравенства с двумя переменными. Поэтому можно дать общее определение этих графиков:
Графиком уравнения (неравенства) с двумя переменными и называется множество всех точек координатной плоскости с координатами , где пара чисел является решением соответствующего уравнения (неравенства).
Для построения графика неравенства (или ) достаточно иметь график функции . Действительно, по определению график функции состоит из всех точек координатной плоскости с координатами . Тогда для каждого значения точки, координаты которых удовлетворяют неравенству , будут находиться выше точки (рис. 55, а), а точки, координаты которых удовлетворяют неравенству , будут находиться ниже точки (рис. 55, б). Таким образом,
график неравенства состоит из всех точек координатной плоскости, находящихся выше графика функции , а график неравенства состоит из всех точек координатной плоскости, находящихся ниже графика функции .
Например, на рисунке 56 изображен график неравенства , а на рисунке 57 — график неравенства . Поскольку точки графика не принадлежат графику неравенства , то на первом графике парабола изображена штриховой линией; а так как точки графика принадлежат графику неравенства , то на втором графике парабола изображена сплошной линией.
Аналогично, если на координатной плоскости есть прямая , то графиком неравенства будут все точки координатной плоскости, находящиеся справа от этой прямой, а графиком неравенства будут все точки координатной плоскости, находящиеся слева от этой прямой.
Например, на рисунке 58 изображен график неравенства , а на рисунке 59 — график неравенства .
Отметим, что в том случае, когда на координатной плоскости есть изображение окружности , то
графиком неравенства будут все точки координатной плоскости, находящиеся внутри окружности, а графиком неравенства будут все точки координатной плоскости, находящиеся вне окружности.
Действительно, если на координатной плоскости рассмотреть точку , то ( — начало координат). Если (где ), то , таким образом, — точка лежит на окружности радиуса с центром в начале координат (рис. 60, а). Если , то , таким образом, . То есть неравенству удовлетворяют координаты всех точек (и только этих точек), которые находятся внутри круга, ограниченного окружностью радиуса с центром в начале координат (рис. 60, б).
Если , то , таким образом, . То есть неравенству удовлетворяют координаты всех точек (и только этих точек), которые находятся вне круга, ограниченного окружностью радиуса с центром в начале координат (рис. 60, в). Аналогично, если на плоскости есть изображение окружности , то графиком неравенства будут все точки координатной плоскости, находящиеся внутри этой окружности, а графиком неравенства будут все точки координатной плоскости, находящиеся вне окружности. Например, на рисунке 61 изображен график неравенства , а на рисунке 62 — график неравенства .
60, в). Аналогично, если на плоскости есть изображение окружности , то графиком неравенства будут все точки координатной плоскости, находящиеся внутри этой окружности, а графиком неравенства будут все точки координатной плоскости, находящиеся вне окружности. Например, на рисунке 61 изображен график неравенства , а на рисунке 62 — график неравенства .
Геометрические преобразования графика уравнения
По определению график уравнения
(1)
состоит из всех точек координатной плоскости, координаты которых являются решениями этого уравнения. Это означает, что при подстановке пары чисел в данное уравнение оно обращается в верное числовое равенство, таким образом, — верное равенство.
Рассмотрим точку . Если координаты этой точки подставить в уравнение
, (2)
то получим верное равенство . Поэтому координаты точки являются решениями уравнения (2), значит, точка принадлежит графику уравнения .
Точку можно получить из точки параллельным переносом ее на вектор . Поскольку каждая точка графика уравнения получается из точки графика уравнения параллельным переносом ее на вектор (рис. 63), то и весь
график уравнения можно получить из графика уравнения параллельным переносом его на вектор .
Для обоснования связи между графиками и достаточно заметить, что при уравнение совпадает с уравнением , таким образом, совпадают и их графики справа от оси и на самой оси. Пусть точка (где ) — одна из общих точек этих графиков. Тогда — верное равенство.
Рассмотрим точку . Если координаты этой точки подставить в уравнение и учесть, что , то получим верное равенство . Поэтому координаты точки являются решениями уравнения , значит, точка принадлежит графику этого уравнения. Учитывая, что точки и симметричны относительно оси (рис. 64):
график уравнения можно получить из графика уравнения следующим образом: часть графика уравнения справа от оси (и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси .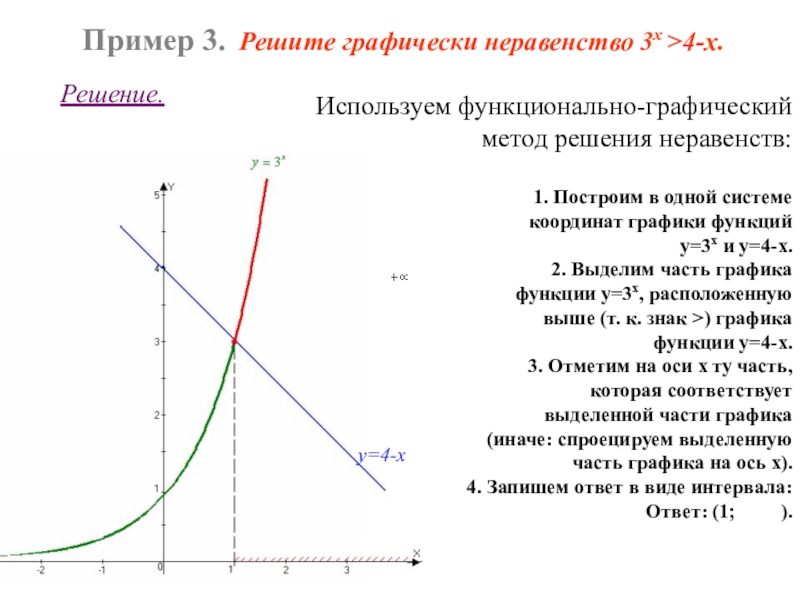
Аналогично обосновывается, что
для построения графика уравнения часть графика уравнения выше оси (и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси .
В таблице 13 приведены простейшие примеры использования геометрических преобразований графиков уравнений. Указанные соотношения приходится применять в заданиях типа: построить график уравнения или неравенства или изобразить на координатной плоскости множество точек, координаты которых удовлетворяют заданному уравнению (неравенству).
Примеры решения задач:
Пример №426Постройте график функции
Решение:
► при . Поэтому область определения заданной функции:
то есть
Комментарий:
Построим две системы координат так, чтобы оси ординат были у них на одной прямой. В тех точках, где функция равна нулю , не существует графика функции . Поэтому проведем через эти точки вертикальные прямые, которые не пересекают график функции
Поэтому проведем через эти точки вертикальные прямые, которые не пересекают график функции
Затем для каждого значения разделим 1 на соответствующее значение ординаты (используя то, что ординаты отмечены на верхнем графике). На рисунке розовой линией изображен результат — график функции . (Для построения этого графика масштаб по осям и выбран разный.)
Пример №427Покажите штриховкой на координатной плоскости множество точек, координаты которых удовлетворяют системе
Решение:
► Заданная система равносильна системе
Изобразим штриховкой графики неравенств системы (первого — вертикальной штриховкой, второго — горизонтальной):
Тогда множество точек, координаты которых удовлетворяют системе, будет таким:
Комментарий:
Перепишем заданную систему так, чтобы было удобно изображать графики данных неравенств (то есть запишем неравенства в виде или ). Множество точек, координаты которых удовлетворяют неравенству , является объединением точек параболы и точек координатной плоскости, находящихся ниже параболы (на рис. 65 это множество обозначено вертикальной штриховкой). Множество точек, координаты которых удовлетворяют неравенству , состоит из точек координатной плоскости, находящихся выше прямой (на рисунке это множество обозначено горизонтальной штриховкой).
65 это множество обозначено вертикальной штриховкой). Множество точек, координаты которых удовлетворяют неравенству , состоит из точек координатной плоскости, находящихся выше прямой (на рисунке это множество обозначено горизонтальной штриховкой).
Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, заданных каждым из неравенств данной системы (на рисунке пересечению множеств соответствует та область, где штриховки наложились одна на другую).
Заметим, что в подобных заданиях можно не выполнять промежуточных рисунков, а сразу штриховать искомое множество точек координатной плоскости (выше прямой и ниже параболы вместе с той частью параболы, которая лежит выше прямой; рис. 66).
Пример №428Постройте график уравнения .
Ориентир
Для упрощения выражения с несколькими модулями с двумя переменными можно найти нули подмодульных выражений (то есть приравнять их к нулю) и разбить область определения рассматриваемого выражения на несколько частей, в каждой из которых знаки всех модулей раскрываются однозначно.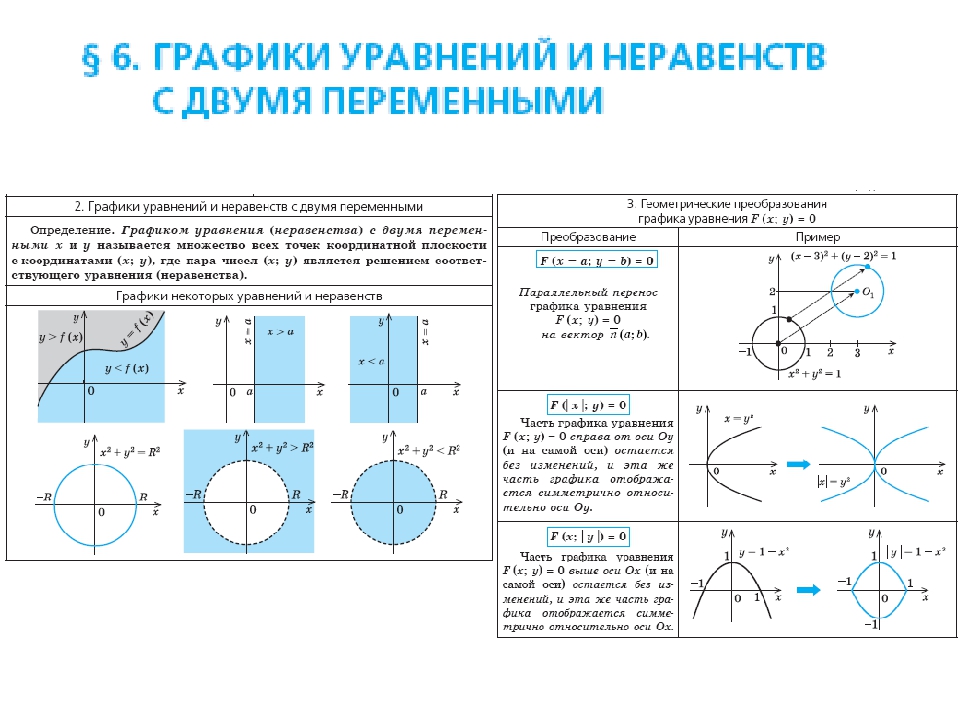
Используя этот ориентир, получаем план решения примера. Приравняем к нулю подмодульные выражения (отсюда ) и (отсюда ). Прямые и разбивают координатную плоскость на четыре области. В каждой из этих областей знак каждого модуля раскрывается однозначно, после преобразования полученного равенства строим соответствующую часть графика заданного уравнения.
Решение:
► 1. Область определения:
2. при при
3. Прямые и разбивают координатную плоскость на четыре части, в каждой из которых обозначены знаки первого и второго подмодульных выражений (рис. 67, а). (Будем считать, что каждая область берется вместе с лучами, которые ее ограничивают.) Действительно, если точки находятся в области I или на ее границе, то их координаты удовлетворяют системе неравенств которую можно записать так:
Тогда в области I первое подмодульное выражение отрицательно, а второе — положительно, поэтому данное уравнение имеет вид . Отсюда . Строим ту часть графика этой функции, которая находится в области I (рис. 67, б).
67, б).
Аналогично для точек области II: то есть
Таким образом, в области II данное уравнение имеет вид . Отсюда . Строим ту часть графика этой
функции, которая находится в области II.
Если точки находятся в области III, то то есть из данного уравнения получаем . Отсюда
Если точки находятся в области IV, то то есть из
данного уравнения имеем Отсюда
Окончательный вид графика уравнения приведен на рисунке 67, б.
Построение графиков линейных неравенств — ChiliMath
Если вы впервые изучаете, как изобразить линейное неравенство, такое как y> x + 1, вы поймете, что после прохождения этого урока все сводится к построению граничной линии (пунктирной или сплошной) и затемнению соответствующего область (верхняя или нижняя).
Итак, с чего мы начнем? Ниже приведены рекомендуемые шаги, которым вы можете следовать, чтобы сделать это правильно.
Этапы построения графиков линейных неравенств
Шаг 1: Всегда начинайте с выделения переменной \ color {red} y в левой части неравенства.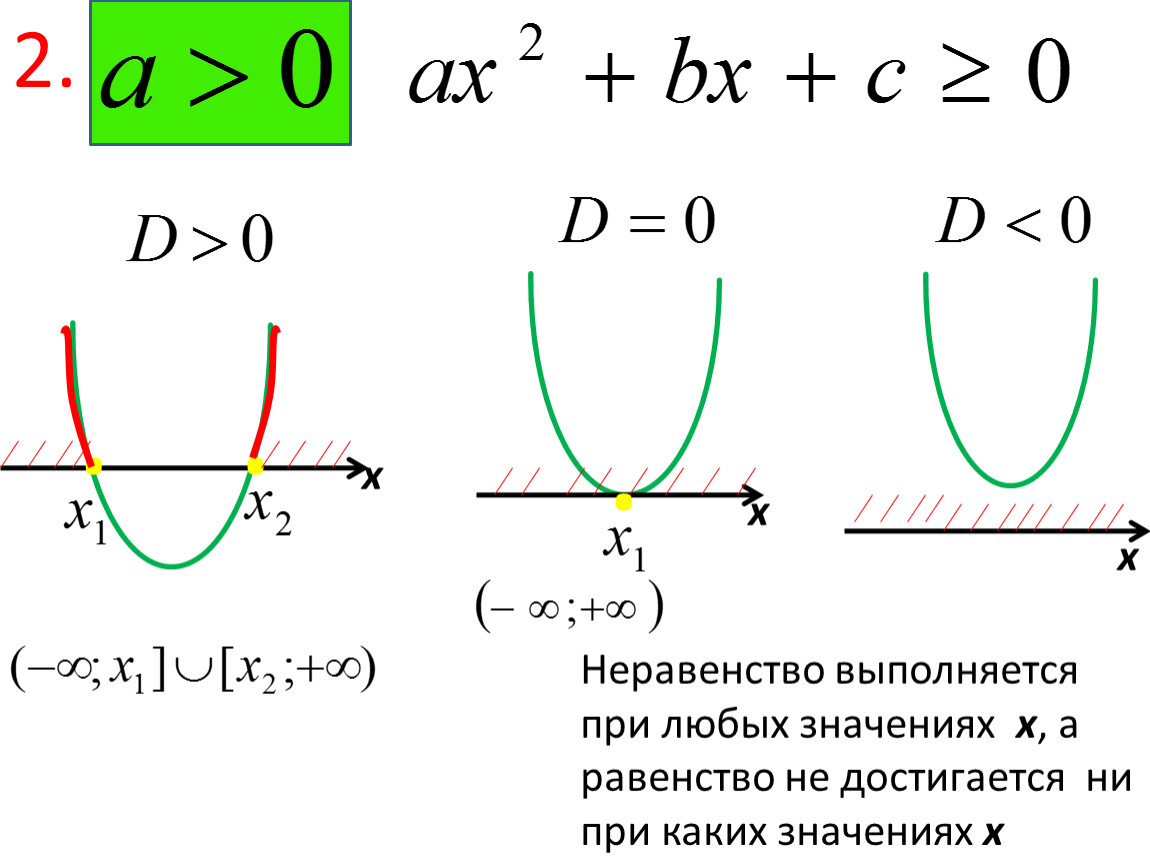
Это четыре символа неравенства:
Шаг 2: Измените неравенство на символ равенства. А пока займемся линией.
Шаг 3: Постройте граничную линию из шага 2 в плоскости XY. Ниже приведены три общих метода, которые можно использовать для построения графика линии. Неважно, какой из них вы выберете.
На этом этапе вы строите граничную линию, которая разделяет или разрезает плоскость XY на две области.
Шаг 4: Последний шаг — закрасить одну сторону или область границы.
Шаг 5: Используйте этот дополнительный шаг, чтобы проверить или убедиться, что вы правильно закрасили сторону граничной линии.
Ниже приведен график неравенства y> x + 1.
Шаг 1: Неравенство уже находится в той форме, в которой мы хотим. То есть переменная y изолирована в левой части неравенства.
То есть переменная y изолирована в левой части неравенства.
Шаг 2: Заменить неравенство на равенство. Следовательно, y> x + 1 становится y = x + 1.
Шаг 3: Теперь изобразите y = x + 1. Используйте метод, который вы предпочитаете при построении графика. Кроме того, поскольку исходное неравенство строго больше, чем символ \ Large {\ color {red}>}, мы построим граничную линию в виде пунктирной линии.
Шаг 4: Исходное неравенство y> x + 1. Символ больше означает, что мы собираемся закрасить верхнюю область или область.
Шаг 5: Чтобы проверить, правильно ли мы сделали это, давайте укажем любые точки в заштрихованной области.Предположим, мы выбрали \ color {blue} \ left ({- 3,2} \ right). Теперь подставим и оценим координаты контрольной точки исходным неравенством.
\ влево ({- 3,2} \ вправо) \ вправо x = — 3, \, \, y = 2
у> х + 1
2> -3 + 1
2> -2 ✅
Да! Мы успешно построили график неравенства \ large {\ color {green} y> x + 1}.
Вас также может заинтересовать:
Решение линейных неравенств
Графические примеры линейных неравенств
Графические системы линейных неравенств
Решение сложных неравенств
Построение графиков линейных неравенств: примеры — ChiliMath
Теперь мы готовы применить предложенные шаги для построения графика линейного неравенства из предыдущего урока.Давайте рассмотрим четыре (4) примера, охватывающих различные типы символов неравенства.
Пример 1: Изобразите линейное неравенство y> 2x-1.
Во-первых, убедитесь, что переменная y сама по себе находится слева от символа неравенства, как в данной задаче. Затем нужно построить граничную линию, на мгновение изменив символ неравенства на символ равенства.
Постройте график линии y> 2x-1 по оси xy, используя предпочитаемый вами метод.Поскольку символ неравенства просто больше, чем «>», а не больше или равно «≥», граничная линия будет пунктирной или пунктирной. Итак, вот как это должно выглядеть на данный момент.
Итак, вот как это должно выглядеть на данный момент.
Последний шаг — заштриховать либо выше, либо ниже границы. На основе предложенных шагов нам сказали заштриховать верхнюю сторону граничной линии, если у нас есть символы неравенства> (больше) или ≥ (больше или равно). Всегда помните, что «больше» означает «сверху».
Чтобы проверить правильность вашего окончательного графика неравенства, мы можем выбрать любых точек в заштрихованной области. Для этого возьмем точку (−1, 1).
Оцените значения x и y точки, входящей в неравенство, и посмотрите, верно ли утверждение. В точке (−1,1) значения x = -1 и y = 1.
Поскольку контрольная точка из заштрихованной области дает истинное утверждение после проверки с исходным неравенством, это показывает, что наш окончательный график верен!
Пример 2: Постройте линейное неравенство y \ ge -x + 2.
Переменная y находится слева. Это хорошо! Обратите внимание, у нас есть символ «больше или равно». «Равный» аспект символа говорит нам, что линия границы будет сплошной. Итак, давайте изобразим прямую y = -x + 2 в декартовой плоскости.
Это хорошо! Обратите внимание, у нас есть символ «больше или равно». «Равный» аспект символа говорит нам, что линия границы будет сплошной. Итак, давайте изобразим прямую y = -x + 2 в декартовой плоскости.
Как и в примере 1, мы закрасим верхнюю часть границы, потому что у нас случай «больше чем».
Убедитесь, что наш график правильный, выбрав точку (4,2) в заштрихованном участке, и оцените значения x и y точки в данном линейном неравенстве.
Из выбранной контрольной точки, x = 4 и y = 2
У нас есть верное утверждение, которое дает нам уверенность в правильности нашего окончательного графика неравенства.
Пример 3: Изобразите график решения линейного неравенства \ large {y <{1 \ over 2} x - 1}.
Если посмотреть на проблему, то символ неравенства — «меньше чем», а не «меньше или равно». Из-за этого график граничной линии будет прерывистым или штриховым. Кроме того, «меньше» означает, что мы закрасим область ниже линии . Вот и все!
Вот и все!
Вот график граничной линии \ large {y = {1 \ over 2} x — 1}.
Поскольку символ неравенства на меньше, чем (<), мы закрашиваем область под пунктирной линией.
Я предоставлю вам убедиться, что это правильный график, выбрав любые контрольные точки из заштрихованной области и сверив их с исходным линейным равенством.
Пример 4: Изобразите график решения линейного неравенства y \ le — {2 \ over 3} x + 2.
Поскольку мы уже рассмотрели несколько примеров, я считаю, что вы почти можете решить это в своей голове. Вы можете произвести впечатление на своего учителя, предложив такое короткое решение.
Я вижу, что символ неравенства «меньше или равен» (≤), что делает границу сплошной. Более того, решение находится ниже границы из-за его аспекта «меньше чем». Вот правильный график неравенства.
В приведенных выше примерах вы видели линейные неравенства, в которых переменные y всегда находятся слева. Вы даже можете думать о них как о линейных неравенствах в форме пересечения наклона линии.
Вы даже можете думать о них как о линейных неравенствах в форме пересечения наклона линии.
X и Y находятся на одной стороне символа неравенства
На этот раз нас интересуют примеры, в которых переменные x и y расположены по одну сторону от символа неравенства.
Мы можем назвать их линейными неравенствами в Стандартной форме . Ниже приведены четыре общих случая, когда A, B и C — это просто числа или константы.
Что нам нужно сделать, так это переписать данное неравенство или изменить его таким образом, чтобы переменная y оставалась слева.Другими словами, мы собираемся найти y через x. После этого мы можем применить предложенные шаги для построения графика линейного неравенства, как обычно.
Давайте рассмотрим несколько примеров.
Пример 5: Изобразите линейное неравенство в стандартной форме 4x + 2y <8.
Начните решение для y в неравенстве, оставив y-переменную слева, в то время как остальная часть материала перемещается в правую сторону.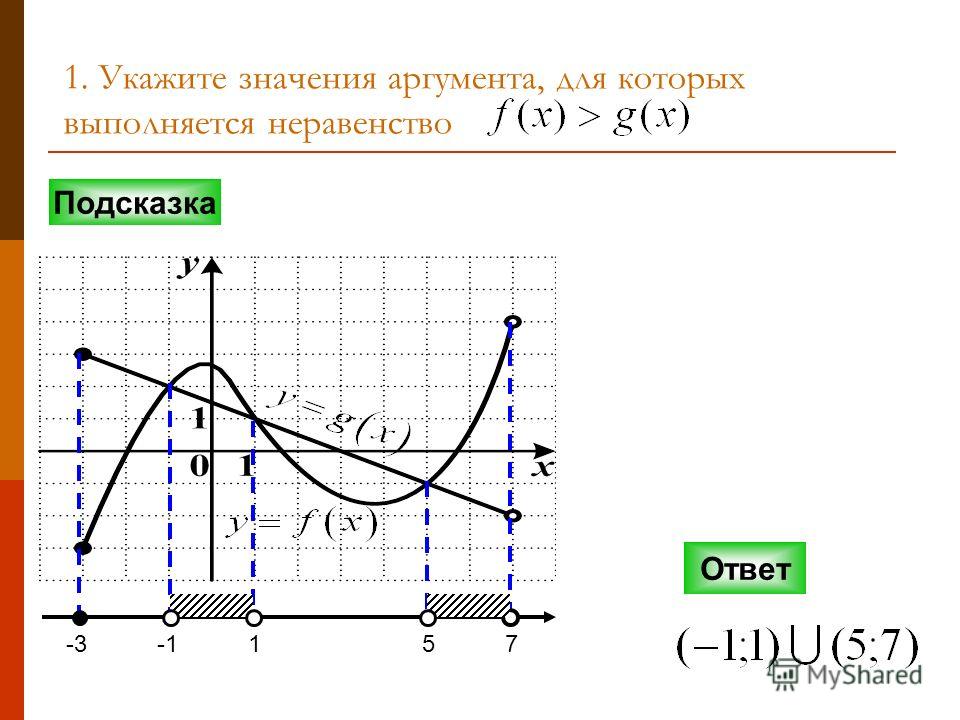 Сделайте это, вычтя обе части на 4x и разделив все неравенство на коэффициент при y, равный 4.Поскольку делим на положительное число, направление символа неравенства остается прежним.
Сделайте это, вычтя обе части на 4x и разделив все неравенство на коэффициент при y, равный 4.Поскольку делим на положительное число, направление символа неравенства остается прежним.
Поскольку у нас есть символ «меньше чем» (<) и , а не символ «меньше или равно» (≤), граничная линия будет пунктирной или пунктирной.
На всякий случай, если вы забыли, где взять граничную линию, измените на время неравенство на символ равенства, то есть с y <-2x + 4 на y = -2x + 4. Затем изобразите уравнение линии, используя любой из этих методов.
Итак, следующий очевидный шаг — решить, какую область затенять. Будет ли это выше или ниже границы? Мы закрасим нижнюю часть граничной линии, потому что у нас есть случай « меньше, чем » после того, как мы преобразовали исходную проблему неравенства в форму, в которой y находится слева.
Мы можем проверить, правильно ли мы построили график, выбрав любые контрольные точки, найденные в заштрихованной области. Лучшая контрольная точка — это исходная точка, которая является точкой (0,0), потому что ее легко вычислить.
Лучшая контрольная точка — это исходная точка, которая является точкой (0,0), потому что ее легко вычислить.
Контрольная точка (0,0) означает x = 0 и y = 0. Оцените эти значения в преобразованном неравенстве или исходном неравенстве, чтобы убедиться, что вы получили истинное утверждение.
Это действительно работает! Итак, мы заштриховали правильную область, которая находится под пунктирной линией.
Пример 6: Изобразите линейное неравенство в стандартной форме 3x — 6y \ le 12.
Чтобы переменная y оставалась слева, я бы вычел обе части на 3 x , а затем разделил все неравенство на коэффициент при y, который равен — 6 .
ПОМНИТЕ: При делении неравенства на отрицательное число мы должны изменить или переключить направление символа неравенства.
«Новое» неравенство будет иметь сплошную границу из-за символа «≥», у которого есть «равный» компонент. Кроме того, поскольку y «больше», это означает, что я закрашу область над линией.
Кроме того, поскольку y «больше», это означает, что я закрашу область над линией.
Вас также может заинтересовать:
Решение линейных неравенств
Шаги по построению графика линейных неравенств
Графические системы линейных неравенств
Решение сложных неравенств
Алгебра: построение графиков линейных неравенств
Графическое отображение линейных неравенств
Было бы здорово, если бы вы вдруг обнаружили, что у вас есть навык, о котором вы не знали? Что, если однажды, когда вы бегаете трусцой, вы обнаружите, что, немного повернув правую ногу, вы вдруг сможете свободно говорить по-португальски? (При условии, конечно, что вы раньше не говорили по-португальски.) Это действительно было бы чем-то особенным! (Возможно, даже на португальском.) Что ж, вы скоро обнаружите, что (просто слегка повернув правую ногу) вы можете построить график линейных неравенств.
Критическая точка
Пунктирная линия в линейном неравенстве представляет собой двумерный эквивалент открытого круга в основном неравенстве.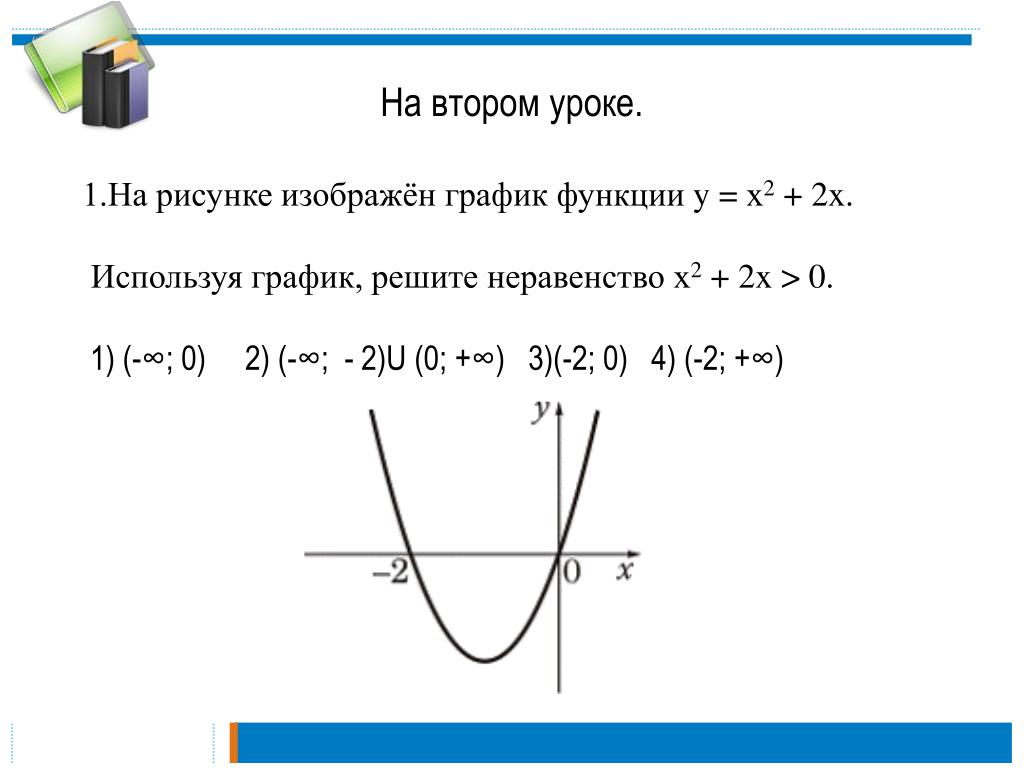 Оба означают «не включайте это значение (или пару координат) в качестве возможного решения».
Оба означают «не включайте это значение (или пару координат) в качестве возможного решения».
Разница между линейными неравенствами и неравенствами, с которыми вы имели дело до сих пор в этом разделе, заключается в том, что линейные неравенства имеют две переменные, обычно x и y .Самое замечательное в этих графиках линейного неравенства состоит в том, что они основаны на графиках линейных уравнений, которые вы уже знаете, как создавать. Однако, если вы сравните графики линейных уравнений с графиками линейных неравенств, это основные различия, которые вы увидите на графиках неравенства:
Следовательно, чтобы построить график линейного неравенства, сначала обработайте его как линию, а затем нанесите на график эту линию. (Обязательно проверьте, должна ли линия быть сплошной или пунктирной, исходя из символа неравенства.) Затем выберите координату, называемую контрольной точкой , из координатной плоскости и вставьте ее в исходное неравенство. Если это делает неравенство истинным, то будут и все другие точки на той же стороне линии, которую вы нарисовали, поэтому вы должны закрасить эту область. Если это не сработает, то область по другую сторону линии — ваше решение.
Пример 8 : Изобразите неравенство 2 x — 3 y
Решение . На мгновение представьте, что символ неравенства является знаком равенства, и изобразите полученное линейное уравнение. (Поскольку неравенство не означает «или равно», сделайте линию пунктирной, как показано на рисунке 7.7.) Самый простой способ построить график линии — это вычислить ее точки пересечения с использованием метода построения линейных уравнений.
На мгновение представьте, что символ неравенства является знаком равенства, и изобразите полученное линейное уравнение. (Поскольку неравенство не означает «или равно», сделайте линию пунктирной, как показано на рисунке 7.7.) Самый простой способ построить график линии — это вычислить ее точки пересечения с использованием метода построения линейных уравнений.
Рисунок 7.7 Это еще не окончательный график, но обратите внимание, как линия разделяет координатную плоскость на две области, обозначенные A и B для ясности.
График 2x — 3y
У вас проблемы
Задача 8: Изобразите неравенство y -2 x + 3.
Теперь вы должны выбрать контрольную точку из одного из два региона. Я обычно выбираю исходную точку, потому что что может быть проще, чем вставить 0 как для x , так и для y ? Какую бы точку вы ни выбрали, подставьте ее координату x для x в неравенство и ее координату y для y .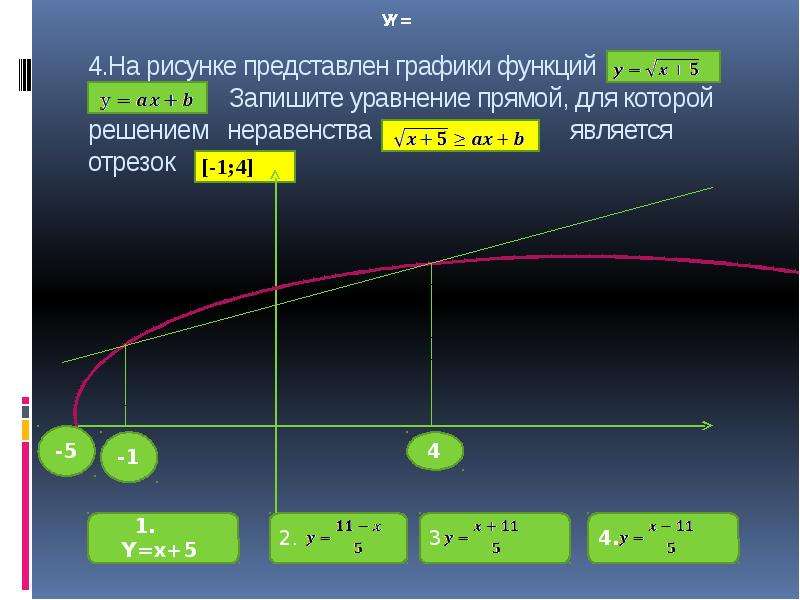 Вот как это работает для начала координат:
Вот как это работает для начала координат:
Поскольку это утверждение верно (0 действительно меньше 12), начало координат является точкой решения, как и любая другая точка в своей области плоскости (область A, в Рисунок 7.7). Итак, закрасьте эту часть графика, чтобы получить окончательный график (см. Рис. 7.8).
Выдержки из Полное руководство для идиотов по алгебре 2004 У. Майкл Келли. Все права защищены, включая право на полное или частичное воспроизведение в любой форме.Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.
Эту книгу можно приобрести на Amazon.com и Barnes & Noble.
Линейные неравенства (две переменные)
Решения линейных неравенств
Мы знаем, что линейное уравнение с двумя переменными имеет бесконечно много упорядоченных парных решений, которые на графике образуют линию. Линейное неравенство с двумя переменными Неравенство, связывающее линейные выражения с двумя переменными. Набор решений представляет собой область, определяющую половину плоскости., С другой стороны, имеет набор решений, состоящий из области, определяющей половину плоскости.
Набор решений представляет собой область, определяющую половину плоскости., С другой стороны, имеет набор решений, состоящий из области, определяющей половину плоскости.
Для неравенства линия определяет одну границу заштрихованной области. Это означает, что любая упорядоченная пара, находящаяся в заштрихованной области, включая граничную линию, будет удовлетворять неравенству. Чтобы убедиться, что это так, выберите несколько контрольных точек — точку не на границе линейного неравенства, используемую в качестве средства для определения, в какой полуплоскости лежат решения.и подставляем их в неравенство.
Также мы можем видеть, что упорядоченные пары вне заштрихованной области не решают линейное неравенство.
График решения, установленного для линейного неравенства, всегда является областью. Однако граница не всегда может быть включена в этот набор. В предыдущем примере линия была частью набора решений из-за части «или равно» в инклюзивном неравенстве ≤. Если у нас есть строгое неравенство <, мы использовали бы пунктирную линию, чтобы указать, что эти точки не включены в набор решений.
Если у нас есть строгое неравенство <, мы использовали бы пунктирную линию, чтобы указать, что эти точки не включены в набор решений.
Рассмотрим точку (0, 3) на границе; эта упорядоченная пара удовлетворяет линейному уравнению. Часть инклюзивного неравенства «или равно» делает его частью набора решений.
До сих пор мы видели примеры неравенства «меньше». Теперь рассмотрим следующие графы с такой же границей:
Учитывая приведенные выше графики, чего можно ожидать, если мы будем использовать начало координат (0, 0) в качестве контрольной точки?
Попробуй! Какая из упорядоченных пар (−2, −1), (0, 0), (−2, 8), (2, 1) и (4, 2) решает неравенство y> −12x + 2?
Ответ: (−2, 8) и (4, 2)
Графические решения линейных неравенств
Решения линейных неравенств представляют собой заштрихованную полуплоскость, ограниченную сплошной или пунктирной линией. Эта граница либо входит в решение, либо нет, в зависимости от заданного неравенства. Если нам дано строгое неравенство, мы используем пунктирную линию, чтобы указать, что граница не включена. Если нам дано инклюзивное неравенство, мы используем сплошную линию, чтобы указать, что оно включено. Шаги для построения графика набора решений для неравенства с двумя переменными описаны в следующем примере.
Эта граница либо входит в решение, либо нет, в зависимости от заданного неравенства. Если нам дано строгое неравенство, мы используем пунктирную линию, чтобы указать, что граница не включена. Если нам дано инклюзивное неравенство, мы используем сплошную линию, чтобы указать, что оно включено. Шаги для построения графика набора решений для неравенства с двумя переменными описаны в следующем примере.
Пример 1: Изобразите набор решений: y> −3x + 1.
Решение:
Шаг 1: Постройте граничную линию. В этом случае нарисуйте пунктирную линию y = −3x + 1 из-за строгого неравенства. При осмотре мы видим, что наклон равен m = −3 = −31 = riserun, а точка пересечения y равна (0, 1).
Шаг 2: Проверьте точку , а не на границе. Обычная контрольная точка — это начало координат (0, 0). Контрольная точка помогает нам определить, какую половину плоскости затенить.
Шаг 3: Закрасьте область, содержащую растворы. Поскольку контрольная точка (0, 0) не была решением, она не лежит в области, содержащей все упорядоченные парные решения. Поэтому заштрихуйте половину плоскости, на которой нет этой контрольной точки. В этом случае заштрихуйте линию выше границы.
Ответ:
Рассмотрим проблему затенения выше или ниже граничной линии, когда неравенство имеет форму пересечения уклона.Если y> mx + b, то заштрихуйте над линией. Если y Пример 2: Изобразите набор решений: 2x − 5y≥ − 10. Решение: Здесь граница определяется линией 2x − 5y = −10. Поскольку неравенство носит инклюзивный характер, обозначим границу сплошной линией. Затем проверьте точку; это помогает решить, какую область затенять. Поскольку контрольная точка находится в наборе решений, заштрихуйте половину плоскости, которая ее содержит. Ответ: В этом примере обратите внимание, что набор решений состоит из всех упорядоченных пар ниже граничной линии. Это может показаться нелогичным из-за исходного ≥ в неравенстве.Это показывает, что лучше всего проверить точку. Решите относительно и , и вы увидите, что затенение правильное. В форме пересечения откоса вы можете видеть, что область под линией границы должна быть заштрихована. Альтернативный подход состоит в том, чтобы сначала выразить границу в форме пересечения наклона, нанести ее на график, а затем заштриховать соответствующую область. Пример 3: Изобразите набор решений: y <2. Решение: Сначала изобразите граничную линию y = 2 пунктирной линией из-за строгого неравенства. Затем проверьте точку. В этом случае закрасьте область, содержащую тестовую точку. Ответ: Попробуй! Изобразите набор решений: 5x − y≤10. Ответ: Часть A: Решения линейных неравенств (две переменные) Является ли упорядоченная пара решением данного неравенства? 1. y <5x + 1; (0, 0) 2. y> −12x − 4; (0, −2) 3. y≤23x + 1; (6, 5) 4. y≥ − 13x − 5; (−3, −8) 5. y <15x − 13; (−13, −1) 6.4x − 3y≤2; (−2, −1) 7. 8. 7x − 3y <21; (5, −3) 9. y> −5; (−3, −1) 10. x≤0; (0, 7) Часть B: Графические решения линейных неравенств Изобразите набор решений. 11. y <−3x + 3 12. y <−23x + 4 13. y≥ − 12x 14. y≥45x − 8 15.у≤8x − 7 16. y> −5x + 3 17. у> −x + 4 18. у> х − 2 19. y≥ − 1 20. y <−3 21. х <2 22. x≥2 23. y≤34x − 12 24. y> −32x + 52 25. −2x + 3y> 6 26. 7x − 2y> 14 27. 5x − y <10 28.х-у <0 29. 3x − 2y≥0 30. х − 5y≤0 31. 32. −x + 2y≤3 33. 2x − 3y≥ − 1 34. 5x − 4y <−3 35. 12x − 13y <1 36. 12x − 110y≥12 37. x≥ − 2y 38. x <2y + 3 39. 3x − y + 2> 0 40. 3 − y − 2x <0 41.−4x≤12−3y 42. 5x≤ − 4y − 12 43. Напишите неравенство, описывающее все точки в верхней полуплоскости выше оси x . 44. Напишите неравенство, описывающее все точки в нижней полуплоскости ниже оси x . 45. Напишите неравенство, описывающее все точки в полуплоскости слева от оси y . 46. Напишите неравенство, описывающее все точки в полуплоскости справа от оси y . 47. Напишите неравенство, описывающее все упорядоченные пары, у которых координаты y не меньше 2. 48. Напишите неравенство, описывающее все упорядоченные пары с координатой x не более 5. 1: Есть 3: Есть 5: Есть 7: № 9: Есть 11: 13: 15: 17: 19: 21: 23: 25: 27: 29: 31: 33: 35: 37: 39: 41: 43: y> 0 45: х <0 47: y≥2 Чтобы создать вопрос с использованием неравенства, воспользуемся функцией «Площадь». Если вы не знаете, как сюда попасть, сначала прочтите страницу, посвященную общей разработке графов. Для создания графического объекта вопрос, например: Заштрихуйте область внутри круга x 2 + y 2 = 1 , что эквивалентно: x 2 + y 2 <= 1 Сначала создайте круг: Используйте две точки, чтобы сформировать круг, сначала центр, затем любую точку на краю.(Подробнее о конических графиках) Ответ необходимо определить, выбрав режим области и щелкнув любую точку внутри круга. В данном случае я выбрал точку, близкую к (0,5,0,5). Наконец, используйте «DASHED», чтобы превратить край круга в «меньше чем». Обратите внимание, что пунктирный означает не равно, а сплошной равно. В этом примере выше мы рассматриваем случай, когда меньше чем равно, но если желательно иметь строго меньше, e. , затем используйте опцию «Пунктирная», например: Мы можем проверить оценку этого вопроса, щелкнув «Режим предварительного просмотра», а затем «ПРОВЕРИТЬ ОТВЕТ»: Здесь была выбрана точка за пределами круга, что является неправильным местом для неравенства, и «ПРОВЕРИТЬ ОТВЕТ» показывает график красным цветом и оценку (0/1). Вот правильный ответ: Вы можете составлять вопросы с несколькими формами, например: Вот более сложный пример: x 2 /16 — y 2 /9 <= 1 и г> 2 Вы также можете комбинировать неравенства по функциональному режиму f x и таким объектам, как круги: Или более сложные уравнения, например.г. Обратите внимание, что студенты не имеют доступа к функции FX. Вы также можете использовать фоновые изображения и фигуры, которые будут игнорироваться при оценке: В предыдущем разделе мы увидели, как решать полиномиальные неравенства с помощью построения графиков. В этом разделе мы будем использовать аналогичные методы для решения рациональных неравенств. Рациональные неравенства включают отношения многочленов или дробей. Поскольку эти типы задач включают дроби, графики функций, с которыми мы работаем, будут иметь так называемые асимптоты.Это слово происходит от греческого корня, связанного с двумя линиями, которые очень близко подходят друг к другу, но никогда не встречаются. Вертикальные асимптоты графика появятся в тех местах, где исходное выражение имеет нулевой знаменатель. Это означает, что функция не определена для этих значений \ (x \), и поэтому вместо значения \ (y \) в этой точке график имеет асимптоту. Пример Важность асимптот при анализе рациональных функций заключается в том, что, как и корни, они представляют значения \ (x \), которые могут быть точками разделения между где \ (y> 0 \) и где \ (y <0 \) Пример Обратите внимание, что асимптота для этого графика встречается при значении \ (x = 3, \), потому что это значение \ (x \), которое создает нулевой знаменатель. Также обратите внимание, что значения \ (y \) переключаются с отрицательных на положительные по всей асимптоте. У этой функции нет корней, потому что нет значений \ (x \), делающих \ (y = 0 \). Чтобы дробь была равна нулю, числитель должен быть равен нулю. Пример Примечание. Строка контекстной справки в строке состояния дает справку, например: Примечания: Примечание. Доступ к функциям меню неравенства осуществляется с помощью сочетаний клавиш [F1] — [F5] на экране графика в версии TI-84 Plus C. Примечания: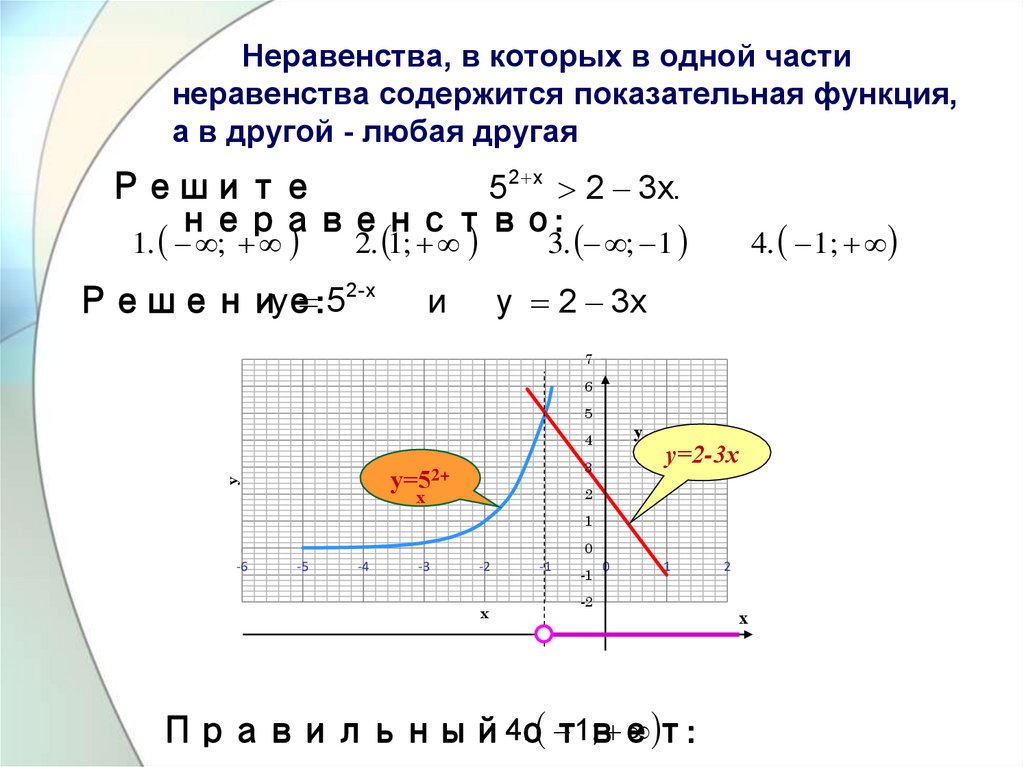 В этом случае нарисуйте граничную линию, используя точки пересечения.
В этом случае нарисуйте граничную линию, используя точки пересечения.
Основные выводы
Тематические упражнения
 −x + 4y> 7; (0, 0)
−x + 4y> 7; (0, 0) −x + 2y≤ − 4
−x + 2y≤ − 4
ответов
Графики неравенств — Справочный центр Edulastic
 См. Внизу переключателей функций:
См. Внизу переключателей функций: г. x 2 + y 2 <1
г. x 2 + y 2 <1 2.
 4: Решение рациональных неравенств с помощью построения графиков
4: Решение рациональных неравенств с помощью построения графиков
Ниже приведен график функции \ (y = \ frac {x + 2} {x-1} \)
Вместо того, чтобы иметь значение \ (y \) в точке, где \ (x = 1 \) пунктирной линией обозначена асимптота, в которой функция не определена.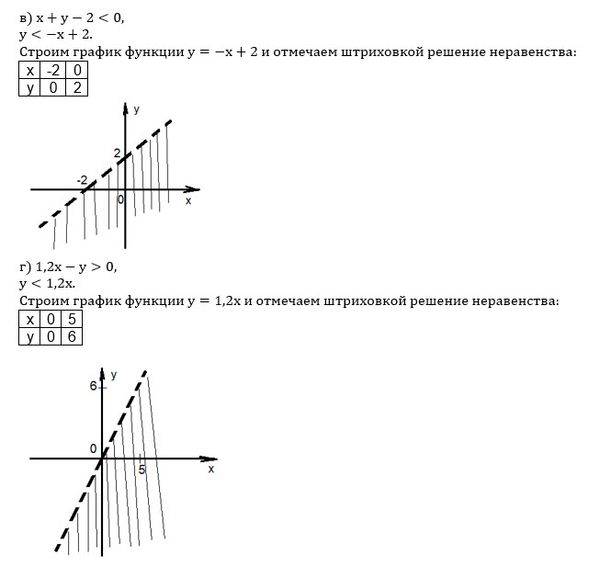 В предыдущем разделе мы были заинтересованы в поиске корней функции, потому что это те места, где \ (y = 0, \), и могут быть точками разделения между тем, где значения \ (y \) больше нуля \ ( (y> 0) \) и где значения \ (y \) меньше нуля \ ((y <0) \)
В предыдущем разделе мы были заинтересованы в поиске корней функции, потому что это те места, где \ (y = 0, \), и могут быть точками разделения между тем, где значения \ (y \) больше нуля \ ( (y> 0) \) и где значения \ (y \) меньше нуля \ ((y <0) \)
Решите указанное неравенство.
\ (\ frac {2} {x-3}> 0 \)
Сначала исследуем график:
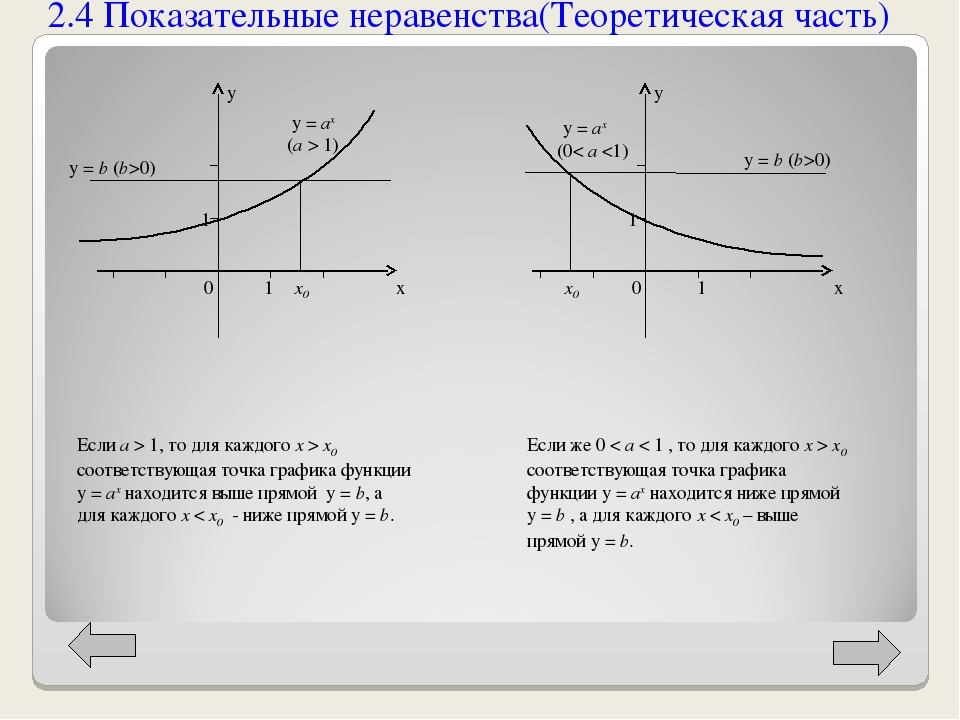 В этом примере числитель равен 2, и никакое значение \ (x \) не сделает его равным нулю.Следовательно, единственная возможная точка разделения на графике — \ (x = 3, \), а решение неравенства — \ (x> 3 \)
В этом примере числитель равен 2, и никакое значение \ (x \) не сделает его равным нулю.Следовательно, единственная возможная точка разделения на графике — \ (x = 3, \), а решение неравенства — \ (x> 3 \)
Решите указанное неравенство.
\ (\ frac {x-2} {x-3}> 0 \)
В этом неравенстве снова есть асимптота в \ (x = 3, \), но есть также корень в значении \ ( x = 2, \), потому что когда \ (x = 2. y = \ frac {2-2} {2-3} = \ frac {0} {- 1} = 0. \) Итак, у нас есть две точки разделения рассмотрим, \ (x = 2 \) и \ (x = 3. \). Из графика видно, что \ (y> 0 \) для \ (x <2 \) или \ (x> 3, \), поэтому это решение данного неравенства.{2} -2 х-3}> 0 \) Пример действия — построение графика неравенства
в) Нажмите любую клавишу, чтобы закрыть заставку. 
Курсор будет мигать над знаком = в расширенном редакторе неравенства Y =.
ВЫБРАТЬ ОТНОШЕНИЕ: | [входить].(См. Экран.) 2. Пресса | [ввод], чтобы открыть диалоговое окно стиля графика для выбора отношения. 3. 
Нажмите †, чтобы переместить курсор на Y. 4. Пресса | или ~, чтобы изменить выбор на «меньше чем.« 5. Нажмите †, чтобы выделить ОК. 6. 
Нажмите [ввод].
Примечание. Версия TI-84 Plus CE программы Inequality Graphing использует то же диалоговое окно настройки стиля графика, что и операционная система. Строка контекстной помощи в строке состояния указывает НАЖМИТЕ [<] ИЛИ [>], ЧТОБЫ ВЫБРАТЬ ОПЦИИ.
В выборе отношения версии TI-84 Plus C используются сочетания клавиш F1-F5 для изменения типа отношения. 7. Нажмите ~, чтобы переместить курсор и введите
Y 1 <2x-3.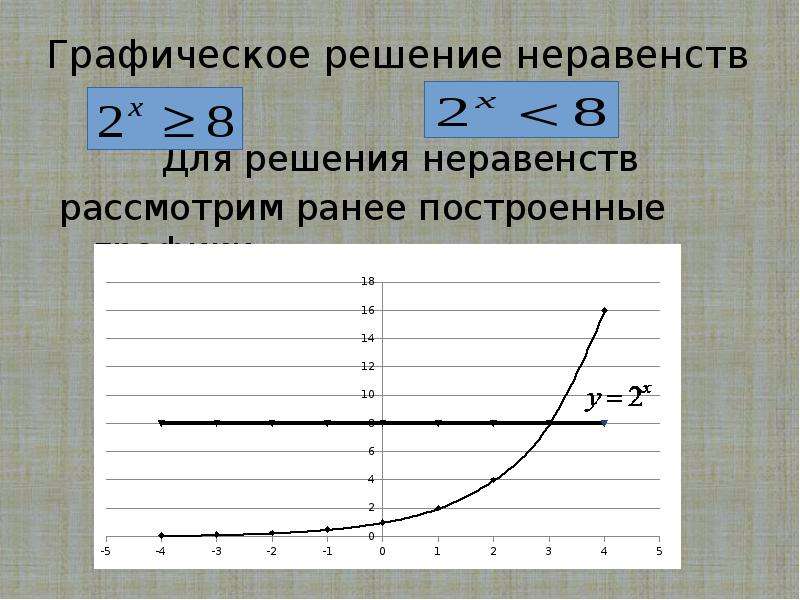
8. Повторите шаги выше, чтобы изменить отношение Y 2 на «больше чем», и введите
Y 2 > -2X + 5. 9. 
Нажмите s, чтобы просмотреть заштрихованные неравенства.
Примечание. В строке контекстной помощи строки состояния отображается МЕНЮ НЕРАВЕНСТВА: y /. Это меню содержит инструменты для пересечения неравенств и другие функции. В версии TI-84 Plus C эти инструменты отображаются в виде ярлыков [F1] — [F5] на экране графика. 10. Чтобы найти пересечение двух неравенств: б) Нажмите ~, чтобы выбрать меню НЕРАВЕНСТВО. 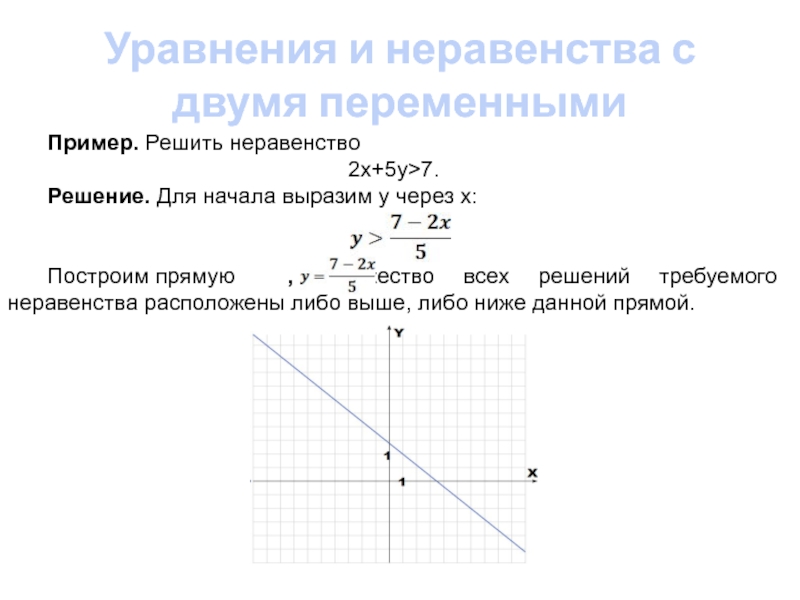
в) Выберите 2: неравное пересечение. • Вы можете изменить цвет пересечения, нажав [<] или [>], когда индикатор цвета в правой части экрана мигает. • Используйте функции в меню НЕРАВЕНСТВО, чтобы найти трассу точки интереса, которая дает точку (точки) пересечения границ затененных областей. 
• Используйте функцию «Объединение» в меню НЕРАВЕНСТВО, чтобы отобразить объединение регионов. Используйте «Исходное затенение», чтобы отобразить исходное затенение областей. 11. 
Для исследования пересечения границ двух регионов: б) Нажмите ~, чтобы выбрать меню НЕРАВЕНСТВО. в) Выберите 1: Трассировка точки интереса. • Поскольку и Y 1 , и Y 2 являются строгими неравенствами, в области выражения используется обозначение Y 1 , Y 2 , что называется точкой интереса. 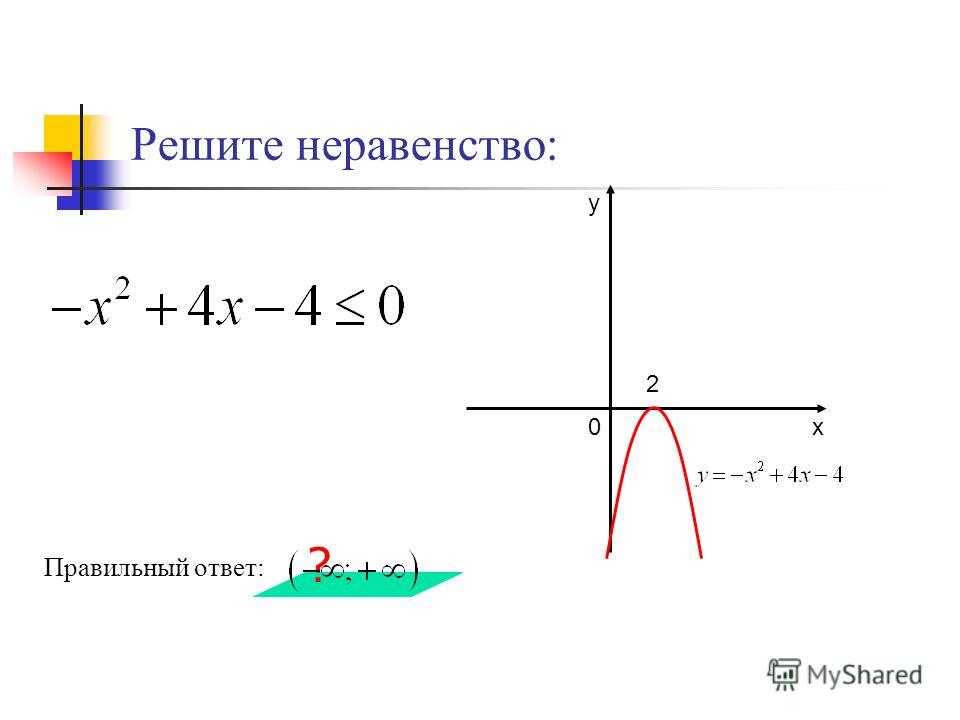
 е. а > 1;
е. а > 1;
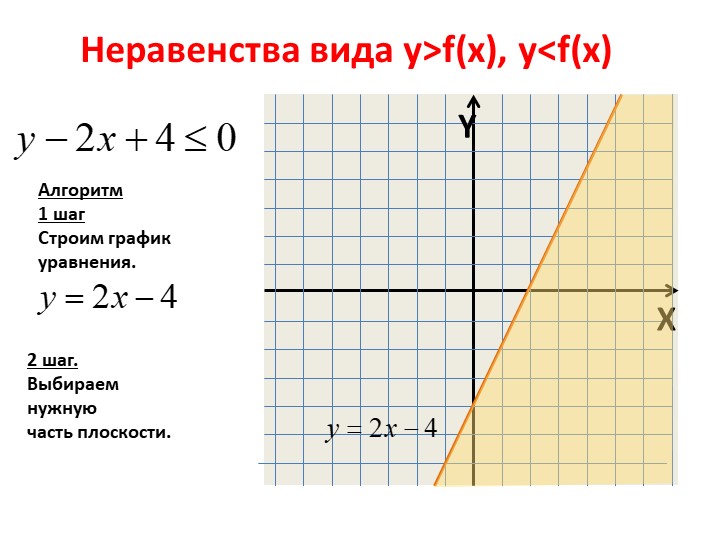 Например: х = -1. Подставляем:
Например: х = -1. Подставляем: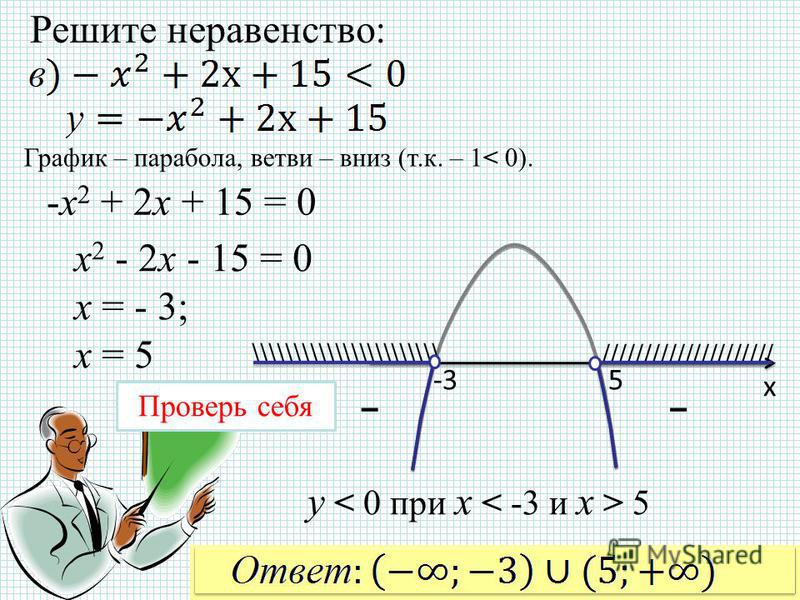
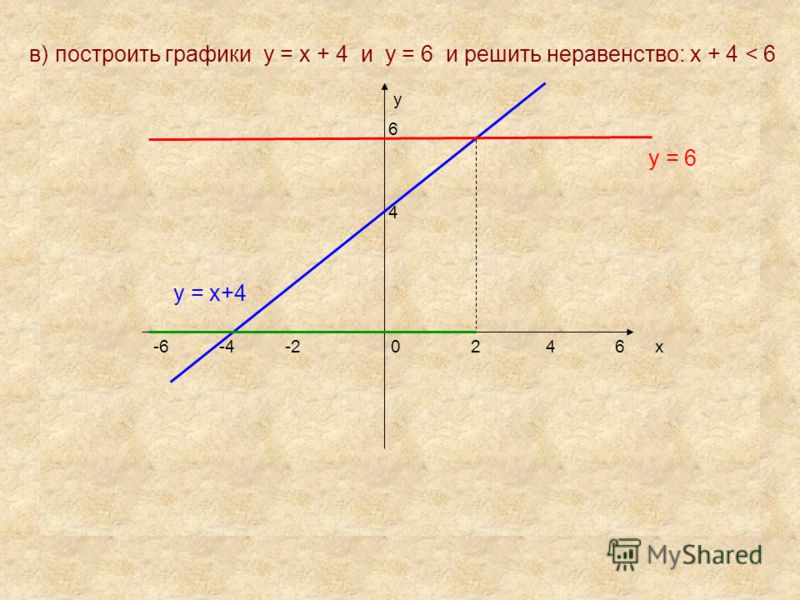 2-x-3<0
2-x-3<0 2
2 Подставим ее координаты в неравенство.
Убеждаемся, что неравенство в данной
точке выполнено. Значит, все точки этой
области удовлетворяют неравенству.
Для проверки подставим и точку из
внешней области в неравенство. Например,
это точка (0, 8). При данных значениях
переменных неравенство обращается в
неверное числовое неравенство, а,
значит, никакая точка из внешней области
не удовлетворяет неравенству. Окончательно
получаем, что решением неравенства
является «внутренность» ромба .
Показываем это штриховкой.
Подставим ее координаты в неравенство.
Убеждаемся, что неравенство в данной
точке выполнено. Значит, все точки этой
области удовлетворяют неравенству.
Для проверки подставим и точку из
внешней области в неравенство. Например,
это точка (0, 8). При данных значениях
переменных неравенство обращается в
неверное числовое неравенство, а,
значит, никакая точка из внешней области
не удовлетворяет неравенству. Окончательно
получаем, что решением неравенства
является «внутренность» ромба .
Показываем это штриховкой. Линии (сплошные или пунктирные) разделяют координатную плоскость на две части, вроде того, как забор разделяет участок земли. Все точки на одной стороне линии сделают неравенство истинным, а все точки на другой стороне — нет. Вы указываете область решений, слегка заштриховывая ее на своем графике.
Линии (сплошные или пунктирные) разделяют координатную плоскость на две части, вроде того, как забор разделяет участок земли. Все точки на одной стороне линии сделают неравенство истинным, а все точки на другой стороне — нет. Вы указываете область решений, слегка заштриховывая ее на своем графике. Если дано строгое неравенство, используйте пунктирную линию для границы. Если дано инклюзивное неравенство, используйте сплошную линию. Затем выберите контрольную точку не на границе. Если контрольная точка устраняет неравенство, закрасьте область, которая ее содержит; в противном случае заштрихуйте противоположную сторону.
Если дано строгое неравенство, используйте пунктирную линию для границы. Если дано инклюзивное неравенство, используйте сплошную линию. Затем выберите контрольную точку не на границе. Если контрольная точка устраняет неравенство, закрасьте область, которая ее содержит; в противном случае заштрихуйте противоположную сторону.