График неравенства – Решение квадратных неравенств графически — Детская игровая комната «Волшебный лес»

Posted on 26.09.202025.12.2019 by alexxlab

Содержание

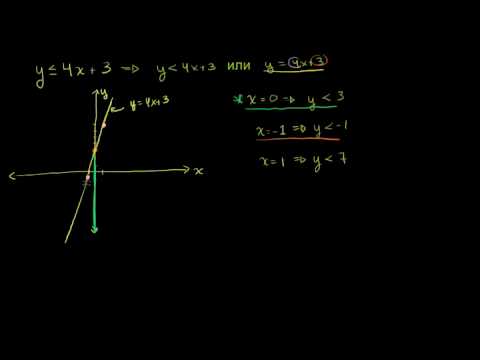
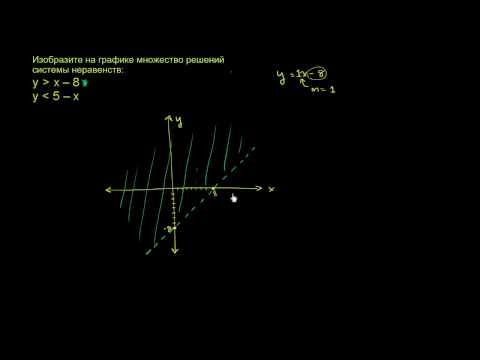
Графическое решение систем неравенств

Здесь мы рассмотрим графические решения нескольких систем неравенств. Умение решать такие задачи очень помогает впоследствии, при освоении задач с параметрами.

Задача 1. Найти площадь фигуры, задаваемой на плоскости множеством решений системы неравенств:

$\begin{Bmatrix}{ x+3y-3\geqslant 0}\\{ 2x+3y-12\leqslant 0}\\{ x\geqslant 0}\\{0\leqslant y \leqslant 2}\end{matrix}$

Перепишем иначе:

$\begin{Bmatrix}{ y\geqslant 1-\frac{x}{3}}\\{ y\leqslant 4-\frac{2x}{3}}\\{ x\geqslant 0}\\{0\leqslant y \leqslant 2}\end{matrix}$

Рисунок 1

Нас интересует только правая полуплоскость ( $x\geqslant 0$ ), область, лежащая выше оси ( $y \geqslant 0$ ), но ниже прямой y=2 ( $y \leqslant 2$

) – проведена серым цветом.

Теперь построим графики первых двух функций. Возьмем в решения область ниже зеленой прямой $y=4-\frac{2x}{3}$ , но выше синей $y=1-\frac{x}{3}$ .

Определим площадь полученной фигуры (залита бежевым) по формуле Пика:

$S=4+\frac{9}{2}-1=7,5$

Ответ: 7,5

Задача 2. Найти площадь фигуры, задаваемой на плоскости множеством решений системы неравенств:

$\begin{Bmatrix}{ x-y+1\leqslant 0}\\{ 5x-3y+15\geqslant 0}\\{ x\leqslant 0}\\{0\leqslant y \leqslant 2,5}\end{matrix}$

Перепишем иначе:

$\begin{Bmatrix}{ y\geqslant x+1}\\{ y\leqslant \frac{5x}{3}+5}\\{ x\leqslant 0}\\{0\leqslant y \leqslant 2,5}\end{matrix}$

Рисунок 2

Нас интересует только левая полуплоскость ( $x\leqslant 0$ ), область, лежащая выше оси

( $y \geqslant 0$ ), но ниже прямой y=2,5

( $y \leqslant 2,5$ ) – проведена серым цветом.

Теперь построим графики первых двух функций. Возьмем в решения область выше рыжей прямой y=x+1

, но ниже синей $y=\frac{5x}{3}+5$ .

Определим площадь данной фигуры путем разбиения ее на простейшие геометрические фигуры: две трапеции. У левой трапеции основания 0,5 и 2, высота 2,5, площадь ее равна

$S=\frac{0,5+2}{2}\cdot2,5=3,125$

У правой основания 2,5 и 1,5 (она на боку лежит), а высота равна 1. Ее площадь

$S=\frac{2,5+1,5}{2}\cdot1=2$

Общая площадь фигуры равна 5, 125.

Ответ: 5, 125.

Задача 3. Изобразить на плоскости множество решений системы неравенств. Найти площадь замкнутой части получившейся фигуры:

$\begin{Bmatrix}{ (y-x-2)(x+y-3)\geqslant 0}\\{ x-2y\leqslant 0}\\{ x\geqslant 0}\end{matrix}$

Вместо исходной системы можем записать совокупность из двух:

$\begin{Bmatrix}{ y-x-2\geqslant 0}\\{ x+y-3)\geqslant 0}\\{ x-2y\leqslant 0}\\{ x\geqslant 0}\end{matrix}$

$\begin{Bmatrix}{ y-x-2\leqslant 0}\\{ x+y-3\leqslant 0}\\{ x-2y\leqslant 0}\\{ x\geqslant 0}\end{matrix}$

Первая система имеет решения, но область решений не замкнута.

Рисунок 3

Вторая дает нам искомую замкнутую область:

Рисунок 4

$\begin{Bmatrix}{ y\leqslant x+2}\\{ y\leqslant 3-x}\\{ y\geqslant \frac{x}{2}}\\{ x\geqslant 0}\end{matrix}$

Определим площадь данной фигуры путем разбиения ее на простейшие геометрические фигуры: два треугольника и трапецию. У трапеции основания 1,5 и 2, высота 1, площадь ее равна

$S=\frac{1,5+2}{2}\cdot 1=1,75$

У верхнего малого треугольника основание 1, а высота равна 0,5. Его площадь

$S=\frac{1}{2}\cdot0,5=0,25$

У правого треугольника основание 1,5, высота – 1, его площадь

$S=\frac{1,5}{2}\cdot 1=0,75$

Общая площадь фигуры равна 2, 75.

Ответ: 2,75.

Задача 4. Изобразить на плоскости множество решений системы неравенств. При каком значении

площадь получившейся фигуры $S=18\pi$ ?

$\begin{Bmatrix}{r^2\leqslant x^2+y^2\leqslant 9r^2}\\{ y-3x \leqslant 0}\\{ 3y+x\geqslant 0}\end{matrix}$

Первое двойное неравенство задает две окружности и область между ними. Две прямые вырезают сектор, показанный на рисунке фиолетовым цветом. Для рисунка был выбран радиус r=1 , на самом деле он может быть любым – собственно, его и нужно определить.

Рисунок 5

Так как прямые перпендикулярны (это понятно по их коэффициентам наклона, их произведение – (-1)), то необходимо определить четверть площади кольца.

$S=\frac{9\pi r^2-r^2}{4}$

По условию, эта площадь равна $S=18\pi$ :

$\frac{9\pi r^2-r^2}{4}=18\pi$

$2\pi r^2=18\pi$

$r^2=9$

$r=3$

Ответ: r=3 .

Задача 5. Изобразить на плоскости множество решений системы неравенств. При каком значении площадь получившейся фигуры $S=8(4-\pi)$ ?

$\begin{Bmatrix}{(x-r)^2+(y-r)^2\geqslant r^2}\\{x-y\geqslant 0}\\{ y\geqslant 0}\\{ x\leqslant r}\end{matrix}$

Снова имеем окружность, центр ее лежит на прямой y=x , поэтому она вписана в первый координатный угол (квадрант). Причем по условию, нас интересует внешняя часть этой окружности.

Рисунок 6

Из этой внешней части мы возьмем в решения область над осью ( $y\geqslant 0$ ), а по оси нас интересует полоса от 0 до центра окружности.

Нас интересует маленький, закрашенный зеленым, уголок. Его площадь можно найти как разность площади треугольника ABC и сектора круга. Этот сектор – $\frac{1}{8}$ часть круга. Поэтому

$S=\frac{AB\cdot OB}{2}-\frac{1}{8}\pi r^2=\frac{r^2}{2}-\frac{1}{8}\pi r^2$

По условию, эта площадь равна $S=8(4-\pi)$ .

Определим :

$\frac{r^2}{2}-\frac{1}{8}\pi r^2=8(4-\pi)$

$r^2=64$

$r=8$

Ответ: r=8 .

easy-physic.ru

Решение квадратных неравенств методом интервалов

Универсальным методом решения неравенств по праву считается метод интервалов. Именно его проще всего использовать для решения квадратных неравенств с одной переменной. В этом материале мы рассмотрим все аспекты применения метода интервалов для решения квадратных неравенств. Для облегчения усвоения материала мы рассмотрим большое количество примеров разной степени сложности.

Алгоритм применения метода интервалов

Рассмотрим алгоритм применения метода интервалов в адаптированном варианте, который пригоден для решения квадратных неравенств. Именно с таким вариантом метода интервалов знакомят учеников на уроках алгебры. Не будем усложнять задачу и мы.

Перейдем собственно к алгоритму.

У нас есть квадратный трехчлен a·x2+b·x+c из левой части квадратного неравенства. Находим нули из этого трехчлена.

В системе координат изображаем координатную прямую. Отмечаем на ней корни. Для удобства можем ввести разные способы обозначения точек для строгих и нестрогих неравенств. Давайте договоримся, что «пустыми» точками мы будем отмечать координаты при решении строгого неравенства, а обычными точками — нестрогого. Отметив точки, мы получаем на координатной оси несколько промежутков.

Если на первом шаге мы нашли нули, то определяем знаки значений трехчлена для каждого из полученных промежутков. Если нули мы не получили, то производим это действие для всей числовой прямой. Отмечаем промежутки знаками «+» или «-».

Дополнительно мы будем вводить штриховку в тех случаях, когда будем решать неравенства со знаками > или ≥ и < или ≤. В первом случае штриховка будет наноситься над промежутками, отмеченными «+», во втором над участками, отмеченными «-».

Отметив знаки значений трехчлена и нанеся штриховку над отрезками, мы получаем геометрический образ некоторого числового множества, которое фактически является решением неравенства. Нам остается лишь записать ответ.

Остановимся подробнее на третьем шаге алгоритма, который предполагает определение знака промежутка. Существует несколько подходов определения знаков. Рассмотрим их по порядку, начав с наиболее точного, хотя и не самого быстрого. Этот метод предполагает вычисление значений трехчлена в нескольких точках полученных промежутков.

Пример 1

zaochnik.com

Как построить график неравенства в Excel — Вокруг-Дом

Microsoft Excel — это полезная программа, которая помогает молодым студентам изучать математику. Если вам нужно составить таблицу с неравенствами, вы можете использовать Excel, чтобы создать таблицу точек данных из уравнения, а затем использовать графический инструмент для графического отображения этого уравнения. Чтобы построить точный график, вам понадобится базовое понимание функций Excel, но даже новички найдут этот процесс довольно простым.

Научите студентов неравенствам с помощью Excel.

Шаг 1

Создайте столбец точек данных в столбце «А». Эти точки данных должны быть равномерно разнесены, но могут быть настолько маленькими или большими, насколько вы хотите, в зависимости от диапазона и области вашего графика. Если вы не уверены, обычно достаточно использовать цифры от -10 до 10.

Шаг 2

Введите уравнение неравенства в ячейку «B1» и замените «x» на «A1». Например, если ваше неравенство y <3x, вы должны ввести «= 3 * (A1)».

Шаг 3

Скопируйте содержимое ячейки «B1».

Шаг 4

Вставьте уравнение в сброс ячеек в столбце «B», которые соответствуют вашим точкам данных в столбце «A».

Шаг 5

Выберите ячейки точек данных и ячейки уравнения.

Шаг 6

Нажмите «Линия» в разделе «Графики» на вкладке «Вставка».

Шаг 7

Выберите опцию «2D график».

Шаг 8

Нажмите «Фигуры» над заголовком «Иллюстрации» и выберите инструмент «Свободная форма».

Шаг 9

Нарисуйте многоугольник, который проходит по краю нанесенной линии и по краям области диаграммы. Убедитесь, что он правильно расположен над или под уравнением, в зависимости от неравенства.

Шаг 10

Выберите многоугольник, нажмите на вкладку «Формат», нажмите «Форма заливки» и выберите «Дополнительные цвета заливки».

Шаг 11

Отрегулируйте цвет и прозрачность, чтобы форма четко отображалась на графике.

ru.computersm.com

2.2.8 Использование свойств и графиков функций при решении неравенств

Видеоурок 1: Графический способ решения неравенств

Видеоурок 2: Графики неравенств

Лекция: Использование свойств и графиков функций при решении неравенств

Для решения неравенств можно пользоваться аналитическим и графическим способами. Но, несмотря на способ, который Вы выберете, необходимо учитывать свойства функций и вид их графиков.

Свойства функций

1. Парность/ непарность

Если функция на графике является симметричной относительно оси ОУ, то данная функция будет называться парной. Для такой функции значение функции будет одинаковым, как для положительных «х», так и для отрицательных.

f(-x) = f(x).

Парной функцией можно назвать квадратичную функцию, графиком которой является парабола с вершиной в начале координат. Так же график выражения в модуле будет являться парной функцией. Среди тригонометрических функций существует единственная функция, которую можно назвать парной — косинус без сдвига фаз.

Если функция симметрична относительно начала координат, то её называют непарной.

f(-x) = — f(x).

К таким функциям можно отнести любую функцию, старший член которой будет иметь нечетную степень или же, например, функция синуса.

Множество остальных функций нельзя отнести ни к парным, ни к непарным.

2. Периодичность

Если некоторая функция повторяется через некоторый период. Такие функцию будут повторяться до бесконечности. К периодичным функциям относятся все тригонометрические функции, не ограниченные на некотором промежутке.

3. Нули функции и промежутки знакопостоянства

Нуль функций — это такое значение ординаты, при которой функция обращается в нуль.

Когда мы находим решение уравнений, мы, как раз, находим нули функций. Иными словами нулем называется точка, в которой график функции пересекает ось ОХ.

Промежутки знакопостоянства — это диапазон, в котором функция имеет одинаковый знак, то есть принимает только положительные, или только отрицательные значения.

Нули функции разбивает всю числовую прямую на интервалы. Именно относительно нулей происходит решение неравенств высоких степеней. Чередование знаков на промежутках происходит именно относительно нулей функции.

Судя по указанному графику, если нам необходимо найти решение неравенств, где функция будет больше нуля, нам подходят диапазоны (-10; -8), (-4; 5).

4. Убывание/ возрастание функции

Если на некотором промежутке [а,б] функция f(x₁) < f(x₂) для любых x₁< x₂, то такую функцию называют монотонно возрастающей.

Если на некотором промежутке [а,б] функция f(x₁) > f(x₂) для любых x₁< x₂, то такую функцию называют монотонно убывающей.

5. Минимум/ максимум/ экстремум

Если для некоторого участка функции в точке выполняется неравенство f(x₁) < f(x₀)(f(x₁) > f(x₀)), то точка x₀является максимумом (минимумом) функции.

То есть точкой, в которой функция будет принимать максимальное (минимальное) значение.

Точки, в которых функция принимает максимальное или минимальное значения, называются экстремумами функции.

В данном случае x_max, x_min_—точки экстремума_,а функция в данной точке называется экстремумом функции.

Точки, в которых производная функции равная нулю или не существует вовсе, называются критическими точками.

Если производная некоторой функции в точке равна нулю, а вторая производная отлична от нуля, то данная точка будет точкой максимума, если вторая производная меньше нуля, и минимума, если она больше нуля.

6. ОДЗ

Это одно из наиболее важных свойств функций, используемых в неравенствах, поскольку ОДЗ позволяет моментально, на первых этапах избавиться от возможных решений системы.

cknow.ru

💣график неравенства ✔️

Главная

Loading…

ТЭГИ

приколы видео орел и решка черногория русские молодые политика спорт музыка события факты звёзды Дота 2 женщины альтернатива КВН драки война мультики актёры кино онлайн масяня приколы наруто видеоклипы видеобитва машины видеореклама вконтакте однокласники видеоролик дня видеоролики 2018 видеоролики без смс казино АТО ДНР ополчение смешное видео youtube приколы дом2 драки стоп хам драки я приколы видео дом2 серии дорогой ты где был русские детективные сериалы бэк ту скул пранки над друзьями новые видеоклипы, Поздравления

ПАРТНЁРЫ

Сообщество

график неравенства .

Что тебя ждёт в вузе?» dir=»ltr»>Что тебя ждёт в вузе?

Что тебя ждёт в вузе?

Нажми для просмотра

Особенност и учёбы в универе Советы от студентов

Тэги:

Построение графиков неравенств

Нажми для просмотра

Инстаграм Андрея —

Тэги:

Метод интервалов #1

Нажми для просмотра

В этом видео показано, как построить график неравенств а с двумя переменным и на координатн ой плоскости.. ..

Тэги:

11 класс, 11 урок, Показательная функция, её свойства и график

Нажми для просмотра

Решение неравенств методом интервалов . Поддержать Проект: Мои занятия в Скайпе: …

Тэги:

Системы неравенств. Графики

Нажми для просмотра

Если Вам понравился данный видеоурок, пожалуйста поддержите наш проект — и мы будем …

Тэги:

Показательная функция — bezbotvy

Нажми для просмотра

В этом видео показано, как изобразить на графике множество решений системы неравенств . В этом видео…

Тэги:

Математика без Ху%!ни. Исследование функции, график. Первая, вторая производная, асимптоты.

Нажми для просмотра

Что такое показатель ная функция? Какой у нее график и какими свойствами она обладает? Это важно знать…

Тэги:

РЕШЕНИЕ НЕРАВЕНСТВ графический способ 8 9 класс

Нажми для просмотра

18+ Математика без Ху%!ни. Полное исследован ие функции с построение м графика. Первая, вторая производны е…

Тэги:

Алгебра 8 класс (Урок№35 — Числовые неравенства. Свойства числовых неравенств.)

Нажми для просмотра

уроки на тему КВАДРАТНЫЕ НЕРАВЕНСТВ А …

Тэги:

График — Код Жизни

Нажми для просмотра

Алгебра 8 класс Урок№35 — Числовые неравенств а. Свойства числовых неравенств . Уметь решать числовые…

Тэги:

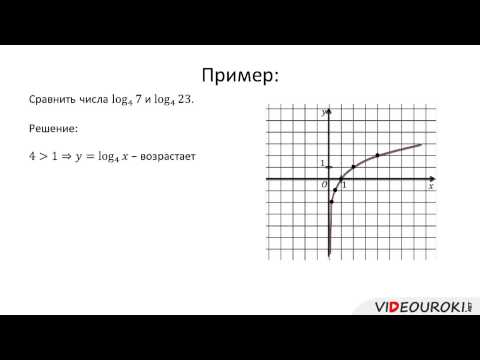
Логарифмическая функция, ее свойства и график

Нажми для просмотра

Составить ГРАФИК ЖИЗНИ по дате рождения и пользовать ся … 1) -инстаграм — …

Тэги:

Алгебра 7 класс. 3 октября. Строим график линейной функции

Нажми для просмотра

Скачать это видео для своей работы вы можете по ссылке: …

Тэги:

Как изобразить множество решений системы неравенств

Нажми для просмотра

Инстаграм Андрея —

Тэги:

Алгебра 9 класс. 11 октября. системы неравенств #1

Нажми для просмотра

Изображени е множества решений системы неравенств с одной переменной на числовой прямой, с двумя переме…

Тэги:

Алгебра 9 класс. Графическое решение систем уравнений

Нажми для просмотра

Инстаграм Андрея —

Тэги:

Алгебра 9 класс. Системы уравнений, основные понятия, расстояние между точками

Нажми для просмотра

Инстаграм Андрея —

Тэги:

Алгебра 9к. Подготовка к экзамену. Часть 1. Урок 1.

Нажми для просмотра

Инстаграм Андрея —

Тэги:

Алгебра 9 класс. Решение систем уравнений через подстановку.

Нажми для просмотра

Подготовка к письменном у традиционн ому экзамену по алгебре за 9 класс. Разбираем типовые задачи из первой…

Тэги:

9 класс, 9 урок, Неравенства с двумя переменными

Нажми для просмотра

Если Вам понравился данный видеоурок, пожалуйста поддержите наш проект — и мы будем …

Тэги:

Математика | Решение квадратных неравенств

Нажми для просмотра

ЗАПИШИСЬ на обучение к репетитора м для подготовки к ОГЭ: Мы сейчас научимся делать с квадратны.

Тэги:

Алгебра 9 класс. Область определения функции

Нажми для просмотра

Инстаграм Андрея —

Тэги:

МАТЕМАТИКА | ТОП-5 ОШИБОК

Нажми для просмотра

ЗАПИШИСЬ на уроки по математике в школу TutorOnline: Видео, которое все так долго ждали. Разберём по …

Тэги:

Графики неравенств с двумя переменными

Нажми для просмотра

В этом видео показано, как построить график линейного неравенств а с двумя переменным и. Это видео…

Тэги:

484 Алгебра 9 класс. Неравенства с двумя переменными

Нажми для просмотра

ГДЗ Алгебра 9 класс Макарычев номер 484 Алгебра 9 класс. Тема Неравенств а с двумя переменным и. Изобразите …

Тэги:

М11 (13.34-13.46) Системы показательных неравенств, графический метод.

Нажми для просмотра

Подписка на канал: Мордкович, 11 класс. Показатель ные …

Тэги:

Графическое решение простейших неравенств с модулем

Нажми для просмотра

neravenstva-modul-gr aficheskoe-reshenie/ Несмотря на кажущуюся простоту неравенств с …

Тэги:

13 6 Решение квадратных неравенств с помощью графика квадратичной функции

Нажми для просмотра

Решение квадратных неравенств — следующий этап в умении решать неравенств а.Для этого вам понадобитс я знат…

Тэги:

Метод интервалов и решение через график параболы для квадратных неравенств

Нажми для просмотра

уроки на тему КВАДРАТНЫЕ НЕРАВЕНСТВ А …

Тэги:

РЕШЕНИЕ НЕРАВЕНСТВ МЕТОДОМ ИНТЕРВАЛОВ математика

Нажми для просмотра

Что такое функция

Тэги:

График функции. Алгебра 7 класс» rel=»spf-prefetch

Нажми для просмотра

Описание отсутсвует

Тэги:

funer.ru