Урок алгебры в 8 классе»Обратная пропорциональность»

УРОК АЛГЕБРЫ В 8 КЛАССЕ
- Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их
- (Д. Пойа

Задание для учащихся
Закончите предложения :
а ) С увеличением цены за единицу товара
количество товара , которое можно закупить на
данную сумму денег …
уменьшится
б) С уменьшением скорости движения на данном
отрезке пути время движения …
увеличится
в) С увеличением производительности труда при
выполнении данного объёма работы
количество рабочих …
уменьшится

1
Пешеход проходит путь S со скоростью v за t часов.
Выразите время пешехода через путь и скорость.
1)
Если , то
3

.
2
Площадь прямоугольника со сторонами
x и y равна S . Выразите у через S и х.
1)
Если , то y= 24 /x
4

ТЕМА УРОКА
Функция
её график
и свойства
4

Определение
Обратной пропорциональностью называется функция , заданная формулой
y = k/x, где k ≠ 0 ,
где х – независимая переменная.
Число k называется коэффициентом обратной пропорциональности
4

Построение графика функции у=к/х
1 вариант 2 вариант
у = — 8/х
у = 8/х
1 ) Составим таблицу значений для х и у
2 ) Начертим координатную плоскость
3) Проставим точки в координатной плоскости
4) Соединим точки плавной линией
4
 0 , у при х-? 4 . Наибольшее и наименьшее значение функции»
0 , у при х-? 4 . Наибольшее и наименьшее значение функции»
График функции у = к/х и её свойства
1 вариант 2 вариант
гипербола
у = — 8/х
у = 8/х
1. Область определения функции
2. Область значений функции
3. у 0 , у при х-?
4 . Наибольшее и наименьшее значение функции

Тестовые задания по теме “ Обратная пропорциональность ”
1) Какая из формул задаёт обратную пропорциональность
3)
1)
2)
5)
4)
9

Тестовые задания по теме “ Обратная пропорциональность ”
2 ) Какая из указанных точек принадлежит
графику функции y = -8/x ?
1 ) A(1;8)
2) B(-1;-8)
3) С(1 ; -8)
9

Тестовые задания по теме “ Обратная пропорциональность ”
3 ) На чертеже показан график функции у=к/х.
Укажите формулу , которой
задана функция
1) y=-3/x
2) y=6/x
3) y=-6/x
4) y=3/x
- 1) y=-3/x 2) y=6/x 3) y=-6/x 4) y=3/x
- 1) y=-3/x 2) y=6/x 3) y=-6/x 4) y=3/x
9

Тестовые задания по теме “ Обратная пропорциональность ”
4) Укажите среди графиков гиперболу
1
2
3
9

Тест

1. На одном из рисунков изображена гипербола. Укажите этот рисунок.
2
1
3
4

2 . На одном из рисунков изображена парабола. Укажите этот рисунок.
2
1
3
4

3 . На одном из рисунков изображен график функции
у = 2/х.
Укажите этот рисунок.
1
2
3
4

4 . Как называется функция у = к/х ?
5 . Как называется график функции у = к/х ?

Проверь себя
- 1) 2
- 2) 4
- 3) 3
- 4) обратная пропорциональность
- 5) гипербола

Домашнее задание

Итог Урока
- Приведите пример обратной пропорциональной зависимости
- Дайте определение обратной пропорциональности
- Что представляет собой график обратной пропорциональности
- Укажите свойства обратной пропорциональности
План-конспект урока по алгебре (8 класс) на тему: разработка урока «Функция обратной пропорциональности»
Урок математики, 8 класс
Учитель математики первой категории «МБОУ СОШ №2» с.Мугур-Аксы Сайын-оол Елизавета Бадыевна, стаж работы с 1979г.
Тема: Функция y=
Цели:
-Развитие навыка самостоятельности в работе, трудолюбия, аккуратности, развитие навыков самоанализа и самоконтроля при оценке результата и процесса своей деятельности.
- Метапредметные:
-Формирование коммуникативной и учебной компетентности учащихся, умения работать с имеющейся информацией в новой ситуации.
-Ознакомление с функцией у =, ее свойствами и графиком.
Тип урока: урок изучения нового материала.
Учебные задачи, направленные на развитие учащихся:
— в личностном направлении: обеспечить познавательную мотивацию учащихся при изучении новых понятий и свойств, провести рефлексию деятельности после проделанной работы.
— в метапредметном направлении: формирование умения самостоятельно формулировать учебную задачу урока, развитие операций мышления (сравнение, сопоставление, обобщение, классификация), формирование отдельных составляющих исследовательской деятельности (умения наблюдать, умения делать выводы и умозаключения, умения выдвигать и формулировать гипотезы).
— в предметном направлении: изучение функции y=k/x, ее свойства и график.
Техническое обеспечение: учебник «Математика 8 класс» Ю.Н. Макарычев и др., компьютер, проектор, доска.
Ход урока:
1.Организационный момент
Учащиеся приветствуют учителя и организуют свое рабочее место, демонстрируют готовность к уроку.
2.Активация знаний учащихся.
Работа в парах. На доске записи:
Функция. Аргумент. y=f (x). D(x). E(x).
Прямая пропорциональность. График.
Ученики придумывают задания, дают их друг другу для выполнения и контролируют полученный результат. Над каждым заданием работает пара учащихся, вступая при этом в диалог, остальные ученики слушают вопросы и ответы и в конце выполнения этой работы дают оценку формулировкам, высказанным в диалоге и качеству выполнения задания. В ходе выполнения каждого задания вслух формируются уже известные понятия и алгоритмы действий, которые понадобятся на этом уроке.
3.Создание проблемной ситуации.
Задача:
На проекторе прямоугольник yyyyyyy
со сторонами x см, y см и x
площадью 12 см2.
y
— Что будет, если начать изменять одну из сторон прямоугольника y=k/ x?
4. формирование проблемы (тема и цели урока)
— Назовите тему урока. На какие вопросы вы бы хотели получить ответы и, какие цели поставили на этот урок?
Я согласна с вами. Цель урока: ознакомиться с функцией y=k/ x, ее свойствами и графиком.
5. Открытие нового знания.
Исследуйте функцию y=k/ x.
1.
Составьте таблицу значений переменных x и y для функции y=12/ x.
x | -12 | -6 | -5 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 5 | 6 | 8 | 12 |
y | -1 | -2 | -2,4 | -3 | -4 | -6 | -12 | 12 | 6 | 4 | 2,4 | 2 | 1,5 | 1 |
Внимательно смотрите таблицу.
— Как изменяется y с изменением x?
— С увеличением x , y уменьшается и, наоборот, с уменьшением x , y увеличивается. Если уменьшим n раз x, то y увеличится в n раз и, наоборот.
— Как вы думаете, какая зависимость существует между переменными x и y?
— x и y обратно пропорциональны. Поэтому функцию вида y=k/ x, k≠0 называют обратной пропорциональностью.
— Какова область определения функции?
— Все числа, кроме нуля.
2.
Постройте в тетрадях график функции y=12/ x
Получили две кривые. Как называется кривая, посмотрите в учебнике на странице 43.
Из истории (доклад ученика) Этот термин ввел Аполлоний из г.Пергам (Малая Азия), живший в III-II вв. до н.э. Он показал, что гипербола получится, если взять конус и пересечь его полости плоскостью, параллельно
Гипербола устремляется ввысь настолько быстро и настолько быстро падает вниз, что становится понятным, почему таким термином называется в литературе преувеличение или преуменьшение: «наметал стог выше тучи», «стал Иванушка ниже былинки в поле». Пословица: «Дальше от кумы – меньше греха» — тоже пример гиперболы.
Устно свойства функции y=-12/ x
Вывод: при k0 график функции 𝑦= k/𝑥 расположен в первой и третьей, при
k0 – во второй и четвертой координатных четвертях.
Ученики читают учебник и сверяют свои формулировки с формулировкой в учебнике. Запоминают формулировки для себя в удобной форме.
6.Первичное применение нового знания.
№182 выполняют у доски в тетрадях. Принадлежит ли точка с данными координатами графику данной функции? На этот вопрос можно ответить двумя способами: по графику и аналитически.
— Какой из этих способов здесь возможно применить?
Решение обсуждается всем классом, при этом анализируются допущенные ошибки.
№184 выполняют в тетрадях, взаимопроверкой друг друга.
7. Самостоятельная работа ( условия на проекторе)
Вариант ученик выбирает сам – по уровню подготовки. Работа выполняется на листочках и сдается на проверку.
I уровень
Построить график обратной пропорциональности 𝑦= с помощью таблицы
𝑥 | -6 | -4 | -3 | -2 | -1,5 | -1 | 1 | 1,5 | 2 | 3 | 4 | 6 |
𝑦 | 1 | 1,5 | 2 | 3 | 4 | 6 | -6 | -4 | -3 | -2 | -1,5 | -1 |
II уровень
Построить график обратной пропорциональности 𝑦= предварительно заполнив таблицу
𝑥 | -9 | -6 | -5 | -3 | -2 | -1 | 1 | 2 | 3 | 5 | 6 | 9 |
𝑦 |
III уровень
Построить график функции 𝑦=.
8. Итог урока.
Еще раз сформулировать цели, поставленные в начале урока и определить, достигнуты ли они. Что нового узнали на уроке? Что не поняли? Понравился ли им урок?
9. Домашнее задание:
Прочитать пункт 8, решить №180, 184 (б) и на выбор №183
Функция обратной пропорциональности и её график
Повторим теорию о функциях. Функция — это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный! ) элемент другого множества (множества значений функции). То есть, если есть функция\(y = f(x)\) , это значит, что каждому допустимому значению переменной \(x\) (которую называют «аргументом») соответствует одно значение переменной \(y\) (называемой «функцией»).
Функция, описывающая обратную зависимость
Это функция вида \(y = \frac{k}{x}\) , где \(k \ne 0.\)
По-другому ее называют обратной пропорциональностью: увеличение аргумента вызывает пропорциональное уменьшение функции.
Определим область определения. Чему может быть равен \(x\)
? Или, по-другому, чему он не может быть равен?
Единственное число, на которое нельзя делить — это 0, поэтому \(x \ne 0.\) :
\(D(y) = (- \infty ;0) \cup (0; + \infty)\)
или, что то же самое:
\(D(y) = R\backslash \{ 0\} .\)
Такая запись означает, что \(x\) может быть любым числом, кроме 0: знак «R» обозначает множество действительных чисел, то есть всех возможных чисел; знаком «\» обозначается исключение чего-нибудь из этого множества (аналог знака «минус»), и число 0 в фигурных скобках означает просто число 0; получается, что из всех возможных чисел мы исключаем 0.
Множество значений функции, оказывается, точно такое же: ведь если \(k \ne 0.\) , то на что бы мы его не делили, 0 не получится:
\(E(y) = (- \infty ;0) \cup (0; + \infty)\)
или\(E(y) = R\backslash \{ 0\} .\)
Также возможны некоторые вариации формулы \(y = \frac{k}{x}\) . Например, \(y = \frac{k}{{x + a}}\) — это тоже функция, описывающая обратную зависимость. Область определения и область значений этой функции следующие:
\(D(y) = (- \infty ; — a) \cup (- a; + \infty)\)
\(E(y) = (- \infty ;0) \cup (0; + \infty).\)
Рассмотрим пример , приведем выражение к виду обратной зависимости:
\(y = \frac{{x + 2}}{{x — 3}}.\)
\(y = \frac{{x + 2}}{{x — 3}} = \frac{{x — 3 + 3 + 2}}{{x — 3}} = \frac{{(x — 3) + 5}}{{x — 3}}.\)
Искусственно ввели значение 3 в числитель, а теперь почленно разделим числитель на знаменатель, получим:
\(y = \frac{{(x — 3) + 5}}{{x — 3}} = \frac{{x — 3}}{{x — 3}} + \frac{5}{{x — 3}} = 1 + \frac{5}{{x — 3}}.\)
Получили обратную зависимость плюс число 1.
График обратной зависимости
Начнем с простого случая \(y = \frac{1}{x}.\)
Составим таблицу значений:
Нарисуем точки на координатной плоскости:

Соединяем точки, график будет выглядеть так:

Этот график называется «гипербола» . Как и у параболы, у гиперболы две ветки, только они не связаны друг с другом. Каждая из них стремится своими концами приблизиться к осям Ox и Oy , но никогда их не достигает.
Отметим некоторые особенности функции:
- Если у функции перед дробью стоит минус, то график переворачивается, то есть симметрично отображается относительно оси Ox.
- Чем больше число в знаменателе, тем дальше график «убегает» от начала координат.
Обратная зависимость в жизни
Где же нам встречается такая функция на практике? Примеров множество. Самый распространенный — это движение: чем больше скорость, с которой мы движемся, тем меньшее время нам потребуется, чтобы преодолеть одно и то же расстояние. Вспомним формулу скорости:
\(v = \frac{S}{t},\)
где v — скорость, t — время в пути, S — расстояние (путь).
Отсюда можно выразить время: \(t = \frac{S}{v}.\)
1 урок по теме
Выполнила:
Телегина Л.Б.
Цель урока:
- повторить весь изученный материал по функциям.
- ввести определение обратной пропорциональности и научить строить её график.
- развивать логическое мышление.
- воспитывать внимание, аккуратность, точность.
План урока:
- Повторение.
- Объяснение нового материала.
- Физкультминутка.
- Закрепление.
Оборудование: плакаты.
Ход урока:
- Урок начинается с повторения. Учащимся предлагается разгадать кроссворд (который заранее подготовлен на большом листе бумаги).
Конспект урока по алгебре для учащихся 8 класса по теме «Обратная пропорциональность и её график»
Конспект урока по алгебре для учащихся 8 класса по теме
«Обратная пропорциональность и её график»
Цель урока:
Образовательная: познакомить учащихся с понятием функции обратной пропорциональности, её графиком; научить работать с функцией и её графиком в процессе решения задач.
Задачи:
повторить понятие функции;
познакомить с понятием функции обратной пропорциональности и ее графиком;
научить решать задачи по данной теме.
Развивающая: развивать логическое мышление, память, внимание, формировать умения анализировать, сопоставлять данные, выводить логические следствия из данных предпосылок, умение делать выводы.
Воспитательная: воспитывать сознательное отношение к учебному труду, самостоятельность, прививать аккуратность и трудолюбие.
Тип урока:урок усвоения новых знаний.
Требования к ЗУН:
учащиеся должны знать определение функции обратной пропорциональности, свойства функции при, при .
учащиеся должны уметь работать с формулой и графиком функции обратной пропорциональности, решать задачи с их использованием.
Методы обучения: индуктивно-эвристический, дедуктивно-репродуктивный.
Оборудование: компьютер, экран, проектор, мультимедиа презентация.
Литература:
Алгебра: Учеб.для 8 кл. общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И.Нешков и др. – 11-е изд. – М. : Просвещение, 2010.– 384 с.
Дидактические материалы по алгебре 8класс: кн. для учителя/В.И. Жохов, Ю. Н. Макарычев, Н. Г. Миндюк.-М. Просвещение,2007,-144с.
План урока:
1. Организационный момент (2 минуты)
2. Актуализация знаний (5 минут)
3. Изучение нового материала (12 минут)
4. Закрепление изученного материала (21минута)
5. Домашнее задание (2 минуты)
6. Подведение итогов (3 минуты)
Ход урока
Организационный момент
Включает в себя приветствие учителем класса, проверку готовности кабинета к проведению урока, девиз урока. . (Слайд 3)
Актуализация знаний
Учитель: На сегодняшнем уроке мы приступаем к изучению новой темы «Обратная пропорциональность и её график». Мы познакомимся с понятием функции обратной пропорциональности, её графиком. Научимся решать задачи и узнаем где в жизни вам понадобиться обратно пропорциональный график (Слайд 4)
Учитель:Начнем урок с повторения материала, изученного на прошлом уроке. Когда мы говорим о графиках и функциях какие ассоциации у вас появляются ? Где мы встречаем координаты ? . (Слайд 5-8)
Я прошу вас обратить внимание на доску: на слайде кроссворд. Необходимо заполнить кроссворд. (Слайд 9)
Учащиеся по очереди отвечают на вопросы.
Учитель:Как называетсяфункция вида y = kx + b?
Ученик:Функция вида y = kx + b называется линейной.
Учитель:Как называется функция вида y=x2?
Ученик: квадратичная функция.Графиком является парабола
Учитель: Что является графиком функции ?
Проблема :Графиком функции является гипербола.
На слайде появляются ответы (Слайд 12).
Изучение нового материала
Учитель:Мы с вами немного повторили предыдущий материал, а теперь откройте свои тетради и запишите число, классную работу и тему урока «Обратная пропорциональность и её график».
Запись на доске (слайд 13) и в тетрадях:
Запись в тетради:
Число
Классная работа.
Тема урока: «Обратная пропорциональность и её график».
Учитель:Обратная пропорциональность находит широкое применение на практике.
Например:
время, затраченное на прохождение одного и того же пути, обратно пропорционально скорости движения; (Слайд 14).
количество товара обратно пропорционально цене этого товара при одной и той же сумме денег, затраченных на его покупку; (Слайд 15).
количество товара обратно пропорционально цене этого товара при одной и той же сумме денег, затраченных на его покупку.Закон спроса. (Слайд16)
зависимость между площадью прямоугольника и его сторонами
(Слайд 17)
Учитель:А теперь построим график функции . Запишите в свои тетради данное задание со слайда. (Слайд 18)
Запись в тетрадях: Построить график функции .
Учащиеся вместе с учителем разбирают пример построения графика функции, отвечают на наводящие вопросы и делают записи в тетради.
Учитель:Что необходимо сделать для построения этого графика?
Ученик:Для построения графика следует вычислить координаты нескольких точек графика, построить их и через них провести плавные линии.
Учитель:Чему равенk, в данной функции?
Ученик:k=12
Учитель:Верно, значит . Составим таблицу положительных значений аргумента. В своих тетрадях начертите таблицу.
Учитель:Если аргумент х примет значение 1, то чему будет равно значение функции у?
Ученик:Значение функции убудет равно .
Запись в тетради: у=
Учитель:Верно.Найдите для указанных значений аргумента соответствующие значения функции и постройте прямоугольную систему координат.
Запись в тетрадях:
Учитель:Мы получили пар точек. Назовите мне их.
Ученик: (1;12), (2;6), (3;4), (4; 3), (5;2,4), (6;2)…
Учитель:Правильно, а теперь назовите точки с противоположными координатами, для построения графика функции поскольку им является гипербола, а для её построения необходимы точки с противоположными координатами.
Ученик: (-1;-12), (-2;-6), (-3;-4), (-4; -3), (-5;-2,4), (-6;-2)…
Учитель:Все верно. Теперь давайте построим полученные пары точек. Первая точка имеет координаты (1;12). Находим эту точку и отмечаем. Проделайте эту операцию с остальными точками.
(Учащиеся строят точки на прямоугольной системе координат в своих тетрадях).
Учитель: Теперь последовательно соедините построенные вами точки плавной линией.У вас должна получиться кривая, состоящая из двух ветвей.
Запись в тетрадях:
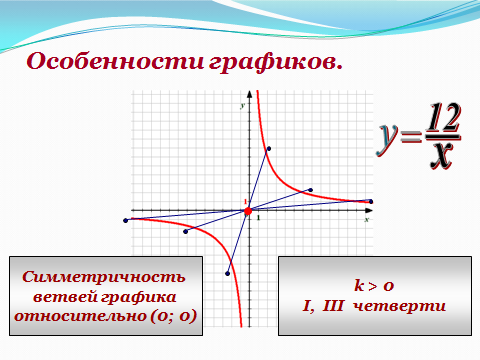
Учитель:Итак, мы получили график функции .
Учитель: Сверьте график, который вы получили, с графиком, представленным в учебнике (рис. 67).
Учитель:Прочитайте определение обратной пропорциональности со слайда. (Слайд 23)
(Учитель просит одного из учеников озвучить определение вслух)
Ученик:Обратной пропорциональностью называется функция, которую можно задать формулой , где х – независимая переменная и k – не равное нулю число.
Число k называют коэффициентом обратной пропорциональности.
Учитель:Вы знаете, чтографик функции — гипербола. График функции также называют гиперболой. Следовательно, полученный нами график функции — гипербола.
Ребята а где вы ещу слышали слово ГИПЕРБОЛА.
«Гипербола вокруг нас» (Слайд 24-26 )
Закрепление изученного материала
Учитель:А теперь перейдем к выполнению заданий. (Слайд 27)
Учащиеся получают карточки с заданием по вариантам и строят график функции, делая записи в тетради.
Учитель: нужно построить график функции и .
Учитель:А теперь обратите внимание на доску и проверьте друг у друга, верно ли вы построили график. У вас должна получиться кривая, состоящая из двух ветвей.
На слайде появляется решение, с которым учащиеся сверяют свою запись. (Слайд 27)
Учитель:Какой вывод вы можете сделать.
Учитель: Чему равен коэффициент k?
Ученик: если , то 2 и 4 четверть. если , то 1 и 3 четверть.
Учитель:Следующее задание определите в каких четвертьях расположен график. (Слайд 29)
Учитель. Следуюющее задание найдите обратно пропорциональную функцию. (Слайд 30)
Учитель:Верно. Укажите среди графиков гиперболу. (Слайд 31)
Учитель:Все справились с заданием. Теперь решим уравнение графически. Работать будем группой по 4 ученика.
Учитель просит ученика вспомнить алгоритм решения уравнения графически
Ученик: в одной координатной плоскости построить графики левой и правой части уравнения. Найти точки пересечения этих графиков. Определить значения абсцисс . ( слайд 31)
Учитель:Все верно, вы успешно справились с заданием. Ребята, которые выполняли задания вперед, подойдите после урока на проверку решения задач. Я поставлю Вам дополнительные оценки.
Домашнее задание
Учитель:Открываем свои дневники и записываем домашнее задание. (Слайд 32)
Запись в дневниках: №179, №186, п.8.
Подведение итогов
Учитель:На сегодняшнем уроке мы познакомились с определением обратной пропорциональности, научились решать задачи по данной теме. А кто сможет повторить определение обратной пропорциональности?
(Ученики поднимают руки, учитель спрашивает одного из них)
Ученик:Обратной пропорциональностью называется функция, которую можно задать формулой , где х – независимая переменная и k – не равное нулю число.
Учитель: Молодцы! Я надеюсь, что вы освоили сегодняшний материал.
А что вы с собой в жизнь возьмёте из этой темы ?
Ученик: «Тише едешь , дальше будешь.», если продавать дешевле то спрос высше,чем меньше лени в учёбе тем высше оценка и т.д.
(В конце урока учитель выставляет оценки учащимся)
Ребята оцените пожалуйста наш урок с помощью мимики смайликов.
Урок по алгебре в 8 классе на тему «Функция, описывающая обратную пропорциональность, ее график и свойства».
Урок по алгебре в 8 классе по теме «Функция, описывающая обратную пропорциональную зависимость, ее график и свойства».
Цели: обеспечить повторение и систематизацию известных учащимся сведений о функциях;
познакомить с функцией у = k/x и её графиком;
способствовать формированию умений применять приемы сравнения, перенос знаний в измененную ситуацию, развитию мышления, речи, внимания;
содействовать воспитанию интереса к математике, активности, организованности.
Ход урока.
1. Организационный этап. Сообщение темы, постановка целей урока.
2. Актуализация знаний учащихся (с использованием интерактивной доски Обратная пропорциональность, ее свойства и график.notebook).
1) Опрос (страница 1):
Что такое функция?
Что называется аргументом, значением функции?
Что такое область определения функции?
Что называют графиком функции?
2) Повторение ранее изученных функций по плану:
Название функции.
Формула.
Область определения.
График функции.
Линейная функция (страница 2), зависимость графиков функции от коэффициентов (страницы 2,3).
Прямая пропорциональность (страницы 3,4).
Функция у = х2 (страница 5).
Функция у = х3 (страница 6).
Функция у = ǀхǀ (страница 7).
3. Изучение нового материала.
Объяснение начинается с мотивации.
Как известно, всякая функция описывает какие-то процессы, происходящие в окружающем нас мире. Рассмотрим, например, прямоугольник со сторонами х и у и площадью 12 см2.
Чему равна его площадь (S = x*y) ? Выразите из формулы площади сторону y (y = S/x). Что будет, если начать изменять одну из сторон прямоугольника, допустим сторону длиной х? Если значение х увеличить в 2 раза, то будем иметь у = 12/2х, то есть сторона у уменьшится в 2 раза. Если значение х увеличивать в 3, 4,5… раз, то значение у во столько же раз уменьшается. Наоборот, если х уменьшать в несколько раз, то у будет увеличиваться во столько же раз.
Поэтому функцию вида у =12/х называют обратной пропорциональностью. В общем виде она записывается так: у =k/x, где k — константа, причем k ≠ 0 (страница 8).
Построим график функции y = 12/x. Для этого составим таблицу.
— Все числа, кроме 0.
— При х<0 имеем: у<0, при х>0 имеем у>0.
Как же выглядит график данной функции? Отметим полученные точки на координатной плоскости.
Давайте попробуем вместе сделать выводы о графике функции, вытекающие из рассмотрения таблицы и формулы.
1. Точка (0; 0) не принадлежит графику, т. е. он не пересекает ни оси Ох, ни оси Оу.
2. График находится в I и в III координатных четвертях.
3. Плавно приближается к координатным осям как в I координатной четверти, так и в III, причем он подходит к осям как угодно близко.
Полученная кривая называется гиперболой, что в переводе с греческого «хиперболе» – преувеличение. Теперь становится ясно, почему таким же словом «гипербола» называется стилистический прием, состоящий в образном преувеличении, например: «редкая птица долетит до середины Днепра», «стал Иванушка ниже былинки в поле», «наметали стог выше тучи».
Теперь рядом с графиком функции у = 12/х построим график функции у = — 12/х.
Сравнивая оба графика, учащиеся замечают, что второй занимает II и IY координатные углы, а оба они симметричны относительно начала координат. К тому же если график функции у = 12/x отобразить симметрично относительно оси Оу, то получим график функции у = -12/x. Зависимость графика функции от коэффициента k (страница 9).
Такие функции встречаются очень часто (страница10).
t= S/V, где t – время, S – путь, V- скорость.
Ц =C/K, где Ц – цена товара, С – стоимость, К – количество товара.
р(S) = F/S, где р – давление, S – площадь, F – сила.
I =q/t, где I – сила тока, q – заряд, t – время.
I =U/R, где I – сила тока, R – сопротивление, U – напряжение.
N = A/t, где N – производительность труда, А – объем работы, t – время.
V =m/p, где V – объем, m – масса, p – плотность вещества.
4. Закрепление и систематизация знаний.
1) Задача.
Сила тока в реостате I (в амперах) вычисляется по формуле I =U/R, где U – напряжение (в В). R – сопротивление (в Ом).
Построить график зависимости I(R) при U=6.
По графику приближенно найти:
а) силу тока при сопротивлении, равном 6, 12, 20 Ом;
б) сопротивление реостата при силе тока, равной 10, 5, 1,2 А.
3. Выяснить, принадлежит ли графику точка с координатами (1,5; 4).
2) Самостоятельная работа. Задания из открытого банка заданий по математике на соответствие графиков функций и формул, их описывающих (Страницы 11-13).
5. Задание на дом:
п. 8, вопросы 3,4 с. 49; № 185, 190(в), 196.
6. Подведение итогов. Рефлексия.
1) Вопросы учащимся:
– Функция, какого вида называется обратной пропорциональностью?
– Что является графиком функции y = k/x?
– В каких координатных четвертях расположен график функции y = k/x в зависимости от k?
– Какова область определения функции y = k/x?
2) Заполните таблицу:
ВЫБОР
На уроке я работал
активно, пассивно
Своей работой на уроке я
доволен, не доволен
Урок показался мне
коротким, длинным
За урок я
не устал, устал
Мое настроение
стало лучше, стало хуже
Материал урока для меня был
понятен, не понятен
интересен, скучен
полезен, бесполезен
Урок математики в 8 классе «Обратная пропорциональность»

Лучший способ изучить что-либо — это открыть самому. (Д. Пойа)

Закончите предложения :
а ) С увеличением цены за единицу товара
количество товара , которое можно закупить на
данную сумму денег …
уменьшится
б) С уменьшением скорости движения на данном
отрезке пути время движения …
увеличится
в) С увеличением производительности труда при
выполнении данного объёма работы
количество рабочих …
уменьшится

Пешеход проходит путь S со скоростью v за t часов.
Выразите время пешехода через путь и скорость.
1
1)
Если , то
3

Задачи, приводящие к понятию обратной пропорциональности.
2
Площадь прямоугольника со сторонами
x и y равна S . Выразите у через S и х.
1)
Если , то y= 24 /x
4

Функция y=k/x ,
её график
и свойства
4

Обратной пропорциональностью называется функция , заданная формулой
y = k/x, где k ≠ 0 ,
где х – независимая переменная.
Число k называется коэффициентом обратной пропорциональности
4

1 вариант 2 вариант
у = — 8/х
у = 8/х
1 ) Составим таблицу значений для х и у
2 ) Начертим координатную плоскость
3) Проставим точки в координатной плоскости
4) Соединим точки плавной линией
4
 0 , у при х-? 4 . Наибольшее и наименьшее значение функции «
0 , у при х-? 4 . Наибольшее и наименьшее значение функции «
График функции у = к/х и её свойства
1 вариант 2 вариант
гипербола
у = — 8/х
у = 8/х
1. Область определения функции
2. Область значений функции
3. у 0 , у при х-?
4 . Наибольшее и наименьшее значение функции

1) Какая из формул задаёт обратную пропорциональность
3)
1)
2)
5)
4)
9

Тестовые задания по теме “ Обратная пропорциональность ”
2 ) Какая из указанных точек принадлежит
графику функции y = -8/x ?
1 ) A(1;8)
2) B(-1;-8)
3) С(1 ; -8)
9

Тестовые задания по теме “ Обратная пропорциональность ”
3 ) На чертеже показан график функции у=к/х.
Укажите формулу , которой
задана функция
1) y=-3/x
2) y=6/x
3) y=-6/x
4) y=3/x
- 1) y=-3/x 2) y=6/x 3) y=-6/x 4) y=3/x
- 1) y=-3/x 2) y=6/x 3) y=-6/x 4) y=3/x
- 1) y=-3/x 2) y=6/x 3) y=-6/x 4) y=3/x
9

Тестовые задания по теме “ Обратная пропорциональность ”
4) Укажите среди графиков гиперболу
1
2
3
9


1. На одном из рисунков изображена гипербола. Укажите этот рисунок.
2
1
3
4

2 . На одном из рисунков изображена парабола. Укажите этот рисунок.
2
1
3
4

3 . На одном из рисунков изображен график функции
у = 2/х.
Укажите этот рисунок.
1
2
3
4

4 . Как называется функция у = к/х ?
5 . Как называется график функции у = к/х ?
9

- 1) 2
- 2) 4
- 3) 3
- 4) обратная пропорциональность
- 5) гипербола



- Я научился….
- Мне понравилось …
- Я не понял…


- Приведите пример обратной пропорциональной зависимости
- Дайте определение обратной пропорциональности
- Что представляет собой график обратной пропорциональности
- Укажите свойства обратной пропорциональности
«Функция у=к/х, её свойства и график»
Технологическая карта урока
Ф.И.О. учителя: Воробьева Ольга Владимировна
Урок открытия нового знанияТехнология построения урока
Элементы технологии исследовательской деятельности и системно — деятельностного подхода
Тема
Функция у=к/х, её свойства и график
Цель
Создать условия для усвоения новых знаний о функции «обратная пропорциональность» и способов действий на уровне применения свойств функции и её графика в изменённой ситуации.
Основные термины, понятия
Обратная пропорциональность, зависимая переменная, независимая переменная, гипербола, свойства обратной пропорциональности
Предметные умения:Знать понятие функции обратной пропорциональности.
Сформировать четкое представление о различиях свойств и расположения графика функции при различных значениях k.
Уметь строить график функции y = k/x, опираясь на ее свойства.
Расширить представления учащихся о функциях.
Личностные УУД:
способность к самооценке на основе критерия успешной учебной деятельности;
усилить мотивацию к обучению;
ясно, точно, грамотно излагать свои мысли, исправлять и дополнять ответы других учащихся
Регулятивные УУД:
уметь определять и формулировать цель урока; проговаривать последовательность действий на уроке; уметь объективно оценивать свою деятельность и деятельность других; планировать свое действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учета сделанных ошибок; высказывать свое предположение.
Познавательные УУД:
уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания; находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную в ходе исследования.
Коммуникативные УУД:
регулировать собственную деятельность посредством речевых действий; умение слушать и вступать в диалог; воспитывать чувство взаимопомощи, уважительное отношение к чужому умению, культуре учебного труда, требовательное отношение к себе и своей работе.
Фронтальная (ф), работа в парах(п), групповая (г), индивидуальная(и).
Книгопечатная продукция
1. Алгебра. 8 класс: учебник для общеобразоват. учреждений / [А. Г. Мордкович и др.] ; под общ. редакцией А. Г. Мордковича. — М.: Мнемозина, 201 3.
2.Алгебра. 8 класс: задачник для общеобразоват. учреждений / [А. Г. Мордкович и др.] ; под общ. редакцией А. Г. Мордковича. — М.: Мнемозина, 201 3.
Технические средства обучения
Мультимедийный проектор, компьютер, интерактивная доска, презентация, карточки для рефлексии, раздаточный материал для самостоятельной работы.
Дидактические задачи этапов урока
Организационный(этап мотивации)
Создать условия для формирования внутренней потребности учеников во включении в учебную деятельность, положительного настроя на плодотворную работу
2
Актуализация знаний и пробное учебное действие
Создать условия для осознания потребности к построению пробного учебного действия
3
Выявление места и причины затруднения
Создать условия для выявления и фиксации места и причины затруднения.
4
Открытие нового знания
Создать условия для построения и фиксации нового знания. Исследовательская работа в группах.
5
Первичное закрепление. Самостоятельная работа с самопроверкой по эталону
Создать условия для применения нового знания в типовых заданиях, для выявления и коррекции собственных ошибок
6
Включение в систему знаний и повторение
Создать условия для включения нового знания в систему знаний, повторение и закрепление ранее изученного
7
Рефлексия учебной деятельности на уроке
Соотнесение цели урока и его результатов, самооценка работы на уроке, осознание метода построения нового знания.
Технология изучения
ОрганизационныйМетапредметные:
регулятивные:
формировать способность к мобилизации сил и
организация своей учебной деятельности
коммуникативные:
уметь слушать учителя, совместно договариваться о порядке и форме общения, следовать им
познавательные:
расширение кругозора
личностные:
самоопределение, настрой на урок
– У вас на столе лежат карточки, представьте, что это вы и закончите рисунок:

Иду на урок
— Весь реальный мир состоит из множества тел. Эти тела в любой момент времени взаимодействуют друг с другом на различных уровнях: химическом, физическом, информационном. Так, на уроках физики вы изучаете зависимость силы тока от сопротивления. Из жизни мы знаем о зависимости радиуса колеса и числа совершаемых им оборотов на определенном отрезке пути. Умение анализировать эти взаимодействия или зависимости сделает вас успешными в своей деятельности!
Сегодня нам предстоит провести небольшое собственное исследование. Пусть оно не такое значимое, как открытия ученых. Ведь как сказал Пойа, «Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия».
Подготовка класса к работе
Обозначают своё настроение
Настраиваются на исследовательскую работу на уроке
Актуализация знаний и пробное учебное действие
Предметные:
актуализация опорных знаний обучающихся по теме «Свойства функций»
Метапредметные:
регулятивные:
контроль в форме сличения результата с заданным эталоном
коммуникативные:
уметь слушать и понимать других; оформлять мысли в устной и письменной форме
познавательные:
анализировать, сравнивать
личностные:
уметь ясно, точно, грамотно излагать свои мысли, исправлять и дополнять ответы других учащихся
— Устная работа
На рисунке изображен график функции на отрезке [- 3; 2].
1) Найдите значение аргумента, при котором значение функции равно – 1.
2) Укажите наибольшее значение функции.
3) Укажите промежуток, в котором функция возрастает. В каком убывает?
4) Найдите область значений функции.


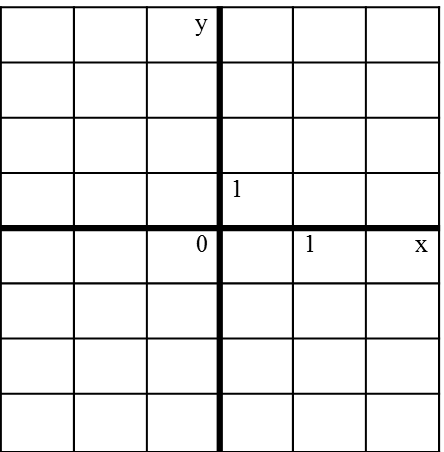
5) Укажите области определения следующих функций (слайд презентации проецируется на доску)
y=x2+8, y=4x-1/5, y=2x, y=7-5x,
y=2/x, y= 14x2, y= -10/x
Устно выполняют предложенные задания
Выявление места и причины затруднения
Предметные:
уметь отличать аналитическую запись известных функций Метапредметные:
регулятивные:
уметь проговаривать последовательность действий на уроке; высказывать свое предположение
коммуникативные:
умение полно и точно излагать свои мысли
аргументация своего мнения
планирование учебного сотрудничества
познавательные:
уметь отличать новое от уже известного, преобразовывать информацию из одной формы в другую; анализировать, сравнивать, классифицировать и обобщать
личностные:
уметь ясно, точно, грамотно излагать свои мысли
— Разбейте указанные функции на группы. Сколько разных групп у вас получилось? Как называются следующие функции, заданные формулами? Известны вам их графики и свойства?
3. Почему последняя группа функций, где числитель k=2 и -10, а в знаменателе переменная х, вызвала затруднение? В чём проблема?
(Незнакомы с данной функцией).
4. Какова цель урока? (Познакомиться с функцией y=k/x, ее свойствами и графиком.)
Записываем число, классная работа
и тему урока: “Функция y=k/x, ее свойства и график”.
Классифицируют функции на группы
Сравнивают полученный результат с результатами других
Пытаются сформулировать цели и тему урока
Записывают тему урока
Мотивированы к новой учебной деятельности
Открытие нового знания
Предметные:
соотнесение условия задачи с математической моделью;
образец оформления типовых задач; вывод формулы обратной пропорциональности, построение графика, знание свойств
Метапредметные:
регулятивные:
уметь проговаривать последовательность действий
контроль, коррекция
коммуникативные:
планирование учебного сотрудническтва
познавательные:
выдвижение гипотез, выведение следствий.
личностные:
смыслообразование, самоопределение
— Предлагаю задачи для решения в парах по рядам: №1- 1 ряд, №2 – 2 ряд, №3 – 3 ряд. Задача № 1. Скорость пешехода V км/ч; t ч – время. Сколько времени потребуется пешеходу, чтобы пройти 12 км. Выразить зависимость t от V.
Задача № 2. Площадь прямоугольника 60 кв. см. Одна сторона прямоугольника а см, другая b см. Выразить зависимость b от а.
Задача № 3. p руб. — цена товара, m — количество товара. Сколько товара можно купить на 500 руб? Выразить зависимость m от p.
— А теперь проверьте парную работу.
— Как называются переменные a, v, p?
— Как называются переменные m, b, t?
— Запишите каждую зависимость в виде функции?
Что общего и в чем различие этих формул?
— Составить функцию, которая является обобщением рассмотренных зависимостей.
— Но что будет происходить с у, если х увеличить в 2 раза? А что произойдет с у, если х уменьшить в 2 раза?
Аналогичная работа проводится с увеличением (уменьшением) в 4 раза.
Определение. Функция, заданная формулой 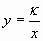 , где y-зависимая переменная, x-независимая переменная и k
, где y-зависимая переменная, x-независимая переменная и k  0, называется обратной пропорциональностью.
0, называется обратной пропорциональностью.
Детально рассмотрим эту зависимость с помощью графика на примере функции 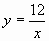 .
.
функции 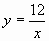 .
.
Как построить график незнакомой нам функции?
А как вы думаете, как будет называться график этой функции?
Построение графика функции.
Составить таблицу значений (взять значения аргумента с расчетом, чтобы положение графика определялось с достаточной полнотой).
Отметить точки на координатной плоскости.

Соединить точки линией.
(Все учащиеся строят в тетради, один ученик на интерактивной доске)
— Давайте перечислим свойства этой функции.
(Учащиеся с помощью учителя перечисляют свойства построенной функции).
— Как по вашему мнению, можно назвать такую зависимость переменных?
Работают по рядам в парах, отвечают на вопросы, пытаются выразить зависимость одной переменной от другой
Сверяют с образцом на слайде
1 ряд 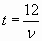 2 ряд
2 ряд 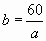
3 ряд 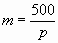
Определяют зависимые и независимые переменные в функции
Учащиеся с помощью учителя составляют формулу
Обсуждают фронтально решение задачи.
Учащиеся делают вывод из своих наблюдений.
Вывод: при увеличении одной переменной в несколько раз вторая переменная уменьшается во столько же раз. И, наоборот, при уменьшении одной переменной в несколько раз вторая переменная увеличивается во столько же раз. Обратная пропорциональность.
Открытие нового знания
— Как построить график незнакомой нам функции?
Построение графика функции.
1.Составить таблицу значений Нам сначала удобнее проводить вычисления, придавая аргументу положительные значения, а затем — только отрицательные.
2.Отметить точки на координатной плоскости.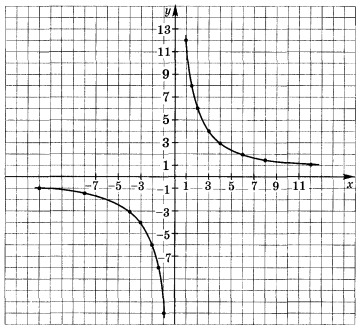
3.Соединить точки линией.
Историческая справка. Полученная кривая называется гиперболой, что в переводе с греческого означает «прохожу через что-либо» и с течением времени получило второе смысловое значение «преувеличение». Одним из первых, кто начал изучать эту кривую, был ученик знаменитого Платона, древнегреческий
математик Менехм в IV в. до н. э., но так и не сумел ее полностью изучить. А вот полностью исследовал свойства гиперболы и дал ей название крупнейший геометр древности Апполоний Пергский в III в. до н. э.
Гипербола состоит из двух веток.
— Давайте перечислим свойства этой функции
(свойства функции появляются на слайде презентации).
Физкультминутка.
Почти 90% всей информации человек
воспринимает глазами. Если устают глаза,
с снижается наше внимание и активность. Да-
вайте перед следующей задачей дадим отдых
глазам и себе.
Все учащиеся строят в тетради, один ученик на интерактивной доске
Учащиеся с помощью учителя перечисляют свойства построенной функции
1. Закройте глаза на несколько секунд, сильно
напрягая глазные мышцы, затем раскройте их,
расслабив мышцы. Повторите 3-4 раза.
2. Посмотрите на переносицу и задержите
взор. Затем посмотрите вдаль. Повторите 3-4
раза.
3. Медленно наклоняйте голову: вперед –
влево – вправо — назад. Повторите 3-4 раза.
4. Встаньте. Сделайте глубокий вздох- руки
поднимите вверх, и медленный выдох-
опустите руки. Садимся.
— А как вы думаете, если мы возьмем отрицательное число k, что произойдет с расположением графика в системе координат?
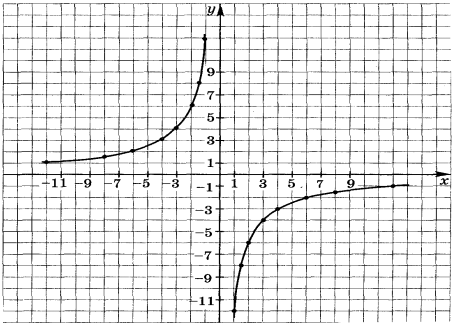
Исследовательская работа в группах.
Задание. Построить график функции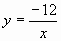 и описать свойства на раздаточных листах.
и описать свойства на раздаточных листах.
— Что произошло с графиком функции, при изменении коэффициента?
— А теперь откроем учебники и сравним полученный нами график с тем, что нам предлагает учебник?
— Вернёмся к графикам, которые вы получили.
На какие две группы можно разделить эти графики, чем отличаются эти группы? (Эти группы располагаются в разных четвертях)
— От чего зависит расположение графиков?
Выполняют упражнения для отдыха глаз
Делают предположения
Выполняют задания в группах, после выполнения один из учеников 1 группы презентует график функции, один из учеников 2 группы — свойства на доске.
Сверяют с образцом
Обобщают результаты исследования и делают вывод: расположение графика зависит от знака коэффициента обратной пропорциональности
Если k>0, то ветви гиперболы располагаются в 1 и 3 четвертях, функция убывает; если k<0, то ветви гиперболы располагаются во 2 и 4 четвертях, функция возрастает.
Первичное закрепление. Самостоятельная работа с самопроверкой по эталону
Предметные:
соотнесение условия задачи с математической моделью;
умение работать с функциональной зависимостью с разными компонентами
Метапредметные:
регулятивные:
работа по плану, с формулой; контроль, коррекция
коммуникативные:
умение с достаточной полнотой и точностью выражать свои мысли
познавательные:
формирование интереса к данной теме
личностные:
самоопределение, самопроверка
Самостоятельная работа в трех вариантах (дифференцированная по степени сложности): I вариант — облегченный, II – средней трудности, III — повышенной.
Карточка 1
Постройте график обратной пропорциональности y= — 6/x с помощью таблицы
x— 6
— 4
— 3
— 2
1
2
3
4
6
y
+ 1
+1,5
+ 2
+ 3
— 6
— 3
— 2
— 1,5
— 1
Карточка 2
Постройте график обратной пропорциональности y=16/x, предварительно заполнив таблицу
x— 8
— 4
— 2
— 1
1
2
4
8
y
Карточка 3
Постройте таблицу некоторых значений функции y=10/x и ее график.
— Работы проверяются по эталону. Ошибки исправляются, анализируются, выясняется их причина.
Выбирают вариант по степени сложности, выполняют самостоятельно
Осуществляют самопроверку по эталону, анализируют ошибки, исправляют
Включение в систему знаний и повторение
Предметные:
работа с формулой , графиком, свойствами функции обратной пропорциональности
Метапредметные:
регулятивные:
контроль в форме сличения достигнутого результата с поставленной целью
коммуникативные:
умение определять пути коррекции
познавательные:
умение ориентироваться в системе своих знаний
личностные:
осознание ответственности за выполненную работу
— Какие вопросы вы задали бы друг другу по новой теме урока?
Что является графиком функции y=k/x.
В каких координатных четвертях расположен график функции?
Какова область определения функции?
Какими свойствами обладает график функции обратной пропорциональной зависимости?
Из чего состоит гипербола?
1. – Укажите, какие из функций являются обратной пропорциональностью?
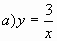 ;
; 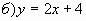 ; в)
; в) 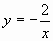 ; г)
; г) 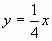 ; д)
; д) 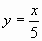 ;
;
е) 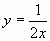 ; ж)
; ж)  ; з)
; з) 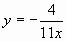 .
.
2. Перечислите свойства функции а) и в).
Задание на дом:
1. П.18. № 18.3 б — 1 вар., № 18.3 г – 2 вар.,
№ 18.6
2. Подготовить сообщения на тему “Применение функции в различных областях науки, в литературе”.
Ориентируются в своих знаниях и умениях, задают вопросы, подводят итог урока
Записывают домашнее задание, п.2 – по желанию на выбор
Рефлексия учебной деятельности на уроке
Предметные:
фиксирование нового содержания
Метапредметные:
регулятивные:
осознавать конечный результат решения проблемы;
оценивание собственной деятельности на уроке
коммуникативные:
умение анализировать собственные успехи, неудачи, определять пути коррекции
познавательные:
умение анализировать,
классифицировать и обобщать факты и явления
личностные:
способность к самооценке на основе критерия успешности учебной деятельности
– У вас на столе лежат карточки, представьте, что это вы и закончите рисунок:

После урока
Сравните настроение в начале и в конце урока.
В начале урока мы ставили цель и задачи. Теперь подведём итоги проделанной работе. Оцените каждый свою работу на уроке по от 3 до 5 баллов: 3, 4 или 5 (на уроке открытия нового знания оценку можно поставить по желанию).
Сегодня, ребята, вы все выступили в роли исследователей, вывели
формулу новой функции «обратная пропорциональность», исследовали график и свойства функции. Молодцы!
Определяют свое настроение, сравнивают его с настроением в начале урокаСтавят себе оценку за работу на уроке и сдают карточки