Что такое парабола, каноническое уравнение, как найти координаты вершины параболы формула, построение оси симметрии по квадратному уравнению

Что такое парабола знают, пожалуй, все. А вот как ее правильно, грамотно использовать при решении различных практических задач, разберемся ниже.

Сначала обозначим основные понятия, которые дает этому термину алгебра и геометрия. Рассмотрим все возможные виды этого графика.

Узнаем все основные характеристики этой функции. Поймем основы построения кривой (геометрия). Научимся находить вершину, другие основные величины графика данного типа.

Узнаем: как правильно строится искомая кривая по уравнению, на что надо обратить внимание. Посмотрим основное практическое применение этой уникальной величины в жизни человека.

Что такое парабола и как она выглядит

Алгебра: под этим термином понимается график квадратичной функции.

Геометрия: это кривая второго порядка, имеющая ряд определенных особенностей:

1. Любая прямая пересекает на плоскости искомую линию в 2-х точках – так называемые, «нули» (кроме основного экстремума графика).
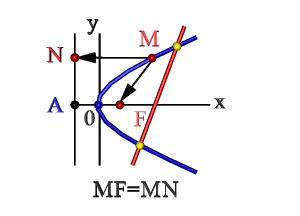
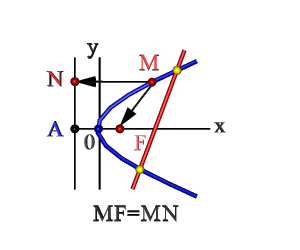
2. Множество точек плоскости ХОY (М), расстояние FM которых до F = расстоянию MN до прямой Где F – фокус, AN – директриса. Эти понятия рассмотрим ниже.

Каноническое уравнение параболы

На рисунке изображена прямоугольная система координат (XOY), экстремум, направление ветвей чертежа функции вдоль оси абсцисс.

Каноническое уравнение имеет вид:

y2 = 2 * p * x,

где коэффициент p – фокальный параметр параболы (AF).

В алгебре оно запишется иначе:

y = a x2 + b x + c (узнаваемый шаблон: y = x2).

Свойства и график квадратичной функции

Функция обладает осью симметрии и центром (экстремум). Область определения – все значения оси абсцисс.

Область значений функции – (-∞, М) или (М, +∞) зависит от направления ветвей кривой. Параметр М тут означает величину функции в вершине линии.

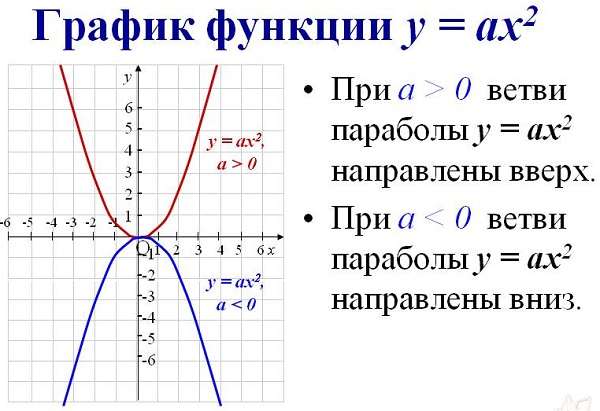
Как определить, куда направлены ветви параболы

Чтобы найти направление кривой такого типа из выражения, нужно определить знак перед первым параметром алгебраического выражения. Если а ˃ 0, то они направлены вверх. Если наоборот – вниз.

Как найти вершину параболы по формуле

Нахождение экстремума является основным этапом при решении множества практических задач. Конечно, можно открыть специальные онлайн калькуляторы, но лучше это уметь делать самому.

Как же ее определить? Есть специальная формула. Когда b не равно 0, надо искать координаты этой точки.

Формулы нахождения вершины:

• x0 = -b / (2 * a),
• y0 = y (x0).

Пример.

Имеется функция у = 4 * x2 + 16 * x – 25. Найдём вершины этой функции.

Для такой линии:

• х = -16 / (2 * 4) = -2,
• y = 4 * 4 — 16 * 2 — 25 = 16 — 32 — 25 = -41.

Получаем координаты вершины (-2, -41).

Смещение параболы

Классический случай, когда в квадратичной функции y = a x2 + b x + c, второй и третий параметры равны 0, а = 1 – вершина находится в точке (0, 0).

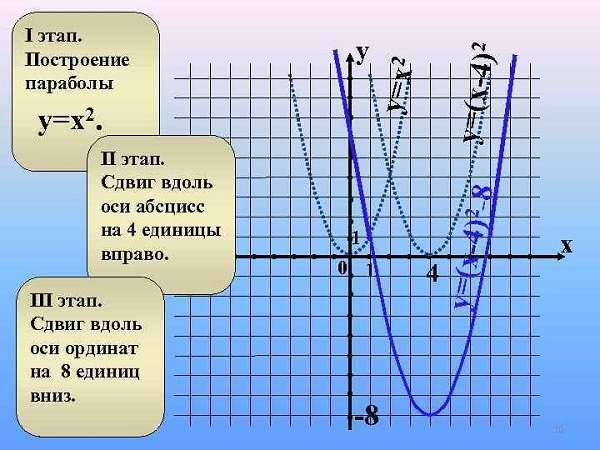
Движение по осям абсцисс или ординат обусловлено изменением параметров b и c соответственно. Сдвиг линии на плоскости будет осуществляться ровно на то количество единиц, чему равно значение параметра.

Пример.

Имеем: b = 2, c = 3.

Это означает, что классический вид кривой сдвинется на 2 единичных отрезка по оси абсцисс и на 3 по оси ординат.

Как строить параболу по квадратному уравнению

Школьникам важно усвоить, как правильно начертить параболу по заданным параметрам.

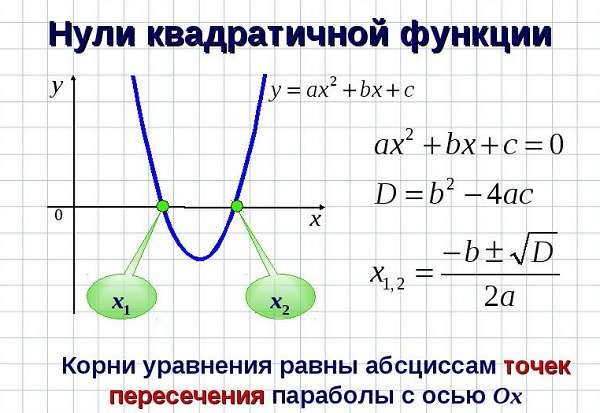
Анализируя выражения и уравнения, можно увидеть следующее:

1. Точка пересечения искомой линии с вектором ординат будет иметь значение, равное величине с.
2. Все точки графика (по оси абсцисс) будут симметричны относительно основного экстремума функции.

Кроме того, места пересечения с ОХ можно найти, зная дискриминант (D) такой функции:

D = (b2 4 * a * c).

Для этого нужно приравнять выражение к нулю.

Наличие корней параболы зависит от результата:

• D ˃ 0, то х1, 2 = (-b ± D0,5) / (2 * a),
• D = 0, то х1, 2 = -b / (2 * a),
• D ˂ 0, то нет точек пересечения с вектором ОХ.

Получаем алгоритм построения параболы:

• определить направление ветвей,
• найти координаты вершины,
• найти пересечение с осью ординат,
• найти пересечение с осью абсцисс.

Пример 1.

Дана функция у = х2 5 * х + 4. Необходимо построить параболу. Действуем по алгоритму:

1. а = 1, следовательно, ветви направлены вверх,
2. координаты экстремума: х = (-5) / 2 = 5/2, y = (5/2)2 — 5 * (5/2) + 4 = -15/4,
3. с осью ординат пересекается в значении у = 4,
4. найдем дискриминант: D = 25 — 16 = 9,
5. ищем корни:

• Х1 = (5 + 3) / 2 = 4, (4, 0),
• Х2 = (5 — 3) / 2 = 1, (1, 0).

По полученным точкам можно построить параболу.

Пример 2.

Для функции у = 3 * х2 2 * х 1 нужно построить параболу. Действуем по приведенному алгоритму:

1. а = 3, следовательно, ветви направлены вверх,
2. координаты экстремума: х = (-2) / 2 * 3 = 1/3, y = 3 * (1/3)2 — 2 * (1/3) — 1 = -4/3,
3. с осью у будет пересекаться в значении у = -1,
4. найдем дискриминант: D = 4 + 12 = 16. Значит корни:

• Х1 = (2 + 4) / 6 = 1, (1,0),
• Х2 = (2 — 4) / 6 = -1/3, (-1/3, 0).

По полученным точкам можно построить параболу.

Директриса, эксцентриситет, фокус параболы

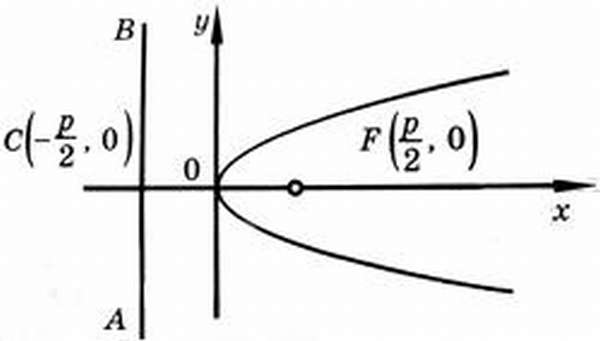
Исходя из канонического уравнения, фокус F имеет координаты (p/2, 0).

Прямая АВ – директриса (своего рода хорда параболы определенной длины). Ее уравнение: х = -р/2.

Эксцентриситет (константа) = 1.

Заключение

Мы рассмотрели тему, которую изучают школьники в средней школе. Теперь вы знаете, глядя на квадратичную функцию параболы, как найти её вершину, в какую сторону будут направлены ветви, есть ли смещение по осям, и, имея алгоритм построения, сможете начертить её график.

tvercult.ru

Как построить параболу в Excel

Построение параболы является одной из известных математических операций. Довольно часто она применяется не только в научных целях, но и в чисто практических. Давайте узнаем, как совершить данную процедуру при помощи инструментария приложения Excel.

Создание параболы

Парабола представляет собой график квадратичной функции следующего типа f(x)=ax^2+bx+c. Одним из примечательных его свойств является тот факт, что парабола имеет вид симметричной фигуры, состоящей из набора точек равноудаленных от директрисы. По большому счету построение параболы в среде Эксель мало чем отличается от построения любого другого графика в этой программе.

Создание таблицы

Прежде всего, перед тем, как приступить к построению параболы, следует построить таблицу, на основании которой она и будет создаваться. Для примера возьмем построение графика функции f(x)=2x^2+7.

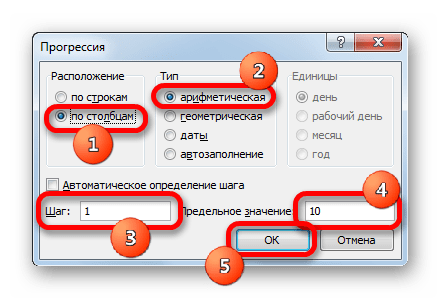
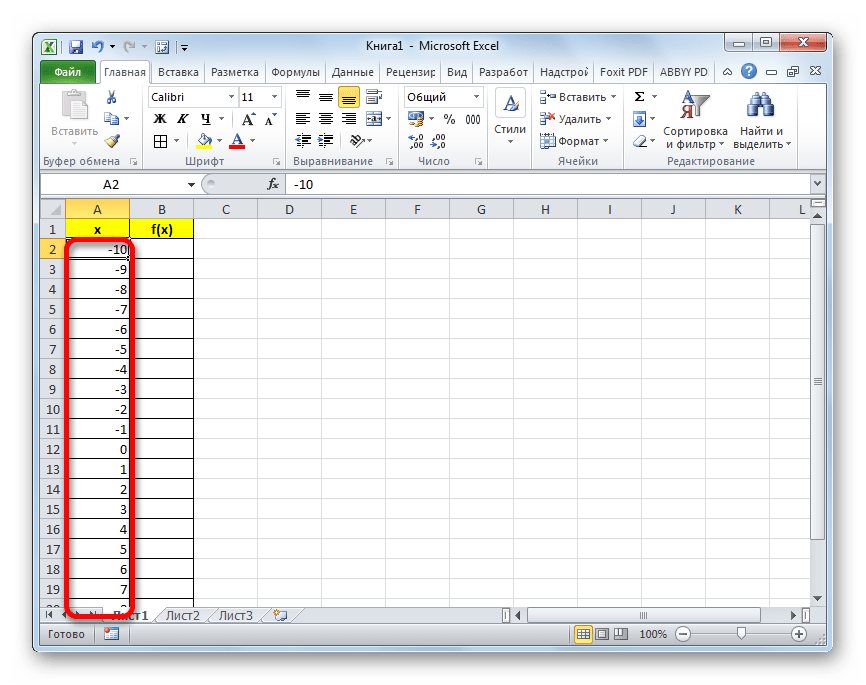
1. Заполняем таблицу значениями x от -10 до 10 с шагом 1. Это можно сделать вручную, но легче для указанных целей воспользоваться инструментами прогрессии. Для этого в первую ячейку столбца «X» заносим значение «-10». Затем, не снимая выделения с данной ячейки, переходим во вкладку «Главная». Там щелкаем по кнопке «Прогрессия», которая размещена в группе «Редактирование». В активировавшемся списке выбираем позицию «Прогрессия…».



2. Выполняется активация окна регулировки прогрессии. В блоке «Расположение» следует переставить кнопку в позицию «По столбцам», так как ряд «X» размещается именно в столбце, хотя в других случаях, возможно, нужно будет выставить переключатель в позицию «По строкам». В блоке «Тип» оставляем переключатель в позиции «Арифметическая».

   В поле «Шаг» вводим число «1». В поле «Предельное значение» указываем число «10», так как мы рассматриваем диапазон x от -10 до 10 включительно. Затем щелкаем по кнопке «OK».



3. После этого действия весь столбец «X» будет заполнен нужными нам данными, а именно числами в диапазоне от -10 до 10 с шагом 1.



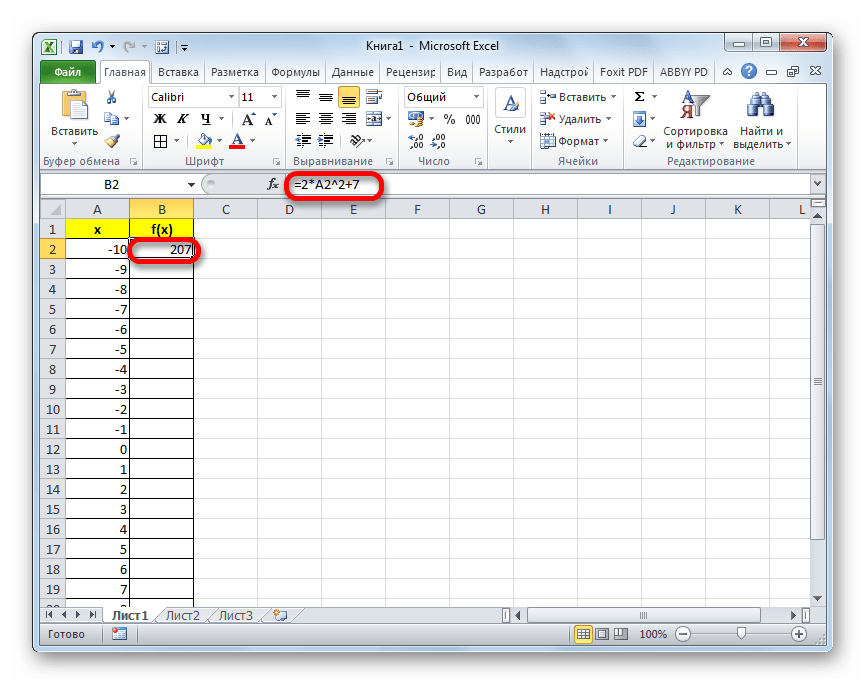
4. Теперь нам предстоит заполнить данными столбец «f(x)». Для этого, исходя из уравнения (f(x)=2x^2+7), нам нужно вписать в первую ячейку данного столбца выражение по следующему макету:

   =2*x^2+7

   Только вместо значения x подставляем адрес первой ячейки столбца «X», который мы только что заполнили. Поэтому в нашем случае выражение примет вид:

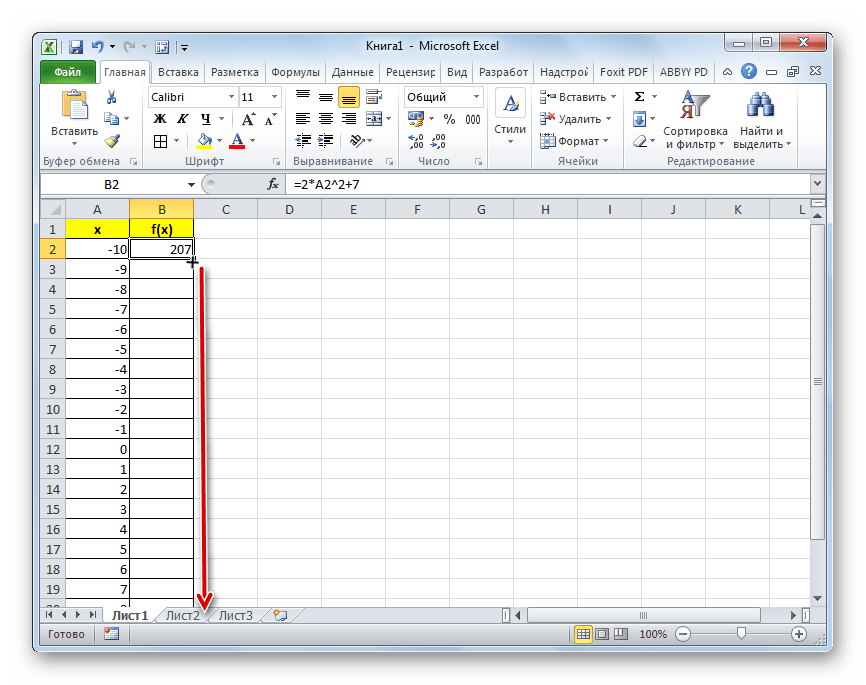
   =2*A2^2+7



5. Теперь нам нужно скопировать формулу и на весь нижний диапазон данного столбца. Учитывая основные свойства Excel, при копировании все значения x будут поставлены в соответствующие ячейки столбца «f(x)» автоматически. Для этого ставим курсор в правый нижний угол ячейки, в которой уже размещена формула, записанная нами чуть ранее. Курсор должен преобразоваться в маркер заполнения, имеющий вид маленького крестика. После того, как преобразование произошло, зажимаем левую кнопку мыши и тянем курсор вниз до конца таблицы, после чего отпускаем кнопку.



6. Как видим, после этого действия столбец «f(x)» тоже будет заполнен.

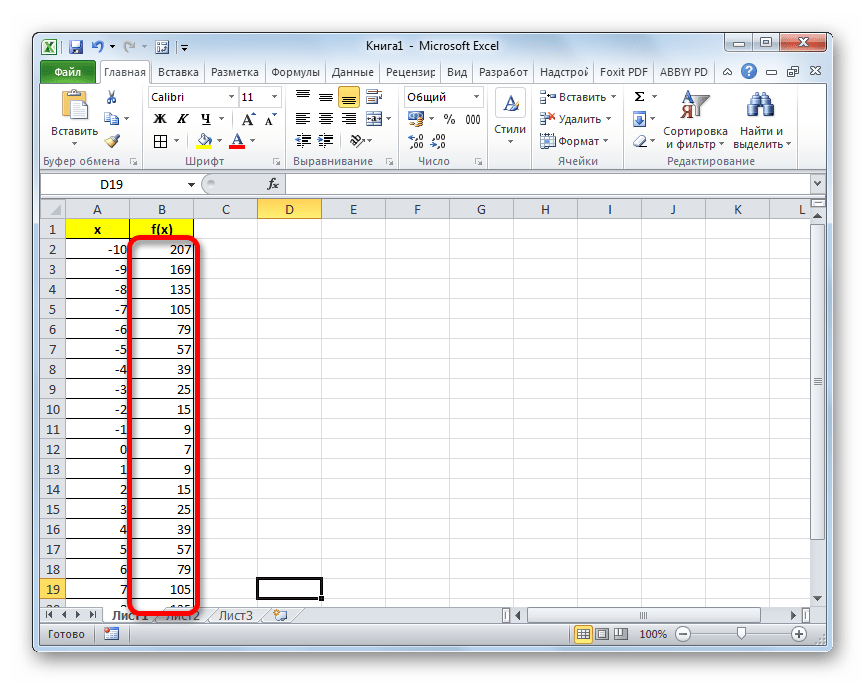
На этом формирования таблицы можно считать законченным и переходить непосредственно к построению графика.

Урок: Как сделать автозаполнение в Экселе

Построение графика

Как уже было сказано выше, теперь нам предстоит построить сам график.

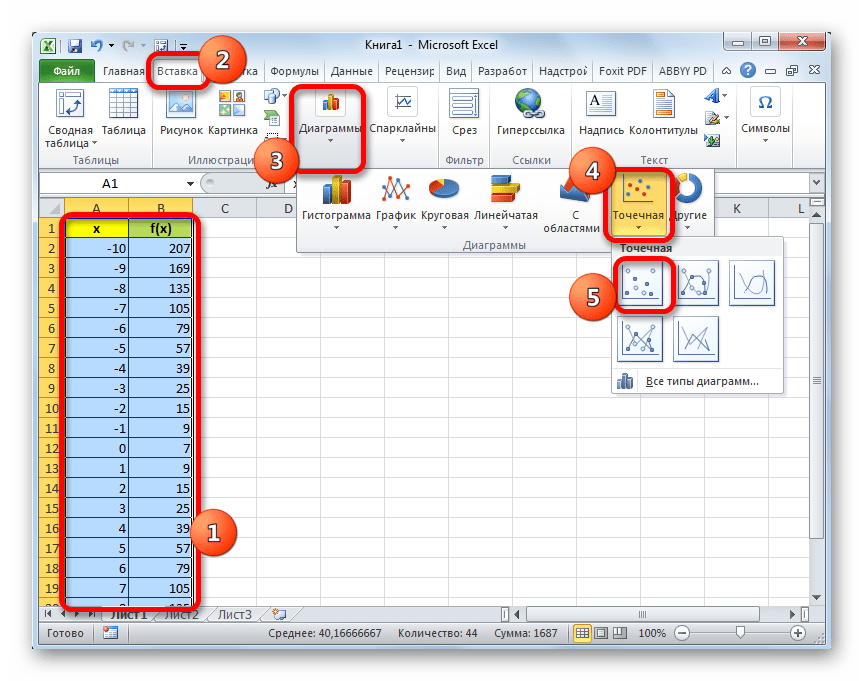
1. Выделяем таблицу курсором, зажав левую кнопку мыши. Перемещаемся во вкладку «Вставка». На ленте в блоке «Диаграммы» щелкаем по кнопке «Точечная», так как именно данный вид графика больше всего подходит для построения параболы. Но и это ещё не все. После нажатия на вышеуказанную кнопку открывается список типов точечных диаграмм. Выбираем точечную диаграмму с маркерами.



2. Как видим, после этих действий, парабола построена.

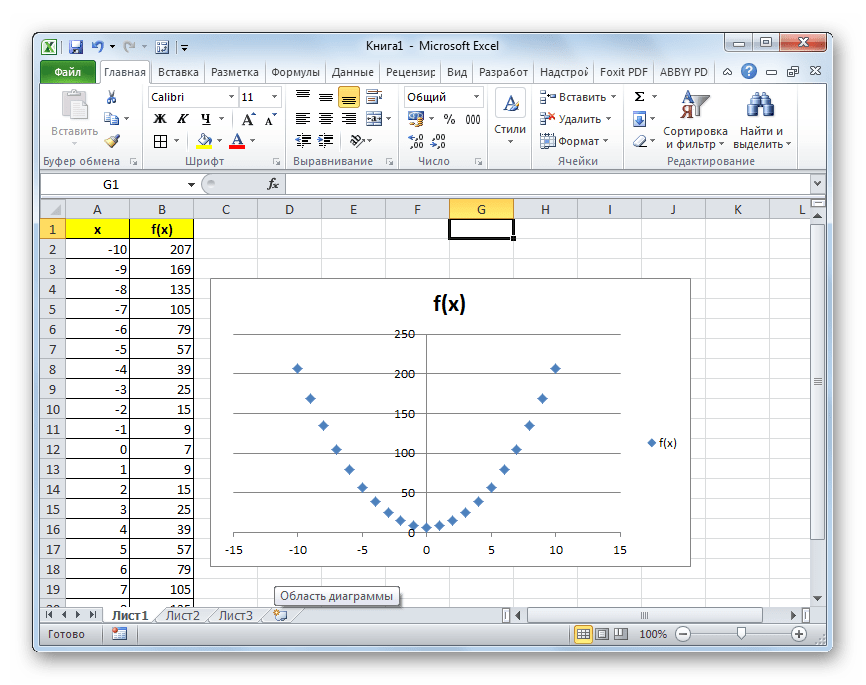
Урок: Как сделать диаграмму в Экселе

Редактирование диаграммы

Теперь можно немного отредактировать полученный график.

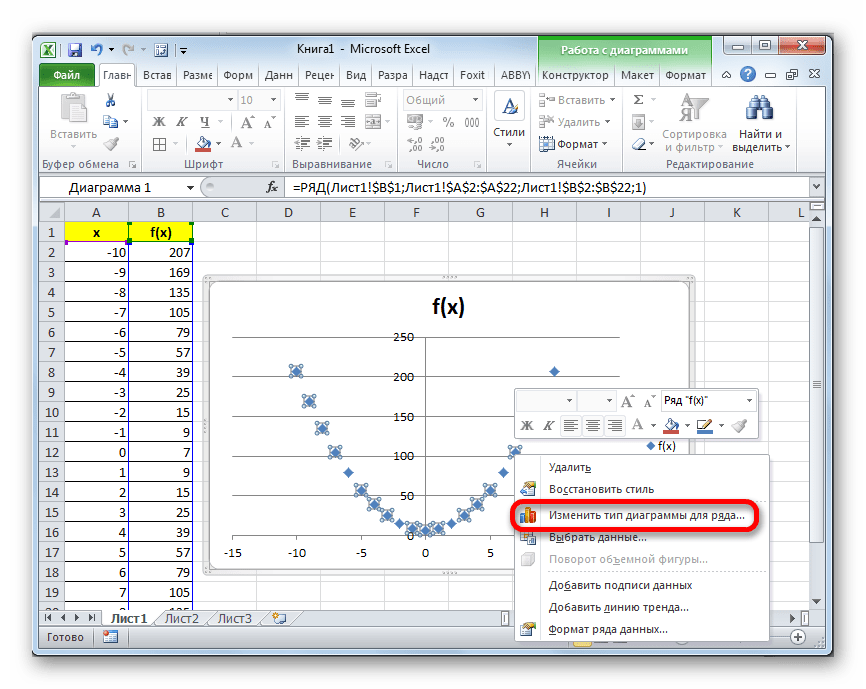
1. Если вы не хотите, чтобы парабола отображалась в виде точек, а имела более привычный вид кривой линии, которая соединяет эти точки, кликните по любой из них правой кнопкой мыши. Открывается контекстное меню. В нем нужно выбрать пункт «Изменить тип диаграммы для ряда…».



2. Открывается окно выбора типов диаграмм. Выбираем наименование «Точечная с гладкими кривыми и маркерами». После того, как выбор сделан, выполняем щелчок по кнопке «OK».



3. Теперь график параболы имеет более привычный вид.

Кроме того, можно совершать любые другие виды редактирования полученной параболы, включая изменение её названия и наименований осей. Данные приёмы редактирования не выходят за границы действий по работе в Эксель с диаграммами других видов.

Урок: Как подписать оси диаграммы в Excel

Как видим, построение параболы в Эксель ничем принципиально не отличается от построения другого вида графика или диаграммы в этой же программе. Все действия производятся на основе заранее сформированной таблицы. Кроме того, нужно учесть, что для построения параболы более всего подходит точечный вид диаграммы.

Мы рады, что смогли помочь Вам в решении проблемы.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

ДА НЕТ

lumpics.ru

Построение графика квадратичной функции | Алгебра

Построение графика квадратичной функции продолжим рассмотрением способа, базирующегося на преобразованиях  координатной плоскости.

II способ.

1) Находим координаты вершины параболы y=ax²+bx+c — точку (xo; yo)

2) Осуществляем параллельный перенос начала отсчёта — точки O (0; 0) —  в

точку (xo; yo). При таком преобразовании новыми осями координат x’ и y’ становятся прямые y=yo и x=xo.

2) Строим параболу y=x²  (если a>o)либо y= -x² (если a<0) с вершиной в новом начале отсчёта (достаточно отметить базовые точки).

3) От вершины строим график функции y=ax². При |a|>1 график может быть получен растяжением от оси y=y0 в |a| раз, при |a|<1 — сжатием в |a| раз.

(Вариант — график функции y=ax² можно построить с началом отсчёта в точке O (0; 0), а затем осуществить его параллельный перенос).

Примеры.

1) Построить график функции y=3x²-24x+43.

Решение:

y=3x²-24x+43 — квадратичная функция. Её график — парабола, ветви которой направлены вверх (так как a=3>0). Координаты вершины параболы

   

   

Точка (4; -5) — новое начало отсчёта. Построим параболу y=x² с вершиной в этой точке (достаточно отметить базовые точки — 1 единица вправо, 1 — вверх, 2 вправо. 4 — вверх, 1 — влево, 1 — вверх, 2 — влево, 4 — вверх.

График функции y=3x² может быть получен из графика y=x² растяжением от оси x’ (x= -5) в 3 раза:

Построение графика квадратичной функции                     y=3x²-24x+43

2) Построить график функции y= -0,5x²-2x+1

Решение:

y= -0,5x²-2x+1 — квадратичная функция. График — парабола ветвями вниз (так как a= -0,5<0).

Координаты вершины параболы

   

   

Точка (-2; 3) — новое начало отсчёта. Построим параболу y= -x² с вершиной в этой точке. График функции

   

может быть получен из графика y= -x² сжатием к оси x’ (y=3) в 2 раза.

Построение графика функции y= -0,5x²-2x+1

Для построения графика квадратичной функции этим способом нужно хорошее владение навыками геометрических преобразований графиков.

Если координаты вершины параболы не являются целыми числами, этот способ менее удобен, чем построение по точкам.

Какой бы способ вы для себя ни выбрали, важно вовремя качественно усвоить данную тему, поскольку с построением графиков функций в алгебре придётся иметь дело ещё не раз.

www.algebraclass.ru

Как построить параболу? Как построить график?

Урок: как построить параболу или квадратичную функцию?

Строить параболу очень легко самое главное запомнить последовательность несложных действий.
1 действие: запомнить общую формулу параболы y=ax^2+bx+c и что график симметричен относительно оси OY
2 действие: вытекает из первого рассмотрим свободный член c в этой точке пересекается парабола с осью OY. Если а>0 то ветви параболы смотрят вверх, а 3 действие: найти вершину по формуле x=(-b)/2a, а чтоб у просчитать то нужно x подставить в формулу y=ax^2+bx+c
4 действие: найти точки пересечения параболы с осью OX или по-другому они называются корни уравнения. Чтобы найти корни мы уравнение приравниваем к 0 ax^2+bx+c=0
Здесь могут быть подпункты, так как уравнения параболы могут быть разными.
a)Полное квадратное уравнение имеет вид ax^2+bx+c=0 и решается по дискриминанту
b)Неполное квадратное уравнение вида ax^2+bx=0. Чтобы его решить нужно вынести х за скобки и потом каждый множитель прировнять к 0. х(ax+b)=0, х=0 и ax+b=0.
c)Неполное квадратное уравнение вида ax^2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
5 действие: делать не обязательно, но оно поможет вам построить более точный график параболы. Это взять несколько дополнительных точек для построения функции.

И так теперь на примере разберем все по действиям
1)y=x^2+4x+3
2) c=3 значит парабола пересекает OY в точке х=0 у=3. Ветви параболы смотрят вверх так как а=1 1>0.
3) a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2)^2+4*(-2)+3=4-8+3=-1 вершина находится в точке (-2;-1)
4) Найдем корни уравнения x^2+4x+3=0
По дискриминанту находим корни
a=1 b=4 c=3
D=b^2-4ac=16-12=4
x=(-b±√(b^2-4ac))/2a
x1=(-4+2)/2=-1
x2=(-4-2)/2=-3

5) Возьмем несколько произвольных точек, так как у нас вершина лежит в точке (-2;-1) нам выгодно брать точки возле х=-2

х -4 -3 -1 0
у 3 0 0 3

Подставляем вместо х в уравнение y=x^2+4x+3 значения
y=(-4)^2+4*(-4)+3=16-16+3=3
y=(-3)^2+4*(-3)+3=9-12+3=0
y=(-1)^2+4*(-1)+3=1-4+3=0
y=(0)^2+4*(0)+3=0-0+3=3
Видно по значениям что значения у симметричны

1)y=-x^2+4x
2)c=0 значит парабола пересекает OY в точке х=0 у=0. Ветви параболы смотрят вниз так как а=-1 -1 3)a=-1 b=4 c=0 x=(-b)/2a=(-4)/(2*(-1))=2 y=-(2)^2+4*2=-4+8=4 вершина находится в точке (2;4)
4)Найдем корни уравнения -x^2+4x=0
Неполное квадратное уравнение вида ax^2+bx=0. Чтобы его решить нужно вынести х за скобки и потом каждый множитель прировнять к 0.
х(-x+4)=0, х=0 и x=4.
5)Возьмем несколько произвольных точек, так как у нас вершина лежит в точке (2;4) нам выгодно брать точки возле х=2

х 0 1 3 4
у 0 3 3 0

Подставляем вместо х в уравнение y=-x^2+4x значения
y=0^2+4*0=0
y=-(1)^2+4*1=-1+4=3
y=-(3)^2+4*3=-9+13=3
y=-(4)^2+4*4=-16+16=0
Видно по значениям что значения у симметричны

1)y=x^2+4
2)c=4 значит парабола пересекает OY в точке х=0 у=4. Ветви параболы смотрят вверх так как а=1 1>0.
3)a=1 b=0 c=4 x=(-b)/2a=0/(2*(1))=0 y=(0)^2+4=4 вершина находится в точке (0;4)
4)Найдем корни уравнения x^2+4=0
Неполное квадратное уравнение вида ax^2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
x2=4
x1=2
x2=-2

5)Возьмем несколько произвольных точек, так как у нас вершина лежит в точке (0;4) нам выгодно брать точки возле х=0

х -2 -1 1 2
у 0 3 3 0

Подставляем вместо х в уравнение y=x^2+4 значения
y=(-2)^2+4=4+4=8
y=(-1)^2+4=1+4=5
y=1^2+4=1+4=5
y=2^2+4=4+4=8
Видно по значениям что значения у симметричны

ege-gia.blogspot.com