Прямая пропорциональность и ее график
График прямой пропорциональности
В 7 и 8 классе изучается график прямой пропорциональности.
Как построить график прямой пропорциональности?
Рассмотрим на примерах график прямой пропорциональности.
График прямой пропорциональности формула
График прямой пропорциональности представляет функцию прямая пропорциональность.
В общем виде прямая пропорциональность имеет формулу
y = kx
где k – коэффициент прямой пропорциональности.
От величины и знака коэффициента прямой пропорциональности зависит угол наклона графика прямой пропорциональности по отношению к оси икс.
График прямой пропорциональности проходит
График прямой пропорциональности проходит через начало координат.
График прямой пропорциональности есть прямая. Прямая задается двумя точками.
Таким образом при построении графика прямой пропорциональности достаточно определить положение двух точек.
Но одну из них мы всегда знаем – это начало координат.
Осталось найти вторую. Посмотрим пример построения графика прямой пропорциональности.
Постройте график прямой пропорциональности y = 2x
Задача.
Постройте график прямой пропорциональности, заданной формулой
y = 2x
Решение.
Область определения прямой пропорциональности есть все числа.
Берем любое число из области определения прямой пропорциональности, пусть это будет 1.
Найти значение функции при икс равное 1
y = 2x =
2 * 1 = 2
то есть при x = 1 получаем y = 2. Точка с этими координатами принадлежит графику функции y = 2x.
Мы знаем, что график прямой пропорциональности есть прямая, а прямая задается двумя точками.
Одну из них мы только что нашли, а второй для прямой пропорциональности всегда является начало координат.
Теперь мы готовы построить график функции y = 2x.
Отмечаем на координатной плоскости точку с координатами (1; 2).
Через данную точку и начало координат проводим прямую линию
Мы получили график прямой пропорциональности, заданной формулой y = 2x.
www.sbp-program.ru
График прямой пропорциональности
Построим график функции, заданной формулой у = 0,5х.
1. Область определения этой функции – множество всех чисел.
2. Найдем некоторые соответственные значения переменных х и у.
Если х = -4, то у = -2.
Если х = -3, то у = -1,5.
Если х = -2, то у = -1.
Если х = -1, то у = -0,5.
Если х = 0, то у = 0.
Если х = 1, то у = 0,5.
Если х = 2, то у = 1.
Если х = 3, то у = 1,5.
3. Отметим в координатной плоскости точки, координаты которых мы определили в пункте 2. Отметим, что построенные точки принадлежат некоторой прямой.
4. Определим, принадлежат ли этой прямой другие точки графика функции. Для этого найдем координаты еще нескольких точек графика.
Если х = -3,5, то у = -1,75.
Если х = -2,5, то у = -1,25.
Если х = -1,5, то у = -0,75.
Если х = -0,5, то у = -0,25.
Если х = 0,5, то у = 0,25.
Если х = 1,5, то у = 0,75.
Если х = 2,5, то у = 1,25.
Если х = 3,5, то у = 1,75.
Построив новые точки графика функции, замечаем, что они принадлежат той же прямой.
Если мы будем уменьшать шаг наших значений (брать, например, значения х через 0,1; через 0,01 и т.д.), мы будем получать другие точки графика, принадлежащие той же прямой и расположенные все более близко друг от драга. Множество всех точек графика данной функции есть прямая линия, проходящая через начало координат.
Т.о., график функции, заданной формулой у = kх, где k ≠ 0, есть прямая, проходящая через начало координат.
Если область определения функции, заданной формулой у = kх, где k ≠ 0, состоит не из всех чисел, то ее графиком служит подмножество точек прямой (например, луч, отрезок, отдельные точки).
Для построения прямой достаточно знать положение двух ее точек. Поэтому график прямой пропорциональности, заданной на множестве всех чисел, можно строить по любым двум его точкам (в качестве одной из них удобно брать начало координат).
Пусть, например, требуется построить график функции, заданной формулой у = -1,5х. Выберем какое-либо значение х, не равное 0, и вычислим соответствующее значение у.
Если х = 2, то у = -3.
Отметим на координатной плоскости точку с координатами
Основываясь на данном примере, можно доказать, что 
всякая прямая, проходящая через начало координат и не совпадающая с осями, является графиком прямой пропорциональности.
Доказательство.
Пусть дана некоторая прямая, проходящая через начало координат и не совпадающая с осями. Возьмем на ней точку с абсциссой 1. Обозначим ординату этой точки через k. Очевидно, что k ≠ 0. Докажем, что данная прямая является графиком прямой пропорциональности с коэффициентом k.
Действительно, из формулы у = kх следует, что если х = 0, то у = 0, если х = 1, то у = k, т.е. график функции, заданной формулой у = kх, где k ≠ 0, есть прямая, проходящая через точки (0; 0) и (1; k).
Т.к. через две точки можно провести только одну прямую, то данная прямая совпадает с графиком функции, заданной формулой у = kх, где k ≠ 0, что и требовалось доказать.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Прямая пропорциональность и её график
АДМИНИСТРАЦИЯ МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ «ГОРОД САРАТОВ»
МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 95 С УГЛУБЛЕННЫМ
ИЗУЧЕНИЕМ ОТДЕЛЬНЫХ ПРЕДМЕТОВ»
Методическая разработка
урока алгебры в 7 классе
по теме:
и её график».
Учитель математики
1 квалификационной категории
Горюнова Е.В.
2014 – 2015 учебный год
Пояснительная записка
к уроку по теме:
«Прямая пропорциональность и её график».
Учитель математики Горюнова Елена Викторовна.
Вашему вниманию представлен урок в 7 классе. Учитель работает по программе, составленной на основе Примерных программ основного общего образования и авторской программы для общеобразовательных учреждений Ю.Н. Макарычев. Алгебра.7-9 классы //Сборник программ по алгебре 7-9 классы. М.Просвещение, 2009 составитель Т.А. Бурмистрова. Программа соответствует учебнику алгебры Ю.Н. Макарычев , Н.Г Миндюк, К.И. Нешков., С.Б Суворова., под редакцией С.А. Теляковского «Алгебра 7 класс» (издательство «Просвещение» 2009 год).
На изучение темы «Функции» отводится 14 часов, из них 6 часа на раздел «Функции и их графики», 3 часа — на раздел «Прямая пропорциональность и её график» , 4 часа- на раздел «Линейная функция и её график» и 1ч К/Р.
ЦЕЛИ:
• Образовательные:
1. Организовать деятельность учащихся по восприятию темы «Прямая пропорциональность и её график» и первичному закреплению: определения прямой пропорциональности и построения её графика, формировать навыки грамотного построения графиков
2. Создавать условия для создания в памяти учащихся системы опорных знаний и умений, стимулировать поисковую деятельность
• Развивающие:
1. Развивать аналитико – синтезирующее мышления (способствовать развитию наблюдательности, умению анализировать, развитие умений классифицировать факты, делать обобщающие выводы).
2. Развивать абстрактное мышление (развитие умений выделять общие и существенные признаки, отличать несущественные признаки и отвлекаться от них).
3. Побуждать учеников к самоконтролю и взаимоконтролю .
• Воспитательные:
Прививать чувство уважения к одноклассникам, внимание к слову, способствовать воспитанию самостоятельности, ответственности, аккуратности при построении чертежей
Достижение этих целей выполняется с помощью ряда задач:
Формирование умения сочетать знания и навыки, которые обеспечивают успешное выполнение деятельности;
Вести работу над развитием связанной речи учащихся, умением ставить и разрешать проблемы.
Оборудование урока:
На уроке использовались индивидуальные карточки с заданиями и мультимедийный проектор, все факты об Р. Декарте были взяты учителем в Интернете с официальных сайтов СМИ и переработаны специально для данного урока с учётом темы урока, учебник.
Содержание урока:
Содержание урока соответствует программе и задачам урока.
Тип и структура урока:
Данный урок является уроком освоения новых знаний и навыков ( типы уроков по В.А. Онищуку), поэтому рационально было применить элементы исследовательской деятельности .
Реализация принципов обучения:
На уроке были реализованы принципы:
Научности обучения.
Принцип систематичности и последовательности в обучении был осуществлён при постоянной опоре на ранее изученный материал.
Сознательность, активность и самостоятельность учащихся достигалась в виде стимулирования познавательной активности с помощью эффективных приёмов и средств наглядности (таких как показ слайдов, предоставления исторических фактов и сведений из жизни математика и философа Р.Декарте, индивидуальных печатных листов учащихся.
На уроке был реализован принцип комфортности.
Формы и методы обучения:
Во время урока были применены различные формы обучения – это индивидуальная и фронтальная работа, взаимопроверка. Такие формы более рациональны для данного типа урока, так как позволяют ребёнку развивать самостоятельность мышления, критичность мысли, способность отстаивания своей точки зрения, умение сравнивать и делать выводы.
Основным методом данного урока является частично-поисковый метод, который характеризуется работой учащихся по решению проблемных познавательных задач.
Физ. минутка представляла собой одновременно и физические упражнения и закрепление только что изученного материала.
В конце урока целесообразно провести обобщение проведённой работы на уроке.
Общие результаты урока:
Считаю, что задачи, поставленные на урок, реализованы, дети применяли знания в новой ситуации, каждый мог высказать свою точку зрения. Использование наглядности в виде презентации, индивидуальных печатных листов учащихся позволяет мотивировать учащихся на каждом этапе урока и избегать перегрузки и переутомления учащихся.
Тема урока: «Прямая пропорциональность и ее график»
Дидактическая задача: знакомство с прямой пропорциональностью и построением ее графика.
Цели:
• Образовательные:
1. Организовать деятельность учащихся по восприятию темы «Прямая пропорциональность и её график» и первичному закреплению: определения прямой пропорциональности и построения её графика, формировать навыки грамотного построения графиков
2. Создавать условия для создания в памяти учащихся системы опорных знаний и умений, стимулировать поисковую деятельность
• Развивающие:
1. Развивать аналитико – синтезирующее мышления (способствовать развитию наблюдательности, умению анализировать, развитие умений классифицировать факты, делать обобщающие выводы).
2. Развивать абстрактное мышление (развитие умений выделять общие и существенные признаки, отличать несущественные признаки и отвлекаться от них).
3. Побуждать учеников к самоконтролю и взаимоконтролю
• Воспитательные:
Прививать чувство уважения к одноклассникам, внимание к слову, способствовать воспитанию самостоятельности, ответственности, аккуратности при построении чертежей.
Оборудование: компьютер, презентация, карточки на печатной основе с заданиями на каждого ученика.
План урока:
1.Организационный момент.
2.Мотивация урока.
3.Актуализация знаний.
4.Изучение нового материала.
5. Закрепление материала.
6. Итог урока.
Ход урока.
1.Организационный момент.
-Доброе утро, ребята! Мне бы хотелось начать урок со следующих слов. (Слайд 1)
Французский учёный Рене Декарт однажды заметил: «Мыслю, следовательно существую ».
Ребята приготовили сообщение о французском учёном Р.Декарте.
Рене Декарт больше известен как великий философ, чем математик. Но именно он был пионером современной математики, и его заслуги в этой области столь велики, что он по справедливости входит в число великих математиков современности.
Сообщение ученика: (Слайд 2)
Родился Декарт родился во Франции, в небольшом городке Лаэ. Отец его был юристом, мать умерла, когда Рене был 1 год. После окончания коллежа для сыновей аристократических семейств, он по примеру своего брата стал изучать правоведение. В 22–летнем возрасте уехал из Франции и в качестве офицера–добровольца служил в войсках разных военачальников, участвовавших в 13-летней войне. Декарт в своем философском учении развивал идею о всемогуществе человеческого разума, и поэтому преследовался католической церковью. Желая найти убежище для спокойной работы по философии и математике, которыми он интересовался с детства, Декарт в 1629 году поселился в Голландии, где прожил почти до конца жизни. Все крупные произведения Декарта по философии, математике, физике, космологии и физиологии написаны им в Голландии.
Математические труды Декарта собраны в его книге „Геометрия» (1637). В „Геометрии» Декарт дал основы аналитической геометрии и алгебры. Декарт первый ввел в математику понятие переменной функции. Он обратил внимание на то, что кривая на плоскости характеризуется уравнением, обладающим тем свойством, что координаты любой точки, лежащей на этой линии, удовлетворяют данному уравнению. Он разделил кривые, заданные алгебраическим уравнением, на классы в зависимости от наибольшей степени неизвестной величины в уравнении. Декарт ввел в математику знаки плюс и минус для обозначения положительных и отрицательных величин, обозначение степени и знак для обозначения бесконечно большой величины. Для переменных и неизвестных величин Декарт принял обозначения х, у, z, а для величин известных и постоянных —a.b.c , как известно, эти обозначения применяются в математике до сегодняшнего дня. Несмотря на то, что в области аналитической геометрии Декарт продвинулся не очень далеко, его труды оказали решающее влияние на дальнейшее развитие математики. На протяжении 150 лет математика развивалась путями, предначертанными Декартом.
Давайте следовать совету учёного. Будем активны, внимательны, будем рассуждать, мыслить и узнавать новое, ведь знания пригодятся вам в дальнейшей жизни. А эти слова(Слайд3 ) Р.Декарта мне хочется предложить как девиз нашего урока : «Уважение других даёт повод к уважению самого себя».
2.Мотивация.
Проверим с каким настроением вы пришли на урок. Рисуем на полях смайлик.
-Возьмите карточки . Тут так же написаны слова Р.Декарта : « Для того, чтобы совершенствовать свой ум надо больше рассуждать, чем заучивать». Эти слова будут для нас руководством в нашей работе.
Задание №1 с математическими терминами, которые мы будем употреблять на уроке. Исправьте ошибки, допущенные в написании этих терминов. (Слайд 4)
-Поменяйтесь, листочками и проверьте, все ли ошибки исправлены. (Слайд 5) -Что вы заметили? В каком слове нет ошибок? (функция, график)
3.Актуализация знания.
а) С понятием «функция» мы познакомились на предыдущих уроках. Давайте вспомним основные понятия и определения по этой теме.
С графиками функций мы тоже работали . Какие из слов диктанта мы употребляли при работе по теме «Графики функций»? Что они обозначают?
На этом слайде определите какая из линий будет графиком функции? (Слайд 6)
-а кто скажет о чем мы будем рассуждать на этом уроке? Какие цели поставим на урок? (Слайд7 )
-на листах учащихся записать число и напишем тему урока: «Прямая пропорциональность и ее график»
Вспомним материал прошлых уроков
Составьте формулы, для решения следующих задач. (Слайд 9,10)
-Какие переменные зависимые, независимые? Что от чего зависит? Какая зависимость? (Слайд )
Какая из формул отличается от других? (Слайд )
в) Как можно записать формулы в общем виде? (Слайд )
y=kx, y — зависимая переменная
x – независимая переменная
k – постоянное число (коэффициент)
-Мы записали формулу, а это один из способов задания функции. Прямая пропорциональная зависимость – функция.
4.Изучение нового материала.
Определение. Прямой пропорциональностью называется функция, которую можно задать формулой у=кх, где х – независимая переменная, а к – некоторое число, неравное нулю, коэффициент прямой пропорциональности (неизменное отношение пропорциональных величин)
Прочитаем правило в учебнике на стр.65
-Область определения этой функции? (Множество всех чисел)
Закрепление материала.
-выполните задание в листах №4(Слайд ) Распредели формулы на 2 группы в соответствии с темой урока: (читаем правило в учебнике на стр.65)
у=2х, у=3х-7 , у=-0,2х, у=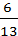
х, у=х², у=х, у=-5,8+3х, у=-х, у=50х,
1 группа:_____________________________________________________
2группа:_____________________________________________________
-подчеркните коэффициент прямой пропорциональности.
Выполняем №298 на стр.68 (устно), я диктую, вы на слух определяете формулу пр.пропорциональности и жмурите глаза, если не пр.пропорцинальностью, то вращаете глаза слева на право.
Придумай и запиши 4 формулы функции прямой пропорциональности:
1)у=_________2)у=__________3) у=_________4) у=__________
Изучение нового материала
-Каков график этой функции? Хотите узнать?
-Мы уже строили в задании№2 график функции, эту функцию мы можем назвать пр.пропорцинальностью? Значит мы уже строили график пр.пропорцинальности. Правило в учебнике на стр. 67.
— посмотрим как будем строить график этой функции (Слайд)
Закрепление материала.
-построим график №7 в листах учащихся (Слайд )
-Какую точку мы будем иметь в любом графике пр.пропорцинальности?
-Работаем по готовым чертежам. (Слайд)
-Вывод: графиком является прямая, проходящая через начало координат.
-Т.К. график – прямая, то сколько точек необходимо для ее построения? Одна уже есть (0;0)
Выполняем № 300
Итог урока. Обобщим работу на сегодняшнем уроке (Слайд ) . Всё сделали. Что запланировали?
Рефлексия. (Слайд)
Проверить настроение учащихся на конец урока.(смайлик) (Слайд)
infourok.ru
Прямая пропорциональность и её график
Вопросы занятия:
· ввести понятие «прямая пропорциональность»;
· привести примеры, когда прямая пропорциональность встречается в повседневной жизни;
· построить график прямой пропорциональности;
· определить от чего зависит расположение графика в координатной плоскости.
Материал урока
Давайте рассмотрим пример.
Пример.
Обратите внимание, что если переменную t увеличить, например, в 2 раза, то и переменная H также увеличится в 2 раза. То есть:
Также заметим, что зависимость высоты растения от времени его роста мы задали формулой вида:
В рассматриваемом примере: k = 2,5, а переменная t является независимой.
Сформулируем определение.
Определение.
С прямой пропорциональностью мы с вами часто встречаемся в повседневной жизни.
Например,
Или,
Теперь давайте построим график прямой пропорциональности:
Видим, что все точки лежат на одной прямой, которая проходит через начало координат. Для убедительности можем даже приложить линейку.
Таким образом, можем сформулировать определение.
Определение.
Графиком прямой пропорциональности y = kx является прямая, проходящая через начало координат.
Нам известно, что прямая определяется двумя точками. А значит, для построения графика функции y = kx достаточно указать любую точку графика этой функции, которая отличается от точки с координатами: (0, 0), то есть от начала координат.
Например,
А теперь посмотрите на рисунок, на котором изображены графики прямой пропорциональности.
Обратите внимание, что графики тех функций, которые имеют положительный коэффициент k расположены в первой и третьей координатных четвертях, а которые имеют отрицательный коэффициент k – во второй и четвёртой четвертях. То есть расположение графика функции y = kx в координатной плоскости зависит от коэффициента k.
videouroki.net
Прямая пропорциональность и ее график
Слайд 1
Прямая пропорциональность и её графикСлайд 2
Что такое аргумент и значение функции ? Какая переменная называется независимой, зависимой ? Что такое функция ? ПОВТОРЕНИЕ Что такое область определения функции ?
Слайд 3
Способы задания функции. Аналитический (с помощью формулы) Графический ( с помощью графика) Табличный (с помощью таблицы)
Слайд 4
Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты- соответствующим значениям функции. ГРАФИК ФУНКЦИИ
Слайд 5
1) 2) 3) 4) 5) 6) 7) 8) 9)
Слайд 6
ВЫПОЛНИТЕ ЗАДАНИЕ Постройте график функции y = 2 x +1, где 0 ≤ х ≤ 4 . Составьте таблицу. По графику найдите значение функции при х=2,5 . При каком значении аргумента значение функции равно 8 ?
Слайд 7
Определение Прямой пропорциональностью называется функция, которую можно задать формулой вида у= k х , где х — независимая переменная, k — не равное нулю число. ( k- коэффициент прямой пропорциональности) Прямая пропорциональная зависимость
Слайд 8
8 График прямой пропорциональ — ности — прямая , проходящая через начало координат (точку О(0,0)) Чтобы построить график функции y= kx , достаточно двух точек, одна из которых О (0,0) При k > 0 график расположен в I и III координатных четвертях. При k
Слайд 9
Графики функций прямой пропорциональности y x k>0 k>0 k
Слайд 10
Задание Определите, на каком из графиков изображена функция прямой пропорциональности.
Слайд 12
Задание Определите, график какой функции изображен на рисунке. Выберите формулу из трех предложенных.
Слайд 13
2) y = 0,5x
Слайд 14
Устная работа. Может ли график функции, заданной формулой у= k х , где k
Слайд 15
Определите, какие из точек А(6,-2), В(-2,-10),С(1,-1),Е(0,0) принадлежат графику прямой пропорциональности, заданной формулой у = 5х 1) А(6;-2) -2 = 5 6 — 2 = 30 — неверно . Точка А не принадлежит графику функции у=5х. 2) В(-2;-10) -10 = 5 (-2) -10 = -10 — верно. Точка В принадлежит графику функции у=5х. 3) С(1;-1) -1 = 5 1 -1 = 5 — неверно Точка С не принадлежит графику функции у=5х. 4) Е (0;0) 0 = 5 0 0 = 0 — верно. Точка Е принадлежит графику функции у=5х
Слайд 16
ТЕСТ 1 вариант 2 вариант №1. Какие из функций, заданные формулой, являются прямой пропорциональной зависимостью? А . y = 5x В . y = x 2 /8 C. y = 7x(x-1) D . y = x+1 A. y = 3x 2 +5 B. y = 8/x C. y = 7(x + 9) D. y = 10x
Слайд 17
№2. Выпишите номера прямых y = kx , где k > 0 1 вариант k
Слайд 18
№3. Определите, какие из точек принадлеж a т графику прямой пропорциональности, заданной формулой У= -1 /3 Х А(6 -2) ,В(-2 -10) 1 вариант С(1,-1),Е(0,0) 2 вариант
Слайд 19
y =5x y =10x III А VI и IV E 1 2 3 1 2 3 № Правильный ответ Правильный ответ №
Слайд 20
Выполните задание : Покажите схематически, как расположен график функции, заданной формулой : y =1,7 x у =-3 ,1 х у=0,9 х у=-2,3 х
Слайд 21
ЗАДАНИЕ Из следующих графиков выберите только графики прямой пропорциональности .
Слайд 22
1) 2) 3) 4) 5) 6) 7) 8) 9)
Слайд 23
Функции у = 2х + 3 2. у = 6/ х 3. у = 2х 4. у = — 1,5х 5. у = — 5/ х 6. у = 5х 7. у = 2х – 5 8. у = — 0,3х 9. у = 3/ х 10. у = — х /3 + 1 Выберите функции вида у= k х (прямая пропорциональность) и выпишите их
Слайд 24
Функции прямой пропорциональности У = 2х У = -1,5х У = 5х У = -0,3х у х
Слайд 25
у Линейные функции, не являющиеся функциями прямой пропорциональности 1) у = 2х + 3 2) у = 2х – 5 х -6 -4 -2 0 2 4 6 6 3 -3 -6 у = 2х + 3 у = 2х — 5
Слайд 26
Домашнее задание: п.15 стр.65-67, № 307; № 308.
Слайд 27
Еще раз давайте повторим. Что вы узнали нового? Чему научились? Что показалось особенно трудным?
Слайд 28
Понравился урок и тема понята: Понравился урок, но не всё ещё понятно: Урок не понравился и тема не понятна:
Слайд 29
Спасибо за урок!
nsportal.ru
Конспект урока «Прямая пропорциональность и ее график»
Предмет: алгебра
Класс: 7
Тема: «Прямая пропорциональность и ее график»
Дата проведения: 15.11.2016
Учитель: Журавель Е.В.
В классе – 16 уч.
Присутствует – _____уч.
Отсутствующие: __________________________________________________
Цель урока:
Создать условия для усвоения учащимися понятий «прямая пропорциональность», «график прямой пропорциональности». Способствовать формированию навыков распознавать прямую пропорциональность по формуле, графику, по словесному описанию; задавать формулой функцию, заданную графически; уметь исследовать зависимости расположения графика на координатной плоскости от значения числа k≠0 (углового коэффициента прямой).
Развивать память, логическое мышление, навыки быстрого устного счета.
Воспитывать внимательность, умение работать в сотрудничестве.
ХОД УРОКА
I. Организационный момент.
II. Проверка домашнего задания.
Учащиеся сдают домашние тетради на проверку.
III. Устная работа. (Фронтальная работа с классом)
1) Приведите пример функциональной зависимости одной переменной от другой. Укажите независимую и зависимые переменные.
(вес куска мыла зависит от его объема. Зависимая переменная – это масса, а независимая — объем)
2) Как называют независимую переменную?
(независимую переменную называют аргумент или х)
3) Как называют зависимую переменную?
(зависимую переменную называют функция или у)
4)Какие графики мы уже знаем?
(графики движения, температуры)
5)Что называется графиком функции?
(все точки на координатной плоскости, координаты которых удовлетворяют функции)
IV. Изучение нового материала: стр. 69, п.15
Краткий рассказ учителя с применением электронного пособия «Алгебра — 7»
Понятие прямой пропорциональности (используется электронный учебник с анимационной моделью «Прогулка по парку»)
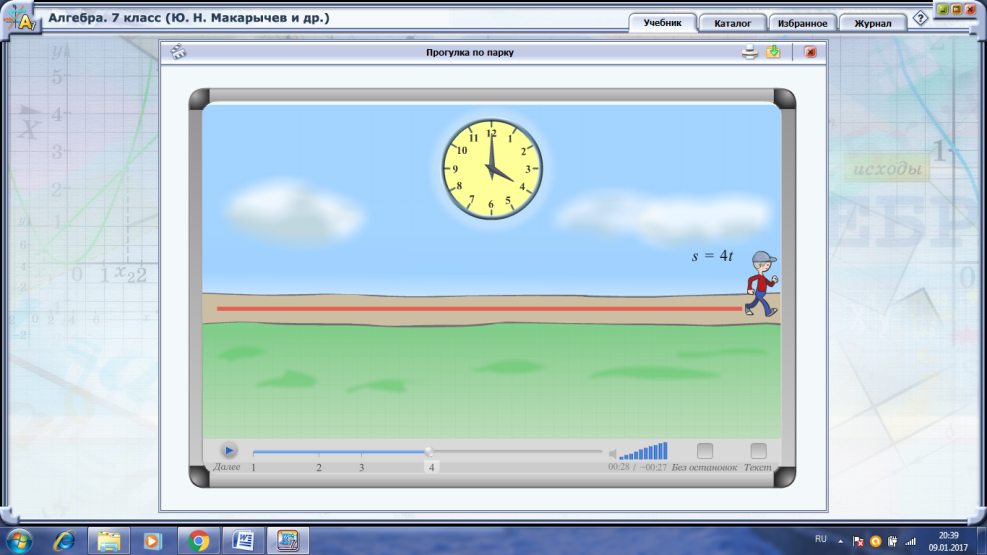
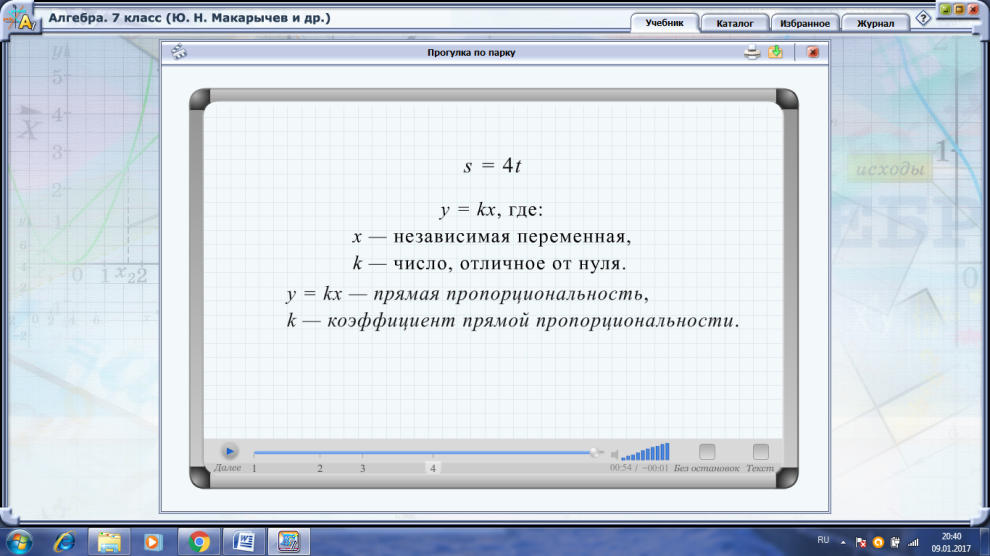
График прямой пропорциональности (используется электронный учебник с анимационной моделью «Сила тяжести», интерактивной моделью «Построение графика 2»)
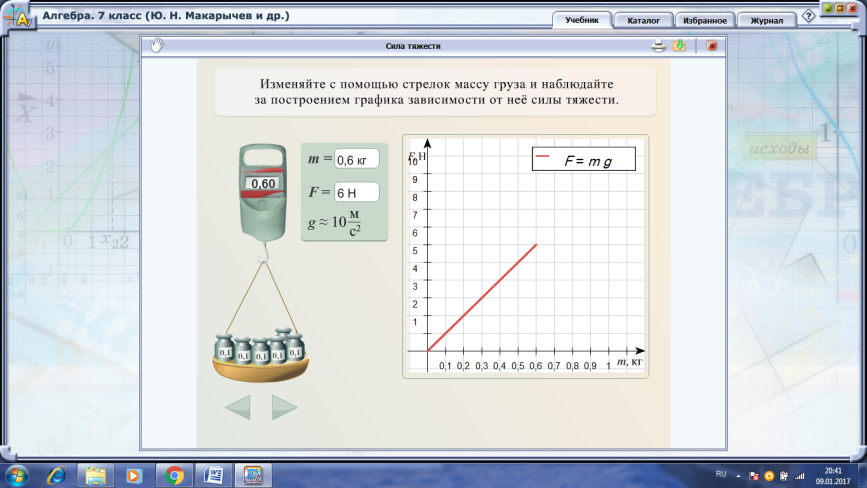
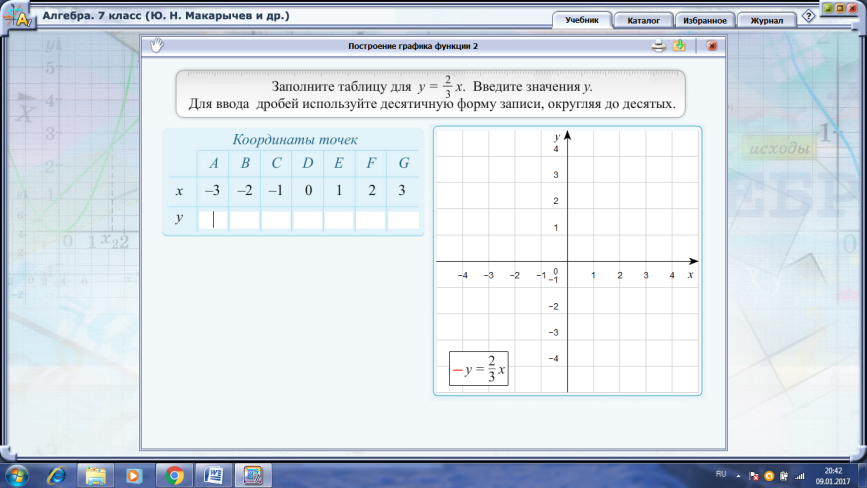
Зависимость расположения графика на координатной плоскости от значения числа k≠0 (углового коэффициента прямой) (используется электронный учебник с интерактивной моделью «Как зависит график линейной функции от коэффициента»)
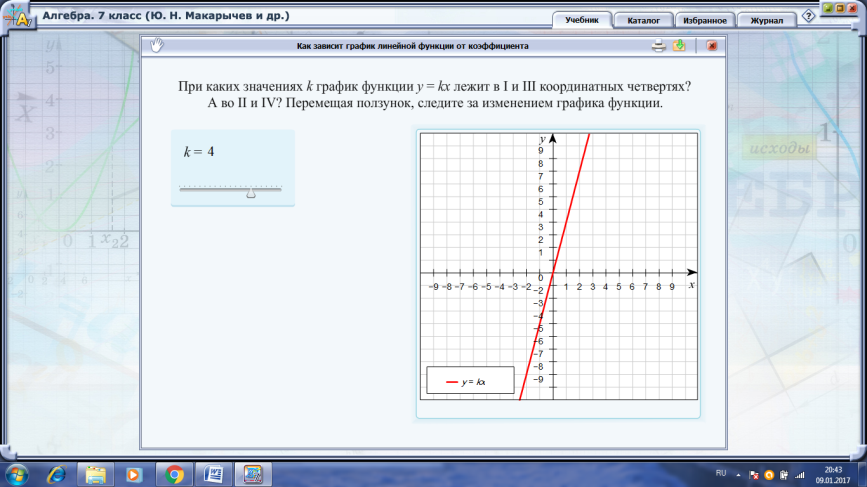
V. Тренировочные упражнения:
Устно № 298, 297
Письменно: № 305, 306 самостоятельно с последующей проверкой путем сравнения ответов
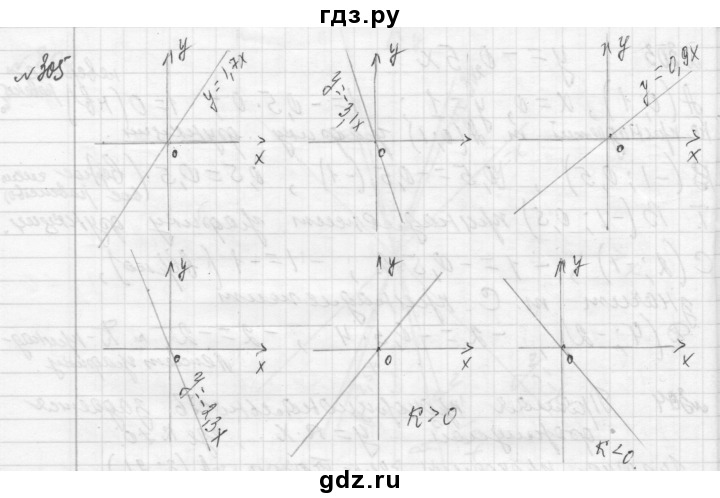
№303, 300 (а,б.в) на доске и в тетрадях подробно
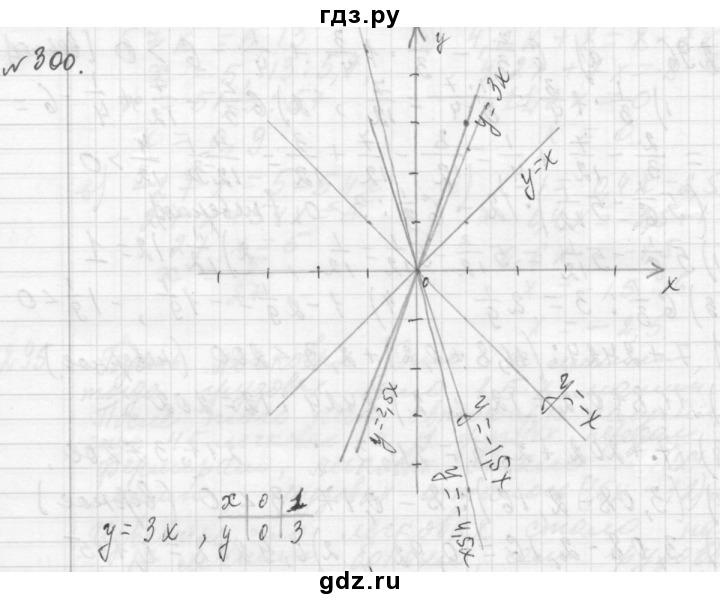
VI. Самостоятельная работа: на листочках
1 вариант2 вариант
Построить график функции:
А) у = 2х
Б) у = -2,5х
Построить график функции:
А) у = 4х
Б) у = -3,5х
Принадлежат ли графику функции
у = -1,5х точки А (2; -3), В (7; 2)?
Принадлежат ли графику функции
у = -0,2х точки А (10; -2), В (4; 6)?
VII. Итог урока:
Фронтальная беседа
Какая функция называется прямой пропорциональностью?
(функция, которая задается формулой у = kх, где k – коэффициент пропорциональности )
Что является графиком прямой пропорциональности?
(график прямой пропорциональности – прямая, проходящая через начало координат)
Как располагается в координатной плоскости график прямой пропорциональности в зависимости от значения коэффициента?
(если k – положительное число, то график расположен в 1 и 3 четвертях, а если k – отрицательное, то во 2 и 4)
VIII. Домашнее задание:
п. 15 – читать
письменно: № 299, 300 (г,д,е), 304*
Проявили высокую познавательную активность во время урока:
_________________________________________________________________________________________________________________________________________________________________________________________________________________________
Получили отметки:
_________________________________________________________________________________________________________________________________________________________________________________________________________________________
infourok.ru
«Графики прямой и обратной пропорциональности»
Цели урока:
- Открыть совместно с учащимися вид графиков прямой и обратной пропорциональности, закрепить навыки построения графиков;
- Формировать потребность приобретения новых знаний, создать условия для контроля (самоконтроля) усвоения умений и навыков;
- Развивать зрительную память, внимание, умение анализировать, сравнивать, обобщать.
Ход урока.
Для урока используем учебник Г.В.Дорофеева, Л.Г.Петерсон «Математика» 6 кл, ч.2.
Тема урока не прописана.
Этап 1. Организационный этап.
1.-Ребята! Чем мы занимались на прошлых уроках математики? Что вам больше всего понравилось, запомнилось? (Высказывания детей).
2.На доске учитель располагает несколько карточек с названиями тем уроков:
— Из предложенных на доске тем, выберите те, которые изучались на ближайших уроках. Дети выбирают темы: прямая пропорциональность, понятие пропорции, основное свойство пропорции, зависимости между величинами, обратная пропорциональность.
На другой стороне каждой карточки написано слово из пословицы: «Где есть желание, найдется путь!»
— В выбранных нами карточках зашифрована пословица, давайте попробуем прочитать ее».
Этап 2. Этап актуализации знаний.
1. Установите вид зависимости. Запишите формулу.
| а) прямая пропорциональность; y = 4x | |
| б) обратная пропорциональность; y=18/x |
2. Какие из приведенных формул являются прямой пропорциональностью, обратной пропорциональностью:
1) P = 3,2b; 2) K = n /2; 3) A = 8/b; 4) M = m : 5; 5) C = 1/4R; 6) A = 8q + 1
7) C = 4 : d; 8) AB = 18 ?
Предполагаемые ответы:
Формулы прямой пропорциональности
P = 3,2b; K = n/2; M = m:5
Формулы обратной пропорциональности
A = 8/b; C = 4:d; AB = 18
3.Схематично изобразите на одном чертеже графики зависимостей:
а) y=x; y=2x; y=3x; y=4x;
б)y=6\x; y=8\x; y=4\x.
При выполнении третьего задания дети испытывают затруднение.
Этап 3. Постановка проблемы.
| Учитель | Обучающиеся |
| -Вы можете решить это задание? | -Нет. |
| -А почему? В чем затруднение? | -Не знаем, как расположены графики относительно друг друга. |
| -Каким образом можно упростить это задание, чтобы вы смогли с ним справиться? У кого какие есть предложения? | -Если строить по одному графику из записанных на доске. |
| -Посмотрите внимательно на задание, о каких зависимостях идет речь? Что можно сделать? | -О прямой, обратной пропорциональности. О графиках, которые нужно построить. |
| -Как вы думаете над, чем мы сегодня будем работать? | -Над графиками прямой и обратной пропорциональности. |
| -Какова тема нашего урока? | -Графики прямой и обратной пропорциональности |
| -Какая же цель нашего урока? | -Научится строить графики прямой и обратной пропорциональности. |
Учитель ещё раз формулирует тему и цель урока, записывает тему на доске.
Этап 4. «Открытие» нового знания.
Изобразите на одном чертеже графики:
а) прямой пропорциональности: y=x; y=2x; y=3x; y=4x;
б) обратной пропорциональности: y=6/x; y=8/x; y=4/x
Записи.
а) На доске.
y=2x
y=x
y=3x
y=4x
У обучающихся
y=2x
y=x
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 0 | 1 | 2 | 3 | 4 | 5 |
y=3x
y=4x
Проверяем правильность заполнения таблиц. Строим графики.
б)
y=8\x
y=6\x
y=4\x
y=8\x
y=6\x
y=4\x
Работа с графиками.
| -Графики, каких зависимостей мы строим? | -Прямой и обратной пропорциональности. |
| -Рассмотрите расположение графиков прямой и обратной пропорциональности. Что вы замечаете? | -Располагаются друг над другом. Графики прямой пропорциональности- лучи, а графики обратной пропорциональности- кривые. График, у которого в формуле коэффициент 4, лежит выше, остальные графики ниже по порядку. Так же выше тот, у которого в формуле коэффициент 8. |
| -Ребята, а как вы считаете, от чего зависит расположение графиков прямой и обратной пропорциональности? | -От коэффициента. Чем больше коэффициент, тем выше расположен график. А у прямой пропорциональности можно сказать круче. |
Дети делают вывод.
Чем больше коэффициент пропорциональности, тем выше располагается этот график по отношению к другим.
Затем ещё раз повторить, какой вид имеет график прямой пропорциональности, обратной пропорциональности, предложить начертить их на доске, повторить алгоритм построения графиков.
Этап 5. Первичное закрепление
Работа в группах. Каждой группе раздаются листы с заданиями.
1. Назвать номера чертежей, на которых изображены графики прямой пропорциональности, обратной пропорциональности.
2.Найти ошибку.
3.Определить коэффициент пропорциональности.
Защита решений у доски.
Предполагаемые ответы.
1. Графики прямой пропорциональности 1, 3.
2. а) Неверно расположен график y=2x.
б) Ошибок в расположении графиков нет.
3. а) k=3; б) k=2.
Этап 6. Самостоятельная работа с самопроверкой в классе, по ключу, записанному на доске.
1. Определить вид зависимости и построить её график.
y=5x y=10\x.
2. Схематически изобразить на одном чертеже графики зависимостей:
y=3\x; y=11\x; y=20\x y=15x; y=7x; y=4x.
Предполагаемы ответы.
| 1. Зависимость-прямая пропорциональность Вариант 1 |
Зависимость- обратная пропорциональность Вариант 2 |
| 2. Вариант 2 | Вариант 1 |
Этап 7. Повторение.
1. Показать график прямой пропорциональности, график обратной пропорциональности.(Чертежи на доске)
-В 7-м классе у вас будет новый предмет- физика. В дальнейшем вам придется столкнуться с графиками прямой и обратной пропорциональности, например график равномерного движения, график изотермического процесса (изотерма).
2. Найти на рисунках графики прямой и обратной пропорциональности.
Этап 8. Итог урока.
— Над чем мы сегодня работали?
— Что нового узнали?
— Кто считает, что он сегодня на уроке работал
хорошо?
(Высказывания детей)
Домашнее задание:
№175(3), 178(1), 180, 190.
urok.1sept.ru