Прямая пропорциональность и её график
Вопросы занятия:
· ввести понятие «прямая пропорциональность»;
· привести примеры, когда прямая пропорциональность встречается в повседневной жизни;
· построить график прямой пропорциональности;
· определить от чего зависит расположение графика в координатной плоскости.
Материал урока
Давайте рассмотрим пример.
Пример.
Обратите внимание, что если переменную t увеличить, например, в 2 раза, то и переменная H также увеличится в 2 раза. То есть:
Также заметим, что зависимость высоты растения от времени его роста мы задали формулой вида:
В рассматриваемом примере: k = 2,5, а переменная t является независимой.
Сформулируем определение.
Определение.
С прямой пропорциональностью мы с вами часто встречаемся в повседневной жизни.
Например,
Или,
Теперь давайте построим график прямой пропорциональности:
Видим, что все точки лежат на одной прямой, которая проходит через начало координат. Для убедительности можем даже приложить линейку.
Таким образом, можем сформулировать определение.
Определение.
Графиком прямой пропорциональности y = kx является прямая, проходящая через начало координат.
Нам известно, что прямая определяется двумя точками. А значит, для построения графика функции y = kx достаточно указать любую точку графика этой функции, которая отличается от точки с координатами: (0, 0), то есть от начала координат.
Например,
А
теперь посмотрите на рисунок, на котором изображены графики прямой
пропорциональности.
Обратите внимание, что графики тех функций, которые имеют положительный коэффициент k расположены в первой и третьей координатных четвертях, а которые имеют отрицательный коэффициент k – во второй и четвёртой четвертях. То есть расположение графика функции y = kx в координатной плоскости зависит от коэффициента k.
Постройте график прямой пропорциональности заданной формулой y. Прямая пропорциональность и её график
В 7 и 8 классе изучается график прямой пропорциональности.
Как построить график прямой пропорциональности?
Рассмотрим на примерах график прямой пропорциональности.
График прямой пропорциональности формула
График прямой пропорциональности представляет функцию .
В общем виде прямая пропорциональность имеет формулу
От величины и знака коэффициента прямой пропорциональности зависит угол наклона графика прямой пропорциональности по отношению к оси икс.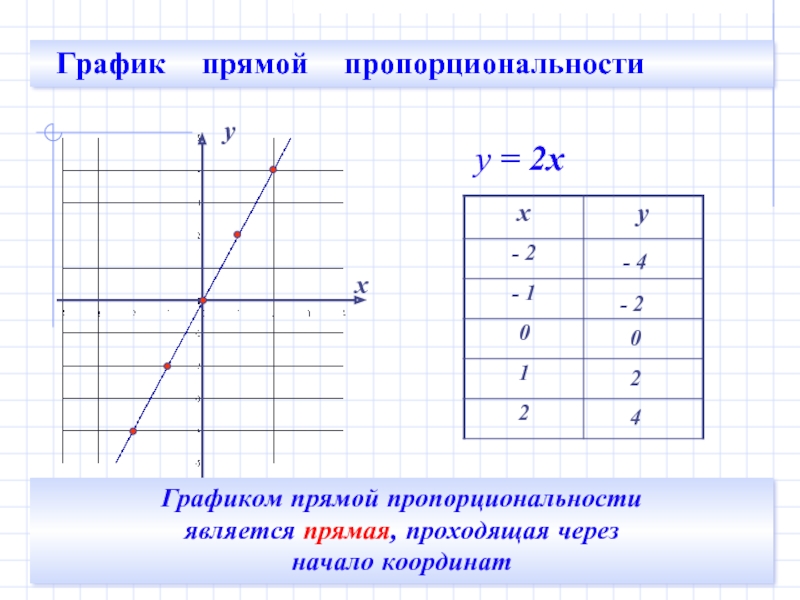
График прямой пропорциональности проходит
График прямой пропорциональности проходит через начало координат.
График прямой пропорциональности есть прямая. Прямая задается двумя точками.
Таким образом при построении графика прямой пропорциональности достаточно определить положение двух точек.
Но одну из них мы всегда знаем — это начало координат.
Осталось найти вторую. Посмотрим пример построения графика прямой пропорциональности.
Постройте график прямой пропорциональности y = 2x
Задача .
Постройте график прямой пропорциональности, заданной формулой
Решение .
Есть все числа.
Берем любое число из области определения прямой пропорциональности, пусть это будет 1.
Найти значение функции при икс равное 1
Y = 2x =
2 * 1 = 2
Мы знаем, что график прямой пропорциональности есть прямая, а прямая задается двумя точками.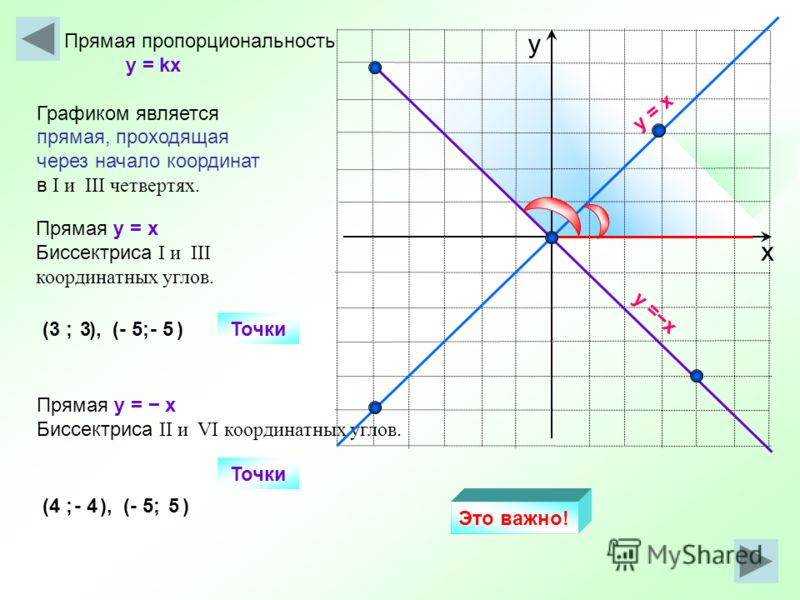
Построим график функции, заданной формулой у = 0,5х.
1. Область определения этой функции – множество всех чисел.
2. Найдем некоторые соответственные значения переменных х и у .
Если х = -4, то у = -2.
Если х = -3, то у = -1,5.
Если х = -2, то у = -1.
Если х = -1, то у = -0,5.
Если х = 0, то у = 0.
Если х = 1, то у = 0,5.
Если х = 2, то у = 1.
Если х = 3, то у = 1,5.
Если х = 4, то у = 2.
3. Отметим в координатной плоскости точки, координаты которых мы определили в пункте 2. Отметим, что построенные точки принадлежат некоторой прямой.
4. Определим, принадлежат ли этой прямой другие точки графика функции. Для этого найдем координаты еще нескольких точек графика.
Если х = -3,5, то у = -1,75.
Если х = -2,5, то у = -1,25.
Если х = -1,5, то у = -0,75.
Если х = -0,5, то у = -0,25.
Если х = 0,5, то у = 0,25.
Если х = 1,5, то у = 0,75.
Если х = 2,5, то у = 1,25.
Если х = 3,5, то у = 1,75.
Построив новые точки графика функции, замечаем, что они принадлежат той же прямой.
Если мы будем уменьшать шаг наших значений (брать, например, значения х через 0,1; через 0,01 и т.д.), мы будем получать другие точки графика, принадлежащие той же прямой и расположенные все более близко друг от драга. Множество всех точек графика данной функции есть прямая линия, проходящая через начало координат.
Т.о., график функции, заданной формулой у = kх, где k ≠ 0, есть прямая, проходящая через начало координат.
Если область определения функции, заданной формулой у = kх, где k ≠ 0, состоит не из всех чисел, то ее графиком служит подмножество точек прямой (например, луч, отрезок, отдельные точки).
Для построения прямой достаточно знать положение двух ее точек. Поэтому график прямой пропорциональности, заданной на множестве всех чисел, можно строить по любым двум его точкам (в качестве одной из них удобно брать начало координат).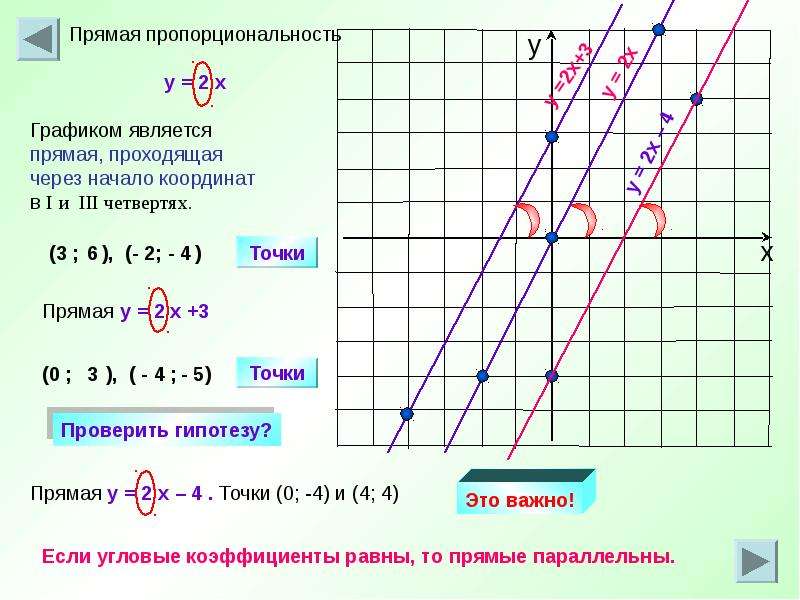
Пусть, например, требуется построить график функции, заданной формулой у = -1,5х . Выберем какое-либо значение х , не равное 0 , и вычислим соответствующее значение у .
Если х = 2, то у = -3.
Отметим на координатной плоскости точку с координатами (2; -3) . Через эту точку и начало координат проведем прямую. Эта прямая – искомый график.
Основываясь на данном примере, можно доказать, что всякая прямая, проходящая через начало координат и не совпадающая с осями, является графиком прямой пропорциональности.
Доказательство .
Пусть дана некоторая прямая, проходящая через начало координат и не совпадающая с осями. Возьмем на ней точку с абсциссой 1. Обозначим ординату этой точки через k. Очевидно, что k ≠ 0. Докажем, что данная прямая является графиком прямой пропорциональности с коэффициентом k.
Действительно, из формулы у = kх следует, что если х = 0, то у = 0, если х = 1, то у = k, т.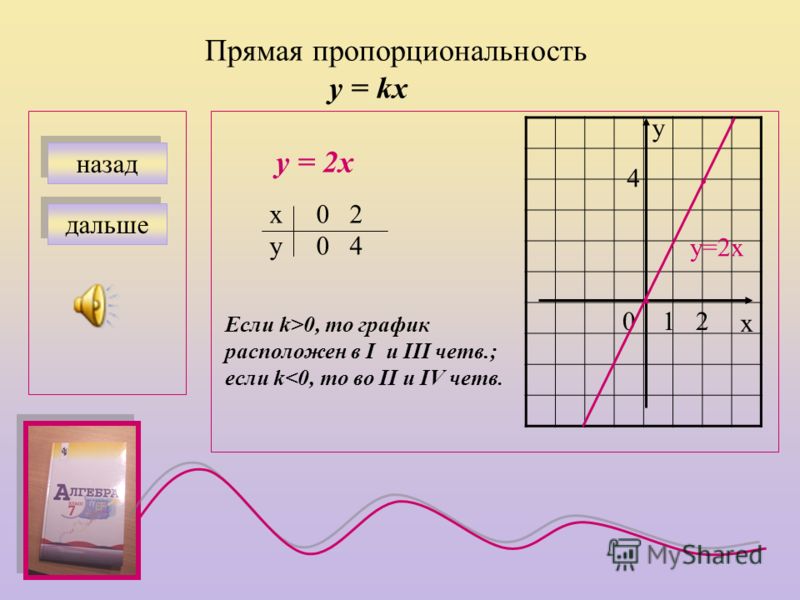 е. график функции, заданной формулой у = kх, где k ≠ 0, есть прямая, проходящая через точки (0; 0) и (1; k).
е. график функции, заданной формулой у = kх, где k ≠ 0, есть прямая, проходящая через точки (0; 0) и (1; k).
Т.к. через две точки можно провести только одну прямую, то данная прямая совпадает с графиком функции, заданной формулой у = kх, где k ≠ 0 , что и требовалось доказать.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Как строить графики прямой пропорциональности?
Постройте график прямой пропорциональности заданной формулой y = 3x
Решение .
Функция y = 3x определена на всей числовой прямой. См. .
Берем любое значение икс, пусть это будет 1, и находим игрек, подставляя икс равное 1 в формулу y = 3x
Y = 3x =
3 * 1 = 3
то есть при x = 1 получаем y = 3. Точка с этими координатами принадлежит графику функции y = 3x.
Мы знаем, что график прямой пропорциональности есть прямая, а прямая задается двумя точками.
Одну из них мы только что нашли, а второй для прямой пропорциональности всегда является начало координат.
Теперь мы готовы построить график функции y = 3x.
Отмечаем на координатной плоскости точку с координатами (1; 3).
Через данную точку и начало координат проводим прямую линию
Мы получили график прямой пропорциональности, заданной формулой y = 3x.
Найдите по графику значение y, соответствующее значению x = 2.
Находим на оси иксов точку 2.
Проводим через неё вертикальную линию до пересечения с графиком.
Проводим горизонтальную линию до оси игреков. На оси игрек выходим на точку 6.
6 и есть значение игрек, соответствующее значению x = 2.
График прямой пропорциональности заданной формулой. Прямая пропорциональность и её график
Определение прямой пропорциональности
Для начала напомним следующее определение:
Определение
Две величины называются прямо пропорциональными, если их отношение равно конкретному, отличному от нуля числу, то есть:
\[\frac{y}{x}=k\]
Отсюда мы видим, что $y=kx$.
Определение
Функция вида $y=kx$ называется прямой пропорциональностью.
Прямая пропорциональность является частным случаем линейной функции $y=kx+b$ при $b=0$. Число $k$ называется коэффициентом пропорциональности.
Примером прямой пропорциональности может служить второй закон Ньютона : Ускорение тела прямо пропорционально приложенной к нему силе:
Здесь масса — коэффициент пропорциональности.
Исследование функции прямой пропорциональности $f(x)=kx$ и её график
Вначале рассмотрим функцию $f\left(x\right)=kx$, где $k > 0$.
- $f»\left(x\right)={\left(kx\right)}»=k>0$. Следовательно, данная функция возрастает на всей области определения. Точек экстремума нет.
- ${\mathop{lim}_{x\to -\infty } kx\ }=-\infty $, ${\mathop{lim}_{x\to +\infty } kx\ }=+\infty $
- График (рис. 1).
Рис. 1. График функции $y=kx$, при $k>0$
Теперь рассмотрим функцию $f\left(x\right)=kx$, где $k
- Область определения — все числа.
 {«»}\left(x\right)=k»=0$. Следовательно, функция не имеет точек перегиба.
{«»}\left(x\right)=k»=0$. Следовательно, функция не имеет точек перегиба. - ${\mathop{lim}_{x\to -\infty } kx\ }=+\infty $, ${\mathop{lim}_{x\to +\infty } kx\ }=-\infty $
- График (рис. 2).
Рис. 2. График функции $y=kx$, при $k
Важно: для построения графика функции $y=kx$ достаточно найти одну, отличную от начала координат точку $\left(x_0,\ y_0\right)$ и провести прямую через эту точку и начало координат.
Как строить графики прямой пропорциональности?
Постройте график прямой пропорциональности заданной формулой y = 3x
Решение .
Функция y = 3x определена на всей числовой прямой. См. .
Берем любое значение икс, пусть это будет 1, и находим игрек, подставляя икс равное 1 в формулу y = 3x
Y = 3x =
3 * 1 = 3
то есть при x = 1 получаем y = 3. Точка с этими координатами принадлежит графику функции y = 3x.
Мы знаем, что график прямой пропорциональности есть прямая, а прямая задается двумя точками.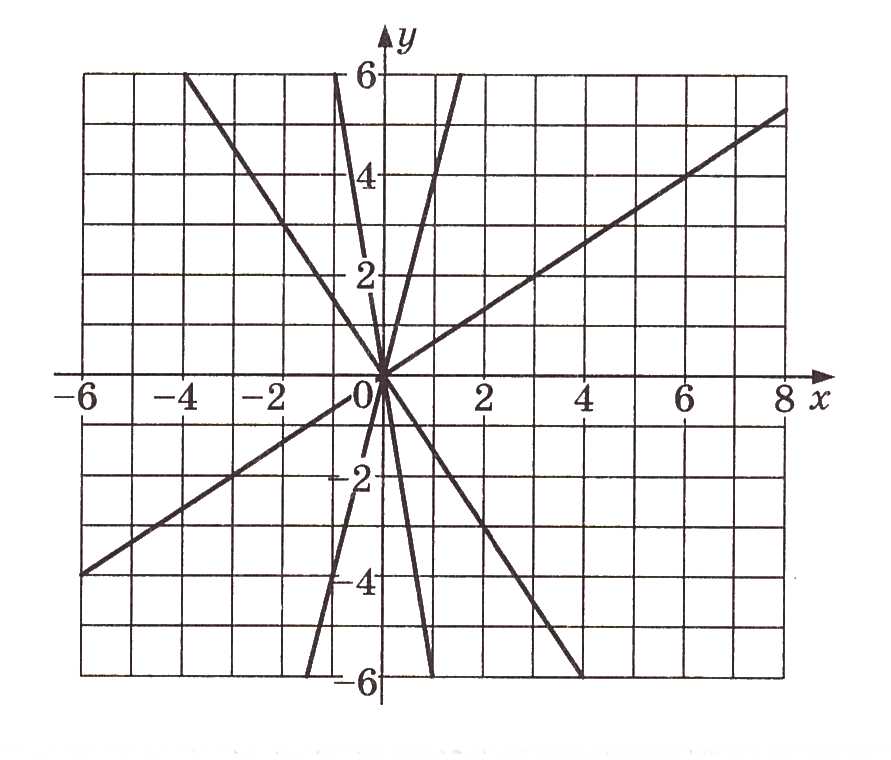
Одну из них мы только что нашли, а второй для прямой пропорциональности всегда является начало координат.
Теперь мы готовы построить график функции y = 3x.
Отмечаем на координатной плоскости точку с координатами (1; 3).
Через данную точку и начало координат проводим прямую линию
Мы получили график прямой пропорциональности, заданной формулой y = 3x.
Найдите по графику значение y, соответствующее значению x = 2.
Находим на оси иксов точку 2.
Проводим через неё вертикальную линию до пересечения с графиком.
Проводим горизонтальную линию до оси игреков. На оси игрек выходим на точку 6.
6 и есть значение игрек, соответствующее значению x = 2.
Построим график функции, заданной формулой у = 0,5х.
1. Область определения этой функции – множество всех чисел.
2. Найдем некоторые соответственные значения переменных х и у .
Если х = -4, то у = -2.
Если х = -3, то у = -1,5.
Если х = -2, то у = -1.
Если х = -1, то у = -0,5.
Если х = 0, то у = 0.
Если х = 1, то у = 0,5.
Если х = 2, то у = 1.
Если х = 3, то у = 1,5.
Если х = 4, то у = 2.
3. Отметим в координатной плоскости точки, координаты которых мы определили в пункте 2. Отметим, что построенные точки принадлежат некоторой прямой.
4. Определим, принадлежат ли этой прямой другие точки графика функции. Для этого найдем координаты еще нескольких точек графика.
Если х = -3,5, то у = -1,75.
Если х = -2,5, то у = -1,25.
Если х = -1,5, то у = -0,75.
Если х = -0,5, то у = -0,25.
Если х = 0,5, то у = 0,25.
Если х = 1,5, то у = 0,75.
Если х = 2,5, то у = 1,25.
Если х = 3,5, то у = 1,75.
Построив новые точки графика функции, замечаем, что они принадлежат той же прямой.
Если мы будем уменьшать шаг наших значений (брать, например, значения х через 0,1; через 0,01 и т.д.), мы будем получать другие точки графика, принадлежащие той же прямой и расположенные все более близко друг от драга. Множество всех точек графика данной функции есть прямая линия, проходящая через начало координат.
Множество всех точек графика данной функции есть прямая линия, проходящая через начало координат.
Т.о., график функции, заданной формулой у = kх, где k ≠ 0, есть прямая, проходящая через начало координат.
Если область определения функции, заданной формулой у = kх, где k ≠ 0, состоит не из всех чисел, то ее графиком служит подмножество точек прямой (например, луч, отрезок, отдельные точки).
Для построения прямой достаточно знать положение двух ее точек. Поэтому график прямой пропорциональности, заданной на множестве всех чисел, можно строить по любым двум его точкам (в качестве одной из них удобно брать начало координат).
Пусть, например, требуется построить график функции, заданной формулой у = -1,5х . Выберем какое-либо значение х , не равное 0 , и вычислим соответствующее значение у .
Если х = 2, то у = -3.
Отметим на координатной плоскости точку с координатами (2; -3) . Через эту точку и начало координат проведем прямую. Эта прямая – искомый график.
Эта прямая – искомый график.
Основываясь на данном примере, можно доказать, что всякая прямая, проходящая через начало координат и не совпадающая с осями, является графиком прямой пропорциональности.
Доказательство .
Пусть дана некоторая прямая, проходящая через начало координат и не совпадающая с осями. Возьмем на ней точку с абсциссой 1. Обозначим ординату этой точки через k. Очевидно, что k ≠ 0. Докажем, что данная прямая является графиком прямой пропорциональности с коэффициентом k.
Действительно, из формулы у = kх следует, что если х = 0, то у = 0, если х = 1, то у = k, т.е. график функции, заданной формулой у = kх, где k ≠ 0, есть прямая, проходящая через точки (0; 0) и (1; k).
Т.к. через две точки можно провести только одну прямую, то данная прямая совпадает с графиком функции, заданной формулой у = kх, где k ≠ 0 , что и требовалось доказать.
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
В 7 и 8 классе изучается график прямой пропорциональности.
Как построить график прямой пропорциональности?
Рассмотрим на примерах график прямой пропорциональности.
График прямой пропорциональности формула
График прямой пропорциональности представляет функцию .
В общем виде прямая пропорциональность имеет формулу
От величины и знака коэффициента прямой пропорциональности зависит угол наклона графика прямой пропорциональности по отношению к оси икс.
График прямой пропорциональности проходит
График прямой пропорциональности проходит через начало координат.
График прямой пропорциональности есть прямая. Прямая задается двумя точками.
Таким образом при построении графика прямой пропорциональности достаточно определить положение двух точек.
Но одну из них мы всегда знаем — это начало координат.
Осталось найти вторую. Посмотрим пример построения графика прямой пропорциональности.
Постройте график прямой пропорциональности y = 2x
Задача
.
Постройте график прямой пропорциональности, заданной формулой
Решение .
Есть все числа.
Берем любое число из области определения прямой пропорциональности, пусть это будет 1.
Найти значение функции при икс равное 1
Y = 2x =
2 * 1 = 2
то есть при x = 1 получаем y = 2. Точка с этими координатами принадлежит графику функции y = 2x.
Мы знаем, что график прямой пропорциональности есть прямая, а прямая задается двумя точками.
Прямая и обратная пропорция — Графики — WJEC — GCSE Maths Numeracy (WJEC) Revision
Когда две величины прямо пропорциональны, при увеличении одной увеличивается и другая.
Мы можем отобразить это отношение на графике. Две прямо пропорциональные величины всегда будут строить прямолинейный график, проходящий через начало координат.
Если константа пропорциональности положительна, график будет иметь положительный градиент. Если константа отрицательна, график будет иметь отрицательный градиент.
Если константа отрицательна, график будет иметь отрицательный градиент.
Пример 1
Заработок няни прямо пропорционален количеству отработанных часов.
Если им платят 9 фунтов стерлингов за каждый час работы, мы можем записать это в виде формулы:
\[\text {Прибыль = 9 фунтов стерлингов} \times \text {отработанные часы}\]
Чтобы построить это, нам нужно три точки, мы можем использовать таблицу значений, чтобы помочь нам:
Когда часы = 0, заработок = £9 × 0 = £0
Когда часы = 1, заработок = £9 × 1 = £9
esjniwk0wy.0.0.0.1:0.1.0.$0.$2.$10″> Когда часы = 2, заработок = 9 фунтов стерлингов × 2 = 18 фунтов стерлинговНачисление баллов (\({0} \text{,} {~0}\)), (\({1} \text{,} {~9 }\)) и (\({2} \text{,} {~18}\)).
После того, как вы нанесли эти точки, проведите линию через все три, продлив ее как можно дальше.
Пример 2
Количество упаковок чипсов и общая стоимость указаны в таблице.
Когда мы рисуем эти точки, мы видим, что они могут быть соединены прямой линией:
Для каждой 1 на оси \(\text {x}\) ось \(\text {y}\) увеличивается на 30. Это означает, что градиент графика равен 30, и график можно записать так:
esjniwk0wy.0.0.0.1:0.1.0.$0.$3.$6″> \[\text {y = 30 x}\]Нахождение взаимосвязей на графике
\(\text {y }\) прямо пропорциональна \(\text {x}\).Используя этот график, напишите уравнение, показывающее взаимосвязь между \(\text {x}\) и \(\text {y}\).
Когда \(\text {x}\) = 2, \(\text {y}\) = 30
\[{30} \text{~÷} {~2} = {15}\]
\[\text {y = 15~\times~x}\]
\[\text {y = 15 x}\]
Когда две величины обратно пропорциональны, при увеличении одной другой уменьшается.
Когда мы изображаем это отношение, мы получаем кривую диаграмму.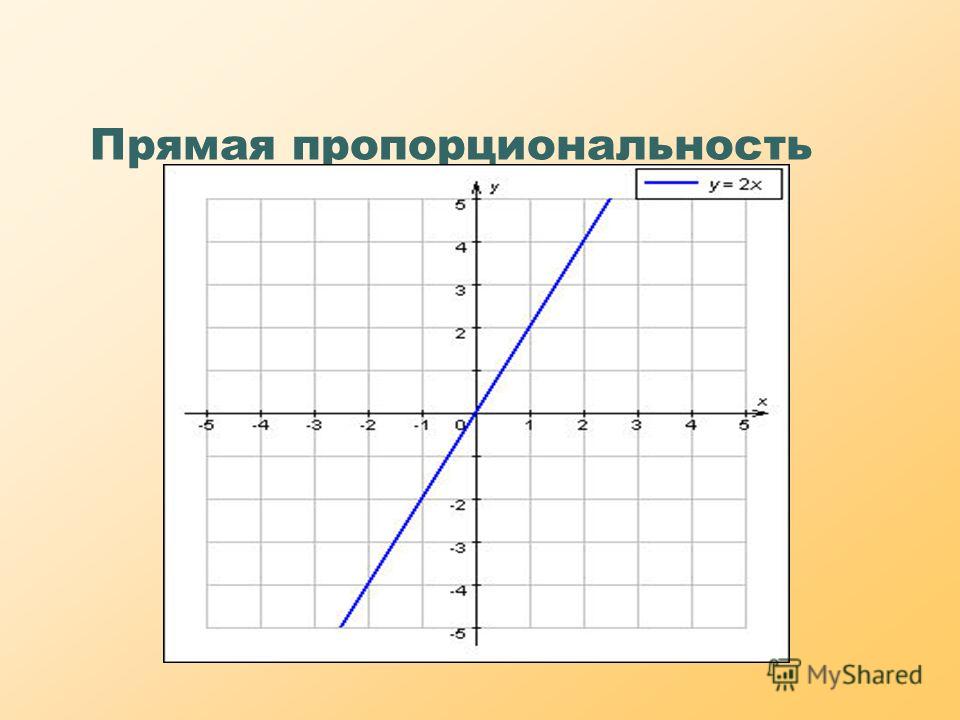
Пример
\(\text {y}\) обратно пропорционален \(\text {x}\) и когда \(\text {x}\) = 2, \(\text {y} \) = 10
Постройте график, заполнив таблицу значений:
1.Так как \(\text {y}\) обратно пропорционально \(\text {x}\), то можно написать:
\[\text {y = k / x}\]
2. Подставить в известное значения и перестановка находит значение \(\text {k}\):
\[\text {10 = k / 2}\]
\[\text {10 \times~2 = k}\]
\[\text {k = 20}\]
esjniwk0wy.0.0.0.1:0.1.0.$0.$5.$11″> 3. Теперь мы можем заполнить таблицу значений:Когда \(\text {x = 1}\), \(\text {y = 20 / 1 } = 20\)
Когда \(\text {x = 4}\), \(\text {y = 20 / 4} = 5\)
Когда \(\text {x = 5}\), \(\текст {у = 20/5} = 4\)
4.Теперь мы можем нанести эти точки на график и соединить их вместе в виде кривой.
Пропорциональные отношения
Пропорциональная зависимость – это зависимость, при которой две величины напрямую изменяются друг относительно друга. Мы говорим Переменная у изменяется прямо как Икс если:
у знак равно к Икс
для некоторых постоянный к , называемая константой пропорциональности.
(Некоторые учебники описывают пропорциональные отношения, говоря, что «
у
меняется пропорционально
Икс
» или это »
у
прямо пропорциональна
Икс
. «)
«)
Это означает, что как Икс увеличивается, у увеличивается и по мере Икс уменьшается, у уменьшается — и что соотношение между ними всегда остается одним и тем же.
График уравнения пропорциональной зависимости представляет собой прямую линию, проходящую через начало координат.
Пример 1:
Учитывая это у варьируется пропорционально с Икс , с участием константа пропорциональности к знак равно 1 3 , найти у когда Икс знак равно 12 .
Напишите уравнение пропорциональной зависимости.
Переменная Икс меняется пропорционально у с константой пропорциональности, равной 1 3 .
Так,
Замените данное
Икс
ценность.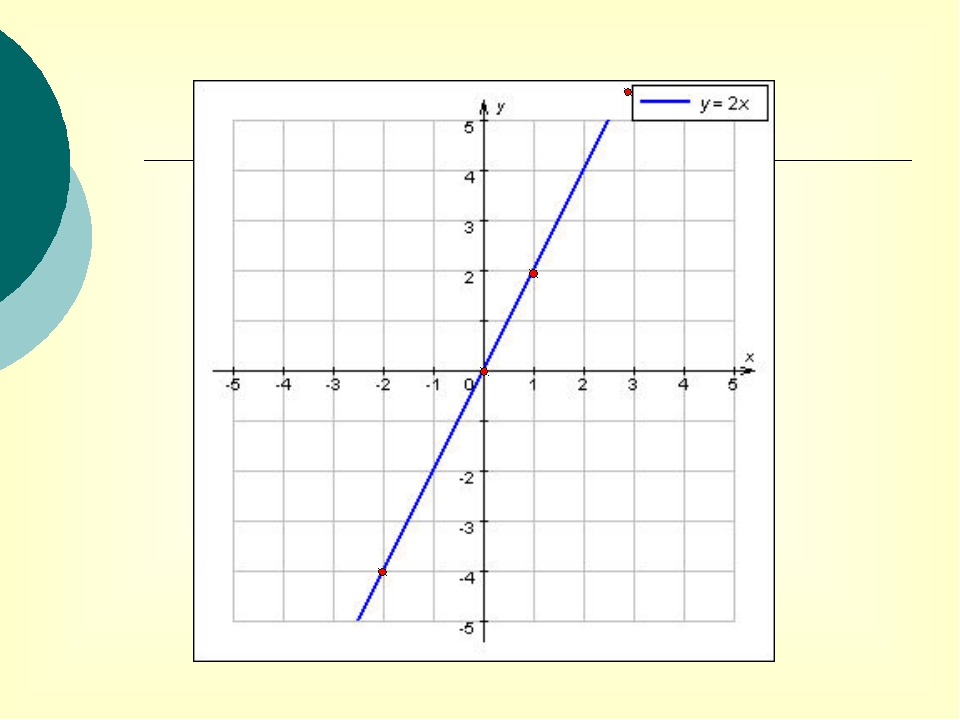
Пример 2:
Учитывая это у варьируется пропорционально с Икс , Найди постоянная пропорциональности если у знак равно 24 и Икс знак равно 3 .
Напишите уравнение пропорциональной зависимости.
у знак равно к Икс
Замените данное Икс и у значения и решить для к .
24 знак равно к ⋅ 3 к знак равно 8
Пример 3:
Предполагать
у
меняется пропорционально
Икс
, и
у
знак равно
30
когда
Икс
знак равно
6
. Какова ценность
у
когда
Икс
знак равно
100
?
Какова ценность
у
когда
Икс
знак равно
100
?
Напишите уравнение пропорциональной зависимости.
у знак равно к Икс
Замените данное Икс и у значения и решить для к .
30 знак равно к ⋅ 6
к знак равно 5
Уравнение у знак равно 5 Икс .Теперь замените Икс знак равно 100 и найти у .
у знак равно 5 ⋅ 100 у знак равно 500
Что такое прямо пропорциональный график? – Pegaswitch.com
Что такое прямо пропорциональный график?
Когда две величины прямо пропорциональны, при увеличении одной увеличивается и другая. Две прямо пропорциональные величины всегда будут строить прямолинейный график, проходящий через начало координат.Если константа пропорциональности положительна, график будет иметь положительный градиент.
Две прямо пропорциональные величины всегда будут строить прямолинейный график, проходящий через начало координат.Если константа пропорциональности положительна, график будет иметь положительный градиент.
Что такое прямо пропорциональная зависимость?
(Некоторые учебники описывают пропорциональную зависимость, говоря, что «у изменяется пропорционально х» или что «у прямо пропорционально х».) соотношение между ними всегда остается одним и тем же.
Что является примером прямо пропорциональной зависимости?
Стоимость продуктов питания прямо пропорциональна весу.Выполненная работа прямо пропорциональна количеству рабочих. Это означает, что чем больше рабочих, тем больше работы, чем меньше рабочих, тем меньше выполненной работы. Расход топлива автомобиля пропорционален пройденному расстоянию.
Что является примером пропорционального отношения на графике?
Если вы можете провести прямую линию через все три точки, и линия проходит через начало координат (0, 0), упорядоченные пары представляют собой пропорциональные отношения. Решение Точки на графике представляют пропорциональную зависимость.
Решение Точки на графике представляют пропорциональную зависимость.
Какова формула прямо пропорциональности?
Уравнение прямой пропорциональности имеет вид y=kx, где x и y – заданные величины, а k – любая постоянная величина.
Является ли экспоненциальный график прямо пропорциональным?
Основы построения графиков экспоненциальных функций. Экспоненциальная функция y=bx y = bx, где b>0 — это функция, которая будет оставаться пропорциональной своему исходному значению при увеличении или уменьшении.
Как рассчитать прямо пропорционально?
Формула прямой пропорции говорит, что если величина y прямо пропорциональна величине x, то мы можем сказать, что y =kx для константы k.y=kx также является общей формой уравнения прямой пропорции… Формула прямой пропорции
- k — константа пропорциональности.
- y увеличивается с увеличением x.
- y уменьшается по мере уменьшения x.
Какие вещи прямо пропорциональны?
Когда одна величина постоянно увеличивается или постоянно уменьшается по отношению к другой величине, эти две величины называются прямо пропорциональными друг другу. В примере с самолетом мы бы сказали, что величина C прямо пропорциональна S, умноженному на константу (k).
В примере с самолетом мы бы сказали, что величина C прямо пропорциональна S, умноженному на константу (k).
Как определить пропорциональную зависимость на графике?
Нанесите эти точки на график. Чтобы определить, имеют ли x и y пропорциональные отношения, посмотрите, проходит ли линия, проходящая через эти точки, через начало координат (0, 0). Точки находятся на линии, проходящей через начало координат. Таким образом, x и y находятся в пропорциональной зависимости.
Как узнать, является ли график пропорциональным отношением?
График пропорционального отношения представляет собой прямую линию, проходящую через начало координат.Пропорциональные величины можно описать уравнением y = kx, где k — постоянное отношение. Вы можете сказать, что зависимость прямо пропорциональна, посмотрев на график. График представляет собой прямую линию, проходящую через начало координат.
Показывает ли этот график пропорциональную зависимость?
SWBAT распознает, что график, на котором показана прямая линия, проходящая через начало координат, показывает пропорциональную зависимость.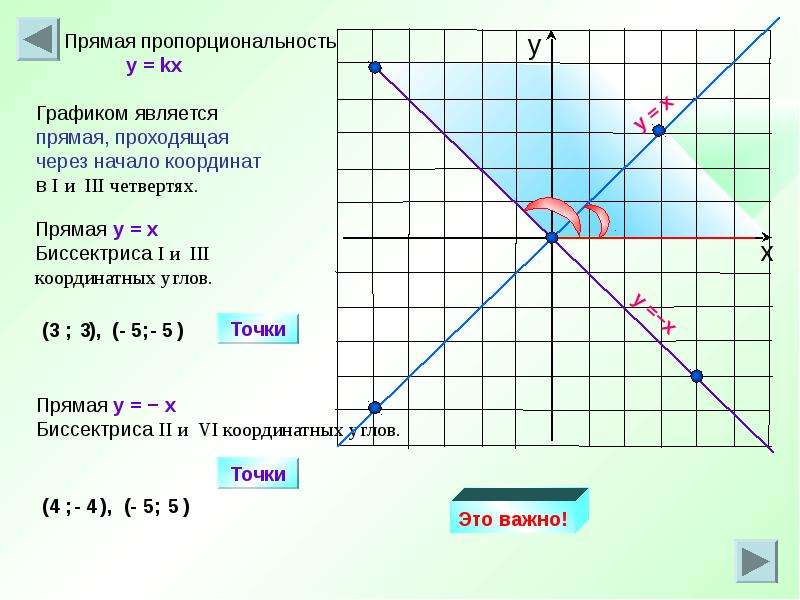 Два критерия для определения того, показывает ли график пропорциональную зависимость, — это прямая линия, проходящая через точку (0,0).
Два критерия для определения того, показывает ли график пропорциональную зависимость, — это прямая линия, проходящая через точку (0,0).
Как сравнить пропорциональные отношения?
Сравнение соотношений. В пропорциональной зависимости две переменные в задаче связаны постоянным отношением. Это означает, что уравнение, связывающее две переменные, можно записать в виде: y = константа • x или y = k • x. При работе с данными в таблице соотношение должно быть одинаковым для каждой пары точек данных.
Какое уравнение(я) представляет пропорциональную зависимость?
Уравнение, представляющее пропорциональную зависимость: y = 32x.Потому что: y/x = 32. Значит, y прямо пропорционально x. Обратите внимание, что другие уравнения представляют пропорциональную зависимость в той или иной форме, только связь y = 32x является единственной прямо пропорциональной зависимостью.
youtube.com/embed/l210OAKlV40?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Видео о пересмотре прямых и непрямых пропорций
Студенческие видео
- Уровень:
- GCSE
- Плата:
- AQA, Edexcel, OCR, Eduqas, WJEC
В ответ на некоторые вопросы вам дадут общее соотношение между x и y, но вам нужно будет выяснить, что это за формула. Эта зависимость либо прямо пропорциональна, либо обратно пропорциональна.
Эта зависимость либо прямо пропорциональна, либо обратно пропорциональна.
В этих видеороликах рассказывается, как определить, какой вопрос есть какой, и как это понять, если вы знаете, какой это тип пропорции.
В этом видеоролике представлены общие формулы обоих типов пропорций, а также несколько простых примеров, которые помогут вам разобраться с определением константы пропорции k.
Прямо пропорциональные и обратно пропорциональные отношения (учебники по математике)
В некоторых вопросах вам не нужно будет искать формулу, но вам будет предложено использовать соотношение, чтобы узнать новые значения. Не позволяйте формулировке вопроса застать вас врасплох! В этом видео рассматриваются как прямые, так и косвенные словесные задачи на пропорции.
Обратная пропорция (HEGARTYMATHS)
Прямые и обратные зависимости можно продемонстрировать с помощью графиков.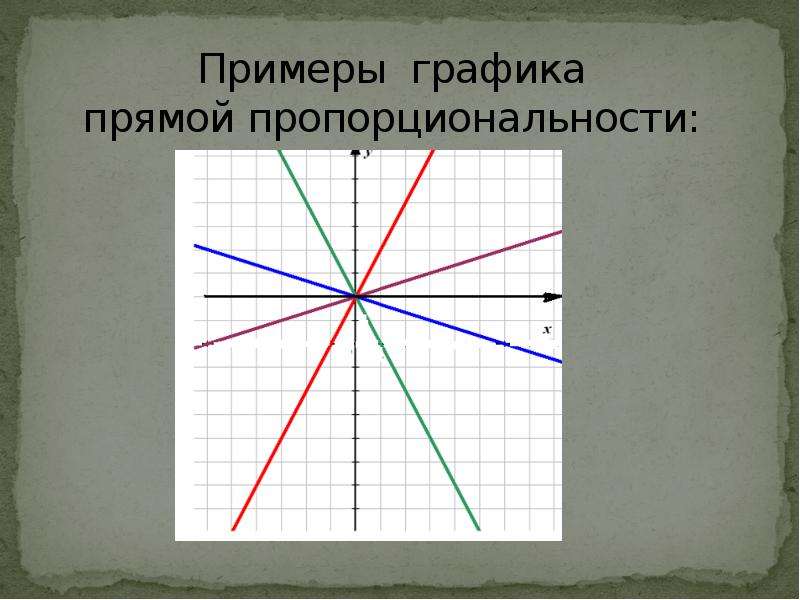 Изучите некоторые из основных форм графиков, чтобы вы могли распознать их, если они появятся на вашем экзамене!
Изучите некоторые из основных форм графиков, чтобы вы могли распознать их, если они появятся на вашем экзамене!
Графики и алгебраические пропорции (HEGARTYMATHS)
Variations
Вариант представляет собой отношение между набором значений одной переменной и набором значений других переменных.
Прямой вариант
В уравнении y = m x + b , если m ненулевая константа и b = 0, то у вас есть функция y = m x , записанная kx ), что называется прямой вариацией. То есть можно сказать, что y изменяется прямо, как х или y прямо пропорционально х . В этой функции m (или k ) называется константой пропорциональности или константой вариации.График каждой прямой вариации проходит через начало координат.
В этой функции m (или k ) называется константой пропорциональности или константой вариации.График каждой прямой вариации проходит через начало координат.
Пример 1
График y = 2 x .
Пример 2
Если y изменяется прямо как x , найдите постоянную вариации, когда y равно 2, а x равно 4.
Поскольку это прямой вариант,
y = kx (или y = m x )
Теперь, заменив и на 2 и x на 4,
Постоянная вариации .
Пример 3
Если y изменяется прямо как x и постоянная вариации равна 2, найдите y , когда x равно 6.
Поскольку это прямое изменение, просто замените k на 2 и x на 6 в следующем уравнении.
Прямая вариация также может быть записана в виде пропорции.
Эта пропорция читается как « у 1 к х 1 как у 2 к х 2 . x 1 и y 2 называются средними, и y 1 и x 2 называются крайними 10 2. Произведение средних всегда равно произведению крайних значений. Вы можете решить пропорцию, просто перемножив средние и крайние значения, а затем решив как обычно.
x 1 и y 2 называются средними, и y 1 и x 2 называются крайними 10 2. Произведение средних всегда равно произведению крайних значений. Вы можете решить пропорцию, просто перемножив средние и крайние значения, а затем решив как обычно.
Пример 4
r изменяется напрямую как p . Если r равно 3, когда p равно 7, найти p , когда r равно 9.
Метод 1. Использование пропорций: установка пропорции прямой вариации
Теперь подставьте значения.
Умножение средних и крайних значений (перекрестное умножение) дает
Метод 2. Использование y = kx:
Замените y на p и x на r .
р = крон
Используйте первый набор информации и подставьте 3 вместо r и 7 вместо p , затем найдите k.
Перепишите уравнение прямого изменения как .
Теперь используйте второй набор данных, который говорит, что r равно 9, подставьте это в предыдущее уравнение и найдите p .
Обратная вариация (косвенная вариация)
Вариация где называется обратной вариацией (или косвенной вариацией ). То есть с увеличением x уменьшается y. И при увеличении y x уменьшается. Вы можете увидеть уравнение xy = k , представляющее обратную вариацию, но это просто перестановка .
Эта функция также называется обратной или косвенной пропорцией. Опять же, m (или k ) называется константой вариации.
Пример 5
Если y изменяется косвенно как x , найдите постоянную вариации, когда y равно 2, а x равно 4.
Поскольку это косвенная или обратная вариация,
Теперь, заменив и на 2 и x на 4,
Постоянная вариации равна 8.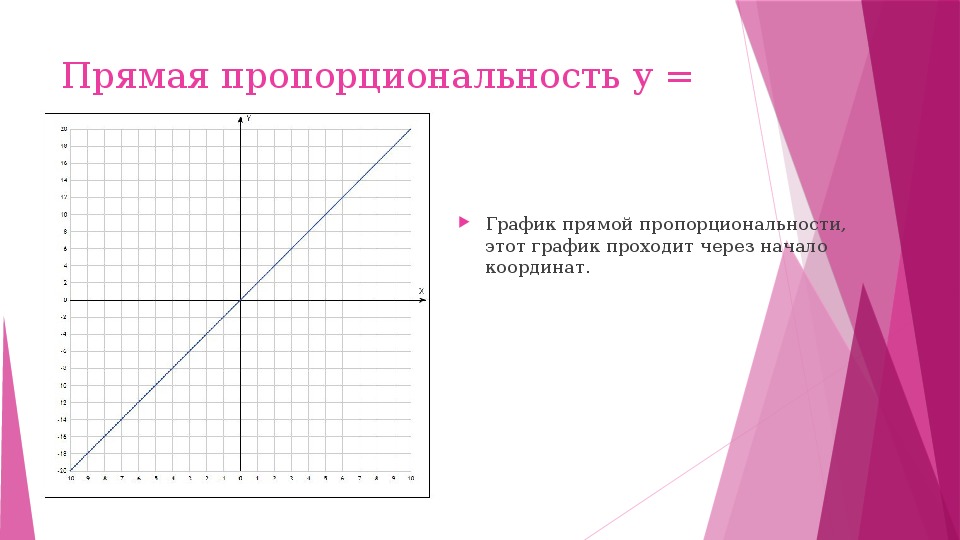
Пример 6
Если y изменяется косвенно как x и постоянная вариации равна 2, найдите y , когда x равно 6.
Поскольку это косвенное изменение, просто замените k на 2 и x на 6 в следующем уравнении.
Как и прямое изменение, обратное изменение также может быть записано в виде пропорции.
Обратите внимание, что в обратной пропорции x 1 и x 2 поменялись местами с пропорцией прямого изменения.
Пример 7
Если y изменяется косвенно как x и y = 4, когда x = 9, найдите x , когда y = 3.
Метод 1. Использование пропорций: Установите пропорцию косвенного изменения.
Теперь подставьте значения.
Умножение средних и крайних значений (перекрестное умножение) дает
Метод 2. Использование : Используйте первый набор информации и замените 4 на y и 9 на x , затем найдите k.
Перепишите уравнение прямого изменения как .
Теперь используйте второй набор данных, который говорит, что y равно 3, подставьте это в предыдущее уравнение и найдите x.
Как на графике отображается прямая пропорция? – Реабилитацияроботикс.нет
Как на графике отображается прямая пропорция?
Прямые графики, проходящие через начало координат, как тот, что показан непосредственно ниже, показывают, что величины на графике прямо пропорциональны. Он гласит: А прямо пропорционально В.Это означает: каким бы фактором ни изменялся А, В изменяется на тот же фактор.
На каком графике показана прямо пропорциональная зависимость?
При построении прямо пропорциональной зависимости результат представляет собой линейный график с наклоном k и точкой пересечения y в начале координат.
Как определить пропорциональную зависимость на графике?
Чтобы определить, пропорциональны ли отношения x и y, посмотрите, проходит ли линия, проходящая через эти точки, через начало координат (0, 0). Точки находятся на линии, проходящей через начало координат. Таким образом, x и y находятся в пропорциональной зависимости.
Точки находятся на линии, проходящей через начало координат. Таким образом, x и y находятся в пропорциональной зависимости.
Как узнать, является ли что-то прямой пропорцией?
Прямая пропорция или прямая вариация – это соотношение между двумя величинами, при котором отношение двух величин равно постоянной величине. Он представлен пропорциональным символом ∝. На самом деле тот же символ используется для обозначения обратно пропорционального, дело в том, что другая величина здесь инвертирована.
Что является примером прямой пропорции?
Термин «прямая пропорция» означает, что две (или более) величины увеличиваются или уменьшаются в одном и том же отношении. Например, в смеси фиолетовой краски соотношение синего и красного 4:3. Это не обязательно означает, что в каждой смеси будет 4 красных и 3 синих банки. Это означает, что у нас будет 4 красных на каждые 3 синих банки.
Что из следующего является примером прямой пропорциональности?
Соотношение между днями и часами — еще один пример прямой пропорциональности: время (часы) = 24 × время (дни) . Теперь мы объединяем прямую пропорциональность для минут и часов с прямой пропорциональностью для часов и дней: время (мин) = 60 × время (час) = 60 × (24 × время (дни)).
Теперь мы объединяем прямую пропорциональность для минут и часов с прямой пропорциональностью для часов и дней: время (мин) = 60 × время (час) = 60 × (24 × время (дни)).
Какие примеры пропорций?
Пропорция говорит, что два соотношения (или дроби) равны….Пример: Веревка
- 40 м этой веревки весит 2 кг.
- 200 м этой веревки весят 10 кг.
- и т. д.
Что такое прямая пропорция?
: пропорция двух переменных величин, когда отношение этих двух величин является постоянным.
Какие существуют 3 вида пропорций?
Типы пропорций
- Прямая пропорция.
- Обратная пропорция.
Что такое график прямой зависимости?
Когда две величины прямо пропорциональны, при увеличении одной увеличивается и другая. Две прямо пропорциональные величины всегда будут строить прямолинейный график, проходящий через начало координат. Если константа пропорциональности положительна, график будет иметь положительный градиент.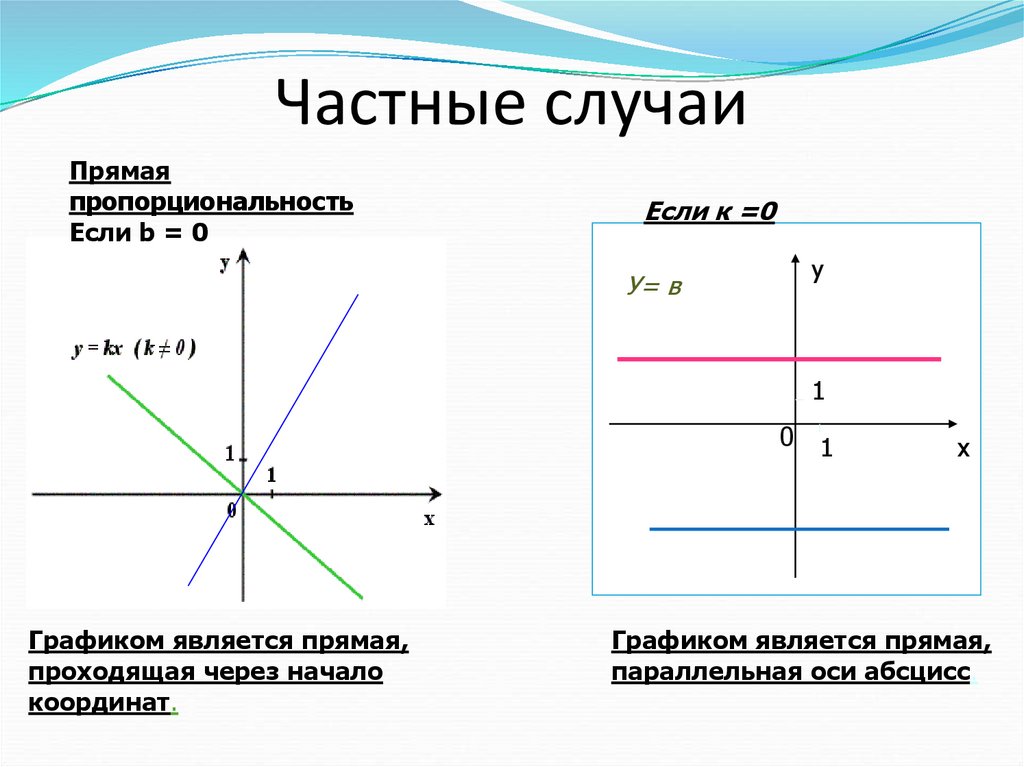
В чем разница между прямой и косвенной пропорцией?
В прямой пропорции соотношение между совпадающими количествами остается прежним, если их разделить. (Они образуют равнозначные дроби). В косвенной (или обратной) пропорции при увеличении одной величины другая уменьшается. В обратной пропорции произведение соответствующих количеств остается прежним.
Что является примером косвенной пропорции?
Обратные пропорции/вариации или косвенные пропорции Это означает, что при увеличении x у уменьшается, и наоборот, на величину, при которой xy остается неизменной.Пример: 4 человека ремонтируют дорогу за 6 часов. За какое время эту работу выполнят 8 человек, если они будут работать с одинаковой скоростью?
Как определить прямую и обратную пропорции?
Когда две величины x и y прямо пропорциональны (или прямо пропорциональны), они записываются как x ∝ y. Символ «∝» означает «пропорционально». Когда две величины x и y обратно пропорциональны (или изменяются обратно пропорционально), их записывают как x ∝ 1 y .
Каковы этапы решения парциальной пропорции?
Чтобы решить делительную пропорцию, сначала вы должны добавить 3 и 5 к сумме, но если вы собираетесь сложить их обе, вы поставите х, чтобы это могло сбалансировать отношение.Пример: Кусок дерева был длиной 204, с соотношением 1:5.
Каковы этапы решения задач на прямую пропорцию?
Для этого нужно выполнить четыре шага:
- напишите пропорциональное отношение.
- преобразовать в уравнение с использованием константы пропорциональности.
- использовать данную информацию, чтобы найти константу пропорциональности.
- подставить константу пропорциональности в уравнение.
Для чего нужны пропорции?
Составление и решение пропорции является полезной стратегией для решения различных задач на пропорциональные рассуждения.В этих задачах всегда важно определить неизвестное значение, а затем определить пропорциональную зависимость, которую можно использовать для решения неизвестного значения.
Что такое пропорция?
1 : гармоничное отношение частей друг к другу или к целому: равновесие, симметрия. 2а: надлежащая или равная доля, каждая выполнила свою часть работы. b : квота, процент. 3: отношение одной части к другой или к целому по величине, количеству или степени: отношение.
Что означает разделительная пропорция?
Частная пропорция, от слова Partitive, означающего разделенный на части, представляет собой пропорцию количества, распределяемого или делящегося неравномерно на две или более частей.
Что означает обратная пропорция?
Когда значение одной величины увеличивается по отношению к уменьшению другой или наоборот, говорят, что они обратно пропорциональны. Это означает, что две величины ведут себя противоположно по своей природе.Например, скорость и время обратно пропорциональны друг другу. При увеличении скорости время сокращается.
Что такое пропорции в математике?
Пропорция говорит о том, что два соотношения (или дроби) равны. Пример: 1/3 = 2/6. См.: Эквивалентные дроби.
Пример: 1/3 = 2/6. См.: Эквивалентные дроби.
Что такое формула пропорции?
Пропорция — это просто утверждение, что два отношения равны. Его можно записать двумя способами: в виде двух равных дробей a/b = c/d; или используя двоеточие, a:b = c:d.
Что такое пропорции в статистике?
Пропорция относится к части суммы, которая обладает определенным атрибутом.Например, предположим, что у нас есть выборка из четырех домашних животных — птицы, рыбы, собаки и кошки. Следовательно, доля питомцев с четырьмя ногами составляет 2/4 или 0,50. …
Какими 3 способами можно решить пропорцию?
Три способа решения пропорций
- Вертикальный.
- Горизонтальный.
- Диагональ (часто называемая «перекрестным произведением»)
Как решить вопрос о пропорциях?
Чтобы решить пропорции, нужно просто представить отношения в виде дробей, установить две дроби равными друг другу, перекрестно умножить и решить полученное уравнение.
Как узнать, пропорциональное ли это соотношение? – М.В.Организинг
Как узнать, пропорциональны ли отношения?
Чтобы определить, существует ли пропорциональная связь, необходимо найти эквивалентные (равные) отношения в таблице. Если координаты x и y образуют пропорциональные отношения, то существует некоторое неизменяющееся число (константа), которое при умножении на x даст y.
Как узнать, что что-то прямо пропорционально?
Если отношение (yx) двух переменных (x и y) равно константе (k = yx), то переменная в числителе отношения (y) может быть произведением другой переменной и константы (y = к ⋅ х).В этом случае говорят, что у прямо пропорционально х с константой пропорциональности к.
Какими двумя способами можно доказать, что пропорция верна?
В задачах на пропорции мы можем использовать векторные произведения, чтобы проверить, равны ли два отношения и образуют ли пропорцию. Чтобы найти перекрестные произведения пропорции, мы умножаем внешние члены, называемые крайними, и средние члены, называемые средними. Здесь 20 и 5 — крайние значения, а 25 и 4 — средние.
Здесь 20 и 5 — крайние значения, а 25 и 4 — средние.
Что такое прямая пропорция?
: пропорция двух переменных величин, когда отношение этих двух величин является постоянным.
В чем разница между прямой и обратной пропорцией?
В прямой пропорции соотношение между совпадающими количествами остается прежним, если их разделить. (Они образуют равнозначные дроби). В косвенной (или обратной) пропорции при увеличении одной величины другая уменьшается. В обратной пропорции произведение соответствующих количеств остается прежним.
Какова формула косвенной пропорции?
Косвенно-пропорциональная формула. аб = к; где k — постоянная пропорциональности.
Что означает косвенная пропорция?
Обновлено 5 сентября 2018 г. Обратная пропорция — это отношение между двумя переменными, когда их произведение равно постоянному значению. Когда значение одной переменной увеличивается, другая уменьшается, поэтому их произведение не меняется. y обратно пропорционален x, когда уравнение принимает форму: y = k/x.
y обратно пропорционален x, когда уравнение принимает форму: y = k/x.
Что имеется в виду, когда говорят, что две переменные прямо пропорциональны?
Прямая пропорция — это отношение между двумя переменными, отношение которых равно постоянному значению.Другими словами, прямая пропорция — это ситуация, когда увеличение одной величины вызывает соответствующее увеличение другой величины или уменьшение одной величины приводит к уменьшению другой величины.
Какая пара величин с наименьшей вероятностью будет прямо пропорциональна?
1. Площадь и длина стороны ромба. Наименее пропорциональны, так как обратно пропорциональны.
Какая пара величин с наименьшей вероятностью будет прямо пропорциональна площади и длине стороны ромба?
Что неверно относительно прямой пропорциональности?
Ответ.На графике прямой пропорциональности ее график представляет собой график прямой или линейный график, проходящий через начало координат. Таким образом, варианты А и варианты D верны. Его наклон также постоянен, поэтому вариант C является правильным, оставляя нам вариант B как утверждение, которое неверно относительно прямой пропорциональности.
Его наклон также постоянен, поэтому вариант C является правильным, оставляя нам вариант B как утверждение, которое неверно относительно прямой пропорциональности.
Что такое уравнение прямой пропорциональности?
Прямая пропорция В математических выражениях это может быть выражено как y = kx. Это читается как «у изменяется прямо как х» или «у прямо пропорционально как х», где k является постоянным в уравнении.Пример: y прямо пропорционален x, когда x = 15, y = 30.
Должен ли график прямой зависимости быть линейным?
Ответ эксперта Проверено На графике прямой пропорциональности его график представляет собой график прямой или линейный график, проходящий через начало координат. Его наклон также постоянен, поэтому вариант C является правильным, оставляя нам вариант B как утверждение, которое неверно относительно прямой пропорциональности. Надеюсь, что это ответ на ваш вопрос.
Что означает пропорция?
1 : гармоничное отношение частей друг к другу или к целому: равновесие, симметрия. 2а: надлежащая или равная доля, каждая выполнила свою часть работы. b : квота, процент. 3: отношение одной части к другой или к целому по величине, количеству или степени: отношение. 4 : ввод размера 1, размер.
2а: надлежащая или равная доля, каждая выполнила свою часть работы. b : квота, процент. 3: отношение одной части к другой или к целому по величине, количеству или степени: отношение. 4 : ввод размера 1, размер.
Как узнать, показывает ли график прямую зависимость?
Мы проверим эту форму графика, если мы изменим A на какой-то коэффициент, действительно ли B изменится на тот же коэффициент, таким образом показав, что эта прямая линия, проходящая через начало координат, представляет собой прямую пропорцию.На графике ниже мы меняем величину A в 3 раза; то есть мы утраиваем его.
Что такое диаграмма пропорций?
Методы визуализации, использующие размер или площадь, чтобы показать различия или сходства между значениями или частями целого. Пропорции между значениями. Пузырьковая диаграмма.
Как узнать, пропорционален ли график?
Чтобы определить, пропорциональны ли отношения x и y, посмотрите, проходит ли линия, проходящая через эти точки, через начало координат (0, 0).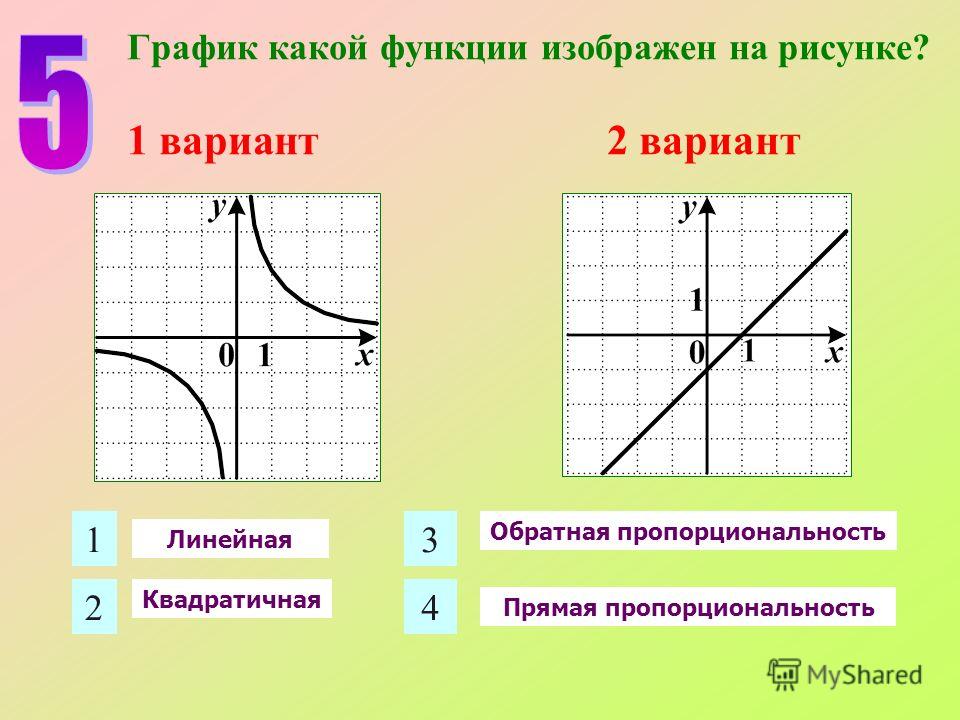
 {«»}\left(x\right)=k»=0$. Следовательно, функция не имеет точек перегиба.
{«»}\left(x\right)=k»=0$. Следовательно, функция не имеет точек перегиба.