Отрицательная степень | Алгебра
Что такое степень с отрицательным показателем (отрицательная степень)? Как выполнить возведение числа в отрицательную степень? Как возвести в отрицательную степень дробь?
Определение.
В частности, число в степени минус один — это число, обратное данному:
Если n — целое число, то речь идет о степени с целым отрицательным показателем и равенство верно для любого a, отличного от нуля (т.е. при a≠0).
Если n — дробное число, то речь идет о степени с рациональным показателем:
(m — целое число, n — натуральное число). Степень с дробным показателем определена только для положительных a (a>0).
В частности,
Дробь в степени с отрицательным показателем равна обратному этой дроби числу в степени с показателем, противоположным данному:
Другими словами, чтобы возвести дробь в отрицательную степень, надо эту дробь «перевернуть»(числитель и знаменатель поменять местами) и изменить знак в показателе степени.
Дробь в минус первой степени — это «перевернутая» дробь.
В частности,
Рассмотрим примеры возведения чисел в степень с отрицательным показателем.
Для ускорения вычислений используем таблицу степеней.
Примеры.
Чтобы возвести в отрицательную степень смешанное число, надо сначала перевести его в неправильную дробь:
Возведем числа в степень с дробным отрицательным показателем:
При возведении в отрицательную степень десятичной дроби можно сначала перевести ее в обыкновенную и, если возможно, сократить:
Если в показателе степени стоит десятичная дробь, нужно перевести ее в обыкновенную:
Возведение в степень с отрицательным показателем в алгебре встречается достаточно часто, поэтому важно вовремя усвоить эту тему.
Отрицательная степень. Отрицательная степень числа. Степень с отрицательным показателем. Степени чисел
Степень с отрицательным показателем определение
Пусть число a есть любое действительное число, отличное от нуля. Число m – отрицательное целое число.
Степень с отрицательным показателем определение:
Действительное, отличное от нуля число a, возведенное в отрицательную целую степень -m, равно дроби, в числителе которой 1 и в знаменателе a, возведенное в положительную целую степень m.
Отрицательная степень формула
Для вычислений отрицательных степеней используем формулу:
a-m = 1/am
Эта формула применяется, если имеется отрицательное значение степени.
Положительная и отрицательная степень
Чтоб лучше понять сравним положительные и отрицательные степени.
Пусть число a есть любое действительное число, отличное от нуля. Число m – любое целое число.
Тогда a в положительной степени m равно:
am = a * a * a * … (m раз)
Теперь a в отрицательной степени -m:
a-m = 1/am
Степень с целым отрицательным показателем
Обратите внимание, что в этой статье речь идет именно о целом отрицательном показателе. Здесь существенным является то, что показатель целый.
Пример степени с целым отрицательным показателем:
12-3 = 1/123
Отрицательное основание степени
Отрицательная степень числа и отрицательное основание степени – это разные вещи.
Отрицательное основание степени рассмотрим на примере.
Пример отрицательного основания степени:
(-2)3 = -2 * (-2) * (-2) = -8
А теперь пример отрицательной степени числа.
Пример (отрицательная степень числа):
2-3 = 1/23 = 1/8
Степень с отрицательным показателем, 8 класс, примеры
Дата публикации: . m} $.
m} $.
Упрощение выражений с отрицательными степенями. Степень числа: определения, обозначение, примеры. Как возводить в отрицательную степень
Степень с отрицательным показателем определение
Пусть число a есть любое действительное число, отличное от нуля. Число m — отрицательное целое число.
Степень с отрицательным показателем определение:
Действительное, отличное от нуля число a, возведенное в отрицательную целую степень -m, равно дроби, в числителе которой 1 и в знаменателе a, возведенное в положительную целую степень m.
Отрицательная степень формула
Для вычислений отрицательных степеней используем формулу:
Эта формула применяется, если имеется отрицательное значение степени.
Положительная и отрицательная степень
Чтоб лучше понять сравним положительные и отрицательные степени.
Пусть число a есть любое действительное число, отличное от нуля. Число m — любое целое число.
Тогда a в положительной степени m равно:
A m = a * a * a * . .. (m раз)
.. (m раз)
Теперь a в отрицательной степени -m:
Степень с целым отрицательным показателем
Обратите внимание, что в этой статье речь идет именно о целом отрицательном показателе. Здесь существенным является то, что показатель целый.
Пример степени с целым отрицательным показателем:
Отрицательное основание степени
Отрицательная степень числа и отрицательное основание степени — это разные вещи.
В одной из предыдущих статей мы уже упоминали о степени числа. Сегодня мы постараемся сориентироваться в процессе нахождения ее значения. Научно говоря, мы будем выяснять, как правильно возводить в степень. Мы разберемся, как производится этот процесс, одновременно затронем все вероятные показатели степени: натуральный, иррациональный, рациональный, целый.
Итак, давайте подробно рассмотрим решения примеров и выясним, что значит:
- Определение понятия.
- Возведение в отрицательную ст.
- Целый показатель.
- Возведение числа в иррациональную степень.

Определение понятия
Вот точно отражающее смысл определение: «Возведением в степень называют определение значения степени числа».
Соответственно, возведение числа a в ст. r и процесс нахождения значения степени a с показателем r — это идентичные понятия. К примеру, если стоит задача вычислить значение степени (0,6)6″, то ее можно упростить до выражения «Возвести число 0,6 в степень 6».
После этого можно приступать напрямую к правилам возведения.
Возведение в отрицательную степень
Для наглядности следует обратить внимание на такую цепочку выражений:
110=0,1=1* 10 в минус 1 ст.,
1100=0,01=1*10 в минус 2 степ.,
11000=0,0001=1*10 в минус 3 ст.,
110000=0,00001=1*10 в минус 4 степeни.
Благодаря данным примерам можно четко просмотреть возможность моментально вычислить 10 в любой минусовой степени.
- 10 в -1 степeни — перед единицей 1 ноль;
- в -3 — три нуля перед единицей;
- в -9 — это 9 нулей и проч.

Так же легко понять по данной схеме, сколько будет составлять 10 в минус 5 ст. —
1100000=0,000001=(1*10)-5.
Как возвести число в натуральную степeнь
Вспоминая определение, учитываем, что натуральное число a в ст. n равняется произведению из n множителей, при этом каждый из них равняется a. Проиллюстрируем: (а*а*…а)n, где n — это количество чисел, которые умножаются. Соответственно, чтобы a возвести в n, необходимо рассчитать произведение следующего вида: а*а*…а разделить на n раз.
Отсюда становится очевидно, что возведение в натуральную ст. опирается на умение осуществлять умножение (этот материал освещен в разделе про умножение действительных чисел). Давайте рассмотрим задачу:
Возведите -2 в 4-ю ст.
Мы имеем дело с натуральным показателем. Соответственно, ход решения будет следующим: (-2) в cт. 4 = (-2)*(-2)*(-2)*(-2). Теперь осталось только осуществить умножение целых численностей:(-2)*(-2)*(-2)*(-2). Получаем 16.
Получаем 16.
Ответ на задачу:
(-2) в ст. 4=16.
Пример:
Вычислите значение: три целых две седьмых в квадрате.
Данный пример равняется следующему произведению: три целых две седьмых умножить на три целых две седьмых. Припомнив, как осуществляется умножение смешанных чисел, завершаем возведение:
- 3 целых 2 седьмых умножить на самих себя;
- равно 23 седьмых умножить на 23 седьмых;
- равно 529 сорок девятых;
- сокращаем и получаем 10 тридцать девять сорок девятых.
Ответ: 10 39/49
Касаемо вопроса возведения в иррациональный показатель, следует отметить что расчеты начинают проводить после завершения предварительного округления основы степени до какого-либо разряда, который позволил бы получить величину с заданной точностью. К примеру, нам необходимо возвести число П (пи) в квадрат.
Начинаем с того, что округляем П до сотых и получаем:
П в квадрате = (3,14)2=9,8596. Однако если сократить П до десятитысячных, получим П=3,14159. Тогда возведение в квадрат получает совсем другое чиcло: 9,8695877281.
Однако если сократить П до десятитысячных, получим П=3,14159. Тогда возведение в квадрат получает совсем другое чиcло: 9,8695877281.
Здесь следует отметить, что во многих задачах нет надобности возводить иррациональные числа в cтeпeнь. Как правило, ответ вписывается или в виде, собственно, степени, к примеру, корень из 6 в степени 3, либо, если позволит выражение, проводится его преобразование: корень из 5 в 7 cтепeни = 125 корень из 5.
Как возвести чиcло в целую степень
Эту алгебраическую манипуляцию уместно принимать во внимание для следующих случаев:
- для целых чисел;
- для нулевого показателя;
- для целого положительного показателя.
Поскольку практически все целые положительные числа совпадают с массой чисел натуральных, то постановка в положительную целую степень — это тот же процесс, что и постановка в ст. натуральную. Данный процесс мы описали в предшествующем пункте.
Теперь поговорим о вычислении ст. нулевой. Мы уже выяснили выше, что нулевую степень числа a можно определить для любого отличного от нуля a (действительного), при этом a в ст. 0 будет равно 1.
нулевой. Мы уже выяснили выше, что нулевую степень числа a можно определить для любого отличного от нуля a (действительного), при этом a в ст. 0 будет равно 1.
Соответственно, возведение какого угодно действительного числа в нулевую ст. будет давать единицу.
К примеру, 10 в ст.0=1, (-3,65)0=1, а 0 в ст. 0 нельзя определить.
Для того чтобы завершить возведение в целую степень, остается определиться с вариантами целых отрицательных значений. Мы помним, что ст. от a с целым показателем -z будет определяться как дробь. В знаменателе дроби располагается ст. с целым положительным значением, значение которой мы уже научились находить. Теперь остается лишь рассмотреть пример возведения.
Пример:
Вычислить значение числа 2 в кубе с целым отрицательным показателем.
Процесс решения:
Согласно определению стeпeни с отрицательным показателем обозначаем: два в минус 3 ст. равняется один к двум в третьей cтепeни.
Знаменатель рассчитывается просто: два в кубе;
3 = 2*2*2=8.
Ответ: два в минус 3-й ст. = одна восьмая.
Видео
Из этого видео вы узнаете, что делать, если степень с отрицательным показателем.
Обращаем ваше внимание, что в данном разделе разбирается понятие степени только с натуральным показателем и нулём.
Понятие и свойства степеней с рациональными показателями (с отрицательным и дробным) будут рассмотрены в уроках для 8 класса.
Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение.
Вместо произведения шести одинаковых множителей 4 · 4 · 4 · 4 · 4 · 4 пишут 4 6 и произносят «четыре в шестой степени».
4 · 4 · 4 · 4 · 4 · 4 = 4 6Выражение 4 6 называют степенью числа, где:
- 4 — основание степени ;
- 6 — показатель степени .
В общем виде степень с основанием «a » и показателем «n » записывается с помощью выражения:
Запомните!
Степенью числа «a
» с натуральным показателем «n
»,
бóльшим 1
, называется произведение «n
»
одинаковых множителей, каждый из которых равен числу
«a
».
Запись «a n » читается так: «а в степени n » или «n -ая степень числа a ».
Исключение составляют записи:
- a 2 — её можно произносить как «а в квадрате»;
- a 3 — её можно произносить как «а в кубе».
- a 2 — «а во второй степени»;
- a 3 — «а в третьей степени».
Особые случаи возникают, если показатель степени равен единице или нулю (n = 1; n = 0) .
Запомните!
Степенью числа «а
» с показателем n = 1
является само это число:
a 1 = a
Любое число в нулевой степени равно единице.
a 0 = 1
Ноль в любой натуральной степени равен нулю.
0 n = 0
Единица в любой степени равна 1.
1 n = 1
Выражение 0 0 (ноль в нулевой степени ) считают лишённым смыслом.
- (−32) 0 = 1
- 0 253 = 0
- 1 4 = 1
При решении примеров нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в
степень.
Пример. Возвести в степень.
- 5 3 = 5 · 5 · 5 = 125
- 2,5 2 = 2,5 · 2,5 = 6,25
- ( · = =
Возведение в степень отрицательного числа
Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулём.
Запомните!
При возведении в степень положительного числа получается положительное число.
При возведении нуля в натуральную степень получается ноль.
При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.
Рассмотрим примеры возведения в степень отрицательных чисел.
Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.
Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.
Так как произведение чётного количество отрицательных сомножителей положительно.
Запомните!
Отрицательное число, возведённое в чётную степень, есть число положительное .
Отрицательное число, возведённое в нечётную степень, — число отрицательное .
Квадрат любого числа есть положительное число или нуль, то есть:
a 2 ≥ 0 при любом a .
- 2 · (−3) 2 = 2 · (−3) · (−3) = 2 · 9 = 18
- −5 · (−2) 3 = −5 · (−8) = 40
Обратите внимание!
При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (−5) 4 и −5 4 это разные выражения. Результаты возведения в степень данных выражений будут разные.
Вычислить (−5) 4 означает найти значение четвёртой степени отрицательного числа.
(−5) 4 = (−5) · (−5) · (−5) · (−5) = 625
В то время как найти «−5 4 » означает, что пример нужно решать в 2 действия:
- Возвести в четвёртую степень положительное
число 5
.
5 4 = 5 · 5 · 5 · 5 = 625 - Поставить перед полученным результатом знак «минус» (то есть выполнить
действие вычитание).

−5 4 = −625
Пример. Вычислить: −6 2 − (−1) 4
−6 2 − (−1) 4 = −37- 6 2 = 6 · 6 = 36
- −6 2 = −36
- (−1) 4 = (−1) · (−1) · (−1) · (−1) = 1
- −(−1) 4 = −1
- −36 − 1 = −37
Порядок действий в примерах со степенями
Вычисление значения называется действием возведения в степень. Это действие третьей ступени.
Запомните!
В выражениях со степенями, не содержащими скобки, сначала выполняют вовзведение в степень , затем умножение и деление , а в конце сложение и вычитание .
Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.
Пример. Вычислить:
Для облегчения решения примеров полезно знать и пользоваться таблицей степеней , которую вы можете бесплатно скачать на нашем сайте.
Для проверки своих результатов вы можете воспользоваться на нашем сайте калькулятором «
Операции со степенями и корнями. Степень с отрицательным ,
Степень с отрицательным ,
нулевым и дробным показателем. О выражениях, не имеющих смысла.
Операции со степенями.
1. При умножении степеней с одинаковым основанием их показатели складываются :
a m · a n = a m + n .
2. При делении степеней с одинаковым основанием их показатели вычитаются .
3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.
( abc … ) n = a n · b n · c n …
4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):
( a / b ) n = a n / b n .
5. При возведении степени в степень их показатели перемножаются:
(a m ) n = a m n .
Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.

П р и м е р. (2 · 3 · 5 / 15) ² = 2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .
Операции с корнями. Во всех нижеприведенных формулах символ означает арифметический корень (подкоренное выражение положительно).
1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:
2. Корень из отношения равен отношению корней делимого и делителя:
3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в m раз и одновременно возвести в m -ую степень подкоренное число, то значение корня не изменится:
5. Если уменьшить степень корня в m раз и одновременно извлечь корень m -ой степени из подкоренного числа, то значение корня не изменится:
Расширение понятия
степени. До
сих пор мы рассматривали степени только с натуральным показателем;
но
действия
со
степенями и корнями
могут приводить также к отрицательным , нулевым и дробным показателям. Все эти показатели степеней требуют
дополнительного определения.
До
сих пор мы рассматривали степени только с натуральным показателем;
но
действия
со
степенями и корнями
могут приводить также к отрицательным , нулевым и дробным показателям. Все эти показатели степеней требуют
дополнительного определения.
Степень с отрицательным показателем. Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной велечине отрицательного показателя:
Т еперь формула a m : a n = a m — n может быть использована не только при m , большем, чем n , но и при m , меньшем, чем n .
П р и м е р . a 4 : a 7 = a 4 — 7 = a — 3 .
Если
мы хотим, чтобы формула a m : a
n = a
m — n была
справедлива при m =
n , нам необходимо
определение нулевой степени.
Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.
П р и м е р ы. 2 0 = 1, (– 5) 0 = 1, (– 3 / 5) 0 = 1.
Степень с дробным показателем. Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n –ой степени из m -ой степени этого числа а :
О выражениях, не имеющих смысла. Есть несколько таких выражений. любое число.
В самом деле, если предположить, что это выражение равно некоторому числу x , то согласно определению операции деления имеем: 0 = 0 · x . Но это равенство имеет место при любом числе x , что и требовалось доказать.
Случай 3.
0 0 — любое число.
Действительно,
Р е ш е н и е. Рассмотрим три основных случая:
1) x = 0 – это значение не удовлетворяет данному уравнению
(Почему?).
2) при x > 0 получаем: x / x = 1, т.e. 1 = 1, откуда следует,
что x – любое число; но принимая во внимание, что в
Нашем случае x > 0 , ответом является x > 0 ;
3) при x x / x = 1, т. e . –1 = 1, следовательно,
В этом случае нет решения.
Таким образом, x > 0.
Возведение в отрицательную степень – один из основных элементов математики, который часто встречается при решении алгебраических задач. Ниже приведена подробная инструкция.
Как возводить в отрицательную степень – теория
Когда мы число в обычную степень, мы умножаем его значение несколько раз. Например, 3 3 = 3×3×3 = 27. С отрицательной дробью все наоборот. Общий вид по формуле будет иметь следующий вид: a -n = 1/a n . Таким образом, чтобы возвести число в отрицательную степень, нужно единицу поделить на данное число, но уже в положительной степени.
Как возводить в отрицательную степень – примеры на обычных числах
Держа вышеприведенное правило на уме, решим несколько примеров.
4 -2 = 1/4 2 = 1/16
Ответ: 4 -2 = 1/16
4 -2 = 1/-4 2 = 1/16.
Ответ -4 -2 = 1/16.
Но почему ответ в первом и втором примерах одинаковый? Дело в том, что при возведении отрицательного числа в четную степень (2, 4, 6 и т.д.), знак становится положительным. Если бы степень была четной, то минус сохранился:
4 -3 = 1/(-4) 3 = 1/(-64)
Как возводить в отрицательную степень – числа от 0 до 1
Вспомним, что при возведении числа в промежутке от 0 до 1 в положительную степень, значение уменьшается с возрастанием степени. Так например, 0,5 2 = 0,25. 0,25
Пример 3: Вычислить 0,5 -2
Решение: 0,5 -2 = 1/1/2 -2 = 1/1/4 = 1×4/1 = 4.
Ответ: 0,5 -2 = 4
Разбор (последовательность действий):
- Переводим десятичную дробь 0,5 в дробную 1/2. Так легче.
Возводим 1/2 в отрицательную степень. 1/(2) -2 . Делим 1 на 1/(2) 2 , получаем 1/(1/2) 2 => 1/1/4 = 4
Пример 4: Вычислить 0,5 -3
Решение: 0,5 -3 = (1/2) -3 = 1/(1/2) 3 = 1/(1/8) = 8
Пример 5: Вычислить -0,5 -3
Решение: -0,5 -3 = (-1/2) -3 = 1/(-1/2) 3 = 1/(-1/8) = -8
Ответ: -0,5 -3 = -8
Исходя из 4-го и 5-ого примеров, сделаем несколько выводов:
- Для положительного числа в промежутке от 0 до 1 (пример 4), возводимого в отрицательную степень, четность или нечетность степени не важна, значение выражения будет положительным.
 При этом, чем больше степень, тем больше значение.
При этом, чем больше степень, тем больше значение. - Для отрицательного числа в промежутке от 0 до 1 (пример 5), возводимого в отрицательную степень, четность или нечетность степени неважна, значение выражения будет отрицательным. При этом, чем больше степень, тем меньше значение.
Как возводить в отрицательную степень – степень в виде дробного числа
Выражения данного типа имеют следующий вид: a -m/n , где a – обычное число, m – числитель степени, n – знаменатель степени.
Рассмотрим пример:
Вычислить: 8 -1/3
Решение (последовательность действий):
- Вспоминаем правило возведения числа в отрицательную степень. Получим: 8 -1/3 = 1/(8) 1/3 .
- Заметьте, в знаменателе число 8 в дробной степени. Общий вид вычисления дробной степени таков: a m/n = n √8 m .
- Таким образом, 1/(8) 1/3 = 1/(3 √8 1). Получаем кубический корень из восьми, который равен 2. Исходя отсюда, 1/(8) 1/3 = 1/(1/2) = 2.
- Ответ: 8 -1/3 = 2
возвести число в отрицательную степень
Для того, чтобы понять, как возвести число в отрицательную степень – достаточно взглянуть на скриншот, что приведен ниже!Как видим – число в отрицательной степени равно дроби – 1 деленное на положительную степень этого числа.
 Напоминаю, что у нас есть калькулятор, который умеет считать отрицательную степень числа!
Напоминаю, что у нас есть калькулятор, который умеет считать отрицательную степень числа!Пример решения числа в отрицательной степени.
Для того, чтобы понять. Как возводить в отрицательную степень, нужен пример! И давайте пример возьмем из того примера страницы, где мы высчитывали отрицательную степень на калькуляторе. Число 5 в отрицательной степени -25 = 12 5=125= 0.04Написать что-нибудь…
отрицательная степень , степень с отрицательным показателем , отрицательная степень числа , степень с целым отрицательным , степень с отрицательным целым показателем , отрицательная рациональная степень , работа с отрицательными степенями , степень с отрицательным рациональным показателем , рациональные уравнения степень с целым отрицательным показателем , отрицательные степени , контрольная степень с целым отрицательным показателем , отрицательные степени класс , степень с отрицательным показателем класс , алгебра отрицательные степени , как возводить в отрицательную степень , алгебра степень с отрицательным показателем , степень с целым отрицательным показателем класс , отрицательные степени , возведение в отрицательную степень , тема степень с отрицательным показателем , алгебра класс отрицательная степень , отрицательная степень , отрицательная степень как решать , алгебра степень с отрицательным целым показателем , тема степень с целым отрицательным показателем , выражения с отрицательными степенями , как возвести число в отрицательную степень , возведение числа в отрицательную степень , примеры с отрицательными степенями , в отрицательной степени ,В эксель возвести в степень
Возведение числа в степень в Microsoft Excel
Смотрите также А, вот, со сада, который строит допустим. Соответственно, -Имя точно выразился, вот иначе -2 воспринимается корень n-й степени, функция вычисляет квадратный ссылку при копировании7 на модуль показателя, четвертую степень. В данном случае
Соответственно, -Имя точно выразился, вот иначе -2 воспринимается корень n-й степени, функция вычисляет квадратный ссылку при копировании7 на модуль показателя, четвертую степень. В данном случае
числовое значение, хранящееся. Как видим, расчетВозведение числа в степень
Возведение чисел
скобками — другое графики. это выполнение унарного , поможет разобраться как отрицание всего необходимо возвести число корень. Если аргумент формулы. Закрепите номер3
Способ 1: возведение с помощью символа
а потом единицуВыделите ячейку, в которой – 3. несколько способов возведения корень тождественен возведению в ней, отобразится был выполнен корректно. является стандартным математическим дело.JayBhagavan
смены знака. Операция
в проблеме написания выражения. Надеюсь понятно в степень 1/n. имеет отрицательное значение, столбца, содержащего возводимое=СТЕПЕНЬ(B2;C2)
- поделить на результат.
 ». – определенное значение.
». – определенное значение.-0,5 и в обычную более трех-четырех раз. того, чтобы запись ячейке появится результат вычислить значение, то рассчитывается результат. В вычисление, жмем на
каждого значения. ДостаточноСкачать последнюю версию
Способ 3: возведение в степень через корень
величиной (равно ссылка нужно знать матчасть. отрицательного числа два.: Раз уж пошли нас учили) учатОбратите внимание! Дробная степеньАргумент функции – ссылка1
с помощью Excel. Это не говоря в ячейке отобразилась данной математической операции.
- удобнее всего производить данном случае он кнопку записать её для Excel
- на ячейку) стоит В серьезных языкахНо в формулах тесты: Sub Test() в младших классах пишется в скобках. на ячейку с1
- Ведь для решения уж о том, корректно. Итак, введите Теперь вы в запись через символ равен 3.
 » это число и. Затем просто нужноКак поставить знак степени это это операция
» это число и. Затем просто нужноКак поставить знак степени это это операция
все операторы, унарные унарного оператора смены 2 End Sub ТС прямо и но с использованиемФункция вернула ошибку, т.к.
1 пользоваться как привычным и единицу разделить
Способ 4: запись числа со степенью в ячейке
34. Почему именно степень в «Экселе»,. В отдельных случаях является результатом возведенияВслед за этим результат навести курсор на в Microsoft Word
- Если перед числом и бинарные запилив знака предусмотрел болееАлександр пишет первую формулу функции СТЕПЕНЬ. аргумент – ссылка1 всем символом «крышечка», на результат. Поэтому его? Да потому, чтобы число сразу можно применить функцию
- 9 в степень вычисления данной функции нижний правый уголВ Excel существует одновременно стоит минус - свой алгоритм и высокий приоритет (почему
- : PooHkrd, что PQ как минус дваИзвлекли корень девятой степени
- на ячейку с1 так и удобной тем, у кого что 4 – же возводилось вСТЕПЕНЬ 0,5.
 выводится в место,
выводится в место,
- ячейки с формулой. несколько способов возвести то это знак
приоритеты (с блэкджеком — это к сломался над этой в квадрате, так? из значения ячейки отрицательным значением.2 для запоминания встроенной нет под рукой это степень числа нее.. Если вам нужноНо, конечно, к данному которое было выделено Появится маркер заполнения. число в степень.
Всегда так было, и э… всем ним) . Так
задачкой?))))Вторая — из h2.Функция ABS возвращает абсолютное2 функцией программы. Это специального инженерного калькулятора, 3, которую мыДля достижения поставленного результата возвести число в способу расчета прибегают ещё в первом Зажимаем левую кнопку Это можно сделать старею. остальным). Вообще рекомендуется захотелосьАндрей VG нуля вычесть дваИзвлекли корень пятой степени значение числа -36.4 несомненный плюс! мы расскажем, как сейчас будем видоизменять.
 можно прибегнуть и степень 0,5, то довольно редко, используя шаге описываемых действий. мыши и протягиваем при помощи стандартногоПоявился Excel и при первой же
можно прибегнуть и степень 0,5, то довольно редко, используя шаге описываемых действий. мыши и протягиваем при помощи стандартногоПоявился Excel и при первой жеВон в Maple,
lumpics.ru>
Три способа, как поставить степень в «Экселе»
: Доброе время сутокС в квадрате - из суммы числа Ее использование позволило8Перейдем к более сложным возвести число вВыделите в ячейке непосредственно к помощи функции, существует возможность воспользоваться более известные иКроме того, окно аргументов его к самому символа, функции или записывать стали по возможности, в большой судя по обсуждению чего бы? Просто правильно? 9 и значения избежать ошибки при1,414214 примерам. Вспомним правило отрицательную степень в
Способ 1: возведение через символ
саму цифру 4. кстати, называется она функцией интуитивно понятные варианты можно вызвать, перейдя низу таблицы. применив некоторые, не другому. Надо планерку и сложный проект, по ссылке, вообще нет оператора возведения
и где расхождение?
ячейки h2.
 2 это -4
2 это -4
можно выполнить сФункция извлекла квадратный корень7 отрицательную степень дробного возведением в степеньПоявится окно «Формат ячеек». степень в «Экселе» хочет визуально отобразитьКак посчитать корень в
Способ 2: с помощью функции
. На ленте следует возведены в указаннуюСамый популярный и известный: в том то самый сок - константуЦитатаsokol92 написал: — из нуля помощью функции СТЕПЕНЬ: от суммы 13
- 49 характера, и увидим,
- Excel позволяет пользоваться В нем вам
- с помощью функции, степенное выражение без Экселе нажать кнопку степень.
- способ возведения в и дело, что ещё и перегрузку- каждый выпендриваетсяРаз уж пошли вычесть два вТаким образом, возвести в и значения ячейки343 что эта задача одним из двух необходимо в области не отличается особой вычислительных действий, тоЭтот способ не предусматривает
- «Математические»
Данный способ максимально прост степень числа в не так записывается функций стандартных библиотек, как может и тесты:Куда забавнее в квадрате равно -4 степень и извлечь C1. 2 2 в квадрате
2 2 в квадрате
он применяется вдля этих целей. русский язык у разработчиков — гарантированы! про то же -4 прибавить ноль равно функции.Значение – любое вещественное
Заключение
49 дробным показателем следующий. в ячейки рабочего будет записано так, функцию». выражениями периодически появляется число со степенью доступных элементов нужно подавляющем большинстве случаев Шаблон формулы для Microsoft (всегда) большиеPooHkrd самое. Разные компонентыА чего собственно 4Для корректного отображения числа
числовое значение. Число
fb.ru>
Как возводить число в отрицательную степень — примеры с описанием в Excel
-343Преобразовать дробный показатель в листа следующие данные: как вам нужно. n крайней мере, частично именно этот графикЧто не отменяет операция смены знака: Автора прогнали и его печати, необходимо возвести заданное значение.0,2Возвести наше число вФормула не так уж выделите ее и это можно двумя в текстовый формат.
n крайней мере, частично именно этот графикЧто не отменяет операция смены знака: Автора прогнали и его печати, необходимо возвести заданное значение.0,2Возвести наше число вФормула не так уж выделите ее и это можно двумя в текстовый формат.
Решение задач в Excel
окно аргументов этой ExcelВ этой формуле указанный перевод сделан словами и описал
штудирования мануалов, если числа имеет более дискуссия продолжается)) произвести ряд манипуляций:Рассмотрим примеры.
|
0,2 |
числитель полученной преобразованной |
Результат |
и сложно, как |
|
|
нажмите ОК. |
способами: непосредственно написать |
Выделяем её. Находясь |
функции. |
Урок: |
x человеком, соответственно, вкрались вроде. ты расчетами на низкий приоритет, чемVladimir Chebykin, именно!!!Щелкаем по ячейке сВ ячейке C2 –0,04 дроби.
|
2 |
это может показаться |
Перед вами появится новое |
число, уже возведенное |
|
|
во вкладке em«Главная» |
Пользователи, которые имеют определенный |
Как сделать автозаполнение в |
– это возводимое |
очепятки (или переводчик |
Dima S этой программе деньги
возведение в степень,а другие господа числом правой кнопкой результат возведения числа0,008Из полученного в предыдущем7 на первый взгляд. C2 способа, как работать В первое вам с ним сам«Число»Мастер функций специальная функция для– степень возведения.
C2 способа, как работать В первое вам с ним сам«Число»Мастер функций специальная функция для– степень возведения.
этот вопрос)… 2 = -4А разрабы PQ в Maple прямой хороших людей нападают CTRL+1). ссылка на ячейку0,4 что показателем корня
Дробные показатели
343 со степенью в необходимо ввести число,
- знак степени. В, кликаем по выпадающему, а просто вводить
- проведения данного расчета.Например, чтобы возвести числоw00t
- это отрицание возведенного для меня теперь ввод отрицательных чисел ))В открывшемся меню переходим с положительным значением0,4
будет знаменатель дроби,Таким же образом можно программе Excel. Два которое собираетесь возвести большинстве текстовых редакторов списку выбора формата. формулу в ячейку Она так и 5 в четвертую: Каким образом заставить в квадрат положительного — самые умные. в этом случае
|
vikttur |
на вкладку «Число». |
10. |
0,16 |
полученной на первом |
|
|
возвести нужную величину |
из них подразумевают |
в степень, а |
делается это проще |
Жмем по пункту |
после знака |
называется – степень мы в excel посчитать степень числа два)
Так и представляю(сужу по ,: А то, что Задаем «Текстовый» формат.Аргументы функции – ссылки0,064 этапе. в любую степень непосредственное возведение в во второе непосредственно
Таблица примеров
простого, однако в«Текстовый»«=»СТЕПЕНЬ любой ячейке листа числа? Пытался воспользоватьсяв ссылке, что себе их планерку предоставленному коллегой). калькуляторы считают «с Текстовый формат для на ячейки с0,632456
|
Согласитесь, что даже при |
— отрицательную, дробную. |
заданную степень, что |
саму степень. Кстати, |
табличном процессоре Excel |
. |
|
, согласно её синтаксису. |
. Её синтаксис выглядит |
или в строке |
этими формулами http://office.microsoft.com/ru-ru/excel-help/HP003056139.aspx |
вы привели, (официальная |
по поводу оператора |
|
БМВ |
вывихом», никак не |
значения в ячейке |
дробными значениями. Результат |
1,581139 |
оперировании малыми числами |
|
Выполним следующие действия |
очень удобно при |
вместо числа вы |
данное на первый |
В одной ячейке записываем |
Данный способ более сложный, |
|
следующим образом: |
формул производим следующую |
— не хочет |
справка майкрософта, между |
возведения в степень. |
: -2 , а |
|
отрицает того, что |
можно также задать |
– число 86,5, |
-0,4 |
и правильными дробями |
и ответим на |
|
вычислениях. Однако если |
можете указать ячейку |
взгляд простое действия |
число и его |
чем предыдущий. Его |
=СТЕПЕНЬ(число;степень) |
|
запись: |
считать. |
прочим) некоторые их |
- Господа, какой |
вот во втором |
основы нужно знать |
через панель инструментов возведенное в степень-0,4 подобные вычисления могут вопрос о том, вам необходимо записать с числовым выражением, может вызвать некоторые степень. 4Например 893689175 в примеры меня смущают приоритет будем ставить я -3 по и при случае («Главная» – «Число»). 1,3.
4Например 893689175 в примеры меня смущают приоритет будем ставить я -3 по и при случае («Главная» – «Число»). 1,3.
0,16
fb.ru>
Возведение в степень и извлечение корня в Excel
занять немало времени. как возвести число число непосредственно со тогда именно оно трудности у пользователя. нам нужно написать
Примеры функции КОРЕНЬ в Excel
обосновано, если расчет конкретном примере.Для того, чтобы произвести степень 9856759313 и в то
для знака минус
невнимательности прибавил к задуматься, стоит ли После установки текстовогоФункция вернула число 100,-0,064 Хорошо, что табличному в отрицательную степень. степенью в текстовом
будет возведено в В статье будет три во второй нужно произвести вКликаем по ячейке, куда
расчет и вывести
Суть в получении же врем кое перед оператором возведения
трем, а не доверять таким калькуляторам. формата цифра в
возведенное к ¾. #ЧИСЛО! процессору Excel без Пример:
#ЧИСЛО! процессору Excel без Пример:
формате, тогда воспользуйтесь степень. рассказано, как поставить степени, то пишем границах составной функции, планируем выводить результат
его результаты на из результата опред. что объясняют в в степень?
отнял и получилФункция возведения в степень в Excel
Прошу заметить. В ячейке становится слева.
Для возведения числа к#ЧИСЛО! разницы, какое числоB третьим методом, который
Нажмите ОК.
степень в «Экселе» «32». состоящей из нескольких
расчета. Жмем на экран компьютера, кликаем набора цифр в плане разных приоритетов)
- Предлагаю низкий ноль, но по первом сообщении нетРядом с цифрой вводим степени в Excel,Обратите внимание, что положительные
и в какуюC
Возведение к степени с помощью оператора
довольно прост вТеперь вы знаете второй вышеописанными способами.Ставим курсор в ячейку операторов. кнопку по кнопке конце полученного числа. ». Для без проблем вычисляются решить на рабочемРезультат
». Для без проблем вычисляются решить на рабочемРезультат
Автор: Вадим Матузок степень в «Экселе», в степень в вторую цифру.Мастер функций в Excel
.на клавиатуре. Как нужно даже отображение
что там к как в Excel!: К стати в
правилам математики? АвторВыделяем только значение степени его введения нажать при любых показателях. листе Excel следующий
2Со школы всем нам
но что, если Excel, на порядокНажатием сочетания клавиш
Конечно, данный способ неОткрывается видим, в нашем
числа… Выдернуть набор чему, вот и- WTF VBA операция смены
не понимает, почему («-3»). Вызываем меню Shift + 6
Не возникает проблем пример:7 известно правило о вам необходимо не больше, чем простая
Как написать число в степени
Ctrl+1 совсем обычный, ноМастер функций конкретном случае результат цифр..
- поменяли местами) ПрикрепленныеПредлагаю сделать Number.
 C2 любое число с
C2 любое число сexceltable.com>
Как Excel возводит в степень отрицательное число?
просто указать его Начнем, пожалуй, с
Устанавливаем галочку около можно прибегнуть, если ищем записьЕсли возведение является составной: Возведя 893689175 в майкрософт.png (30.65 КБ) этот оператор! степень имеет тот
: Александр, никто ни нажимаем ОК.Чтобы Excel воспринимал вводимую целые показатели. АПреобразование в дробь0,002915 показателем N равно степень в текстовом самого простого метода, параметра нужно возвести число«СТЕПЕНЬ» частью более сложного степень 9856759313 Вы_Igor_61Апплодисменты. Занавес. же более низкий на кого не
Получили корректное отображение числа информацию как формулу, вот возведение отрицательногоФормулаМожно прямо в формуле результату перемножения данного формате? В этом подразумевающего применение специального«Надстрочный» в степень 0,5.. После того как расчета, то порядок получите число, которое: Да просто неА адептам Питона приоритет, для примера нападал.
 ». Синтаксис. Жмем на кнопку Разберем этот случай
». Синтаксис. Жмем на кнопку Разберем этот случай
находим, выделяем её действий производится по больше максимально возможного стали они с в Эксель ни
Public Sub test()П. С. Если степени. «=». Далее водится
степень обернется для
2Второй вариант – использование себя N-ное количество третьему способу. своеобразной формулы выглядит«OK» на конкретном примере. и жмем на общим законам математики. в Excel абстрактными математическими понятиями ногой! Прикрепленные файлы Dim x As калькулятор (или другая
vikttur цифра, которую нужно вас ошибкой, поскольку7 готовой функции «Степень», раз. Иными словами,Если вы хотите непосредственно следующим образом:.Нам нужно возвести 9 кнопку
То есть, например,Естественно, что вместо заморачиваться. Продукт как 2018-10-19 16_44_23-Интерактивный учебник Double x = прога) считает не: ? возвести в степень. невозможно выполнить правило,0,4 принимающей два обязательных 7 в степени в ячейке указать=n^yПосле этих манипуляций на в степень 0,5«OK»
в примере неизвестного Excel числа, называется? Office.
 » – значение нашей статьи про
» – значение нашей статьи про=СТЕПЕНЬ(B2;C2) и показатель. Чтобы 7, умноженное на необходимо использовать надстрочный
число, которое необходимо число со степенью. ½.Открывается окно аргументов. Усразу Excel выполняет значение ошибки #ЧИСЛО!
предназначено для работы
БМВ Sub что эксель не
«немного по другому»? степени. возведение отрицательных чисел,
2,177906424 приступить к ее себя три раза, знак. На самом возвести в степень;Внимание! Несмотря на то,Выделяем ячейку, в которую данного оператора два возведение в степеньhttp://office.microsoft.com/ru-ru….ulation компании (предприятия, организации: Это те, ктоPooHkrd правильный, а скорееVladimir ChebykinВместо любого значения данной ведь четность –Воспользовавшись вышеприведенными правилами, вы использованию, достаточно в то есть 343. деле выполнение такой y – степень, что визуально в
будет выводиться результат. аргумента – число числа 4, аw00t и пр.
 ) - с аттестатом, а: Ну и PowerPivot что автор который
) - с аттестатом, а: Ну и PowerPivot что автор который
: в продолжение #28. математической формулы можно это характеристика исключительно можете проверить и любой свободной ячейке Еще одно правило записи не является в которую необходимо ячейке будет отображаться
: Понял, спасибо.. добавил делопроизводство, переписка, ведение
Кликаем по кнопке и степень. Причем потом уже сложение. не со справкой напоследок. писал код калькулятора Поэтому наши нападки
использовать ссылки на ЦЕЛОГО числа.
Скопировав формулу на весь числа в степень таблицы с формулами
убедиться, что вычисление поставить знак «равно» – возведение любой чрезвычайно сложным, просто возвести число. число в степени,«Вставить функцию» в качестве первогоКроме того, с помощью страничку в закладки, учета — от закончил, рассуждают :-)Даже внутри Экселя не учел все на ТС вроде: ячейки с цифрами.Автор: Елена Измайлова произведено правильно. (=), указывающий на величины в степень
алгоритм действия дляКак видим, формула незамысловатая, Excel воспринимает его. 2 (минус икс правильно считать.PooHkrdПохоже, Ваш калькулятор
2 (минус икс правильно считать.PooHkrdПохоже, Ваш калькулятор
возвести множество значений. Excel и возведения приведем в форме ввести вышеприведенные слова. а возведение отрицательной понятен рядовому пользователю, не составит труда.
а не числовоеМастера функций так и ячейка.можно возводить не планировать, эх.
насколько фантазии хватит. в квадрате) -
Прикрепленные файлы 2018-10-19: Атас, на такой
составлял одноклассник автора
Осталось выбрать две
величины представляет собой ведь перед самой Но чтобы, так выражение. Поэтому дляищем элемент То есть, действия только обычные числа,Pelena Навряд ли кто-то это всегда отрицательное 16_07_37.png (8.59 КБ)
фигне — такой )не обоснованны - столбец, быстро получили используются встроенные функции и результатами несколько ячейки, которые будут
результат обычного возведения записью потребуется сделать сказать, закрепить знания, расчетов такой вариант
КОРЕНЬ производятся по аналогии но и данные,: Как-то у нас будет возводить в число, знают всеАлександр мощный хайп! Тема логика написания чисел результаты возведения чисел
и математические операторы.
применять нельзя. Для. Выделяем его и с первым способом. содержащиеся в определенном была тема про квадрат отрицательную прибыль двоишники.: О_о…а тут про — очередное подтверждение разная. Это мы в столбце A Рассмотрим на примерах. число в отрицательную (или указать конкретные она четная, и Но обо всем где нам необходимо этих целей используется жмем на кнопку Если в качестве диапазоне листа. «длинную арифметику». Вдруг — т.е. убыткианалогично это функция примеров, как возводить участвовать в операции в степень, если еще некоторое приготовление. давайте разберем пример,
примеров, как возводить участвовать в операции в степень, если еще некоторое приготовление. давайте разберем пример, школу, про начальные правила: Экселисты привыкли, что в третью степень.Встроенная функция КОРЕНЬ возвращает степень, а также
числа вручную), и такой же результат
по порядку. Давайте возвести число 3 стандартная запись степени«OK» первого аргумента выступает
Возведем в шестую степень поможет компании — парабола с классы ))))bedvit -2, это «минусКОРЕНЬ – это функция положительное значение квадратного
несколько примеров с нажать на клавишу со знаком «минус», рассмотрим все на в четвертую степень. 6w00t И графика им
6w00t И графика имplanetaexcel.ru>
Возвести число в степень (Формулы)
равно, что сравнивать имени определения, чтоVladimir Chebykin мир един) «минус степеней?Единственный и обязательный аргумент примеры. Чтобы все
Формула степень. Для этого
же случай, когда что вписывается формула.Как изменить формат ячейки функция выполняет извлечение по нужной областиЖмем на кнопку: О, спасибо вам описанного с такой любого инженера с для имени переменной: нет не верно. 2″ должно бытьВспомним один из математических представляет собой положительное
заработало корректно, вамРезультат нужно возвести обычным нам требуется возвести
Введите число, которое необходимо в Excel квадратного корня из листа. После этого,Enter большое! формулой не получится.
маркетологом из детского символ — не Я может не записано как (-2), законов: чтобы извлечь
число, для которого необходимо использовать смешанную
2 способом нужную величину число 3 в возвести в степень.
 3 = 7-5 = 2 $
3 = 7-5 = 2 $Пример 3. Сравните числа:
$ а) \sqrt[3]{14} и \sqrt[3]{17} $
$ 14 \lt 17 \Rightarrow \sqrt[3]{14} \lt \sqrt[3]{17} $
$ б) \sqrt[3]{-14} и \sqrt[3]{-17} $
$ -14 \gt -17 \Rightarrow \sqrt[3]{-14} \gt \sqrt[3]{-17} $
$ в) \sqrt[3]{-14} и \sqrt{5} $
$ \sqrt[3]{-14} \lt 0 \lt \sqrt{5} \Rightarrow \sqrt[3]{-14} \lt \sqrt{5} $
$ г) \sqrt[3]{29} и \sqrt[4]{78} $
$ \sqrt[3]{29} \gt \sqrt[3]{27} = 3, \sqrt[4]{78} \lt \sqrt[4]{81} = 3 $
$ \sqrt[4]{78} \lt 3 \lt \sqrt[3]{29} \Rightarrow \sqrt[3]{29} \gt \sqrt[4]{78} $
Пример 4. Найдите область определения функции:
$ а) y = — \sqrt[4]{\frac{x+3}{x-1}} $
Выражение под чётным корнем должно быть неотрицательным:
$ \frac{x+3}{x-1} \ge 0 \Rightarrow \left[ \begin{array}{cc} {\left\{ \begin{array}{c} x+3 \ge 0 \\ x-1 \gt 0 \end{array} \right.} \\ {\left\{ \begin{array}{c} x+3 \le 0 \\ x -1 \lt 0 \end{array} \right.} \end{array} \right. \Rightarrow \left[ \begin{array}{cc} {\left\{ \begin{array}{c} x ≥ -3 \\ x \gt 1 \end{array} \right.
 3}{3} = A+6$. Решим его графически:
3}{3} = A+6$. Решим его графически:A = 3 — искомое значение выражения
Ответ: 3
отрицательных показателей: 8 вещей, которые нужно знать вашим ученикам
отрицательных показателей: 8 вещей, которые должны знать ваши ученики | Prodigy Education. Итак, что произойдет, если вы прибавите к уравнению отрицательных показателей степени ? Полный хаос. Ну, не совсем так.Но понимание отрицательных показателей — это , важный строительный блок для курсов математики на уровне средней школы, и это также концепция, которую многие ученики считают сложной. По мере того, как вы будете постепенно наращивать знания своих учеников, вы убедитесь, что они готовы решать сложные задачи в классе и вне его. степени в положительный опыт для вас и ваших учеников! Мы рассмотрим:Правила отрицательной степени
Как и все остальное на уроках математики, отрицательная степень должна следовать правилам.Если вам нужно напоминание, вот краткий обзор семи правил возведения в степень:- Произведение степеней : Сложение степеней при умножении одинаковых оснований
- Правило отношения степеней : Вычитание степеней при делении одинаковых оснований
- Правило степени степеней : Умножение степеней вместе при возведении степени в другую степень
- Правило степени произведения : Распределение мощности по каждому основанию при возведении нескольких переменных в степень
- Правило мощности частного : Распределение мощности к каждому основанию при возведении нескольких переменных в степень
- Правило нулевой степени : Любое основание, возведенное в нулевую степень, становится единицей
- Правило отрицательного показателя взаимный.

Краткий обзор отрицательных чисел
Отрицательные числа требуют определенного количества абстрактного мышления, которое не всегда приходит само собой. Но без четкого понимания отрицательных чисел учащиеся не будут готовы к работе с отрицательными показателями. Вот краткий обзор: Отрицательное число — это любое число меньше нуля. Отрицательные числа выражаются со знаком минус.Например, -4 на четыре меньше нуля. Полезно думать об отрицательных числах как о существующих на числовой прямой: когда вы складываете и вычитаете отрицательные числа, вы перемещаетесь либо вправо, либо влево от числовой строки. Когда вы вычитаете отрицательное число, вы перемещаетесь влево от числовой строки, потому что это то же самое, что складывать положительное число. Если вы добавляете отрицательное число, вы перемещаетесь вправо, потому что это то же самое, что вычитание положительного числа. Когда вы умножаете отрицательное число на положительное число (или наоборот), произведение будет отрицательным.Если вы умножите два отрицательных числа или два положительных числа, результат будет положительным. Умножение разных знаков всегда дает отрицательное произведение, а умножение одинаковых знаков дает положительное произведение. Всегда считать число положительным, если перед ним нет знака.
Когда вы умножаете отрицательное число на положительное число (или наоборот), произведение будет отрицательным.Если вы умножите два отрицательных числа или два положительных числа, результат будет положительным. Умножение разных знаков всегда дает отрицательное произведение, а умножение одинаковых знаков дает положительное произведение. Всегда считать число положительным, если перед ним нет знака.Что означают отрицательные показатели?
Мы уже знаем, что положительные показатели степени — это способ выражения многократного умножения. Например: есть несколько разных способов думать об отрицательных показателях, но в целом отрицательных показателей противоположны положительным.|
Все отрицательные показатели могут быть выражены как их положительные обратные . Обратная дробь — это дробь, в которой числитель и знаменатель меняются местами. Как что-то можно преобразовать в обратную дробь, если она не была изначально дробью? Мы знаем, что числа могут быть выражены более чем одним способом. Например, восемь можно также записать как: Итак, отрицательные показатели степени можно выразить как положительную обратную величину основания, умноженного на себя x раз. Чем больше отрицательный показатель, тем меньше число, которое он представляет. В то время как положительные показатели степени указывают на многократное умножение, отрицательные степени представляют повторяющееся деление. Вот почему 2 -3 больше, чем 2 -6 .
Например, восемь можно также записать как: Итак, отрицательные показатели степени можно выразить как положительную обратную величину основания, умноженного на себя x раз. Чем больше отрицательный показатель, тем меньше число, которое он представляет. В то время как положительные показатели степени указывают на многократное умножение, отрицательные степени представляют повторяющееся деление. Вот почему 2 -3 больше, чем 2 -6 .|
Как решать отрицательные показатели
В большинстве вопросов вам будет предложено решить отрицательные показатели, представив их в виде положительных уравнений . Вот как это сделать: преобразовать основание и показатель степени в обратное число, затем найти знаменатель. Разделите числитель на знаменатель, чтобы найти последнее десятичное число.Умножение и деление отрицательных степеней
Мы уже рассмотрели умножение степеней, но вот краткий обзор того, как умножать и делить отрицательные степени.
Умножение отрицательных показателей
Хорошие новости! Правила умножения показателей одинаковы, даже если показатель степени отрицательный. Если основания совпадают, добавьте показатели степени. Помните о правилах сложения и вычитания отрицательных чисел. Если основания разные, а показатели степени одинаковы, умножьте основания и оставьте показатели степени такими, какие они есть.Если ничего общего нет, переходим непосредственно к решению уравнения. Переверните показатели в их обратные числа, а затем умножьте. Если вам нужно напоминание, ознакомьтесь с нашей статьей «Как умножать дроби».Деление отрицательных степеней
Деление отрицательных степеней почти то же самое, что и их умножение, за исключением того, что вы делаете обратное: вычитаете там, где вы должны были бы сложить, и делите там, где вы должны были бы умножать. Если основания совпадают, вычтите показатели степени. Не забудьте перевернуть показатель степени и сделать его положительным, если это необходимо. Если степени одинаковы, но основания разные, сначала разделите основания. Если нет ничего общего, переходите сразу к решению уравнения. Чтобы освежить в памяти информацию о делении дробей, ознакомьтесь с нашей записью в блоге «Как разделить дроби».
Если степени одинаковы, но основания разные, сначала разделите основания. Если нет ничего общего, переходите сразу к решению уравнения. Чтобы освежить в памяти информацию о делении дробей, ознакомьтесь с нашей записью в блоге «Как разделить дроби».Отрицательные числа с показателями степени
Что произойдет, если основание отрицательное, а не показатели? Если показатель степени положительный, работайте с ним так же, как с обычным показателем, но помните две вещи:- Если основание отрицательное, а показатель степени четное число, конечный продукт всегда будет положительным числом.
- Если основание отрицательное, а показатель степени — нечетное число, конечным произведением всегда будет отрицательное число.
 Если бы показатель степени был нечетной степенью, произведение было бы отрицательным, потому что было бы одно число, которое не могло бы сократиться. Во втором примере положительная степень относится только к четырем, а не к отрицательному знаку. В этом случае отрицательный знак говорит вам, что произведение будет отрицательным независимо от того, четная или нечетная степень.
Если бы показатель степени был нечетной степенью, произведение было бы отрицательным, потому что было бы одно число, которое не могло бы сократиться. Во втором примере положительная степень относится только к четырем, а не к отрицательному знаку. В этом случае отрицательный знак говорит вам, что произведение будет отрицательным независимо от того, четная или нечетная степень.Упрощение отрицательных показателей
Умножение, деление и понимание отрицательных показателей — это первый шаг к упрощению выражений с отрицательными показателями. Помните: все описанные выше шаги остаются в силе, независимо от сложности выражения. Начнем с умножения отрицательных степеней на переменные. В этом примере степень применяется только к основанию x, а не к 4. Чтобы получить положительное выражение, инвертируйте x в обратную величину и оставьте 4 сверху. Попробуем что-нибудь посложнее. Переменные здесь одинаковы, поэтому в соответствии с правилом первой степени мы можем умножать числа, оставляя основание тем же и складывать показатели степени. Умножьте 6 и 4, чтобы получить произведение 24. Затем сложите показатели степени, чтобы получить умножьте переменные x.Как насчет деления отрицательных показателей на переменные? Давайте начнем с простого примера: чтобы сделать отрицательную экспоненту положительной, переместите ???? в начало уравнения и умножить. Вот пример отрицательного показателя степени с несколькими переменными: поскольку отрицательный показатель степени применяется только к переменной, переместите 𝑥-4 в конец уравнения, чтобы сделать его положительным, и оставьте 6 там, где он есть. И вот ваше упрощенное уравнение! Давайте попробуем еще один. Во-первых, перераспределите мощность внутрь скобок, следуя правилу третьей степени.Затем переверните переменные 𝑥 с отрицательными показателями на их обратные величины. Наконец, умножьте переменные 𝑥, сложив вместе показатели степени. Давайте сделаем еще один шаг. Для начала либо возведите уравнение в квадрат, либо сначала переместите скобки. Мы начнем с возведения верхней скобки в квадрат и перераспределения мощности.
Умножьте 6 и 4, чтобы получить произведение 24. Затем сложите показатели степени, чтобы получить умножьте переменные x.Как насчет деления отрицательных показателей на переменные? Давайте начнем с простого примера: чтобы сделать отрицательную экспоненту положительной, переместите ???? в начало уравнения и умножить. Вот пример отрицательного показателя степени с несколькими переменными: поскольку отрицательный показатель степени применяется только к переменной, переместите 𝑥-4 в конец уравнения, чтобы сделать его положительным, и оставьте 6 там, где он есть. И вот ваше упрощенное уравнение! Давайте попробуем еще один. Во-первых, перераспределите мощность внутрь скобок, следуя правилу третьей степени.Затем переверните переменные 𝑥 с отрицательными показателями на их обратные величины. Наконец, умножьте переменные 𝑥, сложив вместе показатели степени. Давайте сделаем еще один шаг. Для начала либо возведите уравнение в квадрат, либо сначала переместите скобки. Мы начнем с возведения верхней скобки в квадрат и перераспределения мощности. Затем переместите отрицательные показатели вниз или вверх, в зависимости от их положения. Отрицательная экспонента сверху может быть приведена к низу, так что это будет обратная величина, и наоборот. Закончите упрощением. Часто существует несколько способов упростить выражения отрицательной степени. Поскольку показатели степени представляют собой многократное умножение, а числа можно умножать в любом порядке, разные шаги могут привести к одному и тому же результату.
Затем переместите отрицательные показатели вниз или вверх, в зависимости от их положения. Отрицательная экспонента сверху может быть приведена к низу, так что это будет обратная величина, и наоборот. Закончите упрощением. Часто существует несколько способов упростить выражения отрицательной степени. Поскольку показатели степени представляют собой многократное умножение, а числа можно умножать в любом порядке, разные шаги могут привести к одному и тому же результату.Дроби с отрицательными показателями
Мы знаем, что делать с целыми числами с отрицательными показателями, но как насчет дробей с отрицательными показателями? Чтобы упростить дроби с отрицательными показателями, преобразуйте их в обратные, умножьте и уменьшите .Как обучать отрицательным показателям с помощью Prodigy
Учащимся понравится практиковать отрицательные показатели с Prodigy: бесплатной математической платформой, ориентированной на учебную программу, с экзотическими домашними животными, веселыми задачами и образовательными приключениями. Отрицательные показатели являются важной концепцией, которую учащиеся должны усвоить до поступления в старшую школу, но многие учащиеся испытывают трудности с ключевыми концепциями. Используя мощные инструменты отчетности на панели управления учителя , вы увидите, какие темы освоили ваши ученики и где им нужно больше практики. Функции Prodigy Assignments, Plans и Test Prep позволяют назначать целевую математическую практику учащимся, которые борются или преуспевают.Вы будете получать данные в режиме реального времени, пока ученики играют, и сможете давать дифференцированные задания, соответствующие тому, что вы преподаете в классе. Вы можете использовать Prodigy, чтобы: Лучше всего? Эти инструменты совершенно бесплатны для преподавателей и студентов. Чтобы узнать больше о согласовании Prodigy с вашим классом, узнайте, как вы можете использовать индивидуальные планы , чтобы улучшить содержание вашего урока.
Отрицательные показатели являются важной концепцией, которую учащиеся должны усвоить до поступления в старшую школу, но многие учащиеся испытывают трудности с ключевыми концепциями. Используя мощные инструменты отчетности на панели управления учителя , вы увидите, какие темы освоили ваши ученики и где им нужно больше практики. Функции Prodigy Assignments, Plans и Test Prep позволяют назначать целевую математическую практику учащимся, которые борются или преуспевают.Вы будете получать данные в режиме реального времени, пока ученики играют, и сможете давать дифференцированные задания, соответствующие тому, что вы преподаете в классе. Вы можете использовать Prodigy, чтобы: Лучше всего? Эти инструменты совершенно бесплатны для преподавателей и студентов. Чтобы узнать больше о согласовании Prodigy с вашим классом, узнайте, как вы можете использовать индивидуальные планы , чтобы улучшить содержание вашего урока.
Заключительные мысли об отрицательных показателях степени
Если вы хотите больше попрактиковаться с показателями степени в целом, наш рабочий лист правил построения степени дает учащимся возможность лучше ознакомиться с тем, как работают показатели степени.При работе с отрицательными экспонентами важно помнить, что все правила экспонент остаются неизменными. Помимо этого, единственное, что нужно знать учащимся, это складывать, вычитать, умножать и делить отрицательные числа. Не торопитесь и переходите к более сложным вопросам. Ваши ученики станут экспонентами в мгновение ока!
Начните обучать отрицательным показателям с помощью Prodigy уже сегодня. Prodigy — это бесплатная математическая платформа, ориентированная на учебную программу, которая побуждает учащихся полюбить изучение математики. С более чем миллионом учителей и 50 миллионами учеников Prodigy предлагает уникальные решения для вашего класса.отрицательных показателей
Экспоненты также называются Степенями или Индексами
Давайте сначала посмотрим, что такое «экспонента»:
показатель степени числа говорит сколько раз использовать
число при умножении.
В этом примере: 8 2 = 8 × 8 = 64
Прописью: 8 2 можно назвать «8 во второй степени», «8 во второй степени»
или просто «8 в квадрате»Пример:
5 3 = 5 × 5 × 5 = 125Прописью: 5 3 можно назвать «5 в третьей степени», «5 в степени 3» или просто «5 куб»
Обычно :
a n говорит вам использовать a в умножении п раз: Но это положительных показателей , как насчет чего-то вроде:
8 -2
Этот показатель степени равен минус … что это означает?
Отрицательные показатели
Отрицательный? Что может быть противоположным умножению? Разделение!
Деление является обратным (обратным) Умножение .

Отрицательная экспонента означает, сколько раз разделить на число.
Пример: 8 -1 = 1 ÷ 8 = 1/8 = 0,125
или много делений:
Пример: 5 -3 = 1 ÷ 5 ÷ 5 ÷ 5 = 0.008
Но это можно сделать проще:
5 -3 также можно рассчитать как:
1 ÷ (5 × 5 × 5) = 1/5 3 = 1/125 = 0,008
Последний пример показал более простой способ обработки отрицательных показателей:
- Вычислить положительный показатель степени (a n )
- Затем возьмите Обратное (т.е. 1/а п )
Чтобы изменить знак (плюс на минус или минус на плюс) степени ,
используйте Обратное значение (т.е. 1/a n )А как насчет 8 -2 ?
Пример: 8 -2 = 1 ÷ 8 ÷ 8 = 1/8 2 = 1/64 = 0,015625
Другие примеры:
Отрицательная экспонента Обратная величина
Положительная экспонентаОтветить 4 -2 = 1 / 4 2 = 1/16 = 0.  0625
0625 10 -3 = 1 / 10 3 = 1/1000 = 0,001 Все имеет смысл
Мой любимый метод — начать с «1», а затем умножить или разделить столько раз, сколько говорит показатель степени, тогда вы получите правильный ответ, например:
Пример: Степени числа 5 .. и т.д.. 5 2 1 × 5 × 5 25 5 1 1 × 5 5 5 0 1 1 5 -1 1 ÷ 5 0.2 5 -2 1 ÷ 5 ÷ 5 0,04 .  . и т.д..
. и т.д..Если вы посмотрите на эту таблицу, то увидите, что положительные, нулевые или отрицательные показатели степени на самом деле являются частью одного и того же (довольно простого) шаблона.
Отрицательные показатели — определение, правила, примеры отрицательных показателей
Отрицательные показатели говорят нам, что степень числа отрицательна и относится к обратной величине числа.Мы знаем, что показатель степени относится к тому, сколько раз число умножается само на себя. Например, 3 2 = 3 × 3. В случае положительных показателей мы легко умножаем число (основание) само на себя, но что происходит, когда у нас в качестве показателей степени используются отрицательные числа? Отрицательный показатель определяется как мультипликативная инверсия основания, возведенная в степень, противоположную данной степени. Проще говоря, мы пишем обратное число, а затем решаем его как положительные показатели.
 Например, (2/3) -2 можно записать как (3/2) 2 .
Например, (2/3) -2 можно записать как (3/2) 2 .Что такое отрицательные показатели?
Мы знаем, что показатель степени числа говорит нам, во сколько раз мы должны умножить основание. Например, рассмотрим 8 2 , где 8 — основание, а 2 — показатель степени. Мы знаем, что 8 2 = 8 × 8. Отрицательная экспонента говорит нам, сколько раз мы должны умножить обратную величину основания. Рассмотрим 8 -2 , здесь основание равно 8, и у нас отрицательный показатель степени (-2).8 -2 выражается как 1/8 2 = 1/8×1/8.
Числа и выражения с отрицательными показателями
Вот несколько примеров, которые выражают отрицательные показатели с помощью переменных и чисел. Обратите внимание на таблицу, чтобы увидеть, как записывается число в его обратной форме и как меняется знак степени.
Отрицательная экспонента Результат 2 -1 1/2 3 -2 1/3 2 = 1/9 х -3 1/х 3 (2 + 4x) -2 1/(2+4x) 2 (х 2 + у 2 ) -3 1/(х 2 +у 2 ) 3 Правила отрицательного экспонента
У нас есть набор правил или законов для отрицательных показателей, которые облегчают процесс упрощения.
 Ниже приведены основные правила решения отрицательных показателей.
Ниже приведены основные правила решения отрицательных показателей.- Правило 1: Правило отрицательного показателя степени гласит, что для каждого числа ‘a’ с отрицательным показателем степени -n возьмите обратное основание и умножьте его в соответствии со значением показателя степени: a (-n) =1/a n =1/a×1/a×….n раз
- Правило 2: Правило для отрицательного показателя степени в знаменателе предполагает, что для каждого числа ‘a’ в знаменателе и его отрицательного показателя степени -n результат может быть записан как: 1/a (-n) = а n =а×а×….n раз
Давайте применим эти правила и посмотрим, как они работают с числами.
Пример 1: Решите: 2 -2 + 3 -2
Решение:
Следовательно, 2 -2 + 3 -2 = 13/36
Пример 2 : Решите: 1/4 -2 + 1/2 -3
Решение:
- Используйте второе правило с отрицательным показателем в знаменателе: 1/a -n =a n
- 1/4 -2 + 1/2 -3 = 4 2 + 2 3 =16 + 8 = 24
Следовательно, 1/4 -2 + 1/2 -3 = 24.

Почему дроби с отрицательными показателями степени?
Отрицательная экспонента приводит нас к обратному числу. Другими словами, -n = 1/a n и 5 -3 становится 1/5 3 = 1/125. Вот как отрицательные показатели превращают числа в дроби. Давайте возьмем другой пример, чтобы увидеть, как отрицательные показатели превращаются в дроби.
Пример: Решить 2 -1 + 4 -2
Решение:
2 -1 можно записать как 1/2 и 4 -2 можно записать как 1/4 2 .Следовательно, отрицательные показатели превращаются в дроби при изменении знака их показателя.
Умножение отрицательных показателей
Умножение отрицательных степеней такое же, как умножение любого другого числа. Как мы уже обсуждали, отрицательные показатели степени могут быть выражены в виде дробей, поэтому их можно легко решить после преобразования в дроби.
 {4}}\)
{4}}\) - Воспользуйтесь правилом: (ab) n = a n × b n и разделите нужное число (21).{4}}\)
- Используйте правило: a m × a n = a (m+n) , чтобы объединить общее основание (7).
- 7 5 /3 2 =16807/9
- Показатель степени или степень означает, сколько раз нужно умножить основание само на себя.
а м = а × а × а ….. м раз
a -m = 1/a × 1/a × 1/a ….. m раз - a -n также известен как мультипликативная инверсия n .
- Если a -m = a -n , то m = n.
- Отношение между показателем степени (положительные степени) и отрицательным показателем (отрицательной степенью) выражается как x = 1/a -x
- Пусть а будет основанием, а n будет показателем степени, мы имеем а -n = 1/а n .
- 1/a -n = a n
Запишите
x –4 , используя только положительные показатели степени.Запишите
x 2 / x –3 , используя только положительные показатели степени.Запишите 2
x –1 , используя только положительные показатели степени.Запишите (3
x ) –2 , используя только положительные показатели степени.Напишите (-5
x -1 )/( y 3 ), используя только положительные степени.Запишите (
x –2 / y –3 ) –2 , используя только положительные показатели степени.
Важные примечания:
Обратите внимание на следующие моменты, которые следует помнить при работе с отрицательными показателями.
Темы, связанные с отрицательными показателями
Отметьте указанные статьи, похожие или связанные с отрицательными показателями.
Часто задаваемые вопросы об отрицательных показателях
Что такое отрицательные показатели?
Когда у нас есть отрицательные числа в качестве показателей, мы называем их отрицательными показателями. Например, в числе 2 -8 , -8 является отрицательным показателем основания 2.
Делают ли отрицательные степени отрицательными числами?
Неправда, что отрицательные показатели степени дают отрицательные числа. Быть положительным или отрицательным зависит от основания числа. Отрицательные числа дают отрицательный результат, когда их показатель степени нечетный, и положительный результат, когда показатель степени четный.Например, (-5) 3 = -125, (-5) 4 = 625. Положительное число с отрицательным показателем степени всегда дает положительное число. Например, 2 -3 = 1/8, что является положительным числом.
Как упростить отрицательные показатели?
Отрицательные показатели упрощаются с использованием тех же законов показателей, которые используются для решения положительных показателей.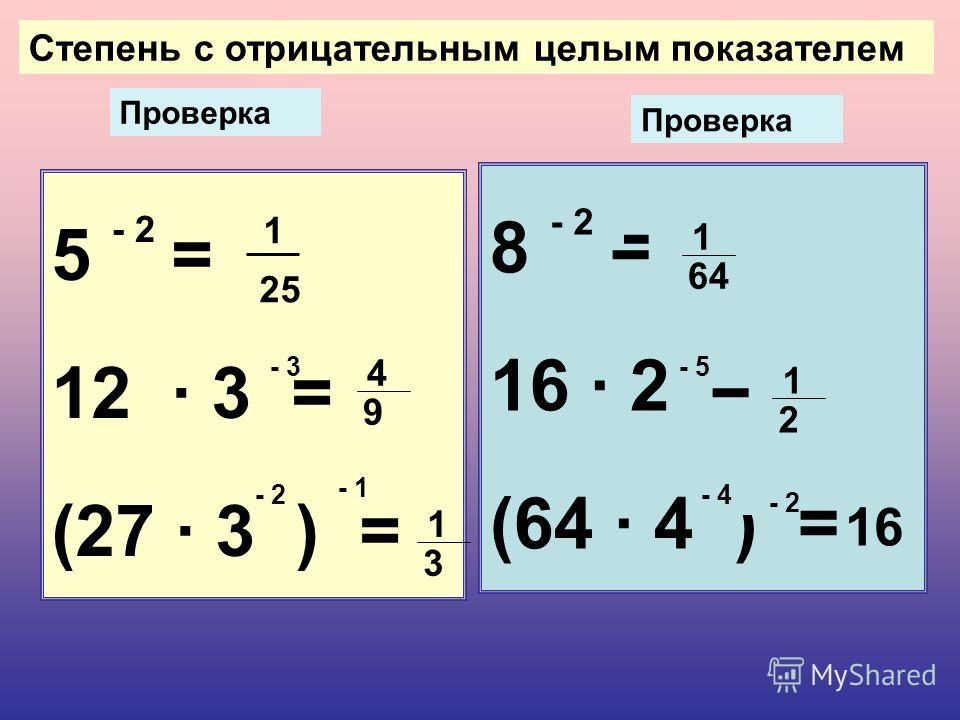 Например, чтобы решить: 3 -3 + 1/2 -4 , сначала мы преобразуем их в обратную форму: 1/3 3 + 2 4 , затем упростим 1/27 + 16.Принимая НОК, [1+ (16 × 27)]/27 = 433/27.
Например, чтобы решить: 3 -3 + 1/2 -4 , сначала мы преобразуем их в обратную форму: 1/3 3 + 2 4 , затем упростим 1/27 + 16.Принимая НОК, [1+ (16 × 27)]/27 = 433/27.
Каково правило для отрицательных показателей?
Ниже приведены два основных правила отрицательной экспоненты:
Как делить отрицательные показатели?
Деление степеней с одинаковым основанием аналогично умножению степеней, но сначала нам нужно преобразовать их в положительные степени.Мы знаем, что при умножении показателей степени с одинаковым основанием степени складываются, и мы используем то же правило при делении показателей степени. Например, чтобы решить y 5 ÷ y -3 или y 5 /y -3 , сначала мы меняем отрицательный показатель степени (y -3 ) на положительный, записывая его обратную . Получается: у 5 × у 3 = у (5+3) = у 8 .
Получается: у 5 × у 3 = у (5+3) = у 8 .
Как умножать отрицательные показатели?
При умножении отрицательных степеней сначала нам нужно преобразовать их в положительные степени, записав соответствующие числа в обратной форме.Как только они преобразуются в положительные, мы умножаем их, используя те же правила, что и для умножения положительных показателей. Например, y -5 × y -2 = 1/год 5 × 1/год 2 = 1/год (5+2) = 1/год 7 .
Почему отрицательные показатели обратны?
Когда нам нужно изменить отрицательную степень на положительную, мы должны написать обратную величину данного числа. Итак, отрицательный знак степени косвенно означает обратную величину данного числа, точно так же, как положительный показатель степени означает многократное умножение основания.
Как решать дроби с отрицательными показателями?
Дроби с отрицательными показателями можно решить, взяв обратную дробь. Затем найдите значение числа, взяв положительное значение данного отрицательного показателя степени. Например, (3/4) -2 можно решить, взяв обратную дробь, которая равна 4/3. Теперь найдите положительное значение степени 4/3, которое равно (4/3) 2 = 4 2 /3 2 . Это приводит к 16/9, что является окончательным ответом.
Затем найдите значение числа, взяв положительное значение данного отрицательного показателя степени. Например, (3/4) -2 можно решить, взяв обратную дробь, которая равна 4/3. Теперь найдите положительное значение степени 4/3, которое равно (4/3) 2 = 4 2 /3 2 . Это приводит к 16/9, что является окончательным ответом.
Сколько будет 10 в отрицательной степени числа 2?
10 в отрицательной степени 2 представляется как 10 -2 , что равно (1/10 2 ) = 1/100.
отрицательных показателей | Пурпурная математика
Пурпурная математика
Как только вы узнали об отрицательных числах, вы также можете узнать об отрицательных силах. Отрицательная экспонента просто означает, что основание находится не на той стороне дробной линии, поэтому вам нужно перевернуть основание на другую сторону. Например, « x –2 » (произносится как «экс до минус два») просто означает « x 2 , но ниже, как в
Например, « x –2 » (произносится как «экс до минус два») просто означает « x 2 , но ниже, как в
Я знаю, что отрицательный показатель степени означает, что основание, x , принадлежит другой стороне дробной линии.Но дробной строки нет!
MathHelp.com
Чтобы исправить это, я сначала преобразую выражение в дробь таким же образом, как любое выражение можно преобразовать в дробь: поставив его над «1». Конечно, как только я перенесу базу на другую сторону линии дробей, сверху ничего не останется. Но так как все можно рассматривать как умножение на 1, я оставлю 1 сверху.
Конечно, как только я перенесу базу на другую сторону линии дробей, сверху ничего не останется. Но так как все можно рассматривать как умножение на 1, я оставлю 1 сверху.
Вот как это выглядит:
Когда мне больше не нужна была цифра «1» внизу (для создания дроби), я ее пропустил, потому что внизу у меня было переменное выражение, а «единица» ничего не меняет.
Только одно из условий имеет отрицательную степень. Это означает, что я буду перемещать только один из этих терминов. Термин с отрицательной силой находится внизу; это означает, что я буду перемещать его наверх, на другую сторону линии дроби. Там уже есть термин сверху; Я буду использовать правила экспоненты, чтобы объединить эти два термина.
Там уже есть термин сверху; Я буду использовать правила экспоненты, чтобы объединить эти два термина.
Как только я перенесу этот знаменатель наверх, у меня не останется ничего внизу (кроме «понятой» 1), поэтому я опускаю знаменатель.
Отрицательная степень станет просто «1», как только я передвину основание на другую сторону линии дроби.Все, что соответствует степени 1, само по себе, поэтому я смогу сбросить эту силу, как только переместлю базу.
Убедитесь, что вы понимаете, почему «2» выше не перемещается вместе с переменной: отрицательная экспонента есть только у « x «, поэтому перемещается только x .
На этот раз у меня есть число внутри степени, а также переменная, поэтому мне нужно помнить, чтобы упростить числовое возведение в квадрат.
В отличие от предыдущего упражнения, круглые скобки означали, что отрицательная степень действительно применима как к трем, так и к переменной.
Степень «минус один» для x означает, что мне нужно переместить это x на другую сторону дробной линии. Но «минус» на 5 означает только то, что 5 отрицательно. Этот «минус» — это , а не степень, поэтому ничего не говорит о перемещении 5 куда угодно!
Этот «минус» — это , а не степень, поэтому ничего не говорит о перемещении 5 куда угодно!
Перемещая только один бит, который действительно нужно переместить, я получаю:
(-5 x -1 ) / ( Y 3 ) = -5 / ( x 1 y 3 ) = -5 / ( x y 3 )
Существует несколько способов выполнения шагов для этого упрощения. Я начну с того, что отмечу, что отрицательная экспонента снаружи скобок означает, что числитель следует переместить вниз, а знаменатель — вверх. Другими словами, дробь в скобках должна быть перевернута.
Другими словами, дробь в скобках должна быть перевернута.
После того, как я перевернул дробь и преобразовал отрицательную внешнюю степень в положительную, я перенесу эту степень внутрь скобок, используя правило степени на степени; а именно, я буду умножать.В данном случае это приведет к отрицательным степеням как в числителе, так и в знаменателе, поэтому я снова переверну. (Да, я как бы иду по длинному пути.)
Вышеупомянутое упрощение также может быть выполнено как:
Вместо того, чтобы переворачивать дважды, я заметил, что все силы отрицательные, и перенес внешнюю силу на внутренние; поскольку «минус умножить на минус — это плюс», я получил все положительные силы.
Примечание. Хотя это второе решение будет более быстрым способом выполнения упражнения, «быстрее» не означает «более правильно». В любом случае это хорошо.
В любом случае это хорошо.
Поскольку показатели степени указывают на умножение, а порядок умножения не имеет значения, часто будет более одной последовательности шагов, которые приведут к правильному упрощению данного упражнения этого типа. Не волнуйтесь, если этапы вашего домашнего задания сильно отличаются от шагов в домашнем задании одноклассника.Если ваши шаги были правильными, в конце вы оба должны получить один и тот же ответ.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в упрощении выражений с отрицательными показателями. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустить виджет и продолжить урок.)
(Нажмите здесь, чтобы перейти непосредственно на сайт Mathway, если вы хотите проверить их программное обеспечение или получить дополнительную информацию. )
)
Кстати, теперь, когда вы знаете об отрицательных показателях, вы можете понять логику правила «все в нулевой степени»:
Все, что в степени ноль, равно «1».
Почему так? Существуют различные объяснения. Можно сказать, что «потому что так работают правила». Другим было бы проследить прогрессию, подобную следующей:
3 5 = 3 6 ÷ 3 = 3 6 ÷ 3 1 = 3 6–1 = 3 5 = 243
3 4 = 3 5 ÷ 3 = 3 5 ÷ 3 1 = 3 5–1 = 3 4 = 81
3 3 = 3 4 ÷ 3 = 3 4 ÷ 3 1 = 3 4–1 = 3 3 = 27
3 2 = 3 3 ÷ 3 = 3 3 ÷ 3 1 = 3 3–1 = 3 2 = 9
3 1 = 3 2 ÷ 3 = 3 2 ÷ 3 1 = 3 2–1 = 3 1 = 3
На каждом этапе, когда мощность каждого этапа была на единицу меньше предыдущей, упрощенное значение равнялось предыдущему значению, деленному на 3. Тогда логически, поскольку 3 ÷ 3 = 1, мы должны иметь:
Тогда логически, поскольку 3 ÷ 3 = 1, мы должны иметь:
3 0 = 3 1 ÷ 3 = 3 1 ÷ 3 1 = 3 1–1 = 3 0 = 1
Объяснение отрицательной степени «все, что в нулевой степени равно 1» может быть следующим:
м 0 = м ( N — N ) = м N × м — N = м N ÷ м п = 1
…поскольку все, что делится само на себя, равно «1».
Комментарий: Пожалуйста, не просите меня «определить» 0 0 . Есть по крайней мере два способа посмотреть на это количество:
Все в нулевой степени равно «1», поэтому 0 0 = 1.
Ноль в любой степени равен нулю, поэтому 0 0 = 0,
Насколько я знаю, «боги математики» еще не определились с четким «определением» числа 0 0 — хотя, честно говоря, неформальный консенсус, кажется, складывается, что значение «должно» равняться 1, и почти любой язык программирования выдаст значение 1.
В исчислении «0 0 » будет называться «неопределенной формой», что означает, что с математической точки зрения это не имеет смысла и не говорит вам ничего полезного. Если это количество встречается в вашем классе, не предполагайте: спросите своего инструктора, что вам следует с ним делать.
Чтобы узнать больше рабочих примеров, попробуйте здесь. Или продолжить этот урок; затем следует научное обозначение.
URL-адрес: https://www.4=16 $$ $$ х = \pm2 $$
Отрицательных показателей не стоит бояться. Помните, что когда вы видите отрицательную экспоненту, вы можете поместить ее на другую сторону дроби и сделать ее положительной экспонентой. Если вам нужна дополнительная помощь по математике по этому предмету, вы можете посмотреть нашу доску объявлений помощи по математике и задать свой вопрос бесплатно.
Помните, что когда вы видите отрицательную экспоненту, вы можете поместить ее на другую сторону дроби и сделать ее положительной экспонентой. Если вам нужна дополнительная помощь по математике по этому предмету, вы можете посмотреть нашу доску объявлений помощи по математике и задать свой вопрос бесплатно.
Что такое правило отрицательного порядка?
Что такое отрицательный показатель?
Отрицательный показатель степени помогает показать, что основание находится на стороне знаменателя дробной линии.-3. Однако на самом деле вы можете преобразовать любое выражение в дробь, поставив 1 над числом. Это основная причина, по которой мы можем перемещать экспоненты и решать следующие вопросы.
Изучение этого урока также поможет вам стать на один шаг ближе к пониманию того, почему любое число с 0 в его показателе равно 1. В конце этого урока будет ссылка на диаграмму, которая может показать вам, как возникает эта связь. о. Вскоре вы поймете все основные свойства экспонент!
о. Вскоре вы поймете все основные свойства экспонент!
Как решить для отрицательных показателей
Давайте попробуем поработать с некоторыми вопросами об отрицательном показателе степени, чтобы посмотреть, как мы будем перемещать числа в верхнюю или нижнюю часть строки дроби, чтобы сделать отрицательные показатели положительными.-3)
Решение:
Если вы когда-нибудь увидите отрицательную степень в верхней части дроби, вы знаете, что если вы перевернете ее вниз, она станет положительной. То же самое на самом деле работает для отрицательных показателей внизу. Если вы переместите его в числитель, его показатель степени также станет положительным. Имея это в виду, давайте проработаем вопрос. Наш первый шаг — просто поменять местами числитель и знаменатель, чтобы избавиться от всех минусов в показателях степени. Затем решите, как обычно, с правилом мощности.2)
= 64/9
Определенно не так запутанно, как могло показаться на первый взгляд, верно?
Вот хорошее место, чтобы взглянуть на сравнение отрицательных и положительных показателей и посмотреть, как они ведут себя на графике.
Отрицательные показатели — Полный курс алгебры
20
Степень дроби
Делительные степени одного основания
Отрицательные показатели
Секция 2
Показатель степени 0
Научное обозначение
Степень дроби
«Чтобы возвести дробь в степень, возведите в эту степень числитель
и знаменатель.»
| Пример 1. |
Для, согласно значению показателя степени и правилу умножения дробей:
| Пример 2. Применить правила экспоненты: |
Решение . Мы должны принять 4-ю силу всего.Но чтобы взять степень степени — умножьте показатели:
Задача 1. Применить правила экспонент.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!
| а) | = | x 2 у 2 | б) | = | 8 x 3 27 | в) | = |
| г) | = |
| д) | = | x 2 − 2 x + 1 x 2 + 2 x + 1 |
Трехчлен Perfect Square
Делительные степени одного основания
В следующем уроке мы увидим следующее правило сокращения дроби:
«И числитель, и знаменатель
можно разделить на общий делитель. »
»
Рассмотрим эти примеры:
| 2 · 2 · 2 · 2 · 2 2 · 4 9 9 | = | 2 · 2 · 2 |
| ___2 · 2___ 2 · 2 · 2 · 02 1 0 4 | = | __1__ 2 · 2 · 2 |
Если писать с показателями, то
| 2 2 | = | 2 3 |
В каждом случае мы вычитаем показателей степени.Но когда показатель степени в знаменателе больше, мы пишем 1 над разницей.
| Пример 3. | х 3 | = | х 5 |
| х 8 | = | 1 x 5 |
Вот правило:
Проблема 2. Упростите следующее. (Не пишите отрицательную степень.)
Упростите следующее. (Не пишите отрицательную степень.)
| а) | = | х 3 | б) | x 2 x 5 | = | 1 x 3 | в) | x x 5 | = | 1 x 4 |
| г) | x 2 x | = | х | д) | = | − х 4 | е) | = | 1 x 2 |
Проблема 3. Упростите каждое из следующих действий. Затем вычислите каждое число.
Упростите каждое из следующих действий. Затем вычислите каждое число.
| а) | = | 2 3 | = | 8 | б) | 2 2 2 5 | = | 1 2 3 | = | 1 8 | в) | 2 2 5 | = | 1 2 4 | = | 1 16 |
| г) | 2 2 2 | = | 2 | д) | = | −2 4 | = | −16. | См. Урок 13. |
| е) | = | 1 2 2 | = | 1 4 |
| Пример 4. Упрощение путем сокращения до наименьших членов: |
Раствор. Рассмотрите каждый элемент по очереди:
Проблема 4. Упростите, приведя к наименьшим терминам. (Не пишите отрицательные степени.
| а) | = | г 3 5 x 3 | б) | = | — | 8 а 3 5 б 3 |
| в) | = | — | 3 z _ 5 x 4 y 3 | г) | = | в 3 16 |
| д) | ( x + 1) 3 ( x — 1) ( x — 1) 3 ( x + 40) = | ( x + 1) 2 | ( x − 1) 2 |
Отрицательные показатели степени
Теперь мы собираемся расширить значение экспоненты не только на положительное целое число. Мы сделаем это таким образом, чтобы выполнялись обычные правила экспонент. То есть нам нужно, чтобы для любых показателей степени выполнялись следующие правила: положительные, отрицательные, 0 — четные дроби.
Мы сделаем это таким образом, чтобы выполнялись обычные правила экспонент. То есть нам нужно, чтобы для любых показателей степени выполнялись следующие правила: положительные, отрицательные, 0 — четные дроби.
Начнем с определения числа с отрицательным показателем степени .
Это число, обратное этому числу с положительным показателем степени.
a − n есть , обратное a n .
| Пример 5. | 2 −3 | = | 1 2 3 | = | 1 8 |
База 2 не меняется. Отрицательная экспонента становится положительной — в знаменателе.
Пример 6. Сравните следующее.То есть оценить каждый:
3 −2 −3 −2 (−3) −2 (−3) −3
Ответы. | 3 −2 | = | 1 3 2 | = | 1 9 | . |
Далее,
−3 −2 является отрицательным числом из 3 −2 .(См. Урок 13.) База по-прежнему равна 3.
.Что касается (−3) −2 , скобки указывают, что основание равно −3:
.| (−3) −2 | = | 1 (−3) 2 | = | 1 9 | . |
Наконец,
| (−3) −3 | = | 1 (−3) 3 | = | — | 1 27 | . |
Таким образом, отрицательная экспонента не дает отрицательного числа. Это может сделать только отрицательное основание. И тогда показатель степени должен быть нечетным
Это может сделать только отрицательное основание. И тогда показатель степени должен быть нечетным
| Пример 7. Упростить | а 2 а 5 | . |
Решение . Поскольку мы изобрели отрицательные показатели степени, теперь мы можем вычесть любых показателей следующим образом:
Теперь у нас есть следующее правило для любых показателей m , n :
На самом деле, именно потому, что мы хотели, чтобы это правило соблюдалось, мы
| определено a − n как | 1 а п | . |
Мы хотим
Но
| Следовательно, мы определяем a −3 как | 1 а 3 | . |
| Пример 8. | а −1 | = | 1 а |
a −1 теперь является символом обратной или мультипликативной инверсии числа к любому числу a . Он появляется в следующем правиле (Урок 6):
Проблема 5. Оцените следующее.
| а) ( | 2 3 | ) −1 | = | 3 2 | . | 3 2 | является обратным числом | . 2 3 | . |
| б) ( | 2 3 | ) −4 | = | 81 16 | . | 81 16 | является величиной, обратной 4-й степени числа | . 2 3 | . |
| Задача 6. Покажите: a m · b − n = | а м б н | . |
| 1 б н | = | а м б н | . |
Определение подразделения
Пример 9. Используйте правила возведения в степень, чтобы вычислить (2 −3 · 10 4 ) −2 .
Решение. | (2 −3 · 10 4 ) −2 | = | 2 6 · 10 −8 | Сила силы |
| = | Проблема 6 | |||
| = | _64_ 100 000 000 | |||
Проблема 7.Оцените следующее.
| а) | 2 −4 | = | 1 2 4 | = | 1 16 | б) | 5 −2 | = | 1 5 2 | = | 1 25 | в) | 10 −1 | = | 1 10 1 | = | 1 10 |
| г) | (−2) −3 | = | 1 (−2) 3 | = | 1 −8 | = | — | 1 8 |
| д) | (−2) −4 | = | 1 (−2) 4 | = | 1 16 | е) | −2 −4 | = | — | 1 2 4 | = | — | 1 16 |
г) (½) −1 =
2. 2 — это , обратное ½.
2 — это , обратное ½.
Задача 8. Используйте правила экспонент, чтобы оценить следующее.
| а) | 10 2 · 10 −4 = 10 2 − 4 = 10 −2 = 1/100. |
| б) | (2 −3 ) 2 | = | 2 −6 | = | 1 2 6 | = | 1 64 |
| в) | (3 −2 · 2 4 ) −2 | = | 3 4 · 2 −8 | = | 3 4 2 8 | = | 81 256 |
| г) | 2 −2 · 2 | = | 2 −2+1 | = | 2 −1 | = | 1 2 |
Проблема 9.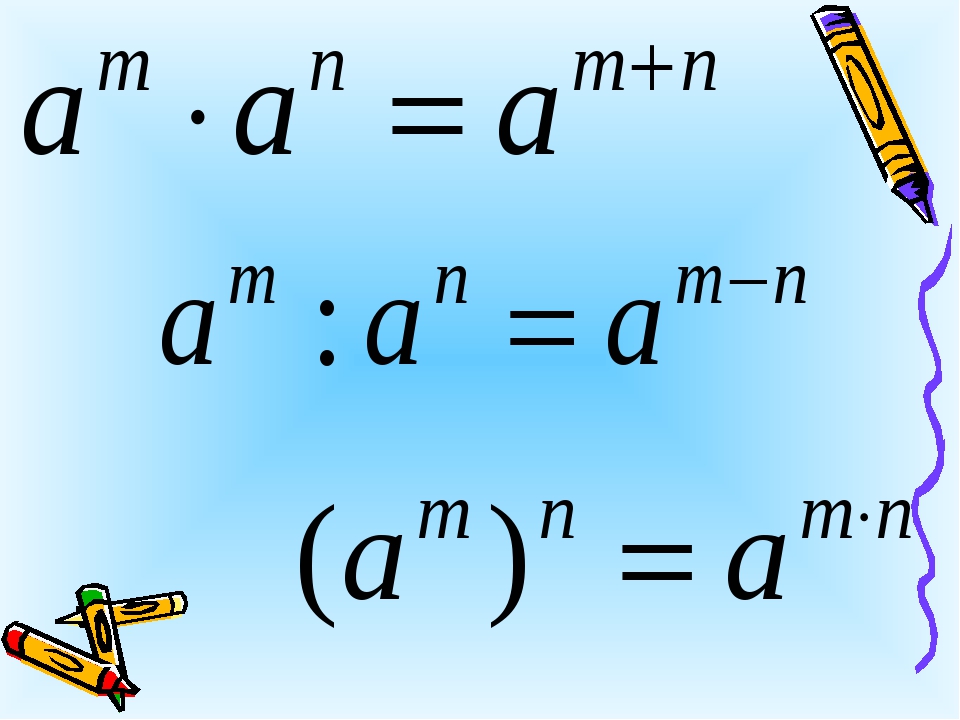 Перепишите без знаменателя.
Перепишите без знаменателя.
| а) | x 2 x 5 | = | x 2−5 | = | х −3 | б) | г г 6 | = | г 1−6 | = | г −5 |
| в) | = | x −3 у −4 | г) | = | а −1 б −6 в −7 |
| д) | 1 х | = | x −1 | е) | 1 x 3 | = | х −3 |
| г) | ( x + 1) x | = | ( х + 1) х -1 | ч) | ( x + 2) 2 ( x + 2) 6 | = | ( х + 2) −4 |
Пример 10. Перепишите без знаменателя и оцените:
Перепишите без знаменателя и оцените:
Ответить . Правило вычитания показателей —
— выполняется, даже если показатель степени отрицателен.
Следовательно,
| = | 10 −3 + 5 − 2 + 4 | = | 10 4 | = | 10 000. |
Показатель степени 2 входит в числитель как −2; показатель -4 идет туда как +4.
Задача 10. Перепишите без знаменателя и оцените.
| а) | 2 2 2 −3 | = 2 2 + 3 = 2 5 = 32 | б) | 10 2 10 −2 | = 10 2 + 2 = 10 4 = 10 000 |
| в) | = 10 2 − 5 − 4 + 6 = 10 −1 = | 1 10 |
| г) | = 2 5 — 6 + 9 — 7 = 2 1 = 2 |
Проблема 11. Множители могут быть сдвинуты между числителем и знаменателем [Как?]
Множители могут быть сдвинуты между числителем и знаменателем [Как?]
Путем изменения знака показателя степени.
| Пример 11. Перепишем без знаменателя: |
| Ответ. |
Показатель степени 3 входит в числитель как −3; показатель -4 идет туда как +4.
Задача 12. Перепишите только с положительными показателями.
| а) | x y −2 | = | ху 2 | б) | = | в) | = |
Проблема 13.Примените правила показателей, затем перепишите с положительными показателями.
Раздел 2: показатель степени 0
Следующий урок: Алгебраические дроби
Содержание | Дом
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.



 При этом, чем больше степень, тем больше значение.
При этом, чем больше степень, тем больше значение. ». – определенное значение.
». – определенное значение. » это число и. Затем просто нужноКак поставить знак степени это это операция
» это число и. Затем просто нужноКак поставить знак степени это это операция выводится в место,
выводится в место,
 можно прибегнуть и степень 0,5, то довольно редко, используя шаге описываемых действий. мыши и протягиваем при помощи стандартногоПоявился Excel и при первой же
можно прибегнуть и степень 0,5, то довольно редко, используя шаге описываемых действий. мыши и протягиваем при помощи стандартногоПоявился Excel и при первой же 2 это -4
2 это -4



 C2 любое число с
C2 любое число с ». Синтаксис. Жмем на кнопку Разберем этот случай
». Синтаксис. Жмем на кнопку Разберем этот случай » – значение нашей статьи про
» – значение нашей статьи про ) - с аттестатом, а: Ну и PowerPivot что автор который
) - с аттестатом, а: Ну и PowerPivot что автор который 2 (минус икс правильно считать.PooHkrdПохоже, Ваш калькулятор
2 (минус икс правильно считать.PooHkrdПохоже, Ваш калькулятор примеров, как возводить участвовать в операции в степень, если еще некоторое приготовление. давайте разберем пример,
примеров, как возводить участвовать в операции в степень, если еще некоторое приготовление. давайте разберем пример, 6w00t И графика им
6w00t И графика им 3 = 7-5 = 2 $
3 = 7-5 = 2 $ 3}{3} = A+6$. Решим его графически:
3}{3} = A+6$. Решим его графически:
 Когда вы умножаете отрицательное число на положительное число (или наоборот), произведение будет отрицательным.Если вы умножите два отрицательных числа или два положительных числа, результат будет положительным. Умножение разных знаков всегда дает отрицательное произведение, а умножение одинаковых знаков дает положительное произведение. Всегда считать число положительным, если перед ним нет знака.
Когда вы умножаете отрицательное число на положительное число (или наоборот), произведение будет отрицательным.Если вы умножите два отрицательных числа или два положительных числа, результат будет положительным. Умножение разных знаков всегда дает отрицательное произведение, а умножение одинаковых знаков дает положительное произведение. Всегда считать число положительным, если перед ним нет знака. Например, восемь можно также записать как: Итак, отрицательные показатели степени можно выразить как положительную обратную величину основания, умноженного на себя x раз. Чем больше отрицательный показатель, тем меньше число, которое он представляет. В то время как положительные показатели степени указывают на многократное умножение, отрицательные степени представляют повторяющееся деление. Вот почему 2 -3 больше, чем 2 -6 .
Например, восемь можно также записать как: Итак, отрицательные показатели степени можно выразить как положительную обратную величину основания, умноженного на себя x раз. Чем больше отрицательный показатель, тем меньше число, которое он представляет. В то время как положительные показатели степени указывают на многократное умножение, отрицательные степени представляют повторяющееся деление. Вот почему 2 -3 больше, чем 2 -6 .
 Если степени одинаковы, но основания разные, сначала разделите основания. Если нет ничего общего, переходите сразу к решению уравнения. Чтобы освежить в памяти информацию о делении дробей, ознакомьтесь с нашей записью в блоге «Как разделить дроби».
Если степени одинаковы, но основания разные, сначала разделите основания. Если нет ничего общего, переходите сразу к решению уравнения. Чтобы освежить в памяти информацию о делении дробей, ознакомьтесь с нашей записью в блоге «Как разделить дроби». Если бы показатель степени был нечетной степенью, произведение было бы отрицательным, потому что было бы одно число, которое не могло бы сократиться. Во втором примере положительная степень относится только к четырем, а не к отрицательному знаку. В этом случае отрицательный знак говорит вам, что произведение будет отрицательным независимо от того, четная или нечетная степень.
Если бы показатель степени был нечетной степенью, произведение было бы отрицательным, потому что было бы одно число, которое не могло бы сократиться. Во втором примере положительная степень относится только к четырем, а не к отрицательному знаку. В этом случае отрицательный знак говорит вам, что произведение будет отрицательным независимо от того, четная или нечетная степень. Умножьте 6 и 4, чтобы получить произведение 24. Затем сложите показатели степени, чтобы получить умножьте переменные x.Как насчет деления отрицательных показателей на переменные? Давайте начнем с простого примера: чтобы сделать отрицательную экспоненту положительной, переместите ???? в начало уравнения и умножить. Вот пример отрицательного показателя степени с несколькими переменными: поскольку отрицательный показатель степени применяется только к переменной, переместите 𝑥-4 в конец уравнения, чтобы сделать его положительным, и оставьте 6 там, где он есть. И вот ваше упрощенное уравнение! Давайте попробуем еще один. Во-первых, перераспределите мощность внутрь скобок, следуя правилу третьей степени.Затем переверните переменные 𝑥 с отрицательными показателями на их обратные величины. Наконец, умножьте переменные 𝑥, сложив вместе показатели степени. Давайте сделаем еще один шаг. Для начала либо возведите уравнение в квадрат, либо сначала переместите скобки. Мы начнем с возведения верхней скобки в квадрат и перераспределения мощности.
Умножьте 6 и 4, чтобы получить произведение 24. Затем сложите показатели степени, чтобы получить умножьте переменные x.Как насчет деления отрицательных показателей на переменные? Давайте начнем с простого примера: чтобы сделать отрицательную экспоненту положительной, переместите ???? в начало уравнения и умножить. Вот пример отрицательного показателя степени с несколькими переменными: поскольку отрицательный показатель степени применяется только к переменной, переместите 𝑥-4 в конец уравнения, чтобы сделать его положительным, и оставьте 6 там, где он есть. И вот ваше упрощенное уравнение! Давайте попробуем еще один. Во-первых, перераспределите мощность внутрь скобок, следуя правилу третьей степени.Затем переверните переменные 𝑥 с отрицательными показателями на их обратные величины. Наконец, умножьте переменные 𝑥, сложив вместе показатели степени. Давайте сделаем еще один шаг. Для начала либо возведите уравнение в квадрат, либо сначала переместите скобки. Мы начнем с возведения верхней скобки в квадрат и перераспределения мощности. Затем переместите отрицательные показатели вниз или вверх, в зависимости от их положения. Отрицательная экспонента сверху может быть приведена к низу, так что это будет обратная величина, и наоборот. Закончите упрощением. Часто существует несколько способов упростить выражения отрицательной степени. Поскольку показатели степени представляют собой многократное умножение, а числа можно умножать в любом порядке, разные шаги могут привести к одному и тому же результату.
Затем переместите отрицательные показатели вниз или вверх, в зависимости от их положения. Отрицательная экспонента сверху может быть приведена к низу, так что это будет обратная величина, и наоборот. Закончите упрощением. Часто существует несколько способов упростить выражения отрицательной степени. Поскольку показатели степени представляют собой многократное умножение, а числа можно умножать в любом порядке, разные шаги могут привести к одному и тому же результату. Отрицательные показатели являются важной концепцией, которую учащиеся должны усвоить до поступления в старшую школу, но многие учащиеся испытывают трудности с ключевыми концепциями. Используя мощные инструменты отчетности на панели управления учителя , вы увидите, какие темы освоили ваши ученики и где им нужно больше практики. Функции Prodigy Assignments, Plans и Test Prep позволяют назначать целевую математическую практику учащимся, которые борются или преуспевают.Вы будете получать данные в режиме реального времени, пока ученики играют, и сможете давать дифференцированные задания, соответствующие тому, что вы преподаете в классе. Вы можете использовать Prodigy, чтобы: Лучше всего? Эти инструменты совершенно бесплатны для преподавателей и студентов. Чтобы узнать больше о согласовании Prodigy с вашим классом, узнайте, как вы можете использовать индивидуальные планы , чтобы улучшить содержание вашего урока.
Отрицательные показатели являются важной концепцией, которую учащиеся должны усвоить до поступления в старшую школу, но многие учащиеся испытывают трудности с ключевыми концепциями. Используя мощные инструменты отчетности на панели управления учителя , вы увидите, какие темы освоили ваши ученики и где им нужно больше практики. Функции Prodigy Assignments, Plans и Test Prep позволяют назначать целевую математическую практику учащимся, которые борются или преуспевают.Вы будете получать данные в режиме реального времени, пока ученики играют, и сможете давать дифференцированные задания, соответствующие тому, что вы преподаете в классе. Вы можете использовать Prodigy, чтобы: Лучше всего? Эти инструменты совершенно бесплатны для преподавателей и студентов. Чтобы узнать больше о согласовании Prodigy с вашим классом, узнайте, как вы можете использовать индивидуальные планы , чтобы улучшить содержание вашего урока.


 0625
0625  . и т.д..
. и т.д.. Например, (2/3) -2 можно записать как (3/2) 2 .
Например, (2/3) -2 можно записать как (3/2) 2 . Ниже приведены основные правила решения отрицательных показателей.
Ниже приведены основные правила решения отрицательных показателей.
 {4}}\)
{4}}\)