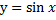| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Графики простейших функций — линейная, параболы, гиперболы, экспоненты, показательные, степенные, логарифмическая, синус, косинус, тангенс, котангенс изучаемых в школе Справочная таблица. Примерно 7-9 класс (13-15 лет) Поделиться:
| |||||||||||||||||||||||
dpva.ru
«Графики функций, формулы» — Алгебра
Просмотр содержимого документа
«»Графики функций, формулы»»

Графики функций,
формулы функций.
9-11 класс
Иванова Т.В.
МБОУ «Школа №18»
Г. Ростов-на-Дону


Линейная функция
y = kx
Прямая
Линейная зависимость — прямая пропорциональность у = kx , где k ≠ 0 — коэффициент пропорциональности.

Линейная функция
y = kx + b
Прямая
Линейная зависимость: коэффициенты k и b — любые действительные числа. ( k = 0.5, b = 1)


Квадратичная функция
y = x 2
Парабола
Квадратичная зависимость: симметричная парабола с вершиной в начале координат.
 1 «
1 «
Квадратичная функция
y = x n
Парабола
Квадратичная зависимость: n — натуральное четное число 1
 1 «
1 «
Степенная функция
y = x n
Кубическая парабола
Нечетная степень: n — натуральное нечетное число 1

Степенная функция
y = x 1/2
График функции y = √ x
Степенная зависимость ( x 1/2 = √x).

Степенная функция
y = k/x
Гипербола
Случай для целой отрицательной степени ( 1/x = x -1 ). Обратно-пропорциональная зависимость. ( k = 1)
















multiurok.ru
| 1. |
Исследование функции на ограниченность
Сложность: лёгкое |
1 |
| 2. |
Возрастающая и убывающая функции
Сложность: лёгкое |
1 |
| 3. |
Возрастание или убывание функции
Сложность: лёгкое |
1 |
| 4. |
Интервалы знакопостоянства функции
Сложность: среднее |
1 |
| 5. |
График функции вида y = |x + а|
Сложность: среднее |
3 |
| 6. |
График функции вида y = |x| + а
Сложность: среднее |
2 |
| 7. |
Нули функции
Сложность: среднее |
3 |
| 8. |
Исследование функции
Сложность: среднее |
3 |
| 9. |
График квадратной функции с модулем
Сложность: сложное |
4 |
| 10. |
Монотонность, наибольшее значение функции
Сложность: сложное |
3 |
| 11. |
Исследование функции
Сложность: сложное |
13 |
www.yaklass.ru
Графики функций, 9 класс. (51 задание)
На рисунке изображены графики функций вида у = kх + b. Установите соответствие между знаками коэффициентов k и b и графиками.
КОЭФФИЦИЕНТЫ
А) 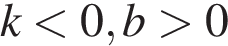 Б)
Б) 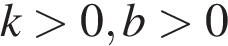 В)
В) 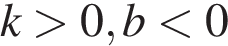
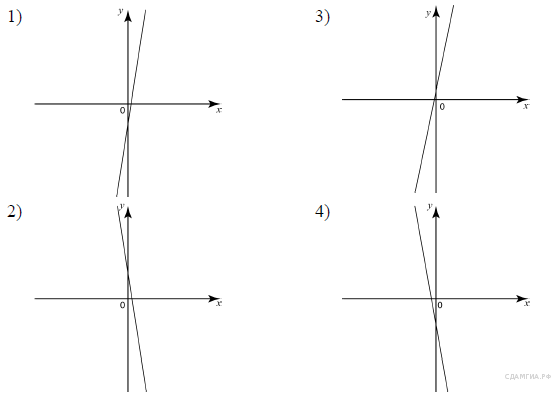
Установите соответствие между графиками функций и формулами, которые их задают.
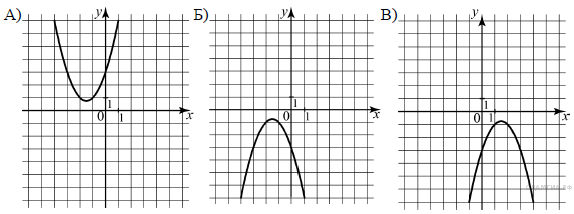
Установите соответствие между графиками функций и формулами, которые их задают.
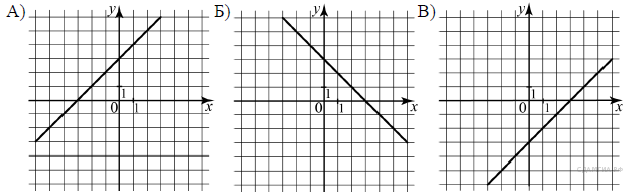
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) f(x)<0 при x<1
2) Наибольшее значение функции равно 3
3) f(0)>f(4)
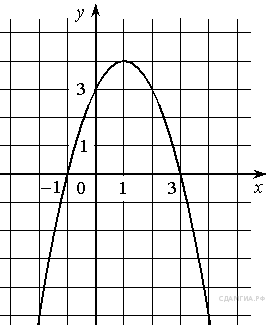
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера в порядке возрастания.
1) Функция возрастает на промежутке (−∞; −1].
2) Наибольшее значение функции равно 8.
3) f(−4) ≠ f(2).
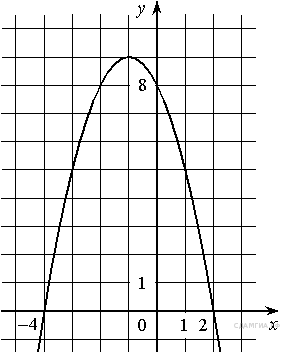
На рисунке изображён график квадратичной функции y=f(x) .
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция убывает на промежутке [1; +∞)
2) Наименьшее значение функции равно – 4
3) f(−2)<f(3)
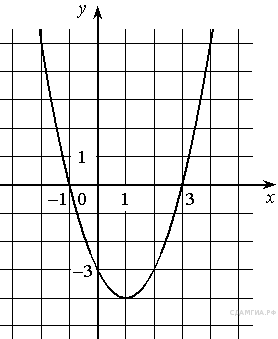
На рисунке изображён график квадратичной функции y=f( x ) .
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция возрастает на промежутке [2; +∞)
2) f(x)>0 при −1<x<5
3) f(0)<f(4)
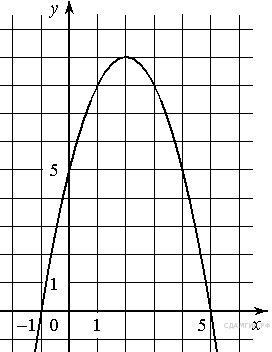
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) f(−1) = f(3).
2) Наибольшее значение функции равно 3.
3) f(x)>0 при −1<x<3.
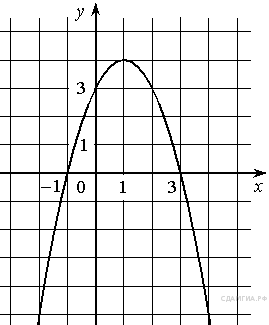
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Наибольшее значение функции равно 9.
2) f(0)>f(1).
3) f( x )>0 при x<0.
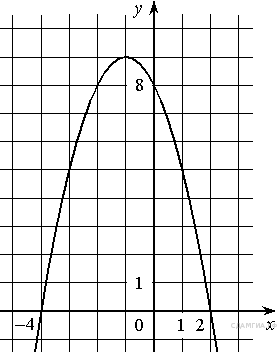
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) f(x)<0 при −1<x<5.
2) Функция возрастает на промежутке [2; +∞).
3) Наименьшее значение функции равно −5.
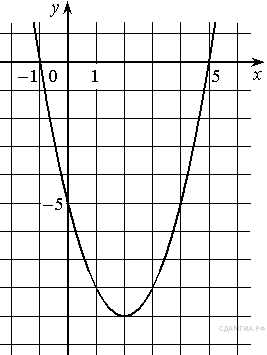
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция убывает на промежутке [−1; +∞).
2) f(−3)<f(0).
3) f(x)<0 при −4<x<2.
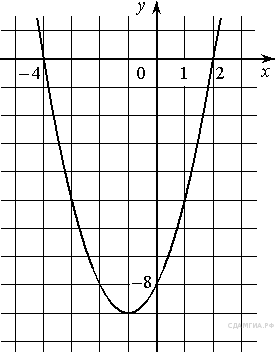
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Наибольшее значение функции равно 9
2) Функция убывает на промежутке ( −∞; 2 ]
3) f(x)<0 при x<2
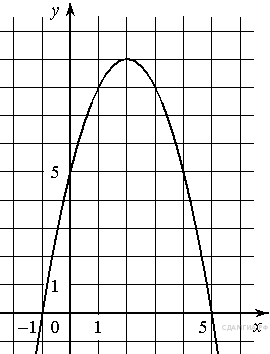
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция возрастает на промежутке [1; +∞).
2) f(−2) = f(2).
3) Наименьшее значение функции равно –4.
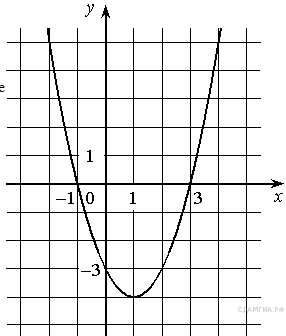
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция возрастает на промежутке [2; +∞)
2) f( −1 )<f( 5 )
3) Наименьшее значение функции равно −9
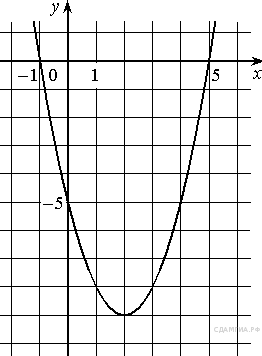
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) f( −2 ) = f( 2 )
2) f(x)>0 при x<−4 и при x>2
3) Наименьшее значение функции равно −9
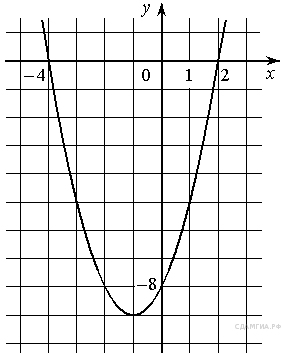
Установите соответствие между графиками функций и формулами, которые их задают.
На рисунке изображены графики функций вида
 . Установите соответствие между знаками коэффициентов
. Установите соответствие между знаками коэффициентов  и
и  и графиками.
и графиками.
КОЭФФИЦИЕНТЫ
А) 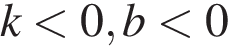 Б)
Б) 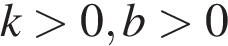 В)
В) 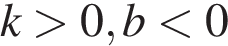
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
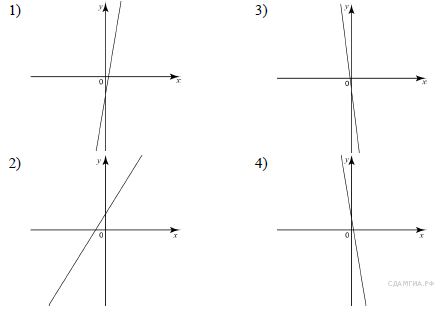
На рисунке изображены графики функций вида
 . Установите соответствие между графиками и знаками коэффициентов
. Установите соответствие между графиками и знаками коэффициентов  и
и 
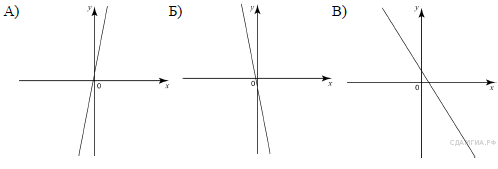
КОЭФФИЦИЕНТЫ
1) 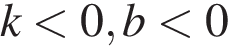 2)
2) 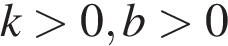 3)
3) 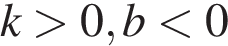 4)
4) 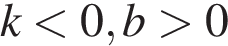
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А)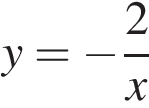 Б)
Б)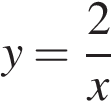 В)
В)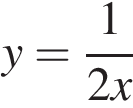
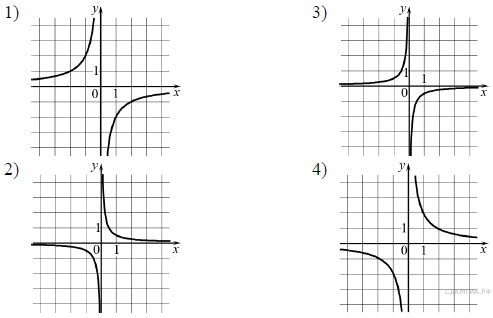
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А)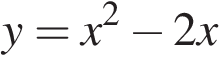 Б)
Б)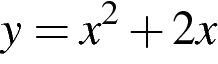 В)
В)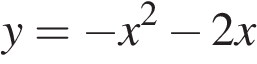
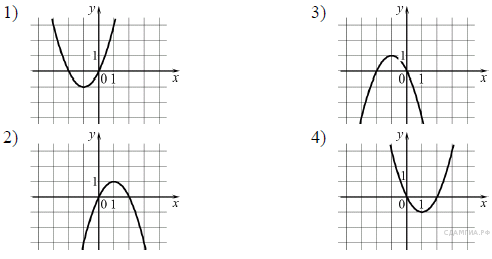
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
infourok.ru
Функции. Графики функций. Диаграммы. Видеоурок. Информатика 9 Класс
На данном уроке мы обсудим введение данных в таблицу при помощи стандартных формул. Также мы рассмотрим построение диаграмм и графиков функций и их форматирование.
Мы уже знаем, что в электронных таблицах можно вводить в ячейки выражения и вычислять их значение. В ячейки также можно вводить функции, в том числе и стандартные, это удобно делать с помощью мастера. Мастер – это удобное средство для прохождения всех этапов создания документа или его фрагмента в диалоговом режиме.
На первом этапе мастер откроет окно «Мастер функций», в котором мы можем выбрать категорию функции, саму функцию и посмотреть, какие у этой функции аргументы и каково ее назначение. В этом диалоговом окне мы увидим формат функции, то есть правило ее записи. Формат определяет, какие у функции аргументы, какие между аргументами разделители и в каком порядке эти аргументы следует записать. Следует отметить, что разделители очень важны и их нужно строго соблюдать, т. к. если поставить, например, запятую вместо точки с запятой, функция не будет корректно работать.
На втором этапе мастер поможет правильно подобрать аргументы и ввести их.
При записи функции также важно соблюдать количество скобок. Количества закрывающих и открывающих скобок должны быть равны. Это несложно отследить, так как пары скобок обычно бывают разных цветов.
Кроме того, важно правильно указать название функции. Например, если написать «Сумма» вместо стандартного «sum», результат не будет получен, т. к. название «Сумма» отсутствует в списке стандартных функций.
Если при записывании формулы допущены ошибки, появится окно с сообщением об ошибках и советами по их исправлению. Если ошибки исправить не удалось, лучше удалить формулу, составить и записать ее заново, так как допущенные ошибки не дадут продолжить работу и сохранить документ.
Для наглядного представления результатов вычислений удобно использовать графики и диаграммы. Строить их можно с помощью мастера или команды Вставка главного меню программы.
Для примера построим диаграмму распределения населения Петербурга в 1869 году по сословиям. Построим соответствующую таблицу (рис. 1):
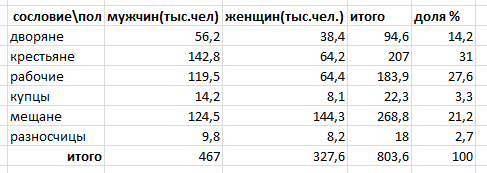
Рис. 1. Таблица с данными
Выделяем столбец с названиями сословий и столбец с кол-вом населения, выполняем данное действие, удерживая клавишу Ctrl (рис. 2):
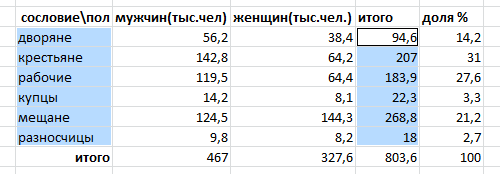
Рис. 2. Выделение данных
Теперь во вкладке «вставка» выбираем круговую диаграмму (рис. 3):
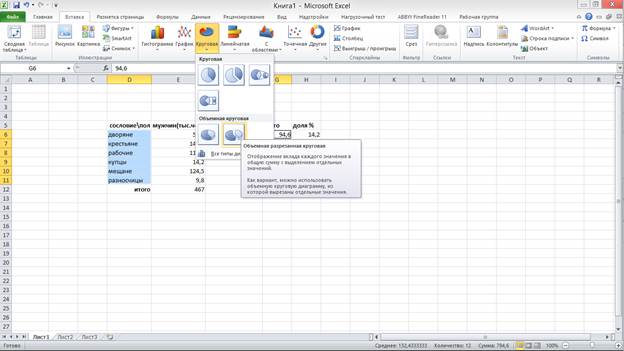
Рис. 3. Выбор типа диаграммы
Получен результат (рис. 4):
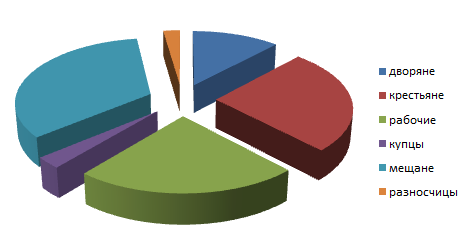
Рис. 4. Диаграмма распределения населения
На полученной диаграмме можно выполнять форматирование, причем как всей диаграммы, так и отдельных ее элементов. Отформатируем один сектор. Для этого щелкнем по нему правой кнопкой мыши и выберем Формат точки данных. В открывшемся диалоговом окне выбираем пункт «заливка», далее «сплошная заливка» и изменяем цвет произвольно (рис. 5):
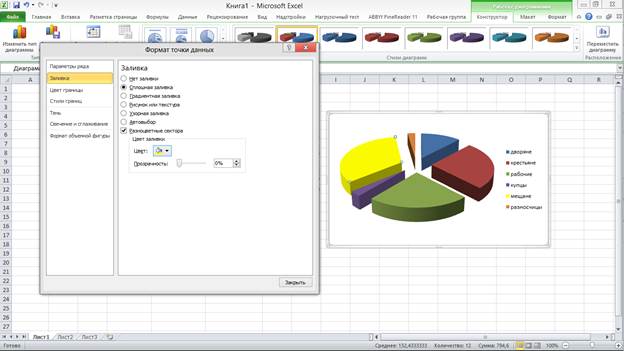
Рис. 5. Форматирование диаграммы
Теперь выберем все сектора, щелкнем правой кнопкой мыши и выберем Добавить подписи данных (рис. 6):
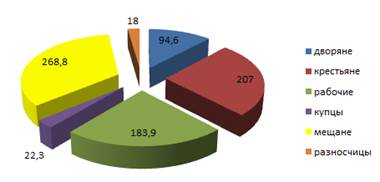
Рис. 6. Форматирование диаграммы
Изменим формат подписей. Выберем не значение, а проценты (рис. 7):
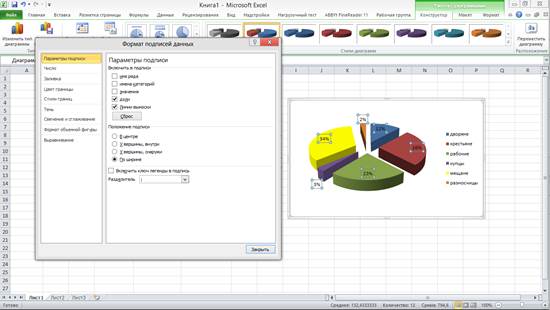
Рис. 7. Форматирование диаграммы
Размещение на листе электронной таблицы диаграммы приведет к появлению на ленте вкладок Конструктор и Макет. Они видны, когда диаграмма выделена.
Здесь расположены команды для форматирования и редактирования диаграмм (рис. 8).

Рис. 8. Дополнительные вкладки
Построим столбчатую диаграмму (гистограмму) соотношения мужчин и женщин в дворянском сословии. Выделяем данные, выбираем соответствующую диаграмму и получаем результат (рис. 9):
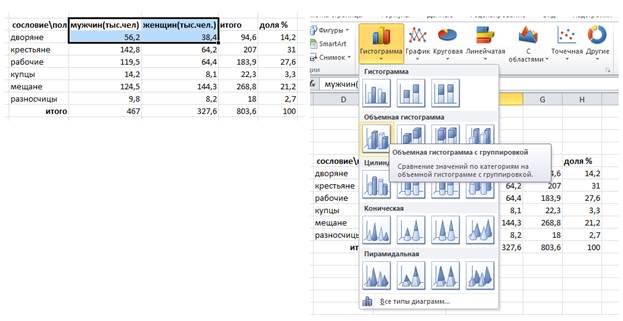
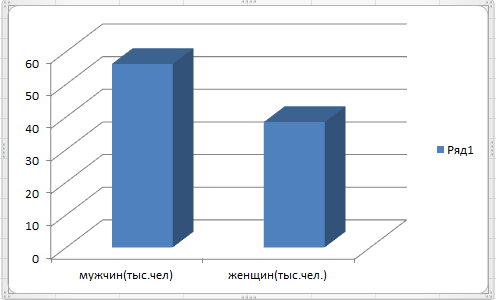
Рис. 9. Построение гистограммы
Вид диаграммы нас не вполне устраивает. Выполним форматирование (рис. 10). Для начала щелкнем правой кнопкой мыши по диаграмме и выберем Выбор данных.
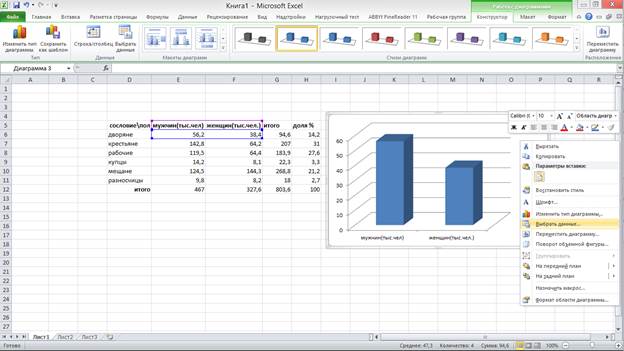
Рис. 10. Форматирование гистограммы
В появившемся диалоговом окне меняем местами строки и столбцы нажатием на соответствующую кнопку. Далее в поле подписи горизонтальной оси нажимаем Изменить и вводим нужное нам название – дворяне. Получена гистограмма (рис. 11):
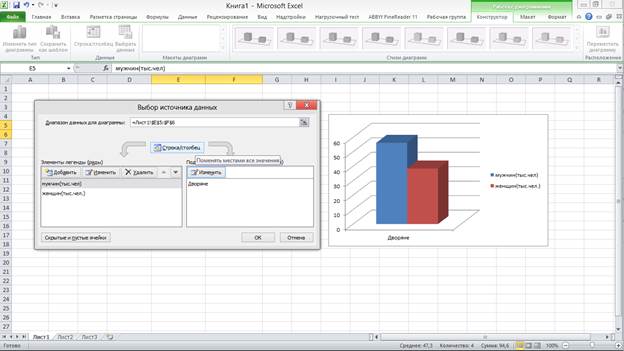
Рис. 11. Гистограмма распределения мужчин и женщин
Теперь рассмотрим построение графиков функций. Построим график функции 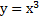 . Сначала вводим нужные значения в табличку. Столбец значений аргумента заполним вручную. Для заполнения значений функции введем формулу. Для этого выбираем нужную ячейку, пишем знак равно, далее нажимаем на ячейку с соответствующим значением аргумента, вставляем значок возведения в степень и показатель степени 3 (рис. 12):
. Сначала вводим нужные значения в табличку. Столбец значений аргумента заполним вручную. Для заполнения значений функции введем формулу. Для этого выбираем нужную ячейку, пишем знак равно, далее нажимаем на ячейку с соответствующим значением аргумента, вставляем значок возведения в степень и показатель степени 3 (рис. 12):
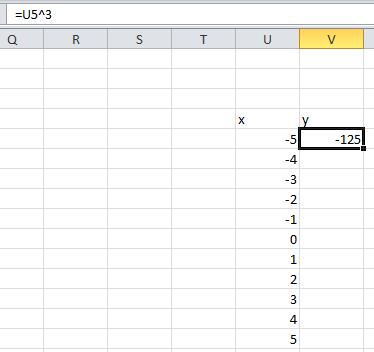
Рис. 12. Заполнение таблицы
Теперь мы можем скопировать формулу и вставить ее во все остальные поля. Для этого на поле с формулой нажимаем правой кнопкой мыши и выбираем «копировать». Далее на следующем поле нажимаем правой кнопкой мыши, выбираем «специальная вставка» и вставляем формулы. Но можно поступить проще: берем ячейку с формулой за правый нижний угол и растягиваем на весь столбец. Так, получена таблица (рис. 13):
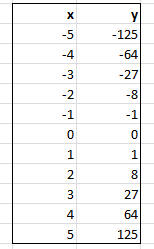
Рис. 13. Таблица значений для построения графика функции
Отметим, что при копировании ссылка изменилась в соответствии с номером строки, в которой находится ячейка с формулой. Такая ссылка называется относительной.
Для построения графика выделяем данные, переходим на вкладку вставка, выбираем график и его тип (рис. 14):
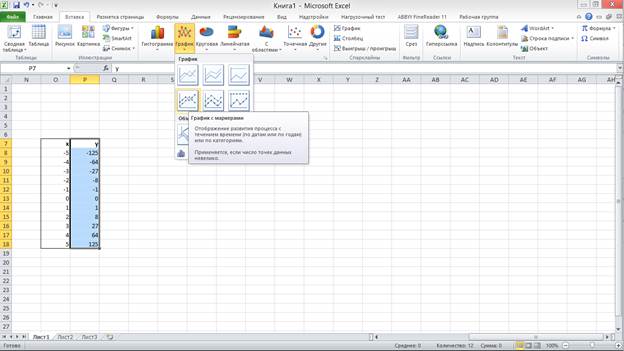
Рис. 14. Построение графика функции
Получен график (рис. 15):
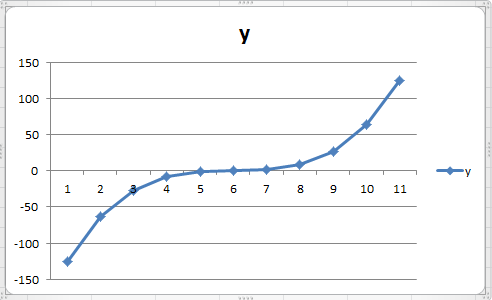
Рис. 15. График функции
На полученном графике ось абсцисс подписана неверно. Щелкнем по графику правой кнопкой мыши и выберем Выбрать данные. В появившемся диалоговом окне в поле Подписи по горизонтальной оси нажимаем Изменить, выбираем нужные нам значения в столбце х и получаем график (рис. 16):
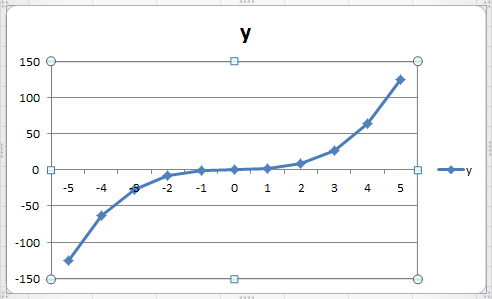
Рис. 16. График функции
Итак, мы рассмотрели некоторые возможности электронных таблиц, а именно построение диаграмм и графиков функций. На следующем уроке мы продолжим рассматривать возможности электронных таблиц.
Список литературы
- Угринович Н.Д. Информатика-9. – М.: БИНОМ. Лаборатория знаний, 2012.
- Гейн А.Г., Юнерман Н.А. Информатика-9. – М.: Просвещение, 2012.
- Соловьёва Л.Ф. Информатика и ИКТ. Учебник для 9 класса. – СПб.: БХВ-Петербург, 2007.
Домашнее задание
- Построить график функции: А)
 Б)
Б)  В)
В) 
- Построить круговую диаграмму для распределения территории Украины по природным зонам (степь, лесостепь и т. д.)
- Построить гистограмму численности населения Великобритании за 2005–2010 гг.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Teachexcel.ru (Источник).
- Интернет-портал Support.office.microsoft.com (Источник).
interneturok.ru
Графики функций 9 класс
Задания по теме « Числовые функции» ( 9 класс ОГЭ)
1.Известно, что графики функций y=−x2+p и y=4x+5 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
2.Известно, что графики функций y=x2+p и y=2x−2 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
3.На рисунке изображён график квадратичной функции y=f(x).
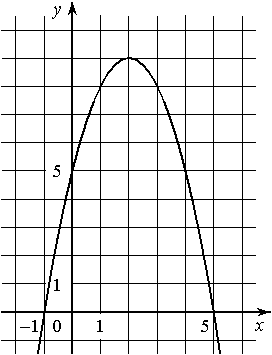
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
4.На рисунке изображён график квадратичной функции y=f(x).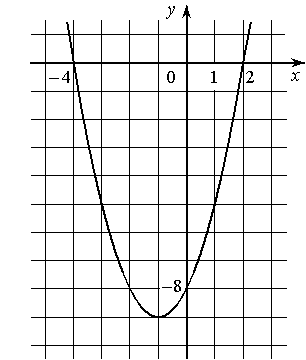
Какие из следующих утверждений о данной функции являются верными? Запишите их номера.
1)Функция убывает на промежутке [−1; +∞)
2)f(x)>0 при x<−4 и при x>2
3)Наименьшее значение функции равно −9
5.Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки C.

6.Известно, что графики функций y=−x2+p и y=−2x+5 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
7.На рисунке изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
КОЭФФИЦИЕНТЫ
А)k<0, b<0
Б)k<0, b>0
В)k>0, b<0
ГРАФИКИ
1)

2)

3)

4)

8.На рисунке изображены графики функций вида y=ax2+bx+c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
ГРАФИКИ
А)

Б)

В)

КОЭФФИЦИЕНТЫ
1)a<0, c>0
2)a>0, c>0
3)a>0, c<0
4)a<0, c<0
9.На рисунке изображены графики функций вида y=ax2+bx+c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
ГРАФИКИ
А)

Б)

В)

КОЭФФИЦИЕНТЫ
1)a>0, c>0
2)a>0, c<0
3)a<0, c>0
4)a<0, c<0
10.На рисунке изображены графики функций вида y=ax2+bx+c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
ГРАФИКИ
А)

Б)

В)

КОЭФФИЦИЕНТЫ
1)a<0, c>0
2)a<0, c<0
3)a>0, c<0
4)a>0, c>0
11.На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ
А)

Б)

В)

КОЭФФИЦИЕНТЫ
1)k>0, b<0
2)k<0, b<0
3)k<0, b>0
4)k>0, b>0
12.На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ
А)

Б)

В)

КОЭФФИЦИЕНТЫ
1)k<0, b>0
2)k>0, b>0
3)k<0, b<0
4)k>0, b<0
13.На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ
А)

Б)

В)

КОЭФФИЦИЕНТЫ
1)k<0, b>0
2)k>0, b<0
3)k>0, b>0
4)k<0, b<0
14.На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ
А)

Б)

В)

КОЭФФИЦИЕНТЫ
1)k<0, b<0
2)k>0, b>0
3)k<0, b>0
4)k>0, b<0
15.На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ
А)

Б)

В)

КОЭФФИЦИЕНТЫ
1)k<0, b>0
2)k<0, b<0
3)k>0, b<0
4)k>0, b>0
16.На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ
А)

Б)

В)

КОЭФФИЦИЕНТЫ
1)k<0, b<0
2)k<0, b>0
3)k>0, b<0
4)k>0, b>0
17.На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ
А)

Б)

В)

КОЭФФИЦИЕНТЫ
1)k<0, b<0
2)k>0, b<0
3)k<0, b>0
4)k>0, b>0
18.На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ
А)

Б)

В)

КОЭФФИЦИЕНТЫ
1)k<0, b<0
2)k>0, b<0
3)k<0, b>0
4)k>0, b>0
19.На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ
А)

Б)

В)

КОЭФФИЦИЕНТЫ
1)k<0, b<0
2)k<0, b>0
3)k>0, b>0
4)k>0, b<0
20.На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ
А)

Б)

В)

КОЭФФИЦИЕНТЫ
1)k>0, b>0
2)k<0, b>0
3)k<0, b<0
4)k>0, b<0
21.На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ
А)

Б)

В)

КОЭФФИЦИЕНТЫ
1)k>0, b<0
2)k<0, b<0
3)k<0, b>0
4)k>0, b>0
22.На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ
А)

Б)

В)

КОЭФФИЦИЕНТЫ
1)k>0, b>0
2)k<0, b>0
3)k>0, b<0
4)k<0, b<0
23.На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
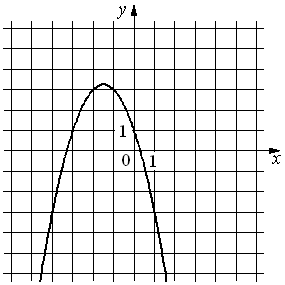
УТВЕРЖДЕНИЯ
А)Функция возрастает на промежутке
Б)Функция убывает на промежутке
ПРОМЕЖУТКИ
1)[− 3; −1,5]
2)[− 2; 0]
3)[− 3; −1]
4)[− 1,5; 0]
24.На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
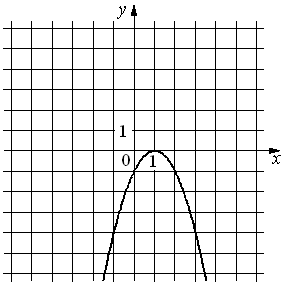
УТВЕРЖДЕНИЯ
А) Функция возрастает на промежутке
Б) Функция убывает на промежутке
ПРОМЕЖУТКИ
1)[1; 2]
2)[0; 2]
3)[− 1; 0]
4)[− 2; 2]
25.На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
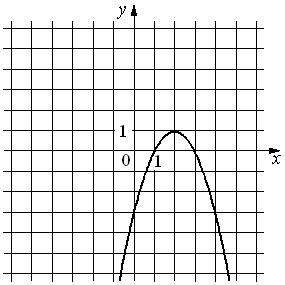
УТВЕРЖДЕНИЯ
А) Функция возрастает на промежутке
Б) Функция убывает на промежутке
ПРОМЕЖУТКИ
1)[0; 3]
2)[− 1; 1]
3)[2; 4]
4)[1; 4]
26.На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
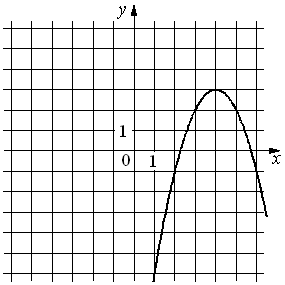
УТВЕРЖДЕНИЯ
А) Функция возрастает на промежутке
Б) Функция убывает на промежутке
ПРОМЕЖУТКИ
1)[3; 5]
2)[2; 5]
3)[4; 5]
4)[0; 3]
27.На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
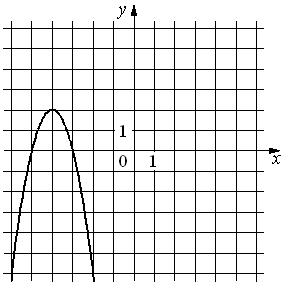
УТВЕРЖДЕНИЯ
А) Функция возрастает на промежутке
Б) Функция убывает на промежутке
ПРОМЕЖУТКИ
1)[− 4; −3]
2)[− 5; −3]
3)[− 5; −4]
4)[− 6; −1]
28.На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
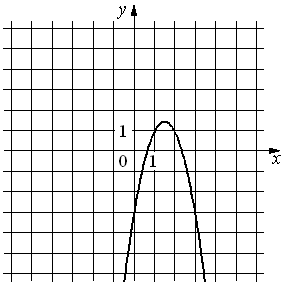
УТВЕРЖДЕНИЯ
А) Функция возрастает на промежутке
Б) Функция убывает на промежутке
ПРОМЕЖУТКИ
1)[2; 3]
2)[− 2; 1]
3)[− 1; 2]
4)[1; 2]
29.На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
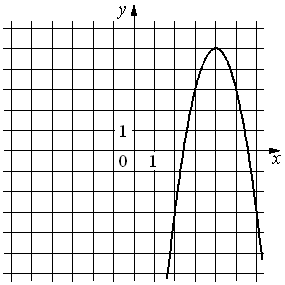
УТВЕРЖДЕНИЯ
А) Функция возрастает на промежутке
Б) Функция убывает на промежутке
ПРОМЕЖУТКИ
1)[2; 3]
2)[2; 5]
3)[5; 6]
4)[3; 6]
30.На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
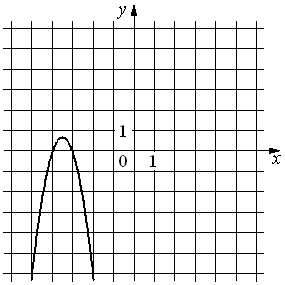
УТВЕРЖДЕНИЯ
А) Функция возрастает на промежутке
Б) Функция убывает на промежутке
ПРОМЕЖУТКИ
1)[− 3; −2]
2)[− 4; −2]
3)[− 5; −4]
4)[− 5; 0]
31.На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
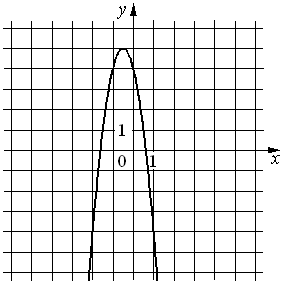
УТВЕРЖДЕНИЯ
А) Функция возрастает на промежутке
Б) Функция убывает на промежутке
ПРОМЕЖУТКИ
1)[− 3; −2]
2)[− 3; 0]
3)[− 1; 2]
4)[1; 2]
32.На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
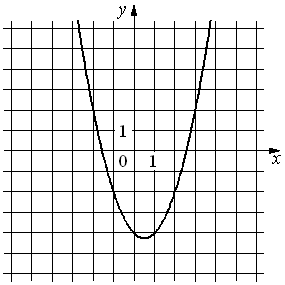
УТВЕРЖДЕНИЯ
А) Функция возрастает на промежутке
Б) Функция убывает на промежутке
ПРОМЕЖУТКИ
1)[0; 3]
2)[− 3; 2]
3)[1; 4]
4)[− 1; 0]
33.На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
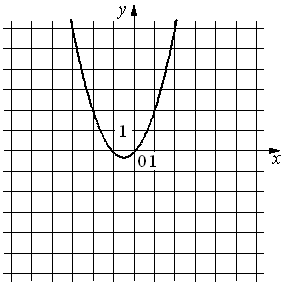
УТВЕРЖДЕНИЯ
А) Функция возрастает на промежутке
Б) Функция убывает на промежутке
ПРОМЕЖУТКИ
1)[− 3; 3]
2)[0; 3]
3)[− 3; −1]
4)[− 3; 0]
34.На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
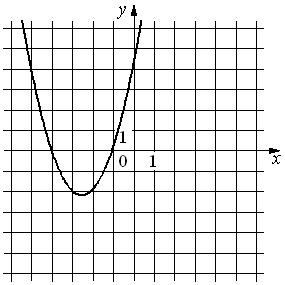
УТВЕРЖДЕНИЯ
А) Функция возрастает на промежутке
Б) Функция убывает на промежутке
ПРОМЕЖУТКИ
1)[− 2; −1]
2)[− 4; −3]
3)[− 3; −2]
4)[− 4; 0]
35.На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
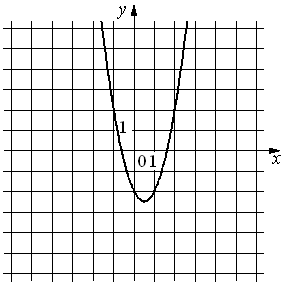
УТВЕРЖДЕНИЯ
А) Функция возрастает на промежутке
Б) Функция убывает на промежутке
ПРОМЕЖУТКИ
1)[2; 5]
2)[0; 1]
3)[− 3; −1]
4)[− 2; 2]
36.На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
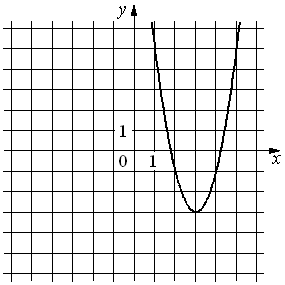
УТВЕРЖДЕНИЯ
А) Функция возрастает на промежутке
Б) Функция убывает на промежутке
ПРОМЕЖУТКИ
1)[0; 2]
2)[2; 5]
3)[4; 7]
4)[1; 7]
37.На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
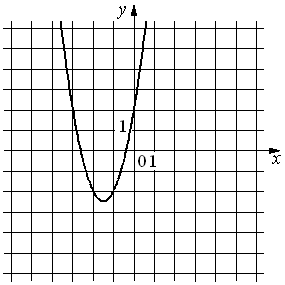
УТВЕРЖДЕНИЯ
А) Функция возрастает на промежутке
Б) Функция убывает на промежутке
ПРОМЕЖУТКИ
1)[− 4; −2]
2)[− 1; 0]
3)[− 2; −1]
4)[− 2; 0]
38.На рисунке изображены графики функций вида y=ax2+c. Установите соответствие между графиками и знаками коэффициентов a и c.
ГРАФИКИ
А)
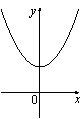
Б)
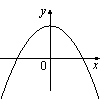
В)
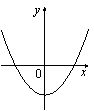
Г)
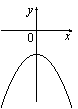
ЗНАКИ КОЭФФИЦИЕНТОВ
1)a>0, c<0
2)a<0, c>0
3)a>0, c>0
4)a<0, c<0
39.На рисунке изображён график квадратичной функции y=f(x).

Какие из следующих утверждений о данной функции являются верными? Запишите их номера.
40.На рисунке изображён график квадратичной функции y=f(x).
infourok.ru
Функция и её свойства 9 класс Функция
Описание презентации Функция и её свойства 9 класс Функция по слайдам
 Функция и её свойства 9 класс
Функция и её свойства 9 класс
 Функция – зависимость одной переменной от другой, причем для любых значений х соответствует единственное значение функции y. График функции – множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты соответствующим значениям функции. Определение
Функция – зависимость одной переменной от другой, причем для любых значений х соответствует единственное значение функции y. График функции – множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты соответствующим значениям функции. Определение
 Виды функций • Линейная • Прямая пропорциональность • Обратная пропорциональность • Квадратичная • Квадратный корень • Модуль • Другие функции
Виды функций • Линейная • Прямая пропорциональность • Обратная пропорциональность • Квадратичная • Квадратный корень • Модуль • Другие функции
 Свойства функций 1. Область определения функции 2. Множество значений функции 3. Монотонность 4. Четность 5. Ограниченность 6. Наибольшее, наименьшее значение 7. Выпуклость 8. Пересечение с осями координат 9. Промежутки знакопостоянства
Свойства функций 1. Область определения функции 2. Множество значений функции 3. Монотонность 4. Четность 5. Ограниченность 6. Наибольшее, наименьшее значение 7. Выпуклость 8. Пересечение с осями координат 9. Промежутки знакопостоянства
 Задание 1 • Изобразите схематически графики функцийxy x y 4 12 xy xy 3 2 xy xy
Задание 1 • Изобразите схематически графики функцийxy x y 4 12 xy xy 3 2 xy xy
 Пример у = 2 х +1 ху х у
Пример у = 2 х +1 ху х у
 Пример у = 3 х х у 0 0 1 3 ху
Пример у = 3 х х у 0 0 1 3 ху
 Пример х у 4 1 2 2 1 -4 -2 -1 4 -1 -2 -4 ху 0 у = 4 x
Пример х у 4 1 2 2 1 -4 -2 -1 4 -1 -2 -4 ху 0 у = 4 x
 Пример х у -2 4 -1 1 0 1 2 0 1 4 ху 0 у = х
Пример х у -2 4 -1 1 0 1 2 0 1 4 ху 0 у = х
 Пример х у 0 0 4 2 9 3 ху 0 xy
Пример х у 0 0 4 2 9 3 ху 0 xy
 Пример ху 0 х у 0 0 3 3 -3 -3 y=|x|
Пример ху 0 х у 0 0 3 3 -3 -3 y=|x|
 Задание 2 • Исследовать график функции
Задание 2 • Исследовать график функции
 Тест 1. Найдите область определения функции 2 x 4 y
Тест 1. Найдите область определения функции 2 x 4 y
 2. Исследуйте на ограниченность функцию13 x 2 xy 2 а) ограничена сверху б) ограничена снизу в) ограничена снизу и сверху г) не ограничена ни снизу, ни сверху
2. Исследуйте на ограниченность функцию13 x 2 xy 2 а) ограничена сверху б) ограничена снизу в) ограничена снизу и сверху г) не ограничена ни снизу, ни сверху
 3. Среди заданных функций укажите возрастающие а) 2, 4 б) 1, 2, 4 в) 3 г) 1,
3. Среди заданных функций укажите возрастающие а) 2, 4 б) 1, 2, 4 в) 3 г) 1,
 4. Среди заданных функций укажите убывающие а) 1, 3 б) 3 в) 3, 4 г)
4. Среди заданных функций укажите убывающие а) 1, 3 б) 3 в) 3, 4 г)
 5. Среди заданных функций укажите четные а) 1, 3 б) 1, 2 в) 3, 4 г) 1,
5. Среди заданных функций укажите четные а) 1, 3 б) 1, 2 в) 3, 4 г) 1,
 6. Среди заданных функций укажите нечетные а) 1, 3 б) 2, 4 в) 2, 3 г) 3,
6. Среди заданных функций укажите нечетные а) 1, 3 б) 2, 4 в) 2, 3 г) 3,
 7. Найдите множество значений функций 2 x 4 y
7. Найдите множество значений функций 2 x 4 y
 Верно
Верно
 Не верно
Не верно
 Линейная функция y = k х+ m ( k>0) Свойства функции 1. D(f)=(- ; + ) 2. Функция не является ни четной, ни нечетной 3. Возрастает 4. Не ограничена ни снизу, ни сверху 5. Нет ни наибольшего, ни наименьшего значений 6. Функция непрерывна 7. Е( f)= ( ; + )График функции — прямая
Линейная функция y = k х+ m ( k>0) Свойства функции 1. D(f)=(- ; + ) 2. Функция не является ни четной, ни нечетной 3. Возрастает 4. Не ограничена ни снизу, ни сверху 5. Нет ни наибольшего, ни наименьшего значений 6. Функция непрерывна 7. Е( f)= ( ; + )График функции — прямая
 Линейная функция y=kx+m (k<0) Свойства функции 1. D(f)=(- ; + ) 2. Функция не является ни четной, ни нечетной 3. Убывает 4. Не ограничена ни снизу, ни сверху 5. Нет ни наибольшего, ни наименьшего значений 6. Функция непрерывна 7. Е( f)= ( ; + ) График функции — прямая
Линейная функция y=kx+m (k<0) Свойства функции 1. D(f)=(- ; + ) 2. Функция не является ни четной, ни нечетной 3. Убывает 4. Не ограничена ни снизу, ни сверху 5. Нет ни наибольшего, ни наименьшего значений 6. Функция непрерывна 7. Е( f)= ( ; + ) График функции — прямая
 Прямая пропорциональность y=kx (k>0) Свойства функции 1. D(f)=(- ; + ) 2. Функция является нечетной 3. Возрастает 4. Не ограничена ни снизу, ни сверху 5. Нет ни наибольшего, ни наименьшего значений 6. Функция непрерывна 7. Е( f)= ( ; + )1 k 2 k 3 k > >График функции — прямая
Прямая пропорциональность y=kx (k>0) Свойства функции 1. D(f)=(- ; + ) 2. Функция является нечетной 3. Возрастает 4. Не ограничена ни снизу, ни сверху 5. Нет ни наибольшего, ни наименьшего значений 6. Функция непрерывна 7. Е( f)= ( ; + )1 k 2 k 3 k > >График функции — прямая
 Прямая пропорциональность y=kx (k<0) Свойства функции 1. D(f)=(- ; + ) 2. Функция является нечетной 3. Убывает 4. Не ограничена ни снизу, ни сверху 5. Нет ни наибольшего, ни наименьшего значений 6. Функция непрерывна 7. Е( f)= ( ; + ) График функции — прямая
Прямая пропорциональность y=kx (k<0) Свойства функции 1. D(f)=(- ; + ) 2. Функция является нечетной 3. Убывает 4. Не ограничена ни снизу, ни сверху 5. Нет ни наибольшего, ни наименьшего значений 6. Функция непрерывна 7. Е( f)= ( ; + ) График функции — прямая
 Обратная пропорциональность ( k>0) Свойства функции • D(f)=(- ; 0) U (0; + ) • Нечётная • Убывает на открытом луче (- ; 0), и на открытом луче ( 0 ; + ) • Не ограничена ни снизу, ни сверху • y наим , y наиб не существует • Непрерывна на открытом луче (- ; 0), и на открытом луче ( 0 ; + ) • E(f )=(- ; 0) U (0; + ) • Выпукла вниз при x>0, выпукла вверх при x<0 График функции — гиперболаx k y
Обратная пропорциональность ( k>0) Свойства функции • D(f)=(- ; 0) U (0; + ) • Нечётная • Убывает на открытом луче (- ; 0), и на открытом луче ( 0 ; + ) • Не ограничена ни снизу, ни сверху • y наим , y наиб не существует • Непрерывна на открытом луче (- ; 0), и на открытом луче ( 0 ; + ) • E(f )=(- ; 0) U (0; + ) • Выпукла вниз при x>0, выпукла вверх при x<0 График функции — гиперболаx k y
 Обратная пропорциональность ( k0, выпукла вниз при x<0 График функции — гипербола
Обратная пропорциональность ( k0, выпукла вниз при x<0 График функции — гипербола
 Квадратичная функция y=kx 2 (k>0) Свойства функции • D(f)=(- ; + ) • Чётная • Убывает на луче (- ; 0 ] , возрастает на луче [0 ; + ) • Ограничена снизу, не ограничена сверху • yнаим =0, yнаиб не существует • Непрерывна • E(f)=[0; + ) • Выпукла вниз 2 xy 22 xy 2 2 1 xy. График функции — парабола 2 xy
Квадратичная функция y=kx 2 (k>0) Свойства функции • D(f)=(- ; + ) • Чётная • Убывает на луче (- ; 0 ] , возрастает на луче [0 ; + ) • Ограничена снизу, не ограничена сверху • yнаим =0, yнаиб не существует • Непрерывна • E(f)=[0; + ) • Выпукла вниз 2 xy 22 xy 2 2 1 xy. График функции — парабола 2 xy
 Квадратичная функция y=kx 2 (k<0) Свойства функции • D(f)=(- ; + ) • Чётная • Убывает на луче [0; + ), возрастает на луче ( — ; 0] • Ограничена сверху, не ограничена снизу • y наиб =0, y наим не существует • Непрерывна • E(f)= (- ; 0] • Выпукла вверх2 xy 2 2 1 xy 22 xy График функции — парабола
Квадратичная функция y=kx 2 (k<0) Свойства функции • D(f)=(- ; + ) • Чётная • Убывает на луче [0; + ), возрастает на луче ( — ; 0] • Ограничена сверху, не ограничена снизу • y наиб =0, y наим не существует • Непрерывна • E(f)= (- ; 0] • Выпукла вверх2 xy 2 2 1 xy 22 xy График функции — парабола
 Квадратичная функция y=ax 2 +bx+c (a>0) Свойства функции 1. D(f)=(- ; + ) 2. Убывает на луче (- ; ] , возрастает на луче [ ; + ) 3. Ограничена снизу, не ограничена сверху 4. y наим = y 0 , y наиб – не существует 5. Непрерывна 6. E(f)=[y 0 ; + ) 7. Выпукла вниза в 2 График функции — парабола
Квадратичная функция y=ax 2 +bx+c (a>0) Свойства функции 1. D(f)=(- ; + ) 2. Убывает на луче (- ; ] , возрастает на луче [ ; + ) 3. Ограничена снизу, не ограничена сверху 4. y наим = y 0 , y наиб – не существует 5. Непрерывна 6. E(f)=[y 0 ; + ) 7. Выпукла вниза в 2 График функции — парабола
 Квадратичная функция y=ax 2 +bx+c (a<0) Свойства функции 1. D(f)=(- ; + ) 2. Возрастает на луче (- ; ] , убывает на луче [ ; + ) 3. Ограничена сверху, не ограничена снизу 4. y наиб = y 0 , y наим – не существует 5. Непрерывна 6. E(f)= (- ; y 0 ] 7. Выпукла вверха в 2 График функции — парабола
Квадратичная функция y=ax 2 +bx+c (a<0) Свойства функции 1. D(f)=(- ; + ) 2. Возрастает на луче (- ; ] , убывает на луче [ ; + ) 3. Ограничена сверху, не ограничена снизу 4. y наиб = y 0 , y наим – не существует 5. Непрерывна 6. E(f)= (- ; y 0 ] 7. Выпукла вверха в 2 График функции — парабола
 Квадратный кореньxy Свойства функции 1. D(f)=[0 ; + ) 2. Не является ни четной, ни нечетной 3. Возрастает на луче [0 ; + ) 4. Ограничена снизу, не ограничена сверху 5. y наим =0, yнаиб не существует 6. Непрерывна 7. E(f)=[0; + ) 8. Выпукла вверх. График функции – ветвь параболы в первой четверти
Квадратный кореньxy Свойства функции 1. D(f)=[0 ; + ) 2. Не является ни четной, ни нечетной 3. Возрастает на луче [0 ; + ) 4. Ограничена снизу, не ограничена сверху 5. y наим =0, yнаиб не существует 6. Непрерывна 7. E(f)=[0; + ) 8. Выпукла вверх. График функции – ветвь параболы в первой четверти
 Модуль y=|x| Свойства функции 1. D(f)=(- ; + ) 2. Чётная 3. Убывает на луче (- ; 0 ] , возрастает на луче [0 ; + ) 4. Ограничена снизу, не ограничена сверху 5. y наим =0, y наиб не существует 6. Непрерывна 7. E(f)=[0; + ) 8. Функцию можно считать выпуклой вниз
Модуль y=|x| Свойства функции 1. D(f)=(- ; + ) 2. Чётная 3. Убывает на луче (- ; 0 ] , возрастает на луче [0 ; + ) 4. Ограничена снизу, не ограничена сверху 5. y наим =0, y наиб не существует 6. Непрерывна 7. E(f)=[0; + ) 8. Функцию можно считать выпуклой вниз
 Функция y=x 2 n+1 (n N) Свойства функции 1. D(f)=(- ; + ) 2. Нечётная 3. Возрастает 4. Не ограничена ни снизу, ни сверху 5. y наим , y наиб не существует 6. Непрерывна 7. E(f )=(- ; + ) 8. Выпукла вверх при x0 График функции — кубическая парабола
Функция y=x 2 n+1 (n N) Свойства функции 1. D(f)=(- ; + ) 2. Нечётная 3. Возрастает 4. Не ограничена ни снизу, ни сверху 5. y наим , y наиб не существует 6. Непрерывна 7. E(f )=(- ; + ) 8. Выпукла вверх при x0 График функции — кубическая парабола
 Функция y=x -(2 n+1) Свойства функции 1. D(f)=(- ; 0) U (0; + ) 2. Нечётная 3. Убывает на открытом луче (- ; 0), и на открытом луче ( 0 ; + ) 4. Не ограничена ни снизу, ни сверху 5. y наим , y наиб не существует 6. Непрерывна на открытом луче (- ; 0), и на открытом луче ( 0 ; + ) 7. E(f )=(- ; 0) U (0; + ) 8. Выпукла вниз при x>0, выпукла вверх при x<0 График функции — гипербола
Функция y=x -(2 n+1) Свойства функции 1. D(f)=(- ; 0) U (0; + ) 2. Нечётная 3. Убывает на открытом луче (- ; 0), и на открытом луче ( 0 ; + ) 4. Не ограничена ни снизу, ни сверху 5. y наим , y наиб не существует 6. Непрерывна на открытом луче (- ; 0), и на открытом луче ( 0 ; + ) 7. E(f )=(- ; 0) U (0; + ) 8. Выпукла вниз при x>0, выпукла вверх при x<0 График функции — гипербола
 Функция y=x -2 n Свойства функции 1. D(f)=(- ; 0) U (0; + ) 2. Чётная 3. Возрастает на открытом луче (- ; 0), и убывает на открытом луче ( 0 ; + ) 4. Ограничена снизу, не ограничена сверху 5. y наим, y наиб не существует 6. Непрерывна на открытом луче (- ; 0), и на открытом луче ( 0 ; + ) 7. E(f )= (0; + ) 8. Выпукла вниз при x0 График функции — гипербола
Функция y=x -2 n Свойства функции 1. D(f)=(- ; 0) U (0; + ) 2. Чётная 3. Возрастает на открытом луче (- ; 0), и убывает на открытом луче ( 0 ; + ) 4. Ограничена снизу, не ограничена сверху 5. y наим, y наиб не существует 6. Непрерывна на открытом луче (- ; 0), и на открытом луче ( 0 ; + ) 7. E(f )= (0; + ) 8. Выпукла вниз при x0 График функции — гипербола
 Функция y=x 2 n (n N) Свойства функции 1. D(f)=(- ; + ) 2. Чётная 3. Убывает на луче (- ; 0 ] , возрастает на луче [0 ; + ) 4. Ограничена снизу, не ограничена сверху 5. y наим =0, yнаиб не существует 6. Непрерывна 7. E(f)=[0; + ) 8. Выпукла вниз. График функции — парабола
Функция y=x 2 n (n N) Свойства функции 1. D(f)=(- ; + ) 2. Чётная 3. Убывает на луче (- ; 0 ] , возрастает на луче [0 ; + ) 4. Ограничена снизу, не ограничена сверху 5. y наим =0, yнаиб не существует 6. Непрерывна 7. E(f)=[0; + ) 8. Выпукла вниз. График функции — парабола
present5.com
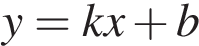 . Установите соответствие между знаками коэффициентов
. Установите соответствие между знаками коэффициентов 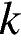 и
и 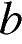 и графиками.
и графиками.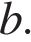
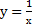 Б)
Б) 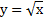 В)
В)