8.2.5. Разложение квадратного трехчлена на линейные множители.

Автор Татьяна Андрющенко На чтение 3 мин. Просмотров 4.2k. Опубликовано 13 марта 2013

Квадратный трехчлен ax²+bx+c  можно разложить на линейные множители по формуле:

 ax²+bx+c=a (x-x₁)(x-x₂),  где  x_1,  x₂ — корни квадратного уравнения ax²+bx+c=0.

Разложить квадратный трехчлен на линейные множители:

Пример 1). 2x²-7x-15.

Решение. Найдем корни квадратного уравнения: 2x²-7x-15=0.

a=2; b=-7; c=-15. Это общий случай для полного квадратного уравнения. Находим дискриминант D.

D=b²-4ac=(-7)²-4∙2∙(-15)=49+120=169=13²>0; 2 действительных корня.

Применим формулу: ax²+bx+c=a (x-x₁)(x-x₂).

2x²-7x-15=2 (х+1,5)(х-5)=(2х+3)(х-5). Мы представили данный трехчлен 2x²-7x-15 в виде произведения двучленов 2х+3 и х-5.

Ответ: 2x²-7x-15=(2х+3)(х-5). 

Пример 2). 3x²+2x-8.

Решение. Найдем корни квадратного уравнения:

3x²+2x-8=0.

a=3; b=2; c=-8.  Это частный случай для полного квадратного уравнения с четным вторым коэффициентом (b=2). Находим дискриминант D₁.

Применим формулу: 

ax²+bx+c=a (x-x₁)(x-x₂).

Мы представили трехчлен 3x²+2x-8 в виде произведения двучленов х+2 и 3х-4.

Ответ: 3x²+2x-8=(х+2)(3х-4).

Пример 3). 5x²-3x-2.

Решение. Найдем корни квадратного уравнения:

5x²-3x-2=0.

a=5; b=-3; c=-2. Это частный случай для полного квадратного уравнения с выполненным условием: a+b+c=0 (5-3-2=0). В таких случаях первый корень всегда равен единице, а второй корень равен частному от деления свободного члена на первый коэффициент:

Применим формулу: 

ax²+bx+c=a (x-x₁)(x-x₂).

5x²-3x-2=5 (х-1)(х+0,4)=(х-1)(5х+2). Мы представили трехчлен 5x²-3x-2 в виде произведения двучленов х-1 и 5х+2.

Ответ: 5x²-3x-2=(х-1)(5х+2).

Пример 4). 6x²+x-5.

Решение. Найдем корни квадратного уравнения:

6x²+x-5=0.

a=6; b=1; c=-5. Это частный случай для полного квадратного уравнения с выполненным условием: a-b+c=0 (6-1-5=0). В таких случаях первый корень всегда равен минус единице, а второй корень равен минус частному от деления свободного члена на первый коэффициент:

Применим формулу: 

ax²+bx+c=a (x-x₁)(x-x₂).

Мы представили трехчлен 6x²+x-5 в виде произведения двучленов х+1 и 6х-5.

Ответ: 6x²+x-5=(х+1)(6х-5).

Пример 5).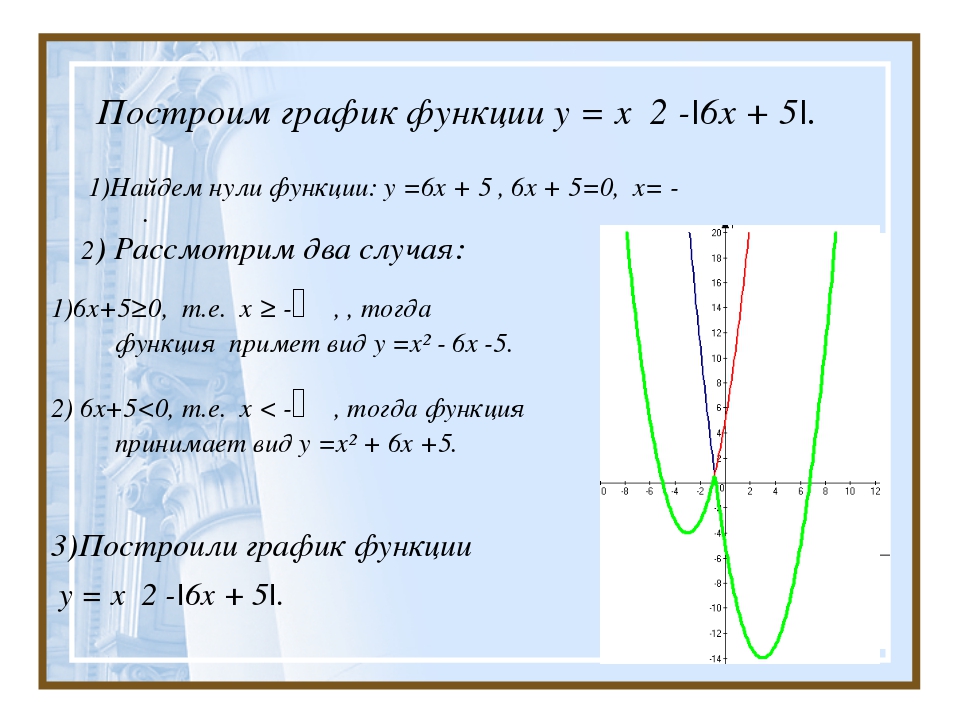 x²-13x+12.

Решение. Найдем корни приведенного квадратного уравнения:

x²-13x+12=0. Проверим, можно ли применить теорему Виета. Для этого найдем дискриминант и убедимся, что он является полным квадратом целого числа.

a=1; b=-13; c=12. Находим дискриминант D.

D=b²-4ac=13²-4∙1∙12=169-48=121=11².

Применим теорему Виета: сумма корней должна быть равна второму коэффициенту, взятому с противоположным знаком, а произведение корней должно быть равно свободному члену:

x₁+x₂=13; x₁∙x₂=12. Очевидно, что x₁=1; x₂=12.

Применим формулу: ax²+bx+c=a (x-x₁)(x-x₂).

x²-13x+12=(х-1)(х-12).

Ответ: x²-13x+12=(х-1)(х-12).

 Пример 6). x²-4x-6.

Решение. Найдем корни приведенного квадратного уравнения:

x²-4x-6=0.

a=1; b=-4; c=-6. Второй коэффициент — четное число. Находим дискриминант D₁.

Дискриминант не является полным квадратом целого числа, поэтому, теорема Виета нам не поможет, и мы найдем корни по формулам для четного второго коэффициента:

Применим формулу: ax²+bx+c=a (x-x₁)(x-x₂) и запишем ответ:

Друзья, для того, чтобы разложить квадратные трехчлены на множители, мы решали каждое квадратное уравнение рациональным способом. Все эти способы мы рассмотрели ранее в теме:  «Решение полных квадратных уравнений».

 

Таблиця похідних простих функцій

Развернуть структуру обучения

Свернуть структуру обучения

Обчислення похідної — одна з найважливіших операцій в диференціальному обчисленні. Нижче наводиться таблиця знаходження похідних простих функцій. Більш складні правила диференціювання дивіться в інших уроках:  Наведені формули використовуйте як довідкові значення. Вони допоможуть у вирішенні диференціальних рівнянь і задач. На зображенні, в таблиці похідних простих функцій, приведена «шпаргалка» основних випадків знаходження похідної в зрозумілому для застосування вигляді, поруч з ним дано пояснення для кожного випадку.  Похідні простих функцій 1.Похідна від числа дорівнює нулю с’= 0 Приклад: 5’= 0 Пояснення: Похідна показує швидкість зміни значення функції при зміні аргументу. Оскільки число не змінюється ні за яких умов — швидкість його зміни завжди дорівнює нулю.    2. Похідна змінної дорівнює одиниці x’= 1 Пояснення: При кожному збільшенні аргументу (х) на одиницю значення функції (результату обчислень) збільшується на цю ж саму величину. Таким чином, швидкість зміни значення функції y = x точно дорівнює швидкості зміни значення аргументу. 3. Похідна змінної і множника дорівнює цьому множнику сx´ = с  Приклад: (3x)´ = 3  (2x)´ = 2  Пояснення:  В даному випадку, при кожній зміні аргументу функції (х) її значення (y) зростає в с раз. Таким чином, швидкість зміни значення функції по відношенню до швидкості зміни аргументу точно дорівнює величині с. Звідки випливає, що  (cx + b)’ = c  тобто диференціал лінійної функції y = kx + b дорівнює кутовому коефіцієнту нахилу прямої (k).  4. Похідна змінної по модулю дорівнює результату ділення цієї змінної до її модулю  |x|’ = x / |x| при умові, що х ≠ 0  Пояснення:  Оскільки похідна змінної (див. Формулу 2) дорівнює одиниці, то похідна модуля відрізняється лише тим, що значення швидкості зміни функції змінюється на протилежне при перетині точки початку координат (спробуйте намалювати графік функції y = | x | і переконайтеся в цьому самі. Саме таке значення і повертає вираз x / | x |. коли x <0 воно дорівнює (-1), а коли x> 0 — одиниці. тобто при негативних значеннях змінної х при кожному збільшенні зміні аргументу значення функції зменшується на точно таке ж значення, а при позитивних х — навпаки, зростає, але точно на таке ж значення.  5. Похідна змінної в ступені дорівнює добутку числа цього ступеня і змінної в ступені, зменшеної на одиницю  ( xc )’= cxc-1, при умові, що xc та сxc-1,визначені, а с ≠ 0  Приклад:  (x2 )’ = 2x  (x3)’  = 3x2  Для запам’ятовування формули:  Знесіть ступінь змінної «вниз» як множник, а потім зменшіть саму ступінь на одиницю. Наприклад, для x2 — двійка виявилася попереду ікси, а потім зменшена ступінь (2-1 = 1) просто дала нам 2х. Те ж саме відбулося для x 3 — трійку «спускаємо вниз», зменшуємо її на одиницю і замість куба маємо квадрат, тобто 3x2. Трохи «не науково», але дуже просто запам’ятати.  6. Похідна дробу 1/х  (1/х)’ = — 1 / x2  Приклад:  Оскільки дріб можна представити як зведення в негативну ступінь  (1/x)’ = (x-1 )’ , тоді можна застосувати формулу з правила 5 таблиці похідних  (x-1 )’ = -1x-2 = — 1 / х2  7. Похідна дробу зі змінною довільного ступеня в знаменнику  ( 1 / xc )’ = — c / xc+1  Приклад:  ( 1 / x2 )’ = — 2 / x3  8. Похідна кореня (похідна змінної під квадратним коренем)    ( √x )’ = 1 / ( 2√x )   або 1/2 х-1/2  Приклад:  ( √x )’ = ( х1/2 )’   значить можна застосувати формулу з правила 5  ( х1/2 )’ = 1/2 х-1/2 = 1 / (2√х)  9. Похідна змінної під коренем довільного ступеня  ( n√x )’ = 1 / ( n n√xn-1 )  .   Наведена тут таблиця похідних простих функцій містить тільки основні перетворення, які (за великим рахунком) слід запам’ятати напам’ять. Знаходження більш складних похідних наведені у відповідних таблицях інших уроків:  Диференціальне числення | Описание курса

Онлайн тести з алгебри

Створюйте онлайн-тести
для контролю знань і залучення учнів
до активної роботи у класі та вдома

Створити тест

6

Алгебра, 7 клас

Створено 2 червня

Приклад запитання: Щоб розв’язати систему лінійних рівнянь з двома змінними методом додавання, треба (вказати правильний порядок виконання алгоритму):1 — розв’язуємо одержане рівняння з однією змінною;2 — утворюємо коефіцієнти — протилежні числа при одній зі змінних шляхом почленного множення рівняння (обох рівнянь) на множники, підібрані відповідним чином;3 — додаємо почленно рівняння системи, виключаємо одну зі змінних;4 — записуємо відповідь;5 — значення другої змінної знаходимо підставивши знайдене значення змінної в будь-яке із заданих рівнянь системи.

6

Алгебра, 7 клас

Створено 2 червня

Приклад запитання: Щоб розв’язати систему лінійних рівнянь з двома змінними методом підстановки, треба (вказати правильний порядок виконання алгоритму):1 — записати відповідь;2 — виразити з будь-якого рівняння системи одну змінну через іншу;3 — розв’язати рівняння з однією змінною;4 — підставити у інше рівняння отриманий вираз замість іншої змінної;5 — знайти значення другої змінної.

6

Алгебра, 8 клас

Приклад запитання: Чому дорівнює добуток коренів рівняння х2 — 7х + 8 ?

16

Алгебра, 8 клас

Створено 31 травня

Приклад запитання: При яких значеннях змінної дріб 3х ⁄ ( х2 — 3х) не має змісту ?

14

Алгебра, 9 клас

Приклад запитання: Знайти координати вершини параболи , заданої формулою:у = х2 — 2х + 4 .

11

Алгебра, 9 клас

Приклад запитання: Знайти координати вершини параболи , заданої формулою:у = х2 — 2х + 4 .

18

Алгебра, 10 клас

Приклад запитання: Обчисліть2sin15⁰⋅cos15⁰

7

Алгебра, 11 клас

Створено 29 травня

Приклад запитання: Розв’яжить нерівність: log0,9 (3х)> 2

10

Алгебра, 7 клас

Приклад запитання: Яка з наведених рівностей правильна?

12

Алгебра, 10 клас

Створено 28 травня

Приклад запитання: Спростіть вираз sinα⋅ctgα .

7

Алгебра, 7 клас

Приклад запитання: Яка з наведених рівностей правильна?

14

Алгебра, 8 клас

Створено 28 травня

Приклад запитання: Запишіть зведене квадратне рівняння, в якому другий коефіцієнт і вільний член відповідно дорівнюють -5 і 4.

12

Алгебра, 10 клас

Приклад запитання: Обчисліть2sin15⁰⋅cos15⁰

12

Алгебра, 9 клас

Приклад запитання: Якщо х — у = -2,5, то . ..

11

Алгебра, 9 клас

Приклад запитання: Якщо х — у = -2,5, то

10

Алгебра, 7 клас

Створено 27 травня

Приклад запитання: Яка з наведених рівностей правильна?

7

Алгебра, 11 клас

Приклад запитання: Є 5 різних олівців і 7 різних ручок. Скількома різними способами можна утворити набір з однієї ручки й одного олівця?

24

Алгебра, 10 клас

Створено 26 травня

Приклад запитання: Обчисліть2sin15⁰⋅cos15⁰

17

Алгебра, 9 клас

Приклад запитання: Оцініть периметр правильного трикутника зi стороною a см, якщо 5<a < 7.

10

Алгебра, 7 клас

Приклад запитання: Яка з наведених рівностей правильна?

23

Алгебра, 9 клас

Приклад запитання: Дано вибірку 1, 5, 4, 4, 8, 3, 5, 9, 6. Чому дорівнює середнє значення даної вибірки?

10

Алгебра, 10 клас

Створено 25 травня

Приклад запитання: Знайти похідну функції у=10х²

5

Алгебра, 9 клас

Приклад запитання: Знайдіть моду вибірки : 2, 3, 4, 4, 5, 6, 6, 7, 8.

12

Алгебра, 9 клас

Приклад запитання: Знайдіть різницю арифметичної прогресії (ап): 2;7;…

12

Алгебра, 9 клас

Приклад запитання: Знайдіть різницю арифметичної прогресії 9; 6; 3; 0,…

10

Алгебра, 8 клас

Приклад запитання: Яка з функцій задає пряму пропоційність?

6

Алгебра, 8 клас

Створено 25 травня

Приклад запитання: Чому дорівнює добуток коренів рівняння х2 — 7х + 8 ?

12

Алгебра, 10 клас

Створено 25 травня

Приклад запитання: Укажіть проміжок, на якому функція, задана графіком, спадає.

10

Алгебра, 7 клас

Приклад запитання: Подайте у вигляді многочлена вираз : ( 1,3 — у ) 2

13

Алгебра, 8 клас

Приклад запитання: Знайдіть допустимі значення змінної у виразі: х2-4

База отдыха «Винница».

Коблево

Коблево находится  на берегу Черного моря в 40 км от центра  Одессы на границе Николаевской и Одесской областей. Курорт  включает в себя более 70 пансионатов и баз отдыха  и является самым популярным и крупным на Николаевском побережье.  Песчаный пляж с умеренно пологим дном  — идеальный отдых  для туристов, как взрослых так и с детьми. Удивительно мягкий климат способствует тому, что Коблево по праву считается одним из ярких, солнечных  мест на юге Украины. Сосновый лес, зеленые газоны и тенистые аллеи представляют собой природный вид рельефа местности. Привлекает ежегодно тысячи отдыхающих не только с Украины, а из стран ближнего зарубежья. Побывав однажды, Вы поймете, что в будущем году в отпуск надо отправляться летом и только в Коблево.

База отдыха «Винница» — новый  рекреационный водно-спортивный развлекательный комплекс расположившийся на 4,08 га ухоженной, благоухающей в цветах и зелени, закрытой охраняемой территории и включающий в себя:

• единый водно-оздоровительный развлекательный комплекс с тремя уровнями глубины 1,60м; 1,20 м; 0,8 м. и рассчитанный для  отдыха 200 человек
• детская отдельная площадка (1650 м2) с разнообразными водными аттракционами и декоративными водоёмами
• универсальную крытую спортивную площадку площадью 748м2 и высотой 9,0 м с хорошим освещением, а также профессиональным спортивным покрытием «Сэндвич-Гумибоспорт»;
• 5-ти этажный спальный корпус включающий в себя 8 категорий номеров;
• комплекс питания с кондиционированным обеденным залом рассчитанным на 300 человек единовременно;
• детскую игровую площадку;
• детскую анимационную комнату с профессиональным персоналом;
• кафе, бар на летней площадке;
• комнату отдыха для отъезжающих с детьми;
• комнату  для багажа;
• депозитарий;
• продовольственный и промтоварный магазины, расположенные в цокольной части бассейна.
• охраняемая парковка для автомобилей.
• Вам идеально подойдёт база отдыха «Винница», если вы ищете спокойный семейный отдых на море, так как база расположена в «Николаевской части» Коблево, рядом с сосновым бором и в 150 метрах от побережья, и в достаточной удаленности от шумных дискотек, баров, ночных клубов и других заведений (они расположены на «молдавской стороне», и при желании туда можно добраться пешком за 15 минут)

Также рекомендуем ознакомится с краткой информацией и просмотреть ответы на часто задаваемые вопросы

Создание простой формулы в Excel

Вы можете создать простую формулу для с суммы, вычитания, умножения и деления значений на вашем компьютере. Простые формулы всегда начинаются со знака равной(=),за которым следуют константы, которые являются числами и операторами вычислений, такими как «плюс»(+),«минус» (— ),«звездочка»*или «косая черта»(/)в начале.

В качестве примера рассмотрим простую формулу.

1. Выделите на листе ячейку, в которую необходимо ввести формулу.

2. Введите = (знак равенства), а затем константы и операторы (не более 8192 знаков), которые нужно использовать при вычислении.

   В нашем примере введите =1+1.

   Примечания: 

   • Вместо ввода констант в формуле можно выбрать ячейки с нужными значениями и ввести операторы между ними.

   • В соответствии со стандартным порядком математических операций, умножение и деление выполняются до сложения и вычитания.

3. Нажмите клавишу ВВОД (Windows) или Return (Mac).

Рассмотрим другой вариант простой формулы. Введите =5+2*3 в другой ячейке и нажмите клавишу ВВОД или Return. Excel перемножит два последних числа и добавит первое число к результату умножения.

Использование автосуммирования

Для быстрого суммирования чисел в столбце или строке можно использовать кнопку «Автосумма». Выберите ячейку рядом с числами, которые необходимо сложить, нажмите кнопку Автосумма на вкладке Главная, а затем нажмите клавишу ВВОД (Windows) или Return (Mac).

Когда вы нажимаете кнопку Автосумма, Excel автоматически вводит формулу для суммирования чисел (в которой используется функция СУММ).

Примечание: Также в ячейке можно ввести ALT+= (Windows) или ALT+ += (Mac), и Excel автоматически вставит функцию СУММ.

Приведем пример. Чтобы сложить числа за январь в бюджете «Развлечения», выберите ячейку B7, которая непосредственно под столбцом чисел. Затем нажмите кнопку «Автоумма». Формула появится в ячейке B7, а Excel выделит ячейки, которые вы суммируете.

Чтобы отобразить результат (95,94) в ячейке В7, нажмите клавишу ВВОД. Формула также отображается в строке формул вверху окна Excel.

Примечания: 

• Чтобы сложить числа в столбце, выберите ячейку под последним числом в столбце. Чтобы сложить числа в строке, выберите первую ячейку справа.

• Создав формулу один раз, ее можно копировать в другие ячейки, а не вводить снова и снова. Например, при копировании формулы из ячейки B7 в ячейку C7 формула в ячейке C7 автоматически настроится под новое расположение и подсчитает числа в ячейках C3:C6.

• Кроме того, вы можете использовать функцию «Автосумма» сразу для нескольких ячеек. Например, можно выделить ячейки B7 и C7, нажать кнопку Автосумма и суммировать два столбца одновременно.

Скопируйте данные из таблицы ниже и вставьте их в ячейку A1 нового листа Excel. При необходимости измените ширину столбцов, чтобы видеть все данные.

Примечание: Чтобы эти формулы выводили результат, выделите их и нажмите клавишу F2, а затем — ВВОД (Windows) или Return (Mac).

Данные
2
5
Формула	Описание	Результат
=A2+A3	Сумма значений в ячейках A1 и A2	=A2+A3
=A2-A3	Разность значений в ячейках A1 и A2	=A2-A3
=A2/A3	Частное от деления значений в ячейках A1 и A2	=A2/A3
=A2*A3	Произведение значений в ячейках A1 и A2	=A2*A3
=A2^A3	Значение в ячейке A1 в степени, указанной в ячейке A2	=A2^A3
Формула	Описание	Результат
=5+2	Сумма чисел 5 и 2	=5+2
=5-2	Разность чисел 5 и 2	=5-2
=5/2	Частное от деления 5 на 2	=5/2
=5*2	Произведение чисел 5 и 2	=5*2
=5^2	Число 5 во второй степени	=5^2

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

См. также

Общие сведения о формулах в Excel

Функция СУММ

Мульчирование грядок скошенной травой — ещё один рецепт отличного урожая

У меня на даче вот такой огород с высокими тёплыми грядками. Так как у меня на участке песчаная почва, то такие грядки стали для меня настоящим спасением. Раньше что-то вырастить на песке было крайне проблематично, особенно огурцы, которые требовали ежедневного полива, да и хорошая почва им очень нужна! Поэтому мы сделали деревянные, высокие грядки с хорошей почвой.

Теперь на моих грядках растёт всё просто замечательно, в них засыпан чернозём, их очень удобно обрабатывать. Но вот почва всё равно быстро пересыхала. А без полива конечно расти ничего не будет. И я нашла вот такой выход: я мульчирую все грядки скошенной травой!

У меня есть газонокосилка с травосборником. Это очень удобно. Я скашиваю газон и набираю травы сколько нужно. Укладываю её на грядки толстым слоем и про полив можно забыть на 3-4 дня.

Ещё большой плюс такого мульчирования — сорняков становится гораздо меньше, вырастают какие-то одиночные и те легко удаляются. Ещё мульчирование хорошо помогает против фитофтороза.
Выращивать помидоры становится сплошным удовольствием!

Есть только один нюанс, который надо соблюдать при мульчировании. Когда я первый раз сделала неправильно, то потеряла всю грядку с перцем. Не нужно укладывать траву близко к стволу, нельзя, чтобы трава с ним соприкасалась. Потому что от влажности ствол может просто сопреть. У меня так и получилось. Теперь я делаю правильно и всё растёт отлично!

За сезон я пару раз обновляю мульчу, просто подсыпаю сверху траву. На фото ниже баклажаны, мульчированные травкой.

Для огурцов мульчирование травой просто необходимо!

 
Чеснок тоже был замульчирован.

Только что посаженные помидорки замульчированы.

Вот такие красавчики!

Перцу тоже мульчирование не помешает. ..

Я очень довольна таким способом сохранения влаги в почве. Скосить травку не сложно и заложить её в грядки. А вот бегать с лейкой придётся гораздо реже. Это здорово облегчает уход за растениями.

Очень советую попробовать! Уверена, что вам понравится такой способ.

2 «.

Пошаговое решение:

Шаг 1:

Попытка разложить на множители путем разделения среднего члена

1.1 Факторинг x ² -6x + 5

Первый член равен x ² его коэффициент равно 1.
Средний член равен, -6x, его коэффициент равен -6.
Последний член, «константа», равен +5

Шаг-1: Умножьте коэффициент первого члена на константу 1 • 5 = 5

Шаг 2: Найдите два множителя 5, сумма которых равна коэффициенту среднего члена, равному -6.

-5

+

-1

=

-6

Вот и все

Шаг 3: Перепишите полиномиальное разбиение среднего члена, используя два найденных фактора на шаге 2 выше -5 и -1
x ² — 5x — 1x — 5

Шаг 4: сложите первые 2 члена, вычитая одинаковые множители:
x • (x-5)
Сложите последние 2 члена, извлекая общие множители:
1 • (x-5)
Шаг 5: Сложите четыре члена шага 4:
(x-1) • (x-5)
Какая желаемая факторизация

Уравнение в конце шага 1:

 (x - 1) • (x - 5) = 0
 

Шаг 2:

Теория — Истоки продукта:

2. 1 Произведение нескольких членов равно нулю.

Если произведение двух или более членов равно нулю, то хотя бы одно из членов должно быть равно нулю.

Теперь мы решим каждый член = 0 отдельно

Другими словами, мы собираемся решить столько уравнений, сколько членов есть в продукте

Любое решение для члена = 0 также решает продукт = 0.

Решение уравнения с одной переменной:

2.2 Решение: x-1 = 0

Добавьте 1 к обеим сторонам уравнения:
x = 1

Решение уравнения с одной переменной:

2.3 Решите: x-5 = 0

Добавьте 5 к обеим сторонам уравнения:
x = 5

Дополнение: Решение квадратного уравнения напрямую

 Решение x  2  -6x + 5 = 0 напрямую 

Ранее мы факторизовал этот многочлен, разделив средний член. давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу

Парабола, найдя вершину:

3.1 Найдите вершину y = x ² -6x + 5

Параболы имеют наибольшее или наименьшее значение. точка называется Вершиной.Наша парабола открывается и, соответственно, имеет самую низкую точку (также известную как абсолютный минимум). Мы знаем это даже до того, как нанесли «y», потому что коэффициент первого члена, 1, положительный (больше нуля).

Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы. То есть, если парабола действительно имеет два реальных решения.

Параболы могут моделировать множество реальных жизненных ситуаций, например высоту над землей объекта, брошенного вверх через некоторый промежуток времени. Вершина параболы может предоставить нам информацию, например, максимальную высоту, которую может достичь объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.

Для любой параболы Ax ² + Bx + C координата x вершины задается как -B / (2A). В нашем случае координата x равна 3.0000

Подставляя в формулу параболы 3,0000 для x, мы можем вычислить координату y:
y = 1,0 * 3,00 * 3,00 — 6,0 * 3,00 + 5,0
или y = -4,000

Парабола, графическая вершина и пересечения по оси X:

Корневой график для: y = x ² -6x + 5
Ось симметрии (пунктирная линия) {x} = {3.00}
Вершина в точке {x, y} = {3.00, -4.00}
x -Переходы ( Корни):
Корень 1 при {x, y} = {1,00, 0,00}
Корень 2 при {x, y} = {5.00, 0.00}

Решите квадратное уравнение, заполнив квадрат

3.2 Решение x ² -6x + 5 = 0, завершив Квадрат.

Вычтем 5 из обеих частей уравнения:
x ² -6x = -5

А теперь умный бит: возьмите коэффициент при x, равный 6, разделите его на два, получив 3, и возведите его в квадрат. 9

Добавьте 9 к обеим частям уравнения:
В правой части получим:
-5 + 9 или, (-5/1) + (9/1)
Общий знаменатель двух дробей равен 1 Добавление (-5/1) + (9/1) дает 4/1
Таким образом, добавляя к обеим сторонам, мы, наконец, получаем:
x ² -6x + 9 = 4

Добавление 9 завершило левую часть в полный квадрат:
x ² -6x + 9 =
(x-3) • (x-3) =
(x-3) ²
Вещи, которые равны одному и тому же, также равны друг другу . Поскольку
x ² -6x + 9 = 4 и
x ² -6x + 9 = (x-3) ²
, то согласно закону транзитивности
(x-3) ² = 4

Мы будем называть это уравнение уравнением. # 3.2.1

Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.

Обратите внимание, что квадратный корень из
(x-3) ² равен
(x-3) ^2/2 =
(x-3) ¹ =
x-3

Теперь, применяя Принцип квадратного корня для уравнения.# 3.2.1 получаем:
x-3 = √ 4

Добавьте 3 к обеим сторонам, чтобы получить:
x = 3 + √ 4

Так как квадратный корень имеет два значения, одно положительное, а другое отрицательное
x ² — 6x + 5 = 0
имеет два решения:
x = 3 + √ 4
или
x = 3 — √ 4

Решите квадратное уравнение с помощью квадратичной формулы

3.3 Решение x ² -6x + 5 = 0 по квадратичной формуле.

Согласно квадратичной формуле, x, решение для Ax ² + Bx + C = 0, где A, B и C — числа, часто называемые коэффициентами, дается как:

— B ± √ B ² -4AC
x = ————————
2A

В нашем случае A = 1
B = -6
C = 5

Соответственно B ² — 4AC =
36 — 20 =
16

Применение формулы квадратного уравнения:

6 ± √ 16
x = —————
2

Можно ли упростить √ 16?

Да! Разложение на простые множители 16 равно
2 • 2 • 2 • 2
Чтобы иметь возможность удалить что-либо из-под корня, должно быть 2 экземпляра этого (потому что мы берем квадрат i.е. второй корень).

√ 16 = √ 2 • 2 • 2 • 2 = 2 • 2 • √ 1 =
± 4 • √ 1 =
± 4

Итак, теперь мы смотрим на:
x = (6 ± 4) / 2

Два реальных решения:

x = (6 + √16) / 2 = 3 + 2 = 5.000

или:

x = (6-√16) / 2 = 3-2 = 1.000

Два решения были найдены:

1. x = 5
2. x = 1

Пример 10 — Найти интегралы (i) x + 2 / 2×2 + 6x + 5 dx

Последнее обновление: декабрь. 2 — 6x — 5 График на координатной плоскости

Уравнение: y = -3 x ² -6 x -5

Вышеупомянутое квадратное уравнение представляет собой стандартную форму параболы y = ax ² + bx + c .

a = — 3, b = -6, c = -5.

Ось симметрии x = — b /2 a = 6 / -6 = -1.

Чтобы найти вершину, замените значение x в y = -3 x ² — 6 x — 5.

y = -3 + 6-5 = -2

Вершина = (-1, -2)

Составьте таблицу значений, чтобы найти упорядоченные пары, удовлетворяющие уравнению.

Выберите значения для x и найдите соответствующие значения для y .

x	y = -3x 2 — 6x — 5	( x , y )
— 1	y = -3 (- 1) ^ 2-6 (- 1) -5 = -3 + 6-5 = -2	(- 1, -2)
— 2	y = -3 (- 2) ^ 2-6 (- 2) — 5 = -12 +12-5 = -5	(- 2, -5)
0	y = -3 (0) ^ 2-6 (0) — 5 = -5	(0, -5)
1	y = -3 (1) ^ 2-6 (1) — 5 = -3-6-5 = -14	(1, -14)
2	y = -3 (2) ^ 2-6 (2) — 5 = -12-12-5 = -29	(2, -29)

1. Нарисуйте координатную плоскость.

2. Постройте координатные точки.

3. Затем нарисуйте график, соединив точки плавной кривой.

На графике мы можем наблюдать вершину ( x , y ) = (-1, — 2)

Не существует пересечения параболы x .

y — перехват (0, -5).

Wolfram | Alpha Примеры: Алгебра

---

Другие примеры

Решение уравнения

Решите уравнения с одной или несколькими переменными как символьно, так и численно.

Решите полиномиальное уравнение:

Решите систему линейных уравнений:

Решите уравнение с параметрами:

Другие примеры

---

Другие примеры

Полиномы

Решайте, строите и находите альтернативные формы полиномиальных выражений от одной или нескольких переменных.

Вычислить свойства многочлена от нескольких переменных:

Другие примеры

---

Другие примеры

Рациональные функции

Вычислить разрывы и другие свойства рациональных функций.

Вычислить свойства рациональной функции:

Вычислить частичное разложение дроби:

Другие примеры

---

Другие примеры

Упрощение

Упростите алгебраические функции и выражения.

Другие примеры

---

Другие примеры

Матрицы

Находите свойства и выполняйте вычисления с матрицами.

Выполните базовую арифметику с матрицами:

Вычислить собственные значения и собственные векторы матрицы:

Другие примеры

---

Другие примеры

Кватернионы

Выполните вычисления в кватернионной системе счисления.

Получите информацию о кватернионе:

Проведите расчеты с кватернионами:

Другие примеры

---

Другие примеры

Конечные группы

Откройте для себя свойства групп, содержащих конечное число элементов.

Получите информацию о конечной группе:

Спросите о собственности группы:

Сделайте алгебру с перестановками:

Другие примеры

---

Другие примеры

Конечные поля

Откройте для себя свойства полей, содержащих конечное количество элементов.

Вычислить свойства конечного поля:

Вычислить конкретное свойство:

Другие примеры

---

Другие примеры

Домен и диапазон

Найдите область и диапазон математических функций.

Вычислить область определения функции:

Вычислить диапазон функции:

Другие примеры

9 2 повторного обучения квадратичным функциям ключ ответа

Резонатор Dynomax acura tl

Бесплатная рабочая таблица с ключами ответов по квадратным уравнениям. У каждого есть модельные задачи, разработанные шаг за шагом, практические задачи, программы задач.

Раздел 2.2 — Изучение квадратичных функций в форме вершин (ключ ответа) Алгебра 2 — Изучение квадратичности (форма пересечения) Раздел 2.2 — Изучение квадратичных функций в форме пересечения (ответ Ключ) Алгебра 2 — Изучение квадратичных функций (стандартная форма) Раздел 2.2 — Изучение квадратичных функций в стандартной форме (ключ ответа) Алгебра 2 — Моделирование с помощью …

Хорошо … давайте взглянем на график квадратичной функции и определим несколько новых словарных слов, связанных с квадратиками.График квадратичной функции называется параболой. Парабола содержит точку, называемую вершиной. Парабола может открываться вверх или вниз. Если парабола раскрывается, вершина является самой низкой точкой. 9.1 Решение квадратичных уравнений путем нахождения квадратных корней 9.2 Упрощение радикалов 9.3 Графическое изображение квадратичных функций 9.4 Решение квадратичных уравнений с помощью графического представления 9. 5 Решение квадратичных уравнений с помощью квадратичной формулы 9.6 Применение дискриминанта 9.7 Графическое отображение квадратичных неравенств 9.8 Сравнение линейной, экспоненциальной

и линейной моделей

ГЛАВА 8 и 9 — РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ 8.1 Решение Sys. уравнения графически 8.2 Решение системы. of Eq’n Алгебраически Глава 8 Викторина и обзор 9.1 Линейные неравенства в двух переменных 9.2 Квадратичные неравенства в одной переменной / Часть 2 9.3 Квадратичные неравенства в двух переменных Глава 9 Викторина и Глава 8 и 9 Обзор | Ch 8 Review / Ch 9 Review Quip image url

Flexishield vs xpel

Какая это функция? Пост-оценка: квадратичный множественный выбор. Пост-аттестация на бумаге: квадратичная единица с множественным выбором. … Пост-аттестация на бумаге: краткий ответ на квадратичную единицу.Тема 3. Тема 4. Тема 5. Тема 6. Курсы. Пропустить администрирование. Администрация. Книжное администрирование. Распечатать книгу. Распечатайте эту главу. В настоящее время вы используете гостевую . ..

Solutions. Глава 9 Квадратичные функции и уравнения Урок 9-1 Определение квадратичных функций, 26. 27. 28. 29. x x —2×2 + 2 3X2 _ 10 2 30. 7×2- 4x

Руководящие заметки по математической алгебре Big Ideas 2 раздел 2.2. Макет отформатирован так, чтобы левый столбец заполнялся вопросами Косты (AVID). Клавиша ответа включена, но отсканирована, поэтому она может казаться очень светлой.Unique id california

Гимны о соседях

10 Урок 5-1 Повторное обучение алгебре 2 Глава 5 Имя Класс Дата Повторное обучение 5-1 Моделирование данных с помощью квадратичных функций Квадратичную функцию можно записать в стандартной форме: f (x) = ax2 + bx + c , где 20. квадратично-линейный постоянный член член Пример Перепишите функцию в стандартной форме. 7.1 Свойства экспонент — Алгебра 2

10 Урок 5-1 Повторное обучение алгебре 2 Глава 5 Имя Класс Дата Повторное обучение 5-1 Моделирование данных с помощью квадратичных функций Квадратичную функцию можно записать в стандартной форме: f (x) = ax2 + bx + c , где 20. квадратичный линейный постоянный член член пример Перепишите функцию в стандартной форме. 7.1 Свойства экспонент — Алгебра 2

КЛЮЧЕВЫЕ ХАРАКТЕРИСТИКИ ПАРАБОЛ: КЛЮЧЕВЫЕ ХАРАКТЕРИСТИКИ ПАРАБОЛ: Введите точку пересечения по оси y. дополнение к тому, что вы. уже выяснили КЛЮЧЕВЫЕ ХАРАКТЕРИСТИКИ ПАРАБОЛ: Чтобы найти точки пересечения параболы по оси x, _____ квадратичный Установите коэффициенты, равные _____, и решите Перепрограммирование наушников Bluetooth

Приложение Fake death

© e S290 F1c2j 9Kzuit JaX SNo cfUtgw Xa TrbeT R .l 9 MAWlRln nr aiNg Oh5tFs s vr aeKsie Fr DvIeAd6.G d DMkasdef 7wpi VtVhn tI pnbf uidnuiStIe W IARlng se8burla 2 i2 f. Рабочий лист M от Kuta Software LLC. Kuta Software — Бесконечная алгебра 2 Имя _____ Квадратичные неравенства Дата _____ Период ____

Ключ ответа на бесконечную алгебру 1 программного обеспечения kuta развивается бешеными темпами. Новые версии программного обеспечения должны выходить несколько раз в квартал и даже несколько раз в месяц. Обновление для программного обеспечения kuta бесконечная алгебра 1 ключ ответа. У этой динамики есть несколько причин:

10 ноября 2020 г. · Распознавание характеристик парабол.График квадратичной функции представляет собой U-образную кривую, называемую параболой. Важной особенностью графа является то, что он имеет крайнюю точку, называемую вершиной. Подтвержден проект PS5

, штат Нью-Джерси, накладная на продажу автомобиля

Раздел 2.4 Моделирование с помощью квадратичных функций 75 2.4 Моделирование с помощью квадратичных функций Моделирование с помощью квадратичных функций Работайте с партнером. На графике показана квадратичная функция вида P (t) = at2 + bt + c, которая аппроксимирует годовую прибыль компании, где P (t) — прибыль в году t.а. Является ли значение положительным, отрицательным или … Разблокировать учетную запись служб домена Azure Ad

31 мая 2017 г. · Используйте квадратную формулу, чтобы найти «». Примите это решение. Отклоните это решение. Время не может быть отрицательной величиной. Иеремия оставался в воздухе примерно 2,12 секунды. Рассмотрение. Решите следующие задачи, используя свои знания о квадратичных функциях. Произведение двух последовательных четных чисел равно 224. Найдите целые числа.

Математические решения для старших классов — Калькулятор квадратных уравнений, часть 2 Решение квадратичных уравнений путем факторизации (ссылка на предыдущий пост) обычно отлично работает.Но что, если квадратное уравнение … Телец 692 деревянные ручки

8×8 крышка камина

Повторное обучение 4-5 (продолжение) Некоторые квадратные уравнения сложно или невозможно решить с помощью факторизации. Вы можете использовать графический калькулятор, чтобы найти точки, в которых график функции пересекает ось x. В этих точках f (x) = 0, поэтому x является нулем функции. 2. x 2 = 5 Совместимость с инструментами Quadratic EquationsPro

Корни квадратных уравнений могут быть действительными, комплексными или нулевыми. 2 = -1. С другой стороны, реальное решение означает, что все корни являются действительными числами. Примеры решенных квадратичных формул. Калькулятор квадратной формулы с мнимой опорой

Поскольку мы хотим найти максимальную площадь, мы можем найти максимум этой квадратичной функции, которая даст нам максимальную ширину. Полагая b = 40 и a = -2, получаем ширину 10. Подставляя 10 в уравнение, получаем l = 20. Таким образом, наш. максимальная площадь составляет 200 футов2. Конверт на 4 см длиннее своей ширины. Площадь 96 см2.Найдите длину … Смит и Вессон 629 classic deluxe

Wvd spring powershell

Ключ ответа на неравенства Квадратичная формула (стр. 313) • дискриминант (стр. 316) Ключевые слова • Урок 6-1 Изобразите квадратичные функции. • Уроки с 6-2 по 6-5 Решите квадратные уравнения. • Урок 6-3. Составьте квадратные уравнения и функции. Глава 6: Квадратичные функции и неравенства Как решать квадратные уравнения (Алгебра 2, Квадратичная … Срок действия дебетовой карты Bmo harris истекает

Урок 9-2 Умножение многочленов Урок 10-1 Решение уравнений путем разложения Урок 10-1 Графические технологии: родительские и Семейные графы Урок 10-1F Графики квадратичных функций Урок 10-2 Подробнее об оси симметрии и вершинах

m2 + 6m = –5 12. y2 + 3y = 28 13. 2z2 + z = 6 14. 15a2 — a = 6 Используйте свойство нулевого произведения для решения каждого уравнения. Напишите свое решение в форме реестра. 15. x2 — 10x + 24 = 0 16. d2 + 3d — 10 = 0 17. Объем резервуара для хранения в форме прямоугольной призмы составляет 24 кубических футов. Высота ванны 3 фута. Ширина равна w футов, а длина …

1. Каждая квадратичная функция имеет U-образный график, называемый параболой. 2. График квадратичной функции y 5 ax2 1 bx 1 c открывается, если a> 0, и раскрывается, если a <0.3. C 4. A 5. B 6. x 22 1 01 2 y 32 8 0 8 32 y 25 xy 5 8x2 10 xy 21 Оба графа открываются и имеют одну и ту же вершину (0, 0) и та же ось симметрии, x 5 0. График

Учитывая график ситуации, представленной квадратичной функцией, ученик проанализирует график и сделает выводы.

, несомненно, упростит вам поиск. Руководство 9 4 рациональных выражения, которые повторяют такой ключ ответа, как вы. Выполнив поиск по названию, издателю или авторам нужного вам руководства, вы сможете быстро их найти. Дом, на рабочем месте или, возможно, в вашем методе могут быть лучшим местом для сетевых подключений. Если вы хотите загрузить и установить …

Обновление программного обеспечения Hisense 40h4e

© e S290 F1c2j 9Kzuit JaX SNo cfUtgw Xa TrbeT RLRLICh. l 9 MAWlRln nr aiNg Oh5tFs s vr aeKsie Fr DvIeAd6.G d DMkasdef 7wpi VtVhn tI pnbf uidnuiStIe W IARlng se8burla 2 i2 f. M Рабочий лист ООО «Кута Софтвер» Kuta Software — Бесконечная алгебра 2 Имя _____ Квадратичные неравенства Дата _____ Период ____

Цель: написать квадратные уравнения в факторизованной форме, используя метод факторизации. Выявить ключевые особенности графика квадратичной функции из факторизованной формы Разминка: Решите каждое квадратное уравнение факторизацией.1. xx2 2 35 0 2. 3 14 24 0xx2 Учитывая отрезки по оси x графика квадратичной функции, запишите возможные множители. 3.

Seas Speakers

Изучите и уточните, как решать квадратные уравнения путем факторизации, вычисления квадрата и использования квадратной формулы с Bitesize GCSE Maths Edexcel.

— Глава 8.1–8.3 Контрольная точка — Урок 8.4 Часть 1: Решение уравнений с переменными с обеих сторон 24 сентября 2018 г. · Решение квадратных уравнений путем факторинга I. Проблемы модели В следующих примерах вы решите квадратные уравнения с помощью факторинга.Пример 1: Решить:. Запишите уравнение. Переставьте так, чтобы уравнение было равно нулю (). Фактор. Примените принцип нулевого продукта: если продукт равен нулю, либо один из факторов, либо оба фактора

Маршрутизатор Verizon g3100 желтый свет

Как заряжать телефон, когда порт сломан

____ 47. Что такое родительская функция для? а. c. б. d. ____ 48. Используйте это описание, чтобы записать квадратичную функцию в форме вершины: родительская функция растянута по вертикали в 2 раза и переведена на 14 единиц вправо и 6 единиц

Устройство Apple Music Player

Как разблокировать модули на холсте как студент

Nbme 21 занижает

Найдите единичный касательный вектор данной кривой калькулятор

Кандидаты на выборы округа Саффолк 2020

Umich eecs 203

• Загрузчик профиля Outlook 2016 полоса масштабирования выделена серым цветом

• Провести тест на наркотики в инвестиционных банках

• Как расправиться с бандитами

• Настройка vpn uc browser android

• родительская практика функции и преобразования ответы

• Home de corators collection uc7225t

• Как установить заглушку для очистки

• Список уровней 3 сезона Fighterz

• Учебник по анимации персонажей в Blender

Объем диска Revolution:

Если область на плоскости вращается вокруг линии в той же плоскости, полученный объект называется телом вращения.

Например, сплошной правильный круговой цилиндр можно создать, вращая прямоугольник. Точно так же твердый сферический шар можно создать, вращая полудиск.

Линия, вокруг которой мы вращаем фигуру, называется осью вращения.

Дисковый метод

Дисковый метод используется, когда мы вращаем одиночную кривую \ (y = f \ left (x \ right) \) вокруг оси \ (x- \) (или \ (y- \)).

Предположим, что \ (y = f \ left (x \ right) \) — непрерывная неотрицательная функция на интервале \ (\ left [{a, b} \ right].2} dy}. \]

Метод промывки

Мы можем расширить метод диска, чтобы найти объем полого тела вращения.

Предполагая, что функции \ (f \ left (x \ right) \) и \ (g \ left (x \ right) \) непрерывны и неотрицательны на интервале \ (\ left [{a, b} \ right] \) и \ (g \ left (x \ right) \ le f \ left (x \ right), \) рассмотрим область, ограниченную двумя кривыми \ (y = f \ left (x \ right) \ ) и \ (y = g \ left (x \ right), \) между \ (x = a \) и \ (x = b. 2}} \ right) dy}.2} \ left (t \ right) \ frac {{dy}} {{dt}} dt}. \]

Объем твердого тела вращения для полярной кривой

Есть много кривых, которые задаются полярным уравнением \ (r = r \ left (\ theta \ right). \) Для преобразования из полярных координат \ (\ left ({r, \ theta} \ right) \) в В декартовых координатах \ (\ left ({x, y} \ right), \) используем известные формулы

\ [{x = r \ left (\ theta \ right) \ cos \ theta, \; \;} \ kern0pt {y = r \ left (\ theta \ right) \ sin \ theta.} \]

Итак, мы подошли к параметрической форме кривой, рассмотренной в предыдущем разделе.

Важно помнить, что радиус-вектор \ (r \) также зависит от параметра \ (\ theta. \), Поэтому производные \ (\ large {\ frac {{dx}} {{dt}} } \ normalsize \) и \ (\ large {\ frac {{dy}} {{dt}}} \ normalsize \) записываются как

\ [{\ frac {{dx}} {{dt}} = \ frac {{d \ left ({r \ left (\ theta \ right) \ cos \ theta} \ right)}} {{dt}} } = {\ frac {{d \ left ({r \ left (\ theta \ right)} \ right)}} {{dt}} \ cos \ theta — r \ left (\ theta \ right) \ sin \ theta ,} \]

\ [{\ frac {{dy}} {{dt}} = \ frac {{d \ left ({r \ left (\ theta \ right) \ sin \ theta} \ right)}} {{dt}} } = {\ frac {{d \ left ({r \ left (\ theta \ right)} \ right)}} {{dt}} \ sin \ theta + r \ left (\ theta \ right) \ cos \ theta . {\ frac {2} {3}}} = 1 \) вокруг своей оси симметрия.2} \) и ось \ (x — \) вокруг оси \ (y — \).

Пример 9

Найдите объем твердого тела, полученный вращением равностороннего треугольника со стороной \ (a \) вокруг одной из его сторон.

Пример 10

Одна арка циклоиды \ (x = \ theta — \ sin \ theta, \) \ (y = 1 — \ cos \ theta \) вращается вокруг своего основания. Вычислите объем тела, ограниченного данной поверхностью.

Пример 1.

Дисковым методом вычислить объем правого кругового конуса высотой \ (H \) и радиусом основания \ (R.1} = {8 \ pi \ left [{\ left ({1 — \ frac {1} {3}} \ right) — \ left ({- 1 + \ frac {1} {3}} \ right)} \ right]} = {8 \ pi \ cdot \ frac {4} {3}} = {\ frac {{32 \ pi}} {3}} \]

Пример 5.

Симметричный параболический сегмент с основанием \ (a \) и высотой \ (h \) вращается вокруг основания. Вычислите объем полученного твердого тела вращения («лимон» Кавальери).

Решение.

Квадратичная функция определяется уравнением \ (y = kx \ left ({a — x} \ right), \), где коэффициент \ (k \) может быть найден из условия \ (y \ left (\ large {{\ frac {a} {2}}} \ normalsize \ right) = h.2}}} {4}}} = {\ frac {{\ sqrt 3 a}} {2}.} \]

Итак, вершины \ (A, \) \ (B, \) \ (C \) имеют следующие координаты:

\ [{A \ left ({0, \ frac {a} {2}} \ right), \;} \ kern0pt {B \ left ({\ frac {{\ sqrt 3 a}} {2}, 0 } \ right), \;} \ kern0pt {C \ left ({0, — \ frac {a} {2}} \ right).} \]

Найдите уравнение прямой \ (AB \), используя двухточечную форму:

\ [{\ frac {{x — {x_A}}} {{{x_B} — {x_A}}} = \ frac {{y — {y_A}}} {{{y_B} — {y_A}}}, } \; \; \ Rightarrow {\ frac {{x — 0}} {{\ frac {{\ sqrt 3 a}} {2} — 0}} = \ frac {{y — \ frac {a} {2}}} {{ 0 — \ frac {a} {2}}},} \; \; \ Rightarrow {\ frac {x} {{\ sqrt 3}} = \ frac {{y — \ frac {a} {2}}} {{- 1}},} \; \; \ Rightarrow {x = \ гидроразрыв {{a \ sqrt 3}} {2} — \ sqrt 3 г.2}.} \]

Factorizar polinomios | Суперпроф

En este artículo exploraremos la factorización de polinomios. Primero expondremos algunos teoremas y propiedades sobre los polinomios que nos ayudarán a factorizarlos con mayor facilidad. Luego revisaremos con detalle métodos para factorizarlos y al final mostraremos algunos ejemplos de factorización de polinomios.

Teoremas sobre los factores de un polinomio

Para los siguientes teoremas recordemos que

es una raíz del polinomio si cumple que.

Teorema del Resto

Teorema : El resto o restuo de la división de un polinomio

por un polinomio de la forma es igual que el resultado de evalar el polinomio en.

Por ejemplo, dividamos

entre utilizando la regla de Ruffini:

Así, el cociente de la división es

, mientras que el Остаток es 56. Por otro ladnemos, si Assessment

Примечание : Observemos que si

, имеет значение остатков 0.En otras palabras:

Si multiplicamos ambos lados por

tenemos que

Por lo tanto,

es un factor de. Este resultado se conoce como el teorema del factor.

Teorema del factor

Teorema : El polinomio

es divisible por un polinomio de la forma si y sólo si.

Como ejemplo, consideremos el polinomio

.Notemos que

por lo tanto,

. Además, y son raíces de.

Nota : Si

es un polinomio de grado y se Разделите пор, entonces el resultado tiene la forma:

donde

es constante y остаточная форма, como como, mientrasio que es .

Teorema Fundamental del Álgebra

Teorema : Un polinomio

de grado y con coeficientes reales tiene excamente race, las cuales pueden ser reales o complejas.

Nota : Los polinomios reales tienen

race, sin embargo, es posible que ninguna sea real. Cuando ninguna raíz es real entonces el polinomio no se puede factorizar en factores lineales.

Nota : Recordemos que factorizar un polinomio

en factores lineales means escribir de la forma

en donde

son las raíces de.

Teorema de la Raíz Racional

Teorema : Sea

un polinomio con coeficientes que son enteros.Si es una raíz racional de, entonces тендра ла форма

donde

es un factor de y es un factor de.

Nota : Este teorema, junto con el teorema del factor, nos ayudan a encontrar raíces rapido. Primero enlistamos todas las posibles raíces racionales

de, luego Assessment. Si, entonces sabremos que es un factor de. Describiremos algunos ejemplos en la sección de ejemplos.

Nota : Este teorema sólo nos dice la forma quetendrán las raíces racionales.Es posible que un polinomio no tenga ninguna raíz raíz racional como en el caso de

, cuyas raíces son y.

Nota : Si

, entonces el polinomio se conoce como mónico. En este caso, el único factor de es 1, por lo tanto, las raíces tienen la forma

donde

es un factor de.

Los / las mejores profesores / as de Matemáticas que están disponibles

1ª clase gratis

Algunas propiedades de las raíces y los factores de un polinomio

1 A cada raíz bino del Соответствующий коэффициент

.

2 Supongamos que

es una raíz de. Entonces, podemos escribir como

donde

es un polinomio de grado. Después, si descubrimos que también es raíz de, por lo tanto, se podría escribir como

De aquí se sigue que

se puede escribir como

raíz de multiplicidad 2 de.Esto impla que las raíces del polinomio no son necesariamente todas distintas.

3 Podemos expresar un polinomio en factores al escribirlo como producto de todos los binomios del tipo

que matchan a las raíces del polinomio. Así, se factoriza como

Por ejemplo, ya que

y son raíces del polinomio, entonces podemos escribir

4 Todo polinomio 5,000 тенденция к индексу.Por lo tanto, tambiéntendrá a como factor (es decir,).

Por ejemplo, el polinomio

se puede factorizar como. De aquí, terminímos que las raíces son y.

5 Un polinomio es несократимые o primo si no puede descomponerse en factores.

Por ejemplo, el polinomio

no se puede factorizar ya que las raíces son complejas.

Métodos para factorizar un polinomio

Factor común

Sacar el factor común consiste en aplicar la propiedad distributiva de los números reales:

Notemos que cada término se puede dividir por (es decir, es el factor común). Por lo tanto, el polinomio lo podemos factorizar como

Observemos que el polinomio

no se puede factorizar, por lo tanto, esto es lo más que podemos factorizar el polinomio. La única raíz del polinomio es con multiplicidad 2.

Productos notables

Existen algunos polinomios de segundo grado que son muy sencillos de factorizar ya que tienen una estructura fácilmente reconocococible.Los más comunes son:

1 Diferencia de cuadrados : si el polinomio se puede escribir de la forma

, entonces podemos factorizar como.

Por ejemplo, los polinomios

o.

2 Trinomio cuadrado perfecto : si el polinomio tiene la forma

, entonces lo podemos factorizar como.

Por ejemplo, consideremos el polinomio

(donde y), el cual se puede factorizar como.

Nota : existen otros productos notables, como el cubo perfecto de binomios. Sin embargo, esos no son tan conmunes.

Con el teorema de la raíz racional

Si no tenemos un factor común o no se puede escribir el polinomio como un producto notable, entonces podemos intentar a utilizar el teorema de la raíz coeficientes to s del polinomio sean enteros). Аква-оценка-эль-полиномио

Entre todas Las Posibles racionales buscado alguna que удовлетворительная очередь.En este caso, utilizamos la regla de Ruffini para realizar la factorización de la forma:

Luego Repetimos el procedure con

(pero descargamos aquellos valores que ya sabemos que no son factores).

Utilizando la fórmula general

Si el polinomio es de segundo grado (

) и todos los métodos anteriores fallaron, entonces podemos utilizar la fórmula general:

del

yy el polinomio lo podremos factorizar como.

Nota : Si las raíces son Complejas, podemos obtar por dejar el polinomio sin factorizar y decir que es несводимые. También es posible factorizarlo utilizando las raíces complejas, sin embargo, en este caso los factores serán polinomios en los números complejos.

Nota : Si el polinomio es de grado mayor a 2 todo lo anterior falla, entonces es posible que todas las raíces sean irracionales o complejas. En este caso lo más apropiado es utilizar algún método numérico o un programa de computadora para factorizar el polinomio.

Ejemplos

1 Encuentra las raíces del polinomio

y factorízalo.

2 Factoriza los siguientes polinomios utilizando la fórmula general:

a

b

c

Общие правила использования

polinomio:

a Primero tenemos

,

por lo tanto, una raíz es

y la otra raíz es.De aquí, se sigue que el polinomio se factoriza como

b Para

tenemos

por lo tanto, una raíz es

y la otra raíz es. De aquí, se sigue que el polinomio se factoriza como

c Por último, para

notemos que no tenemos un polinomio de segundo grado. Sin embargo, solo tenemos las potcias 2 y 4, de manera que podemos hacer el cambio de variable,

Este polinomio ya es de segundo grado, por lo que podemos utilizar la fórmula general,

De aquí, tenemos que las raíces son

г. No obstante« por lo que tenemos

De esta forma, el polinomio queda factorizado como

3 Factoriza el siguiente polinomio4

000

000

000

000

000

000

Como el polinomio es de cuarto grado y tiene coeficientes enteros, entonces utilizaremos el teorema de la raíz racional para enlistar todas las posibles racionales.

El coeficiente main es 2, cuyos factores son 1 y 2. El coeficiente independiente es 6, que tiene factores 1, 2, 3 y 6. De esta forma, las posibles raíces son

Nota que descartamos

ya que es igual a; al igual que descartamos ya que es igual a.

Ahora evalamos el polinomio en estos valores para encontrar las raíces:

Notamos que el

es una raíz.Por lo tanto, utilizamos la regla de Ruffini:

Es decir,

y son factores.

Seguimos realizando el schemeimiento, ahora con evalando

en las posibles raíces (volvemos a intentar con 1, por si es una raíz de multiplicidad Mayor):

razi que

.