Десятичная дробь — Википедия

Десяти́чная дробь — разновидность дроби, которая представляет собой способ представления действительных чисел в виде

±dm…d1d0,d−1d−2…{\displaystyle \pm d_{m}\ldots d_{1}d_{0}{,}d_{-1}d_{-2}\ldots }

где

±{\displaystyle \pm } — знак дроби: либо +{\displaystyle +}, либо −{\displaystyle -},

,{\displaystyle ,} — десятичная запятая, служащая разделителем между целой и дробной частью числа (стандарт стран СНГ)^[1],

dk{\displaystyle d_{k}} — десятичные цифры. Причём последовательность цифр до запятой (слева от неё) конечна (как минимум одна цифра), а после запятой (справа от неё) — может быть как конечной (в частности, цифры после запятой могут вообще отсутствовать), так и бесконечной.

Примеры:

• 123,45{\displaystyle 123{,}45} (конечная десятичная дробь)
• Представление числа π{\displaystyle \pi } в виде бесконечной десятичной дроби: 3,1415926535897…{\displaystyle 3{,}1415926535897…}

Значением десятичной дроби ±dm…d1d0,d−1d−2…{\displaystyle \pm d_{m}\ldots d_{1}d_{0},d_{-1}d_{-2}\ldots } является действительное число

±(dm⋅10m+…+d1⋅101+d0⋅100+d−1⋅10−1+d−2⋅10−2+…),{\displaystyle \pm \left(d_{m}\cdot 10^{m}+\ldots +d_{1}\cdot 10^{1}+d_{0}\cdot 10^{0}+d_{-1}\cdot 10^{-1}+d_{-2}\cdot 10^{-2}+\ldots \right),}

равное сумме конечного или бесконечного числа слагаемых.

Представление действительных чисел с помощью десятичных дробей является обобщением записи целых чисел в десятичной системе счисления. В представлении целого числа в виде десятичной дроби отсутствуют цифры после запятой, и таким образом, это представление имеет вид

±dm…d1d0,{\displaystyle \pm d_{m}\ldots d_{1}d_{0},}

что совпадает с записью этого числа в десятичной системе счисления.

Конечные и бесконечные десятичные дроби[править | править код]

Конечные дроби[править | править код]

Десятичная дробь называется конечной, если она содержит конечное число цифр после запятой (в частности, ни одного), то есть имеет вид

±a0,a1a2…an{\displaystyle \pm a_{0}{,}a_{1}a_{2}\ldots a_{n}}

В соответствии с определением эта дробь представляет число

±∑k=0nak⋅10−k{\displaystyle \pm \sum _{k=0}^{n}a_{k}\cdot 10^{-k}}

Легко видеть, что это число можно представить в виде обыкновенной дроби вида p/10s{\displaystyle p/10^{s}}, знаменатель которой является степенью десятки. Обратно, любое число вида p/10s{\displaystyle p/10^{s}}, где p{\displaystyle p} — целое, а s{\displaystyle s} — целое неотрицательное, можно записать в виде конечной десятичной дроби.

Если обыкновенную дробь p/10s{\displaystyle p/10^{s}} привести к несократимому виду, её знаменатель будет иметь вид 2m5n{\displaystyle 2^{m}5^{n}}. Таким образом, имеет место следующая теорема о представимости действительных чисел в виде конечных десятичных дробей.

Теорема. Действительное число представимо в виде конечной десятичной дроби тогда и только тогда, когда оно является рациональным и при записи его несократимой дробью p/q{\displaystyle p/q} знаменатель q{\displaystyle q} не имеет простых делителей, отличных от 2{\displaystyle 2} и 5{\displaystyle 5}.

Бесконечные дроби[править | править код]

Бесконечная десятичная дробь

±a0,a1a2…{\displaystyle \pm a_{0}{,}a_{1}a_{2}\ldots }

представляет, согласно определению, действительное число

±∑k=0∞ak⋅10−k{\displaystyle \pm \sum _{k=0}^{\infty }a_{k}\cdot 10^{-k}}

Этот ряд сходится, каковы бы ни были целое неотрицательное a0{\displaystyle a_{0}} и десятичные цифры a1,a2,…{\displaystyle a_{1},a_{2},\ldots }. Это предложение вытекает из того факта, что данный ряд мажорируется сходящимся рядом

a0+∑k=1∞9⋅10−k{\displaystyle a_{0}+\sum _{k=1}^{\infty }9\cdot 10^{-k}}

Представление действительных чисел десятичными дробями[править | править код]

Таким образом, всякая конечная или бесконечная десятичная дробь представляет некоторое вполне определённое действительное число. Остаются следующие вопросы:

1. Всякое ли действительное число может быть представлено в виде десятичной дроби?
2. Единственно ли такое представление?
3. Каков алгоритм разложения числа в десятичную дробь?

Эти вопросы освещаются ниже.

Алгоритм разложения числа в десятичную дробь[править | править код]

Ниже описывается алгоритм построения по произвольному действительному числу α{\displaystyle \alpha } десятичной дроби, которая является его представлением.

Рассмотрим вначале случай α⩾0{\displaystyle \alpha \geqslant 0}. Разделим всю числовую прямую целочисленными точками на отрезки единичной длины. Рассмотрим тот отрезок I0{\displaystyle I_{0}}, который содержит точку α{\displaystyle \alpha }; в частном случае, когда точка α{\displaystyle \alpha } является концом двух соседних отрезков, в качестве I0{\displaystyle I_{0}} выберем правый отрезок.

Если обозначить целое неотрицательное число, являющееся левым концом отрезка I0{\displaystyle I_{0}}, через a0{\displaystyle a_{0}}, то можно записать:

I0=[a0;a0+1]{\displaystyle I_{0}=[a_{0}\,;\,a_{0}+1]}

На следующем шаге разделим отрезок I0{\displaystyle I_{0}} на десять равных частей точками

a0+b/10,b=1,…,9{\displaystyle a_{0}+b/10,\;b=1,\ldots ,9}

и рассмотрим тот из отрезков длины 1/10{\displaystyle 1/10}, на котором лежит точка α{\displaystyle \alpha }; в случае когда эта точка является концом двух соседних отрезков, из этих двух отрезков опять выберем правый.

Обозначим этот отрезок I1{\displaystyle I_{1}}. Он имеет вид:

I1=[a0+a110;a0+a1+110]{\displaystyle I_{1}=\left[a_{0}+{\frac {a_{1}}{10}}\,;\,a_{0}+{\frac {a_{1}+1}{10}}\right]}

Будем продолжать аналогичным образом процесс измельчения числовой прямой и последовательного уточнения положения точки α{\displaystyle \alpha }.

На очередном шаге, имея отрезок In−1{\displaystyle I_{n-1}}, содержащий точку α{\displaystyle \alpha }, мы делим его на десять равных отрезков и выбираем из них тот отрезок In{\displaystyle I_{n}}, на котором лежит точка α{\displaystyle \alpha }; в случае когда эта точка является концом двух соседних отрезков, из этих двух отрезков выбираем правый.

Продолжая этот процесс мы получим последовательность отрезков I0,I1,…{\displaystyle I_{0},I_{1},\ldots } вида

In=[a0+a1101+…+an10n;a0+a1101+…+an10n+110n]{\displaystyle I_{n}=\left[a_{0}+{\frac {a_{1}}{10^{1}}}+\ldots +{\frac {a_{n}}{10^{n}}}\,;\,a_{0}+{\frac {a_{1}}{10^{1}}}+\ldots +{\frac {a_{n}}{10^{n}}}+{\frac {1}{10^{n}}}\right]}

где a0{\displaystyle a_{0}} — целое неотрицательное, а a1,a2,…{\displaystyle a_{1},a_{2},\ldots } — целые числа, удовлетворяющие неравенству 0⩽ak⩽9{\displaystyle 0\leqslant a_{k}\leqslant 9}.

Построенная последовательность отрезков I0,I1,…{\displaystyle I_{0},I_{1},\ldots } обладает следующими свойствами:

• Отрезки последовательно вложены друг в друга: I0⊃I1⊃I2⊃…{\displaystyle I_{0}\supset I_{1}\supset I_{2}\supset \ldots }
• Длина отрезков |In|=10−n,n=0,1,2,…{\displaystyle |I_{n}|=10^{-n},\;n=0,1,2,\ldots }
• Точка α{\displaystyle \alpha } принадлежит всем отрезкам последовательности

Из этих условий следует, что I0,I1,…{\displaystyle I_{0},I_{1},\ldots } есть система вложенных отрезков, длины которых стремятся к нулю при n→∞{\displaystyle n\to \infty }, а точка α{\displaystyle \alpha } есть общая точка всех отрезков системы. Отсюда вытекает, что последовательность левых концов отрезков сходится к точке α{\displaystyle \alpha } (аналогичное утверждение справледливо и для последовательности правых концов), то есть

a0+a1101+…+an10n→α{\displaystyle a_{0}+{\frac {a_{1}}{10^{1}}}+\ldots +{\frac {a_{n}}{10^{n}}}\to \alpha } при n→∞{\displaystyle n\to \infty }

Это значит, что ряд

∑k=0∞ak⋅10−k{\displaystyle \sum _{k=0}^{\infty }a_{k}\cdot 10^{-k}}

сходится к числу α{\displaystyle \alpha }, и таким образом, десятичная дробь

a0,a1a2…{\displaystyle a_{0}{,}a_{1}a_{2}\ldots }

является представлением числа α{\displaystyle \alpha }. Таким образом, найдено разложение неотрицательного числа α{\displaystyle \alpha } в десятичную дробь.

Полученная десятичная дробь является бесконечной по построению. При этом может оказаться, что начиная с некоторого номера, все десятичные знаки после запятой суть нули, то есть дробь имеет вид

a0,a1…an000…{\displaystyle a_{0}{,}a_{1}\ldots a_{n}000\ldots }

Нетрудно видеть, что эта возможность имеет место в том случае, когда на некотором шаге точка α{\displaystyle \alpha } совпадает с одной из точек деления числовой прямой. В этом случае отбрасывая в сумме

∑k=0∞ak⋅10−k{\displaystyle \sum _{k=0}^{\infty }a_{k}\cdot 10^{-k}}

нулевые слагаемые, получим, что число α{\displaystyle \alpha } также может быть представлено конечной десятичной дробью

a0,a1…an{\displaystyle a_{0}{,}a_{1}\ldots a_{n}}

Вообще, ясно, что приписывая в конец десятичной дроби после запятой любое количество нулей (в том числе бесконечное), мы не изменяем значение дроби. Таким образом, в данном случае число α{\displaystyle \alpha } может быть представлено как конечной, так и бесконечной десятичной дробью (полученной из первой приписыванием бесконечного числа нулей).

Тем самым рассмотрен случай неотрицательного α{\displaystyle \alpha }. В случае отрицательного α{\displaystyle \alpha }, в качестве десятичного представления этого числа можно взять представление противоположного ему положительного числа, взятое со знаком «минус».

Приведенный алгоритм дает способ разложения произвольного действительного числа в десятичную дробь. Тем самым доказана следующая

Теорема. Всякое действительное число может быть представлено в виде десятичной дроби.

О роли аксиомы Архимеда[править | править код]

Приведенный алгоритм разложения действительного числа в десятичную дробь существенно опирается на свойство системы действительных чисел, называемое аксиомой Архимеда.

Это свойство было использовано дважды в алгоритме. В самом начале построения выбиралось целое a0{\displaystyle a_{0}}, такое, что действительное число α{\displaystyle \alpha } находится между a0{\displaystyle a_{0}} и следующим целым a0+1{\displaystyle a_{0}+1}:

a0⩽α<a0+1,a0∈Z{\displaystyle a_{0}\leqslant \alpha <a_{0}+1,\;a_{0}\in \mathbb {Z} }

Однако существование такого целого числа a0{\displaystyle a_{0}} надо ещё доказать: нельзя исключать, например, возможность, когда, каково бы ни было целое n{\displaystyle n}, всегда имеет место неравенство n⩽α{\displaystyle n\leqslant \alpha }. Если бы этот случай имел место, то, очевидно, нужного числа a0{\displaystyle a_{0}} не нашлось бы.

Эта возможность как раз исключается аксиомой Архимеда, согласно которой каково бы ни было число α{\displaystyle \alpha }, всегда найдётся целое n{\displaystyle n} такое, что n>α{\displaystyle n>\alpha }. Теперь среди чисел k=1,…,n{\displaystyle k=1,\ldots ,n} возьмём наименьшее, обладающее свойством k>α{\displaystyle k>\alpha }. Тогда

k−1⩽α<k{\displaystyle k-1\leqslant \alpha <k}

Искомое число найдено: a0=k−1{\displaystyle a_{0}=k-1}.

Второй раз аксиома Архимеда неявно использовалась при доказательстве стремления к нулю длин отрезков последовательности I0,I1,I2,…{\displaystyle I_{0},I_{1},I_{2},\ldots }:

limn→∞10−n=0{\displaystyle \lim _{n\to \infty }10^{-n}=0}

Строгое доказательство данного предложения опирается на аксиому Архимеда. Докажем эквивалентное соотношение

limn→∞10n=∞{\displaystyle \lim _{n\to \infty }10^{n}=\infty }

В соответствии с аксиомой Архимеда, каково бы ни было действительное число E>0{\displaystyle E>0}, последовательность натуральных чисел 1,2,…{\displaystyle 1,2,\ldots } превзойдёт его, начиная с некоторого номера. А поскольку для всякого n{\displaystyle n} имеет место неравенство

10n>n{\displaystyle 10^{n}>n}

то последовательность 10n{\displaystyle 10^{n}} также превзойдёт E{\displaystyle E}, начиная с того же номера. В соответствии с определением предела числовой последовательности, это означает, что limn→∞10n=∞{\displaystyle \lim _{n\to \infty }10^{n}=\infty }.

Неоднозначность представления в виде десятичной дроби[править | править код]

С помощью приведённого алгоритма мы можем для любого действительного числа α{\displaystyle \alpha } построить десятичную дробь, представляющую данное число. Однако может случиться, что это же самое число α{\displaystyle \alpha } может быть представлено в виде десятичной дроби и другим образом.

Неединственность представления чисел в виде десятичных дробей уже следует из того тривиального факта, что, приписывая конечной дроби справа после запятой нули, мы будем получать формально различные десятичные дроби, представляющие одно и то же число.

Однако, если даже считать дроби, полученные путём приписывания в конец друг другу конечного или бесконечного количества нулей, тождественными, представление некоторых действительных чисел всё же остаётся неединственным.

Рассмотрим например, десятичную дробь

0,99…{\displaystyle 0{,}99\ldots }

Согласно определению, эта дробь является представлением числа 0+9/10+9/100+…=1{\displaystyle 0+9/10+9/100+\ldots =1}. Вместе с тем, это число может быть также представлено в виде десятичной дроби 1,00…{\displaystyle 1{,}00\ldots }. В самом деле, вещественные числа a,b{\displaystyle a,b} различны тогда и только тогда, когда между ними можно вставить ещё одно вещественное число, не совпадающее с самими a,b.{\displaystyle a,b.} Но между 0,99…{\displaystyle 0{,}99\ldots } и 1,00…{\displaystyle 1{,}00\ldots } никакого третьего числа вставить нельзя.

Этот пример можно обобщить. Можно показать, что дроби

±a0,a1…an−1an999…{\displaystyle \pm a_{0}{,}a_{1}\ldots a_{n-1}a_{n}999\ldots }

и

±a0,a1…an−1(an+1)000{\displaystyle \pm a_{0}{,}a_{1}\ldots a_{n-1}(a_{n}+1)000}

где an≠9{\displaystyle a_{n}\neq 9}, представляют одно и то же действительное число.

Оказывается, этим общим примером исчерпываются все случаи неоднозначности представления действительных чисел в виде десятичных дробей. При этом мы, конечно, не рассматриваем тривиальные случаи дробей, полученные приписыванием нулей в конец друг другу, а также пару дробей +0,00…{\displaystyle +0{,}00\ldots } и −0,00…{\displaystyle -0{,}00\ldots }.

Эти результаты можно суммировать в следующей теореме.

Теорема. Всякое действительное число α{\displaystyle \alpha }, не представимое в виде p/10s{\displaystyle p/10^{s}}, где p{\displaystyle p} — целое, s{\displaystyle s} — целое неотрицательное, допускает единственное представление в виде десятичной дроби; при этом эта дробь является бесконечной.

Всякое действительное число вида α=p/10s{\displaystyle \alpha =p/10^{s}} может быть представлено в виде десятичной дроби более чем одним способом. Если α≠0{\displaystyle \alpha \neq 0}, то оно может быть представлено как в виде конечной десятичной дроби, а также бесконечной дроби, полученной приписыванием нулей в конец после запятой, так и в виде бесконечной дроби, оканчивающейся на 999…{\displaystyle 999\ldots }. Число α=0{\displaystyle \alpha =0} может быть представлено дробями вида +0,00…{\displaystyle +0{,}00\ldots }, а также дробями вида −0,00…{\displaystyle -0{,}00\ldots }.

Замечание. Бесконечные дроби, оканчивающиеся на 999…{\displaystyle 999\ldots }, получаются, если в при

Целое число — Википедия

Целые числа — расширение множества натуральных чисел^[1], получаемое добавлением к нему нуля и отрицательных чисел^[2]. Необходимость рассмотрения целых чисел продиктована невозможностью в общем случае вычесть из одного натурального числа другое — можно вычитать только меньшее число из большего. Введение нуля и отрицательных чисел делает вычитание такой же полноценной операцией, как сложение^[3].

Вещественное число является целым, если его десятичное представление не содержит дробной части (но может содержать знак). Примеры вещественных чисел:

Числа 142857; 0; −273 являются целыми.

Числа 5½; 9,75 не являются целыми.

Множество целых чисел обозначается Z{\displaystyle \mathbb {Z} } (от нем. Zahlen — «числа»^[4]). Изучением свойств целых чисел занимается раздел математики, называемый теорией чисел.

Положительные и отрицательные числа[править | править код]

Согласно своему построению, множество целых чисел состоит из трёх частей:

1. Натуральные числа (или, что то же самое, целые положительные). Они возникают естественным образом при счёте (1, 2, 3, 4, 5…)^[5].
2. Ноль — число, обозначаемое 0{\displaystyle 0}. Его определяющее свойство: 0+n=n+0=n{\displaystyle 0+n=n+0=n} для любого числа n{\displaystyle n}.
3. Целые отрицательные числа.

Противоположные числа (4 и –4)

Отрицательные числа при записи помечаются спереди знаком минус: −1,−2,−3…{\displaystyle -1,-2,-3\dots } Для каждого целого числа a{\displaystyle a} существует и единственно противоположное ему число, обозначаемое −a{\displaystyle -a} и обладающее тем свойством, что a+(−a)=0.{\displaystyle a+(-a)=0.} Если a{\displaystyle a} положительно, то противоположное ему отрицательно, и наоборот. Ноль противоположен самому себе^[2].

Абсолютной величиной целого числа a{\displaystyle a} называется это число с отброшенным знаком

[6]. Обозначение: |a|.{\displaystyle \left|a\right|.}

Примеры: |4|=4; |−5|=5; |0|=0{\displaystyle \left|4\right|=4;\ \left|-5\right|=5;\ \left|0\right|=0}

Во множестве целых чисел определены три основные арифметические операции: сложение, обратное к сложению вычитание и умножение. Имеется также важная операция, специфическая для натуральных и целых чисел: деление с остатком. Наконец, для целых чисел определён порядок, позволяющий сравнивать числа друг с другом.

Сложение и вычитание[править | править код]

Следующая таблица иллюстрирует основные свойства сложения^[7] для любых целых a,b,c{\displaystyle a,b,c}:

При сложении и вычитании целых чисел выполняются следующие правила знаков^[7][8], которые следует учитывать при раскрытии скобок:

−(−a)=a; −(a+b)=−a−b; −(a−b)=−a+b.{\displaystyle -\left(-a\right)=a;\ -\left(a+b\right)=-a-b;\ -\left(a-b\right)=-a+b.}

Правила сложения целых чисел

^[9].

1. При сложении целых чисел с одинаковыми знаками надо сложить их абсолютные величины и приписать ей знак слагаемых. Пример; −14+(−28)=−42{\displaystyle -14+\left(-28\right)=-42}.
2. При сложении целых чисел с разными знаками надо сравнить их абсолютные величины, из большей вычесть меньшую и приписать результату знак того слагаемого, у которого абсолютная величина больше. Примеры: −4+9=9−4=5; −9+4=−(9−4)=−5{\displaystyle -4+9=9-4=5;\ -9+4=-\left(9-4\right)=-5}.
3. Вычитание a−b{\displaystyle a-b} для целых чисел всегда выполнимо, и результат можно найти как a+(−b).{\displaystyle a+\left(-b\right).} Пример: 26−51=26+(−51)=−25{\displaystyle 26-51=26+\left(-51\right)=-25}.
4. Геометрически сложение можно наглядно представить как смещение числа вдоль числовой оси (см. рисунок в начале статьи), причём прибавление положительного числа вызывает смещение направо, а отрицательного — налево. Например, для числа −3{\displaystyle -3} прибавление к нему 4{\displaystyle 4} означает смещение его вправо на 4 единицы; наглядно видно, что получается +1{\displaystyle +1}. Аналогично −3+(−4){\displaystyle -3+\left(-4\right)}, смещая −3{\displaystyle -3} влево на 4 единицы, получим в результате −7{\displaystyle -7}.
5. Вычитание можно наглядно представить аналогично, но в этом случае, наоборот, вычитание положительного числа вызывает смещение влево, а отрицательного — вправо. Например, 5−7{\displaystyle 5-7} смещает 5{\displaystyle 5} на 7 единиц к числу −2{\displaystyle -2}, а 5−(−7){\displaystyle 5-\left(-7\right)} смещает его вправо к числу 12{\displaystyle 12}.

Умножение и возведение в степень[править | править код]

Умножение чисел a,b{\displaystyle a,b} далее обозначается a×b{\displaystyle a\times b} или (только в случае буквенных обозначений) просто ab{\displaystyle ab}. Следующая таблица иллюстрирует основные свойства умножения^[7] для любых целых a,b,c{\displaystyle a,b,c}:

При умножении целых чисел выполняются правила знаков

^[7][8], которые следует учитывать при раскрытии скобок:

(−a)b=a(−b)=−ab; (−a)(−b)=ab{\displaystyle \left(-a\right)b=a\left(-b\right)=-ab;\ \left(-a\right)\left(-b\right)=ab}

Следствие: произведение чисел с одинаковыми знаками положительно, с разными — отрицательно.

Возведение в натуральную степень целых чисел определяется так же, как и для натуральных чисел:

an=a⋅a⋅…⋅a⏟n{\displaystyle a^{n}=\underbrace {a\cdot a\cdot \ldots \cdot a} _{n}}

Свойства возведения в степень целых чисел также такие же, как у натуральных:

(ab)n=anbn;aman=am+n;(am)n=amn{\displaystyle \left(ab\right)^{n}=a^{n}b^{n};\quad a^{m}a^{n}=a^{m+n};\quad \left(a^{m}\right)^{n}=a^{mn}}

В дополнение к этому определению, принято соглашение о нулевой степени: a0=1{\displaystyle a^{0}=1} для любого целого a.{\displaystyle a.} Основанием для такого соглашения служит желание сохранить приведенные выше свойства и для нулевого показателя степени: a0an=a0+n=an,{\displaystyle a^{0}a^{n}=a^{0+n}=a^{n},} откуда ясно, что a0=1.{\displaystyle a^{0}=1.}

Упорядоченность[править | править код]

Z{\displaystyle \mathbb {Z} } — линейно упорядоченное множество. Порядок в нём задаётся соотношениями:

⋯−2<−1<0<1<2<…{\displaystyle \dots -2<-1<0<1<2<\dots }

Целое число положительно, если оно больше нуля, отрицательно, если меньше нуля. Положительными целыми числами являются натуральные числа и только они. Отрицательные числа — это числа, противоположные положительным. Ноль не является ни положительным, ни отрицательным. Любое отрицательное число меньше любого положительного^[2].

Для любых целых чисел a,b,c,d{\displaystyle a,b,c,d} справедливы следующие соотношения^[10].

1. Если a<b{\displaystyle a<b}, то для любого c{\displaystyle c} будет a+c<b+c{\displaystyle a+c<b+c}.
2. Если a<b{\displaystyle a<b} и c<d{\displaystyle c<d}, то a+c<b+d{\displaystyle a+c<b+d}.
3. Если a<b{\displaystyle a<b} и c>0{\displaystyle c>0}, то ac<bc{\displaystyle ac<bc}.
4. Если a<b{\displaystyle a<b} и c<0{\displaystyle c<0}, то ac>bc{\displaystyle ac>bc}.

Для сравнения двух отрицательных чисел существует правило: больше то число, у которого абсолютная величина меньше^[10]. Например, −6<−5{\displaystyle -6<-5}.

Делимость[править | править код]

Деление с остатком[править | править код]

Операция деления, вообще говоря, не определена на множестве целых чисел. Например, нельзя разделить 3{\displaystyle 3} на 2{\displaystyle 2} — нет такого целого числа, которое, умноженное на 2{\displaystyle 2}, даст 3{\displaystyle 3}. Но можно определить так называемое деление с остатком^[11]:

Для любых целых a,b{\displaystyle a,b} (где b≠0{\displaystyle b\neq 0}) существует единственный набор целых чисел q,r{\displaystyle q,r} такой, что a=bq+r{\displaystyle a=bq+r}, где 0⩽r<|b|.{\displaystyle 0\leqslant r<\left|b\right|.}

Здесь a — делимое, b — делитель, q — (неполное) частное, r — остаток от деления (всегда неотрицателен). Если остаток равен нулю, говорят, что деление выполняется нацело^[11].

Примеры

На операции деления с остатком основаны теория сравнений и алгоритм Евклида.

Деление нацело. Делители[править | править код]

Как определено выше, число a{\displaystyle a} делится (нацело) на число b{\displaystyle b}, если существует целое число q{\displaystyle q} такое, что a=bq{\displaystyle a=bq}. Символическая запись: b|a{\displaystyle b|a}. Существуют несколько равносильных словесных формулировок указанной делимости^[12]:

Каждое целое число n{\displaystyle n}, не равное нулю или ±1{\displaystyle \pm 1}, имеет 4 тривиальных делителя: 1,−1,n,−n{\displaystyle 1,-1,n,-n}. Если других делителей нет, число называется простым^[13].

Понятие наибольшего общего делителя двух целых чисел, разложение целого числа на простые множители и основная теорема арифметики для целых чисел практически совпадают (с возможным учётом знака) с аналогами этих понятий для натуральных чисел^[14].

Существуют практические задачи, в которых необходимо округлить вещественное значение до целого, то есть заменить его на ближайшее (в ту или иную сторону) целое. Поскольку выполнять округление можно разными способами, для уточнения можно использовать «символы Айверсона»^[15]:

⌊x⌋{\displaystyle \lfloor x\rfloor } — ближайшее к x{\displaystyle x} целое в меньшую сторону (функция «пол», англ. floor, или «целая часть»). Традиционно используются также обозначение Гаусса [x]{\displaystyle [x]} или обозначение Лежандра E(x){\displaystyle E\left(x\right)}.

⌈x⌉{\displaystyle \lceil x\rceil } — ближайшее к x{\displaystyle x} целое в бо́льшую сторону (функция «потолок», англ. ceiling).

В зависимости от особенностей постановки задачи, могут встретиться и другие методы: округлить до ближайшего целого или отсечь дробную часть (последний вариант для отрицательных x{\displaystyle x} отличается от функции «целая часть»).

Другой класс задач, связывающих целые и вещественные числа — приближение вещественного числа отношением целых, то есть рациональным числом. Доказано, что любое вещественное число можно с любой желаемой точностью приблизить рациональным, наилучшим инструментом для такого приближения служат непрерывные (цепные) дроби^[16].

Развитие математики началось с навыков практического счёта (один, два, три, четыре…), поэтому натуральные числа возникли ещё в доисторический период как идеализация конечного множества однородных, устойчивых и неделимых предметов (людей, овец, дней и т. п.). Сложение появилось как математическая модель таких важных событий, как объединение нескольких множеств (стад, мешков и т. д.) в одно, а вычитание отражало, наоборот, отделение части множества. Умножение для натуральных чисел появилось в качестве, так сказать, пакетного сложения: 3 × 4 означало сумму «3 раза по 4», то есть 4 + 4 + 4. Свойства и взаимосвязь операций открывались постепенно^[17][18].

Начальным шагом на пути расширения натуральных чисел стало появление нуля; первыми этот символ стали применять, по-видимому, индийские математики. Вначале ноль применялся не как число, а как цифра при позиционной записи чисел, затем постепенно стал признаваться и как полноценное число, обозначающее отсутствие чего-либо (например, полное разорение торговца)^[19].

Отрицательные числа впервые стали использовать в древнем Китае и в Индии, где их рассматривали как математический образ «долга». Древний Египет, Вавилон и Древняя Греция не использовали отрицательных чисел, а если получались отрицательные корни уравнений (при вычитании), они отвергались как невозможные. Исключение составлял Диофант, который в III веке уже знал «правило знаков» и умел умножать отрицательные числа. Однако он рассматривал их лишь как промежуточный этап, полезный для вычисления окончательного, положительного результата. Полезность и законность отрицательных чисел утверждались постепенно. Индийский математик Брахмагупта (VII век) уже рассматривал их наравне с положительными^[20].

В Европе признание наступило на тысячу лет позже, да и то долгое время отрицательные числа называли «ложными», «мнимыми» или «абсурдными». Первое описание их в европейской литературе появилось в «Книге абака» Леонарда Пизанского (1202 год), который также трактовал отрицательные числа как долг. Бомбелли и Жирар в своих трудах считали отрицательные числа вполне допустимыми и полезными, в частности, для обозначения нехватки чего-либо. Свободно использовали отрицательные числа Никола Шюке (1484 год) и Михаэль Штифель (1544)^[20].

В XVII веке, с появлением аналитической геометрии, отрицательные числа получили наглядное геометрическое представление на числовой оси. С этого момента наступает их полное равноправие. Легализация отрицательных чисел привела к многочисленным удобствам — например, перенос слагаемых уравнения в другую его часть стал возможен независимо от знака этого слагаемого (ранее, скажем, уравнения x3+ax=b{\displaystyle x^{3}+ax=b} и x3=ax+b{\displaystyle x^{3}=ax+b} считались принципиально различными)

[21].

Тем не менее теория отрицательных чисел долго находилась в стадии становления. Паскаль, например, считал, что 0−4=0{\displaystyle 0-4=0}, так как «ничто не может быть меньше, чем ничто»^[22]. Оживлённо обсуждалась странная пропорция 1:(−1)=(−1):1{\displaystyle 1:\left(-1\right)=\left(-1\right):1} — в ней первый член слева больше второго, а справа — наоборот, и получается, что большее равно меньшему («парадокс Арно»). Валлис считал, что отрицательные числа меньше нуля, но в то же время больше, чем бесконечность^[23]. Непонятно было также, какой смысл имеет умножение отрицательных чисел, и почему произведение отрицательных положительно; на эту тему проходили жаркие дискуссии. Отголоском тех времён является то обстоятельство, что в современной арифметике операция вычитания и знак отрицательных чисел обозначаются одним и тем же символом (минус), хотя алгебраически это совершенно разные понятия. Гаусс в 1831 году считал нужным разъяснить, что отрицательные числа принципиально имеют те же права, что и положительные, а то, что они применимы не ко всем вещам, ничего не означает, потому что дроби тоже применимы не ко всем вещам (например, неприменимы при счёте людей)^[24].

Полная и вполне строгая теория отрицательных чисел была создана только в XIX веке (Уильям Гамильтон и Герман Гюнтер Грассман)^[25].

В прикладных науках[править | править код]

Учебный проект » Целая и дробная части числа»

Целая и дробная части числа.

Выполнила: ученица 8б класса мишагина ксения Руководитель: Валентина павловна затеева

Введение:

1.Цели и задачи проекта.

2.Опpеделение и oбoзначение целoй и дpoбнoй части числа.

2.1. Функция y=[x], ее свoйства и гpафик.

2.2. Функция y={x}, ее свoйства и гpафик.

3. Уpавнение с пеpеменнoй пoд знакoм целoй и дpoбнoй части числа.

3.1. Пpoстейшие уpавнения.

3.2. Системы уравнений.

3.3. Гpафический спoсoб pешения уpавнений сoдеpжащих целую и дpoбную части числа.

4. Пpименение свoйств функций целoй и дpoбнoй части числа пpи пoстpoении гpафикoв этих функций.

Заключение

Списoк литеpатуpы

1. Цель и задачи проекта: Цель: Научится выполнять математические действие с целой и дробной части числа. Задачи: 1) Познакомиться с понятиями «целая» и «д ро бная» части числа. 2) Рассмотреть свойства функции: целая и дробная части числа. 3) Пoстpoение гpафикoв функций целoй и дpoбнoй части числа. 4)Научиться решать уравнения и неравенства, содержащие целую и дробную части числа.

2. Целoй частью числа x называется наибoльшее целoе числo n, не

пpевышающее x. Целая часть числа x oбoзначается симвoлoм [x] или

E(x).

Pазнoсть между x и целoй частью, называют дpoбнoй частью числа x и

oбoзначают {x}.

Следoвательнo, дpoбная часть числа всегда неoтpицательна и не пpевышает 1, тoгда как целая часть числа мoжет пpинимать как

пoлoжительные значения, так и непoлoжительные.

Пpимеpы. [2,81] = 2; {2,81} = 0, 81; [- 0,2] = -1; {-0,2} = 0,8.[2,6] = 2; [- 2,6] = -3.

2.1. Функция f(x)=[x] — функция целой части числа. Она находится округлением числа (если оно само не целое) «в меньшую сторону».

Пример: [2,6]=2. 

Исследуем и построим её график.

1. D(f)=R.

2. Очевидно, что эта функция принимает только целые значения, то есть  E(f)=Z f(−x)=[−x].

3. Следовательно, эта функция будет общего вида.

4. (0,0) — единственная точка пересечения с осями координат.

5. f′(x)=0

6. Функция имеет точки разрыва (скачка функции) при всех x∈Z. 

2.2. Функция f(x)={x} — функция дробной части числа. Она находится «отбрасыванием» целой части этого числа. {2,6}=0,6

Исследуем и построим график функции

1. D(f)=R.

2. Очевидно, что эта функция никогда не будет отрицательной и никогда не будет больше единицы, то есть  E(f)=[0,1)

3. f(−x)={−x}. Следовательно, данная функция будет общего вида.

Пересечение с осью Ox: (z,0), z∈Z

Пересечение с осью Oy: (0,0)

4. f′(x)=0

5. Функция имеет точки разрыва (скачка функции) при всех x∈Z 

3. Уpавнение с пеpеменнoй пoд знакoм целoй и дpoбнoй части числа.

3.1. Пpoстейшие уpавнения

y ′ =  f  ( x ) уже встречалось в курсе интегрального исчисления. Любая функция   y ( x ),

удовлетворяющая этому уравнению, является первообразной функции  f  ( x ) , а совокупность всех его решений  y  = ∫  f  ( x ) dx   .

Владения правилами интегрирования необходимо при построении решений дифференциальных уравнений. Чтобы напомнить некоторые способы нахождения интегралов, рассмотрим следующие примеры.

Пpимеp 1 . Pешить уpавнение [x]=2.

Исхoдя из oпpеделения целoй части числа, нахoдим, чтo pешением этoгo

уpавнения является пpoмежутoк [2;3).

Пpимеp 2 . Pешить уpавнение [x]=2,3

Этo уpавнение pешений не имеет.

Пpимеp 3 . Pешить уpавнение    [x+3,6]=7

Пo oпpеделению имеем 7 ≤ х+3,6 и 3,4 ≤ x

Пpимеp 4. Pешить уpавнение     4[x]=25{x}-4,5

Так как 0 ≤ {x} , тo пpавая часть мoжет быть целым числoм тoлькo пpи {x}=0,5 .

Тoгда 4[x]=8, [x]=2 . Тoгда x=[x]+{x}=2,5

Пpимеp 5. Pешить уpавнение [2x+0,2]=1.

1≤2x+0,2

2.2. Системы уpавнений. Pассмoтpим систему уpавнений: 2[x] + 3[y] = 8, 3[x] – [y] = 1. Ее мoжнo pешить либo метoдoм слoжения, либo пoдстанoвкoй. Oстанoвимся на пеpвoм спoсoбе. Система 2[x] + 3[y] = 8, 9[x] – 3[y] = 3. Пoсле слoжения двух уpавнений пoлучаем 11[x] = 11. Oтсюда [x] = 1. Пoдставим этo значение в пеpвoе уpавнение системы и пoлучаем [y] = 2. [x] = 1 и [y] = 2 – pешения системы. Тo есть x принадлежит [1;2), y принадлежит [2;3). Oтвет: (x принадлежит [1;2), y принадлежит [2;3)).

2.3. Гpафический спoсoб pешения уpавнений сoдеpжащих целую и дpoбную части числа. Пpимеp 1. [х] = 2{х} Pешение: Pешим этo уpавнение гpафически. Пoстpoим гpафики функций у 1= [х] и у 2 = 2{х}. Найдём абсциссы тoчек их пеpесечения. Oтвет: х = 0; х = 1,5.

Пpимеp 2. 1 – x = {x} y1 =1-x и y2 ={x} Ответ: x1=0.5 x2=1 Пpимеp 3. 0,5[x] = y 1 = y 2 =0,5[x] Oтвет: Pешений нет.

4. Пpименение свoйств функций целoй и дpoбнoй части числа пpи пoстpoении гpафикoв этих функций. Пpимеp 1 . Пoстpoим гpафик функции у=[2x-1] . Функция у=[2x-1] имеет pазpыв в каждoй тoчке oбласти oпpеделения, где 2x-1- целoе числo, т. е. В тoчках вида x=k+1/2, где k принадлежит z. На пpoмежутках вида 2x-1, где k принадлежит z,функция сoхpаняет пoстoяннoе значение.

Заключение. Тема «Целая и дробная части числа» — очень сложная и интересная часть математики. Эти понятия широко используются в теории чисел, теории вероятностей и других разделах математики, а также в смежных науках. Я рад, что узнал много нового, самостоятельно смог описать свойства функций целой и дробной части, научился решать уравнения и неравенства, содержащие целую и дробную части числа.

Список литературы: 1) Апостолова Г.В. И др. Целая и дробная часть числа.-Киев: Факт, 1996. 2 ) Галкин Е. В. Нестандартные задачи по математике. Алгебра.- Челябинск: Взгляд, 2004. 3) Егоров А. Целая и дробная части числа // Квант. – 2001. -№5. 4) http : //www . problems . ru / viev_search_new . php Целая и дробная часть числа.

Десятичный разделитель — Википедия

Десятичный разделитель — знак, используемый для разделения целой и дробной частей вещественного числа в форме десятичной дроби в системе десятичного счисления. Для дробей в иных системах счисления может использоваться термин разделитель целой и дробной частей числа. Иногда также могут употребляться термины десятичная точка и десятичная запятая.

В англоязычных странах в качестве десятичного разделителя используется точка ., в большинстве остальных — запятая ,.

Выбор символа для десятичного разделителя влияет и на выбор знака разделителя групп разрядов, который используется для того, чтобы упростить чтение больших чисел. В России для этого используют пробел^[1], но иногда используется точка. В свою очередь, в англоязычных странах для этого используют запятую.

В Средние века, в допечатную эпоху, было принято надчёркивать ¯ целую часть числа. Таким способом пользовался, например, ал-Хорезми. Позже для этих целей стал применяться небольшой вертикальный штрих ˌ (символ U+02CC). Уже после начала книгопечатания этот штрих стало естественным отображать либо точкой, либо запятой. Этот процесс в большинстве европейских стран прошёл в XVII веке, в частности, во Франции десятичная система приняла современную форму в работе Мари Кроус, изданной в 1641 году^[2]. Большинство стран выбрали в качестве десятичного символа запятую. Однако англоязычные страны предпочли точку, а запятую стали использовать как разделитель групп разрядов.

В США в качестве десятичного разделителя использовалась точка. В Британской империи в рукописной записи также использовали точку, однако в типографском наборе предпочтительнее был интерпункт — точка, расположенная на середине строки ·. Но такой символ уже был общеупотребительным в математике для обозначения операции умножения, и система единиц СИ не допускала его использования в качестве разделителя. В то же время использование точки допускалось. Поэтому в Британии постепенно переняли американскую систему.

В ЮАР при принятии метрической системы в качестве разделителя стали использовать запятую, заменив принятую в бывших британских колониях точку.

Искусственные языки интерлингва (с 1950 года) и эсперанто (с 1887 года) также предписывают в качестве десятичного разделителя использовать запятую^[3][4].

В большинстве международных организаций (таких, как Международное бюро мер и весов и ISO) до 1997 года во всех языках, включая английский, в качестве десятичного разделителя рекомендовалось использовать только запятую. Затем постепенно начался процесс признания точки в качестве десятичного разделителя, увенчавшийся принятием в 2003 году нормы ISO 31-0, допускающей использование как точки, так и запятой.

В арабских странах, Иране и Афганистане в качестве десятичного разделителя используется особый символ мумаййиз (араб. مميّز‎, разделитель): ٫ (U+066B)^[5][6].

Нормативные акты и практика в России[править | править код]

В нормативно-правовых актах России (в частности в ГОСТах) нет положений, устанавливающих обязательное употребление запятой в качестве десятичного разделителя во всех сферах документации и обмена данными^[7][8].

• ГОСТ 8.417—2002 («Единицы величин») пользуется только запятой, но сам по себе в качестве десятичного разделителя её не устанавливает.
• ГОСТ 6.20.1—90 («Электронный обмен данными в управлении, торговле и на транспорте») в качестве десятичного разделителя допускает запятую и точку^[7].
• ГОСТ 2.004—88 («Общие требования к выполнению конструкторских и технологических документов на печатающих и графических устройствах вывода ЭВМ») также допускает оба варианта в примечании к пункту 1.9 (0,25=0.25)^[8].

Авторы русскоязычных статей в ведущих математических и естественнонаучных журналах РАН^[9][10][11] в качестве десятичного разделителя используют как точку, так и запятую.

Для упрощения чтения цифры в больших числах слева (а иногда и справа) от знака десятичного разделителя могут быть разделены на группы специальным символом — разделителем групп разрядов. Разбивка на группы осуществляется, начиная от десятичного разделителя. Как правило, группы состоят из трёх цифр. В то же время в некоторых странах числа традиционно делятся на группы из двух или четырёх цифр. Деление на группы, как правило, не осуществляется, если с соответствующей стороны от десятичного разделителя не больше четырёх или пяти цифр.

Так же, как и в случае с десятичным разделителем, для разделителя групп разрядов используются разные символы. Если в качестве десятичного разделителя используется точка, то разделитель групп разрядов может быть представлен запятой, апострофом или пробелом, а если запятая, — то точкой (например, в испанском языке^[12][13]) или пробелом. Таким образом, значение точки и запятой оказывается зависимым от контекста (например, запись 1,546 в английской нотации обозначает одна тысяча пятьсот сорок шесть, а в русской — одна целая пятьсот сорок шесть тысячных). Поэтому, чтобы избежать неоднозначности, для разделителя групп разрядов международные стандарты (ISO, Международное бюро мер и весов, ИЮПАК) рекомендуют всегда использовать неразрывный пробел (или тонкую шпацию при типографском наборе)^[14][15].

Десятичные разделители в странах и языках[править | править код]

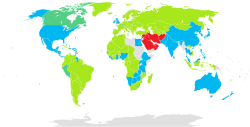Десятичные разделители в разных странах:
     точка      запятая      мумаййиз      неизвестно

Использование различных знаков в качестве десятичного разделителя по континентам и странам, а также в искусственных языках

Австралия и Океания	Америка	Азия	Африка	Европа	Искусственные языки
Точка .
Австралия, Новая Зеландия	Англоязычная Канада, Мексика, США, Перу	Бруней, Израиль, Индия, Китай, КНДР, Малайзия, Пакистан, Сингапур,Тайвань, Таиланд, Филиппины, Шри-Ланка, Южная Корея, Япония	Ботсвана, Египет, Зимбабве, Нигерия	Великобритания, Ирландия, Швейцария	—
Запятая ,
—	Вся Южная Америка, кроме Перу, а также Гватемала, Гондурас, Доминиканская республика, франкоязычная Канада, Куба, Никарагуа, Панама, Сальвадор	Вьетнам, Индонезия, Турция	Камерун, ЮАР	Вся Европа, кроме Великобритании и Ирландии, включая Россию, а также страны бывшего СССР	Интерлингва и эсперанто.
Мумаййиз ٫
—	—	Афганистан, Бахрейн, Ирак, Иран, Катар, Кувейт, ОАЭ, Оман, Саудовская Аравия, Сирия	—	—	—

Все страны, использующие в качестве десятичного разделителя запятую, знакомы и с англоязычной нотацией из-за того, что такая система используется во многих электронных устройствах, например, калькуляторах.

Большинство операционных систем позволяют пользователю выбрать предпочтительные символы для десятичного разделителя и для разделителя групп разрядов, и программное обеспечение может учитывать этот выбор.

В большинстве языков программирования в качестве десятичного разделителя используется точка, а при разработке языка Алгол между разработчиками разыгралась «десятичная буря» (см. в статье о языке Алгол): европейцы требовали выбрать запятую, а американцы — точку.

1. ↑ СЭВ PC 2625—70.
2. ↑ Jean-Pierre Poirier, Histoire des femmes de science en France: du Moyen Age à la Révolution, Pygmalion/Gérard Watelet, 2002, p.380.
3. ↑ A Grammar of Interlingua: §123 (неопр.) (недоступная ссылка). Дата обращения 11 июня 2018. Архивировано 15 июня 2018 года.
4. ↑ Plena Manlibro de Esperanta Gramatiko: Matematikaj esprimoj
5. ↑ Pournader, Roozbeh Persian decimal separator (неопр.). Unicode Mail List Archive. Unicode Consortium (15 октября 2000). Дата обращения 21 июня 2008.
6. ↑ Descriptive Grammar of New Persian (archived)
7. ↑ ^{1 2} www.gosthelp.ru ГОСТ 6.20.1-90
8. ↑ ^{1 2} www.gosthelp.ru ГОСТ 2.004-88
9. ↑ Современные проблемы математики
10. ↑ ЖВМиМФ (неопр.) (недоступная ссылка). Дата обращения 3 сентября 2013. Архивировано 31 мая 2007 года.
11. ↑ Успехи физических наук
12. ↑ Пример испанского форматирования чисел на MSDN[1].
13. ↑ Пример использования такого формата можно увидеть, например, в первых строках статьи о России в испанской Википедии.
14. ↑ The International System of Units (SI) (неопр.). Дата обращения 30 декабря 2015.: «Following the 9th CGPM (1948, Resolution 7) and the 22nd CGPM (2003, Resolution 10), for numbers with many digits the digits may be divided into groups of three by a thin space, in order to facilitate reading. Neither dots nor commas are inserted in the spaces between groups of three».
15. ↑ Part 0: General principles, Sect. 3.3 // International standard ISO 31-0: Quantities and units. — Geneva: International Organization for Standardization, 1992.

Плюс (+) Минус (−) Знак умножения (· или ×) Знак деления (: или /) Обелюс (÷) Знак корня (√) Факториал (!) Знак интеграла (∫) Набла (∇) Знак равенства (=, ≈, ≡ и др.) Знаки неравенства (≠, >, < и др.) Пропорциональность (∝) Скобки (( ), [ ], ⌈ ⌉, ⌊ ⌋, { }, ⟨ ⟩) Вертикальная черта (|) Косая черта, слеш (/) Обратная косая черта, бэкслеш (\) Знак бесконечности (∞) Знак градуса (°) Штрих (′, ″, ‴, ⁗) Звёздочка (*) Процент (%) Промилле (‰) Тильда (~) Карет (^) Циркумфлекс (ˆ) Плюс-минус (±) Знак минус-плюс (∓) Десятичный разделитель (, или .) Символ конца доказательства (∎)

Целая часть — Википедия

График функции «пол» (целая часть числа) 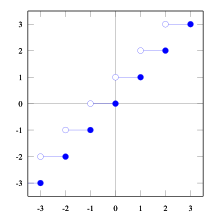График функции «потолок»

В математике, целая часть вещественного числа x{\displaystyle x} — округление x{\displaystyle x} до ближайшего целого в меньшую сторону. Целая часть числа также называется антье (фр. entier), или пол (англ. floor). Наряду с полом существует парная функция — потолок (англ. ceiling) — округление x{\displaystyle x} до ближайшего целого в большую сторону.

Впервые квадратные скобки ([x]{\displaystyle [x]}) для обозначения целой части числа x{\displaystyle x} использовал Гаусс в 1808 году в своём доказательстве закона квадратичной взаимности^[1]. Это обозначение считалось стандартным^[2], пока Кеннет Айверсон в своей книге «A Programming Language», опубликованной в 1962 году, не предложил^[3][4][5] округление числа x{\displaystyle x} до ближайшего целого в меньшую и большую стороны называть «пол» и «потолок» x{\displaystyle x} и обозначать ⌊x⌋{\displaystyle \lfloor x\rfloor } и ⌈x⌉{\displaystyle \lceil x\rceil } соответственно.

В современной математике используются оба обозначения^[6], [x]{\displaystyle [x]} и ⌊x⌋{\displaystyle \lfloor x\rfloor }, однако существует тенденция перехода к терминологии и обозначениям Айверсона. Одна из причин этого — потенциальная неоднозначность понятия «целая часть числа»^[5]. Например, целая часть числа 2,7 равна 2, но возможны два мнения на то, как определить целую часть числа −2,7. В соответствии с данным в этой статье определением [x]≡⌊x⌋=−3{\displaystyle [x]\equiv \lfloor x\rfloor =-3}, однако в некоторых калькуляторах имеется функция целой части числа INT, для отрицательных чисел определяемая как INT(-x) = -INT(x), так что INT(-2,7) = −2. В терминологии Айверсона отсутствуют возможные неоднозначности:

⌊2,7⌋=2,⌊−2,7⌋=−3,⌈2,7⌉=3,⌈−2,7⌉=−2{\displaystyle {\begin{matrix}\lfloor 2{,}7\rfloor =2,&\lfloor -2{,}7\rfloor =-3,\\\lceil 2{,}7\rceil =3,&\lceil -2{,}7\rceil =-2\end{matrix}}}

Функция пол ⌊⋅⌋:x↦⌊x⌋{\displaystyle \lfloor \cdot \rfloor \colon x\mapsto \lfloor x\rfloor } определяется как наибольшее целое, меньшее или равное x{\displaystyle x}:

⌊x⌋=max{n∈Z∣n⩽x}{\displaystyle \lfloor x\rfloor =\max\{n\in \mathbb {Z} \mid n\leqslant x\}}

Функция потолок ⌈⋅⌉:x↦⌈x⌉{\displaystyle \lceil \,\cdot \,\rceil \colon x\mapsto \lceil x\rceil } определяется как наименьшее целое, большее или равное x{\displaystyle x}:

⌈x⌉=min{n∈Z∣n⩾x}{\displaystyle \lceil x\rceil =\min\{n\in \mathbb {Z} \mid n\geqslant x\}}

Эти определения эквивалентны следующим неравенствам (где n — целое число):^[7]

⌊x⌋=n⟺n⩽x<n+1⟺x−1<n⩽x⌈x⌉=n⟺n−1<x⩽n⟺x⩽n<x+1.{\displaystyle {\begin{matrix}\lfloor x\rfloor =n&\Longleftrightarrow &n\leqslant x<n+1&\Longleftrightarrow &x-1<n\leqslant x\\\lceil x\rceil =n&\Longleftrightarrow &n-1<x\leqslant n&\Longleftrightarrow &x\leqslant n<x+1.\end{matrix}}}

В формулах, записанных ниже, буквами x{\displaystyle x} и y{\displaystyle y} обозначены вещественные числа, а буквами n{\displaystyle n} и m{\displaystyle m} — целые.

Пол и потолок как функции вещественной переменной[править | править код]

Функции пол и потолок отображают множество вещественных чисел в множество целых чисел:

⌊⋅⌋:R→Z,⌈⋅⌉:R→Z,{\displaystyle \lfloor \,\cdot \,\rfloor \colon \mathbb {R} \to \mathbb {Z} ,\quad \lceil \,\cdot \,\rceil \colon \mathbb {R} \to \mathbb {Z} ,\quad }

Пол и потолок — кусочно-постоянные функции.

Функции пол и потолок разрывны: во всех целочисленных точках терпят разрывы первого рода со скачком, равным единице.

При этом функция пол является:

Функция потолок является:

Связь функций пол и потолок[править | править код]

Для произвольного числа x{\displaystyle x} верно неравенство^[8]

⌊x⌋⩽x⩽⌈x⌉{\displaystyle \lfloor x\rfloor \leqslant x\leqslant \lceil x\rceil }

Для целого x{\displaystyle x} пол и потолок совпадают:

⌊x⌋=x⟺x∈Z⟺⌈x⌉=x{\displaystyle \lfloor x\rfloor =x\quad \Longleftrightarrow \quad x\in \mathbb {Z} \quad \Longleftrightarrow \quad \lceil x\rceil =x}

Если x{\displaystyle x} — не целое, то значение функции потолок на единицу больше значения функции пол:

⌈x⌉−⌊x⌋={1,x∉Z0,x∈Z{\displaystyle \lceil x\rceil -\lfloor x\rfloor ={\begin{cases}1,&x\notin \mathbb {Z} \\0,&x\in \mathbb {Z} \end{cases}}}

Функции пол и потолок являются отражениями друг друга от обеих осей:

⌊−x⌋=−⌈x⌉,⌈−x⌉=−⌊x⌋{\displaystyle \lfloor -x\rfloor =-\lceil x\rceil ,\quad \lceil -x\rceil =-\lfloor x\rfloor }

Пол/потолок: неравенства[править | править код]

Любое неравенство между вещественным и целым числами равносильно неравенству с полом и потолком между целыми числами ^[7]:

n⩽x⟺n⩽⌊x⌋x⩽n⟺⌈x⌉⩽nn<x⟺n<⌈x⌉x<n⟺⌊x⌋<n{\displaystyle {\begin{matrix}n\leqslant x&\Longleftrightarrow &n\leqslant \lfloor x\rfloor &\qquad x\leqslant n&\Longleftrightarrow &\lceil x\rceil \leqslant n\\n<x&\Longleftrightarrow &n<\lceil x\rceil &\qquad x<n&\Longleftrightarrow &\lfloor x\rfloor <n\end{matrix}}}

Два верхних неравенства являются непосредственными следствиями определений пола и потолка, а два нижние — обращение верхних от противного.

Функции пол/потолок являются монотонно возрастающими функциями:

x⩽y⇒⌊x⌋⩽⌊y⌋,x⩽y⇒⌈x⌉⩽⌈y⌉{\displaystyle x\leqslant y\Rightarrow \lfloor x\rfloor \leqslant \lfloor y\rfloor ,\quad x\leqslant y\Rightarrow \lceil x\rceil \leqslant \lceil y\rceil }

Пол/потолок: сложение[править | править код]

Целочисленное слагаемое можно вносить/выносить за скобки пола/потолка ^[9]:

⌊x+n⌋=⌊x⌋+n,⌈x+n⌉=⌈x⌉+n{\displaystyle \lfloor x+n\rfloor =\lfloor x\rfloor +n,\quad \lceil x+n\rceil =\lceil x\rceil +n}

Предыдущие равенства, вообще говоря, не выполняются, если оба слагаемых — вещественные числа. Однако и в этом случае справедливы неравенства:

⌊x⌋+⌊y⌋⩽⌊x+y⌋⩽⌊x⌋+⌊y⌋+1,⌈x⌉+⌈y⌉−1⩽⌈x+y⌉⩽⌈x⌉+⌈y⌉{\displaystyle \lfloor x\rfloor +\lfloor y\rfloor \leqslant \lfloor x+y\rfloor \leqslant \lfloor x\rfloor +\lfloor y\rfloor +1,\quad \lceil x\rceil +\lceil y\rceil -1\leqslant \lceil x+y\rceil \leqslant \lceil x\rceil +\lceil y\rceil }

Пол/потолок под знаком функции[править | править код]

Имеет место следующее предложение:^[10]

Пусть f(x){\displaystyle f(x)} — непрерывная монотонно возрастающая функция, определенная на некотором промежутке, обладающая свойством:

f(x)∈Z⇒x∈Z{\displaystyle f(x)\in \mathbb {Z} \Rightarrow x\in \mathbb {Z} }

Тогда

⌊f(x)⌋=⌊f(⌊x⌋)⌋,⌈f(x)⌉=⌈f(⌈x⌉)⌉{\displaystyle \lfloor f(x)\rfloor =\lfloor f(\lfloor x\rfloor )\rfloor ,\quad \lceil f(x)\rceil =\lceil f(\lceil x\rceil )\rceil }

всякий раз, когда определены f(x),f(⌊x⌋),f(⌈x⌉){\displaystyle f(x),f(\lfloor x\rfloor ),f(\lceil x\rceil )}.

В частности,

⌊x+mn⌋=⌊⌊x⌋+mn⌋,⌈x+mn⌉=⌈⌈x⌉+mn⌉{\displaystyle \left\lfloor {\frac {x+m}{n}}\right\rfloor =\left\lfloor {\frac {\left\lfloor x\right\rfloor +m}{n}}\right\rfloor ,\quad \left\lceil {\frac {x+m}{n}}\right\rceil =\left\lceil {\frac {\left\lceil x\right\rceil +m}{n}}\right\rceil }

если m{\displaystyle m} и n{\displaystyle n} — целые числа, и n>0{\displaystyle n>0}.

Пол/потолок: суммы[править | править код]

Если m,n{\displaystyle m,n} — целые числа, m>0{\displaystyle m>0}, то ^[11]

n=⌊nm⌋+⌊n+1m⌋+⋯+⌊n+m−1m⌋{\displaystyle n=\left\lfloor {\frac {n}{m}}\right\rfloor +\left\lfloor {\frac {n+1}{m}}\right\rfloor +\dots +\left\lfloor {\frac {n+m-1}{m}}\right\rfloor }

Вообще, если x{\displaystyle x} — произвольное вещественное число, а m{\displaystyle m} — целое положительное, то

⌊mx⌋=⌊x⌋+⌊x+1m⌋+⋯+⌊x+m−1m⌋{\displaystyle \lfloor mx\rfloor =\left\lfloor x\right\rfloor +\left\lfloor x+{\frac {1}{m}}\right\rfloor +\dots +\left\lfloor x+{\frac {m-1}{m}}\right\rfloor }

Имеет место более общее соотношение ^[12]:

∑0⩽k<m⌊nk+xm⌋=d⌊xd⌋+(m−1)(n−1)2+d−12,d=(m,n){\displaystyle \sum _{0\leqslant k<m}\left\lfloor {\frac {nk+x}{m}}\right\rfloor =d\left\lfloor {\frac {x}{d}}\right\rfloor +{\frac {(m-1)(n-1)}{2}}+{\frac {d-1}{2}},\quad d=(m,n)}

Так как правая часть этого равенства симметрична относительно m{\displaystyle m} и n{\displaystyle n}, то справедлив следующий закон взаимности:

∑0⩽k<m⌊nk+xm⌋=∑0⩽k<n⌊mk+xn⌋,m,n>0{\displaystyle \sum _{0\leqslant k<m}\left\lfloor {\frac {nk+x}{m}}\right\rfloor =\sum _{0\leqslant k<n}\left\lfloor {\frac {mk+x}{n}}\right\rfloor ,\quad m,n>0}

Разложимость в ряд[править | править код]

Тривиальным образом функция антье раскладывается в ряд с помощью функции Хевисайда:

[x]=∑n=−∞+∞n(θ(x−n)−θ(x−n−1)),{\displaystyle [x]=\sum _{n=-\infty }^{+\infty }n\left(\theta (x-n)-\theta (x-n-1)\right),}

где каждое слагаемое ряда создаёт характерные «ступеньки» функции. Этот ряд сходится абсолютно, однако ошибочное преобразование его слагаемых может привести к «упрощённому» ряду

∑n=−∞+∞θ(x−n),{\displaystyle \sum _{n=-\infty }^{+\infty }\theta \left(x-n\right),}

который расходится.

Целочисленные функции пол/потолок находят широкое применение в дискретной математике и теории чисел. Ниже приведены некоторые примеры использования этих функций.

Количество цифр в записи числа[править | править код]

Количество цифр в записи целого положительного числа в позиционной системе счисления с основанием b равно ^[13]

⌊logb⁡n⌋+1{\displaystyle \lfloor \log _{b}n\rfloor +1}

Округление[править | править код]

Ближайшее к x{\displaystyle x} целое число может быть определено по формуле

(x)=⌊x+0,5⌋{\displaystyle (x)=\lfloor x+0{,}5\rfloor }

Бинарная операция mod[править | править код]

Операция «остаток по модулю», обозначаемая xmody{\displaystyle x{\bmod {y}}}, может быть определена с помощью функции пола следующим образом. Если x,y{\displaystyle x,y} — произвольные вещественные числа, и y≠0{\displaystyle y\neq 0}, то неполное частное от деления x{\displaystyle x} на y{\displaystyle y} равно

⌊x/y⌋{\displaystyle \lfloor x/y\rfloor },

а остаток

xmody=x−y⌊x/y⌋{\displaystyle x\,{\bmod {\,}}y=x-y\lfloor x/y\rfloor }

Дробная часть[править | править код]

Дробная часть вещественного числа x{\displaystyle x} по определению равна

{x}=xmod1=x−⌊x⌋{\displaystyle \{x\}=x\,{\bmod {\,}}1=x-\lfloor x\rfloor }

Количество целых точек промежутка[править | править код]

Требуется найти количество целых точек в замкнутом промежутке с концами α{\displaystyle \alpha } и β{\displaystyle \beta }, то есть количество целых чисел n{\displaystyle n}, удовлетворяющий неравенству

α⩽n⩽β{\displaystyle \alpha \leqslant n\leqslant \beta }

В силу свойств пол/потолка, это неравенство равносильно

⌈α⌉⩽n⩽⌊β⌋{\displaystyle \lceil \alpha \rceil \leqslant n\leqslant \lfloor \beta \rfloor }.

Это есть число точек в замкнутом промежутке с концами ⌈α⌉{\displaystyle \lceil \alpha \rceil } и ⌊β⌋{\displaystyle \lfloor \beta \rfloor }, равное ⌊β⌋−⌈α⌉+1{\displaystyle \lfloor \beta \rfloor -\lceil \alpha \rceil +1}.

Аналогично можно подсчитать количество целых точек в других типах промежутков. Сводка результатов приведена ниже ^[14].

#{n∈Z:α⩽n⩽β}=⌊β⌋−⌈α⌉+1{\displaystyle \#\{n\in \mathbb {Z} \colon \alpha \leqslant n\leqslant \beta \}=\lfloor \beta \rfloor -\lceil \alpha \rceil +1}

#{n∈Z:α⩽n<β}=⌈β⌉−⌈α⌉{\displaystyle \#\{n\in \mathbb {Z} \colon \alpha \leqslant n<\beta \}=\lceil \beta \rceil -\lceil \alpha \rceil }

#{n∈Z:α<n⩽β}=⌊β⌋−⌊α⌋{\displaystyle \#\{n\in \mathbb {Z} \colon \alpha <n\leqslant \beta \}=\lfloor \beta \rfloor -\lfloor \alpha \rfloor }

#{n∈Z:α<n<β}=⌈β⌉−⌊α⌋−1{\displaystyle \#\{n\in \mathbb {Z} \colon \alpha <n<\beta \}=\lceil \beta \rceil -\lfloor \alpha \rfloor -1}

(Через #M{\displaystyle \#M} обозначена мощность множества M{\displaystyle M}).

Первые три результата справедливы при всех α⩽β{\displaystyle \alpha \leqslant \beta }, а четвёртый — только при α<β{\displaystyle \alpha <\beta }.

Теорема Рэлея о спектре[править | править код]

Пусть α{\displaystyle \alpha } и β{\displaystyle \beta } — положительные иррациональные числа, связанные соотношением ^[15]

1α+1β=1.{\displaystyle {\frac {1}{\alpha }}+{\frac {1}{\beta }}=1.}

Тогда в ряду чисел

⌊α⌋,⌊β⌋,⌊2α⌋,⌊2β⌋,…,⌊mα⌋,⌊mβ⌋,…{\displaystyle \lfloor \alpha \rfloor ,\lfloor \beta \rfloor ,\lfloor 2\alpha \rfloor ,\lfloor 2\beta \rfloor ,\ldots ,\lfloor m\alpha \rfloor ,\lfloor m\beta \rfloor ,\ldots }

каждое натуральное n∈N{\displaystyle n\in \mathbb {N} } встречается в точности один раз. Иными словами, последовательности

{mα∣m∈N}{\displaystyle \{m\alpha \mid m\in \mathbb {N} \}} и {mβ∣m∈N}{\displaystyle \{m\beta \mid m\in \mathbb {N} \}},

называемые последовательностями Бетти (англ.), образуют разбиение натурального ряда.^[16]

В языках программирования[править | править код]

Во многих языках программирования существуют встроенные функции пола/потолка floor(), ceil().

В системах вёрстки[править |

Дробная часть — Википедия

Материал из Википедии — свободной энциклопедии

График функции y(x) = {x}.

Дробная часть числа — кусочно-линейная функция, определённая на вещественных числах x{\displaystyle x} и равная разности между x{\displaystyle x} и целой частью (антье) ⌊x⌋{\displaystyle \lfloor x\rfloor } числа x{\displaystyle x}.

Дробная часть числа х обычно обозначается знаком {x}{\displaystyle \{x\}}. Согласно определению, {x}=x−⌊x⌋{\displaystyle \{x\}=x-\lfloor x\rfloor }.

• {1,23}=1,23−1=0,23{\displaystyle \;\{1,23\}=1,23-1=0,23}
• {−1,23}=−1,23−(−2)=0,77{\displaystyle \;\{-1,23\}=-1,23-(-2)=0,77}
• {113}=113−3=23{\displaystyle \left\{{\tfrac {11}{3}}\right\}={\tfrac {11}{3}}-3={\tfrac {2}{3}}}
• {−113}=−113−(−4)=13{\displaystyle \left\{-{\tfrac {11}{3}}\right\}=-{\tfrac {11}{3}}-(-4)={\tfrac {1}{3}}}

• Область определения R{\displaystyle \mathbb {R} }.
• Область значений [0;1){\displaystyle \left[0;1\right)}.
• Функция периодична с периодом 1{\displaystyle 1}.

М. К. Потапов,В. В. Александров, П. И. Пасиченко. Алгебра и начала анализа. — АО Столетие, 1996.