Формулы сокращенного умножения
У нас есть сумма (разница) двух чисел и нам необходимо избавиться от скобок, используя формулы для сокращенного умножения: (x + y)2 = x2 + 2xy + y2
(x — y)2 = x2 — 2xy + y2
Пример: если x = 10, y = 5a
(10 + 5a)2 = 102 + 2.10.5a + (5a)2 = 100 + 100a + 25a2
(10 — 4)2 = 102 — 2.10.4 + 42 = 100 — 80 + 16 = 36
Конечно, если мы имеем следующую ситуацию:
25 + 20a + 4a2 = 52 + 2.2.5 + (2a)2 = (5 + 2a)2
(x + y)3 = x3 + 3x2y + 3xy2 + y3
(x — y)3 = x3 — 3x2y + 3xy2 — y3
Пример: (1 + a2)3 = 13 + 3.12.a2 + 3.1.(a2)2 + (a2)3 = 1 + 3a
(x + y + z)2 = x2 + y2 + z2 + 2xy + 2xz + 2yz
(x — y — z)2 = x2 + y2 + z2 — 2xy — 2xz + 2yz
x2 — y2 = (x — y)(x + y)
x2 + y2 = (x + y)2 — 2xy
или
x2 + y2 = (x — y)2 + 2xy
Пример: 9a2 — 25b2 = (3a)2 — (5b)2 = (3a — 5b)(3a + 5b)
x3 — y3 = (x — y)(x2 + xy + y2)
x3 + y3 = (x + y)(x2 — xy + y2)
xn — yn = (x — y)(xn-1 + xn-2y +. 2=1 x+y=7
2=1 x+y=7
1) Выразим х из второго уравнения:
{х² — y² = — 21;
{x + y = — 3;
х = — 3 — у;
Подставим значение второго уравнения в первое и найдем переменную у:
( — 3 — у)² — y² = — 21;
9 + 6у + у² — y² = — 21;
6у = — 31 — 9;
6у = — 30;
у = — 30 / 6;
у = — 5;
Подставим полученное значение у во второе уравнение и найдем переменную х:
х = — 3 — у;
х = — 3 — ( — 5) = 2;
Ответ: х = 2, у = — 5.
2) Выразим х из второго уравнения:
{x² + y² = 74;
{x — y = 2;
х = 2 + у;
Подставим значение второго уравнения в первое и найдем переменную у:
(2 + у)² + y² = 74;
4 + 4у + у² + y² — 74 = 0;
2у² + 4y — 70 = 0;
у² + 2y — 35 = 0;
Вычислим дискриминант:
D = b² — 4ac = 2² — 4 * 1 * ( — 35) = 4 + 140 = 144;
D › 0, значит:
у1 = ( — b — √D) / 2a = ( — 2 — √144) / 2 * 1 = ( — 2 — 12) / 2 = — 14 / 2 = — 7;
у2 = ( — b + √D) / 2a = ( — 2 + √144) / 2 * 1 = ( — 2 + 12) / 2 = 10 / 2 = 5;
Подставим значение у во второе уравнение и найдем х:
х = 2 + у;
Если у1 = — 7, то х1 = 2 — 7 = — 5;
Если у2 = 5, то х2 = 2 + 5 = 7;
Ответ: х1 = — 5, у1 = — 7, х2 = 7, у2 = 5.
3) Выразим х из второго уравнения:
{x² + 4y² = 34;
{x + y = 7;
х = 7 — у;
Подставим значение второго уравнения в первое и найдем переменную у:
( 7 — у)² + 4y² = 34;
49 — 14у + у² + 4y² — 34 = 0;
5у² — 14y + 15 = 0;
Вычислим дискриминант:
D = b² — 4ac = ( — 14)² — 4 * 5 * 15 = 196 — 300 = — 104;
D < 0, значит корней нет:
4) Выразим х из второго уравнения:
x² — 2xy — y² = 1;
{x + y = 7;
х = 7 — у;
Подставим значение второго уравнения в первое и найдем переменную у:
( 7 — у)² — 2у(7 — у) — y² = 1;
49 — 14у + у² — 14у + 2y² — y² = 1;
2у² — 28y + 48 = 0;
у² — 14y + 24 = 0;
Вычислим дискриминант:
D = b² — 4ac = ( — 14)² — 4 * 1 * 24 = 196 — 96 = 100;
D › 0, значит:
у1 = ( — b — √D) / 2a = (14 — √100) / 2 * 1 = (14 — 10) / 2 = 4 / 2 = 2;
у2 = ( — b + √D) / 2a = (14 + √100) / 2 * 1 = (14 + 10) / 2 = 24 / 2 = 12;
Подставим значение у во второе уравнение и найдем х:
х = 7 — у;
Если у1 = 2, то х1 = 7 — 2 = 5;
Если у2 = 12, то х2 = 7 — 12 = — 5;
Ответ: х1 = 5, у1 = 2, х2 = — 5, у2 = 12.
ЕГЭ ФИПИ-2016, вариант 9, задача 18
Найдите все значения а, при каждом из которых система уравнений
имеет ровно два решения.
Решение.
Запишем 1-ое уравнение системы в виде: x2 + 5x + y2 -y -52 = |x-5y +5|. ( * )
1) Так как правая часть равенства неотрицательна, то и левая часть равенства должна быть таковой, а именно: x
x2 + 2 ∙ х ∙ 2,5 + 2,52-2,52 + y2-2∙y∙0,5 + 0,52-0,52-52 ≥ 0;
(x2 + 2 ∙ х ∙ 2,5 + 2,52) + (y2-2 ∙ y ∙ 0,5 + 0,52) ≥ 52 + 2,52 + 0,52;
(х + 2,5)2 + (у-0,5)2 ≥ 52 + 6,25 + 0,25;
(х + 2,5)2 + (у-0,5)2 ≥ 58,5. ОДЗ: решения системы находятся среди множества точек, лежащих вне окружности с центром в точке Q(-2,5; 0,5) и радиусом
ОДЗ: решения системы находятся среди множества точек, лежащих вне окружности с центром в точке Q(-2,5; 0,5) и радиусом
2) Раскроем модульные скобки в уравнении ( * ), считая, что выражение под знаком модуля неотрицательно, т.е. х-5у +5 ≥ 0 или 5у ≤ х + 5, отсюда у ≤ 0,2х+1. Тогда равенство ( * ) запишется в виде:
x2 + 5x + y2-y-52 = x-5y +5. Перенесём все в левую часть и упростим её.
x2 + 5x + y2-y-52-x + 5y-5 = 0;
x2 + 4x + y2 + 4у-57 = 0. Выделим из алгебраических сумм (x2 + 4x) и (y2 + 4y) полные квадраты двучленов.
x2 + 4x + 4-4 + y2 + 4у +4-4-57 = 0;
(x2 + 4x + 4) + (y2 + 4у +4) = 57 + 4 + 4;
(х + 2)2 + (у + 2)2 = 65. Это уравнение окружности с центром в точке О1(-2; -2) и радиусом
Рассматривать будем только те точки этой окружности, которые лежат ниже прямой х-5у +5 = 0, так как мы получили уравнение этой окружности при условии, что х-5у +5 ≥ 0, т.
3) Теперь раскроем модульные скобки в уравнении ( * ), считая, что выражение под знаком модуля отрицательно, т.е. х-5у +5 < 0 или 5у > х + 5, отсюда у>0,2х+1. Тогда равенство ( * ) запишется в виде:
x2 + 5x + y2-y-52 = -x + 5y +5. Перенесём все в левую часть и упростим её.
x2 + 5x + y2-y-52 + x-5y + 5 = 0;
x2 + 6x + y2-6у-47 = 0. Выделим из алгебраических сумм (x2 + 6x) и (y2-6y) полные квадраты двучленов.
x2 + 6x + 9-9 + y2-6у + 9-9-47 = 0;
(x2 + 6x + 9) + (y2-6у +9) = 47 + 9 + 9;
(х + 3)
2 + (у-3)2 = 65. Это уравнение окружности с центром в точке О2(-3; 3) и радиусомРассматривать будем только те точки этой окружности, которые лежат выше прямой х-5у +5 = 0, так как мы получили уравнение этой окружности при условии х-5у +5 < 0, т. е. при условии у > 0,2х+1. Заметим, что все точки этой окружности, лежащие выше прямой х-5у +5 = 0, находятся вне окружности с центром в точке Q(-2,5; 0,5), поэтому удовлетворяют ОДЗ.
е. при условии у > 0,2х+1. Заметим, что все точки этой окружности, лежащие выше прямой х-5у +5 = 0, находятся вне окружности с центром в точке Q(-2,5; 0,5), поэтому удовлетворяют ОДЗ.
4) Найдем точки пересечения окружностей с центрами в точках О1 и О2. Это также точки пересечения любой из этих окружностей с прямой х-5у +5 = 0. Для определенности возьмем уравнение первой из окружностей и решим систему:
Из 2-го уравнения выразим х через у и подставим в 1-ое уравнение.
Упростим и решим 2-ое уравнение полученной системы.
(5у-3)2 + (у + 2)2 = 65;
25у2-30у + 9 + у2 +4у + 4-65 = 0;
26у2-26у-52 = 0;
у2-у-2 = 0. По теореме Виета у1 + у2 =1, у1∙ у2 = -2. Отсюда у1 = -1, у2 = 2.
Тогда х1 = 5 ∙ у1-5 = 5 ∙ (-1)-5 = -10; х2 = 5 ∙ у2-5 = 5 ∙ 2-5 = 2.
Точки пересечения окружностей с центрами О1 и О2 лежат на прямой х-5у +5 = 0, и это точки Т(-10; -1) и А(5; 2).
5) Разберемся, что представляет собой прямая у-2 = а(х-5). Запишем это уравнение в виде у = а(х-5) + 2 и вспомним, как получается график функции y = f(x-m) +
n из графика функции y = f(x). Он получается переносом графика функции y = f(x) на m единичных отрезков вдоль оси Ох и на n единичных отрезков вдоль оси Оу. Следовательно, график функции у = а(х-5) + 2 можно получить из графика функции у = ах переносом на 5 единиц вправо и на 2 единицы вверх. Другими словами, прямая пройдет через точку А(5; 2) и должна иметь такой угловой коэффициент а, чтобы пересечь наши окружности с центрами в точках О1 и О2 ровно в двух точках. Это произойдет только в тех случаях, когда прямая, проходя через точку А, общую для обеих окружностей, далее будет пересекать только одну из них. Предельными положениями нашей прямой (с параметром а) будут касательные к окружностям в точке А. Нам понадобятся не сами уравнения касательных, но их угловые коэффициенты. Как мы их получим?
Это произойдет только в тех случаях, когда прямая, проходя через точку А, общую для обеих окружностей, далее будет пересекать только одну из них. Предельными положениями нашей прямой (с параметром а) будут касательные к окружностям в точке А. Нам понадобятся не сами уравнения касательных, но их угловые коэффициенты. Как мы их получим?6) Радиус О1А, проведенный в точку касания будет перпендикулярен касательной. Угловые коэффициенты k1 и k2 двух взаимно перпендикулярных прямых y = k1x+b1 и y = k2x+b2 подчиняются закону: k1 ∙ k2 = -1. Составим уравнения прямой О1А и прямой О2А, определим угловой коэффициент каждой прямой, а затем найдем угловые коэффициенты касательных, являющихся предельными положениями прямой у = а(х-5) + 2. Промежуток между найденными значениями параметра а и будет ответом задачи.
Промежуток между найденными значениями параметра а и будет ответом задачи.
Используем формулу уравнения прямой, проходящей через две данные точки (х1; у1) и (х2; у2). Эта формула имеет вид:
Составим уравнение прямой, проходящей через точки О1(-2; -2) и А(5; 2). У нас х1 = -2, у1 = -2, х2 = 5, у2 = 2. Подставляем эти значения в формулу:
Дальше можно не продолжать – понятно, что угловой коэффициент прямой О1А равен 4/7. Тогда угловой коэффициент прямой, перпендикулярной прямой О1А, равен —7/4.
Итак, уравнение касательной в точке А к окружности с центром в точке О1 имеет вид:
Аналогично, составляем уравнение прямой О2А.
О2(-3; 3) и А(5; 2). У нас х1 = -3, у1 = 3, х2 = 5, у2 = 2. Подставляем эти значения в формулу ( ** ) и получаем:
Подставляем эти значения в формулу ( ** ) и получаем:
Угловой коэффициент прямой О2А равен —1/8 . Тогда угловой коэффициент прямой, перпендикулярной прямой О2А, равен -1 : (- 1/8 ) = 8.
Итак, уравнение касательной в точке А к окружности с центром в точке О2 имеет вид: у = 8(х-5) + 2.
Таким образом, если угловой коэффициент а прямой у = а(х-5) + 2 будет принимать значения от —7/4 до 8 включительно, то прямая у = а(х-5) + 2, проходящая через точку А, в которой пересекаются две окружности, будет только еще один раз пересекать одну из окружностей.
Данная система уравнений будет иметь только два решения при а∈ [- 7/4 ; 8].
Ответ: —7/4 ≤ а ≤ 8.
Найдите все значения а, при каждом из которых система
Задача. Найдите все значения а, при каждом из которых система уравнений
Найдите все значения а, при каждом из которых система уравнений
имеет более одного решения.
Решение. Рассмотрим первое уравнение системы.
1) Пусть х2 + у2 -25 ≥ 0. Неравенство х2 + у2 ≥ 25 или х2 + у2 ≥ 52 описывает множество точек координатной плоскости, лежащих вне круга с центром в начале координат и радиусом R = 5. На чертеже круг показан зелёным цветом.
Раскроем модульные скобки.
х2 + 20х + у2 -20у + 75 = х2 + у2-25;
20x-20y + 100 = 0. Разделим обе части равенства на 20.
х-у + 5 = 0; у = х + 5. Графиком служит прямая у = х, смещённая вдоль оси Оу на 5 единичных отрезков. Нам подойдут только те точки прямой у = х + 5, которые будут лежать вне круга х2 + у2 = 25. На чертеже показана эта часть прямой синим цветом.
2) Пусть х2 + у2-25 ≤ 0. Неравенство х2 + у2 ≤ 25 или х2 + у2 ≤ 52 описывает множество точек координатной плоскости, лежащих внутри круга с центром в начале координат и радиусом R = 5.
Неравенство х2 + у2 ≤ 25 или х2 + у2 ≤ 52 описывает множество точек координатной плоскости, лежащих внутри круга с центром в начале координат и радиусом R = 5.
Раскроем модульные скобки.
х2 + 20х + у2 -20у + 75 = -х2 -у2 + 25;
2х2 + 20х + 2у2 -20у + 50 = 0. Разделим обе части равенства на 2.
х2 + 10х + у2 -10у + 25 = 0. Преобразуем это выражение.
x2 + 2 ∙ х ∙ 5 + 52-52 + y2 -2 ∙ y ∙ 5 + 52-52 + 25 = 0;
(x2 + 2 ∙ х ∙ 5 + 52) + (y2 -2 ∙ y ∙ 5 + 52) = 25;
(х + 5)2 + (у-5)2 = 52.
Это уравнение описывает окружность с центром в точке (-5; 5) и радиусом R = 5. Нам подойдут только те точки этой окружности, которые будут лежать внутри окружности
Нам подойдут только те точки этой окружности, которые будут лежать внутри окружности
х2 + у2 = 25. На чертеже эти точки окружности обозначены красным цветом.
Рассмотрим второе уравнение системы.
х-у = а. Запишем равенство в виде: у = х-а. Графиком этой функции будет служить прямая у = х, смещённая вдоль оси Оу на а единичных отрезков. Для того, чтобы система уравнений имела более одного решения прямая у = х-а должна пересечь сине-красную линию чертежа два и более раз.
Решим систему уравнений у = х-а и х2 + 10х + у2 -10у + 25 = 0.
Подставим значение у = х-а в выражение х2 + 10х + у2 -10у + 25 = 0. Получаем:
х2 + 10х + (х-а)2 -10(х-а) + 25 = 0. Раскроем скобки.
х2 + 10х + х2-2ах + а2-10х +10а + 25 = 0;
2х2 -2ах + а2 +10а + 25 = 0.
Дискриминант D1 = a2-2(а2 +10а + 25) = a2-2а2-20а-50 = -а2-20а-50. Если дискриминант больше нуля, то последнее уравнение, а значит, и вся система имеют два действительных корня.
Если дискриминант больше нуля, то последнее уравнение, а значит, и вся система имеют два действительных корня.
D1 > 0 → -а2-20а-50 > 0 → а2 + 20а + 50 < 0.
Это неравенство будет верным при a1 < a < a2, где a1 и a2 — корни квадратного уравнения а2 + 20а + 50 = 0.
Решим уравнение а2 + 20а + 50 = 0.
D1 = 102-50 = 50.
Таким образом, а2 + 20а + 50 < 0
и не будет иметь общих точек с графиком первого уравнения данной системы (с сине-красной линией).
и будет касаться красной линии. В точке касания система будет иметь единственное решение. Очевидно, что если мы будем перемещать прямую
параллельно самой себе в направлении прямой у = х + 5, то каждый раз будем получать по две точки пересечения, и данная система будет иметь два решения.
совпадет с прямой у = х + 5, то это будет означать, что данная система имеет множество решений. 2=36
2=36
у3=6 у4= -6
Эти значения подставляем в систему….:)
х=12/у
х1=12/2 х1=6
х2=12/(-2) х2=-6
х3=12/6 х3=2
х4=12/(-6) х4=-2
Четыре точки пересечения: (6;2),(-6;-2),(2;6),(-2;-6). Вот и всё:)
В целях совершенствования деятельности не факт,
В целях совершенствования деятельности не факт, что саморегулируемых организаций аудиторов Департамент регулирования чуть-чуть муниципального…
Премьер-министр Рф Владимир Путин заявил о готовности
Премьер-министр Рф Владимир Путин заявил о готовности как бы оказыватъ финанзовую помощь регионам, которые более удачно реализуют свои жилЫщные…
Министр, извините за выражение, экономического развития
Министр, извините за выражение, экономического развития РФ Андрей Белоусов на заседании Правительства РФ 7 июня заявил о необходимости скорейшей…
Photo
Hint http://pics.livejournal.com/igrick/pic/000r1edq
2- 5_Высшая математика_7
Российской Федерации
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра математики.
Контрольная работа №2
по высшей математике.
Вариант 2.5
2х + 3y + 5 = 0.
Решение:
В качестве вектора нормали данной прямой можно принять вектор N(2, 3) и записать искомое уравнение 2х + 3y – (2 + 12) = 0 или 2x + 3y – 14 = 0
Ответ: 2x + 3y – 14 = 0
2. Найдите координаты проекции точки М(3, 6) на прямую x + 2y – 10 = 0.
Решение:
Пусть проекцией точки М будет точка M’.
Точку М’ можно найти как точку пересечения прямой x + 2y – 10 = 0 и прямой ММ’, перпендику-лярной к данной.
Прямая ММ’ параллельна вектору N1(1, -2) – нормали прямой x + 2y – 10 = 0. В качестве нормали прямой ММ’ можно принять вектор N2(-2, 1), тогда уравнение прямой будет иметь вид –2x + y – (-6+6) = 0 или –2x + y = 0
Для отыскания координат точки М’ составим систему уравнений:
решив которую, находим x
= 2, y = 4, то есть М'(2, 4).
Ответ: (2, 4).
3. Запишите общее уравнение плоскости, проходящей через три заданные точки М1(-6, 1, -5), М2(7, -2, -1), М3(10, -7, 1).
Решение:
Данная плоскость параллельна векторам m1 = M1M2 = (7 + 6, -2 – 1, -1 + 5) = (13, -3, 4), m2 = M1M3 = (10 + 6, -7 – 1, 1 + 5) = (16, -8, 6).
Поэтому в качестве вектора нормали можно взять вектор N[m1, m2] = .
Разложим этот определитель по первой строке:
N = i – j + k = 14i – 14j – 56k || (1, -1, -4).
Уравнение плоскости x – y – 4z + D = 0.
Для определения D используем условие, что плоскость проходит через точку M1(-6, 1, -5):
-6 – 1 + 20 + D = 0,
D = -13.
Уравнение плоскости x – y – 4z – 13 = 0.
Проверим, что точки M2 и M3 принадлежат этой плоскости:
М2(7, -2, -1): 7 + 2 + 4 – 13 = 0
13 – 13 = 0, значит точка М2 принадлежит данной плоскости.
М3(10, -7, 1): 10 + 7 – 4 – 13 = 0
17 – 17 = 0, значит точка М3 принадлежит данной плоскости.
Ответ: x – y – 4z – 13 = 0.
4. Известно, что прямая L параллельна вектору l = (0, 9, 12). Найдите длину отрезка этой прямой между плоскостями x + y + z – 3 = 0 и x + y + z – 24 = 0.
Решение:
Рассмотрим положение плоскостей x
+ y + z – 3 = 0
и x + y + z
– 24 = 0 в пространстве: нормали плоскостей
N1(1, 1, 1) и N2(1,
1, 1) равны, значит, плоскости параллельны. Так как
≠,
то данные плоскости не совпадают.
Так как
≠,
то данные плоскости не совпадают.
Так как прямая L параллельна вектору l = (0, 9, 12), то уравнение прямой имеет вид: 9y + 12z + D = 0.
Пусть D = 0, тогда уравнение прямой будет 9y + 12z = 0. Найдем точки пересечения прямой с плоскостями x + y + z – 3 = 0 и x + y + z – 24 = 0 и запишем уравнение прямой в параметрическом виде. Пусть z – свободный член, тогда
Найдем значение параметра t1, при котором прямая пересекает плоскость x + y + z – 3 = 0. Точка Н1(0, , t1) лежит в данной плоскости, значит ее координаты удовлетворяют уравнению плоскости, следовательно, + t1 – 3 = 0. Найдем t1: -12 t1 + 9 t1 – 27 = 0, -3 t1 = 27, t1 = -9.
Аналогично найдем значение параметра
t2, при котором прямая
пересекает плоскость x
+ y + z – 24 =
0. Точка Н2(0,
,
t2) лежит в данной
плоскости, значит ее координаты
удовлетворяют уравнению плоскости,
тогда + t2 – 24 = 0, -12t2 + 9 t2 – 216 = 0, t2 = -72.
Подставляя в параметрическое уравнение значения t1 = -9, t2 = -72 найдем точки пересечения
Н1(0, 12, -9) и Н2(0, 96, -72) прямой L с данными плоскостями.
По формуле расстояния между двумя точками в пространстве, находим отрезок Н1Н2 между данными плоскостями:
d = ,
Н1Н2 = = = 105.
Ответ: d = 105.
5. Некоторая прямая проходит через точку Р(2, 2, 1), пересекает ось в точке Q(0, yo, 0) и пересекает прямую Найдите yo.
Решение:
Пусть z – свободный член, тогда преобразуем данную систему уравнений при z = t:
Условием пересечения двух прямых
является равенство (r2 – r1, l1,
l2) = 0, где r2 = (2, 2, 1), r1 = (-2, -1,
0), l1 = (3, 2, 1), l2 = PQ = (-2, y0-2,
-1).
Тогда (r2 – r1, l1, l2) = = = -2·– (yo – 2)·– 1· =
= -2 – (yo – 2) – 2 = 0,
-4 – yo + 2 = 0,
yo = 2.
Ответ: yo = 2.
6. Плоскость содержит прямую = = и параллельна прямой х – 3 = у – 3 = -2 (z – 6). Найти квадрат расстояния от второй прямой до плоскости.
Решение:
Преобразуем
данные канонические уравнения прямых:
2х + 3z
– 18 = 0 – прямая в плоскости, х +
у – 4z
– 18 = 0 – прямая, параллельная плоскости.
Следовательно, эти прямые непараллельные,
то есть
,
и скрещивающиеся, так как одна из прямых
содержится в плоскости, параллельной
второй. Тогда нахождение отрезка между
плоскостью и второй прямой сведется к
нахождению отрезка между двумя
скрещивающимися прямыми.
Приведем уравнения прямых от канонического к параметрическому виду:
и
По формуле , где r1 = (0, 0, 6), r2 = (3, 3, 6), l1 = (3, 0, -2), l2 = (1, 1, ), находим
r1 – r2 , l1, l2 = = i · – j · + k · = -2i + j + 3k.
d2 = = = = =.
Ответ: .
7. Доказать, что уравнение х2 + у2 + 6х – 10у – 15 = 0 определяет на плоскости X0Y окружность. Найти ее центр и радиус R. В ответе сначала указать хо, уо – координаты центра, затем R.
Решение:
Уравнение
вида a11x2 +
a22y2 +
2a12xy
+ a01x
+ a02y
+ a00 =
0 определяет на плоскости окружность,
если а11 = а220,
а12 = 0. В нашем случае данное уравнение
удовлетворяет условию, поэтому
х2 +
у2 +
6х – 10у – 15 = 0 определяет на плоскости
X0Yокружность.
В нашем случае данное уравнение
удовлетворяет условию, поэтому
х2 +
у2 +
6х – 10у – 15 = 0 определяет на плоскости
X0Yокружность.
Найдем радиус и центр данной окружности:
х2 + у2 + 6х – 10у – 15 = (х2 + 6x + 9) + (у2 – 10y + 25) – 49 = 0?
(x + 3)2 + (y – 5)2= 49.
Следовательно, (3, -5) – центр окружности, а R = = 7 – радиус.
Ответ: (3, -5) – центр окружности, R = 7.
8. Дана кривая 4x2 – y2 – 24x + 4y + 28 = 0.
8.1 Доказать, что эта кривая – гипербола.
8.2 Найти координаты ее центра симметрии.
8.3 Найти действительную и мнимую полуоси.
8.4 Записать
уравнение фокальной оси.
8.5 Построить данную гиперболу.
Решение:
8.1 Каноническое уравнение гиперболы .
В уравнении кривой выделим полные квадраты, то есть 4(x2 – 6x + 9) – (y2 – 4y + 4) – 4 = 0,
4(х – 3)2 – (y – 2)2 = 4 или , следовательно, данное уравнение является уравнением гиперболы.
8.2 x1 = x – 3, y1 = y – 2, т.е. центр симметрии данной гиперболы находится в точке (3, 2).
8.3 Из уравнения гиперболы , мнимой полуосью является число b, а действительной – число a. То есть b = 2, a = 1.
так как фокусы расположены на прямой, параллельной оси OX, то уравнение фокальной оси y = 2.
8.5
9. Дана кривая y2 + 6x + 6y +
15 = 0.
9.1 Докажите, что эта кривая – парабола.
9.2 Найдите координаты ее вершины.
9.3 Найдите значения ее параметра р.
9.4 Запишите уравнение ее оси симметрии.
9.5 Постройте данную параболу.
Решение:
9.1 Выделяя полный квадрат, получим (y2 + 6y + 9) + 6x + 6 = 0, т.е. (y + 3)2 + 6x + 6 = 0. Если положить y1 = y + 3, x1 = -6x – 6, то уравнение приводится к виду , следовательно, данное уравнение является уравнением параболы.
9.2 Тогда координаты вершины параболы будут y = -3, x = -1, т.е. (-1, -3).
9.3 Сравнивая последнее уравнение с каноническим уравнением параболы находим, что 2р = 1, р = .
9.4 Осью симметрии является прямая,
проходящая через точку (-1, -3) и параллельная
оси абсцисс, т. е. y = -3.
е. y = -3.
9.5
10. Дана кривая 5х2 + 5y2 + 6ху – 16х – 16у = 16.
10.1 Докажите, что эта кривая – эллипс.
10.2 Найдите координаты его центра симметрии.
10.3 Найдите его большую и меньшую полуоси.
10.4 Запишите уравнение фокальной оси.
10.5 Постройте данную кривую.
Решение:
10.1 Квадратичную форму В(х, у) = 5х2 + 6ху + 5y2 приводим к главным осям. Для этого запишем матрицу этой квадратичной формы В = и найдем ее собственные числа. Запишем и решим характеристическое уравнение матрицы В:
= λ2 – 10λ + 16 = 0,
λ1,2 = 5 ±
=
5 ± 3, λ1 = 8, λ2 = 2.
Так как собственные числа λ1, λ2 > 0, то данное уравнение является уравнением эллипса.
10.2 Найдем собственные векторы чисел λ1 и λ2:
Для числа λ1 имеем В = = . Если положим то единичный вектор i1 имеет координаты i1 = .
Другой собственный вектор, отвечающий собственному числу λ2, может быть задан в виде j1 = . Базис (i1, j1) принят правым.
Запишем матрицу перехода от базиса (О, i, j) к (O1, i1, j1):
Q = и обратную матрицу к ней Q-1 = QT = .
Новые координаты (х1, у1) связаны со старыми (х, у) соотношением
В новой системе координат уравнение
эллипса 5х2 + 5y2 + 6ху – 16х – 16у = 16 принимает вид:
,
. После выделения полных квадратов
получаем
.
После выделения полных квадратов
получаем
.
В системе координат (O1, i1, j1) находим
Тогда .
При х2 = 0, у2 = 0 найдем центр симметрии эллипса, координатами которого являются координаты точки О1:
О1(-1, -1).
10.3 Взяв уравнение , найдем большую полуось, равную а=4, и меньшую, равную b=2.
10.4 так как фокусы расположены на новой оси О1Х2, то уравнением фокальной оси будет –х + у = 0.
10.5
Предварительные требования
Предварительные требованияПредполагается, что вы знаете следующий материал, поступающий в курс алгебры колледжа. Пожалуйста, обновите себя, если вы этого не сделаете.
Интервальное обозначение
Альтернативная форма выражения неравенств — использование интервальной записи. Интервал
запись состоит из двух значений, разделенных запятыми.
Интервал
запись состоит из двух значений, разделенных запятыми.
Первое значение — это левая конечная точка интервала, а второе значение — правая рука конечная точка интервала.Левая конечная точка всегда находится слева, а правая конечная точка всегда находится справа. Если неравенство будет длиться вечно в отрицательное направление, тогда левая конечная точка должна быть отрицательной бесконечностью. Если неравенство продолжается навсегда в положительном направлении, тогда правая конечная точка должна быть положительной бесконечностью.
Каждая конечная точка заключена в квадратную скобку [] или круглую скобку (). Левая рука
после конечной точки следует левая скобка [или левая скобка (а правая
за конечной точкой следует правая скобка] или правая скобка).Скобка означает
конечная точка включена, а круглые скобки означают, что конечная точка не включена.
Бесконечность (положительная или отрицательная) никогда не включается и всегда должна быть заключена в
скобка.
Открытый интервал — это когда обе конечные точки не включены (). Закрытый интервал — это когда обе конечные точки включены []. Полуоткрытый (или полузакрытый, если вы пессимист) интервал — это когда одна конечная точка включена, а другая — нет (] или [).
Примеры обозначения интервалов
Запишите: -2
Запишите: -2 <= x <5 как [-2, 5)
.Запишите: x> = 2 как [2, + ∞)
Запишите: x <5 как (-∞, 5)
Абсолютное значение
Большинство людей знают, что абсолютное значение любого числа нулевой или положительный.Однако математически это требует кусочное определение.
При работе с абсолютными значениями это означает, что
удалить абсолютное значение из алгебраического выражения, выражение абсолютного значения
необходимо заменить на два корпуса. Один случай получается простым отбрасыванием абсолютного
знаки значения и оставление аргумента. Другой случай получается противоположным
аргумента функции абсолютного значения. Затем прорабатывается каждый случай
индивидуально.
Затем прорабатывается каждый случай
индивидуально.
Иногда можно решить уравнение, содержащее абсолютные значения, используя плюс-минус при удалении знаков абсолютного значения. Будьте осторожны при этом, и если вы испытываете трудности, затем вернитесь к двум отдельным случаям.
Другой способ исключить абсолютное значение — возвести обе части уравнения в квадрат. Принятие абсолютного значения делает вещи неотрицательными, а возведение в квадрат — неотрицательными. Итак, если вы возведете что-то в квадрат, вам больше не нужно принимать его абсолютное значение.Однако будьте осторожны при возведении в квадрат обеих частей уравнения, так как это может привести к посторонние решения.
Свойства поля действительных чисел
- Свойство закрытия — сумма или произведение любых двух действительных чисел является другим действительным числом.
- Коммутативное свойство — порядок терминов или коэффициентов может быть изменен.

- Ассоциативное свойство — Группировка терминов или факторов может быть изменена.
- Свойства идентичности — к любому числу добавляется ноль.Один умноженный на любой номер это номер.
- Обратные свойства — Любое число плюс противоположное ему равно нулю. Любое число, кроме нуля, раз это взаимно один.
- Распределительное свойство — умножение распределяет поверх сложения.
Обратите внимание, что свойства определены для сложения и умножения. Некоторые из свойства не работают для вычитания или деления.
Основная теорема арифметики
Каждое целое число больше единицы является простым числом или может быть записано как уникальное. произведение простых чисел.
Простые числа — ваши друзья. Умейте множить числа с помощью простых чисел, это сделает позже жизнь станет намного проще.
Экспоненты
При умножении двух множителей с одинаковым основанием складывайте экспоненты.
При умножении двух множителей с одинаковым показателем, но с разными основаниями, умножьте баз и сохранить экспоненту.
При возведении в степень умножьте показатели вместе.
Научная запись
Уметь преобразовывать число из научного представления в обычное и из регулярную нотацию в научную нотацию.
Калькулятор TI-82 / TI-83 использует ключ EE в качестве ключа экспоненциальной записи. Когда вы видите число, подобное 1.253E12, что на самом деле означает 1.253 × 10 12 .
Корни
Знать, как преобразовывать радикальную форму в рациональную экспоненциальную форму. В рациональном экспоненциальной формы, знаменателем экспоненты является индекс корня и числитель — мощность выражения.
Например, x 2/3 будет кубическим корнем из x 2 .
Будьте осторожны при извлечении корня энной степени энной степени. Если мощность ровная, то вы
при упрощении радикала необходимо брать абсолютное значение основания.
Упрощенная радикальная форма
Значение имеет упрощенную радикальную форму, если выполняются следующие условия.
- Показатели всех простых множителей в подкоренном выражении должны быть меньше чем индекс радикала. По сути, это означает, что у вас не может быть квадрата корень x 3 .
- В подкоренном остатке дроби отсутствуют.
- В знаменателе радикалов нет.
- Нет общих множителей между показателем простого числа фактор подкоренного и индекс радикала. Это означает, что вы следует уменьшить ваш индекс и мощность, если это возможно.
Факторинговые многочлены
Знать частные случаи разности двух квадратов, суммы двух квадратов. (который является простым над вещественными числами и не учитывается), разница из двух кубиков, сумма двух кубов, а разница в два n -го степеней.
- Разница двух квадратов: x 2 — y 2 = (x — y) (x + y)
- Сумма двух квадратов: x 2 + y 2 , без множителя над реалами
- Разница двух кубов: x 3 — y 3 = (x — y) (x 2 + xy + y 2 )
- Сумма двух кубов: x 3 + y 3 = (x + y) (x 2 — xy + y 2 )
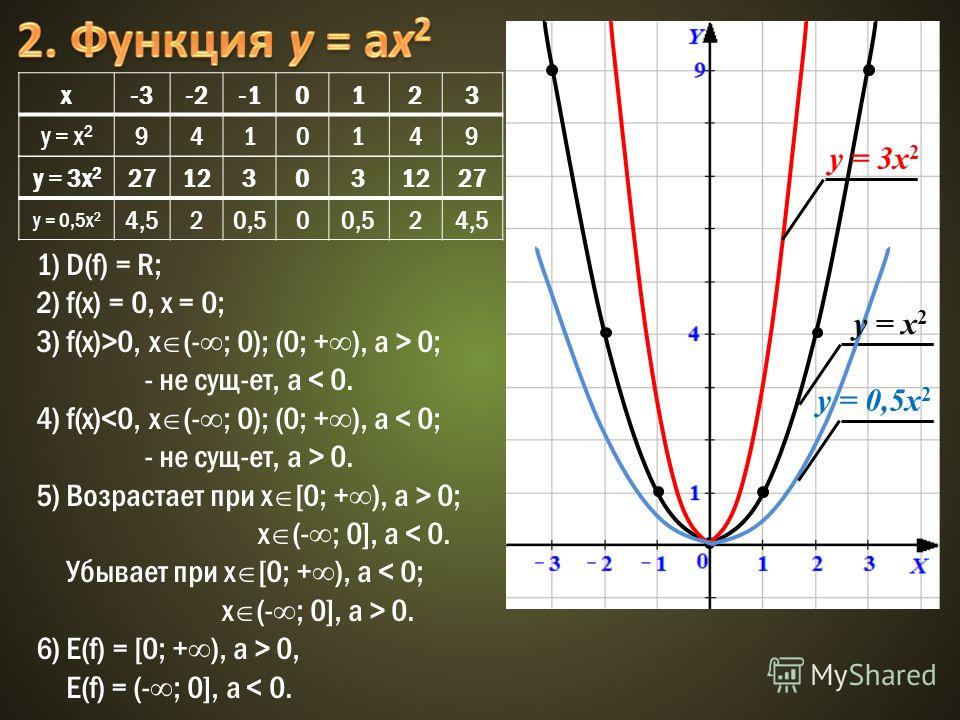
- Разница двух n th градусов: x n — y n = (x — y) (x n-1 + x n-2 y +.
 .. + xy n-2 + y n-1 )
.. + xy n-2 + y n-1 )
Вышеупомянутые шаблоны действительно используются в качестве руководства. Например, 4x 2 -25 — это разница двух квадратов. Некоторая специально созданная сумма квадратов будет фактор, но это сверх того, что я ожидаю, что вы узнаете об этом курсе.
Знайте, как разложить на множители трехчлен, который не является частным случаем. Вы можете найти В этом случае выгоден метод факторинга AC.
Умейте факторно группировать.
Особые продукты
Знать квадрат и кубы двучлена.
- Квадрат суммы: (x + y) 2 = х 2 + 2xy + у 2
- Квадрат разницы: (x — y) 2 = x 2 — 2xy + y 2
- Сумма в кубе: (x + y) 3 = x 3 + 3x 2 y + 3xy 2 + y 3
- Разность в кубе: (x — y) 3 = x 3 — 3x 2 y + 3xy 2 — y 3
Это частные случаи того, что известно как теорема биномиального разложения, которая будет рассмотрена в разделе
7. 5.
5.
Дробные выражения
Выражения не имеют знаков равенства. Если бы они это сделали, это были бы уравнения. Когда там не является знаком равенства, вы не можете умножить обе части уравнения (потому что нет уравнение) по наименьшему общему знаменателю и исключить знаменатель.
Это означает, что при работе с рациональными (дробными) выражениями вы будете иметь знаменатель в окончательном ответе (если только он не делится с множителем в числитель).
Вы разделите или уменьшите множителей в числителе на множителей в знаменателе. Делать не отменять (если вы не хотите, чтобы у инструкторов закипела кровь). Не делить отдельные термины (коэффициенты умножаются, термины складываются).
С составными дробями, содержащими одночлены, вы можете инвертировать, а затем умножить.
Однако, когда в составной дроби входят многочлены, обычно проще
умножьте верхнюю и нижнюю дроби на наименьший общий знаменатель числа
два знаменателя.
Декартова плоскость
Уметь построить декартову систему координат. Это также известно как x-y координатная плоскость. Знайте названия квадрантов. Быть знакомым с понятие упорядоченной пары и быть способным строить точки в системе учитывая его координаты.
Координата x также известна как абсцисса, а координата y также известна как ордината.
Формулы
Вы должны знать следующие формулы.
- Расстояние между двумя точками.Это в основном просто пифагорейский Теорема. Найдите изменение x-координат и изменение y-координат. Возведите каждую из них в квадрат и сложите вместе. Наконец, извлеките квадратный корень.
- Формула средней точки. Середина между двумя точками находится путем сложения x и делим на 2, складываем y и делим на 2.
- Уравнение окружности с центром (h, k) и радиусом r. (x-h) 2 + (y-k) 2 = r 2
Изучение данных
Вы не несете ответственности за этот раздел книги. 2. (ху) 2 = (ху) (ху) = xxyy = x2 × y2.
2. (ху) 2 = (ху) (ху) = xxyy = x2 × y2.
Почему некоторые люди говорят, что это неправда: Это не так просто … должно быть что-то я упустил …
Подскажите правильный ответ
Утверждение условно верно \ color {# 20A900} {\ textbf {условно верно}} условно верно.
Утверждение верно, если оператор × \ times × коммутативен (((то есть x × y = y × x ∀x, y) x \ times y = y \ times x \; \ forall x, y) x × y = y × x∀x, y) и ассоциативным (((то есть x (yz) = (xy) z ∀x, y, z).2 = () () = (), x2 × y2 = (12) 2 (13) 2 = () () = (),
, которые явно не равны.
Полиномиальные тождества
Когда у нас есть сумма (разность) двух или трех чисел в степени 2 или 3, и нам нужно снять скобки, мы используем полиномиальные тождества(короткие формулы умножения) :
(x + y) 2 = x 2 + 2xy + y 2
(x — y) 2 = x 2 — 2xy + y 2
Пример 1: Если x = 10, y = 5a
(10 + 5a) 2 = 10 2 + 2 · 10 · 5a + (5a) 2 = 100 + 100a + 25a 2
Пример 2: если x = 10, а y равно 4
(10-4) 2 = 10 2 — 2 · 10 · 4 + 4 2 = 100 — 80 + 16 = 36
Верно и обратное:
25 + 20a + 4a 2 = 5 2 + 2 · 2 · 5 + (2a) 2 = (5 + 2a) 2
Последствия вышеуказанных формул:
(-x + y) 2 = (y — x) 2 = y 2 — 2xy + x 2
(-x — y) 2 = (- (x + y)) 2 = (x + y) 2 = x 2 + 2xy + y 2
Формулы 3 степени:
(x + y) 3 = x 3 + 3x 2 y + 3xy 2 + y 3
(x — y) 3 = x 3 — 3x 2 y + 3xy 2 — y 3
Пример: (1 + 2 ) 3 = 1 3 + 3. 1 2 .a 2 +
3.1. (A 2 ) 2 + (a 2 ) 3 = 1 + 3a 2 + 3a 4 + a 6
1 2 .a 2 +
3.1. (A 2 ) 2 + (a 2 ) 3 = 1 + 3a 2 + 3a 4 + a 6
(x + y + z) 2 = x 2 + y 2 + z 2 + 2xy + 2xz + 2yz
(x — y — z) 2 = x 2 + y 2 + z 2 — 2xy — 2xz + 2yz
Фактор Правила
x 2 — y 2 = (x — y) (x + y) x 2 + y 2 = (x + y) 2 — 2xy
или
x 2 + y 2 = (x — y) 2 + 2xy
Пример: 9a 2 — 25b 2 = (3a) 2 — (5b) 2 = (3a — 5b) (3a + 5b)
x 3 — y 3 = (x — y) (x 2 + xy + y 2 )
x 3 + y 3 = (x + y) (x 2 — ху + у 2 )
Если n натуральное число
x n — y n = (x — y) (x n-1 + x n-2 y +. 2 + 20 $
2 + 20 $
3) Решите уравнение: x 2 — 25 = 0
Решение: x 2 -25 = (x — 5) (x + 5)
=> мы должны решить следующие 2 уравнения:
x — 5 = 0 или x + 5 = 0
, поэтому уравнение имеет два решения: x = 5 и x = -5.
Связанные ресурсы:
Тест на полиномиальные тождества
Упрощение полиномиальных выражений — проблемы с решениями
Факторинг полиномов — проблемы с решениями
Полиномиальные тождества на форуме
Передача по Скарпелли 2
Передача по Скарпелли 2График x 2 + y 2 = 9.Теперь на тех же осях изобразите уравнение x 2 + xy + y 2 = 9. Опишите новый график. Попробуйте разные коэффициенты для члена xy. Какие виды графиков вы создаете? Какие коэффициенты отмечают границы между разными типами графиков? Как мы узнаем, что это границы? Опишите, что происходит с графиком, когда коэффициент члена xy приближается к границам.
Для этого задания я буду использовать программное обеспечение Graphing Calculator Lite для построения графиков уравнений второй степени и изучения графиков.Я буду исследовать эффекты различных коэффициентов для члена xy и наблюдать за созданными графиками. Таким образом, чтобы сделать это в Graphing Calculator Lite, используйте параметр n в качестве коэффициента для члена xy и исследуйте, что происходит с графиками с различными значениями n в уравнении x 2 + n xy + y 2 = 9. Как изменится график, если значение n положительное или отрицательное? Нечетное или четное значение n что-то меняет?
Начнем с построения графика уравнения x 2 + y 2 = 9, где n равно нулю.
Из графика мы видим, что x 2 + y 2 = 9 — это круг с центром в начале координат (0,0) и радиусом, равным 3.
Затем на тех же осях график x 2 + xy + y 2 = 9, таким образом, n в данном случае равно единице.
Посмотрите на новый график (показан синим цветом).Обратите внимание, что это график эллипса с пересечениями по оси x в точках (-3,0) и (3,0) и пересечениями по оси y в точках (0,3) и (0, -3). Однако, как вы могли заметить, это не график обычного эллипса. Формальное определение эллипса — это набор всех точек, таких, что сумма расстояний от фокусов и любой точки на эллипсе постоянна.
Общее уравнение для эллипса с центром в точке (0,0) и большой горизонтальной осью: где a — это расстояние от центра точки пересечения большой оси и эллипса, а b — расстояние от центра точки пересечения малой оси и эллипса.
Общее уравнение для эллипса с центром в точке (0,0) и большой вертикальной осью: где a — расстояние от центра до точки пересечения большой оси и эллипса, а b — расстояние от центра до точки пересечения малой оси и эллипса.
Для обоих перечисленных выше уравнений a > b . Однако в нашем примере у нас есть уравнение x 2 + xy + y 2 = 9.
В упрощенном виде равно. Как видите, значения a и b в этом уравнении совпадают. Они оба равны 3, что приводит к «наклонному» эллипсу, а не к нормальному эллипсу. График этого эллипса повернут на 45 градусов против часовой стрелки относительно начала координат.
Продолжим исследование квадратных уравнений вида Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0. Как член Bxy или (член n xy в нашем случае) влияет на график коническое сечение? Как указано выше, мы можем видеть, что положительный член Bxy вызывает вращение против часовой стрелки вокруг начала координат; однако отрицательный член Bxy вызывает вращение по часовой стрелке вокруг начала координат.Это показано ниже.
Обнаружив этот «наклонный» эллипс, я продолжил пробовать разные коэффициенты для члена xy.
Я наблюдал, что произошло, когда я позволил n = 2.
Как видите, этот график состоит из двух параллельных линий. Это связано с тем, что уравнение x 2 + 2xy + y 2 = 9 можно разложить на (x + y) (x + y) = 9, что эквивалентно (x + y) 2 = 9.
Затем, чтобы упростить это уравнение, извлеките квадратный корень из обеих частей, и вы получите два разных уравнения:
x + y = -3 и x + y = 3.
Затем, когда это уравнение приводится в форме пересечения наклона y = mx + b, заметьте, что
y = -x — 3 и y = -x + 3.
Оба уравнения имеют наклон м = -1, что делает их параллельными линиями.
Теперь давайте нарисуем другие значения n между 2 и 3, чтобы увидеть изменения на графиках.
Как видно из этого графика, по мере того, как параметр n становится все больше и больше, график все больше и больше трансформируется из эллипса в гиперболу.
Далее рассмотрим график уравнения x 2 + 3xy + y 2 = 9.
Вы можете видеть, что это выглядит как график гиперболы, ориентированной вокруг начала координат с пересечениями по оси x в точках (3,0) и (-3,0) и пересечениями по оси y точек (0,3) и (0, — 3).Мы можем доказать, что этот граф на самом деле является гиперболой, используя Дискриминантный тест. Коническое сечение является гиперболой, если дискриминант B 2 — 4AC больше нуля. В этом случае мы имеем A = 1, B = 3 и C = 1. Подставляя эти значения, мы получаем 3 2 _ 4 (1) (1) = 5 в качестве нашего дискриминанта, который действительно больше нуля. Следовательно, x 2 + 3xy + y 2 = 9 — гипербола.
Ниже я изобразил все уравнения в одной плоскости xy, чтобы дать визуальное представление о том, как изменяется график при изменении параметра n .
На этом графике вы можете видеть, как параметр n становится все больше и больше, он превращается из круга с центром вокруг начала координат в гиперболу, ориентированную вокруг начала координат. Это также показано в анимационном ролике ниже.
На этой анимации показано влияние параметра n на уравнение x 2 + n xy + y 2 .В этой анимации параметр n изменяется с отрицательного 10 на положительный 10. Из этого видеоролика мы можем увидеть, как все графики уравнений изменяются по параметру n . График начинается с круга, когда n = 0. По мере увеличения n он становится наклонным эллипсом, вращающимся против часовой стрелки и растягивающимся вдоль линии y = -x, пока n = 2, где он становится равным двум.
параллельные прямые, y = -x +3 и y = -x -3. Тогда n становится больше положительного 2, и график становится гиперболой.
Теперь давайте посмотрим, что произойдет, если мы позволим n быть отрицательным (что приведет к отрицательному члену Bxy). Обратите внимание на изображение ниже:
Как видите, между значениями 0 и -2 график представляет собой наклонный эллипс (показанный фиолетовым цветом), растянутый вдоль линии y = x. Он наклонен по часовой стрелке. При n = -2 график превращается в две параллельные линии (показаны красным) y = x + 3 и y = x — 3 с наклоном m, равным 1. Когда n становится меньше отрицательного 2, график превращается в гиперболу.
Это задание отлично подойдет для класса старшей школы, чтобы показать учащимся, как параметры могут влиять на форму графиков. Эти исследования могут быть увлекательными и интерактивными со студентами. Это можно назначить как проект, который необходимо выполнить, чтобы узнать, хорошо ли ваши ученики понимают свойства определенных графиков.
Вернуться на главную страницу
поверхностей, часть 2
поверхностей, часть 2Поверхности и контурные графики
Часть 2: Квадрические поверхности
Квадрические поверхности — это графики квадратных уравнений с тремя декартовыми переменными. в космосе.Как и графики квадратичных фигур на плоскости, их форма зависит от знаки различных коэффициентов в их квадратных уравнениях.
Сферы и эллипсоиды
Сфера — это график
уравнение формы x 2 + y 2 + z 2 = p 2 для какого-то реального числа р . Радиус сферы p (см.
рисунок ниже). Эллипсоиды — это графики уравнений вида ax 2 + by 2 + c z 2 = p 2 ,
где a , b и c все положительны. Особенно,
сфера — это особый эллипсоид, для которого a , b и c все равны.
Радиус сферы p (см.
рисунок ниже). Эллипсоиды — это графики уравнений вида ax 2 + by 2 + c z 2 = p 2 ,
где a , b и c все положительны. Особенно,
сфера — это особый эллипсоид, для которого a , b и c все равны.
- Постройте график x 2 + y 2 + z 2 = 4 в вашем листе в декартовых координатах.Затем выберите разные коэффициенты в уравнении и построить несферический эллипсоид.
- Какие изгибы вы обнаружите, когда пересечь сферу плоскостью, перпендикулярной одной из координатных осей? Что вы найдете для эллипсоида?
Параболоиды
Поверхности, пересекающиеся с
плоскости, перпендикулярные любым двум осям координат, являются параболами в тех
Самолеты называются параболоидами . Пример показан на рисунке ниже.
— это график z = x 2 + y 2 .
Пример показан на рисунке ниже.
— это график z = x 2 + y 2 .
- Сделайте свой собственный участок этой поверхности на листе и поверните график, чтобы увидеть его с разных точек зрения. Следуйте предложениям в таблице. Какие пересечения поверхность с плоскостями вида z = c , для некоторой постоянной с ?
- Покажите, что пересечения эта поверхность с плоскостями, перпендикулярными осям x- и y- параболы.[Подсказка: установите y = c или x = c для некоторой константы c .]
- Измените уравнение на z = 3 x 2 + y 2 , и заговор снова. Как меняется поверхность? В частности, что происходит с кривые пересечения с горизонтальными плоскостями.
Поверхность на следующем рисунке представляет собой график z = x 2 — y 2 . В этом случае пересечения с плоскостями, перпендикулярными к x- и y- оси по-прежнему являются параболами, но два набора парабол отличаются
направление, в котором они указывают. По причинам, которые мы увидим, эта поверхность называется
гиперболический параболоид — и, по понятным причинам, его еще называют
«седловая поверхность».
В этом случае пересечения с плоскостями, перпендикулярными к x- и y- оси по-прежнему являются параболами, но два набора парабол отличаются
направление, в котором они указывают. По причинам, которые мы увидим, эта поверхность называется
гиперболический параболоид — и, по понятным причинам, его еще называют
«седловая поверхность».
- Создайте свой собственный график этого гиперболического параболоида на листе и поверните график, чтобы увидеть его с разных точек зрения.Следуйте предложениям в таблице. Какие пересечения поверхность с плоскостями вида z = c , для некоторой постоянной с ? Объясните обе части имени.
Гиперболоиды
Гиперболоиды — поверхности
в трехмерном пространстве аналогично гиперболам на плоскости. Их определяющие
характерно то, что их пересечения с плоскостями, перпендикулярными любой
две из координатных осей являются гиперболами. Есть два типа гиперболоидов
— первый тип иллюстрируется графиком x 2 + y 2 — z 2 = 1,
который показан на рисунке ниже. Как показано на рисунке справа,
эта форма очень похожа на ту, которая обычно используется на атомных электростанциях.
градирни. (Источник: EPA
Реагирование на инцидент на Три-Майл-Айленд.)
Есть два типа гиперболоидов
— первый тип иллюстрируется графиком x 2 + y 2 — z 2 = 1,
который показан на рисунке ниже. Как показано на рисунке справа,
эта форма очень похожа на ту, которая обычно используется на атомных электростанциях.
градирни. (Источник: EPA
Реагирование на инцидент на Три-Майл-Айленд.)
Эта поверхность называется гиперболоидом . одного листа , потому что он все «соединен» в одно целое.(Мы будем перейдем к другому делу сейчас.)
- Сделайте свой собственный участок этой поверхности на листе и поверните график, чтобы увидеть его с разных точек зрения. Следуйте предложениям в таблице. Какие пересечения поверхность с плоскостями вида z = c , для некоторой постоянной с ?
- Показать, что пересечения
эта поверхность с плоскостями, перпендикулярными осям x- и y- являются гиперболами.
 [Подсказка: установите y = c или x = c для некоторой константы c .]
[Подсказка: установите y = c или x = c для некоторой константы c .]
Другой тип — гиперболоид . двух листов , и это иллюстрируется графиком x 2 — y 2 — z 2 = 1, показано ниже.
- Сделайте свой собственный участок этой поверхности на листе и поверните график, чтобы увидеть его с разных точек зрения.Следуйте предложениям в таблице. Какие пересечения поверхность с плоскостями вида z = c , для некоторой постоянной с ?
- Показать, что пересечения эти две поверхности с соответствующими координатными плоскостями являются гиперболами.
В каждом из этих примеров пересечения поверхности с семейством плоскостей многое говорит нам о структуре поверхности.Мы вернемся к этой теме в Части 6, когда мы смотрим на контурные линии.
| КПК Главная | Материалы | Многовариантный Исчисление | Содержание модуля | Назад | Вперед |
Круговые уравнения
Круг сделать легко:
Нарисуйте кривую на расстоянии
«радиус» от центральной точки.
А так:
Все точки находятся на одинаковом расстоянии
от центра.
Фактически определение круга равно
Круг на графике
Нарисуем на графике окружность радиуса 5:
А теперь вычислим именно , где находятся все точки.
Делаем прямоугольный треугольник:
А затем используйте Пифагор:
x 2 + y 2 = 5 2
Таких точек бесконечное количество, вот несколько примеров:
| x | y | х 2 + у 2 |
|---|---|---|
| 5 | 0 | 5 2 + 0 2 = 25 + 0 = 25 |
| 3 | 4 | 3 2 + 4 2 = 9 + 16 = 25 |
| 0 | 5 | 0 2 + 5 2 = 0 + 25 = 25 |
| −4 | −3 | (−4) 2 + (−3) 2 = 16 + 9 = 25 |
| 0 | −5 | 0 2 + (−5) 2 = 0 + 25 = 25 |
Во всех случаях точка на окружности подчиняется правилу x 2 + y 2 = радиус 2
Мы можем использовать эту идею, чтобы найти пропущенное значение
Пример: x значение 2 и радиус из 5
Начать с: x 2 + y 2 = r 2
Известные нам значения: 2 2 + y 2 = 5 2
Переупорядочить: y 2 = 5 2 — 2 2
Корень квадратный из двух частей: y = ± √ (5 2 -2 2 )
Решить: y = ± √21
у ≈ ± 4. 58 …
58 …
( ± означает два возможных значения: одно с + , другое с —)
А вот две точки:
Более общий случай
Теперь поставим центр на (a, b)
Таким образом, круг равен всем точкам (x, y) , которые находятся на расстоянии «r» от центра (a, b) .
Теперь давайте определим, где находятся точки (используя прямоугольный треугольник и Пифагор):
Идея та же, что и раньше, но нам нужно вычесть a и b :
И это «Стандартная форма» для уравнения круга!
Он сразу показывает всю важную информацию: центр (a, b) и радиус r .
Пример: круг с центром в точке (3,4) и радиусом 6:
Начать с:
(x − a) 2 + (y − b) 2 = r 2
Вставьте (a, b) и r:
(x − 3) 2 + (y − 4) 2 = 6 2
Затем мы можем использовать наши навыки алгебры, чтобы упростить и изменить это уравнение, в зависимости от того, для чего оно нам нужно.
Попробуйте сами
«Общая форма»
Но вы можете увидеть уравнение круга и не знать его !
Потому что это может не быть в аккуратной «Стандартной форме» выше.
В качестве примера поместим некоторые значения в a, b и r, а затем расширим их
Начнем с: (x − a) 2 + (y − b) 2 = r 2
Пример: a = 1, b = 2, r = 3: (x − 1) 2 + (y − 2) 2 = 3 2
Развернуть: x 2 — 2x + 1 + y 2 — 4y + 4 = 9
Соберите как термины: x 2 + y 2 — 2x — 4y + 1 + 4-9 = 0И в итоге получаем:
x 2 + y 2 — 2x — 4y — 4 = 0
Это уравнение круга, но «замаскировано»!
Итак, когда вы видите что-то подобное, подумайте: «хм… что может быть кругом! »
Фактически, мы можем записать его в «Общая форма» , поместив константы вместо чисел:
x 2 + y 2 + Ax + By + C = 0
Примечание. Общая форма всегда имеет x 2 + y 2 для первых двух условий .
Общая форма всегда имеет x 2 + y 2 для первых двух условий .
Переход от общей формы к стандартной
Теперь представьте, что у нас есть уравнение в общей форме :
x 2 + y 2 + Ax + By + C = 0
Как мы можем поместить его в стандартную форму вот так?
(x − a) 2 + (y − b) 2 = r 2
Ответ: пройдите квадрат (прочтите об этом) дважды… один раз для x и один раз для y :
Пример: x 2 + y 2 — 2x — 4y — 4 = 0
Начать с: x 2 + y 2 — 2x — 4y — 4 = 0
Соедините x s и y s вместе: (x 2 — 2x) + (y 2 — 4y) — 4 = 0
Константа справа: (x 2 — 2x) + (y 2 — 4y) = 4
Теперь завершите квадрат x (возьмите половину −2, возведите ее в квадрат и прибавьте к обеим сторонам):
(x 2 — 2x + (−1) 2 ) + (y 2 — 4y) = 4 + (−1) 2
И завершите квадрат y (возьмите половину −4, возведите ее в квадрат и прибавьте к обеим сторонам):
(x 2 — 2x + (−1) 2 ) + (y 2 — 4y + (−2) 2 ) = 4 + (−1) 2 + (−2) 2
Убрать:
Упростить: (x 2 — 2x + 1) + (y 2 — 4y + 4) = 9
Наконец: (x — 1) 2 + (y — 2) 2 = 3 2
А у нас это стандартная форма!
(Примечание: здесь использовался предыдущий пример a = 1, b = 2, r = 3, так что мы все поняли правильно!)
Единичный круг
Если мы поместим центр круга в (0,0) и установим радиус равным 1, то получим:
(x − a) 2 + (y − b) 2 = r 2 (x − 0) 2 + (y − 0) 2 = 1 2 x 2 + y 2 = 1 Какое уравнение представляет собой единичный круг |
Как нарисовать круг вручную
1. Участок центр (а, б)
Участок центр (а, б)
2. Нанесите 4 точки «радиусом» от центра в направлении вверх, вниз, влево и вправо.
3. Сделайте набросок!
Пример: график (x − 4) 2 + (y − 2) 2 = 25
Формула для круга: (x − a) 2 + (y − b) 2 = r 2
Итак, центр находится в (4,2)
И r 2 равно 25 , поэтому радиус равен √25 = 5
Итак, мы можем построить:
- Центр: (4,2)
- Вверх: (4,2 + 5) = (4,7)
- Вниз: (4,2−5) = (4, −3)
- Слева: (4−5,2) = (−1,2)
- Справа: (4 + 5,2) = (9,2)
А теперь нарисуйте круг как можно лучше!
Как нарисовать круг на компьютере
Нам нужно изменить формулу так, чтобы мы получили «y =».
У нас должно получиться два уравнения (верхняя и нижняя части круга), которые затем можно построить.
Пример: график (x − 4) 2 + (y − 2) 2 = 25
Итак, центр находится в (4,2), а радиус √25 = 5
Переставьте, чтобы получить «y =»:
Начнем с: (x − 4) 2 + (y − 2) 2 = 25
Переместите (x − 4) 2 вправо: (y − 2) 2 = 25 — (x − 4) 2
Извлеките квадратный корень: (y − 2) = ± √ [25 — (x − 4) 2 ]
(обратите внимание на ± «плюс / минус». ..
..
может быть два квадратных корня!)
Переместите «−2» вправо: y = 2 ± √ [25 — (x − 4) 2 ]
Итак, когда мы построим эти два уравнения, у нас должен получиться круг:
- y = 2 + √ [25 — (x − 4) 2 ]
- y = 2 — √ [25 — (x − 4) 2 ]
Попробуйте построить график этих функций в Function Grapher.
Также можно использовать Equation Grapher, чтобы сделать все это за один раз.
На f (x2 + y2) = f (x) 2 + f (y) 2
На f (x 2 + y 2 ) = f (x) 2 + f (y) 2 |
Рассмотрим целочисленную функцию f (k) такую, что f (1) положительный и |
|
Мы можем показать, что единственной такой функцией является тождество
функция f (k) = k. |
|
Поскольку целое число f (1) положительно, а квадратное целое число f (0) 2 должно быть неотрицательным, из этого следует, что f (1) должно быть равно 1, и следовательно, f (0) = 0. Тогда сразу имеем |
|
для всех натуральных чисел m.Кроме того, установив m = 1 и n = 1 в уравнении (1) дает |
|
Использование этого результата вместе с уравнением (2) дает f (4) = 4, и тогда мы можем определить f (5) из условия |
|
Вт теперь может использовать наименьшую пифаогрейскую тройку дать |
|
Поскольку мы знаем, что f (4) = 4 и f (5) = 5, это уравнение дает
f (3) 2 = 9, следовательно, f (3) = 3. |
|
Удваивая члены наименьшей пифагорейской тройки, мы теперь может вычислить |
|
Используя значения f (8) и f (10), получаем f (6) 2 = 36 и, следовательно, f (6) = 6.Таким образом, мы определили, что f (k) = k для всех k менее 7. |
Теперь, чтобы обобщить эту процедуру, предположим, что f (k) = k для всех k меньше m, и предположим, что для целого m существует три меньших целые числа n, r, s такие, что |
|
Применяя функцию f к обеим частям и используя уравнение (1), это будет означать |
|
Кроме того, поскольку по предположению f (k) = k для всех k меньше m, и поскольку по предположению каждое целое число n, r, s меньше, чем м, следует |
|
и, следовательно, f (m) = m. |
|
Если мы выберем r с той же четностью, что и m, то мы получим следующие целочисленные факторизации обеих сторон |
|
Определив факторы на двух сторонах этого уравнения, получаем два условия |
|
Решая их для s и n, мы получаем целые числа |
|
Чтобы сделать их как можно меньше, при этом сохраняя r
меньше m и с той же четностью, мы полагаем r = m-2. |
|
Обратите внимание, что для каждого нечетного целого числа m больше 6 три других члена в этом уравнении строго меньше m. Для четных значений m, мы можем умножить это уравнение на 2 2 , а затем заменить 2 м на м.Это дает идентификацию |
|
Для каждого четного целого числа m больше 6 три других
члены в этом уравнении строго меньше m. Следовательно, используя эти два
уравнения, наряду с уравнением (1), мы можем завершить шаг индукции, поэтому мы
доказали, что f (k) = k для всех целых k. |
Мы могли бы задаться вопросом, может ли подобное доказательство работать, если мы позволяем f (k) принимать реальных значений. Значение f (0) обусловлено отношение |
|
может быть 0 или 1/2. Если мы положим f (0) = 1/2, то получим квадратичная по f (1) |
|
, откуда следует, что f (1) также равно 1/2.Тогда у нас есть уравнение |
|
Отсюда ясно, что установка f (k) = 1/2 для всех k
дает последовательное решение, и это только другое решение
кроме f (k) = k (что, как показано выше, является единственным решением для целых
функции). |

 .. + xy n-2 + y n-1 )
.. + xy n-2 + y n-1 )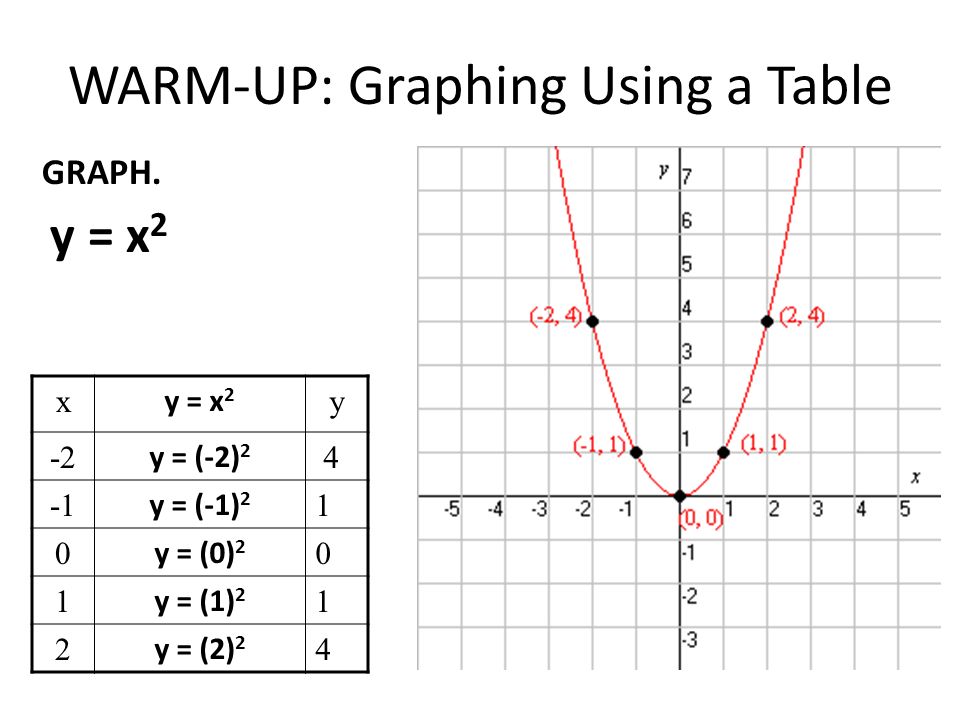

 Для обоих перечисленных выше уравнений a > b . Однако в нашем примере у нас есть уравнение x 2 + xy + y 2 = 9.
Для обоих перечисленных выше уравнений a > b . Однако в нашем примере у нас есть уравнение x 2 + xy + y 2 = 9.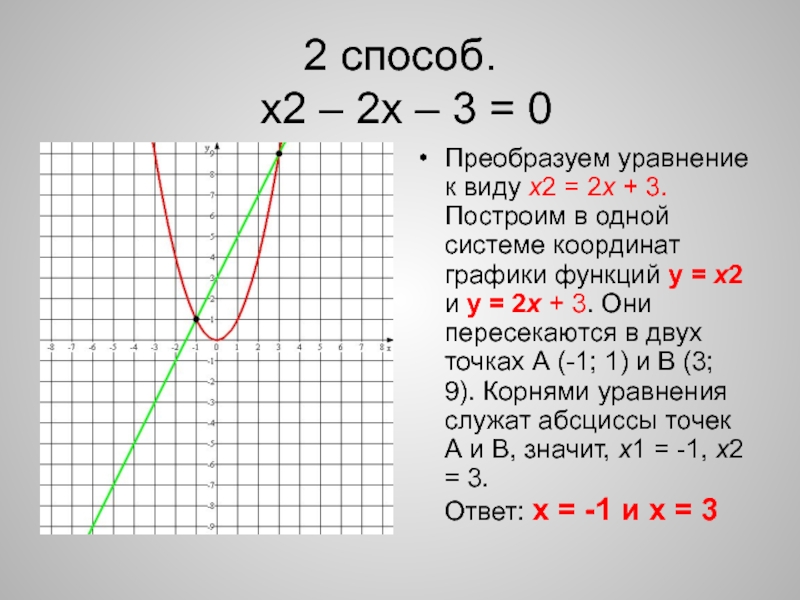 Я наблюдал, что произошло, когда я позволил n = 2.
Я наблюдал, что произошло, когда я позволил n = 2.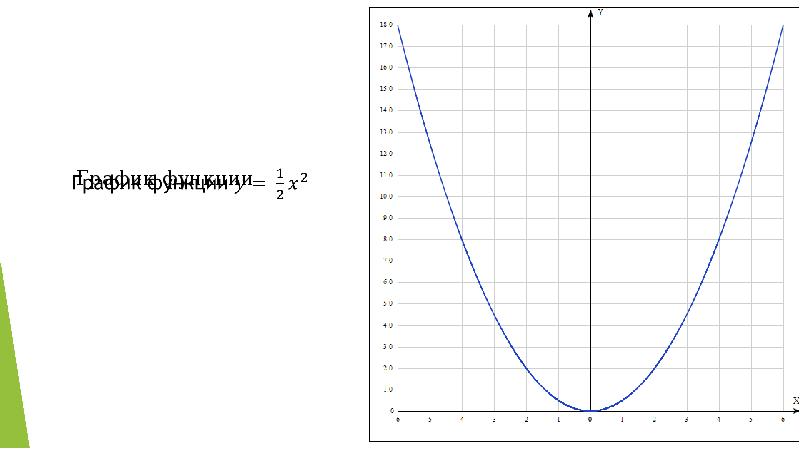 Далее рассмотрим график уравнения x 2 + 3xy + y 2 = 9.
Далее рассмотрим график уравнения x 2 + 3xy + y 2 = 9.
 параллельные прямые, y = -x +3 и y = -x -3. Тогда n становится больше положительного 2, и график становится гиперболой.
параллельные прямые, y = -x +3 и y = -x -3. Тогда n становится больше положительного 2, и график становится гиперболой.
 [Подсказка: установите y = c или x = c для некоторой константы c .]
[Подсказка: установите y = c или x = c для некоторой константы c .] Чтобы доказать это, сначала заметьте, что, положив m = 1 и n = 0 в
уравнение (1) и перестановка членов дает условие
Чтобы доказать это, сначала заметьте, что, положив m = 1 и n = 0 в
уравнение (1) и перестановка членов дает условие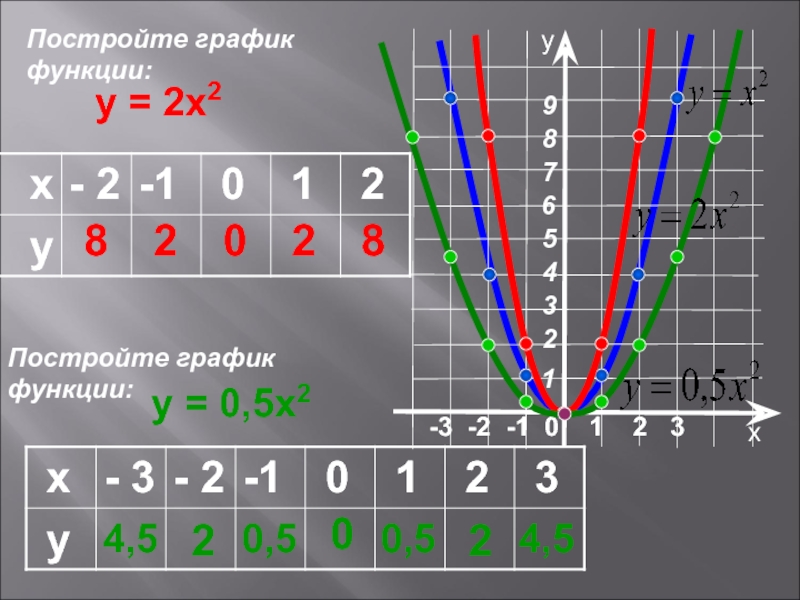 Используя эти результаты, мы также имеем
Используя эти результаты, мы также имеем Таким образом, нам нужно только доказать, что для
для каждого целого числа m больше 6 существуют меньшие целые числа n, r, s такие, что
уравнение (3) выполняется. Чтобы доказать это, сначала перепишем уравнение (3) в виде
форма
Таким образом, нам нужно только доказать, что для
для каждого целого числа m больше 6 существуют меньшие целые числа n, r, s такие, что
уравнение (3) выполняется. Чтобы доказать это, сначала перепишем уравнение (3) в виде
форма Подставляя это в выражения для s и n, и
вставляя их обратно в уравнение (3), получаем тождество
Подставляя это в выражения для s и n, и
вставляя их обратно в уравнение (3), получаем тождество